MP Board Class 12th Maths Book Solutions Chapter 6 अवकलज के अनुप्रयोग Ex 6.5

In this article, we share MP Board Class 12th Maths Book Solutions Chapter 6 अवकलज के अनुप्रयोग Ex 6.5 Pdf, These solutions are solved by subject experts from the latest MP Board books.

MP Board Class 12th Maths Book Solutions Chapter 6 अवकलज के अनुप्रयोग Ex 6.5

प्रश्न 1.
निम्नलिखित दिए गए फलनों के उच्चतम या निम्नतम मान, यदि कोई हो तो ज्ञात कीजिए
(i) f (x) = (2x – 1)² + 3
(ii) f (x) = 9x² + 12x + 2
(iii) f (x) = – (x – 1)² + 10
(iv) g (x) = x² + 1
हल:
(i) f (x) = (2x – 1)² + 3
(2x – 1)² का कम – से – कम मान = 0
∴ f(x) का निम्नतम मान = 3

(ii) f (x) = 9x² + 12x + 2 = 9x² + 12x + 4 – 2
= (3x + 2)² – 2
(3x + 2)² का निम्नतम मान = 0
∴ f (x) का निम्नतम मान = – 2

(iii) f (x) = – (x – 1)² + 10
– (x – 1)² का अधिकतम मान = 0
∴ f का उच्चतम मान = 10

(iv) g (x) = x³ + 1
g'(x) = 3x² जो x ϵ R के लिए धनात्मक है।
∴ g एक वर्धमान फलन है; अतः इसका कोई न्यूनतम तथा अधिकतम मान नहीं है।

प्रश्न 2.
निम्नलिखित दिए गए फलनों के उच्चतम मान या निम्नतम मान, यदि कोई हो तो ज्ञात कीजिए
(i) f (x) |x + 2| – 1
(ii) g (x) = – |x + 1| + 3
(iii) h (x) = sin (2x) + 5
(iv) f (x) = |sin 4x + 3|
(v) h(x) = x + 1, x ϵ ( – 1, 1)
हल:
(i) f(x) = |x + 2| – 1
|x + 2| का न्यूनतम मान 0 है।
∴ f का निम्नतम मान = – 1
अतः उच्चतम मान का अस्तित्व नहीं है।

(ii) g (x) = -|x + 1| + 3
– |x + 1| का अधिकतम मान = 0
∴ g (x) = – |x + 1| + 3 का उच्चतम मान 0 + 3 = 3
निम्नतम मान का अस्तित्व नहीं है।

(iii) h (x) = sin (2x) + 5
sin 2x का अधिकतम मान = 1
∴ h(x) = sin 2x + 5 का उच्चतम मान, 1 + 5 = 6
sin 2x का न्यूनतम मान = – 1
∴ h (x) = sin 2x + 5 का निम्नतम मान = – 1 + 5 = 4

(iv) f (x) = |sin 4x + 3|
sin 4x का अधिकतम मान = 1
f(x) = |sin 4x + 3| का उच्चतम मान = |1 + 3| = 4
तथा sin 4x का निम्नतम मान = – 1
f (x) = |sin 4x + 3| का निम्नतम मान = |- 1 + 3| = 2

(v) h (x) = x + 1 .
h'(x) = 1 = धनात्मक
h वर्धमान फलन है।
इसका कोई उच्चतम या निम्नतम मान नहीं है।

प्रश्न 3.
निम्नलिखित फलनों के स्थानीय उच्चतम या निम्नतम, यदि कोई हो तो ज्ञात कीजिए तथा स्थानीय उच्चतम या स्थानीय निम्नतम मान,जैसी स्थिति हो, भी ज्ञात कीजिए।
(i) f (x) = x²
(ii) g (x) = x³ – 3x
(iii) h(x) = sin x + cos x, o < x < \(\frac{\pi}{2}\)
(iv) f (x) = sin x – cos x, 0 < x < 2π
(v) f (x) = x³ – 6x² + 9x + 15
(vi) g (x) = \(\frac{x}{2}+\frac{2}{x}\), x > 0
(vii) g (x) = \(\frac{1}{x^{2}+2}\)
(viii) f (x) = \(x \sqrt{1-x}\), x > 0
हल:
(i) f (x) = x²
f'(x) = 2x
यदि f'(x) = 0 तब 2x = 0 या x = 0
f'(x) जैसे ही x = 0 से होकर आगे बढ़ता है तो इसका चिह्न ऋणात्मक से धनात्मक में बदल जाता है।
∴ x = 0 पर f स्थानीय निम्नतम है।
स्थानीय निम्नतम मान = f (0) = 0

(ii) g(x) = x³ – 3x
∴ g'(x) = 3x² – 3 = 3 (x² – 1) = 3 (x – 1) (x + 1)
यदि g’ (x) = 0 तब 3x² – 3 = 0
⇒ x² – 1 = 0 ⇒ x = ± 1
x = – 1 पर g'(x) का चित – – = +
– + = –
जैसे ही x, x = – 1 से होकर आगे बढ़ता है, g’ का चिह्न + ve से – ve में परिवर्तित होता है।
∴ x = – 1 पर g उच्चतम है।
उच्चतम मान = g (- 1) = (- 1)³ – 3 (- 1) = – 1 + 3 = 2
x = 1 पर g'(x) के चिह्न जैसे ही x, x = 1 से होकर आगे बढ़ता है,
– + = –
+ + = +
g’ (x), ऋणात्मक से धनात्मक में परिवर्तित हो जाता है।
x = 1 पर g निम्नतम है।
निम्नतम मान = g(1) = 1³ – 3 = – 2

(iii) h(x) = sin x + cos x, 0 < x < \(\frac{\pi}{2}\)
h'(x) = cos x – sin x = cos x(1 – tan x)
यदि h'(x) = 0 तब 1 – tan x = 0 या tan x = 1 या x = \(\frac{\pi}{4}\)
x = \(\frac{\pi}{4}\) पर x का मान \(\frac{\pi}{4}\) से थोड़ा कम करने से tan x, 1 से कम होगा और x का मान \(\frac{\pi}{4}\) से थोड़ा अधिक रखने पर tan x, 1 से अधिक होगा।
इस प्रकार 1 – tan x का चिह्न + ve से – ve में परिवर्तित होता है। cos x में चिह्न में कोई परिवर्तन नहीं होता।
∴ x = \(\frac{\pi}{4}\) उच्चतम है।
स्थानीय उच्चतम मान

(v) f (x) = x³ – 6x² + 9x + 15
∴ f'(x) = 3x² – 12x + 9 = 3 (x² – 4x + 3)
= 3(x – 1)(x – 3)
यदि f'(x) = 0 ⇒ x – 1 = 0 या x – 3 = 0
∴ x = 1 .या x = 3

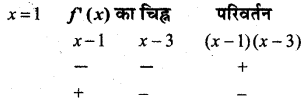
x का मान 1 से थोड़ा कम रखने पर
x का मान 1 से थोड़ा अधिक रखने पर
इस प्रकार f'(x) का चिह्न, जैसे ही x, x = 1 से होकर आगे बढ़ता है, + ve से – ve में परिवर्तित होता है।
⇒ x = 1, पर स्थानीय उच्चतम बिन्दु है।
स्थानीय उच्चतम मान = f (1) = 1 – 6 + 9 + 15 = 19

x का मान 3 से थोड़ा कम रखने पर,
x का मान 3 से थोड़ा अधिक रखने पर,
∴ f'(x) का चिह्न धनात्मक से ऋणात्मक में परिवर्तित होता है, जब x, x = 3 बिन्दु से होकर जाता है।
∴ x = 3 पर स्थानीय निम्नतम बिन्दु है।
∴ स्थानीय निम्नतम मान = f (3) = 27 – 54 + 27 + 15
= 69 – 54 = 15

x का मान 2 से थोड़ा कम रखने पर,
x का मान 2 से थोड़ा अधिक रखने पर,
g'(x) का चिह्न – – ve से + ve में परिवर्तित होता है, जब x,x = 2 से होकर आगे बढ़ता है।
∴ f, x = 2 पर स्थानीय निम्नतम है।
स्थानीय निम्नतम मान = g (2) = \(\frac{2}{2}+\frac{2}{2}=2\)

प्रश्न 4.
सिद्ध कीजिए कि निम्नलिखित फलनों का उच्चतम यो निम्नतम मान नहीं है
(i) f (x) = e^x
(ii) g (x) = log x
(iii) h(x) = x³ + x² + x + 1
हल:
(i) f(x) = e^x

अतः दिया गया फलन न तो उच्चतम है और न ही न्यूनतम
(iii) h(x) = x³ + x² + x + 1
= h'(x) = 3x² + 2x + 1
यदि h'(x) = 0
⇒ 3x² + 2x + 1 = 0
⇒ \(\frac{-2 \pm \sqrt{4-12}}{6}=\frac{-1 \pm \sqrt{-2}}{3}\)
जो कि काल्पनिक संख्या है
अत: ∀ x ϵ R, h'(x) ≠0
अतः h का कोई भी मान उच्चतम या निम्नतम नहीं है।

प्रश्न 5.
प्रदत्त अन्तरालों में निम्नलिखित फलनों के निरपेक्ष उच्चतम मान और निरपेक्ष निम्नतम मान ज्ञात कीजिए।
(i) f (x) = x³, x ϵ [- 2,2]
(ii) f (x) = sin x + cos x x ϵ [0, 1]
(iii) f (x) = 4x – \(\frac{1}{2}\)x², x ϵ [-2, \(\frac{9}{2}\)]
(iv) f (x) = (x – 1)² + 3, x ϵ [- 3, 1]
हल:
(i) f (x) = x³, अन्तराल [ – 2, 2]
∴ (x) = 3x²
यदि f’ (x) = 0, तब 3x² = 0 ∴ x = 0
f(- 2) = (- 2)³ = – 8
f (0) = (0)³ = 0
तथा f (2) = (2)³ = 8
निरपेक्ष उच्चतम मान = 8
निरपेक्ष निम्नतम मान = – 8

(ii) f(x) = sinx + cosx, x ϵ [0, π]
⇒ f'(x) = cosx – sin x
उच्चतम व निम्नतम मान के लिए
f'(x) = 0
⇒ cosx – sin x = 0
⇒ tan x = 1
⇒ x = π/4
अब x = \(\frac{\pi}{4}\), 0, π पर f(x) का मान ज्ञात करना है।

f(0) = sin 0° + cos0° = 0 + 1 = 1
f(π) = sin π + cos π = 0 – 1 = – 1
अत: फलन f(x) का निरपेक्ष उच्चतम मान x = \(\frac{\pi}{4}\) पर \( \sqrt{{2}} \) है।
तथा x = π पर f(x) का निरपेक्ष निम्नतम मान – 1 है।

अंत: x = 4 पर f(x) का निरपेक्ष उच्चतम मान = 8
तथा x = – 2 पर f(x) का निरपेक्ष निम्नतम मान = – 10

(iv) यहाँ f (x) = (x – 1)² + 3, [- 3, 1]
∴ f'(x) = 2(x – 1)
यदि f'(x) = 0, 2(x – 1) = 0, x = 1
f(1) = (1 – 1)² + 3 = 0 + 3 = 3
f(- 3) = (- 3 – 1)² + 3 = 16 + 3 = 19
अतः निरपेक्ष उच्चतम मान = 19
तथा निरपेक्ष निम्नतम मान = 3

प्रश्न 6.
यदि लाभ फलन P(x) = 41 – 72x – 18x² से प्रदत्त है तो किसी कम्पनी द्वारा अर्जित उच्चतम लाभ ज्ञात कीजिए।
हल:
दिया है लाभ फलन
P(x) = 41 – 72x – 18x²

⇒ 36x = – 72
x = – 2
∴ x = – 2 पर
\(\frac{d^{2} P}{d x^{2}}\) = – 36 < 0
अतः x = – 2 पर लाभ फलन का मान उच्चतम है।
अतः उच्चतम लाभ = P( – 2)
= 41 – 72(- 2) – 18(- 2)²
= 41 + 144 – 72
= 113

प्रश्न 7.
अन्तराल [0, 3] पर 3x⁴ – 8x³ + 12x² – 48x + 25 के उच्चतम मान और निम्नतम मान ज्ञात कीजिए।
हल:
यहाँ f(x) = 3x⁴ – 8x² + 12x² – 48x + 25
∴ f'(x) = 12x³ – 24x² + 24x – 48
= 12[x³ – 2x² + 2x – 4] = 12[x² (x – 2) + 2(x – 2)]
= 12(x – 2)(x² + 2)
यदि f'(x) = 0, तब
x – 2 = 0 ∴ x = 2
अन्तराल (0, 3) पर,
f (0) = 25
f(2) = 3(2)⁴ – 8(2)³ + 12(2)² – 48(2) + 25
= 3 × 16 – 8 × 8 + 12 × 4 – 48 × 2 + 25
= 48 – 64 + 48 – 96 + 25 = – 39
तथा f(3) = 3(3)⁴ – 8(3)³ + 12(3)² – 48(3) + 25
= 3 × 81 – 8 × 27 + 12 × 9 – 48 × 3 + 25
= 243 – 216 + 108 – 144 + 25 = 16
∴ निरपेक्ष उच्चतम मान = 25
निरपेक्ष निम्नतम मान = – 39

प्रश्न 8.
अन्तराल [0, 2 π] के किन बिन्दुओं पर फलन sin 2x अपना उच्चतम मान प्राप्त करता है।
हल:
यहाँ f (x) = sin 2x,[0, π] पर
∴ (x) = 2cos 2x
यदि f'(x) = 0 ⇒ 2cos 2x = 0

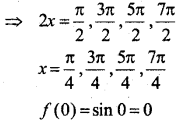
प्रश्न 9.
फलन sin x + cos x का उच्चतम मान क्या है?
हल:
यहाँ f(x) = sin x + cos x, [0, 2π] पर,
∴ f(x) = cos x – sin x
f'(x) = 0 = cos x – sin x = 0 ⇒ tan x = 1

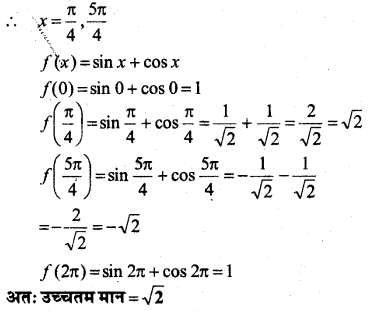
प्रश्न 10.
अन्तराल [1,3] में 2x³ – 24x + 107 का महत्तम मान ज्ञात कीजिए।इसी फलन का अन्तराल [- 3, – 1]में भी महत्तम मान ज्ञात कीजिए।
हल:
यहाँ f (x) = 2x³ – 24x + 107, [1, 3]
∴ f(x) = 6x² – 24
उच्चतम व निम्नतम मान के लिए,
f'(x) = 0
⇒ 6x² – 24 = 0 ⇒ 6x² = 24 ⇒ x² = 4 ∴ x = ± 2
अन्तराल [1, 3] के लिए,
f(1) = 2(1)³ – 24 (1) + 107 = 2 – 24 + 107 = 85
f(2) = 2(2)³ – 24 (2) + 107 = 16 – 48 + 107 = 75
f(3) = 2(3)³ – 24 (3) + 107 = 54 – 72 + 107 = 89
इस प्रकार अधिकतम f (x) = 89, x = 3 पर, अन्तराल [- 3, – 1] के लिए हम x = – 3, – 2, – 1 पर f (x) का मान ज्ञात करते हैं।
f(- 3) = 2(- 3)³ – 24(- 3) + 107
= – 54 + 72 + 107 = – 54 + 179 = 125
f(- 2) = 2(- 2)³ – 24 (- 2) + 107
= – 16 + 48 + 107 = 139
f(- 1) = 2(- 1)³ – 24(- 1) + 107 = – 2 + 24 + 107 = 129
इस प्रकार अधिकतम मान f (x) = 139, x = – 2 पर

प्रश्न 11.
यदि दिया है कि अन्तराल [0, 2] में x = 1 पर फलन x⁴ – 62x³ + ax + 9 उच्चतम मान प्राप्त करता है तो a का मान ज्ञात कीजिए।
हल:
यहाँ f (x) = x⁴ – 62x³ + ax + 9
∴ f'(x) = 4x³ – 124x + a
उच्चतम व निम्नतम मान के लिए, f'(x) = 0
⇒ 4x³ – 124x + a = 0
x = 1, पर f उच्चतम है ⇒ f (1) = 0
∴ 4 × – 124 × 1 + a = 0 ⇒ 4 – 124 + a = 0
⇒ – 120 + a = 0
∴ a = 120
f(x) = 4x³ = 124x + a
f(x) = 12x² – 124
f(1) = 12 – 124 = – 112 < 0
अतः x = 1, उच्चतम है जब a = 120

प्रश्न 12.
[0, 2π] पर x + sin 2x का उच्चतम और निम्नतम मान ज्ञात कीजिए।
हल:
माना f(x) = x + sin 2x
∴ f(x) = 1 + 2cos 2x
उच्चतम व निम्नतम बिन्दु के लिए, f'(x) = 0
⇒ 1 + cos 2x = 0 ⇒ cos 2x = – 1


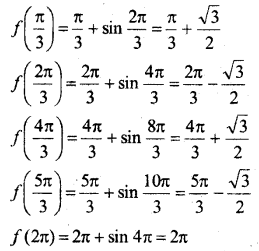
f(x) का उच्चतम मान = 2π
f (x) का उच्चतम मान = 0

प्रश्न 13.
ऐसी दो संख्याएँ ज्ञात कीजिए जिनका योग 24 है और जिनका गुणनफल उच्चतम हो।
हल:
माना अभीष्ट संख्याएँ x तथा 24 – x हैं।
माना उनका गुणनफल P है।
∴ P = x(24 – x)
P = 24x – x²

अतः x = 12 के लिए P (संख्याओं का गुणनफल) उच्चतम है।

प्रश्न 14.
ऐसी दो धन संख्याएँ x और y ज्ञात कीजिए ताकि x + y = 60 और xy³ उच्चतम हो।
हल:
∵ x + y = 60
माना P = xy³
⇒ P = (60 – y) y³
(∵ x + y = 60
⇒ x = 60 – y)
⇒ P = 60y³ – y⁴


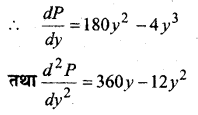
अत: x = 15, y = 45 के लिए P = xy³ उच्चतम है।

प्रश्न 15.
ऐसी दो धन संख्याएँ x और y ज्ञात कीजिए जिनका योग 35 हो और गुणनफल x²y² उच्चतम हो।
हल:
दो धन संख्याएँ x, y हैं।
x + y – 35
∴ y = 35 – x
गुणनफल P = x²y⁵
y का मान समी० (2) में रखने पर
P = x² (35 – x)⁵
x के सापेक्ष अवकलन करने पर

केवल 10 स्वीकृत मान है जैसे कि x = 0, 35 अस्वीकृत कर दिए जाते हैं।
x = 10 पर,
जब x, 10 के निकट और 10 की बाईं ओर हो तो
\(\frac{d P}{d x}\) = (1)(+ 1)(+ 1) = + ve
जब x, 10 के निकट और 10 की दाई ओर हो तो
\(\frac{d P}{d x}\) = (+)(+)(-) = – ve
इस प्रकार x, 10 से होता हुआ आगे बढ़ता है
\(\frac{d P}{d x}\) + ve से – ve को परिवर्तित होता है।
x = 10 पर P उच्चतम है।
∴ y = 35 – 10 = 25
अतः अभीष्ट संख्याएँ 10 और 25 हैं।

प्रश्न 16.
ऐसी दो धन संख्याएँ ज्ञात कीजिए जिनका योग 16 हो और जिनके घनों का योग निम्नतम हो।
हल:
माना x और 16 – x दो धन संख्याएँ हैं।
प्रश्नानुसार, घनों का योग S = x³ + (16 – x)³
अवकलन करने पर,
\(\frac{d S}{d x}\) = 3x² + 3(16 – x)² ( – 1)
= 3x² – 3(16 – x)²
= 3x² – 3(256 + x² – 32x)
= 3x² – 3 × 256 – 3x² + 3 × 32x
= 3(32x – 256)
उच्चतम व निम्नतम बिन्दु के लिए,

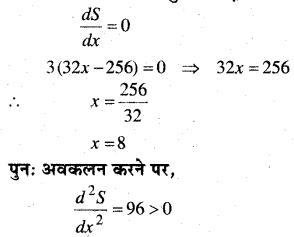
अतः अभीष्ट संख्याएँ 8 और (16 – 8)अर्थात् 8 और 8 हैं।

प्रश्न 17.
18 cm भुजा के टिन के किसी वर्गाकार टुकड़े से प्रत्येक कोने पर एक वर्ग काटकर तथा इस प्रकार बने टिन के फलकों को मोड़कर ढक्कन रहित एक सन्दूक बनाना है। काटे जाने वाले वर्ग की भुजा कितनी होगी जिससे सन्दूक का आयतन उच्चतम हो?
हल:
माना वर्ग की प्रत्येक भुजा x सेमी काटी गई है।
∴ सन्दूक के लिए,
लम्बाई = 18 – 2x
चौड़ाई = 18 – 2x
ऊँचाई = x
∴ आयतन V = ल० × चौ० × ॐ
= x (18 – 2x)(18 – 2x) = x (18 – 2x)².1


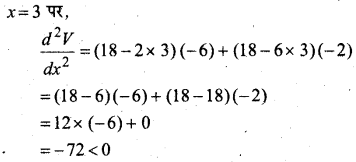
∴ x = 3 पर आयतन अधिकतम होगा। अर्थात् वर्ग की भुजा प्रत्येक कोने से 3 सेमी काटी गई है तो आयतन उच्चतम होगा।

प्रश्न 18.
45 cm × 24 cm की टिन की आयताकार चादर के कोनों पर वर्ग काटकर तथा इस प्रकार बने टिन के फलकों को मोड़कर ढक्कन रहित एक सन्दूक बनाना है। काटे जाने वाले वर्ग की भुजा कितनी होगी जिससे सन्दूक का आयतन उच्चतम हो?
हल:
माना प्रत्येक कोने से x सेमी भुजा काटी गई है।
∴ आयताकार सन्दूक की भुजाएँ
l = 45 – 2x
b = 24 – 2x
h = x सेमी


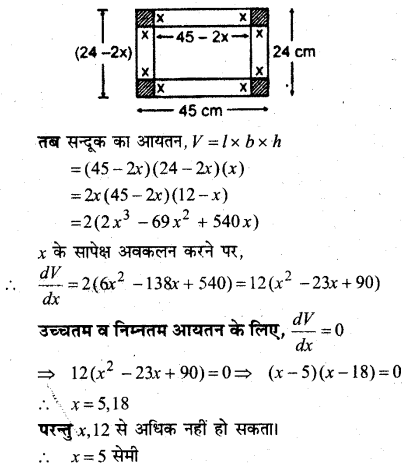
अतः x = 5 के लिए आयतन उच्चतम है।

प्रश्न 19.
सिद्ध कीजिए कि एक दिए वृत्त के अन्तर्गत सभी आयतों में वर्ग का क्षेत्रफल उच्चतम होता है।
हल:
माना a त्रिज्या के वृत्त के अन्तर्गत आयतन की लम्बाई x तथा चौड़ाई y है।

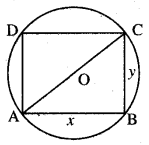
∴ x² + y² = (2a)²
⇒ x² + y² = 4a² …(1)
∴ आयतन का क्षेत्रफल = xy

जब x बिन्दु x = \( \sqrt{{2}} \) a से होकर जाता है तो A’ (x) का चिह्न धनात्मक से ऋणात्मक में बदल जाता है। अतः आयत का क्षेत्रफल उच्चतम होगा, जब x = \( \sqrt{{2}} \)a और y = \( \sqrt{{2}} \)a होगा। अर्थात् आयत वर्ग होगा।

प्रश्न 20.
सिद्ध कीजिए कि प्रदत्त पृष्ठ एवं महत्तम आयतन के बेलन की ऊँचाई आधार के व्यास के बराबर होती है।
हल:
माना बेलन का पृष्ठीय क्षेत्रफल = S
त्रिज्या = r
ऊँचाई = h
आयतन = V
पृष्ठीय क्षेत्रफल S = 2πr² + 2πrh


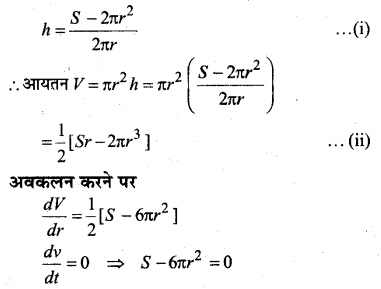
अतः जब बेलन की ऊँचाई आधार के व्यास के बराबर है तो आयतन अधिकतम होता है।

प्रश्न 21.
100 cm³ आयतन वाले डिब्बे सभी बंद बेलनाकार (लम्ब वृत्तीय) डिब्बों में से न्यूनतम पृष्ठ क्षेत्रफल वाले डिब्बे की विमाएँ ज्ञात कीजिए।
हल:
माना बेलनाकार डिब्बों की त्रिज्या और ऊँचाई क्रमश: r और h है।
आयतन = πr²h = 100 cm³


⇒ S न्यूनतम होगा।
अतः कुल पृष्ठीय क्षेत्रफल न्यूनतम होगा।

प्रश्न 22.
एक 28 cm लम्बे तार को दो टुकड़ों में विभक्त किया जाना है। एक टुकड़े से वर्ग तथा दूसरे से वृत्त बनाया जाना है। दोनों टुकड़ों की लम्बाई कितनी होनी चाहिए जिससे वर्ग एवं वृस का सम्मिलित क्षेत्रफल न्यूनतम हो?
हल:
माना तार के एक भाग की लम्बाई x सेमी है तब दूसरा भाग = (28 – x) सेमी होगा।
माना x लम्बाई वाला भाग । त्रिज्या वाले वृत्त में बदला गया है।

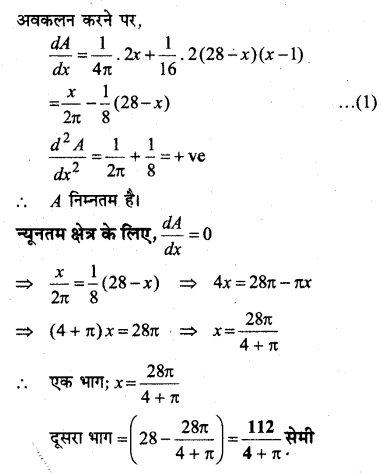
प्रश्न 23.
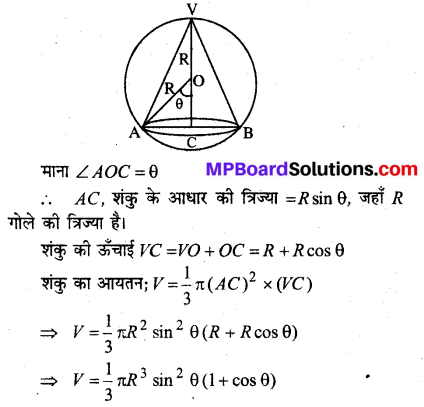
सिद्ध कीजिए कि R त्रिज्या के गोले के अन्तर्गत विशालतम शंकु का आयतन गोले के आयतन का \(\frac{8}{27}\) होता है।
हल:
माना V AB गोले के अन्तर्गत विशालतम शंकु का आयतन है।
स्पष्टतयाः अधिकतम आयतन के लिए शंकु का अक्ष गोले . की ऊँचाई के साथ होना चाहिए।

प्रश्न 24.
सिद्ध कीजिए कि न्यूनतम पृष्ठ पर दिए आयतन के लम्ब वृत्तीय शंकु की ऊँचाई, आधार की त्रिज्या की 72 गुनी होती है।
हल:
माना शंकु की त्रिज्या = r
शंकु की ऊँचाई = h


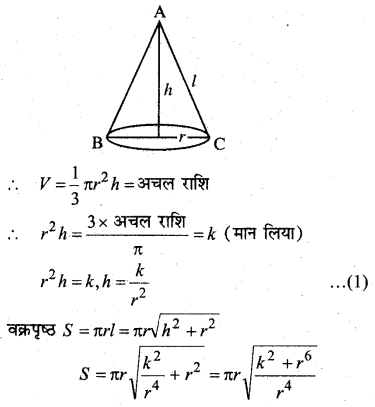
∴ S न्यूनतम है जब h = \( \sqrt{{2}} \)r
अतः न्यूनतम वक्र पृष्ठ वाला लम्ब वृत्तीय शंकु की ऊँचाई, त्रिज्या की \( \sqrt{{2}} \) गुनी है।

प्रश्न 25.
सिद्ध कीजिए कि दी हुई तिर्यक ऊँचाई और महत्तम आयतन वाले शंकु का अर्थ शीर्ष कोण tan^-1\( \sqrt{{2}} \) होता है।
हल:
माना शंकु की त्रिज्या = r
ऊँचाई = l
ऊर्ध्वाधर ऊँचाई = AM = lcosθ
शंकु की त्रिज्या = MC = lsinθ

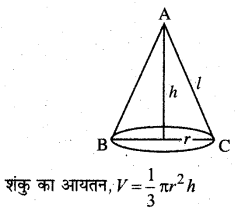
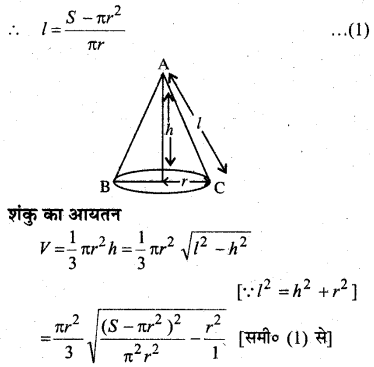
प्रश्न 26.
सिद्ध कीजिए कि दिए हुए पृष्ठ और महत्तम आयतन वाले लम्ब वृत्तीय शंकु का अर्द्ध शीर्ष कोण sin^-1\(\left(\frac{1}{3}\right)\) होता है।
हल:
माना शंकु का पृष्ठीय क्षेत्रफल S तथा आयतन V है। शंकु की त्रिज्या , ऊँचाई h तथा तिर्यक ऊँचाई l है।
शंकु का पृष्ठीय क्षेत्रफल = πrl + πr²

नोट – प्रश्न संख्या 27 से 29 में सही उत्तर का चुनाव कीजिए।
प्रश्न 27.
वक्र x² = 2y पर (0, 5) से न्यूनतम दूरी पर स्थित बिन्दु है
(A) (2\( \sqrt{{2}} \), 4)
(B) (2\( \sqrt{{2}} \), 0)
(C) (0, 0)
(D) (2, 2)
हल:
माना वक्र x² = 2y पर कोई बिन्दु P (x, y) है।
दिया हुआ बिन्दु A (0, 5) है।
PA² = (x – 0) + (y – 5)² = Z (माना)
∴ Z = x² + (y – 5) …(1)
तथा वक्र x² = 2y …(2)
x² का मान समी० (1) में रखने पर,
Z = 2y + (y – 5)² = 2y + y² + 25 – 10y
= y² + 25 – 8y
अवकलन करने पर,

अतः विकल्प (A) सही है।

प्रश्न 28.
x के सभी वास्तविक मानों के लिए \(\frac{1-x+x^{2}}{1+x+x^{2}}\) का न्यूनतम मान है
(A) 0
(B) 1
(C) 3
(D) \(\frac{1}{3}\)
हल:

प्रश्न 29.
[x(x – 1) + 1]^1/3, 0 ≤ x ≤ 1का उच्चतम मान है-
(A) \(\left(\frac{1}{3}\right)^{\frac{1}{3}}\)
(B) \(\frac{1}{2}\)
(C) 1
(D) 0
हल:
यहाँ y = [x(x – 1) + 1]^1/3
x के सापेक्ष अवकलन करने पर,

उच्चतम मान = 1
अतः विकल्प (C) सही है।