In this article, we share MP Board Class 12th Maths Book Solutions Chapter 13 प्रायिकता Ex 13.2 Pdf, These solutions are solved by subject experts from the latest MP Board books.
MP Board Class 12th Maths Book Solutions Chapter 13 प्रायिकता Ex 13.2
प्रश्न 1.
यदि P (A) = \(\frac{3}{5}\), P (B) = \(\frac{1}{5}\) और A तथा B स्वतंत्र घटनाएँ हैं तो P (ARB) ज्ञात कीजिए।
हल:
∵ A तथा B स्वतंत्र घटनाएँ हैं
∴ P(A ∩ B) = P (A)x P (B)
= \(\frac{3}{5} \times \frac{1}{5}=\frac{3}{25}\)
प्रश्न 2.
52 पत्तों की एक गड्डी में से यादृच्छया बिना प्रतिस्थापित किए गए दो पत्ते निकाले गए। दोनों पत्तों के काले रंग का होने की प्रायिकता ज्ञात कीजिए।
हल:
पत्तों की कुल संख्या = 52
गड्डी में काले पत्तों की कुल संख्या = 26
∴ एक पत्ता यादृच्छया खींचने पर काले पत्ते की प्रायिकता
= \(\frac{26}{52}\)
P(E1) = \(\frac{1}{2}\)
एक पत्ता खींचने पर शेष पत्तों की संख्या = 52 – 1 = 51
तथा काले पत्तों की संख्या = 26 – 1 = 25
∴ दूसरा काला पत्ता होने की प्रायिकता F2 = \(\frac{25}{51}\)
अतः दोनों पत्ते काले रंग के होने की प्रायिकता
= E1 x E2
= \(\frac{1}{2} \times \frac{25}{51}=\frac{25}{102}\)
प्रश्न 3.
संतरों के एक डिब्बे का निरीक्षण उसमें से तीन संतरों को यादृच्छया बिना प्रतिस्थापित किए हुए निकाल कर किया जाता है। यदि तीनों निकाले गए संतरे अच्छे हों तो डिब्बे को बिक्री के लिए स्वीकृत किया जाता है अन्यथा अस्वीकृत कर देते हैं। एक डिब्बा जिसमें 15 संतरे हैं जिनमें से 12 अच्छे व 3 खराब संतरे हैं, के बिक्री के लिए स्वीकृत होने की प्रायिकता ज्ञात कीजिए।
हल:
डिब्बा जिसमें 12 अच्छे और 3 खराब सन्तरे हैं।
12 संतरों में से 3 अच्छे संतरे निकालने के प्रकार = 12C3
15 सन्तरों में से 3 सन्तरे निकालने के प्रकार = 15C3
स्वीकृत होने की प्रायिकता =3 अच्छे सन्तरों को चुनने की प्रायिकता
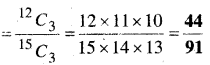
![]()
प्रश्न 4.
एक न्याय्य सिक्का और एक अभिनत पासे को उछाला गया। मान लें A घटना ‘सिक्के पर चित प्रकट होता है’ और B घटना ‘पासे पर सख्या 3 प्रकट होती है’ को निरूपित करते हैं। निरीक्षण कीजिए कि घटनाएँ A और B स्वतन्त्र हैं या नहीं?
हल:
घटना A पर, चित आने की प्रायिकता P(A) = \(\frac{1}{2}\)
घटना B पर 3 प्रकट होने की प्रायिकता P(B) = \(\frac{1}{6}\) जब पासे और सिक्के को उछाला जाता है, तब कुल संख्या
= [HI, H2, H3. H4, Hz, H6 ]
= [TI,T2,T3,TA,TH,T6]
अब H3 का प्रकट होना एक ही तरीके से हो सकता है।
3 और चित आने की प्रायिकता = \(\frac{1}{12}\)
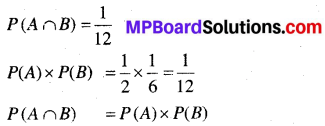
अतः A और B स्वतन्त्र घटनाएँ हैं।
प्रश्न 5.
एक पासे पर 1,2,3 लाल रंग से और 4, 5, 6 हरे रंग से लिखे गए हैं। इस पासे को उछाला गया। मान लेंA घटना ‘संख्या सम है’ और Bघटना संख्या लाल रंग से लिखी गई है’ को निरूपित करते हैं। क्या A और B स्वतन्त्र हैं?
हल:
पासे पर सम संख्याएँ 2, 4, 6 हैं।
घटना A पर सम संख्या आने की प्रायिकता
P(A) = \(\frac{3}{6}=\frac{1}{2}\)
पासे पर दो रंग लाल और हरा है।
घटना (B) पर लाल रंग आने की प्रायिकता P(B) = \(\frac{1}{2}\)
लाल रंग में सम संख्या 2 है।
लाल रंग और सम संख्याएँ होने की प्रायिकता
P(A ∩ B) = \(\frac{1}{6}\)
≠P(A ∩ B)
A और B स्वतन्त्र घटना नहीं है।
प्रश्न 6.
मान लें E तथा F दो घटनाएँ इस प्रकार हैं कि P(E) = \(\frac{3}{5}\), P(F) = \(\frac{3}{10}\) और P(E ∩ F) = \(\frac{1}{5}\) तब क्या E तथा F स्वतन्त्र हैं।
हल:
∵ P(E) = \(\frac{3}{5}\) तथा P(F) = \(\frac{3}{10}\) तथा P(E ∩ F) = \(\frac{1}{5}\)
∴ P(E) x P(F) = \(\frac{3}{5} \times \frac{3}{10}=\frac{9}{50}\)
∵ P(E ∩ F) ≠ P(E) x P(F)
अतः E तथा F स्वतन्त्र घटनाएँ नहीं हैं।
प्रश्न 7.
A और B ऐसी घटनाएँ दी गई हैं जहाँ P(A)= \(\frac{1}{2}\), P(AUB) = \(\frac{3}{5}\) तथा P(B) = P
p का मान ज्ञात कीजिए यदि
(i) घटनाएँ परस्पर अपवर्जी हैं
(ii) घटनाएँ स्वतन्त्र हैं।
हल:
माना P(A ∩ B) =x
अब P(A) = \(\frac{1}{2}\), P(A ∪ B) = \(\frac{3}{5}\), P(B) = P
P(A U B) = P(A) + P(B) – P(A ∩ B)

(i) जब घटनाएँ A और B परस्पर अपवर्जी हैं x = 0
∴ P = \(\frac{1}{10}\)
(ii) जब घटनाएँ A और B स्वतन्त्र हैं
P(A ∩ B) = P(A) x P(B)

![]()
प्रश्न 8.
मान लें A और B स्वतन्त्र घटनाएँ हैं तथा P(A) = 0.3 और P(B) = 0.4 तब .
(i) P(A ∩ B)
(ii) P(A U B)
(iii) \(P\left(\frac{A}{B}\right)\)
(iv) \(P\left(\frac{B}{A}\right)\) ज्ञात कीजिए।
हल:
(i) दिया है :
P(A) = 0.3, P(B) = 0.4
जब A और B स्वतन्त्र घटना है
P(A ∩ B) = P(A) x P(B)
= 0.3 x 0.4 = 0.12
(ii) P(A U B) = P(A) + P(B) – P(A ∩ B)
= 0.3 + 0.4 – 0.12
= 0.7 – 0.12 = 0.57
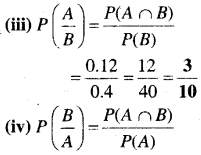
= \(\frac{0.12}{0.3}=\frac{12}{30}=\frac{2}{5}\)
प्रश्न 9.
दी गई घटनाएँ A और B ऐसी हैं, जहाँ P(A) = \(\frac{1}{4}\), P(B) =\(\frac{1}{2}\) और P(A ∩ B) = तब P(A – नहीं और B – नहीं) ज्ञात कीजिए।
हल:

अत: P(A – नहीं और B – नहीं) = \(\frac{3}{8}\)
प्रश्न 10.
मान लें A तथा B स्वतन्त्र घटनाएँ हैं और P(A) = \(\frac{1}{2}\) तथा P(B) = \(\frac{7}{12}\) और P(A – नहीं और B – नहीं) = \(\frac{1}{4}\) क्या A और B स्वतन्त्र घटनाएँ हैं?
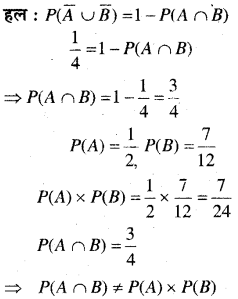
A और B स्वतन्त्र घटनाएँ नहीं हैं।
![]()
प्रश्न 11.
A और B स्वतन्त्र घटनाएँ दी गई हैं जहाँ P(A) = 0.3, P (B)= 0.6 तो
(i) P(A और B)
(ii) P(A और B – नहीं)
(iii) P(A या B)
(iv) P(A और B में कोई भी नहीं ) का मान ज्ञात कीजिए।
हल:
दिया है : A और B स्वतन्त्र घटनाएँ हैं
(i) ∴ P (A और B) = P(A ∩ B)
=P(A) × P (B) [∵P (A)= 0.3, P (B)= 0.6]
= 0.3 x 0.6 = 0.18
(ii) P (A और B नहीं)
=P(A ∩ \(\overline{\mathbf{B}}\))
= P(A) – P(A ∩ B)
= 0.3 – 0.18 [∵ P(A ∩ B) = 0.18]
= 0.12
(iii) यहाँ P (A) = 0.3, P (B) = 0.6,
P (A ∩ B) = 0.18
∴ P(A ∪ B) = P (A) + P (B) – P (A ∩ B)
= 0.3 + 0.6 – 0.18
= 0.72
⇒ P(A या B) = 0.72
(iv) P(A और B में कोई नहीं) = P(\(\overline{\mathbf{A}}\) ∩ \(\overline{\mathbf{B}}\))
= P(\(\overline{\mathbf{A}}\))x P (\(\overline{\mathbf{B}}\))
∴ P(\(\overline{\mathbf{A}}\) ∩ \(\overline{\mathbf{B}}\)) = P (\(\overline{\mathbf{A}}\)) x P(\(\overline{\mathbf{B}}\))
= [1 – P (A)] x [1 – P (B)]
=[1 – 0.3] x [1 – 0.6]
= 0.7 x 0.4
= 0.28
प्रश्न 12.
एक पासे को तीन बार उछाला जाता है तो कम-से-कम एक बार विषम संख्या प्राप्त होने की प्रायिकता ज्ञात कीजिए।
हल:
पासे को एक बार उछालने पर विषम संख्या प्राप्त होने की प्रायिकता = \(\frac{3}{6}=\frac{1}{2}\)
तथा सम संख्या प्राप्त होने की प्रायिकता = \(\frac{3}{6}=\frac{1}{2}\)
इसलिए पासे को तीन बार उछालने पर सम संख्या प्राप्त होने की प्रायिकता = \(\frac{1}{2} \times \frac{1}{2} \times \frac{1}{2}=\frac{1}{8}\)
अतः पासे को तीन बार उछालने पर कम से कम 1 बार विषम संख्या प्राप्त होने की प्रायिकता = \(1-\frac{1}{8}=\frac{7}{8}\)
प्रश्न 13.
दो गेंद एक बॉक्स से बिना प्रतिस्थापित किए निकाली जाती है। बॉक्स में 10 काली और 8 लाल गेंदें हैं तो प्रायिकता ज्ञात कीजिए-(i) दोनों गेंदें लाल हों, (i) प्रथम काली एवं दूसरी लाल हो, (iii) एक काली तथा दूसरी लाल
हो।
हल:
(i) प्रथम गेंद लाल होने की प्रायिकता
= \(\frac{C_{1}}{^{18} C_{1}}=\frac{8}{18}=\frac{4}{9}\)
दूसरी गेंद भी लाल प्राप्त होने की प्रायिकता = \(\frac{4}{9}\)
दोनों गेंद लाल प्राप्त होने की प्रायिकता
= \(\frac{4}{9} \times \frac{4}{9}=\frac{16}{81}\)
(ii) प्रथम गेंद काली प्राप्त होने की प्रायिकता
= \(\frac{10}{18} C_{1}=\frac{10}{18}=\frac{5}{9}\)
दूसरी गेंद लाल प्राप्त होने की प्रायिकता
= \(\frac{^{8} C_{1}}{^{18} C_{1}}=\frac{8}{18}=\frac{4}{9}\)
प्रथम काली एवं दूसरी लाल गेंद प्राप्त होने की प्रायिकता
= \(\frac{5}{9} \times \frac{4}{9}=\frac{20}{81}\)
(iii) प्रथम गेंद काली और दूसरी लाल प्राप्त होने की प्रायिकता
= \(\frac{10}{18} \times \frac{8}{18}=\frac{5}{9} \times \frac{4}{9}=\frac{20}{81}\)
प्रथम गेंद लाल औ दूसरी गेंद काली प्राप्त होने की प्रायिकता
= \(\frac{8}{18} \times \frac{10}{18}=\frac{4}{9} \times \frac{5}{9}=\frac{20}{81}\)
∴ एक काली तथा दूसरी लाल गेंद प्राप्त होने की प्रायिकता
= \(\frac{20}{81}+\frac{20}{81}=\frac{40}{81}\)
प्रश्न 14.
एक विशेष समस्या को A और B द्वारा स्वतन्त्र रूप से हल करने की प्रायिकताएँ क्रमशः \(\frac{1}{2}\) और \(\frac{1}{3}\) हैं। यदि दोनों, स्वतंत्र रूप से, समस्या हल करने का प्रयास करते हैं तो प्रायिकता ज्ञात कीजिए कि –
(i) समस्या हल हो जाती है।
(ii) उनमें से तथ्यतः कोई एक समस्या हल कर लेता है।
हल:
(i) A द्वारा समस्या हल करने की प्रायिकता =\(\frac{1}{2}\) = P(A)
∴ A के द्वारा समस्या हल न होने की प्रायिकता
= \(1-\frac{1}{2}=\frac{1}{2}\) = P(A)
तथा B के द्वारा समस्या हल करने की प्रायिकता
= \(\frac{1}{3}\) =P(B)
∴ समस्या हल न करने की प्रायिकता = \(1-\frac{1}{3}=\frac{2}{3}\) = P(B)
स्वतन्त्र रूप से प्रश्न हल नहीं होने की प्रायिकता
= \(\frac{1}{2} \times \frac{2}{3}=\frac{1}{3}\)
इसलिए समस्या हल हो जाने की प्रायिकता = \(1-\frac{1}{3}=\frac{2}{3}\)
अत: दोनों द्वारा समस्या हल होने की प्रायिकता = \(\frac{2}{3}\)
(ii) उनमें से तथ्यत: कोई एक प्रश्न हल करने की प्रायिकता
= P(A\(\overline{B}\)) + P(\(\overline{A}\)B)
= P(A).P(\(\overline{B}\)) + P(\(\overline{A}\)).P(B) (∵A तथा B स्वतन्त्र घटनाएँ हैं)
= \(\frac{1}{2} \times \frac{2}{3}+\frac{1}{2} \times \frac{1}{3}=\frac{1}{3}+\frac{1}{6}=\frac{1}{2}\)
![]()
प्रश्न 15.
ताश के 52 पत्तों की एक सुमिश्रित गड्डी से एक पत्ता यादृच्छया निकाला जाता है।
निम्नलिखित में से किन दशाओं में घटनाएँ E और F स्वतन्त्र हैं?
(i) E : ‘निकाला गया पत्ता हुकुम का है’
F : ‘निकाला गया पत्ता इक्का है’
(ii) E : ‘निकाला गया पत्ता काले रंग का है’
F : ‘निकाला गया पत्ता एक बादशाह है’
(iii)E : ‘निकाला गया पत्ता एक बादशाह या एक बेगम है’
F: “निकाला गया पत्ता एक बेगम या एक गुलाम है’
हल:
ताश के 52 पत्तों की एक गड्डी है।
(i) हुकुम के पत्तों की संख्या = 13
∴ निकाले गए हुकुम के पत्ते की प्रायिकता
= \(\frac{13}{52} \frac{C_{1}}{C_{1}}=\frac{13}{52}\)
∴ P (E) = \(\frac{13}{52}=\frac{1}{4}\)
ताशों की एक गड्डी में चार इक्के हैं।
निकाला गया पत्ता इक्का की प्रायिकता
= \(\frac{^{4} C_{1}}{^{52} C_{1}}=\frac{4}{52}=\frac{1}{13}\)
⇒ P(F) = \(\frac{1}{13}\)
केवल एक पत्ता है जिसमें हुकुम का एक इक्का है।
निकाला गया हुकुम का इक्का की प्रायिकता = \(\frac{1}{52}\)
∴ P(E ∩ F) = \(\frac{1}{52}=\frac{1}{4} \times \frac{1}{13}\)
= P(E) x P(F)
⇒ P(E ∩ F) = P(E) x P(F)
E तथा F स्वतन्त्र घटनाएँ हैं।
(ii) ताश के 52 पत्तों की गड्डी में 26 काले रंग के पत्ते हैं।
एक काला पत्ता खींचने की प्रयिकता = \(\frac{26}{52} \frac{C_{1}}{C_{1}}=\frac{26}{52}=\frac{1}{2}\)
∴ P(E) = \(\frac{1}{2}\)
ताश के 52 पत्तों की एक गड्डी में 4 पत्ते बादशाह हैं।
∴ एक बादशाह खींचने की प्रायिकता
= \(\frac{^{4} C_{1}}{^{52} C_{1}}=\frac{4}{51}=\frac{1}{13}\)
∴ P(F) = \(\frac{1}{13}\)
यहाँ काले रंग में दो बादशाह हैं।
∴ काले रंग की एक बादशाह खींचने की प्रायिकता
= P(E ∩ F) = \(\frac{2}{52}=\frac{1}{26}\)
अब, P(E) x P(F) = \(\frac{1}{2} \times \frac{1}{13}=\frac{1}{26}\)
= P(E ∩ F)
अतः P(E ∩ F) = P(E) x P(F)
⇒ E और F स्वतन्त्रघटनाएँ हैं।
(iii) यहाँ 4 बेगम और 4 बादशाह के पत्ते हैं।
∴ एक बादशाह या एक बेगम खींचने की प्रायिकता
= \(\frac{^{8} C_{1}}{^{52} C_{1}}\)
= \(\frac{8}{52}=\frac{2}{13}\)
∴ P(E) = \(\frac{2}{13}\)
यहाँ 4 बेगम और 4 गुलाम के पत्ते हैं।
∴ एक बेगम या एक गुलाम की प्रायिकता = \(\frac{8}{52}=\frac{2}{13}\)
यहाँ दोनों ही दशाओं में 4 बेगम उभयनिष्ठ हैं।
∴ एक बेगम का पत्ता खींचने की प्रायिकता = \(\frac{4}{52}=\frac{1}{13}\)
= P(E ∩ F)
P(E) x P(F) = \(\frac{2}{13} \times \frac{2}{13}\)
= \(\frac{4}{169}\) ≠ P(E ∩ F)
अतः E और F स्वतन्त्र घटनाएँ नहीं हैं।
प्रश्न 16.
एक छात्रावास में 60% विद्यार्थी हिन्दी का, 40% अंग्रेजी का और 20% दोनों अखबार पढ़ते हैं। एक छात्रा को यादृच्छया चुना जाता है।
(a) प्रायिकता ज्ञात कीजिए कि वह न तो हिन्दी और न ही अंग्रेजी का अखबार पढ़ती है।
(b) यदि वह हिन्दी का अखबार पढ़ती है तो उसके अंग्रेजी का अखबार भी पढ़ने वाली होने की प्रायिकता ज्ञात कीजिए।
(c) यदि वह अंग्रेजी का अखबार पढ़ती है तो उसके हिन्दी का अखबार भी पढ़ने वाली होने की प्रायिकता ज्ञात कीजिए।
हल:
(a) माना छात्रों के हिन्दी और अंग्रेजी के अखबार पढ़ने की घटनाओं को क्रमश: H और E से निरूपित करते हैं।
P(H) = 60% = \(\frac{60}{100}\) =0.6
P(E) = 40% = \(\frac{10}{100}\) = 0.4
P(H ∩ E) = 20% = \(\frac{20}{100}\) = 0.2
छात्रों के कम से कम एक अखबार पढ़ने की प्रायिकता
=P(H U E)
P(H) = 0.6, P(E) = 0.4, P(H U E) = 0.2
∴ P(H U E) = 0.6 + 0.4 – 0.2
=1 – 0.2 = 0.8
∴ छात्रों के न तो हिन्दी और न ही अंग्रेजी का अखबार पढ़ने की प्रायिकता
=1 – P(H U E) = 1 – 0.8
= 0.2 = 20%
स्पष्ट है कि 20% विद्यार्थी अखबार नहीं पढ़ते
(b) यदि वह हिन्दी का अखबार पढ़ती है तो उसमें अंग्रेजी का अखबार भी पढ़ने वाली होने की प्रायिकता

(c) यदि वह अंग्रेजी का अखबार पढ़ती है तो उसके हिन्दी | का अखबार भी पढ़ने वाली होने की प्रायिकता
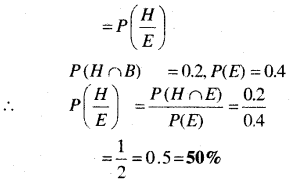
![]()
प्रश्न 17.
यदि पासों का एक जोड़ा उछाला जाता है तो प्रत्येक पासे पर सम अभाज्य संख्या प्राप्त करने की प्रायिकता निम्नलिखित में से क्या है?
(A) 0
(B) \(\frac{1}{3}\)
(C) \(\frac{1}{12}\)
(D) \(\frac{1}{36}\)
हल:
यहाँ समअभाज्य संख्या केवल 2 है। जब पासा उछाला जाता है तब सम अभाज्य संख्या प्राप्त होने की प्रायिकता = \(\frac{1}{6}\)
जब पासों का एक जोड़ा उछाला जाता है तब समअभाज्य संख्या प्राप्त करने की प्रायिकता
= \(\frac{1}{6} \times \frac{1}{6}=\frac{1}{36}\)
अतः विकल्प (D) सही है।
प्रश्न 18.
दो घटनाओंA और B को परस्पर स्वतन्त्र कहते हैं, यदि
(A) A और B परस्पर अपवर्जी हैं
(B) P (A’B’ ) = [1 – P(A)][1 – P(B)]
(C) P (A) = P(B)
(D) (A) + P(B)=1
हल:
दो घटनाएँ स्वतन्त्र हैं।
यदि P(A ∩ B) = P(A)x P(B)
या P(A’ ∩ B’) = P(A’). P(B’)
= [1 – P(A)] [1 – P(B)]
अतः विकल्प (B) सही है।