In this article, we share MP Board Class 12th Maths Book Solutions Chapter 13 प्रायिकता Ex 13.1 Pdf, These solutions are solved by subject experts from the latest MP Board books.
MP Board Class 12th Maths Book Solutions Chapter 13 प्रायिकता Ex 13.1
प्रश्न 1.
यदि E और F इस प्रकार की घटनाएँ हैं कि P(E) = 0.6, P (F) == 0.3 और P(E ∩F) = 0.2, तो \(\boldsymbol{P}\left(\frac{\boldsymbol{E}}{\boldsymbol{F}}\right)\) और \(\boldsymbol{P}\left(\frac{\boldsymbol{F}}{\boldsymbol{E}}\right)\) ज्ञात कीजिए।
हल:
ज्ञात है
P(E) = 0.6
P(F) =03
तथा P(EMF) = 0.2

प्रश्न 2.
\(P\left(\frac{A}{B}\right)\) ज्ञात कीजिए, यदि P (B) = 0.5 और P(A ∩ B) = 0.32
हल:
∵ P(B) =0.5
तथा P (A ∩ B) =0.32
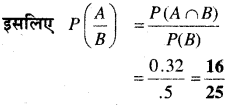
प्रश्न 3.
यदि P(A) = 0.8, P(B) = 0.5 और \(P\left(\frac{B}{A}\right)\) = 0.4 ज्ञात कीजिए।
(i) P (A ∩ B)
(ii) P\(P\left(\frac{A}{B}\right)\)
(iii) P(AUB)
हल:
दिया है :
P(A) = 0.8, P(B) = 0.5
और \(P\left(\frac{B}{A}\right)\)=0.4

(iii) ∵ P(A U B) = P(A) + P(B) – P(A ∩B)
= 0.8 + 0.5 – 0.32
=1.3 – 0.32
= 0.98
![]()
प्रश्न 4.
P (AUB) ज्ञात कीजिए यदि 2P (A) = P(B) = \(\frac{5}{13}\) और \(P\left(\frac{A}{B}\right) = \frac{2}{5}\)

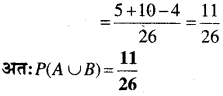
प्रश्न 5.
यदि P(A) = \(\frac{6}{11}\) P (B) = \(\frac{5}{11}\) और P(AUB) = \(\frac{7}{11}\) तो ज्ञात कीजिए
(i) P (A∩B)
(ii) \(P\left(\frac{A}{B}\right)\)
(iii) \(P\left(\frac{B}{A}\right)\)

निम्नलिखित प्रश्न 6 से 9 तक \(P\left(\frac{E}{F}\right)\) ज्ञात कीजिए।
प्रश्न 6.
एक सिक्के को तीन बार उछाला गया है-
(i) E : तीसरे उछाल पर चित F : पहली दोनों उछालों पर चित।
(ii) E : न्यूतनम दो चित F : अधिकतम एक चित।
(iii) E : अधिकतम दो पट F : न्यूनतम एक पट।
हल:
सम्भावित परिणाम =8
(i) E = {HHH, HTH, THH, TTH}
तथा F = {HHH, HHT}
E∩F = {HHH}
⇒P(E∩F) = \(\frac{1}{8}\) , P(F) = \(\frac{1}{4}\)
∴ 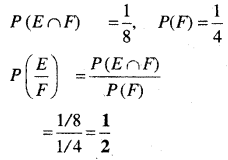
(ii) ∵ E : न्यूनतम दो चित
∴ E = {HHH, HTH, THH, HHT}
F: अधिकतम दो चित
∴ F = {TTT, HTT, THT, HTT, HHT, HTH,THH}
∴ E ∩ F = {HHT, HTH, THH}

(iii) E : अधिकतम दो पट
∴ E = {HTT, THT, TTH, HHT, HTH,THH, HHH}
F : न्यूनतम दो पट
F = {THH, HTH, HHT, TTH, THT, HTT, TTT}
∴ E ∩ F = {HTT,THT,TTH,THH, HTH, HHT}

प्रश्न 7.
दो सिक्कों को एक बार उछाला गया है –
(i) E : एक सिक्के पर पट प्रकट होता है F : एक सिक्के पर चित प्रकट होता है।
(ii)E : कोई पट प्रकट नहीं होता F: कोई चित प्रकट नहीं होता है।
हल : (i) E = एक सिक्के पर पट प्रकट होता है।
= {TH, HT}
F = एक सिक्के पर चित प्रकट होता है।
= {HT, TH}
∴ E ∩F = {TH, HT}
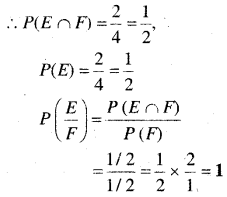
(ii) E = कोई पट प्रकट नहीं होता है
= {H, H}
F = कोई चित प्रकट नहीं होता है
= {TT}
∴ E ∩ F=ϕ
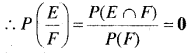
![]()
प्रश्न 8.
एक पासे को तीन बार उछाला गया है
E : तीसरी उछाल पर संख्या 4 प्रकट होना
F : पहली दो उछालों पर क्रमशः 6 तथा 5 प्रकट होना।
हल:
E = तीसरी उछाल पर संख्या 4 प्रकट होना
= (1, 1, 4), (1, 2, 4), (1, 3, 4), …(1, 6, 4)
=(2, 1, 4), (2, 2, 4), (2, 3, 4), …(2, 6, 4)
= (3, 1, 4), (3, 2, 4), (3, 3, 4), …(3, 6, 4)
= (4,1, 4), (4, 2, 4), (4, 3, 4), …(4, 6, 4)
= (5, 1, 4), (5, 2, 4), (5, 3, 4), …(5, 6, 4)
=(6, 1, 4), (6, 2, 4), (6, 3, 4), … (6, 6, 4)
= 36 परिणाम
F = पहली दो उछालों पर क्रमश: 6 तथा 5 प्रकट होना
= {(6, 5, 1), (6, 5, 2), ( 6, 5, 3), ( 6, 5, 4), ( 6, 5, 5), (6, 5, 6)} = 6 परिणाम
∴ E ∩ F = {6, 5, 4}

प्रश्न 9.
एक पारिवारिक चित्र में माता, पिता व पुत्र या यादृच्छया खड़ें हैं –
E : पुत्र एक सिरे पर खड़ा है F : पिता मध्य में खड़े हैं।
हल:
माना पुत्र (s), पिता (f) तथा माता (m) यादृच्छया खड़े है।
E = पुत्र एक सिरे पर खड़ा है।
= {smf, sfm, fms, mfs}
तथा F : पिता मध्य में खड़े हैं।
∴ F = { mfs, sin}
⇒ E ∩ F = {mfs, sfm}
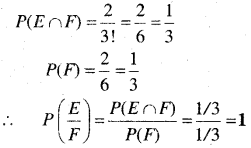
प्रश्न 10.
एक काले और एक लाल पासे को उछाला गया हैं –
(a) पासों पर प्राप्त संख्याओं का योग 9 से अधिक होने की सप्रतिबन्ध प्रायिकता ज्ञात कीजिए यदि यह ज्ञात हो कि काले पासे पर 5 प्रकट हुआ है।
(b) पासों पर प्राप्त संख्याओं का योग 8 होने की सप्रतिबन्ध प्रायिकता ज्ञात कीजिए यदि यह ज्ञात हो कि लाल पासे पर प्रकट संख्या 4 से कम है।
हल:
(a) जब दो पासे उछाले जाएँ तो उनका योग 9 से अधिक हो
A = {(4, 6), (5, 5), (6, 4), (5, 6), (6, 5), (6, 6)}
B = काले पासे पर 5 प्रकट हुआ है।
= {(5,1), (5, 2), (5, 3), (5, 4), (5, 5), (5, 6)}
A∩B = {(5, 5), (5, 6)}
P(A∩B) = \(\frac{2}{36}\)= \(\frac{1}{18}\)

(b) A = प्राप्त संख्याओं का योग 8 है।
= {(2, 6), (3, 5), (4, 4), (5, 3), (6, 2)}
B = लाल पासे पर प्रकट संख्या 4 से कम है।
B = {(1, 1), (1, 2), (1, 3), (1, 4), (1, 5), (1, 6), (2, 1), (2, 2), (2, 3), (2, 4), (2, 5), (2, 6), (3, 1), (3, 2), (3, 3), (3, 4), (3, 5), (3, 6)}
A ∩ B = {(2, 6), (3, 5)}
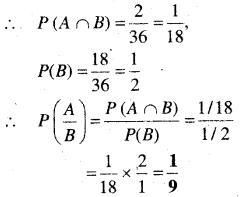
प्रश्न 11.
एक न्याय्य पासे को उछाला गया है। घटनाओं E = {1, 3, 5}, F = {2, 3} और G = {2, 3, 4,5} के लिए
निम्नलिखित ज्ञात कीजिए –
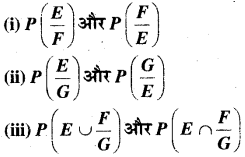
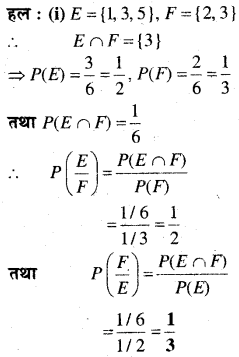

(iii) E = {1, 3, 5}, F = {2, 3}, G = {2, 3, 4, 5}
⇒E ∩ G = {3, 5} E ∩ G = {2, 3},
(E ∩ F) ∩ G = {3}
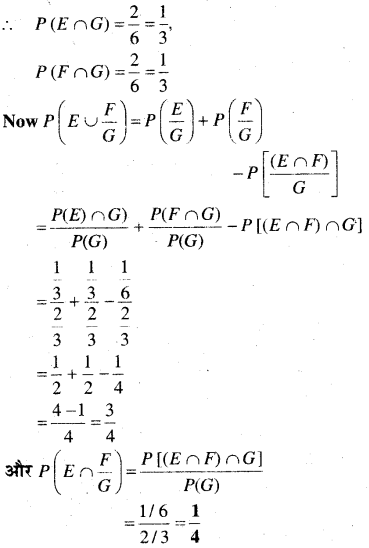
प्रश्न 12.
मान लें कि जन्म लेने वाले बच्चे का लड़का या लड़की होना समसंभाव्य है। यदि किसी परिवार में दो बच्चे हैं तो दोनों बच्चों के लड़की होने की सप्रतिबन्ध प्रायिकता क्या है, यदि यह दिया गया है कि
(i) सबसे छोटा बच्चा लड़की है
(ii) न्यूनतम एक बच्चा लड़की है।
हल:
माना पहले तथा दूसरे बच्चे, लड़कियाँ G1,G2, तथा लड़के B1, B2 हैं।
∴ S = {(G1.G2), (G1, B2), (G2, B1), (B1, B2)}
माना A = दोनों बच्चे लड़कियाँ हैं।
= {G1G2}
B = सबसे छोटा बच्चा लड़की है।
= {G1G2. B1G2}
C = न्यूनतम एक बच्चा लड़की है।
= {G1B2,G1G2, B1G2}
A ∩ B = {G1G2}, A ∩ C = {G1G2}
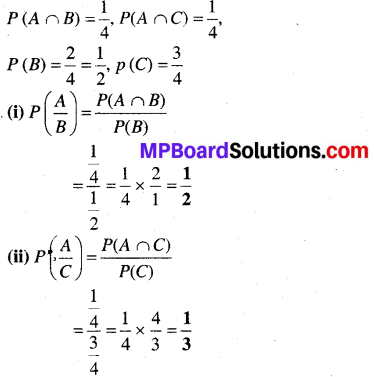
![]()
प्रश्न 13.
एक प्रशिक्षक के पास 300 सत्य/असत्य प्रकार के आसान प्रश्न, 200 सत्य/असत्य प्रकार के कठिन प्रश्न, 500 बहुविकल्पीय प्रकार के आसान प्रश्न और 400 बहुविकल्पीय प्रकार के कठिन प्रश्नों का संग्रह है। यदि प्रश्नों के संग्रह से एक प्रश्न यादृच्छया चुना जाता है तो एक आसान प्रश्न की बहुविकल्पीय होने की प्रायिकता क्या होगी?
हल:
दिए गए आँकड़ों की टेबिल निम्न प्रकार है –
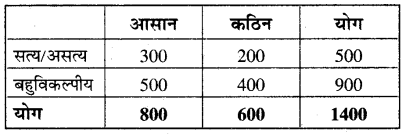
माना E = सरल प्रश्न, D = कठिन प्रश्न, T = सत्य/असत्य प्रश्न, M = बहुविकल्पीय प्रश्न
सरल बहुविकल्पीय प्रश्नों की संख्या = 500
कुल प्रश्नों की संख्या = 1400
P(E ∩ M) = आसन और बहुविकल्पीय प्रश्नों की प्रायिकता
\( = \frac{500}{1400} = \frac{5}{14}\)
बहुविकल्पीय प्रश्नों की कुल संख्या = 500 + 400 = 900
P(M) = एक बहुविकल्पीय प्रश्नों की प्रायिकता
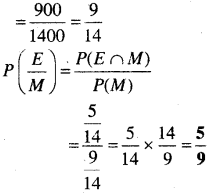
प्रश्न 14.
यह दिया गया है कि दो पासों को फेंकने पर प्राप्त संख्याएँ भिन्न-भिन्न हैं। दोनों संख्याओं का योग 4 होने की प्रायिकता ज्ञात कीजिए।
हल:
दो पासों को फेंकने से प्रतिदर्श समष्टि के परिणाम
= 6 x 6 =36
माना A = दो संख्याओं का योग 4
= [(1,3), (2, 2), (3,1)]
दो पासों को फेंकने पर समान संख्या वाले परिणाम
= {(1, 1), (2, 2), (3,3),(4, 4) (5,5), (6, 6)}
B = जब संख्या भिन्न हो तो ऐसे परिणाम
=36 – 6 = 30
A∩B = [(1, 3), (3, 1)]
P(A∩B) = \(\frac{2}{36}\),
P(B) =\(\frac{30}{36}\)
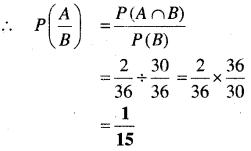
प्रश्न 15.
एक पासे को फेंकने के परीक्षण पर विचार कीजिए। यदि पासे पर प्रकट संख्या 3 का गुणज है तो पासे को पुनः फेंकें और यदि कोई अन्य संख्या प्रकट हो तो एक सिक्के को उछालें। घटना न्यूनतम एक पासे पर संख्या 3 प्रकट होना’ दिया गया है तो घटना ‘सिक्के पर पट प्रकट होने’ की सप्रतिबन्ध प्रायिकता ज्ञात कीजिए।
हल:
माना यहाँ 3 का गुणज प्रत्येक समय n बार फेंका गया।
एक उछाल में 3 के गुणज की प्रायिकता प्राप्त होगी = \(\frac{2}{6}=\frac{1}{3}\)
n उछालों में 3 के गुणज की प्रायिकता प्राप्त होगी = \(=\left(\frac{1}{3}\right)^{n}\)
एक उछाल में 6 की प्रायिकता प्राप्त होगी = \(\frac{1}{6}\)
∴ n उछालों में 6 की प्रायिकता प्राप्त होगी = \(\left(\frac{1}{6}\right)^{n}\)
⇒n उछालों में कम-से-कम 3 की प्रायिकता प्राप्त होगी
= \(\left(\frac{1}{3}\right)^{n}-\left(\frac{1}{6}\right)^{n}\)
∴ (n +1)th उछाल में 1, 2, 3, 4, 5 (3 का गुणज नहीं है) की प्रायिकता प्राप्त होगी
=\(\frac{4}{6}=\frac{2}{3}\)
अगली उछाल में एक सिक्का उछाला गया और पट आया।
∴ पट आने की प्रायिकता = \(\frac{1}{2}\)
अन्त में (n + 2)th उछाल में कम-से-कम 3 और पट प्राप्त होने की प्रायिकता
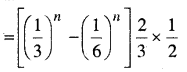
यदि n→∞; एक पासे पर संख्या 3 प्रकट होना, दिया गया है तो सिक्के पर पट होने की सप्रतिबन्ध प्रायिकता
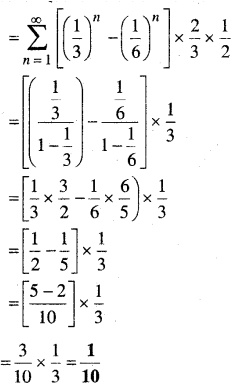
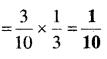
निम्नलिखित प्रश्नों में से प्रत्येक में सही उत्तर चुनें।
प्रश्न 16.
यदि P(A) = \(\frac{1}{2}\), P(B) = 0 तब \(P\left(\frac{A}{B}\right)\) है –
(A) 0
(B) \(\frac{1}{2}\)
(C) परिभाषित नहीं
(D) 1
हल:
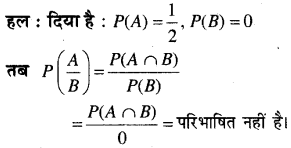
![]()
प्रश्न 17.
यदि A और B दो घटनाएँ इस प्रकार हैं कि \(\boldsymbol{P}\left(\frac{\boldsymbol{A}}{\boldsymbol{B}}\right)^{\prime}=\boldsymbol{P}\left(\frac{\boldsymbol{B}}{\boldsymbol{A}}\right)\) ≠ 0 तब
(A) A ⊂ B
(B) A = B
(C) A ∩B = ϕ
(D) P(A)=P(B)
हल:
