In this article, we share MP Board Class 12th Maths Book Solutions Chapter 12 प्रायिकता Ex 12.2 Pdf, These solutions are solved by subject experts from the latest MP Board books.
MP Board Class 12th Maths Book Solutions Chapter 12 प्रायिकता Ex 12.2
प्रश्न 1.
रेशमा दो प्रकार के भोज्य P और Q को इस प्रकार मिलाना चाहती है कि मिश्रण में विटामिन अवयवों में 8 मात्रक विटामिन A तथा 11 मात्रक विटामिन B हों। भोज्य P की लागत Rs 60/kg और भोज्य ए की लागत Rs 80/kg है। भोज्य P में 3 मात्रक/kg विटामिन A और 5 मात्रक/kg विटामिन B है जबकि भोज्य में 4 मात्रक/kg विटामिन A और 2 मात्रक/kg विटामिन है। मिश्रण की न्यूनतम लागत ज्ञात कीजिए।
हल:
माना मिश्रण में भोज्य पदार्थ P की मात्रा x kg और Q की मात्रा y kg है।
स्पष्टतः x ≥ 0, y ≥ 0
प्रदत्त आंकड़ों से निम्नलिखित सारणी बनाते हैं।
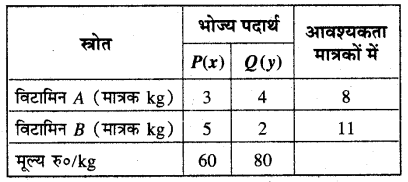
∴ मिश्रण में विटामिन A के 8 मात्रक और विटामिन B के 11 मात्रक होने चाहिए अतः निम्न अवरोध प्राप्त होते हैं।
3x + 4 ≤ 8
5x + 2y ≥ 11
भोज्य P के x kg और Q के y kg खरीदने का कुल मूल्य z है तब
Z = 60x + 80y
अतः समस्या का गणितीय समीकरण निम्नलिखित है।
निम्न व्यवरोधों के अन्तर्गत
3x + 4y ≥ 8 …(i)
5x + 2y ≥ 11 …(ii)
x, y ≥ 0 …(iii)
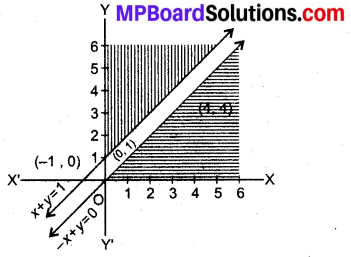
असमीकरणों
(i) व
(iii) तक के आलेखों द्वारा निर्धारित सुसंगत क्षेत्र X APDY हैं तथा सुसंगत क्षेत्र अपरिवद्ध है।
P\(\left(2, \frac{1}{2}\right)\) प्रतिच्छेदत बिन्दु हैं।
AB: 3x + 4y = 8
और 5x + 2y = 11
Z के मान की गणना प्रत्येक कोणीय बिन्दु पर करने पर
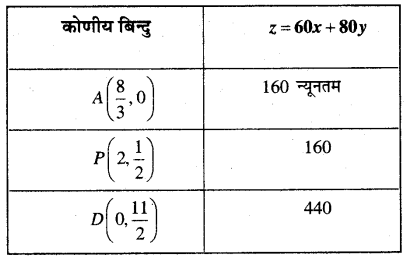
स्पष्ट है कि 2 का न्यूनतम मान 160 है। परन्तु सुसंगत क्षेत्र अपरिवद्ध है।
अब हमें असमीकरण का आलेख खींचना पड़ेगा।
60x + 80y < 160
या 3x + 4y < 8
यह रेखा के बीच का क्षेत्र प्रदर्शित करता है।
AB: 3x + 4y = 8
आलेख से ज्ञात होता है कि यह क्षेत्र तथा सुसंगत क्षेत्रों के बीच कोई बिन्दु उभयनिष्ठ नहीं है।
अतः z का न्यूनतम मूल्य 160 रु० है, जो कि \(\left(\frac{8}{3}, 0\right)\) और \(\left(2, \frac{1}{2}\right)\) को मिलाने वाली रेखाखण्ड के सभी बिन्दुओं पर न्यूनतम
प्रश्न 2:
एक प्रकार के केक को 200 g आटा तथा 25g वसा (fat) की आवश्यकता होती है तथा दूसरी प्रकार के केक के लिए 100 g आटा तथा 50g वसा की आवश्यकता होती है। केकों की अधिकतम संख्या बताओ जो 5 किलो आटे तथा 1 किलो वसा से बन सकते हैं, यह मान लिया गया है कि केकों को बनाने के लिए अन्य पदार्थों की कमी नहीं रहेगी।
हल:
माना पहली प्रकार के केक x तथा दूसरी प्रकार के केक y हैं।
∴ कुल केकों की संख्या z =x+y
St 200x + 100y ≤ 5000 (आटा)
25x + 50y ≤ 1000 (वसा)
अतः समस्या का गणितीय सूत्रीकरण निम्न हैं-
उच्च अवरोधों के अन्तर्गत
z = x + y
या 2x + y ≤ 50
x + 2y ≤ 40 और x,y ≥ 0
असमीकरणों का आलेख बनाने पर सुसंगत क्षेत्र OAEB प्राप्त होता है।
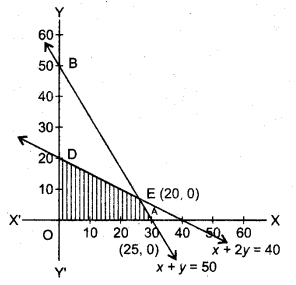
रेखाओं AB: 2x + y = 50 और CD: x +2y = 40 के प्रतिच्छेद बिन्दु E (20,10) हैं।
अब z की गणना प्रत्येक कोणीय बिन्दु पर करने पर
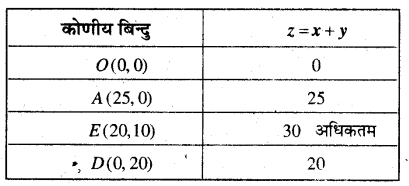
अतः केकों की अधिकतम संस्था = 30 एक प्रकार की तथा 10 अन्य प्रकार की हैं।
प्रश्न 3.
एक कारखाने में टेनिस के रैकेट तथा क्रिकेट के बल्ले बनते हैं। एक टेनिस रैकेट बनाने के लिए 1.5 घंटा यांत्रिक समय तथा 3 घंटे शिल्पकार का समय लगता है। एक क्रिकेट बल्ले को तैयार करने में 3 घंटे यांत्रिक समय तथा 1 घंटा शिल्पकार का समय लगता है। एक दिन में कारखाने में विभिन्न यंत्रों पर उपलब्ध यांत्रिक समय के 42 घंटे और शिल्पकार समय के 24 घंटे से अधिक नहीं हैं।
(i) रैकेटों और बल्लों को कितनी संख्या में बनाया जाए ताकि कारखाना पूरी क्षमता से कार्य करे?
(ii) यदि रैकेट और बल्ले पर लाभ क्रमश: Rs 20 तथा Rs 10 हों तो कारखाने का अधिकतम लाभ ज्ञात कीजिए यदि कारखाना पूरी क्षमता से कार्य करे।
हल:
माना रैकेटों की संख्या = x तथा बल्लों की संख्या = y
(i) अधिकतम
z = x + y
St 15x + 3y ≤ 42
3x + y ≤ 24
x, y ≥ 0
असमीकरणों का आलेख बनाने पर सुसंगत क्षेत्र OABC है तथा रेखाओं x +2y = 28 तथा 3x +y = 24 का प्रतिच्छेद बिन्दु B(4,12) है।
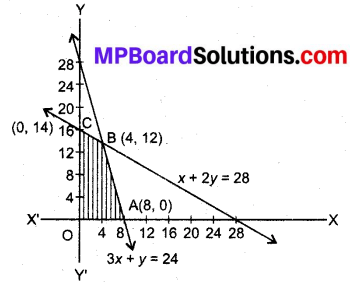
अब र की प्रत्येक कोणीय बिन्दु पर गणना करने पर

∵ 2 का अधिकतम मात्रा 16 है,
∵ 4 रैकेट तथा 12 बल्ले।
(ii) लाभ z = 20x + 10y
At D(0, 0), z = 0
At A(8, 0), z = 160
At B(4, 12), z = 200
At C(0, 14), z = 14
∴ अधिकतम लाभ 200 रु० हैं।
![]()
प्रश्न 4.
एक निर्माणकर्ता नट और बोल्ट का निर्माण करता है। एक पैकेट नटों के निर्माण में मशीन A पर एक घंटा और मशीन B पर 3 घंटे काम करना पड़ता है, जबकि एक पैकेट बोल्ट के निर्माण में 3 घंटे मशीन A पर और 1 घंटा मशीन B पर काम करना पड़ता है। वह नटों से Rs 17.50 प्रति पैकेट और बोल्टों पर Rs 7.00 प्रति पैकेट लाभ कमाता है। यदि प्रतिदिन मशीनों का अधिकतम उपयोग 12 घंटे किया जाए तो प्रत्येक (नट और बोल्ट) के कितने पैकेट उत्पादित किए जाएँ ताकि अधिकतम लाभ कमाया जा सके।
हल:
माना बोल्ट के पैकिट = x तथा y पैकेट नटों का निर्माण हुआ
तब दिये गये अवरोध का गणितीय सूत्रीकरण निम्नलिखित है-
अधिकतम z = 17.50x + 7y
या x + 3y ≤ 12
3x + y ≤ 12
x, y ≥ 0
अब असमीकरणों का आलेख बनाने पर सुसंगत क्षेत्र OABC प्राप्त होता है
रेखाओं x + 3y = 12 और 3x + y = 12 का प्रतिच्छेद बिन्दु B(3,3) हैं।
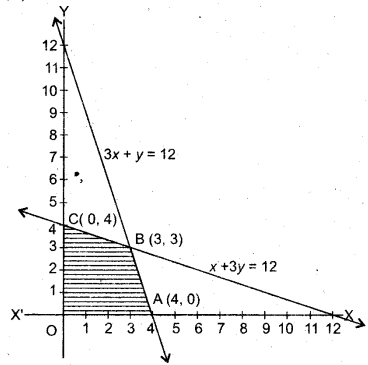
अब z की गणना प्रत्येक कोणीय बिन्दु पर करने पर
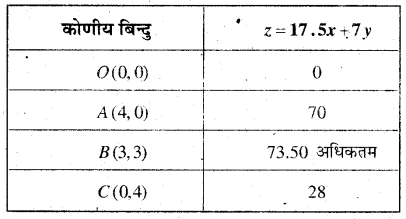
अतः नट के तीन पैकेट तथा बोल्ट के तीन पैकेट और अधिकतम लाभः = 73.50 रु० हैं।
प्रश्न 5.
एक कारखाने में दो प्रकार के पेंच A और B बनते हैं। प्रत्येक के निर्माण में दो मशीनों के प्रयोग की आवश्यकता होती है, जिसमें एक स्वचालित और दूसरी हस्तचालित है। एक पैकेट पेंच A के निर्माण में 4 मिनट स्वचालित और 6 मिनट हस्तचालित मशीन, तथा एक पैकेट पेंच B के निर्माण में 6 मिनट स्वचालित और 3 मिनट हस्तचालित मशीन का कार्य होता है। प्रत्येक मशीन किसी भी दिन के लिए अधिकतम 4घंटे काम के लिए उपलब्ध है। निर्माता पेंच के प्रत्येक पैकेट पर Rs7 और पेंच B के प्रत्येक पैकेट पर Rs 10 का लाभ कमाता है। यह मानते हुए कि कारखाने में निर्मित सभी पेंचों के पैकेट बिक जाते हैं, ज्ञात कीजिए कि प्रतिदिन कितने पैकेट विभिन्न पेंचों के बनाए जाएँ जिससे लाभ अधिकतम हो तथा
अधिकतम लाभ ज्ञात कीजिए।
हल:
माना x पैकेट पेंच A के तथा y पैकेट पेंच B के उत्पादित होने चाहिए।
इसलिए गणितीय सूत्रीकरण निम्नलिखित होगा-
अधिकतम : z = 7x + 10y (लाभ)
St 4x + 6y ≤ 240 (स्वचालित मशीन)
2x + 3y ≤ 120
6x + 3y ≤ 240 (हस्तचालित मशीन)
x, y ≥ 0
2x + y ≤ 80
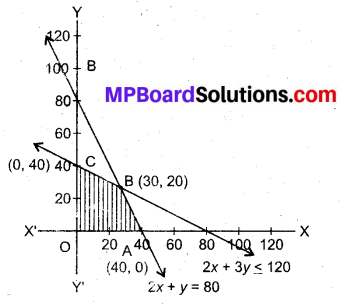
अब असमीकरणों का आलेख बनाने पर सुसंगत क्षेत्र OABC प्राप्त होता है।
रेखाओं 2x + 3y = 120 और 2x + y = 80 का प्रतिच्छेद बिन्दु B (30, 20) है।
अब z की गणना प्रत्येक कोणीय बिन्दु पर करने पर
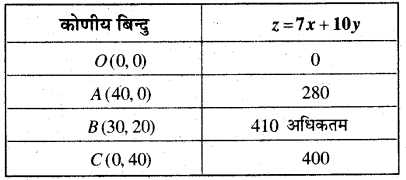
इसलिए 30 पैकिट A प्रकार के पेंच तथा 20 पैकेट B प्रकार के पेंचों के तथा अधिकतम लाभ = 410 रु० है।
प्रश्न 6.
एक कुटीर उद्योग निर्माता पैडेस्टल लैंप और लकड़ी के शेड बनाता है। प्रत्येक के निर्माण में एक रगड़ने/काटने और एक स्प्रेयर की आवश्यकता पड़ती है। एक लैंप के निर्माण में 2 घंटे रगड़ने/काटने और 3 घंटे स्प्रेयर की आवश्यकता होती है, जबकि एक शेड के निर्माण में 1 घंटा रगड़ने/काटने और 2 घंटे स्प्रेयर की आवश्यकता होती है। स्प्रेयर की मशीन प्रतिदिन अधिकतम 20 घंटे और रंगड़ने/काटने की मशीन प्रतिदिन अधिकतम 12 घंटे के लिए उपलब्ध है। एक लैंप की बिक्री पर Rs 5 और एक शेड की बिक्री पर Rs 3 का लाभ होता है। यह मानते हुए कि सभी निर्मित लैंप और शेड बिक जाते हैं, तो बताइए वह निर्माण की प्रतिदिन कैसी योजना बनाए कि लाभ अधिकतम हो?
हल:
माना x लैंप तथा y लकड़ी के शेड उत्पादित होते हैं। इस समस्या को गणितीय सूत्रीकरण करने पर अधिकतम
लाभ
z = 5x + 3y
St 2x + y ≤ 12 (रगड़ना/काटना)
3x + 2y ≤ 20 (स्प्रेयर)
x, y ≥ 20
अब आलेख बनाने पर सुसंगत क्षेत्र OAPD प्राप्त होता है।
रेखाओं 2x + y = 12 तथा 3x + 2y = 20 का प्रतिच्छेद बिन्दु P(4,4) है।
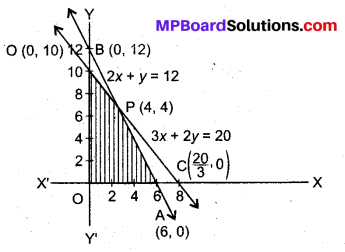
अब z की गणना प्रत्येक कोणीय बिन्दु पर करने पर कोणीय बिन्दु
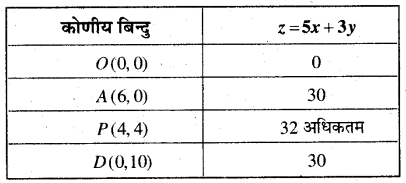
इसलिए 4 लैंप तथा 4 लकड़ी के शेड तथा अधिकतम लाभ = 32 रु० है।
![]()
प्रश्न 7.
एक कंपनी प्लाईवुड के अनूठे स्मृति चिह्न का निर्माण करती है। A प्रकार के प्रति स्मृति चिह्न के निर्माण में 5 मिनट काटने और 10 मिनट जोड़ने में लगते हैं। B प्रकार के प्रति स्मृति चिह्न के लिए 8 मिनट काटने और 8 मिनट जोड़ने में लगते हैं। दिया गया है कि काटने के लिए कुल समय 3 घंटे 20 मिनट तथा जोड़ने के लिए 4 घंटे उपलब्ध हैं। प्रत्येक A प्रकार के स्मृति चिह्न पर Rs 5 और प्रत्येक B प्रकार के स्मृति चिह्न पर Rs 6 का लाभ होना है। ज्ञात कीजिए कि लाभ के अधिकतमीकरण के लिए प्रत्येक प्रकार के कितने-कितने स्मृति चिह्नों का कंपनी द्वारा निर्माण होना चाहिए?
हल:
माना A प्रकार के स्मृति चिह्नों की संख्या x तथा B प्रकार के स्मृति चिह्नों की संख्या y हैं।
दी गई समस्या का गणितीय समीकरण करने पर
अधिकतम = 5x + 6y (लाभ)
St 5x + 8y ≤ 200 (कटिंग)
10x + 8y ≤ 240 (जोड़ना)
x, y ≥ 0
अब आलेख बनाने पर सुसंगत क्षेत्र OABC प्राप्त होते हैं।
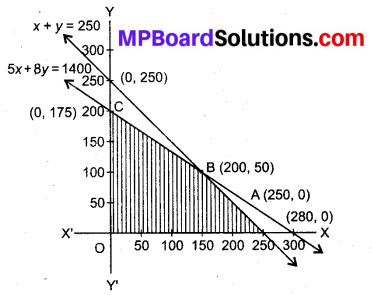
अब z की गणना प्रत्येक कोणीय बिन्दु पर करने पर
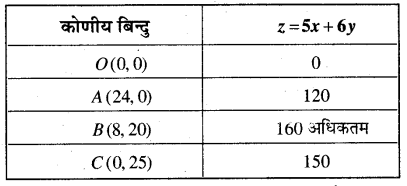
क्योंकि B(8, 20) पर 2 का मान अधिकतम है अत: A प्रकार के स्मृति चिह्नों की संख्या 8 तथा B प्रकार के स्मृति चिह्नों की संख्या 20 है तथा अधिकतम लाभ 160 रु० है।
प्रश्न 8.
एक सौदागर दो प्रकार के निजी कंप्यूटर-एक डेस्कटॉप नमूना और दूसरा पोर्टेबल नमूना, जिनकी कीमतें क्रमश: Rs 25,000 और Rs 40,000 होगी, बेचने की योजना बनाता है। वह अनुमान लगाता है कि कंप्यूटरों की कुल मासिक माँग 250 नगों से अधिक नहीं होगी। प्रत्येक प्रकार के कंप्यूटरों के नगों की संख्या ज्ञात कीजिए जिसे सौदागर अधिकतम लाभ प्राप्त करने के लिए संग्रह करें यदि उसके पास निवेश के लिए Rs 70 लाख से अधिक नहीं है और यदिडेस्कटॉप नमूने पर उसका लाभ Rs 4500 और पोर्टेबल नमूने पर Rs 5000 लाभ हो।
हल:
माना डेस्कटॉप की संख्या x तथा पोर्टेबल की संख्या y है। तब समस्या का गणितीय समीकरण करने पर
अधिकतम z = 4500x + 5000y (लाभ)
25000x + 40000y ≤ 70,00,000 (लागत मूल्य)
5x + 8y ≤ 1400
x + y ≤ 250 (माँग)
x, y ≥ 0
अब समस्या का आलेख बनाने पर सुसंगत क्षेत्र OABC प्राप्त होता है जहाँ कोणीय बिन्दुओं 0,A, B, C के निर्देशांक
क्रमशः (0,0), (250,0), (200,50) और (0,175) हैं।

अब z की गणना प्रत्येक कोणीय बिन्दु पर करने पर
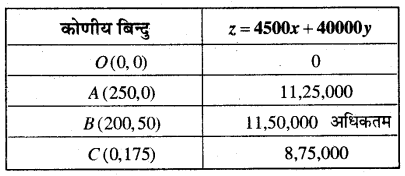
अत: डेस्कटोंपों के नमूनों की संख्या 200 तथा पोर्टेबल नमूनों की संख्या 50 है तथा अधिकतम लाभ = 1150,000 रु० हैं।
प्रश्न 9.
एक भोज्य पदार्थ में कम से कम 80 मात्रक विटामिन A और 100 मात्रक खनिज होना चाहिए। दो प्रकार के भोज्य F1 और F2 उपलब्ध हैं। भोज्य F1 की लागत Rs 4 प्रति मात्रक और F2 की लागत Rs 5 प्रति मात्रक है। भोज्य F1 की एक इकाई में कम से कम 3 मात्रक विटामिन A और 4 मात्रक खनिज है। F2की प्रति इकाई में कम से कम 6 मात्रक विटामिन A और 3 मात्रक खनिज हैं। इसको एक रैखिक प्रोग्रामन समस्या के रूप में सूत्रबद्ध कीजिए। उस आहार का न्यूनतम मूल्य ज्ञात कीजिए, जिसमें इन दो भोज्यों का मिश्रण है और उसमें न्यूनतम पोषक तत्त्व हैं।
हल:
माना x मात्रक भोज्य पदार्थ F1 के तथा y मात्रक भोज्य पदार्थ F2 के हैं। तब गणितीय सूत्रीकरण करने पर
न्यूनतम z = 4x + 6y
St 3x + 6y ≥ 80 (लागत)
4x + 3y ≥ 100 (विटामिन A)
x, y ≥ 0 (विटामिन B)
अब आलेख बनाने पर सुसंगत क्षेत्र X AEDY प्राप्त होता है जो कि अपरिवद्ध है।
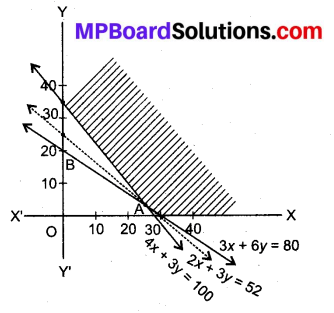
कोणीय बिन्दु A, E तथा D के निर्देशांक क्रमशः
\(\left(\frac{80}{3}, 0\right)\left(24, \frac{4}{3}\right)\) तथा \(\left(0, \frac{100}{3}\right)\) हैं।
अब z की गणना प्रत्येक कोणीय बिन्दु पर करने पर
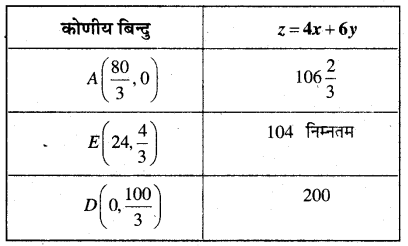
सारणी से स्पष्ट है कि – का न्यूनतम मान 104 है अतः न्यूनतम मूल्य = 104 रु०।
![]()
प्रश्न 10.
दो प्रकार के उर्वरक F1 और F2 हैं। F1 में 10% नाइट्रोजन और 6% फास्फोरिक अम्ल है। तथा F2 में 5% नाइट्रोजन तथा 10% फास्फोरिक अम्ल है। मिट्टी की स्थितियों का परीक्षण करने के पश्चात् एक किसान पाता है कि उसे अपनी फसल के लिए 14 kg नाइट्रोजन और 14 kg फास्फोरिक अम्ल की आवश्यकता है। यदि F1 की कीमत Rs. 6/kg और F2 की कीमत Rs. 5/kg है, प्रत्येक प्रकार का कितना उर्वरक उपयोग के लिए चाहिए ताकि न्यूनतम मूल्य पर वांछित पोषक तत्व मिल सके। न्यूनतम लागत क्या है?
हल:
माना मिश्रण में x kg F1 के तथा y kg F2 के मिश्रित है।
तब न्यूनतम z = 6x + 5y (लागत)

x, y ≥ 0 या न्यूनतम z = 6x +5y
St 2x + y ≥ 280
3x + 5y ≥ 2700
x, y ≥ 0
अब असमीकरणों का आलेख बनाने पर सुसंगत क्षेत्र Y ABCX प्राप्त है जो अपरिबद्ध है।
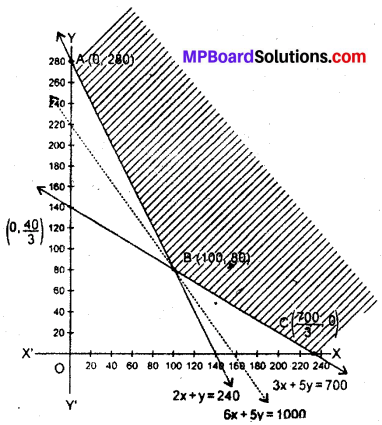
अब z की गणना प्रत्येक कोणीय बिन्दु पर करने पर कोणीय बिन्दु

इसलिए सारणी से z का निम्नतम मान 1000 है तथा बिन्दु B(100, 80) पर है, परन्तु सुसंगत क्षेत्र अपरिबद्ध है इसलिए असमीकरण 6x + 5y < 1000 लेने पर।
क्योंकि यहाँ पर कोई बिन्दु उभयनिष्ठ नहीं है। अतः उर्वरक F1 के 100 kg तथा उर्वरक F2 के 80 kg मात्रा है, और न्यूनतम मूल्य 1000 रु० है।
प्रश्न 11.
निम्नलिखित असमीकरण निकाय : 2x + y ≤ 10, x+3y ≤ 15, x, y ≥ 0 से निर्धारित सुसंगत क्षेत्र के कोणीय बिन्दु (0,0), (5,0), (3,4) और (0, 5) हैं। माना कि Z = px + qy, जहाँ p, q>0, p तथा q के लिए निम्नलिखित में कौन प्रतिबन्ध उचित है ताकि Z का अधिकतम (3, 4) और (0, 5) दोनों पर घटित होता है।
(A) p = q
(B) p = 2q
(C) p = 3q
(D) q = 3p
हल:
दिया है : Z = px + qy
बिन्दु (3, 4) पर, Z = 3p + 4q
बिन्दु (0, 5) पर, Z = 0 + 5q = 5q
∴ 3p + 4q=5q
⇒ 3p = 5q – 4q
⇒ 3p = q
अतः विकल्प (D) सही है।