In this article, we share MP Board Class 12th Maths Book Solutions Chapter 12 प्रायिकता Ex 12.1 Pdf, These solutions are solved by subject experts from the latest MP Board books.
MP Board Class 12th Maths Book Solutions Chapter 12 प्रायिकता Ex 12.1
ग्राफीय विधि से निम्न रैखिक प्रोग्रामन समस्याओं को हल कीजिए।
प्रश्न 1.
निम्न अवरोधों के अन्तर्गत Z = 3x + 4y का अधिकतमीकरण कीजिए-
x + y ≤ 4, x ≥ 0, y ≥ 0
हल:
अधिकतम
Z = 3x +4y
x + y ≤ 4
x ≥ 0, y ≥ 0
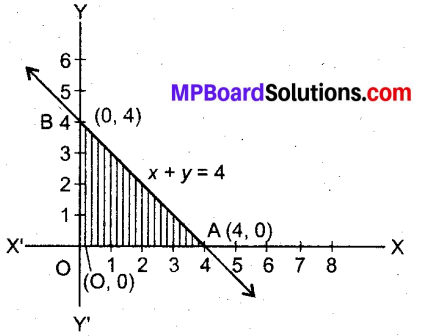
पहले सभी समस्याओं को समीकरण के रूप में लिखने पर
x + y = 4
x = 0 ….(ii)
y = 0 …(iii)
अब ग्राफ बनाने पर सुसंगत क्षेत्र OAB प्राप्त होता है।
Z के मान की गणना प्रत्येक कोणीय बिन्दु पर करने पर
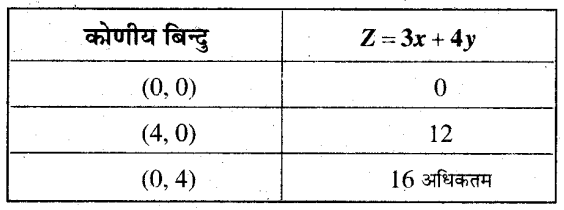
अतः Z का अधिकतम मान 16 बिन्दु (0, 4) पर है।
प्रश्न 2.
निम्न अवरोधों के अन्तर्गत Z = – 3x + 4y का न्यूनतमीकरण कीजिए-
x + 2y ≤ 8, 3x + 2y ≤ 12, x ≥ 0, y ≥ 0
हल:
सर्वप्रथम सभी असमीकरणों को समीकरण के रूप में लिखने पर
x + 2y = 8 ……(i)
3x + 2y = 12 ……(ii)
x = 0, y = 0 ……(iii)
अब आलेख बनाने पर सुसंगत क्षेत्र OABC प्राप्त होता है।
समी०
(i) व
(ii) को हल करने पर
x = 2, y = 3 प्राप्त होता है।
∵ रेखा
(i) व
(ii) बिन्दु (2, 3) पर मिलती हैं।
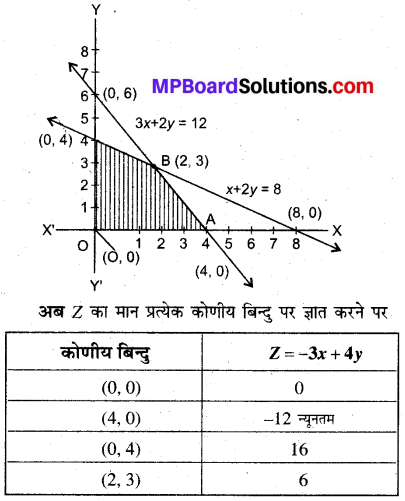
अतः बिन्दु (4,0) पर Z का मान न्यूनतम है।
![]()
प्रश्न 3:
निम्न अवरोधों के अन्तर्गत Z = 5x + 3y का अधिकतमीकरण कीजिए
3x + 5y ≤ 15, 5x + 2y ≤ 10, x ≥ 0, y ≥ 0
हल:
सर्वप्रथम असमीकरणों को समीकरणों के रूप में लिखने पर,
3x + 5y =15 ….(i)
5x + 2y=10 …(ii)
x = 0 …(iii)
y = 0 …(iv)
अब समीकरणों का ग्राफ बनाने पर सुसंगत क्षेत्र OABC प्राप्त होता है।
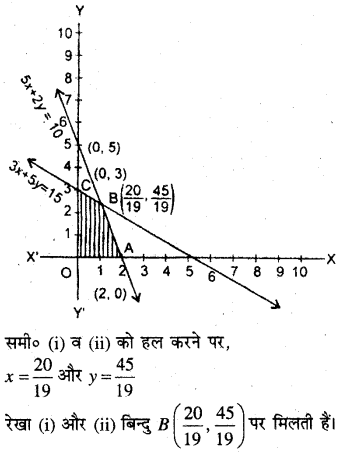
अब Z का मान प्रत्येक कोणीय बिन्दु पर ज्ञात करने पर
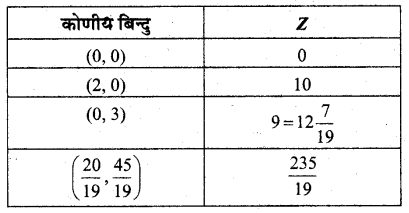
अतः बिन्दु Z का अधिकतम मान \(\frac{245}{19}\) है।
\(\left(\frac{20}{19}, \frac{45}{19}\right)\)
प्रश्न 4.
निम्न अवरोधों के अन्तर्गत z = 3x + 5y का न्यूनतमीकरण कीजिए-
x + 3y ≥ 3, x + y ≥ 2, x ≥ 0, y ≥ 0
हल:
सर्वप्रथम सभी असमीकरणों को समीकरणों के रूप में लिखने पर,
x + 3y =3 …(i)
x + y=2 …(ii)
x = 0 …(iii)
y = 0 …(iv)
अब ग्राफ बनाने पर सुसंगत क्षेत्र X ABCY प्राप्त होता हो।
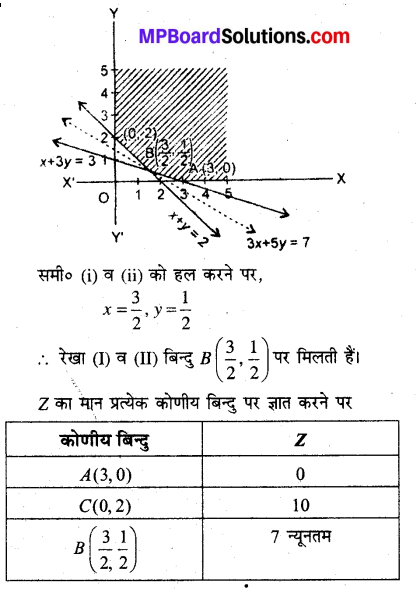
सारणी से Z का न्यूनतम मान बिन्दु B\(\left(\frac{3}{2}, \frac{1}{2}\right)\) पर 7 है।
प्रश्न 5.
निम्न अवरोधों के अन्तर्गत Z = 3x +2y का अधिकतमीकरण कीजिए-
x + 2y ≤ 10, 3x + y ≤ 15, x, y ≥ 0
हल:
सर्वप्रथम असमीकरणों को समीकरणों के रूप में लिखने पर
x + 2y = 10 …(i)
3x + y = 15 …(ii)
x = 0, y = 0 …(iii)
अब ग्राफ बनाने पर सुसंगत क्षेत्र OABC प्राप्त होता है।
समीकरण (i) व (ii) को हल करने पर,
x =4, y=3
ये रेखाएँ बिन्दु B(4,3) पर प्रतिच्छेदित करती हैं।
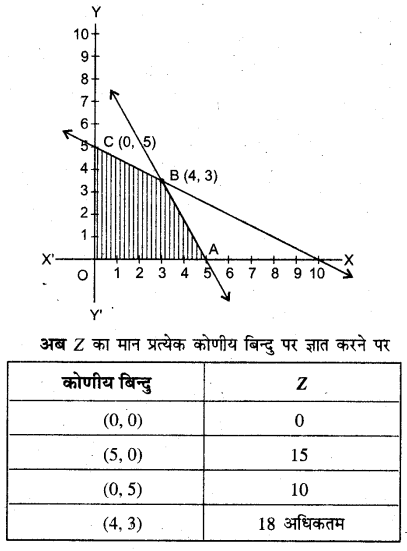
सारणी से बिन्दु (4,3) पर Z का अधिकतम मान 18 है।
![]()
प्रश्न 6.
निम्न अवरोधों के अन्तर्गत Z = x+2y का न्यूनतमीकरण कीजिए-
2x+y ≥ 3, x+2y ≥ 6, x,y ≥ 0
हल:
सर्वप्रथम असमीकरणों को समीकरणों के रूप में लिखने पर
2x + y =3 ….(i)
x + 2y =6 …(ii)
x = 0, y = 0 …(iii)
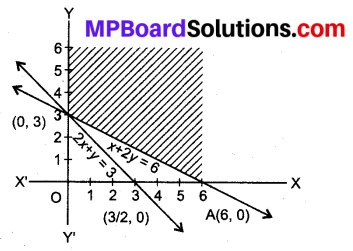
ग्राफ बनाने पर सुसंगत क्षेत्र XABY प्राप्त होता है।
z का मान प्रत्येक कोणीय बिन्दु पर ज्ञात करने पर
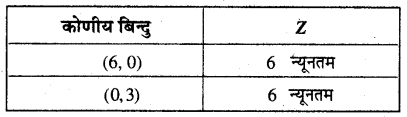
यहाँ z का प्रत्येक मान 6 है।।
अतः बिन्दुओं (6,0) और (0,3) को मिलाने वाली रेखा खण्ड पर स्थित सभी बिन्दुओं पर Z का न्यूनतम मान 6 है।
दिखाइए कि z का न्यूनतम मान दो बिन्दुओं से अधिक बिन्दुओं पर घटित होता है।
प्रश्न 7.
निम्न अवरोधों के अन्तर्गत Z = 5x + 10y का न्यूनतमीकरण तथा अधिकतमीकरण कीजिए-
x + 2y ≤ 120; x + y ≥ 60, x – 2y ≥ 0, x, y ≥ 0
हल:
दिया है : उद्देश्य फलन : Z = 5x + 10y
अवरोध : x + 2y ≤ 120, x + y ≥ 60
x – 2y ≥ 0, x, y ≥ 0
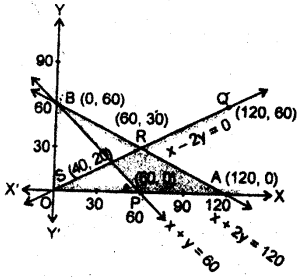
(1) x +2y ≤ 120 का आरेख,
रेखा x + 2y =120, बिन्दु A(120, 0) और बिन्दु B(0, 60) से होकर जाती है।
∴ x + 2y =120 का आरेख रेखा AB है।
x + 2y ≤ 120 में x = 0, y = 0 रखने पर,
0 ≤ 120, जो सत्य है।
∴ x +2y ≤ 120 के क्षेत्र में बिन्दु रेखा AB पर और उसके नीचे मूल बिन्दु की ओर स्थित है।
(2) x + y ≥ 60 का आरेख
रेखा x + y = 60, बिन्दु P(60, 0), B(0, 60) से होकर जाती है।
∴ x + y = 60 का आरेख रेखा PB है।
x + y ≥ 60 में x = 0, y = 0 रखने पर, 0 ≥ 60 जो सत्य नहीं है।
⇒ x +y ≥ 60 क्षेत्र के बिन्दु रेखा PB पर और उसके ऊपर होते हैं।
(3) x – 2y ≥ 0 का आरेख
रेखा x – 2y = 0 मूल बिन्दु 0 और Q(120, 60) से होकर जाती है।
∴ x – 2y ≥ 0 का आरेख रेखा OQ है।
x – 2y ≥ 0 में x =1, y = 0 रखने पर 1 ≥ 0 जो सत्य है।
⇒ (1, 0) इस क्षेत्र में स्थित है। x – 2y ≤ 0 क्षेत्र के बिन्दु रेखा OQ पर और इसके नीचे (1, 0) की ओर हैं।
(4) x ≥ 0 क्षेत्र के बिन्दु y- अक्ष पर और y- अक्ष के दायीं ओर है।
(5) y ≥ 0 क्षेत्र के बिन्दु x- अक्ष पर और इसके ऊपर हैं।
इस समस्या का सुसंगत क्षेत्र PSRA है।
जबकि बिन्दु S(40, 20) PB: x + y = 60 और OQ: x – 2y = 0 का प्रतिच्छेद बिन्दु है।
और R(60, 30), AB: x + 2y =120 और x – 2y = 0 का प्रतिच्छेद बिन्दु है।
उद्देश्य फलन : Z = 5x + 10y
बिन्दु A(120, 0) पर,
Z = 5 x 120 + 10 x 0 = 600
बिन्दु R(60, 30) पर,
Z = 5 x 60 + 10 x 30
= 300 + 300 = 600
बिन्दु S(40, 20) पर,
Z = 5 x 40 + 10x 20
= 200 + 200 = 400
बिन्दु P(60, 0) पर,
Z = 5 x 60 + 10 x 0
= 300 + 0 = 300
⇒ Z का न्यूनतम मान P(60, 0) पर 300 है।
और Z का अधिकतम मान RA के सभी बिन्दुओं पर 600 है।
![]()
प्रश्न 8.
निम्न अवरोधों के अन्तर्गत Z = x + 2y का न्यूनतमीकरण तथा अधिकतमीकरण कीजिए-
x + 2y ≥ 100, 2x – y ≤ 0, 2x +y ≤ 200, x, y ≥ 0
हल:
सर्वप्रथम असमीकरणों को समीकरणों के रूप में लिखने पर
x + 2y = 100
2x – y = 0
2x + y = 200
x = 0 y=0
ग्राफ बनाने पर सुसंगत क्षेत्र BEDC प्राप्त होता है।
समी० 2x + y = 200 तथा 2x – y = 0 को हल करने पर x = 50, y = 100 प्राप्त होता है।
⇒ D(50,100)
पुनः समी० x + 2y = 100 तथा 2x – y = 0 को हल करने पर, x = 20, y = 40 प्राप्त होता है।
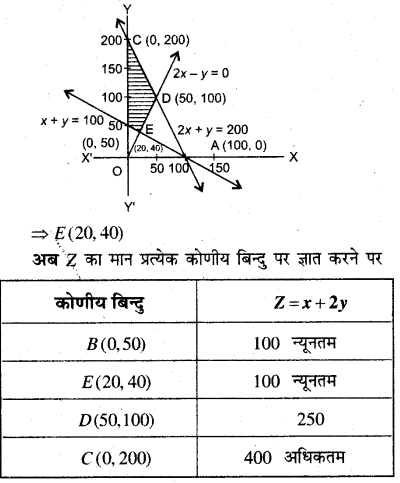
अतः Z का न्यूनतम मान 100 है तथा अधिकतम मान बिन्दु (0, 200) पर 400 है।
प्रश्न 9.
निम्न अवरोधों के अन्तर्गत Z = – x + 2y का अधिकतमीकरण कीजिए-
x ≥ 3, x + y ≥ 5, x + 2y ≥ 6, y ≥ 0
हल:
दिया है : उद्देश्य फलन :
Z = – x + 2y
(1) x + y ≥ 5 का आरेख
रेखा x + y =5, बिन्दु A(5, 0) और B(0, 5) से होकर जाती है।
∴ x + y =5 का आरेख रेखा AB है।
x + y ≥ 5 में x =0, y=0 रखने पर,
0 ≥ 5 जो सत्य नहीं है।
∴ x + y ≥ 5 क्षेत्र के बिन्दु रेखा AB पर और उसके ऊपर है।
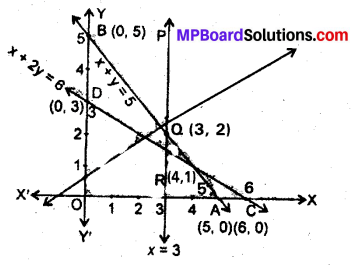
(2) x + 2y ≥ 6 का आरेख
रेखा x + 2y = 6, बिन्दु C (6, 0) और D (0, 3) से होकर जाती है।
∴ x + 2y = 6 रेखा का आरेख रेखा CD है।
⇒ x + 2y ≥ 6 में x =0, y = 0 रखने पर, 0 ≤ 6 जो सत्य नहीं है।
∴ x + 2y ≥ 6 का क्षेत्र के बिन्दु CD पर या उसके ऊपर है।
(3) x ≥ 3 क्षेत्र के बिन्दु रेखा PQ: x =3 पर या उसके दायीं ओर है।
(4) y ≥ 0 क्षेत्र के बिन्दु x- अक्ष पर और उसके ऊपर होते हैं। समस्या का सुसंगत क्षेत्र PQRCX है।
बिन्दु रेखा PQ =3 और AB: x + y =5 का प्रतिच्छेदन बिन्दु Q के निर्देशांक (3, 2) है।
बिन्दु R रेखा CD: x + 2y = 6 और AB: x + y =5 का प्रतिच्छेदन बिन्दु (4, 1) है।
उद्देश्य फलन : Z = – x + 2y
अब, बिन्दु Q (3, 2) पर,
Z = – 3 + 2 x 2 = – 3 + 4 =1
बिन्दु R(4, 1) पर,
Z = – 4 + 2 x 1 = – 4 + 2 = – 2
बिन्दु C(6, 0) पर,
Z = – 6 + 0 = – 6
⇒ z का अधिकतम मान 1 है परन्तु सुसंगत क्षेत्र अपरिबद्ध है तो – x + 2y > 1 क्षेत्र पर विचार करें। .
– x + 2y > 1 तथा सुसंगत क्षेत्र में अनेकों बिन्दु उभयनिष्ठ है।
अतः Zका कोई अधिकतम मान नहीं है।
![]()
प्रश्न 10.
निम्न अवरोधों के अन्तर्गत Z = x + y का अधिकतमीकरण कीजिए-
x – y ≤ – 1, – x + y ≤ 0, x, y ≥ 0
हल:
(i) x – y ≤ -1 का क्षेत्र
रेखा x – y = – 1 बिन्दु A(-1,0), B(0, 1) से होकर जाती है, जो AB आरेख है।
x – y ≤ – 1 में x =0, y = 0 रखने पर,
0 ≤ -1 जो सत्य नहीं है।
⇒ x – y ≤ – 1 के क्षेत्र बिन्दु रेखा AB पर और उसके ऊपर है।
(ii) – x + y ≤ का क्षेत्र
रेखा – x + y = 0, मूल बिन्दु O और C(1, 1) से होकर जाती है।
– x + y ≤ 0 में x = 1, y = 0 रखने पर, -1 ≤ 0 जो सत्य है।
⇒ – x + y ≤ 0 के क्षेत्र बिन्दु OC पर या उसके नीचे (1,0) ओर हैं।
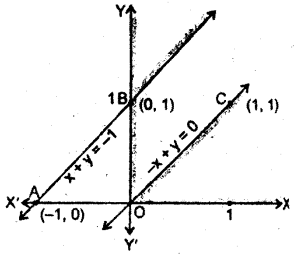
(iii) x ≥ 0 क्षेत्र के बिन्दु y- अक्ष पर और -अक्ष के दायीं ओर हैं।
(iv) y ≥ 0 क्षेत्र के बिन्दु x- अक्ष पर और x- अक्ष के ऊपर स्थित हैं।
इस समस्या का कोई सुसंगत क्षेत्र नहीं है।
अतः Z का अधिकतम मान नहीं है।