MP Board Class 12th Maths Important Questions Chapter 9 Differential Equations
Differential Equations Important Questions
Differential Equations Objective Type Questions
Question 1.
Choose the correct answer:
Question 1.
Degree of the differential equation
\(\frac { d^{ 2 }y }{ d^{ 2 }x } \) + x2 \(\frac{dy}{dx}\) = ex is:
(a) 1
(b) 2
(c) 3
(d) does not exist
Answer:
(c) 3
Question 2.
Solution of differential equation (1 + x) y dx + (1 – y) xdy = 0 is:
(a) log xy + x + y = c
(b) logxy + x – y = c
(c) log xy – x – y = c
(d) log xy – x + y = c.
Answer:
(b) logxy + x – y = c
![]()
Question 3.
The differential equation of all circles which passes through the origin whose center lie on the A – axis is:
(a) x2 = y2+ xy \(\frac{dy}{dx}\)
(b) x2 = y2 + 3xy \(\frac{dy}{dx}\)
(c) y2 = x2 + 2xy \(\frac{dy}{dx}\)
(d) y2 = x2 – 2xy \(\frac{dy}{dx}\)
Answer:
(c) y2 = x2 + 2xy \(\frac{dy}{dx}\)
Question 4.
Solution of the differential equation \(\frac{dy}{dx}\) + y = ex, y(o) = 0 is:
(a) y = e-x(x – 1)
(b) y = xex
(c) y = xe-x + 1
(d) y = xe-x
Answer:
(d) y = xe-x
Question 5.
The straight line which satisfies the differential equation \(\frac{dy}{dx}\) = m and cuts an intercept 3 on the positive y – axis is:
(a) y = mx + c
(b) y = mx +3
(c) y = mx – 3
(d) y = – mx + 3.
Answer:
(b) y = mx +3
Question 2.
Fill in the blanks:
- The corresponding differential equation of the equation x2 + y2 = a2 is ……………………………
- The differential equation of the curve y = ecx is …………………….. where c is arbitrary constant.
- The integration factor of the linear differential equation \(\frac{dy}{dx}\) + Py = Q is …………………………….
- In the linear differential equation \(\frac{dy}{dx}\) + Py = Q. P and Q are …………………………….
- The form of differential equation (x + y + 1) dy = dx is ……………………………
- Solution of the differential equation e-x+y \(\frac{dy}{dx}\) = 1 is ……………………………
Answer:
- y \(\frac{dy}{dx}\) + x = 0
- x \(\frac{dy}{dx}\) = y log y
- e∫pdx
- constant
- linear differential equation
- e-y = e-x + c
![]()
Question 3.
Write True/False:
- Order of differential equation y = x \((\frac { dy }{ dx } )^{ 2 }\) + \(\frac { d^{ 2 }y }{ dx^{ 2 } } \) is 2.
- Degree of differential equation \((\frac { d^{ 3 }y }{ dx^{ 3 } } )^{ 4/5 }\) – 2 \((\frac { dy }{ dx } )\) \((\frac { d^{ 2 }y }{ dx^{ 2 } } )^{ 2 }\) = 0 is 5.
- The integration factor of linear differential equation x \(\frac{dy}{dx}\) – y = 2x2 is e-x
- Solution of differential equation dy = sin xdx is y + cos x – c = 0.
- Solution of differential equation ydx + (x – y3) dy = 0 is xy = \(\frac { y^{ 4 } }{ 4 } \) + c.
Answer:
- True
- False
- False
- True
- True
Question 4.
Write the answer is one word/sentence:
- Write the integration factor of differential equation (1 + y2) + (2xy – cot y) \(\frac{dy}{dx}\) = 0.
- Find the solution of the differential equation (1 + x2) dy = (1 + y2) dx.
- Find the sum of order and degree of the differential equation y = x \((\frac { dy }{ dx } )^{ 3 }\) + \(\frac { d^{ 2 }y }{ dx^{ 2 } } \)
- Find the integration factor of the differential equation x logx \(\frac{dy}{dx}\) + y = 2 log x
- Find he solution of the differential equation \(\frac{dy}{dx}\) + \(\frac{1}{x}\) = \(\frac { e^{ y } }{ x^{ 2 } } \)
Answer:
- 1 + y2
- x – y = c(1 + xy)
- 3
- log x
- 2xe-y = cx2 + 1.
Differential Equations Very Short Answer Type Questions
Question 1.
Find the order and degree of \(\frac{dy}{dx}\) + y = e-x?
Answer:
1, 1
Question 2.
Find the degree and order of \((\frac { dy }{ dx } )^{ 3 }\) = \(\sqrt { 1+(\frac { dy }{ dx } )^{ 2 } } \)?
Answer:
1, 6
Question 3.
Find the degree and order of \(\frac { d^{ 2 }y }{ dx^{ 2 } } \) + \(\sqrt { 1+(\frac { dy }{ dx } )^{ 3 } } \) = 0?
Answer:
2, 2
![]()
Question 4.
Find the differential equation corresponding to equation of circle x2 + y2 = a2?
Answer:
y \(\frac{dy}{dx}\) + x = 0
Question 5.
Find the differential equation of line y = mx + c?
Answer:
\(\frac{dy}{dx}\) = m
Question 6.
Solve the differential equation \(\frac{dy}{dx}\) = 4y?
Answer:
y = c.e4x
Question 7.
Solve the differential equation x2 \(\frac{dy}{dx}\) = 2?
Answer:
y = c – \(\frac{2}{x}\)
![]()
Question 8.
Find the solution of differential equation dy = sinxdx?
Answer:
y + cos x = c
Question 9.
Find the solution of differential equation \(\frac{dy}{dx}\) + Px = Q?
Answer:
xe∫pdy. dy + c
Question 10.
Solve the differential equation (1 – y2) \(\frac{dy}{dx}\) + yx = ay?
Answer:
\(\frac { 1 }{ \sqrt { 1-y^{ 2 } } } \)
Differential Equations Short Answer Type Questions
Question 1.
Solve the differential equation xlog xdy – ydx = 0?
Solution:
x log x dy – ydx = 0 (given)
⇒ x log x = ydx
⇒ \(\frac{1}{y}\) \(\frac{dy}{dx}\) = \(\frac{1}{xlogx}\) dx
⇒ ∫\(\frac{1}{y}\) dy = ∫\(\frac{1}{xlogx}\) dx
⇒ log y = ∫\(\frac{1}{t}\) dt , (let log x = t ⇒ \(\frac{1}{x}\) dx = dt)
⇒ log y = log t + log c
⇒ log y = log log x + log c
Question 2.
Solve the differential equation \(\frac{dy}{dx}\) = ex-y + x.e-y?
Solution:
\(\frac{dy}{dx}\) = ex-y + x.e-y (given)
⇒ \(\frac{dy}{dx}\) = e-y (ex + x)
⇒ eydy = (ex + x) dx
Integrating both sides,
∫eydy = ∫(ex + x) dx
ey = ex + \(\frac { x^{ 2 } }{ 2 } \) + c
![]()
Question 3.
Prove that solution of y = 4sin 3x is \(\frac { d^{ 2 }y }{ dx^{ 2 } } \) + 9y = 0?
Solution:
y = 4 sin 3x (given)
Differentiating with respect to x,
∴\(\frac{dy}{dx}\) = 12 cos 3x
Again differentiating with respect to x,
\(\frac { d^{ 2 }y }{ dx^{ 2 } } \) = – 36 sin 3x = – 9 × 4 sin 3x
⇒ \(\frac { d^{ 2 }y }{ dx^{ 2 } } \) = -9y, [from eqn.(1)]
⇒ \(\frac { d^{ 2 }y }{ dx^{ 2 } } \) + 9y = 0. Proved.
Question 4.
Solve the differential equation \(\frac{dy}{dx}\) = sec2 x + 2x?
Solution:
\(\frac{dy}{dx}\) = sec x (sec x + tan x) (given)
⇒ dy = (sec2 x + sec x tan x ) dx
⇒ ∫dy = ∫sec2 dx + ∫sec x tan x dx
∴y = tan x + sec x + c.
Question 5.
Solve the differential equation \(\frac{dy}{dx}\) = sec2 x + 3x2?
Solution:
\(\frac{dy}{dx}\) = sec2 x + 3x2 (given)
⇒ dy = (sec2 x + 3x2) dx
⇒ ∫dy = ∫sec2 xdx + 3∫x2 dx
⇒ y = tan x + \(\frac { 3x^{ 3 } }{ 3 } \) + c
⇒ y = tan x + x3 + c.
Question 6.
Solve the differential equation \(\frac{dy}{dx}\) = sec2 x + 2x?
Solution:
Solve as Q.No . 5
![]()
Question 7.
Solve the differential equation \(\frac{dy}{dx}\) = (3x2 x + 2)?
Solution:
\(\frac{dy}{dx}\) = (3x2 + 2) (given)
⇒ dy = (3x2 + 2) dx
⇒ ∫dy = ∫(3x2 + 2) dx
⇒ y = 3 × \(\frac { x^{ 3 } }{ 3 } \) + 2x = c = x2 + 2x + c.
Question 8.
Solve the differential equation x2 \(\frac{dy}{dx}\) = 2?
Solution:
x2 \(\frac{dy}{dx}\) = 2 (given)
⇒ dy = 2.x-2 dx
⇒ ∫dy = 2∫x-2 dx
⇒ y = 2 \((\frac { -1 }{ x } )\) + c
Question 9.
Solve the differential equation \(\frac{dy}{dx}\) = x3 + sin 4x?
Solution:
\(\frac{dy}{dx}\) = x3 + sin 4x (given)
⇒ dy = (x3 + sin 4x) dx
⇒ ∫dy = ∫x3 dx + ∫sin 4x dx
⇒ y = \(\frac { x^{ 4 } }{ 4 } \) + \((\frac { -cos4x }{ 4 } )\) + c
⇒ y = \(\frac { x^{ 4 } }{ 4 } \) – \(\frac { -cos4x }{ 4 } \) + c
Question 10.
Solve the differential equation \(\frac{dy}{dx}\) + 2x = e3x?
Solution:
\(\frac{dy}{dx}\) + 2x = e3x (given)
⇒ \(\frac{dy}{dx}\) = e3x – 2x
⇒ dy = (e3x – 2x) dx
⇒ ∫dy = ∫3x dx – 2∫x dx
⇒ y = e3x. \(\frac{1}{3}\) e3x – x2 + c
![]()
Question 11.
Solve the differential equation \(\frac{dy}{dx}\) = \(\frac { cos^{ 2 }y }{ sin^{ 2 }x } \) (given)
⇒ \(\frac { 1 }{ cos^{ 2 }y } \) dy = \(\frac { 1 }{ sin^{ 2 }x } \) dx
⇒ sec2 ydy = cosec2 xdx
⇒ ∫sec2 ydy = ∫cosec2 xdx
⇒ tan y = – cot x + c
Question 12.
Solve the differential equation (x2 + 1) \(\frac{dy}{dx}\) = 1?
Solution:

Question 13.
Solve the differential equation \(\frac{dy}{dx}\) = sin x sin y?
Solution:
\(\frac{dy}{dx}\) = sin x sin y
⇒ cosec y dy = sin x dx
On integrating,
– loge (cosec y + cot y) = – cos x + c
⇒ cos x – loge (cosec y + cot y) = c
Question 14.
Solve the differential equation \(\frac{dy}{dx}\) = y sin x?
Solution:
\(\frac{dy}{dx}\) = y sin x
⇒ \(\frac{1}{y}\) \(\frac{dy}{dx}\) = sin x
⇒ ∫\(\frac{1}{y}\) dy = ∫sin x dx
⇒ log y = – cos x + c
![]()
Question 15.
Solve the differential equation \(\frac{dy}{dx}\) = x cos x?
Solution:
Given:
\(\frac{dy}{dx}\) = x cos x
⇒ dy = x cos x dx
⇒ ∫dy = ∫x cos x dx
⇒ y = xsin x – ∫1. sin x dx + c
⇒ y = xsin x + cos x + c
Question 16.
Solve the differential equation \(\frac{dy}{dx}\) = x3 + sin 4x?
Solution:
\(\frac{dy}{dx}\) = x3 + sin 4x (given)
⇒ dy = (x3 + sin 4x) dx
⇒ ∫dy = ∫x3 dx + ∫sin 4x dx
⇒ y = \(\frac { x^{ 4 } }{ 4 } \) + \((\frac { -cos4x }{ 4 } )\) + c
⇒ y = \(\frac { x^{ 4 } }{ 4 } \) – \(\frac { cos4x }{ 4 } \) + c
Question 17.
Solve the differential equation \(\frac{dy}{dx}\) + 2x = e3x?
Solution:
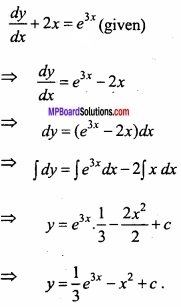
Question 18.
Solve the differential equation \(\frac{dy}{dx}\) = \(\frac { cos^{ 2 }y }{ sin^{ 2 }x } \)?
Solution:
\(\frac{dy}{dx}\) = \(\frac { cos^{ 2 }y }{ sin^{ 2 }x } \)
⇒ \(\frac { 1 }{ cos^{ 2 }y } \) dy = \(\frac { 1 }{ sin^{ 2 }x } \) dx
⇒ sec2 ydy = cosec2 xdx
∴∫sec2 ydy = ∫cosec2 xdx + c
tan y = – cotx + c
Question 19.
Solve the differential equation \(\frac{dy}{dx}\) = 1 – x + y – xy?
Solution:
\(\frac{dy}{dx}\) = 1 – x + y – xy (given)
⇒ \(\frac{dy}{dx}\) = (1 – x) + y (1 – x)
⇒ \(\frac{dy}{dx}\) = (1 – x) (1 + y)
⇒ \(\frac{dy}{1+y}\) = (1 – x) dx
⇒ ∫\(\frac{dy}{1+y}\) = ∫(1 – x) dx
⇒ loge (1 + y) = x – \(\frac { x^{ 2 } }{ 2 } \) + c
![]()
Question 20.
Solve the differential equation \(\frac{dy}{dx}\) = (1 + x) (1 + y2)?
Solution:
\(\frac{dy}{dx}\) = (1 + x) (1 + y2) (given)
⇒ \(\frac { 1 }{ 1+y^{ 2 } } \) dy = (1 + x) dx
Integrating both sides,
⇒ tan-1y = x + \(\frac { x^{ 2 } }{ 2 } \) + c.
Question 21.
Solve the differential equation:
\(\frac{dy}{dx}\) = cot2 x?
Solution:
\(\frac{dy}{dx}\) = cot2 x (given)
⇒ dy = cot2 x
⇒ ∫dy = ∫cot2 x dx
⇒ y = ∫(cosec2 x – 1) dx
⇒ y = – cot x – x + c
Differential Equations Long Answer Type Questions – II
Question 1.
(A) Solve the differential equation \(\frac{dy}{dx}\) + y tan x = sec x?
Solution:
\(\frac{dy}{dx}\) + y tan x = sec x (given)
Comparing the equation with \(\frac{dy}{dx}\) + Py = Q,
P = tan x, Q = sec x
∴L.F. = e∫P dx = e∫tanx dx = elog secx
⇒ L.F. = sec x
Applying formula
y × (1.F.) = ∫Q × (I.F.) dx + c
⇒ ∫sec2 x dx + c
⇒ y sec x = tan x + c
(B) Solve the differential equation \(\frac{dy}{dx}\) + y tan x = sin x?
Solution:
Solve as Q.No.1 (A).
![]()
Question 2.
Solve the differential equation \(\frac{dy}{dx}\) = \(\frac { \sqrt { 1-y^{ 2 } } }{ \sqrt { 1-x^{ 2 } } } \)?
Solution:

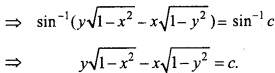
Question 3.
Solve the differential equation 3x2 dy = (3xy + y2)dx?
Solution:
3x2 dy = (3xy + y2) dx (given)
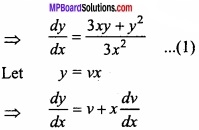
Putting in eqn. (1),
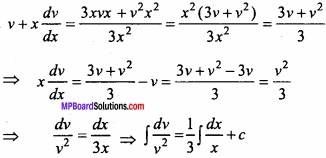
⇒ – \(\frac{1}{v}\) = \(\frac{1}{3}\) log x + c
∴- \(\frac{1}{y}\) = \(\frac{1}{3}\) log x + c
Question 4.
Solve the differential equation (1 + x2) \(\frac{dy}{dx}\) + 2xy = 4x2?
Solution:

The required solution will be:
![]()

Question 5.
Solve the differential equation (1 + x2) \(\frac{dy}{dx}\) + 2xy = cos x?
Solution:
(1 + x2) \(\frac{dy}{dx}\) + 2xy = cos x (given)
⇒ \(\frac{dy}{dx}\) + \(\frac { 2x }{ (1+x^{ 2 }) } \)
Comparing with \(\frac{dy}{dx}\) + Py = Q,
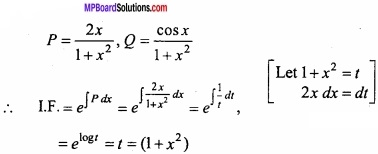
The required solution of eqn. (1) is:

Question 6.
Marginal cost price of making anything is given by equation c'(x) = \(\frac{dc}{dx}\) = 2 + 0.15 x. Find the total cost price c(x) for making it? [Given c (0) = 100]
Solution:
c'(x) = \(\frac{dc}{dx}\) = 2 + 0.15 x (given)
Integrating both sides
∫c'(x) dx = ∫ (2 + 0.15 x) dx
c(x) = 2x + 0.15 \(\frac { x^{ 2 } }{ 2 } \) + A …………. (1)
If x = 0
c(0) = 2 × 0 + \(\frac { 0.15 }{ 2 } \) × 02 + A
⇒ c(0) = A
∴ A = 100, [∵ c(0) = 100]
Putting in eqn. (1),
c(x) = 2x + 0.075 x2 + 100
Question 7.
Solve the differential equation x\(\sqrt { 1+y^{ 2 } } \) dx + y \(\sqrt { 1+x^{ 2 } } \) dy = 0?
Solution:
x\(\sqrt { 1+y^{ 2 } } \) dx + y \(\sqrt { 1+x^{ 2 } } \) dy = 0 (given)
⇒ \(\frac { y }{ \sqrt { 1+y^{ 2 } } } \) dy = – \(\frac { x }{ \sqrt { 1+x^{ 2 } } } \) dx
Integrating both sides,

Question 8.
Solve the differential equation (x + y + 1) \(\frac{dy}{dx}\) = 1?
Solution:
(x + y + 1) \(\frac{dy}{dx}\) = 1 (given)
⇒ \(\frac{dy}{dx}\) = x + y + 1
⇒ \(\frac{dy}{dx}\) – x = y + 1
Comparing the equation with \(\frac{dx}{dy}\) + Px = Q?
P = – 1 and Q = y + 1
∴I.F. = e∫pdy = e-∫dy = e-y
Here the required solution is:
⇒ x.e∫pdy = ∫e∫pdy. Qdy
⇒ x.e-y = ∫e-y (y + 1) dy + c
⇒ x.e-y = – (y + 1)e-y – ∫1(-e-y) dy + c
⇒ x = -(y + 1) -1 + cey
x + y + 2 = cey
Question 9.
Solve the differential equation sec2x tany dx + sec2 y tan xdy = 0?
Solution:
sec2x tany dx + sec2 y tan xdy = 0 (given)

⇒ log y = – log x + log c
⇒ log x + log y = log c
⇒ log xy = log c
⇒ xy = c
Question 10.
Solve the differential equation \(\frac{dy}{dx}\) = y tanx – 2 sin x?
Solution:
\(\frac{dy}{dx}\) – y tanx = – 2 sin x (given)
Comparing with \(\frac{dy}{dx}\) + Py = Q,
P = – tan x, Q = – 2 sin x
L.F. = e∫pdx = e-∫tanxdx
= elogecosx = cos x
The required solution is:
y.(I.F.) = ∫Q.I.F. dx + c
⇒ ycos x = -2∫sin x cos x dx + c
⇒ ycosx = -∫sin2xdx + c
⇒ ycosx = \(\frac { cos2x }{ 2 } \) + c.
![]()
Question 11.
Solve the differential equation \(\frac{dy}{dx}\) + 2y = 4x?
Solution:
Solution:
\(\frac{dy}{dx}\) + 2y = 4x
Comparing with \(\frac{dy}{dx}\) + Py = Q,
P = 2, Q = 4x
I.F. = e∫pdx = e∫2dx = e2x
The required differential solution is:
y. (I.F) = ∫Q.I.F. dx + c
⇒ ye2x = ∫4xe2x dx + c
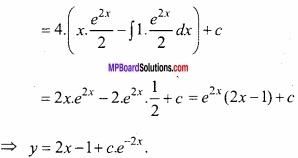
Question 12.
Solve the differential equation cos2 x \(\frac{dy}{dx}\) + y = 2?
Solution:
cos2 x \(\frac{dy}{dx}\) + y = 2
⇒ \(\frac{dy}{dx}\) + sec2 x. y = 2 sec2 x
Comparing with \(\frac{dy}{dx}\) + P y = Q,
P = sec2 x, Q = 2 sec2 x
I.F. = e∫sec2 xdx
Required solution is:
y. (I.F) = ∫Q.I.F. dx + c
⇒ y.etanx = ∫2 sec2 x. etanx dx + c
⇒ y.etanx = 2.∫et dt + c, (Let tan x = t ⇒ sec2 xdx = dt)
= 2.etanx + c
⇒ etanx (y – 2) = c.
![]()
Question 13.
Solve the differential equation cos x \(\frac{dy}{dx}\) + y = sin x?
Solution:
cos x \(\frac{dy}{dx}\) + y = sin x
⇒ \(\frac{dy}{dx}\) + sec x.y = tan x
Comparing with \(\frac{dy}{dx}\) + Py = Q,
P = secx, Q = tanx
L.F. = e∫secxdx
= eloge(sec x + tan x) dx + c
Required Solution y.I.F. = ∫Q.I.F. dx + c
⇒ y. (sec x + tan x) = ∫tan x.(sec x + tan x) dx + c
= ∫sec x tan x dx + ∫tan2 xdx + c
= sec x + ∫(sec2 x – 1) dx = sec x + tan x = – x + c.
Question 14.
Solve the differential equation (1 + y2) dx = (tan-1 y – x) dy? (CBSE 2015)
Solution:
(1 + y2) dx = (tan-1 y – x) dy (given)
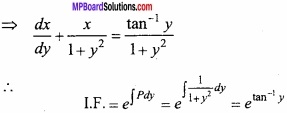
The required solution is:

Question 15.
Solve the differential equation (1 + y2) + ( x – etan-1 y) \(\frac{dy}{dx}\) = 0? (CBSE 2016)
Solution:
The given equation is:

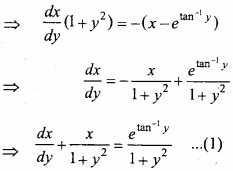
Comparing with \(\frac{dx}{dy}\) + Px = Q,

The required solution is:
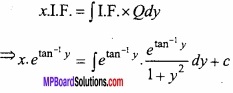
Put tan-1 y = t,

Question 16.
Solve the differential equation (1 + x2) \(\frac{dy}{dx}\) + 2xy = \(\frac { x }{ 1+x^{ 2 } } \). Where, y = 0 and x = 1? (NCERT)
Solution:

Comparing with \(\frac{dy}{dx}\) + Py = Q,

The required solution is:

y = 0 and x = 1 (given)
0 (1 + 1)2 = tan-1 1 + c
⇒ 0 = \(\frac { \pi }{ 4 } \) + c
⇒ c = – \(\frac { \pi }{ 4 } \)
From eqn. (2),
y. (1 + x2) = tan-1 x – \(\frac { \pi }{ 4 } \).
![]()
Question 17.
Solve the differential equation \(\frac{dy}{dx}\) + y cot x = 4x cosec x. Given: y = 0 and x = \(\frac { \pi }{ 2 } \)? (NCERT; CBSE, 2012)
Solution:
\(\frac{dy}{dx}\) + y cot x = 4x cosec x (given)
Comparing with eqn. (1) \(\frac{dy}{dx}\) + Py = Q,
P = cot x, Q = 4x cosec x
I.F. = e∫pdx
= e∫cot xdx = elog(sinx) = sin x
The required solution is:
y.I.F = ∫I.F. × Qdx
⇒ y.sin x = ∫sin x × 4x cosec x dx
⇒ y sin x = 4∫\(\frac { xsinx }{ sinx } \) dx
⇒ y sin x = 4∫xdx
⇒ ysin x = \(\frac { 4x^{ 2 } }{ 2 } \) + c
⇒ y sin x = 2x2 + c
When x = \(\frac { \pi }{ 2 } \) and y = 0,
0 (sin \(\frac { \pi }{ 2 } \)) = 2 ( \(\frac { \pi }{ 2 } \) ) 2 + c
⇒ 0 = \(\frac { 2\pi ^{ 2 } }{ 4 } \) + c
∴ c = \(\frac { -\pi ^{ 2 } }{ 2 } \)
Putting in eqn. (1),
y. sin x = 2x2 – \(\frac { -\pi ^{ 2 } }{ 2 } \).