MP Board Class 12th Maths Important Questions Chapter 8 समाकलनों के अनुप्रयोग

MP Board Class 12th Maths Important Questions Chapter 8 समाकलनों के अनुप्रयोग

समाकलनों के अनुप्रयोग Important Questions

समाकलनों के अनुप्रयोग वस्तुनिष्ठ प्रश्न

प्रश्न 1.
सही विकल्प चुनकर लिखिए –

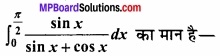
(a) π
(b) \(\frac { \pi }{ 2 } \)
(c) \(\frac { \pi }{ 4 } \)
(d) \(\frac { -\pi }{ 4 } \)
उत्तर:
(c) \(\frac { \pi }{ 4 } \)

प्रश्न 2.
दीर्घवृत्त \(\frac { x^{ 2 } }{ y^{ 2 } } \) + \(\frac { y^{ 2 } }{ b^{ 2 } } \) = 1 के प्रथम चतुर्थांश का क्षेत्रफल होगा –
(a) πab
(b) \(\frac{1}{2}\) πab
(c) \(\frac{1}{4}\) πab
(d) \(\frac{1}{8}\) πab
उत्तर:
(c) \(\frac{1}{4}\) πab

प्रश्न 3.
\(\int_{2}^{4} x^{3} d x\) का मान है –
(a) 60
(b) 50
(c) 70
(d) 256.
उत्तर:
(a) 60

प्रश्न 4.
\(\int_{0}^{2 a} f(x) d x=0\) होगा यदि –
(a) f (2a – x) = f (x)
(b) f (2a – x) = – f (x)
(c) f (x) सम फलन हो
(d) f (x) विषम फलन हो
उत्तर:
(b) f (2a – x) = – f (x)

प्रश्न 5.
\(\int_{0}^{2 \pi}|\sin x| d x\) बराबर है –
(a) 2
(b) \(\sqrt{3}\)
(c) 4
(d) 0.
उत्तर:
(c) 4

प्रश्न 2.
रिक्त स्थानों की पूर्ति कीजिये –

उत्तर:

1. 0
2. 0
3. 17
4. 0
5. \(\frac { \pi }{ 4 } \)
6. πa²

प्रश्न 3.
निम्न कथनों में सत्य/असत्य बताइए –

उत्तर:

1. सत्य
2. सत्य
3. असत्य
4. असत्य
5. सत्य
6. सत्य

प्रश्न 4.
सही जोड़ी बनाइए –

उत्तर:

1. (b)
2. (a)
3. (d)
4. (c)
5. (f)
6. (e)

प्रश्न 5.
एक शब्द/वाक्य में उत्तर दीजिए –

उत्तर:

1. 1
2. \(\frac { -\pi }{ 2 } \) log 2
3. 2
4. \(\frac { \pi }{ 2 } \)
5. -4
6. \(\frac { \pi }{ 12 } \)

समाकलनों के अनुप्रयोग दीर्घ उत्तरीय प्रश्न – II

प्रश्न 1.
दो वक्रों x² = 8y तथा y² = 8x के बीच घिरे क्षेत्र का क्षेत्रफल समाकल विधि से ज्ञात कीजिए।
हल:
दिये हुए परवलयों के समीकरण हैं:
x² = 8y ………… (1)
तथा y² = 8x ……………….. (2)
समी. (1) और (2) को हल करने पर,
( \(\frac { x^{ 2 } }{ 8 } \) )² = 8x
⇒ \(\frac { x^{ 4 } }{ 64 } \) = 8x
⇒ x⁴ = 64 × 8x = 8 × 8 × 8 × x
⇒ x³ = (8)³ या x = 8
समी. (1) से,

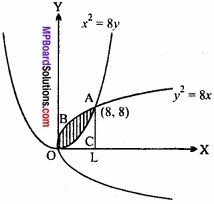
(8)² = 8y ⇒ y = 8
A के निर्देशांक (8, 8) हैं।
परवलय बिन्दु तथा A पर मिलते हैं।
∴ उभयनिष्ठ क्षेत्रफल = क्षेत्रफल OBALO – क्षेत्रफल OCALO

प्रश्न 2.
चक्र y = cosx, X – अक्ष और x = 0 तथा x = 2π से घिरे क्षेत्र का क्षेत्रफल समाकलन विधि से ज्ञात कीजिए।
हल:
y = f (x) = cos x
जब x ∈ [0, \(\frac { \pi }{ 2 } \) ], cos x ≥ 0;
जब x ∈ [ \(\frac { \pi }{ 2 } \), \(\frac { 3\pi }{ 2 } \) ], cos x ≤ 0
जब x ∈ [ \(\frac { 3\pi }{ 2 } \), 2π], cos x ≥ 0

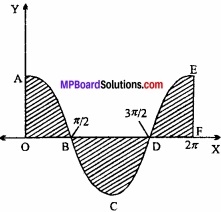
अभीष्ट क्षेत्रफल = OAB का क्षेत्रफल + BCD का क्षेत्रफल + DEF का क्षेत्रफल

प्रश्न 3.
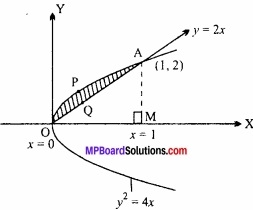
वक्र y² = 4x तथा रेखा y = 2x के बीच का क्षेत्रफल ज्ञात कीजिए। (समाकलन विधि से)
हल:
दिया गया वक्र और रेखा है –
y² = 4x और y = 2x
y² = 4x में y = 2x रखने पर,

(2x)² = 4x
⇒ 4x² = 4x
⇒ x² – x = 0
⇒ x(x – 1) = 0
∴ x = 0 या x = 1
तब y = 2x = 0 या y = 2x = 2 × 1 = 2
अत: वक्र y² = 4x तथा रेखा y = 2x के प्रतिच्छेद बिन्दु O(0, 0) एवं (1, 2) होंगे।
अत: अभीष्ट छायांकित क्षेत्र
= क्षेत्र (OPAMO) – क्षेत्र (OQAMO)

जहाँ y_c = वक्र y² = 4x तथा y_s = रेखा y = 2x के लिए,

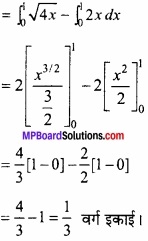
= \(\frac{4}{3}\) [1 – 0] – \(\frac{2}{2}\) [1 – 0]
= \(\frac{4}{3}\) – 1 = \(\frac{1}{3}\) वर्ग इकाई।

प्रश्न 4.
समाकलन विधि द्वारा वक्रों x² = 4y तथा x = 4y – 2 के अंतर्गत क्षेत्रफल ज्ञात कीजिए।
हल:
प्रश्न क्रमांक 3 की भाँति हल करें।

प्रश्न 5.
समाकलन विधि से रेखाओं |x| + |y| = a से घिरे क्षेत्र का क्षेत्रफल ज्ञात कीजिए।
हल:
दी गयी रेखाओं |x| + |y| = a द्वारा निरूपित रेखायें निम्न होंगी –
x + y = a ……………… (1)
– x – y = a ………………. (2)
x – y = a …………….. (3)
– x + y = a …………….. (4)
⇒ \(\frac{x}{a}\) + \(\frac{y}{a}\) = 1, \(\frac{x}{-a}\) + \(\frac{y}{-a}\) = 1
⇒ \(\frac{x}{a}\) + \(\frac{y}{-a}\) = 1, \(\frac{x}{-a}\) + \(\frac{y}{a}\) = 1

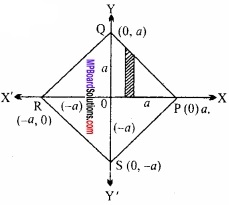
उक्त रेखाओं के ग्राफ से स्पष्ट है, कि उक्त रेखाएँ क्रमशः PQ, RS, PS और QR रेखाओं द्वारा निरूपित हैं।
अतः उक्त रेखाओं द्वारा घिरा क्षेत्रफल
= 4 × ∆OPQ का क्षेत्रफल

= 4 × \(\frac { a^{ 2 } }{ 2 } \) = 2a² वर्ग इकाई।

प्रश्न 6.
वृत्त x² + y² का क्षेत्रफल समाकलन विधि से ज्ञात कीजिए।
हल:
दिया है:
वृत्त x² + y² = a²
⇒ y² = a² – x²
⇒ y = \(\sqrt { a^{ 2 }-x^{ 2 } } \)
वृत्त X – अक्ष तथा Y – अक्ष के सापेक्ष सममित आकृति है अतः
वृत्त का क्षेत्रफल = 4 × ∆ABC का क्षेत्रफल

प्रश्न 7.
वृत्त x² + y² = 25 का क्षेत्रफल समाकलन विधि से ज्ञात कीजिए।
हल:
प्रश्न क्रमांक 6 की भाँति हल करें। [संकेत – a = 5 रखें।]

प्रश्न 8.
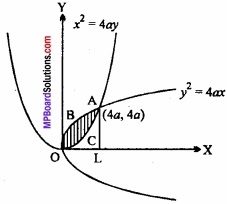
वक्रों y² = 4ax तथा x² = 4ay, a > 0 के अन्तर्गत क्षेत्रफल ज्ञात कीजिए। (समाकलन विधि द्वारा)
हल:
दिये हुए परवलयों के समीकरण हैं:
y² = 4ax ………….. (1)
तथा x² = 4ay ……………. (2)
समी. (1) और (2) को हल करने पर,

\(\frac { x^{ 4 } }{ 16a^{ 2 } } \) = 4ax
⇒ x⁴ – 64a³x = 0
⇒ x(x³ – 64a³) = 0
अतः या तो x = 0 अथवा x³ – 64a³ = 0
जब x³ – 64a³ = 0
जब x³ – 64a³ = 0 तो x = 4a
जब x = 0 तो y = 0
और जब x = 4a तो y = 4a
अत: दोनों परवलय बिन्दुओं (0, 0), (4a, 4a) पर मिलते हैं।
∴ उभयनिष्ठ क्षेत्रफल = क्षेत्रफल OBALO – क्षेत्रफल OCALO

प्रश्न 9.
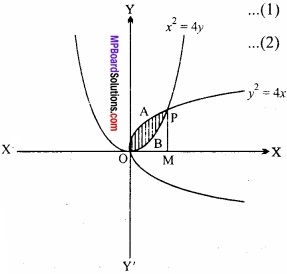
वक्रों y² = 4x और x² = 4y के बीच का क्षेत्रफल समाकलन विधि से ज्ञात कीजिए।
हल:
दिए हुए वक्रों के समीकरण हैं:
y² = 4x ……………… (1)
xc = 4y ………………. (2)
समी. (2) से y का मान समी. (1) में रखने पर,

⇒ \(\frac { x^{ 4 } }{ 16 } \) = 4x
⇒ x⁴ – 64x = 0
⇒ x(x³ – 64) = 0
⇒ x = 0 या x³ = 64
⇒ x = 0 या x = 4
∴ बिन्दु 0 पर x = 0 तथा बिन्दु M पर x = 4
अतः अभीष्ट क्षेत्रफल = क्षेत्र. OAPBO
= क्षेत्र. OAPMO – क्षेत्र. OBPMO

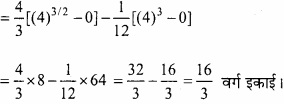
प्रश्न 10.
वक्र y² = x और x² = y के बीच का क्षेत्रफल समाकलन विधि से ज्ञात कीजिए।
हल:
प्रश्न क्रमांक 9 की भाँति हल करें।

प्रश्न 11.
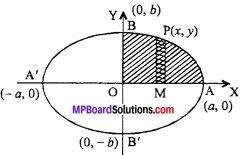
दीर्घवृत्त \(\frac { x^{ 2 } }{ a^{ 2 } } \) + \(\frac { y^{ 2 } }{ b^{ 2 } } \) = 1 से घिरे क्षेत्र का क्षेत्रफल ज्ञात कीजिए। (समाकलन विधि द्वारा)
हल:
दिया हुआ वक्र X – अक्ष और Y – अक्ष के सापेक्ष सममित है। अतएव सम्पूर्ण क्षेत्रफल क्षेत्र OAB का 4 गुना होगा।
यहाँ y = \(\frac{b}{a}\) \(\sqrt { a^{ 2 }-x^{ 2 } } \)
वक्र पर बिन्दु P लिया। तब पट्टी PM का क्षेत्रफल ydx होगा।
x का मान O पर शून्य तथा A पर x = a है।

प्रश्न 12.
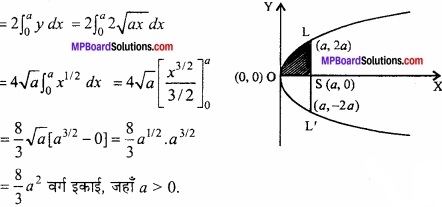
परवलय y² = 4ax तथा इसकी नाभिलम्ब जीवा से घिरे क्षेत्र का क्षेत्रफल ज्ञात कीजिए। (समाकलन विधि द्वारा)
हल:
परवलय का समीकरण है:
y² = 4ax
⇒ y = ± 2\(\sqrt{ax}\)
LSL’ नाभिलम्ब है तथा S(a, 0) और 0(0, 0) है।
अतः अभीष्ट क्षेत्रफल = 2 × क्षेत्रफल OSL

प्रश्न 13.
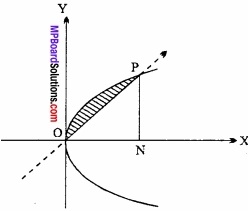
परवलय y² = 4ax और रेखा y = mx के बीच घिरे क्षेत्र का क्षेत्रफल ज्ञात कीजिए।
हल:
परवलय का समी. y² = 4ax ……………. (1)
रेखा का समी. y = mx …………….. (2)
मूलबिन्दु O(0, 0) है। P परवलय और रेखा का प्रतिच्छेद बिन्दु है। समी. (1) और (2) को हल करने पर,
y² = 4ax
⇒ (mx)² = 4ax
⇒ m²x² – 4ax = 0
⇒ x(m²x – 4a) = 0
∴ x = 0, x = \(\frac { 4a }{ m^{ 2 } } \)

प्रश्न 14.
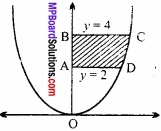
प्रथम चतुर्थांश में x² = 4y, y = 2, y = 4 एवं Y – अक्ष से घिरे क्षेत्र का क्षेत्रफल ज्ञात कीजिए। (NCERT)
हल:
दिए गए वक्र का समीकरण है:
x² = 4y
⇒ x = 2\(\sqrt{y}\)
∴ अभीष्ट क्षेत्रफल = ABCD का क्षेत्रफल

प्रश्न 15.
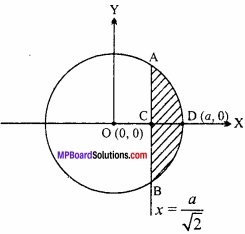
छेदक रेखा x = \(\frac { a }{ \sqrt { 2 } } \) द्वारा वृत्त x² + y² = a² के छोटे भाग का क्षेत्रफल ज्ञात कीजिए। (NCERT)
हल:
वृत्त का समीकरण है:
x² + y² = a²
y² = a² – x²
y = \(\sqrt { a^{ 2 }-x^{ 2 } } \)
रेखा का समीकरण है –
x = \(\frac { a }{ \sqrt { 2 } } \)
समी. (1) और (2) को हल करने पर,

( \(\frac { a }{ \sqrt { 2 } } \) )² + y² = a²
y² = a² – \(\frac { a^{ 2 } }{ 2 } \) = \(\frac { a^{ 2 } }{ 2 } \)
y = \(\frac { a }{ \sqrt { 2 } } \)
वृत्त और रेखा का प्रतिच्छेद बिन्दु A( \(\frac { a }{ \sqrt { 2 } } \), \(\frac { a }{ \sqrt { 2 } } \) ) है।
D के निर्देशांक (a, 0) होंगे।
∴ अभीष्ट क्षेत्रफल = ABD का क्षेत्रफल = 2 × ACD का क्षेत्रफल

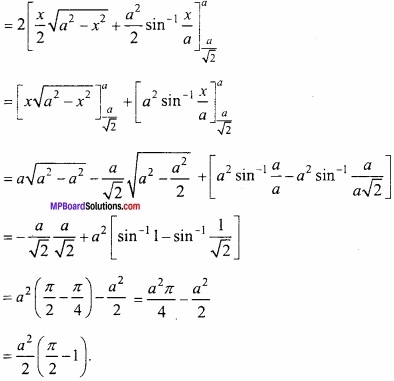
प्रश्न 16.
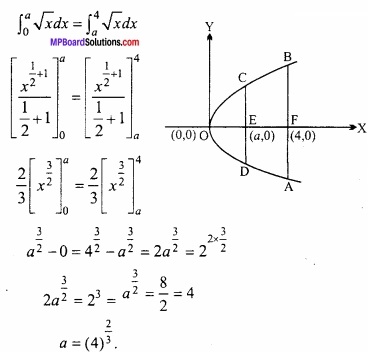
यदि वक्र x = y² एवं रेखा x = 4 से घिरा हुआ क्षेत्रफल x = a द्वारा दो बराबर भागों में विभाजित होता है, तो a का मान ज्ञात कीजिए। (NCERT)
हल:
परवलय का समीकरण है:
x = y²
⇒ y = \(\sqrt{x}\) ………… (1)
परवलय तथा रेखा x = 4 से घिरे क्षेत्रफल को रेखा x = a दो बराबर भागों में विभाजित करती है।
क्षेत्रफल OEC = क्षेत्रफल EFCB

प्रश्न 17.
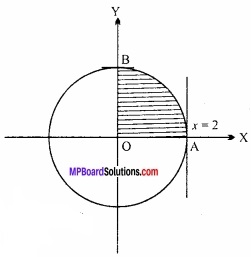
प्रथम चतुर्थांश में वृत्त x² + y² = 4 एवं रेखाओं x = 0, x = 2 से घिरे क्षेत्र का क्षेत्रफल ज्ञात कीजिए। (NCERT)
हल:
वृत्त का समीकरण है:
x² + y² = 4
⇒ y² = 4 – x²
⇒ y = \(\sqrt { (2)^{ 2 }-x^{ 2 } } \)

प्रश्न 18.
प्रथम चतुर्थांश में वृत्त x² + y² = 32 रेखा y = x एवं X – अक्ष द्वारा घिरे क्षेत्र का क्षेत्रफल ज्ञात कीजिए। (NCERT; CBSE 2018)
हल:
दिए गए वृत्त का समीकरण है:
x² + y² = 32
y² = 32 – x²
वृत्त का समीकरण y = \(\sqrt { 32-x^{ 2 } } \)
रेखा का समीकरण है:
समी. (1) और (2) को हल करने पर,
x² + x² = 32
2x² = 32
x² = 16
x = 4

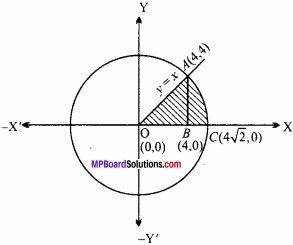
x का मान समी. (2) में रखने पर,
y = 4
रेखा और वृत्त का प्रतिच्छेद बिन्दु O(0,0) तथा A(4, 4) है। B के निर्देशांक (4, 0) तथा C के निर्देशांक (4\(\sqrt{2}\),0) हैं।
अभीष्ट क्षेत्रफल = क्षेत्रफल OACBO
= क्षेत्रफल OAB + क्षेत्रफल ABC

प्रश्न 19.
उस त्रिभुज का क्षेत्रफल समाकलन द्वारा ज्ञात कीजिए जिसकी भुजाएँ y = 2x + 1, y = 3x + 1 तथा x = 4 हैं। (NCERT)
हल:
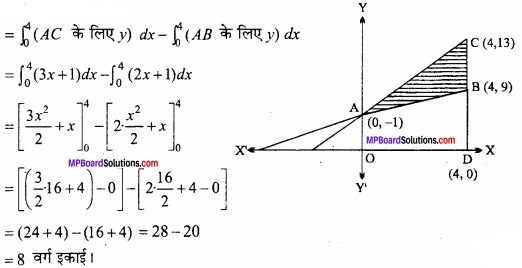
माना कि ∆ABC की भुजाओं AB, AC तथा BC के समीकरण क्रमशः हैं –
y = 2x + 1 ……….. (1)
y = 3x + 1 ……….. (2)
और x = 4 ……….. (3)
समी. (1) और (2) को हल करने पर, बिन्दु A (0, 1)
समी. (1) और (3) को हल करने पर, बिन्दु B (4, 9) और
समी. (2) और (3) को हल करने पर, बिन्दु C (4, 13) हैं।
अत: अभीष्ट क्षेत्रफल

MP Board Class 12 Maths Important Questions