MP Board Class 12th Chemistry Solutions Chapter 4 रासायनिक बलगतिकी
रासायनिक बलगतिकी NCERT पाठ्यनिहित प्रश्न
प्रश्न 1.
R → Pअभिक्रिया के लिये अभिकारक की सान्द्रता 25 मिनट में परिवर्तित होकर 0.03 M से 0.02 M हो जाती है। औसत वेग की गणना सेकण्ड तथा मिनट दोनों इकाइयों में कीजिये।
हल
अभिक्रिया R → P
अभिक्रिया की औसत दर (वेग) = –\(\frac{\Delta[\mathrm{R}]}{\Delta t}\)
= –\(\frac{[0 \cdot 02-0.03]}{25}\)
= \(\frac{0.01}{25}\)
= 4 × 10-4M मिनट -1
यदि समय सेकण्ड में लिया जाये, तब
अभिक्रिया की औसत दर = –\(\frac{\Delta[\mathrm{R}]}{\Delta t}\)
= \(-\frac{[0.02-0.03]}{25 \times 60}\)
= 6.66 × 10-6M सेकण्ड-1
प्रश्न 2.
2A → उत्पाद अभिक्रिया में A की सान्द्रता 10 मिनट में 0.5 मोल L-1 से घटकर 0.4 मोल L-1 रह जाती है। इस समयांतराल के लिये अभिक्रिया वेग की गणना कीजिये।
हल
औसत दर = –\(\frac{1}{2} \frac{\Delta[\mathrm{A}]}{\Delta t}\)=-\(\frac{1}{2} \frac{[0.4-0.5]}{10}\)
= 0.005 मोल लीटर -1 मिनट -1।
प्रश्न 3.
एक अभिक्रिया, A+ B → उत्पाद के लिये वेग नियमr=k[A]1/2 [B]2 दिया गया है। अभिक्रिया की कोटि क्या है ?
हल
अभिक्रिया की कोटि = \(\frac{1}{2}\) + 2 = 2 \(\frac{1}{2}\) = 2.5.
प्रश्न 4.
अणु x का Y में रूपांतरण द्वितीय कोटि की बलगतिकी के अनुरूप होता है। यदि x की सान्द्रता तीन गुनी कर दी जाये तो Y के निर्माण होने के लिए वेग पर क्या प्रभाव पड़ेगा?
हल
अभिक्रिया X → Y के लिये, जैसा कि इसमें द्वितीय कोटि की बलगतिकी (Kinetics) है। इसका दर नियम समीकरण होगा —
दर = k[X]2 = ka2 (यदि x = a मोल L-1 )
यदि X की सान्द्रता 3 गुनी बढ़ायी जाये तो यह
[X] = 3a मोल L-1 हो जायेगी।
दर = k(3a)2 = 9ka2
अत: अभिक्रिया की दर 9 गुनी हो जायेगी। अर्थात् Y के बनाने की दर 9 गुनी बढ़ जायेगी।
प्रश्न 5.
एक प्रथम कोटि की अभिक्रिया का वेग स्थिरांक 1.15 x 10-3S-1 है। इस अभिक्रिया में अभिकारक की 5g मात्रा घटकर 3g होने में कितना समय लगेगा?
हल

प्रश्न 6.
SO2Cl2 को अपनी प्रारम्भिक मात्रा से आधी मात्रा में वियोजित होने में 60 मिनट का समय लगता है। यदि अभिक्रिया प्रथम कोटि की हो, तो वेग स्थिरांक की गणना कीजिये।
हल
t1/2 = 60 मिनट = 60 × 60s
∴ k = \(\frac{0.693}{t_{1 / 2}}\) = \(\frac{0.693}{60 \times 60}\)
= 1.925 × 10-4 सेकण्ड-1
प्रश्न 7.
ताप का वेग स्थिरांक पर क्या प्रभाव होगा?
उत्तर
10°C ताप बढ़ाने पर अभिक्रिया का वेग स्थिरांक लगभग दुगुना हो जाता है। वेग स्थिरांक की ताप पर निर्भरता आीनियस समीकरण द्वारा प्रदर्शित की जाती है। k = \(\mathrm{A} e^{-\mathrm{E}_{a} / \mathrm{RT}}\) जहाँ, A आवृत्ति कारक तथा Ea अभिक्रिया की सक्रियण ऊर्जा है।
प्रश्न 8.
परम ताप, 298 K में 10 K की वृद्धि होने पर रासायनिक अभिक्रिया का वेग दुगुना हो जाता है। इस अभिक्रिया के लिये E, की गणना कीजिये।
हल
दिया गया है – k2 = 2k, T1 = 298 K, T2 = 308 K,
R = 8-314JK-1 mol-1
हम जानते हैं कि –

प्रश्न 9.
581 K ताप पर अभिक्रिया 2HI(g) → H2(g) + I2(g) के लिये सक्रियण ऊर्जा का मान 209.5 kJ मोल -1 है। अणुओं के उस अंश की गणना कीजिये जिसकी ऊर्जा सक्रियण ऊर्जा के बराबर अथवा इससे अधिक है।
हल
प्रश्नानुसार,
Ea = 209.5 kJ मोल -1
= 209.5 × 103 J मोल-1
T = 581 K
अणुओं का प्रभाज जिसकी ऊर्जा सक्रियण ऊर्जा के बराबर या उससे ज्यादा है, को इसके द्वारा प्रदर्शित किया जाता है
x = \(e^{-\mathrm{E}_{a} / \mathrm{RT}}\) (R= 8.314J)
लॉग का उपयोग करने पर,
logx =-\(\frac{\mathrm{E} a}{2 \cdot 303 \mathrm{RT}}\)
logx = –\(\frac{209.5 \times 10^{3}}{2.303 \times 8.314 \times 581}\)
या logx = -18.832
या x = Antilog[-18.832]
या x = 1.472 x 10-19.
रासायनिक बलगतिकी NCERT पाठ्य-पुस्तक प्रश्नोत्तर
प्रश्न 1.
निम्न अभिक्रियाओं के वेग व्यंजकों से इनकी अभिक्रिया कोटि तथा वेग स्थिरांकों की इकाइयाँ ज्ञात कीजिए –
(i) 3NO(g) → N2O(g) वेग = k[NO]2
(ii) H2O2(aq) + 3I(aq) + 2H+ → 2H2O(l) + I–3 – वेग = k[H2O2] [I–]
(iii) CH3CHO(g) → CH4(g) + CO(g) – वेग = k[CH3CHO]3/2
(iv) C2H5Cl(g) → C2H4(g) + HCl(g)
वेग = k[C2H5Cl]
उत्तर

प्रश्न 2.
अभिक्रिया 2A + B→ A2B के लिए वेग = k[A] [B]2, यहाँk का मान 2.0 x 10-6 mol-2L2s-1 है। प्रारम्भिक वेग की गणना कीजिए; जब [A] = 0-1 mol L-1 एवं [B] = 0.2 molL -1हो तथा अभिक्रिया वेग की गणना कीजिए जब [A] घटकर 0.06 mol L-1रह जाए।
हल
दिया गया है –
दर = k[A] [B]2
प्रारम्भिक दर = 2 × 10-6 × [0.1] [0.2]2
= 8 ×10-9 मोल लीटर-1 सेकण्ड -1
A की सान्द्रता में कमी
अर्थात् Δ[A] = 0.1 – 0.06
= 0.04 मोल लीटर -1
B की सान्द्रता में कमी
अर्थात् Δ[B] = \(\frac{1}{2}\) × 0.04 = 0.02 मोल लीटर -1
B की बची सान्द्रता = 0.2 – 0.02 = 0.18 M
दर = k[A] [B]2
= 2 × 10-6 × 0.06 × [0.18]2
= 3.89 × 10-9 मोल लीटर-1 सेकण्ड -1
प्रश्न 3.
प्लैटिनम सतह पर NH3 का अपघटन शून्य कोटि की अभिक्रिया है। N2 एवं H2 के उत्पादन की दर क्या होगी जब k का मान 2.5 × 10-4mol L-1s-1 हो?
हल
2NH3 → N2 + 3H2

शून्यं कोटि अभिक्रिया के लिये –
दर = k = 2.5 × 10-4 Ms-1
N2 बनने की दर = \(\frac{d\left[\mathbf{N}_{2}\right]}{d t}\)
= 2.5 × 10-4
= 2.5 × 10-4 Ms-1.
H2 बनने की दर =\(\frac{d\left[\mathrm{H}_{2}\right]}{d t}\) = 3 × 2.5 ×10-4
= 7.5 × 10-4 Ms-1.
प्रश्न 4.
डाईमेथिल ईथर के अपघटन से CH4, H2 तथा CO बनते हैं। इस अभिक्रिया का वेग निम्न समीकरण द्वारा दिया जाता है –
वेग = k[CH3OCH3]3/2
अभिक्रिया के वेग का अनुगमन बंद पात्र में बढ़ते दाब द्वारा किया जाता है, अत: वेग समीकरण को डाईमेथिल ईथर के आंशिक दाब के पद में भी दिया जा सकता है। अतः वेग = k(PCH3OCH3)3/2
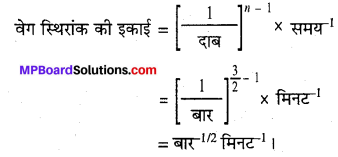
यदि दाब को bar में तथा समय को मिनट में मापा जाये तो अभिक्रिया के वेग एवं वेग स्थिरांक की इकाइयाँ क्या होंगी?
हल
अभिक्रिया के दर नियमानुसार,
दर = k(PCH3OCH3)3/2
दर = दाब परिवर्तन / समय परिवर्तन
दर की इकाई = बार मिनट -1
प्रश्न 5.
रासायनिक अभिक्रिया के वेग पर प्रभाव डालने वाले कारकों का उल्लेख कीजिए।
उत्तर
अभिक्रिया का वेग निम्नलिखित कारकों पर निर्भर करता है –
(i) अभिकारकों की सान्द्रता,
(ii) ताप,
(iii) उत्प्रेरक,
(iv) अभिकारक की प्रकृति आदि।
प्रश्न 6.
किसी अभिक्रियक के लिए एक अभिक्रिया द्वितीय कोटि की है।अभिक्रिया का वेग कैसे प्रभावित होगा; यदि अभिक्रियक की सान्द्रता –
(i) दुगुनी कर दी जाए,
(ii) आधी कर दी जाए।
हल
माना कि अभिक्रिया A → B, A के लिये द्वितीय कोटि की अभिक्रिया है –
\(\frac{d x}{d t}\) = k[A]2 = ka2
(i) जब [A] की सान्द्रता दुगुनी कर दी जाये –
A = 2a
अभिक्रिया की नयी दर –
\(\frac{d x^{\prime \prime}}{d t}\) = k[2a]2 = 4ka2
या
= 4\(\frac{d x}{d t}\)
अतः अभिक्रिया की दर चार गुनी हो जाती है, जब सान्द्रता दुगुनी की जाती है।
(ii) जब [A] की सान्द्रता 1/2 कर दी जाये –
A = \(\frac{a}{2}\)
इसलिये अभिक्रिया की नयी दर,
\(\frac{d x^{\prime}}{d t}=k\left[\frac{a}{2}\right]\)
= \(\frac{1}{4}\)ka2 =\(\frac{1}{4} \frac{d x}{d t}\)
अतः अभिक्रिया की दर 1/4 गुनी हो जाती है, जब सान्द्रता 1/2 गुनी की जाती है।
प्रश्न 7.
वेग स्थिरांक पर ताप का क्या प्रभाव पड़ता है ? ताप के इस प्रभाव को मात्रात्मक रूप में कैसे प्रदर्शित कर सकते हैं ?
उत्तर
अभिक्रिया का वेग स्थिरांक ताप के साथ बढ़ता है। अभिक्रिया ऊष्माशोषी है या ऊष्माक्षेपी इससे प्रभावित नहीं होती है। आर्टीनियस समीकरण से वेग स्थिरांक ताप पर निर्भरता को दर्शाता है –
k =\(\mathrm{A} e^{-\mathrm{E}_{a} / \mathrm{KT}}\)
प्रश्न 8.
जल में एस्टर के छद्म प्रथम कोटि के जल-अपघटन के निम्नलिखित आँकड़े प्राप्त हुए –

(i) 30 से 60 सेकण्ड समय अंतराल में औसत वेग की गणना कीजिए।
(ii) एस्टर के जल-अपघटन के लिए छद्म प्रथम कोटि अभिक्रिया वेग स्थिरांक की गणना कीजिए।
हल
(i)

(ii)

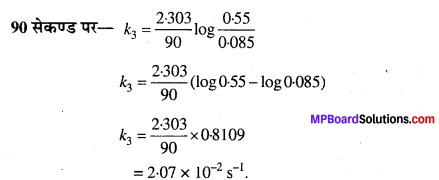
प्रश्न 9.
एक अभिक्रिया A के प्रति प्रथम तथा B के प्रति द्वितीय कोटि की है –
(i) अवकलन वेग समीकरण लिखिए।
(ii) B की सान्द्रता तीन गुनी करने से वेग पर क्या प्रभाव पड़ेगा?
(iii) A तथा B दोनों की सान्द्रता दुगुनी करने से वेग पर क्या प्रभाव पड़ेगा ?
हल
(i) अवकलन वेग समीकरण, \(\frac{d[\mathrm{R}]}{d t}\) = k[A]1 [B]2
दर (r) = k[A]1 [B]2 यदि [A] = x तथा [B] = y होने पर दर (r1) = kxy2 …………………(1)
(ii) जब [B] = 3y
r2kx (3y)2 …………………..(2)
समीकरण (2) को (1) से भाग देने पर,
r2 = 9r1
अतः दर 9 गुना बढ़ती है।
(ii) जब [A] तथा [B] दोनों दुगुना हो क्तजाता है
r3 = k(2x) (2y)2
(3) समीकरण (3) को (1) से भाग देने पर,
r3 = 8 r1
अर्थात् दर 8 गुनी बढ़ जायेगी।
प्रश्न 10.
A और B के मध्य अभिक्रिया में A और B की विभिन्न प्रारम्भिक सान्द्रताओं के लिए प्रारम्भिक वेग (r0 ) नीचे दिए गए हैं –
A और B के प्रति अभिक्रिया की कोटि क्या है?

हल
माना कि अभिक्रिया की कोटि A के सन्दर्भ में x तथा B के संदर्भ में y हो, तो
r1 = k[A]x [B]y
∴ दर r1 = k[0.20]x [0.30]y
= 5.07 x 10-5………………………….(1)
तथा दर r2 = k[0.20]x [0.10]y
= 5.07 x 10-5
\(\frac{r_{1}}{r_{2}}\) = \(\frac{(0.30)^{y}}{(0.10)^{y}}\) = 1
3y = 1 या 3y = 3°
∴ y= 0
दर r3 = k[0.40]x [0.05]y
= 1.43 x 10-4
समीकरण (3) को (2) से भाग देने पर,
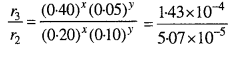
2x + \(\frac{1}{2^{y}}\) = 2.8
jab y= 0
∴ 2x + \(\frac{1}{2^{0}}\) = 2.8
या 2x = 2.8
दोनों तरफ लॉग लेने पर,
x log 2 = log 2.8
या x = \(\frac{\log 2.8}{\log 2}\)
= \(\frac{0.45}{0.3010}\) = 1.5
अत: A के प्रति अभिक्रिया की कोटि = 1.5
तथा B के प्रति अभिक्रिया की कोटि = 0.
प्रश्न 11.
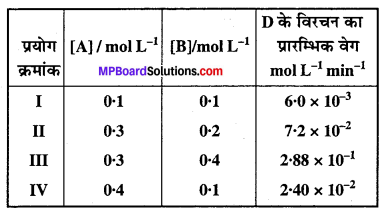
2A + B → C + D अभिक्रिया की बलगतिकी अध्ययन करने पर निम्नलिखित परिणाम प्राप्त हुए। अभिक्रिया के लिए वेग नियम तथा वेग स्थिरांक ज्ञात कीजिए।
हल
प्रयोग I तथा IV की तुलना करने तथा मान रखने पर ज्ञात होता है कि ‘B’ की सान्द्रता स्थिर है, अतः हमें A के सापेक्ष कोटि प्राप्त होती है।
r1 = k (0.1)x (0.1)y = 6.0 × 10-3 ……………..(1)
r2 = k (0.4)x (0.1)y = 2.40 × 10-2 ……………..(2)
(2) समीकरण (2) को (1) से भाग देने पर,
\(\frac{(0.4)^{x}}{(0.1)^{y}}=\frac{2.40 \times 10^{-2}}{6.0 \times 10^{-3}}=4\)
या 4x = 4
या 4x = 41
∴ x = 1
इसी प्रकार, प्रयोग II तथा III की तुलना करने पर B के सापेक्ष में कोटि प्राप्त होती है।
r2 = k (0.3)x (0.2)y = 7.2 × 10-2 ……………..(3)
r3 = k (0.3)x (0.4)y = 2.88 × 10-1 ……………..(4)
समीकरण (4) को (3) से भाग देने पर,
\(\frac{(0.4)^{x}}{(0.2)^{x}}\) =\(\frac{2.88 \times 10^{-1}}{7.2 \times 10^{-2}}\) = 4
(2)y = 4
या (2)y = (2)2
∴y = 2
अतः दर नियम व्यंजक है –
दर = k[A] [B]2
समीकरण (1) में मान रखने पर,
6.0 x 10-3 = k(0.1) (0.1)2
या k = \(\frac{6 \cdot 0 \times 10^{-3}}{(0.1)(0.1)^{2}}\)
= 6.0 मोल -2 लीटर2 मिनट-1।
प्रश्न 12.
A तथा B के मध्य अभिक्रिया A के प्रति प्रथम तथा B के प्रति शन्य कोटि की है। निम्न तालिका में रिक्त स्थान भरिएप्रयोग –

हल
दिया गया है कि A तथा B के मध्य अभिक्रियाA के प्रति प्रथम कोटि तथा B के प्रति शून्य कोटि की है।
∴ दर = k[A]1 [B]0
परन्तु [B]0 = 1
∴ दर = k[A]
प्रयोग I से,
2 × 10-2 = k(0.1)
⇒ k= 0.2 मिनट-1
प्रयोग II से,
4 × 10-2 = 0.2 [A]
⇒ [A] = 0.2 मोल लीटर-1।
प्रयोग III से,
दर = (0.2) (0.4)
= 0.08 मोल लीटर-1 मिनट-1।
प्रयोग IV से,
2 × 10-2= 0.2[A]
⇒ [A] = 0.1 मोल लीटर -1।
प्रश्न 13.
नीचे दी गई प्रथम कोटि की अभिक्रियाओं के वेग स्थिरांक से अर्धायु की गणना कीजिए(i) 200 s-1, (ii) 2 min-1, (iii) 4 year-1.
हल
(i) t1/2 = \(\frac{0.693}{k}\)
= \(\frac{0.693}{200}\)
= 3.465 x 10-3 सेकण्ड।
(ii) t1/2 = \(\frac{0.693}{k}\)
= \(\frac{0.693}{2}\)
= 0.3465 मिनट।
(iii) t1/2 = \(\frac{0.693}{k}\)
= \(\frac{0.693}{4}\)
= 0.1732 वर्ष।
प्रश्न 14.
14C के रेडियोएक्टिव क्षय की अर्धायु 5730 वर्ष है। एक पुरातत्व कलाकृति की लकड़ी में, जीवित वृक्ष की लकड़ी की तुलना में 80% 14C की मात्रा है। नमूने की आयु का परिकलन कीजिए।
हल
रेडियोएक्टिव विघटन की प्रथम कोटि की बलगतिकी होती है।
विघटन स्थिरांक; k = \(\frac{0.693}{t_{1 / 2}}\)
∴ k = \(\frac{0.693}{t_{1 / 2}}\) वर्ष -1
प्रथम कोटि बलगतिकी समीकरण से,
\(t=\frac{2 \cdot 303}{k} \log \frac{a}{a-x}\)
माना a = 100
(a-x) = 80
t = \(\frac{2 \cdot 303}{(0.693 / 5730)} \log \frac{100}{80}\)
या t = 1845.37 वर्ष -1
प्रश्न 15.
गैस प्रावस्था में 318 K पर N2O5 के अपघटन की [2N2O5 → 4N2 + O2] अभिक्रिया के आँकड़े नीचे दिए गए हैं –

(i) [N2O5] एवं । के मध्य आलेख खींचिए।
(ii) अभिक्रिया के लिए अर्धायु की गणना कीजिए।
(iii) log [N2O5] एवं t के मध्य ग्राफ खींचिए।
(iv) अभिक्रिया के लिए वेग नियम क्या है ?
(v) वेग स्थिरांक की गणना कीजिए।
(vi) k की सहायता से अर्धायु की गणना कीजिए तथा इसकी तुलना (ii) से कीजिए।
हल
(i) समय व [N2O5] के मध्य खींचा गया ग्राफ आगे दिखाया गया है –
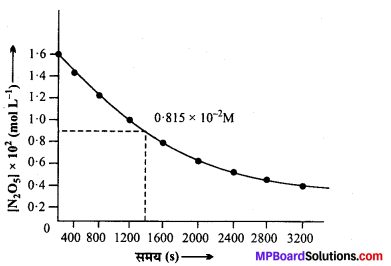
(ii) N2O5 की प्रारम्भिक सान्द्रता = 1.63 × 102M
प्रारम्भिक सान्द्रता का आधा = 1.63 × 102 × \(\frac{1}{2}\)
= 0.815 × 102M
ग्राफ से प्रारम्भिक सान्द्रता के आधे (t1/2) के संगत समय = 1440 सेकण्ड।
(iii) log [N2O5] तथा समय के मध्य ग्राफ –
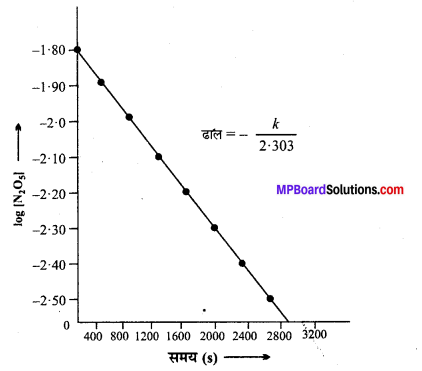
(iv) चूँकि log[N2O5] तथा समय का ग्राफ सरल रेखा है, अतः अभिक्रिया 1st कोटि की है
दर = k[N2O5].
(v) रेखा का ढाल = –\(\frac{k}{2 \cdot 303}\) =-2.10 × 10-4
k = -2.10 ×10-4 × (-2.303)
= 4.84 × 10-4s-1
(vi) t1/2 = \(\frac{0.693}{k}=\frac{0.693}{4.84 \times 10^{-4}}\)
= 1432 s.
प्रश्न 16.
प्रथम कोटि की अभिक्रिया के लिए वेग स्थिरांक 60s-1 है। अभिक्रियक को अपनी प्रारम्भिक सान्द्रता से 1/16 वाँ भाग रह जाने में कितना समय लगेगा?
हल
t = \(\frac{2 \cdot 303}{k} \log \frac{a}{a-x}\)
a = 1, k = 60 सेकण्ड-1, (a-x) = \(\frac{1}{16}\)
∴ 60 = \(\frac{2 \cdot 303}{t} \log \frac{1}{1 / 16}\)
या t= 0.046 सेकण्ड।
प्रश्न 17.
नाभिकीय विस्फोट का 28.1 वर्ष अर्धायु वाला एक उत्पाद 90Sr होता है। यदि कैल्सियम के स्थान पर 1μg, 90Sr नवजात शिशु की अस्थियों में अवशोषित हो जाए और उपापचयन से ह्रास न हो तो इसकी 10 वर्ष एवं 60 वर्ष पश्चात् कितनी मात्रा रह जाएगी ?
हल
k = \(\frac{0.693}{t_{1 / 2}}\); t1/2 =281वर्ष
∴ k = \(\frac{0.693}{28 \cdot 1}\)= 0.0247 वर्ष -1
k = \(\frac{2 \cdot 303}{t} log \frac{a}{(a-x)}\)
90Sr की प्रारम्भिक सान्द्रता =1μg
मान लीजिए 90Sr की 10 वर्ष बाद सान्द्रता = x μg
0.0247 = \(\frac{2.303}{10} \log \frac{1 \mu \mathrm{g}}{x \mu \mathrm{g}}\)
या log \(\frac{1}{x}\) = \(\frac{0.0247 \times 10}{2.303}\) = 0.1072
या \(\frac{1}{x}\)= 1.280
या x=0.782 μg
10 वर्ष बाद 90Sr की सान्द्रता = 0.782 μg .
मान लीजिए 60 वर्षों बाद 90Sr की सान्द्रता = y μg
∴ 0.0247 = \(\frac{2 \cdot 303}{60} log \frac{1 \mu \mathrm{g}}{y \mu \mathrm{g}}\)
या \(log\frac{1}{y}\) = \(\frac{0.247 \times 60}{2.303}\) = 0.6435
या \(\frac{1}{y}\) = 4.40
y= 0.228 μg
60 वर्ष बाद 90sr की सान्द्रता = 0.228 μg .
प्रश्न 18.
दर्शाइए कि प्रथम कोटि की अभिक्रिया में 99% अभिक्रिया पूर्ण होने में लगा समय 90% अभिक्रिया पूर्ण होने में लगने वाले समय से दुगुना होता है।
हल
मान लीजिए 90% पूर्ण होने तथा 99% पूर्ण होने में लगे समय को क्रमशः t0.90 तथा t0.99 से प्रदर्शित किया जाये।
प्रथम कोटि बलगतिकी से, k =\(\frac{2 \cdot 303}{t} log \frac{a}{a-x}\)
90% पूर्ण होने के लिए, k = \(\frac{2 \cdot 303}{t_{0.99}} log \frac{100}{1}\)
या k = \(\frac{2 \cdot 303}{t_{0.99}} \times 2\) ………………..(1)
90% पूर्ण होने के लिए,
k = \(\frac{2.303}{t_{0.90}} log \frac{100}{10}\)
या k = \(\frac{2 \cdot 303}{t_{0.90}} \times 1\)
समीकरण (1) तथा (2) से हमें प्राप्त होता है –
to.99 = 2 x t0.90
प्रश्न 19.
एक प्रथम कोटि की अभिक्रिया में 30% वियोजन होने में 40 मिनट लगते हैं। t1/2 की गणना कीजिए।
हल
प्रथम कोटि अभिक्रिया के लिये,
k = \(\frac{2 \cdot 303}{t} log \frac{a}{a-x}\)
t = 40 मिनट, a = 100, x = 30
उपर्युक्त समीकरण में मान रखने पर,
k = \(\frac{2 \cdot 303}{40} log \frac{100}{70}\)
या k = \(\frac{2 \cdot 303}{40} log 1.43\)
या k = \(\frac{2 \cdot 303}{40}\) × 0.1554
या k = 8.94 × 10-3
t1/2= \(\frac{0.693}{k}\) = \(\frac{0.693}{8.94 \times 10^{-3}}\)
= 77.7 मिनट।
प्रश्न 20.
543K ताप पर एजोआइसोप्रोपेन के हेक्सेन तथा नाइट्रोजन में विघटन के निम्न आँकड़े प्राप्त हुए। वेग स्थिरांक की गणना कीजिए –

हल
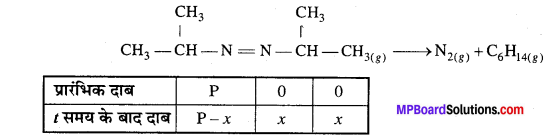


प्रश्न 21.
स्थिर आयतन पर, SO2Cl2 के प्रथम कोटि के ताप अपघटन पर निम्न आँकड़े प्राप्त
हुए
SO2Cl2(g) → SO2(g) + Cl2(g)
अभिक्रिया वेग की गणना कीजिए जब कुल दाब 0.65 atm हो –
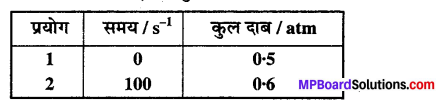
हल
अभिक्रिया है –
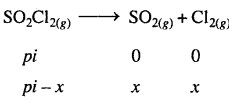
दाब के संदर्भ में प्रथम कोटि अभिक्रिया के लिये –
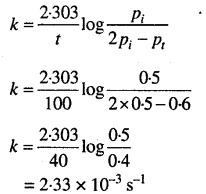
हम जानते हैं (व्यंजक देखिये)
x= Pt- Pi
x= 0.65 – 0.5
x= 0.15
(Pi-x) अर्थात्
SO2Cl2(g)) का शेष दाब = 0.5 – 0.15
= 0.35 वायुमण्डलीय
दर = k x pso2cI2
= 2.23x 10-4 x 0.35
= 7.805 x 10-4 वायुमण्डलीय सेकण्ड-1
प्रश्न 22.
विभिन्न तापों पर N2O5 के अपघटन के लिए वेग स्थिरांक नीचे दिए गये हैं –

In k एवं 1/T के मध्य ग्राफ खींचिए तथा A एवं Ea की गणना कीजिए।30°C तथा 50°C पर वेग स्थिरांक को ज्ञात कीजिए।
हल
1/T को logk के विरुद्ध ग्राफ खींचने पर हम नीचे दिये गये आँकड़ों में इस प्रकार पुनः लिख सकते हैं –
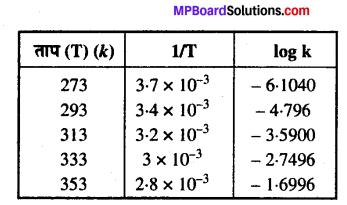
नीचे दर्शायी गयी आकृति के अनुसार ग्राफ खींचते हैं। ग्राफ से हमें पता चलता है –
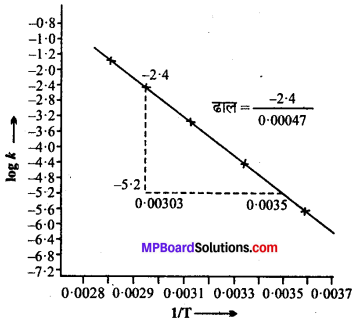
ढाल = \(\frac{-2 \cdot 4}{0.0047}\) = -5106.38
Ea = – ढाल × 2.303 xR
=(-5106.38) × 2.303 × 8.314
= 97772.58 J मोल -1
=97.77258 kJ मोल -1
हम जानते हैं कि
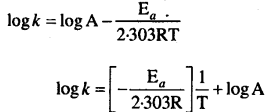
इसकी तुलना y = mx + c से करने पर,
log A = माना जो y अक्ष को काटता हैअर्थात् log k अक्ष पर,
[y2– y1] = -1 – (-7.2)
= (-1 + 7.2) = 6.2
log A = 6.2
A = Antilog 6.2
= 1.585 x 106s-1
वेग स्थिरांक k का मान ग्राफ से इस प्रकार प्राप्त करते हैं –

हम k का मान निम्नलिखित सूत्र से भी निकाल सकते हैं –
log k = log A – \(\frac{\mathrm{E}_{a}}{2 \cdot 303 \mathrm{RT}}\)
प्रश्न 23.
546 K ताप पर हाइड्रोकार्बन के अपघटन में वेग स्थिरांक 2.418 x 10-5s-1 है। यदि सक्रियण ऊर्जा 179.9 kJ/mol हो तो पूर्व-घातांकी गुणन का मान क्या होगा?
हल
प्रश्नानुसारवेग स्थिरांक (K) = 2.418 x 10-5s-1
ताप (T)= 546K
सक्रियण ऊर्जा (Ea) = 179.9 kJ mol-1
log A = log k + \(\frac{\mathrm{E}_{a}}{2.303 \mathrm{RT}}\)
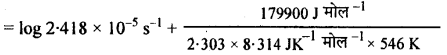
= -4.6184 + 17:21
log A = -4.6184 + 17.21
log A = 12.5916
A = Antilog 12.5916
= 3.9 × 1012s-1.
प्रश्न 24.
किसी अभिक्रिया A → उत्पाद के लिए k = 2.0 x 10-2S-1 है। यदि A की प्रारम्भिक सान्द्रता 1.0 mol L-1 हो तो 100 s के पश्चात् इसकी सान्द्रता क्या रह जाएगी?
हल
k की इकाई s -1 है।
∴ अभिक्रिया प्रथम कोटि की है।


प्रश्न 25.
अम्लीय माध्यम में सुक्रोज का ग्लूकोज एवं फ्रक्टोज़ में विघटन प्रथम कोटि की अभिक्रिया है। इस अभिक्रिया की अर्धायु 3-0 घंटे है। 8 घंटे बाद नमूने में सुक्रोज का कितना अंश बचेगा ?
हल –
k = \(\frac{0.693}{t_{1 / 2}}=\frac{0.693}{3.0}\) = 0.231 घंटा -1
माना कि सुक्रोज (Sucrose) की प्रारम्भिक सान्द्रता (a) = 1 M
8 घंटे बाद सान्द्रता = (a-x)
जहाँ ‘x’ सुक्रोज की विघटित मात्रा है।
k = \(\frac{2 \cdot 303}{t} \log \frac{a}{(a-x)}\)
या 0.231 = \(\frac{0.303}{8} \log \frac{1}{1-x}\)
या log \(\frac{1}{1-x}\) = \(\frac{0 \cdot 231 \times 8}{2 \cdot 303}\) = 0.8024
या \(\frac{1}{1-x}\) = 6.345
या 1 = 6.345 – 6.345x
∴ x = \(\frac{5 \cdot 345}{6 \cdot 345}\) = 0.842
8 घंटे बाद सुक्रोज की शेष सान्द्रता = 1 – 0.842
= 0.158 M.
प्रश्न 26.
हाइड्रोकार्बन का विघटन निम्न समीकरण के अनुसार होता है।E. की गणना कीजिए –
k = (4.5 x 1011s-1)e-28000 K/T
हल
k = (4.5 x 1011s-1)e-28000 K/T
समीकरण की तुलना आर्चीनियस समीकरण से करने पर,
k = \(\mathrm{A} e^{-\mathrm{E}_{a} / \mathrm{RT}}\)
\(\frac{-\mathrm{E}_{a}}{\mathrm{R}}\) = -28000 K
∴ Ea= 28000 x 8.314
= 232792 J मोल -1
= 232.792 kJ मोल -1।
प्रश्न 27.
H2O2 के प्रथम कोटि के विघटन को निम्न समीकरण द्वारा लिख सकते हैं –
logk = 14.34 – 1.25 x 104\(\frac{\mathbf{K}}{\mathbf{T}}\)
इस अभिक्रिया के लिए E, की गणना कीजिए। कितने ताप पर इस अभिक्रिया की अर्धायु 256 मिनट होगी?
हल
(i) हम जानते हैं कि
k=\(\mathrm{A} e^{-\mathrm{E}_{a} / \mathrm{RT}}\)…………………….(1)
समीकरण (1) के दोनों तरफ लॉगरिथ्म लेने पर हमें प्राप्त होता है –
log k = log A – \(\frac{\mathrm{E}_{a}}{2 \cdot 303 \mathrm{RT}}\)………………..(2)
दिया गया है –
logk = 14.34 – 1.25 x 104 \(\frac{\mathbf{K}}{\mathbf{T}}\) …………….(3)
समीकरण (2) तथा (3) की तुलना करने पर हमें प्राप्त होता है –
\(\frac{\mathbf{E}_{a}}{2 \cdot 303 \mathrm{R}}\) = 1. 25 × 104K
∴ Ea = (1.25×104 K) (2.303) ……………………. ((8.214JK-1मोल -1))
Ea = 239339J मोल-1 …………..(4)
(ii) t1/2 = 256 मिनट = 256 × 60 सेकण्ड
∴ k = \(\frac{0.693}{t_{1 / 2}}\)
= \(\frac{0.693}{256 \times 60}\)
4.5 ×10-5s-1…………………(5)
समीकरण (5) से k के इस मान को समीकरण (3) में रखने पर,
log(45 × 10-5)= 14.34 – \(\frac{1 \cdot 25 \times 10^{4} \mathrm{K}}{\mathrm{T}}\)
∴ T= 668.9 K.
प्रश्न 28.
10°C ताप पर A के उत्पाद में विघटन के लिए k का मान 4.5 x 103s-1तथा सक्रियण ऊर्जा 60 kJ mol-1 है। किस ताप पर k का मान 1.5 x 104s-1 होगा?
हल
दिया गया है, k1 = 4.5 x 103s-1,
k1 = 1.5 x 104 s-1,
T1 = 10°C = 10 + 273 = 283 K,
Ea = 60 kJ मोल -1 = 60000 J मोल -1
आर्चीनियस समीकरण का प्रयोग करने तथा इस मान को समीकरण में रखने पर हमें प्राप्त होता है —
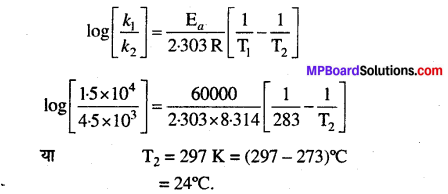
प्रश्न 29.
298 K ताप पर प्रथम कोटि की अभिक्रिया के 10% पूर्ण होने का समय 308 K ताप पर 25% अभिक्रिया पूर्ण होने में लगे समय के बराबर है। यदि A का मान 4 × 1010S-1 हो तो 318 K ताप पर k तथा Ea की गणना कीजिए।
हल

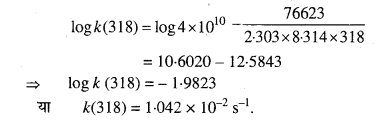
प्रश्न 30.
ताप में 293 K से 313 K तक वृद्धि करने पर किसी अभिक्रिया का वेग चार गुना हो जाता है। इस अभिक्रिया के लिए सक्रियण ऊर्जा की गणना यह मानते हुए कीजिए कि इसका मान ताप के साथ परिवर्तित नहीं होता।
उत्तर
\(\log \frac{k_{2}}{k_{1}}=\frac{\mathrm{E}_{a}}{2 \cdot 303 \mathrm{R}}\left[\frac{\mathrm{T}_{2}-\mathrm{T}_{1}}{\mathrm{T}_{1} \mathrm{T}_{2}}\right]\)
इस प्रक्रम में, k2 = 4k1
T1 = 293 K, T2 = 313 K,
R = 8.314 JK-1 mol-1
उपरोक्त समीकरण में ये मान रखने पर,
\(\log 4=\frac{E_{a}}{2 \cdot 303 \times 8 \cdot 314}\left[\frac{313-293}{293 \times 313}\right]\)
E = 52859.8 J / मोल
= 52.8 kJ मोल -1।
रासायनिक बलगतिकी अन्य महत्वपूर्ण प्रश्नोत्तर
रासायनिक बलगतिकी वस्तुनिष्ठ प्रश्न
1. सही विकल्प चुनकर लिखिए
प्रश्न 1.
अधिकांश अभिक्रियाओं का ताप गुणांक किसके मध्य स्थित होता है –
(a) 1 तथा 3
(b) 2 तथा 3
(c) 1 तथा 4
(d) 2 तथा 4.
उत्तर
(b) 2 तथा 3
प्रश्न 2.
प्रथम कोटि की अभिक्रिया के लिए t1/2 का मान होता है –
(a) \(\frac{0.693}{k_{1}}\)
(b) \(\frac{2 \cdot 303}{k_{1}}\)
(c) \(\frac{0.303}{k_{1}}\)
(d) \(\frac{0.693}{t}\)
उत्तर
(a) \(\frac{0.693}{k_{1}}\)
प्रश्न 3.
एक प्रथम कोटि की अभिक्रिया 32 मिनट में 75% पूर्ण होती है, 50% पूर्ण होने में लगा होगा –
(a) 24 मिनट
(b) 16 मिनट
(c) 8 मिनट
(d) 4 मिनट।
उत्तर
(b) 16 मिनट
प्रश्न 4.
अभिक्रिया H2(g) + Br2(g) → 2HBr(g) के लिए प्रायोगिक आँकड़े दर्शाते हैं कि
अभिक्रिया दर =k1 [H2] [Br2]1/2
अभिक्रिया की आण्विकता तथा कोटि है, क्रमश: –
(a) 2,\(\frac{3}{2}\)
(b) \(\frac{3}{2},\frac{3}{2}\)
(c) 1,1
(d) 1,\(\frac{1}{2}\)
उत्तर
(a) 2,\(\frac{3}{2}\)
प्रश्न 5.
निम्नलिखित अभिक्रिया
2FeCl3 + SnCl2 → 2FeCl2 + SnCl4 उदाहरण है –
(a) प्रथम कोटि की अभिक्रिया का
(b) द्वितीय कोटि की अभिक्रिया का
(c) तृतीय कोटि की अभिक्रिया का
(d) इनमें से कोई नहीं।
उत्तर
(d) इनमें से कोई नहीं।
प्रश्न 6.
अभिक्रिया 2A + B → A2B में अभिकारक A के समाप्त होने की दर –
(a) B के घटने की दर की आधी है
(b) B के घटने की दर के समान है
(c) B के घटने की दर की दो गुनी है
(d) A2B के उत्पादन की दर के समान है।
उत्तर
(b) B के घटने की दर के समान है
प्रश्न 7.
इक्षु शर्करा का ग्लूकोज एवं फ्रक्टोज में अभिक्रिया
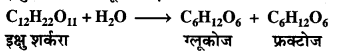
के अनुसार प्रतिलोमन होना एक उदाहरण है –
(a) प्रथम कोटि की अभिक्रिया का
(b) द्वितीय कोटि की अभिक्रिया का
(c) तृतीय कोटि की अभिक्रिया का
(d) शून्य कोटि की अभिक्रिया का।
उत्तर
(a) प्रथम कोटि की अभिक्रिया का
प्रश्न 8.
एक दिये गये ताप पर अभिक्रिया की गति मन्द हो जाती है जबकि –
(a) सक्रियण की प्रात्यतम ऊर्जा उच्चतर होती है
(b) सक्रियण की प्रात्यतम ऊर्जा निम्नतर होती है
(c) एण्ट्रॉपी परिवर्तित होती है
(d) अभिकारकों की प्रारंभिक सान्द्रता स्थिर होती है।
उत्तर
(a) सक्रियण की प्रात्यतम ऊर्जा उच्चतर होती है
प्रश्न 9.
पौधे स्टार्च का निर्माण करते हैं –
(a) फ्लैश फोटोलिसिस से
(b) फोटोलिसिस से
(c) प्रकाश-संश्लेषण से
(d) इनमें से कोई नहीं।
उत्तर
(c) प्रकाश-संश्लेषण से
प्रश्न 10.
प्रथम कोटि की अभिक्रिया के लिए विशिष्ट अभिक्रिया स्थिरांक निर्भर करता है –
(a) अभिकारकों की सान्द्रता पर
(b) उत्पाद की सान्द्रता पर
(c) समय पर
(d) ताप पर।
उत्तर
(d) ताप पर।
प्रश्न 11.
A तथा B से C प्राप्त करने की अभिक्रिया में A में प्रथम कोटि गतिज तथा B में द्वितीय कोटि प्रदर्शित करती है। दर समीकरण लिखा जाएगा –
(a) दर = k[A]2[B]
(b) दर = k[A][B]2
(c) दर = k[A]1/2[B]
(d) दर = k[A][B]1/2
उत्तर
(b) दर = k[A][B]2
प्रश्न 12.
शर्करा के प्रतीपन की अभिक्रिया की आण्विकता है –
(a) 3
(b) 2
(c) 1
(d) 0.
उत्तर
(c) 1
प्रश्न 13.
अणुओं के अभिक्रिया में भाग लेने हेतु न्यूनतम आवश्यक ऊर्जा कहलाती है –
(a) स्थितिज ऊर्जा
(b) गतिज ऊर्जा
(c) नाभिकीय ऊर्जा
(d) सक्रियण ऊर्जा।
उत्तर
(d) सक्रियण ऊर्जा।
प्रश्न 14.
2A + B → A2B रासायनिक अभिक्रिया में यदि A का सान्द्रण दुगुना एवं B का सान्द्रण स्थिर कर दिया जाता है, तो अभिक्रिया की दर –
(a) चार गुना बढ़ जाएगी
(b) दो गुना कम हो जाएगी
(c) दो गुना बढ़ जाएगी
(d) अपरिवर्तित रहेगी।
उत्तर
प्रश्न 15.
द्वितीय कोटि की अभिक्रिया में अर्द्ध-आयुकाल
(a) प्रारंभिक सान्द्रण के समानुपाती होती है
(b) प्रारंभिक सान्द्रण पर निर्भर नहीं करती
(c) प्रारंभिक सान्द्रण के व्युत्क्रमानुपाती होती है
(d) प्रारंभिक सान्द्रण के वर्ग के व्युत्क्रमानुपाती होती है।
उत्तर
(d) प्रारंभिक सान्द्रण के वर्ग के व्युत्क्रमानुपाती होती है।
प्रश्न 16.
2H2O2 → 2H2O + O2 अभिक्रिया है –
(a) शून्य कोटि की अभिक्रिया
(b) प्रथम कोटि की अभिक्रिया
(c) द्वितीय कोटि की अभिक्रिया
(d) तृतीय कोटि की अभिक्रिया।
उत्तर
(c) द्वितीय कोटि की अभिक्रिया
प्रश्न 17.
एक यौगिक का ऊष्मीय अपघटन प्रथम कोटि का है। यदि यौगिक के एक नमूने का 120 मिनट में 50% अपघटन होता है, तो 90% अपघटन में कितना समय लगेगा –
(a) लगभग 240 मिनट
(b) लगभग 480 मिनट
(c) लगभग 450 मिनट
(d) लगभग 400 मिनट।
उत्तर
(b) लगभग 480 मिनट
प्रश्न 18.
आीनियस समीकरण है –
(a) k = \(e^{-\mathrm{E}_{n} \mathrm{RT}}\)
(b) k = \(\frac{E_{a}}{R T}\)
(c) k = \(\frac{E_{a}}{R T}\)
(d) k = \(\mathrm{A} e^{-\mathrm{E}_{a} / \mathrm{RT}}\)
उत्तर
(d) k = \(\mathrm{A} e^{-\mathrm{E}_{a} / \mathrm{RT}}\)
प्रश्न 19.
जब ताप में वृद्धि होता है, तो अभिक्रिया का दर बढ़ जाता है। इसका कारण –
(a) सक्रियण ऊर्जा में कमी होता है
(b) संघटनों की संख्या में वृद्धि होता है
(c) सक्रियित अणुओं की संख्या में कमी होता है
(d) संघटनों की संख्या में कमी होना।
उत्तर
(b) संघटनों की संख्या में वृद्धि होता है
प्रश्न 20.
द्वितीय कोटि की रासायनिक अभिक्रिया के वेग स्थिरांक की इकाई है –
(a) मोल-1 लिटर-1 सेकण्ड-1
(b) मोल लिटर-1 सेकण्ड-1
(c) मोल लिटर सेकण्ड
(d) मोल-1 लिटर सेकण्ड-1 |
उत्तर
(d) मोल-1 लिटर सेकण्ड-1 |
प्रश्न 21.
अभिक्रिया 2N2O5 ⇌ 2NO2O4+O2 है –
(a) द्वि-अणुक एवं द्वितीय कोटि की
(b) एक-अणुक एवं प्रथम कोटि की
(c) द्वि-अणुक एवं प्रथम कोटि की
(d) द्वि-अणुक एवं शून्य कोटि की।
उत्तर
(c) द्वि-अणुक एवं प्रथम कोटि की
प्रश्न 22.
प्रथम कोटि की अभिक्रिया में वेग स्थिरांक की इकाई है
(a) mol L-1S-1
(b) mol-1LS-1
(c) S-1
(d) mol L-1S.
उत्तर
(c) S-1
प्रश्न 23.
एक प्रथम कोटि की अभिक्रिया के लिए 90% पूर्ण होने में लगने वाला समय लगभग होता है –
(a) अर्द्ध-आयु का 1.1 गुना
(b) अर्द्ध-आयु का 2.2 गुना
(c) अर्द्ध-आयु का 3.3 गुना
(d) अर्द्ध-आयु का 4.4 गुना।
उत्तर
(c) अर्द्ध-आयु का 3.3 गुना
प्रश्न 24.
रासायनिक अभिक्रिया की दर निर्भर करती है –
(a) सक्रिय द्रव्यमान पर
(b) परमाणु द्रव्यमान पर
(c) तुल्यांकी भार पर
(d) आण्विक द्रव्यमान पर।
उत्तर
(a) सक्रिय द्रव्यमान पर
प्रश्न 25.
द्रव्य-अनुपाती क्रिया के नियम का प्रतिपादन किसने किया –
(a) डॉल्टन ने
(b) गुल्डवर्ग तथा वागे ने
(c) हुण्ड तथा मुलीकन ने
(d) आर्टीनियस ने।
उत्तर
(b) गुल्डवर्ग तथा वागे ने
प्रश्न 26.
अभिक्रिया दर का मात्रक है –
(a) मोल लिटर -1 सेकण्ड-1
(b) मोल -1 लिटर सेकण्ड-1
(c) मोल -1 लिटर-1 सेकण्ड
(d) मोल लिटर सेकण्ड।
उत्तर
(a) मोल लिटर -1 सेकण्ड-1
2. रिक्त स्थानों की पूर्ति कीजिए –
- किसी अभिक्रिया की दर अभिकारक स्पीशीज के सान्द्रण पर निर्भर नहीं है, तो उस अभिक्रिया की कोटि है ………………..।
- किसी रेडियोधर्मी तत्व का अर्द्ध-आयुकाल 140 दिन है, आरम्भ में 1g तत्व लेने पर 560 दिनों के बाद बच जाएगा ………………….. gm.
- तीव्र अभिक्रियाएँ ………………. सेकण्ड से भी कम समय में सम्पन्न हो जाती है।
- किसी अभिक्रिया की क्रियाविधि में मन्द गति से चलने वाला पद ……………….. कहलाता है।
- ………………… द्वारा तीव्र गति से चलने वाली अभिक्रियाओं का अध्ययन किया जाता है।
- तृतीय कोटि की अभिक्रिया के लिए दर स्थिरांक की इकाई ………………… होती है।
- अभिकारकों की निम्नतम तथा उच्चतम ऊर्जा अवस्था का अन्तर ………………… कहलाती है।
- वे अभिक्रियाएँ जो विकिरण के अवशोषण से सम्पन्न होती हैं ………………. कहलाती हैं।
- अभिक्रिया में भाग लेने वाले कुल अणुओं की संख्या ………………. कहलाती है।
- ………………… से अभिक्रिया की क्रियाविधि के संबंध में जानकारी मिलती है।
- एथिल एसीटेट का अम्लीय माध्यम में जल-अपघटन एक ………… कोटि की अभिक्रिया है।
- अणुसंख्यता सदैव …………. होती है।
- एक मोल अभिकारक को उत्तेजित करने के लिए …………. फोटॉन की आवश्यकता होती है।
- समय के किसी विशेष क्षण पर किसी अभिकारक के सान्द्रण में परिवर्तन की दर उस समय की ……………. दर कहलाती है।
- अभिक्रिया की दर अभिकारक के सान्द्रण के …………… होता है।
- cm-1…………… का मात्रक है।
उत्तर
- शून्य,
- \(\frac{1}{16}\) gm,
- 10-9
- दर-निर्धारक पद,
- फ्लैश फोटोलिसिस,
- लिटर 2 मोल 2 सेकण्ड -1,
- सक्रियण ऊर्जा,
- प्रकाश-रासायनिक अभिक्रियाएँ,
- आण्विकता,
- अभिक्रिया की कोटि,
- आभासी एक अणुक,
- पूर्णांक संख्या,
- एक मोल,
- तात्क्षणिक,
- समानुपाती,
- सेल स्थिरांक।
3. उचित संबंध जोड़िए –

उत्तर
1. (c), 2. (e), 3. (a), 4. (b), 5. (d), 6. (g), 7. (1).
4. एक शब्द/वाक्य में उत्तर दीजिए –
- देहली ऊर्जा और सक्रियण ऊर्जा में क्या संबंध है ?
- प्रथम कोटि की अभिक्रिया के लिए दर-स्थिरांक का व्यंजक क्या है ?
- आर्चीनियस समीकरण का समाकलित रूप लिखिए।
- अभिक्रिया A + B → Cशून्य कोटि की हो, तो दर समीकरण लिखिए।
- किसी अभिक्रिया के लिए दर समीकरण
दर = k [NO2]2 [Cl2]
हो, तो Cl2 के सापेक्ष तथा NO2 के सापेक्ष अभिक्रिया की कोटि तथा अभिक्रिया की कुल कोटि बताइए। - अभिकारकों तथा उत्पादों के सान्द्रण के आधार पर निम्नलिखित अभिक्रियाओं के लिए दर व्यंजक लिखिए- ‘
2NO2 → 2NO + O2. - दर निर्धारक पद क्या होता है ?
- शून्य कोटि की अभिक्रिया का एक उदाहरण लिखिए।
- क्वाण्टम दक्षता क्या है ?
- आीनियस समीकरण लिखिए।
- प्रथम कोटि की अभिक्रिया के अर्द्ध-आयुकाल ज्ञात करने का व्यंजक लिखिए।
- अभिकारक के पृष्ठ क्षेत्रफल का अभिक्रिया की दर पर क्या प्रभाव पड़ता है ?
- तात्क्षणिक दर किसे कहते हैं ?
- अभिक्रिया का अर्द्ध-आयुकाल क्या है ?
- शून्य कोटि की अभिक्रिया के लिए दर स्थिरांक की इकाई लिखिए।
- देहली ऊर्जा को समझाइए।
- तीव्र अभिक्रियाएँ किसे कहते हैं ?
- शून्य कोटि की अभिक्रिया के लिए t1/2 किसके समानुपाती है ?
उत्तर
- सक्रियण ऊर्जा = देहली ऊर्जा – अणुओं की आद्य अवस्था में ऊर्जा ।
या देहली ऊर्जा = सक्रियण ऊर्जा + अणुओं की मूल अवस्था में ऊर्जा। - k =\(\frac{2 \cdot 303}{t}\) \(\log _{10} \frac{a}{a-x}\)
- \(\log _{10} \frac{k_{2}}{k_{1}}\) = \(\frac{E_{a}}{2 \cdot 303 R}\left[\frac{T_{2}-T_{1}}{T_{1} T_{2}}\right]\)
- –\(\frac{d x}{d r}\) = K[A]0[B]0
- Cl2 के सापेक्ष कोटि = 1
NO2 के सापेक्ष कोटि = 2
अतः कुल कोटि = 1 + 2 = 3 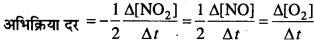
- अभिक्रिया के पदों में सबसे धीमा At
विघटित अणुओं की संख्या पद, 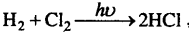

- k =\(\mathrm{A} e^{-\mathrm{E}_{a} / \mathrm{RT}}\)
- \(t_{1 / 2}=\frac{0.693}{k}\)
- पृष्ठ क्षेत्रफल अधिक होने से अभिक्रिया की दर बढ़ जाती है,
- समय के किसी विशेष क्षण पर किसी अभिकारक या उत्पाद के सान्द्रण में परिवर्तन की दर, उस समय की तात्क्षणिक दर कहलाती है,
- किसी अभिक्रिया का अर्द्ध-आयुकाल वह समय है जिसमें अभिक्रिया का सान्द्रण घटकर आधा रह जाता है,
- लिटर मोल-1सेकण्ड-1,
- ऊर्जा की उस न्यूनतम मात्रा को देहली ऊर्जा कहते हैं, जो उन अणुओं के पास होती है जो प्रभावी कारकों द्वारा अभिक्रिया को सम्पन्न करते हैं,
- वे अभिक्रियाएँ जो 10-9 सेकण्ड अथवा उससे कम समय में भी संपन्न हो जाती हैं, तीव्र अभिक्रियाएँ कहलाती हैं,
- प्रारंभिक सांद्रण।
रासायनिक बलगतिकी अति लघु उत्तरीय प्रश्न
प्रश्न 1.
प्रथम कोटि की अभिक्रिया किसे कहते हैं ?
उत्तर
वे अभिक्रियाएँ, जिनमें अभिक्रिया का वेग केवल एक अणु के सान्द्रण पर निर्भर करता है, प्रथम कोटि की अभिक्रियाएँ कहलाती हैं।
प्रश्न 2.
ऊर्जा अवरोध क्या है ?
उत्तर
उस न्यूनतम ऊर्जा को जिसे प्राप्त करने के बाद ही अभिकारक अणु उत्पाद में परिवर्तित हो सकते हैं, ऊर्जा अवरोध कहलाते हैं । अभिकारी अणु जब तक इस शिखर की ऊँचाई (सक्रियण ऊर्जा) तक नहीं पहुँचते तब तक वे सक्रियित संकुल नहीं बना सकते और उत्पाद में परिवर्तित नहीं हो सकते।
प्रश्न 3.
दर निर्धारक पद को समझाइए।
उत्तर
कुछ रासायनिक अभिक्रियाएँ एक से अधिक पदों में संपन्न होती है। अभिक्रिया की दर का निर्धारण सबसे धीमी गति से होने वाले पद द्वारा होता है, जिसे दर निर्धारक पद (Rate determining step) कहते हैं।
प्रश्न 4.
प्रकाश-रासायनिक अभिक्रियाओं की विशेषताएँ लिखिए। (कोई तीन)
उत्तर
विशेषताएँ-
- इन अभिक्रियाओं के लिए चुम्बकीय विकिरणों का अवशोषण होना आवश्यक है।
- ये अभिक्रियाएँ ताप से अप्रभावित रहती है, किन्तु विकिरणों की तीव्रता इनकों प्रभावित करती है।
- क्रियाकारी अणुओं को सक्रिय करने के लिये प्रकाश का होना आवश्यक है।
प्रश्न 5.
आर्चीनियस समीकरण की क्या उपयोगिता है ? (कोई दो)
उत्तर
उपयोगिता-
- सक्रियण ऊर्जा की गणना करने में।
- किसी अभिक्रिया के लिए एक ताप पर वेग स्थिरांक ज्ञात होने पर दूसरे ताप पर वेग स्थिरांक ज्ञात करने में।
प्रश्न 6.
प्रकाश-रासायनिक अभिक्रिया किसे कहते हैं ? एक उदाहरण दीजिए।
उत्तर
ऐसी अभिक्रियाएँ जो प्रकाश अथवा किसी अन्य विद्युत्-चुम्बकीय विकिरणों के कारण प्रेरित होती है, प्रकाश-रासायनिक अभिक्रियाएँ कहलाती है। इन विकिरणों की तरंगदैर्घ्य 2000Å से 8000Å तक होती है।
उदाहरण-

प्रश्न 7.
विशिष्ट अभिक्रिया दर किसे कहते हैं ?
उत्तर
किसी अभिक्रिया की विशिष्ट अभिक्रिया दर दिये गये ताप पर अभिक्रिया की उस दर के बराबर होती है, जब प्रत्येक अभिकारक का सान्द्रण इकाई में लिया गया हो।
अभिक्रिया A2(g) + B2(g) →2AB(g)
अभिक्रिया दर ∝ [A2][B2]
= K[A2][B2]
यदि, [A2] = [B2] = 1 हो, तो
अभिक्रिया दर =K
जहाँ, K विशिष्ट अभिक्रिया दर-स्थिरांक हैं।
प्रश्न 8.
अभिक्रिया की औसत दर का मान कब उसकी तात्कालिक अभिक्रिया दर के बराबर हो जाता है ?
उत्तर
जब समय अंतराल At का मान लगभग शून्य हो जाता है या जब समय अनंत रूप से सूक्ष्म होता है, तब अभिक्रिया की औसत दर उसकी तात्कालिक अभिक्रिया दर के तुल्य हो जाती है। अत: अभिक्रिया की तात्कालिक दर \(\frac{d x}{d t}=\lim _{\Delta t \rightarrow 0} \frac{\Delta x}{\Delta t}\) होती है।
प्रश्न 9.
छद्म एकाणुक अभिक्रिया को उदाहरण सहित समझाइए।
उत्तर
कुछ अभिक्रियाएँ ऐसी होती है, जिनकी अणुसंख्यता दो होती है किन्तु उनका गतिक अध्ययन करने पर ज्ञात होता है कि उनकी अभिक्रिया कोटि एक है। ऐसी अभिक्रियाएँ को छद्म एकाणुक अभिक्रियाएँ कहते हैं।
उदाहरण –
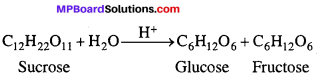
उपर्युक्त अभिक्रिया द्विअणुक है, लेकिन जल की सान्द्रता अभिक्रिया की दर को प्रभावित नहीं करती हैं। अतः अभिक्रिया की दर केवल शर्करा की सान्द्रता के समानुपाती होती है।
दर = k[C12H22O11]
अतः शर्करा का प्रतिलोमन प्रथम कोटि की अभिक्रिया है। इसे छद्म एकाणुक अभिक्रिया कहते हैं।
प्रश्न 10.
तापमान गुणांक किसे कहते हैं ?
उत्तर
कुछ रासायनिक अभिक्रियाओं में केवल ताप में 10°C वृद्धि करने पर अभिक्रिया दर दो गुना या तीन गुना हो जाता है।
ताप के इस प्रभाव को तापमान गुणांक द्वारा दर्शाते हैं,

इसे तापमान गुणांक कहते है।
विभिन्न समय पर अभिक्रिया दर का अनुपात जिनके मध्य 10°C ताप का अंतर हो, उसे तापमान गुणांक कहते हैं।
रासायनिक बलगतिकी लघु उत्तरीय प्रश्न
प्रश्न 1.
रासायनिक अभिक्रिया की दर से आप क्या समझते हैं ? इसकी इकाई लिखिए।
उत्तर
किसी रासायनिक अभिक्रिया की दर इकाई समय अन्तराल में अभिकारक अथवा उत्पाद के सान्द्रण में परिवर्तन के बराबर होती है।
![]()
समयान्तराल अभिक्रिया दर की इकाई, सान्द्रण की इकाई तथा समय की इकाई पर निर्भर करती है। यदि सान्द्रण को मोल प्रति लीटर में तथा समय को सेकण्ड में व्यक्त किया जाये तो अभिक्रिया की दर की इकाई मोल प्रति लीटर प्रति सेकण्ड प्राप्त होती है। यदि समय को मिनट में दर्शाया जाये तो अभिक्रिया दर की इकाई मोल प्रति लीटर प्रति मिनट होगी ।
प्रश्न 2.
अभिक्रिया की तात्कालिक दर से क्या तात्पर्य है ?
उत्तर
किसी विशेष क्षण पर निकाली गई अभिक्रिया की दर को तात्कालिक दर (Instantaneous reaction rate) कहते हैं। किसी अभिक्रिया की दर अभिकारकों के सान्द्रण पर निर्भर करती है। समय बीतने पर अभिकारकों का सान्द्रण कम होता जाता है, अतः अभिक्रिया की दर भी कम होने लगती है। किसी अभिक्रिया की दर को अधिक यथार्थ रूप में दर्शाने के लिए उसकी तात्कालिक दर अधिक यथार्थ मान प्रस्तुत करती है ।
तात्कालिक या तात्क्षणिक वेग = \(\left[-\frac{\Delta \mathrm{A}}{\Delta t}\right]_{\Delta \mathrm{T} \rightarrow 0}
= -\frac{d[\mathrm{A}]}{d t}\)
जहाँ, d[A] सान्द्रण में अति अल्प परिवर्तन है, जो अति अल्प समय अन्तराल dt में होता है।
प्रश्न 3.
किसी अभिक्रिया की आण्विकता (अणुसंख्यता) से आप क्या समझते हैं ?
उत्तर
अभिक्रिया की अणुसंख्यता (Molecularity of a reaction)- कई रासायनिक अभिक्रियाएँ एक से अधिक पदों में सम्पन्न होती हैं । अभिक्रिया की दर का निर्धारण सबसे धीमी गति से होने वाले पद द्वारा होता है। इस पद को दर निर्धारक पद (Rate determining step) कहते हैं।
“दर निर्धारक पद में भाग लेने वाले अणुओं, परमाणुओं तथा आयनों की संख्या को अणुसंख्यता (Molecularity) कहते हैं ।” अथवा
“किसी रासायनिक अभिक्रिया के सम्पन्न होने के लिए उसके आरम्भिक पद (Elementary step) में भाग लेने वाले अणुओं की संख्या को अणुसंख्यता कहते हैं ।”
O3 → O2 +O (एकाणुक अभिक्रिया)
NO + O3 →NO2 +O2 (द्विअणुक अभिक्रिया)
प्रश्न 4.
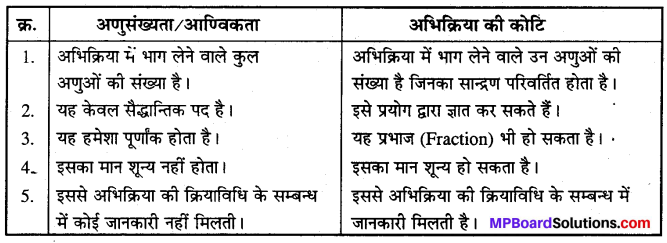
अभिक्रिया की आण्विकता और अभिक्रिया की कोटि में चार अन्तर लिखिए।
उत्तर
अभिक्रिया की आण्विकता और अभिक्रिया की कोटि में अन्तर –
प्रश्न 5.
रासायनिक अभिक्रिया की दर को प्रभावित करने वाले किन्हीं चार कारकों को संक्षेप में । समझाइए।
उत्तर
किसी रासायनिक अभिक्रिया की दर को प्रभावित करने वाले कारक निम्नलिखित हैं
- अभिकारकों का सान्द्रण-किसी भी अभिक्रिया का वेग क्रियाकारकों की सान्द्रता के समानुपाती होता है । अभिकारकों का सान्द्रण बढ़ाने पर अभिक्रिया की दर में वृद्धि हो जाती है। समय के साथ क्रियाकारकों का सान्द्रण कम होने पर अभिक्रिया की दर भी कम हो जाती है।
- अभिक्रिया का ताप-ताप वृद्धि का अभिक्रिया की दर पर अत्यधिक प्रभाव पड़ता है। उच्च ताप पर अभिक्रिया की दर बढ़ जाती है।
- उत्प्रेरक की उपस्थिति उत्प्रेरक अभिक्रिया की दर को बढ़ा या घटा देते हैं। धनात्मक उत्प्रेरक क्रिया की दर में वृद्धि करते हैं तथा ऋणात्मक उत्प्रेरक क्रिया की दर घटा देते हैं।
- क्रियाकारकों की प्रकृति-क्रियाकारकों की प्रकृति का भी अभिक्रिया की दर पर बड़ा प्रभाव पड़ता है । किसी भी रासायनिक अभिक्रिया में कुछ पुराने बन्ध टूटते हैं व नये बन्ध बनते हैं। अतः अणु जितने सरल होंगे उतने ही उसमें कम बन्ध टूटेंगे और अभिक्रिया की गति तेज हो जाएगी जबकि जटिल अणुओं में अधिक बन्ध टूटेंगे अतः उनका वेग कम हो जाएगा।
- विकिरण का प्रभाव-कुछ अभिक्रियाओं का वेग विशिष्ट विकिरणों के अवशोषण से भी बढ़ जाता है। उदाहरणार्थ, प्रकाश की अनुपस्थिति में हाइड्रोजन तथा क्लोरीन के मध्य अभिक्रिया धीमी गति से होती है, किन्तु प्रकाश की उपस्थिति में यह अभिक्रिया तीव्र गति से होती है।
प्रश्न 6.
दर-स्थिरांक के लक्षण बताइए।
उत्तर
दर-स्थिरांक के लक्षण निम्नलिखित हैं –
- दर-स्थिरांक (k) अभिक्रिया की दर की माप होती है।
- प्रत्येक अभिक्रिया के लिए दर-स्थिरांक (k) के मान भिन्न-भिन्न होते हैं।
- निश्चित ताप पर k का मान निश्चित होता है।
- दर-स्थिरांक, अभिक्रिया की कोटि पर निर्भर करता है।
प्रश्न 7.
अभिक्रिया की कोटि से आप क्या समझते हैं ? उदाहरण दीजिए। .
उत्तर
अभिक्रिया की कोटि (Order of Reaction)-किसी अभिक्रिया की कोटि को हम इस प्रकार परिभाषित कर सकते हैं –
“किसी अभिक्रिया की कोटि उन समस्त घातों का योग है जिन्हें अभिक्रिया की प्रेक्षित दर को दर्शाने के लिए दर-नियम समीकरण में सान्द्रण-पदों पर लगाया जाना चाहिए।”
मानलो सामान्य अभिक्रिया aA + bB + cC → Products के लिए दर-नियम समीकरण इस प्रकार हैं –
दर = –\(\frac{d x}{d t}\) = k[A]p[B]q [C]r”
तो सम्पूर्ण अभिक्रिया की कोटि n = p+q+r
जिसमें p,q तथा r क्रमश: A, B तथा C के सापेक्ष अभिक्रिया की कोटि हैं। अभिक्रिया की कुल कोटि n घातों के योग p+q+r के बराबर होती है।
n= 1 हो, तो अभिक्रिया की कोटि एक तथा n = 2 हो तो अभिक्रिया की कोटि 2 होती है, आदि। उदाहरणार्थ, अमोनियम नाइट्राइट का विघटन इस प्रकार होता है –
NH4NO2 → N2 + 2H2O
अभिक्रिया की दर = –\(\frac{d x}{d t}\) = k[NH4NO2]
अतः इस अभिक्रिया की कोटि 1 होगी।
प्रश्न 8.
शून्य कोटि की अभिक्रिया किसे कहते हैं ? इसका एक उदाहरण दीजिए।
उत्तर
ऐसी अभिक्रियाएँ जिनकी दर अभिकारकों के सान्द्रण पर निर्भर नहीं करती, शून्य कोटि की अभिक्रिया कहलाती हैं।
उदाहरण-Au, Pt जैसी धातुओं के सम्पर्क में आने पर अमोनियो का विघटन हो जाता है, जो शून्य कोटि की अभिक्रिया है।
![]()
यह पाया गया है कि इस अभिक्रिया की दर अमोनिया के सान्द्रण पर निर्भर नहीं होती है।
अभिक्रिया दर = –\(\frac{d x}{d t}\) = k[NH3]°
इस अभिक्रिया की कोटि शून्य होती है।
प्रश्न 9.
किसी अभिक्रिया का वेग ताप पर किस प्रकार निर्भर करता है ? समझाइए।
उत्तर
ताप वृद्धि से सामान्यतः किसी रासायनिक अभिक्रिया की दर में वृद्धि हो जाती है। कई रासायनिक अभिक्रियाओं में 10 K ताप वृद्धि से अभिक्रिया की दर दुगुनी से पाँच गुनी तक बढ़ जाती है।
10°C ताप वृद्धि से अभिक्रिया का वेग दो से तीन गुना तक बढ़ जाता है। यदि एक ताप t °C पर किसी अभिक्रिया का वेग स्थिरांक kt है और उससे 10°C अधिक अर्थात् (t+10)°C ताप पर उसका वेग स्थिरांक kt +10°C है, तो उसका ताप गुणांक (Temperature coefficient)
\(\frac{k_{t}+10}{k_{t}} = 2\) से 3 के बीच
समांगी गैसीय अभिक्रियाओं में ताप परिवर्तन से वेग स्थिरांक में होने वाला परिवर्तन आर्टीनियस समीकरण द्वारा दिया जा सकता है जो निम्न प्रकार है
k =\(\mathrm{A} e^{-\mathrm{E}_{a} / \mathrm{RT}}\)
प्रश्न 10.
सक्रियण ऊर्जा पर संक्षिप्त टिप्पणी लिखिए।
उत्तर
सक्रियण ऊर्जा—ऊर्जा की वह न्यूनतम मात्रा जो देहली ऊर्जा से कम ऊर्जा वाले अणुओं को प्राप्त करनी पड़ती है, ताकि वे ऊर्जा अवरोध को पार कर सकें, सक्रियण ऊर्जा कहलाती है।
किसी अभिक्रिया के सम्पन्न होने के लिए यह आवश्यक है कि अभिकारकों की ऊर्जा सक्रियण ऊर्जा के बराबर तो होनी ही चाहिए। उत्प्रेरक की उपस्थिति से इसके मान को कम किया जा सकता है जिससे कम ऊर्जा पाकर भी अभिक्रिया सम्पन्न हो सकती है। सक्रियण ऊर्जा को Ea लिखा जाता है।
सक्रियण ऊर्जा को आीनियस समीकरण के आधार पर ज्ञात किया जा सकता है –
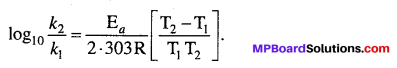
प्रश्न 11.
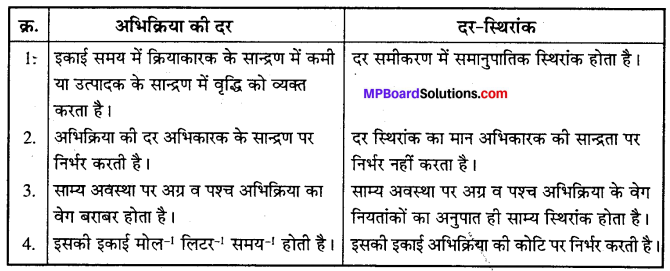
अभिक्रिया की दर तथा दर-स्थिरांक में अंतर दीजिए।
उत्तर
अभिक्रिया की दर तथा दर-स्थिरांक में अंतर –
प्रश्न 12.
सिद्ध कीजिए कि शून्य कोटि की अभिक्रिया का अर्द्ध-आयुकाल अभिकारक की प्रारंभिक सान्द्रता के समानुपाती होता है।
उत्तर
यदि अभिक्रिया का वेग अभिकारकों के सान्द्रता पर निर्भर नहीं करता है तो वह अभिक्रिया शून्य कोटि की अभिक्रिया कहलाती है। . शून्य कोटि की अभिक्रिया के लिए दर-स्थिरांक व सान्द्रण के संबंध को निम्न समीकरण से व्यक्त करते है –
k=\(\frac{[\mathrm{A}]_{0}-[\mathrm{A}]}{t}\) ……………..(1)
अर्द्ध-आयुकाल t1/2 पर [A] = \(\frac{1}{2}\)[A]o
यह मान समी. (1) में रखने पर, .
K = \(\frac{[\mathrm{A}]_{0}-\frac{1}{2}[\mathrm{A}]}{t_{1 / 2}}\)
या t1/2 = \(\frac{1}{2} \frac{[\mathrm{A}]_{0}}{\mathrm{K}}\)
या t1/2 ∝ [A]0
अर्थात शून्य कोटि की अभिक्रिया का अर्द्ध-आयुकाल अभिकारक के प्रारंभिक सान्द्रता के समानुपाती होता है।
प्रश्न 13.
सिद्ध कीजिए कि प्रथम कोटि की अभिक्रिया का अर्द्ध-आयुकाल अभिकारक के प्रारंभिक सान्द्रण पर निर्भर नहीं होता।
उत्तर
प्रथम कोटि की अभिक्रिया का अर्द्ध-आयुकाल अभिकारक के प्रारंभिक सान्द्रण पर निर्भर नहीं होता सिद्ध करना –
किसी अभिक्रिया का अर्द्ध-आयुकाल वह समय है, जिसमें आधी अभिक्रिया पूर्ण हो जाती है। अर्द्धआयुकाल को t1/2 द्वारा दर्शाते हैं। प्रथम कोटि की अभिक्रिया के लिए अर्द्ध-आयुकाल की गणना इस प्रकार की जा सकती है। प्रथम कोटि की अभिक्रिया के लिए समाकलित दर समीकरण (Integrated rate equation) इस प्रकार है

समीकरण (6) यह दर्शाता है कि प्रथम कोटि की अभिक्रिया के लिए अर्द्ध-आयुकाल का मान अभिकारक के प्रारंभिक सान्द्रण पर निर्भर नहीं होता।
प्रश्न 14.
समाकलित दर नियम विधि क्या है ? टिप्पणी लिखिए।
उत्तर
प्रथम कोटि की अभिक्रिया के लिए समाकलित दर समीकरण निम्न प्रकार है –
k = \(\frac{2 \cdot 303}{t} \log \frac{a}{(a-x)}\)
इस समीकरण से अभिक्रिया की कोटि की गणना की जा सकती है। अभिकारक की प्रारम्भिक सान्द्रता
(a) ज्ञात करके किसी निश्चित समय पर सान्द्रता (a-x) का पता कर लेते हैं।
इस प्रकार यदि हम देखें तो उपर्युक्त समीकरण में है तथा (a-X) के मानों को रखकर k के मान की गणना करते हैं, इस प्रकार यदि k का मान निश्चित अथवा स्थिर रहे तो यह निश्चित है कि अभिक्रिया प्रथम कोटि की है। प्रथम कोटि की अभिक्रिया के लिए सान्द्रता के login (a-x) और 1 के मध्य ग्राफ खींचने पर सीधी रेखा प्राप्त होती है। अन्य अभिक्रिया की कोटि के लिए प्राप्त गतिज समीकरण द्वारा अभिक्रिया की उचित कोटि का निर्धारण करते हैं।
प्रश्न 15.
एक प्रथम कोटि की अभिक्रिया 40 मिनट में 90% पूर्ण हो जाती है। इस अभिक्रिया का अर्द्ध-आयुकाल ज्ञात कीजिए। [log 2 = 0.3010]
हल
माना कि अभिकारक की प्रारंभिक सान्द्रता (a) = 100, t = 40 मिनट
40 मिनट में 90% क्रिया पूर्ण होती है, अतः
x= 90
∴ 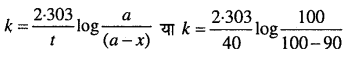
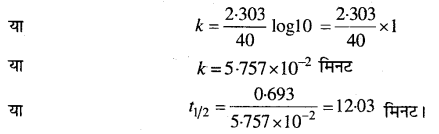
प्रश्न 16.
दर्शाइए कि प्रथम कोटि की अभिक्रिया के लिये 99.9% अभिक्रिया पूर्ण होने में लगा समय उसके अर्द्ध-आयुकाल का लगभग 10 गुना होता है।
हल
यदि अभिकारक की प्रारंम्भिक सान्द्रता a हो, तो x = 0.999a के लिये t = ? प्रथम कोटि की अभिक्रिया के लिये,

प्रश्न 17.
अभिक्रिया की कोटि क्या है ? शून्य कोटि, प्रथम कोटि एवं द्वितीय कोटि की अभिक्रिया के लिए दर-स्थिरांक k का मात्रक लिखिए।
उत्तर
किसी अभिक्रिया की कोटि अभिकारकों के अणुओं की वह संख्या है जिनकी सान्द्रता अभिक्रिया की दर को प्रभावित करती है।
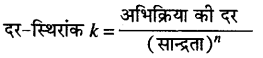
यहाँ, n = अभिक्रिया की कोटि है।
शून्य कोटि के लिये k का मात्रक,
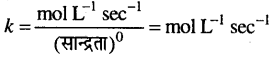
प्रथम कोटि के लिए k का मात्रक,
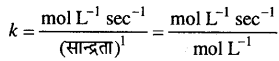
k की इकाई = sec-1
द्वितीय कोटि के लिए k का मात्रक,
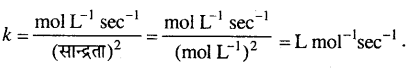
प्रश्न 18.
(a) 2N2O5→ 4NO2 +O22 (b) H2 +I2 → 2HI. अभिक्रिया (a) प्रथम कोटि की है, जबकि अभिक्रिया (b) द्वितीय कोटि की है, क्यों ?
उत्तर
(a) अभिक्रिया 2N2O5→ 4NO2 +O2 के लिए पहले अभिक्रिया की दर और [N2O5] के मध्य ग्राफ खींचते हैं। इसके पश्चात् दूसरा ग्राफ अभिक्रिया की दर तथा [N2O5]2 के मध्य खींचते हैं। यह पाया गया है, कि पहले ग्राफ में सरल रेखा प्राप्त होती है।
अतः दर ∝ [N2O5]
दर = k[N2O5]
अतः अभिक्रिया 2N2O5 → 4NO2 +O2 प्रथम कोटि की है।
(b) अभिक्रिया H2 +I2 → 2HI के लिए अभिक्रिया की दर और [H2][I2] के मध्य खींचा गया ग्राफ सरल रेखा है।
अतः दर = k [H2] [I2]
अर्थात् यह अभिक्रिया द्वितीय कोटि की है।
रासायनिक बलगतिकी दीर्घ उत्तरीय प्रश्न
प्रश्न 1.
शून्य-कोटि की अभिक्रिया के लिए दर-स्थिरांक का व्यंजक ज्ञात कीजिए।
उत्तर
यदि किसी अभिक्रिया का वेग अभिकारकों की सान्द्रता पर निर्भर नहीं करता तो उसे शून्य कोटि की अभिक्रिया कहते हैं।
माना शून्य कोटि की अभिक्रिया निम्न है –
A → B
जहाँ, A तथा B अभिकारक तथा उत्पाद की सान्द्रता हैं। इस प्रकार की अभिक्रिया में अभिक्रिया का वेग अभिकारकों की सान्द्रता पर निर्भर नहीं करता, अभिकारक की सान्द्रता में परिवर्तन की दर स्थिर रहती है।
अभिक्रिया की दर = स्थिरांक
अभिकारक A की प्रारंभिक सान्द्रता a मोल/लीटर है। t समय में A का x मोल उत्पाद में परिवर्तित होता है। अतः t समय बाद A की सान्द्रता (a-x) मोल/लीटर रह जाती है।
–\(\frac{d[\mathbf{A}]}{d t}\) या \(\frac{d x}{d t} \propto(a-x)^{0}\)
या \(\frac{d x}{d t}\) = k0(a-x)0 …………….(1)
जहाँ, k0 = शून्य कोटि की अभिक्रिया का वेग स्थिरांक है।
\(\frac{d x}{d t}\) = k0……………………..(2)
\(\frac{d x}{d t}\) = k0dt ……………………..(3)
समीकरण (3) का समाकलन करने पर,
x= k0t + C ……………………..(4)
जहाँ, C = समाकलन स्थिरांक (Integration constants) है।
जब t = 0 तब x = 0 होता है। यह मान समीकरण (4) में रखने पर,
0 =k0 × 0 + C
अतः C=0 ……………………..(5)
समीकरण (5) का मान समीकरण (4) में रखने पर,
x = k0t ……………..(6)
\(k_{0}=\frac{x}{t}\)………………….(7)
समीकरण (7) शून्य कोटि की अभिक्रिया के लिए दर-स्थिरांक का व्यंजक है। k की इकाई
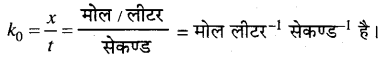
प्रश्न 2.
आर्चीनियस समीकरण पर संक्षिप्त टिप्पणी लिखिए।
उत्तर-आर्चीनियस ने समांगी गैसीय अभिक्रियाओ में ताप से होने वाले परिवर्तन से वेग स्थिरांक में होने वाले परिवर्तन को निम्नलिखित व्यंजक द्वारा दर्शाया –
k = \(\mathrm{A} e^{-\mathrm{E}_{a} / \mathrm{RT}}\)
इसे आर्टीनियस का समीकरण कहते हैं ।
जिसमें A = आवृत्ति कारक (Frequency factor), Ea = सक्रियण ऊर्जा तथा T = परम ताप है। A तथा Ea अभिक्रिया पर निर्भर करते हैं अभिकारकों पर नहीं।
समीकरण का लॉगरिथ्म लेने पर,
\(\ln k=-\frac{\mathrm{E}_{a}}{\mathrm{RT}}+\ln \mathrm{A}\)
या logk = \(\log \mathrm{A}-\frac{\mathrm{E}_{a}}{2 \cdot 303 \mathrm{RT}}\) …………..(1)
यह एक सरल रेखा का समीकरण है। यदि भिन्न-भिन्न तापों पर log10 k तथा \(\frac{1}{\mathrm{T}}\) के मध्य ग्राफ खींचें तो एक सरल रेखा प्राप्त होगी, जिसका ढाल = \(\frac{\mathrm{-E}_{a}}{2 \cdot 303 \mathrm{R}}\) होगा। ग्राफ द्वारा ढाल = \(\frac{\mathrm{E}_{a}}{2 \cdot 303 \mathrm{R}}\) का मान ज्ञात करके सक्रियण ऊर्जा Ea का मान ज्ञात किया जा सकता है।
Ea की गणना एक दूसरी विधि द्वारा भी कर सकते हैं।
मानलो ताप T1 तथा T2 पर किसी अभिक्रिया के वेग स्थिरांक क्रमशः k1 तथा k2 हों, तो समीकरण (1) के अनुसार,
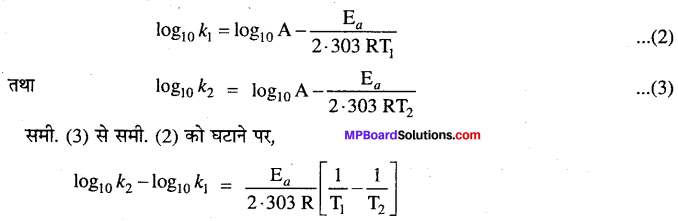
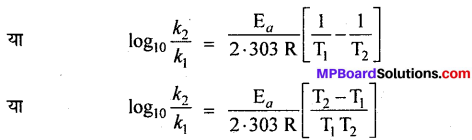
इस समीकरण की सहायता से सक्रियण ऊर्जा E, का मान ज्ञात किया जा सकता है ।
प्रश्न 3.
आीनियस समीकरण को सीधी रेखा के समीकरण के रूप में लिखिए। इस समीकरण में ग्राफ का ढाल क्या होगा ? किसी अपघटन अभिक्रिया के अपघटन के लिए \(\frac{1}{\mathrm{T}}\) तथा log k के बीच खींचे गये ग्राफ से वक्र का ढाल –9920 प्राप्त हुआ। क्रिया के सक्रियण ऊर्जा की गणना कीजिए।
उत्तर
आीनियस समीकरण-आर्चीनियस ने समांगी गैसीय अभिक्रियाओं में ताप से होने वाले परिवर्तन से वेग स्थिरांक k में होने वाले परिवर्तन को निम्नलिखित व्यंजक द्वारा दर्शाया –
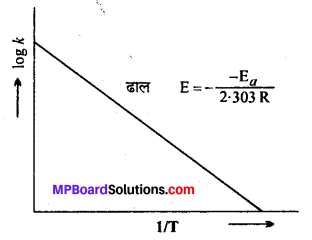
k = \(\mathrm{A} e^{-\mathrm{E}_{a} / \mathrm{RT}}\)
इसे आर्टीनियस का समीकरण कहते हैं।
जहाँ, A = आवृत्ति कारक, Ea = सक्रियण ऊर्जा तथा T = परम ताप है।
समीकरण का लॉगरिथ्म लेने पर,
In k = –\(\frac{\mathrm{E}_{a}}{\mathrm{R} \mathrm{T}}\)
या logk = \(\log \mathrm{A}-\frac{\mathrm{E}_{a}}{2 \cdot 303 \mathrm{RT}}\)
यह एक सरल रेखा का समीकरण है। यदि भिन्न-भिन्न तापों पर log10k तथा \frac{1}{\mathrm{T}} के मध्य ग्राफ खींचें तो एक सरल रेखा प्राप्त होगी, जिसका ढाल (Slope) = \(\frac{-\mathrm{E}_{a}}{2 \cdot 303 \mathrm{R}}\) होगा। ग्राफ द्वारा ढाल =\(\frac{-\mathrm{E}_{a}}{2 \cdot 303 \mathrm{R}}\) का मान ज्ञात करके सक्रियण ऊर्जा Ea का मान ज्ञात किया जा सकता है।
ढाल = \(\frac{-\mathrm{E}_{a}}{2 \cdot 303 \mathrm{R}}\) (सक्रियण ऊर्जा)
उत्तर
या Ea = ढाल x 2.303 x R
या Ea =-9920 x 2.303 x (-4.58)
∴ Ea = 104633.5808 कैलोरी प्रति ग्राम अणु।
प्रश्न 4.
प्रथम कोटि की अभिक्रिया के लिए वेग स्थिरांक का व्यंजक ज्ञात कीजिए।
उत्तर
वे अभिक्रियाएँ, जिनमें अभिक्रिया का वेग केवल एक अणु के सान्द्रण पर निर्भर करता है प्रथम कोटि की अभिक्रियाएँ कहलाती हैं। मानलो प्रथम कोटि की सामान्य अभिक्रिया इस प्रकार है –
A → Product
माना अभिकारक A का प्रारम्भिक सान्द्रण a ग्राम अणु है। सेकण्ड पश्चात x ग्राम अणु, क्रिया कर लेते हैं तो शेष पदार्थ की मात्रा (a-X) ग्राम अणु होगी।
अतः t समय पश्चात् अभिक्रिया की दर A की सान्द्रता (a -x) के समानुपाती होगी।
अर्थात्
\(\frac{d x}{d t}\) ∝A
\(\frac{d x}{d t}\) = a – x
या \(\frac{d x}{d t}\) = k(a-x),
या \(\frac{d x}{(a-x)}=k \cdot d t\) …(1)
सम्पूर्ण क्रिया का वेग ज्ञात करने के लिए समी. (1) का समाकलन करने पर,
\(\int \frac{d x}{a-x}=\int k \cdot d t\)
In(a-x) =kt+c, (यहाँ c समाकलन स्थिरांक है) …(2)
यदि t=0 है तो x = 0 होगा, अतः ये मान समी. (2) में रखने पर,
-In a =c ……………(3)
समी. (3) से c का मान समी. (2) में रखने पर,
-In (a – x) = kt – In a
या In a – In (a-x) = kt
या In \(\frac{a}{a-x}\) = kt
अतः k =\(\frac{1}{t} \ln \frac{a}{a-x}\)
log का आधार e से 10 करने पर,
k = \(\frac{2 \cdot 303}{t} \log \frac{a}{a-x}\)
यह प्रथम कोटि की अभिक्रिया के लिए वेग स्थिरांक k का व्यंजक है।