MP Board Class 11th Physics Solutions Chapter 9 ठोसों के यांत्रिक गुण

MP Board Class 11th Physics Solutions Chapter 9 ठोसों के यांत्रिक गुण

ठोसों के यांत्रिक गुण अभ्यास के प्रश्न एवं उनके उत्तर

प्रश्न 9.1.
4.7 m लम्बे व 3.0 x 10^-5 m²अनुप्रस्थ काट के स्टील के तार तथा 3.5 m लंबे व 4.0 x 10^-5m² अनुप्रस्थ काट के ताँबे के तार पर दिए गए समान परिमाण के भारों को लटकाने पर उनकी लंबाइयों में समान वृद्धि होती है। स्टील तथा ताँबे के यंग प्रत्यास्थता गुणांकों में क्या अनुपात है?
उत्तर:
दिया है: स्टील के तार के लिए
तार की लम्बाई, I₁ = 4.7 m
अनुप्रस्थ काट का क्षेत्रफल
a₁ = 3.0 × 10^-5 m²
माना लम्बाई में वृद्धि,
∆I₂ = ∆l; F₂ = F
माना स्टील व ताँबे के तार के यंग प्रत्यास्थता गुणांक Y₁, व Y₂ हैं।

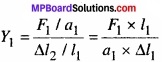
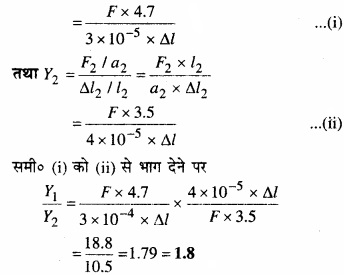
प्रश्न 9.2.
नीचे चित्र में किसी दिए गए पदार्थ के लिए प्रतिबल – विकृति वक्र दर्शाया गया है। इस पदार्थ के लिए –

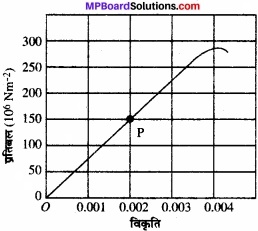
(a) यंग प्रत्यास्थता गुणांक तथा –
(b) सन्निकट पराभव सामर्थ्य क्या है?
उत्तर:
(a) ग्राफ पर स्थित बिन्दु P पर विकृति, E = 0.002
प्रतिबल, σ = 150 × 10⁶ न्यूटन/मीटर²
सूत्र यंग प्रत्यास्थता गुणांक, Y = \(\frac{σ}{E}\) से
y = \(\frac { 150\times 10^{ 6 } }{ 0.002 } \)
= 7.5 × 10¹⁰ न्यूटन/मीटर²
(b) परास व सामर्थ्य = ग्राफ के उच्चतम बिन्दु के संगत प्रतिबल
= 290 × 10⁶ न्यूटन प्रति मीटर ²

प्रश्न 9.3.
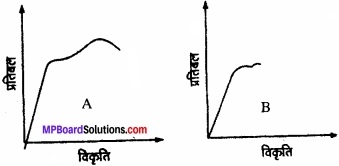
दो पदार्थों A और R के लिए प्रतिबल-विकृति ग्राफ चित्र में दर्शाए गए हैं।
इन ग्राफों को एक ही पैमाना मानकर खींचा गया है।

1. किस पदार्थ का यंग प्रत्यास्थता गुणांक अधिक है?
2. दोनों पदार्थों में कौन अधिक मजबूत है?

उत्तर:

1. ∵ पदार्थ A के ग्राफ का ढाल दूसरे ग्राफ की तुलना में अधिक है; अत: पदार्थ A का यंग गुणांक अधिक है।
2. दोनों ग्राफों पर पराभव बिन्दुओं की ऊँचाई लगभग बराबर है परन्तु पदार्थ A के ग्राफ, पदार्थ B की तुलना में प्लास्टिक क्षेत्र अधिक सुस्पष्ट है; अत: पदार्थ A अधिक मजबूत है।

प्रश्न 9.4.
निम्नलिखित दो कथनों को ध्यान से पढ़िये और कारण सहित बताइये कि वे सत्य हैं या असत्य –

1. इस्पात की अपेक्षा रबड़ का यंग गुणांक अधिक है;
2. किसी कुण्डली का तनन उसके अपरूपण गुणांक से निर्धारित होता है।

उत्तर:

1. असत्य, चूँकि इस्पात व रबड़ से बने एक जैसे तारों में समान विकृति उत्पन्न करने के लिए इस्पात के तार में रबड़ की अपेक्षा अधिक प्रतिबल उत्पन्न होता है। इससे स्पष्ट है कि इस्पात का यंग गुणांक रबड़ से अधिक है।’
2. सत्य, चूँकि हम किसी कुण्डली या स्प्रिंग को खींचते हैं तो न तो स्प्रिंग निर्माण में लगे तार की लम्बाई में कोई परिवर्तन होता है और न ही उसका आयतन परिवर्तित होता है। स्प्रिंग का केवल रूप बदलता है। अतः स्प्रिंग का तनन उसके अपरूपण गुणांक से निर्धारित होता है।

प्रश्न 9.5.
0.25 cm व्यास के दो तार, जिनमें एक इस्पात का तथा दूसरा पीतल का है, चित्र के अनुसार भारित है। बिना भार लटकाए इस्पात तथा पीतल के तारों की लम्बाइयाँ क्रमश: 1.5 m तथा 1.0 m हैं। यदि इस्पात तथा पीतल के यंग गुणांक क्रमश: 2.0 × 10 ¹¹ Pa तथा 0.91 × 10¹¹ Pa हों तो इस्पात तथा पीतल के तारों में विस्तार की गणना कीजिए।
उत्तर:
दिया है: R_s = R_B = 0.125 cm
= 1.25 × 10^-3 m
L_s = 1.5 m, L_B = 1.0 m
Y_s = 2.0 × 10 ¹¹ Pa,
Y_B = 0.91 × 10 ¹¹ Pa
जहाँ S व B क्रमशः इस्पात
(Steel) तथा पीतल (Brass) को प्रदर्शित करते हैं।
पीतल के तार पर केवल 6.0 kg द्रव्यमान के पिंड का भार लगा है, जबकि इस्पात के तार पर (6.0 + 4.0 = 10.0 kg) का भार लगा है।
∴F_B = 6.0 kg × 9.8 Nkg^-1 = 58.8 N
F_S = 10.0 kg × 9.8 Nkg^-1 = 98 N
प्रत्येक का अनुप्रस्थ क्षेत्रफल A = πR²
= 3.14 × (1.25 × 10^-3 m)²
= 4.91 × 10^-6 m²


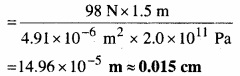
= 14.96 × 10 ^-5 m = 0.015 cm

प्रश्न 9.6.
ऐल्युमिनियम के किसी घन के किनारे 10 cm लम्बे हैं। इसकी एक फलक किसी ऊर्ध्वाधर दीवार से कसकर जुड़ी हुई है। इस घन के सम्मुख फलक से 100 kg का एक द्रव्यमान जोड़ दिया गया है। ऐल्युमीनियम का अपरूपण गुणांक 25 GPa है। इस फलक का ऊर्ध्वाधर विस्थापन कितना होगा?
उत्तर:
दिया है:
अपरूपण गुणांक G = 25 GPa
= 25 × 10⁹ Nm^-2
बल – आरोपित फलक का क्षेत्रफल A =10 cm × 10 cm = 100 × 10 ^-4m²

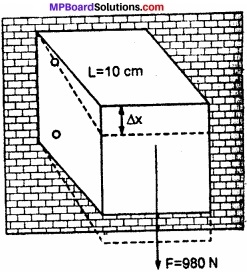
आरोपित बल
F = 100 kg × 9.8 Nkg^-1 = 980 N
माना फलक का ऊर्ध्व विस्थापन = ∆x
जबकि L = 10 cm = 0.1 m

प्रश्न 9.7.
मृदु इस्पात के चार समरूप खोखले बेलनाकार स्तम्भ 50,000 kg द्रव्यमान के किसी बड़े ढाँचे को आधार दिये हुए हैं। प्रत्येक स्तम्भ की भीतरी तथा बाहरी त्रिज्याएँ क्रमश: 30 तथा 60 cm हैं। भार वितरण को एकसमान मानते हुए प्रत्येक स्तम्भ की संपीडन विकृति की गणना कीजिये।
उत्तर:
दिया है:
आन्तरिक त्रिज्या (भीतरी त्रिज्या)
R_ext = 30 सेमी = 0.3 मीटर
बाहरी त्रिज्या, R_ext = 60 सेमी = 0.6 मीटर
प्रत्येक स्तम्भ का अनुप्रस्थ काट का क्षेत्रफल A = πR²_ext – πR²_int
= 3.14 [(0.6)²² – (0.3)²]
= 0.85 मीटर ²
ढाँचे का सम्पूर्ण भार,
W = 50,000 × 9.8
= 4.9 × 10 ⁵ न्यूटन
अतः प्रत्येक स्तम्भ पर भार, F₁ = \(\frac{1}{4}\) = 1.225 × 10⁵ न्यूटन
हम जानते हैं कि इस्पात का यंग गुणांक,
Y = 2 × 10¹¹ न्यूटन/मीटर²
सूत्र Y = \(\frac { FL }{ A\Delta L } \)
प्रत्येक स्तम्भ पर संपीडन विकृति
= \(\frac { \Delta L }{ L } \) = \(\frac { F_{ 1 }O }{ AY } \)
= \(\frac { 1.225\times 10^{ 5 } }{ 0.85\times 10^{ 2 }\times 2\times 10^{ 11 } } \)
= 0.72 × 10 ^-6
चारों स्तम्भों पर संपीडन विकृति
= (0.72 × 10 ^-6) × 4
= 32.88 × 10 ^-6

प्रश्न 9.8.
ताँबे का एक टुकड़ा, जिसका अनुप्रस्थ परिच्छेद 15.2 mm × 19.1 mm का है, 44,500 N बल के तनाव से खींचा जाता है, जिससे केवल प्रत्यास्थ विरूपण उत्पन्न हो। उत्पन्न विकृति की गणना कीजिये।
उत्तर:
दिया है, Y = 1.1 × 10¹¹ Nm^-2
A = परिच्छेद क्षेत्रफल
= 15.2 mm × 19.1 mm
= 15.2 × 10^-3 m × 19.1 × 10^-3 m
बल F = 44500N
परिणामी = विकृति = ?
Y = प्रतिबल/विकृति
या विकृति प्रतिबल/Y = \(\frac{F}{AY}\)
या अनुदैर्ध्य विकृति
= \(\frac { 44500 }{ 15.2\times 19.1\times 10^{ -6 }\times 1.1\times 10^{ 11 } } \)
= 139.34 × 10^-3 = 0.139

प्रश्न 9.9.
1.5 cm त्रिज्या का एक इस्पात का केबिल भार उठाने के लिए इस्तेमाल किया जाता है। यदि इस्पात के लिए अधिकतम अनुज्ञेय प्रतिबल 10⁸ Nm^-2 है तो उस अधिकतम भार की गणना कीजिए जिसे केबिल उठा सकता है।
उत्तर:
दिया है: इस्पात के तार की त्रिज्या, r = 1.5 सेमी
= 1.5 × 10^-2 मीटर ²
अधिकतम अनुज्ञेय प्रतिबल × अनुप्रस्थ काट का क्षेत्रफल
= 10 ⁸ × π × (1.5 × 10 ^-2)²
= 3.14 × 2.25 × 10 ⁴ न्यूटन

प्रश्न 9.10.
15 kg द्रव्यमान की एक दृढ़ पट्टी को तीन तारों, जिनमें प्रत्येक की लंबाई 2 m है, से सममित लटकाया गया है। सिरों के दोनों तार ताँबे के हैं तथा बीच वाला लोहे का है। तारों के व्यासों के अनुपात निकालिए, प्रत्येक पर तनाव उतना ही रहना चाहिए।
उत्तर:
माना कि ताँबे व लोहे के यंग गुणांक क्रमशः Y₁ व Y₂ है।
Y₁ = 110 × 10⁹ न्यूटन/मीटर² व
Y₂ = 190 × 10⁹ न्यूटन/मीटर²
माना कि ताँबे व लोहे के अनुप्रस्थ काट के क्षेत्रफल क्रमश:
a₁, व a₂ हैं तथा इनके व्यास क्रमश: a₁ व d₂ हैं।
सूत्र क्षेत्रफल = T (व्यास/2)₂ से,

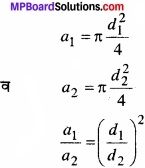
दिया है:
L = 2 मीटर
माना प्रत्येक तार में उत्पन्न वृद्धि ∆l है तथा प्रत्येक तार में उत्पन्न तनाव F है।
सूत्र Y = प्रतिबल/विकृति से,
ताँबे के तार की विकृति = \(\frac { F/a_{ 1 } }{ Y_{ 2 } } \)
या अनुप्रस्थ परिच्छेद
= \(\frac { 44500 }{ 15.2\times 19.1\times 10^{ -6 }\times 1.1\times 10^{ 11 } } \)
= 139.34 × 10^-3 = 0.139

प्रश्न 9.11.
एक मीटर अतानित लंबाई के इस्पात के तार के एक सिरे से 14.5 kg का द्रव्यमान बाँध कर उसे एक ऊर्ध्वाधर वृत्त में घुमाया जाता है, वृत्त की तली पर उसका कोणीय वेग 2 rev/s है। तार के अनुप्रस्थ परिच्छेद का क्षेत्रफल 0.065 cm ²है। तार में विस्तार की गणना कीजिए जब द्रव्यमान अपने पथ के निम्नतम बिंदु पर है।
उत्तर:
निम्नतम बिन्दु पर द्रव्यमान के घूर्णन के कारण तार में उत्पन्न बल,
T – mg = \(\frac { m }{ \omega ^{ 2 } } \)
जहाँ T = तार में तनाव है।
T = mg + \(\frac { m }{ \omega ^{ 2 } } \)
= 14.5 × 9.8 + 14.5 × 1 × (4π)²
= 14.5 (9.8 + 16 × 9.87)
= 14.5 (9.8 + 157.92)
= 2431.94 N
प्रतिबल = \(\frac{T}{A}\) = \(\frac { 2431.94 }{ 65\times 10^{ 7 } } \)
विकृति = \(\frac{∆L}{l}\) = \(\frac{∆L}{l}\) = ∆L
सम्बन्ध

प्रश्न 9.12.
नीचे दिये गये आँकड़ों से जल के आयतन प्रत्यास्थता गुणांक की गणना कीजिए, प्रारंभिक आयतन = 100.0 L दाब में वृद्धि = 100.0 atm (1 atm = 1.013 × 10⁵ Pa), अंतिम आयतन = 100.5 L। नियत ताप पर जल तथा वायु के आयतन प्रत्यास्थता गुणांकों की तुलना कीजिए। सरलं शब्दों में समझाइये कि यह अनुपात इतना अधिक क्यों है?
उत्तर:
दिया है:
P = 100 वायुमण्डलीय दाब = 100 × 1.013 × 10⁵ Pa (∴1 atm = 1.013 × 10⁵ Pa)
प्रारम्भिक आयतन,
V₁ = 100 litre = 100 × 10^-3 m^-3
अन्तिम आयतन,
V₂ = 100.5 litre = 100.5 × 10^-3 m^-3
आयतन में परिवर्तन = ∆V = V₂ – V₁
= (100.5 – 100) × 10^-3 m^-3
= 0.5 × 10^-3 m^-3
जल का आयतन गुणक = K_W = ?
सूत्र K_W = \(\frac { P/\Delta V }{ V } \) से
K_W = \(\frac { PV }{ \Delta V } \)
= \(\frac { PV }{ \Delta V } \)
= \(\frac { 100\times 1.013\times 10^{ 5 }\times 100\times 10^{ -3 } }{ 0.5\times 10^{ -3 } } \) (∵V = V₁
या
K_W = 2.026 × 10⁹ Pa
पुनः हम जानते हैं की STP पर वायु का आयतन गुणांक
K_air = 1.0 × 10^-4 GPa
= 1 × 10^-4 × 10⁹ Pa = 10⁵ Pa
\(\frac { K_{ W } }{ K_{ air } } \) = \(\frac { 2.026\times 10^{ 9 } }{ 10^{ 5 } } \) = 2.026 × 10⁴
= 20260
यहाँ अनुपात बहुत आदिक है अयथार्थ जल का आयतन प्रत्यास्थता वायु की आयतन प्रत्यास्थता से बहुत अधिक है। इसका कारण यह है कि समान दाब द्वारा जल के आयतन में होने वाली कमी, वायु के आयतन में होने वाली कमी की तुलना में नगण्य होती है।

प्रश्न 9.13.
जल का घनत्व उस गहराई पर, जहाँ दाब 80.0 atm हो, कितना होगा? दिया गया है कि पृष्ठ पर जल का घनत्व 1.03 × 103 kgm^-3, जल की संपीडता 45.8 × 10^-11 Pa^-1 (1 Pa = 1Nm^-2)
उत्तर:
दिया है:
P = 80 atm = 80 × 1.013 × 10⁵ Pa
\(\frac { 1 }{ k } \) = 45.8 × 10^-11 Pa^-1
पृष्ठ पर जल का घनत्व,
ρ = 1.03 × 10³ किग्रा प्रति मीटर³
माना दी हुई गहराई पर जल का घनत्व ρ है।
माना M द्रव्यमान के जल के द्वारा पृष्ठ व दी हुई गहराई पर आयतन क्रमश: V व V’ है।
अत:
V = \(\frac { M }{ \rho } \) तथा V’ = \(\frac { M }{ \rho’ } \)
∴ आयतन में परिवर्तन
∆V = V – V’ = M (\(\frac { 1 }{ \rho } -\frac { 1 }{ \rho ^{ ‘ } } \))
∴ आयतनात्मक विकृति
\(\frac { \Delta V }{ V } \) = M(\(\frac { 1 }{ \rho } -\frac { 1 }{ \rho ^{ ‘ } } \)) × \(\frac { \rho }{ M } \) = (1 – \(\frac { \rho }{ \rho ^{ ‘ } } \))
या \(\frac { \Delta V }{ V } \) = (1 – \(\frac { 1.03\times 10^{ 3 } }{ \rho ^{ ‘ } } \))
पुनः हम जानते हैं कि जल का आयतन गुणांक निम्नवत्

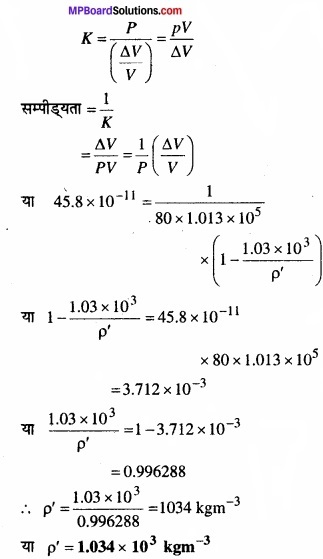
p’ = 1.034 × 10³ kgm^-3

प्रश्न 9.14.
काँच के स्लेब पर 10 atm का जलीय दाब लगाने पर उसके आयतन में भिन्नात्मक अंतर की गणना कीजिए।
उत्तर:
दिया है:
P = 10 atm = 10 × 1.013 × 10⁵ Pa
सारणी से, काँच के गुटके के लिए,
K = 37 × 10⁹ Nm^-2
काँच के गुटके के आयतन में भिन्नात्मक अन्तर
= \(\frac { \Delta V }{ V } \) = ?

= 0.0274 × 10^-3
= 2.74 × 10^-5
= 0.0274 × 10^-3 % = 0.003 %

प्रश्न 9.15
ताँबे के एक ठोस घन का एक किनारा 10 cm का है। इस पर 7.0 x 10⁶ Pa का जलीय दाब लगाने पर इसके आयतन में संकुचन निकालिए।
उत्तर:
दिया है:
L = 10 cm = 0.1 m
ताँबे का आयतन गुणांक
= 140 × 10⁹ Pa
P = 7 × 10⁶ Pa
ठोस ताँबे के घन में आयतन सम्पीडन
= ∆V = ?
V = L³ = (0.1)³ = 0.001 m³
सूत्र, K = – \(\frac { P }{ \frac { \Delta V }{ V } } \) से
\(\frac { \Delta V }{ V } \) = \(\frac { -PV }{ K } \)
= \(\frac { 7\times 10^{ 6 }\times 0.001 }{ 140\times 10^{ 9 } } \)
= \(\frac { -1 }{ 20 } \) × 10^-6m³
= – 0.05 × 10^-6 m³ = – 0.05cm³
यहाँ ऋणात्मक चिह्न से स्पष्ट होता है कि आयतन संकुचित होता है।

प्रश्न 9.16.
1 लीटर जल पर दाब में कितना अन्तर किया जाए कि वह 0.10% सम्पीडित हो जाए।
उत्तर:
दिया है:
V = 1 लीटर
∆V = – 0.10 % of V
= \(\frac { -0.10 }{ 100 } \) × 1 = \(\frac{1}{1000}\) लीटर
माना ∆p = 1 लीटर जल संकुचित करने के लिए आवश्यक दाब
पानी का आयतन प्रसार गुणांक
K = 2.2 × 10⁹ Nm^-2

ठोसों के यांत्रिक गुण अतिरिक्त अभ्यास के प्रश्न एवं उनके उत्तर

प्रश्न 9.17.
हीरे के एकल क्रिस्टलों से बनी निहाइयों, जिनकी आकृति चित्र में दिखाई गयी है, का उपयोग अति उच्च दाब के अंतर्गत द्रव्यों के व्यवहार की जाँच के लिए किया जाता है। निहाई के संकीर्ण सिरों पर सपाट फलकों का व्यास 0.50 mm है। यदि निहाई के चौड़े सिरों पर 50.000 N का बल लगा हो तो उसकी नोंक पर दाब ज्ञात कीजिए।

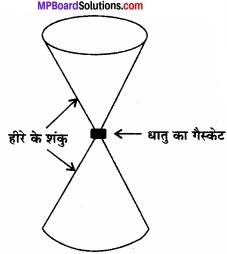
उत्तर:
दिया है: आरोपित बल, F = 5 × 10⁴ न्यूटन
व्यास, D = 5 × 10^-4 मीटर
त्रिज्या, r = \(\frac{D}{2}\) = 2.5 × 10^-4
क्षेत्रफल, A = πr²
= \(\frac{22}{7}\) × (2.5 × 10^-4)²
नोंक पर दाब, P = ?
सूत्र P = \(\frac{F}{A}\) से,
P = \(\frac { 5\times 10^{ 4 } }{ \frac { 22 }{ 7 } \times (2.5\times 10^{ -4 })^{ 2 } } \)
= 0.225 × 10¹²Pa
= 2.55 × 10¹¹Pa

प्रश्न 9.18.
1.05 m लंबाई तथा नगण्य द्रव्यमान की एक छड़ को बराबर लंबाई के दो तारों, एक इस्पात का (तार A) तथा दूसरा ऐल्युमीनियम का तार (तार B) द्वारा सिरों से लटका दिया गया है, जैसा कि चित्र में दिखाया गया है। A तथा B के तारों के अनुप्रस्थ परिच्छेद के
क्षेत्रफल क्रमशः 1.0 mm² और 2.0 mm² हैं। छड़ के किसी बिन्दु से एक द्रव्यमान m को लटका दिया जाए ताकि इस्पात तथा एल्युमीनियम के तारों में (a) समान प्रतिबल तथा (b) समान विकृति उत्पन्न हो।

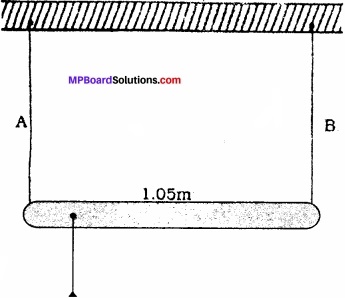
उत्तर:
माना कि स्टील तथा एल्युमीनियम के दो तारों क्रमश: A व B की लम्बाई L है।
माना कि A तथा B के अनुप्रस्थ क्षेत्रफल क्रमश: a₁ व a₂, हैं।
a₁ = 1 मिमी₂ = (10^-3)₂ = 10^-6 मीटर m²
a₂ = 2 मिमी² = 2 × 10^-6 मीटर ²
सारणी से, स्टील के लिए,
Y₁ = 2 × 10¹¹ न्यूटन मीटर ²
एल्युमीनियम के लिए,
Y₂ = 7 × 10¹⁹ न्यूटन मीटर^-2 माना तारों के निचले सिरों पर लगाए गए बल F₁ व F² हैं।
(a) A तथा B पर प्रतिबल क्रमश: F₁/a₁ व F₂/a₂ हैं। जब दोनों प्रतिबल बराबर हैं, तब
\(\frac { F_{ 1 } }{ a_{ 1 } } \) = \(\frac { F_{ 1 } }{ a_{ 2 } } \) या \(\frac { F_{ 1 } }{ F_{ 2 } } \)
= \(\frac { a_{ 1 } }{ a_{ 2 } } \)
माना कि दोनों छड़ों से x व y दूरी पर लटकाए गए भार mg द्वारा आरोपित बल F₁ व F₂ हैं। तब
F₁x = F₂Y
या \(\frac { F_{ 1 } }{ F_{ 2 } } \) = \(\frac{Y}{x}\)
समी० (i) व (ii) से,
\(\frac{y}{x}\) = \(\frac { a_{ 1 } }{ a_{ 2 } } \)
या
x = \(\frac { a_{ 2 } }{ a_{ 1 } } \) y
परन्तु x + y = 1.05 m
y = 1.05 – x
समी० (iii) व (iv) से,
x = \(\frac { a_{ 2 } }{ a_{ 1 } } \) (1.05 – x)
या a₁x = 1.05 a₂ – xa₂
या x (a₁ + a₂) = 1.05a₂
x = \(\frac { 1.05\times 2\times 10^{ -6 } }{ (1+2)\times 10^{ -6 } } \)
x = \(\frac { 1.05\times 2 }{ 3 } \) = 0.70m
y = 1.05 – 70 = 0.35 m
अतः द्रव्यमान m को A (स्टील तार.) से 0.7 मीटर या B (Al) से 0.35 मीटर की दूरी पर लटकाना चाहिए।
सूत्र y = प्रतिबल/विकृति से, विकृति = \(\frac { F_{ 1 }/a_{ 2 } }{ Y_{ 2 } } \)
चूँकि विकृतियाँ समान हैं।

Y = 1.05 – x = 1.05 – 0.43 = 0.62m
अतः द्रव्यमान m को A से 0.43 मीटर दूरी पर लटकाना चाहिए।

प्रश्न 9.19
मृदु इस्पात के एक तार, जिसकी लंबाई 1.0 m तथा अनुप्रस्थ परिच्छेद का क्षेत्रफल 0.50 × 10^-2 cm² है, को दो खम्भों के बीच क्षैतिज दिशा में प्रत्यास्थ सीमा के अंदर ही तनित किया जाता है। तार के मध्य बिंदु से 100g का एक द्रव्यमान लटका दिया जाता है। मध्य बिंदु पर अवनमन की गणना कीजिए।
उत्तर:
दिया है: 1 = 1 मीटर
क्षेत्रफल: A = 0.5 × 10^-2 cm²
= 0.5 × 10^-2 × 10^-2 × (10^-2 m)²
= 0.5 × 10 ^-6m²
द्रव्यमान:
m = 100 g = 0.1 kg
भार W = mg = 0.1 × 9.8 N
माना तार की त्रिज्या r है।
A = πr² = 0.5 × 10^-6 m²
r² = \(\frac { 0.5\times 10^{ -6 } }{ \pi } \) m²
स्टील के लिए, y = 2 × 10¹¹ Pa
अवनमन δ = ? = ?

= 0.051 m = 0.01m

प्रश्न 9.20.
धातु के दो पहियों के सिरों को चार रिवेट से आपस में जोड़ दिया गया है। प्रत्येक रिवेट का व्यास 6 mm है। यदि रिवेट पर अपरूपण प्रतिबल 6.9 × 10⁷ Pa से अधिक नहीं बढ़ना हो तो रिवेट की हुई पट्टी द्वारा आरोपित तनाव का अधिकतम मान कितना होगा? मान लीजिए कि प्रत्येक रिवेट एक चौड़ाई भार वहन करता है।
उत्तर:
माना रिवेट पर w भार लगाया जाता है।

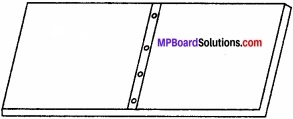
प्रत्येक रिवेट पर आरोपित बल = \(\frac{w}{4}\)
प्रत्येक रिवेट पर अधिकतम अपरूपण प्रतिबल
= 6.9 × 10⁷ Pa
माना अपरूपण बल प्रत्येक रिवेट के A क्षेत्रफल पर लगाया जाता है।

माना रिवेट पट्टी द्वारा लगाया गया अधिकतम तनाव w_max है।
अतः
\(\frac { w_{ max } }{ 4A } \) = 6.9 × 10⁷
या w_max = 4A = 6.9 × 10⁷
दिया है:
प्रत्येक रिवेट का व्यास
D = 6 mm = 6 × 10^-3
A = \(\frac { \pi D^{ 2 } }{ 4 } \)
= \(\frac { 3.142\times (6\times 10^{ -3 })^{ 2 } }{ 4 } \)
समी० (i) व (ii) से,
W_max = 4 × \(\frac { 3.142\times 36\times 10^{ -6 } }{ 4 } \) × 6.9 × 10^-3
= 7804.73N = 7.8 × 10³N

प्रश्न 9.21.
प्रशांत महासागर में स्थित मैरिना नामक खाई एक स्थान पर पानी की सतह से 11 km नीचे चली जाती है और उस खाई में नीचे तक 0.32 m³ आयतन का इस्पात का एक गोला गिराया जाता है, तो गोले के आयतन में परिवर्तन की गणना करें।खाई के तल पर जल का दाब 1.1 × 10⁸ Pa है और इस्पात का आयतन गुणांक 160 GPa है।
उत्तर:
दिया है: h = 11 km = 11 × 10³ m
जल का घनत्व, ρ = 10³ kgm^-3
खाई के तल पर जल के 11 किमी स्तम्भ द्वारा लगाया गया दाब
P = hpg
= 11 × 10³ × 10³ × 10 Pa
= 1.1 × 10⁸ Pa
V = 0.32 m³
∆V = ?
जल का आयतन गुणांक = K
= 2.2 × 10⁴
= 2.2 × 10⁴ × 10⁵ Pa
= 2.2 × 10⁹Pa (∴ 1 atm = 10⁵ Pa)

= 0.016 m³

MP Board Class 11 Physics Solutions