MP Board Class 11th Physics Important Questions Chapter 8 Gravitation

Students get through the MP Board Class 11th Physics Important Questions Chapter 8 Gravitation which are most likely to be asked in the exam.

MP Board Class 11th Physics Important Questions Chapter 8 Gravitation

Gravitation Class 11 Important Questions Very Short Answer Type

Question 1.
Write the difference between gravitation and gravity.
Answer:
Gravitation : The force of attraction between any two material bodies in the universe is called force of gravitation.
Gravity: If one of the attracting bodies is earth or some other planet or natural satel¬lite, then the force of attraction is called force of gravity.

Question 2.
Explain Newton’s universal gravitational laws.
Answer:
Every body of the universe attract each other. The force of attraction between two bodies is directly proportional to the product of their masses and inversely proportional to the square of the distance between them and it acts along the line joining the two bodies.

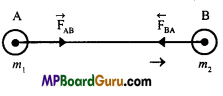
\(\vec{F}\)AB → Force given by B on A, \(\vec{F}\)BA → Force given by A on B. Let two bodies of mass m₁ and m₂ are kept d distance apart.
∴ (i) F ∝ m₁m₂and
(ii) F ∝ \(\frac{1}{d^{2}}\)
Combining both the laws,
F ∝\(\frac{m_{1} m_{2}}{d^{2}}\)
F = G\(\frac{m_{1} m_{2}}{d^{2}}\)
Where, G is constant called universal gravitational constant.

Question 3.
Define universal gravitational constant.
Answer:
We know that, F = G\(\frac{m_{1} m_{2}}{d^{2}}\)
If m₁ = m₂= 1 and d= 1, then F= G
Hence, the universal gravitational constant is numerically equal to the force of attraction between the two bodies each of mass unity, kept at unit distance apart.

Question 4.
Find out the unit and dimensional formula of universal gravitational constant. Also, write the value.
Answer:
Since, F = \(\frac{G m_{1} m_{2}}{d^{2}}\)
or
G = \(\frac{F d^{2}}{m_{1} m_{2}}\)
Unit: S.I. unit of G will \(\frac{\mathrm{Nm}^{2}}{\mathrm{~kg} \mathrm{~kg}}\) = Nm² kg^-2 .
Dimensional formula : [G] = \(\frac{\left[\mathrm{MLT}^{-2}\right]\left[\mathrm{L}^{2}\right]}{[\mathrm{M}][\mathrm{M}]}\) = [M^-1L³T^-2]
Value : Value of G = 6.67 × 10^-11 Nm² kg ^-2.

Question 5.
The value of G = 6.67 × 10^-11 Nm² kg ^-2. What does it means? Why G is called universal constant?
Answer:
When two bodies, each of mass 1 kg are kept 1 m apart, then the force of attraction between them is 6.67 × 10^-11 N.
The value of G does not depend upon nature, medium, time, temperature etc. There-fore, it is called universal constant.

Question 6.
What is acceleration due to gravity ? What is its standard value?
Answer:
The acceleration produced in a body due to force of gravity is called acceleration due to gravity.
or
The rate of change of velocity in a body falling freely is called acceleration due to gravity.
It is denoted by g and its standard value is 9.8 m × s^-2.

Question 7.
Write the relation between ‘g’ and ‘G’.
Answer:
g = \(\frac{\dot{G} M}{R^{2}}\)

Question 8.
What is the value of ‘g’ at the centre of earth?
Answer:
The value of ‘g’ at the centre of earth is zero.

Question 9.
On what factors the weight of a body depends upon a planet?
Answer:

• Size of planet,
• Daily rotation of planet,
• Position of body in planet.

Question 10.
How the magnitude of ‘g’ changes on the surface of earth?
Answer:
From equator to pole value of ‘g’ increases. It is minimum at equator and maxi¬mum at pole.

Question 11.
At which place value of ‘g’ is minimum and maximum?
Answer:
Value of ‘g’ is minimum at centre of earth and maximum at pole.

Question 12.
A body is taken to moon from the centre of the earth. What change will occur in the weight and the mass of the body?
Answer:
The weight of a body at the centre of the earth is zero. When the body is moved towards the moon, the weight of the body will increase. On the surface of the earth the weight will be maximum. Further the weight will decrease and on the moon it will be \(\frac{1}{6}\) th of the weight on the surface of earth. The mass will remain same.

Question 13.
What is the value of g at the centre of the earth? What will be its weight?
Answer:
Zero, zero.

Question 14.
How does the value of g change on the surface of earth ? Where it is maximum and minimum?
Answer:
The value of g increases when the body is taken from equator to poles. The value of g is maximum at poles and minimum at the equator.

Question 15.
Can the gravity of earth be zero, at some height?
Answer:
No as F ∝ \(\frac{1}{r^{2}}\)

Question 16.
If the earth stops rotation about its axis, what will happen to the weight of the body? What change will occur in the body placed at the poles?
Answer:
If the earth stops rotation the weight of the bodies will increase. The weight of the body placed at poles will remain same.

Question 17.
A man can jump six times more on the moon, than on the earth. Why?
Answer:
Because the value of acceleration due to gravity is six times less than that of earth.

Question 18.
The gravitational mass on earth is \(\frac{g}{6}\). If a body is taken to moon from the earth, then what will happen to weight, inertial mass and gravitational mass ?
Answer:
The weight will be \(\frac{1}{6}\) time that of earth. The inertial mass and gravitational mass will not change.

Question 19.
The gravitational potential energy of a body on the surface of earth is 6.4 × 10⁶ joule. Explain.
Answer:
The work done required to throw a body away from gravitational field of earth will be 6.4 × 10⁶ joule.

Question 20.
Weight of a body at equatorial line is less than its weight at pole. Why?
Answer:
Because value of ‘g’ at equator is less than pole and since weight = Mass × ‘g’ Weight at equator is less than pole.

Question 21.
What is escape velocity? On what factors does it depend?
Answer:
It is the least velocity with which a body must be thrown vertically upwards so that it just escapes the gravitational pull of earth.
It depends upon

• Radius of planet and
• Acceleration due to gravity of the planet.

Question 22.
What are the value of escape velocities of earth and moon?
Answer:
Escape velocity of earth, = 11.2 kms^-1
and that of moon = 2.38 kms^-1

Question 23.
What is an artificial satellite?
Answer:
The man made satellite which revolves around the earth are called artificial satellite.

Question 24.
What is geo-stationary satellite or synchronous satellite ? What is its height above the earth?
Answer:
A satellite revolving around the earth in west to east direction; in the equatorial plane perpendicular to the axis of rotation with time-period equal to that of earth i.e., 24 hours, is called geo-stationary satellite.
Its height from the surface of earth is nearly 36000 km.

Question 25.
What is parking orbit? What is its radius?
Answer:
The orbit in which the geo-stationary satellite is launched is called parking orbit. Its radius is nearly 42309 km.

Question 26.
Why the orbit of artificial satellite is set out of the atmosphere?
Answer:
The orbit of satellite is set out of the atmosphere so that the satellite may not bum due to the friction with air.

Question 27.
What do you mean by weightlessness in the satellite?
Answer:
The necessary centripetal force to revolve in a circular orbit is provided by the gravity of earth. Hence, the net force on the satellite and the bodies inside it will be zero. Therefore, the weight of the body becomes zero.

Question 28.
Weightlessness is not felt on the moon, why?
Answer:
Due to gravity of moon, the bodies have weights on the moon, of course it is a satellite of earth.

Question 29.
Can a satellite be launched in an orbit which is not in the plane, passing through the centre of earth?
Answer:
No, because under this condition, the horizontal component of the force of at-traction between earth and satellite cannot balance the centripetal force. As a result, the satellite will be attracted towards the equatorial plane and its orbit will not be stable.

Question 30.
Can a satellite be launched in an orbit, so that it can be seen always above
Delhi?
Answer:
No, this is because Delhi is not on equator line.

Question 31.
What is the relation between orbital velocity and escape velocity?
Answer:
Escape velocity = √2 × Orbital velocity.

Question 32.
What is the direction of revolution of a geo-stationary satellite?
Answer:
The direction of revolution of geo-stationary satellite is same as the direction of rotation of earth about its own axis, i.e., west to east.

Question 33.
What is the angle between the plane of revolution of satellite and axis of rotation ?
Answer:
90°.

Question 34.
In an artificial satellite a bob is hanging with a string, what will be the tension in the string ?
Answer:
Zero.

Question 35.
Can the velocity of a body be equal to the velocity of light?
Answer:
No, as the mass of a body increases with the velocity. When its velocity becomes equal to that of light, the mass of the body will be infinite, which is not possible.

Question 36.
If the height of the parking orbit of a satellite in space is increased then its orbital velocity decreases, why?
Answer:
Since orbital velocity ν₀ = R\(\sqrt{\frac{g}{R+h}}\)
Here, R and g are constant.
∴ ν₀∝ \(\frac{1}{\sqrt{h}}\)
i.e., if h increases then ν₀ decreases.

Question 37.
To find out time in a satellite pendulum clock is used or spring clock.
Answer:
Spring clock is used to determine time at satellite because pendulum clock will get stop there.

Question 38.
In an artificial satellite a mass of 2 kg is kept at spring balance. What will be the reading of spring balance ?
Answer:
Zero.

Question 39.
What will happen if a glass full of water is tilt in an artificial satellite?
Answer:
Water will start swinging as a droplet inside an artificial satellite due to weightlessness.

Question 40.
Inside an artificial satellite a body of mass 1 kg is hanged with a string. What will be the tension in the string ?
Answer:
Zero.

Question 41.
Escape velocity of 5 gram object in earth is 11.2 km/s. What will be the escape velocity for 10 gram object?
Answer:
Escape velocity of 10 gram object will be 11.2 km/s because escape velocity does not depend upon the mass of the object.

Question 42.
From where a satellite obtain the centripetal force required to revolve around a planet?
Answer:
Any satellite gets the required centripetal force to revolve around the planet from the gravitation force of the planet.

Question 43.
Sun attracts earth toward itself with its gravitational force, but earth does not move toward sun, explain with reason.
Answer:
Earth is not stationary, it revolves around the sun in a circular orbit. Centripetal force required to revolve around the sun is obtained by earth from the gravitational force of sun. In this way earth remains in equilibrium.

Question 44.
On which factor the period of revolution of geo-stationary satellite depends?
Answer:
Period of revolution of geo-stationary satellite depends on distance of it from earth surface. If the distance from earth surface increases, its period of revolution also increases.

Question 45.
How the orbital velocity of a satellite depends upon the distance of its from the earth surface?
Answer:
When the distance of satellite from earth surface increases, its orbital velocity decreases.

Question 46.
Why total energy of a satellite is negative?
Answer:
Since, energy is required for satellite to place it at orbit in infinity. So total energy of a satellite is negative.

Question 47.
Gravitational potential energy of any object at earth surface is 6.4 × 10⁶ joule. Explain its meaning.
Answer:
It means energy required to send an object out of gravitational field is 6.4 × 10⁶ joule.

Gravitation Class 11 Important Questions Short Answer Type

Question 1.
Establish the relation between g and G.
Answer:
Let the mass of the earth be M and its radius be R. A body of mass m is placed on it. Therefore, the force of attraction by the earth on the body :
By Newton’s laws of gravitation,
F = \(\frac{G M m}{R^{2}}\) …(1)
But, the force with which a body is attracted towards the earth gives the weight of body.
F = mg …(2)
Equating eqns. (1) and (2), we get
mg= \(\frac{G M m}{R^{2}}\)
or
g = \(\frac{G M}{R^{2}}\)
It is the required relation.

Question 2.
Explain with mathematical calculation, how the value of g changes with altitude?
or
How does the value of ‘g’ change above the surface of the earth ? Find out the expression and explain.
Answer:
The value of g decreases with the increase of altitude.
Let the mass of earth is M and its radius is R.
∴ g = \(\frac{G M}{R^{2}}\) …(1)
If at point P at height h from the surface of earth is g’, then
g’ = \(\frac{G M}{(R+h)^{2}}\) …(2)
∴ By eqns. (1) and (2), we get

Hence, g’ < g.
Thus as height increases the value of g decreases.

Question 3.
How the value of g changes with the increase of depth? Find the value of g
at the centre of earth.
or
Prove that the value of g at the centre of earth is zero.
Answer:
Assuming the earth to be a homogeneous sphere of mass M, radius R and acceleration due to gravity on the surface is g. Let ρ be the mean density of earth.
We know that, g = \(\frac{G M}{R^{2}}\) …(1)
∵ M = Volume × Density
or
M = \(\frac{4}{3}\)πR³ × ρ …(2)
Putting the value of Min eqn. (1),
g = \(\frac{G \frac{4}{3} \pi R^{3} \times \rho}{R^{2}}\)
or
g = \(\frac{4}{3}\)πRGρ …(3)

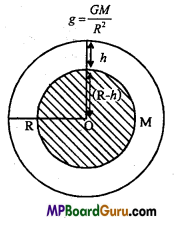
Now, let the body be taken to depth h, below the free sur¬face hence the distance of the body from the centre of earth will be (R-h). Hence, the force of attraction on the body will be acted by the sphere of radius (R-h). Mass of earth of radius (R-h) will be M’.
∴ M’ = \(\frac{4}{3}\)π(R – h)³ ρ
If g_d be the acceleration due to gravity at depth h, then using eqn. (1),

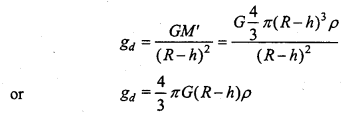
Dividing eqn. (4) by eqn. (3), we have

Hence, from eqn. (5), the value of g decreases with the increase of depth. At the centre
ofearth, h=R
∴ g_d = g\(\left(1-\frac{R}{R}\right)\)
or
g_d= g(1 – 1)g × 0
∴ g_d= 0
Hence, value of g at the centre of earth is zero.

Question 4.
How does the value of ‘g’ change due to shape of the earth?
Answer:
The earth is not perfectly spherical in shape. It is slightly flattened at the poies
and is bulged at the equators
Let R_p and R_e be polar and equational radius respectively.,
Hence, g_p =\(\frac{G M}{R_{p}^{2}}\) and g_e =\(\frac{G M}{R_{p}^{2}}\)
Where g_p and g_e are the acceleration due to gravity at the poles and equator respectively.

Now \(\frac{g_{e}}{g_{p}}=\frac{G M}{R_{e}^{2}} \times \frac{R_{p}^{2}}{G M}=\left(\frac{R_{p}}{R_{e}}\right)^{2}\)
∵ R_p < R_e
∴ \(\left(\frac{R_{p}}{R_{e}}\right)^{2}\) < 1, hense \(\frac{g_{e}}{g_{p}}\) < 1
or
g_e < g_p

Question 5.
Show that the gravitational potential energy of an object near the earth
surface is ΔU = mgh.
Answer:
If a particle is raised from the surface of the earth to a height h above, then r_{1 =} R (earth radius) and r₂ = R + h (see figure).
So that, the change in potential energy )

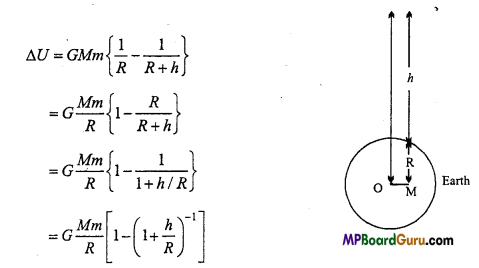
Using Binomial theorem and neglecting the higher powers of h/R, we get

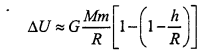
or
ΔU = G \(\frac{M m h}{R^{2}}\)
But, \(\frac{G M}{R_{p}^{2}}\)= g, (acceleration due to gravity at the surface of the earth).
Hence, ΔU = mgh
Thus, when a body of mass m is taken h distance above the earth’s surface, its potential energy increases by mgh.

Question 6.
What do you mean by gravitational field intensity? Establish relation be-tween intensity of gravitational field and acceleration due to gravity.
Answer:
Gravitational field :
The space around a material body in which its gravita-tional pull can be experienced is called its gravitational field.
Gravitational field intensity:
The intensity of gravitational field of a body at a point in a field is defined as the force experienced by a body of unit mass placed at that point provided the presence of unit mass does not disturb the original gravitational field.
i.e.. E = \(\frac{F}{m}\)

Let an object of mass M is at point O and at a distance of r from it at point P, we have to find out the intensity.
Let us consider a unit mass (m = 1) is placed at point P, therefore force of attraction applied by mass M on unit mass will be
F = \(\frac{G M \cdot 1}{r^{2}}=\frac{G M}{r^{2}}\)
Intensity at point P
E = \(=\frac{F}{m}=\frac{G M}{r^{2}} / 1=\frac{G M}{r^{2}}\) …(1)
and we know, acceleration due to gravity
g = \(\frac{G M}{r^{2}}\) …(2)
From eqns. (1) and (2), we get E = g
i.e., Intensity of gravitational field is equal to acceleration due to gravity of any point.

Question 7.
What is orbital velocity? Derive an expression for the orbital velocity. Obtain an expression if satellite is near to the surface of earth.
Answer:
Orbital velocity:
Orbital velocity is the velocity which is given to an artificial satellite, a few hundred kilometre above the earth’s surface so that it may start revolving round the earth.
Let the mass of satellite is m and the radius of orbit from the centre of earth is r, revolving with a velocity of ν_o
∴ Centripetal force = \(\frac{m v_{o}^{2}}{r}\) …(1)
Also, by Newton’s law of gravitation,
F = \(\sqrt{\frac{G M m}{r^{2}}}\) …(2)
Since, centripetal force is provided by gravitation force, then

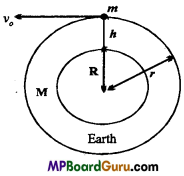
\(\frac{m v_{o}^{2}}{r}=\frac{G M m}{r^{2}}\)
or
ν_o² = \(\frac{G M}{r}\)
∴ ν_o = \(\sqrt{\frac{G M}{r}}\) …(3)
If the radius of earth is R and height of satellite from the surface of earth is h, then
r = R + h
But g = \(\frac{G M}{R^{2}}\)
or
GM = gR²
Putting the values of GM = gR² and r = R + h in eqn. (3), we get
ν_o = \(\sqrt{\frac{g R^{2}}{R+h}}=R \sqrt{\frac{g}{R+h}}\)
If the satellite is near to the surface of earth,then h<<R, then R + h ≈ R
∴ ν_o = R\(\sqrt{\frac{g}{R}}=\sqrt{g R}\)

Question 8.
What is meant by the period of revolution ? Derive an expression for It.
Answer:
Period of revolution :
The time taken to complete one revolution is called period of revolution of satellite.
Let the period of revolution is Tand the radius of orbital is r.
∴ Orbital velocity = \(\frac{\text { Total path travelled }}{\text { Total time taken }}\)
ν_o = \(\frac{2 \pi r}{T}\)
or
T = \(\frac{2 \pi r}{v_{o}}\)
But r = R + h
∴ T = \(\frac{2 \pi(R+h)}{v_{o}}\)
But we have
ν_o = R \(\sqrt{\frac{g}{R+h}}\)
∴ T = \(\frac{2 \pi(R+h)}{R \sqrt{\frac{g}{R+h}}}\)
or
T = 2π(R + h)\(\frac{\sqrt{(R+h)}}{R \sqrt{g}}\)
∴ T = \(\frac{2 \pi}{R} \sqrt{\frac{(R+h)^{3}}{g}}\)

Question 9.
Determine the revolution time of a satellite, near to earth.
Answer:
We have T = \(\frac{2 \pi}{R} \sqrt{\frac{(R+h)^{3}}{g}}\)
If h<<R, then
T = \(\frac{2 \pi}{R} \sqrt{\frac{R^{3}}{g}}\)
= \(2 \pi \sqrt{\frac{R}{g}}\)
Now
R = 6.38 × 10⁶ m,g = 9.8ms^-2
∴ T = \(2 \times 3 \cdot 14 \sqrt{\frac{6 \cdot 38 \times 10^{6}}{9 \cdot 8}}\)
= 84.4 min.(approx.).

Question 10.
Planet A is heavier than planet B. Which will have the greater escape velocity?
Answer:
We have, ν = \(\sqrt{\frac{2 G M}{R}}\)
If R is constant, then
ν ∝ √M
∴ \(\frac{v_{A}}{v_{B}}=\sqrt{\frac{M_{A}}{M_{B}}}\)
∵ M_A>M_B
∴ ν _A> ν_B
Hence, escape velocity of planet A will be greater than that of planet B.

Question 11.
Establish the relation between escape velocity and orbital velocity.
Answer:
Escape velocity : ν_e = \(\sqrt{2 g R}\) …(1)
Orbital velocity : ν_o = \(\sqrt{g R}\) …(2)
Dividing eqn. (1) by eqn. (2), we get
\(\frac{v_{e}}{v_{o}}=\frac{\sqrt{2 g R}}{\sqrt{g R}}=\sqrt{2}\)
∴ ν_e = \(\sqrt{2} v_{o}\)

This is the required relation between escape velocity and orbital velocity.

Question 12.
What are the characteristics of geo-stationary satellite?
Answer:

• The geo-stationary satellite revolves around the earth in equatorial plane, perpendicular to the axis of rotation of earth.
• Its direction is from west to east.
• Its time-period of revolution is 24 hours.

Question 13.
What is geo-stationary satellite ? Prove that its height from the surface of earth is 36000 km.
Answer:
Geo-stationary satellite:
A satellite revolving around the earth in west to east direction; in the equatorial plane perpendicular to the axis of rotation with time-period equal to that of earth i.e., 24 hours, is called geo-stationary satellite.
Its height from the surface of earth is nearly 36000 km.
Now, we have

= 42.22 × 10⁶ m = 42220 km (Approx.)
∴ h=(R + h) – R
= 42.22 × 10⁶ – 6.38 × 10⁶ = 35840 km
or
h = 36000 km (Approx.) Proved.

Question 14.
Why the moon has no atmosphere?
Or
Why the moon has no atmosphere while Jupiter and Saturn have dense atmosphere?
Answer:
The escape velocity for moon is 2.38 kms^-1, while the r.m.s. speed of molecules of gases at 500 K is 2.5 kms^-1, hence the molecules of gases escape from the gravity of moon. The escape velocities of Jupiter and Saturn are greater, therefore, they have atmosphere.

Question 15.
What conclusion did Newton obtain from Kepler’s law of planetary motion?
Answer:
Conclusions obtained by Newton : On the basis of Kepler’s law, Newton pro-pounded the following:
(i) The path of the planets round the sun can be approximately taken as circular, for which the necessary centripetal force can be obtained from the gravitational force of attraction between the planet and sun. The force acting on the planet is always towards the sun.

(ii) By the third law :
T² ∝ r³
For the circular path of planet, the centripetal force acting will be
F = \(\frac{m v^{2}}{r}=\frac{m(r \omega)^{2}}{r}\) = mrω²
or
F = mr \(\left(\frac{2 \pi}{T}\right)^{2}=\frac{4 \pi^{2}}{T^{2}}\) mr …(1)
Since T² ∝ r³ ⇒ T² = Kr³
Putting the value of T²in eqn (1),we get
F = \(\frac{4 \pi^{2}}{K r^{3}}\) mr = \(\frac{4 \pi^{2} m}{K r^{2}}\)
But,\(\frac{4 \pi^{2} m}{K}\) is a Constant.
∴ F = \(\frac{\text { Constant }}{r^{2}}\)
or
F ∝ \(\frac{1}{r^{2}}\)
Hfence, the force acting on the planet is inversely proportional to the square of dis-tance between them.

(iii) The force acting on the planet is directly proportional to its mass.
ie., F∝m.

Gravitation Class 11 Important Questions Long Answer Type

Question 1.
Derive an expression for the escape velocity. Does it depend upon mass?
Answer:
Escape velocity : It is the least velocity with which a body must be thrown vertically upwards so that it just escapes the gravitational pull of earth.
It depends upon

• Radius of planet and
• Acceleration due to gravity of the planet.

Let the mass of earth be M and its radius is R .At any time let the body is at a distance x from the centre of earth.
∴ Force on the body due to earth, F = \(\frac{G M m}{x^{2}}\)
∴ Work done in moving the body through dx distance, against gravity,
dW = Fdx = \(\frac{G M m}{x^{2}}\) .dx
∴ Work done in moving up to infinity,

∴ W = \(\frac{G M m}{R}\)
If the escape velocity is ν_e, then

This is the required expression.
Since, the formula is free from the mass of the body, hence the escape velocity does not deppnd upon the mass of the body.

Gravitation Class 11 Important Numerical Questions

Question 1.
Two masses, each of 1 gm, are kept 1 cm apart. Calculate the force of at-traction between them in kg wt.
Solution:
Given : m₁, = m₂ = 1 gm = 10^-3 kg, r = 1 cm = 10^-2 m and
G = 6.67 × 10^-11 Nm²kg^-2
Now F = \(\frac{G m_{1} m_{2}}{r^{2}}\)
\(=\frac{6 \cdot 67 \times 10^{-11} \times 10^{-3} \times 10^{-3}}{\left(10^{-2}\right)^{2}}\)
\(=\frac{6 \cdot 67 \times 10^{-17}}{10^{-4}}\)
6.67 × 10^-13 N
\(=\frac{6 \cdot 67 \times 10^{-13}}{10}\) kg wt
∴ F = 6.67 × 10^-14kg wt

Question 2.
The mass of a planet is 10¹⁸ kg and its radius is 10³ m. Calculate the acceleration due to gravity on that planet.
Solution:
Given : M = 10¹⁸kg, R = 10³m and G = 6.67 × 10^-11 Nm²kg^-2.
Now, g = \(\frac{G M}{R^{2}}\)
∴ g = \(\frac{6 \cdot 67 \times 10^{-11} \times 10^{18}}{\left(10^{3}\right)^{2}}\)
\(=\frac{6 \cdot 67 \times 10^{7}}{10^{6}}\)
or
g = 6.67 × 10= 66.7ms^-2.

Question 3.
Calculate the value of g at 600 km height above the surface of earth. Given the radius of earth R = 6400 km and g = 9.8 ms^-2.
Solution:
Given : R = 6400 km = 6400 × 10³ m, g = 9.8 ms ^-2,
h = 600 km = 600 × 10³ m
Formula \(\frac{g^{\prime}}{g}=\frac{R^{2}}{(R+h)^{2}}\)
0r
\(\frac{g^{\prime}}{9 \cdot 8}=\left(\frac{6400 \times 10^{3}}{(6400+600) \times 10^{3}}\right)^{2}=\left(\frac{6400}{7000}\right)^{2}\)
∴ g’ = 9.8 × \(\left(\frac{64}{70}\right)^{2}\)
= 8.192ms^-2

Question 4.
At what height the weight of a body be \(\frac{1}{3}\) times that of the surface of earth
Solution:
Given:


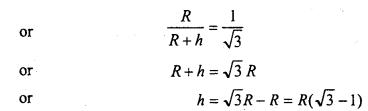
∴ h = R(1.732 – 1) = 0.732Rm

Question 5.
What would be the angular velocity of earth so that the weight of a body at equator becomes zero?
Solution:
Now, we have at equator,
g’ = g – Rω²
But, g’ = 0
∴ g – Rω² = 0
or
-Rω² = -g
or
ω²=g|R
or
ω = \(\sqrt{\frac{g}{R}} \text { . }\)

Question 6.
Calculate the potential energy of a body of mass 100 kg placed at a height 600 km above the surface of earth (M = 6 × 10²⁴ kg, R = 6400 km)-
Solution:
Given : M = 6 × 10²⁴ kg,R = 6400 km = 6400 × 10³m,
h = 600 km = 600 × 10³m,m = 100 kg.
Formula U = \(-\frac{G M m}{r}\)
\(=-\frac{6 \cdot 67 \times 10^{-11} \times 6 \times 10^{24} \times 100}{(6400+600) \times 10^{3}}\) (r = R +h)
\(=-\frac{6 \cdot 67 \times 6 \times 10^{15}}{7000 \times 10^{3}}\)
U = – 5.717 10⁹ joule.

Question 7.
The gravitational field intensity at a point 8000 km away from the earth surface is 6 N/kg. What is gravitational potential at that point?
Solution:
Given : E = 6 N/kg, d – 8000 km = 8000 × 10³m
∴ Formula V = -E × d
Gravitational potential V = -6 × 8000 × 10³
= -48 × 10⁶
= -4.8 × 10⁷Nm/kg.

Question 8.
An artificial satellite is revolving around the earth at height 3600 km above the surface of earth. Calculate
(i) Orbital velocity,
(ii) Period of revolution.
Solution:
Given : h = 3600 km = 3600 × 10³m, g = 9.8 m/s² and R = 6.38 × 10⁶m.
Formula: ν_o = \(\sqrt{\frac{g R^{2}}{R+h}}\)

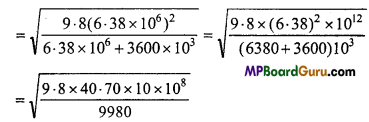
= 10⁴ × 0.6322m/s
= 6.322 × 10³m/s = 6.322m/s

= 626744 × 1.58 = 9913.9 sec
= 2.734 hours

Question 9.
The mass of planet A Is 4 times that of planet I? and radius of A, ¡s 2 times
that of B. Compare their escape velocities.
Solution:
Given : M₁= 4M₂and R₁ = 2R₂

Question 10.
The distance of planet A is three times that of planet B. If the time of revolution of B is 6 months, then find the time of revolution of A.
Solution:By kepler’s law,
T² ∝ r³

Question 11.
The time of revolution ofaplanet revolving in a circular orbit of radius R is T. Find the time of revolution of a planet revolving in an orbit of radius 4R.
Solution:
Given: = T₁ = T, r₁ = R,r₂ = 4R.
By Kepler’s law,
\(\left(\frac{T_{1}}{T_{2}}\right)^{2}=\left(\frac{r_{1}}{r_{2}}\right)^{3}\)
or
\(\left(\frac{T}{T_{2}}\right)^{2}=\left(\frac{R}{4 R}\right)^{3}=\frac{1}{64}\)
or
\(\frac{T}{T_{2}}=\frac{1}{8}\)
∴ T₂ = 8T

Question 12.
If the radius of the moon is 1.74 × 10⁶ m and its mass is 7.36 × 10²² kg, then calculate the escape velocity from the surface of the moon.
Solution:
Given: R = 1.74 × 10⁶ m, M = 7.36 × 10²² kg,
G = 6.67 × 10^-11Nm²/kg²
∵ Escape velocity, ν_e = \(\sqrt{\frac{2 G M}{R}}\)
∴ ν_e = \(\sqrt{\frac{2 \times 6 \cdot 67 \times 10^{-11} \times 7 \cdot 36 \times 10^{22}}{1 \cdot 74 \times 10^{6}}}\)
= 2.38 × 10³ m/sec = 2.38 km/sec.

Question 13.
The escape velocity of earth is 11 kms1. If the radius of a planet is double of earth’s radius and mean density are same, then find the escape velocity of that planet.
Solution:
Escape velocity,
ν = \(\sqrt{\frac{2 G M}{R}}\)

or
ν₂ = 22 km/s.

Question 14.
The mass of a planet is 3 × 10²⁴ kg and radius is 5 × 10⁶ m. What will be the energy required to move, 5 kg body to infinity ?
Solution:
Given : M = 3 × 10²⁴kg,R = 5 × 10⁶m, m = 5kg,
G = 6.67 × 10¹¹ Nm²kg^-2.
Formula U = \(\frac{G M m}{2 R}\)
\(=\frac{6 \cdot 67 \times 10^{-11} \times 3 \times 10^{24} \times 5}{2 \times 5 \times 10^{6}}\)
U = 100.05 × 10⁶ = 1010⁸ joule.

Gravitation Class 11 Important Questions Objective Type

1. Multiple- choice questions:

Question 1.
Newton’s laws of gravitation is true for :
(a) All bodies
(b) Only for heavenly bodies
(c) Only for small bodies
(d) Only for charged objects.
Answer:
(a) All bodies

Question 2.
Value of ‘g’ at moon with comparison to earth is :
(a) \(\frac{1}{2}\)
(b) \(\frac{1}{3}\)
(c) \(\frac{1}{5}\)
(d) \(\frac{1}{6}\)
Answer:
(d) \(\frac{1}{6}\)

Question 3.
value of universal gravitational constant G is :
(a) Same at all places
(b) Unequal at all places
(c) Zero
(d) Infinity.
Answer:
(b) Unequal at all places

Question 4.
Relation between g and G is :
(a) g = GM
(b) gR² = GM
(c) gM = GR²
(d) gM/GR².
Answer:
(b) gR² = GM

Question 5.
Magnitude of g outside the gravitational field is:
(a) Infinity
(b) Zero
(c) 9.8 m/s²
(d) 980 newton.
Answer:
(b) Zero

Question 6.
Magnitude of g at the centre of earth is:
(a) Zero
(b) Infinity
(c) 9.8 newton
(d) 980 dyne.
Answer:
(a) Zero

Question 7.
Magnitude of g at pole is:
(a) Less
(b) More
(c) Zero
(d) None of these.
Answer:
(b) More

Question 8.
Magnitude of g at equator:
(a) More
(b) Less
(c) Infinity
(d) Zero
Answer:
(b) Less

Question 9.
Formula for gravitational potential energy is:
(a) \(\frac{G M m}{r}\)
(b) \(\frac{G m}{r}\)
(c) \(\frac{R}{G M}\)
(d) gR² = GM.
Answer:
(a) \(\frac{G M m}{r}\)

Question 10.
Formula for escape velocity is:
(a) gR
(b) MR .
(c) \(\sqrt{2 g R}\)
(d) \(\text { (d) } \sqrt{g R} \text { . }\)
Answer:
(c) \(\sqrt{2 g R}\)

Question 11.
There is no atmosphere at moon, because :
(a) Moon is closer to earth
(b) It revolves round the earth
(c) It gets light from sun
(d) Escape velocity of gas molecules is less than their root mean-square velocity.
Answer:
(d) Escape velocity of gas molecules is less than their root mean-square velocity.

Question 12.
If a body is projected at angle of 50° then its escape velocity will be :
(a) 11.6 km/s
(b) 11.2km/s
(c) 12.8 km/s
(d) 16.2 km/s.
Answer:
(b) 11.2km/s

Question 13.
Distance of geo-stationary satellite from earth surface :
(a) 6 R
(b) 7 R
(c) 5 R
(d) 3 R.
Answer:
(a) 6 R

Question 14.
Kepler’s second law is based on :
(a) Newton’s first law
(b) Theory of Relativity
(c) Newton’s second law
(d) Laws of conservation of angular momentum.
Answer:
(d) Laws of conservation of angular momentum.

Question 15.
Period of revolution of geo-stationary satellite is :
(a) 20 hours
(b) 22 hours
(c) 24 hours
(d) 25 hours.
Answer:
(c) 24 hours

Question 16.
Formula for orbital velocity is :
(a) gR
(b) g² R²
(c) g³R³
(d) \(\sqrt{g R}\)
Answer:
(c) g³R³

Question 17.
Who invented first the laws of planetary motion :
(a) Newton
(b) Kepler
(c) Galileo
(d) Aryabhatt.
Answer:
(b) Kepler

Question 18.
Radius of parking orbit is :
(a) 36000 km
(b) 42309 km
(c) 6400 km
(d) 80000 km.
Answer:
(b) 42309 km

2. Fill in the blanks:

1. The acceleration of body due to gravity is called …………………..
Answer:
acceleration due to gravity

2. Gravitational force in nature is a …………………….. force.
Answer:
weak

3. Acceleration due to gravity does not depend upon ………………. of the body.
Answer:
mass

4. At height the value of ‘g’ is ………………………
Answer:
less

5. At centre of earth the value of ‘g’ is ………………………
Answer:
Zero

6. G is a ……………… quantity.
Answer:
scalar

7. Gravitational mass and inertial mass are …………………… to each other.
Answer:
equal

8. Gravitational intensity is equal to ……………………..
Answer:
acceleration due to gravity

9. Gravitational potential energy at infinity is ……………………..
Answer:
zero

10. Magnitude of ‘g’ at equatorial position is …………………..
Answer:
minimum

11. Magnitude of ‘g’ at pole is ……………..
Answer:
maximum

12. Orbital velocity does not depend upon ………………… of a body.
Answer:
mass

13. Escape velocity does not depend upon …………….. of the body.
Answer:
mass

14. Magnitude of escape velocity is ……………… km/s.
Answer:
11.2

15. The time-period of geo-stationary satellite is ………………. hours.
Answer:
24

3. Match the following:
I.

Column ‘A’	Column ‘B’
1. Kepler’s Law	(a) Zero
2. Weight of man in space	(b) \(-\frac{G M m}{2 r}\)
3. Escape velocity	(c) Planetary motion
4. Binding energy of satellite	(d) Time-period of revolution is 24 hours
5. Geo-stationary satellite	(e) \(\sqrt{2 g R}\)

Answer:
1. (c) Planetary motion
2. (a) Zero
3. (e) \(\sqrt{2 g R}\)
4. (b) \(-\frac{G M m}{2 r}\)
5. (d) Time-period of revolution is 24 hours

II.

Column ‘A’	Column ‘B’
1. Acceleration due to gravity	(a) Weak force
2. Gravitational constant	(b) Scalar quantity
3. Gravitational potential	(c) Variable
4. Gravitational force	(d) E = mc2
5. Mass-energy equivalence equation	(e) Vector.

Answer:
1. (e) Vector.
2. (c) Variable
3. (b) S calar quantity
4. (a) Weak force
5. (d) E = mc²

4. Write true or false:

1. Newton’s laws is universal.
Answer:
True

2. Magnitude of G is different at different places.
Answer:
False

3. Magnitude of ‘g’ is equal at any point on surface of earth.
Answer:
False

4. Ratio of gravitational mass and inertial mass is one.
Answer:
True

5. Gravitational potential is negative at every point on earth surface.
Answer:
True

6. Principle of superposition is not applicable for gravitation.
Answer:
False

7. Value of escape velocity of a body depends upon its mass.
Answer:
False

8. Height of polar satellite from earth surface is 36000 km.
Answer:
False

9. Magnitude of gravitation potential energy at infinity is zero.
Answer:
True

10. Gravitational force is a conservative force.
Answer:
True