MP Board Class 11th Physics Important Questions Chapter 7 System of Particles and Rotational Motion

Students get through the MP Board Class 11th Physics Important Questions Chapter 7 System of Particles and Rotational Motion which are most likely to be asked in the exam.

MP Board Class 11th Physics Important Questions Chapter 7 System of Particles and Rotational Motion

System of Particles and Rotational Motion Class 11 Important Questions Very Short Answer Type

Question 1.
Define the rotational motion.
Answer:
When a force is applied on a rigid body then it revolves about its own axis. This motion of the body is called rotational motion.

Question 2.
Define the term rigid body.
Answer:
A body is said to be a rigid body if an applying external force or during its motion the distance between constituent particle remain unchanged.

Question 3.
Differentiate rotatory motion and circular motion.
Answer:
In rotatory motion the axis of motion lies within the body while in circular motion the axis lies outside the body.

Question 4.
What is torque? Write its unit and dimensional formula.
Answer:
The turning effect of a force, to rotate a body about an axis is called torque. The torque is equal to product of force and perpendicular distance of force from the axis of rotation.
Torque = Force × Moment arm
τ = F × d
Unit: Its S.I. unit is.N × m.
Dimensional formula: [ML²T^-2].

Question 5.
What do you mean by angular velocity and angular acceleration. Write its S.I. units and dimensional formula.
Answer:
Angular velocity : Rate of Change of angular displacement per unit time.
Its unit is radian/second and dimensional formula is [M⁰L⁰T^-1].
Angular acceleration : The rate of change in angular velocity of the body about the given axis of rotaion.
Its unit is radian/second² and dimensional formula is [M⁰L⁰T^-2]

Question 6.
What do you mean by angular momentum?
Answer:
It is defined on the product of linear momentum and perpendicular distance of line of action of linear vector from the axis of rotation.
Angular momentum = Linear momentum × perpendicular distance of linear momentum from the axis of rotation.
Its SI unit is J × s. and dimensional formula is [ML²T^-1 ].

Question 7.
Define moment of inertia and give its unit and dimensional formula.
Answer:
Moment of inertia of a rotating body is the property by virtue of which, it opposes the torque applied to change its position of rest or rotational motion.
If the mass of a body is m and its distance from the axis of rotation is r, then moment of inertia, I = mr²
Unit: Its S.I. unit is kg × m².
Dimensional formula: [ML²T⁰].

Question 8.
Define radius of gyration and give its unit.
Answer:
The radius of gyration of a body is equal to the perpendicular distance from the axis of rotation of a point at which if the mass of a body is assumed to be concentrated the moment of inertia is the same as the actual ‘moment of inertia of the body about that axis. It is represented by k.
UnIt: Its S.I. unit is metre.

Question 9.
On what factors does the moment of inertia of a body depend?
Answer:
(a) On mass of body (2) Distribution of mass from the axis of rotation.

Question 10.
What will be the effect on moment of inertia if the direction of motion of the body is changed?
Answer:
There will be no effect on moment of inertia.

Question 11.
Is it essential to apply moment of couple to a rotating body? Explain with reason?
Answer:
No, it is not essential to apply moment of couple to a rotating body because moment of couple only create angular acceleration.

Question 12.
It is easy to rotate a stone tied with a small string, than that of a longer. Why?
Answer:
We know that, τ = Iω. If the string is long its moment of inertia will be greater and therefore greater torque will be required to rotate the stone. But, for small string less torque is required. Therefore, it is easy to rotate the stone with smaller string.

Question 13.
Write the relation between torque and angular momentum.
Answer:
τ = \(\frac{d L}{d t}\)

Question 14.
Write the relation between angular momentum and moment of inertia.
Answer:
Angular momentum = Moment of inertia × Angular velocity.

Question 15.
Why the spokes are used in a wheel?
Answer:
The spokes increases the distance of rim from the axis of rotation, hence its moment of inertia increases, which makes the rotation of wheel uniform and maintains its rotation.

Question 16.
The handle of a door is fixed away from the hinge. Why?
Answer:
The handle is fixed away from the hinge because, it increases the perpendicular distance between the line of action of force and hinge. Hence, the torque increases.

Question 17.
The handle of a hand pump is made long, why?
Answer:
Long handle increases the distance between the piston and the force, thus the torque increases, so less force is required to pump the water.

Question 18.
What will be the velocity of a point on a rotational axis in rotational motion?
Answer:
The velocity of a point situated in rotation axis in rotational motion is zero.

Question 19.
Differentiate inertia and moment of inertia.
Answer:
Difference between Inertia and Moment of inertia :

Inertia	Moment of inertia
1. Its importance is in linear motion.	1. Its importance is in rotatory motion.
2. The inertia depends upon the mass of the body.	2. It depends upon mass and the perpendicular distance from the axis of rotation.
3. It is constant for a body.	3. It changes with the position of axis and distribution of mass.

Question 20.
What is the physical importance of moment of inertia?
Answer:
To rotate a body about an axis from the rest or to change angular velocity or angular acceleration of rotating body, a torque is applied, more the moment of inertia more will be the torque. This is the physical importance of moment of inertia.

Question 21.
What do you mean by mechanical equilibrium of a system?
Answer:
When the vector addition of total forces and vector addition of total moment of inertia is’ zero then the system is said to be in mechanical equilibrium.

Question 22.
Write the principle of moments.
Answer:
According to this principle anti clockwise moments are taken positive and clockwise moments are taken negative when the body is in rotational equilibrium.

Question 23.
What is moment of couple? Write its SI unit and dimensional formula. Write the factor on which it depends.
Answer:

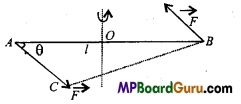
The product of a force and the perpendicular distance between the line of action of forces is called moment of couple.
Moment of couple = Force × Couple arm
Unit: Its S.I. unit is N × m.
The factor it depends are :

• Magnitude of force.
• Perpendicular distance between the line of action of forces.

Question 24.
What is the physical importance of angular momentum?
Answer:
We know that,
Torque = Force × Perpendicular distance of line of action from the axis and
Angular momentum = Linear momentum × Perpendicular distance of particle from the
axis.
Hence, as the torque measures the tinning effect, similarly angular momentum measures the rotational motion.

Question 25.
What is geometrical meaning of angular momentum?
Answer:
The angular momentum is equal to twice of the product of mass and areal velocity of a particle.
i.e., Angular momentum = 2 × Mass × Areal velocity

Question 26.
A dancer is rotating with stretched hands, when the closes her hands, her speed of rotation increases. Why?
Answer:
We know that in the absence of external force the angular momentum of a rotating body is conserved and is equal to Iω. When the dancer closes her hands, her moment of inertia I decreases hence ω i.e., angular velocity increases.

Question 27.
When a rotating stone tied with a string is stoped, the string winds up in the hand fastly. Why?
Answer:
When the string is started wind up in the hand, the length of string decreases and hence the moment of inertia of stone decreases. But, we know that angular momentum Iω is constant. As I decreases ω increases, therefore the string winds up very fast.

Question 28.
Which factor depends on moment of inertia of the body that moves around a body.
Answer:
We know I = Σmr²
Therefore moment of inertia,

• Is directly proportional to the mass.
• Is directly proportional to the square of distance from the axis of rotation.

Question 29.
Is centre of mass a reality?
Answer:
No, it is only a mathematical concept.

Question 30.
It is difficult to open the door by pushing it or pulling it at the hinge. Why?
Answer:
Because at the hinge the distance of the point of application of the force from the axis of rotation is negligible, so the torque is very small.

Question 31.
Why a helicopter must necessarily have two propellors?
Answer:
If there were only one propellor in the helicopter, then it would have to turn in the opposite direction to conserve its angular momentum.

System of Particles and Rotational Class 11 Important Questions Short Answer Type

Question 1.
Define vector product of two vectors and give one example of vector product. Also write its properties.
Answer:

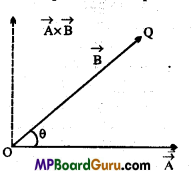
Let the angle between two vectors \(\vec{A} \text { and } \vec{B}\) is θ, then their cross product is defined as
\(\vec{A} \times \vec{B}=A B \sin \theta \hat{n}\)
Where, \(\hat{n}\) is unit vector perpendicular to the plane consisting vectors \(\vec{A} \text { and } \vec{B}\) .
The direction of \(\vec{A} \times \overrightarrow{\vec{B}}\) follows the screw rule, as shown in the figure.

Example : Let a force \(\vec{F}\) is acting at a point whose position vector is \(\vec{r}\) , then the torque \(\vec{τ}\) is given by the cross product of \(\vec{F}\) and \(\vec{r}\)
i.e.. \(\vec{\tau}=\vec{r} \times \vec{F}\)
Properties: I. Vector product of two vector is always a vector quantity.
2. It does not obey commutative law
\(\vec{a} \times \vec{b} \neq \vec{b} \times \vec{a}\)
3. It does not obey associative law
\(\vec{a} \times(\vec{b} \times \vec{c}) \neq(\vec{a} \times \vec{b}) \times \vec{c}\)
4. \(\vec{a} \times \vec{a}\) = 0 (zero vector)

Question 2.
Show that the area of the triangle contained between the vectors  \(\vec{a} \text { and } \vec{b}\) is one half of the magnitude of a× b.
Answer:

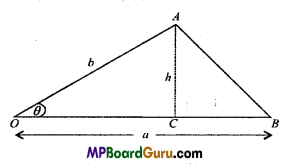
Let the vectors \(\vec{a} \text { and } \vec{b}\) represent the two adjacent sides of ΔAOB such that
OA =b, OB = a
Let angle between a and b be θ.
Such that∠AOB= θ
and also let h be the height of the triangle such that
h=AC
Now in right angled ΔOCA,
sinθ = \(\frac{A C}{O A}\)
or
AC=OA sinθ
or
h = b sinθ … (1)
We know that the area of the triangle AOB, is given b
= \(\frac{1}{2}\) × base × height
= \(\frac{1}{2}\) × OB x AC
= \(\frac{1}{2}\) × a × h
= \(\frac{1}{2}\) × a × b sinθ
= \(\frac{1}{2}\)absinθ …(2)
Also by the definition of cross-product of two vectors, we know that
a × b = ab sinθ\(\hat{n}\)
or
\(|a \times b|=|a b \sin \theta \hat{n}|\)
= ab sinθ\(|\hat{n}|\)
= ab sinθ (\(|\hat{n}|\)
= absinθ, (\(|\hat{n}|\)
= absinθ, (∵ (\(|\hat{n}|\) = 1) …(3)
∴ From eqns. (2) and (3), we get
Area of ΔAOB = \(\frac{1}{2} \mid a \times b\)
= \(\frac{1}{2}\) [magnitude of a × b].

Question 3.
Give the location of the centre of mass of a
(i) sphere
(ii) cylinder
(iii) ring and
(iv) cube each of uniform mass density. Does the centre of mass of a body neccessarily lie inside the body?
Answer:
C.M. lies at the :
(i) Centre of sphere.
(ii) Mid-point of axis of symmetry of the cylinder i.e., its geometrical centre.
(iii) Centre of ring.
(iv) Point of intersection of diagonals i.e., at its geometrical centre.

No, in some cases, C.M. of a body like ring, hollow cylinder, hollow sphere and hollow cube etc. may lie outside.

Question 4.
Define work in rotational motion.
Answer:
As work is define as product of force and displacement in direction of force in linear motion, same like that work done by a torque in rotational motion is define as product of torque and angular displacement.
Work W = τ.d.θ

Question 5.
Derive an expression for the angular momentum of a body in rotational motion.
Or
Prove that J = Iω
Answer:
Consider a body which is made up number of particles of masses m₁,m₂,m₃,…. situated at the distances r₁,r₂, r₃ from the axis of rotation. If the linear velocities are
ν₁, ν₂, ν₃,…. respectively, then
Linear momentum of m₁ = m₁ν₁ = m₁r₁ω , (∵ ν = r ω)
and Angular momentum = m₁r₁ω x r₁ = m₁r₁² ω
Similarly, angular momentum of m₂,m₃,…. will be m₂r₂² ω,m₃r₃² ω,…..
∴ Angular momentum of whole body = m₁r₁²ω + m₂r₂² ω, + m₃r₃² ω, +….
or
J = ω (m₁r₁² +m₂r₂² +m₃r₃² +….)
= ωΣ mr²
or
J = ωI
∴ Angular momentum = Angular velocity × Moment of inertia.

Question 6.
What do you understand by angular momentum? Establish the relation between angular momentum and rotational K.E.
Answer:
Angular momentum : If a particle is moving about an axis, then the moment of linear momentum is called its angular momentum about that axis.
∴ Angular momentum = Linear momentum × Perpendicular distance of particle from the axis of rotation

Relation between angular momentum and rotational K.E.: We know that rotational kinetic energy (E_k) is given by the formula
E_k = \(\frac{1}{2}\) Iω² …(1)
But, Angular momentum, J = Iω
or
ω = \(\frac{J}{I}\)
Putting the value of ω in eqn. (1), we get
E_k = \(\frac{1}{2}\) I\(\left(\frac{J}{I}\right)^{2}\) = \(\frac{1}{2}\) \(\frac{J^{2}}{I}\)
or
J² =2I E_k
or
J = \(\sqrt{2 I E_{k}}\) …(2)
Eqn. (2) is the required relation.
If angular momentum remains conserved, then \(\sqrt{2 I E_{k}}\) lEk will be constant
or
2I E_k = Constant
or
E_k = \(\frac{\text { Constant }}{2 I}\)
or
E_k ∝ \(\frac{1}{I}\)

Question 7.
What is the law of conservation of angular momentum? Prove it.
Answer:
Law of conservation of angular momentum: In the absence of external torque, the angular momentum of a system remains constant.
i.e., J = a constant
Then, Iω = a constant
Now, we know that rate of change of angular momentum is equal to the external torque
applied.
i.e., τ = \(\frac{d J}{d t}\)
If τ = 0
Then, \(\frac{d J}{d t}\) = 0
or
J = a constant
or
J = Iω
If in two different conditions the moment of inertia of a body are I₁ and I₂and angular velocities are ω₁and ω₂respectively, then
I₁ω₁ = I₂ω₂

Question 8.
Prove that the rate of change of angular momentum is equal to the torque applied.
Or
Prove that τ = \(\frac{d J}{d t}\)
Answer:
Let a torque τ is applied on a body of moment of inertia I, so that its angular
acceleration becomes α, then
τ = I.α ….(1)
But, α = \(\frac{d \omega}{d t}\)
∴ τ = I.\(\frac{d \omega}{d t}\) …(2)
Also we have J = Iω
∴ \(\frac{d J}{d t}=\frac{d}{d t}\) (Iω) = \(\frac{d \omega}{d t}\)
From eqn. (2), we get
Or
\(\frac{d J}{d t}\) = Iω = τ [ from eqn .(1)]
Hence, rate of change of angular momentum is equal to the torque applied.

Question 9.
Derive an expression for the moment of inertia of a rigid body.
Or
Prove that I = Σ mr².
Answer:

Let a body rotating about an axis XY supposing that the body is made up of number of particles of masses m₁,m₂,m₃,…. situated at the distances r₁,r₂,r₃, from the axis of rotation.
∴ The moment of inertia of the particles will be m₁r₁² , m₂r₂² , m₃r₃²,
Hence, the moment of inertia of whole body,
I = m₁r₁² + m₂r₂² + m₃r₃² +
or
I = Σmr²
Where, Σ is the sign of summation.

Question 10.
Compare the different derivatives in linear motion and rotational motion.
Answer:
Different derivatives in linear and rotational motion :

Linear motion	Rotational motion
1. Displacement = x	1. Angular displacement = θ
2. Linear velocity ν = \(\frac{d x}{d t}\)	2. Angular velocity ω = \(\frac{d θ}{d t}\)
3. Linear acceleration a = \(\frac{d ν }{d t}\)	3. Angular acceleration α = \(\frac{d \omega}{d t}\)
4. Mass = m	4. Moment of inertia = I
5. Force = F	5. Moment of force (Torque) = τ
6. Linear momentum p = m. ν	6. Angular momentum J = I.ω
7. Force F = \(\frac{d p }{d t}\)	7. Torque τ = \(\frac{d J}{d t}=\frac{d}{d t}\)
8. Kinetic energy = \(\frac{1}{2}\)mν2	8. Rotational kinetic energy = \(\frac{1}{2}\) Iω2
9. Equation of a linear motion v = u + at s = ut + \(\frac{1}{2}\)at2 ν2 = u2 + 2as.	9. Equation of angular motion ω = ω0 + αt θ = ω0t + \(\frac{1}{2}\) αt2 ω2 = ω02 +2αθ

Question 11.
A planet is revolving around a sun in an elliptical orbit. How angular velocity and linear velocity get changes in the orbit?
Answer:
(1) Since angular momentum L = mr²ω is constant. Therefore when planet go
far from sun r increases and hence co decreases and when planet go near to sun r decreases
and hence co increases.
(2) Since L = mνr constant. Therefore when planet go far from sun r increases and
hence ν decreases and when planet is close to sun r decreases and hence ν increases.
[∵ ν ∝\(\frac{1}{r}\)

Question 12.
A ladder is at rest against a wall. Is the ladder more likely to slip when a person climb up why?
Answer:
It is more likely to slip when a man climb upward in the ladder because due to the fact that the weight of the man will provide an extra torque for the slipping of the ladder.

Question 13.
What do you understand by angular momentum? Derive its’s expression.
Answer:
If a particle is moving about an axis, then the moment of linear momentum is called its angular momentum about that axis.
Angular momentum = Linear momentum × Perpendicular distance of particle from the axis of rotation.
Let’ m’ be the mass of a particle P whose position vector be V with respect to origin
O and its linear momentum be \(\vec{p}(=m \vec{v})\) and angular momentum be \(\vec{J}=(\vec{p} \times \overrightarrow{O N})\) = pr sinθ
In right angled Δ OPN,

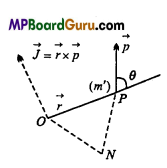
ON = OP sinθ =r sinθ
or
J=rp sinθ
Where θ is angle between \(\vec{r} \text { and } \vec{p}\)
or
\(\vec{J}=\vec{r} \times \vec{p}\)
or
\(\vec{J}=\vec{r} \times(m \cdot \vec{v})\)
or
\(\vec{J}=m(\vec{r} \times \vec{v})\)

Question 14.
What do you understand by angular acceleration? Prove that :a = r × α.
Answer:
Angular acceleration : Rate of change in angular velocity is defined as angular acceleration.
Angular acceleration = \([latex]\frac{\text { Angular velocity }}{\text { Time interval }}\)[/latex]
If Δω be the change in angular velocity in time Δt, then average angular acceleration = \(\frac{\Delta \omega}{\Delta t}\)
or instantaneous angular acceleration α = \(\lim _{\Delta t \rightarrow 0} \frac{\Delta \omega}{\Delta t}=\frac{d \omega}{d t}\)
But ν = rω .where r is the distance of particle, from axis of rotation,
∴ Integration both side, we get
\(\frac{d ν}{d t}\) = r \(\frac{d ω }{d t}\) = r.α

Question 15.
Prove that the radius of gyration of a body is equal to the root mean square of>the distances of particles from the axis of rotation.
Answer:
Expression for the radius of gyration : Let the mass of a body is M and its radius of gyration is K,
Moment of inertia of the body
∴ I = MK²
Also I = Σmr²
∴ MK² = Σmr²
or
MK² = m₁ r₁² + m₂r₂² + m₃r₃ ² +….
If m₁ = m₂ = m₃ =….= m (let), then
MK² = mr₁² +mr₂² +mr₃² + ……
MK² = m(r₁² + r₂² + r₃ ² + …..)
But M = m × N(where N is number of particles)
∴ mNK² = m(r₁² + r₂² + r₃ ² + …..)
or
K² = \(\frac{r_{1}^{2}+r_{2}^{2}+r_{3}^{2}+\ldots}{N}\)
∴ K = \(\sqrt{\frac{r_{1}^{2}+r_{2}^{2}+r_{3}^{2}+\ldots}{N}}\)
Hence, Radius of gyration = r.m.s. of distance of particle from the axis of rotation.

Question 16.
Derive an expression for the K. E. of a rotation.
Or
Prove that the kinetic energy of rotation of a rigid body =\(\frac{1}{2}\)ω², where I is moment of inertia and co is angular velocity.
Or
Define the rotational kinetic energy and derive its formula.
Answer:
Let a body is rotating about an axis XY, with an angular velocity ω. The body consists of number of particle and angular velocity of each particel will be same. But the distances of all the particles are different, therefore each particle will have different linear velocity.
Let the distances of the particles of masses m₁m₂m₃are r₁, r₂, r₃,…. and their
linear velocities are v₁ v₂, v₃,…. respectively.
Then, K.E. of particles will be

System of Particles and Rotational Class 11 Important Questions Long Answer Type

Question 1.
State perpendicular axes theorem and prove it. Is it applied to every body?
Or
State theorem of perpendicular axis of moment of inertia and prove it.
Answer:
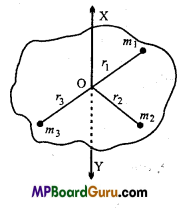
Perpendicular axes theorem :
According to this theorem. The moment of inertia of a plane lamina about an axis perpendicular to its plane is equal to the sum of the moment of inertia of the body about two mutually perpendicular axes lying in the plane of the body and intersecting at the point through which the perpendicular axis passes.

Proof:
Let P be a particle on a lamina, at distances x,y and r from the axes of X, Y and Z and OP = r.
If the mass of the particle is m, then
M.I. about X – axis, I_x = Σ my²
M.I. about y – axis, I_y = Σ mx²
and M.I. about Z-axis, I_z = Σ mr²
From right angle Δ PMO,
r² = x² + y²
∴ mr² = mx² + my²
or
Σmr² = Σmx² + Σmy²
or
I_z = I_x + I_y

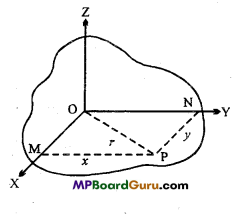
This threorem is true for all types of bodies. The solid body is divided into laminas and the theorem can be applied.

Question 2.
State theorem of parallel axes and prove it. Is it applicable for all the bddies?
Answer:
Parallel axes theorem :
According to this theorem, the moment of inertia of a body about the given axis is equal to the sum of the moment of inertia of the body about an axis through the centre of mass and parallel to the given axis and the product of the mass of the body and the square of distance between the two axes.

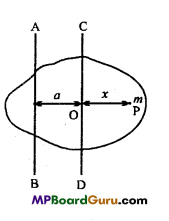
Proof:
Let CD is the axis passing through centre of mass of the body and AB is the axes parallel to CD at a distance a.
Consider a particle P of mass m at a distance x from CD.
∴ M.I. of P about axis AB = m(a + x)²
∴ M.I. of whole body about AB
I =Σm(a+ x)²
or
I = Σm(a² + 2ax + x²)
or
I = Σma² + Σ2amx + Σmx²
or
I = a²Σm + 2.a Σmx + Σmx²
But, Σmx² = I_cm and Σm = M.
∴ Now, Σx is the moment of body about the axis passing through centre of mass. .•.
∴ Σmx = 0
Hence, by eqn. (1)
I = a²M + 0 + I_cm
or
I = I_cm + Ma²
This theorem is applicable for all the bodies.

Question 3.
Write the equations of rotational motion and derive them.
Answer:
If the initial angular velocity is ω₀, angular acceleration is α and after t sec. the displacement is θ and angular velocity becomes ω, then equations are :
(i) ω = ω₀ + αt
(ii) θ = ω₀t + \(\frac{1}{2}\)αt²
(iii) ω² = ω₀² +2αθ

(i) Derivation of first equation :ω = ω₀ + αt
By the definition of angular acceleration,
α = \(=\frac{\omega-\omega_{0}}{t}\)
or
ω – ₀ = αt
∴ ω = ω₀ + αt

(ii) Derivation of second equation: θ = ω₀t + \(\frac{1}{2}\)αt²
The body is rotating with uniform angular acceleration, therefore
Average angular velocity = \(\frac{\omega+\omega_{0}}{2}\)
But, from the first eqn., ω = ω₀ + αt
∴ Average angular velocity = \(\frac{\omega_{0}+\alpha t+\omega_{0}}{2}\)
= ω₀ + \(\frac{1}{2}\)αt
Now, Angular displacement = Average angular velocity × Time
θ = \(\left(\omega_{0}+\frac{1}{2} \alpha t\right)\) × t
or
θ = ω₀t +\(\frac{1}{2}\) αt²

(iii) Derivation of third equation : ω² = ω₀² + 2αθ
Now, by first equation, we have
ω = ω₀ + αt
Squaring both the sides, we get
ω² = ( ω₀ + αt)²
or
ω² = ω₀² + 2ω₀αt + α²t²
or
ω² = ω₀² + 2α\(\left(\omega_{0} t+\frac{1}{2} \alpha t^{2}\right)\)
But, from second eqn., we have
ω₀t + \(\frac{1}{2}\)at² = θ
∴ ω² = ω₀²+ 2 α θ

Question 4.
Derive the expression of kinetic energy in rolling motion.
Answer:
When the body is rolling over any surface, its kinetic energy is the sum of translatory kinetic energy and rotatory kinetic energy.

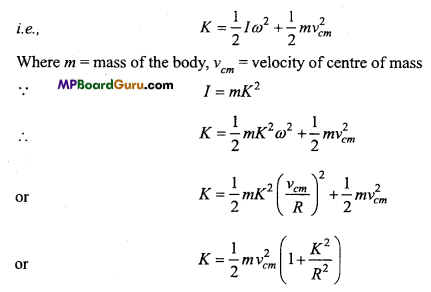
The above formula is applicable for cylinder, disc and sphere.

System of Particles and Rotational Class 11 Important Numerical Questions

Question 1.
Two circular disc made of different metals having same mass and diameter dA and dB (dA > dB). If the moment of inertia about the axis perpendicular to its plane and passing through its centre is I_A and I_B. Find which is more I_A or I_B ?
Solution:
Let the mass of each disc b e‘m’ and radius be r_Aand r_B.

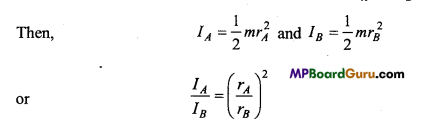
If the thickness of the disc is ‘t then

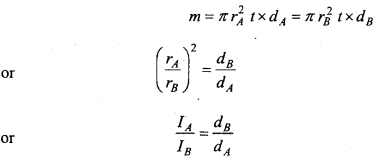
Since, d_A > d_B
There fore I_A < I_B

Question 2.
A solid sphere of mass M and radius R is rolling over a horizontal surface with velocity ν. What will be its kinetic energy?
Solution:
Total kinetic energy = Rotatory kinetic energy + Linear kinetic energy

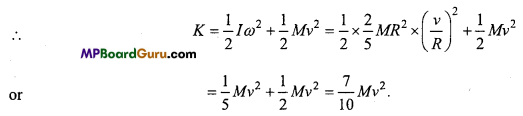
Question 3.
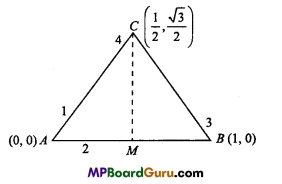
Three particles of massess 2, 3, 4 kilogram are kept at three vertices of a triangle of side 1 metre. Find out centre of mass of the system.
Solution:
Let the vertices A be at origin (0, 0) and B be at X-axis of a ΔABC, then the
coordinates will be : A (0,0), B (1,0) and C\(\left(\frac{1}{2}, \frac{\sqrt{3}}{2}\right)\)
∴ Centre of mass of the system

Question 4.
(a) Find the moment of inertia of a sphere about a tangent to the sphere, given the moment of inertia of the sphere about any of its diameters to be 2MR²/5, where M is the mass of the sphere and R is the radius of the sphere.
(b) Given the moment of inertia of a disc of mass M and radius R about any of its diameters to the MR²/4. Find its moment of inertia about an axis normal to the disc and passing through a point on its edge.
Solution:
(a) The moment of inertia of sphere about its diameter be
I_cm = \(\frac{2}{5}\)MR²
By the theorem of parallel axis
I = I_cm + Ma²
= \(\frac{2}{5}\)MR² + MR², [∵ a = R]
= \(\frac{7}{5}\)MR²

(b) The moment of inertia of disc about its diameter

I_d = \(\frac{1}{4}\)MR²
By the theorem of perpendicular axis the moment of inertia of disc about an axis AB passing through its centre, perpendicular to its plane be
I_cm = \(\frac{1}{4}\)MR² + \(\frac{1}{4}\)MR² [∵I_z=I_x+I_y]
= \(\frac{1}{2}\)MR²
By the theorem of parallel axis the moment of inertia about an axis passing through a point on its edge and perpendicular to the disc be
I = I_cm + Ma² = \(\frac{1}{2}\)MR² + MR² , [∵ a=R]
= \(\frac{3}{2}\)MR²

Question 5.
A solid sphere of mass 0.5 kg and radius 1 metre is rolling over a smooth surface with a velocity of 5 m/s. Find its total energy. What is the percentage of rotational kinetic energy in total energy ?
Solution:
Given : m = 0.5 kg, 2r = 1 m, r = 0.5 m, ν =5 m/s.

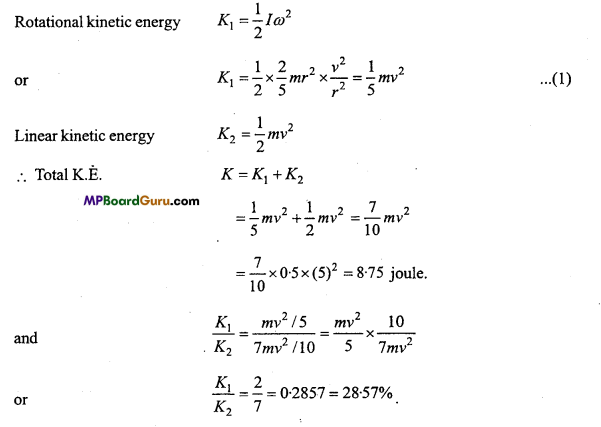
Question 6.
If = \(\vec{a}=3 \hat{i}-4 \hat{j}+\hat{k}\) and \(\vec{r}=5 \hat{i}-6 \hat{j}+6 \hat{k}\) then find out the magnitude of linear velocity.
Solution:
\(\vec{a}=3 \hat{i}-4 \hat{j}+\hat{k}, \vec{r}=5 \hat{i}-6 \hat{j}+6 \hat{k}\)
From \(\vec{v}=\vec{a} \times \vec{r}\)
\(=\left|\begin{array}{ccc}
\hat{i} & \hat{j} & \hat{k} \\
3 & -4 & 1 \\
5 & -6 & 6
\end{array}\right|\)
or
\(\vec{v}=\hat{i}(-24+6)-\hat{j}(18-5)+\hat{k}(-18+20)\)
\(=-18 \hat{i}-13 \hat{j}+2 \hat{k}\)

Question 7.
A metre stick is balanced on a knife edge at its centre. When two coins, each of mass 5 gm are put one on top of the other at the 12.0 cm mark, the stick is found to be balanced at
45.0 cm. What is the mass of the metre stick?
Solution:
Given : AB = 1 m = 100 cm
AG = BG = 50 cm AC = 12 cm;

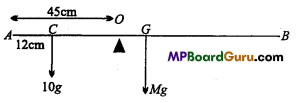
For the rotational equilibrium about point O
10g × OC = Mg × OG
or
10g (45 -12)= Mg (50 -45)
or
10 × 33 =M × 5
∴ M = \(\frac{10 \times 33}{5}\) = 66 gm.

Question 8.
Moment of inertia of a flywheel is 4 kg/m². Find out the angular acceleration of it if the torque acting on it is 10 newtonmetre.
Solution:
Given : I = 4 kg/m², τ = 10 newton-metre
From torque τ = Iα, we get
α = \(\frac{\tau}{I}=\frac{10}{4}\) = 2.5 rad/s²

Question 9.
The oxygen molecule has a mass of 5.30 × 10^-26 kg and a moment of inertia
1.94 × 10^-46kgm² about an axis through its centre perpendicular to the lines joining the two atoms. Suppose the mean speed of such a molecule in a gas is 500 m/s and that if kinetic energy of rotation is two thirds of its kinetic energy of translation. Find the average anglular velocity of the molecule.
Solution:
Given, M = 5.30 × 10^-26kg; I = 1.94 × 10^-46kgm² and ν = 500 m/s
Rotational K.E. = \(\frac{2}{3}\) × Translatory K.E.

= 6.75 x 10¹²rad/s.

Question 10.
Find out the moment of inertia of a circular disc of mass 2 kg and radius 0.5 metre along:
(i) Its geometrical axis,
(ii) Its diameter,
(iii) Tangential direction on its circum-ference.
Solution:
Given : M= 2 kg, R = 0.5 m
(i) M.I. along its geometrical axis
I = MR² = 2 × (0.5)²
= 2 × (0.25)
= 0.5 kg m².

(ii) M.I. along diameter
I_d = \(\frac{1}{2}\)I = \(\frac{1}{2}\)MR²
= \(\frac{1}{2}\).2 × (0.5 )²
= (0.5)2 = 0.25 kgm²

(iii) M.I. in tangential direction on its circumference
I_T =I_d + Ma²
= \(\frac{M R^{2}}{2}\) + MR² = \(\frac{3}{2}\) MR²
= \(\frac{3}{2}\).2 × (0.5)²
= 3 × 0.25 =0.75 kgm².

Question 11.
The mass of a circular ring is 2 kg and its radius is 2m. The speed of its centre of mass is 20 cm × s^-1 Calculate the K.E. of rotation of ring. (M. I. of ring = MR²)
Solution:
Given : r = 2 m,M = 2kg,ν = 20 cm × s^-1 = 20 × 10 ms^-1.
Total K.E. = \(\frac{1}{2} I \omega^{2}+\frac{1}{2} M v^{2}\)
\(=\frac{1}{2} M r^{2} \frac{v^{2}}{r^{2}}+\frac{1}{2} M v^{2}\)
\(=\frac{1}{2} M v^{2}+\frac{1}{2} M v^{2}\) = Mν²
= 2 × (20 × 10^-2 )² = 8 × 10^-2 joule.

Question 12.
The wheel of a train revolve 6 revolution per second. On applying brakes it get stopped after 12 sec. Find out angular acceleration produced by brake.
Solution:
Given : Frequency n = 6 revolution/sec, t = 12 sec, ω = 0
and ω₀ = 2πn = 12π rad/sec
By the formula ω = ω₀ + α.t, we get
0 = 12π – α × 12
or
α = \(\frac{12 \pi}{12}\) = π
or
α = 3.14 rad/sec ²

Question 13.
A man is standing on a rotating table with hands stretched, the moment of inertia is 50 kg m2 and angular velocity is 3 rad/s. Now, the man closes his hands thus the moment of inertia becomes 30 kg m². Calculate the angular velocity.
Soution:
Given: I₁=50kgm², ω₁ =3rad × s^-1, I₂=30kgm².
We have, I₁ ω₁ = I₂ ω₂
∴ ω₂ = \(\frac{I_{1} \omega_{1}}{I_{2}}\)
or
ω₂ = \(\frac{50 \times 3}{30}\) = 5rad s^-1

Question 14.
If the diameter of the earth reduces to half of it, then what will be the duration of the day?
Solution:
We know I₁ ω₁ = I₂ ω₂
or
\(\frac{2}{5} M R^{2} \times \frac{2 \pi}{T_{1}}=\frac{2}{5}\left(\frac{R}{2}\right)^{2} M \times \frac{2 \pi}{T_{2}}\)
∴ \(\frac{1}{T_{1}}=\frac{1}{4 T_{2}}\)
or
T₂ = \(\frac{T_{1}}{4}=\frac{24}{4}\) = 6 hr

Question 16.
If the radius of revolving disc is made half keeping mass same, then what will be its angular velocity?
Solution:
From = I₁ ω₁ = I₂ ω₂
Or
MR²ω₁ = \(\left(\frac{R}{2}\right)^{2}\)M ω₂
∴ ω₂ = 4ω₁
i.e., Angular velocity will become 4 times of the earlier.

Question 17.
Angular momentum of a body changes from 220 kg m2 to 340 kg m2 in 10 sec. Find out the torque acting on it.
Solution:
Since τ = \(\frac{d J}{d t}\)
∴ τ = \(\frac{340-220}{10}=\frac{120}{10}\)
τ = 12 N-m.

Question 18.
The mass of a fly-wheel is 25 kg and its radius is 0.2 m. How much force
will be applied in tangential direction to produce angular acceleration of 2 rad × s^-2?
Solution:
Given : M = 25 kg, R = 0.2 m, α = 2 rad × s^-2, d = 0.2m.
Now,
I = MR²
= 25 × (0.2 )² = 1 kgm
Again, τ =I.α
= 1 × 2=2 N-m
Also, τ=F × d
∴ F = \(\frac{\tau}{d}\)
= \(\frac{2}{0 \cdot 2}\)
= 10N

Question 19.
A ball of mass 1 kg is tied at one end of a 20 cm long string and it is rotated in horizontal phase in such a way that it revolves 8 revolution per second. Find out the following :
(i) Ahgular velocity,
(ii) Linear velocity,
(iii) Moment of inertia along the finger of hand,
(iv) Angular momentum.
Solution:
Given : r = 20cm =20 × 10^-2m, m= 1 kg, υ =8rev/sec

(i) Angular velocity ω = 2πυ
or
ω = 2π × 8 = 16π rad/sec.

(ii) Linear velocity v = r.ω
or
ν = 20 × 10^-2 × 16π
ν = 3.2π m/s.

(iii) Moment of inertia I = mr²
or
I = 1 × (20 × 10^-2)²
or
I = 0.04 kg m².

(iv) Angular momentum J = Iω
or
J = 0.04 × 16π
= 0.64π kg m²/sec.

Question 20.
A ball tied with a string takes 4 second for one revolution rotating in cicular path. If the radius of the circular path is made half, then what will be the time taken by the ball to complete one revolution.
Solution:
By the laws of conservation of momentum
= I₁ ω₁ = I₂ ω₂
Let the mass of the ball be ‘wi’ and radius be ‘r’.
Then, I₁ = mr²

System of Particles and Rotational Class 11 Important Questions Objective Type

1. Multiple- choice questions:

Question 1.
In rotational motion, moment of inertia has the same importance as the physical quantity in linear motion :
(a) Velocity
(b) Acceleration
(c) Mass
(d) Force
Answer:
(c) Mass

Question 2.
Centre of mass of moving object:
(a) Remain stationary
(b) Does not get influenced by internal forces
(c) Does not get influenced by external forces
(d) None of these.
Answer:
(b) Does not get influenced by internal forces

Question 3.
The moment of linear momentum is called :
(a) Couple
(b) Torque
(c) Impulse
(d) Angular momentum.
Answer:
(d) Angular momentum.

Question 4.
Which relation is incorrect:
(a) L = Iω
(b )I = MK²
(c )E = \(\frac{1}{2}\)Iω
(d) τ = \(\frac{d L}{d t}\)
Answer:
(c )E = \(\frac{1}{2}\)Iω

Question 5.
Moment of inertia depends upon :
(a) Angular velocity
(b) Mass
(c) Distribution of mass
(d) On axes of rotation and mass distribution.
Answer:
(d) On axes of rotation and mass distribution.

Question 6.
What is the formula for rotational kinetic energy of an object:
Moment of inertia Angular Acceleration
(a) R.K.E. = \(\frac{1}{2}\) × Moment of inertia × (Angular velocity)²
(b) R.K.E. = \(\frac{\text { Moment of inertia }}{\text { Angular Acceleration }}\)
(c) R.K.E. = \(\frac{\text { Force }}{\text { Time }}\)
(d) R.K.E. = \(\frac{\text { Time }}{\text { Displacement }}\)
Answer:
(a) R.K.E. = \(\frac{1}{2}\) × Moment of inertia × (Angular velocity)²

Question 7.
Rate of change in angular velocity is known as :
(a) Angular displacement
(b) Angular speed
(c) Angular acceleration
(d) Angular momentum.
Answer:
(c) Angular acceleration

Question 8.
Moment of inertia of a solid cylinder of mass M and radius R along geometrical axis is:
(a) \(\frac{2}{3}\)MR²
(b) \(\frac{4}{3}\)MR²
(c) \(\frac{5}{4}\)MR²
(d) \(\frac{1}{2}\)MR².
Answer:
(d) \(\frac{1}{2}\)MR²

Question 9.
In a merry-go-around, a boy suddenly comes and sits down which physical quantity will be conserved :
(a) Linear momentum
(b) Kinetic energy
(c) Angular momentum
(d) None of the above.
Answer:
(c) Angular momentum

Question 10.
The unit of moment of inertia is :
(a) kg/m²
(b)kg/m
(c)kg² × m
(d)kg × m²
Answer:
(d)kg × m²

2. Fill in the blanks:

1. Formula for angular momentum is …………………….
Answer:
Moment of inertia × Angular velocity

2. If the axis of rotation changes, then its ………………… also changes.
Answer:
Moment of inertia

3. The rate of change of angular velocity is called ………………..
Answer:
Angular acceleration

4. Angular momentum gives a measure of ………………… of body.
Answer:
Rotational motion

5. The angular momentum of a body is …………….. the product of its mass and areal
velocity.
Answer:
Twice

6. ‘In rotational motion, work = moment of force × …………….
Answer:
Perpendicular distance from rotational axis.

3. Match the following:
I.

Column ‘A’	Column ‘B’
1. The position \((\overrightarrow{\mathrm{R}})\) of center of mass of two particle system	(a) \(\frac{d \overrightarrow{\mathrm{R}}}{d t}\)
2. Velocity of center of mass	(b) \(\frac{m_{1} \vec{r}_{1}+m_{2} \vec{r}_{2}}{m_{1}+m_{2}}\)
3. Torque \((\vec{\tau})\)	(c) Σmr2
4. Moment of inertia (I)	(d) \(\frac{1}{2}\)Iω2
5. Rotational Kinetic Energy (K.E.)	(e) \(\vec{r} \times \overrightarrow{\mathrm{F}}\)

Answer:
1. (b) \(\frac{m_{1} \vec{r}_{1}+m_{2} \vec{r}_{2}}{m_{1}+m_{2}}\)
2. (a) \(\frac{d \overrightarrow{\mathrm{R}}}{d t}\)
3. (e) \(\vec{r} \times \overrightarrow{\mathrm{F}}\)
4. (c) Σmr²
5. (d) \(\frac{1}{2}\)Iω²

II.

Column ‘A’	Column ‘B’
1. Moment of Inertia	(a) m/sec2
2. Torque	(b) \(\frac{5}{2}\)MR2
3. Radius of Gyration	(c) F × r
4. Moment of inertia of solid sphere	(d) MR2
5. Acceleration	(e) \(\sqrt{\frac{I}{M}}\)

Answer:
1. (d) MR²
2. (c) F × r
3. (e) \(\sqrt{\frac{I}{M}}\)
4. (b) \(\frac{5}{2}\)MR²
5. (a) m/sec²

4. Write true or false:
1. If two particles have equal mass, then their position of center of mass is at the center of the line joining them.
Answer:
True

2. If internal force acting on a system is zero, then its momentum will be zero.
Answer:
False

3. If no entemal force acts on a system, then the velocity of its center of mass will remain constant.
Answer:
True

4. During motion, the volume or shape of a rigid body may change.
Answer:
False

5. The center of mass always lies inside the body.
Answer:
False

6. According to theorem of parallel axis for moment of inertia I = I_o + Ma² where symbols used have their, usual meanings.
Answer:
True