MP Board Class 11th Maths Solutions Chapter 9 अनुक्रम तथा श्रेणी Ex 9.4
प्रश्न 1 से 7 तक प्रत्येक श्रेणी के n पदों का योग ज्ञात कीजिए :
प्रश्न 1.
1 × 2 + 2 × 3 + 3 × 4 + 4 × 5 + ….
हल:
1 × 2 + 2 × 3 + 3 × 4 + 4 × 5 +……
प्रत्येक पद के दो गुणनखण्ड हैं।
पहले गुणनखंडों से बनी श्रेढ़ी 1, 2, 3, 4……
∴ n वाँ पद = n
दूसरे गुणनखंडों से बनी श्रेढ़ी 2, 3, 4, 5……
n वाँ पद = (n + 1)
1 × 2 + 2 × 3 + 3 × 4+…. का n वाँ पद = n(n + 1) = n2 + n

प्रश्न 2.
1 × 2 × 3 + 2 × 3 × 4+ 3 × 4 × 5 +…..
हल:
1 × 2 × 3 + 2 × 3 × 4 + 3 × 4 × 5 +……
पहले गुणनखंडों की श्रेढ़ी 1, 2, 3, 4, …..n
n वाँ पद = n
दूसरे गुणनखंडों की श्रेढ़ी 2, 3, 4, 5,….
n वाँ पद = (n + 1)
तीसरे गुणनखंडों की श्रेढ़ी. 3, 4, 5….
n वाँ पद = (n + 2)
∴ 1 × 2 × 3 + 2 × 3 × 4 + 3 × 4 × 5 +…… का n वाँ पद
= n(n + 1)(n + 2) = n(n2 + 3n + 2)
=n3+ 3n2 + 2n

![]()
प्रश्न 3.
3 × 12 + 5 × 22 + 7 × 32 +……
हल:
3 × 12 + 5 × 22 + 7 × 32 +…..
पहले गुणनखंड 3, 5, 7,….. का n वाँ पद = 3 + (n – 1). 2 = 2n + 1
दूसरे गुणनखंड 12, 22, 32….. का nवाँ पद = n2
∴ 3 × 12 + 5 × 22 + 7 × 32 +…… का गवाँ पद
= (2n + 1) n2 = 2n3 + n2

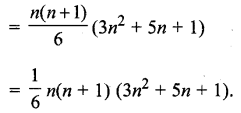
प्रश्न 4.
\(\frac{1}{1 \times 2}+\frac{1}{2 \times 3}+\frac{1}{3 \times 4}\) +…….
हल:
\(\frac{1}{1 \times 2}+\frac{1}{2 \times 3}+\frac{1}{3 \times 4}\) +…….
1, 2, 3,….. का गवाँ पद = n
2, 3, 4,……का n वाँ पद = (n + 1)

प्रश्न 5.
52 + 62 + 72 +….+ 202.
हल:
n वें पद वाली इस श्रेणी में,
(n + 4)2 = n2 + 8n + 16
Sn = ΣTn = Σn2 + 8 Σn + (16 + 16 +……n. पदों तक)
= \(\frac{n(n+1)(2 n+1)}{6}\) + 8 × \(\frac{n(n+1)}{2}\) + 16n
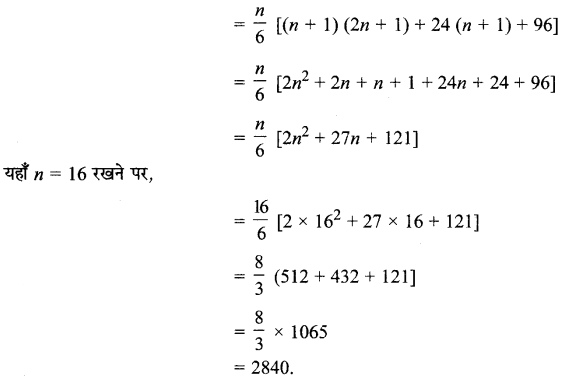
![]()
प्रश्न 6.
3 × 8 + 6 × 11 + 9 × 14 +…..
हल:
3 × 8 + 6 × 11 + 9 × 14 +….
3, 6, 9 का n वाँ पद = 3n
8, 11, 14,…..का n वाँ पद = 8 + (n – 1). 3 = 3n + 5
∴ 3 × 8 + 6 × 11 + 9 × 14 +……का nवाँ पद = 3n(3n + 5)
= 3 (3n2 + 5n)
दी हुई श्रेढ़ी के n पदों का योगफल

प्रश्न 7.
12 + (12 + 22) + (12 + 22 + 32) +…..
हल:
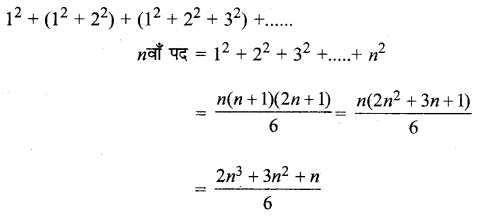
दी हुई श्रेढ़ी के n पदों का योगफल

प्रश्न 8 से 10 तक प्रत्येक श्रेणी के n पदों का योग ज्ञात कीजिए जिसका nवाँ पद दिया है :
प्रश्न 8.
n(n + 1)(n + 4).
हल:
Tn = n(n + 1)(n + 4) = n(n2 + 5n + 4)
= n3 + 5n2 + 4n
दी हुई श्रेढ़ी के n पदों का योग = Σn3 + 5Σn2 + 4Σn
= \(\frac{n^{2}(n+1)^{2}}{4}+\frac{5 n(n+1)(2 n+1)}{6}+\frac{4 n(n+1)}{2}\)
= \(\frac{n(n+1)}{12}\)[3n(n + 1) + 10(2n + 1) + 24]
= \(\frac{n(n+1)}{12}\)[3n2 + 3n + 20n + 10 + 24]
= \(\frac{n(n+1)}{12}\)[3n2 + 23n + 34]
प्रश्न 9.
n2 + 2n.
हल:
दी हुई श्रेढ़ी के n पदों का योग
= Σn2 + Σ2n
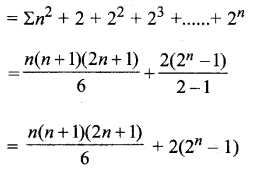
![]()
प्रश्न 10.
(2n – 1).
हल:
Tn = (2n – 1)2 = 4n2 – 4n + 1
दी हुई श्रेढ़ी के n पदों का योग
