MP Board Class 11th Maths Solutions Chapter 5 सम्मिश्र संख्याएँ और द्विघातीय समीकरण Ex 5.2
प्रश्न 1 से 2 तक सम्मिश्र संख्याओं में प्रत्येक का मापांक और कोणांक ज्ञात कीजिए :
प्रश्न 1.
z = -1 – i\( \sqrt{{3}} \).
हल:
मान लीजिए : = – 1 – i\( \sqrt{{3}} \) = r(cos θ + i sin θ)
अर्थात् r cos θ = -1, r sin θ = – \( \sqrt{{3}} \)
वर्ग करके जोड़ने पर, r2 = 1 + 3 = 4 या r = 2
z का मापांक = 2
अब cosθ = \(-\frac{1}{2}\) = – cos \(\frac{\pi}{3}\)

प्रश्न 2.
–\( \sqrt{{3}} \) + i
हल:
मान लीजिए x = –\( \sqrt{{3}} \) + i = r (cos θ + i sin θ)
D r cos θ = –\( \sqrt{{3}} \), r sin θ = 1
वर्ग करके जोड़ने पर,
r2(cos2θ + sin2θ) = 3 + 1 = 4 ,
∴ r2 = 4 या r = 2

प्रश्न 3 से 8 तक सम्मिश्र संख्याओं में प्रत्येक को ध्रुवीय रूप में रूपांतरित कीजिए :
प्रश्न 3.
1 – i.
हल:
मान लीजिए z = 1 – i = r(cos θ + i sinθ)
∴ r cos θ = 1 तथा rsin θ = -1
वर्ग करके जोड़ने पर,
r2 cos2 θ + r2 sin2θ = 1 + 1 = 2
या r2 (cos2θ + sin2θ) = 2
या r2 = 2 या r = –\( \sqrt{{2}} \)
अब cos θ धनात्मक है और sin θ ऋणात्मक है।
∴ θ चौथे चतुर्थांश में है।

![]()
प्रश्न 4.
-1 + i.
हल:
मान लीजिए z = -1 + i = r(cos θ + isin θ)
⇒ r cosθ = – 1 और r sin θ = 1
इनका वर्ग करके जोड़ने पर,
r2cos2θ + r2 sin2θ = 1
या (cos2 θ + sin2θ) = 1
r2 = 2 या r = \( \sqrt{{2}} \)
यहाँ cos θ ऋणात्मक तथा sin θ धनात्मक है
⇒ θ दूसरे चतुर्थांश में है।
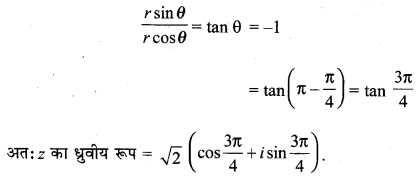
प्रश्न 5.
-1 – i
हल:
मान लीजिए z = – 1 – i = r(cos θ + i sin θ)
∴ rcos θ = – 1, r sin θ = -1
इनका वर्ग करके जोड़ने पर,
∴ r2 cos2θ + r2 sin2 θ = 1 + 1 = 2
या r2(cos2 θ + sin2θ) = 2
∴ r2 = 2 या r = \( \sqrt{{2}} \)
यहाँ cos θ और sin θ दोनों ही ऋणात्मक हैं।
∴ θ तीसरे चतुर्थांश में है।

प्रश्न 6.
-3.
हल:
मान लीजिए z = – 3 = r (cos θ + sin θ)
∴ r cos θ = – 3, r sin θ = 0
इनका वर्ग करके जोड़ने पर,
∴ r2cos2θ + r2 sin2 θ = 9
r2 (cos2θ + sin2 θ) = r2 = 9 या r = 3
अब \(\frac{r \sin \theta}{r \cos \theta}=\frac{0}{-3}=0\) परन्तु r cos θ ऋणात्मक है।
∴ θ = π
∴ z का ध्रुवीय रूप = 3(cos π + i sin π).
![]()
प्रश्न 7.
\( \sqrt{{3}} \) + i.
हल:
मान लीजिए z = \( \sqrt{{3}} \) + i = r(cos θ + i sin θ)
∴ rcos θ = \( \sqrt{{3}} \), r sin θ = 1
वर्ग करके जोड़ने पर,
r2 cos2 θ + r2 sin2 θ = 3 + 1 = 4
या r2(cos2 θ + sin2 θ) = 4
r2 = 4 या r = 2
∴ cos2 = \(\frac{\sqrt{3}}{2}\) और sin θ = \(\frac{1}{2}\)
sin θ और cos θ दोनों ही धनात्मक है।
∴ θ पहले चतुर्थांश में है।
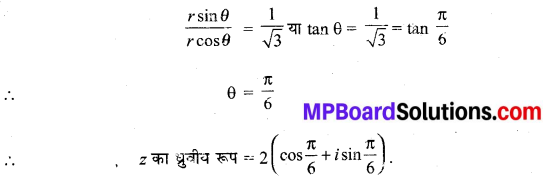
प्रश्न 8.
i.
हल:
मान लीजिए z = i = r(cos θ + i sin θ)
⇒ r cos θ = 0 और r sin θ = 1
वर्ग करके जोड़ने पर,
r2cos2θ + r2 sin2θ = 0 + 1
या r2(sin2θ + cos2θ) = 1 .
या r2 = 1 या r = 1
