MP Board Class 11th Maths Solutions Chapter 10 सरल रेखाएँ Ex 10.3

MP Board Class 11th Maths Solutions Chapter 10 सरल रेखाएँ Ex 10.3

प्रश्न 1.
निम्नलिखित समीकरणों को ढाल अंतःखण्ड रूप में रूपान्तरित कीजिए और उनके ढाल तथा y-अंतः खण्ड ज्ञात कीजिए :
(i) x + 7y = 0,
(ii) 6x + 3y – 5 = 0,
(iii) y = 0.
हल:
(i) x + 7y = 0
∴ y = – \(\frac{1}{7}\)x + 0
∴ ढाल = – \(\frac{1}{7}\), y-अंत: खण्ड = 0.
(ii) 6x + 3y – 5 = 0,
3y = – 6x + 5
∴ y = – 2x + \(\frac{5}{3}\)
ढाल = – 2, y-अंत: खण्ड = \(\frac{5}{3}\)
(iii) y = 0
या y = 0. x + 0.
ढाल = 0, y-अंत: खण्ड = 0

प्रश्न 2.
निम्नलिखित समीकरणों को अंतःखण्ड रूप में रूपान्तरित कीजिए और अक्षों पर इनके द्वारा काटे गए अंतःखण्ड ज्ञात कीजिए :
(i) 3x + 2y – 12 = 0,
(ii) 4x – 3y = 6,
(iii) 3y + 2 = 0.
हल:
(i) 3x + 2y – 12 = 0
या 3x + 2y = 12
12 से दोनों पक्षों में भाग देने पर
\(\frac{x}{4}+\frac{y}{6}\) = 1
अतः अंत: खण्ड 4 तथा 6 हैं।
(ii) 4x – 3y = 6
6 से दोनो पक्षों में भाग देने पर,
\(\frac{4 x}{6}-\frac{3 y}{6}\) = 1
\(\frac{x}{\frac{3}{2}}+\frac{y}{-2}\) = 1.
अत: अंत:खण्ड \(\frac{3}{2}\) तथा – 2 हैं।
3y + 2 = 0
या 3y = – 2
y = – \(\frac{2}{3}\).
अन्त: खण्ड हेतु समीकरण का रूप:
\(\frac{x}{0}+\frac{y}{-\frac{2}{3}}\) = 1
अंत:खण्ड 0 और –\(\frac{2}{3}\) हैं।

प्रश्न 3.
निम्नलिखित समीकरणों को लम्ब रूप में रूपान्तरित कीजिए। उनकी मूल बिन्दु से लांबिक दूरियाँ और लम्ब तथा धन x-अक्ष के बीच का कोण ज्ञात कीजिए :
(i) x – \(\sqrt{3}\)y + 8 = 0,
(ii) y – 2 = 0,
(iii) x – y = 4.
हल:

(ii) y – 2 = 0 या y = 2
0·x + y·1 = 2
x cos 90° + y sin 90° = 2 [∵ cos 90° = 0, sin 90° = 1]
∴ p = 2, α = 90°.
(iii) x – y =4
\(\sqrt{2}\) से भाग देने पर
\(\frac{1}{\sqrt{2}} x+\left(-\frac{1}{\sqrt{2}}\right) y\) = 2\(\sqrt{2}\)
\(\frac{1}{\sqrt{2}}\) = cos (360° – 45°) = cos 315°
और – \(\frac{1}{\sqrt{2}}\) = sin 315०
∴ x – y = 4 का लम्ब रूप
x cos 315° + y sin 315° = 4
की तुलना x cos α + y sin α = p से करने पर,
p = 2\(\sqrt{2}\) , α = 315°.

प्रश्न 4.
बिन्दु (- 1, 1) की रेखा 12(x + 6) = 5(y – 2) से दूरी ज्ञात कीजिए।
हल:
12(x + 6) = 5(y – 2).
या 12x + 72 = 5y – 10
12x – 5y + 82 = 0

प्रश्न 5.
x-अक्ष पर बिन्दुओं को ज्ञात कीजिए जिनकी रेखा \(\frac{x}{3}+\frac{y}{4}\) = 1 से दूरियाँ 4 इकाई हैं।
हल:
दिया गया समीकरण है: \(\frac{x}{3}+\frac{y}{4}\) = 1
12 से गुणा करने पर
4x + 3y – 12 = 0 …(1)
x- अक्ष पर माना कोई बिन्दु (a, 0) हो, तो बिन्दु (a, 0) से रेखा (1) की दूरी
= \(\frac{4 a+0-12}{\sqrt{16+9}}\) = ± \(\frac{4 a-12}{5}\)
∴ ± \(\frac{4 a-12}{5}\) = 4
या ± (4a – 12) = 20
+ ve चिन्ह लेकर 4a = 32 या a = 8
x-अक्ष पर अभीष्ट बिन्दु (8, 0) है।
– ve चिन्ह लेकर, –\(\frac{4 a-12}{5}\) = 4 या – 4a + 12 = 20
4a = – 8, a = – 2
दूसरा अभीष्ट बिन्दु (- 2, 0) है।

प्रश्न 6.
समान्तर रेखाओं के बीच की दूरी ज्ञात कीजिए
(i) 15x + 8y – 34 = 0 और 15x + 8y + 31 = 0
(ii) l(x +y) + p = 0 और l(x + y) – r= 0
हल:

प्रश्न 7.
रेखा 3x – 4y + 2 = 0 के समान्तर और बिन्दु (-2, 3) से जाने वाली रेखा का समीकरण ज्ञात कीजिए।
हल:
3x – 4y + 2 = 0
या 4y = 3x +2
∴ y = \(\frac{3}{4} x+\frac{2}{4}\)
∴ रेखा की ढाल = \(\frac{3}{4}\)
दिया गया बिन्दु (- 2, 3) और ढाल m = \(\frac{3}{4}\) से जाने वाली रेखा का समीकरण
y – y₁ = m(x – x₁)
y – 3 = \(\frac{3}{4}\)(x + 2)
या 4y – 12 = 3x + 6
या 3x – 4y + 18 = 0.
दूसरी विधि : कोई भी रेखा ax + by + c = 0 के समान्तर ax + by + k = 0 के रूप में लिखी जा सकती है।
∴ 3x – 4y + 2 = 0 के समान्तर रेखा 3x – 4y + k = 0 है
यह (- 2, 3) से होकर जाती है।
∴ 3 x (- 2) – 4 x 3 + k = 0 या k = 18
अभीष्ट समान्तर रेखा का समीकरण: 3x – 4y + 18 = 0.

प्रश्न 8.
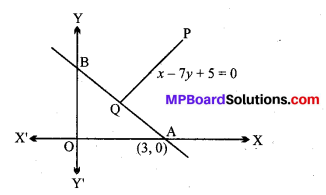
रेखा x – 7y + 5 = 0 पर लम्ब और x-अन्तः खण्ड 3 वाली रेखा का समीकरण ज्ञात कीजिए।
हल:
∵ x-अंत:खण्ड = 3
∴ रेखा A(3, 0) से होकर जाती है।
रेखा PQ : x – 7y + 5 = 0
या 7y = x +5
या y = \(\frac{1}{7}\) x + \(\frac{5}{7}\)

इसलिए PQ की ढाल = \(\frac{1}{7}\)
∵ PQ ⊥ AB
∴ A से होकर जाने वाली रेखा AB की ढाल = – 7
∴ बिन्दु (3, 0) से रेखा AB का समीकरण,
y – 0 = – 7(x – 3).
= – 7x + 21
या 7x + y – 21 = 0.
दूसरी विधि : ax + by + c = 0 की लम्ब कोई रेखा bx – ay + k = 0
∴ x – 7y + 5 = 0 की लम्ब रेखा 7x + y + k = 0
यह रेखा (3, 0) से होकर जाती है।
∴ 7 x 3 + 0 + k = 0, अर्थात् k = – 21
∴ अभीष्ट रेखा का समीकरण 7x + y – 21 = 0.

प्रश्न 9.
रेखाओं \(\sqrt{3}\)x + y =1 और x +\(\sqrt{3}\)y =1 के बीच का कोण ज्ञात कीजिए।
हल:

θ = 30° = \(\frac{\pi}{6}\) रेडियन। .

प्रश्न 10.
बिन्दुओं (h, 3) और (4, 1) से जाने वाली रेखा, रेखा 7x – 9y – 19 = 0 को समकोण पर प्रतिच्छेद करती है। का मान ज्ञात कीजिए।

माना रेखा AB बिन्दु A(h, 3), B(4, 1) से जाने वाली रेखा की ढाल,

चूँकि दोनों रेखाएँ एक-दूसरे को समकोण पर प्रतिच्छेद करती हैं, ∴ m₁,m₂ = – 1
\(\frac{2}{h-4} \times \frac{7}{9}\) = – 1
14 = – 9(h – 4) = – 9h + 36
∴ 9h = 36 – 14 = 22
h = \(\frac{22}{9}\)

प्रश्न 11.
सिद्ध कीजिए कि बिन्दु (x₁, y₁) से जाने वाली और रेखा Ax + By + C = 0 के समान्तर रेखा का समीकरण
A(x – x₁) + B(y – y₁) = 0 है।
हल:
रेखा Ax + By + C = 0
या y= – \(\frac{A}{B}\)x – \(\frac{C}{B}\)
रेखा की ढाल = – \(\frac{A}{B}\)
∴ समान्तर रेखा की ढाल = – \(\frac{A}{B}\)

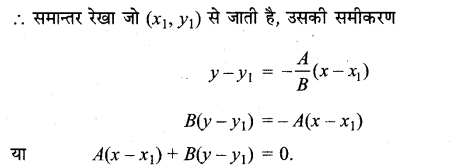
प्रश्न 12.
बिन्दु (2, 3) से जाने वाली दो रेखाएँ परस्पर 60° के कोण पर प्रतिच्छेद करती हैं। यदि एक रेखा की ढाल 2 है तो दूसरी रेखा का समीकरण ज्ञात कीजिए।
हल:
माना दूसरी रेखा की ढाल m है।
दोनों रेखाओं के बीच कोण
tan θ = \(\frac{m_{1}-m_{2}}{1+m_{1} m_{2}}\)
जहाँ θ = 60°, m₁ = m और m₂ = 2
∴ tan 60 = ± \(\frac{m-2}{1+2 m}\) = \(\sqrt{3}\)

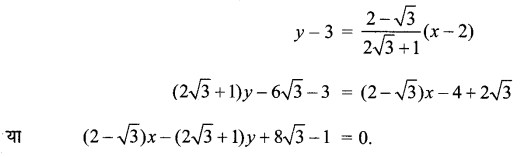
प्रश्न 13.
बिन्दुओं (3, 4) और (- 1, 2) को मिलाने वाली रेखाखण्ड के लम्ब समद्विभाजक रेखा का समीकरण ज्ञात कीजिए।
हल:
माना बिन्दुओं A(3, 4) और B(- 1, 2) को मिलाने वाले रेखाखण्ड का मध्य बिन्दु

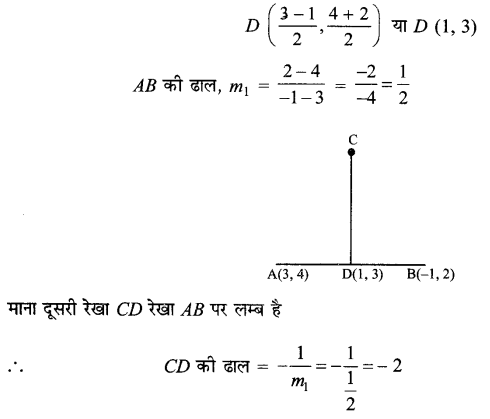
रेखा CD बिन्दु D से होकर जाती है
∴ रेखा CD का समीकरण
y – 3 = – 2(x – 1)
= – 2x + 2
∴ 2x + y – 5 = 0.

प्रश्न 14.
बिन्दु (- 1, 3) से रेखा 3x – 4y – 16 = 0 पर डाले गए लम्बपाद के निर्देशांक ज्ञात कीजिए।
हल:
मान लीजिए रेखा AB का समीकरण, 3x – 4y – 16 = 0 …(i)
या y = \(\frac{3}{4}\)x – 4
रेखा AB की ढाल = \(\frac{3}{4}\)
बिन्दु C(- 1, 3) से AB पर डाला गया लम्ब CD है
∴ AB ⊥ CD.

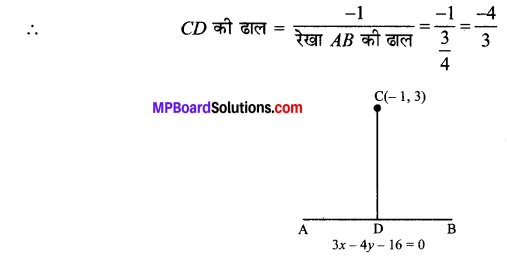
अतः रेखा CD का समीकरण,
y – y₁ = m(x – x₁)
y – 3 = \(\frac{-4}{3}\)(x + 1)
या 3y – 9 = – 4x – 4
या 4x + 3y – 5 = 0 …(ii)
समी (i) को 3 से और (ii) को 4 से गुणा करने पर,
9x – 12y = 48
16x + 12y = 20
इनको जोड़ने पर
25x = 68 या x = \(\frac{68}{25}\)
x का मान (i) में रखने पर,

प्रश्न 15.
मूल बिन्दु से रेखा y = mx + c पर डाला गया लम्ब रेखा से बिन्दु (-1, 2) पर मिलता है। m और … c के मान ज्ञात कीजिए।
हल:
माना रेखा AB का समीकरण, y = mx + c
रेखा AB की ढाल = m

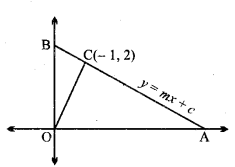
O से रेखा AB पर लम्ब OC डाला गया है जो बिन्दु C(- 1, 2) पर मिलता है।
∴ लम्ब रेखा OC की ढाल = –\(\frac{1}{m}\)
अब रेखा OC का समीकरण,
y – 0 = –\(\frac{1}{m}\)(x – 0)
या x + my = 0
OC की प्रवणता = \(\frac{2-0}{-1-0}\) = – 2
∴ लम्ब रेखा OC की ढाल = –\(\frac{1}{m}\)
बिन्दु C (- 1, 2) निम्न रेखा पर स्थित है :
y = mx + c
⇒ 2 = – m + c
m = \(\frac{1}{2}\) रखने पर,
2 = – \(\frac{1}{2}\) + c
∴ c = 2+ \(\frac{1}{2}\) = \(\frac{5}{2}\)
अतः m = \(\frac{1}{2}\), c = \(\frac{5}{2}\)

प्रश्न 16.
यदि p और q क्रमशः मूल बिन्दु से रेखाओं x cos θ – y sin θ = k cos 2θ और x sec θ +y cosec θ = k पर लम्ब की लंबाइयाँ हैं तो सिद्ध कीजिए कि
p₂ + 4q₂ = k₂.
हल:
मूल बिन्दु (0, 0) से x cos θ – y sin θ = k cos 2θ की दूरी,

समीकरण (1) और (2) को वर्ग करके जोड़ने पर,
k₂ = p₂ + 4q₂
अतः p₂ + 4q₂ = K₂.

प्रश्न 17.
शीर्षों A(2, 3), B(4, – 1) और C(1, 2) वाले त्रिभुज ABC के शीर्ष A से उसकी सम्मुख भुजा पर लम्ब डाला गया है। लम्ब की लम्बाई तथा समीकरण ज्ञात कीजिए।
हल:
मान लीजिए AM रेखा BC पर लंब डाला गया है
(i) रेखा BC की ढाल

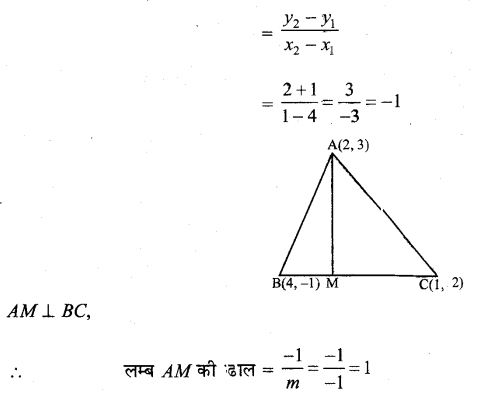
रेखा AM बिन्दु A से जाती है और ढाल = 1 है।
∴ AM का समीकरण
y – y₁ = m(x – x₁)
y – 3 = 1. (x – 2)
या x – y + 1 = 0
(ii) बिन्दु B(4, – 1) और C(1, 2) से होकर जाने वाली रेखा BC का समीकरण

प्रश्न 18.
यदि p मूल बिन्दु से उस रेखा पर डाले गए लम्ब की लम्बाई हो जिसस पर अक्षों पर कटे अंत: खण्ड a और b हों, तो दिखाइए कि \(\frac{1}{p^{2}}=\frac{1}{a^{2}}+\frac{1}{b^{2}}\).
हल:
उस रेखा का समीकरण, जिसकी अक्षों पर कटे अंत:खण्ड a और b हों,
\(\frac{x}{a}+\frac{y}{b}\) = 1 (अंत:खण्ड समीकरण)
मूल बिन्दु (0, 0) बसे इस रेखा पर डाले गए लम्ब की लम्बाई

MP Board Class 11th Maths Solutions