MP Board Class 11th Maths Solutions Chapter 10 सरल रेखाएँ Ex 10.1

MP Board Class 11th Maths Solutions Chapter 10 सरल रेखाएँ Ex 10.1

प्रश्न 1.
कार्तीय तल में एक चतुर्भुज खींचिए जिसके शीर्ष (- 4, 5), (0, 7), (5, – 5) और (- 4, – 2) हैं। इसका क्षेत्रफल भी ज्ञात कीजिए।
हल:
दिए गए बिन्दुओं (- 4, 5), (0, 7), (5, -5) और (- 4, – 2) क्रमशः A, B, C, D द्वारा दर्शाया गया है। चतुर्भुज ABCD को दो भागों में बाँटा गया है। जो ∆ABD तथा ∆BDC के रूप में हैं।

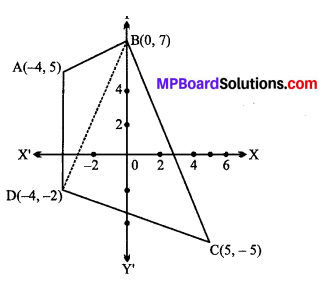
∆ABD के शीर्ष A(- 4, 5), B(0, 7), D(- 4, – 2) हैं।
∴ ∆ABD का क्षेत्रफल = \(\frac{1}{2}\)|[ – 4(7 + 2) +0(- 2 – 5)+ (- 4)(5 – 7)]|
= \(\frac{1}{2}\)|[-36+8]|= \(\frac{1}{2}\) x 28
= 14 वर्ग इकाई
∆BDC के शीर्ष B(0, 7), D(-4, – 2), C ( 5, – 5) हैं।
∆BDC का क्षेत्रफल = \(\frac{1}{2}\)[0(- 2 + 5) – 4( – 5 – 7) + 5(7 + 2)]
= \(\frac{1}{2}\) [48 +45] = = \(\frac{1}{2}\) × 93
= 46.5 वर्ग इकाई
∴ चतुर्भुज ABCD का क्षेत्रफल = ∆ABD का क्षेत्रफल + ∆BDC का क्षेत्रफल
= 14+ 46.5
= 60.5 वर्ग इकाई।

प्रश्न 2.
2a भुजा के समबाहु त्रिभुज का आधार y-अक्ष के अनुदिश इस प्रकार है कि आधार का मध्य बिन्दु मूल बिन्दु पर है। त्रिभुज के शीर्ष ज्ञात कीजिए।
हल:
माना ∆ABC की भुजा BC, y- अक्ष के अनुदिश है जिसका मध्य बिन्दु मूल बिन्दु O है।
⇒ B और C के शीर्ष बिन्दु (0, a) और (0, – a) हैं।
बिन्दु A, x- अक्ष पर है, AB = 2a, OB = a

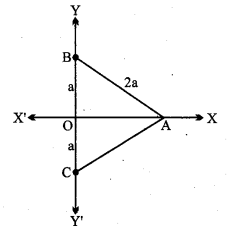
समकोण त्रिभुज OAB में,
OA² = AB² – OB² = (2a)² – a²
= 4a² – a² = 3a²
∴ OA = \(\sqrt{3}\)a
∴ A के निर्देशांक (\(\sqrt{3}\)a,0) हैं।
अतः AABC के निर्देशांक (\(\sqrt{3}\)a,0), (0, a), (0 – a) हैं।

प्रश्न 3.
P(x₁,y₁) और Q(x₂, Y₂) के बीच की दूरी ज्ञात कीजिए जब :
(i) PQ,y- अक्ष के समांतर है,
(ii) PQ, x- अक्ष के समांतर है।
हल:
(i) जब कोई रेखा y-अक्ष के समांतर होती है तो उस पर जितने भी बिन्दु होंगे उनके x- निर्देशांक बराबर होते हैं अर्थात् X₁ = X₂.

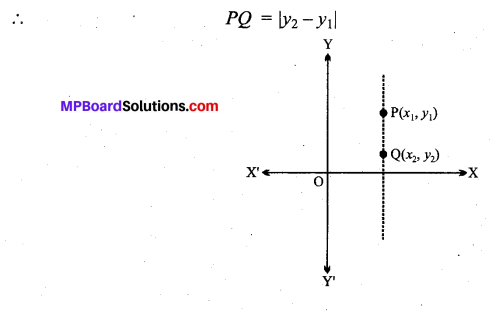
(ii) जब कोई रेखा x-अक्ष के समांतर होती है तो उसके प्रत्येक बिन्दु का y- निर्देशांक बराबर होता है।
अर्थात् y₁ = Y₂

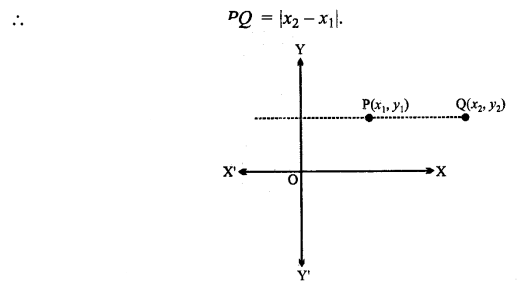
प्रश्न 4.
x- अक्ष पर एक बिन्दु ज्ञात कीजिए जो (7, 6) और (3, 4) बिन्दुओं से समान दूरी पर है।
हल:
मान लीजिए x- अक्ष पर बिन्दु A(a, 0), बिन्दु B(7, 6) और C(3, 4) से समान दूरी पर है।

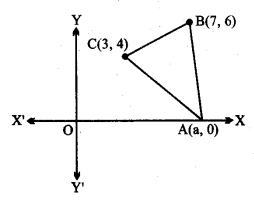
अर्थात् AB = AC
या AB₂ = AC₂
या (a – 7)₂ + (0 – 6)₂ = (a – 3)₂ + (0 – 4)₂
∴ a₂ – 14a + 49 + 36 = a₂ – 6a + 9+ 16
– 14a + 6a = 25 – 85
= – 60
या – 8a = – 60
या a = \(\frac{60}{8}=\frac{15}{2}\)
अतः बिन्दु 4 के निर्देशांक \(\left(\frac{15}{2}, 0\right)\) है।

प्रश्न 5.
रेखा की ढाल ज्ञात कीजिए जो मूल बिन्दु और P(0, -4) तथा B(8, 0) बिन्दुओं को मिलाने वाले रेखाखंड के मध्य बिन्दु से जाती है।
हल:
बिन्दु P(0, – 4) और B(8, 0) को मिलाने वाले रेखाखंड का मध्य बिन्दु

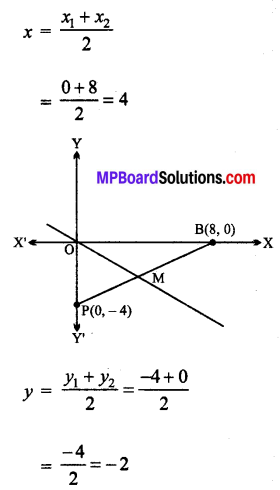
⇒ PB का मध्य बिन्दु M के निर्देशांक (4, -2) है।
मूल बिन्दु 0 के निर्देशांक (0, 0) हैं।
∴ OM की ढाल = \(\frac{y_{2}-y_{1}}{x_{2}-x_{1}}=\frac{-2-0}{4-0}=\frac{-2}{4}=-\frac{1}{2}\).

प्रश्न 6.
पाइथागोरस प्रमेय के प्रयोग बिना दिखलाइए कि बिन्दु (4, 4), (3, 5) और (- 1, – 1) एक समकोण त्रिभुज के शीर्ष हैं।
हल:
माना दिए गए बिन्दु A(4, 4), B(3, 5) और C(- 1, – 1) हैं, तब

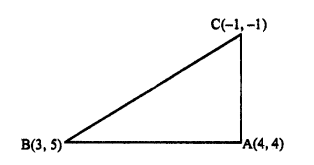
प्रश्न 7.
उस रेखा का समीकरण ज्ञात कीजिए जो y- अक्ष की धन दिशा से वामावर्त्त मापा गया 30° का कोण बनाती है।
हल:
माना रेखा OP, y- अक्ष से वामावर्त्त 30° का कोण बनाती है।
∴ x- अक्ष की धन दिशा से 90° + 30° = 120° का कोण बनाती है।
⇒ रेखा OP की ढाल = tan 120 = – \(\sqrt{3}\)

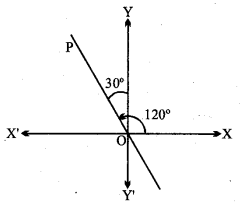
यह रेखा मूल बिन्दु (0, 0) से होकर जाती है। रेखा का बिन्दु ढाल रूप है
y – y₁ = m(x – x₁)
∴ OP का समीकरण y – 0 = – \(\sqrt{3}\) (x – 0)
या y = – \(\sqrt{3}\)x.

प्रश्न 8.
x का वह मान ज्ञात कीजिए जिसके लिए बिन्दु (x,- 1), (2, 1) और (4, 5) सरेख हैं।
हल:
मान लीजिए बिन्दु A (x, – 1), B(2, 1), C(4, 5) संरेख हैं यदि
AB की ढाल = \(\frac{y_{2}-y_{1}}{x_{2}-x_{1}}=\frac{1+1}{2-x}=\frac{2}{2-x}\) …(1)
BC की ढाल = \(\frac{5-1}{4-2}=\frac{4}{2}\) = 2 …(2)
∴ समीकरण (1) और (2) से,
\(\frac{2}{2-x}\) = 2
या 1 = 2 – x .
x = 1.

प्रश्न 9.
दूरी सूत्र का प्रयोग किए बिना दिखलाइए कि बिन्दु (-2,-1), (4,0), (3, 3) और (-3, 2) एक समांतर चतुर्भुज के शीर्ष हैं।
हल:
मान लीजिए एक चतुर्भुज के शीर्ष A(- 2, – 1), B(4, 0), C(3, 3), तथा D(- 3, 2) हैं।

अर्थात् BC || AD
अतः AB || DC, BC || AD
अतः ABCD एक मांस चतुर्भुज है।

प्रश्न 10.
x- अक्ष और (3, – 1) और (4, – 2) बिन्दुओं को मिलाने वाली रेखा के बीच का कोण ज्ञात कीजिए।
हल:
माना 4(3, – 1), B(4, – 2) को मिलाने वाली रेखा AB की ढाल = \(\frac{-2+1}{4-3}=\frac{-1}{1}\) = – 1
यदि x- अक्ष और AB के बीच θ कोण हो, तो
tan θ = – 1 = tan 135°
θ = 135°.

प्रश्न 11.
एक रेखा की ढाल दूसरी रेखा की ढाल का दुगुना है। यदि दोनों के बीच के कोण की स्पर्शज्या (tangent) \(\frac{1}{3}\) है तो रेखाओं की ढाल ज्ञात कीजिए।
हल:
माना रेखाओं की ढाल m₁, m₂ हों, तब
∴ m₁ = 2m₂ यदि दोनों रेखाओं के बीच कोण हो, तो
tan θ = \(\frac{1}{3}\)

– ve चिन्ह लेने पर, \(1+2 m_{2}^{2}=-3 m_{2}\) या \(2 m_{2}^{2}+3 m_{2}\) +1 = 0
या (m₂ + 1) (2m₂ + 1) = 0 अर्थात् m₂ = – 1, – \(\frac{1}{2}\)
∴ रेखा की ढाल – 2, – 1, तथा – 1, – \(\frac{1}{2}\)

प्रश्न 12.
एक रेखा (x₁, y₁) और (h, k) से जाती है। यदि रेखा की ढाल m है तो दिखाइए
k – y₁ = m(h – x₁).
हल:
माना रेखा AB बिन्दु A(x₁, y₁) और B(h, k) से गुजरती हो, तब
∴ AB की ढाल = \(\frac{k-y_{1}}{h-x_{1}}\) = m
अर्थात् k – y₁ = m(h – x₁)

प्रश्न 13.
यदि तीन बिन्दु (h, 0), (a, b) और (0, k) एक रेखा पर हैं तो दिखाइए कि \(\frac{a}{h}+\frac{b}{k}\) = 1
हल:
मान लीजिए बिन्दु A (h, 0), B(a, b), तथा C(0, k) एक रेखा पर हों, तब

या (a – h) (k – b) = – ab
या ak – ab – hk + hb = – ab
∴ ak + hb = hk
hk से भाग देने पर, \(\frac{a}{h}+\frac{b}{k}\) = 1

प्रश्न 14.
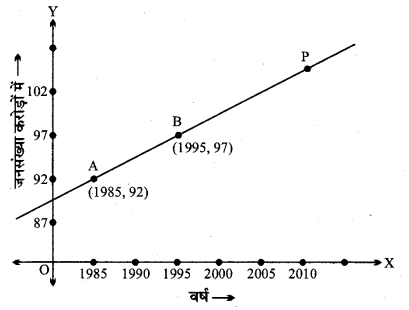
जनसंख्या और वर्ष के निम्नलिखित लेखाचित्र पर विचार कीजिए। (देखिए आकृति में) रेखा AB की ढाल ज्ञात कीजिए और इसके प्रयोग से बताइए कि वर्ष 2010 में जनसंख्या कितनी होगी ?
हल:
दी गयी आकृति में रेखा AB बिन्दु A(1985, 92) और B(1995,97) से होकर जाती है।
∴ AB की ढाल = \(\frac{97-92}{1995-1985}=\frac{5}{10}=\frac{1}{2}\)
मान लीजिए सन् 2010 में जनसंख्या y₁ करोड़ होगी जो बिन्दु P(2010, y₁), AB पर पड़ता है।

∴ ABP सरेखीय हैं।
या AB की ढाल = BP की ढाल
\(\frac{1}{2}=\frac{y_{1}-97}{2010-1995}=\frac{y_{1}-97}{15}\)
∴ 2(y₁ – 97) = 15
2y₁ = 15 + 2 × 97
= 15 + 194 = 209
∴ y₁ = \(\frac{209}{2}\) = 104.5
सन् 2010 में जनसंख्या 104.5 करोड़ होगी।

MP Board Class 11th Maths Solutions