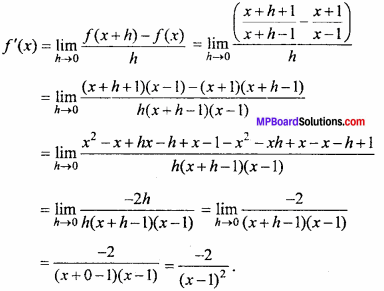MP Board Class 11th Maths Important Questions Chapter 13 Limits and Derivatives

MP Board Class 11th Maths Important Questions Chapter 13 Limits and Derivatives

Limits and Derivatives Important Questions

Limits and Derivatives Short Answer Type Questions

Evaluate the following limits :

Question 1.

Solution:

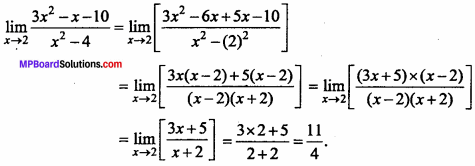
Question 2.

Solution:

Question 3.

Solution:

Question 4.

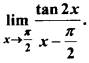
Solution:

Question 5.

Solution:

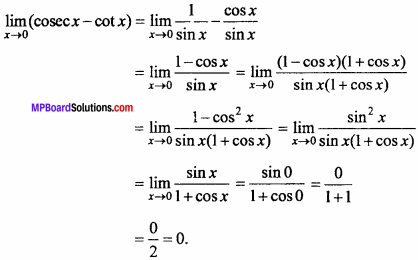
Question 6.

Solution:

Question 7.

Solution:

Question 8.

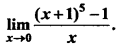
Solution:

Question 9.
If 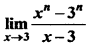= 405, then find the value of n.
Solution:

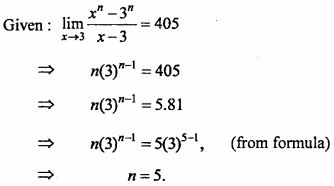
Question 10.
Find the value of :

Solution:

Question 11.

Solution:

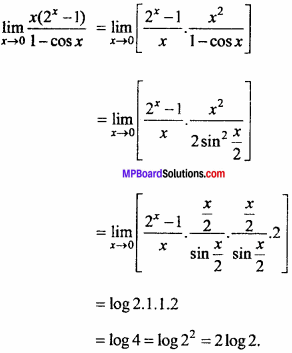
Question 12.
If y = e^x cos x, then find the value of \(\frac { dy }{ dx }\)
Solution:
y = e^x.cos x
I II
\(\frac { dy }{ dx }\) = \(\frac { d }{ dx }\)(e^x.cos x)
= e^x.\(\frac { d }{ dx }\)cos x + cos x\(\frac { d }{ dx }\)e^x
= e^x( – sin x) + cos x\(\frac { d }{ dx }\)e^x
= e^x[cos x – sin x].

Question 13.
If y = e^x cos x, then find the value of \(\frac { dy }{ dx }\)
Solution:
y = e^x.sin x
I II
\(\frac { dy }{ dx }\) = \(\frac { d }{ dx }\)(e^x.sin x)
= e^x.\(\frac { d }{ dx }\)sin x + sin x\(\frac { d }{ dx }\)e^x
= e^xcos x + ^x.e^x
= e^x(cos x + sin x).

Question 14.
Differentiate sin(x + a) w.r.t. x.
Solution:
Let y = sin(x + a)
y = sin x cos a + cos x sin a
∴\(\frac { dy }{ dx }\) = \(\frac { d }{ dx }\)(sin x cos a + cos x sin a)
= cos a\(\frac { d }{ dx }\) sin x + sin\(\frac { d }{ dx }\)cos x
= cos a cos x – sin a sin x
⇒ \(\frac { dy }{ dx }\) = cos(x + a).

Question 15.
Differentiate cosecx.cotx w.r.t. x.
Solution:
Let y = cosec x. cot x
⇒ \(\frac { dy }{ dx }\) = \(\frac { d }{ dx }\)[cosec x. cot x]
⇒ \(\frac { dy }{ dx }\) = cot x\(\frac { d }{ dx }\) cosec x + cosec x\(\frac { d }{ dx }\) cot x
= – cot xcosec x cot x – cosec x.cosec² x
\(\frac { dy }{ dx }\) = – cosec x[cot² x + cosec² x].

Question 16.
Differentiate \(\frac { cos x }{ 1 + sin x }\) w.r.t. x.
Solution:
Let y = \(\frac { cos x }{ 1 + sin x }\)

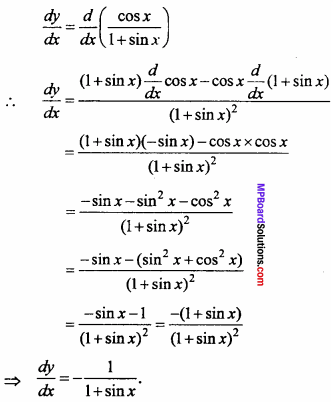
Question 17.
Differentiate \(\frac { sec c – 1 }{ sec x + 1 }\) w.r.t. x.
Solution:
Let y = \(\frac { sec c – 1 }{ sec x + 1 }\)

Question 18.
Differentiate sinⁿ x w.r.t. x.
Solution:
Let y = sinⁿ x
\(\frac { dy }{ dx }\) = \(\frac { d }{ dx }\)(sinⁿ x )
Put sin x = t,
\(\frac { dy }{ dx }\) = \(\frac { d }{ dx }\)tⁿ = \(\frac { d }{ dt }\)tⁿ. \(\frac { dt }{ dx }\) = n sin^{n – 1}\(\frac { d }{ dx }\)(sin x)
⇒ \(\frac { dy }{ dx }\) = n sin^{n – 1}x cos x.

Limits and Derivatives Long Answer Type Questions

Question 1.
Let f(x) =
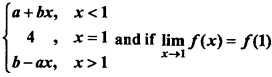, then find the value of a and b.
Solution:

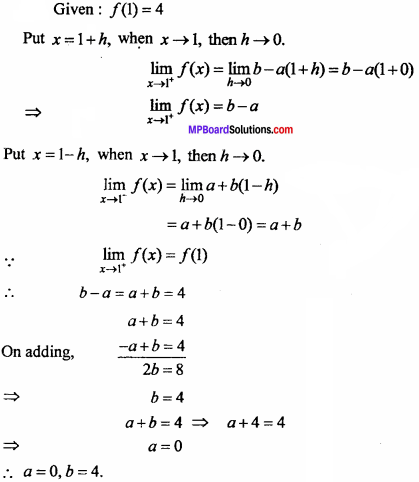
Question 2.
Find the value of , where

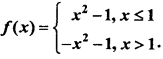
Solution:

Question 3.
f(x) is defined such that
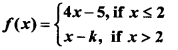and is exist x = 2, then find the value of k.
Solution:

Question 4.
If the function f(x) satisfies= π, then find the value of
Solution:

Question 5.
Find the differential coefficient of the following functions by using first principle method :
(i) sin(x + 1), (ii) cos(x – \(\frac { π }{ 8 }\),
Solution:
(i) Let f(x) = sin(x + 1)
∴ f(x + h) = sin[x + h + 1]
By definition of first principle,

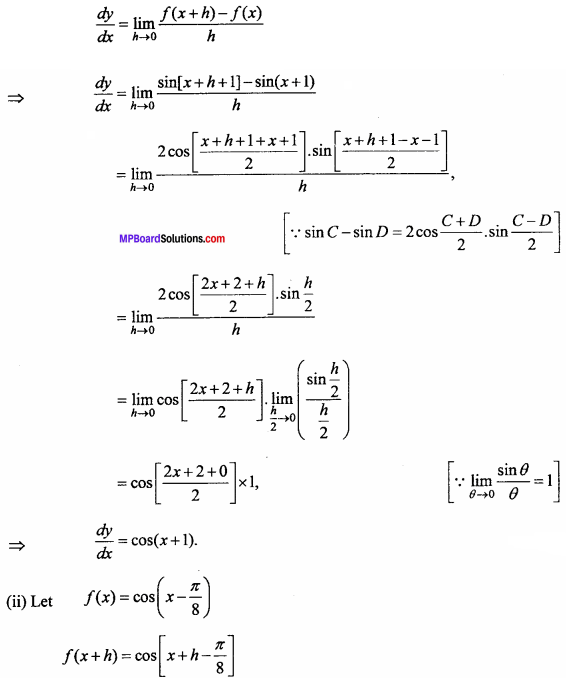
By definition of first principle,

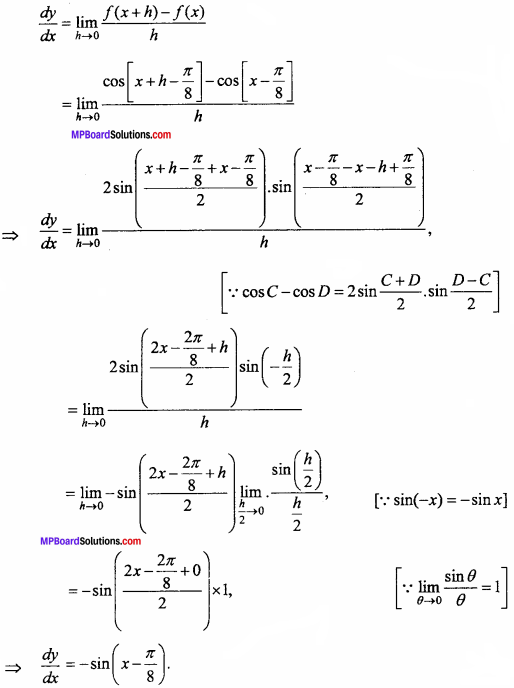
Find the differential coefficient of the following functions

Question 6.
(ax² + sin x)(p + q cos x). (NCERT)
Solution:
Let y = (ax² + sin x)(p + q cos x).
∴ \(\frac { dy }{ dx }\) = \(\frac { d }{ dx }\)[(ax² + sin x)(p + q cos x)]
⇒ \(\frac { dy }{ dx }\) = (p + q cos x)\(\frac { d }{ dx }\)(ax² + sin x) + (ax² + sin x)\(\frac { d }{ dx }\) (p + q cos x)
⇒ \(\frac { dy }{ dx }\) = (p + q cos x)(2a + cos x) + (ax² + sin x)(0 – q sin x)
⇒ \(\frac { dy }{ dx }\) = – q sin x(ax² + sin x) + (p + q cos x)(2a + cos x)

Question 7.
(x + cos x)(x – tan x) (NCERT)
Solution:
Let y = (x + cos x)(x – tan x)
∴ \(\frac { dy }{ dx }\) = \(\frac { d }{ dx }\)[(x + cos x)(x – tan x)]
⇒ \(\frac { dy }{ dx }\) = (x – tan x)\(\frac { d }{ dx }\)(x + cos x) + (x + cos x)\(\frac { d }{ dx }\)(x – tan x)
⇒ \(\frac { dy }{ dx }\) = (x – tan x)(1 – sinx) + (x + cos x)(1 – sec² x)
= (x – tan x)(1 – sinx) + (x + cos x)(sec² x – 1)
⇒ \(\frac { dy }{ dx }\) = (x – tan x)(1 – sinx) – tan² x(x + cos x)

Question 8.
\(\frac { 4x + 5sin x }{ 3x + 7 cos x}\)
Solution:
Let y = \(\frac { 4x + 5sin x }{ 3x + 7 cos x}\)

Question 9.
\(\frac{x^{2} \cos \frac{\pi}{4}}{\sin x}\)
Solution:
Let y = \(\frac{x^{2} \cos \frac{\pi}{4}}{\sin x}\)

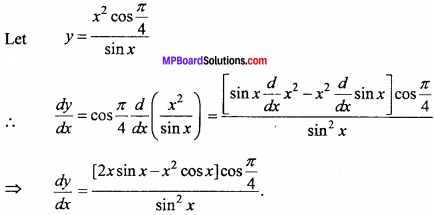
Question 10.
\(\frac { x }{ 1 + tan x}\)
Solution:
Let y = \(\frac { x }{ 1 + tan x}\)

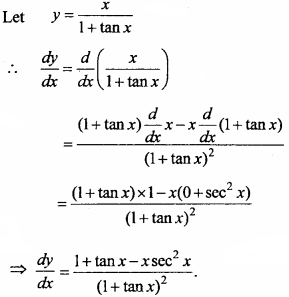
Question 11.
Find the differential coefficient of \(\frac { sec x – 1 }{ sec x + 1}\)
Solution:
Let y = \(\frac { sec x – 1 }{ sec x + 1}\)

Question 12.
If y = \(\frac { x }{ x + 4 }\), then prove that:
x\(\frac { dy }{ dx}\) = y(1 – y)
Solution:
Given : y = \(\frac { x }{ x + 4 }\)

Question 13.
If y = \(\sqrt {x}\) + \(\frac{1}{\sqrt{x}}\), then prove that : 2x\(\frac { dy }{ dx}\) + y – 2 \(\sqrt {x}\) = 0
Solution:
Given : y = \(\sqrt {x}\) + \(\frac{1}{\sqrt{x}}\)

Question 14.
Find the differential coefficient of \(\frac { sin(x + a) }{ cos x }\)
Solution:
Let y = \(\frac { sin(x + a) }{ cos x }\)
⇒ y = \(\frac { sin x + cos a + cos x sin a }{ cos x }\)
⇒ y = \(\frac { sin x + cos a }{ cos x }\) + \(\frac { cos x + sin a }{ cos x }\)
⇒ y = cos a tan x + sin a
∴ \(\frac { dy }{ dx}\) = \(\frac { d }{ dx}\)(cos a tan x + sin a)
= cos a \(\frac { d }{ dx}\) tan x + \(\frac { d }{ dx}\) sin a
= cos a x sec² x + 0
= sec²x. cos a.

Question 15.
If f(x) = \(\frac { { x }^{ 100 } }{ 100 } +\frac { { x }^{ 99 } }{ 100 }\)+……..\(\frac { { x }^{ 2 } }{ 2 }\) + x +1, then prove that:
f'(1) = 100 f'(0). (NCERT)
Solution:
Put x = 1, we get
f'(1) = 1 + 1 + ………. 1 + 1 (100 times)
f’(1) = 100 …. (1)
Put x = 0, we get
f'(0) = 0 + 0 + ……… 0 + 1
f’(0) = 1 …. (2)
From equation (1) and (2),
f'(1) = 100 f'(0).

Question 16.
Find the differential coefficient of cos x by first principle method. (NCERT)
Solution:
Let f(x) = cosx
∴ f(x + h) = cos(x + h)
By definition of first principle

Question 17.
Find the differential coefficient of f(x) = \(\frac { x + 1 }{ x – 1 }\) by first principle method.
Solution:
Given : f(x) = \(\frac { x + 1 }{ x – 1 }\)
f(x + h) = \(\frac { x + h + 1}{ x + h – 1 }\)
By definition of first principle,

MP Board Class 11th Maths Important Questions