In this article, we will share MP Board Class 10th Maths Book Solutions Chapter 6 Triangles Ex 6.4 Pdf, These solutions are solved subject experts from the latest edition books.
MP Board Class 10th Maths Solutions Chapter 6 Triangles Ex 6.4
Question 1.
Let ∆ABC ~ ∆DEF and their areas be, respectively, 64 cm2 and 121 cm2. If EF = 15.4 cm, find BC.
Solution:
We have ar(∆ABC) = 64 cm2
ar(∆DEF) = 121 cm2 and EF = 15.4 cm[Given]
∵ ∆ABC ~ ∆DEF
∴ \(\frac { { ar }(\Delta ABC) }{ { ar }(\Delta DEF) } =\left( \frac { BC }{ EF } \right) ^{ 2 }\)
[Ratios of areas of two similar triangles is equal to the ratio of the squares of their corresponding sides]
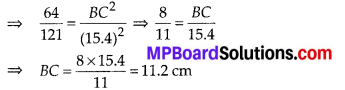
Thus, BC = 11.2 cm
Question 2.
Diagonals of a trapezium ABCD with AB || DC intersect each other at the point O. If AB = 2CD, find the ratio of the areas of triangles AOB and COD.
Solution:
In trapezium ABCD, AB || DC. Diagonals AC and BD intersect at O.
In ∆AOB and ∆COD,
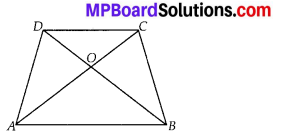
∠AOB = ∠COD [Vertically opposite angles]
∠OAB = ∠OCD [Alternate angles]
∴ Using AA criterion of similarity, we have
∆AOB ~ ∆COD
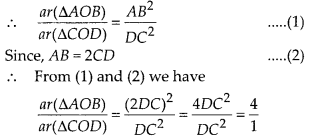
i. e., ar(∆AOB) : ar(∆COD) = 4 : 1
![]()
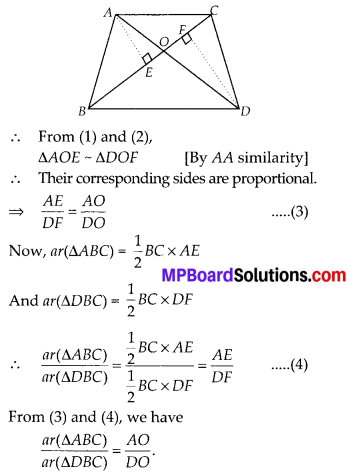
Question 3.
In the figure, ABC and DBC are two triangles on the same base BC. If AD intersects BC at O, show that \(\frac { { ar }(\Delta ABC) }{ { ar }(\Delta DBC) } =\frac { AO }{ DO } \)
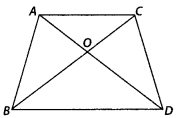
Solution:
We have, ∆ABC and ∆DBC are on the same base BC. Also BC and AD intersect at O.
Let us draw AE⊥BC and DF⊥BC.
In ∆AOE and ∆DOF,
∠AEO = ∠DFO = 90° ……….. (1)
Also, ∠AOE = ∠DOF …………… (2)
[Vertically Opposite Angles]
Question 4.
If the areas of two similar triangles are equal, prove that they are congruent.
Solution:
We have ∆ABC and ∆DEF, such that ∆ABC ~ ∆DEF and ar(∆ABC) = ar(∆DEF).
Since the ratio of areas of two similar triangles is equal to the square of the ratio of their corresponding sides.

i.e., the corresponding sides of ∆ABC and ∆DEF are equal.
⇒ ∆ABC ≅ ∆DEF [By SSS congruency]
Question 5.
D, E and F are respectively the mid-points of sides AB, BC and CA of ∆ABC. Find the ratio of the areas of ∆DEF and ∆ABC.
Solution:
We have a ∆ABC in which D, E and F are mid points of AB, BC and CA respectively. D, E and F are joined to form ∆DEF.
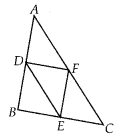
Now, in ∆ABC, D and F are the mid-points of sides AB and AC.
∴ \(\frac{A D}{D B}=\frac{A F}{F C}\) = 1
∴ By the converse of the basic proportion¬ality theorem, we have,
DF||BC ⇒ DF||BE
Similarly; EF||AB ⇒ EF||BD
Since, DF||BE and DB||EF
∴ Quadrilateral BEFD is a parallelogram.
⇒ FE = BD = \(\frac{1}{2}\)AB …………. (1)
Similarly, quadrilateral ECFD is a parallelogram.
⇒ DF = EC = \(\frac{1}{2}\)BC ………… (2)
and DE = FC = \(\frac{1}{2}\)AC ………….. (3)
Now, in ∆ABC and ∆DEF

Question 6.
Prove that the ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding medians.
Solution:
We have two triangles ABC and DEF such that ∆ABC ~ ∆DEF
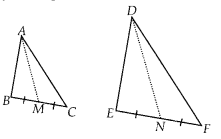
AM and DN are medians corresponding to BC and EF respectively.
∵ ∆ABC ~ ∆DEF
∴ The ratio of their areas is equal to the square of the ratio of their corresponding sides.

![]()
Question 7.
Prove that the area of an equilateral triangle described on one side of a square is equal to half the area of the equilateral triangle described on one of its diagonals.
Solution:
We have a square ABCD, whose diagonal is AC. Equilateral ∆BQC is described on the side BC and another equilateral ∆APC is described on the diagonal AC.
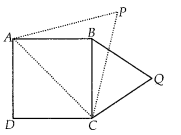
∵ All equilateral triangles are similar.
∴ ∆APC ~ ∆BQC
∴ The ratio of their areas is equal to the square of the ratio of their corresponding sides.
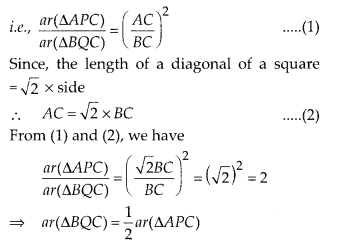
Tick the correct answer and justify:
Question 8.
ABC and BDE are two equilateral triangles such that D is the mid-point of BC. Ratio of the areas of triangles ABC and BDE is
(A) 2 : 1
(B) 1 : 2
(C) 4 : 1
(D) 1 : 4
Solution:
(C) : We have an equilateral ∆ABC and D is the mid point of BC. DE is drawn such that BDE is also an equilateral traingle. Since all equilateral triangles are similar,
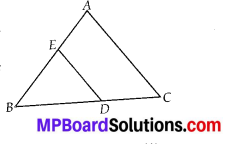
∴ ∆ABC ~ ∆BDE
⇒ The ratio of their areas is equal to the square of the ratio of their corresponding sides.
∴ \(\frac { { ar }(\Delta ABC) }{ { ar }(\Delta BDE) } =\left( \frac { AB }{ BD } \right) ^{ 2 }\) …………. (1)
∵ AB = AC = BCfsides of equilateral AABC]
and BD = \(\frac{1}{2}\)BC [∵ D is the mid point of BC]
⇒ BC = 2BD = AB …………… (2) [∵ AB = BC]
From (1) and (2), we have
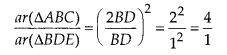
⇒ ar(∆ABC) : ar(∆BDE) = 4 : 1
Question 9.
Sides of two similar triangles are in the ratio 4:9. Areas of these triangles are in the ratio
(A) 2 : 3
(B) 4 : 9
(C) 81 : 16
(D) 16 : 81
Solution:
(D) : We have two similar triangles such that the ratio of their corresponding sides is 4 : 9.
∴ The ratio of areas of two similar triangles is equal to the square of the ratio of their corresponding sides.
∴ \(\frac { { ar }(\Delta -I) }{ { ar }(\Delta -II) } =\left( \frac { 4 }{ 9 } \right) ^{ 2 }=\frac { 16 }{ 81 } \)
⇒ ar(∆-I): ar(∆-II) = 16 : 81