In this article, we will share MP Board Class 10th Maths Book Solutions Chapter 6 त्रिभुज Ex 6.2 Pdf, These solutions are solved subject experts from the latest edition books.
MP Board Class 10th Maths Solutions Chapter 6 त्रिभुज Ex 6.2
प्रश्न 1.
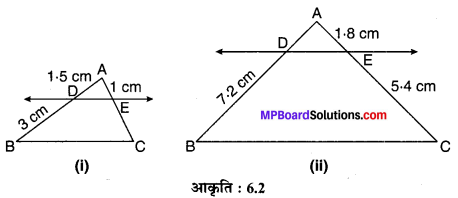
संलग्न आकृत्ति 6.2
(i) और
(ii) में DE || BC है।
आकृति
(i) में EC और
(ii) में AD ज्ञात कीजिए।
हल :
(i) ∵
DE || BC

1.5 EC = 1 x 3 = 3
EC = \(\frac { 3 }{ 1.5 }\)
= 2cm
⇒ अतः EC का अभीष्ट मान 2 cm है।
(ii) चूँकि DE || BC
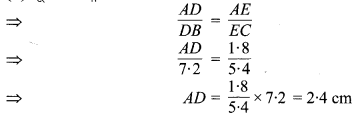
अत: AD का अभीष्ट मान 2.4 cm है।
प्रश्न 2.
किसी ∆PQR की भुजाओं PQ और PR पर क्रमशः बिन्द E और F स्थित हैं। निम्नलिखित में से प्रत्येक स्थिति के लिए बताइए कि क्या EF || QR है?
(i) PE = 3.9 cm, EQ = 3 cm, PF = 3.6 cm और FR = 2.4 cm
(ii) PE = 4 cm, QE = 4:5 cm, PF = 8 cm और RF = 9 cm
(iii) PQ = 1.28 cm, PR = 2.56 cm, PE = 0.18 cm और PF = 0.36 cm
हल :
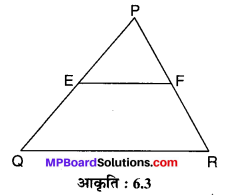
एक ∆PQR दिया है जिसकी भुजा PQ एवं PR पर क्रमश: E एवं F बिन्दु स्थित हैं। (देखिए संलग्न आकृति)
अब (i) ∵
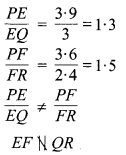
अतः EF QR के समान्तर नहीं है।
(ii) ∵
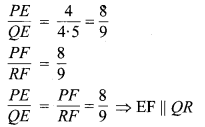
अतः EF एवं QR समान्तर हैं।
(iii) ∵
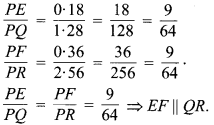
अत: EF एवं QR समान्तर हैं।
प्रश्न 3.
संलग्न आकृति 6.4 में यदि LM || CB और LN || CD हो, तो सिद्ध कीजिए कि \(\frac{A M}{A B}=\frac{A N}{A D}\) है।
हल :
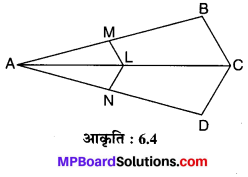
चूँकि ∆ABC में LM || CB (दिया है)
\(\frac{A M}{A B}=\frac{A L}{A C}\) …(1)
चूँकि ∆ACD में, LN || CD (दिया है)
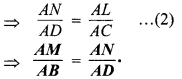
[समीकरण (1) एवं (2) से]
इति सिद्धम्
![]()
प्रश्न 4.
संलग्न आकृति 6.5 में DE || AC और DF || AE है। सिद्ध कीजिए कि \(\frac { 1 }{ 2 }\) है।
हल :
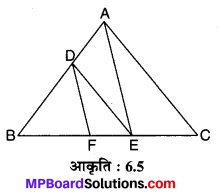
चूँकि ∆BAC में, DE || AC (दिया है)
\(\frac{B E}{E C}=\frac{B D}{D A}\) ……(1)
चूँकि ∆BAE में, DF || AE (दिया है)
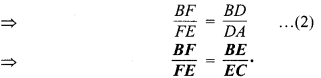
(समीकरण (1) एवं (2) से)
इति सिद्धम्
प्रश्न 5.
संलग्न आकृति 6.6 में DE || OQ और DF || OR है। दर्शाइए कि EF || QR है।
हल :
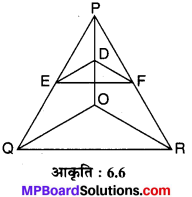
चूँकि ∆PQO में, ED || QO (दिया है)
\(\frac{P E}{E Q}=\frac{P D}{D O}\) …(1)
चूँकि ∆POR में, DF || OR (दिया है)
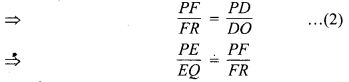
[समीकरण (i) एवं (ii) से]
⇒ EF, ∆PQR की भुजाओं PQ एवं PR को क्रमशः E और F पर समानुपात में विभाजित कर रही है।
इति सिद्धम्
प्रश्न 6.
संलग्न आकृति 6.7 में क्रमशः OP, OQ और OR पर स्थित बिन्दु A, B और C इस प्रकार हैं कि AB || PQ और AC || PR है। दर्शाइए कि BC || QR.
हल :
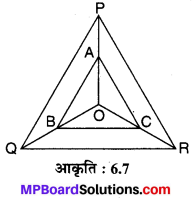
चूँकि ∆OPQ में, AB || PQ (दिया है)
\(\frac{O B}{B Q}=\frac{O A}{A P}\) …(1)
चूँकि ∆OPR में AC || PR (दिया है)
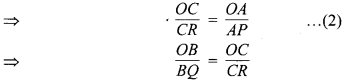
[समीकरण (1) एवं (2) से]
⇒ ∆OQR की भुजाओं OQ एवं OR को BC क्रमशः B और C पर समानुपात में विभाजित कर रही है।
BC || QR.
इति सिद्धम्
![]()
प्रश्न 7.
प्रमेय 6.1 का प्रयोग करते हुए सिद्ध कीजिए कि एक त्रिभुज की एक भुजा के मध्य-बिन्दु से होकर दूसरी भुजा के समान्तर खींची गई रेखा तीसरी भुजा को समद्विभाजित करती है।
हल :
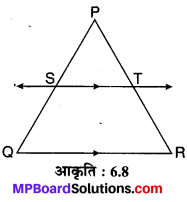
मान लीजिए ∆POR एक दिया हुआ त्रिभुज है जिसकी भुजा PQ के मध्य-बिन्दु S से ST||QR एक रेखा खींची गई है जो PR को बिन्दु T पर प्रतिच्छेद करती है। (देखिए संलग्न आकृति 6.8) चूँकि S, PQ का मध्य-बिन्दु दिया है।
PS = SQ
⇒\(\frac { PS }{ SQ }\) ..(1)
चूँकि ∆PQR में, ST||QR
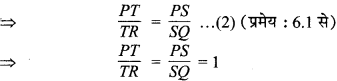
[समीकरण (1) एवं (2) से] .
PT = TR
⇒ ST, PR को समद्विभाजित करती है।
अतः किसी त्रिभुज में एक भुजा के मध्य-बिन्दु से दूसरी भुजा के समान्तर खींची गई रेखा तीसरी भुजा को समद्विभाजित करती है।
इति सिद्धम्
प्रश्न 8.
प्रमेय 6.2 का प्रयोग करते हुए सिद्ध कीजिए कि एक त्रिभुज की किन्हीं दो भुजाओं के मध्य-बिन्दुओं को मिलाने वाली रेखा तीसरी भुजा के समान्तर होती है।
हल :
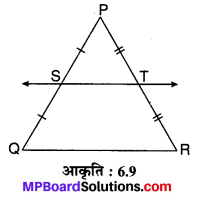
मान लीजिए ∆PQR एक दिया हुआ त्रिभुज है, जिसकी भुजाओं PQ और PR के मध्य-बिन्दु क्रमशः S एवं T हैं। ST को मिलाया गया है। (देखिए संलग्न आकृति)
चूँकि PS = SQ एवं PT = TR (दिया है)
\(\frac { PS }{ SQ }=1\) …(1)
\(\frac { PT }{ TR }\) ….(2)
समीकरण (1) व (2) से,
⇒ \(\frac{P S}{S Q}=\frac{P T}{T R}\) (समानुपाती हैं)
⇒ रेखा ST, ∆POR की दो भुजाओं PQ एवं PR को क्रमशः S एवं T बिन्दुओं पर 1 : 1 के समानुपात में विभाजित करती है।
⇒ ST || QR (प्रमेय : 6.2 से)
अतः एक त्रिभुज की किन्हीं दो भुजाओं के मध्य-बिन्दुओं को मिलाने वाली रेखा तीसरी भुजा के समान्तर होती है।
इति सिद्धम्
प्रश्न 9.
ABCD एक समलम्ब है, जिसमें AB || DC है तथा इसके विकर्ण परस्पर बिन्दु O पर प्रतिच्छेद करते हैं। दर्शाइए कि \(\frac{A O}{B O}=\frac{C O}{D O}\) है।
हल :
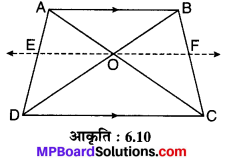
ज्ञातहैः एकसमलम्बचतुर्भुज ABCD जिसकीभुजाएँ AB||DC एवं जिसके विकर्ण AC एवं BD परस्पर O बिन्दु पर प्रतिच्छेद करते हैं (देखिए संलग्न आकृति 6.10)
रचना : एक रेखा EF || AB || DC खींचिए।
अब चूँकि ∆ADC में, EF || DC (रचना से)
⇒ \(\frac{A E}{E D}=\frac{A O}{C O}\) ….(1) [प्रमेय : 6.1 से]
चूँकि ∆DAB में, EF || AB (रचना से)
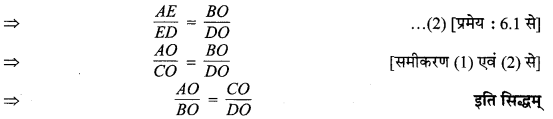
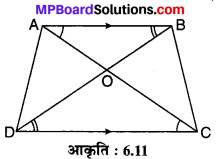
वैकिल्पक विधि:
समलम्ब ₹ ABCD में AB || DC एवं विकर्ण AC एवं BD बिन्दु O पर प्रतिच्छेद करते हैं। (देखिए संलग्न आकृति 6.11)
चूँकि AB || DC (दिया है)
एवं AC तिर्यक रेखा है।
∠OAB = ∠OCD …(1) (एकान्तर कोण हैं)
चूँकि AB || DC (दिया है) एवं BD तिर्यक रेखा है।
∠OBA = ∠ODC ….(2) (एकान्तर कोण हैं)
चूँकि ∠AOB = ∠DOC …(3) (शीर्षाभिमुख कोण हैं)
∆AOB एवं ∆COD के तीनों संगत कोण बराबर हैं। [समीकरण (1), (2) एवं (3) से]
∆AOB ~ ∆COD [AAA समरूपता]
\(\frac{B O}{D O}=\frac{A O}{C O}\)
\(\frac{A O}{B O}=\frac{C O}{D O}\)
इति सिद्धम्
![]()
प्रश्न 10.
एक चतुर्भुज ABCD के विकर्ण परस्पर बिन्दु O पर इस प्रकार प्रतिच्छेद करते हैं कि \(\frac{A O}{B O}=\frac{C O}{D O}\) है। दर्शाइए कि ABCD एक समलम्ब है।
हल :
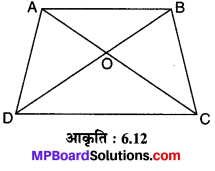
ABCD एक चतुर्भुज दिया है, जिसके विकर्ण AC और BD परस्पर O बिन्दु पर इस प्रकार प्रतिच्छेद करते हैं कि
\(\frac{A O}{B O}=\frac{C O}{D O}\)
त्रिभुज OAB एवं त्रिभुज OCD में,
∠AOB = ∠COD [शीर्षाभिमुख कोण हैं]
\(\) [समानुपात में हैं।
[ये बराबर कोणों को अन्तर्गत करने वाली भुजाएँ हैं।]
⇒ ∆OAB ~ ∆OCD [SAS समरूपता]
⇒ ∠OAB = ∠OCD [संगत कोण बराबर होते हैं।]
लेकिन ये एकान्तर कोण हैं।
⇒ AB || DC
अतः ABCD एक समलम्ब है।
इति सिद्धम्