In this article, we will share MP Board Class 10th Maths Book Solutions Chapter 3 दो चरों वाले रैखिक समीकरण युग्म Ex 3.7 Pdf, These solutions are solved subject experts from the latest edition books.
MP Board Class 10th Maths Solutions Chapter 3 दो चरों वाले रैखिक समीकरण युग्म Ex 3.7
प्रश्न 1.
दो मित्रों अनी और बीजू की आयु में 3 वर्ष का अन्तर है। अनी के पिता धरम की आयु अनी की आयु की दुगुनी और बीजू की आयु अपनी बहन कैथी की आयु की दुगुनी है। कैथी और धरम की आयु का अन्तर 30 वर्ष है। अनी और बीजू की आयु ज्ञात कीजिए।
हल:
मान लीजिए अनी और बीजू की आयु क्रमशः x वर्ष एवं y वर्ष है, तो प्रश्नानुसार
x – y = 3 ….(1)
अनी के पिता धरम की आयु = 2x
एवं कैथी (बीजू की बहिन) की आयु = \(\frac { y }{ 2 } \)
तब 2x – \(\frac { y }{ 2 } \) = 30
⇒ 4x – y = 60 ….(2)
⇒ 3x = 57 [समीकरण (2) – समीकरण (1) से]
⇒ x = \(\frac { 57 }{ 3 } \) = 19 वर्ष
x का मान समीकरण (1) में, रखने पर
19 – y = 3 ⇒ y = 19 – 3 = 16 वर्ष
अतः अनी एवं बीजू की अभीष्ट आयु क्रमशः 19 वर्ष एवं 16 वर्ष है।
![]()
प्रश्न 2.
एक मित्र दूसरे से कहता है, “यदि मुझे एक सौ दे दो, तो मैं आपसे दो गुना धनी बन जाऊँगा।” दूसरा उत्तर देता है, “यदि आप मुझे दस दे दें, तो मैं आपसे छः गुना धनी बन जाऊँगा।” बताइए कि उनकी क्रमशः क्या सम्पत्तिया हैं? [भास्कर – II की बीजगणित से]
हल:
मान लीजिए कि दोनों की सम्पत्तियों क्रमशः x एवं y हैं तो
प्रथम शर्तानुसार, x + 100 = 2 (y – 100) = 2y – 200
⇒ x – 2y = – 300 ….(1)
एवं द्वितीय शार्तानुसार, y + 10 = 6 (x – 10) = 6x – 60
⇒ 6x – y = 70 ….(2)
⇒ 12x – 2y = 140 ….(3) [समीकरण (2) × 2 से]
⇒ 11x = 440 [समीकरण (3) में से समीकरण (1) को घटाने पर]
⇒ x = \(\frac { 440 }{ 11 } \) = ₹40
x का मान समीकरण (1) में रखने पर,
40 – 2y = – 300
⇒ 2y = 40 + 300 = 340
⇒ y = \(\frac { 340 }{ 2 } \) = ₹ 170
अत: दोनों मित्रों के पास क्रमश: ₹ 40 एवं ₹ 170 हैं।
प्रश्न 3.
एक रेलगाड़ी कुछ दूरी समान चाल से तय करती है। यदि रेलगाड़ी 10 km/hr अधिक तेज चलती होती, तो उसे नियत समय से 2 घण्टे कम लगते और यदि रेलगाड़ी 10 km/hr धीमी चली होती, तो उसे नियत समय से 3 घण्टे अधिक लगते। रेलगाड़ी द्वारा तय की गई दूरी ज्ञात कीजिए।
हल:
मान लीजिए रेलगाड़ी द्वारा तय की गयी दूरी = x km एवं उसकी नियत चाल = y km/hr तो उसकी यात्रा में लगा समय = \(\frac { x }{ y } \) hr
अब प्रथम शर्तानुसार, \(\frac { x }{ (y+10) } \) = \(\frac { x }{ y } \) -2 ….(1)
एवं द्वितीय शर्तानुसार, \(\frac { x }{ (y-10) } \) = \(\frac { x }{ y } \) + 3 ….(2)
⇒ xy = xy + 10x – 2y (y + 10) [समीकरण (1) से]
⇒ 2y2 + 20y = 10x ….(3)
एवं xy = xy – 10x + 3y2 – 30y
⇒ 3y2 – 30y = 10x ….(4)
⇒ y2 – 50y = 0 [समीकरण (4) – समीकरण (3) से]
⇒ y (y – 50) = 0
⇒ या तो y = 0 (जो असम्भव है)
अथवा y – 50 = 0 ⇒ y = 50
अब y का मान समीकरण (1) में रखने पर प्राप्त होता है:
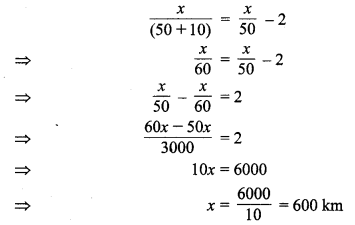
अतः रेलगाड़ी द्वारा तय की गई अभीष्ट दूरी = 600 km.
प्रश्न 4.
एक कक्षा के विद्यार्थियों को पंक्तियों में खड़ा होना है। यदि पंक्ति में 3 विद्यार्थी अधिक होते तो एक पंक्ति कम होती है। यदि पंक्ति में 3 विद्यार्थी कम होते तो 2 पंक्तियाँ अधिक बनतीं हैं। कक्षा में विद्यार्थियों की संख्या ज्ञात कीजिए।
हल:
मान लीजिए कक्षा में विद्यार्थियों की कुल संख्या x है तथा प्रत्येक पंक्ति में । विद्यार्थी रखे जाते हैं तो कुल पंक्तियों की संख्या = \(\frac { x }{ y } \)
अब प्रथम शर्तानुसार, \(\frac{x}{y+3}=\frac{x}{y}-1\)
⇒ xy = xy + 3x – y2 – 3y
⇒ y2 + 3y = 3x ….(1)
एवं द्वितीय शर्तानुसार, \(\frac{x}{y-3}=\frac{x}{y}+2\)
⇒ xy = xy – 3x + 2y2 – 6y
⇒ 2y2 – 6y = 3x ….(2)
⇒ y2 – 9y = 0 [समीकरण (2) – समीकरण (1) से]
⇒ y (y – 9) = 0
⇒ या तो y = 0 (जो असम्भव है)
अथवा y = 9
अब y का मान समीकरण (1) में रखने पर,
(9)2 + 3 (9) = 3x
⇒ 81 +27 = 3x
⇒ 3x = 108 ⇒ x = \(\frac { 108 }{ 3 } \) = 36
अतः कक्षा में अभीष्ट छात्रों की संख्या = 36.
प्रश्न 5.
एक ∆ABC में ∠C = 3 ∠B = 2 (∠A+ ∠B) है तो त्रिभुज के तीनों कोण ज्ञात कीजिए
हल:
दिया है: ∠C = 3 ∠B = 2(∠A + ∠B) …..(1)
हम जानते हैं कि ∠A + ∠B + ∠C = 180° ….(2)
⇒ \(\frac { 1 }{ 2 } \) ∠C + ∠C = 180° [समीकरण (2) एवं समीकरण (1) से]
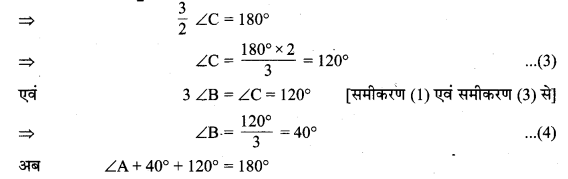
[समीकरण (2) में ∠B एवं ∠C के मान रखने पर]
∠A = 180° – 40° – 120° = 180° – 160° = 20°
अतः त्रिभुज के तीनों कोणों का अभीष्ट मान ∠A = 20°, ∠B = 40° एवं ∠C = 120° है।
प्रश्न 6.
समीकरणों 5x – y = 5 और 3x – y = 3 के ग्राफ खींचिए। इन रेखाओं और y-अक्ष से बने त्रिभुज के शीर्षों के निर्देशांक ज्ञात कीजिए। इस प्रकार बने त्रिभुज के क्षेत्रफल का परिकलन कीजिए।
हल:
∵ 5x – y = 5 ….(1)
⇒ y = 5x – 5
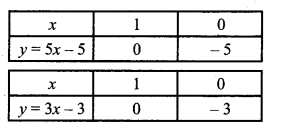
एवं 3x – y = 3 ….(2)
⇒ y = 3x – 3
ग्राफीय निरूपण :
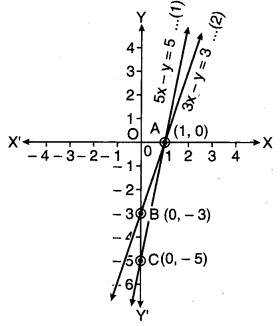
आकृति : 3.10
अतः त्रिभुज के अभीष्ट शीर्षों के निर्देशांक (1, 0), (0, – 3) एवं (0, – 5) हैं (ग्राफ के अनुसार)।
अब ∆ABC का क्षेत्रफल
चूँकि y – अक्ष और दत्त रेखाओं के मध्य ∆ABC बना है जिसका आधार BC = 2 इकाई एवं शीर्षलम्ब OA = 1 इकाई
∵ ar (∆ABC) = \(\frac { 1 }{ 2 } \) × BC × OA
⇒ ar (∆ABC) = \(\frac { 1 }{ 2 } \) × 2 × 1 = 1 वर्ग इकाई
अतः ग्राफ एवं y-अक्ष से बने ∆ABC का अभीष्ट क्षेत्रफल = 1 वर्ग इकाई।
![]()
प्रश्न 7.
निम्न रैखिक समीकरणों के युग्मों को हल कीजिए :
(i) px + qy = p – q; qx – py = p + q
(ii) ax + by = c; bx + ay = 1 + c
(iii) \(\frac { x }{ a } \) – \(\frac { y }{ b } \) = 0; ax + by = a2 + b2
(iv) (a – b) x + (a + b)y = a2 – 2ab – b2; (a + b) (x + y) = a2 + b2
(v) 152x – 378y = -74; – 378x + 152y = – 604
हल:
(i) चूंकि px + qy = p – q ⇒ px + qy – (p – q) = 0 ….(1)
एवं qx – py = p + q ⇒ qx – py – (p + q) = 0 ….(2)
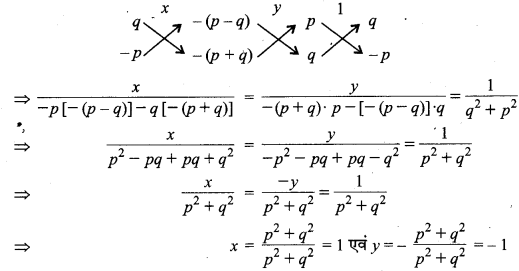
अतः दत्त समीकरण युग्म का अभीष्ट हल x = 1 एवं y = -1 है।
(ii) चूंकि ax + by = c ⇒ ax + by – c = 0 ….(1)
एवं bx + ay = 1 + c ⇒ bx + ay – (c + 1) = 0 ….(2)
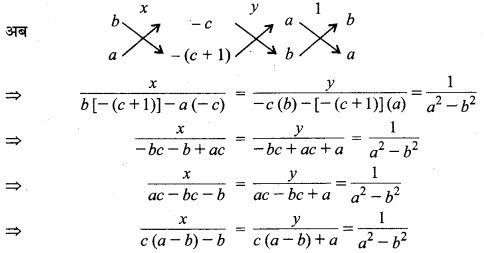
![]()
(iii) चूँकि \(\frac{x}{a}-\frac{y}{b}=0 \Rightarrow b x-a y=0\) …..(1)
एवं ax + by = a2 + b2 …..(2)
समीकरण (1) से x = \(\frac { a }{ b } \) y समीकरण (2) में रखने पर प्राप्त होता है:
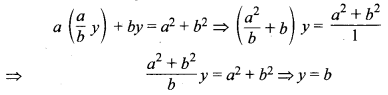
y का मान समीकरण (1) में रखने पर,
\(\frac{x}{a}-\frac{b}{b}=0 \Rightarrow \frac{x}{a}=1 \Rightarrow x=a\)
अत: दत्त समीकरण युग्म का अभीष्ट हल x = a एवं y = b है।
(iv) चूँकि (a – b) x + (a + b) y = a2 – 2ab – b2 …..(1)
एवं (a + b) (x + y) = a2 + b2 ….(2)
समीकरण (2) से \(\left(\frac{a^{2}+b^{2}}{a+b}-x\right)\) समीकरण (1) में रखने पर प्राप्त होता है :
\((a-b) x+(a+b)\left(\frac{a^{2}+b^{2}}{a+b}-x\right)=a^{2}-2 a b-b^{2}\)
⇒ (a – b)x + [(a2 + b2) – x (a + b)] = a2 – 2ab – b2
⇒ a2 + b2 + (a -b – a – b)x = a2 – 2ab – b2
⇒ -2bx = -2b2 – 2ab = -2b (b + a)
⇒ x = b + a = a + b
x का मान समीकरण (1) में रखने पर,
(a – b) (a + b) + (a + b)y = a2 – 2ab – b2
⇒ a2 – b2 + (a + b)y = a2 – b2 – 2ab
⇒ (a + b)y = -2ab
⇒ y = – \(\frac { 2ab }{ a+b } \)
अतः दत्त समीकरण युग्म का अभीष्ट हल x = (a + b) एवं y = \(\frac { -2ab }{ a+b } \) है।
(v) चूँकि 152x – 378y = – 74
⇒ 152x – 378y + 74 = 0 ….(1)
एवं -378x + 152y = – 604
⇒ -378x + 152y + 604 = 0 ….(2)
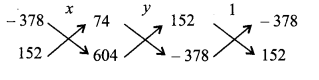

अतः दत्त समीकरण युग्म का अभीष्ट हल x = 2 एवं y = 1 है।
![]()
प्रश्न 8.
ABCD एक चक्रीय चतुर्भुज है। (देखिए संलग्न आकृति 3.11) इस चक्रीय चतुर्भुज के कोण ज्ञात कीजिए।
हल:
संलग्न आकृति के अनुसार, ∠A = 4y + 20
∠B = 3y – 5
∠C = -4x
एवं ∠D = – 7x + 5
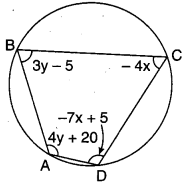
अब हम जानते हैं कि
∵ ∠A + ∠C = 180°
[चक्रीय चतुर्भुज के सम्मुख कोण हैं।]
⇒ 4y + 20 + (-4x) = 180°
⇒ – 4x + 4y + 20 = 180°
⇒ – 4x + 4y = 180° – 20° = 160°
⇒ -x + y = 40 …(1)
एवं ∠B + ∠D = 180° (चक्रीय चतुर्भुज के सम्मुख कोण हैं)
⇒ 3y – 5 – 7x + 5 = 180°
⇒ – 7x + 3y = 180°…..(2)
एवं – 7x + 7y = 280 …..(3) [समीकरण (1) × 7 से]
⇒ 4y = 100 [समीकरण (3) – समीकरण (2) से]
⇒ y = \(\frac { 100 }{ 4 } \) = 25
y का मान समीकरण (1) में रखने पर,
-x + 25 = 40
⇒ -x = 40 – 25 = 15
⇒ x = – 15
अब ∠A = 4y + 20
= 4 × 25 + 20 = 100 + 20 = 120°
∠B = 3y – 5
= 3 × 25 – 5 = 75 – 5 = 70°
∠C = -4x
= -4(-15) = 60°
∠D = – 7x + 5
= -7 (- 15) + 5
= 105 + 5 = 110°
अतः दिए चक्रीय चतुर्भुज के अभीष्ट कोण हैं ∠A = 120°, ∠B = 70°, ∠C = 60° एवं ∠D = 110°.