In this article, we will share MP Board Class 10th Maths Book Solutions Chapter 2 बहुपद Ex 2.3 Pdf, These solutions are solved subject experts from the latest edition books.
MP Board Class 10th Maths Solutions Chapter 2 बहुपद Ex 2.3
प्रश्न 1.
विभाजन एल्गोरिथ्म का प्रयोग करके, निम्न में p (x) को g (x) से भाग देने पर भागफल तथा शेषफल ज्ञात कीजिए :
(i) p(x) = x3 – 3x2 + 5x – 3,g (x) = x2 – 2
(ii) p(x) = x4 – 3x2 + 4x + 5,g (x) = x2 + 1 – x
(iii) P (x) = x4 – 5x + 6, g (x) = 2 – x2
हल:
(i) p (x) = x3 – 3x2 + 5x – 3 एवं g (x) = x2 – 2
चरण 1 : भागफल का प्रथम पद प्राप्त करने के लिए भाज्य के उच्चतम घात वाले पद x3 को भाजक के उच्चतम घात वाले पद x2 से भाग दीजिए। यह x आता है तब भाग देने की प्रक्रिया कीजिए, जो शेष बचता है, वह 3x2 + 7x – 3 है।
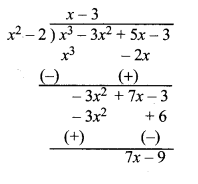
चरण 2 : अब भागफल का दूसरा पद ज्ञात करने के लिए नए भाज्य के उच्चतम घात वाले पद -3x2 को भाजक के उच्चतम घात वाले पद x2 से भाग दीजिए। यह -3 आता है तब भाग देने की प्रक्रिया कीजिए।
चरण 3 : अब शेष बचे 7x – 9 की घात भाजक x2 – 2 की घात से कम है। इसलिए हम भाग की क्रिया को और नहीं कर सकते।
अतः, अभीष्ट भागफल = x – 3 एवं शेषफल = 7x – 9 है।
(ii) p (x) = x4 – 3x2 + 4x + 5,g (x) = x2 + 1 – x यहाँ भाज्य तो भाजक रूप में है, लेकिन भाजक g (x) = x2 + 1 – x मानक रूप में नहीं है अत: मानक रूप में व्यवस्थित करने पर भाजक g (x) = x2 – x + 1 प्राप्त होगा।
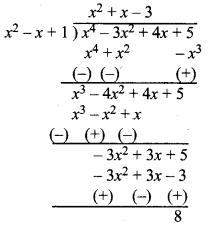
चरण 1 : भागफल का प्रथम पद प्राप्त करने के लिए भाज्य की उच्चत्तम घात वाले पद x4 को भाजक के उच्चत्तम घात वाले पद x2 से भाग दीजिए यह x2 आता है तब भाग देने की प्रक्रिया कीजिए, जो शेष बचता है वह x3 – 4x2 + 4x + 5 है।
चरण 2 : अब भागफल का दूसरा पद ज्ञात करने के लिए नए भाज्य के उच्चतम घात वाले पद x3 को भाजक के उच्चतम घात वाले पद x2 से भाग दीजिए। यह x आता है तब भाग देने की प्रक्रिया कीजिए जो शेष बचता है वह – 3x2 + 3x + 5 है।
चरण 3 : अब भागफल का तीसरा पद ज्ञात करने के लिए नए भाज्य के उच्चतम घात वाले पद -3x2 को भाजक के उच्चतम घात वाले पद x2 से भाग दीजिए। यह -3 आता है तब भाग देने की प्रक्रिया कीजिए, जो शेष बचता है वह 8 है।
चरण 4: अब शेष बचे 8 की घात भाजक x2 – x + 1 की घात से कम है। इसलिए हम भाग की प्रक्रिया को और नहीं कर सकते।
अतः, अभीष्ट भागफल = x2 + x – 3 एवं शेषफल = 8 है।
(iii) p (x) = x4 – 5x + 6, g (x) = 2 – x2
यहाँ भाज्य तो मानक रूप में है लेकिन भाजक g (x)= 2 – x2 मानक रूप में नहीं है, इसलिए भाजक को मानक रूप में व्यवस्थित करने पर g (x) = – x2 +2 प्राप्त होगा।
चरण 1 : भागफल का प्रथम पद प्राप्त करने के लिए भाज्य के उच्चतम घात वाले पद x4 को भाजक के उच्चतम घात वाले पद -x2 से भाग दीजिए, यह – x2 आता है, तब भाग देने की प्रक्रिया कीजिए। जो शेष बचता है, वह 2x2 -5x + 6
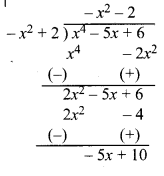
चरण 2 : अब भागफल का द्वितीय पद ज्ञात करने के लिए नए भाज्य के उच्चतम घात वाले पद 2x2 को भाजक के उच्चतम घात वाले पद -x2 से भाग दीजिए। यह – 2 आता है, तब भाग देने की प्रक्रिया कीजिए। जो शेष बचता है, वह – 5x + 10 है।
चरण 3 : अब शेष बचे – 5x + 10 की घात भाजक – x2 + 2 से कम है। इसलिए हम भाग की प्रक्रिया को और नहीं कर सकते।
अतः, अभीष्ट भागफल = -x2 – 2 एवं शेषफल = -5x + 10 है।
![]()
प्रश्न 2.
पहले बहुपद से दूसरे बहुपद को भाग करके जाँच कीजिए कि क्या प्रथम बहुपद द्वितीय बहुपद का एक गुणनखण्ड है :
(i) t2 – 3, 2t4 + 3t3 – 2t2 – 9t – 12
(ii) x2 + 3x + 1, 3x4 + 5x3 – 7x2 + 2x + 2
(iii) x3 – 3x + 1, x5 – 4x3 + x2 + 3x + 1
हल:
(i) यहाँ भाजक t2 – 3 एवं भाज्य 2t4 + 3t3 – 2t2 – 9t – 12 हैं जो मानक रूप में व्यवस्थित हैं।
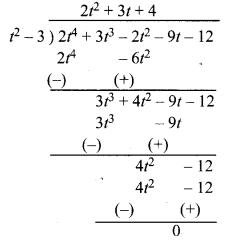
चूँकि यहाँ शेषफल शून्य आया है।
अतः, दिया हुआ प्रथम बहुपद, द्वितीय बहुपद का एक गुणनखण्ड है।
(ii) यहाँ भाजक x2 + 3x + 1 तथा भाज्य 3x4 + 5x3 – 7x2 + 2x + 2 हैं जो मानक रूप में व्यवस्थित हैं।
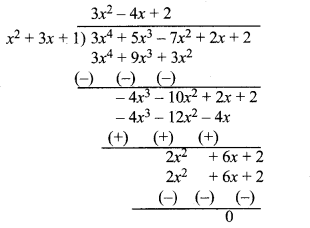
चूँकि यहाँ शेषफल शून्य आया है।
अतः, दिया हुआ प्रथम बहुपद द्वितीय बहुपद का एक गुणनखण्ड है।
(iii) यहाँ भाजक x3 – 3x + 1 एवं भाज्य x5 – 4x3 + x2 + 3x + 1 हैं जो मानक रूप में व्यवस्थित हैं।
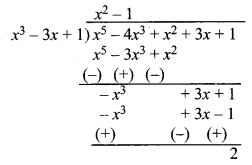
यहाँ शेषफल 2 आया है, शून्य नहीं है।
अतः, दिया हुआ प्रथम बहुपद, द्वितीय बहुपद का एक गुणनखण्ड नहीं है।
![]()
प्रश्न 3.
3x4 + 6x3 – 2x2 – 10x – 5 के अन्य सभी शून्यक ज्ञात कीजिए, यदि इसके दो शून्यक \(\sqrt{\frac{5}{3}}\)
और – \(\sqrt{\frac{5}{3}}\) हैं।
हल:
चूँकि \(\sqrt{\frac{5}{3}}\) एवं –\(\sqrt{\frac{5}{3}}\) दिए गए बहुपद के दो शून्यक हैं, इसलिए (x – \(\sqrt{\frac{5}{3}}\))(x + \(\sqrt{\frac{5}{3}}\)) अर्धात (x2 – \(\frac { 5 }{ 3 } \)) दिए गए बहुपद का एक गुणक होगा। अब विभाजन एल्गोरिथ्म का प्रयोग दिए गए बहुपद एवं (x2 – \(\frac { 5 }{ 3 } \)) के लिए करते हैं :

इसलिए 3x4 + 6x3 – 2x2 – 10x – 5 = (x2 – \(\frac { 5 }{ 3 } \)) (3x2 + 6x + 3)
अब 3x2 + 6x + 3 के गुणनखण्ड 3 (x + 1)2 प्राप्त होते हैं इसलिए इसके शून्यक x = -1 एवं x = -1 होंगे।
अतः, दिए बहुपद के अन्य शून्यक -1 और -1 है।
प्रश्न 4.
यदि x3 – 3x2 + x + 2 को एक बहुपदg (x) से भाग देने पर भागफल और शेषफल क्रमशः x – 2 और – 2x + 4 हैं, तो g (x) का मान ज्ञात कीजिए।
हल:
यूक्लिड की विभाजन प्रमेयिका का प्रयोग करने पर हम पाते हैं:
g (x).(x – 2) + (-2x + 4) = x3 – 3x2 + x + 2
⇒ g (x).(x – 2) x3 – 3x2 + x + 2 + 2x – 4
x3 – 3x2 + 3x – 2
⇒ g(x) = \(\frac{x^{3}-3 x^{2}+3 x-2}{x-2}\)
इसलिए g (x) का मान ज्ञात करने के लिए हम बहुपद x3 – 3x2 + 3x – 2 को व्यंजक x – 2 से विभाजित करेंगे
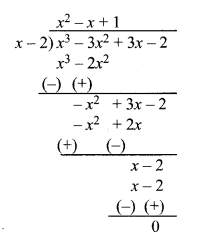
अतः,g (x) का अभीष्ट मान x2 – x + 1 है।
प्रश्न 5.
बहुपदों p (x), g (x), q (x) और r (x) के ऐसे उदाहरण दीजिए जो विभाजन एल्गोरिथ्म को सन्तुष्ट करते हों तथा
(i) घात p (x) = घात q(x)
(ii) घात q (x) = घात r (x)
(ii) घात r (x) = 0
हल:
(i) p (x) = 2x2 – 2x + 14, g (x) = 2,
q(x) = x2 – x + 7 एवं r (x) = 0
(ii) p (x) = x3 + x2 + x + 1, g (x) = x2 – 1,
q(x) = x + 1 एवं r (x) = 2x +2
(iii) p (x) = x3 + 2x2 – x + 2, g (x) = x2 – 1,
q(x) = x + 2 एवं r (x) = 4
ज्ञातव्य : उपर्युक्त तीनों प्रश्नों (i), (ii) एवं (iii) के अनेक उदाहरण हो सकते हैं।
![]()