MP Board Class 10th Maths Solutions Chapter 2 बहुपद Ex 2.2

In this article, we will share MP Board Class 10th Maths Book Solutions Chapter 2 बहुपद Ex 2.2 Pdf, These solutions are solved subject experts from latest edition books.

MP Board Class 10th Maths Solutions Chapter 2 बहुपद Ex 2.2

प्रश्न 1.
निम्न द्विघात व्यंजकों के शून्यक ज्ञात कीजिए और शून्यकों तथा गुणांकों के बीच के सम्बन्ध की जाँच कीजिए:
(i) x² – 2x – 8
(ii) 4s² – 4s + 1
(iii) 6x² – 3 – 7x
(iv) 4u² + 8u
(v) t² – 15
(vi) 3x² – x – 4
हल:
(i) x² – 2x – 8 = (x – 4) (x + 2) [गुणनखण्ड करने पर]
चूँकि x² – 2x – 8 का मान शून्य होगा जब या तो x – 4 = 0
⇒ x = 4
अथवा x + 2 = 0 ⇒ x = – 2
अतः, x² – 2x – 8 के शून्यक 4 एवं – 2 होंगे।

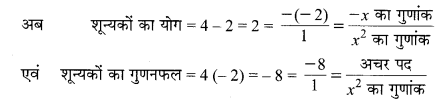
अतः, शून्यकों तथा गुणांकों के बीच सम्बन्धों की सत्यता प्रमाणित होती है।

(ii) 4s² – 4s + 1 = (2s – 1)²
चूँकि 4s² – 4s + 1 का मान शून्य होगा जब
25 – 1 = 0 ⇒ 2s = 1 ⇒ s = \(\frac { 1 }{ 2 } \)
अतः, 4s² – 4s + 1 के प्रत्येक शून्यक का मान = \(\frac { 1 }{ 2 } \)

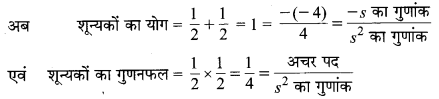
अतः, शून्यकों तथा गुणांकों के बीच सम्बन्धों की सत्यता प्रमाणित होती है।

(iii) 6x² – 3 – 7x = 6x² – 7x – 3 = (2x – 3) (3x + 1)
चूँकि 6x² – 3 – 7x का मान शून्य होगा जब या तो
2x – 3 = 0 ⇒ 2x = 3 ⇒ x = \(\frac { 3 }{ 2 } \)
अथवा 3x + 1 = 0
⇒ 3x = -1 ⇒ x = –\(\frac { 1 }{ 3 } \)
अतः, 6x² – 3 – 7x के शून्यक \(\frac { 3 }{ 2 } \) और –\(\frac { 1 }{ 3 } \) होंगे।

अतः, शून्यकों तथा गुणांकों के बीच सम्बन्धों की सत्यता प्रमाणित होती है।

(iv) 4u² + 8u = 4u (u + 2)
चूँकि 4u² + 8u का मान शून्य होगा जब या तो u = 0
अथवा u + 2 = 0 ⇒ u = -2
अतः, 4u² + 8u के शून्यक 0 और -2 होंगे।
अब शून्यकों का योग = 0 + (-2) = -2

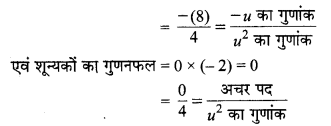
अतः, शून्यकों तथा गुणांकों के बीच सम्बन्धों की सत्यता प्रमाणित होती है।

(v) t² – 15 = (t)² – (\(\sqrt { 15 }\))² = (t + \(\sqrt { 15 }\)) (t – \(\sqrt { 15 }\))
चूँकि t² – 15 का मान शून्य होगा जब या तो
t + \(\sqrt { 15 }\) = 0 ⇒ t = – \(\sqrt { 15 }\)
अथवा t – \(\sqrt { 15 }\) = 0
⇒ t = \(\sqrt { 15 }\)
अतः, t² – 15 के शून्यक – \(\sqrt { 15 }\) और \(\sqrt { 15 }\) होंगे।
अब शून्यकों का योग = – \(\sqrt { 15 }\) + \(\sqrt { 15 }\) = 0 = \(\frac { -0 }{ 1 } \)

अतः, शून्यकों तथा गुणांकों के बीच सम्बन्धों की सत्यता प्रमाणित होती है।

(vi) 3x² – x – 4 = (3x – 4) (x + 1)
चूँकि 3x² – x – 4 का मान शून्य होगा जब
या तो 3x – 4 = 0 ⇒ 3x = 4 ⇒ x = \(\frac { 4 }{ 3 } \)
अथवा x + 1 = 0 ⇒ x = – 1
अतः, 3x² – x – 4 के शून्यक \(\frac { 4 }{ 3 } \) और -1 होंगे।

अतः, शून्यकों तथा गुणांकों के बीच सम्बन्धों की सत्यता प्रमाणित होती है।

प्रश्न 2.
एक द्विघात बहुपद ज्ञात कीजिए, जिसके शून्यकों के योग तथा गुणनफल क्रमशः दी गई संख्या हैं:
(i) \(\frac { 1 }{ 4 } \), -1
(ii) \(\sqrt { 2 }\), \(\frac { 1 }{ 3 } \)
(iii) 0, \(\sqrt { 5 }\)
(iv) 1,1
(v) –\(\frac { 1 }{ 4 } \),\(\frac { 1 }{ 4 } \)
(vi) 4,1
हल:
(i) मान लीजिए कि अभीष्ट द्विघात बहुपद ax² + bx + c है जिसके शून्यक a एवं B हैं तो हम पाते हैं कि
α + β = \(\frac { 1 }{ 4 } \) = – \(\frac { b }{ a } \) = \(\frac { -(-1) }{ 4 } \)
और α.β = -1 = \(\frac { c }{ a } \) = \(\frac { (-4) }{ 4 } \) (हर समान करने पर)
⇒ यदि a = 4 तब b = -1 एवं c = – 4 होगा।
अतः, एक द्विघात बहुपद जिसमें दी गई शर्ते सन्तुष्ट होती हैं, 4x² – x – 4 है एवं अन्य कोई द्विघात बहुपद जो इन शर्तों को सन्तुष्ट करे k (4x² – x – 4) होगा, जहाँ k एक वास्तविक संख्या है।

(ii) मान लीजिए अभीष्ट द्विघात बहुपद ax² + bx + c है जिसके शून्यक α एवं β हैं, तो हम पाते हैं कि
\(\alpha+\beta=-\frac{b}{a}=\sqrt{2}=-\frac{(-3 \sqrt{2})}{3}\)
और \(\alpha \cdot \beta=\frac{c}{a}=\frac{1}{3}\) (हर समान करने पर)
⇒ यदि a= 3 तब b = – 3 \(\sqrt { 2 }\) एवं c = 1 होगा।
अतः, एक द्विघात बहुपद जिसमें दी गई शर्ते सन्तुष्ट होती हैं, 3x² – 3\(\sqrt { 2 }\) x + 1 है एवं अन्य कोई द्विघात बहुपद जो इन शर्तों को सन्तुष्ट करे k (3x² – 3\(\sqrt { 2 }\) x + 1) होगा, जहाँ k एक वास्तविक संख्या है।

(iii) मान लीजिए अभीष्ट द्विघात बहुपद ax² + bx + c है जिसमें शून्यक α एवं β हैं तो हम पाते हैं कि
\(\alpha+\beta=-\frac{b}{a}=0=-\frac{0}{1}\)
और α.β = \(\frac { c }{ a } \) = \(\sqrt { 5 }\) = \(=\frac{\sqrt{5}}{1}\)
⇒ यदि a = 1 तब b = 0 एवं c = \(\sqrt { 5 }\) होगा।
अतः, एक द्विघात बहुपद जिसमें दी गई शर्ते सन्तुष्ट होती हैं: x² + 0.x + \(\sqrt { 5 }\) अर्थात् x² + \(\sqrt { 5 }\) है एवं अन्य कोई द्विघात बहुपद जो इन शर्तों को सन्तुष्ट करे k (x² + \(\sqrt { 5 }\)) होगा, जहाँ k एक वास्तविक संख्या है।

(iv) मान लीजिए अभीष्ट द्विघात बहुपद ax² + bx + c है जिसके शून्यक α एवं β हैं, तो हम पाते ‘हैं कि
\(\alpha+\beta=-\frac{b}{a}=1=-\frac{(-1)}{1}\)
और α.β = \(\frac { c }{ a } \) = 1 = \(\frac { 1 }{ 1 } \)
⇒ यदि a = 1 तब b = -1 एवं c = 1 होगा।
अतः, एक द्विघात बहुपद जिसमें दी गई शर्ते सन्तुष्ट होती हैं, x² + x + 1 है एवं अन्य कोई द्विघात बहुपद जो इन शर्तों को सन्तुष्ट करे k (4x² + x + 1) होगा, जहाँ k एक वास्तविक संख्या है।

(v) मान लीजिए अभीष्ट द्विघात बहुपद ax² + bx + c है जिसके शून्यक α एवं β हैं, तो हम पाते हैं कि
α + β = – \(\frac { b }{ a } \) = – \(\frac { 1 }{ 4 } \)
और α.β = \(\frac { c }{ a } \) = \(\frac { 1 }{ 4 } \)
⇒ यदि a = 4 तब b = 1 एवं c = 1 होगा।
अतः, एक द्विघात बहुपद जिसमें दी गई शर्ते सन्तुष्ट होती हैं, 4x² + x + 1 है एवं अन्य कोई द्विघात बहुपद जो इन शर्तों को सन्तुष्ट करे k (4x² + x + 1) होगा, जहाँ k एक वास्तविक संख्या है।

(vi) मान लीजिए अभीष्ट द्विघात बहुपद ax² + bx + c है जिसके शून्यक α एवं β हैं तो हम पाते हैं कि
α + β = – \(\frac { b }{ a } \) = 4 = – \(\frac { (-4) }{ 1 } \)
और α.β = \(\frac { c }{ a } \) = 1 = \(\frac { 1 }{ 1 } \)
⇒ यदि a = 1 तब b = – 4 एवं c = 1 होगा।
अतः, एक द्विघात बहुपद जिसमें दी गई शर्ते सन्तुष्ट होती हैं,: x² + 1 है एवं अन्य कोई द्विघात बहुपद जो इन शर्तों को सन्तुष्ट करे k (4x² – 4x + 1) होगा, जहाँ k एक वास्तविक संख्या है।