In this article, we will share MP Board Class 10th Maths Book Solutions Chapter 13 पृष्ठीय क्षेत्रफल एवं आयतन Ex 13.3 Pdf, These solutions are solved subject experts from the latest edition books.
MP Board Class 10th Maths Solutions Chapter 13 पृष्ठीय क्षेत्रफल एवं आयतन Ex 13.3
प्रश्न 1.
त्रिज्या 4.2 cm वाले धातु के एक गोले को पिघलाकर त्रिज्या 6 cm वाले एक बेलन के रूप में ढाला जाता है। बेलन की ऊँचाई ज्ञात कीजिए।
हल :
माना,
बेलन की ऊँचाई = h cm है, तो प्रश्नानुसार,
बेलन का आयतन = गोले का आयतन
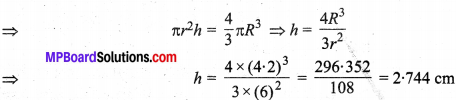
अतः, बेलन की अभीष्ट ऊँचाई = 2.744 cm है।
प्रश्न 2.
क्रमशः 6 cm, 8 cm और 10 cm त्रिज्याओं वाले धातु के तीन ठोस गोलों को पिघलाकर एक बड़ा ठोस गोला बनाया जाता है। इस गोले की त्रिज्या ज्ञात कीजिए।
हल :
मान लीजिए बड़े गोले की त्रिज्या = R cm है, तो प्रश्नानुसार,
बड़े गोले का आयतन = तीन छोटे गोलों के आयतनों का योग
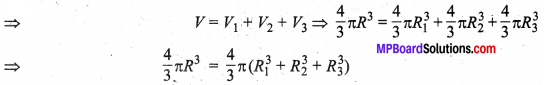
R³ = (6)³ + (8) + (10)³
R³ = 216 + 512 + 1000
= 1728
= (12)³
R = 12 cm
अतः, बड़े गोले की अभीष्ट त्रिज्या = 12 cm है।
प्रश्न 3.
व्यास 7m वाला 20 m गहरा एक कुआँ खोदा जाता है और खोदने से निकली हुई मिट्टी को समान रूप में फैलाकर 22 m x 14 m वाला एक चबूतरा बनाया जाता है। इस चबूतरे की ऊँचाई ज्ञात कीजिए।
हल :
चूँकि कुएँ का व्यास 2r = 7m ⇒ r = \(\frac { 7 }{ 2 }\)m है एवं कुएँ की गहराई d = 20 m मान लीजिए चबूतरे की ऊँचाई hm है, तो प्रश्नानुसार, चबूतरे की मिट्टी की आयतन = कुएँ का आयतन
22 m x 14 m x hm = \(\pi r^{2} d=\frac{22}{7} \times\left(\frac{7}{2}\right)^{2} \times 20\)
\(h=\frac{22 \times 49 \times 20}{7 \times 4 \times 22 \times 14}=\frac{5}{2} \mathrm{m}\)
= 2.5 m
अतः, चबूतरे की अभीष्ट ऊँचाई = 2.5 m है।
![]()
प्रश्न 4.
व्यास 3 m का एक कुआँ 14m की गहराई तक खोदा जाता है। इससे निकली हुई मिट्टी को कुएँ के चारों ओर 4 m चौड़ी एक वृत्ताकार वलय (Ring) बनाते हुए समान रूप से फैलाकर एक प्रकार का बाँध बनाया जाता है। इस बाँध की ऊँचाई ज्ञात कीजिए।
हल :
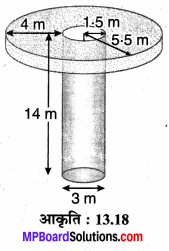
मान लीजिए बाँध की ऊँचाई = x m है।
कुएँ का व्यास d = 2r1 = 3 m ⇒ r1 = \(\frac { 3 }{ 2 }\) = 1.5 m तथा गहराई h = 14 m
बाँध की चौड़ाई = 4 m
⇒ बाँध की बाह्य त्रिज्या r2 = 4 + 1.5 = 5.5 m
∴ वलयाकार बाँध का आयतन = π(r22 – r12)x,
V = π[(5.5)² – (1.5)²] × x
= πx(30.25 – 2.25)
= 28πx m³
∴ कुएँ का आन्तरिक आयतन = πr12h
V = π(1.5)² × 14
= 31.5 π
बाँध का आयतन = कुएँ का आन्तरिक आयतन
⇒ 28π x = 31.5 π
⇒ x = \(\frac { 31.5 }{ 28 }\) = 1.125 m
अतः, बाँध की अभीष्ट ऊँचाई = 1.125 m है।
प्रश्न 5.
व्यास 12 cm और ऊँचाई 15 cm वाले एक लम्ब वृत्तीय बेलन के आकार का बर्तन आइसक्रीम से पूरा भरा हुआ है। इस आइसक्रीम को ऊँचाई 12 cm और व्यास 6 cm वाले शकओं में भरा जाना है, जिनका ऊपरी सिरा अर्द्धगोलाकार होगा। इन शंकुओं की संख्या ज्ञात कीजिए जो इस आइसक्रीम से भरे जा सकते हैं।
हल :
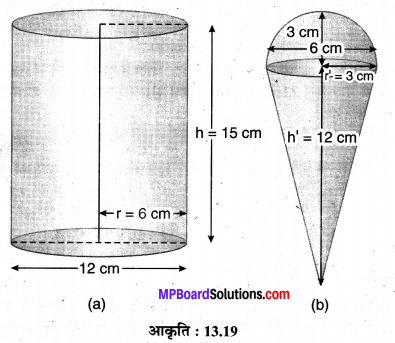
मान लीजिए बेलनाकार बर्तन की ऊँचाई h = 15 cm तथा व्यास d = 2r = 12 cm (दिया है)
त्रिज्या r = \(\frac { 12 }{ 2 }\) = 6 cm
शंक की ऊँचाई h’ = 12 cm
शंकु का व्यास = अर्द्धगोले का व्यास
d’ = 2r’ = 6 cm (दिया है)
r’ = \(\frac { 6 }{ 2 }\) = 3 cm
बेलन का आयतन V = πr²h
= π(6)² x 15
= 540π cm³
एवं शंकु का कुल आयतन = V’ = \(\frac { 1 }{ 3 }\)π(r’)²h’ + \(\frac { 2 }{ 3 }\) π(r’)³
= \(\frac { 1 }{ 3 }\) π(r’)² (h’ + 2r’)
= \(\frac { 1 }{ 3 }\) π(3)² (12 + 2 x 3)
= \(\frac { 1 }{ 3 }\) π x 9 x 18
= 54 π cm³
![]()
अतः, आइसक्रीम शंकुओं की अभीष्ट संख्या = 10 है।
प्रश्न 6.
विमाओं 5.5 cm x 10 cm x 3.5 cm वाला एक घनाभ बनाने के लिए 1.75 cm व्यास और 2 mm मोटाई वाले कितने सिक्कों को पिघलाना पड़ेगा?
हल :
माना सिक्कों की संख्या = n है दिया है। घनाभ की विमाएँ 5.5 cm x 10 cm x 3.5 cm तथा सिक्कों की मोटाई x = 2 mm = 0.2 cm एवं व्यास d = 2r = 1.75 cm
r = \(\frac { 1.75 }{ 2 }\) cm दिया है।
घनाभ का आयतन = 5.5 cm x 10 cm x 3.5 cm = 192.5 cm³.
n सिक्कों का कुल आयतन = n × πr²x
= \(n \times \frac{22}{7} \times\left(\frac{1 \cdot 75}{2}\right)^{2} \times 0 \cdot 2=\frac{13 \cdot 475}{28} n\)
चूँकि सिक्कों का कुल आयतन = घनाभ का आयतन
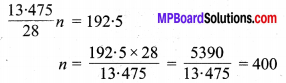
अतः, सिक्कों की अभीष्ट संख्या = 400 है।
![]()
प्रश्न 7.
32 cm ऊँची और आधार त्रिज्या 18 cm वाली एक बेलनाकार बाल्टी रेत से भरी हुई है। इस बाल्टी को भूमि पर खाली किया जाता है और इस रेत की एक शंक्वाकार ढेरी बनाई जाती है। यदिशंक्वाकार ढेरी की ऊँचाई 24 cm है, तो इस ढेरी की त्रिज्या और तिर्यक ऊँचाई ज्ञात कीजिए।
हल :
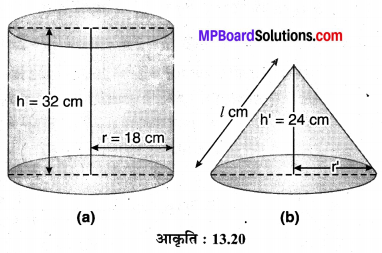
माना लीजिए बेलनाकार बाल्टी की ऊँचाई h = 32 cm तथा त्रिज्या r = 18 cm दी गयी है तथा इसको भरे हुए रेत से एक शंक्वाकार ढेरी बनानी है जिसकी ऊँचाई h’ = 24 cm है। पुनः मान लीजिए कि शंक्वाकार ढेरी की त्रिज्या = r’ cm एवं तिर्यक ऊँचाई = l cm है, तो प्रश्नानुसार,
शंक्वाकार ढेरी का आयतन = बेलनाकार बाल्टी का आयतन
![]()

अतः, शंक्वाकार ढेरी की अभीष्ट त्रिज्या = 36 cm एवं उसकी अभीष्ट तिर्यक ऊँचाई = 12√13 cm है।
प्रश्न 8.
6m चौड़ी और 1.5 m गहरी एक नहर में पानी 10 km/h चाल से बह रहा है। 30 मिनट में यह नहर कितने क्षेत्रफल की सिंचाई कर पायेगी जबकि ऊँचाई के लिए 8 cm गहरे पानी की आवश्यकता होती है?
हल :
मान लीजिए नहर एक घनाभ के आकार की है जिसकी चौड़ाई b = 6 m और गहराई h = 1.5m जिसमें 10 km/h की चाल से पानी बह रहा है। पुनः मान लीजिए यह 30 मिनट में x वर्ग मीटर क्षेत्रफल की सिंचाई करेगा जिसमें पानी की गराई d = 8 cm = 0.08 m है।
30 मिनट में जल धारा की लम्बाई = \(\frac { 30 }{ 60 }h\) x 10 km/h = 5 km
l = 5000 m
जल धारा का 30 मिनट में आयतन = lbh = 5000 x 6 x 1.5 m³
V = 45000 m³.
प्रश्नानुसार,
x × 0.08 = 45000
x = \(\frac{45000}{0.08}=\frac{45000 \times 100}{8} \mathrm{m}^{2}\)
x = 562500 m²
= 56.25 हेक्टेअर
अतः, अभीष्ट क्षेत्रफल = 562500 m² अथवा 56.25 हेक्टेअर है।
प्रश्न 9.
एक किसान अपने खेत में 10 m व्यास वाली और 2 m गहरी एक बेलनाकार टंकी को आन्तरिक व्यास 20 cm वाले एक पाइप द्वारा एक नहर से जोड़ता है। यदि पाइप में पानी 3 km/h की चाल से बह रहा है, तो कितने समय बाद टंकी पूरी भर जायेगी?
हल :
बेलनाकार टंकी की गहराई h = 2 m तथा व्यास d = 2r = 10 m
r = \(\frac { 10 }{ 2 }\) = 5 m दिया है।
पाइप का आन्तरिक व्यास d’ = 2r’ = 20 cm = 0.2 m
r’ = 0.1 m है।
जल धारा की पाइप में 1 घण्टे में लम्बाई 3 km = 3000 m होगी।
टंकी का आयतन = πr²h
= π(5)² x 2
= 50π m³
1 घण्टे में नल से प्राप्त जल का आयतन = π(r’)²l
= π(0.1)² x 3000 m³
= 30π m³.

अतः, टंकी को भरने में लगा अभीष्ट समय = 100 मिनट है।
![]()