MP Board Class 10th Maths Solutions Chapter 12 वृतों से संबंधित क्षेत्रफल Additional Questions

In this article, we will share MP Board Class 10th Maths Book Solutions Chapter 12 वृतों से संबंधित क्षेत्रफल Additional Questions Pdf, These solutions are solved subject experts from the latest edition books.

MP Board Class 10th Maths Solutions Chapter 12 वृतों से संबंधित क्षेत्रफल Additional Questions

MP Board Class 10th Maths Chapter 12 अतिरिक्त परीक्षोपयोगी प्रश्न

MP Board Class 10th Maths Chapter 12 दीर्घ उत्तरीय प्रश्न

प्रश्न 1.
संलग्न आकृति 12.35 में ABCD एक आयत है, जिसकी विमाएँ 21 cm x 14 cm है। BC को व्यास मानकर एक अर्द्धवृत्त खींचा गया है। आकृति में छायांकित भाग का क्षेत्रफल तथा परिमाप ज्ञात कीजिए।
हल :

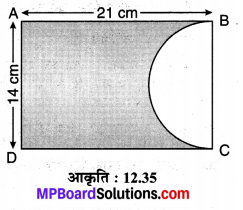
ज्ञात है : एक आयत जिसकी विमाएँ 21 cm x 14 cm
तथा एक अर्द्धवृत्त जिसका व्यास 14 cm, दिया है
अर्द्धवृत्त की त्रिज्या = \(\frac { 14 }{ 2 }\) = 7 cm
आयत का क्षेत्रफल = 21 x 14 = 294 cm²
अर्द्धवृत्त का क्षेत्रफल = \(\frac{1}{2} \pi r^{2}=\frac{1}{2} \times \frac{22}{7} \times(7)^{2}\)
= 77 cm²
चूँकि ar (छायांकित भाग) = ar (आयत) – ar (अर्द्धवृत्त)
ar (छायांकित भाग) = 294 – 77 = 217 cm²
छायांकित भाग की परिमाप = AB + DC + AD + πr
छायांकित भाग की परिमाप = 21 + 21 + 14 + \(\frac { 22 }{ 7 }\) x 7
= 21 + 21 + 14 + 22
= 78 cm
अतः छायांकित भाग का अभीष्ट क्षेत्रफल = 217 cm² एवं अभीष्ट परिमाप = 78 cm है।

प्रश्न 2.
संलग्न आकृति 12.36 में O केन्द्र वाले दो संकेन्द्रीय वृत्तों की त्रिज्याएँ 21 cm एवं 42 cm है यदि ∠AOB = 60° है, तो छायांकित भाग का क्षेत्रफल ज्ञात कीजिए। (\(\pi=\frac{22}{7}\) का प्रयोग कीजिए।)
हल :

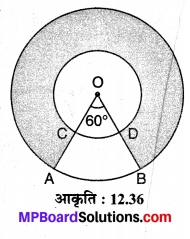
ज्ञात है : बाह्य वृत्त की त्रिज्या r1 = 42 cm एवं आन्तरिक वृत्त की त्रिज्या r2 = 21 cm. छोटे वृत्त के दीर्घ त्रिज्यखण्ड का शीर्ष कोण θ2 = 360° – 60° = 300° तथा बड़े वृत्त के त्रिज्यखण्ड का शीर्ष कोण θ1 = 60° है।
∵ar (दीर्घ त्रिज्यखण्ड) = \(\frac{\theta_{2}}{360^{\circ}} \times \pi r_{2}^{2}\)
⇒ ar (दीर्घ त्रिज्यखण्ड) = \(\frac{300^{\circ}}{360^{\circ}} \times \frac{22}{7} \times(21)^{2}\)
= 5 x 11 x 21
= 1155 cm²
∵ ar (बड़े वृत्त का त्रिज्यखण्ड) = \(\frac{\theta_{1}}{360^{\circ}} \times \pi\left(r_{1}\right)^{2}\)
= \(\frac{60^{\circ}}{360^{\circ}} \times \frac{22}{7} \times(42)^{2}=924 \mathrm{cm}^{2}\)
= 924 cm²
∵ बड़े वृत्त का क्षेत्रफल = \(\pi r_{1}^{2}=\frac{22}{7} \times(42)^{2}\)
⇒ ar (दीर्घ वृत्त) = 5544 cm²
ar (छायांकित भाग) = ar (दीर्घ वृत्त) – ar (छोटे वृत्त का दीर्घ त्रिज्यखण्ड) – ar (छोटे वृत्त का लघु त्रिज्यखण्ड)
⇒ ar (छायांकित भाग) = 5544 – 1155 – 924
= 5544 – 2079
= 3465 cm²
अतः छायांकित भाग का अभीष्ट क्षेत्रफल = 3465 cm² है।

प्रश्न 3.
दी गई आकृति में, प्रत्येक 3 cm व्यास के तीन अर्द्धवृत्त, 4.5 cm त्रिज्या का एक अर्द्धवृत्त बनाए गए है। छायांकित भाग का क्षेत्रफल ज्ञात कीजिए।
हल :

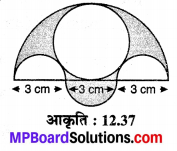
चूँकि 4.5 cm त्रिज्या के अर्द्धवृत्त का क्षेत्रफल

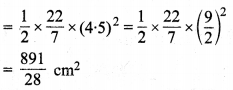
चूँकि 4.5 cm व्यास अर्थात् \(\frac { 9 }{ 4 }\) cm त्रिज्या वाले वृत्त का क्षेत्रफल = \(\frac{22}{7}\left(\frac{9}{4}\right)^{2}=\frac{891}{56} \mathrm{cm}^{2}\)
चूँकि 3 cm व्यास अर्थात् \(\frac { 3 }{ 2 }\) cm त्रिज्या के एक अर्द्धवृत्त का क्षेत्रफल

कुल क्षेत्रफल = ar ( \(\frac { 9 }{ 2 }\) cm त्रिज्या का अर्द्धवृत्त ) + ar (\(\frac { 3 }{ 2 }\) cm त्रिज्या का अर्द्धवृत्त)
कुल क्षेत्रफल

रिक्त स्थान का क्षेत्रफल = ar(\(\frac { 9 }{ 4 }\) cm त्रिज्या का वृत्त) + 2 x ar (\(\frac { 3 }{ 2 }\) cm त्रिज्या का अर्द्धवृत्त)

ar (छायांकित भाग) = कुल क्षेत्रफल – रिक्त स्थान का क्षेत्रफल

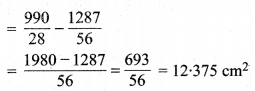
अतः छायांकित भाग का अभीष्ट क्षेत्रफल = 12.375 cm² है।

प्रश्न 4.
संलग्न आकृति में केन्द्र वाले वृत्त का एक त्रिज्यखण्ड OAP दर्शाया गया है जिसका केन्द्र पर अन्तरित कोण θ है। AB वृत्त की त्रिज्या OA पर लम्ब है जो OP को बढ़ाने पर बिन्दु B पर काटता है। सिद्ध कीजिए कि रेखांकित भाग का परिमाप \(r\left[\tan \theta+\sec \theta+\frac{\pi \theta}{180}-1\right]\) है।
हल :

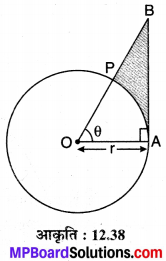
समकोण ∆OAB में,
tan θ = \(\frac { AB }{ r }\) ⇒ AB = r tan θ …(1)
एवं sec θ = \(\frac { OB }{ r }\) ⇒ OB = r sec θ …(2)
तथा चाप \(AP=\frac{\theta}{180^{\circ}} \pi r\) …(3)
चूँकि छायांकित भाग की परिमाप = AB + PB + चाप AP
= AB + (OB – OP) + चाप AP

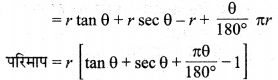
अत: अभीष्ट परिमाप = \(r\left[\tan \theta+\sec \theta+\frac{\pi \theta}{180}-1\right]\) है।
इति सिद्धम्

प्रश्न 5.
संलग्न आकृति 12:39 में दो संकेन्द्रीय वृत्तों, जिनकी त्रिज्याएँ 7 cm तथा 14 cm है, के बीच घिरे छायांकित क्षेत्र का क्षेत्रफल ज्ञात कीजिए जबकि ∠AOC = 40° है। (\(\pi=\frac{22}{7}\) लीजिए।)
हल :

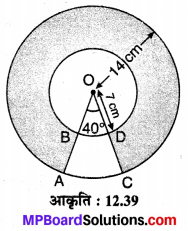
ज्ञात है : बड़े वृत्त की त्रिज्या r1 = 14 cm
छोटे वृत्त की त्रिज्या r2 = 7 cm तथा त्रिज्यखण्ड AOC का शीर्ष कोण θ1 = 40° है। छोटे वृत्त के दीर्घ त्रिज्यखण्ड का कोण θ2 = 360° – 40° = 320°
बड़े वृत्त का क्षेत्रफल

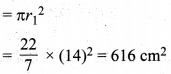
छोटे वृत्त के दीर्घ त्रिज्यखण्ड का क्षेत्रफल

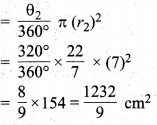
बड़े वृत्त के लघु त्रिज्यखण्ड का क्षेत्रफल

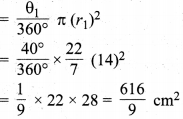
रिक्त स्थान का क्षेत्रफल = दीर्घ त्रिज्यखण्ड का क्षेत्रफल + लघु त्रिज्यखण्ड का क्षेत्रफल

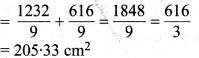
छायांकित भाग का क्षेत्रफल = बड़े वृत्त का क्षेत्रफल – रिक्त स्थान का क्षेत्रफल
= 616 – 205.33
= 410.67 cm²
अतः छायांकित भाग का अभीष्ट क्षेत्रफल = 410.67 cm² है।

प्रश्न 6.
संलग्न आकृति 12.40 में O केन्द्र वाले वृत्त का व्यास AB = 13 cm है तथा AC = 12 cm है। BC को मिलाया गया है। छायांकित क्षेत्र का क्षेत्रफल ज्ञात कीजिए। (π = 3.14 लीजिए।)
हल :

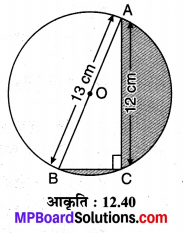
ज्ञात है : ∆ACB में ∠C समकोण है (चूँकि अर्द्धवृत्त का कोण है), विकर्ण AB = 13 cm तथा AC = 12 cm, वृत्त का व्यास AB = 13 cm तो त्रिज्या r = \(\frac { 13 }{ 2 }\) cm
या समकोण ∆ACB में पाइथागोरस प्रमेय से

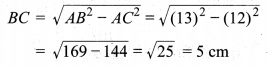
समकोण ∆ACB का क्षेत्रफल

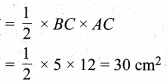
अर्द्धवृत्त का क्षेत्रफल

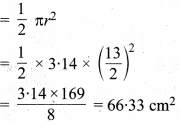
ar (छायांकित क्षेत्र) = ar (अर्द्धवृत्त) – ar (ABC)
= 66.33 – 30
= 36.33 cm²
अतः छायांकित भाग का अभीष्ट क्षेत्रफल = 36.33 cm² है।

प्रश्न 7.
संलग्न आकृति में PQRS एक वर्गाकार लॉन है जिसकी भुजा PQ = 42 m है। दो वृत्ताकार फूलों की क्यारियाँ भुजा PS तथा QR पर हैं जिनका केन्द्र इस वर्ग के विकर्णों का प्रतिच्छेदन बिन्दु O है। दोनों फूलों की क्यारियों (छायांकित भाग) का कुल क्षेत्रफल ज्ञात कीजिए।
हल :

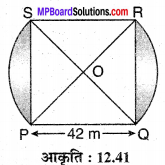
दिया है PQRS एक वर्गाकार लॉन जिसकी भुजा PQ = 42 m है अर्थात् PS = PQ = QR = RS = 42 m. हम जानते हैं कि वर्ग के विकर्ण समकोण पर समद्विभाजित करते हैं। मान लीजिए OP = r वृत्त की त्रिज्या है। समकोण ∆SOP में पाइथागोरस प्रमेय से,
OP² + OS² = PS²
⇒ r² + r² = (42)²
⇒ 2r² = 42 x 42
⇒ r² = 21 x 42

ar (छायांकित वृत्तखण्ड) = ar (त्रिज्यखण्ड) – ar (POS)
= 693 – 441
= 252 m²
कुल छायांकित भाग का क्षेत्रफल = 2 x 252
= 504 m²
अतः दोनों फूलों की क्यारियों (छायांकित भाग) का अभीष्ट क्षेत्रफल = 504 m² है।

प्रश्न 8.
14 cm त्रिज्या वाले उस लघु वृत्तखण्ड का क्षेत्रफल ज्ञात कीजिए, जिसका केन्द्रीय कोण 60° है। संगत दीर्घ वृत्तखण्ड का क्षेत्रफल भी ज्ञात कीजिए। (\(\pi=\frac{22}{7}\) लीजिए)।
हल :

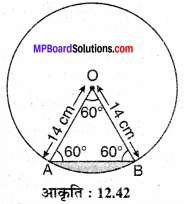
मान लीजिए O केन्द्र वाले वृत्त की त्रिज्या r = OA = OB = 14 cm तथा OA और OB के बीच केन्द्र पर बना कोण (लघु वृत्तखण्ड का केन्द्रीय कोण) θ = 60° दिया है।
∆OAB एक समबाहु त्रिभुज होगा जिसकी भुजा a = OA = AB = OB = 14 cm है।
∵त्रिज्यखण्ड का क्षेत्रफल

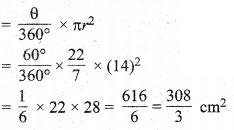
∵समबाहु ∆OAB का क्षेत्रफल

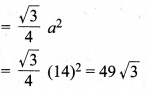
∵वृत्तखण्ड का क्षेत्रफल = त्रिज्यखण्ड का क्षेत्रफल – त्रिभुज का क्षेत्रफल

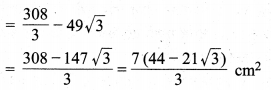
अतः लघु वृत्तखण्ड का क्षेत्रफल = \(\frac{7(44-21 \sqrt{3})}{3} \mathrm{cm}^{2}\) है।
∵वृत्त का क्षेत्रफल = πr² = \(\frac { 22 }{ 7 }\) x (14)²
= 22 x 28
= 616 cm²
∵दीर्घ वृत्तखण्ड का क्षेत्रफल = वृत्त का क्षेत्रफल – लघु वृत्तखण्ड का क्षेत्रफल

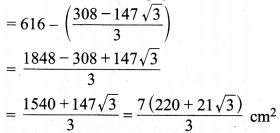
अतः दीर्घ वृत्तखण्ड का क्षेत्रफल \(\frac{7(220+21 \sqrt{3})}{3} \mathrm{cm}^{2}\) है।

प्रश्न 9.
एक वृत्ताकार खेल के मैदान का क्षेत्रफल 22176 m² है। इसकी चारदीवारी लगवाने का खर्च कितना होगा यदि दर Rs 50 प्रति मीटर हो।
हल :
वृत्ताकार मैदान का क्षेत्रफल = πr² = 22176
\(\frac { 22 }{ 7 }\) r² = 22176
r² = \(\frac { 22176 \times 7 }{ 22 }\) = 7056
r = √7056
= 84 m
वृत्ताकार मैदान की परिधि = 2πr = 2 x \(\frac { 22 }{ 7 }\) x 84
= 528 m
चार दीवार लगवाने का व्यय = दर x परिधि
= 50 x 528
= Rs 26,400
अतः वृत्ताकार खेल के मैदान की चारदीवारी लगवाने का अभीष्ट व्यय = Rs 26,400 होगा।

प्रश्न 10.
एक त्रिभुजाकार मैदान की भुजाएँ 15 m, 16 m एवं 17 m हैं। मैदान के कोनों में एक गाय, एक भैंस एवं एक घोड़ा अलग-अलग 7 m लम्बे रस्से से प्रत्येक को घास चरने के लिए बाँधा गया है। मैदान के उस भाग का क्षेत्रफल ज्ञात कीजिए जिसको चरा नहीं गया है।

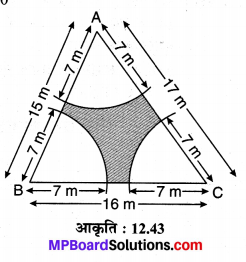
हल :
मान लीजिए त्रिभुजाकार मैदान ABC की भुजाएँ AB = 15 m, BC = 16 m एवं CA = 17 m हैं। शीर्ष A, B एवं C से 7 m लम्बे रस्से में क्रमशः गाय, भैंस एवं घोड़ा बाँधा गया है जो 7 m त्रिज्या वाले तथा शीर्ष कोण क्रमश: ∠A, ∠B, ∠C वाले त्रिज्यखण्डों से घास चर सकेंगे तथा छायांकित भाग मैदान का वह भाग होगा जहाँ से घास नहीं चरी जा सकेगी।

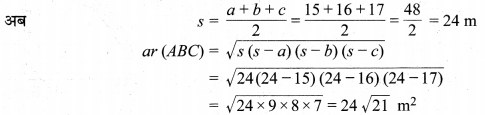
तीनों पशुओं द्वारा चरे गए मैदान के भाग का क्षेत्रफल

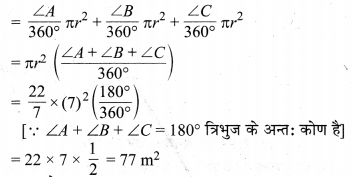
चरे नहीं जा सकने वाले मैदान के भाग का क्षेत्रफल
= (24 √21 – 77) m²
अतः चरे नहीं जा सकने वाले मैदान के भाग का अभीष्ट क्षेत्रफल
= (24 √21 – 77) m² है।

प्रश्न 11.
12 cm त्रिज्या वाले वृत्त के उस वृत्तखण्ड का क्षेत्रफल ज्ञात कीजिए जिसके संगत त्रिज्यखण्ड का केन्द्र पर बना कोण 60° है। (π = 3.14 का प्रयोग करें।)
हल :

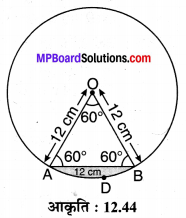
मान लीजिए OA = OB = 12 cm त्रिज्या तथा O केन्द्र वाला एक वृत्त है जिसका त्रिज्यखण्ड OADB तथा संगत वृत्तखण्ड ADB है। त्रिज्यखण्ड का केन्द्रीय कोण θ = ∠AOB = 60°
∠O = ∠A = ∠B = 60°
∆OAB एक समबाहु त्रिभुज है जिसकी प्रत्येक भुजा a = 12 cm है।

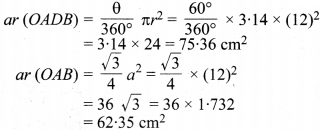
ar (छायांकित भाग) = 75.36 – 62.35
ar (ADB) = 13.01 cm²
अतः वृत्तखण्ड का अभीष्ट क्षेत्रफल = 13.01 cm² है।

प्रश्न 12.
एक वृत्ताकर पोखर (तालाब) का व्यास 17.5 m है। यह 2 m चौड़े रास्ते से घिरा हुआ है। Rs 25 प्रति m² की दर से रास्ते को बनवाने का व्यय ज्ञात कीजिए।
हल :

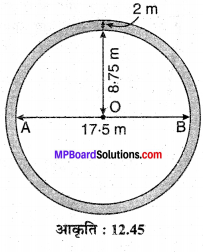
ज्ञात है : O केन्द्र वाले वृत्ताकार तालाब का व्यास d = 2r1 = 17.5 m
r1 = 8.75 m = \(\frac { 35 }{ 4 }\) = m
इसके चारों ओर 2 m चौड़ा रास्ता है।
बाह्य वृत्त की त्रिज्या r2 = 8.75 + 2 = 10.75 m = \(\frac { 43 }{ 4 }\)m

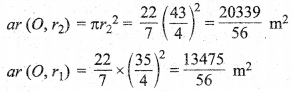
रास्ते का क्षेत्रफल = ar (O, r2) – ar (O, r1)

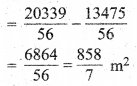
रास्ते के बनवाने का कुल व्यय = दर x क्षेत्रफल
= Rs 25 x \(\frac { 858 }{ 7 }\)
= \(\frac { 21450 }{ 7 }\)
= Rs 3064.29
अतः रास्ते को बनवाने का अभीष्ट व्यय = Rs 3064.29 है।

प्रश्न 13.
संलग्न आकृति 12.46 में ABCD एक समलम्ब चतुर्भुज है जिसमें AB || DC, AB = 18 cm, DC = 32 cm एवं AB तथा DC के बीच दूरी = 14 cm है। यदि A, B, C एवं D को केन्द्र लेकर क्रमशः 7 cm की त्रिज्या के चाप खींचे गए हैं। छायांकित भाग का क्षेत्रफल ज्ञात कीजिए।
हल :

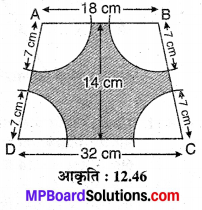
ज्ञात है कि एक समलम्ब चतुर्भुज ABCD जिसमें AB || DC, AB = 18 cm, DC = 32 cm एवं AB तथा DC के मध्य दूरी = 14 cm. शीर्ष A, B,C एवं D से 7 cm त्रिज्या के चाप काटे हैं।
समलम्ब चतुर्भुज क्षेत्रफल = \(\frac { 1 }{ 2 }\) (AB + DC) x बीच की दूरी
ar (ABCD) = \(\frac { 1 }{ 2 }\) (18+32) x 14 cm²
= \(\frac { 1 }{ 2 }\) x 50 x 14 = 350 cm²
अब शीर्षों पर बने त्रिज्यखण्डों के क्षेत्रफल,

ar (छायांकित भाग) = ar (ABCD) – ar (चारों त्रिज्यखण्ड)
= 350 – 154
= 196 cm²
अतः छायांकित भाग का अभीष्ट क्षेत्रफल = 196 cm² है।

प्रश्न 14.
3.5 cm प्रत्येक त्रिज्या वाले तीन वृत्त इस प्रकार खींचे गए हैं कि प्रत्येक वृत्त शेष दो वृत्तों को बाह्यतः स्पर्श करे। इन वृत्तों से बीच घिरे क्षेत्र का क्षेत्रफल ज्ञात कीजिए।
हल :
मान लीजिए r = 3.5 cm = \(\frac { 7 }{ 2 }\) cm त्रिज्या वाले तीन वृत्त जिनके केन्द्र P, Q एवं R है। संलग्न आकृति 12.47 के अनुसार खींचे गए हैं। उनसे घिरे छायांकित भाग का क्षेत्रफल ज्ञात करना है। चूँकि ∆PQR एक समबाहु त्रिभुज है जिसकी प्रत्येक भुजा की लम्बाई a = \(\frac{7}{2}+\frac{7}{2}\) = 7 cm है तथा इसके अन्तर्गत प्रत्येक त्रिज्यखण्ड की त्रिज्या r = \(\frac { 7 }{ 2 }\) cm एवं केन्द्रीय कोण θ = 60° है।

ar (छायांकित भाग) = ar (PQR) – 3 ar (त्रिज्यखण्ड)
= 21.217 – 19.25
= 1.967 cm²
अतः छायांकित भाग अर्थात् वृत्तों के मध्य घिरे हुए क्षेत्र का अभीष्ट क्षेत्रफल =1.967 cm² है।

प्रश्न 15.
5 सेमी त्रिज्या वाले उस त्रिज्यखण्ड का क्षेत्रफल ज्ञात कीजिए जिसके संगत चाप की लम्बाई 3.5 cm है।
हल :

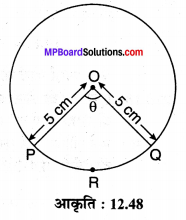
मान लीजिए O केन्द्र का एक वृत्त है जिसकी त्रिज्या r = 5 cm है तथा, चाप \(\widehat{P R Q}\) की लम्बाई 3.5 cm है केन्द्र पर θ कोण अन्तरित करता है। इसका संगत त्रिज्यखण्ड OPRQ है।

चूँकि त्रिज्यखण्ड OPRQ का क्षेत्रफल

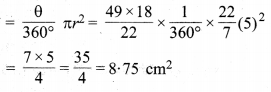
अतः त्रिज्यखण्ड का अभीष्ट क्षेत्रफल = 8.75 cm² है।

प्रश्न 16.
7 cm त्रिज्या वाले 4 वृत्ताकार समान कार्ड बोर्ड के टुकड़े आपस में सटाकर एक कागज पर इस प्रकार रखे हैं कि प्रत्येक शेष तीन वृत्तों में से दो को स्पर्श करता है। इन चारों के बीच घेरे हुए कागज के क्षेत्र का क्षेत्रफल ज्ञात कीजिए।
हल :

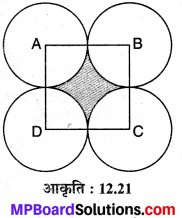
ABCD वर्ग की प्रत्येक भुजा a = 14 cm दिया है। चित्रानुसार
प्रत्येक वृत्त की त्रिज्या = \(\frac{a}{2}=\frac{14}{2}\) = 7 cm.
वर्ग में से चार वृत्त-चतुर्थांश अर्थात् एक वृत्त क्षेत्रफल को हटाकर शेष भाग छायांकित किया गया है।
⇒ छायांकित भाग का क्षेत्रफल = वर्ग का क्षेत्रफल – वृत्त का क्षेत्रफल
= a² – πr²
= (14)² – \(\frac { 22 }{ 7 }\) x (7)²
= 196 – 154
= 42 cm²
अतः छायांकित भाग का अभीष्ट क्षेत्रफल = 42 cm² है।

प्रश्न 17.
784 cm² क्षेत्रफल वाले एक वर्गाकार कार्ड बोर्ड पर चार समान (सर्वांगसम) अधिकतम माप की वृत्ताकार प्लेटें इस प्रकार रखी गयी हैं कि प्रत्येक शेष में से दो को बाह्यतः स्पर्श करें तथा वर्ग की प्रत्येक भुजा दो वृत्ताकार प्लेटों की स्पर्श रेखा हो, तो A. इन प्लेटों से अनाच्छादित कार्ड बोर्ड के रिक्त क्षेत्र का क्षेत्रफल ज्ञात कीजिए।
हल:

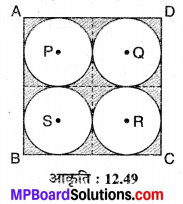
मान लीजिए एक वर्गाकार कार्ड बोर्ड ABCD है जिसका क्षेत्रफल 784 cm² है। आकृति के अनुसार चार सर्वांगसम वृत्ताकार प्लेटें P, Q, R एवं S रखी हैं। चूँकि दो प्लेटें परस्पर स्पर्श कर रही हैं ।

कार्ड बोर्ड के अनाच्छादित क्षेत्र का क्षेत्रफल
ar (छायांकित क्षेत्र) = ar (ABCD) – 4ar (वृत्त)
= 784 – 616 [∵ ar (ABCD) = 784 दिया है।]
= 168 cm²
अतः कार्ड बोर्ड के अनाच्छादित रिक्त क्षेत्रफल का अभीष्ट क्षेत्रफल = 168 cm² है।

प्रश्न 18.
एक वृत्त के केन्द्रीय कोण 200° वाले त्रिज्यखण्ड का क्षेत्रफल 770 cm² है। इस त्रिज्यखण्ड के संगत चाप की माप ज्ञात कीजिए।
हल :
मान लीजिए एक वृत्त (O, r) है जिसका θ = 200° केन्द्रीय कोण वाला दीर्घ त्रिज्यखण्ड OQRP है तथा संगत चाप QRP है तथा ar (OQRP) = 770 cm² (दिया है)। चूँकि त्रिज्यखण्ड का क्षेत्रफल


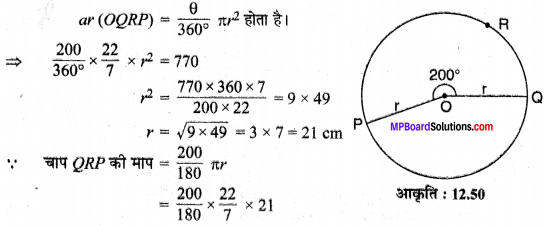
अतः चाप की अभीष्ट माप = \(73\frac { 1 }{ 3 }\) cm है।

प्रश्न 19.
7 cm एवं 21 cm त्रिज्याओं वाले दो वृत्तों के क्रमशः केन्द्रीय कोण 120° एवं 40° वाले त्रिज्यखण्ड हैं। दोनों त्रिज्यखण्डों के क्षेत्रफल तथा उनके संगत चापों के माप ज्ञात कीजिए। आप क्या प्रेक्षित करते है?
हल :

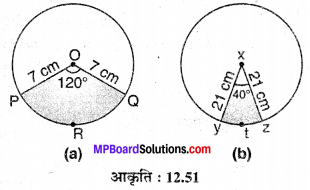
मान लीजिए O एवं x केन्द्र वाले दो वृत्तों की त्रिज्याएँ क्रमशः r1 = 7 cm एवं r2 = 21 cm है तथा केन्द्रीय कोण θ1 = 120° एवं θ2 = 40° वाले त्रिज्यखण्ड क्रमशः OPRQ एवं xytz हैं
जिनके संगत चाप क्रमशः \(\widehat{P R Q}\) एवं \(\widehat{y t z}\) है।

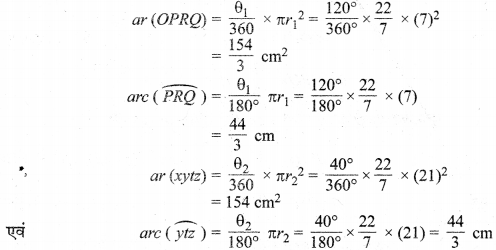
अत: दोनों त्रिज्यखण्डों के अभीष्ट क्षेत्रफल क्रमश: \(\frac { 154 }{ 3 }\) cm² एवं 154 cm² हैं तथा संगत चापों की माप क्रमशः \(\frac { 44 }{ 3 }\) cm एवं \(\frac { 44 }{ 3 }\) cm हैं जो बराबर हैं। इस प्रकार हम प्रेक्षित करते हैं कि चाप बराबर होते हुए भी उनके संगत त्रिज्यखण्डों के क्षेत्रफल अलग-अलग हैं।

प्रश्न 20.
एक वृत्ताकार पहिए द्वारा 176 m दूरी तय करने में लगाए गए चक्करों की संख्या ज्ञात कीजिए जबकि उसका क्षेत्रफल = 1.54 m².
हल :
चूँकि वृत्त का क्षेत्रफल = πr²
\(\frac { 22 }{ 7 }\) r² = 1.54
r² = \(\frac { 1.54 \times 7 }{ 22 }\)
= 0.49
चूँकि वृत्त की परिधि (एक चक्कर में चली गई दूरी) = 2πr
= 2 x \(\frac { 22 }{ 7 }\) x 0.7 = 4.4 m

अतः चक्करों की अभीष्ट संख्या = 40 चक्कर है।

प्रश्न 21.
केन्द्र पर 90° का कोण अन्तरित करने वाले तथा 5 cm लम्बाई की जीवा द्वारा किसी वृत्त को विभाजित करने पर बने दोनों वृत्तखण्डों के क्षेत्रफलों का अन्तर ज्ञात कीजिए।
हल :

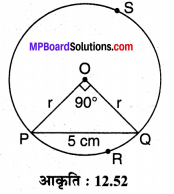
वृत्त (O,r) की जीवा PQ द्वारा केन्द्र O पर ∠POQ = 90° अन्तरित किया गया है, जहाँ जीवा PQ, ∆POQ का कर्ण है, तो समकोण ∆POQ में,
OP² + OQ² = PQ²
2r² = (5)² = 25
r² = \(\frac { 25 }{ 2 }\) …(1)
लघु त्रिज्यखण्ड OPRQ का क्षेत्रफल = \(\frac{\theta}{360^{\circ}} \pi r^{2}\)

दीर्घ त्रिज्यखण्ड OQSP का क्षेत्रफल = \(\frac{360^{\circ}-\theta}{360^{\circ}} \pi r^{2}\)

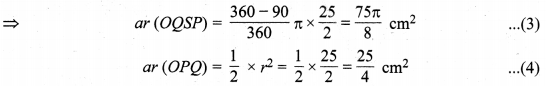
वृत्तखण्ड PRQ का क्षेत्रफल = ar (OPRQ) – ar (OPQ)

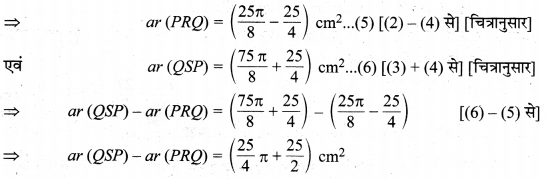
अतः दोनों वृत्तखण्डों का अभीष्ट अन्तर = \(\left(\frac{25}{4} \pi+\frac{25}{2}\right) \mathrm{cm}^{2}\) है।

प्रश्न 22.
21 cm त्रिज्या वाले वृत्त के केन्द्रीय कोण 120° वाले त्रिज्यखण्ड का उसके संगत दीर्घ त्रिज्यखण्ड के क्षेत्रफलों का अन्तर ज्ञात कीजिए।
हल :

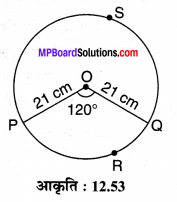
मान लीजिए r = 21 cm त्रिज्या वाले वृत्त (O, r) का केन्द्रीय कोण θ1 = 120° वाला एक त्रिज्यखण्ड OPRQ तथा इसके संगत दीर्घ त्रिज्यखण्ड OQSP है जिसका केन्द्रीय कोण θ2 = 360° – 120° = 240° है।


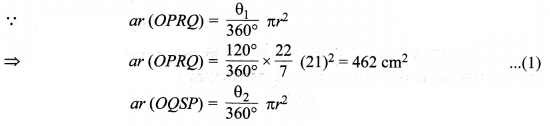
ar (OQSP) – ar (OPRQ) = 924 – 462
= 462 cm²
अतः दोनों त्रिज्यखण्डों के क्षेत्रफलों में अभीष्ट अन्तर = 462 cm² है।

MP Board Class 10th Maths Chapter 12 लघु उत्तरीय प्रश्न

प्रश्न 1.
उस वृत्त की त्रिज्या ज्ञात कीजिए जिसकी परिधि 15 cm एवं 18 cm त्रिज्याओं वाले दो वृत्तों की परिधियों का योग है।
हल :
मान लीजिए कि वृत्त की अभीष्ट त्रिज्या = r हो तो प्रश्नानुसार,
2πr = 2π (15) + 2π (18)
2πr = 2π (15 + 18)
r = 15 + 18
= 33 cm
अतः वृत्त की अभीष्ट त्रिज्या = 33 cm है।

प्रश्न 2.
28 cm त्रिज्या वाले उस त्रिज्यखण्ड का क्षेत्रफल ज्ञात कीजिए जिसका केन्द्रीय शीर्ष कोण 45° हो।
हल :
चूँकि त्रिज्यखण्ड का क्षेत्रफल

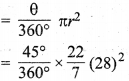
= 308 cm²
अतः त्रिज्यखण्ड का अभीष्ट क्षेत्रफल = 308 cm² है।

प्रश्न 3.
एक मोटर साइकिल के पहिये की त्रिज्या 35 cm है। वह 1 मिनट में कितने चक्कर लगाएगा जबकि उसकी चाल 66 km/h हो।
हल :
मोटर साइकिल द्वारा 1 मिनट में चली गयी दूरी
= चाल x समय = 66 km/h x \(\frac { 1 }{ 60 }\) h = 1.1 km
= 1100 m
= 110000 cm.
पहिये की परिधि = 2πr = 2 x \(\frac { 22 }{ 7 }\) x 35 = 220 cm

अतः मोटरसाइकिल का पहिया 500 चक्कर लगायेगा।

प्रश्न 4.
एक गाय 14 m लम्बी रस्सी से एक आयत के शीर्ष से बधी है जिसकी विमाएँ 20 m x 16 m है। गाय द्वारा चरे जा सकने वाले क्षेत्र का क्षेत्रफल ज्ञात कीजिए।
हल :
गाय एक 14 m त्रिज्या के चतुर्थांश की घास को चर पायेगी
⇒ चरे जाने वाले क्षेत्र का क्षेत्रफल = \(\frac{1}{4} \pi r^{2}\)
= \(\frac{1}{4} \times \frac{22}{7} \times(14)^{2}\)
= 154 m²
अतः गाय द्वारा चरे जा सकने वाले क्षेत्रफल का अभीष्ट क्षेत्रफल = 154 m² है।

प्रश्न 5.
एक 14 cm त्रिज्या वाले वृत्त के लघु वृत्तखण्ड का क्षेत्रफल ज्ञात कीजिए जबकि उसके संगत त्रिज्यखण्ड का शीर्ष कोण 60° है।
हल :
वृत्त (O, r) की त्रिज्या r = 14 cm तथा अवधा PRQ के संगत त्रिज्यखण्ड OPRQ का शीर्ष कोण θ = ∠POQ = 60° है तो त्रिभुज समबाहु ∆ होगा जिसकी भुजा a = r = 14 cm त्रिज्यखण्ड का

अत: लघु वृत्तखण्ड का अभीष्ट क्षेत्रफल = \(\left(\frac{308}{3}-49 \sqrt{3}\right) \mathrm{cm}^{2}\) है।

प्रश्न 6.
संलग्न आकृति में ABCD एक वर्ग है जिसकी भुजा a = 12 cm जिसमें उसके शीर्षों A, B, C एवं D को केन्द्र लेकर इस प्रकार चाप खींचे गए हैं कि ये चाप वर्ग की भुजाओं AB, BC, CD और DA को उनके मध्य-बिन्दुओं क्रमशः P, Q, R और S पर प्रतिच्छेद करते हैं। छायांकित क्षेत्र PORS का क्षेत्रफल ज्ञात कीजिए। π = 3.14 का प्रयोग कीजिए।
हल :

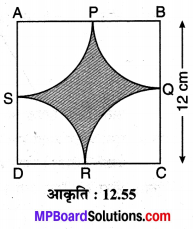
वृत्त के चार चतुर्थांश ASP, BPQ, CQR एवं DRS हैं जिनमें प्रत्येक की त्रिज्या r = \(\frac { 12 }{ 2 }\) = 6 cm है। वर्ग ABCD का क्षेत्रफल = ar (ABCD) = a² = 12² = 144 cm²
चारों वृत्तखण्डों का क्षेत्रफल = 4 x \(\frac { 1 }{ 4 }\) πR²
= 4 x \(\frac { 1 }{ 4 }\) x 3.14 x (6)
= 113.04 cm²
छायांकित भाग का क्षेत्रफल = वर्ग का क्षेत्रफल – चतुर्थांशों का क्षेत्रफल
= 144 – 113.04
= 30.96 cm²
अतः छायांकित भाग का अभीष्ट क्षेत्रफल = 30.96 cm² है।

प्रश्न 7.
संलग्न आकृति में 10 cm भुजा वाले समबाहु त्रिभुज ABC के शीर्ष A, B एवं C को लेकर चाप खींचे गए है जो भुजाओं BC, CA एवं AB को उनके मध्य बिन्दुओं क्रमशः D, E एवं F पर प्रतिच्छेद करते हैं। छायांकित क्षेत्र का क्षेत्रफल ज्ञात कीजिए। π = 3.14 का प्रयोग कीजिए।
हल :

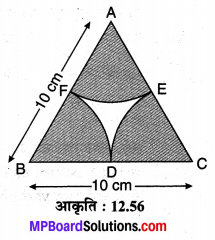
छायांकित भाग तीन सर्वांसगम त्रिज्यखण्डों से बना है जिनमें प्रत्येक की त्रिज्या r = \(\frac { 10 }{ 2 }\) = 5 cm तथा केन्द्रीय शीर्ष कोण θ = 60° (समबाहु ∆ के कोण) है।
ar (छायांकित क्षेत्र)

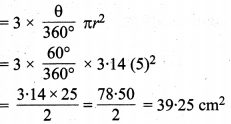
अतः छायांकित भाग का अभीष्ट क्षेत्रफल = 39.25 cm² है।

प्रश्न 8.
संलग्न आकृति में ∆POR के शीर्षों P, Q एवं R को केन्द्र लेकर 14 cm त्रिज्या के चाप खींचे गए हैं। छायांकित भाग का क्षेत्रफल ज्ञात कीजिए।
हल :

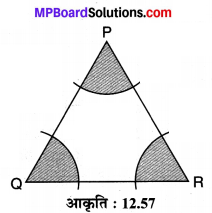
छायांकित भाग तीन त्रिज्यखण्डों के योग से बना है जिनमें प्रत्येक की त्रिज्या r = 14 cm दी है तथा मान लीजिए उनके शीर्ष कोण क्रमशः ∠P, ∠Q और ∠R हैं तो
छायांकित भाग का क्षेत्रफल

अतः छायांकित भाग का अभीष्ट क्षेत्रफल = 308 cm² है।

प्रश्न 9.
एक वृत्ताकर पार्क चारों ओर से एक 21 m चौड़ी सड़क से घिरा है। यदि पार्क की त्रिज्या 105 m हो, तो सड़क का क्षेत्रफल ज्ञात कीजिए।
हल :

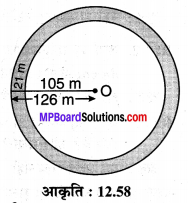
सड़क एक वृत्ताकार वलय है जिसकी आन्तरिक त्रिज्या r1 = 105 m दी है तथा इसकी बाह्य त्रिज्या r2 = 105 m + 21 m = 126 m है।
सड़क का क्षेत्रफल = π (R₂² – R₁²)
= \(\frac { 22 }{ 7 }\) x [(126)² – (105)²]
= \(\frac { 22 }{ 7 }\) (126 + 105) (126 – 105)
= \(\frac { 22 }{ 7 }\) x 231 x 21
= 15246 m²
अतः सड़क का अभीष्ट क्षेत्रफल = 15246 m² है।

प्रश्न 10.
संलग्न आकृति 12.59 में चतुर्भुज ABCD के शीर्ष A, B, C एवं D को केन्द्र लेकर 21 cm त्रिज्या के चाप खींचे गए हैं। छायांकित क्षेत्र का क्षेत्रफल ज्ञात कीजिए।
हल :

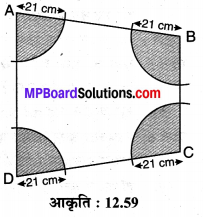
चारों शीर्षों पर चार त्रिज्यखण्ड बने हैं जिनमें प्रत्येक की त्रिज्या r = 21 cm तथा शीर्ष केन्द्रीय कोण ∠A, ∠B, ∠C एवं ∠D हैं।

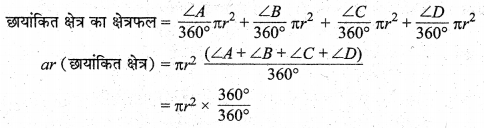
[∴ ∠A+ ∠B + ∠C+ ∠D = 360° चतुर्भुज के शीर्ष कोणों का योग]
= πr²
= \(\frac { 22 }{ 7 }\) (21)²
= 22 x 63
= 1386 cm² .
अतः छायांकित क्षेत्र का अभीष्ट क्षेत्रफल = 1386 cm² है।

प्रश्न 11.
20 cm लम्बा एक तार का टुकड़ा एक वृत्त की चाप की शक्ल में मोड़ा गया है, जो वृत्त के केन्द्र पर 60° का कोण अन्तरित करता है। वृत्त की त्रिज्या ज्ञात कीजिए।
हल :
चाप की लम्बाई = 20 cm तथा केन्द्र पर कोण θ = 60° अन्तरित है।
चूँकि

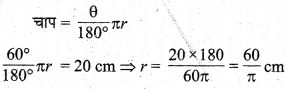
अतः वृत्त की अभीष्ट त्रिज्या = \(\frac{60}{\pi}\) cm है।

MP Board Class 10th Maths Chapter 12 अति लघु उत्तरीय प्रश्न

प्रश्न 1.
क्या एक वर्ग जिसकी भुजा a cm है के अन्तर्वृत्त का क्षेत्रफल πa² cm होगी? अपने उत्तर का कारण बताइए।
हल :
नहीं हो सकता, क्योंकि इसकी त्रिज्या \(\frac { a }{ 2 }\) होगी तथा क्षेत्रफल \(\frac{1}{4} \pi a^{2} \mathrm{cm}^{2}\).

प्रश्न 2.
क्या यह कहना सत्य होगा कि एक वर्ग की परिमाप जो a cm त्रिज्या वाले वृत्त का परिगत है, 8a cm होगी। अपने उत्तर का कारण दीजिए।
हल :
हाँ, यह कथन सत्य है, क्योंकि वर्ग की भुजा 2a cm है।

प्रश्न 3.
क्या यह कहना सत्य है कि किसी वृत्तखण्ड का क्षेत्रफल संगत त्रिज्यखण्ड के क्षेत्रफल से कम है? और क्यों?
हल :
यह सदैव सत्य नहीं। यह केवल लघु वृत्तखण्ड एवं लघु त्रिज्यखण्ड के लिए सत्य है।

प्रश्न 4.
क्या यह कहना सत्य है कि किसी वृत्तखण्ड का क्षेत्रफल = संगत त्रिज्यखण्ड क्षेत्रफल-संगत त्रिभुज का क्षेत्रफल? और क्यों?
हल :
यह कथन सदैव सत्य नहीं है। यह केवल लघु वृत्तखण्ड एवं लघु त्रिज्यखण्ड के लिए सत्य है।

प्रश्न 5.
क्या यह सत्य है कि किसी d cm व्यास वाले पहिए द्वारा एक चक्कर में चली गयी दूरी 2πd cm होगी? और क्यों?
हल :
नहीं क्योंकि यह πd cm होगी।

प्रश्न 6.
r त्रिज्या वाले किसी पहिए द्वारा s m की दूरी तय करने में उसे \(\frac{\boldsymbol{S}}{2 \pi \boldsymbol{r}}\) चक्कर लगाने पड़ेंगे। क्या यह कथन सत्य हैं? और क्यों?
हल :
हाँ कथन सत्य है क्योंकि 1 चक्कर में चली गयी दूरी = 2πr m.

प्रश्न 7.
किसी वृत्त के क्षेत्रफल का संख्यात्मक मान उसकी परिधि के संख्यात्मक मान के बराबर होगा। क्या यह कथन सत्य है? और क्यों?
हल :
यह कथन सदैव सत्य नहीं है, क्योंकि वह त्रिज्या r के मान पर निर्भर करेगा और जब r का मान 2 मात्रक होगा तभी यह सत्य होगा।

प्रश्न 8.
किसी r मात्रक त्रिज्या के वृत्त का चाप दूसरे 2r मात्रक त्रिज्या के वृत्त के चाप के बराबर है। तो प्रथम वृत्त के संगत त्रिज्यखण्ड का शीर्ष (केन्द्रीय) कोण दूसरे वृत्त के संगत त्रिज्यखण्ड के शीर्ष (केन्द्रीय) कोण का दूना होगा। क्या यह कथन असत्य है? और क्यों?
हल :
नहीं, कथन सत्य है, क्योंकि चाप = कोण x त्रिज्या।

प्रश्न 9.
दो भिन्न वृत्तों के समान संगत चापों द्वारा निर्मित त्रिज्यखण्डों के क्षेत्रफल समान होंगे। क्या यह कथन सत्य है? और क्यों?
हल :
यह कथन सदैव सत्य नहीं है क्योंकि यह केवल समान वृत्तों के लिए ही सत्य है।

प्रश्न 10.
दो विभिन्न वृत्तों के त्रिज्यखण्डों के क्षेत्रफल यदि समान हों, तो क्या यह आवश्यक है कि उनके संगत चापों की लम्बाई समान होगी? और क्यों?
हल :
यह कथन सदैव सत्य नहीं है। यह केवल समान वृत्तों के चापों के लिए ही सत्य है।

प्रश्न 11.
क्या a cm लम्बाई एवं b cm चौड़ाई वाले आयत (जहाँ a > b) के अन्तर्गत खींचे गए। बड़े-से-बड़े वृत्त का क्षेत्रफल πb² cm² होगा? और क्यों?
हल :
नहीं, क्योंकि वृत्त की त्रिज्या b/2 होगी।

प्रश्न 12.
दो भिन्न वृत्तों के क्षेत्रफल बराबर हैं, तो क्या यह आवश्यक है कि उनकी परिधियाँ की बराबर होंगी? और क्यों?
हल :
हाँ, क्योंकि उनकी त्रिज्याएँ बराबर हैं।

प्रश्न 13.
दो वृत्तों की परिधियाँ बराबर हैं, तो क्या यह आवश्यक है कि उनके क्षेत्रफल भी बराबर होंगे? और क्यों?
हल :
हाँ क्योंकि उनकी त्रिज्याएँ बराबर हैं।

प्रश्न 14.
क्या यह कहना सत्य होगा कि एक वृत्त के अन्तर्गत बने वर्ग का क्षेत्रफल p² cm² होगा यदि वृत्त का व्यास p cm हो? और क्यों?
हल :
नहीं, क्योंकि वर्ग का विकर्ण p cm होगा।

MP Board Class 10th Maths Chapter 12 वस्तुनिष्ठ प्रश्न

MP Board Class 10th Maths Chapter 12 बहु-विकल्पीय प्रश्न

प्रश्न 1.
वृत्त का चाप, वृत्त की त्रिज्या और चाप द्वारा केन्द्र पर बने कोण में क्या सम्बन्ध है :
(a) कोण = चाप x त्रिज्या
(b) चाप = कोण x त्रिज्या
(c) त्रिज्या = चाप x कोण
(d) इनमें से कोई नहीं।
उत्तर:
(b) चाप = कोण x त्रिज्या

प्रश्न 2.
यदि किसी वृत्त का क्षेत्रफल 154 cm² है, तो इसकी परिमाप होगी :
(a) 11 cm
(b) 22 cm
(c) 44 cm
(d) 55 cm.
उत्तर:
(c) 44 cm

प्रश्न 3.
त्रिज्या के वृत्त के एक त्रिज्यखण्ड का केन्द्रीय कोण θ(डिग्री में) है, तो त्रिज्यखण्ड का क्षेत्रफल होगा:

उत्तर:
\(\frac{\pi r^{2} \theta}{360^{\circ}}\)

प्रश्न 4.
यदि त्रिज्याओं R₁ एवं R₂ वाले वृत्तों के क्षेत्रफलों का योगफल तीसरे R त्रिज्या वाले वृत्त के क्षेत्रफल के बराबर हो, तो :
(a) R₁ + R₂ = R
(b) R₁² + R₂² = R²
(c) R₁ + R₂ < R
(d) R₁² + R₁² < R².
उत्तर:
(b) R₁² + R₂² = R²

प्रश्न 5.
यदि त्रिज्याओं R1 एवं R2 वाले वृत्तों की परिधियों का योगफल तीसरे R त्रिज्या वाले वृत्त की परिधि के बराबर हो, तो :
(a) R₁ + R₂ = R
(b) R₁ + R₂ > R
(c) R₁ + R₂ < R
(d) नहीं कह सकते।
उत्तर:
(a) R₁ + R₂ = R

प्रश्न 6.
r त्रिज्या वाले अर्द्धवृत्त के अन्तर्गत खींचे गए बड़े-से-बड़े त्रिभुज का क्षेत्रफल होगा :
(a) r² वर्ग मात्रक
(b) \(\frac { 1 }{ 2 }\) r² वर्ग मात्रक
(c) 2r² वर्ग मात्रक
(d) √2 r² वर्ग मात्रक।
उत्तर:
(a) r² वर्ग मात्रक

प्रश्न 7.
एक वृत्त की परिधि एक वर्ग की परिमाप के बराबर हो तो उनके क्षेत्रफलों का अनुपात होगा :
(a) 22 : 7
(b) 14 : 11
(c) 7 : 22
(d) 11 : 14.
उत्तर:
(b) 14 : 11

प्रश्न 8.
एक एकल वृत्ताकार पार्क बनाना प्रस्तावित है जिसका क्षेत्रफल दो छोटे वृत्ताकार पार्कों के क्षेत्रफल के योगफल के बराबर है। यदि छोटे पार्कों के व्यास क्रमश: 16 m एवं 12 m हों, तो नए पार्क की त्रिज्या होगी :
(a) 10 m
(b) 15 m
(c) 20 m
(d) 24 m.
उत्तर:
(a) 10 m

प्रश्न 9.
6 cm भुजा वाले वर्ग के अन्तर्गत खींचे गए वृत्त का क्षेत्रफल होगा :
(a) 36π cm²
(b) 18π cm²
(c) 12π cm²
(d) 9π cm².
उत्तर:
(d) 9π cm².

प्रश्न 10.
8 cm त्रिज्या के वृत्त के अन्तर्गत बनने वाले वर्ग का क्षेत्रफल होगा :
(a) 256 cm²
(b) 128 cm²
(c) 64√2 cm²
(d) 64 cm².
उत्तर:
(b) 128 cm²

प्रश्न 11.
एक वृत्त की परिधि 36 cm एवं 20 cm त्रिज्याओं वाले दो वृत्तों की परिधियों का योग है, तो उस वृत्त की त्रिज्या होगी:
(a) 56 cm
(b) 42 cm
(c) 28 cm
(d) 16 cm.
उत्तर:
(c) 28 cm

प्रश्न 12.
एक वृत्त का क्षेत्रफल 24 cm एवं 7 cm त्रिज्याओं वाले दो वृत्तों के क्षेत्रफल का योग है, तो उस वृत्त का व्यास होगा:
(a) 31 cm
(b) 25 cm
(c) 62 cm
(d) 50 cm.
उत्तर:
(d) 50 cm.

रिक्त स्थानों की पूर्ति

1. वृत्त के अनुदिश एक बार चलने में तय की गई दूरी उस वृत्त की ………… कहलाती है।
2. वृत्त की परिधि के मध्य घिरे हुए क्षेत्र की माप उस वृत्त का ………… कहलाता है।
3. एक वृत्तीय क्षेत्र का वह भाग जो दो त्रिज्याओं और संगत चाप से घिरा (परिबद्ध) हो उस वृत्त का एक ………….. कहलाता है।
4. त्रिज्यखण्ड की संगत चाप की माप उस चाप की ………… कहलाती है।
5. वृत्तीय क्षेत्र का वह भाग जो जीवा और संगत चाप से परिबद्ध हो उस वृत्त का ………… कहलाता है।
5. कोण θ वाले त्रिज्यखण्ड का क्षेत्रफल का सूत्र ………… है। (2019)
उत्तर-
1. परिधि (परिमाप),
2. क्षेत्रफल,
3. त्रिज्यखण्ड,
4. लम्बाई,
5. वृत्तखण्ड,
6. त्रिज्यखण्ड का क्षेत्रफल = \(\frac{\theta}{360^{\circ}} \pi r^{2}\)

जोड़ी मिलाना

उत्तर-
1.→(c),
2.→(d),
3.→(e),
4.→(a),
5.→(b).

सत्य/असत्य कथन

1. सर्वांगसम वृत्तों के क्षेत्रफल सदैव बराबर होते हैं।
2. समरूप वृत्तों के क्षेत्रफल सदैव बराबर होते हैं।
3. सर्वांगसम वृत्तों की परिमाप सदैव बराबर होती है।
4. समरूप वृत्तों की परिमाप सदैव बराबर होती है।
5. यदि एक वृत्त की परिधि एवं एक वर्ग की परिमाप बराबर है तो वृत्त का क्षेत्रफल > वर्ग का क्षेत्रफल
उत्तर-
1. सत्य,
2. असत्य
3. सत्य,
4. असत्य,
5. सत्य।

एक शब्द/वाक्य में उत्तर

1. एक वृत्त के व्यास d एवं परिधि में क्या सम्बन्ध है?
2. एक वृत्त के व्यास d एवं उसके क्षेत्रफल में क्या सम्बन्ध है?
उत्तर-
1. परिधि = πd,
2. वृत्त का क्षेत्रफल = \(\frac{1}{4} \pi d^{2}\)