Category: Class 7

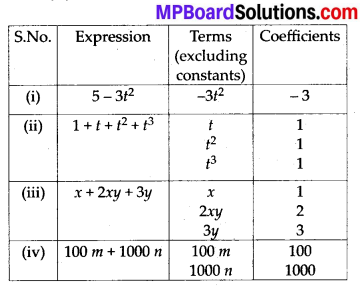
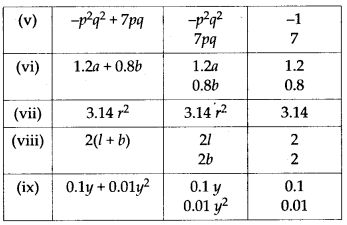
MP Board Class 7th Maths Solutions Chapter 11 Perimeter and Area Ex 11.2

Question 1.
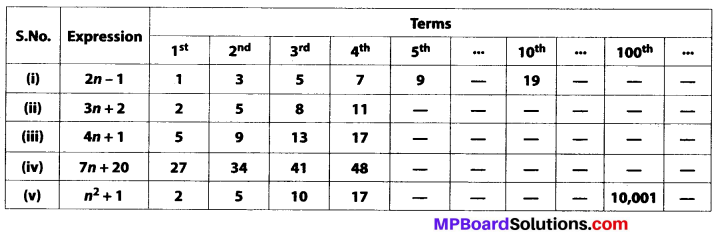
Find the area of each of the following parallelograms:

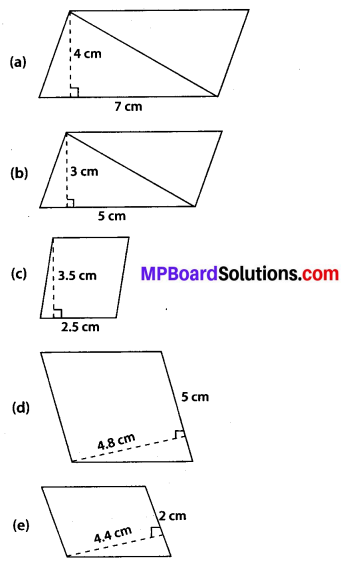
Solution:
Area of parallelogram = Base × Height
(a) Height = 4 cm, Base = 7 cm
Area of parallelogram = 7 × 4 = 28 cm²

(b) Height = 3 cm, Base = 5 cm
Area of parallelogram = 5 × 3 = 15 cm²

(c) Height = 3.5 cm, Base = 2.5 cm
Area of parallelogram = 2.5 × 3.5 = 8.75 cm²

(d) Height = 4.8 cm, Base = 5 cm
Area of parallelogram = 5 × 4.8 = 24 cm²

(e) Height = 4.4 cm, Base = 2 cm
Area of parallelogram = 2 × 4.4 = 8.8 cm²

Question 2.
Find the area of each of the following triangles:


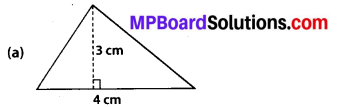
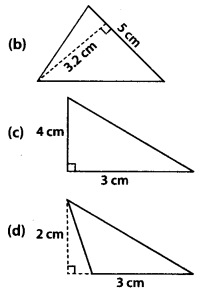
Solution:
Area of triangle = \(\frac{1}{2}\) × Base × Height
(a) Base = 4 cm, height = 3 cm
Area = \(\frac{1}{2}\) × 4 × 3 = 6 cm²

(b) Base = 5 cm, height = 3.2 cm
Area = \(\frac{1}{2}\) × 5 × 3.2 = 8 cm²

(c) Base = 3 cm, height = 4 cm
Area = \(\frac{1}{2}\) × 3 × 4 = 6cm²

(d) Base = 3 cm, height = 2 cm
Area = \(\frac{1}{2}\) × 3 × 2 = 3 cm²

Question 3.
Find the missing values:

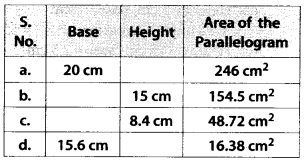
Solution:
Area of parallelogram = Base × Height
(a) Base = 20 cm
Let height = h
Area of parallelogram = 246 cm²
∴ 20 × h = 246
⇒ h = \(\frac{246}{20}\) = 12.3 cm
Therefore, the height of parallelogram is 12.3 cm.

(b) Let base = b
Height = 15 cm
Area of parallelogram = 154.5 cm²
∴ b × 15 = 154.5
⇒ b = \(\frac{154.5}{15}\) = 10.3 cm
Therefore, the base of parallelogram is 10.3 cm.

(c) Let base = b
Height = 8.4 cm
Area of parallelogram = 48.72 cm²
∴ b × 8.4 = 48.72
⇒ b = \(\frac{48.72}{8.4}\) = 5.8 cm
Therefore, the base of parallelogram is 5.8 cm.

(d) Base = 15.6 cm
Let height = h
Area of parallelogram = 16.38 cm²
∴15.6 × h = 16.38
⇒ h = \(\frac{16.38}{15.6}\) = 1.05 cm
Therefore, the height of parallelogram is 1.05 cm.

Question 4.
Find the missing values:

Solution:
Area of triangle = \(\frac{1}{2}\) × Base × Height
Let b be the base of triangle and h be the height of triangle.
(i) b = 15 cm

Therefore, the height of triangle is 11.6 cm.

(ii) h = 31.4 mm
Area = \(\frac{1}{2}\) × b × h = 1256 mm²

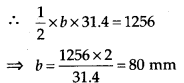
Therefore, the base of triangle is 80 mm.

(iii) b = 22 cm

Therefore, the height of triangle is 15.5 cm.

Question 5.
PQRS is a parallelogram (see the given figure). QM is the height from Q to SR and QN is the height from Q to PS. If SR = 12 cm and QM = 7.6 cm. Find:
(a) the area of the parallelogram PQRS
(b) QN, if PS = 8 cm

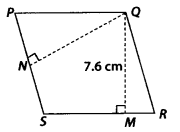
Solution:
(a) Area of parallelogram = Base × Height
= SR × QM
= 12 × 7.6 = 91.2 cm²

(b) PS = 8 cm
Area of parallelogram = Base × Height
= PS × QN = 91.2 cm²
⇒ 8 × QN = 91.2
⇒ QN = \(\frac{91.2}{8}\) = 11.4 cm

Question 6.
DL and BM are the heights on sides AB and AD respectively of parallelogram ABCD (see the given figure).

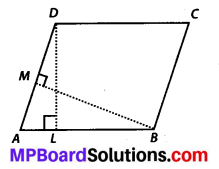
If the area of the parallelogram is 1470 cm², AB = 35 cm and AD = 49 cm, find the length of BM and DL.
Solution:
Area of parallelogram = Base × Height
= AB × DL
⇒ 1470 = 35 × DL
⇒ DL = \(\frac{1470}{35}\) = 42 cm
Also, area of parallelogram = AD × BM
⇒ 1470 = 49 × BM
∴ BM = \(\frac{1470}{49}\) = 30 cm

Question 7.
∆ABC is right angled at A (see the given figure). AD is perpendicular to BC. If AB = 5 cm, BC – 13 cm and AC = 12 cm, find the area of ∆ABC. Also find the length of AD.

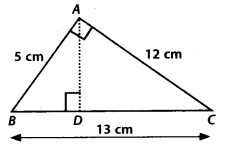
Solution:

Question 8.
∆ABC is isosceles with AB = AC= 7.5 cm and BC = 9 cm (see the given figure). The height AD from A to BC, is 6 cm. Find the area of ∆ABC. What will be the height from C to AB i. e., CE?

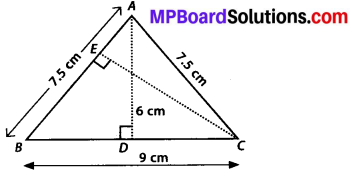
Solution:

MP Board Class 7th Maths Solutions

MP Board Class 7th Maths Solutions Chapter 8 Comparing Quantities Ex 8.2

Question 1.
Convert the given fractional numbers to percents.

Solution:

Question 2.
Convert the given decimal fractions to percents.
(a) 0.65
(b) 2.1
(c) 0.02
(d) 12.35
Solution:

Question 3.
Estimate what part of the figures is coloured and hence find the percent which is coloured.

Solution:
(i) Here, 1 part out of 4 equals parts is shaded which represents the fraction \(\frac{1}{4}\).

(ii) Here, 3 parts out of 5 equal parts are shaded which represents the fraction \(\frac{3}{5}\).

(iii) Here 3 parts out of 8 equal parts are shaded which represents the fraction \(\frac{3}{8}\).

Question 4.
Find:
(a) 15% of 250
(b) 1% of 1 hour
(c) 20% of ₹ 2500
(d) 75% of 1 kg
Solution:

Question 5.
Find the whole quantity if
(a) 5% of it is 600
(b) 12% of it is? 1080
(c) 40% of it is 500 km
(d) 70% of it is 14 minutes
(e) 8% of it is 40 litres
Solution:
Let the whole quantity be x.

Question 6.
Convert given percents to decimal fractions and also to fractions in simplest forms:
(a) 25%
(b) 150%
(c) 20%
(d) 5%
Solution:

Question 7.
In a city, 30% are females, 40% are males and remaining are children. What percent are children?
Solution:
It is given that 30% are females and 40% are males.
Children = 100% – (40% + 30%)
= 100% – 70% = 30%

Question 8.
Out of 15,000 voters in a constituency, 60% voted. Find the percentage of voters who did not vote. Can you now find how many actually did not vote?
Solution:
Percentage of voters who voted = 60%
Percentage of those who did not vote = 100% – 60%
= 40%
Number of people who did not vote = 40% of 15000
= 40% × 15000

Therefore, 6000 people did not vote.

Question 9.
Meeta saves ₹ 400 from her salary. If this is 10% of her salary. What is her salary?
Solution:
Let Meeta’s salary be ₹ x.
Given that, 10% of x = 400

Therefore, Meeta’s salary is ₹ 4000.

Question 10.
A local cricket team played 20 matches in one season. It won 25% of them. How many matches did they win?
Solution:
Number of games won = 25% of 20
\(=\frac{25}{100} \times 20=5\)
Therefore, the team won 5 matches.

MP Board Class 7th Maths Solutions

MP Board Class 7th Maths Solutions Chapter 11 Perimeter and Area Ex 11.1

Question 1.
The length and the breadth of a rectangular piece of land are 500 m and 300 m respectively. Find
(i) its area
(ii) the cost of the land, if 1 m² of the land costs ₹ 10,000.
Solution:
Length (l) = 500 m
Breadth (b) = 300 m
(i) Area = Length × Breadth = 500 × 300 = 150000 m²
(ii) Cost of 1 m² land = ₹ 10000
∴ Cost of 150000 m² land
= 150000 × 10000 = ₹ 1500000000

Question 2.
Find the area of a square park whose perimeter is 320 m.
Solution:
Perimeter of the square park = 320 m
∴ 4 × Length of the side of park = 320
Length of the side of park = \(\frac{320}{4}\) = 80 m
Area = (Length of the side of park)²
= (80)² = 6400 m²

Question 3.
Find the breadth of a rectangular plot of land, if its area is 440 m² and the length is 22 m. Also find its perimeter.
Solution:
Area of a rectangular plot = 440 m²
Length = 22 m
Area = Length x Breadth = 440 m²
∴ 22 × Breadth = 440
⇒ Breadth = \(\frac{440}{22}\) = 20 m
∴ Perimeter = 2 (Length + Breadth)
= 2 (22 + 20) = 2(42) = 84 m

Question 4.
The perimeter of a rectangular sheet is 100 cm. If the length is 35 cm, find its breadth. Also find the area.
Solution:
Length = 35 cm
Perimeter = 100 cm
∴ 2 (35 + Breadth) = 100
⇒ 35 + Breadth = 50
⇒ Breadth = 50 – 35 = 15 cm
∴ Area = Length × Breadth
= 35 × 15 = 525 cm²

Question 5.
The area of a square park is the same as of a rectangular park. If the side of the square park is 60 m and the length of the rectangular park is 90 m, find the breadth of the rectangular park.
Solution:
Side of the square park = 60 m
Length of the rectangular park = 90 m
Area of the square park = (side)² = (60)² = 3600 m²
Area of rectangular park = Length × Breadth
= 90 × Breadth
It is given that area of square park = area of rectangular park
∴ 3600 = 90 × Breadth
⇒ Breadth = 40 m

Question 6.
A wire is in the shape of a rectangle. Its length is 40 cm and breadth is 22 cm. If the same wire is rebent in the shape of a square, what will be the measure of each side. Also find which shape encloses more area?
Solution:
Length of rectangle = 40 cm
Breadth of rectangle = 22 cm
Perimeter of rectangle = Perimeter of square
∴ 2 (Length + Breadth) = 4 × Side of square
⇒ 2 (40 + 22) = 4 × Side of square
⇒ 2 × 62 = 4 × Side of square
∴ Side of square = \(\frac{124}{4}\) = 31 cm
Now, area of rectangle = 40 × 22 = 880 cm²
Area of square = (Side)² = 31 × 31 = 961 cm²
As 961 > 880.
Therefore, the square-shaped wire encloses more area than rectangle – shaped wire.

Question 7.
The perimeter of a rectangle is 130 cm. If the breadth of the rectangle is 30 cm, find its length. Also find the area of the rectangle.
Solution:
Breadth = 30 cm
Perimeter = 130 cm
∴ 2 (Length + 30) = 130
⇒ Length + 30 = 65
⇒ Length = 65 – 30 = 35 cm
Now, area = Length × Breadth
= 35 × 30 = 1050 cm²

Question 8.
A door of length 2 m and breadth 1 m is fitted in a wall. The length of the wall is 4.5 m and the breadth is 3.6 m (see the given figure). Find the cost of white washing the wall, if the rate of white washing the wall is ₹ 20 per m².

Solution:
Length of wall = 4.5 m
Breadth of wall = 3.6 m
Area of wall = Length × Breadth
= 4.5 × 3.6
= 16.2 m²
Area of door = 2 × 1 = 2 m²
Area to be white-washed
= Area of wall – Area of door
= 16.2 – 2 = 14.2 m²
Cost of white-washing 1 m² area = ₹ 20 2.
∴ Cost of white-washing 14.2 m² area
= 14.2 × 20 = ₹ 284

MP Board Class 7th Maths Solutions

MP Board Class 7th Maths Solutions Chapter 12 Algebraic Expressions Ex 12.4

Question 1.
Observe the patterns of digits made from line segments of equal length. You will find such segmented digits on the display of electronic
watches or calculators,

If the number of digits formed is taken to be n, the number of segments required to form n digits is given by the algebraic expression appearing on the right of each pattern. How many segments are required to form 5, 10, 100 digits of the kind

Solution:
(a) It is given that the number of segments required to form n digits of the kind
is (5n + 1).
Number of segments required to form 5 digits = (5 × 5 + 1) = 25 + 1 = 26
Number of segments required to form 10 digits = (5 × 10 + 1) = 50 + 1 = 51
Number of segments required to form 100 digits = (5 × 100 + 1) = 500 + 1 = 501

(b) It is given that the number of segments required to form n digits of the kind
[ is (3n +1).
Number of segments required to form 5 digits = (3 × 5 + 1) = 15 + 1 = 16
Number of segments required to form 10 digits = (3 × 10 + 1) = 30 + 1 = 31
Number of segments required to form 100 digits = (3 × 100 + 1) = 300 + 1 = 301

(c) It is given that the number of segments required to form n digits of the kind
is (5n + 2).
Number of segments required to form 5 digits = (5 × 5 + 2) = 25 + 2 = 27
Number of segments required to form 10 digits = (5 × 10 + 2) = 50 + 2 = 52
Number of segments required to form 100 digits = (5 × 100 + 2) = 500 + 2 = 502

Question 2.
Use the given algebraic expression to complete the table of number patterns.

Solution:
(i) Number pattern for expression 2n – 1
Put n = 1, 2, 3,…. and so on, we get

(ii) For expression 3 n + 2, 5^th, 10^th term and 100th term of the pattern are 3 × 5 + 2 = 17, 3 × 10 + 2 = 32 and 3 × 100 + 2 = 302 respectively.
(iii) For expression 4n +1, 5^th, 10^th and 100^th term of the pattern are 4 × 5 +1 = 21, 4 × 10 + 1 = 41 and 4 × 100 + 1 = 401 respectively.
(iv) For expression 7n + 20, 5^th, 10^th and 100^th term of the pattern are 7 × 5 + 1 = 36, 7 × 10 + 20 = 90 and 7 × 100 + 20 = 720 respectively.
(v) For expression n² + 1, 5^th and 10th term of the pattern are 5² + 1 = 26 and 10² + 1 = 101 respectively.

MP Board Class 7th Maths Solutions

MP Board Class 7th Maths Solutions Chapter 8 Comparing Quantities Ex 8.1

Question 1.
Find the ratio of:
(a) ₹ 5 to 50paise
(b) 15 kg to 210 g
(c) 9 m to 27 cm
(d) 30 days to 36 hours
Solution:
(a) ₹ 5 to 50 paise
1 rupee = 100 paise
∴ 5 rupee = 500 paise
Hence, the required ratio is

(b) 15 kg to 210 g
1kg = 1000g
15 kg = 15000 g
Hence, the required ratio is

(c) 9 m to 27 cm
1m = 100 cm
9 m = 900 cm
Hence, the required ratio is

(d) 30 days to 36 hours
1 day = 24 hours
30 days = 24 × 30 = 720 hrs
Hence, the required ratio is

Question 2.
In a computer lab, there are 3 computers for every 6 students. How many computers will
be needed for 24 students?
Solution:
For 6 students, number of computers required = 3
For 1 student, number of computers required = \(\frac{3}{6}\)
For 24 students, number of computers required = \(24 \times \frac{3}{6}=12\)
Hence, 12 computers are required for 24 students.

Question 3.
Population of Rajasthan = 570 lakhs and population of UP = 1660 lakhs.
Area of Rajasthan = 3 lakhs km² and Area of UP = 2 lakhs km²
(i) How many people are there per km² in both these states ?
(ii) Which states is less populated?
Solution:
(i) Population of Rajasthan in 3 lakhs km²
area = 570 lakhs
Population of rajasthan in 1 km² area
\(=\frac{570}{3}=190\) lakhs
Population of U.P. in 2 km² = 1660 lakhs
Population of U.P. in 1 km² = \(\frac{1660}{2}\)
= 830 lakhs

(ii) It can be observed that population per km² area is lesser for Rajasthan. Therefore, Rajasthan is less populated.

MP Board Class 7th Maths Solutions

MP Board Class 7th Maths Solutions Chapter 12 Algebraic Expressions Ex 12.3

Question 1.
If m = 2, find the value of:
(i) m – 2
(ii) 3m – 5
(iii) 9 – 5m
(iv) 3m² – 2m – 7
(v) \(\frac{5 m}{2}\) – 4
Solution:
(i) m – 2 = 2 – 2 = 0
(ii) 3m – 5 = (3 × 2) – 5 = 6 – 5 = 1
(iii) 9 – 5m = 9 – (5 × 2) = 9 – 10 = -1
(iv) 3m² – 2m – 7 = 3 × (2 × 2) – (2 × 2) – 7
= 12 – 4 – 7 = 1
(v) \(\frac{5 m}{2}\) – 4 = \(\left(\frac{5 \times 2}{2}\right)\) – 4 = 5 – 4 = 1

Question 2.
If p = -2, find the value of:
(i) 4p + 7
(ii) -3p² + 4p + 7
(iii) -2p³ – 3p² + 4p + 7
Solution:
(i) 4p + 7 = 4 × (-2) + 7 = -8 + 7 = -1
(ii) -3p² + 4p + 7 = -3 × (-2) × (-2) + 4 × (-2) + 7 = -12 – 8 + 7 = -13
(iii) -2p³ – 3p² + 4p + 7
= -2 × (-2) × (-2) × (-2) – 3 × (-2) × (-2) + 4 × (-2) + 7
= 16 – 12 – 8 + 7 = 3

Question 3.
Find the value of the following expressions, when x = -1:
(i) 2x – 7
(ii) -x + 2
(iii) x² + 2x + 1
(iv) 2x² – x – 2
Solution:
(i) 2x – 7 = 2 × (-1) – 7 = -2 – 7 = -9
(ii) – x + 2 = – (-1) + 2 = 1 + 2 = 3
(iii) x² + 2x + 1 = (-1) × (-1) + 2 × (-1) + 1 = 1 – 2 + 1 = 0
(iv) 2x² – x – 2 = 2 × (-1) × (-1) – (-1) – 2 = 2 + 1 – 2 = 1

Question 4.
If a = 2, b = -2, find the value of:
(i) a² + b²
(ii) a² + ab + b²
(iii) a² – b²
Solution:
(i) a² + b² = 2 × 2 + (-2) × (-2) = 4 + 4 = 8
(ii) a² + ab + b² = (2 × 2) + 2 × (-2) + (-2) × (-2) = 4 – 4 + 4 = 4
(iii) a² – b² = 2 × 2 – (-2) × (-2) = 4 – 4 = 0

Question 5.
When a = 0, b = -1, find the value of the given expressions:
(i) 2a + 2b
(ii) 2a² + b² + 1
(iii) 2a²b + 2ab² + ab
(iv) a² + ab + 2
Solution:
(i) 2a + 2b = 2 × (0) + 2 × (-1) = 0 – 2 = – 2
(ii) 2a² + b² + 1 = 2 × (0) × (0) + (-1) × (-1) + 1 = 0 + 1 + 1 = 2
(iii) 2a²b + 2ab² + ab = 2 × (0) × (0) × (-1) + 2 × (0) × (-1) × (-1) + 0 × (-1)
= 0 + 0 + 0 = 0
(iv) a² + ab + 2 = (0) × (0) + 0 × (-1) + 2
= 0 + 0 + 2 = 2

Question 6.
Simplify the expressions and find the value, if x is equal to 2.
(i) x + 7 + 4 (x – 5)
(ii) 3(x + 2) + 5x – 7
(iii) 6x + 5(x – 2)
(iv) 4(2x – 1) + 3x+ 11
Solution:
(i) x + 7 + 4(x – 5) = x + 7 + 4x – 20
= (1 + 4)x + (7 – 20) = 5x – 13
Putting x = 2 we get,
5x – 13 = (5 × 2) – 13 = 10 – 13 = -3

(ii) 3 (x + 2) + 5x – 7 = 3x + 6 + 5x – 7
= (3 + 5)x + (6 – 7) = 8x – 1
Putting x = 2 we get,
8x – 1 = (8 × 2) – 1 = 16 – 1 = 15

(iii) 6x + 5(x – 2) = 6x + 5x – 10
= (6 + 5)x – 10 = (11x – 10)
Putting x = 2 we get,
11x – 10 = (11 × 2) – 10 = 22 – 10 = 12

(iv) 4(2x – 1) + 3x + 11 = 8x – 4 + 3x + 11
= (8 + 3) × + (11 – 4) = 11x + 7
Putting x = 2 we get,
11x + 7= (11 × 2) + 7 = 22 + 7 = 29

Question 7.
Simplify these expressions and find their values if x = 3, a = -1, b = -2.
(i) 3x – 5 – x + 9
(ii) 2 – 8x + 4x + 4
(iii) 3a + 5 – 8o + 1
(iv) 10 – 3b – 4 – 5b
(v) 2a – 2b – 4 – 5 + a
Solution:
(i) 3x – 5 – x + 9 = (3 – 1) x + (-5 + 9)
= 2x + 4 = (2 × 3) + 4 [∵ x = 3]
= 6 + 4 = 10

(ii) 2 – 8x + 4x + 4 = 2 + 4 + (- 8 + 4)x
= 6 – 4x = 6 – (4 × 3) = 6 – 12 = -6 [∵ x = 3]

(iii) 3a + 5 – 8a +1 = (3 – 8)a + (5 + 1)
= -5a + 6
= -5 × (-1) + 6     [∵ a = -1]
= 5 + 6 = 11

(iv) 10 – 3b – 4 – 5b = 10 – 4 + (- 3 – 5)b
= 6 – 8b = 6 – 8 × (-2) [∵ b = -2]
= 6 + 16 = 22

(v) 2a – 2b – 4 – 5 + a = (2 + 1)a – 2b – 4 – 5
= 3a – 2b – 9
= 3 × (-1) – 2 × (-2) – 9 [∵ a = -1, b = -2]
= -3 + 4 – 9 = -8

Question 8.
(i) If z = 10, find the value of z³ – 3(z – 10).
(ii) If p = -10, find the value of p² – 2p -100.
Solution:
(i) For z = 10,
z³ – 3z + 30
= (10 × 10 × 10) – (3 × 10) + 30
= 1000 – 30 + 30 = 1000

(ii) For p = -10,
p² – 2p – 100
=(-10) × (-10) – 2 × (-10) – 100
= 100 + 20 – 100 = 20

Question 9.
What should be the value of a if the value of 2x² + x – a equals to 5, when x = 0?
Solution:
When x = 0; 2x² + x – a = 5,
∴ (2 × 0) + 0 – a = 5
⇒ 0 – a = 5
⇒ a = -5

Question 10.
Simplify the expression and find its value when a = 5 and b = -3.
2(a² + ab) + 3 – ab
Solution:
2(a² + ab) + 3 – ab = 2a² + 2ab + 3 – ab
= 2a² + (2 – 1) ab + 3 = 2a² + ab + 3
= 2 × (5 × 5) + 5 × (-3) + 3       [ ∵ a = 5, b = – 3]
= 50 – 15 + 3 = 38

MP Board Class 7th Maths Solutions

MP Board Class 7th Maths Solutions Chapter 7 Congruence of Triangles Ex 7.2

Question 1.
Which congruence criterion do you use in the following?
(a) Given: AC = DF
AB = DE
BC = EF
So, ∆ABC ≅ ∆DEF

(b) Given: ZX = RP
RQ = ZY
∠PRQ = ∠XZY
So, ∆PQR ≅ ∆XYZ

(c) Given: ∠MLN = ∠FGH
∠NML = ∠HFG
ML = FG
So, ∆LMN ≅ ∆GFH

(d) Given EB = BD

AE = CB
∠A = ∠C = 90°
So, ∆ABE ≅ ∆CDB
Solution:
(a) SSS, as all three sides of AABC are equal to the corresponding sides of ∆DEF.
(b) SAS, as two sides and the angle included between these sides of ∆PQR are equal to the corresponding sides and included angle of ∆XYZ.
(c) ASA, as two angles and the side included between these angles of ∆LMN are equal to the corresponding angles and included side of ∆GFH.
(d) RHS, as in the given two right-angled triangles, one side and the hypotenuse are respectively equal.

Question 2.
You want to show that ∆ART ≅ ∆PEN,
(a) If you have to use SSS criterion, then you need to show
(i) AR =
(ii) RT =
(iii) AT =
(b) If it is given that ∠T = ∠N and you are to use SAS criterion, you need to have
(i) RT = and
(ii) PN =
(c) If it is given that AT = PN and you are to use ASA criterion, you need to have

Solution:
(a) (i) AR = PE
(ii) RT = EN
(iii) AT = PN

(b) (i) RT = EN
(ii) PN = AT

(c) (i) ∠ATR = ∠PNE
(ii) ∠RAT = ∠EPN

Question 3.
You have to show that ∆AMP ≅ ∆AMQ
In the following proof, supply the missing reasons.

Solution:
(i) Given
(ii) Given
(iii) Common
(iv) SAS congruence criterion, as the two sides and the angle included between these sides of ∆AMP are equal to corresponding sides and included angle of ∆AMQ.

Question 4.
In ∆ABC, ∠A = 30°, ∠B = 40° and ∠C = 110°
In ∆PQR, ∠P = 30°, ∠Q = 40° and ∠R = 110°
A student says that ∆ABC ≅ ∆PQR by AAA congruence criterion. Is he justified? Why or why not?
Solution:
No. This property represents that these triangles have their respective angles of equal measure. However, this does not give any information about their sides. The sides of these triangles may have a ratio different from 1 : 1. Therefore, AAA property does not prove that two triangles are congruent.

Question 5.
In the figure, the two triangles are congruent. The corresponding parts are marked. We can write ∆RAT ≅ ?

Solution:
It can be observed that,
∠RAT = ∠WON
∠ART = ∠OWN
AR = OW
Therefore, ∆RAT ≅ ∆WON, by ASA criterion.

Question 6.
Complete the congruence statement:

Solution:
In ∆BCA and ∆BTA,
BC = BT (given)
TA = CA (given)
BA is common.
Therefore, ∆BCA ≅ ∆BTA
(by SSS congruence criterion)
Now, in AQRS and ATPQ,
∠RQS = ∠PTQ (given)
RQ = PT (given)
∠SRQ = ∠QPT (given)
Therefore, ∆QRS = ∆TPQ
(by ASA congruence criterion)

Question 7.
In a squared sheet, draw two triangles of equal areas such that
(i) the triangles are congruent.
(ii) the triangles are not congruent. What can you say about their perimeters?
Solution:

Here, ∆ABC and ∆PQR have the same area and are congruent to each other also. Also the perimeter of both the triangles will be the same.

Here, ∆ABC and ∆PQR have the same height and same base. Thus, their areas are equal. However, these triangles are not congruent to each other. Also, the perimeter of both the triangles will not be the same.

Question 8.
Draw a rough sketch of two triangles such that they have five pairs of congruent parts but still the triangles are not congruent.

Solution:
∆ABC & ∆DEF are not congruent to each other but have five congruent parts i.e., ∠BAC = ∠EFD, ∠ABC = ∠DEF, ∠BCA = ∠EDF, AB = DF and BC = EF

Question 9.
If ∆ABC and ∆PQR are to be congruent, name one additional pair of corresponding parts. What criterion did you use?

Solution:
∠ABC = ∠PQR = 90° and
∠BCA = ∠QRP (Given)
For triangles to be congruent, BC = QR
∆ABC ≅ ∆PQR (ASA congruence criterion)

Question 10.
Explain, why ∆ABC ≅ ∆FED

Solution:
Given that, ∠ABC = ∠FED = 90° and ∠BAC = ∠EFD
The two angles of ∆ABC are equal to the two respective angles of ∆FED. Also, the sum of all interior angles of a triangle is 180°. Therefore, third angle of both triangles will also be equal in measure.
∴ ∠BCA = ∠EDF
Now, in ∆ABC and ∆FED,
∠ABC = ∠FED, BC = ED and ∠BCA = ∠EDF
⇒ ∆ABC = ∆FED
(ASA congruence criterion)

MP Board Class 7th Maths Solutions

MP Board Class 7th Social Science Solutions Miscellaneous Questions 2

Choose the correct answer

Question 1.
The founder of the slave dynasty was:
(a) Mohammed Ghori
(b) Ill-tutmish
(c) Qutub-ud-din Aibak
(d) Alauddin Khilji
Answer:
(c) Qutub-ud-din Aibak

Question 2.
The Chariman of the National Human Rights Commission is appointed by:
(a) Prime Minister
(b) President
(c) Governor
(d) Chief Minister
Answer:
(b) President

Question 3.
The first battle of Panipat was fought in:
(a) 1526 AD
(b) 1556 AD
(c) 1529 AD
(d) 1527 AD
Answer:
(a) 1526 AD

Question 4.
The percentage of land area on earth is:
(a) 71%
(b) 72%
(c) 28%
(d) 29%
Answer:
(d) 29%

Question 5.
Spring tide occurs on:
(a) Fifth day
(b) full moon day
(c) 8th day
(d) 4th day
Answer:
(b) full moon day

Fill in the blanks:

1. The founder of the Khilji dynasty was ………….
2. Guru Nanak was bom in ………….. village.
3. The tenure of the Vice President is …………….. year.
4. ………….. is used to measure rainfall.
5. There are …………….number of seasons in India.

Answer:

1. Alauddin Khilji
2. Talwandi
3. Five years
4. Rain grange
5. three.

Match column ‘A’with column ‘B’

Answer:
1. (b) Issue of copper coins
2. (c) Riddles-mukris
3. (a) Iqta system
4. (e) Witty, advisor
5. (d) Waves

Answer the following questions in detail:

Question 1.
What are effects of ocean currents on human life?
Answer:
Ocean currents are streams of water flowing constantly in a definite direction at or near the surface of the ocean.
Ocean currents are caused by prevailing or planetary winds. They are also caused by die variation of temperature. The variation of saline water in the sea water causes ocean currents.

The ocean currents influence the climate of the regions such as coastal areas or islands. The warm currents raise the temperature whereas the cold currents reduce the temperature. Due to warm currents the harbors at higher latitudes remain, open through out the jar i. e. The harbors of Norway and Japan. The warm winds blowing over warm currents absorbs a lot of moisture and the nearby areas receive lots of rainfall.

Question 2.
Describe the administrative set up of Shershah.
Answer:
Shershah was an efficient administrator. The interest of the people ranked above everything. He started many reforms in military administration, land revenue etc that was followed by Akbar. Shershah divided his empire into Sarkars, which were again subdivided into parganas.

Officer in charge of sarkars and panganas were periodically transferred. He enforced equal law for justice and introduced a reformed system of currency. The silver coin known as the Rupee which lasted throughout the Mughal period and was maintained by the East India company down to 1835 AD.

Question 3.
Explain the process of the formation of Vidhan Sablia.
Answer:
The representatives of the Vidhan Sabha are elected in such a way that the seats are proportionately represented. If a person is elected from more than one constituency then he will have to resign from the rest retaining only one seat If there is a controversy about the election of any candidate, then a petition can be filed in the High court. After accepting the petition, the High Court gives its verdict It can also be against the candidate.

A person can appeal to the Supreme Court if the Verdict goes against him. The verdict of the Supreme Court is final.
The term of Vidhan Sabha is 5 years. In a case of emergency, it can be dissolved, Vidhan Sabha has a speaker and a Deputy Speaker. The Speaker conducts the business of the state Vidhan Sabha. The Deputy Speaker discharges duties in the absence of the Speaker.

Question 4.
What are the advantages of Ocean?
Answer:

• Rain on land – All the rain on land are due to the evaporation of sea water. Rains are useful for vegetation, animal life and human beings.
• Balance of temperature – Ocean shelp to maintain balance of temperature on land.
• Means of transport – The international trade is possible because of the oceans and seas, which joins the continents.

Question 5.
Write the main features of the architecture of the Sultanate period.
Answer:

• The caste rules were strictly followed. The women did not enjoy much freedom and the purdah system became very common.
• The practice of child marriage, polygamy and sati stystem was prevalent in the society.

MP Board Class 7th Social Science Solutions Miscellaneous Questions 2 Short Answer Type Questions

Question 1.
Explain the market control policy of Alauddin Khilji.
Answer:
Alauddin controlled prices in the market Those traders who did not sell goods at fixed prices or who weighed something less, were given severe punishment.

Question 2.
Write the advantages of tides.
Answer:

• The tides help in fishing.
• They increase the depth of the shallow harbors. This helps in bringing ships into the harbors.
• They increase the depth of estuaries.
• They keep rivers deep enough so to help ships placed in the rivers.

Question 3.
What is meant by ordinance?
Answer:
Ordinance is the order of the Chief Executive issued at a time when the Legislature is not in session. As soon as the legislature is convened, the ordinance is approved by it. If the legislature does not approve them, they are withdrawn.

Question 4.
Write about the progress made in the field of architecture during the reign of Shahjahan.
Answer:
Under Shahjahan Mughal architecture reached die climax. He built magnificent buildings, forts, mosques, tombs in Agra, Lahore, Delhi, Kabul, Kandhar, Ajmer, Ahamdabad etc. He built Moti-Masjid, Diwan-e-Aam, Diwan-e-Khas in the Fort at Agra. The most famous building of his time is the Tajmahal. It is made of white marble. It is regarded as jewel in the builder’s art.

Question 5.
Write a short note on cyclonic rains.
Answer:
When the hot and cold air meet, die hot air rises upwards and the cold air rushes to occupy the low-pressure area in the center. As a result there is circular movement which causes the whirling air in the center to rise upwards. This rising air cools down, condenses and brings rains. This type of rainfall is called cyclonic rain.

Question 6.
Explain the main features of Akbar’s Mansabdari system.
Answer:
‘Mansabdari System’ was a special feature of the Mughal rule. By ‘Mansab’ is meant a post or title. Each ‘Mansabdar’ was recognised as big or small as per the number of soldiers under him. It ranged between 10,000 to 50,000 soliders and the emperor could use their armies as per his wishes.

Question 7.
What was the effect of Bhakti movement on the life of the people?
Answer:
Bhakti movement had a great effect on the Indian society. The leaders of this movement used die local language which put great impact on the minds of die common people. This movement helped in arousing consciousness among people. It removed the false notions and bad practices. It also tried to bring the society together by bridging the gap between Hindu and Muslim.

MP Board Class 7th Social Science Solutions

MP Board Class 7th Maths Solutions Chapter 12 Algebraic Expressions Ex 12.2

Question 1.
Simplify by combining like terms:
(i) 21b – 32 +7b – 20b
(ii) -z² + 13z² – 5z + 7z³ – 15z
(iii) p – (p – q) – q – (q – p)
(iv) 3a – 2b – ab – (a – b + ab) + 3ab + b – a
(v) 5x²y – 5x² + 3yx² – 3y² + x² – y² + 8xy² – 3y²
(vi) (3y² + 5y – 4) – (8y – y² – 4)
Solution:
(i) 21b – 32 + 7b – 20b
= 21b + 7b – 20b – 32
= (21 + 7 – 20)b – 32
= 8b – 32

(ii) -z² + 13z² – 5z + 7z³ – 15z
= 7z³ + (-1 + 13) z² + (-5 -15) z
= 7z³ + 12z² – 20z

(iii) p – (p – q) – q – (q – p)
= p – p + q – q – q + p
= p – q

(iv) 3a – 2b – ab – (a – b + ab) + 3ab + b – a
= 3a – 2b – ab – a + b – ab + 3 ab + b – a
= (3 – 1 – 1)a + (-2 + 1 + 1)b + (-1 – 1 + 3)ab
= a + ab

(v) 5x²y – 5x² + 3yx² – 3y² + x² – y² + 8xy² – 3y²
= (5 + 3) x²y + (-5 + 1) x² + (- 3 – 1 – 3 )y² + 8xy²
= 8x²y – 4x² – 7y² + 8xy²

(vi) (3y² + 5y – 4) – (8y – y² – 4)
= 3y² + 5y – 4 – 8y + y² + 4
= (3 + 1) y² + (5 – 8) y + 4 – 4
= 4y² – 3y

Question 2.
Add:
(i) 3mn, -5mn, 8mn, -4mn
(ii) t – 8tz, 3tz – z, z – 1
(iii) -7mn + 5, 12mn + 2, 9mn – 8, -2mn – 3
(iv) a + b – 3, b – a + 3, a – b + 3
(v) 14x + 10y – 12xy – 13, 18 – 7x – 10y + 8xy, 4xy
(vi) 5m – 7n, 3n – 4m + 2, 2m – 3mn – 5
(vii) 4x²y, -3xy², 5xy², 5x²y
(viii) 3 p²q² – 4pq + 5, -10p²q², 15 + 9pq + 7p²q²
(ix) ab – 4a, 4b – ab, 4a – 4b
(x) x² – y² – 1, y² – 1 – x², 1 – x² – y².
Solution:
(i) 3 mn + (-5 mn) + 8 mn + (-4 mn)
= (3 – 5 + 8 – 4 )mn = 2 mn

(ii) (t – 8tz) + (3tz – z) + (z – t)
= t – 8tz + 3tz – z + z – t
= (1 – 1)t + (- 8 + 3)tz + (-1 + 1)z
= -5 tz

(iii) (-7mn + 5) + (12mn + 2) + (9mn – 8) + (-2mn – 3)
=-7mn + 5 + 12mn + 2 + 9mn – 8 – 2mn – 3
= (-7 + 12 + 9 – 2)mn + (5 + 2 – 8 – 3)
= 12mn – 4

(iv) (a + b – 3) + (b – a + 3) + (a – b + 3)
= a + b – 3 + b – a + 3 + a – b + 3
= (1 -1 + 1)a + (1 + 1 – 1)b + (- 3 + 3 + 3)
= a + b + 3

(v) (14x + 10y – 12xy – 13) + (18 – 7x – 10y + 8xy) + 4xy
= 14x + 10y – 12xy – 13 + 18 – 7x – 10y + 8xy + 4xy
= (14 – 7)x + (10 – 10)y + (12 + 8 + 4 )xy + (-13 + 18)
= 7x + 5

(vi) (5m – 7n) + (3n – 4m + 2) + (2m – 3mn – 5)
= 5m – 7n + 3n – 4m + 2 + 2m – 3mn – 5
= (5 – 4 + 2)m + (- 7 + 3)n – 3mn + (2 – 5)
= 3m – 4n – 3mn – 3

(vii) (4x²y) + (-3xy²) + (-5xy²) + (5x²y)
= 4x²y – 3xy² – 5xy² + 5x²y
= (4 + 5) x²y + (-3 – 5) xy²
= 9x²y – 8xy²

(viii) (3p²q² – 4pq + 5) + (-10p²q²) + (15 + 9pq +7p²q²)
= 3p²q² – 4pq + 5 – 10p²q² + 15 + 9pq + 7p²q²
= (3 – 10 + 7) p²q² + (-4 + 9)pq + (5 + 15)
= 5pq + 20

(ix) (ab – 4a) +(4 b – ab) + (4a- 4b)
= ab – 4a + 4b – ab + 4a – 4b
= (1 – 1)ab + (-4 + 4 )a + (4 – 4)b = 0

(x) (x² – y² – 1) + (y² – 1 – x²) + (1 – x² – y²)
= x² – y² – 1 + y² – 1 – x² + 1 – x² – y²
= (1 – 1 – 1)x² + (-1 + 1 – 1)y² + (-1 – 1 + 1)
= -x² – y² – 1

Question 3.
Subtract:
(i) -5y² from y²
(ii) 6xy from -12xy
(iii) (a – b) from (a + b)
(iv) a(b – 5) from b (5 – a)
(v) – m2 + 5 mn from 4mi2 – 3mn + 8
(vi) -x² + 10x – 5 from 5x – 10
(vii) 5a² – 7ab + 5b² from 3ab – 2a² – 2b²
(viii) 4pq – 5q² – 3p² from 5p² + 3q² – pq
Solution:
(i) y² – (-5y²) = y² + 5y² = 6y²
(ii) -12xy – (6xy) = -12xy – 6xy = -18xy
(iii) (a + b) – (a – b) = a + b – a + b = 2b

(iv) b(5 – a) – a(b – 5)
= 5b – ab – ab + 5a
= 5a + 5b – 2ab

(v) (4m² – 3mn + 8) – (- m² + 5mn)
= 4m² – 3mn + 8 + m² – 5mn
= (4 + 1)m² + (- 3 – 5 )mn + 8
= 5m² – 8mn + 8

(vi) (5x – 10) – (-x² + 10x – 5)
= 5x – 10 + x² – 10x + 5
= x² + (5 – 10)x + (-10 + 5)
= x² – 5x – 5

(vii) (3ab – 2a² – 2b²) – (5a² – 7ab + 5b²)
= 3ab – 2a² – 2b² – 5a² + 7ab – 5b²
= (3 + 7)ab + (- 2 – 5)a² + (- 2 – 5 )b²
= 10ab – 7a² – 7b²

(viii) (5p² + 3q² – pq) – (4pq – 5a² – 3p²)
= 5p² + 3q² – pq – 4pq + 5q² + 3p²
= (5 + 3 )p² + (3 + 5 )q² + (-1 – 4 )pq
= 8p² + 8q² – 5pq

Question 4.
(a) What should be added to x² + xy + y² to obtain 2x² + 3xy?
(b) What should be subtracted from 2a + 8b + 10 to get – 3a + 7b + 16?
Solution:
(a) Let a be the required term.
∴ a + (x² + y² + xy) = 2x² + 3xy
⇒ a = 2x² + 3xy – (x² + y² + xy)
= 2x² + 3xy – x² – y² – xy
= (2 – 1) x² – y² + (3 – 1)xy
= x² – y² + 2xy

(b) Let p be the required term.
∴ (2a + 8b + 10) -p = -3a + 7b + 16
⇒ p = 2a + 8b + 10 – (- 3a + 7b + 16)
= 2a + 8b + 10 + 3a – 7b – 16
= (2 + 3)a + (8 – 7)b + (10 – 16)
= 5a + b – 6

Question 5.
What should be taken away from 3x² – 4y² + 5xy + 20 to obtain -x² – y² + 6xy + 20 ?
Solution:
Required term
= (3x² – 4y² + 5xy + 20) – (-x² – y² + 6xy + 20)
= 3x² – 4y² + 5xy + 20 + x² + y² – 6xy – 20
= (3 + 1)x² + (- 4 + 1) y² + (5 – 6)xy + (20 – 20)
= 4x² – 3y² – xy

Question 6.
(a) From the sum of 3x – y + 11 and -y – 11, subtract 3x – y – 11.
(b) From the sum of 4 + 3x and 5 – 4x + 2x², subtract the sum of 3x² – 5x and -x² + 2x + 5.
Solution:
(a) Sum of 3x – y + 11 and – y – 11
= (3x – y + 11) + (-y – 11)
= 3x – y + 11 – y – 11
= 3x + (- 1 – 1) y + (11 – 11)
= 3x – 2y
Now, required difference
= (3x – 2y) – (3x – y – 11)
= 3x – 2y – 3x + y + 11
= (3 – 3)x + (- 2 + 1) y + 11
= -y + 11

(b) Sum of 4 + 3x and 5 – 4x + 2x²
= (4 + 3x) + (5 – 4x + 2x²)
= 4 + 3x + 5 – 4x + 2x²
= (3 – 4)x + 2x² + 4 + 5
= – x + 2x² + 9
Now, sum of 3x² – 5x and -x² + 2x + 5
= (3x² – 5x) + (-x² + 2x + 5)
= 3x² – 5x – x² + 2x + 5
= (3 – 1) x² + (- 5 + 2)x + 5
= 2x² – 3x + 5
Required difference
= (- x + 2x² + 9) – (2x² – 3x + 5)
= -x + 2x² + 9 – 2x² + 3x – 5
= (-1 + 3)x + (2 – 2) x² + (9 – 5)
= 2x + 4

MP Board Class 7th Maths Solutions

MP Board Class 7th Maths Solutions Chapter 12 Algebraic Expressions Ex 12.1

Question 1.
Get the algebraic expressions in the following cases using variables, constants and arithmetic operations.
(i) Subtraction of z from y.
(ii) One-half of the sum of numbers x and y.
(iii) The number z multiplied by itself.
(iv) One-fourth of the product of numbers p and Q.
(v) Numbers x and y both squared and added.
(vi) Number 5 added to three times the product of numbers m and n.
(vii) Product of numbers y and z subtracted from 10.
(viii) Sum of numbers a and b subtracted from their product.
Solution:
(i) y – z
(ii) \(\frac{1}{2}\)(x + y)
(iii) z²
(iv) \(\frac{1}{4}\)(pq)
(v) x² + y²
(vi) 5 + 3 (mn)
(viii) ab – (a + b)

Question 2.
(i) Identify the terms and their factors in the following expressions. Show the terms and factors by tree diagrams.
(a) x – 3
(b) 1 + x + x²
(c) y – y³
(d) 5xy² + 7x²y
(e) -ab + 2b² – 3a²

(ii) Identify terms and factors in the expressions given below:
(a) -4x + 5
(b) -4x + 5y
(c) 5y + 3y²
(d) xy + 2x²y²
(e) pq + q
(f) 1.2ab – 2.4b + 3.6a
(g) \(\frac{3}{4}\)x + \(\frac{1}{4}\)
(h) 0.1p² + 0.2q²
Solution:
(i)

Question 3.
Identify the numerical coefficients of terms (other than constants) in the following expressions:
(i) 5 – 3t²
(ii) 1 + t + t² + t³
(iii) x + 2xy + 3y
(iv) 100m + 1000n
(v) -p²q² + 7pq
(vi) 1.2a + 0.8b
(vii) 3.14 r²
(viii) 2(l + b)
(ix) 0.1y + 0.01y²
Solution:

Question 4.
(a) Identify terms which contains x and give the coefficient of x.
(i) y²x + y
(ii) 13y² – 8yx
(iii) x + y + 2
(iv) 5 + z + zx
(v) 1 + x + xy
(vi) 12xy² + 25
(vii) 7x + xy²
(b) identify terms which contains y² and give the coefficient of y².
(i) 8 – xy²
(ii) 5y² + 7x
(iii) 2x²y – 15xy² + 7y²
Solution:
(a)

Question 5.
Classify into trinomials.
(i) 4y – 7z
(ii) y²
(iii) x + y – xy
(iv) 100
(v) ab – a – b
(vi) 5 – 3t
(vii) 4p²q – 4pq²
(viii) 7mn
(ix) z² – 3z + 8
(x) a² + b²
(xi) z² + z
(xii) 1 + x + x²
Solution:
The monomials, binomials and trinomials have 1, 2 and 3 unlike terms in it respectively.
(i) 4y – 7z Binomial
(ii) y² Monomial
(iii) x + y – xy Trinomial
(iv) 100 Monomial
(v) ab – a – b Trinomial
(vi) 5 – 3t Binomial
(vii) 4p²q – 4pq² Binomial
(viii) 7mn Monomial
(ix) z² – 3z + 8 Trinomial
(x) a² + b² Binomial
(xi) z² + z Binomial
(xii) 1 + x + x² Trinomial

Question 6.
State whether a given pair of terms is of like or unlike terms.
(i) 1,100
(ii) -7x, \(\frac{5}{2}\)x
(iii) -29x, -29y
(iv) 14xy, 42yx
(v) 4m²p, 4mp²
(vi) 12xz, 12x²z²
Solution:
The terms which have same algebraic factors are called like terms. However, when terms have different algebraic factors, these are called unlike terms.
(i) 1,100 Like
(ii) -7x, \(\frac{5}{2}\)x Like
(iii) -29x, -29y Unlike
(iv) 14xy, 42yx Like
(v) 4m²p, 4mp² Unlike
(vi) 12xz, 12x²z² Unlike

Question 7.
Identify like terms in the following:
(a) -xy², -4yx², 8x², 2xy², 7y, -11x², -100x, -11yx, 20x²y, -6x², y, 2xy, 3x
(b) 10pg, 7p, 8q, -p²q², -7qp, – 100q, -23, 12q²p², – 5p², 41, 2405p, 78qp, 13p²g, qp²,701p²
Solution:
(a) -xy² and 2xy²; -4yx² and 20x²y; 8x², -11x² and -6x²; 7y and y, -100x and 3x; -11yx and 2xy

(b) 10pq, -7qp and 78qp; 7p and 2405p; 8q and -100y; -p²q² and 12q²p², -23 and 41; -5p² and 701 p²; 13p2²q and qp²

MP Board Class 7th Maths Solutions