Prasanna

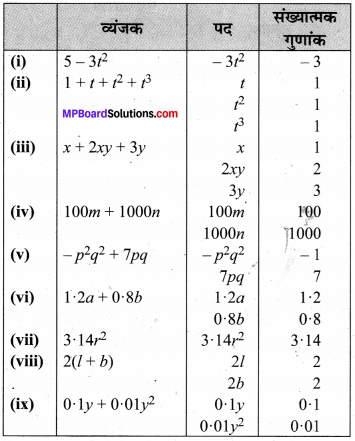
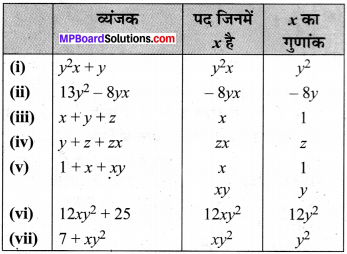
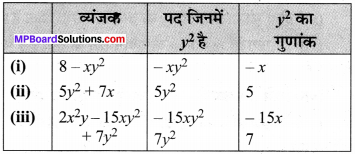
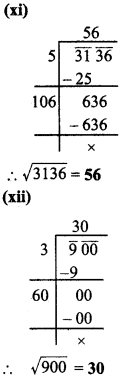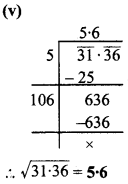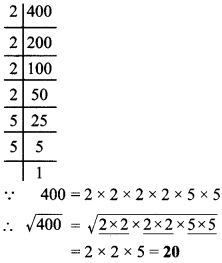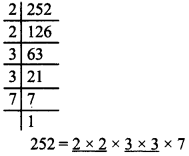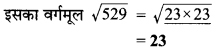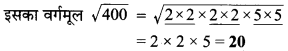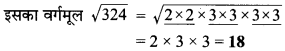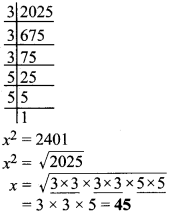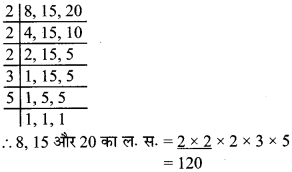MP Board Class 8th Maths Solutions Chapter 7 घन और घनमूल Intext Questions

MP Board Class 8th Maths Chapter 7 पाठान्तर्गत प्रश्नोत्तर

पाठ्य-पुस्तक पृष्ठ संख्या # 117

भूमिका हार्डी-रामानुजन संख्या

प्रश्न 1.
1729 सबसे छोटी हार्डी-रामानुजन संख्या है। इस प्रकार की अनेक संख्याएँ हैं : उनमें से कुछ हैं 4104 (2,16; 9,5), 13832 (18, 20; 2,024)। कोष्ठकों में दी हुई संख्याएँ लेकर इसकी जाँच कीजिए।
हल:
जाँच –

• 4104 = 4096 + 8 = 16³ + 2³ और
• 4104 = 3375 + 729 = 15³ + 9³
• 13832 = 5832 + 8000 = 18³ + 20³
• और 13832 = 13824 + 8 = 24³ + 2³

घन –

प्रश्न 1.
1 सेमी भुजा वाले कितने घनों से 2 सेमी भजा वाला एक घन बनेगा?
हल:
2 सेमी भुजा वाला एक घन बनाने के लिए 1 सेमी भुजा वाले 2 x 2 x 2 = 8 घनों की आवश्यकता होगी।

प्रश्न 2.
1 सेमी भुजा वाले कितने घनों से 3 सेमी भुजा वाला एक घन बनेगा?
हल:
3 सेमी भुजा वाला एक घन बनाने के लिए 1 सेमी भुजा वाले 3 x 3 x 3 = 27 घनों की आवश्यकता होगी।

पाठ्य-पुस्तक पृष्ठ संख्या # 118

प्रश्न 1.
क्या आप बता सकते हैं कि इनको ये नाम क्यों दिए गए हैं?
हल:
हाँ, बता सकते हैं। इनको ये नाम इसलिए दिए गए हैं क्योंकि इसमें एक संख्या को स्वयं उसी से तीन बार गुणा किया जाता है।

प्रश्न 2.
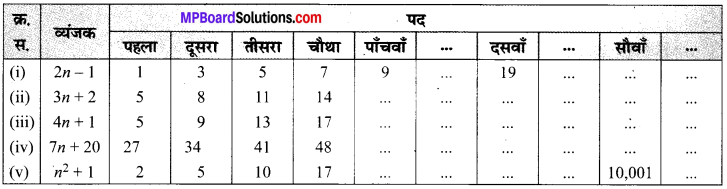
नीचे 1 से 10 तक की संख्याओं के घन दिए गए हैं:

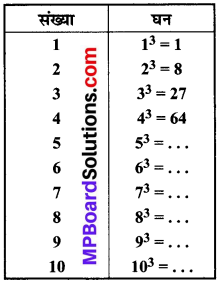
पूर्ण कीजिए।
हल:

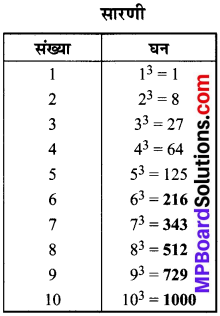
प्रश्न 3.
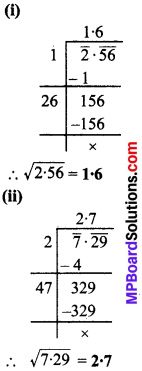
यहाँ 1 से 1000 तक दस पूर्ण घन हैं। (इसकी जाँच कीजिए), 1 से 100 तक कितने पूर्ण धन हैं?
हल:
जाँच –

• 1 = 1 x 1 x 1
• 8 = 2 x 2 x 2
• 27 = 3 x 3 x 3
• 64 = 4 x 4 x 4
• 125 = 5 x 5 x 5
• 216 = 6 x 6 x 6
• 343 = 7 x 7 x 7
• 512 = 8 x 8 x 8
• 729 = 9 x 9 x 9
• 1000 = 10 x 10 x 10.

यहाँ स्पष्ट है कि संख्या को उसी संख्या से 3 बार गुणा करने पर संख्याएँ 1, 8, 27, 64, 125, 216, 343, 512, 729 और 1000 प्राप्त होती है।
∴ 1, 8, 27, 64, 125, 216, 343, 512, 729 और 1000 पूर्ण घन संख्याएँ हैं।
यहाँ 1 से 100 तक 1, 8, 27 और 64, 4 पूर्ण घन हैं।

प्रश्न 4.
सम संख्याओं के घनों को देखिए। क्या ये सभी सम हैं? आप विषम संख्याओं के घनों के बारे में क्या कह सकते हैं?
हल:
हाँ, सम संख्याओं के सभी घन सम हैं। विषम संख्याओं के घन विषम हैं।

पाठ्य-पुस्तक पृष्ठ संख्या # 119

प्रश्न 1.
ऐसी कुछ संख्याओं पर विचार कीजिए जिनकी इकाई का अंक 1 है। इनमें से प्रत्येक संख्या का घन ज्ञात कीजिए। उस संख्या के घन के इकाई के अंक के बारे में आप क्या कह सकते हैं, जिसकी इकाई का अंक 1 है।?
इसी प्रकार, उन संख्याओं के घनों की इकाई के अंकों के बारे में पता कीजिए, जिनकी इकाई के अंक 2,3,4 इत्यादि हैं।
हल:
1, 11, 21, 31,41,… आदि कुछ ऐसी संख्याएँ हैं जिनके इकाई का अंक 1 है। इन संख्याओं के घन हैं –

• 1³ = 1
• 11³ = 1331
• 21³ = 9261
• 31³ = 29791
• 41³ = 68921

आदि यहाँ यह स्पष्ट है कि ऐसी संख्याएँ जिनके इकाई का अंक 1 है उन संख्याओं के घनों का इकाई अंक भी 1 है।
इन संख्याओं के घन जिनके इकाई अंक 2, 3, 4, …… आदि हैं –

• 2 → 23 = 8 12³ = 1728 – 22³ = 10648
• 3 → 33 = 27 13³ =2197 – 23³ = 12167
• 4 → 43 = 64 14³ = 2744 – 24³ = 13824
• 5 → 53 = 125 15³ = 3375 – 25³ = 15625
• 6 → 63 = 216 16³ =4096 – 26³ = 17576
• 7 → 73 = 343 17³ = 4913 – 27³ = 19683
• 8 → 83 = 512 18³ = 5832 – 28³ = 21952
• 9 → 93 = 729 19³ = 6859 – 29³ =24389
• 10 → 103 = 1000 20³ = 8000 – 30³ = 27000 .. इत्यादि।

यहाँ यह स्पष्ट है कि जिन संख्याओं के इकाई अंक 2, 3, 4, 5, 6, 7, 8, 9, 0 हैं उनके घनों के इकाई अंक क्रमशः 8, 7, 4, 5, 6, 3, 2, 9 और 0 हैं।

प्रयास कीजिए (क्रमांक 7.1)

प्रश्न 1.
निम्नलिखित संख्याओं में से प्रत्येक के घन के इकाई अंक ज्ञात कीजिए:

1. 3331
2. 8888
3. 149
4. 1005
5. 1024
6. 77
7. 5022
8. 53

हल:
संख्याओं के घन के इकाई अंक –

1. 3331 → 1³ = 1 x 1 x 1 = 1; इकाई अंक =1
2. 8888 → 8³ = 8 x 8 x 8 = 512; इकाई अंक = 2
3. 149 → 9³ = 9 x 9 x 9 = 729; इकाई अंक = 9
4. 1005 → 5³ = 5x5x5 = 125; इकाई अंक = 5
5. 1024 → 4³ = 4 x 4 x 4 = 64; इकाई अंक = 4
6. 77 → 7³ = 7 x 7 x 7 = 343; इकाई अंक = 3
7. 5022 → 2³ = 2 x 2 x 2 = 8; इकाई अंक = 8
8. 53 → 3³ = 3 x 3 x 3 = 27; इकाई अंक = 7

कुछ रोचक प्रतिरूप

क्रमागत विषम संख्याओं को जोड़ना

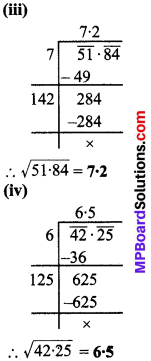
विषम संख्याओं के योगों के निम्नलिखित प्रतिरूप को देखिए –

• 1 = 1 = 1³
• 3 + 5 = 8 = 2³
• 7 + 9 + 11 = 27 = 3³
• 13 + 15 + 17 + 19 = 64 = 4³
• 21 + 23 + 25 + 27 + 29 = 125 = 5³

प्रश्न 1.
क्या यह रोचक नहीं है? योग 10³ प्राप्त करने के लिए कितनी क्रमागत विषम संख्याओं की आवश्यकता होगी?
हल:
हाँ, यह रोचक है। उपर्युक्त प्रतिरूप से स्पष्ट है कि योग 103 प्राप्त करने के लिए 10 क्रमागत विषम संख्याओं की आवश्यकता होगी।

प्रयास कीजिए (क्रमांक 7.2)

प्रश्न 1.
उपर्युक्त प्रतिरूप का प्रयोग करते हुए, निम्नलिखित संख्याओं को विषम संख्याओं के योग के रूप में व्यक्त कीजिए –

1. 6³
2. 8³
3. 7³

हल:

1. 6³ = 31 + 33 + 35 + 37 + 39 + 41 = 216
2. 8³ = 57 + 59 + 61 + 63 + 65 + 67 + 69 + 71 = 512
3. 7³ = 43 + 45 + 47 + 49 + 51 + 53 + 55 = 343

प्रश्न 2.
निम्नलिखित प्रतिरूप को देखिए:

• 2³ – 1³ = 1 + 2 x 1 x 3
• 3³ – 2³ = 1 + 3 x 2 x 3
• 4³ – 3³ = 1 + 4 x 3 x 3

उपर्युक्त प्रतिरूप का प्रयोग करते हुए, निम्नलिखित के मान ज्ञात कीजिए:

1. 7³ – 6³
2. 12³ – 11³
3. 20³ – 19³
4. 51³ – 50³

हल:
उपर्युक्त प्रतिरूप का प्रयोग करते हुए –

1. 7³ – 6³ = 1 + 7 x 6 x 3 = 1 + 126 = 127
2. 12³ – 11³ = 1 + 12 x 11 x 3 = 1 + 396 = 397
3. 20³ – 19³ = 1 + 20 x 19 x 3 = 1 + 1140 = 1141
4. 51³ – 50³ = 1 + 51 x 50 x 3 = 1 + 7650 = 7651

पाठ्य-पुस्तक पृष्ठ संख्या # 120

प्रश्न 1.
यदि किसी संख्या के अभाज्य गुणनखण्ड में प्रत्येक गुणनखण्ड तीन बार आता है, तो क्या वह संख्या एक पूर्ण घन होती है?
हल:
यदि किसी संख्या के अभाज्य गुणनखण्डन में प्रत्येक गुणनखण्ड तीन बार आता है, तो वह संख्या एक पूर्ण घन होती

प्रश्न 2.
क्या 729 पूर्ण घन है?
हल:
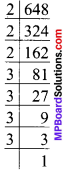
∴ 729 = 3 x 3 x 3 x 3 x 3 x 3
प्रश्न 3.
क्या आपको याद है कि a^m x b^m = (a x b)^m होता है?
हल:
हाँ, याद है कि a^m x b^m = (a x b)^m

प्रयास कीजिए (क्रमांक 7.3)

प्रश्न 1.
निम्नलिखित में से कौन-सी संख्याएँ पूर्ण घन हैं?

1. 400
2. 3375
3. 8000
4. 15625
5. 9000
6. 6859
7. 2025
8. 10648.

हल:
1.

संख्याओं के त्रिक बनाने पर 2 x 5 x 5 शेष रहता है।
अतः 400 पूर्ण घन नहीं है।

2.

यहाँ प्रत्येक गुणनखण्ड तीन बार आया है।
अत: 3375 एक पूर्ण घन है।

3.

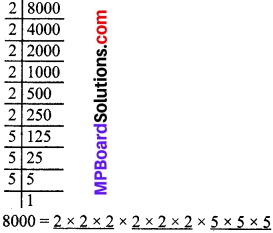
यहाँ प्रत्येक गुणनखण्ड तीन बार आया है।
अतः 8000 एक पूर्ण घन है।

4.

यहाँ प्रत्येक गुणनखण्ड तीन बार आया है।
अतः 15625 एक पूर्ण घन है।

5.

संख्याओं के त्रिक बनाने पर 3 x 3 शेष रहता है।
अत: 9000 पूर्ण घन नहीं है।

6.

यहाँ प्रत्येक गुणनखण्ड तीन बार आया है।
अत: 6859 एक पूर्ण घन है।

7.

संख्याओं के त्रिक बनाने पर 3 x 5 x 5 शेष रहता है।
अत: 2025 एक पूर्ण घन नहीं है।

8.

यहाँ प्रत्येक गुणनखण्ड तीन बार आया है।
अतः 10648 एक पूर्ण घन है।

पाठ्य-पुस्तक पृष्ठ संख्या # 121
सोचिए, चर्चा कीजिए और लिखिए (क्रमांक 7.1)

प्रश्न 1.
जाँच कीजिए कि निम्नलिखित में से कौन-सी संख्याएँ पूर्ण घन हैं –

1. 2700
2. 16000
3. 64000
4. 900
5. 125000
6. 36000
7. 21600
8. 10000
9. 27000000
10. 1000

इन पूर्ण घनों में आप क्या प्रतिरूप देखते हैं?
हल:
प्रत्येक संख्या के अभाज्य गुणनखण्ड करने पर,
1. 2700 = 2 x 2 x 3 x 3 x 3 x 5 x 5
संख्याओं के त्रिक बनाने पर 2 x 2 x 5 x 5 शेष रहता है।
अतः 2700 एक पूर्ण घन नहीं है।

2. 16000 = 2 x 2 x 2 x 2 x 2 x 2 x 2 x 5 x 5 x 5
संख्याओं के त्रिक बनाने पर 2 शेष रहता है।
अत: 16000 एक पूर्ण घन नहीं है।

3. 64000 = 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 x 5 x 5 x 5
यहाँ प्रत्येक गुणनखण्ड तीन बार आया है।
अतः 64000 एक पूर्ण घन है।

4. 900 = 2 x 2 x 3 x 3 x 5 x 5
यहाँ हम त्रिक बनाकर देखते हैं, तो किसी भी संख्या का त्रिक नहीं बनता है।
अत: 900 एक पूर्ण घन नहीं है।

5. 125000 = 2 x 2 x 2 x 5 x 5 x 5 x 5 x 5 x 5
यहाँ प्रत्येक गुणनखण्ड तीन बार आया है।
अत: 125000 एक पूर्ण घन है।

6. 36000 = 2 x 2 x 2 x 2 x 2 x 3 x 3 x 5 x 5 x 5
संख्याओं के त्रिक बनाने पर 2 x 2 x 3 x 3 शेष रहता है।
अतः 36000 एक पूर्ण घन नहीं है।

7. 21600 = 2 x 2 x 2 x 2 x 5 x 5 x 5 x 5
संख्याओं के त्रिक बनाने पर 2 x 5 शेष रहता है।
अत: 21600 एक पूर्ण घन नहीं है।

8. 10000 = 2 x 2 x 2 x 2 x 5 x 5 x 5 x 5
संख्याओं के त्रिक बनाने पर 2 x 5 शेष रहता है।
अतः 10000 एक पूर्ण घन नहीं है।

9. 27000000 = 2 x 2 x 2 x 2 x 2 x 2 x 3 x 3 x 3 x 5 x 5 x 5 x 5 x 5 x 5
यहाँ प्रत्येक संख्या तीन-तीन बार आयी है।
अत: 27000000 एक पूर्ण घन है।

10. 1000 = 2 x 2 x 2 x 5 x 5 x 5
यहाँ प्रत्येक संख्या तीन बार आई है।
अत: 1000 एक पूर्ण घन है।

MP Board Class 8th Maths Solutions

MP Board Class 7th Maths Solutions Chapter 13 घातांक और घात Ex 13.1

प्रश्न 1.
निम्नलिखित के मान ज्ञात कीजिए :
(i) 2⁶
(ii) 9³
(iii) 11²
(iv) 5⁴
हल:
(i) 2⁶ = 2 × 2 × 2 × 2 × 2 × 2 = 64
(iii) 9³ = 9 × 9 × 9 = 729
(iii) 11² = 11 × 11 = 121
(iv) 5⁴ = 5 × 5 × 5 × 5 = 625

प्रश्न 2.
निम्नलिखित को घातांकीय रूप में व्यक्त कीजिए:
(i) 6 × 6 × 6 × 6
(ii) t × t
(iii) b × b × b × b
(iv) 5 × 5 × 7 × 7 × 7
(v) 2 × 2 × a × a
(vi) a × a × a × c × c × c × c × d
हल:
(i) 6 × 6 × 6 × 6 = 6⁴
(ii) t × t = t²
(iii) b × b × b × b = b⁴
(iv) 5 × 5 × 7 × 7 × 7 = 5² × 7³
(v) 2 × 2 × a × a = 2² × a²
(vi) a × a × a × c × c × c × c × d = a³ × c⁴ × d

प्रश्न 3.
निम्नलिखित संख्याओं में से प्रत्येक को घातांकीय संकेतन में व्यक्त कीजिए :
(i) 512
(ii) 343
(iii) 729
(iv) 3125
हल:

प्रश्न 4.
निम्नलिखित में से प्रत्येक भाग में, जहाँ भी सम्भव हो, बड़ी संख्या को पहचानिए :
(i) 4³ या 3⁴
(ii) 5³ या 3⁵
(iii) 2⁸ या 8²
(iv) 100² या 2¹⁰⁰
(v) 2¹⁰ या 10²
हल:
(i) ∵ 4³ = 4 × 4 × 4 = 64
और 3⁴ = 3 × 3 × 3 × 3 = 81
∵ 81 > 64 ∴ 3⁴ > 4³
अतः 3⁴ बड़ा है।

(ii) ∵ 5³ = 5 × 5 × 5 = 125
और 3⁵ = 3 × 3 × 3 × 3 × 3 = 243
∵ 243 > 125 ∴ 3⁵ > 5³
अतः 3⁵ बड़ा है।

(iii) ∵ 2⁸ = 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2
= 256
और 8² = 8 × 8 = 64
∵ 256 > 64 ∴ 2⁸ > 8²
अतः 28 बड़ा है।

(iv) ∵ 100² = 100 × 100 = 10000
और 2¹⁰⁰ = (2¹⁰)¹⁰
= (2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2)¹⁰
= (1024)¹⁰ = (1024)^5×2
= (1024 × 1024)⁵
= (1048576)⁵
∵ 1048576 > 10000
∴ (1048576)⁵ > 100²
या (2¹⁰)¹⁰ > 100² या 2¹⁰⁰ > 100²
अत: (2¹⁰)¹⁰ बड़ा है।

(v) ∵ 2¹⁰ = 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2
= 1024
और 10² = 10 × 10 = 100
∵ 1024 > 100, ∴ 2¹⁰ > 10²
अतः 2¹⁰ बड़ा है।

प्रश्न 5.
निम्नलिखित में से प्रत्येक को उनके अभाज्य गुणनखण्डों की घातों के गुणनफल के रूप में व्यक्त कीजिए:
(i) 648
(ii) 405
(iii) 540
(iv) 3600
हल:
(i) 648

∴ 648 = 2 × 2 × 2 × 3 × 3 × 3 × 3
= 23 × 34

(ii)405

∴ 405 = 3 × 3 × 3 × 3 × 5
= 34 × 5

(iii) 540

∴ 540 = 2 × 2 × 3 × 3 × 3 × 5
= 22 × 33 × 5

(iv) 3600

∴ 3600 = 2 × 2 × 2 × 2 × 3 × 3 × 5 × 5
= 2⁴ × 3² × 5²

प्रश्न 6.
सरल कीजिए:
(i) 2 × 10³
(ii) 7² × 2²
(iii) 2³ × 5
(iv) 3 × 4⁴
(v) 0 × 10²
(vi) 5² × 3³
(vii) 2⁴ × 3²
(viii) 3² × 10⁴
हल:
(i) 2 × 10³ = 2 × 1000 = 2000
(ii) 7² × 2² = 49 × 4 = 196
(iii) 2³ × 5 = 8 × 5 = 40
(iv) 3 × 4⁴ = 3 × 256 = 768
(v) 0 × 10² = 0 × 100 = 0
(vi) 5² × 3³ = 25 × 27 = 675
(vii) 2⁴ × 3² = 16 × 9 = 144
(viii) 3² × 10⁴ = 9 × 10000 = 90000

प्रश्न 7.
सरल कीजिए:
(i) (-4)³
(ii) (-3) × (-2)³
(iii) (-3)² × (-5)²
(iv) (-2)³ × (-10)³
हल:
(i) (-4)³ = (-4) × (-4) × (-4)
= -64

(ii) (-3) × (-2)³ = (-3) (-2) (-2) (-2)
= (-3) × (-8) = 24

(iii) (-3)² × (-5)² = (-3) (-3) (-5) (-5)
= 9 × 25 = 225

(iv) (-2)³ × (-10)3 = (-2)(-2)(-2) (-10) (-10) (- 10)
= (-8) × (-1000) = 8000

प्रश्न 8.
निम्नलिखित संख्याओं की तुलना कीजिए :
(i) 2.7 × 10¹²; 1.5 × 10⁸
(ii) 4 × 10¹⁴;3 × 10¹⁷
हल:
(i) ∵ 2.7 × 10¹² = \(\frac { 27 }{ 10 } \) × 10¹²
= 27 × 10¹¹ में 13 अंक होंगे।
और 1.5 × 10⁸ = \(\frac { 27 }{ 10 } \) × 10⁸
= 15 × 10⁷ में 9 अंक होंगे।
स्पष्ट है कि 27 × 10¹¹ > 15 × 10⁷
⇒ 2.7 × 10¹² > 1.5 × 10⁸

(ii) ∵ 4 × 10¹⁴ में 15 अंक होंगे
और 3 × 10¹⁷ में 18 अंक होंगे।
∴ 4 × 10¹⁴ < 3 × 10¹⁷

पाठ्य-पुस्तक पृष्ठ संख्या # 270

प्रयास कीजिए

प्रश्न 1.
सरल करके घातांकीय रूप में लिखिए :
(i) 2⁵ × 2³
(ii) p³ × p²
(iii) 4³ × 4²
(iv) a³ × a² × a⁷
(v) 5³ × 5⁷ × 5¹²
(vi) (-4)¹⁰⁰ × (-4)²⁰
हल:
(i) 2⁵ × 2³ = 2⁵⁺³ = 2⁸
(ii) p³ × p² = p³⁺² = p⁵
(iii) 4³ × 4² = 4³⁺² = 4⁵
(iv) a³ × a² × a⁷ = a³⁺²⁺⁷ = a¹²
(v) 5³ × 5⁷ × 5¹² = 5³⁺⁷⁺¹² = 5²²
(vi) (-4)¹⁰⁰ × (-4)²⁰ = (-4)¹⁰⁰⁺²⁰ = (-4)¹²⁰

पाठ्य-पुस्तक पृष्ठ संख्या # 271

प्रयास कीजिए

प्रश्न 1.
सरल करके घातांकीय रूप में लिखिए : उदाहरण के लिए, 116 + 113 = 114
(i) 2⁹ ÷ 2³
(ii) 10⁸ ÷ 10⁴
(iii) 9¹¹ ÷ 9⁷
(iv) 20¹⁵ ÷ 20¹³
(v) 7¹³ ÷ 7¹⁰
हल:
(i) 2⁹ ÷ 2³ = 2^9-3 = 2⁶
(ii) 10⁸ ÷ 10⁴ = 10^8-4 = 10⁴
(iii) 9¹¹ ÷ 9⁷ = 9^11-7 = 9⁴
(iv) 20¹⁵ ÷ 20¹³ = 20^15-13 = 20²
(v) 7¹³ ÷ 7¹⁰ = 7^13-10 = 7³

प्रयास कीजिए

प्रश्न 1.
सरल करके, उत्तर को घातांकीय रूप में व्यक्त कीजिए:
(i) (6²)⁴
(ii) (2²)¹⁰⁰
(iii) (7⁵⁰)²
(iv) (5³)⁷
हल:
(i) (6²)⁴ = 6^2×4 = 68
(ii) (2²)¹⁰⁰ = 2^2×100 = 2²⁰⁰
(iii) (7⁵⁰)² = 7^50×2 = 7¹⁰⁰
(iv) (5³)⁷ = 5^3×7 = 5²¹

पाठ्य-पुस्तक पृष्ठ संख्या # 273

प्रयास कीजिए

प्रश्न 1.
a^m × b^m = (ab)^m का प्रयोग करके, अन्य रूप में बदलिए:
(i) 4³ × 2³
(ii) 2⁵ × b⁵
(iii) a² × t²
(iv) 5⁶ × (-2)⁶
(v) (-2)⁴ × (-3)⁴
हल:
(i) 4³ × 2³ = (4 × 2)³ = (8)³
(ii) 2⁵ × b⁵ = (2 × b)⁵ = (2b)⁵
(iii) a² × t² = (a × t)² = (at)²
(iv) 56 × (-2)² = {5 × (-2)}²
= (-10)⁶ = (10)⁶
(v) (-2)⁴ × (-3)⁴ = {(-2) × (-3)}⁴ = (6)⁴

प्रयास कीजिए

प्रश्न 1.
a^m + b^m = (\(\frac { a }{ b } \))m का प्रयोग करके, अन्य रूप में बदलिए:
(i) 4⁵ ÷ 3⁵
(ii) 2⁵ ÷ b⁵
(iii) (-2)³ ÷ b³
(iv) p⁴ ÷ q⁴
(v) 5⁶ ÷ (-2)⁶
हल:

पाठ्य-पुस्तक पृष्ठ संख्या # 276

MP Board Class 7th Maths Solutions

MP Board Class 7th Maths Solutions Chapter 12 बीजीय व्यंजक Ex 12.4

प्रश्न 1.
बराबर लम्बाई के रेखाखण्डों से बनाए गए अंकों के पैटर्न को देखिए। आप रेखाखण्डों से बने हुए इस प्रकार के अंकों को इलेक्ट्रॉनिक घड़ियों या कैलकुलेटरों पर देख सकते हैं।

यदि बनाए गए अंकों की संख्या n ली जाए, तो उसके लिए आवश्यक रेखाखण्डों की n संख्या दर्शाने वाला बीजीय व्यंजक पैटर्न के दाईं ओर लिखा गया है। 6,4,8 के प्रकार के 5, 10, 100 अंकों को बनाने के लिए कितने रेखाखण्डों की आवश्यकता होगी?
हल:
(i) ∵ 6 की तरह n अंकों को बनाने में लगे रेखाखण्डों की संख्या
= (5n + 1)
∴ 5 अंकों की संख्या के लिए रेखाखण्डों की संख्या
= 5 × 5 + 1 = 25 + 1 = 26
10 अंकों की संख्या के लिए रेखाखण्डों की संख्या
= 5 × 10 + 1 = 50 + 1 = 51
100 अंकों की संख्या के लिए रेखाखण्डों की संख्या
= 5 × 100 + 1 = 500 + 1 = 501

(ii) ∵ 4 की तरह n अंकों को बनाने के लिए रेखाखण्डों की संख्या = (3n + 1)
∴ 5, 10, 100 अंकों को बनाने के लिए रेखाखण्डों की संख्या क्रमशः
3 × 5 + 1 = 15 + 1 = 16
3 × 10 + 1 = 30 + 1 = 31
3 × 100 + 1 = 300 + 1 = 301

(iii) 8 की तरह n अंकों को बनाने में लगे रेखाखण्डों की संख्या = (5n + 2)
∴ 5, 10, 100 को बनाने में लगे रेखाखण्डों की संख्या क्रमशः
5 × 5 + 2 = 25 + 2 = 27
5 × 10 + 2 = 50 + 2 = 52
5 × 100 + 2 = 500 + 2 = 502

प्रश्न 2.
संख्या पैटों की निम्नलिखित सारणी को पूरा करने के लिए, दिए हुए बीजीय व्यंजकों का प्रयोग कीजिए:

हल:
(i) व्यंजक (2n – 1) के लिए
100 वाँ पद = 2 × 100 – 1 = 200 – 1 = 199

(ii) व्यंजक (3n + 2) के लिए
5 वाँ पद = 3 × 5 + 2 = 15 + 2 = 17
10 वाँ पद = 3 × 10 + 2 = 30 + 2 = 32
100 वाँ पद = 3 × 100 + 2 = 300 + 2 = 302

(iii) व्यंजक (4n + 1) के लिए
5 वाँ पद = 4 × 5 + 1 = 20 + 1 = 21
10 वाँ पद = 4 × 10 + 1 = 40 + 1 = 41
100 वाँ पद = 4 × 100 + 1 = 400 + 1 = 401

(iv) व्यंजक 7n + 20 के लिए
5 वाँ पद = 7 × 5 + 20 = 35 + 20 = 55
10 वाँ पद = 7 × 10 + 20 = 70 + 20 = 90
100 वाँ पद = 7 × 100 + 20 = 700 + 20 = 720

(v) व्यंजक n² + 1 के लिए
5 वाँ पद = (5)² + 1 = 25 + 1 = 26
10 वाँ पद = (10)² + 1 = 100 + 1 = 101

MP Board Class 7th Maths Solutions

MP Board Class 8th Social Science Solutions Chapter 18 Revolutionary Movement in India

MP Board Class 8th Social Science Chapter 18 Text Book Exercise

Choose the correct option of the following.

Question 1.
Who was not among the revolutionary activity in foreign country?
(a) Shamji Verma
(b) Sardar Ajeet Singh
(c) Madan Lal Dhingra
(d) Vinayak Damodar Savarkar
Answer:
(b) Sardar Ajeet Singh

Question 2.
Who hoisted Indian Flag in 1907 in Germany?
(a) Bhikaji Camma
(b) Lala Hardayal
(c) Mrs Annie Besant
(d) Lala Lajpat Rai
Answer:
(a)Bhikaji Camma

Question 3.
In which district of Madhya Pradesh Chandra Shekhar Azad was born?
(a) Jhabua
(b) Mandla
(c) Raisen
(d) Panna
Answer:
(a) Jhabua

Question 4.
Azad Hind Fauz was founded by
(a) Subhash Chandra Bose
(b) Capt. Mohan Singh
(c) Capt. Prem Kumar Sehgal
(d) Shahnawaz Khan
Answer:
(b)Capt. Mohan Singh

Fill in the blanks :

1. Shyamji Verma founded in ……….. 1905 in London.
2. In 1908 Khudi Ram Bose threw bomb on ………….
3. Dev Narain Tiwari was hanged to death in …………

Answer:

1. Indian house in London
2. The carriage of the defamed judge Kingsford
3. 1931.

MP Board Class 8th Social Science Chapter 18 Very Short Answer Type Questions

Question 1.
Write the names of prominent revolutionaries of Madhya Pradesh?
Answer:
Chandra Shekhar Azad, Thakur Yashwant Singh, Dev Narain Tiwari, Dalpat Rao were the prominent revolutionaries of Madhya Pradesh.

Question 2.
Which villages were occupied by Basudev Balwant Phadke?
Answer:
Basudev Phadke was the leader of the revolutionary movement with the help of few people he occupied Dhamri, Balte Palspe villages in 1879.

Question 3.
Who was assassinated by Chapekar Brothers?
Answer:
In 1897 Damodar and Balkrishan Chapekar brothers murdered Rand, head of the Plague Committee and Lieutenant Amherst in Pune.

MP Board Class 8th Social Science Chapter 18 Short Answer Type Questions

Question 1.
Describe about the revolutionary activities in abroad?
Answer:
Indian revolutionaries were active in other parts of the world also Shyamji Verma established ‘India House’ in London in 1905. He started sociolongistic magazine and scholarships.Vinayak Damodar Savarkar, Birendranath Chattopadhyay, Tirumal Acharya, Bhikaji Camma, Bhai Permanand, Madan Lal Dhingra and Lala Hardayal were the active members of this society.

Madan Lal Dhingra in 1909 killed Curzon Vailer the Secretary of India. He was hanged and Sarvarkar was sent to cellular jail at Andaman Island. In US the Ghadar party was formed in 1913. Lala Hardayal was the key activist of this party. The Ghadar magazine was published.

As the world was begun Lala Hardayal and his comrades went to Germany, Birendranath Chattopadhyay, Bhupender Dutt and Lala Hardayal founded Independence Committee in
Germany. The revolutionaries with their patriotism and self-sacrifice became the source of inspiration for the Indians.

Question 2.
What was Kakori Conspiracy? Describe it?
Answer:
Money was required to run the revolutionaries movements. A group of revolutionaries were successful in robbing the govt, cash at the Kakori Railway station on August 2. 1925 on Saharanpur-Lucknow line. Many of them were arrested after this incident and they were tried in the Kakori Conspiracy Case.

Four of them Ram Prasad Bismil, Ashfaqullah Khan, Roshan Singh and Rajendra Lahiri were sentenced to death and 17 others were sentenced to long-term imprisonment.

Question 3.
Write the names of key organisation of the second phase revolutionary movement?
Answer:
The following were the main revolutionary organisations of the second phase:

1. Youth sabha founded by the Bhagat Singh, Yeshpal and Chhabildas.
2. Hindustan Democratic Republic
3. Hindustan Socialist Republic Association. In 1928 Chandra Shekhar Azad, Sachidra Nath Sanyal, Ram
4. Prasad Bismil together changed the name of Hindustan. Republic Association as Hindustan Socialist
5. Republic Association.
6. Azad Hind Fauz. It was founded by Captain Mohan Singh.

MP Board Class 8th Social Science Chapter 18 Long Answer Type Questions

Question 1.
What were the reasons of the rise of revolutionary movement?
Answer:
The aim of this movement was to change the system based on injustice and to end the oppression of Indians by the British govt, in India. To free the Indian people and to tolerate hardships to get the freedom from ‘English Rule’.

The main factors of the rise of the revolutionary movements were:

1. Economic Disparity:
At the end of the 19th century and early years of 20th century was the period of famines and epidemics. The apathy by the British govt, on such time added fuel to fire the resentment among Indians.

2. Lord Curzon’s Policy:
The senate system followed after Indian University Act. 1904 was the cause of resentment in educated Indians. The govt, confidential ordinance and Calcutta Corporation ordinance contributed more resentment in the Indian people.

3. Partition of Bengal (1905):
The division of Bengal in two parts under the policy of divide and rule by Lord Curzon angered the whole nation and it created sense of devotion and sacrifice among the young Indians.

4. International events:
The independence movements of America, France, Italy, Germany and Ireland inspired Indian revolutionaries too In 1905 the Japanese won over Russia instilled sense of new awakening among the Indians.

Question 2.
What methods were adopted by the revolutionaries against the British rule?
Answer:
Revolutionaries thought that we can not achieve freedom merely through peaceful movements. They Want freedom from British Rule as early as possible therefore they showed self sacrifice to create the feelings of bravery and patriotism among the Indian youths to embrace struggle for Swaraj.

Initially the revolutionaries could not chalk out their plans and programmes but later on the outlay of programmes came into existence.

They adopted the following methods:

Methods used by Revolutionaries:
The revolutionaries used violent methods. They used to organize themselves into small secret societies and give training to their members in making bombs and firearms. They tried to get anus from other countries and also planned their activities from there.

The revolutionaries were brave and fearless and worked with full determination and mad9 sacrifices. Instead of uniting the common people for the national cause, they made individuals their targets. By their daring activities, they were a great source of inspiration to the Indian people.

Question 3.
Write notes on:

1. Azad Hind Fuaz
2. Chandra Shekher Azad

Answer:
1.Azad Hind Fuaz:
At the initiative of Rashbehari Bose, Captain Mohan Singh (one of the Indian soldiers taken prisoner by Japanese) formed the Azad Hind Fuaz. Subhash Chandra Bose instilled new energy into Azad Hind Fuaz and became famous by the name of Netaji.

In the capacity of leader of Azad Hind Fuaz he formed temporary India Govt, in Singapore on October 23 and took vow to shed last drop of blood for the freedom of the country. In 1944 Azad Hind Fauz was successful in moving up to the eastern border of India.

In 1944 he hoisted Indian flag in Kohima. And then seized Imphal but due to paucity of ration and excess rains he had to retreat from there. Netaji gave the slogan “Give me blood and I will give you freedom”.

In 1944 the position of Japan in world politics had become very weak. So the Azad Hind Fauz began to disintegrate.

2. Chandra Shekher Azad:
Chandra Shekhar Azad was born at Bhavra village in Jhabua district in Madhya Pradesh. He embraced non-cooperation movement at the tender age of 14. When he was arrested he told his name was Azad.

His role in Kakori conspiracy, Saunder’s killing and bombing at the assembly was notable. Finally surrounded by British police at the Alfred park in Allahabad, he shot himself dead. He paid his life for the freedom of India. He will be remembered for his great sacrifice for his motherland.

MP Board Class 8th Social Science Solutions

MP Board Class 7th Maths Solutions Chapter 12 बीजीय व्यंजक Ex 12.3

प्रश्न 1.
यदि m = 2 है, तो निम्नलिखित के मान ज्ञात कीजिए:
(i) m – 2
(ii) 3m – 5
(iii) 9 – 5m
(iv) 3m² – 2m – 7
(v) \(\frac { 5m }{ 2 } \) – 4
हल:
(i) m – 2 ∵ m = 2
∴ m – 2 = 2 – 2 = 0
(ii) 3m – 5 = 3 × 2 – 5 = 6 – 5 = 1

(iii) 9 – 5m = 9 – 5 × 2 = 9 – 10 = -1

(iv) 3m² – 2m – 7
= 3(2)² – 2 × 2 – 7
= 3 × 4 – 4 – 7 = 12 – 11 = 1

(v) \(\frac { 5m }{ 2 } \) – 4 = \(\frac{5 \times 2}{2}\) – 4 = 5 – 4 = 1

प्रश्न 2.
यदि p = -2 है, तो निम्नलिखित के मान ज्ञात कीजिए:
(i) 4p + 7
(ii) -3p + 4p + 7
(iii) -2p³ – 3p² + 4p + 7
हल:
यहाँ p = -2
(i) 4p + 7 = 4 × (-2) + 7 = – 8 + 7 = – 1

(ii) -3p² + 4p + 7
= -3(-2)² + 4(-2) + 7
= -3 × 4 – 8 + 7
= – 12 – 8 + 7 = – 13

(iii) -2p³ – 3p² + 4p + 7
= -2(-2)³ – 3(-2)² + 4(-2) + 7
= -2(-8) – 3 × 4 – 8 + 7
= 16 – 12 – 8 + 7 = 23 – 20 = 3

प्रश्न 3.
निम्नलिखित व्यंजकों के मान ज्ञात कीजिए, जब x = -1 है:
(i) 2x – 7
(ii) -x + 2
(iii) x² + 2x + 1
(iv) 2x² – x – 2
हल:
यहाँ x = -1
(i) 2x – 7 = 2 (-1) – 7 = – 2 – 7 = – 9
(ii) -x + 2 = – (-1) + 2 = 1 + 2 – 3
(iii) x² + 2x + 1 = (-1)² + 2(- 1) + 1
= 1 – 2 + 1 = 2 – 2 = 0
(iv) 2x² – x – 2 = 2 (-1)² – (-1) – 2
= 2 × 1 + 1 – 2 = 2 + 1 – 2 = 1

प्रश्न 4.
यदि a = 2 और b = -2 हो, तो निम्नलिखित के मान ज्ञात कीजिए:
(i) a² + b²
(ii) a² + ab + b²
(iii) a² – b²
हल:
यहाँ, a = 2 और b = -2
(i) a² + b² = (2)² + (-2)² = 4 + 4 = 8
(ii) a² + ab + b² = (2)² + 2 (-2) + (-2)²
= 4 – 4 + 4 = 4
(iii) a² – b² = (2)² – (-2)² = 4 – 4 = 0

प्रश्न 5.
जब a = 0 और b = -1 है, तो दिए हुए व्यंजकों के मान ज्ञात कीजिए:
(i) 2a + 2b
(ii) 2a² + b + 1
(iii) 2a²b + 2ab² + ab
(iv) a² + ab + 2
हल:
यहाँ, a = 0 और b = -1
(i) 2a + 2b = 2 × 0 + 2x (-1)
= 0 – 2 = – 2

(ii) 2a² + b² + 1 = 2 × (0)² + (-1)² + 1
= 2 × 0 + 1 + 1 = 2

(iii) 2a²b + 2ab² + ab = 2 (0)² (-1) + 2 (0) (-1)² + 0 × (-1)
= 0 + 0 + 0 = 0

(iv) a² + ab + 2 = (0) + 0 (-1) + 2
= 0 + 0 + 2 – 2

प्रश्न 6.
इन व्यंजकों को सरल कीजिए तथा इनके मान ज्ञात कीजिए, जब x का मान 2 है:
(i) x + 7 + 4 (x – 5)
(ii) 3(x + 2) + 5x – 7
(iii) 6x + 5(x – 2)
(iv) 4(2x – 1)+ 3x + 11
हल:
(i) x + 7 + 4 (x – 5) = x + 7 + 4x – 20
= x + 4x + 7 – 20
= 5x – 13
x = 2 रखने पर, 5x – 13 = 5 × 2 – 13
= 10 – 13 = -3

(ii) 3 (x + 2) + 5x – 7 = 3x + 6 + 5x – 7
= 3x + 5x + 6 – 7
= 8x – 1
x = 2 रखने पर,
8x – 1 – 8 × 2 – 1 = 16 – 1 = 15

(iii) 6x + 5(x – 2) = 6x + 5x – 10
= 11x – 10
x = 2 रखने पर,
11x – 10 = 11 × 2 – 10
= 22 – 10 = 12

(iv) 4(2x – 1) + 3x + 11
= 8x – 4 + 3x + 11
= 8x + 3x – 4 + 11
= 11x + 7
x = 2 रखने पर,
11x + 7 = 11 × 2 + 7 = 22 + 7 = 29

प्रश्न 7.
इन व्यंजकों को सरल कीजिए तथा इनके मान ज्ञात कीजिए, जब x = 3,4 = -1 और b = -2 है :
(i) 3x – 5 – x +9
(ii) 2 – 8x + 4x + 4
(iii) 3a + 5 – 8a + 1
(iv) 10 – 3b – 4 – 5b
(v) 2a – 2b – 4 – 5 + a
हल:
(i) 3x – 5 – x + 9 = 2x + 4
x = 3 रखने पर,
2x + 4 = 2 × 3 + 4
= 6 + 4 = 10

(ii) 2 – 8x + 4x + 4 = 6 – 4x
x = 3 रखने पर,
6 – 4x = 6 – 4 × 3
= 6 – 12 = -6

(iii) 3a + 5 – 8a + 1 = -5a + 6
a = -1 रखने पर,
-5a + 6 = -5 × (-1) + 6
= 5 + 6 = 11

(iv) 10 – 3b – 4 – 5b = 6 – 8b.
b – 2 रखने पर,
6 – 8b = 6 – 8 × (-2)
= 6 + 16 = 22

(v) 2a – 2b – 4 – 5 + a = 3a – 2b – 9
a = -1, b = – 2 रखने पर,
3a – 2b – 9 = 3(- 1)-2(- 2)- 9
= -3 + 4 -9 = -8

प्रश्न 8.
(i) यदि z = 10 है, तो z³ – 3(z – 10) का मान ज्ञात कीजिए।
(ii) यदि p = -10 है, तो p² – 2p – 100 का मान ज्ञात कीजिए।
हल:
(i) जब z = 10 है, तो 2
z³ – 3(z – 10) = (10)³ – 3(10 – 10)
= 1000 – 3 × 0
= 1000 – 0 = 1000

(ii) जब p = -10 है, तो
p² – 2p – 100 = (-10)2 – 2(-10) – 100
= 100 + 20 – 100
= 20

प्रश्न 9.
यदि x = 0 पर 2x² + x – a का मान 5 के बराबर है, तो a का मान क्या होना चाहिए ?
हल:
x = 0 पर, 2x² + x – a = 5
∴ 2 × (0)² + 0 – a = 5
या 0 + 0 – a = 5 ⇒ a = -5

प्रश्न 10.
व्यंजक 2(a² + ab) + 3 – ab को सरल कीजिए और इसका मान ज्ञात कीजिए, जब a = 5 और b = -3 है।
हल:
2 (a² + ab) + 3 – ab
= 2a² + 2ab + 3 – ab
= 2a² + 2ab – ab + 3
= 2a² + ab + 3
a = 5 और b = – 3 रखने पर,
2a² + ab + 3 = 2(5)2 + 5 × (-3) + 3
= 2 × 25 + (-15) + 3
= 50 – 15 + 3 = 38

पाठ्य-पुस्तक पृष्ठ संख्या # 261

प्रयास कीजिए

पाठ्य-पुस्तक में दिये गये आधारभूत आकारों को लेकर उपर्युक्त प्रकार के पैटर्न बनाइए :
आकारों को बनाने के लिए आवश्यक रेखाखण्डों की संख्या दाईं ओर लिखी हुई है। साथ ही n आकारों को बनाने के लिए आवश्यक रेखाखण्डों को दर्शाने वाला व्यंजक भी दाईं ओर दिया हुआ है। आगे बढ़िए और ऐसी ही और पैटर्नो की खोज कीजिए।
हल:

पाठ्य-पुस्तक पृष्ठ संख्या # 262

n भुजा वाले किसी बहुभुज के एक शीर्ष से हम कुल
(n – 3) विकर्ण खींच सकते हैं। एक सप्तभुज (7 भुजाएँ) और अष्टभुज (8 भुजाएँ) के लिए उनकी आकृतियाँ
खींच करके इसकी जाँच कीजिए। यह संख्या एक त्रिभुज (3 भुजाएँ) के लिए क्या है ?
हल:
(i) सप्तभुज ABCDEFG में, विकर्ण AC, AD, AE, AF हैं, अर्थात् इसमें 4 विकर्ण हैं। यदि n – 3 में n = 7 रखें, तो विकर्ण = 7 – 3 = 4

(ii) अष्टभुज ABCDEFGH में विकर्ण AC, AD, AE, AF, AG हैं अर्थात् इसमें 5 विकर्ण हैं। यदि n – 3 में n = 8 रखें, तो विकर्ण = 8 – 3 = 5

(iii) ∆ABC में कोई विकर्ण नहीं होता है। यदि n – 3 में n = 3 रखें, तो 3 – 3 = 0

अतः प्रत्येक स्थिति में परिणाम सन्तुष्ट होता है।

पाठ्य-पुस्तक पृष्ठ संख्या # 262-263

MP Board Class 7th Maths Solutions

MP Board Class 8th Maths Solutions Chapter 6 वर्ग और वर्गमूल Ex 6.4

प्रश्न 1.
निम्नलिखित संख्याओं का वर्गमूल, भाग विधि से ज्ञात कीजिए –

(i) 2304
(ii) 4489
(iii) 3481
(iv) 529
(v) 3249
(vi) 1369
(vii) 5776
(viii) 7921
(xi) 576
(x) 1024
(xi)3136
(xii) 900.

हल:

प्रश्न 2.
निम्नलिखित संख्याओं में से प्रत्येक के वर्गमूल के अंकों की संख्या ज्ञात कीजिए (बिना गणना के) –

1. 64
2. 144
3. 4489
4. 27225
5. 390625

हल:
1. संख्या 64 में 2 अंक हैं।
∴ \(\sqrt { 64 } \) में अंकों की संख्या = \(\frac{n}{2}\) = \(\frac{n}{2}\) = 1 होगी।

2. संख्या 144 में 3 अंक है।
∴ \(\sqrt { 144 } \) में अंकों की संख्या = \(\frac{3+1}{2}\) = \(\frac{4}{2}\) = 2 होगी।

3. संख्या 4489 में अंकों की संख्या = 4 है।
∴ \(\sqrt { 4489 } \) में अंकों की संख्या = \(\frac{4}{2}\) = 2 होगी।

4. संख्या 27225 में अंकों की संख्या = 5 है।
∴ \(\sqrt { 27225 } \) में अंकों की संख्या = \(\frac{5+1}{2}\) = \(\frac{6}{2}\) = 3 होगी।

5. संख्या 390625 में अंकों की संख्या = 6 है।
∴ \(\sqrt { 390625 } \) में अंकों की संख्या = \(\frac{6}{2}\) = 3 होगी।

प्रश्न 3.
निम्नलिखित दशमलव संख्याओं के वर्गमूल ज्ञात कीजिए –

(i) 2.56
(ii) 7.29
(iii) 51.84
(iv) 42.25
(v) 31.36

हल:

प्रश्न 4.
निम्नलिखित संख्याओं में से प्रत्येक में न्यूनतम संख्या क्या घटाई जाए कि एक पूर्ण वर्ग संख्या प्राप्त हो जाए। इस प्रकार प्राप्त पूर्ण वर्ग संख्याओं का वर्गमूल भी ज्ञात कीजिए –

1. 402
2. 1989
3. 3250
4. 825
5. 4000.

हल:
1.

स्पष्ट है कि 202, 402 से 2 कम है। अतः पूर्ण वर्ग संख्या प्राप्त करने के लिए दी हुई संख्या में से 2 घटाना चाहिए।
∴ अभीष्ट पूर्ण वर्ग संख्या = 402 – 2 = 400
पुनः \(\sqrt { 400 } \) = 20

2.

संख्या का वर्गमूल निकालने पर 53 शेष बचता है।
अतः संख्या में से 53 घटाने पर प्राप्त संख्या पूर्ण वर्ग होगी।
∴ अभीष्ट पूर्ण वर्ग संख्या = 1989 – 53
= 1936
पुनः \(\sqrt { 1936 } \) = 44

3.

संख्या का वर्गमूल निकालने पर 1 शेष बचता है।
अतः संख्या में से 1 घटाने पर प्राप्त संख्या पूर्ण वर्ग होगी।
∴ अभीष्ट पूर्ण वर्ग संख्या = 3250 – 1 = 3249
पुनः \(\sqrt { 3249 } \) = 57

4.

संख्या का वर्गमूल निकालने पर 41 शेष बचता है।
अत: संख्या में से 41 घटाने पर प्राप्त संख्या पूर्ण वर्ग होगी।
∴ अभीष्ट पूर्ण वर्ग संख्या = 825 – 41 = 784
पुनः \(\sqrt { 784 } \) = 28

5.

संख्या का वर्गमूल निकालने पर 31 शेष बचता है।
अतः संख्या में से 31 घटाने पर प्राप्त संख्या पूर्ण वर्ग होगी।
∴ अभीष्ट पूर्ण वर्ग संख्या = 4000 – 31 = 3969
पुनः \(\sqrt { 3969 } \) = 63

प्रश्न 5.
निम्नलिखित संख्याओं में से प्रत्येक में कम से कम कितना जोड़ा जाए कि एक पूर्ण वर्ग संख्या प्राप्त हो जाए ? इस प्रकार प्राप्त पूर्ण वर्ग संख्याओं का वर्गमूल भी ज्ञात कीजिए –

1. 525
2. 1750
3. 252
4. 1825
5. 6412

हल:
1.

स्पष्ट है कि 22² < 525 < 23²
अतः अभीष्ट संख्या = 23² – 525
= 529 – 525
= 4 जोड़ी जाए।
∴ अभीष्ट पूर्ण वर्ग संख्या = 525 + 4 = 529
स्पष्टतः \(\sqrt { 529 } \) = 23

2.

स्पष्ट है कि 41² < 1750 < 42²
अतः अभीष्ट संख्या = 422 – 1750
= 1764 – 1750
= 14 जोड़ी जाए।
∴ अभीष्ट पूर्ण वर्ग संख्या = 1750 + 14 = 1764
स्पष्टतः \(\sqrt { 1764 } \) = 42

3.

स्पष्ट है कि 15² < 252 < 16²
अतः अभीष्ट संख्या = 162 – 252
= 256 – 252 = 4 जोड़ी जाए।
∴ अभीष्ट पूर्ण वर्ग संख्या = 252 + 4 = 256
स्पष्टतः \(\sqrt { 1764 } \) = 16

4.

स्पष्ट है कि 42² < 1825 < 43²
अतः अभीष्ट संख्या = 432 – 1825
= 1849 – 1825
= 24 जोड़ी जाए।
∴ अभीष्ट पूर्ण वर्ग संख्या = 1825 + 24 = 1849
स्पष्टतः \(\sqrt { 1849 } \) = 43

5.

स्पष्ट है कि 802 <6412 <812 अतः अभीष्ट संख्या = 812 – 6412
= 6561 – 6412
=149 जोड़ी जाए।
∴ अभीष्ट पूर्ण वर्ग संख्या = 6412 + 149 = 6561
स्पष्टतः \(\sqrt { 1849 } \) = 81

प्रश्न 6.
किसी वर्ग की भुजा की लम्बाई ज्ञात कीजिए जिसका क्षेत्रफल 441 मी है।
हल:
वर्ग का क्षेत्रफल = (वर्ग की भुजा)²
441 = (वर्ग की भुजा)²
∴ वर्ग की भुजा = \(\sqrt { 441 } \) मीटर
= 21 मीटर

प्रश्न 7.
किसी समकोण त्रिभुज ABC में, ∠B = 90°

(a) यदि AB = 6 सेमी, BC = 8 सेमी है, तो AC ज्ञात कीजिए।
(b) यदि AC = 13 सेमी, BC = 5 सेमी, तो AB ज्ञात कीजिए।

हल:
(a) समकोण ΔABC में, पाइथागोरस प्रमेय से

AC² = AB² + BC²
AC² = 6² + 8²
= 36 + 64 = 100
∴ AC = \(\sqrt { 100 } \) = 10 सेमी

(b) समकोण ΔABC में, पाइथागोरस प्रमेय से

AC² = AB² + BC²
13² = AB² + 5²
169 = AB² + 25
AB² = 169 – 25 = 144
AB = \(\sqrt { 144 } \) = 12 सेमी.

प्रश्न 8.
एक माली के पास 1000 पौधे हैं। इन पौधों को वह इस प्रकार लगाना चाहता है कि पंक्तियों की संख्या और कॉलम की संख्या समान रहे। इसके लिए कम से कम पौधों की संख्या ज्ञात कीजिए जिसकी उसे आवश्यकता हो।
हल:
1000 का वर्गमूल लेने पर,

यह दर्शाता है कि 312, 1000 से 39 कम हैं और 32² = 1024
अतः माली को अभीष्ट पौधों की आवश्यकता होगी = 1024 – 1000 – 24 पौधे

प्रश्न 9.
एक विद्यालय में 500 विद्यार्थी हैं। पी. टी. के अभ्यास के लिए इन्हें इस तरह से खड़ा किया गया कि पंक्तियों की संख्या कॉलम की संख्या के समान रहे। इस व्यवस्था को बनाने में कितने विद्यार्थियों को बाहर जाना होगा?
हल:
500 का वर्गमूल लेने पर,

यह दर्शाता है कि 222 = 484 जो कि 500 से 16 कम है
अतः इस व्यवस्था को बनाने में 16 विद्यार्थियों को बाहर जाना होगा।

MP Board Class 8th Maths Solutions

MP Board Class 7th Maths Solutions Chapter 12 बीजीय व्यंजक Ex 12.2

प्रश्न 1.
समान पदों को संयोजित (मिलान) करके सरल कीजिए:
(i) 21b – 32 + 7b – 20b
(ii) -z² + 13z² – 5z + 7z³ – 15z
(iii)p – (p – q) – q – (q – p)
(iv) 3a – 2b – ab – (a – b + ab) + 3ab + b – a
(v) 5x²y – 5x² + 3yx² – 3y² + x² – 8xy² – 3y²
(vi) (3y² + 5y – 4) – (8y – y² – 4)
हल:
(i) 21b – 32 + 7b – 20b
= 21b + 7b – 20b – 32
= (21 + 7 – 20) b – 32
= 8b – 32

(ii) – z² + 13z² – 5z + 7z³ – 15z
= 7z³ – z² + 13z² – 5z – 15z
= 7z³ + (-1 + 13)z² + (-5 -15) z
= 7z³ + 12z³ – 20z

(iii) p – (p – q) – q – (q – p)
= p – p + q – q – q + p
= p – p + p + q – q – q
= (1 – 1 + 1)p + (1 – 1 – 1)q
= p – q

(iv) 3a – 2b – ab – (a – b + ab) + 3ab + b – a
= 3a – 2b – ab – a + b – ab + 3ab + b – a
= (3a – a – a) + (-2b + b + b) + (-ab -ab + 3ab)
= (3 – 1 – 1)a + (-2 + 1 + 1) b + (- 1 – 1 + 3)ab
= (1)a + (0) b + (1) ab = a + ab

(v) 5x² y – 5x² + 3yx² – 3y² + x² – y² + 8xy²
= (5x²y + 3yx²) + (8xy²) + (-5x² + x²) + (-3y² – y² – 3y²)
= (5 + 3) x²y + 8xy² + (- 5 + 1)x² + (- 3 – 1 – 3) y²
= 8x²y + 8xy² – 4x² – 7y²

(vi) (3y² + 5y – 4) – (8y – y² – 4)
= 3y² + 5y – 4 – 8y + y² + 4
= (3y² + y²) + (5y – 8y) + (- 4 + 4)
= (3 + 1) y² + (5 – 8) y + (- 4 + 4)
= 4y² – 3y + 0 = 4y² – 3y

प्रश्न 2.
जोड़िए:
(i) 3mn, -5mn, 8mn, -4mn
(ii) t – 8tz, 3tz – z, z – 1
(iii) -7mn + 5,12mn + 2, 9mn – 8, -2 mn – 3
(iv) a + b – 3,b – a + 3,a – b + 3
(v) 14x + 10y – 12xy – 13, 18 – 7x – 10y + 8xy,4xy
(vi) 5m – 7n, 3n – 4m + 2, 2m – 3mn – 5
(vii) 4x²y, – 3xy², -5xy², 5x²y
(viii) 3p²q² – 4pq + 5, – 10p²q², 15 + 9pq + 7p²q²
(ix) ab – 4a, 4b – ab, 4a – 4b
(x) x² – y² – 1 – y² – 1 – x², 1 – x² – y²
हल:
(i) अभीष्ट योग
= 3mn + (-5mn) + 8mn + (-4mn)
= [3+ (-5) + 8 + (-4)] mn
= [11 – 9] mn = 2mn

(ii) अभीष्ट योग
= (1 – 8tz) + (3tz – z) + (z – t)
= t – 8tz + 3tz – z + z – t
= (t – t) + (-z + z) + (-8tz + 3tz)
= (1 – 1) t + (- 1 + 1) z + (- 8 + 3) tz
= (0) t + (0) z + (-5)tz = – 5tz

(iii) अभीष्ट योग = (-7mn + 5) + (12mn + 2) + (9mn – 8) + (-2mn – 3)
= -7mn + 5 + 12mn + 2 + 9mn – 8 – 2mm – 3
= (-7mm + 12mn + 9mn – 2mn) + (5 + 2 – 8 – 3)
= (-7 + 12 + 9 – 2) mn + (7 – 11)
= (21 – 9) mn + (-4) = 12mn – 4

(iv) अभीष्ट योग = (a + b – 3) + (b – a + 3) + (a – b + 3)
= a + b – 3 + b – a + 3 + a – b + 3
= ( a – a + a) + (b + b – b) + ( – 3 + 3 + 3)
= (1 – 1 + 1)a + (1 + 1 – 1) b + (- 3 + 6)
= (1) a + (1) b + (3)
= a + b + 3

(v) अभीष्ट योग
= (14x + 10y – 12xy – 13) + (18 – 7x – 10y + 8xy) + 4xy
= 14x + 10y – 12xy – 13 + 18 – 7x – 10y + 8xy + 4xy
= (14x – 7x) + (10y – 10y) + (- 12xy + 8xy + 4xy) + (- 13 + 18)
= (14 – 7) x + (10 – 10)y (- 12 + 8 + 4) xy + (5)
= (7)x + (0)y + (- 12 + 12) xy + (5)
= 7x + (0) y + (0) xy + 5
= 7x + 5.

(vi) अभीष्ट योग
= (5m – 7n) + (3n – 4m + 2) + (2m – 3mn – 5)
= 5m – 7n + 3n – 4m + 2 + 2m – 3mn – 5
= (5m – 4m + 2m) + (-7n + 3n) -3mn + (2 – 5)
= (5 – 4 + 2) m + (- 7 + 3) n – 3 mn – 3
= 3m – 4n – 3mn – 3

(vii) अभीष्ट योग
= 4x²y + (-3xy²) + (-5xy²) + 5x²y
= 4x²y – 3xy – 5xy² + 5x²y
= (4 + 5) x²y + (- 3 – 5) xy²
= 9x²y – 8xy²

(viii) अभीष्ट योग
= (3p²q² – 4pq + 5) + (-10 p²q²) + (15 + 9pq + 7p²q²)
= 3p²q² – 4pq + 5 – 10p²q² + 15 + 9pq + 7p²q²
= 3p²q² – 10p²q² + 7p²q² – 4pq + 9pq + 5 + 15
= (3 – 10 + 7)p²q² + (- 4 + 9) pq + (5 + 15)
= (0)p²q² + 5pq + 20
= 5pq + 20

(ix) अभीष्ट योग
= (ab – 4a) + (4b – ab) + (4a – 4b)
= ab – 4a + 4b – ab + 4a – 4b
= ab – ab – 4a + 4a + 4b – 4b
= (0) ab + (0) a + (0) b
= 0 + 0 + 0 = 0

(x) अभीष्ट योग
= (x² – y² – 1) + (y² – 1 – x²) + (1 – x² – y²)
= x² – y² – 1 + y² – 1 – x + 1 – x² – y²
= x² – x² – x² – y² + y² – y² – 1 – 1 + 1
= (1 – 1 – 1) x² + (- 1 + 1 – 1) y² + (- 1 – 1 + 1)
= – x² – y² – 1

प्रश्न 3.
घटाइए:
(i) y² में से – 5y²
(ii) – 12xy में से 6xy
(iii) (a + b) में से (a – b)
(iv) b (5 – a) में से a (b – 5)
(v) 4m² – 3mn + 8 में से – m² + 5mn
(vi) 5x – 10 में से – x² + 10x – 5
(vii) 3ab – 2a² – 2b² में से 5a² – 7ab + 5b²
(viii) 5p² + 3q² – Pq में से 4pq – 5q² – 3p²
हल:
(i) अभीष्ट अन्तर
y2 – (-5y2)
= y2 + 5 = 6y2

(ii) अभीष्ट अन्तर = – 12xy – 6xy = -18xy

(iii) अभीष्ट अन्तर
= (a + b) – (a – b) = a + b – a + b
= (1 – 1)a + (1 + 1) b = 2b

(iv) अभीष्ट अन्तर
= b (5 – a) – a (b – 5)
= 5b – ab – ab + 5a
= 5a + 5b + ( – 1 – 1) ab
= 5a + 5b – 2ab

(v) अभीष्ट अन्तर
= (4m² – 3mn + 8) – (- m² + 5mn)
= 4m² – 3mn + 8 + m² – 5mn
= 4m² + m² – 3mn – 5mn + 8
= (4 + 1)m + (- 3 – 5)mn + 8
= 5m² – 8mn + 8

(vi) अभीष्ट अन्तर
= (5x – 10) – (- x² + 10x – 5)
= 5x – 10 + x² – 10 x + 5
= x² + (5 – 10) x + (- 10 + 5)
= x² – 5x – 5

(vii) अभीष्ट अन्तर
= (3ab – 2a² – 2b²) – (5a² – 7ab + 5b²)
= 3ab – 2a² – 2b² – 5a² + 7ab – 5b²
= -2a² – 5a² – 2b² – 5b² + 3ab + 7ab
=(- 2 – 5) a² + (- 2 – 5) b² + (3 + 7) ab
= -7a – 7b² + 10ab

(viii) अभीष्ट अन्तर
= (5p² + 3q² – pq) – (4pq – 5q² – 3p²)
= 5p² + 3q² – pq – 4pq + 5q² + 3p²
= 5p² + 3p² + 3q² + 5q² – pq – 4pq
= (5 + 3)p² + (3 + 5) q² + (- 1 – 4)pq
= 8p² + 8q² – 5pq

प्रश्न 4.
(a) 2x² + 3xy प्राप्त करने के लिए x² + xy + ya में क्या जोड़ना चाहिए?
(b) -3a + 7b + 16 प्राप्त करने के लिए 2a + 8b + 10 में से क्या घटाना चाहिए ?
हल:
(a) अभीष्ट व्यंजक
= (2x² + 3xy) – (x² + xy + y²)
= 2x² + 3xy – x² – xy – y²
= 2x² – x² – y² + 3xy – xy
= (2 – 1) x² – y² + (3 – 1)xy
= x² – y² + 2xy

(b) अभीष्ट व्यंजक
= (2a + 8b + 10) – (- 3a + 7b + 16)
= 2a + 8b + 10 + 3a – 7b – 16
= 2a + 3a + 8b – 7b + 10 – 16
= (2 + 3)a + (8 – 7)b + (10 – 16)
= 5a + b – 6

प्रश्न 5.
-x² – y² + 6xy + 20 प्राप्त करने के लिए, 3x² – 4y² + 5xy + 20 में से क्या निकाल लेना चाहिए?
हल:
अभीष्ट व्यंजक = (3x² – 4y² + 5xy + 20) -(- x² – y² + 6xy + 20)
= 3x² – 4y² + 5xy + 20 + x² + y² – 6xy – 20
= 3x² + x² – 4y² + y² + 5xy – 6xy + 20 – 20
= (3 + 1)x² + (- 4 + 1) y² + (5 – 6) xy + (20 – 20)
= 4x² – 3y² – xy + 0
= 4x² – 3y² – xy

प्रश्न 6.
(a) 3x – y + 11 और – y – 11 के योग में से 3x – y – 11 को घटाइए।
(b) 4 + 3x और 5 – 4x + 2x² के योग में से 3x² – 5x और – x² + 2x + 5 के योग को घटाइए।
हल:
(a) 3x – y + 11 और – y – 11 का योग
= (3x – y + 11) + (- y – 11)
= 3x – y + 11 – y – 11
= 3x – y – y + 11 – 11
= 3x – 2y
अब 3x – 2y में से 3x – y – 11 को घटाने पर,
अभीष्ट अन्तर = (3x – 2y) – (3x – y – 11)
= 3x – 2y – 3x + y + 11
= (3x – 3x) + (-2y + y) + 11
= 0 – y + 11
= – y + 11

(b) 4 + 3x और 5 – 4x + 2x² का योग
= 4 + 3x + 5 – 4 x + 2x²
= (4 + 5) + (3x – 4x) + 2x²
= 9 – x + 2x²
3x² – 5x और = x² + 2x + 5 का योग
= 3x² – 5x – x² + 2x + 5
= 3x² – x² – 5x + 2x + 5
= (3 – 1)x² + (- 5 + 2)x + 5
= 2x² – 3x + 5
अब, प्रश्नानुसार
अभीष्ट अन्तर = (9 – x + 2x²) – (2x² – 3x + 5)
= 9 – x + 2x² – 2x² + 3x – 5
= (9 – 5) + (- x + 3x) + (2x² – 2x²)
= 4 + (- 1 + 3)x + (2 – 2) x²
= 4 + (2)x + (0) x²
= 4 + 2x ⇒ 2x +4
पाठ्य-पुस्तक पृष्ठ संख्या # 258

MP Board Class 7th Maths Solutions

MP Board Class 7th Maths Solutions Chapter 12 बीजीय व्यंजक Ex 12.1

प्रश्न 1.
निम्नलिखित स्थितियों में चरों, अचरों और अंकगणितीय संक्रियाओं का प्रयोग करते हुए बीजीय व्यंजक प्राप्त कीजिए –

1. संख्या y में से z को घटाना।
2. संख्याओं x और y के योग का आधा।
3. संख्या z को स्वयं उससे गुणा किया जाता है।
4. संख्याओं p और q के गुणनफल का एक-चौथाई।
5. दोनों संख्याओं x और y के वर्गों को जोड़ा जाता है।
6. संख्याओं m और n के गुणनफल के तीन गुने में संख्या 5 जोड़ना।
7. 10 में से संख्याओं y और z के गुणनफल को घटाना।
8. संख्याओं a और b के गुणनफल में से उनके योग को घटाना।

हल:

1. y – 2
2. \(\frac { 1 }{ 2 } \) = (x + y)
3. z²
4. \(\frac { 1 }{ 4 } \)pq
5. x² + y²
6. 3mn + 5
7. 10 – yz
8. ab – (a + b)

प्रश्न 2.
(i) निम्नलिखित व्यंजकों में पदों और उनके गुणनखण्डों को छाँटिए। पदों और उनके गुणनखण्डों को पेड़ आरेख द्वारा भी दर्शाइए :
(a) x – 3
(b) 1 + x + x²
(c) y – y³
(d) 5x² + 7x²y
(e) – ab + 2b² – 3a²
(ii) नीचे दिए गए व्यंजकों में,पदों और उनके गुणनखण्डों को छाँटिए :
(a) -4x + 5
(b) -4x + 5y
(c) 5y + 3y²
(d) xy + 2x²y²
(e) Pq + q
(f) 1.2ab – 2.4b + 3.6a
(g) \(\frac { 3 }{ 4 } \)x + \(\frac { 1 }{ 4 } \)
(h) 0.12p² + 0.2q²
हल:
(i) (a) x – 3

(b) 1 + x + x²

(c) y – y³

(d) 5x² + 7x²y

(e) – ab + 2b² – 3a²

(ii) हल:

प्रश्न 3.
निम्नलिखित व्यंजकों में पदों के संख्यात्मक गुणांकों जो अचर न हों, की पहचान कीजिए :
(i) 5 – 3t²
(ii) 1 + t + t² + t³
(iii) x + 2xy + 3y
(iv) 100m + 1000n
(v) -p²q² + 7pq
(vi) 1.2a + 0.8b
(vii) 3.14 r²
(viii) 2(l + b)
(ix) 0.1 y + 0.01 y²
हल:

प्रश्न 4.
(a) वे पद पहचानिए जिनमें x है और फिर इनमें x का गुणांक लिखिए:
(i) y²x + y
(ii) 13y² – 8yx
(iii) x + y + z
(iv) y + z + zx
(v) 1 + x + xy
(vi) 12xy + 25
(vii) 7 + xy²

(b) वे पद पहचानिए जिनमें है और फिर इनमें y² का गुणांक लिखिए :
(i) 8 – xy²
(ii) 5y² + 7x
(iii) 2x²y – 15xy² + 7y²
हल:
(a)

(b)

प्रश्न 5.
निम्नलिखित व्यंजकों को एकपदी, द्विपद और त्रिपद के रूप में वर्गीकृत कीजिए :

1. 4y – 7z
2. y²
3. x + y – xy
4. 100
5. ab – a – b
6. 5 – 3t
7. 4p²q – 4pq²
8. 7mn
9. z² – 3z + 8
10. a² + b²
11. z² + z
12. 1 + x + x²

हल:

1. द्विपद
2. एकपदी
3. त्रिपद
4. एकपदी
5. त्रिपद
6. द्विपद
7. द्विपद
8. एकपदी
9. त्रिपद
10. द्विपद
11. द्विपद
12. त्रिपद।

प्रश्न 6.
बताइए कि दिए हुए पदों के युग्म समान पदों के हैं या असमान पदों के हैं :

1. 1,100
2. -7x, \(\frac { 5 }{ 2 } \)x
3. -29x, -29y
4. 14xy, 42yx
5. 4m²p, 4mp²
6. 12xz, 12x²z²

हल:

1. समान पद
2. समान पद
3. असमान पद
4. समान पद
5. असमान पद
6. असमान पद

प्रश्न 7.
निम्नलिखित में समान पदों को छाँटिए :
(a) -xy², -4yx², , 8x², 2xy², 7y, – 11x²,-100x, – 11yx, 20x²y, -6x²,y, 2xy, 3x.
(b) 10pq, 7p, 8q, -p²q², – 7qp, – 100q, – 23, 12q²p², -5p², 41, 2405p, 78qp, 13p²q, qp², 701p²
हल:
(a) दिए हुए पदों में समान पदों के समूह:
-xy², 2ry²; – 4yx², 20x²y; 8x², – 11x²; – 6x²; 7y, y; – 100x, 3x; -11yx, 2xy
(b) दिए हुए पदों में समान पदों के समूह –
10pq, – 7qp, 78qp; 7p, 2405p; 8q, – 100q; – p²q², 12q²p²; – 23, 41; -5p², 701p², 13p²q, qp²

पाठ्य-पुस्तक पृष्ठ संख्या # 253

प्रयास कीजिए

प्रश्न 1.
कम-से-कम ऐसी दो स्थितियों के बारे में सोचिए, जिनमें से प्रत्येक में आपको दो बीजीय व्यंजकों को बनाने की आवश्यकता पड़े और उन्हें जोड़ना या घटाना पड़े।
हल:

• राहुल की मासिक आय दीपक की आय की तीन गुनी है और मीनाक्षी की मासिक आय राहुल और दीपक की प्रति माह आय के योग से ₹ 300 अधिक है। मीनाक्षी की प्रतिमाह आय क्या है?
• दो हवाई जहाज विपरीत दिशाओं में उड़ना आरम्भ करते हैं। एक की औसत चाल, दूसरे की औसत चाल से 100 km/h अधिक है। यदि चार घण्टे बाद उनके बीच की दूरी 4000 km हो, तो उनकी औसत चाल ज्ञात कीजिए।

पाठ्य-पुस्तक पृष्ठ संख्या # 255

प्रयास कीजिए

प्रश्न 1.
जोड़िए और घटाइए:
(i) m – n, m + n
(ii) mn + 5 – 2, mn + 3
हल:
(i) योग : m – n + m + n
= m + m – n + n
= 2m + 0n = 2m
घटाना: (m – n) – (m + n)
= m – n – m – n
= m – m – n – n
= 0 – 2n = -2n

(ii) योग: mn + 5 – 2, mn +3
= mn + 5 – 2 + mn + 3
= mn + mn + 5 – 2 + 3
= 2mn + 6
घटाना: (mn + 5 – 2) – (mn + 3)
= mn + 5 – 2 – mn – 3
= mn – mn + 5 – 2 – 3
= 0 + 0 = 0

पाठ्य-पुस्तक पृष्ठ संख्या # 256

MP Board Class 7th Maths Solutions

MP Board Class 8th Maths Solutions Chapter 6 वर्ग और वर्गमूल Ex 6.3

प्रश्न 1.
निम्नलिखित संख्याओं के वर्गमूल ज्ञात करने में इकाई अंक की क्या सम्भावना है –

1. 9801
2. 99856
3. 998001
4. 657666025

हल:

संख्याओं के वर्गमूल में इकाई अंक की सम्भावना –

1. 9801 में 1 या 9
2. 99856 में 4 या 6
3. 998001 में 1 या 9
4. 657666025 में 5

प्रश्न 2.
बिना गणना किए वह संख्या बताएँ जो वास्तव में पूर्ण वर्ग नहीं है –

1. 153
2. 257
3. 408
4. 441.

हल:
संख्या (i) 153, (ii) 257, तथा (iii) 408 पूर्ण वर्ग नहीं है।

प्रश्न 3.
बार-बार घटाने की विधि से 100 और 169 का वर्गमूल ज्ञात कीजिए।
हल:
1. 100 से 1 से प्रारम्भ करके क्रमागत विषम संख्याओं के घटाने पर,

• 100 – 1 = 99
• 99 – 3 = 96
• 96 – 5 = 91
• 91 – 7 = 84
• 84 – 9 = 75
• 75 – 11 = 64
• 64 – 13 = 51
• 51 – 15 = 36
• 36 – 17 = 19
• 19 – 19 = 0

संख्या 100 से क्रमागत विषम संख्याओं को घटाने पर 10वाँ पद शून्य (0) प्राप्त होता है।
अतः \(\sqrt { 100 } \) = 10

2. 169 से 1 से प्रारम्भ करके क्रमागत विषम संख्याओं को घटाने पर,

• 169 – 1 = 168
• 168 – 3 = 165
• 165 – 5 = 160
• – 160 – 7 = 153
• 153 – 9 = 144
• 144 – 11 = 133
• 133 – 13 = 120
• 120 – 15 = 105
• 105 – 17 = 88
• 88 – 19 = 69
• 69 – 21 = 48
• 48 – 23 = 25
• 25 – 25 = 0.

संख्या 169 से क्रमागत विषम संख्याओं को घटाने पर 13वाँ पद शून्य (0) प्राप्त होता है। अतः \(\sqrt { 169 } \) = 13

प्रश्न 4.
अभाज्य गुणनखण्ड विधि से निम्न संख्याओं का वर्गमूल ज्ञात कीजिए –

1. 729
2. 400
3. 1764
4. 4096
5. 7744
6. 9604
7. 5929
8. 9216
9. 529
10. 8100

हल:
1.

2.

3.

4.

5.

6.

7.

8.

9.

10.

प्रश्न 5.
निम्नलिखित संख्याओं में प्रत्येक के लिए वह सबसे छोटी पूर्ण संख्या ज्ञात कीजिए जिससे इस संख्या को गुणा करने पर यह एक पूर्ण वर्ग संख्या बन जाए। इस पूर्ण वर्ग संख्या का वर्गमूल भी ज्ञात कीजिए –

1. 252
2. 180
3. 1008
4. 2028
5. 1458
6. 768

हल:
1.

हम जानते हैं कि पूर्ण वर्ग संख्या में प्रत्येक पद के जोड़े बनते हैं।
परन्तु यहाँ 7 का जोड़ा नहीं है। अतः यदि 252 में 7 का गुणा कर दें तो संख्या पूर्ण वर्ग बन जाएगी।
∴ सबसे छोटी पूर्ण संख्या 7 होगी।
गुणा करने पर प्राप्त संख्या = 252 x 7 = 1764

2.

अतः दी गई संख्या में 5 का जोड़ा नहीं बन रहा है। जोड़ा बनाने के लिए 5 का गुणा करना आवश्यक है।
∴ सबसे छोटी पूर्ण संख्या 5 होगी।
गुणा करने पर प्राप्त संख्या = 180 x 5 = 900

3.

अतः दी गई संख्या में 7 का जोड़ा नहीं बन रहा है। जोड़ा बनाने के लिए 7 का गुणा करना चाहिए।
∴ सबसे छोटी पूर्ण संख्या 7 होगी।
गुणा करने पर प्राप्त संख्या = 1008 x 7 = 7056

4.

अतः दी गई संख्या में 3 का जोड़ा नहीं बन रहा है। जोड़ा बनाने के लिए 3 का गुणा करेंगे।
∴ सबसे छोटी पूर्ण संख्या 3 होगी।
गुणा करने पर प्राप्त संख्या = 2028 x 3 = 6084

5.

अतः दी गई संख्या में 2 का जोड़ा नहीं बन रहा है। जोड़ा बनाने के लिए 2 का गुणा करना पड़ेगा।
∴ सबसे छोटी पूर्ण संख्या 2 होगी।
गुणा करने पर प्राप्त संख्या= 1458 x 2 = 2916

6.

अतः दी हुई संख्या में 3 का जोड़ा नहीं बन रहा है। जोड़ा बनाने के लिए 3 का गुणा करना पड़ेगा।
∴ सबसे छोटी पूर्ण संख्या 3 होगी। गुणा करने पर प्राप्त संख्या = 768 x 3

प्रश्न 6.
निम्नलिखित संख्याओं में प्रत्येक के लिए सबसे छोटी पूर्ण संख्या ज्ञात कीजिए जिससे इस संख्या को भाग देने पर वह एक पूर्ण संख्या बन जाए। इस तरह ज्ञात की गई संख्या का वर्गमूल भी ज्ञात कीजिए।

1. 252
2. 2925
3. 396
4. 2645
5. 2800
6. 1620

हल:
1.

इसे पूर्ण संख्या बनाने के लिए 7 का भाग करना होगा।
∴ सबसे छोटी पूर्ण वर्ग संख्या 7 होगी।
भाग देने पर प्राप्त संख्या = 36

2.

इसे पूर्ण संख्या बनाने के लिए 13 से भाग करना होगा।
∴ सबसे छोटी पूर्ण संख्या 13 होगी।
भाग देने पर प्राप्त संख्या = 225

3.

इसे पूर्ण संख्या बनाने के लिए 11 से भाग करना होगा।
∴ सबसे छोटी पूर्ण संख्या 11 होगी।
भाग देने पर प्राप्त संख्या = 36

4.

इसे पूर्ण संख्या बनाने के लिए 5 से भाग करना होगा।
∴ सबसे छोटी पूर्ण संख्या 5 होगी।
भाग देने पर प्राप्त संख्या = 529

5.

इसे पूर्ण संख्या बनाने के लिए 7 से भाग करना होगा।
∴ सबसे छोटी पूर्ण संख्या 7 होगी।
भाग देने पर प्राप्त संख्या = 400

6.

इसे पूर्ण संख्या बनाने के लिए 5 से भाग करना होगा।
∴ सबसे छोटी पूर्ण संख्या 5 होगी।
भाग देने पर प्राप्त संख्या = 324

प्रश्न 7.
एक विद्यालय में कक्षा VIII के सभी विद्यार्थियों ने प्रधानमन्त्री राहत कोष में ₹ 2,401 दान में दिए। प्रत्येक विद्यार्थी ने उतने ही रुपये दान में दिए जितने कक्षा में विद्यार्थी थे। कक्षा में विद्यार्थियों की संख्या ज्ञात कीजिए।
हल:
माना कि कक्षा में विद्यार्थियों की संख्या = x है।
अतः विद्यार्थियों द्वारा दान में दी गई कुल धनराशि = ₹ x × x = ₹ x² परन्तु राहत कोष में दिए गए रुपये = ₹ 2,401

अतः कक्षा में विद्यार्थियों की संख्या = 49 है।

प्रश्न 8.
एक बाग में 2025 पौधे इस प्रकार लगाए जाने हैं कि प्रत्येक पंक्ति में उतने ही पौधे हों, जितनी पंक्तियों की संख्या हो। पंक्तियों की संख्या और प्रत्येक पंक्ति में पौधों की संख्या ज्ञात कीजिए।
हल:
माना कि पंक्तियों की संख्या = x है।
और प्रत्येक पंक्ति में पौधों की संख्या = x
∴ कुल पौधों की संख्या =x × x = x²
लेकिन पौधों की संख्या = 2025
अब, प्रश्नानुसार,

अतः पंक्तियों की अभीष्ट संख्या = 45 तथा प्रत्येक पंक्ति में पौधों की संख्या = 45

प्रश्न 9.
वह सबसे छोटी वर्ग संख्या ज्ञात कीजिए जो 4, 9 और 10 प्रत्येक से विभाजित हो जाए।
हल:
वह सबसे छोटी वर्ग संख्या जो 4, 9 और 10 प्रत्येक से विभाजित हो जाए, 4, 9 और 10 का ल. स. होगी।

इस संख्या को पूर्ण वर्ग बनाने के लिए 5 से गुणा करना पड़ेगा।
∴ सबसे छोटी अभीष्ट वर्ग संख्या = 180 x 5 = 900

प्रश्न 10.
वह सबसे छोटी वर्ग संख्या ज्ञात कीजिए जो प्रत्येक 8, 15 और 20 से विभाजित हो जाए।
हल:
8, 15 और 20 से विभाजित होने वाली पूर्ण वर्ग संख्या 8, 15 और 20 का ल. स. होगी।

इसे पूर्ण बर्ग बनाने के लिए 2 x 3 x 5 = 30 से गुणा करना पड़ेगा।
∴ सबसे छोटी अभीष्ट वर्ग संख्या = 120 x 30
= 3600

पाठ्य-पुस्तक पृष्ठ संख्या # 110

प्रश्न 1.
क्या आप हमें 5 या 6 अंकों वाली संख्या के वर्गमूल में अंकों की संख्या बता सकते हैं?
हल:
हाँ, 5 या 6 अंकों वाली संख्या के वर्गमूल में अंकों की संख्या 3 होगी।

पाठ्य-पुस्तक पृष्ठ संख्या # 111

सोचिए, चर्चा कीजिए और लिखिए (क्रमांक 6.2)

प्रश्न 1.
क्या हम कह सकते हैं कि एक पूर्ण वर्ग संख्या में यदि n अंक हैं तो उसके वर्गमूल में \(\frac{n}{2}\) अंक होंगे। यदि n सम है या (\(\frac{n+1}{2}\)) होंगे यदि n विषम है?
हल:
हाँ, हम कह सकते हैं कि यदि n अंकों की कोई पूर्ण वर्ग संख्या है, तो उसके वर्गमूल में –

1. \(\frac{n}{2}\) अंक होंगे यदि n सम है तथा
2. अंक होंगे यदि (\(\frac{n+1}{2}\)) विषम है।

पाठ्य-पुस्तक पृष्ठ संख्या # 112

प्रयास कीजिए (क्रमांक 6.14)

प्रश्न 1.
निम्नलिखित संख्याओं के वर्गमूल में अंकों की संख्या को गणना के बिना ज्ञात कीजिए –

1. 25600
2. 100000000
3. 36864

हल:

1. क्योंकि संख्या 25600 में 5 अंक हैं, अतः इसके वर्गमूल में अंकों की संख्या \(\frac{5+1}{2}\) अर्थात् 3 अंक होगी।
2. क्योंकि संख्या 100000000 में अंकों की संख्या = 9, अतः इसके वर्गमूल में अंकों की संख्या \(\frac{9+1}{2}\) अर्थात् 5 अंक होगी।
3. क्योंकि संख्या 36864 में अंकों की संख्या = 5, अत: इसके वर्गमूल में अंकों की संख्या = \(\frac{5+1}{2}\), अर्थात् 3 अंक होगी।

पाठ्य-पुस्तक पृष्ठ संख्या # 115

प्रयास कीजिए (क्रमांक 6.15)

प्रश्न 1.
निम्नलिखित संख्याओं के निकटतम पूर्ण संख्याओं का अनुमान लगाइए –

1. \(\sqrt { 80 } \)
2. \(\sqrt { 1000 } \)
3. \(\sqrt { 350 } \)
4. \(\sqrt { 500 } \)

हल:
1. हम जानते हैं कि –
64 < 80 < 81
8 < \(\sqrt { 80 } \) < 9
∵ 81, 80 से अधिक निकटतम है।
∴ निकटतम पूर्ण संख्या = 9

2. हम जानते हैं कि –
31² और 32² = 1024
31² \(\sqrt { 1000 } \) < 32
∵ 1000, 1024 के अधिक निकटतम है
∴ निकटतम पूर्ण संख्या = 32

3. हम जानते हैं कि –
18² = 324 और 19² = 361
18 < \(\sqrt { 1000 } \) < 19
क्योंकि 350, 324 की अपेक्षा 361 के अधिक नजदीक है।
∴ निकटतम पूर्ण संख्या = 19

4. हम जानते हैं कि –
22² = 484 और 23² = 529
22 < \(\sqrt { 500 } \) < 23
∴ 500, 529 की अपेक्षा 484 के अधिक निकट है।
∴ निकटतम पूर्ण संख्या = 22

MP Board Class 8th Maths Solutions

MP Board Class 7th Maths Solutions Chapter 11 परिमाप और क्षेत्रफल Ex 11.4

प्रश्न 1.
एक बगीचा 90 m लम्बा और 75 m चौड़ा है। इसके बाहर चारों तरफ 5 m चौड़ा पथ बनाना है। पथ का क्षेत्रफल ज्ञात कीजिए। बगीचे का क्षेत्रफल हेक्टेअर में भी ज्ञात कीजिए।
हल:
बगीचे की लम्बाई (l) = 90 m, चौड़ाई (b) = 75 m

बगीचे का क्षेत्रफल = l × b
= 90 m × 75 m = 6750 m²
= \(\frac { 6750 }{ 10000 } \) हेक्टेअर
= 0.6750 हेक्टेअर
∵ बगीचे के चारों ओर का पथ आयत बनाता है।
∴ बाह्य आयत की लम्बाई = 90 + 5 + 5 = 100 m
व चौड़ाई = 75 + 5 + 5 = 85 m
∴ पथ सहित बगीचे का बाह्य आयत का क्षेत्रफल
= 100 × 85 = 8,500 m²
अतः पथ का क्षेत्रफल = बाह्य आयत का क्षेत्रफल – बगीचे का क्षेत्रफल
= 8500 m² – 6750 m² = 1750 m²

प्रश्न 2.
125 m लम्बाई और 65m चौड़ाई वाले एक आयताकार पार्क के चारों ओर बाहर एक 3 m चौड़ा पथ बना हुआ है। पथ का क्षेत्रफल ज्ञात कीजिए।
हल:
चित्र 11.29 में,
PQ = AB + 2 × पथ की चौड़ाई
= 125 + 2 × 3 = 125 + 6 = 131 m
व QR = BC + 2 × पथ की चौड़ाई
= 65 + 2 × 3 = 65 + 6 = 71 m

अब, पथ का क्षेत्रफल
= बाह्य आयत PORS का क्षेत्रफल – पार्क ABCD का क्षेत्रफल
= PQ × QR – AB × BC
= 131 × 71 – 125 × 65
= 9301 – 8125 = 1176m²

प्रश्न 3.
8 cm लम्बे और 5 cm चौड़े एक गत्ते पर एक चित्र की पेंटिंग इस प्रकार बनाई गई है कि इसकी प्रत्येक भुजाओं के अनुदिश 1.5 cm चौड़ा हाशिया (margin) छोड़ा गया है। हाशिये का कुल क्षेत्रफल ज्ञात कीजिए।
हल:
चित्र 11.30 में,
PQ = 8 cm, QR = 5 cm
AB = PQ – 2 × हाशिये की चौड़ाई
= 8 – 2 × 1.5 = 8 – 3 = 5 cm
BC = QR – 2 × हाशिये की चौड़ाई
= 5 – 2 × 1.5 = 5 – 3 = 2 cm

अब, हाशिये का कुल क्षेत्रफल
= गत्ते का क्षेत्रफल – पेंटिंग का क्षेत्रफल
= PQ × QR – AB × BC = 8 × 5 – 5 × 2 = 40 – 10 = 30 cm²

प्रश्न 4.
5.5m लम्बे और 4 m चौड़े कमरे के चारों ओर बाहर 2-25 m चौड़ा एक बरामदा बनाया गया है। ज्ञात कीजिए:
(i) बरामदे का क्षेत्रफल
(ii) ₹ 200 प्रति m² की दर से बरामदे के फर्श पर सीमेंट कराने का व्यय।
हल:
चित्र 11.31 में,
ABCD कमरा है तथा इसके चारों ओर 2.25 m चौड़ा बरामदा है।
PQ = AB + 2 × बरामदे की चौड़ाई
= 5.5 + 2 × 2.25 = 5.5 + 4.5 = 10 m
QR = BC + 2 × बरामदे की चौड़ाई
= 4 + 2 × 2.25
= 4 + 4.5 = 8.5 m

(i) बरामदे का क्षेत्रफल = बाह्य आयतकार भाग PQRS का क्षेत्रफल – कमरे का क्षेत्रफल
= PQ × QR – AB × CD
= 10 × 8.5 – 5.5 × 4
= 85 – 22 = 63 m²

(ii) ₹ 200 प्रति m² की दर से बरामदे के फर्श पर सीमेंट कराने का कुल व्यय = ₹200 × 63 = ₹ 12,600

प्रश्न 5.
30 m भुजा वाले एक वर्गाकार बगीचे की परिसीमा से लगा भीतर की ओर 1 m चौड़ा पथ बना हुआ है। ज्ञात कीजिए:
(i) पथ का क्षेत्रफल
(ii) ₹ 40 प्रति m² की दर से शेष भाग पर घास लगवाने का व्यय।
हल:
(i) चित्र 11.32 में,
PQRS बगीचा है। इसके भीतर की ओर 1 m चौड़ा पथ है।

AB = PQ – 2 × पथ की चौड़ाई
= 30 – 2 × 1
= 30 – 2 = 28 m.

BC = OR – 2 × पथ की चौड़ाई
= 30 – 2 × 1
= 30 – 2 = 28m
अब, पथ का क्षेत्रफल = बाह्य वर्ग PQRS का क्षेत्रफल
– अन्त:वर्ग ABCD का क्षेत्रफल
= 30 × 30 – 28 × 28
= 900 – 784
= 116 m²

(ii) बगीचे के शेष भाग का क्षेत्रफल
= ABCD का क्षेत्रफल
= (28 × 28) m²
= 784 m²
∴ ₹ 40 प्रति m² की दर से बगीचे के शेष भाग पर घास लगवाने का व्यय
= ₹40 × 784
= ₹ 31,360

प्रश्न 6.
700 m लम्बे और 300 m चौड़े एक आयताकार पार्क के मध्य से होकर जाते 10 m चौड़े दो पथ बने हुए हैं, जो एक-दूसरे पर परस्पर लम्ब और चौपड़ के आकार के हैं। इनमें से प्रत्येक पथ का क्षेत्रफल ज्ञात कीजिए तथा पार्क की भुजाओं को छोड़कर पार्क के शेष भाग का भी क्षेत्रफल ज्ञात कीजिए। उत्तर को हेक्टेयर में दीजिए।
हल:
PQ = EH = KL = KN = 10 m
लम्बाई के अनुदिश सड़क की लम्बाई = 700 m
चौड़ाई के अनुदिश सड़क की लम्बाई = 300 m

सड़कों PQRS व EFGH का क्षेत्रफल
= PQRS का क्षेत्रफल + EFGH का क्षेत्रफल – KLMN का क्षेत्रफल
(300 × 10 + 700 × 10 – 10 × 10) m²
= (3000 + 7000 – 100) m²
= 10000 m² – 100 m² = 9900 m²
= \(\frac { 9900 }{ 10000 } \) = 0.99 हेक्टेयर
अब, सड़कों को छोड़कर पार्क का क्षेत्रफल
= पार्क का क्षेत्रफल – परस्पर लम्ब सड़कों का क्षेत्रफल
= 700 × 300 – 9900
= 210000 – 9900 = 200100 m²
= \(\frac { 200100 }{ 10000 } \) हेक्टेयर = 20.01 हेक्टेयर

प्रश्न 7.
90 m लम्बाई और 60 m चौड़ाई वाले एक आयताकार मैदान में दो पथ बनाए गए हैं, जो भुजाओं के समान्तर हैं, एक-दूसरे को लम्बवत् काटते हैं और मैदान के मध्य से होकर निकलते हैं। यदि प्रत्येक पथ की चौड़ाई 3m हो, तो ज्ञात कीजिए:
(i) पथों द्वारा आच्छादित क्षेत्रफल
(ii) ₹110 प्रति m² की दर से पथ बनाने का व्यय।
हल:
(i) पथ PQRS का क्षेत्रफल = लम्बाई × चौड़ाई
= 90 × 3 = 270 m²

पथ TUVW का क्षेत्रफल = लम्बाई × चौड़ाई
= 60 × 3 = 180 m²
उभयनिष्ठ भाग EFGH का क्षेत्रफल
= 3 × 3 = 9 m²
अत: पथों का कुल क्षेत्रफल = पथ PQRS का क्षेत्रफल + पथ TUVW का क्षेत्रफल – उभयनिष्ठ भाग EFGH का क्षेत्रफल
= 270 m² + 180 m² – 9m²
= 450 m² – 9 m²
= 441 m²

(ii) ₹ 110 प्रति m² की दर से पथ बनाने का व्यय
= ₹ 110 × 441
= ₹ 48,510

प्रश्न 8.
प्रज्ञा 4 cm त्रिज्या वाले एक वृत्ताकार पाइप के चारों ओर एक रस्सी लपेटती है (जैसा दिखाया गया है) और रस्सी की आवश्यक लम्बाई को काट लेती है। इसके बाद वह उसे 4 cm भुजा वाले एक वर्गाकार बॉक्स के चारों ओर लपेटती है(दिखाया गया है)। क्या उसके पास कुछ और रस्सी बचेगी ? (π = 3.14)

हल:
वृत्ताकार पाइप की त्रिज्या (r) = 4 cm
∴ पाइप की परिधि = 2πr
= 2 × 3.14 × 4 = 25.12 cm
∴ पाइप पर लपेटी गई रस्सी की लम्बाई
= 25.12 cm
अब, वर्ग का परिमाप = 4 × a
= 4 × 4 cm = 16 cm
∴ वर्ग पर लपेटी गई रस्सी की लम्बाई = 16 m
∵ 25.12 cm – 16 cm
∴ 25.12 cm – 16 cm = 9.12 cm.
हाँ, उसके पास 9-12 cm रस्सी और बचेगी।

प्रश्न 9.
संलग्न आकृति एक आयताकार पार्क के मध्य में एक वृत्ताकार फूलों की क्यारी को दर्शाती है। ज्ञात कीजिए:

(i) पूरे पार्क का क्षेत्रफल
(ii) फूलों की क्यारी का क्षेत्रफल
(iii) फूलों की क्यारी को छोड़कर, पार्क के शेष भाग का क्षेत्रफल
(iv) क्यारी की परिधि।
हल:
(i) यहाँ, पार्क की लम्बाई (l) = 10m, चौड़ाई = 5 m.
∴ पार्क का क्षेत्रफल = l × b
= 10 × 5 = 50 m²

(ii) फूलों की क्यारी की त्रिज्या (r) = 2 m
∴ फूलों की क्यारी का क्षेत्रफल = 2
= 3.14 × 2 × 2
= 12.56 m²

(iii) फूलों की क्यारी को छोड़कर शेष भाग का क्षेत्रफल
= पार्क का क्षेत्रफल – क्यारी का क्षेत्रफल
= 50 m² – 12.56 m²
= 37.44 m²

(iv) क्यारी की परिधि = 2πr
= 2 × 3.14 × 2
= 12.56 m

प्रश्न 10.
दी गई आकृति में छायांकित भाग का क्षेत्रफल ज्ञात कीजिए।

हल:
(i) आयत ABCD का क्षेत्रफल
= l × b = 18 × 10 = 180 cm²
∆ AEF का क्षेत्रफल = \(\frac { 1 }{ 2 } \) × b × h
= \(\frac { 1 }{ 2 } \) × 10 × 6 = 30 cm²
∆ CBE का क्षेत्रफल = \(\frac { 1 }{ 2 } \) × b × h
= \(\frac { 1 }{ 2 } \) × 8 × 10 = 40 cm²
∴ छायांकित भाग का क्षेत्रफल
= आयत ABCD का क्षेत्रफल
-(∆ AEF का क्षेत्रफल + ∆ CBE का क्षेत्रफल)
= 180 cm2 – (30 cm2 + 40 cm²)
= 180 cm2 – 70 cm = 110 cm²

(ii) वर्ग PQRS का क्षेत्रफल
= भुजा × भुजा
= 20 × 20 = 400 cm²
∆ PQT का क्षेत्रफल = \(\frac { 1 }{ 2 } \) × b × h
\(\frac { 1 }{ 2 } \) × 20 × 10 = 100 cm²
∆ QRU का क्षेत्रफल = \(\frac { 1 }{ 2 } \) × b × h
\(\frac { 1 }{ 2 } \) × 10 × 20 = 100 cm²
∆ TSU का क्षेत्रफल = \(\frac { 1 }{ 2 } \) × b × h
= \(\frac { 1 }{ 2 } \) × 10 × 10 = 50 cm²
अब, छायांकित भाग का क्षेत्रफल = PQRS का क्षेत्रफल
– (∆ PQT का क्षेत्रफल + ∆ QRU का क्षेत्रफल + ∆ TSU का क्षेत्रफल)
= 400 cm² – (100 cm² + 100 cm² + 50 cm²)
= 400 cm² – 250 cm² = 150 cm²

प्रश्न 11.
चतुर्भुज ABCD का क्षेत्रफल ज्ञात कीजिए। यहाँ, AC = 22 cm, BM = 3 cm, DN = 3 cm, और BM ⊥ AC, DN ⊥ AC.

हल:
∆ ABC का क्षेत्रफल = \(\frac { 1 }{ 2 } \) × b × h
\(\frac { 1 }{ 2 } \) × 22 × 3 = 33 cm²
∆ ACD का क्षेत्रफल = \(\frac { 1 }{ 2 } \) × b × h
= \(\frac { 1 }{ 2 } \) × 22 × 3 = 33 cm²
∴ चतुर्भुज ABCD का क्षेत्रफल
= ∆ABC का क्षेत्रफल + ∆ACD का क्षेत्रफल
= 33 cm² + 33 cm² = 66 cm²

MP Board Class 7th Maths Solutions