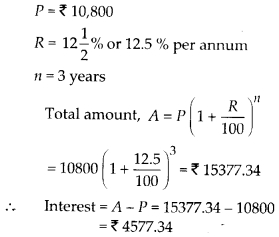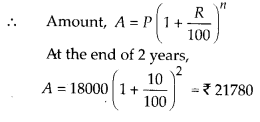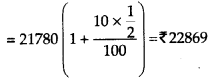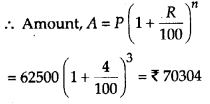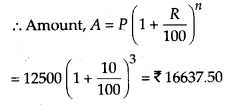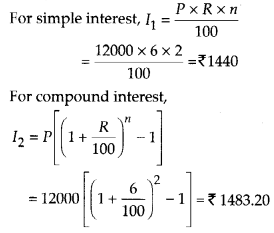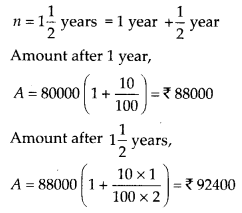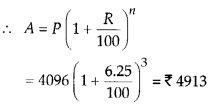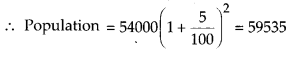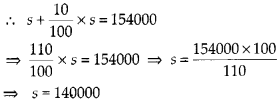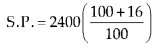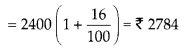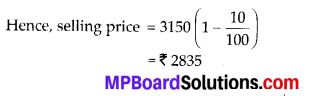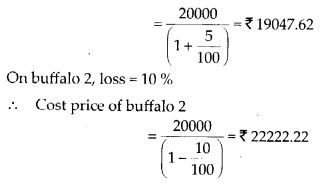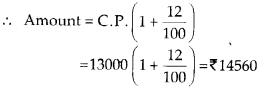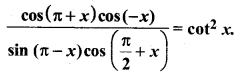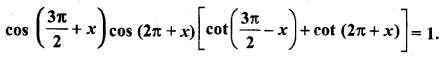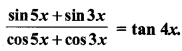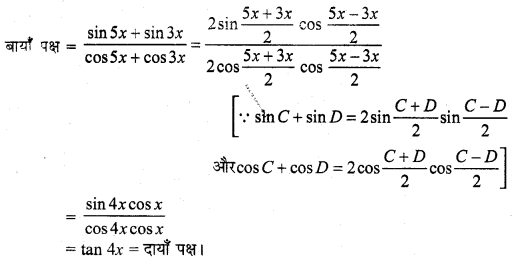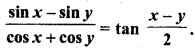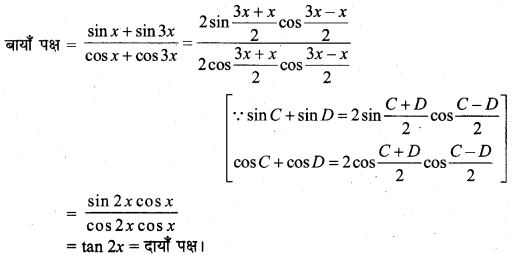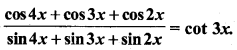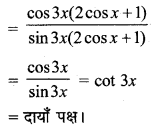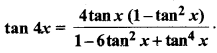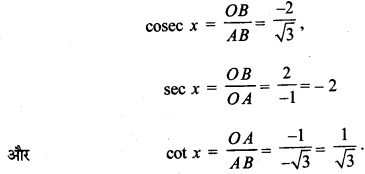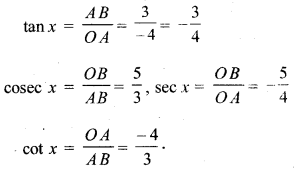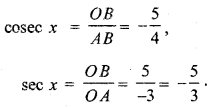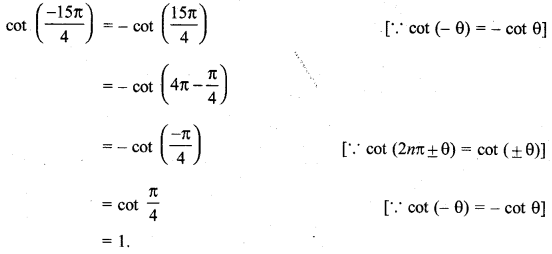Bhagya

MP Board Class 10th General Hindi व्याकरण शब्द विचार

प्रश्न 1.
शब्द की परिभाषा दें।
उत्तर-
शब्द की परिभाषा-निश्चित अर्थ को प्रकट करने वाले वर्ण-समूह को शब्द कहते हैं। जैसे-घर, रोटी, अर्थ, विचार, शब्द आदि।

प्रश्न 2.
शब्द के कितने रूप हैं? उदाहरण सहित समझाएँ।
उत्तरउत्पत्ति के आधार पर हिंदी में शब्द के चार भेद हैं

1. तत्सम,
2. तद्भव,
3. देशज,
4. विदेशी।

1. तत्सम-संस्कृत भाषा के ऐसे शब्द, जो हिंदी में भी अपने मूल रूप में प्रचलित हैं, तत्सम कहलाते हैं। जैसे-वायु, नारी, सत्य, छात्र, समुद्र आदि।
2. तद्भव-जो शब्द संस्कृत भाषा के शब्दों से बिगड़ कर हिंदी में प्रचलित हैं, तद्भव कहलाते हैं। जैसे-सपना (स्वप्न), दूध (दुग्ध)।
3. देशज-जो शब्द स्थानीय पदार्थ के रूप में, कार्य के रूप में अथवा ध्वनि के अनुसार प्रसिद्ध और प्रचलित हैं, देशज कहलाते हैं। ये शब्द देश की विभिन्न बोलियों से लिये गए हैं। जैसे–पेट, खिड़की, थूक, चीनी।
4. विदेशी-वे शब्द, जो अंग्रेज़ी, अरबी, फारसी, तुर्की, पुर्तगाली, फ्रांसीसी आदि विदेशी भाषाओं से हिंदी में आए हैं, विदेशी कहलाते हैं। जैसे-स्कूल, बटन, आलू, गरीब, किताब, लाश।

प्रश्न 3.
तत्सम एवं तद्भव शब्द रूपों के अन्तर उदाहरण सहित समझाएँ।
उत्तर-
तत्सम और तद्भव शब्द-

तत्सम शब्द-
हिंदी में संस्कृत के कुछ शब्दों को ज्यों का त्यों (यथावत्) ले लिया है। ऐसे शब्द तत्सम कहलाते हैं।

तद्भव शब्द-
संस्कृत के कुछ शब्द ऐसे हैं, जिनका रूप परिवर्तन करके हिंदी में अपनाया गया है। ऐसे शब्दों को तद्भव शब्द कहते हैं। यहाँ कुछ तद्भव शब्द और उनके तत्सम रूप दिए जा रहे हैं

प्रश्न 4.
हिन्दी में प्रयुक्त होने वाले कुछ विदेशी शब्दों के उदाहरण दें?
उत्तर-
अंग्रेजी-स्टेशन, राशन, सिनेमा, टेलीविजन, टिकट, फीस, रेडियो, डॉक्टर, बैंक आदि।
अरबी-मौलवी, अदालत, अमीर, मालिक, दुनिया, फकीर, तारीख, किताब, कसर आदि।
फारसी-जिंदगी, बाग, चश्मा, खरगोश, चाकू, कारखाना, रूमाल, शिकायत, जल्दी, खरीद, तमाम, ज़मीन, फौज़, काग़ज़, हज़ार, दुकान, बादाम आदि।
पुर्तगाली-प्याला, आलू, साबुन, नीलाम, पिस्तौल, आदि।
ग्रीक-सुरंग, दाम आदि।
तुर्की-दारोगा, तमगा, काबू, लाश, कालीन, तोप आदि।
फ्रांसीसी-कूपन, अंगरेज़, कारतूस आदि।

MP Board Class 10th Hindi Solutions

MP Board Class 11th Maths Solutions Chapter 3 त्रिकोणमितीय फलन विविध प्रश्नावली

प्रश्न 1.
सिद्ध कीजिए :
2 cos \(\frac{\pi}{13}\) cos\(\frac{9 \pi}{13}\) + cos\(\frac{3 \pi}{13}\) + cos\(\frac{5 \pi}{13}\) = 0.
हल:
बायाँ पक्ष =
2 cos \(\frac{\pi}{13}\) cos\(\frac{9 \pi}{13}\) + cos\(\frac{3 \pi}{13}\) + cos\(\frac{5 \pi}{13}\)

प्रश्न 2.
सिद्ध कीजिए : (sin 3x + sin x) sin x + (cos 3x – cos x) cos x = 0.
हल:
बायाँ पक्ष = (sin 3x + sin x) sin x + (cos 3x – cos x) cosx
= sin 3x sin x + sin²x + cos 3x cos x – cos²x
= (cos 3x cos x + sin 3x sin x) – (cos² x – sin²x)
= cos 2x – cos 2x
= 0 [∵ cos (A – B) = cos A cos B + sin A sin B]
= दायाँ पक्ष।

प्रश्न 3.
सिद्ध कीजिए : (cos x + cos y)² + (sin x – sin y)² = 4 cos²\(\frac{x+y}{2}\).
हल:
बायाँ पक्ष = (cos x + cos y)² + (sin x – sin y)²

प्रश्न 4.
सिद्ध कीजिए : (cos x – cos y)² + (sin x – sin y)² = 4 sin\(\frac{x-y}{2}\).
हल:
बायाँ पक्ष = (cos x – cos y)² + (sin x – sin y)²

प्रश्न 5.
सिद्ध कीजिए : sin x + sin 3x + sin 5x + sin 7x = 4 cos x cos 2x sin 4x.
हल:
बायाँ पक्ष = sin x + sin 3x + sin 5x + sin 7x
= (sin 7x + sin x) + (sin 5x + sin 3x)


= 4 sin 4x cos 2x cos x
= 4 cos x cos 2x sin 4x
= दायाँ पक्ष।

प्रश्न 6.
सिद्ध कीजिए :

हल:

प्रश्न 7.
सिद्ध कीजिए : sin 3x + sin 2x – sin x = 4 sin cos \(\frac{x}{2}\) cos \(\frac{3x}{2}\)
हल:
बायाँ पक्ष = sin 3x + (sin 2x – sin x)

निम्नलिखित प्रत्येक प्रश्न में sin \(\frac{x}{2}\), cos \(\frac{x}{2}\), और tan \(\frac{x}{2}\), ज्ञात कीजिए।
प्रश्न 8.
tan x = –\(\frac{4}{3}\), x द्वितीय चतुर्थाश में हैं।
हल:
∵ x दूसरे चतुर्थांश में है, ∴ \(\frac{x}{2}\) पहले चतुर्थांश में है इसलिए sin \(\frac{x}{2}\), cos \(\frac{x}{2}\), और tan \(\frac{x}{2}\), धनात्मक होंगे।

प्रश्न 9.
cos x = \(-\frac{1}{3}\), x तीसरे चतुर्थांश में है।
हल:
x, तीसरे चतुर्थांश में है।
अर्थात 180° < x < 270°
90° < \(\frac{x}{2}\) < 135
⇒ \(\frac{x}{2}\) दूसरे चतुर्थांश में है।

प्रश्न 10.
sin x = \(\frac{1}{4}\) द्वितीय चतुर्थाश में है।
हल:
x, दूसरे चतुर्थांश में है।
⇒ 90° < \(\frac{x}{2}\) < 180°
2 से भाग देने पर 45° < \(\frac{x}{2}\) < 90°
⇒ \(\frac{x}{2}\) पहले चतुर्थाश में है

MP Board Class 11th Maths Solutions

MP Board Class 8th Maths Solutions Chapter 14 Factorization Ex 14.4

Find and correct the errors in the following mathematical statements.
Question 1.
4(x – 5) = 4x – 5
Solution:
The given statement is incorrect.
The correct statement is 4(x – 5) = 4x – 20.

Question 2.
x(3x + 2) = 3x² + 2
The given statement is incorrect.
The correct statement is x(3x + 2) = 3x² + 2x.

Question 3.
2x + 3y = 5xy
Solution:
The given statement is incorrect.
The correct statement is 2x + 3y = 2x + 3y.

Question 4.
x + 2x + 3x = 5x
Solution:
The given statement is incorrect.
The correct statement is x + 2x + 3x = 6x.

Question 5.
5y + 2y + y – 7y = 0
Solution:
The given statement is incorrect.
The correct statement is 5y + 2y + y – 7y = y.

Question 6.
3x + 2x = 5x²
The given statement is incorrect.
The correct statement is 3x + 2x = 5x.

Question 7.
(2x)² + 4(2x) + 7 = 2x² + 8x + 7
EH The given statement is incorrect.
The correct statement is (2x)² + 4(2x) + 7
= 4x² + 8x + 7.

Question 8.
(2x)² + 5x = 4x + 5x = 9x
EH The given statement is incorrect.
The correct statement is (2x)² + 5x = 4x² + 5x.

Question 9.
(3x + 2)² = 3x² + 6x + 4
Solution:
The given statement is incorrect.
The correct statement is (3x + 2)²
= (3x)² + 2(3x)(2) + 2² = 9x² + 12x + 4.

Question 10.
Substituting x = -3 in
(a) x² + 5x + 4
gives (-3)² + 5 (-3) + 4 = 9 + 2 + 4 = 15
(b) x² – 5x + 4
gives (-3)² – 5(-3) + 4 = 9 – 15 + 4 = -2
(c) x² + 5x gives (-3)² + 5 (-3) = -9 -15 = – 24
Solution:
(a) Incorrect statement
Substituting x = -3 in x² + 5x + 4 gives
(-3)² + 5(-3) + 4 = 9 – 15 + 4 = -2
(b) Incorrect statement
Substituting x = -3 in x² – 5x + 4 gives
(-3)² – 5(-3) + 4 = 9 + 15 + 4 = 28
(c) Incorrect statement
Substituting x = -3 in x² + 5x gives
(-3)² + 5(-3) = 9 – 15 = – 6

Question 11.
(y – 3)² = y² – 9
Solution:
The given statement is incorrect.
The correct statement is (y – 3)² = y² – 6y + 9

Question 12.
(z + 5)² = z² + 25
Solution:
The given statement is incorrect.
The correct statement is (z + 5)² = z² + 10z + 25

Question 13.
(2a + 3b)(a – b) = 2a² – 3b²
Solution:
The given statement is incorrect.
The correct statement is (2a + 3b)(a – b)
= 2a(a – b) + 3b(a – b)
= 2a² – 2ab + 3ab – 3b²
= 2a² + ab – 3b²

Question 14.
(a + 4)(a + 2) = a² + 8
Solution:
The given statement is incorrect.
The correct statement is (a + 4) (a + 2)
= a(a + 2) + 4 (a + 2)
= a² + 2a + 4a + 8 = a² + 6a + 8

Question 15.
(a – 4)(a – 2) = a² – 8
Solution:
The given statement is incorrect.
The correct statement is (a – 4) (a – 2)
= a(a – 2) – 4(a – 2) = a² – 2a – 4a + 8
= a² – 6a + 8

Question 16.
\(\frac{3 x^{2}}{3 x^{2}}\) = o
Solution:
The given statement is incorrect.
The correct statement is
\(\frac{3 x^{2}}{3 x^{2}}\) = 1

Question 17.
\(\frac{3 x^{2}+1}{3 x^{2}}\) = 1 + 1 = 2
Solution:
The given statement is incorrect.
The correct statement is
\(\frac{3 x^{2}+1}{3 x^{2}}=\frac{3 x^{2}}{3 x^{2}}+\frac{1}{3 x^{2}}=1+\frac{1}{3 x^{2}}\)

Question 18.
\(\frac{3 x}{3 x+2}=\frac{1}{2}\)
Solution:
The given statement is incorrect.
The correct statement is
\(\frac{3 x}{3 x+2}=\frac{3 x}{3 x+2}\)

Question 19.
\(\frac{3}{4 x+3}=\frac{1}{4 x}\)
Solution:
The given statement is incorrect.
The correct statement is \(\frac{3}{4 x+3}=\frac{3}{4 x+3}\)

Question 20.
\(\frac{4 x+5}{4 x}\) = 5
Solution:
The given statement is incorrect.
The correct statement is
\(\frac{4 x+5}{4 x}=\frac{4 x}{4 x}+\frac{5}{4 x}=1+\frac{5}{4 x}\)

Question 21.
\(\frac{7 x+5}{5}\) = 7x
Solution:
The given statement is incorrect.
The correct statement is
\(\frac{7 x+5}{5}=\frac{7 x}{5}+\frac{5}{5}=\frac{7 x}{5}+1\)

MP Board Class 8th Maths Solutions

MP Board Class 10th General Hindi व्याकरण वर्तनी

प्रश्न 1.
वर्तनी की परिभाषा दें।
उत्तर-
‘वर्तनी’ का अर्थ है उच्चारण के अनुरूप वर्ण-विन्यास। इसे अंग्रेजी में (spelling) कहते हैं। सामान्यतया लिखने की रीति को वर्तनी कहते हैं। वर्तनी की शुद्धता के लिए उच्चारण की शुद्धता आवश्यक है। यदि उच्चारण गलत हुआ तो वर्तनी भी गलत होती है।

प्रश्न 2.
वर्तनी संशोधन के नियमों पर प्रकाश डालें।
उत्तर-
वर्तनी संबंधी कुछ नियम हैं, जिनका पालन करने से शब्दों के शुद्ध रूप लिखे जा सकते हैं।
1. किसी भी स्वर के साथ किसी अन्य स्वर की मात्रा नहीं लगनी चाहिए।

जैसे-

‘अ’ अिस, ओक, अपर-ये अशुद्ध रूप हैं।
इस, एक, ऊपर-ये शुद्ध रूप हैं।

2. भाववाची-ति, नि, धि, टि से समाप्त होने वाली स्त्रीलिंग संज्ञाओं की अंतिम ‘इ’ ह्रस्व होती है।

जैसे-

भक्ति, शक्ति, नीति, प्रीति, रीति, जाति आदि।

3. संस्कृत के तत्सम पुल्लिंग शब्द के अंतिम इ, उ, प्रायः ह्रस्व होते हैं।

जैसे-

कवि, कपि, हरि, रवि, वाल्मीकि, उदधि आदि।

4. तद्भव तथा विदेशी भाषाओं में आए पुल्लिंग शब्दों के अंतिम इ, उ दीर्घ होते हैं।

जैसे-

अंग्रेजी, फ्रांसीसी, आलू, भालू, डाकू, लड़ाकू।

5. ‘ऋ’ स्वर है। कभी-कभी उसका उच्चारण, रि, रु इस प्रकार करके इसी से शब्द लिखते हैं, वह अशुद्ध रूप है। ‘ऋ’ प्रारंभ में लगने वाले शब्द को ‘र’ से नहीं ‘ऋ’ से लिखना चाहिए

जैसे-

ऋतु लिखना चाहिए, रितु नहीं।
शुद्ध रूप-ऋचा, ऋग्वेद, ऋण, वृष्टि, कृषक, कृष्ण, तृण, तृष्णा आदि।

6. ‘घ’ तथा ‘ध’ वाले शब्द-‘घ’-घर, घोड़ा, घनश्याम, घड़ा, घमण्ड आदि।

‘ध’-धैर्य, धर्म, धन, धमाका, धाम आदि।

7. ‘व’ और ‘ब’ में अंतर-‘व’ के उच्चारण में होठ’ (ओठ) खुले रहते हैं और ‘ब’ के उच्चारण में बंद हो जाते हैं।

‘व’ वाले शब्द-वह, वर्ण, विवाहर, विश्व इत्यादि।
‘ब’ वाले शब्द-बाहर, बंद, बंदर, बँटवारा, बाप, बतासा, बनावट, बारात इत्यादि।

8. श, ष, स का अन्तर-‘श’ वाले शब्द-शहर, शरबत, शेर इत्यादि।

‘ष’ वाले शब्द-षट्कोण, नष्ट, कष्ट, राष्ट्र, युधिष्ठिर, विशिष्ट इत्यादि।
‘स’ वाले शब्द-समाज, सपेरा, समय, सावन, स्वागत, सरौता, सबेरा, स्वर्ग इत्यादि।

प्रश्न 3.
परसर्ग या कारक चिह्न का प्रयोग कहाँ किया जाता है?
उत्तर-
परसर्ग या कारक चिह्न का प्रयोग-संज्ञा शब्दों के साथ होना चाहिए। इस प्रकार जैसे-राम ने, मोहन को, घर में सर्वनाम के साथ प्रयोग-जैसे-मैंने, आपने, उन्होंने, उनको, जिसको इत्यादि।

प्रश्न 4.
योजक चिह्न का प्रयोग सोदाहरण समझाइये।
उत्तर-
योजक चिह्न का प्रयोग समानपद में करना चाहिए।

जैसे-

माता-पिता,
भाई-बहन,
पाप-पुण्य,
सरस्वती – वन्दना,
शोध-संस्था,
रात-दिन आदि।

प्रश्न 5.
शुद्ध एवं अशुद्ध वर्तनी को उदाहरण सहित समझाएँ।
उत्तर-
जैसे-

प्रश्न 6.
वर्ण तथा शब्द में क्या अंतर है?
उत्तर-
ध्वनि का लिखित रूप वर्ण कहलाता है। वर्ण भाषा की सबसे छोटी इकाई है। इन्हें विभाजित नहीं किया जा सकता, परन्तु वर्णों के सार्थक समूह से शब्दों का निर्माण होता है।

जैसे-

अ, आ, इ, ई वर्ण हैं जबकि र् + आ + म् + अ = ‘राम’ शब्द है।

प्रश्न 7.
हिन्दी की लिपि का नाम बताएँ।
उत्तर-
हिन्दी की लिपि का नाम देवनागरी लिपि है। प्रश्न 8. वर्तनी के नियमों में से कोई भी दो नियम लिखिए।
उत्तर-
1. किसी भी स्वर के साथ किसी अन्य स्वर की मात्रा नहीं लगती है।

जैसे-

अशुद्ध-ओक, शुद्ध-एक।

2. ‘ऋ’ स्वर का शुद्ध उच्चारण

जैसे-

रितु-अशुद्ध, ऋतु-शुद्ध शब्द है।

प्रश्न 9.
मानक वर्तनी क्या है? सोदाहरण समझाएँ।
उत्तर-
वर्तनी संबंधी कुछ महत्वपूर्ण नियम हैं। शुद्ध शब्द उच्चारण के लिए, उनका पालन करने से मानक शुद्ध वर्तनी प्रस्तुत होती है।
जैसे-
‘ष’ के स्थान पर ‘श’ संबंधी अशुद्धियाँ।
अशुद्ध शब्द – मानक (शुद्ध) वर्तनी
द्वेश – द्वेष
निर्दोष – निर्दोश

प्रश्न 10.
निम्नांकित शब्दों के (मानक) शुद्ध रूप लिखिए।
उत्तर-
अशुद्ध रूप – मानक (शुद्ध रूप)

1. उज्वल – उज्ज्व ल
2. क्षन – क्षण
3. एकलौता – इकलौता
4. सौंदर्यता – सौंदर्य
5. आशीर्वाद – आशीर्वाद
6. चाहिये – चाहिए
7. अनाधिकार – अनधिकार
8. मैथली – मैथिली
9. उपरोक्त – उपर्युक्त
10. अनुग्रहित – अनुगृहीत

प्रश्न 11.
‘ऋ’ तथा ‘रि’ से बनने वाले कोई चार शब्द लिखिए।
उत्तर-
‘रि’ –

1. रिगवेद
2. रितु
3. रिषि
4. रिचा।।

‘ऋ’ –

1. ऋग्वेद
2. ऋतु
3. ऋषि
4. ऋचा।

MP Board Class 10th Hindi Solutions

MP Board Class 10th General Hindi व्याकरण प्रत्यय

प्रश्न 1.
प्रत्यय किसे कहते हैं?
उत्तर-
मूल शब्दों के अंत में जो शब्दांश जुड़कर नये शब्द बनाए जाते हैं, उन्हें प्रत्यय कहते हैं। दूसरे शब्दों में जो शब्दांश शब्द के अंत में जुड़कर नये-नये शब्दों का निर्माण करते हैं, उन्हें प्रत्यय कहते हैं।

प्रश्न 2.
प्रत्यय कितने प्रकार के होते हैं? उत्तर-प्रत्यय दो प्रकार के होते हैं-कृत और तद्धित।

प्रश्न 3.
कृत प्रत्यय को सोदाहरण समझाएँ:
उत्तर-
कृत प्रत्यय-क्रिया शब्दों के अंत में जो शब्दांश जोड़े जाते हैं, वे कृत प्रत्यय कहलाते हैं,

जैसे-

पढ़ना + ई = पढ़ाई ; लिखना + ई = लिखाई।

क्रिया में प्रत्यय जोड़कर संज्ञाएँ भी बनाई जाती हैं और विशेषण भी। संज्ञा बनाने वाले हिंदी के प्रमुख कृत् प्रत्यय निम्नलिखित हैं-

विशेषण बनाने वाले प्रत्यय

प्रश्न 4.
तद्धित प्रत्यय को सोदाहरण समझाएँ।
उत्तर-
तद्धित प्रत्यय-जो प्रत्यय संज्ञा, सर्वनाम, विशेषण के साथ जुड़कर नये शब्द बनाते हैं, उन्हें तद्धित प्रत्यय कहते हैं।

संज्ञा बनाने वाले तद्धित प्रत्यय-

विशेषण बनाने वाले तद्धित प्रत्यय-

MP Board Class 10th Hindi Solutions

MP Board Class 8th Maths Solutions Chapter 14 Factorization Ex 14.3

Question 1.
Carry out the following divisions.
(i) 28x⁴ ÷ 56x
(ii) -36y³ ÷ 9y²
(iii) 66pq²r³ ÷ 11qr²
(iv) 34x³y³z³ ÷ 51 xy²z³
(v) 12a⁸b⁸ ÷ (- 6a⁶b⁴).
Solution:
(i) 28x⁴ ÷ 56x

Question 2.
Divide the given polynomial by the given monomial.
(i) (5x² – 6x) ÷ 3x
(ii) (3y⁸ – 4y⁶ + 5y⁴) ÷ y⁴
(iii) 8(x³y²z² + x²y³z² + x²y²z³) ÷ 4x²y²z²
(iv) (x³ + 2x² + 3x) ÷ 2x
(v) (p³q⁶ – p⁶q³) ÷ p³q³
Solution:
(i) We have

Question 3.
Work out the following divisions.
(i) (10x – 25) ÷ 5
(ii) (10x- 25) ÷ (2x- 5)
(iii) 10y(6y + 21) ÷ 5(2y + 7)
(iv) 9x²y²(3z – 24) ÷ 27xy(z – 8)
(v) 96abc(3a -12)(5b – 30) ÷ 144(a – 4)(b – 6)
Solution:
(i) We have,
(10x – 25) ÷ 5 = \(\frac{10 x-25}{5}\)
= \(\frac{5(2 x-5)}{5}\) = (2x – 5)

(ii) We have,

Question 4.
Divide as directed.
(i) 5(2x + 1 )(3x + 5) ÷ (2x + 1)
(ii) 26xy(x + 5)(y – 4) ÷ 13x(y – 4)
(iii) 52pqr (p + q)(q + r)(r + p) ÷ 104pq(q + r)(r + p)
(iv) 20(y + 4) (y² + 5y + 3) ÷ 5(y + 4)
(v) x(x + 1)(x + 2)(x + 3) ÷ x(x + 1)
Solution:
(i) We have, 5(2x + 1)(3x + 5) ÷ (2x + 1)

Question 5.
Factorise the expressions and divide them as directed.
(i) (y² + 7y + 10) ÷ (y + 5)
(ii) (m² – 14m – 32) ÷ (m + 2)
(iii) (5p² – 25p + 20) ÷ (p – 1)
(iv) 4yz(z² + 6z – 16) ÷ 2y(z + 8)
(v) 5pq(p² – q²) ÷ 2p(p + q)
(vi) 12xy(9x² – 16y²) ÷ 4xy(3x + 4y)
(vii) 39y³(50y² – 98) ÷ 26y²(5y + 7)
Solution:
(i) We have, y² + 7y + 10
= y² + 5y + 2y + 10
= y(y + 5) + 2(y + 5) = (y + 2) (y + 5)

MP Board Class 8th Maths Solutions

MP Board Class 11th Maths Solutions Chapter 3 त्रिकोणमितीय फलन Ex 3.4

निम्नलिखित समीकरणों का मुख्य तथा व्यापक हल ज्ञात कीजिए (प्रश्न 1 से 4 तक) :
प्रश्न 1.
tan x = \( \sqrt{{3}} \).
हल:

प्रश्न 2.
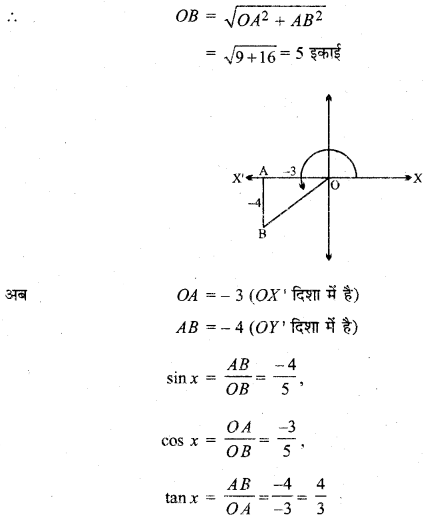
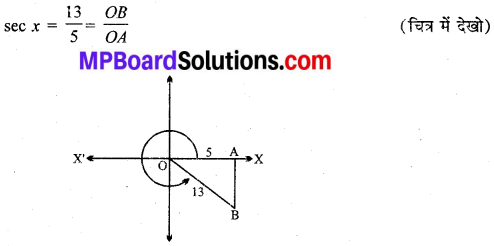
secx = 2.
हल:

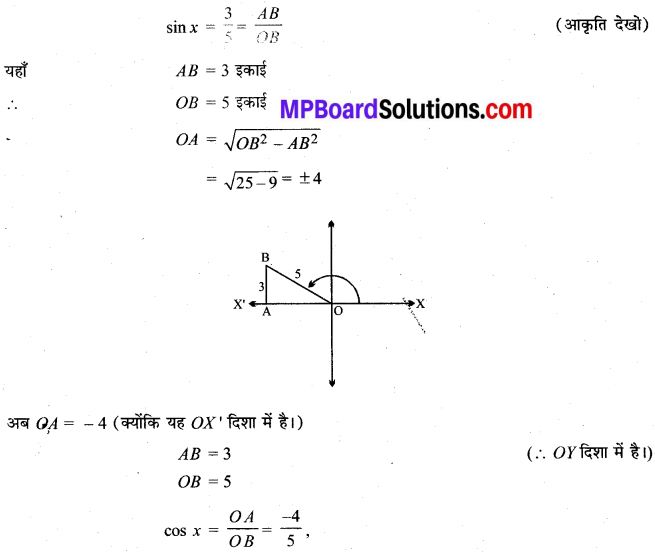
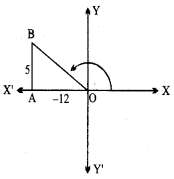
प्रश्न 3.
cot x = \(– \sqrt{{3}} \).
हल:

प्रश्न 4.
cosecx = – 2.
हल:

निम्नलिखित में से प्रत्येक समीकरण का व्यापक हल ज्ञात कीजिए (प्रश्न 5 से 9 तक) :
प्रश्न 5.
cos 4x = cos 2x.
हल:
cos 4x = cos 2x
या cos 4x – cos 2x = 0

प्रश्न 6.
cos 3x + cosx – cos 2x = 0.
हल:
cos 3x + cos x – cos 2x = 0

प्रश्न 7.
sin 2x + cos x = 0.
हल:
sin 2x + cos x = 0
∴ 2 sin x cos x + cos x = 0 [∴ sin 2x = 2 sin x cos x]
या cos x (2 sin x + 1) = 0
(i) जब cos x = 0, x = (2n + 1)\(\frac{\pi}{2}\)

प्रश्न 8.
sec² 2x = 1 – tan 2x.
हल:
sec² 2x = 1 – tan 2x
या 1 + tan² 2x = 1 – tan 2x [∵ sec²A = 1 + tan² A]
या tan² 2x + tan 2x = 0
या tan 2x (tan 2x + 1) = 0
∴ tan 2x = 0, y tan 2x + 1 = 0

प्रश्न 9.
sin x + sin 3x + sin 5x = 0.
हल:
sin x + sin 3x + sin 5x = 0
या (sin 5x + sin x) + sin 3x = 0
या \(2 \sin \frac{5 x+x}{2} \cos \frac{5 x-x}{2}\) + sin 3x = 0 [∵ sin C + sin D = 2 \(\frac{C+D}{2} \cos \frac{C-D}{2}\)]
या 2 sin 3x cos 2x + sin 3x = 0
या sin 3 x (2 cos 2 x + 1) = 0
⇒ sin 3x = 0
या 2 cos 2x + 1 = 0

MP Board Class 11th Maths Solutions

MP Board Class 8th Maths Solutions Chapter 8 Comparing Quantities Ex 8.3

Question 1.
Calculate the amount and compound interest on
(a) ₹ 10,800 for 3 years at 12\(\frac{1}{2}\)% per annum compounded annually.
(b) ₹ 18,000 for 2\(\frac{1}{2}\) years at 10% per annum compounded annually.
(c) ₹ 62,500 for 1\(\frac{1}{2}\) years at 8% per annum compounded half yearly.
(d) ₹ 8,000 for 1 year at 9% per annum compounded half yearly.
(e) ₹ 10,000 for 1 year at 8% per annum compounded half yearly.
Solution:
(a) We have,

(b) We have,
P = ₹ 18000
R = 10 % per annum
n = 2\(\frac{1}{2}\) years or 2.5 years

Now, we calculate S.I. on this amount for \(\frac{1}{2}\) year at 10 % per annum.
∴ Amount after 2.5 years

∴ Interest = A – P = 22869 -18000 = ₹ 4869

(c) We have,
P = ₹ 62500
R = 8 % per annum = 4 % per half year
n = 1\(\frac{1}{2}\) years = 3 half years

∴ Interest = A – P = 70304 – 62500 = ₹ 7804

(d) We have,
P = ₹ 8000
R = 9 % per annum
= 4 % per half year
n = 1 year = 2 half years

∴ Interest = A – P = 8736.20 – 8000 = ₹ 736.20

(e) We have,
P = ₹ 10000
R = 8% per annum = 4 % per half year
n = 1 year = 2 half years

∴ Interest = A – P = 10816 -10000 = ₹ 816

Question 2.
Kamla borrowed ₹ 26,400 from a bank to buy a scooter at a rate of 15% per annum compounded yearly. What amount will she pay at the end of 2 years and 4 months to clear the loan?
(Hint : Find 4 for 2 years with interest is compounded yearly and then find SI on the 2nd year amount for \(\frac{4}{12}\) years).
Solution:
We have,
P = ₹ 26400
R = 15 % per annum
n = 2 years 4 months
At the end of 2 years,

Now, P = ₹ 34914
R = 15 % per annum
n = 4 months = \(\frac{1}{3}\) years
At the end of 2 years and 4 months,

Question 3.
Fabina borrows ₹ 12,500 at 12% per annum for 3 years at simple interest and Radha borrows the same amount for the same time period at 10% per annum, compounded annually. Who pays more interest and by how much?
Solution:
For Fabina, P = ₹ 12500
R = 12 % per annum
n = 3 years
For simple interest,

Interest = 17000 – 12500 = ₹ 4500
For Radha, P = ₹ 12500
R = 10 % per annum
n = 3 years
As this is compound interest

Interest = 16637.50 -12500 = ₹ 4137.50
Hence, Fabina pays more interest by 4500 – 4137.50 = ₹ 362.50

Question 4.
I borrowed ₹ 12,000 from Jamshed at 6% per annum simple interest for 2 years. Had I borrowed this sum at 6% per annum compound interest, what extra amount would I have to pay?
Solution:
We have, P = ₹ 12000
R = 6 % per annum
n = 2 years

So, the extra amount he would have to pay = 1483.20 -1440 = ₹ 43.20

Question 5.
Vasudevan invested X 60,000 at an interest rate of 12% per annum compounded half yearly. What amount would he get
(i) after 6 months?
(ii) after 1 year?
Solution:
We have,
P = ₹ 60000
R = 12 % per annum = 6 % per half year
(i) n = 6 months = 1 half year

Question 6.
Arif took a loan of ₹ 80,000 from a bank. If the rate of interest is 10% per annum, find the difference in amounts he would be paying after 1\(\frac{1}{2}\) years if the interest is
(i) compounded annually.
(ii) compounded half yearly.
Solution:
We have,
P = ₹ 80000
R = 10 % per annum = 5 % per half year
(i) If the interest is compounded annually

(ii) If interest is compounded half yearly

∴ Difference in amounts = 92610 – 92400
= ₹ 210

Question 7.
Maria invested ₹ 8,000 in a business. She would be paid interest at 5% per annum compounded annually. Find
(i) The amount credited against her name at the end of the second year.
(ii) The interest for the 3rd year.
Solution:
We have,
P = ₹ 8000
R = 5 % per annum
(i) n = 2 years

(ii) n = 3 years

Hence, interest for 3^rd year = 9261 – 8820 = ₹ 441

Question 8.
Find the amount and the compound interest on ₹ 10,000 for 1\(\frac{1}{2}\) years at 10% per annum, compounded half yearly. Would this interest be more than the interest he would get if it was compounded annually? Solution:
We have,
P = ₹ 10000
R = 10 % per annum = 5 % per half year
n = 1\(\frac{1}{2}\) years = 3 half years
(i) If interest is compounded half yearly

Interest = 11576.25 – 10000 = ₹ 1576.25

(ii) If interest is compounded annually Amount after 1 year,

Thus, more interest would be generated if interest is calculated half yearly.

Question 9.
Find the amount which Ram will get on ₹ 4096, if he gave it for 18 months at 12\(\frac{1}{2}\) % per annum, interest being compounded half yearly.
Solution:
We have,
P = ₹ 4096
R = 12.5 % per annum = 6.25 % per half year
n = 18 months = 3 half years

Question 10.
The population of a place increased to 54,000 in 2003 at a rate of 5% per annum
(i) find the population in 2001.
(ii) what would be its population in 2005?
Solution:
We have, population in 2003 = 54000
Rate = 5% per annum
(i) Let population in 2001 be x.
The population in 2003

∴ Population = 48980 in 2001

(ii) For population in 2005
n = 2 years

Question 11.
In a laboratory, the count of bacteria in a certain experiment was increasing at the rate of 2.5% per hour. Find the bacteria at the end of 2 hours if the count was initially 5,06,000.
Solution:
Initial count of bacteria = 506000
Rate = 2.5 % per hour
n = 2 hours
∴ Count after 2 hours

Question 12.
A scooter was bought at ₹ 42,000. Its value depreciated at the rate of 8% per annum. Find its value after one year.
Solution:
Initial price = ₹ 42000
Rate of depreciation = 8% per annum
n = 1 year

MP Board Class 8th Maths Solutions

MP Board Class 10th General Hindi व्याकरण उपसर्ग

प्रश्न 1.
उपसर्ग किसे कहते हैं?
उत्तर-
उपसर्ग वे अविकारी (अव्यय) शब्दांश होते हैं, जो किसी शब्द के पूर्व में जुड़कर मूल शब्द के अर्थ में परिवर्तन कर देते हैं।

प्रश्न 2.
उपसर्ग की विशेषता बताइये।
उत्तर-
उपसर्ग किसी भी शब्द को परिवर्तित कर देता है। इससे

1. शब्द के अर्थ में एक नयी विशेषता आ जाती है।
2. शब्द का अर्थ बदल जाता है।
3. कहीं-कहीं शब्द के अर्थ में कोई विशेष अंतर नहीं आता। हिंदी में जो उपसर्ग मिलते हैं, वे संस्कृत, हिंदी और उर्दू भाषा के हैं।

प्रश्न 3.
उपसर्ग कितने तरह के होते हैं? उनके उदाहरण दें।
उत्तर-
संस्कृत उपसर्ग

हिंदी उपसर्ग

MP Board Class 10th Hindi Solutions

MP Board Class 8th Maths Solutions Chapter 14 Factorization Ex 14.2

Question 1.
Factorise the following expressions.
(i) a² + 8o + 16
(ii) p² – 10p + 25
(iii) 25m² + 30m+ 9
(iv) 49y² + 84yz + 36z²
(v) 4x² – 8x + 4
(vi) 121b² – 88bc + 16c²
(vii) (l + m)² – 4lm (Hint: Expand (l + m)² first)
(viii) a⁴ + 2a²b² + b⁴
Solution:
(i) The expression is a² + 8a +16
= a² + 2 × 4 × a + (4)²
= (a + 4)² = (a + 4) (a + 4)

(ii) The expression is p² – 10p + 25
= (p)² – 2 × 5 × p + (5)²
= (P – 5)² = (p – 5)(p – 5)

(iii) The expression is 25m² + 30m + 9
= (5m)² + 2 × 3 × (5m) + (3)² = (5m + 3)²
= (5m + 3) (5m + 3)

(iv) The expression is 49y² + 84yz + 36z²
= (7y)² + 2 × (7y) × (6z) + (6z)² = (7y + 6z)²
= (7y + 6z)(7y + 6z)

(v) The expression is 4x² – 8x + 4
= (2x)² – 2 × (2x) × 2 + (2)² = (2x – 2)²
= [2(x – 1)]² = 4(x – 1)²
= 4(x – 1)(x – 1)

(vi) The expression is 121b² – 88bc + 16c²
= (11b)² – 2 × (11b) (4c) + (4c)² = (11b – 4c)²
= (11b – 4c)(11b – 4c)

(vii) The expression is (l + m)² – 4lm
= l² + 2 × l × m + m² – 4lm [ ∵ (a + b)² = a² + 2ab + b²]
= l² + 2lm + m² – 4lm = l² – 2lm + m²
= (l – m)² = (l – m)(l – m)

(viii)The expression is a⁴ + 2a²b² + b⁴
= (a²)² + 2 × a² × b² + (b²)² = (a² + b²)²
= (a² + b²)(a² + b²)

Question 2.
Factorise.
(i) 4p² – 9q²
(ii) 63a² – 112b²
(iii) 49x² – 36
(iv) 16x⁵ – 144x³
(v) (l + m)² – (l – m)²
(vi) 9x²y² – 16
(vii) (x² – 2xy + y²) – z²
(viii)25a² – 4b² + 28bc – 49c².
Solution:
(i) The expression is 4p² – 9q²
= (2P)² – (3q)² = (2p + 3q) (2p – 3q)

(ii) The expression is 63a² – 112b²
= 7[9a² – 16b²] = 7[(30)² – (4b)²]
= 7(3o + 4b) (3a – 4b).

(iii) The expression is 49x² – 36 = (7x)² – (6)²
= (7x + 6) (7x – 6).

(iv) The expression is 16x⁵ – 144x³
= 16x³(x² – 9) = 16x³ (x² – 3²)
= 16x³ (x + 3)(x – 3).

(v) The expression is (l + m)² – (l – m)²
= (l² + 2lm + m²) – (l² – 2lm + m²)
= l² + 2lm + m² – l² + 2lm – m² = 4lm

(vi) The expression is 9x²y² – 16
= (3xy)² – (4)² = (3xy + 4) (3xy – 4)

(vii) The expression is (x² – 2xy + y²) – z²
= (x – y)² – z² = (x – y + z) (x – y – z)

(viii)The expression is 25a² – 4b² + 28bc – 49c²
= 25a² – [4b² – 28bc + 49c²]
= 25a² – [(2b)² – 2 × (2b) × (7c) + (7c)²]
= (5a)² – (2b – 7c)²
= (5a + 2b – 7c) (5a – 2b + 7c)

Question 3.
Factorise the expressions.
(i) ax² + bx
(ii) 7p² + 21q²
(iii) 2x³ + 2xy² + 2xz²
(iv) am² + bm² + bn² + an²
(v) (lm + l) + m + 1
(vi) y(y + z) + 9(y + z)
(vii) 5y² – 20y – 8z + 2yz
(viii) 10ab + 4a + 5b + 2
(ix) 6xy – 4y + 6 – 9x
Solution:
(i) The expression is ax² + bx = x(ax + b)
(ii) The expression is 7p² + 21q² = 7(p² + 3q² )
(iii) The expression is 2x³ + 2xy² + 2xz²
= 2x(x² + y² + z² ).

(iv) The expression is am² + bm² + bn² + an²
= m² (a + b) + n² (b + a) = (m² + n² ) (a + b)

(v) The expression is (lm + l) + m + 1
= l(m + 1) + 1 (m + 1)= (l + 1) (m + 1)

(vi) The expression is y(y + z) + 9(y + z)
= (y + 9) (y + z).

(vii) The expression is 5y² – 20y – 8z + 2yz
= 5y(y – 4) + 2z(y – 4) = (5y + 2z)(y – 4)

(viii) The expression is 10ab + 4a + 5b + 2
= 2a(5b + 2) + 1 (5b + 2) = (2a + 1) (5b + 2)

(ix) The expression is 6xy – 4y + 6 – 9x
= 2y(3x – 2) – 3 (3x – 2) = (2y – 3) (3x – 2)

Question 4.
Factorise.
(i) a⁴ – b⁴
(ii) p⁴ – 81
(iii) x⁴ – (y + z)⁴
(iv) x⁴ – (x – z)⁴
(v) a⁴ – 2a²b² + b⁴
Solution:
(i) The expression is a⁴ – b²
= (a²)² – (b²)²
= (a² + b²) (a² – b²)
= (a² + b²)(a + b)(a – b).

(ii) The expression is p⁴ – 81 = (p)⁴ – (3)⁴
= (P²)² – (3²)² = (p² + 3²) (p² – 3²)
= (p² + 9) (p + 3) (p – 3)

(iii) The expression is x⁴ – (y + z)⁴
= (x²)² – ((y + z)²)²
= [x² + (y + z)²] [x² – (y + z)²]
= [x² + (y + z)²] (x + y + z) (x – (y + z))
= [x² + (y + z)²] (x + y + z) (x – y – z)

(iv) The expression is x⁴ – (x – z)⁴
= (x²)² – ((x – z)²)²
= (x² – (x – z)²)(x² + (x – z)²)
= (x – x + z)(x + x – z)(x² + x² + z² – 2xz)
= z(2x – z) (2x² – 2xz + z²).

(v) The expression is a⁴ – 2a²b² + b⁴
= (a²)² – 2(a²) (b²) + (b²)² = (a² – b²)²
= [(a + b) (a – b)]² = (a + b)² (a – b)²

Question 5.
Factorise the following expressions.
(i) p² + 6p + 8
(ii) q² – 10q + 21
(iii) p² + 6p – 16
Solution:
(i) The expression is p² + 6p + 8
= p² + 4p + 2p + 8 = p(p + 4) + 2 (p + 4)
= (p + 2) (p + 4)

(ii) The expression is q² – 10q + 21
= q² – 7q – 3q + 21 = q(q – 7) – 3 (q – 7)
= (q – 3) (q – 7)

(iii) The expression is p² + 6p – 16
= p² + 8p – 2p – 16
= p(p + 8) – 2(p + 8) = (p – 2) (p + 8)

MP Board Class 8th Maths Solutions