MP Board Class 8th Maths Solutions Chapter 8 Comparing Quantities Ex 8.3

MP Board Class 8th Maths Solutions Chapter 8 Comparing Quantities Ex 8.3

Question 1.
Calculate the amount and compound interest on
(a) ₹ 10,800 for 3 years at 12\(\frac{1}{2}\)% per annum compounded annually.
(b) ₹ 18,000 for 2\(\frac{1}{2}\) years at 10% per annum compounded annually.
(c) ₹ 62,500 for 1\(\frac{1}{2}\) years at 8% per annum compounded half yearly.
(d) ₹ 8,000 for 1 year at 9% per annum compounded half yearly.
(e) ₹ 10,000 for 1 year at 8% per annum compounded half yearly.
Solution:
(a) We have,

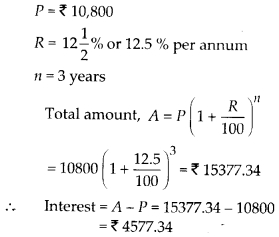
(b) We have,
P = ₹ 18000
R = 10 % per annum
n = 2\(\frac{1}{2}\) years or 2.5 years

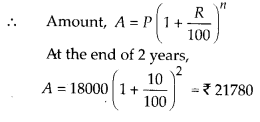
Now, we calculate S.I. on this amount for \(\frac{1}{2}\) year at 10 % per annum.
∴ Amount after 2.5 years

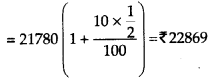
∴ Interest = A – P = 22869 -18000 = ₹ 4869

(c) We have,
P = ₹ 62500
R = 8 % per annum = 4 % per half year
n = 1\(\frac{1}{2}\) years = 3 half years

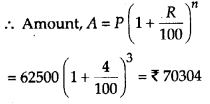
∴ Interest = A – P = 70304 – 62500 = ₹ 7804

(d) We have,
P = ₹ 8000
R = 9 % per annum
= 4 % per half year
n = 1 year = 2 half years

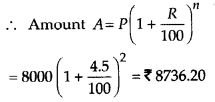
∴ Interest = A – P = 8736.20 – 8000 = ₹ 736.20

(e) We have,
P = ₹ 10000
R = 8% per annum = 4 % per half year
n = 1 year = 2 half years

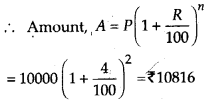
∴ Interest = A – P = 10816 -10000 = ₹ 816

Question 2.
Kamla borrowed ₹ 26,400 from a bank to buy a scooter at a rate of 15% per annum compounded yearly. What amount will she pay at the end of 2 years and 4 months to clear the loan?
(Hint : Find 4 for 2 years with interest is compounded yearly and then find SI on the 2nd year amount for \(\frac{4}{12}\) years).
Solution:
We have,
P = ₹ 26400
R = 15 % per annum
n = 2 years 4 months
At the end of 2 years,

Now, P = ₹ 34914
R = 15 % per annum
n = 4 months = \(\frac{1}{3}\) years
At the end of 2 years and 4 months,

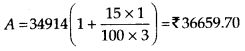
Question 3.
Fabina borrows ₹ 12,500 at 12% per annum for 3 years at simple interest and Radha borrows the same amount for the same time period at 10% per annum, compounded annually. Who pays more interest and by how much?
Solution:
For Fabina, P = ₹ 12500
R = 12 % per annum
n = 3 years
For simple interest,

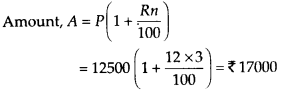
Interest = 17000 – 12500 = ₹ 4500
For Radha, P = ₹ 12500
R = 10 % per annum
n = 3 years
As this is compound interest

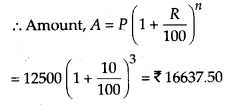
Interest = 16637.50 -12500 = ₹ 4137.50
Hence, Fabina pays more interest by 4500 – 4137.50 = ₹ 362.50

Question 4.
I borrowed ₹ 12,000 from Jamshed at 6% per annum simple interest for 2 years. Had I borrowed this sum at 6% per annum compound interest, what extra amount would I have to pay?
Solution:
We have, P = ₹ 12000
R = 6 % per annum
n = 2 years

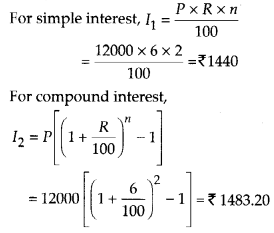
So, the extra amount he would have to pay = 1483.20 -1440 = ₹ 43.20

Question 5.
Vasudevan invested X 60,000 at an interest rate of 12% per annum compounded half yearly. What amount would he get
(i) after 6 months?
(ii) after 1 year?
Solution:
We have,
P = ₹ 60000
R = 12 % per annum = 6 % per half year
(i) n = 6 months = 1 half year

Question 6.
Arif took a loan of ₹ 80,000 from a bank. If the rate of interest is 10% per annum, find the difference in amounts he would be paying after 1\(\frac{1}{2}\) years if the interest is
(i) compounded annually.
(ii) compounded half yearly.
Solution:
We have,
P = ₹ 80000
R = 10 % per annum = 5 % per half year
(i) If the interest is compounded annually

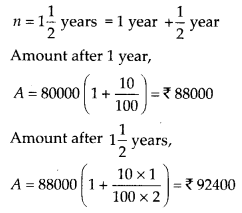
(ii) If interest is compounded half yearly

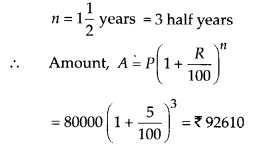
∴ Difference in amounts = 92610 – 92400
= ₹ 210

Question 7.
Maria invested ₹ 8,000 in a business. She would be paid interest at 5% per annum compounded annually. Find
(i) The amount credited against her name at the end of the second year.
(ii) The interest for the 3rd year.
Solution:
We have,
P = ₹ 8000
R = 5 % per annum
(i) n = 2 years

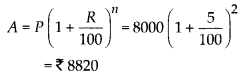
(ii) n = 3 years

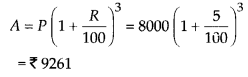
Hence, interest for 3^rd year = 9261 – 8820 = ₹ 441

Question 8.
Find the amount and the compound interest on ₹ 10,000 for 1\(\frac{1}{2}\) years at 10% per annum, compounded half yearly. Would this interest be more than the interest he would get if it was compounded annually? Solution:
We have,
P = ₹ 10000
R = 10 % per annum = 5 % per half year
n = 1\(\frac{1}{2}\) years = 3 half years
(i) If interest is compounded half yearly

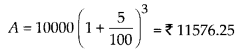
Interest = 11576.25 – 10000 = ₹ 1576.25

(ii) If interest is compounded annually Amount after 1 year,

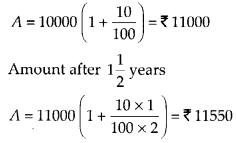
Thus, more interest would be generated if interest is calculated half yearly.

Question 9.
Find the amount which Ram will get on ₹ 4096, if he gave it for 18 months at 12\(\frac{1}{2}\) % per annum, interest being compounded half yearly.
Solution:
We have,
P = ₹ 4096
R = 12.5 % per annum = 6.25 % per half year
n = 18 months = 3 half years

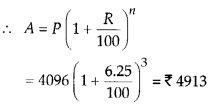
Question 10.
The population of a place increased to 54,000 in 2003 at a rate of 5% per annum
(i) find the population in 2001.
(ii) what would be its population in 2005?
Solution:
We have, population in 2003 = 54000
Rate = 5% per annum
(i) Let population in 2001 be x.
The population in 2003

∴ Population = 48980 in 2001

(ii) For population in 2005
n = 2 years

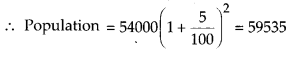
Question 11.
In a laboratory, the count of bacteria in a certain experiment was increasing at the rate of 2.5% per hour. Find the bacteria at the end of 2 hours if the count was initially 5,06,000.
Solution:
Initial count of bacteria = 506000
Rate = 2.5 % per hour
n = 2 hours
∴ Count after 2 hours

Question 12.
A scooter was bought at ₹ 42,000. Its value depreciated at the rate of 8% per annum. Find its value after one year.
Solution:
Initial price = ₹ 42000
Rate of depreciation = 8% per annum
n = 1 year

MP Board Class 8th Maths Solutions