Bhagya

MP Board Class 12th General Hindi व्याकरण पर्यायवाची शब्द

प्रश्न 1.
पर्यायवाची शब्द की परिभाषा सोदाहरण दीजिए।
उत्तर –
पर्यायवाची शब्दों को समानार्थक या प्रतिशब्द भी कहते हैं। जिन शब्दों के अर्थों में समानता हो, उन्हें पर्यायवाची शब्द कहते हैं।

जैसे –
अग्नि – आग, पावक, दहन, अनल, हुताशन, कृशानु।
असुर – दानव, दनुज, दैत्य, राक्षस, तमीचर, रजनीचर।

महत्त्वपूर्ण पर्यायवाची शब्द
1. आकाश – व्योम, गगन, नभ, अम्बर, अन्तरिक्ष, आसमान, अनन्त।
2. कमल – पंकज, सरोज, अरविन्द, शतदल, राजीव, जलज, पद्म, कंज, अम्बुज।
3. चन्द्रमा – हिमांशु, शशि, चन्द्र, सोम, सुधाकर, सुंधाशु, इन्दु, राकापति, राकेश।
4. सूर्य – रवि, दिनकर, भास्कर, पतंग, सविता, आदित्य, भानु।
5. समुद्र – उदधि, सागर, सिन्धु, तोयनिधि, रत्नाकर, पारावार।
6. हवा – वायु, समीर, पवन, प्रभंजन, बयार।
7. तालाब – सर, ताल, सरसी, पुष्कर, जलाशय।
8. अग्नि – पावक, हुताशन, दहन, अनल।
9. जल – नीर, पानी, सलिल, वारि, पय।
10. हाथी – गज, कुंजर, द्विरद, करी, द्वीप, हस्ती।।
11. पर्वत – भूधर, गिरि, नग, तुंग, पहाड़, महीधर।
12. पक्षी – विहग, खग, विहंग, पखेरू, अंडज।
13. घोड़ा – अश्व, हय, बाजि, तुरंग, घोटक।
14. रात – रैन, निशि, रात्रि, यामिनी, तमी।
15. आँख – लोचन, नेत्र, नयन, दृग, चक्षु।
16. सर्प – भुजंग, व्याल, साँप, नाग, फणी, अहि, पन्नग, विषधर।
17. राजा – नृप, भूप, महीप, नरेश, सम्राट, भूपति।
18. फूल – सुमन, पुष्प, कुसुम, प्रसून।
19. अमृत – सुधा, अमी, अभिय, पीयूष।
20. स्त्री – नारी, अबला, बनिता, रमणी, अगना।

21. सोना – स्वर्ण, हेम, कंचन, कनक, कलधौत।
22. विष – गरल, हलाहल, कालकूट।
23. माता – जननी, अम्बिका, अम्बा, धात्री।
24. मयूर – केकी, शिखण्डी, कलापी, मोर, शिखी।
25. पृथ्वी – भू, धरा, भूमि, वसुंधरा, साडी, वसुमती।
26. बिजली – विद्युत, तड़ित, सौदामिनी, शम्पा, चंचला।
27. घर – गृह, गेह, निकेतन, सदन, धाम, मंदिर।
28. सिंह – शेर, नाहर, व्याघ्र, मृगेन्द, मृगराज।
29. भौंरा – भ्रमर, मधुप, मधुकर, अलि, भृग, मलिन्द।
30. जंगल – वन, विपिन, कानन, अरण्य।
31. बन्दर – कपि, मर्कट, शाखामृग, बानर।
32. नदी – सरिता, तरंगिनी, तटनी।
33. पाँव – पद, पैर, चरण, पग।
34. पेड़ – विटप, वृक्ष, पादप, तरु।
35. महादेव – पशुपति, शिव, शंकर, त्रिलोचन, गिरीश, कैलाशपति।
36. आनंद – हर्ष, मोद, प्रमोद, उल्लास।
37. फूल – सुमन, पुष्प, कुसुम, प्रसून।
38. मनुष्य – मानव, नर, मनुज, आदमी।
39. रास्ता – पथ, राह, मार्ग, पन्थ।
40. असुर – दनुज, दानव, राक्षस, दैत्य, निशाचर।
41. गंगा – भागीरथी, सुरसरि, जाह्नवी, मन्दाकिनी।
42. शत्रु – रिपु, बैरी, प्रतिपक्षी।
43. तलवार – कृपाण, करवाल, आलि, खड्ग।
44. गणेश – विनायक, गजानन, गिरजानन्दन।
45. इन्द्र – सुरेश, पुरन्दर, शचीपति।
46. पुत्र – सुत, वत्स, तात, आत्मज, तनय।
47. दुःख – पीड़ा, व्यथा, वेदना, कष्ट, क्लेश।
48. देवता – देव, सुर, अमर, अमर्त्य।
49. कपड़ा – वस्त्र, पट, अम्बर, वसन, चीर, दुकूल।
50. पुत्री – तनया, बेटी, सुता, आत्मजा, दुहिता, नन्दिनी, तनुजा।
51. संसार – जग, जगत, दुनिया, विश्व, लोक।
52. सखा – मित्र, मीत, प्रिय, स्नेही।

अति महत्त्वपूर्ण परीक्षोपयोगी पर्यायवाची शब्द
1. पत्थर – पाषाण, प्रस्तर, पाहन।
2. सेना – कटक, दल, फौज, सैन्य।
3. समूह – वृन्द, गण, पुंज, मण्डी, समुदाय।
4. रक्त – लहू, खून, शोणित, रुधिर।
5. सुन्दर – चारू, रम्य, रुचिर, मनोहर।
6. मछली – मीन, झख, मत्स्य, शफरी।
7. पत्नी – भार्या, बधू, बहू, गृहिणी, तिय।
8. बेल – लता, बल्लरी, बेलि।
9. नौका – नाव, तरिणी, तरी, जलयान।
10. धनुष – चाप, शरासन, कोदण्ड, पिनाक।

MP Board Class 12th Hindi Solutions

MP Board Class 12th General Hindi व्याकरण समोच्चारित भिन्नार्थक शब्द

प्रश्न 1.
समोच्चारित भिन्नार्थक शब्द से क्या समझते हैं? उदाहरण सहित समझाइए।
उत्तर-
हिन्दी में ऐसे अनेक शब्द प्रयुक्त होते हैं जिनका उच्चारण मात्रा या वर्ण के हल्के हेर-फेर के सिवा प्रायः समान होते हैं, किन्तु अर्थ में भिन्नता होती है, उन्हें समोच्चारित भिन्नार्थक शब्द या युग्म शब्द कहा जाता है।

इनके उदाहरण इस प्रकार हैं-

1. अंस = कंधा
अंश = भाग

2. अग = जड़, अगतिशील
अघ = पाप

3. अनल = आग
अनिल = वायु

4. अन्न = अनाज
अन्य = दूसरा

5. अपेक्षा = तुलना में, आवश्यकता
उपेक्षा = अवहेलना

6. अलि = भौंरा
आली = सखी

7. अवलम्ब = सहारा
अविलम्ब = शीघ्र

8. अविराम = निरंतर
अभिराम = सुन्दर

9. आकर = खान
आकार = रूप

10. आदि = आरंभ
आदी = अभ्यस्त

11. आवरण = ढकना
आभरण = अलंकरण

12. आहत = घायल
आहट = आवाज

13. आहुत = हवन किया गया
आहूत = निमंत्रित

14. उद्योत = प्रकाश
उद्योग = प्रयत्न

15. उद्धार = मुक्ति
उधार = ऋण

16. कर्म = काम
क्रम = बारी, सिलसिला

17. कलि = कलयुग
कली = फूल की कली

18. कन = वंश
कुल = किनारा

19. कोप = खजाना
कोस = दूरी का माप (दो मील)

20. क्षति = हानि
क्षिति = पृथ्वी

21. गृह = घर
ग्रह = तारे (बुध, शुक्र आदि)

22. चरम = अंतिग।
चर्म = खाल

23. चीर = वस्त्र
चीड़ = एक वृक्ष का नाम

24. छात्र = विद्यार्थी.
क्षात्र = क्षत्रिय-संबंधी

25. जलज = कमल
जलद = बादल

26. तरणि = सूर्य
तरणी = नाव

27. दूत = संदेश पहुँचाने वाला
द्यूत = जुआ

28. नगर = शहर
नाग = सर्प हाधी

29. निर्वाण = मुक्ति
निर्माण = रचन

30. नीड़ = घोंसला
नीर = पानी

31. पानी = जल
पाणि = हाथ

32. पालतू = पाला हुआ
फालतू = व्यर्थ

33. पुरुष = आदमी
परुष = कठोर

34. प्रणाम = नमस्कार
प्रमाण = सबूत

35. प्रवाह = बहाव
प्रभाव = असर

36. प्रसाद = देवता को चढ़ाया भोग, कृपा
प्रासाद = महल

37. बात = कथन
वात = वायु

38. बेर = एक फल
बैर = शत्रुभाव

39. मध्य = बीच
मद्य = शराब

40. मनोज = कामदेव
मनोज्ञ = सुन्दर

41. मूल = जड़
मूल्य = कीमत

42. याम = पहर
जाम = प्याला

43. रीति = प्रथा
रीती = खाली

44. रेखा = पंक्ति
लेखा = हिसाब

45. लक्ष्य = निशाना
लक्ष = लाख

46. वसन = वस्त्र
व्यसन = कुटेव

47. शुक्ल = स्वच्छ, सफेद
शुल्क = फीस

48. शूर = योद्धा
सूर = सूरदास, अंधा

49. संकर = मिश्रित
शंकर = शिव

50. सकल = पूरा
शकल = टुकड़ा

51. सर = तालाब
शर = बाण

52. सुत = बेटा
सूत = सारथी, कच्चा धागा

53. स्वेद = पसीना
श्वेत = सफेद

54. हर = शिव
हरि = विष्णु

समरूपी भिन्नार्थक शब्द-

MP Board Class 12th Hindi Solutions

MP Board Class 12th General Hindi व्याकरण प्रत्यय

जो शब्दांश किसी शब्द या धातु के अन्त में जुड़कर नए अर्थ का ज्ञान कराते हैं, उन्हें प्रत्यय कहते हैं। जैसे–कड़वाहट, लकड़पन, सज्जनता। ‘हट’, ‘पन’, ‘ता’ ये सभी प्रत्यय के रूप हैं। इस प्रकार हम कह सकते हैं कि शब्द के अंत में प्रत्यय लगने से उनके अर्थ में विशेषता एवं भिन्नता उत्पन्न हो जाती है।

प्रत्यय के दो प्रकार हैं–

1. कृदन्त,
2. तद्धित।

1. कृदन्त प्रत्यय
कृदन्त प्रत्यय वे प्रत्यय होते हैं, जो धातुओं (क्रियाओं) के अन्त में लगाए जाते हैं। हिन्दी में कृदन्त प्रत्यय पाँच प्रकार के होते हैं।

1. कृतवाचक कृदन्त–जो प्रत्यय कर्ता का बोध कराते हैं, वे कृतवाचक कृदन्त होते हैं।
जैसे
(क) राखन + हारा = राखनहारा।
(ख) पालन + हारा = पालनहारा।
(ग) मिलन + सार = मिलनसार।

उदाहरण के लिए कुछ कृदन्त प्रत्यय इस प्रकार हैं

2. कर्मवाचक–ये वे कृदन्त हैं, जो सकर्मक क्रिया में ना, नी, प्रत्यय लगाने से बनते हैं।

जैसे –
नि – चाटना–चटनी, सूंघनी, ओढ़नी।
ना – ओढ़ना–ओढ़ना।
हुआ – लिखना–लिखा

3. क्रिया बोधक–जो क्रिया के अर्थ का बोध कराते हैं, वे क्रिया बोधक कृदन्त कहलाते हैं।
जैसे-
सोता + हुआ = सोता हुआ।
पंच + आयत = पंचायत।
गाता + हुआ = गाता हुआ।
आढ़त + इया = आढ़तिया।

4. करण वाचक–जो क्रिया के साधन का बोध कराते हैं, वे करण वाचक कृदन्त कहलाते हैं। जैसे
कूट + नी = कूटनी।।
चास + नी = चासनी।

उदाहरण के लिए कुछ करण वाचक प्रत्यय–

5. भाववाचक कृदंत–वे कृदंत हैं जो किसी भाव या क्रिया के व्यापार का व्रोध कराते हैं।

जैसे–
थक + आवट = थकावट।
मिल + आवट = मिलावट ।
धुल + आई = धुलाई।

उदाहरण के लिए कुछ भाववाचक कृदन्त

2. तद्धित प्रत्यय

तद्धित प्रत्यय वे होते हैं, जो संज्ञा, सर्वनाम, विशेषण और अव्यय के पीछे लगाए जाते हैं। तद्धित प्रत्यय पाँच प्रकार के होते हैं, जैसे–..
1. कृतवाचक–तद्धित जो कर्ता का बोध कराते हैं, कृतवाचक तद्धित कहलाते हैं,
जैसे –
सोना + आर = सुनार
तेल + इया = तेलिया
गाड़ी + वाला = गाड़ीवाला
माला + ई = माली
घोड़ा + वाला = घोड़ावाला
लकड़ + हारा = लकड़हारा
लोहा + आर = लुहार
भाँग + एड़ी = भँगेड़ी

2. भाववाचक–जिनसे किसी प्रकार का भाव प्रकट होता है, उसे भाववाचक प्रत्यय कहते हैं,

जैसे–
ममता + त्व = ममत्व
बुनाई + वट = बुनावट
बूढ़ा + पा = बुढ़ापा
लड़का + पन = लकड़पन
कड़वा + हट = कड़वाहट
मीठा + स = मिठास

3. अपत्य वाचक–वे तद्धित जो सन्तान के अर्थ का बोध कराते हैं, उन्हें अपत्य वाचक तद्धित कहतें हैं।
जैसे–
अ – वसुदेव, मनु–मानव, रघु–राघव।
इ – मारुत–मारुति।
ई – रामानन्द–समानन्दी, दयानंद–दयानंदी, आयन–नर–नारायण, रामा–रामायण, एव–गंगा–गांगेय, राधा–राधेय।

4. गुण वाचक–जिससे किसी का गुण मालूम हो, उसे गुंण वाचक तद्धित कहते हैं।

जैसे–
गुण + वान = गुणवान
भूख + आ = भूखा
बुद्धि + वान = बुद्धिवान
भ + ई = लोभी
प्यास + आ = प्यासा
चचा + एरा = चचेरा
घर + ऊ = घरू.

5. ऊन वाचक–ऊन वाचक संज्ञाओं में वस्तु की लघुता, ओछापन, हीनता आदि का भाव व्यक्त किया जाता है

जैसे–
लोटा + इया = लुटिया
पहाड़ + ई = पहाड़ी
खाट + इया = खटिया
कोठ + री = कोठरी

MP Board Class 12th Hindi Solutions

MP Board Class 12th General Hindi व्याकरण उपसर्ग

वे शब्दांश जो किसी शब्द में जुड़कर उसका अर्थ परिवर्तित कर देते हैं। उपसर्गों का कोई स्वतंत्र अस्तित्व नहीं होता; फिर भी वे अन्य शब्दों के साथ मिलकर एक विशेष अर्थ का बोध कराते हैं। उपसर्ग सदैव शब्द के पहले आता है, जैसे-‘परा’ उपसर्ग को ‘जय’ के पहले रखने से एक नया शब्द ‘पराजय’ बन जाता है। जिसका अर्थ होता है-हार।

उपसर्ग के शब्द में तीन प्रकार की स्थितियाँ उत्पन्न होती हैं।

जैसे-
1. शब्द के अर्थ में विपरीतता आ जाती है।
2. शब्द के अर्थ में नूतनता आ जाती है।
3. शब्द के अर्थ में कोई नया परिवर्तन नहीं होता।
उत्तर-
हिन्दी भाषा में उपसर्ग तीन भाषाओं के हैं
(a) संस्कृत उपसर्ग
(b) हिन्दी उपसर्ग
(c) उर्दू उपसर्ग।

(a) संस्कृत उपसर्ग

उपसर्ग के समान प्रयुक्त होने वाले कुछ अन्य शब्द

(b) हिन्दी उपसर्ग

(c) उर्दू उपसर्ग

MP Board Class 12th Hindi Solutions

MP Board Class 12th General Hindi व्याकरण समास-विग्रह

जब परस्पर संबंध रखने वाले शब्दों को मिलाकर उनके बीच आई विभक्ति आदि का लोप करके उनसे एक पद बना दिया जाता है, तो इस प्रक्रिया को समास कहते हैं। जिन शब्दों के मूल से समास बना है उनमें से पहले शब्द को पूर्व पद और दूसरे शब्द को उत्तर पद कहते हैं। जैसे–पालन–पोषण में ‘पालन’ पूर्व पद है और ‘पोषण’ उत्तर पद है। और ‘पालन–पोषण’ समस्त पद है।

समास में कभी पहला पद प्रधान होता है, कभी दूसरा पद और कभी कोई अन्य पद प्रधान होता है जिसका नाम प्रस्तुत सामासिक शब्द में नहीं होता और प्रस्तुत सामासिक शब्द तीसरे पद का विशेषण अथवा पर्याय होता है।

कुछ समासों में विशेषण विशेष्य के आधार पर और कुछ में संख्यावाचक शब्दों के आधार पर और कहीं अव्यय की प्रधानता के आधार पर तो कुछ समासों में विभक्ति चिह्नों की विलुप्तता के आधार पर तो कुछ समासों में विभक्ति चिहों की विलुप्तता के आधार पर इस बात का निर्णय किया जाता है कि इसमें कौन–सा समास है।

विग्रह–समस्त पद को पुनः तोड़ने अर्थात् उसके खंडों को पृथक् करके पुनः विभक्ति आदि सहित दर्शाने की प्रक्रिया का नाम विग्रह है।

जैसे–
गंगाजल शब्द का विग्रह होगा गंगा का जल।
इस तरह तत्पुरुष समास के छः भेद होते हैं।

1. अव्ययीभाव समास
इन शब्दों को पढ़िए–

इन सामाजिक शब्दों में प्रथम पद अव्यय और प्रधान या उत्तर पद संज्ञा, विशेषण या क्रिया है।

जिन सामासिक शब्दों में प्रथम पद प्रधान और अव्यय होता है, उत्तर पद संज्ञा, विशेषण या क्रिया–विशेषण होता है वहाँ अव्ययीभाव समास होता है।

2. तत्पुरुष समास
इन शब्दों को पढ़िए–
“शरणागत, तुलसीकृत, सत्याग्रह, ऋणमुक्त, सेनापति, पर्वतारोहण।

उपर्युक्त सामासिक शब्दों में ‘को’, ‘द्वाय’, के लिए, से, का, के, की, ‘पर’ संयोजक शब्द बीच में छिपे हुए हैं जो कारक की विभक्तियाँ हैं। दोनों शब्दों के बीच में कर्ता तथा संबोधन कारकों की विभक्तियों को छोड़कर अन्य कारकों की विभक्तियों का लोप होता है।

जिन सामासिक शब्दों के बीच में कर्म है. लेकर अधिकरण कारक की विभल्लियों का लोप होता है तथा उत्तर पद प्रधान होता है, वे तत्पुरुष समास कहलाते है

(i) कर्म तत्पुरुष समास–
उदाहरण–यशप्राप्त, आशातीत, जेबकतरा, परिलोकगमन।

जिस समस्त पद में कर्म कारक की विभक्ति (को) का लोप होता है उसे कर्म तत्पुरुष कहते हैं।

(ii) करण तत्पुरुष–इन उदाहरणों को देखिए
शब्द – विग्रह
शोकातुर – शोक से आतुर।
मुँहमाँगा – मुँह से माँगा।

जिस समस्त पद में करण कारक (से) की विभक्ति का लोप होता है उसे करण तत्पुरुष कहते हैं।
(ii) सम्प्रदान तत्पुरुष
उदाहरण–
शब्द – विग्रह
विद्यालय – विद्या के लिए घर।
गौशाला – गौ के लिए शाला।
डाक व्यय – डाक के लिए व्यय।

जिसं समस्त पद में सम्प्रदान कारक (के लिए) की विभक्ति का लोप होता है, उसे सम्प्रदान तत्पुरुष कहते हैं।

(iv) अपादान तत्पुरुष
उदाहरण–
शब्द – विग्रह
शक्तिविहीन – शक्ति से विहीन।
पथभ्रष्ट – पथ से भ्रष्ट।
जन्मांध – जन्म से अंधा।
धर्मविमुख – धर्म से विमुख।

जिस सामासिक शब्द में अपादान कारक (से) की विभक्ति का लोप होता है, उसे अपादान तत्पुरुष समास कहते हैं।
नोट–तृतीया विभक्ति करण कारक और पंचमी विभक्ति अपादान कारक की विभक्तियों के चिह्न ‘से’ में एकरूपता होते हुए भी अर्थ में भिन्नता है। करण कारक का ‘से’ का प्रयोग संबंध जोड़ने के अर्थ में प्रयुक्त होता है और अपादान का ‘से’ संबंध–विच्छेद के अर्थ में प्रयुक्त होता है।

(v) संबंध तत्पुरुष समास–
उदाहरण–
शब्द – विग्रह
रामकहानी – राम की कहानी।
प्रेमसागर – प्रेम का सागर।
राजपुत्र – राजा का पुत्र।
पवनपुत्र – पवन का पुत्र।
पराधीन – पर के अधीन।

अर्थात्
जिस सामासिक शब्द में संबंध कारक की विभक्तियों (का, के, की) का लोप . होता है उसे संबंध तत्पुरुष समास कहते हैं।

(vi) अधिकरण तत्पुरुष
उदाहरण–
शब्द – विग्रह
शरणागत – शरण में आया।
घुड़सवार – घोड़े पर सवार।
लोकप्रिय – लोक में प्रिय।

अर्थात्
जिस सामासिक शब्द में अधिकरण (में, पे, पर) कारक की विभक्तियों का लोप होता है उसे अधिकरण तत्पुरुष समास कहते हैं।

3. कर्मधारय समास
महात्मा, शुभागमन, कृष्णसर्प, नीलगाय ।
महात्मा – महान है जो आत्मा।
शुभागमन – जिसका आगमन शुभ है।
कृष्णसर्प – सर्प जो काला है।
नीलगाय – गाय जो नीली है।

उपयुक्त सामासिक शब्दों में पहला पद विशेषण है दूसरा पद विशेष्य अर्थात् दूसरे पद की विशेषता पहला पद बता रहा है।

इन शब्दों को पढ़िए–

शब्द – विग्रह
कनकलता – कनक के समान लता।
कमलनयन – कमल के समान नयन।
घनश्याम – घन के समान श्याम।
चंद्रमुख – चंद्र के समान मुख।
मृगलोचन – मृग के समान नेत्र।

इन शब्दों में पहले पद की तुलना दूसरे पद से की है। अर्थात् पहला पद उपमान और दूसरा पद उपमेय है।

जब सामासिक शब्द में विशेषण विशेष्य का भाव हो या उपमेय उपमान का भाव हो तब कर्मधारय समास होता है।

इस आधार पर कर्मधारय समास भी दो प्रकार के होते हैं
1. विशेषण विशेष्य कर्मधारय–जैसे– नीलकंठ, महाजन, श्वेताम्बर, अधपका।
2. उपमेयोपमान कर्मधारय–जैसे–करकमल, प्राणप्रिय, पाणिपल्लव, हंसगाभिनी।

4. दिगु समास –
इन शब्दों को पढ़िए
पंचतंत्र, शताब्दी, सप्ताह, त्रिभुवन, त्रिलोक, नवरत्न, दशानन, नवनिधि, चतुर्भुज, . दुराहा। इनका विग्रह इस प्रकार होगा– .

शब्द – विग्रह
पंचतंत्र – पाँच तंत्रों का समूह या समाहार।
शताब्दी – सो वर्षों का समाहार या समूह।
सप्ताह – सात दिनों का समूह।
त्रिभुवन – तीन भवनों का समूह।
त्रिलोक – तीन लोकों का समूह।
नवरत्न – नौ रत्नों का समूह।
दशानन – दस मुखों का समूह।
नवनिधि – नौ निधियों का समूह।

इस प्रकार के शब्दों में पहले पद में संख्यावाचक शब्द का प्रयोग हुआ है।
जिस समास में प्रथम पद संख्यावाचक विशेषण हो और समस्त पद के द्वारा समुदाय का बोध हो, उसे द्विगु समास कहते हैं।

5. द्वन्द्व समास–इन शब्दों को पढ़िए–
सीता–राम – सीता और राम।
धर्मा–धर्म – धर्म या अधर्म।

दोनों पद प्रधान होते हैं। सामासिक शब्द में मध्य में स्थित योजक शब्द और अथवा, वा का लोप हो जाता है उसे द्वन्द्व समास कहते हैं।’
इन समासों को पढ़िए माता–पिता, गंगा–यमुना, भाई–बहिन, नर–नारी, रात–दिन, हानि–लाभ
समास विग्रह

शब्द – विग्रह
माता–पिता – माता और पिता।
गंगा–यमुना – गंगा और यमुना।
भाई–बहिन – भाई और बहिन।
रात–दिन – रात और दिन।

उपर्युक्त शब्दों में दोनों पद प्रधान हैं, सामासिक शब्द के बीच में योजक शब्द ‘और’ लुप्त हो गया है। कुछ शब्द इस प्रकार हैं
शब्द – विग्रह
भला–बुरा – भला या बुरा।
छोटा–बड़ा – छोटा या बड़ा।
थोड़ा–बहुत – थोड़ा या बहुत।
लेन–देन – लेन या देन।

इन शब्दों में ‘या’ अथवा ‘व’ योजक शब्दों का लोप रहता है। उपर्युक्त शब्द परस्पर विरोधीभाव के बोधक होते हैं।
इन शब्दों को पढ़िए–

दाल–रोटी – दाल और रोटी।
कहा–सुनी – कहना और सुनना।
रुपया–पैसा – रुपया और पैसा।
खाना–पीना – खाना और पीना।

इन शब्दों में प्रयुक्त पदों के अर्थ के अतिरिक्त उसी प्रकार का अर्थ साथ वाले पद से सूचित होता है। उपर्युक्त उदाहरणों में हमने तीन तरह की स्थितियाँ देखीं।

पहले उदाहरणों में दोनों पद प्रधान हैं, ‘और’ योजक शब्द का लोप हुआ है। इसे इतरेतर द्वन्द्व कहते हैं।
दूसरे उदाहरणों में दोनों पद प्रधान होते हुए परस्पर विरोधी भाव के बोधक हैं, ‘और’ योजक शब्द से जुड़े हैं। इसे वैकल्पिक द्वन्द्व कहते हैं। .
तीसरे उदाहरणों में प्रयुक्त पदों के अर्थ के अतिरिक्त उसी प्रकार का अर्थ द्वितीय पद से सूचित होता है। इसे समाहार द्वन्द्व कहते हैं।

6. बहुब्रीहि समास

इन शब्दों को पढ़िए
1. गिरिधर – गिरि को धारण करने वाला अर्थात् ‘कृष्ण’।
2. चतुर्भुज – चार भुजाएँ हैं जिसकी अर्थात् ‘विष्णु’ ।
3. गजानन – गज के समान आनन (मुख) है जिसका अर्थात् ‘गणेश’।
4. नीलकंठ – नीला है कंठ, जिसका अर्थात् ‘शिव’ ।
5. पीताम्बर – पीले वस्त्रों वाला ‘कृष्ण’ । उपर्युक्त सामासिक शब्दों में दोनों पद प्रधान नहीं हैं। दोनों पद तीसरे अर्थ की ओर संकेत करते हैं।

जैसे–
अर्थात् – कृष्ण।
अर्थात् – विष्णु।

जिन सामासिक शब्दों में दोनों पद किसी तीसरे पद की ओर संकेत करते हैं उन्हें बहुब्रीहि समास कहते हैं।

बहुब्रीहि और कर्मधारय समास में अन्तर–
कर्मधारय समास में दूसरा पद प्रधान होता है और पहला पद विशेष्य के विशेषण का कार्य करता है।

उदाहरण के लिए–
नीलकंठ का विशेषण है नीला–कर्मधारय। नीलकंठ–नीला है कंठ जिसका अर्थात ‘शिव–बहुब्रीहि समास बहुब्रीहि समास में दोनों पद मिलकर तीसरे पद की विशेषता बताते हैं।

बहुब्रीहि और द्विगु में अंतर–जहाँ पहला पद दूसरे पद की विशेषता संख्या में बताता है। वहाँ द्विगु समास होता है। जहाँ संख्यावाची पहला पद और दूसरा पद मिलकर तीसरे पद की विशेषता बताते हैं वहाँ बहुब्रीहि समास होता है।

जैसे–
चतुर्भुज – चार भुजाओं का समूह – द्विगु समास।
चतुर्भुज – चार भुजाएँ हैं जिसकी अर्थात् ‘विष्णु’– बहुब्रीहि समास

समास को पहचानने के कुछ संकेत–

1. अव्ययी भाव समास – प्रथम पद प्रधान और अव्यय होता है।
2. तत्पुरुष समास – दोनों पदों के बीच में कारक की विभक्तियों का लोप होता है और उत्तम पद प्रधान होता है।
3. कर्मधारय समास प्रथम पद विशेषण और दूसरा विशेष्य होता है। या उपमेय उपमान का भाव होता है।
4. द्विगु समास – प्रथम पद संख्यावाचक।
5. द्वन्द्व समास – दोनों पद प्रधान होते हैं और समुच्चय बोधक शब्द से जुड़े होते हैं।
6. बहुब्रीहि समास – दोनों पद को छोड़कर अन्य पद प्रधान होता है।

1. अव्ययी भाव समास

संधि और समास में अन्तर
सन्धि और समास में मख्य रूप से अन्तर यह है कि सन्धि दो वर्णों (अ. आ. इ, क, च आदि) में होती हैं, जबकि समास दो या दो से अधिक शब्दों में होता है। सन्धि में शब्दों को तोड़ने की क्रिया को ‘विच्छेद’ कहते हैं और समास में सामासिक पद को तोड़ने की क्रिया को ‘विग्रह’ कहते हैं। ..

2. तत्पुरुष समास
तत्पुरुष के भेद

(i) कर्म तत्पुरुष

(ii) करण तत्पुरुष

(iii) सम्प्रदान तत्पुरुष

(iv) अपादान तसुरुष

(v) संबंध तत्पुरुष

(vi) अधिकरण तत्पुरुष

एकाधिक शब्दों का लोप-

3. कर्मधारय समास

उपमेयोपमान कर्मधारय समस्त

4. द्विगु समास

5. द्वन्द्व समास

6. बहुब्रीहि समास

MP Board Class 12th Hindi Solutions

MP Board Class 12th Physics Solutions Chapter 6 वैद्युत चुम्बकीय प्रेरण

वैद्युत चुम्बकीय प्रेरण NCERT पाठ्यपुस्तक के अध्याय में पाठ्यनिहित प्रश्न एवं उनके उत्तर

प्रश्न 1.
चित्र 6.1 (a) से (f) में वर्णित स्थितियों के लिए प्रेरित धारा की दिशा की प्रागुक्ति (predict) कीजिए।

उत्तर :
(a) लेन्ज के नियम के अनुसार कुंडली का चुम्बक के दक्षिण ध्रुव के सामने वाला पृष्ठ, चुम्बक की गति का विरोध करेगा अर्थात् यह पृष्ठ दक्षिणी ध्रुव बनेगा। इसके लिए प्रेरित धारा qrpq मार्ग का अनुसरण करेगी।

(b) कुंडली pq का, चुम्बक के दक्षिणी ध्रुव के सामने का पृष्ठ, दक्षिणी ध्रुव के पास आने का विरोध करेगा अर्थात् यह सिरा दक्षिणी ध्रुव बनेगा। इसके लिए प्रेरित धारा prqp मार्ग का अनुसरण करेगी। कुंडली xy का, चुम्बक के उत्तरी ध्रुव के सामने वाला पृष्ठ, उत्तरी ध्रुव के दूर जाने का विरोध करेगा अर्थात् दक्षिणी ध्रुव बनेगा। इसके लिए कुंडली
xy में धारा xyzx मार्ग का अनुसरण करेगी।

(c) जब प्रथम कुंडली से जुड़ी कुंजी दबाते हैं तो इसमें धारा शून्य से महत्तम मान की ओर बढ़ती है। इस बढ़ती हुई धारा के कारण समीपस्थ कुंडली में विपरीत दिशा में धारा प्रेरित होती है। __ अतः समीपस्थ कुंडली में धारा xyzx मार्ग का अनुसरण करेगी।

(d) इंगित दिशा में धारा नियन्त्रक का समंजन बदलने पर परिपथ का प्रतिरोध घटेगा तथा कुंडली में धारा बढ़ेगी। यह बढ़ती हुई धारा समीपस्थ कुंडली में विपरीत दिशा में धारा प्रेरित करेगी। अतः प्रेरित धारा xzyx मार्ग का अनुसरण करेगी।

(e) लेन्ज के नियम के अनुसार कुंजी छोड़ने पर दूसरी कुंडली में धारा की दिशा वही होगी जो कि कुंजी छोड़ने से पूर्व प्रथम कुंडली में थी। अतः प्रेरित धारा xryx मार्ग का अनुसरण करेगी।

(f) तार में प्रवाहित धारा के कारण चुम्बकीय क्षेत्र रेखाएँ, लूप के तल के समान्तर हैं। अत: धारा परिवर्तन के कारण लूप से गुजरने वाले फ्लक्स में कोई परिवर्तन नहीं होगा, अत: लूप में कोई धारा प्रेरित नहीं होगी।

प्रश्न 2.
चित्र 6.2 में वर्णित स्थितियों के लिए लेन्ज के नियम का उपयोग करते हुए प्रेरित विद्युत धारा की दिशा ज्ञात कीजिए।
(a) जब अनियमित आकार का तार वृत्ताकार लूप में बदल रहा हो;
(b) जब एक वृत्ताकार लूप एक सीधे तार में विरूपित किया जा रहा हो।.

उत्तर :
(a) क्रॉस (x) द्वारा एक ऐसे चुम्बकीय क्षेत्र को प्रदर्शित किया गया है जिसकी दिशा कागज के तल के लम्बवत् भीतर की ओर है अनियमित आकार के लूप को वृत्तीय रूप में खींचने पर इससे गुजरने वाला फ्लक्स बढ़ेगा। अत: लूप में प्रेरित धारा इस प्रकार की होगी कि वह निम्नगामी फ्लक्स को बढ़ने से रोकेगी। प्रेरित धारा कागज के तल के लम्बवत् ऊपर की ओर चुम्बकीय क्षेत्र उत्पन्न करेगी। अत: धारा की दिशा adcba मार्ग का अनुसरण करेगी।

(b) चुम्बकीय क्षेत्र कागज के तल के लम्बवत् बाहर की ओर है। लूप के आकार को बदलने पर उससे गुजरने वाला ऊर्ध्वमुखी फ्लक्स घटेगा। अत: लूप में प्रेरित धारा ऊर्ध्वमुखी चुम्बकीय क्षेत्र उत्पन्न करेगी। इसके लिए धारा a’ d’ c b’a’ मार्ग का अनुसरण करेगी।

प्रश्न 3.
एक लम्बी परिनालिका के इकाई सेन्टीमीटर लम्बाई में 15 फेरे हैं। उसके अन्दर 2.0 सेमी का एक छोटा-सा लूप परिनालिका की अक्ष के लम्बवत् रखा गया है। यदि परिनालिका में बहने वाली धारा का मान 0.1सेकण्ड में 2.0 ऐम्पियर से 4.0 ऐम्पियर कर दिया जाए तो धारा परिवर्तन के समय प्रेरित विद्युत वाहक बल कितना होगा?
हल :
परिनालिका में फेरों की संख्या N = 15, लम्बाई 1 = 1 सेमी = 0.01 मीटर, i₁ = 2.0 ऐम्पियर, i₂ = 4.0 ऐम्पियर, ∆t = 0.1 सेकण्ड, लूप का क्षेत्रफल A = 2.0 सेमी² = 2.0 × 10^-4 मीटर²
लूप में प्रेरित वैद्युत वाहक बल

जबकि परिनालिका के अक्ष पर चुम्बकीय क्षेत्र में परिवर्तन

प्रश्न 4.
एक आयताकार लूप जिसकी भुजाएँ 8 सेमी एवं 2 सेमी हैं, एक स्थान पर थोड़ा कटा हुआ है। यह लूप अपने तल के अभिलम्बवत् 0.3 टेस्ला के एकसमान चुम्बकीय क्षेत्र से बाहर की ओर निकल रहा है। यदि लूप के बाहर निकलने का वेग 1 सेमी सेकण्ड^-1 है तो कटे भाग के सिरों पर उत्पन्न वैद्युत वाहक बल कितना होगा, जब लूप की गति अभिलम्बवत् हो (a) लूप की लम्बी भुजा के, (b) लूप की छोटी भुजा के। प्रत्येक स्थिति में उत्पन्न प्रेरित वोल्टता कितने समय तक टिकेगी?
हल :
लम्बी भुजा की लम्बाई l₁ = 0.08 मीटर, छोटी भुजा की लम्बाई l₂ = 0.02 मीटर
B= 0.3 टेस्ला, υ = 1 सेमी सेकण्ड-1 = 0.01 मीटर सेकण्ड^-1
(a) जब लूप लम्बी भुजा के लम्बवत् दिशा में गति कर रहा है तो वैद्युत वाहक बल इसी भुजा के सिरों के बीच उत्पन्न होगा।
∴ वैद्युत वाहक बल e = Bυl₁ = 0.3 × 0.01 × 0.08
= 2.4 × 10^-4 वोल्ट = 0.24 मिलीवोल्ट
यह वैद्युत वाहक बल तभी तक प्रेरित रहेगा जब तक कि लूप पूर्णतः चुम्बकीय क्षेत्र से बाहर नहीं निकल जाता। लगा समय

(b) इस बार वैद्युत वाहक बल छोटी भुजा के सिरों के बीच प्रेरित होगा।
∴ वैद्युत वाहक बल e = Bυl₂ = 0.3x 0.01 x 0.02
= 0.6 × 10^-4 वोल्ट
= 0.06 मिलीवोल्ट।

= 8 सेकण्ड।

प्रश्न 5.
1.0 मीटर लम्बी धातु की छड़ उसके एक सिरे से जाने वाले अभिलम्बवत् अक्ष के परितः 400 रेडियन सेकण्ड^-1 की कोणीय आवृत्ति से घूर्णन कर रही है। छड़ का दूसरा सिरा एक धात्विक वलय से सम्पर्कित है। अक्ष के अनुदिश सभी जगह 0.5 टेस्ला का एकसमान चुम्बकीय क्षेत्र उपस्थित है। वलय तथा अक्ष के बीच स्थापित वैद्युत वाहक बल की गणना कीजिए।
हल :
छड़ की लम्बाई l = 1.0 मीटर, ω = 400 रेंडियन सेकण्ड^-1, B= 0.5 टेस्ला
अक्ष O से x दूरी पर स्थित छड़ के अल्पशि PQ = dx पर विचार कीजिए।

इस अल्पांश का रेखीय वेग υ = xω
∴ इस अल्पांश का विभवान्तर
de = Bυdx = Bxω dx
∴ वलय तथा अक्ष के बीच प्रेरित वैद्युत वाहक बल
e = छड़ के सिरों O तथा A के बीच प्रेरित वैद्युत वाहक बल

प्रश्न 6.
एक वृत्ताकार कुंडली जिसकी त्रिज्या 8.0 सेमी तथा फेरों की संख्या 20 है अपने ऊर्ध्वाधर व्यास के परितः 50 रेडियन सेकण्ड-1 की कोणीय आवृत्ति से 3.0 × 10^-2 टेस्ला के एकसमान चुम्बकीय क्षेत्र में घूम रही है। कुंडली में उत्पन्न अधिकतम तथा औसत प्रेरित वैद्युत वाहक बल का मान ज्ञात कीजिए। यदि कुंडली 10Ω प्रतिरोध का एक बन्द लूप बनाए तो कुंडली में धारा के अधिकतम मान की गणना कीजिए। जूल ऊष्मन के कारण क्षयित औसत शक्ति की गणना कीजिए। यह शक्ति कहाँ से प्राप्त होती है?
हल :
त्रिज्या r = 0.08 मीटर, N = 20, ω = 50 रेडियन सेकण्ड, B= 3.0 × 10^-2 टेस्ला, e_max = ?,
e_aυ = ?
यदि R= 10Ω तब i_max= ?
औसत शक्ति क्षय P_aυ = ?
जब कुंडली चुम्बकीय क्षेत्र में घूमती है तो उसके सिरों के बीच प्रत्यावर्ती वैद्युत वाहक बल उत्पन्न होता है। वै० वा० बल का महत्तम मान
e_max = NBAω
= 20 × 3.0 × 10^-2 × [r × (0.08)²] × 50
⇒ e_max = 0.603 वोल्ट।
जबकि एक पूर्ण चक्र के लिए प्रत्यावर्ती वैद्युत वाहक बल का औसत मान शून्य होगा।
⇒ e_aυ = 0
परिपथ में महत्तम धारा
\(i_{\max }=\frac{e_{\max }}{R}=\frac{0.603}{10}\)
= 0.0603 ऐम्पियर।
परिपथ में औसत शक्ति क्षय
P_aυ = \(\frac{1}{2}\) × e_max × i_max =x emax ximar
= \(\frac{1}{2}\) × 0.603 × 0.0603
= 0.018 वाट।
यह शक्ति कुंडली को घुमाने वाले बाह्य स्रोत के द्वारा किए गए कार्य से प्राप्त होती है।

प्रश्न 7.
पूर्व से पश्चिम दिशा में विस्तृत एक 10 मीटर लम्बा क्षैतिज सीधा तार 0.30 × 10^-4 वेबर मीटर^-2 तीव्रता वाले पृथ्वी के चुम्बकीय क्षेत्र के क्षैतिज घटक के लम्बवत् 5.0 मीटर सेकण्ड^-1 की चाल से गिर रहा है।
(a) तार में प्रेरित वैद्युत वाहक बल का तात्क्षणिक मान क्या होगा?
(b) वैद्युत वाहक बल की दिशा क्या है?
(c) तार का कौन-सा सिरा उच्च विद्युत विभव पर है?
हल :
तार की लम्बाई l = 10 मीटर, υ = 5.0 मीटर सेकण्ड^-1,
चुम्बकीय क्षेत्र B_H = 0.30 × 10^-4 वेबर मीटर^-2

(a) तार में प्रेरत वैद्युत वाहक बल का तात्क्षणिक मान
e = BHU = 0.30 × 10^-4 × 5.0 × 10
= 1.5 × 10^-3 वोल्ट
= 1.5 मिलीवोल्ट।
(b) फ्लेमिंग के दाएँ हाथ के नियम से, वैद्युत वाहक बल की दिशा पश्चिम से पूर्व की ओर होगी।
(c) यह तार जब वैद्युत वाहक बल के स्रोत की भाँति कार्य करेगा तो पूर्वी सिरा उच्च विद्युत विभव पर होगा।

प्रश्न 8.
किसी परिपथ में 0.1 सेकण्ड में धारा 5.0 ऐम्पियर से 0.0 ऐम्पियर तक गिरती है। यदि औसत प्रेरित वैद्युत वाहक बल 200 वोल्ट है तो परिपथ में स्वप्रेरकत्व का आकलन कीजिए।
हल :
i₁ = 5.0 ऐम्पियर, i₂ = 0.0 ऐम्पयर, ∆t = 0.1 सेकण्ड
|e | = 200 वोल्ट, स्वप्रेरकत्व L = ?
सूत्र | e |= \(L \frac{d i}{d t}\)
स्वप्रेरकत्व \(L=\frac{|e|}{d i / d t}=\frac{200}{(5.0-0.0) / 0.1}=\frac{200 \times 0.1}{5.0} \) हेनरी

प्रश्न 9.
पास-पास रखे कुंडलियों के एक युग्म का अन्योन्य प्रेरकत्व 1.5 हेनरी है। यदि एक कुंडली में 0.5 सेकण्ड में धारा 0 से 20 ऐम्पियर परिवर्तित हो तो दूसरी कुंडली की फ्लक्स बंधता में कितना परिवर्तन होगा?
हल :
दिया है : M = 1.5 हेनरी, ∆i = 20 ऐम्पियर – 0 ऐम्पियर = 20 ऐम्पियर, ∆t = 0.5 सेकण्ड दूसरी कुंडली में फ्लक्स बन्धता में परिवर्तन
∆Φ = M∆i = 1.5 × 20 = 30 वेबर।

प्रश्न 10.
एक जेट प्लेन पश्चिम की ओर 1800 किमी/घण्टा वेग से गतिमान है। प्लेन के पंख 25 मीटर लम्बे हैं। इनके सिरों पर कितना विभवान्तर उत्पन्न होगा? पृथ्वी के चुम्बकीय क्षेत्र का मान उस स्थान पर 5 × 10^-4 टेस्ला तथा नति कोण (dip angle) 30° है।
हल :
दिया है : वेग υ = 1800 किमी/घण्टा = 1800 × \(\frac{5}{18}\)
= 500 मीटर सेकण्ड^-1
पंखों की लम्बाई 1 = 25 मीटर,
B= 5 × 10^-4 टेस्ला, नति कोण δ = 30°
∵ प्लेन क्षैतिज दिशा में गतिमान है, अत: प्लेन के पंख पृथ्वी के क्षेत्र के ऊर्ध्व घटक को काटेंगे।
ऊर्ध्व घटक B_V = B sin δ = 5 × 10^-4 × \(\frac{1}{2}\) = 2.5 × 10^-4 टेस्ला
∴ पंखों के सिरों के बीच प्रेरित वैद्युत वाहक बल
e = B_Vυl = 2.5 × 10^-4 × 500 × 25
= 3.125 वोल्ट
= 3.1 वोल्ट।

प्रश्न 11.
मान लीजिए कि प्रश्न 4 में उल्लिखित लूप स्थिर है किन्तु चुम्बकीय क्षेत्र उत्पन्न करने वाले वैद्युत चुम्बक में धारा का मान कम किया जाता है जिससे चुम्बकीय क्षेत्र का मान अपने प्रारम्भिक मान 0.3 टेस्ला से 0.02 टेस्ला सेकण्ड^-1 की दर से घटता है। अब यदि लूप का कटा भाग जोड़ दें जिससे प्राप्त बन्द लूप का प्रतिरोध 1.6Ω हो तो इस लूप में ऊष्मन के रूप में शक्ति ह्रास क्या है? इस शक्ति का स्रोत क्या है?
हल :
लूप का क्षेत्रफल A = 8 × 2 सेमी² = 16 × 10^-4 मीटर²
\(\frac{d B}{d t}\) = 0.02 टेस्ला सेकण्ड^-1, R = 1.6Ω
प्रेरित वैद्युत वाहक बल \(e=\frac{d \phi}{d t}=\frac{d}{d t}(B A)=A \frac{d B}{d t}\)

⇒ e = 16 × 10^-4 × 0.02
= 3.2 × 10^-5 वोल्ट।
∴ प्रेरित धारा: \(\frac{e}{R}=\frac{3.2 \times 10^{-5}}{1.6}\)
= 2.0 × 10^-5 ऐम्पियर।
∴ शक्ति ह्रास P = e × i
= 3.2 × 10^-5 × 2.0 × 10^-5
= 6.4 × 10^-10 वाट।
यह शक्ति, चुम्बकीय क्षेत्र में परिवर्तन करने वाले बाह्य स्रोत द्वारा प्रदान की जाती है।

प्रश्न 12.
12 सेमी भुजा वाला वर्गाकार लूप जिसकी भुजाएँ x एवं Y अक्षों के समान्तर हैं, –दिशा में 8 सेमी सेकण्ड^-1 की गति से चलाया जाता है। लूप तथा उसकी गति का परिवेश धनात्मक –दिशा के चुम्बकीय क्षेत्र का है। चुम्बकीय क्षेत्र न तो एकसमान है और न ही समय के साथ नियत है। इस क्षेत्र की ऋणात्मक दिशा में प्रवणता 10^-3 टेस्ला सेकण्ड^-1 है (अर्थात् ऋणात्मक x-अक्ष की दिशा में इकाई सेन्टीमीटर दूरी पर क्षेत्र के मान में 10^-3 टेस्ला सेकण्ड^-1 की वृद्धि होती है) तथा क्षेत्र के मान में 10^-3 टेस्ला सेकण्ड^-1 की दर से कमी भी हो रही है। यदि कुंडली का प्रतिरोध 4.50 मिलीओम हो तो प्रेरित धारा का परिमाण एवं दिशा ज्ञात कीजिए।
हल :
लूप का प्रतिरोध R = 4.50 × 10^-3Ω, लूप की भुजा a = 12 सेमी
\(\frac{\partial B}{\partial x}\) = – 10^-3 टेस्ला मीटर^-1 = – 10^-1 टेस्ला मीटर^-1
= – 0.1 टेस्ला मीटर^-1 [X-अक्ष की ऋणात्मक दिशा में]
thada \(\frac{\partial x}{\partial t}\) = 8 सेमी सेकण्ड^-1 = 0.08 मीटर सेकण्ड^-1.
\(\frac{\partial B}{\partial t}\) = – 10^-3 टेस्ला सेकण्ड^-1
\(\frac{\partial B}{\partial x}\) तथा \(\frac{\partial B}{\partial t}\) दोनों का चिह्न ऋणात्मक लिया गया है क्योंकि x तथा t दोनों के बढ़ने के साथ चुम्बकीय क्षेत्र घट रहा है।
माना लूप की भुजा की लम्बाई ‘a’ है। x दूरी पर स्थित dx चौड़ाई की एक पट्टी ४ पर विचार कीजिए।
माना इस पट्टी पर चुम्बकीय क्षेत्र B(x, t) है तथा इस पट्टी का क्षेत्रफल dA = adx है।

∴ इस पट्टी से बद्ध चुम्बकीय फ्लक्स
dΦ = BdA = B(x, t) adx
∴ लूप से बद्ध कुल फलक्स

धारा की दिशा ऐसी होगी जो z-दिशा में चुम्बकीय फ्लक्स के घटने का विरोध करेगी। इसके लिए धारी वामावर्त दिशा में प्रवाहित होगी।

प्रश्न 13.
एक शक्तिशाली लाउडस्पीकर के चुम्बक के ध्रुवों के बीच चुम्बकीय क्षेत्र की तीव्रता के परिमाण का मापन किया जाना है। इस हेतु एक छोटी चपटी 2 सेमी क्षेत्रफल की अन्वेषी कुंडली (search coil) का प्रयोग किया गया है। इस कुंडली में पास-पास लिपंटे 25 फेरे हैं तथा इसे चुम्बकीय क्षेत्र के लम्बवत् व्यवस्थित किया गया है और तब इसे द्रुत गति से क्षेत्र के बाहर निकाला जाता है। तुल्यतः एक अन्य विधि में अन्वेषी कुंडली को 90° से तेजी से घुमा देते हैं जिससे कुंडली का तल चुम्बकीय क्षेत्र के समान्तर हो जाए। इन दोनों घटनाओं में कुल 7.5 मिलीकूलॉम आवेश का प्रवाह होता है (जिसे परिपथ में प्रक्षेप धारामापी (ballistic galvanometer) लगाकर ज्ञात किया जा सकता है)। कुंडली तथा धारामापी का संयुक्त प्रतिरोध 0.502 है। चुम्बक की क्षेत्र की तीव्रता का आकलन कीजिए। •
हल :
A = 2 × 10^-4 मीटर², N= 25 फेरे, प्रेरित आवेश q = 7.5×10^-3 कूलॉम
परिपथ का प्रतिरोध R = 0.50Ω
माना चुम्बकीय क्षेत्र की तीव्रता = B.
प्रारम्भिक फ्लक्स Φ₁ = NBA cos 0° = NBA
अन्तिम फ्लक्स Φ₂ = 0
∴ प्रेरित वैद्युत वाहक बल e = \(-\frac{d \phi}{d t}\)

प्रश्न 14.
चित्र 6.5 में एक धातु की छड़ PQ को दर्शाया गया है जो पटरियों AB पर रखी हैं तथा एक स्थायी चुम्बक के ध्रुवों के मध्य स्थित है। पटरियाँ, छड़ एवं चुम्बकीय क्षेत्र परस्पर अभिलम्बवत् दिशाओं में हैं। एक गैल्वेनोमीटर (धारामापी) G को पटरियों से एक स्विच K की सहायता से संयोजित किया गया है। छड़ की लम्बाई = 15 सेमी, B= 0.50 टेस्ला तथा पटरियों, छड़ तथा धारामापी से बने बन्द लूप का प्रतिरोध = 9.0 मिली ओम है। . क्षेत्र को एकसमान मान लें।
(a) माना कुंजी K खुली (open) है तथा छड़ 12 सेमी सेकण्ड -1की चाल से दर्शायी गई दिशा में गतिमान है। प्रेरित वैद्युत वाहक बल का मान एवं ध्रुवणता (polarity) बताइए।

(b) क्या कुंजी K खुली होने पर छड़ के सिरों पर आवेश का आधिक्य हो जाएगा? क्या होगा यदि कुंजी K बंद (close) कर दी जाए।
(c) जब कुंजी K खुली हो तथा छड़ एकसमान वेग से गति में हो तब भी इलेक्ट्रॉनों पर कोई परिणामी बल कार्य नहीं करता यद्यपि उन पर छड़ की गति के कारण चुम्बकीय बल कार्य करता है। कारण स्पष्ट कीजिए।
(d) कुंजी बन्द होने की स्थिति में छड़ पर लगने वाले अवमन्दन बल का मान क्या होगा?
(e) कुंजी बन्द होने की स्थिति में छड़ को उसी चाल (= 12 सेमी सेकण्ड^-1) से चलाने हेतु कितनी शक्ति (बाह्य कारक के लिए) की आवश्यकता होगी?
(f) बन्द परिपथ में कितनी शक्ति का ऊष्मा के रूप में क्षय होगा? इस शक्ति का स्रोत क्या है?
(g) गतिमान छड़ में उत्पन्न वैद्युत वाहक बल का मान क्या होगा यदि चुम्बकीय क्षेत्र की दिशा पटरियों के लम्बवत् होने की बजाय उनके समान्तर हो?
हल :
दिया है : B= 0.50 टेस्ला , l = 0.15 मीटर, υ = 0.12 सेमी सेकण्ड^-1, R= 9.0 × 10^-3Ω
(a) छड़ में प्रेरित वैद्युत वाहक बल e = Bυl = 0.50 × 0.12 × 0.15
= 9 × 10^-3 वोल्ट = 9.0 मिलीवोल्ट।
छड़ का सिरा P धनात्मक तथा Q ऋणात्मक होगा।

(b) हाँ, छड़ के Q सिरे पर इलेक्ट्रॉन एकत्र हो जाएँगे जबकि P सिरे पर धनावेश की अधिकता हो जाएगी।
यदि कुंजी K को बन्द कर दिया जाए तो Q सिरे पर एकत्र होने वाले इलेक्ट्रॉन बन्द परिपथ से होते हुए (G से होकर) सिरे P की ओर गति करने लगेंगे। इस प्रकार परिपथ में स्थायी धारा स्थापित हो जाएगी।
(c) जब कुंजी K खुली है तो P सिरा धनात्मक व Q सिरा ऋणात्मक हो जाता है। इससे छड़ के भीतर सिरे P से सिरे Q की ओर एक वैद्युत क्षेत्र स्थित हो जाता है। इस क्षेत्र के कारण इलेक्ट्रॉनों पर Q से P की ओर वैद्युत बल लगता है जो विपरीत दिष्ट चुम्बकीय बल को सन्तुलित कर लेता है।
इस प्रकार इलेक्ट्रॉनों पर कोई नेट बल कार्य नहीं करता है।
(d) कुंजी K बन्द होने की स्थिति में छड़ PQ से प्रवाहित धारा

∴ छड़ PQ पर चुम्बकीय क्षेत्र के कारण कार्य करने वाला अवमन्दन बल
F = il B sin 90° = 1.0 × 0.15 × 0.50 .
= 75 × 10^-3 न्यूटन = 0.075 न्यूटन।
(e) कुंजी K के बन्द होने पर छड़ को खींचते रहने के लिए व्यय की जाने वाली शक्ति
P = Fυ = 0.075 × 0.12 = 9 × 10^-3 वाट।
(f) परिपथ में व्यय ऊष्मीय शक्ति
. P= i²R = (1.0)² × 9.0 × 10^-3 = 9 × 10^-3 वाट।
इस शक्ति का स्रोत छड़ को एकसमान वेग से खींचते रहने के लिए बाह्य स्रोत द्वारा व्यय की गई शक्ति है।
(g) शून्य; इस स्थिति में छड़ चुम्बकीय बल रेखाओं को नहीं काटेगी। अतः कोई वैद्युत वाहक बल प्रेरित नहीं होगा।

प्रश्न 15.
वायु के क्रोड वाली एक परिनालिका में, जिसकी लम्बाई 30 सेमी तथा अनुप्रस्थ काट का क्षेत्रफल 25 सेमी तथा कुल फेरे 500 हैं, 2.5 ऐम्पियर धारा प्रवाहित हो रही है। धारा को 10^-3 सेकण्ड के अल्पकाल में अचानक बन्द कर दिया जाता है। परिपथ में स्विच के खुले सिरों के बीच उत्पन्न औसत वैद्युत वाहक बल का मान क्या होगा? परिनालिका के सिरों पर चुम्बकीय क्षेत्र के परिवर्तन की उपेक्षा कर सकते हैं?
हल :
फेरों की संख्या N = 500, लम्बाई 1 = 0.30 मीटर, क्षेत्रफल A = 25 × 10^-4 मीटर²,
i₁ = 2.5 ऐम्पियर, i₂ = 0, dt = 10³ सेकण्ड
अक्ष पर चुम्बकीय क्षेत्र को एकसमान मानते हुए प्रारम्भिक चुम्बकीय क्षेत्र \(B_{1}=\mu_{0} \frac{N}{l} i_{1}\)
तथा अन्तिम चुम्बकीय क्षेत्र B_{2}=\mu_{0} \frac{N}{l} i_{2}=0
∴ परिनालिका से बद्ध फ्लक्स बन्धुता में परिवर्तन
dΦ = NB₂A – NB₁A –
= 0 – 500 × 4 π × 10^-7 × \(\frac{500}{0.30}\) × 25 × 10^-4
= – 65.45 × 10^-4 वेबर
अतः स्विच के सिरों के बीच प्रेरित औसत वैद्युत वाहक बल
\(e=-\frac{d \phi}{d t}=\frac{65.45 \times 10^{-4}}{10^{-3}}\)
= 6.545 वोल्ट = 6.5 वोल्ट।

प्रश्न 16.
(a) चित्र 6.6 में दर्शाए अनुसार एक लम्बे, सीधे तार तथा एक वर्गाकार लूप जिसकी एक भुजा की लम्बाई a है, के लिए अन्योन्य प्रेरकत्व का व्यंजक प्राप्त कीजिए।
(b) अब मान लीजिए कि सीधे तार में 50 ऐम्पियर की धारा प्रवाहित हो रही है तथा । लूप एक स्थिर वेग υ = 10 मीटर/सेकण्ड^-1 से दायीं ओर को गति कर रहा है। लूप में प्रेरित वैद्युत वाहक बल का परिकलन उस क्षण पर कीजिए जब x= 0.2 मीटर हो। लूप के | लिए a = 0.1 मीटर लीजिए तथा यह मान लीजिए कि उसका प्रतिरोध बहुत अधिक है।

हल :
(a) यदि अन्योन्य प्रेरण गुणांक M है तो
Φ = Mi

(b) लूप के भीतर तार से 2 दूरी पर स्थित dz चौड़ाई की एक ऐसी पट्टी पर विचार कीजिए जो कि तार के समान्तर है।
इस पट्टी का क्षेत्रफल dA = adz
तार के कारण पट्टी पर चुम्बकीय क्षेत्र \(B=\frac{\mu_{0}}{2 \pi} \cdot \frac{i}{z}\)
यह क्षेत्र पट्टी के तल के लम्बवत् भीतर की ओर है।
∴ पट्टी से बद्ध चुम्बकीय फ्लक्स dΦ = BdA = \(\frac{\mu_{0}}{2 \pi} \cdot \frac{i}{z}\) .adz

दिया है : i = 50 ऐम्पियर, υ = 10 मीटर/सेकण्ड^-1, e= ?, जबकि x = 0.2 मीटर, a = 0.1 मीटर

प्रश्न 17.
किसी M द्रव्यमान तथा R त्रिज्या वाले एक पहिये के किनारे (rim) पर एक रैखिक आवेश स्थापित किया गया है जिसकी प्रति इकाई लम्बाई पर आवेश का मान λ है। पहिये के स्पोक (spoke) हल्के एवं कुचालक हैं तथा वह अपनी अक्ष के परितः घर्षण रहित घूर्णन हेतु स्वतन्त्र है जैसा कि चित्र 6.8 में दर्शाया गया है। पहिये के वृत्तीय भाग पर रिम, के अन्दर एकसमान चुम्बकीय क्षेत्र विस्तरित है। इसे इस प्रकार परिभाषित किया गया है –


चुम्बकीय क्षेत्र को अचानक ‘ऑफ’ (switched off) करने के पश्चात्, पहिये का कोणीय वेग ज्ञात कीजिए।
हल :
माना चुम्बकीय क्षेत्र को स्विच ऑफ करने पर E वैद्युत क्षेत्र उत्पन्न होता है (Note) तथा पहिया ω कोणीय वेग से घूमना प्रारम्भ करता है।
यदि पहिये पर कुल आवेश q है तो एक पूर्ण चक्र के दौरान वैद्युत क्षेत्र द्वारा आवेश को घुमाने में कृत कार्य
w = F x s = qE x 2 1 R

वैद्युत चुम्बकीय प्रेरण NCERT भौतिक विज्ञान प्रश्न प्रदर्शिका (Physics Exemplar Problems) पुस्तक से चयनित महत्त्वपूर्ण प्रश्नों के हल

वैद्युत चुम्बकीय प्रेरण बहुविकल्पीय प्रश्नोत्तर

प्रश्न 1.
x- y तल के किसी प्रदेश में, जहाँ चुम्बकीय क्षेत्र \(B=B_{0}(2 \hat{\mathrm{i}}+3 \hat{\mathrm{j}}+4 \hat{\mathrm{k}}) \mathrm{T}\) है, (यहाँ B₀ कोई नियतांक है), L मीटर भुजा का कोई वर्ग रखा है। इस वर्ग से गुजने वाले फ्लक्स का परिमाण है –
(a) 2B₀L² wb
(b) 3B₀L² Wb
(c) 4B₀L² Wb
(d) 29 B_oL² Wb.
उत्तर :
(c) 4B₀L² Wb

प्रश्न 2.
किसी बेलनाकार छड़ चुम्बक को उसके अक्ष के परित: (चित्र 6.9) घूर्णन कराया जाता है। किसी अ क्ष
तार को इसके अक्ष से संयोजित करके इसके बेलनाकार पृष्ठ से किसी सम्पर्क द्वारा स्पर्श कराया गया है, तब –
(a) ऐमीटर A से दिष्ट धारा प्रवाहित होती है।
(b) ऐमीटर A से दिष्ट धारा प्रवाहित नहीं होती है
(c) ऐमीटर A से आवर्तकाल \(T=\frac{2 \pi}{\omega}\) की प्रत्यावर्ती ज्वावक्रीय धारा प्रवाहित होती है ।
(d) ऐमीटर A से काल परिवर्तित धारा प्रवाहित होती है जो ज्यावक्रीय नहीं होती।

उत्तर :
(a) ऐमीटर A से दिष्ट धारा प्रवाहित होती है।

प्रश्न 3.
चित्र 6.10 में दर्शाए अनुसार A तथा B दो कुण्डलियाँ हैं। जब A को B की ओर गति कराते हैं तो B में चित्र में दर्शाए अनुसार धारा प्रवाहित होने लगती है तथा A के रुकने पर A धारा प्रवाहित होना बन्द हो जाती है। B में धारा वामावर्ती है। जब A गति करता है तो B को स्थिर रखा जाता है तो हम यह निष्कर्ष निकाल सकते हैं कि –
(a) A में दक्षिणावर्ती दिशा में नियत धारा है
(b) A में परिवर्ती धारा है
(c) A में कोई धारा नहीं है
(d) A में वामावर्ती दिशा में नियत धारा है।

उत्तर :
(d) A में वामावर्ती दिशा में नियत धारा है।

प्रश्न 4.
इस प्रश्न में भी स्थिति प्रश्न 6.10 की भाँति है। अन्तर केवल यह है कि अब कुण्डली A को ऊर्ध्वाधर अक्ष के परितः घूर्णन कराया गया है (चित्र-6.11)। यदि A विराम में है तो B में कोई धारा प्रवाहित नहीं होती। जब B में (t = 0 पर) धारा वामावर्ती दिशा में है तथा इस क्षण, t = 0, पर कुंडली A दर्शाए अनुसार है तब कुंडली A में प्रवाहित होती है?

(a) दक्षिणावर्त नियत धारा
(b) दक्षिणावर्त परिवर्ती धारा
(c) वामावर्त परिवर्ती धारा
(d) वामावर्त नियत धारा।
उत्तर :
(a) दक्षिणावर्त नियत धारा

प्रश्न 5.
किसी अनुप्रस्थ काट के क्षेत्रफल A तथा नियत फेरों की संख्या N वाली l लम्बाई की परिनालिका का स्वप्रेरकत्व L बढ़
जाता है –
(a) l तथा A में वृद्धि के साथ
(b) l में कमी तथा A में वृद्धि के साथ
(c) l में वृद्धि तथा A में कमी के साथ
(d) l तथा A में कमी के साथ।
उत्तर :
(b) l में कमी तथा A में वृद्धि के साथ

वैद्युत चुम्बकीय प्रेरण अति लघु उत्तरीय प्रश्नोत्तर

प्रश्न 1.
किसी ऐसे चुम्बक पर विचार कीजिए जो एक ऑन/ऑफ स्विच लगे तार के लूप से घिरा है। यदि स्विच को ऑफ स्थिति (खुले परिपथ) से ऑन स्थिति (बन्द परिपथ) पर लाया जाए तो क्या परिपथ में कोई धारा प्रवाहित होगी?

उत्तर :
तार का कोई भी भाग गतिमान नहीं है, अत: कोई गतिक वैद्युत वाहक बल उत्पन्न नहीं होगा। चुम्बक भी स्थिर है, अत: समय के साथ चुम्बकीय क्षेत्र परिवर्तित नहीं होगा। अत: कोई प्रेरित वैद्युत वाहक बल भी उत्पन्न नहीं होगा। अत: परिपथ में कोई धारा प्रवाहित नहीं होगी।

प्रश्न 2.
कसकर लिपटी परिनालिका के रूप में कोई तार किसी दिष्ट धारा स्रोत से संयोजित है और इसमें विद्युत धारा प्रवाहित हो रही है। यदि कुंडली को इस प्रकार से खींचा जाए कि सर्पिलाकार कुंडली के क्रमागत लपेटों के बीच अन्तराल हो जाए, तो क्या विद्युत धारा बढ़ेगी अथवा घटेगी, स्पष्ट कीजिए।
उत्तर :
कुंडली को खींचकर उसके क्रमागत लपेटों के बीच अन्तराल आ जाने पर इन रिक्त स्थानों से चुम्बकीय फ्लक्स की हानि होगी। अत: लेन्ज के नियमानुसार परिनालिका में एक प्रेरित धारा बहेगी जो चुम्बकीय फ्लक्स में कमी का विरोध करेगी। अतः परिनालिका में प्रवाहित विद्यत धारा बढ़ेगी।

प्रश्न 3.
कोई परिनालिका किसी बैटरी से संयोजित है जिसके कारण उसमें अपरिवर्तित धारा प्रवाहित हो रही है। यदि इस परिनालिका के भीतर कोई लोह क्रोड रख दिया जाए तो विद्युत धारा घटेगी अथवा बढ़ेगी? स्पष्ट कीजिए।
उत्तर :
परिनालिका के भीतर कोई लौह क्रोड रख देने पर चुम्बकीय क्षेत्र में वृद्धि के कारण चुम्बकीय फ्लक्स में वृद्धि हो जाएगी। अत: लेन्ज के नियमानुसार परिनालिका में एक प्रेरित वैद्युत वाहक बल एवं प्रेरित धारा उत्पन्न होगी जोकि फ्लक्स वृद्धि का विरोध करेगी। अतः परिनालिका में प्रवाहित धारा घटेगी।

प्रश्न 4.
धातु के किसी ऐसे छल्ले पर विचार कीजिए जो किसी ऊर्ध्वाधरतः रखी स्थिर परिनालिका (जैसे–कार्ड बोर्ड में जड़ी) के शीर्ष पर रखा है (चित्र 6.13)। छल्ले का केन्द्र परिनालिका के अक्ष के सम्पाती है। यदि अचानक स्विच ऑन करके परिनालिका में धारा प्रवाहित कराएँ तो धातु का छल्ला ऊपर उछलता है। स्पष्ट कीजिए।

उत्तर :
प्रारम्भ में धातु के छल्ले से बद्ध चुम्बकीय फ्लक्स शून्य है। अचानक स्विच ऑन करने पर छल्लों से चुम्बकीय फ्लक्स गुजरता है। लेज के नियमानुसार धातु के छल्ले में एक प्रेरित वैद्युत वाहक बल उत्पन्न होता है जो इस चुम्बकीय फ्लक्स में वृद्धि का विरोध करता है। यह केवल तभी सम्भव है जब छल्ला परिनालिका से दूर अर्थात् ऊपर की ओर गति करे। अत: छल्ला ऊपर की ओर उछलता है।

प्रश्न 5.
1 सेमी आन्तरिक त्रिज्या के किसी धातु के पाइप पर विचार कीजिए। यदि 0.8 सेमी त्रिज्या का कोई बेलनाकार छड़ चुम्बक इस पाइप में गिराया जाए तो वह नीचे गिरने में किसी प्रकार की अचुम्बकित बेलनाकार लौह छड़ की तुलना में अधिक समय लेता है। स्पष्ट कीजिए।
उत्तर :
जब बेलनाकार छड़ चुम्बक को धातु के पाइप में गिराया जाता है तो पाइप में भँवर धाराएँ उत्पन्न होगी, जोकि चुम्बक की गति का विरोध करेंगी। अतः इसकी गति का त्वरण, गुरुत्वीय त्वरण से कम हो जाता है। अचुम्बकित बेलनाकार छड़ को पाइप में गिराने पर, पाइप में भँवर धाराएँ उत्पन्न नहीं होंगी और वह गुरुत्वीय त्वरण से नीचे गिरेंगी। अतः बेलनाकार छड़ चुम्बक पाइप में गिरने में, किसी अचुम्बकित बेलनाकार छड़ से अधिक समय लेती है।

MP Board Class 12th Physics Solutions

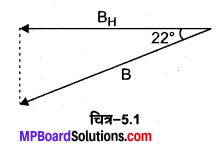
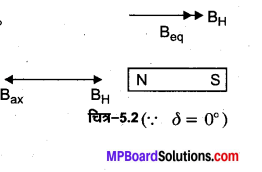
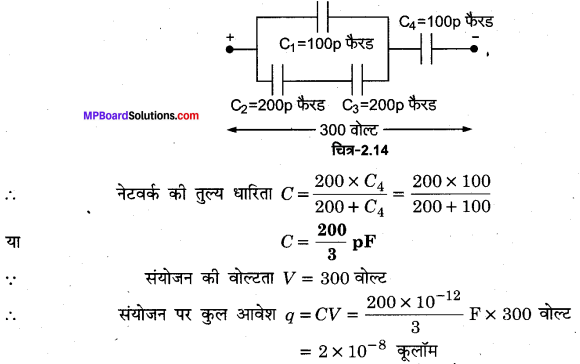
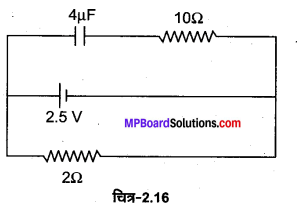
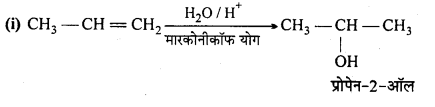
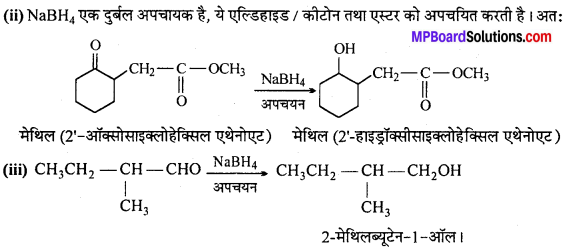
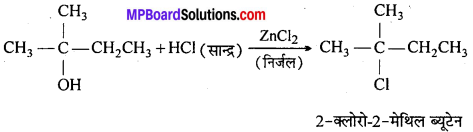
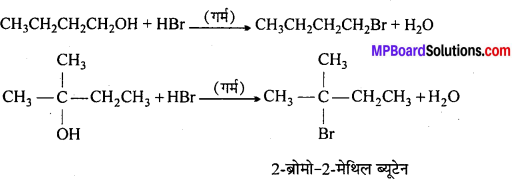
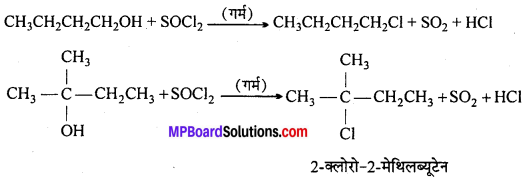
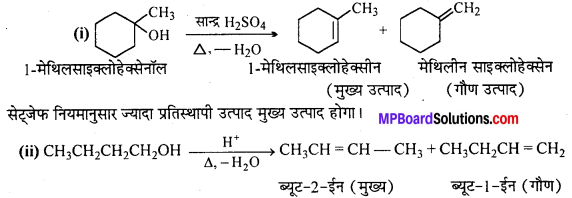
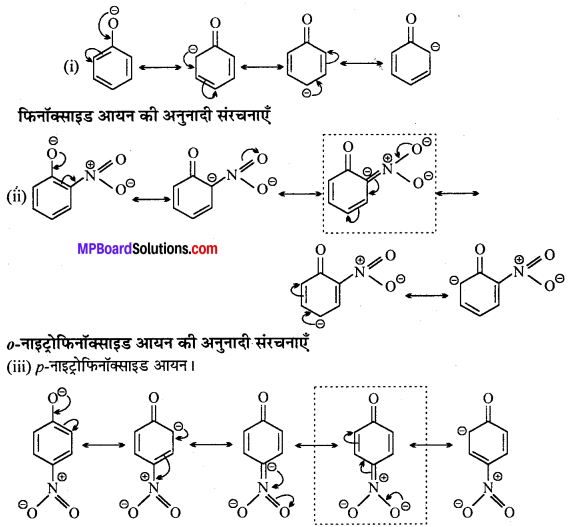
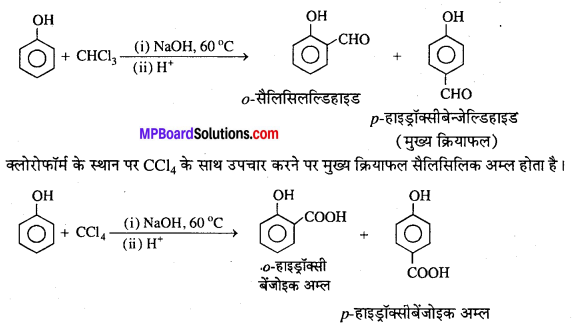
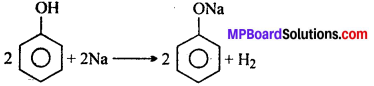
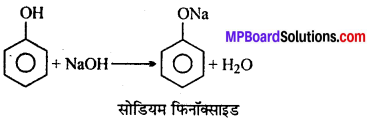
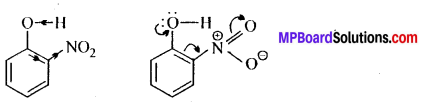
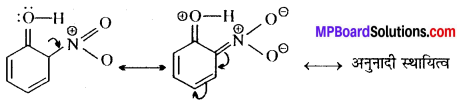
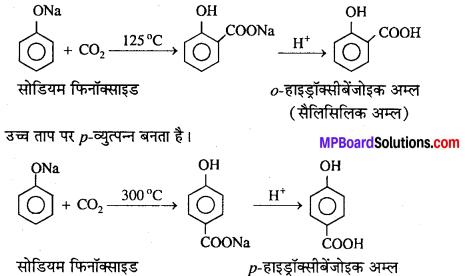
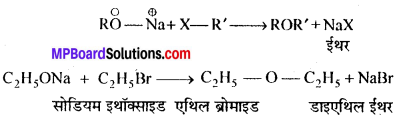
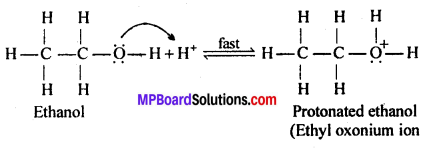
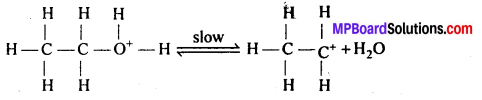
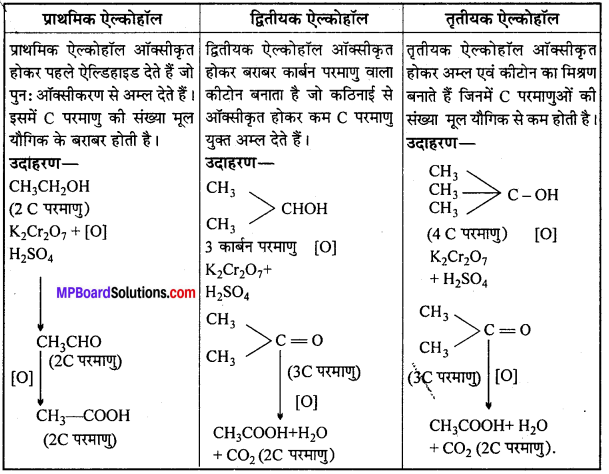
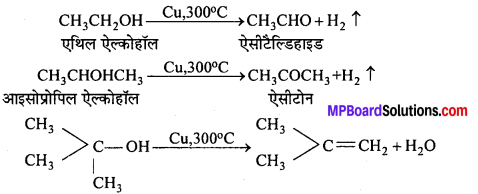
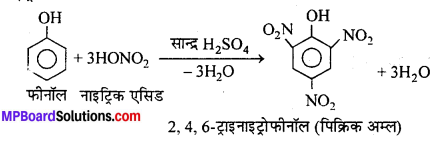
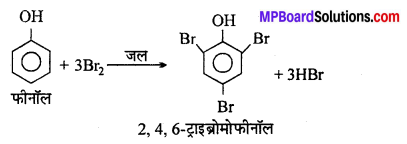
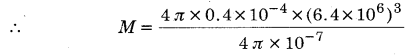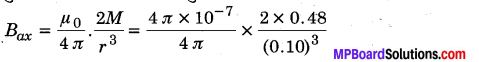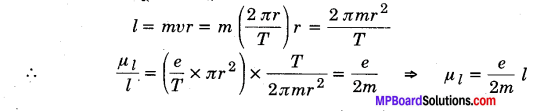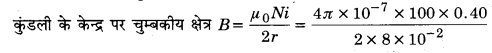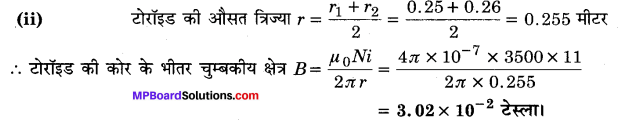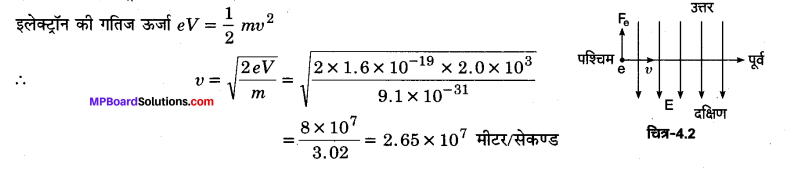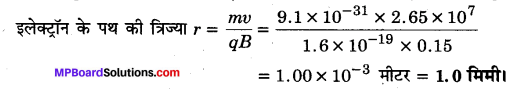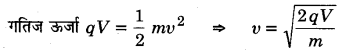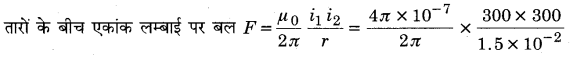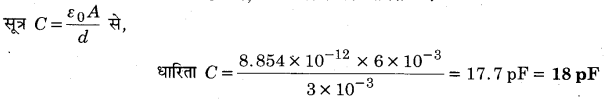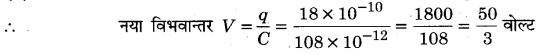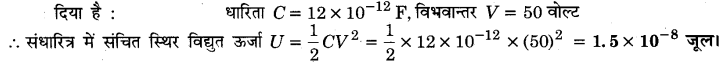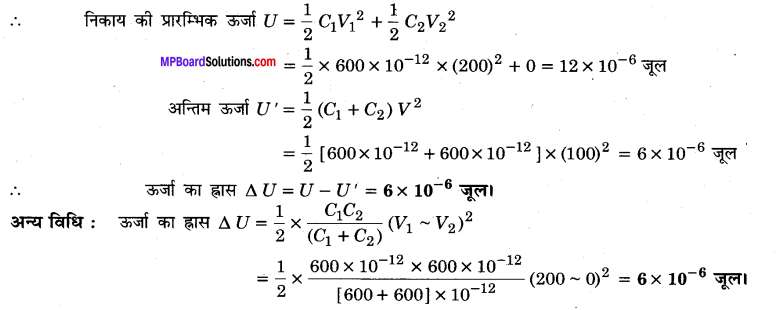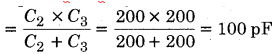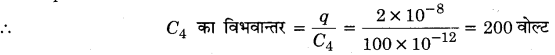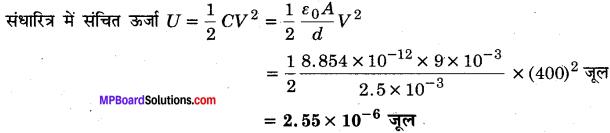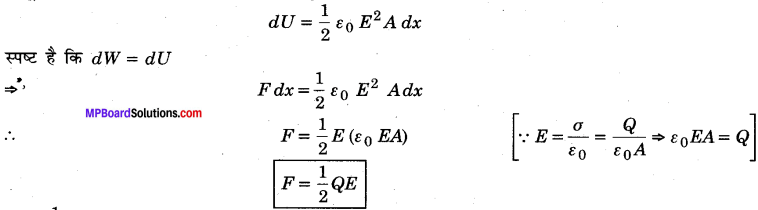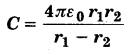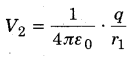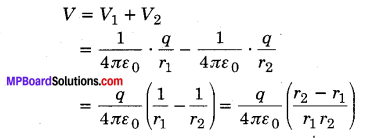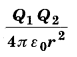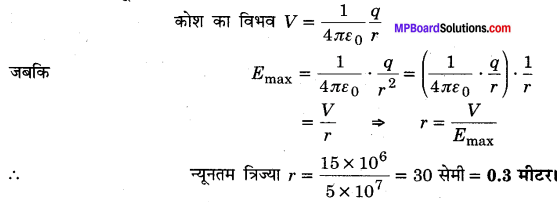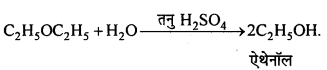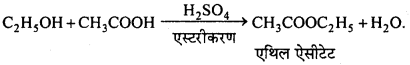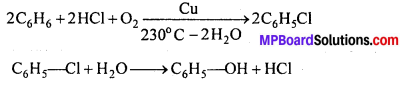MP Board Class 12th General Hindi व्याकरण सन्धि

दो या दो से अधिक वर्षों के परस्पर मिलने से जो विकास या परिवर्तन होता है। उसे सन्धि कहते हैं।

जैसे–

• विद्या + आलय = विद्यालय
• रमा + ईश = रमेश
• सूर्य + उदय = सूर्योदय
• पितृ + आज्ञा = पित्राज्ञा
• सत् + जन = सज्जन
• एक + एक = एकैक

सन्धि तीन प्रकार की होती हैं

1. स्वर संधि,
2. व्यंजन संधि और
3. विसर्ग संधि।

जब स्वर से परे स्वर होने पर उनमें जो विकार होता है, उसे स्वर संधि कहते हैं। दूसरे शब्दों में स्वर के बाद जब कोई स्वर आता है तो दोनों के स्थान में स्वर हो जाता है। उसे स्वर संधि कहते हैं;

जैसे–

• धर्म + अर्थ = धर्मार्थ
• रवि + इन्द्र = रवीन्द्र
• भानु + उदय = भानूदय
• सुर + इन्द्र सुरेन्द्र
• सदा + एव = सदैव
• इति + आदि = इत्यादि
• नै + अक = नायक

स्वर संधि के भेद–स्वर संधि के पाँच भेद हैं–

1. दीर्घ संधि,
2. गुण संधि,
3. वृद्धि संधि,
4. यण संधि, और
5. अयादि संधि।

1. दीर्घ संधि–ह्रस्व या दीर्घ अ, इ, उ, ऋ, के बाद ह्रस्व या दीर्घ अ इ, उ, ऋ क्रमशः आए तो दोनों को मिलाकर एक दीर्घ–स्वर हो जाता है।

जैसे–

• परम + अर्थ = परमार्थ
• राम + आधार = रामाधार
• अभि + इष्ट = अभीष्ट
• भानु + उदय = भानूदय
• मही + इन्द्र = महीन्द्र
• गिरि + ईश = गिरीश
• महा + आशय = महाशय
• अदय + अपि = यद्यपि

2. गुण संधि–अ अथवा आ के पश्चात् ह्रस्व या दीर्घ इ, उ, ऋ आए तो दोनों के स्थान पर क्रमशः ए, ओ तथा अर् हो जाते हैं।

जैसे–

• सुर + इन्द्र = सुरेन्द्र
• सुर + ईश = सुरेश
• सूर्य + उदय = सूर्योदय
• महा + ऋषि = महर्षि
• महा + उत्सव = महोत्सव
• वीर + इन्द्र = वीरेन्द्र
• राज + ऋषि = राजर्षि
• हित + उपदेश = हितोपदेश

3. वृद्धि संधि–हस्व अथवा दीर्घ अ के पश्चात् ए अथवा ऐ आने पर “ऐ” और ओ अथवा औ आने पर दोनों के स्थान पर “औ” हो जाता है।

जैसे–

• सदा + एव = सदैव
• मत + ऐक्य = मतैक्य
• परम + औषधि = परमौषधि
• वन + औषधि = वनौषधि
• महा + ऐश्वर्य = महैश्वर्य
• जल + ओध = जलौध

4. यण सन्धि–हस्व या दीर्घ इ, उ, ऋ से परे अपने से भिन्न स्वर हो जाने पर इनके स्थान पर क्रमशः य, व और र होता है।

जैसे–

• अति + उत्तम = अत्युत्तम
• इति + आदि = इत्यादि.
• प्रति + एक = प्रत्येक
• यदि + अपि = यद्यपि
• सु + आगत = स्वागत
• अति + आचार = अत्याचार
• पित्र + आदेश = पित्रादेश।

5. अयादि संधि–ए, ऐ, ओ, औ के पश्चात् स्वर वर्ण आने पर उनके स्थान .. पर अय, आय तथा अव हो जाते हैं।

जैसे–

• पो + अन = पवन
• पो + अक = पावक
• नै + अक = नायक
• न + अन = नयन
• नै + इका = नायिका

जब व्यंजन और स्वर अथवा व्यंजन से मेल होता है, तो उसे व्यंजन संधि कहते हैं। जैसे

• सत् + जन = सज्जन
• उत् + चारण = उच्चारण
• जगत + नाथ = जगन्नाथ
• दुस + चरित्र = दुश्चरित्र
• शरत् + चन्द्र = शरच्चन्द्र
• महत् + चक्र = महच्चक्र
• षट् + आनन = षडानन
• दिक् + गज = दिग्गज
• सद् + आचार = सदाचार
• दिक् + अम्बर = दिगम्बर
• वाक् + ईश = वागीश
• उत् + गमन = उद्गमन
• उत् + हार = उद्धार
• सम + कल्प = संकल्प
• राम + अयन = रामायन

विसर्ग के साथ जब किसी स्वर या व्यंजन का मेल होता है, तब विसर्ग संधि होती है।
जैसे–

• अति + एव = अतएव
• निः + छल = निश्छल
• धनु + टंकार = धनुष्टंकार
• निः + कपट = निष्कपट
• निः + पाप = निष्पाप
• निः + धन = निर्धन
• नमः +. कार = नमस्कार
• तिरः + कार = तिरस्कार
• पुरः + कार = पुरस्कार
• मनः + योग = मनोयोग
• मनः + रथ = मनोरथ
• पुनः + जन्म = पुनर्जन्म
• दुः + तर = दुस्तर
• सत + आनंद = सदानन्द

अभ्यास के लिए महत्त्वपूर्ण प्रश्न

1. संधि किसे कहते हैं?
2. संधि के कितने प्रकार हैं?
3. निम्नलिखित शब्दों में संधि करो और उनके नाम बताओ

• मत + ऐक्य,
• शुभ + इच्छु
• धन + अभाव,
• उत + लास
• पितृ + अनुमति,
• निः + सन्देह
• जगत + नाथ,
• जगत + ईश
• हित + उपदेश,
• सदा + ऐव
• भोजन + आलय,
• परम + ईश्वर
• मनः + हर,
• निः + बल
• शिव + आलय,
• उत् + गम
• निः + रोग,
• सम + कल्प
• यदि + अपि,
• पो + अन
• नर + इन्द्र,
• परम + अर्थ।

4. निम्नलिखित शब्दों का संधि–विच्छेद करो
व्यवसाय, दुरुपयोग, उद्योग, निश्चल, निर्जन, उज्ज्वल, सूर्योदय, इत्यादि, निर्भय, जगदीश, निश्चिन्त, मनोरथ।

5. नीचे लिखे प्रत्येक शब्द के आगे संधियों के उदाहरण और संधियों के नाम लिखे हैं, किन्तु वे गलत हैं। आप उन्हें सही क्रम में लिखिए–

• मनोरथ – अयादि संधि
• नायक – वृद्धि संधि
• इत्यादि – गुण संधि
• विद्यार्थी – व्यंजन संधि
• महेन्द्र – विसर्ग संधि
• सदैव – दीर्घ संधि
• सज्जन – यण संधि
• सम–कल्प – व्यंजन संधि
• निष्फल – व्यंजन संधि
• मनोयोग – विसर्ग संधि

6. निम्नलिखित शब्दों में से व्यंजन संधि का उदाहरण बताइएं।

• मनोहर,
• पवन,
• जगन्नाथ,
• महाशय।

7. परम + अर्थ, हित + उपदेश, सत् + जन, मनः + विकार उपर्युक्त संधियों में से किन–किन संधियों का उदाहरण है।

MP Board Class 12th Hindi Solutions

MP Board Class 12th General Hindi निबंध साहित्य का इतिहास

निबंध का उदय

आधुनिक युग को गद्य की प्रतिस्थापना का श्रेय जाता है। जिस विश्वास, भावना और आस्था पर हमारे युग की बुनियाद टिकी थी उसमें कहीं न कहीं अनास्था, तर्क और विचार ने अपनी सेंध लगाई। कदाचित् यह सेंध अपने युग की माँग थी जिसका मुख्य साधन गद्य बना। यही कारण है, कवियों ने गद्य साहित्य में भी अपनी प्रतिभा का परिचय दिया।

हिंदी गद्य का आरम्भ भारतेंदु हरिश्चंद्र से माना जाता है। वह कविता के क्षेत्र में चाहे परम्परावादी थे पर गद्य के क्षेत्र में नवीन विचारधारा के पोषक थे। उनका व्यक्तित्व इतना समर्थ था कि उनके इर्द-गिर्द लेखकों का एक मण्डल ही बन गया था। यह वह मण्डल था जो हिंदी गद्य के विकास में महत्त्वपूर्ण स्थान रखते हैं। हिंदी गद्य के विकास में दशा और दिशा की आधारशिला रखने वालों में इस मण्डल का अपूर्व योगदान है। इन लेखकों ने अपनी बात कहने के लिए निबंध विधा को चुना।

निबंध की व्युत्पत्ति, स्वरूप एवं परिभाषा

निबंध की व्युत्पत्ति पर विचार करने पर पता चलता है कि ‘नि’ उपसर्ग, ‘बन्ध’ धातु और ‘धर्म प्रत्यय से यह शब्द बना है। इसका अर्थ है बाँधना। निबंध शब्द के पर्याय के रूप में लेख, संदर्भ, रचना, शोध प्रबंध आदि को स्वीकार किया जाता है। निबंध को हिंदी में अंग्रेजी के एसे और फ्रेंच के एसाई के अर्थ में ग्रहण किया जाता है जिसका सामान्य अर्थ प्रयत्न, प्रयोग या परीक्षण कहा गया है।

निबंध की भारतीय व पाश्चात्य परिभाषाएँ कोशीय अर्थ।

‘मानक हिंदी कोश’ में निबंध के संबंध में यह मत प्रकट किया गया है-“वह विचारपूर्ण विवरणात्मक और विस्तृत लेख, जिसमें किसी विषय के सब अंगों का मौलिक और स्वतंत्र रूप से विवेचन किया गया हो।”

हिंदी शब्द सागर’ में निबंध शब्द का यह अर्थ दिया गया है- ‘बन्धन वह व्याख्या है जिसमें अनेक मतों का संग्रह हो।”

पाश्चात्य विचारकों का मत

निबंध शब्द का सबसे पहले प्रयोग फ्रेंच के मांतेन ने किया था, और वह भी एक विशिष्ट काव्य विधा के लिए। इन्हें ही निबंध का जनक माना जाता है। उनकी रचनाएँ आत्मनिष्ठ हैं। उनका मानना था कि “I am myself the subject of my essays because I am the only person whom I know best.”

अंग्रेजी में सबसे पहले एस्से शब्द का प्रयोग बेकन ने किया था। वह लैटिन । भाषा का ज्ञाता था और उसने इस भाषा में अनेक निबंध लिखे। उसने निबंध कोबिखरावमुक्त चिन्तन कहा है।

सैमुअल जॉनसन ने लिखा, “A loose sally of the mind, an irregular, .. undigested place is not a regular and orderly composition.” “निबंध मानसिक जगत् की विशृंखल विचार तरंग एक असंगठित-अपरिपक्व और अनियमित विचार खण्ड है। निबंध की समस्त विशेषताएँ हमें आक्सफोर्ड इंग्लिश डिक्शनरी में दी गई इस परिभाषा में मिल जाती है, “सीमित आकार की एक ऐसी रचना जो किसी विषय विशेष या उसकी किसी शाखा पर लिखी गई हो, जिसे शुरू में परिष्कारहीन अनियमित, अपरिपक्व खंड माना जाता था, किंतु अब उससे न्यूनाधिक शैली में लिखित छोटी आकार की संबद्ध रचना का बोध होता है।”

भारतीय विचारकों का मत

आचार्य रामचंद्र शक्ल-आचार्य रामचंद्र शक्ल ने निबंध को व्यवस्थित और मर्यादित प्रधान गद्य रचना माना है जिसमें शैली की विशिष्टता होनी चाहिए, लेखक का निजी चिंतन होना चाहिए और अनुभव की विशेषता होनी चाहिए। इसके अतिरिक्त लेखक के अपने व्यक्तित्व की विशिष्टता भी निबंध में रहती है। हिंदी साहित्य के इतिहास में आचार्य रामचंद्र शुक्ल ने निबंध की परिभाषा देते हुए लिखा, “आधुनिक पाश्चात्य लेखकों के अनुसार निबंध उसी को कहना चाहिए जिसमें व्यक्तित्व अर्थात् व्यक्तिगत विशेषता है। बात तो ठीक है यदि ठीक तरह से समझी जाय। व्यक्तिगत विशेषता का यह मतलब नहीं कि उसके प्रदर्शन के लिए विचारकों की श्रृंखला रखी ही न जाए या जान-बूझकर जगह-जगह से तोड़ दी जाए जो उनकी अनुमति के प्रकृत या लोक सामान्य स्वरूप से कोई संबंध ही न रखे अथवा भाषा से सरकस वालों की सी कसरतें या हठयोगियों के से आसन कराये जाएँ, जिनका लक्ष्य तमाशा दिखाने के सिवाय और कुछ न हो।”

बाबू गुलाब राय-बाबू गुलाबराय ने भी निबंध में व्यक्तित्व और विचार दोनों को आवश्यक माना है। वे लिखते हैं- “निबंध उस गद्य रचना को कहते हैं जिसमें एक सीमित आकार के भीतर किसी विषय का वर्णन या प्रतिपादन एक विशेष निजीपन, स्वच्छंदता, सौष्ठव, सजीवता तथा अनावश्यक संगति और संबद्धता के साथ किया गया हो।”

निबंध की परिभाषाओं का अध्ययन करने पर हम इस निष्कर्ष पर पहुँचते हैं कि निबंध एक गद्य रचना है। इसका प्रमुख उद्देश्य अपनी वैयक्तिक अनुभूति, भावना या आदर्श को प्रकट करना है। यह एक छोटी-सी रचना है और किसी एक विषय पर लिखी गई क्रमबद्ध रचना है। इसमें विषय की एकरूपता होनी चाहिए और साथ ही तारतम्यता भी। यह गद्य काव्य की ऐसी विधा है जिसमें लेखक सीमित आकार में अपनी भावात्मकता और प्रतिक्रियाओं को प्रकट करता है।

निबंध के तत्त्व

प्राचीन काल से आज तक साहित्य विधाओं में अनेक बदलाव आए हैं। साधारणतः निबंध में निम्नलिखित तत्त्वों का होना अनिवार्य माना गया है
1. उपयुक्त विषय का चुनाव-लेखक जिस विषय पर निबंध लिखना चाहता है उसे सबसे पहले उपयुक्त विषय का चुनाव करना चाहिए। इसके लिए उसे पर्याप्त सोच-विचार करना चाहिए। निबंध का विषय सामाजिक, वैज्ञानिक, दार्शनिक आर्थिक, ऐतिहासिक, धार्मिक, साहित्यिक, वस्तु, प्रकृति-वर्णन, चरित्र, संस्मरण, भाव, घटना आदि में से किसी भी विषय पर हो सकता है, किंतु विषय ऐसा होना चाहिए कि जिसमें लेखक अपना निश्चित पक्ष व दृष्टिकोण भली-भाँति व्यक्त कर सके।

2. व्यक्तित्व की अभिव्यक्ति-निबंध में निबंधकार के व्यक्तित्व की अभिव्यक्ति दिखनी चाहिए। मोन्तेन ने निबंधों पर निजी चर्चा करते हुए लिखा है, “ये मेरी भावनाएँ हैं, इनके द्वारा मैं स्वयं को पाठकों के समक्ष प्रस्तुत करता हूँ।” भारतीय और पाश्चात्य दोनों ही विचारकों ने निबंध लेखक के व्यक्तित्व के महत्त्व को स्वीकार किया है। निबंध लेखक की आत्मीयता और वैयक्तिकता के कारण ही विषय के सम्बन्ध में निबंधकार के विचारों, भावों और अनुभूति के आधार पर पाठक उनके साथ संबद्ध कर पाता है। इस प्रकार निबंधकार के व्यक्तित्व को निबंध का केंद्रीय गुण कहा जाता है।

3. एकसूत्रता-निबंध बँधी हुई एक कलात्मक रचना है। इसमें विषयान्तर की संभावना नहीं होती, इसलिए निबंध के लिए आवश्यक है कि निबंधकार अपने विचारों को एकसूत्रता के गुण से संबद्ध करके प्रस्तुत करता है। निबंध के विषय के मुख्य भाव या विचार पर अपनी दृष्टि डालते हुए निबंधकार तथ्यों को उसके तर्क के रूप में प्रस्तुत करता है। इन तर्कों को प्रस्तुत करते हुए निबंधकार को यह ध्यान रखना पड़ता है कि तथ्यों और तर्कों के बीच अन्विति क्रम बना रहे। कई निबंधकार निबंध लिखते समय अपनी भाव-तरंगों पर नियन्त्रण नहीं रख पाते, ऐसे में वह विषय अलग हो जाता है। वस्तुतः लेखक का कर्तव्य है कि वह विषयान्तर न हो। अगर विषयान्तर हो भी गया तो उसे इधर-उधर विचरण कर पुनः अपने विषय पर आना ही पड़ेगा। निबंधकार को अपने अभिप्रेत का अंत तक बनाए रखना चाहिए।

4. मर्यादित आकार-निबंध आकार की दृष्टि से छोटी रचना है। इस संदर्भ में हर्बट रीड ने कहा है कि निबंध 3500 से 5000 शब्दों तक सीमित किया जाना चाहिए। वास्तव में निबंध के आकार के निर्धारण की कोई आवश्यकता नहीं है। निबंध विषय के अनुरूप और सटीक तर्कों द्वारा लिखा जाता है। लेखक अपने विचार भावावेश के क्षणों में व्यक्त करता है। ऐसे में वह उसके आकार के विषय में सोचकर नहीं चलता। आवेश के क्षण बहुत थोड़ी अवधि के लिए होते हैं, इसलिए निश्चित रूप से निबंध का आकार स्वतः ही लघु हो जाता है। इसमें अनावश्यक सूचनाओं को कोई स्थान नहीं मिलता।

5. स्वतःपूर्णता-निबंध का एक गुण या विशेषता है कि यह अपने-आप में पूर्ण होना चाहिए। निबंधकार का दायित्व पाठकों को निबंध में चुने हुए विषय की समस्त जानकारी देना है। यही कारण है कि उसे विषय के पक्ष और विपक्ष दोनों पर पूर्णतः विचार करना चाहिए। विषय से संबंधित कोई ज्ञान अधूरा नहीं रहना चाहिए। जिस भाव या विचार या बिंदु को लेकर निबंधकार निबंध लिखता है, निबंध के अंत तक पाठक के मन में संतुष्टि का भाव जागृत होना चाहिए। अगर पाठक के मन में किसी तरह का जिज्ञासा भाव रह जाता है तो उस निबंध को अपूर्ण माना जाता है और इसे निबंध के अवगुण के रूप में शुमार कर लिया जाएगा।

6. रोचकता-निबंध क्योंकि एक साहित्यिक विधा है इसलिए इसमें रोचकता का तत्त्व निश्चित रूप से होना चाहिए। यह अलग बात है कि निबंध का सीधा संबंध बुद्धि तत्त्व से रहता है। फिर इसे ज्ञान की विधा न कहकर रस की विधा कहा जाता है, इसलिए इसमें रोचकता होनी चाहिए, ललितता होनी चाहिए और आकर्षण होना चाहिए। निबंध के विषय प्रायः शुष्क होते हैं, गंभीर होते हैं या बौद्धिक होते हैं।

अगर निबंधकार इन विषयों को रोचक रूप में पाठक तक पहुँचाने में समर्थ हो जाता है तो इसे निबंध की पूर्णता और सफलता कहा जाएगा।

निबंध के भेद

निबंध के भेद, इसके लिए अध्ययन किए गए हैं। विषयों की विविधता से देखा जाए तो इन्हें सीमा में नहीं बाँधा जा सकता। अतः निबंध लेखन का विषय दुनिया के किसी भी कोने का हो सकता है। विद्वानों ने निबंधों का वर्गीकरण तो अवश्य किया है पर यह वर्गीकरण या तो वर्णनीय विषय के आधार पर किया है या फिर उसकी शैली के आधार पर। निबंध का सबसे अधिक प्रचलित वर्गीकरण यह है

1. वर्णनात्मक-वर्णनात्मक निबंध वे कहलाते हैं जिनमें प्रायः भूगोल, यात्रा, ऋतु, तीर्थ, दर्शनीय स्थान, पर्व-त्योहार, सभा- सम्मेलन आदि विषयों का वर्णन किया जाता है। इनमें दृश्यों व स्थानों का वर्णन करते हुए रचनाकार कल्पना का आश्रय लेता है। ऐसे में उसकी भाषा सरल और सुगम हो जाती है। इसमें लेखक निबंध को रोचक बनाने में पूरी कोशिश करता है।

2. विवरणात्मक-इस प्रकार के निबंधों का विषय स्थिर नहीं रहता अपितु गतिशील रहता है। शिकार वर्णन, पर्वतारोहण, दुर्गम प्रदेश की यात्रा आदि का वर्णन जब कलात्मक रूप से किया जाता है तो वे निबंध विवरणात्मक निबंधों की शैली में स्थान पाते हैं। विवरणात्मक निबंधों में विशेष रूप से घटनाओं का विवरण अधिक होता है।

3. विचारात्मक-इस प्रकार के निबंधों में बौद्धिक चिन्तन होता है। इनमें दर्शन, अध्यात्म, मनोविज्ञान आदि विषयगत पक्षों का विवेचन किया जाता है। लेखक अपने अध्ययन व चिन्तन के अनुरूप तर्क-शितर्क और खण्डन का आश्रय लेते हुए विषय का प्रभावशाली विवेचन करता है। इनमें बौद्धिकता तो होती ही है साथ ही भावना और कला कल्पना का समन्वय भी होता है। ऐसे निबंधों में लेखक आमतौर पर तत्सम शैली अपनाता है। समासिकता की प्रधानता भी होती है।

4. भावात्मक-इस श्रेणी में उन निबंधों को स्थान मिलता है जो भावात्मक विषयों पर लिखे जाते हैं। इन निबंधों का निस्सरण हृदय से होता है। इनमें रागात्मकता होती है इसलिए लेखक कवित्व का भी प्रयोग कर लेता है। अनुभूतियाँ और उनके उद्घाटन की रसमय क्षमता इस प्रकार के निबंध लेखकों की संपत्ति मानी जाती हैं। वस्तुतः कल्पना के साथ काव्यात्मकता का पुट इन निबंधों में दृश्यमान होता है।

वर्गीकरण अनावश्यक

गौर से देखा जाए तो इन चारों भेदों की कोई ज़रूरत नहीं है क्योंकि ये निबंध लेखन की शैली हैं। इन्हें वर्गीकरण नहीं कहा जाना चाहिए। अगर कोई कहता है कि वर्णनात्मक निबंध है या दूसरा कोई कहता है कि विवरणात्मक निबंध है तो यह शैली नहीं है तो और क्या है?

वस्तुतः इन्हें विचारात्मक निबंध की श्रेणी में रखा जा सकता है। विचारात्मक निबंधों का विषय मानव जीवन का व्यापक कार्य क्षेत्र है और असीम चिंतन लोक है। इसमें धर्म, दर्शन, मनोविज्ञान आदि विषयों का गंभीर विश्लेषण होता है। इसे निबंध का आदर्श भी कहा जा सकता है। इसमें निबंधकार के गहन चिंतन, मनन, सूक्ष्म अन्तर्दृष्टि और विशद ज्ञान का स्पष्ट रूप देखने को मिलता है। इस संबंध में आचार्य रामचंद्र शुक्ल ने कहा है, “शुद्ध विचारात्मक निबंधों का वहाँ चरम उत्कर्ष नहीं कहा जा सकता है जहाँ एक-एक पैराग्राफ में विचार दबा-दबाकर.टूंसे गए हों, और एक-एक वाक्य किसी विचार खण्ड को लिए हुए हो।’

आचार्य शुक्ल ने अपने निबंधों में स्वयं इस शैली का बखूबी प्रयोग किया है। इसके अतिरिक्त आचार्य हजारी प्रसाद द्विवेदी ने भी इस प्रकार के अनेक निबंध लिखे हैं जिनमें उनके मन की मुक्त उड़ान को अनुभव किया जा सकता है। इन निबंधों में उनकी व्यक्तिगत रुचि और अरुचि का प्रकाशन है। नित्य प्रति के सामान्य शब्दों को अपनाते हुए बड़ी-बड़ी बातें कह देना द्विवेदीजी की अपनी विशेषता है। व्यक्तिगत निबंध जब लेखक लिखता है तो उसका संबंध उसके संपूर्ण निबंध से होता है। आचार्यजी के इसी प्रकार के निबंध ललित निबंध कहलाते रहे हैं। आचार्यजी ने स्वयं कहा है, “व्यक्तिगत निबंधों का लेखन किसी एक विषय को छेड़ता है किंतु जिस प्रकार वीणा के एक तार को छेड़ने से बाकी सभी तार झंकृत हो उठते हैं उसी प्रकार उस एक विषय को छुते ही लेखक की चित्तभूमि पर बँधे सैकड़ों विचार बज उठते हैं।”

आचार्य रामचंद्र शुक्ल व्यक्तित्व व्यंजना को निबंधों का आवश्यक गुण मानते हैं। उन्होंने वैचारिक गंभीरता और क्रमबद्धता का समर्थन किया है। आज हिंदी में दो ही प्रकार के प्रमुख निबंध लिखे जा रहे हैं, “व्यक्तिनिष्ठ और वस्तुनिष्ठ। यों निबंध का कोई भी विषय हो सकता है। साहित्यिक भी हो सकता है और सांस्कृतिक भी। सामाजिक भी और ऐतिहासिक आदि भी। वस्तुतः कोई भी निबंध केवल वस्तुनिष्ठ नहीं हो सकता और न ही व्यक्तिनिष्ठ हो सकता है। निबंध में कभी चिंतन की प्रधानता होती है और कभी लेखक का व्यक्तित्व उभर आता है।”

निबंध शैली

वस्तुतः निबंध शैली को अलग रूप में देखने की परम्परा-सी चल निकली है अन्यथा निबंधों का व करण निबंध शैली ही है। लेखक की रचना ही उसकी सबसे बड़ी शक्ति होती है। शैली ही उसके व्यक्तित्व की पहचान होती है। एक आलोचक ने शैली के बारे में कहा है कि जितने निबंध हैं, उतनी शैलियाँ हैं। इससे यह स्पष्ट होता है कि निबंध लेखन में लेखक के निजीपन का पूरा असर पड़ता है। निबंध की शैली से ही किसी निबंधकार की पहचान होती है क्योंकि एक निबंधकार की शैली दूसरे निबंधकार से भिन्न होती हैं।

मुख्य रूप से निबंध की निम्न शैलियाँ कही जाती हैं-
1. समास शैली-इस निबंध शैली में निबंधकार कम से कम शब्दों में अधिक-से-अधिक विषय का प्रतिपादन करता है। उसके वाक्य सुगठित और कसे हुए होते हैं। गंभीर विषयों के लिए इस शैली का प्रयोग किया जाता है।

2. व्यास शैली-इस तरह के निबंधों में लेखक तथ्यों को खोलता हुआ चला जाता है। उन्हें विभिन्न तर्कों और उदाहरणों के ज़रिए व्याख्यायित करता चला जाता है। वर्णनात्मक, विवरणात्मक और तुलनात्मक निबंधों में निबंधकार इसी प्रकार की शैली का प्रयोग करता है।

3. तरंग या विक्षेप शैली-इस शैली में निबंधकार में एकान्विति का अभाव रहता है। इसमें निबंधकार अपने मन की मौज़,में आकर बात कहता हुआ चलता है पर विषय पर केंद्रित अवश्य रहता है।

4. विवेचन शैली-इंस निबंध शैली में लेखक तर्क-वितर्क के माध्यम से प्रमाण पुष्टि और व्याख्या के माध्यम से, निर्णय आदि के माध्यम से अपने विषय को बढ़ाता हुआ चलता है। इस शैली में लेखक गहन चिंतन के आधार पर अपना कथ्य प्रस्तुत करता चला जाता है। विचारात्मक निबंधों में लेखक इस शैली का प्रयोग करता है। आचार्य रामचंद्र शुक्ल के निबंध इसी प्रकार की शैली के अन्तर्गत माने जाते हैं।

5. व्यंग्य शैली-इस शैली में निबंधकार व्यंग्य के माध्यम से अपने विषयों का प्रतिपादन करता चलता है। इसमें उसके विषय धार्मिक, सामाजिक, राजनीतिक आदि भी हो सकते हैं। इसमें रचनाकार किंचित हास्य का पुट देकर विषय को पठनीय बना देता है। शब्द चयन और अर्थ के चमत्कार की दृष्टि से इस शैली का निबंधकारों में विशेष प्रचलन है। व्यंग्यात्मक निबंध इसी शैली में लिखे जाते हैं।

6. निगमन और आगमन शैली-निबंधकार अपने विषय का प्रतिपादन करने । की दृष्टि से निगमन शैली और आगमन शैली का प्रयोग करता है। इस प्रकार की शैली में लेखक पहले विचारों को सूत्र रूप में प्रस्तुत करता है। तद्उपरांत उस सूत्र के अन्तर्गत पहले अपने विचारों की विस्तार के साथ व्याख्या करता है। बाद में सूत्र रूप में सार लिख देता है। आगमन शैली निनन शैली के विपरीत होती है। इसके अतिरिक्त निबंध की अन्य कई शैलियों को देखा जा सकता है, जैसे प्रलय शैली। इस प्रकार की शैली में निबंधकार कुछ बहके-बहके भावों की अभिव्यंजना करता है। कुछ लेखकों के निबंधों में इस शैली को देखा जा सकता है। भावात्मक निबंधों के लिए कुछ निबंधकार विक्षेप शैली अपनाते हैं। धारा शैली में भी कुछ निबंधकार निबंध लिखते हैं। इसी प्रकार कुछ निबंधकारों ने अलंकरण, चित्रात्मक, सूक्तिपरक, धाराप्रवाह शैली का भी प्रयोग किया है। महादेवी वर्मा की निबंध शैली अलंकरण शैली है।

हिंदी निबंध : विकास की दिशाएँ
हिंदी गद्य का अभाव तो भारतेंदुजी से पूर्व भी नहीं था, पर कुछ अपवादों तक सीमित था। उसकी न तो कोई निश्चित परंपरा थी और न ही प्रधानता। सन् 1850 के बाद गद्य की निश्चित परंपरा स्थापित हुई, महत्त्व भी बढ़ा। पाश्चात्य सभ्यता के संपर्क में आने पर हिंदी साहित्य भी निबंध की ओर उन्मुख हुआ। इसीलिए कहा जाता है कि भारतेंदु युग में सबसे अधिक सफलता निबंध लेखन में मिली। हिंदी निंबध साहित्य को निम्नलिखित भागों में विभाजित किया जा सकता है

• भारतेंदुयुगीन निबंध,
• द्विवेदीयुगीन निबंध,
• शुक्लयुगीन निबंध
• शुक्लयुगोत्तर निबंध एवं
• सामयिक निबंध-1940 से अब तक।

भारतेंदुयुगीन निबंध-भारतेंदु युग में सबसे अधिक सफलता निबंध में प्राप्त हुई। इस युग के लेखकों ने विभिन्न पत्र-पत्रिकाओं के माध्यम से निबंध साहित्य को संपन्न किया! भारतेंदु हरिश्चंद्र से हिंदी निबंध का आरंभ माना जाना चाहिए। बालकृष्ण भट्ट और प्रतापनारायण मिश्र ने इस गद्य विधा को विकसित एवं समृद्ध किया। आचार्य रामचंद्र शुक्ल ने इन दोनों लेखकों को स्टील और एडीसन कहा है। ये दोनों हिंदी के आत्म-व्यंजक निबंधकार थे। इस युग के प्रमुख निबंधकार हैं-भारतेंदु हरिश्चंद्र, प्रतापनारायण मिश्र, बालकृष्ण भट्ट, बदरीनारायण चौधरी ‘प्रेमघन’, लाला श्री निवासदास, राधाचरण गोस्वामी, काशीनाथ खत्री आदि। इन सभी निबंधकारों का संबंध किसी-न-किसी पत्र-पत्रिका से था। भारतेंदु ने पुरातत्त्व, इतिहास, धर्म, कला, समाज-सुधार, जीवनी, यात्रा-वृत्तांत, भाषा तथा साहित्य आदि अनेक विषयों पर निबंध लिखे। प्रतापनारायण मिश्र के लिए तो विषय की कोई सीमा ही नहीं थी। ‘धोखा’, ‘खुशामद’, ‘आप’, ‘दाँत’, ‘बात’ आदि पर उन्होंने अत्यंत रोचक निबंध लिखे। बालकृष्ण भट्ट भारतेंदु युग के सर्वाधिक समर्थ निबंधकार हैं। उन्होंने सामयिक विषय जैसे ‘बाल-विवाह’, ‘स्त्रियाँ और उनकी शिक्षा’ पर उपयोगी निबंध लिखे। ‘प्रेमघन’ के निबंध भी सामयिक विषयों पर टिप्पणी के रूप में हैं। अन्य निबंधकारों का महत्त्व इसी में है कि उन्होंने भारतेंदु, बालकृष्ण भट्ट और प्रतापनारायण मिश्र के मार्ग का अनुसरण किया।

द्विवेदीयुगीन निबंध-भारतेंदु युग में निबंध साहित्य की पूर्णतः स्थापना हो गई थी, लेकिन निबंधों का विषय अधिकांशतः व्यक्तिव्यंजक था। द्विवेदीयुगीन निबंधों में व्यक्तिव्यंजक निबंध कम लिखे गए। इस युग के श्रेष्ठ निबंधकारों में महावीर प्रसाद द्विवेदी (1864-1938), गोविंदनारायण मिश्र (1859-1926), बालमुकुंद गुप्त (1865-1907), माधव प्रसाद मिश्र (1871-1907), मिश्र बंधु-श्याम बिहारी मिश्र (1873-1947) और शुकदेव बिहारी मिश्र (1878-1951), सरदार पूर्णसिंह (1881-1939), चंद्रधर शर्मा गुलेरी (1883-1920), जगन्नाथ प्रसाद चतुर्वेदी (1875-1939), श्यामसुंदर दास (1875-1945), पद्मसिंह शर्मा ‘कमलेश’ (1876-1932), रामचंद्र शुक्ल (1884-1940), कृष्ण बिहारी मिश्र (1890-1963) आदि उल्लेखनीय हैं। महावीर प्रसाद द्विवेदी के निबंध परिचयात्मक या आलोचनात्मक हैं। उनमें आत्मव्यंजन तत्त्व नहीं है। गोंविद नारायण मिश्र के निबंध पांडित्यपूर्ण तथा संस्कृतनिष्ठ गद्यशैली के लिए प्रसिद्ध हैं। बालमुकुंद गुप्त ‘शिवशंभु के चिट्टे’ के लिए विख्यात हैं।

ये चिट्ठे “भारत मित्र’ में छपे थे। माधव प्रसाद मिश्र के निबंध ‘सुदर्शन’ में प्रकाशित हुए। उनके निबंधों का संग्रह ‘माधव मिश्र निबंध माला’ के नाम से प्रकाशित है। सरदार पूर्णसिंह भी इस युग के निबंधकार हैं। इनके निबंध नैतिक विषयों पर हैं। कहीं-कहीं इनकी शैली व्याख्यानात्मक हो गई हैं। चंद्रधर शर्मा गलेरी ने कहानी के अतिरिक्त निबंध भी लिखे। उनके निबंधों में मार्मिक व्यंग्य है। जगन्नाथ प्रसाद चतुर्वेदी के निबंध ‘गद्यमाला’ (1909) और ‘निबंध-निलय’ में प्रकाशित हैं। पद्मसिंह शर्मा कमलेश तुलनात्मक आलोचना के लिए विख्यात हैं। उनकी शैली प्रशंसात्मक और प्रभावपूर्ण है। श्यामसुंदरदास तथा कृष्ण बिहारी मिश्र मूलतः आलोचक थे। इनकी शैली सहज और परिमार्जित है। आचार्य रामचंद्र शुक्ल के प्रारंभिक निबंधों में भाषा संबंधी प्रश्नों और कुछ ऐतिहासिक व्यक्तियों के संबंध में विचार व्यक्त किए गए हैं। उन्होंने कुछ अंग्रेजी निबंधों का अनुवाद भी किया।

इस युग में गणेशशंकर विद्यार्थी, मन्नन द्विवेदी आदि ने भी पाठकों का ध्यान आकर्षित किया। शुक्लयुगीन निबंध-इस युग के प्रमुख निबंधकार आचार्य रामचंद्र शुक्ल हैं आचार्य शुक्ल के निबंध ‘चिंतामणि’ के दोनों खंडों में संकलित हैं। अभी हाल में चिंतामणि का तीसरा खंड प्रकाशित हुआ है। इसका संपादन डॉ. नामवर सिंह ने किया है। इसी युग के निबंधकारों में बाबू गुलाबराय (1888-1963) का उल्लेखनीय स्थान है। ‘ठलुआ क्लब’, ‘फिर निराश क्यों’, ‘मेरी असफलताएँ’ आदि संग्रहों में उनके श्रेष्ठ निबंध संकलित हैं। ल पुन्नालाल बख्शी’ ने कई अच्छे निबंध लिखे। इनके निबंध ‘पंचपात्र’ में संगृहीत हैं। अन्य निबंधकारों में शांति प्रेत द्विवेदी, शिवपूजन सहाय, पांडेय बेचन शर्मा ‘उग्र’, रधुवीर सिंह, माखनलाल चतुर्वेदी आदि मुख्य हैं। इस युग में निबंध तो लिखे गए, पर ललित निबंध कम ही हैं।

शुक्लयुगोत्तर निबंध-शुक्लयुगोत्तर काल में निबंध ने अनेक दिशाओं में सफलता प्राप्त की। इस युग मं समीक्षात्मक निबंध अधिक लिखे गए। यों व्यक्तव्यंजक निबंध भी कम नहीं लिखे गए। शुक्लजी के समीक्षात्मक निबंधों को परंपरा के दूसरे नाम हैं नंददुलारे वाजपेयी। इसी काल के महत्त्वपूर्ण निबंधकार आच हजागे प्रसाद द्विवेदी हैं। उनके ललित निबंधों में नवीन जीवन-बोध है।

शुक्लयुगोत्तर निबंधकारों में जैनेंद्र कुमार का स्थान काफी ऊँचा है। उनके निबंधों में दार्शनिकता है। यह दार्शनिकता निजी है, अतः ऊब पैदा नहीं करती। उनके निबंधों में सरसता है।

हिंदी में प्रभावशाली समीक्षा के अग्रदूत शांतिप्रिय द्विवेदी हैं। इन्होंने समीक्षात्मक निबंध भी लिखे हैं और साहित्येतर भी। इनके समीक्षात्मक निर्बंधों में निर्बध का स्वाद मिलता है। रामधारीसिंह ‘दिनकर’ ने भी इस युग में महत्त्वपूर्ण निबंध लिखे। इनके निबंध विचार-प्रधान हैं। लेकिन कुछ निबंधों में उनका अंतरंग पक्ष भी उद्घाटित हुआ है। समीक्षात्मक निबंधकारों में डॉ. नगेंद्र का स्थान महत्त्वपूर्ण है। उनके निबंधों की कल्पना, मनोवैज्ञानिक दृष्टि उनके व्यक्तित्व के अपरिहार्य अंग हैं। रामवृक्ष बेनीपुरी के निबंध-संग्रह ‘गेहूँ और गुलाब’ तथा ‘वंदे वाणी विनायकौ’ हैं। बेनीपुरी की भाषा में आवेग है, जटिलता नहीं। श्रीराम शर्मा, देवेंद्र सत्यार्थी भी निबंध के क्षेत्र में उल्लेखनीय हैं। वासुदेवशरण अग्रवाल के निबंधों में भारतीय संस्कृति के विविध आयामों को विद्वतापूर्वक उद्घाटित किया गया है। यशपाल के निबंधों में भी मार्क्सवादी दृष्टिकोण मिलता है। बनारसीदास चतुर्वेदी के निबंध-संग्रह ‘साहित्य और जीवन’, ‘हमारे आराध्य’ नाम में यही प्रवृत्ति है। कन्हैयालाल मिश्र प्रभाकर के निबंध में करुणा, व्यंग्य और भावुकता का सन्निवेश है। भगवतशरण उपाध्याय ने ‘ठूठा आम’, और ‘सांस्कृतिक निबंध’ में इतिहास और संस्कृति की पृष्टभूमि पर निबंध लिखे। प्रभाकर माचवे, विद्यानिवास मिश्र, धर्मवीर भारती, शिवप्रसाद सिंह, कुबेरनाथ राय, ठाकुर प्रसाद सिन्हा आदि के ललित निबंध विख्यात हैं।

सामयिक निबंधों में नई चिंतन पद्धति और अभिव्यक्ति देखी जा सकती है। अज्ञेय, विद्यानिवास मिश्र, कुबेरनाथ राय, निर्मल वर्मा, रमेशचंद्रशाह, शरद जोशी, जानकी वल्लभ शास्त्री, रामेश्वर शुक्ल ‘अंचल’, नेमिचंद्र जैन, विष्णु प्रभाकर, जगदीश चतुर्वेदी, डॉ. नामवर सिंह और विवेकी राय आदि ने हिंदी गद्य की निबंध परंपरा को न केवल बढ़ाया है, बल्कि उसमें विशिष्ट प्रयोग किए हैं। समीक्षात्मक निबंधों में गजानन माधव मुक्तिबोध का नाम आता है। उनके निबंधों में बौद्धिकता है और वयस्क वैचारिकता तबोध के ‘नई कविता का आत्मसंघर्ष तथा अन्य निबंध’ नए साहित्य का सौंदर्यशास्त्र, ‘समीक्षा की समस्याएँ’ और ‘एक साहित्यिक की डायरी’ नामक निबंध विशेष उल्लेखनीय हैं। डॉ. रामविलास शर्मा के निबंध शैली में स्वच्छता, प्रखरता तथा वैचारिक संपन्नता है। हिंदी निबंध में व्यंग्य को रवींद्र कालिया ने बढ़ाया है। नए निबंधकारों में रमेशचंद्र शाह का नाम तेजी से उभरा है।

महादेवी वर्मा, विजयेंद्र स्नातक, धर्मवीर भारती, सर्वेश्वरदयाल सक्सेना और रामेश्वर शुक्ल ‘अंचल’ के निबंधों में प्रौढ़ता है। इसके अतिरिक्त विष्णु प्रभाकर कृत ‘हम जिनके ऋणी हैं’ जानकी वल्लभ शास्त्री कृत ‘मन की बात’, ‘जो बिक न सकी’ आदि निबंधों में क्लासिकल संवेदना का उदात्त रूप मिलता है। नए निबंधकारों में : प्रभाकर श्रोत्रिय, चंद्रकांत वांदिवडेकर, नंदकिशोर आचार्य, बनवारी, कृष्णदत्त पालीवाल, प्रदीप मांडव, कर्णसिंह चौहान और सुधीश पचौरी आदि प्रमुख हैं। आज राजनीतिक-सांस्कृतिक विषयों पर भी निबंध लिखे जा रहे हैं। अतः हिंदी निबंध-साहित्य उत्तरोत्तर बढ़ता जा रहा है।

MP Board Class 12th Hindi Solutions

MP Board Class 12th Physics Solutions Chapter 5 चुम्बकत्व एवं द्रव्य

चुम्बकत्व एवं द्रव्य NCERT पाठ्यपुस्तक के अध्याय में पाठ्यनिहित प्रश्न एवं उनके उत्तर

प्रश्न 1.
भू-चुम्बकत्व सम्बन्धी निम्नलिखित प्रश्नों के उत्तर दीजिए
(a) एक सदिश को पूर्ण रूप से व्यक्त करने के लिए तीन राशियों की आवश्यकता होती है। उन तीन स्वतन्त्र राशियों के नाम लिखिए जो परम्परागत रूप से पृथ्वी के चुम्बकीय क्षेत्र को व्यक्त करने के लिए प्रयुक्त होती हैं।
(b) दक्षिण भारत में किसी स्थान पर नति कोण का मान लगभग 18° है। ब्रिटेन में आप इससे अधिक नति कोण की अपेक्षा करेंगे या कम की?
(c) यदि आप ऑस्ट्रेलिया के मेलबोर्न शहर में भू-चुम्बकीय क्षेत्र रेखाओं का नक्शा बनाएँ तो ये रेखाएँ पृथ्वी के अन्दर जाएँगी या इससे बाहर आएँगी?
(d) एक चुम्बकीय सुई जो ऊर्ध्वाधर तल में घूमने के लिए स्वतन्त्र है, यदि भू-चुम्बकीय उत्तर या दक्षिण ध्रुव पर रखी हो तो यह किस दिशा में संकेत करेगी?
(e) यह माना जाता है कि पृथ्वी का चुम्बकीय क्षेत्र लगभग एक चुम्बकीय द्विध्रुव के क्षेत्र जैसा है जो पृथ्वी के केन्द्र पर रखा है और जिसका द्विध्रुव आघूर्ण 8 × 10²²⁵ जूल टेस्ला^-1 है। कोई ढंग सुझाइए जिससे इस संख्या के परिमाण की कोटि जाँची जा सके।
(f) भूगर्भशास्त्रियों का मानना है कि मुख्य N-S चुम्बकीय ध्रुवों के अतिरिक्त, पृथ्वी की सतह पर कई अन्य स्थानीय ध्रुव भी हैं, जो विभिन्न दिशाओं में विन्यस्त हैं। ऐसा होना कैसे सम्भव है?
उत्तर :
(a) पृथ्वी के चुम्बकीय क्षेत्र को व्यक्त करने के लिए प्रयुक्त होने वाली तीन राशियाँ निम्नलिखित हैं-

• नति कोण अथवा नमन कोण δ
• दिक्पात का कोण θ
• पृथ्वी के चुम्बकीय क्षेत्र का क्षैतिज अवयव B_H

(b) चूँकि ब्रिटेन, दक्षिण भारत की तुलना में पृथ्वी के उत्तरी ध्रुव के अधिक समीप है, अतः यहाँ नति कोण अधिक होगा। वास्तव में ब्रिटेन में नति कोण लगभग 70° है।।
(c) ऑस्ट्रेलिया, पृथ्वी के दक्षिण गोलार्द्ध में स्थित है। चूंकि पृथ्वी के दक्षिण ध्रुव से चुम्बकीय क्षेत्र रेखाएँ बाहर निकलती हैं, अत: ये पृथ्वी से बाहर निकलती प्रतीत होंगी।
(d) चूँकि ध्रुवों पर पृथ्वी का चुम्बकीय क्षेत्र ऊर्ध्वाधर होता है, अतः ध्रुवों पर लटकी चुम्बकीय सुई (जो ऊर्ध्वाधर तल में घूमने के लिए स्वतन्त्र है) ऊर्ध्वाधर दिशा की ओर इंगित करेगी।

(e) यदि हम मान लें कि पृथ्वी के केन्द्र पर M चुम्बकीय-आघूर्ण का चुम्बकीय द्विध्रुव रखा है तो पृथ्वी के चुम्बकीय निरक्ष पर स्थित बिन्दुओं की इस द्विध्रुव के केन्द्र से दूरी पृथ्वी की त्रिज्या के बराबर होगी।
निरक्ष पर चुम्बकीय क्षेत्र \(B=\frac{\mu_{0}}{4 \pi} \cdot \frac{M}{r^{3}}\)
∴ \(M=\frac{4 \pi B r^{3}}{\mu_{0}} \)
प्रयोगों द्वारा पृथ्वी के चुम्बकीय निरक्ष पर B = 0.4 गॉस = 0.4 × 10^-4 टेस्ला तथा
r = R_E = 6.4 × 10⁶ मीटर

= 10.5 × 10²²
ऐम्पियर-मीटर 2 स्पष्ट है कि पृथ्वी के चुम्बकीय द्विध्रुव आघूर्ण का यह मान 8 × 10²² जूल टेस्ला^-1 के अत्यन्त निकट है। इस प्रकार पृथ्वी के चुम्बकीय द्विध्रुव आघूर्ण के परिमाण की कोटि की जाँच की जा सकती है।
(f) यद्यपि पृथ्वी का सम्पूर्ण चुम्बकीय क्षेत्र, एकल चुम्बकीय द्विध्रुव के कारण माना जाता है अपितु स्थानीय स्तर पर चुम्बकित पदार्थों के भण्डार अन्य चुम्बकीय ध्रुवों का निर्माण करते हैं।

प्रश्न 2.
निम्नलिखित प्रश्नों के उत्तर दीजिए –
(a) एक जगह से दूसरी जगह जाने पर पृथ्वी का चुम्बकीय क्षेत्र बदलता है। क्या यह समय के साथ भी
साथ भी बदलता है? यदि हाँ, तो कितने समय अन्तराल पर इसमें पर्याप्त परिवर्तन होते हैं?
(b) पृथ्वी के क्रोड में लोहा है, यह ज्ञात है। फिर भी भूगर्भशास्त्री इसको पृथ्वी के चुम्बकीय क्षेत्र का स्रोत नहीं मानते। क्यों?
(c) पृथ्वी के क्रोड के बाहरी चालक भाग में प्रवाहित होने वाली आवेश धाराएँ भू-चुम्बकीय क्षेत्र के लिए उत्तरदायी समझी जाती हैं। इन धाराओं को बनाए रखने वाली बैटरी (ऊर्जा स्रोत) क्या हो सकती है?
(d) अपने 4-5 अरब वर्षों के इतिहास में पृथ्वी अपने चुम्बकीय क्षेत्र की दिशा कई बार उलट चुकी होगी। भूगर्भशास्त्री, इतने सुदूर अतीत के पृथ्वी के चुम्बकीय क्षेत्र के बारे में कैसे जान पाते हैं?
(e) बहुत अधिक दरियों पर (30,000 किमी से अधिक) पृथ्वी का चुम्बकीय क्षेत्र अपनी द्विध्रुवीय आकृति से काफी भिन्न हो जाता है। कौन-से कारक इस विकृति के लिए उत्तरदायी हो सकते हैं?
(1) अन्तरातारकीय अन्तरिक्ष में 10^-12 टेस्ला की कोटि का बहुत ही क्षीण चुम्बकीय क्षेत्र होता है। क्या इस क्षीण चुम्बकीय क्षेत्र के भी कुछ प्रभावी परिणाम हो सकते हैं? समझाइए।
उत्तर :
(a) यद्यपि यह सत्य है कि पृथ्वी का चुम्बकीय क्षेत्र समय के साथ बदलता है, परन्तु चुम्बकीय-क्षेत्र में प्रेक्षण योग्य परिवर्तन के लिए कोई निश्चित समय सीमा निर्धारित नहीं की जा सकती। इसमें सैकड़ों वर्ष का समय भी लग सकता है।
(b) यह सुज्ञात तथ्य है कि पृथ्वी के क्रोड में पिघला हुआ लोहा है परन्तु इसका ताप लोहे के क्यूरी ताप से कहीं अधिक है। इतने उच्च ताप पर यह (लौहचुम्बकीय नहीं हो सकता) कोई चुम्बकीय क्षेत्र उत्पन्न नहीं कर सकता।
(c) यह माना जाता है कि पृथ्वी के गर्भ में उपस्थित रेडियोऐक्टिव पदार्थों के विघटन से प्राप्त ऊर्जा ही आवेश धाराओं की ऊर्जा का स्रोत है।

(d) प्रारम्भ में पृथ्वी के गर्भ में अनेकों पिघली हुई चट्टानें थीं जो समय के साथ धीरे-धीरे ठोस होती चली गईं। इन चट्टानों में मौजूद लौह-चुम्बकीय पदार्थ उस समय के पृथ्वी के चुम्बकीय क्षेत्र के अनुरूप संरेखित हो गए। इस प्रकार भूतकाल का पृथ्वी का चुम्बकीय क्षेत्र इन चट्टानों में चुम्बकीय पदार्थों के अनुरूपण में अभिलेखित है। इन चट्टानों का भूचुम्बकीय अध्ययन उस समय के पृथ्वी के चुम्बकीय क्षेत्र का ज्ञान प्रदान करता है।

(e) पृथ्वी के आयनमण्डल में अनेकों आवेशित कण विद्यमान रहते हैं जिनकी गति एक अलग चुम्बकीय क्षेत्र उत्पन्न करती है। यही चुम्बकीय क्षेत्र, पृथ्वी तल से अधिक दूरी पर पृथ्वी के चुम्बकीय क्षेत्र को विकृत कर देता है। आयनों के कारण उत्पन्न चुम्बकीय क्षेत्र सौर पवन पर निर्भर करता है।

(f) सूत्र R = \(\frac{m v}{q B}\) से, \(R \propto \frac{1}{B}\)
इससे स्पष्ट है कि अत्यन्त क्षीण चुम्बकीय क्षेत्र में गतिमान आवेशित कण अति विशाल त्रिज्या का मार्ग अपनाता है जो कि थोड़ी दूरी में लगभग सरल रेखीय प्रतीत होता है, अत: छोटी दूरियों के लिए सूक्ष्म चुम्बकीय क्षेत्र अप्रभावी प्रतीत होते हैं परन्तु बड़ी दूरियों में ये प्रभावी विक्षेपण उत्पन्न करते हैं।

प्रश्न 3.
एक छोटा छड़ चुम्बक जो एकसमान बाह्य चुम्बकीय क्षेत्र 0.25 टेस्ला के साथ 30° का कोण बनाता है, पर 4.5 × 10^-2 जूल का बल आघूर्ण लगता है। चुम्बक के चुम्बकीय-आघूर्ण का परिमाण क्या है?
हल :
दिया है : B= 0.25 टेस्ला, θ = 30°, r = 4.5 × 10^-2 जूल, M = ?
t= MB sin θ से,
\(M=\frac{\tau}{B \sin \theta}=\frac{4.5 \times 10^{-2}}{0.25 \times 0.5}\) (∵ sin 30° = 0.5)
∴ चुम्बकीय-आघूर्ण M = 0.36 जूल टेस्ला^-1।

प्रश्न 4.
चुम्बकीय-आघूर्ण m = 0.32 जूल टेस्ला^-1 वाला एक छोटा छड़ चुम्बक, 0.15 टेस्ला के एकसमान बाह्य चुम्बकीय क्षेत्र में रखा है। यदि यह छड़ क्षेत्र के तल में घूमने के लिए स्वतन्त्र हो तो क्षेत्र के किस विन्यास में यह (i) स्थायी सन्तुलन और (ii) अस्थायी सन्तुलन में होगा? प्रत्येक स्थिति में चुम्बक की स्थितिज ऊर्जा का मान बताइए।
हल :
दिया है : m = 0.32 जूल टेस्ला^-1
B= 0.15 टेस्ला ।
(i) जब चुम्बक का चुम्बकीय-आघूर्ण क्षेत्र की दिशा में संरेखित होगा तो चुम्बक स्थायी सन्तुलन की स्थिति में होगा।
इस स्थिति में स्थितिज ऊर्जा U₀ = – MB cos 0° [∵ U_θe = – MB cos θ]
= – 0.32 × 0.15 × 1
= – 0.048 जूल
या = 4.8×10^-2 जूल।

(ii) जब चुम्बकीय-आघूर्ण, क्षेत्र के विपरीत दिशा में संरेखित होगा (θ = 180°) तो चुम्बक अस्थायी सन्तुलन की स्थिति में होगा। इस स्थिति में स्थितिज ऊर्जा U_180° = – MB cos 180°
= – 0.32 × 0.15 × (-1)
= + 0.048 जूल
= 4.8 × 10^-2 जूल।

प्रश्न 5.
एक परिनालिका में पास-पास लपेटे गए 800 फेरे हैं तथा इसकी अनुप्रस्थ काट का क्षेत्रफल 2.5 × 10^-4 मीटर² है और इसमें 3.0 ऐम्पियर धारा प्रवाहित हो रही है। समझाइए कि किस अर्थ में यह परिनालिका एक छड़ चुम्बक की तरह व्यवहार करती है? इसके साथ जुड़ा हुआ चुम्बकीय-आघूर्ण कितना है?
हल :
दिया है : N = 800, i = 3.0 ऐम्पियर, A = 2.5 × 10^-4 मीटर²
∴ चुम्बकीय-आघूर्ण M = NiA = 800 × 3.0 × 2.5 × 10^-4
= 0.60 जूल टेस्ला^-1 ।
∵ परिनालिका को किसी चुम्बकीय क्षेत्र में लटकाने पर दण्ड चुम्बक के समान ही इस पर भी एक बल-युग्म कार्य करता है, अत: यह दण्ड-चुम्बक के समान व्यवहार करती है।

प्रश्न 6.
यदि प्रश्न 5 में बताई गई परिनालिका ऊर्ध्वाधर दिशा के परितः घूमने के लिए स्वतन्त्र हो और इस पर क्षैतिज दिशा में एक 0.25 टेस्ला का एकसमान चुम्बकीय क्षेत्र लगाया जाए, तो इस परिनालिका पर लगने वाले बल आघूर्ण का परिमाण उस समय क्या होगा, जब इसकी अक्ष आरोपित क्षेत्र की दिशा से 30° का कोण बना रही हो?
हल :
दिया है : B= 0.25 टेस्ला
पूर्व प्रश्न में,. M = 0.60 जूल टेस्ला^-1
θ = 30°
∴ परिनालिका पर बल-आघूर्ण t = MB sin θ = 0.60 × 0.25 × \(\frac { 1 }{ 2 }\)
= 0.075 जूल = 7.5 × 10^-2 जूल।

प्रश्न 7.
एक छड़ चुम्बक जिसका चुम्बकीय-आघूर्ण 1.5 जूल टेस्ला^-1 है, 0.22 टेस्ला के एक एकसमान चुम्बकीय क्षेत्र के अनुदिश रखा है।
(a) एक बाह्य बल आघूर्ण कितना कार्य करेगा यदि यह चुम्बक को चुम्बकीय क्षेत्र के (i) लम्बवत्, (ii) विपरीत दिशा में संरेखित करने के लिए घुमा दें।
(b) स्थिति (i) एवं (ii) में चुम्बक पर कितना बल आघूर्ण होता है?
हल :
दिया है : M = 1.5 जूल टेस्ला^-1,
B= 0.22 टेस्ला ।
(a) सूत्र W = – MB (cosθ₂ – cosθ₁) से,
(i) चुम्बक को θ₁ = 0° से θ₂ = 90° तक घुमाने में बल-आघूर्ण द्वारा कृत कार्य
W = – 1.5 × 0.22 [cos 90° – cos 0°]
= – 0.33 × (0- 1)= 0.33 जूल। (ii) चुम्बक को 01 = 0° से 02 = 180° तक घुमाने में बल आघूर्ण द्वारा कृत कार्य
W = – 1.5 × 0.22 [cos 180° – cos 0°]
= – 0.33 [ – 1 – 1] = 0.66 जूल।

(b) (i) स्थिति (i) में चुम्बक पर कार्यरत बल आघूर्ण
t= MB sin 90°
= 1.5 × 0.22 × 1 = 0.33 जूल।
(ii) स्थिति (ii) में चुम्बक पर कार्यरत बल-आघूर्ण
T= MB sin 180° = 0

प्रश्न 8.
एक परिनालिका जिसमें पास-पास 2000 फेरे लपेटे गए हैं तथा जिसके अनुप्रस्थ काट का क्षेत्रफल 1.6 × 10^-4 मीटर² है और जिसमें 4.0 ऐम्पियर की धारा प्रवाहित हो रही है, इसके केन्द्र से इस प्रकार लटकाई गई है कि यह एक क्षैतिज तल में घूम सके।
(a) परिनालिका के चुम्बकीय-आघूर्ण का मान क्या है?
(b) परिनालिका पर लगने वाला बल एवं बल आघूर्ण क्या है, यदि इस पर, इसकी अक्ष से 30° का कोण बनाता हुआ 7.5 × 10^-2 टेस्ला का एकसमान क्षैतिज चुम्बकीय क्षेत्र लगाया जाए?
हल :
दिया है : कुल फेरे
N = 2000,
A = 1.6 × 10^-4 मीटर²
i = 4.0 ऐम्पियर
B = 7.5 × 10^-2 टेस्ला

(a) परिनालिका का चुम्बकीय-आघूर्ण
M = NiA = 2000 × 4.0 × 1.6 × 10^-4
= 1.28 ऐम्पियर-मीटर²।

(b) सूत्र t = MB sin θ से,
अक्ष से θ = 30° के कोण पर लगे चुम्बकीय क्षेत्र के कारण बल आघूर्ण
t = 1.28 × 7.5 × 10^-2 × \(\frac { 1 }{ 2 }\)
= 4.8 × 10^-2 न्यूटन-मीटर
= 0.048 न्यूटन-मीटर। :: क्षेत्र एकसमान है, अत: परिनालिका पर कार्यरत बल शून्य होगा।

प्रश्न 9.
एक वृत्ताकार कुंडली जिसमें 16 फेरे हैं, जिसकी त्रिज्या 10 सेमी है और जिसमें 0.75 ऐम्पियर धारा प्रवाहित हो रही है, इस प्रकार रखी है कि इसका तल 5.0 × 10^-2 टेस्ला परिमाण वाले बाह्य क्षेत्र के लम्बवत् है। कुंडली, चुम्बकीय क्षेत्र के लम्बवत् और इसके अपने तल में स्थित एक अक्ष के चारों तरफ घूमने के लिए स्वतन्त्र है। यदि कुंडली को जरा-सा घुमा कर छोड़ दिया जाए तो यह अपनी स्थायी सन्तुलनावस्था के इधर-उधर 2.0 सेकण्ड-1 की आवृत्ति से दोलन करती है। कुंडली का अपने घूर्णन अक्ष के परितः जड़त्व-आघूर्ण क्या है?
हल :
दिया है : N = 16, r = 0.10 मीटर, i = 0.75 ऐम्पियर, B= 5.0 × 10^-2 टेस्ला
घूर्णन आवृत्ति γ = 2.0 सेकण्ड^-1, जड़त्व-आघूर्ण I = ?

कुंडली का चुम्बकीय-आघूर्ण
M = NiA = Ni × πr²
= 16 × 0.75 × 3.14 × (0.10)²
= 0.377 ऐम्पियर-मीटर²
∴ जड़त्व-आघूर्ण \(I=\frac{0.377 \times 5.0 \times 10^{-2}}{4 \times(3.14)^{2} \times(2.0)^{2}}\)
= 1.2 × 10^-4 किग्रा-मीटर।

प्रश्न 10.
एक चुम्बकीय सुई चुम्बकीय याम्योत्तर के समान्तर एक ऊर्ध्वाधर तल में घूमने के लिए स्वतन्त्र है। इसका उत्तरी ध्रुव क्षैतिज से 22° के कोण पर नीचे की ओर झुका है। इस स्थान पर चुम्बकीय क्षेत्र के क्षैतिज अवयव का मान 0.35 गाउस है। इस स्थान पर पृथ्वी के चुम्बकीय-क्षेत्र का परिमाण ज्ञात कीजिए।
हल :
दिया है : चुम्बकीय क्षेत्र का क्षैतिज अवयव
B_H = 0.35 गाउस
जबकि नति कोण δ = 22°
यदि पृथ्वी का सम्पूर्ण चुम्बकीय क्षेत्र B है तो B_H = B cos δ से,

\(B=\frac{B_{H}}{\cos \delta}=\frac{0.35}{\cos 22^{\circ}}\)
\(=\frac{0.35}{0.9272}\) = 0.38 गाउस।

प्रश्न 11.
दक्षिण अफ्रीका में किसी स्थान पर एक चुम्बकीय सुई भौगोलिक उत्तर से 12° पश्चिम की ओर संकेत करती है। चुम्बकीय याम्योत्तर में संरेखित नति-वृत्त की चुम्बकीय सुई का उत्तरी ध्रुव क्षैतिज से 60° उत्तर की
ओर संकेत करता है। पृथ्वी के चुम्बकीय क्षेत्र का क्षैतिज अवयव मापने पर 0.16 गाउस पाया जाता है। इस स्थान पर पृथ्वी के क्षेत्र का परिमाण और दिशा बताइए।
हल :
दिया है : नति कोण 6 = 60° जबकि दिक्पात का कोण θ = 12° उत्तर से पश्चिम की ओर B_H = 0.16 गाउस
B_H = B cos δ से,
\(B=\frac{B_{H}}{\cos \delta}=\frac{0.16}{\cos 60^{\circ}}\)
\(=\frac{0.16}{0.5}\) = 0.32 गाउस
अत: इस स्थान पर पृथ्वी का सम्पूर्ण क्षेत्र 0.32 गाउस है जिसकी दिशा भौगोलिक याम्योत्तर से 12° पश्चिम की ओर क्षैतिज से 60° के कोण पर ऊपर की ओर है।

प्रश्न 12.
किसी छोटे छड़ चुम्बक का चुम्बकीय-आघूर्ण 0.48 जूल टेस्ला^-1 है। चुम्बक के केन्द्र से 10 सेमी की दूरी पर स्थित किसी बिन्दु पर इसके चुम्बकीय क्षेत्र का परिमाण एवं दिशा बताइए यदि यह बिन्दु (i) चुम्बक के अक्ष पर स्थित हो, (ii) चुम्बक के अभिलम्ब समद्विभाजक पर स्थित हो।
हल :
दिया है : M = 0.48 जूल टेस्ला^-1, r = 0.10 मीटर, B= ?
(i) जब बिन्दु चुम्बक के अक्ष पर है तब चुम्बकीय क्षेत्र

= 0.96 × 10^-4 टेस्ला ।
अथवा B_ax = 0.96 गाउस दक्षिणी ध्रुव से उत्तरी ध्रुव की ओर
(ii) जब बिन्दु चुम्बक के लम्ब समद्विभाजक पर है तो चुम्बकीय क्षेत्र
B_eq= \(\frac { 1 }{ 2 }\)B_ax = \(\frac { 1 }{ 2 }\) × 0.96
= 0.48 गाउस ( उत्तरी ध्रुव से दक्षिणी ध्रुव की ओर)।

प्रश्न 13.
क्षैतिज तल में रखे एक छोटे छड़ चुम्बक का अक्ष, चुम्बकीय उत्तर-दक्षिण दिशा के अनुदिश है। सन्तुलन बिन्दु चुम्बक के अक्ष पर, इसके केन्द्र से 14 सेमी दूर स्थित है। इस स्थान पर पृथ्वी का चुम्बकीय क्षेत्र 0.36 गाउस एवं नति कोण शून्य है। चुम्बक के अभिलम्ब समद्विभाजक पर इसके केन्द्र से उतनी ही दूर (14 सेमी) स्थित किसी बिन्दु पर परिणामी चुम्बकीय क्षेत्र क्या होगा?
हल :
दिया है : पृथ्वी का चुम्बकीय क्षेत्र B= 0.36 गाउस, नति कोण δ = 0°

अक्ष पर सन्तुलन बिन्दु की दूरी r = 0.14 मीटर
माना सन्तुलन बिन्दु पर चुम्बक के कारण चुम्बकीय क्षेत्र B_ax है
तब सन्तुलन की अवस्था में ,
B_ax = B_H⇒ B_ax = B cos δ = B
ये क्षेत्र परस्पर विपरीत होंगे।
अभिलम्ब समद्विभाजक पर, इतनी ही दूरी पर चुम्बक के कारण चुम्बकीय क्षेत्र
B_eq = \(\frac { 1 }{ 2 }\)B_ax⇒ B_eq= \(\frac { 1 }{ 2 }\)B
परन्तु यहाँ पृथ्वी का क्षेत्र B_H = B तथा चुम्बक का क्षेत्र दोनों एक ही दिशा में हैं, अतः यहाँ परिणामी क्षेत्र
B₁ = B_eq + B = \(\frac { 1 }{ 2 }\)B + B
= \(\frac { 3 }{ 2 }\)B = \(\frac { 3 }{ 2 }\) × 0.36 = 0.54 गाउस।
इसकी दिशा पृथ्वी के क्षेत्र के अनुदिश होगी।

प्रश्न 14.
यदि प्रश्न 13 में वर्णित चुम्बक को 180° से घुमा दिया जाए तो सन्तुलन बिन्दुओं की नई स्थिति क्या होगी?
हल :
इस स्थिति में, सन्तुलन बिन्दु अभिलम्ब समद्विभाजक पर प्राप्त होगा।
अक्षीय स्थिति में सन्तुलन बिन्दु हेतु

अन्तिम स्थिति में, प्रश्न के अनुसार r_ax = 0.14 मीटर
r_eq = \(\frac{0.14}{(2)^{1 / 3}}\) × 2^-1/3
= 0.111 मीटर = 11.1 सेमी।
अत: सन्तुलन बिन्दु निरक्षीय स्थिति में केन्द्र से 11.1 सेमी की दूरी पर मिलेगा।

प्रश्न 15.
एक छोटा छड़ चुम्बक जिसका चुम्बकीय-आघूर्ण 5.25 × 10^-2 जूल टेस्ला^-1 है, इस प्रकार रखा है कि इसका अक्ष पृथ्वी के क्षेत्र की दिशा के लम्बवत् है। चुम्बक के केन्द्र से कितनी दूरी पर, परिणामी क्षेत्र पृथ्वी के क्षेत्र की दिशा से 45° का कोण बनाएगा, यदि हम (a) अभिलम्ब समद्विभाजक पर देखें, (b) अक्ष पर देखें? इस स्थान पर पृथ्वी के चुम्बकीय क्षेत्र का परिमाण 0.42 गाउस है। प्रयुक्त दूरियों की तुलना में चुम्बक की लम्बाई की उपेक्षा कर सकते हैं।
हल :
दिया है : M = 5.25 × 10^-2जूल टेस्ला^-1
पृथ्वी का क्षेत्र B_H = 0.42 गाउस
(a) माना ऐसा, चुम्बक के निरक्ष पर उसके केन्द्र से r_eq दूरी पर होता है।
इस बिन्दु पर चुम्बक के कारण क्षेत्र

प्रश्न 16.
निम्नलिखित प्रश्नों के उत्तर दीजिए –
(a) ठण्डा करने पर किसी अनुचुम्बकीय पदार्थ का नमूना अधिक चुम्बकन क्यों प्रदर्शित करता है? ( एक ही चुम्बककारी क्षेत्र के लिए)
(b) अनुचुम्बकत्व के विपरीत, प्रतिचुम्बकत्व पर ताप का प्रभाव लगभग नहीं होता। क्यों?
(c) यदि एक टोरॉइड में बिस्मथ का क्रोड लगाया जाए तो इसके अन्दर चुम्बकीय क्षेत्र उस स्थिति की तुलना में (किंचित) कम होगा या (किंचित) ज्यादा होगा, जबकि क्रोड खाली हो?
(d) क्या किसी लौहचुम्बकीय पदार्थ की चुम्बकशीलता चुम्बकीय क्षेत्र पर निर्भर करती है? यदि हाँ, तो उच्च चुम्बकीय क्षेत्रों के लिए इसका मान कम होगा या अधिक? . (e) किसी लौह चुम्बक की सतह के प्रत्येक बिन्दु पर चुम्बकीय क्षेत्र रेखाएँ सदैव लम्बवत् होती हैं [यह तथ्य उन स्थिरविद्युत क्षेत्र रेखाओं के सदृश है जो कि चालक की सतह.के प्रत्येक बिन्दु पर लम्बवत् होती हैं। क्यों?
(f) क्या किसी अनुचुम्बकीय नमूने का अधिकतम सम्भव चुम्बकन, लौहचुम्बक के चुम्बकन के परिमाण की कोटि का होगा?
उत्तर :
(a) ताप के घटने पर पदार्थ के परमाण्वीय चुम्बकों का ऊष्मीय विक्षोभ कम हो जाता है जिसके कारण इन चुम्बकों के बाह्य चुम्बकीय क्षेत्र की दिशा में संरेखित होने की प्रवृत्ति बढ़ जाती है। –
(b) प्रतिचुम्बकीय पदार्थ के परमाणु ऊष्मीय विक्षोभ के कारण, भले ही किसी भी स्थिति में हों, उनमें बाह्य
चुम्बकीय क्षेत्र के कारण, प्रेरित चुम्बकीय-आघूर्ण सदैव ही बाह्य क्षेत्र के विपरीत दिशा में प्रेरित होता है। इस प्रकार प्रतिचुम्बकत्व पर ताप का कोई प्रभाव नहीं होता।
(c) चूँकि बिस्मथ एक प्रतिचुम्बकीय पदार्थ है, अत: चुम्बकीय क्षेत्र अपेक्षाकृत कुछ कम हो जाएगा।
(d) लौहचुम्बकीय पदार्थों की चुम्बकशीलता बाह्य चुम्बकीय क्षेत्र पर निर्भर करती है तथा तीव्र चुम्बकीय, क्षेत्र के लिए इसका मान कम होता है।
(e) जब दो माध्यम किसी स्थान पर मिलते हैं जिनमें से एक के लिए µ >>1 हो तो इनके सीमा पृष्ठ पर क्षेत्र रेखाएँ लम्बवत् हो जाती हैं।
(1) हाँ, किसी अनुचुम्बकीय पदार्थ का अधिकतम सम्भव चुम्बकत्व, लौहचुम्बकीय पदार्थ के चुम्बकन के परिमाण की कोटि का हो सकता है। परन्तु किसी अनुचुम्बकीय पदार्थ को इस कोटि तक चुम्बकित करने के लिए अति उच्च चुम्बकीय क्षेत्र की आवश्यकता होती है जिसे प्राप्त करना व्यवहार में सम्भव नहीं है।

प्रश्न 17.
निम्नलिखित प्रश्नों के उत्तर दीजिए –
(a) लौहचुम्बकीय पदार्थ के चुम्बकन वक्र की अनुत्क्रमणीयता, डोमेनों के आधार पर गुणात्मक दृष्टिकोण से समझाइए।
(b) नर्म लोहे के एक टुकड़े के शैथिल्य लूप का क्षेत्रफल, कार्बन-स्टील के टुकड़े के शैथिल्य लप के क्षेत्रफल से कम होता है। यदि पदार्थ को बार-बार चुम्बकन चक्र से गुजारा जाए तो कौन-सा टुकड़ा अधिक ऊष्मा ऊर्जा का क्षय करेगार
(c) लौह चुम्बक जैसा शैथिल्य लूप प्रदर्शित करने वाली कोई प्रणाली स्मृति संग्रहण की युक्ति है। इस कथन की व्याख्या कीजिए।
(d) कैसेट के.चुम्बकीय फीतों पर परत चढ़ाने के लिए या आधुनिक कम्प्यूटर में स्मृति संग्रहण के लिए, किस तरह के लौहचुम्बकीय पदार्थों का इस्तेमाल होता है? ।
(e) किसी स्थान को चुम्बकीय क्षेत्र से परिरक्षित करना है। कोई विधि सुझाइए।
उत्तर :
(a) जब बाह्य चुम्बकीय क्षेत्र को शून्य कर दिया जाता है तो भी लौहचुम्बकीय पदार्थ के डोमेन अपनी प्रारम्भिक स्थिति में नहीं लौट पाते अपितु उनमें कुछ चुम्बकन शेष रह जाता है। यही कारण है कि लौहचुम्बकीय पदार्थों का चुम्बकन वक्र अनुत्क्रमणीय होता है।
(b) किसी पदार्थ के शैथिल्य लूप का क्षेत्रफल एक पूर्ण चुम्बकन चक्र में होने वाली ऊर्जा-हानि को प्रदर्शित करता है। यह ऊर्जा-हानि ही पदार्थ में ऊष्मा के रूप में उत्पन्न होती है। चूंकि कार्बन-स्टील के शैथिल्य लूप का क्षेत्रफल अधिक है, अत: इसमें अधिक ऊष्मा उत्पन्न होगी अर्थात् कार्बन-स्टील का टुकड़ा अधिक ऊष्मा क्षय करेगा।
(c) किसी लौहचुम्बकीय पदार्थ का चुम्बकन उस पर लगाए गए बाह्य चुम्बकीय-क्षेत्र के चक्रों की संख्या पर निर्भर करता है। इस प्रकार किसी लौह चुम्बकीय पदार्थ का चुम्बकन उस पर लगाए गए चुम्बकन चक्र की सूचना दे सकता है। इस प्रकार चुम्बकन चक्र की स्मृति, चुम्बकित पदार्थ के नमूने में एकत्र हो जाती है।
(d) इस कार्य के लिए सिरेमिक पदार्थों का प्रयोग किया जाता है।
(e) किसी स्थान को चुम्बकीय क्षेत्र से परिरक्षित करने के लिए उस स्थान को नर्म लोहे के रिंग से घेर देना चाहिए। इससे चुम्बकीय क्षेत्र रेखाएँ, नर्म लोहे के रिंग से होकर गुजर जाती हैं तथा रिंग के भीतर प्रवेश नहीं कर पातीं।

प्रश्न 18.
एक लम्बे, सीधे, क्षैतिज केबल में 2.5 ऐम्पियर धारा, 10° दक्षिण-पश्चिम से 10° उत्तर-पूर्व की ओर प्रवाहित हो रही है। इस स्थान पर चुम्बकीय याम्योत्तर भौगोलिक याम्योत्तर के 10° पश्चिम में है। यहाँ पृथ्वी का चुम्बकीय क्षेत्र 0.33 गाउस एवं नति कोण शून्य है। उदासीन बिन्दुओं की रेखा निर्धारित कीजिए। (केबल की मोटाई की उपेक्षा कर सकते हैं।)
(उदासीन बिन्दुओं पर, धारावाही केबल द्वारा चुम्बकीय क्षेत्र, पृथ्वी के क्षैतिज घटक के चुम्बकीय क्षेत्र के समान एवं विपरीत दिशा में होता है।)
हल :
दिया है : पृथ्वी का क्षेत्र B= 0.33 × 10^-4 टेस्ला, नति कोण δ = 0°
∴ पृथ्वी के क्षेत्र का क्षैतिज घटक B_H = B cos δ = 0.33 × 10^-4 टेस्ला
माना उदासीन बिन्दु तार से a दूरी पर है, तब

इस प्रकार, उदासीन बिन्दु रेखा केबल के समान्तर ऊपर की ओर केबल से 1.5 सेमी की दूरी पर होगी।

प्रश्न 19.
किसी स्थान पर एक टेलीफोन केबल में चार लम्बे, सीधे, क्षैतिज तार हैं जिनमें से प्रत्येक में 1.0 ऐम्पियर की धारा पूर्व से पश्चिम की ओर प्रवाहित हो रही है। इस स्थान पर पृथ्वी का चुम्बकीय क्षेत्र 0.39 गाउस एवं नति कोण 35° है। दिक्पात कोण लगभग शून्य है। केबल के 4.0 सेमी नीचे और 4.0 सेमी ऊपर परिणामी चुम्बकीय क्षेत्रों के मान क्या होंगे?
हल :
पृथ्वी का चुम्बकीय क्षेत्र
B = 0.39 × 10^-4 टेस्ला, δ = 35°, i= 1.0 ऐम्पियर
पृथ्वी के क्षेत्र का क्षैतिज अवयव
B_H = B cos δ = 0.39 × cos 35°
= 0.39 × 0.819
= 0.319 गाउस (दक्षिण से उत्तर)
तथा ऊर्ध्वाधर अवयव
B_V = B sin δ = 0.39 × sin 35° = 0.39 × 0.573
= 0.224 गाउस
चार केबलों के कारण उनसे a = 4.0x 10^-2 मीटर की दूरी पर चुम्बकीय क्षेत्र

= 0.2 × 10^-4 टेस्ला = 0.2 गाउस
केबल के ऊपर चुम्बकीय क्षेत्र B’ क्षैतिजतः दक्षिण से उत्तर की ओर तथा केबल के नीचे यह क्षेत्र क्षैतिजतः उत्तर से दक्षिण की ओर होगा।
केबल के नीचे चुम्बकीय क्षेत्र
यहाँ B_H व B’ परस्पर विपरीत हैं।
∴ क्षैतिज अवयव

अत: केबल के नीचे नेट चुम्बकीय क्षेत्र 0.254 गाउस है जो क्षैतिज से 62° के कोण पर है।
केबल के ऊपर चुम्बकीय क्षेत्र
यहाँ B_H व B’ एक ही दिशा में हैं।
∴ क्षैतिज अवयव
B’_H = B_H + B’ = 0.319 + 0.2 = 0.519 गाउस
जबकि B_V = 0.224 गाउस

अत: नेट चुम्बकीय क्षेत्र 0.57 गाउस है जो क्षैतिज से 23° के कोण पर है।

प्रश्न 20.
एक चुम्बकीय सुई जो क्षैतिज तल में घूमने के लिए स्वतन्त्र है, 30 फेरों एवं 12 सेमी त्रिज्या वाली एक कुंडली के केन्द्र पर रखी है। कुंडली एक ऊर्ध्वाधर तल में है और चुम्बकीय याम्योत्तर से 45° का कोण बनाती है। जब कुंडली में 0.35 ऐम्पियर धारा प्रवाहित होती है, चुम्बकीय सुई पश्चिम से पूर्व की ओर संकेत करती है।
(a) इस स्थान पर पृथ्वी के चुम्बकीय क्षेत्र के क्षैतिज अवयव का मान ज्ञात कीजिए।
(b) कुंडली में धारा की दिशा उलट दी जाती है और इसको अपनी ऊर्ध्वाधर अक्ष पर वामावर्त दिशा में (ऊपर से देखने पर ) 90° के कोण पर घुमा दिया जाता है। चुम्बकीय सुई किस दिशा में ठहरेगी? इस स्थान पर चुम्बकीय दिक्पात शून्य लीजिए।
हल :
(a) दिया है : कुंडली में फेरों की संख्या N = 30
धारा i = 0.35 ऐम्पियर, त्रिज्या a = 0.12 मीटर
कंडली के केन्द्र पर चम्बकीय क्षेत्र \(B=\frac{\mu_{0} N i}{2 a}=\frac{4 \pi \times 10^{-7} \times 30 \times 0.35}{2 \times 0.12}\)
= 0.55 गाउस
यह क्षेत्र कुंडली के तल के लम्बवत् है।
∵ चुम्बकीय सुई पूर्व-पश्चिम दिशा में ठहरती है, अतः इस स्थान पर नेट चुम्बकीय क्षेत्र पूर्व पश्चिम दिशा में होगा।
यह तभी सम्भव है जबकि क्षेत्र B का उत्तर-दक्षिण दिशा में अवयव B_H को सन्तुलित कर ले।
अर्थात् B_H = B cos 45° = 0.55 × \(\frac{1}{\sqrt{2}}\)
पृथ्वी के क्षेत्र का क्षैतिज अवयव B_H = 0.39 गाउस।

(b) चित्र-5.4 (b) से स्पष्ट है कि इस बार नेट चुम्बकीय क्षेत्र पूर्व से पश्चिम की ओर होगा। अतः चुम्बकीय सुई पूर्व से पश्चिम की ओर संकेत करेगी।

प्रश्न 21.
एक चुम्बकीय द्विध्रुव दो चुम्बकीय क्षेत्रों के प्रभाव में है। ये क्षेत्र एक-दूसरे से 60° का कोण बनाते हैं और उनमें से एक क्षेत्र का परिमाण 1.2 × 10^-2 टेस्ला है। यदि द्विध्रुव स्थायी सन्तुलन में इस क्षेत्र से 15° का कोण बनाए, तो दूसरे क्षेत्र का परिमाण क्या होगा?
हल :
दिया है : B₁ = 1.2 × 10^-2 टेस्ला, B₂ = ?
∵ द्विध्रुव एक क्षेत्र से 15° का कोण बनाता है, अत: दूसरे क्षेत्र से 45° का कोण बनाएगा।
सन्तुलन की स्थिति में दोनों के कारण द्विध्रुव पर कार्यरत बल-युग्म के आघूर्ण परस्पर सन्तुलित हो जाएँगे।

∴ MB₁ sin 15o = MB₂ sin 45°
B₂= \(\frac{B_{1} \sin 15^{\circ}}{\sin 45^{\circ}}\)
= \(\frac{1.2 \times 10^{-2} \times 0.2588}{0.707}\)
450
150
= 4.39 × 10^-3 टेस्ला
= 4.4 x 10^-3 टेस्ला ।

प्रश्न 22.
एक समोर्जी 18 किलो इलेक्ट्रॉन-वोल्ट वाले इलेक्ट्रॉनों के किरण पुंज पर जो शुरू में क्षैतिज दिशा में गतिमान हैं, 0.04 गाउस का एक क्षैतिज चुम्बकीय क्षेत्र, जो किरण पुंज की प्रारम्भिक दिशा के लम्बवत् है, लगाया गया है। आकलन कीजिए 30 सेमी की क्षैतिज दूरी चलने में किरण पुंज कितनी दूरी ऊपर या नीचे विस्थापित होगा? (me = 9.11 × 10^-31 किग्रा, e= 1.60 × 10^-19 कूलॉम)।
[नोट : इस प्रश्न में आँकड़े इस प्रकार चुने गए हैं कि उत्तर से आपको यह अनुमान हो कि T.V. सेट में इलेक्ट्रॉन गन से पर्दे तक इलेक्ट्रॉन किरण पुंज की गति भू-चुम्बकीय क्षेत्र से किस प्रकार प्रभावित होती है।
हल :
दिया है : B= 0.04 गाउस = 4 x 10^-6 टेस्ला ।

माना इलेक्ट्रॉनों का वेग υ _x है, तब \(\frac { 1 }{ 2 }\)m_eυ _x² = K ⇒ υ _x = \(\sqrt{\frac{2 K}{m_{e}}}[latex]
इलेक्ट्रॉन, चुम्बकीय क्षेत्र के कारण वृत्तीय मार्ग पर गति करते हैं जिसकी त्रिज्या । निम्नलिखित है –

माना इलेक्ट्रॉन-पुंज बिन्दु A पर चुम्बकीय क्षेत्र में क्षैतिज दिशा में प्रवेश करते हैं तथा क्षैतिज दिशा में x = 0.30 मीटर दूरी तय करने तक बिन्दु B पर पहुँच जाते हैं, तब (चित्र से),
sin θ = [latex]\frac{x}{R}=\frac{0.30}{11.3}\)= 0.0265
θ = sin^-1(0.0265) = 1.52°
∴ इलेक्ट्रॉनों का ऊपर अथवा नीचे की ओर विस्थापन
y= OA – OC = R – R cos θ = R (1 – cosθ) = 11.3 (1 – 0.9996)
= 4.0 × 10^-3 मीटर अथवा
y = 4 मिमी।

प्रश्न 23.
अनुचुम्बकीय लवण के एक नमूने में 2.0 × 10²⁴ परमाणु द्विध्रुव हैं जिनमें से प्रत्येक का द्विध्रुव आघूर्ण 1.5 × 10^-23 जूल टेस्ला^-1 है। इस नमूने को 0.64 टेस्ला के एक एकसमान चुम्बकीय क्षेत्र में रखा गया है और 4.2 K ताप तक ठण्डा किया गया। इसमें 15% चुम्बकीय संतृप्तता आ गई। यदि इस नमूने को 0.98 टेस्ला के चुम्बकीय क्षेत्र में 2.8 K ताप पर रखा हो तो इसका कुल द्विध्रुव आघूर्ण कितना होगा? (यह मान सकते हैं कि क्यूरी नियम लागू होता है।)
हल :
दिया है : N = 2.0 × 10²⁴, m = 1.5 × 10^-23 जूल टेस्ला -1, B₁ = 0.64 टेस्ला, T₁= 4.2 K, चुम्बकीय संतृप्तता M₁ = 15%, B₂ = 0.98 टेस्ला, T₂ = 2.8 K,
चुम्बकीय संतृप्तता M₂ = ?
चुम्बकीय संतृप्तता की स्थिति में,
पदार्थ का चुम्बकीय-आघूर्ण M = Nm = 2.0 × 10²⁴ × 1.5 × 10^-23 = 30 जूल टेस्ला^-1
प्रथम स्थिति में,
चम्बकीय-आघूर्ण M₁ = M का 15% = \(\frac{15 M}{100}=\frac{15 \times 30}{100}\) = 4.5 जल टेस्ला^-1
∵ क्यूरी नियम लागू होता है। अतः

प्रश्न 24.
एक रोलैंड रिंग की औसत त्रिज्या 15 सेमी है और इसमें 800 आपेक्षिक चुम्बकशीलता के लौह चुम्बकीय क्रोड पर 3500 फेरे लिपटे हुए हैं। 1.2 ऐम्पियर की चुम्बककारी धारा के कारण इसके क्रोड में कितना घुम्बकीय क्षेत्र (\(\overrightarrow{\mathbf{B}}\)) होगा?
हल :
दिया है : औसत त्रिज्या a = 0.15 मीटर, μ_r = 800, N = 3500, i = 1.2 ऐम्पियर, B= ?

प्रश्न 25.
किसी इलेक्ट्रॉन के नैज चक्रणी कोणीय संवेग \(\overrightarrow{\mathbf{s}}\) एवं कक्षीय कोणीय संवेग \(\overrightarrow{1}\) के साथ जुड़े चुम्बकीय-आघूर्ण क्रमशः \(\overrightarrow{\mu_{\mathrm{S}}}\) और \(\overrightarrow{\mu_{1}}\) हैं। क्वाण्टम सिद्धान्त के आधार पर (और प्रयोगात्मक रूप से अत्यन्त परिशुद्धतापूर्वक पुष्ट) इनके मान क्रमशः निम्न प्रकार दिए जाते हैं –
μ_s = – \(\left(\frac{e}{2 m}\right) \overrightarrow{\mathrm{i}}\) एवं μ_l= – \left(\frac{e}{2 m}\right) \overrightarrow{\mathbf{1}}
इनमें से कौन-सा व्यंजक चिरसम्मत सिद्धान्तों के आधार पर प्राप्त करने की आशा की जा सकती है? उस चिरसम्मत आधार पर प्राप्त होने वाले व्यंजक को व्युत्पन्न कीजिए।
हल :
व्यंजक \(\vec{\mu}_{1}=-\left(\frac{e}{2 m}\right) \overrightarrow{1}\), चिरसम्मत सिद्धान्तों के आधार पर प्राप्त किया जा सकता है।
माना इलेक्ट्रॉन r त्रिज्या की वृत्तीय कक्षा में चक्कर लगा रहा है तथा इसका परिक्रमण काल T है, तब
परिक्रमण के कारण कक्षा में धारा i = \(\frac{e}{T}\)
∴ परिक्रमण के कारण उत्पन्न चुम्बकीय-आघूर्ण का परिमाण

जबकि कक्षा में घूमते इलेक्ट्रॉन का कोणीय संवेग

∵ इलेक्ट्रॉन का आवेश e ऋणात्मक है, अतः \(\vec{\mu}_{1} व \overrightarrow{1}\) सदिशों की दिशाएँ परस्पर विपरीत होंगी। . :
∴ सदिश रूप में लिखने पर, = \(\overrightarrow{\mu_{1}}=-\left(\frac{e}{2 m}\right) \overrightarrow{1}\)

चुम्बकत्व एवं द्रव्य NCERT भौतिक विज्ञान प्रश्न प्रदर्शिका (Physics Exemplar LO Problems) पुस्तक से चयनित महत्त्वपूर्ण प्रश्नों के हल

चुम्बकत्व एवं द्रव्य बहुविकल्पीय प्रश्नोत्तर

प्रश्न 1.
पृथ्वी के चुम्बकीय क्षेत्र को पृथ्वी के केन्द्र पर स्थित बिन्दु द्विध्रुव के क्षेत्र का प्रतिरूप माना जा सकता है। इस द्विध्रुव का अक्ष पृथ्वी के अक्ष से 11.3° का कोण बनाता है। मुम्बई में द्विक्पात लगभग शून्य है, तब –
(a) पृथ्वी पर दिक्पात का मान 11.3° पश्चिम से 11.3° पूर्व के बीच परिवर्तित होता है।
(b) निम्नतम दिक्पात शून्य अंश (0°) है।
(c) द्विध्रुव अक्ष तथा पृथ्ट के अक्ष को धारण करने वाला तल ग्रीनविच से गुजरता है।
(d) समस्त पृथ्वी पर दिक्पात सदैव ऋणात्मक होना चाहिए।
उत्तर :
(a) पृथ्वी पर दिक्पात का मान 11.3° पश्चिम से 11.3° पूर्व के बीच परिवर्तित होता है।

प्रश्न 2.
कमरे के ताप पर किसी स्थायी चुम्बक में –
(a) प्रत्येक अणु का चुम्बकीय-आघूर्ण शून्य होता है
(b) सभी अलग-अलग अणुओं के शून्येतर चुम्बकीय-आघूर्ण होते हैं जो पूर्णत: संरेखित होते हैं।
(c) कुछ डोमेन अंशत: संरेखित होते हैं
(d) सभी डोमेन पूर्णत: संरेखित होते हैं।
उत्तर :
(c) कुछ डोमेन अंशत: संरेखित होते हैं

चुम्बकत्व एवं द्रव्य अतिं लघु उत्तरीय प्रश्नोत्तर

प्रश्न 1.
इलेक्ट्रॉन की भाँति प्रोटॉन में भी चक्रण तथा चुम्बकीय-आघूर्ण होता है, तब पदार्थों के चुम्बकत्व में इसमें प्रभाव की उपेक्षा क्यों की जाती है?
उत्तर :
इलेक्ट्रॉन का चुम्बकीय-आघूर्ण \(\left(\mu_{e}\right)=\frac{e h}{4 \pi m_{e}}\)
इसी प्रकार, प्रोटॉन का चुम्बकीय-आघूर्ण \(\left(\mu_{p}\right)=\frac{e h}{4 \pi m_{p}}\)
परन्तु m_p >> m_e अतः μ_e >> μ_p
अतः पदार्थों के चुम्बकत्व में इलेक्ट्रॉन की तुलना में प्रोटॉन के चुम्बकीय-आघूर्ण की उपेक्षा की जाती है।

प्रश्न 2.
आण्विक दृष्टिकोण से प्रतिचुम्बकत्व, अनुचुम्बकत्व तथा लौहचुम्बकत्व की चुम्बकीय प्रवृत्तियों की ताप निर्भरता की विवेचना कीजिए।
उत्तर :
प्रतिचुम्बकत्व इलेक्ट्रॉनों की कक्षीय गति के कारण उत्पन्न होता है, अतः यह ताप से अधिक प्रभावित नहीं होता है। अनुचुम्बकीय तथा लौहचुम्बकीय पदार्थों के अणुओं में अपना परिणामी । चुम्बकीय-आघूर्ण होता है तथा प्रत्येक अणु स्वयं एक चुम्बकीय द्विध्रुव होता है। इन पदार्थों में चुम्बकत्व इन चुम्बकीय द्विध्रुवों के बाह्य चुम्बकीय क्षेत्र के अनुदिश संरेखण के कारण उत्पन्न होता है। ताप वृद्धि पर संरेखण विक्षोभित होता है जिसके परिणामस्वरूप इन पदार्थों की चुम्बकशीलता ताप वृद्धि पर घट जाती है।

प्रश्न 3.
चित्र में दर्शाए अनुसार तीन सर्वसम छड़ चुम्बकों को समान तल में केन्द्र पर रिवट द्वारा जड़ दिया गया है। इस निकाय को विराम अवस्था में किसी धीरे-धीरे परिवर्तित होने वाले चुम्बकीय क्षेत्र में रखा गया है। यह पाया गया है कि चुम्बकों के निकाय में कोई गति नहीं हुई। एक चुम्बक के उत्तर-दक्षिण ध्रुवों को चित्र में दर्शाया गया है। अन्य दो चुम्बकों के ध्रुव निर्धारित कीजिए।
उत्तर :

चुम्बकों के निकाय में कोई गति नहीं हुई है, अत: परिणामी चुम्बकीय-आघूर्ण m = 0.
इसके लिए एकमात्र सम्भव स्थिति चित्र में दर्शायी गई है।

MP Board Class 12th Physics Solutions