Bhagya

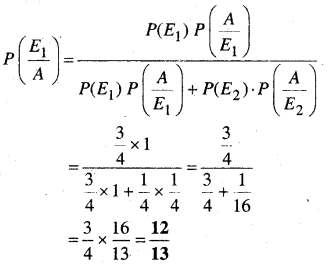
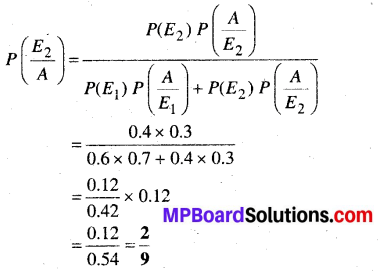
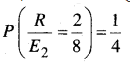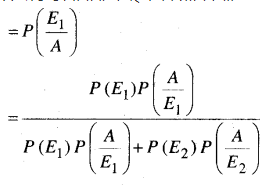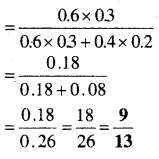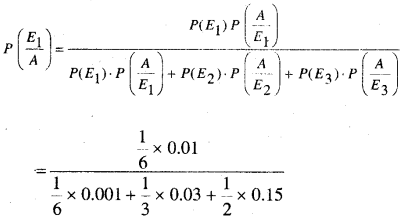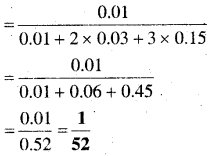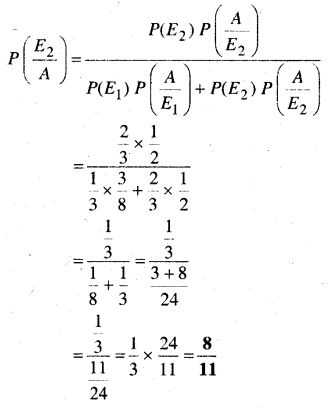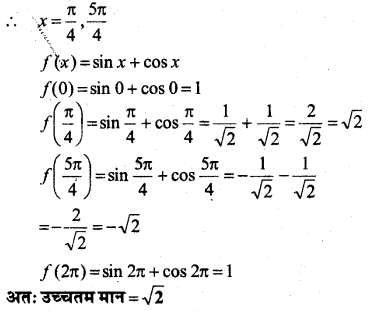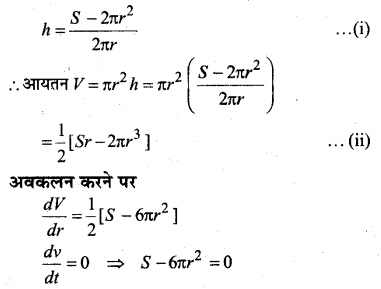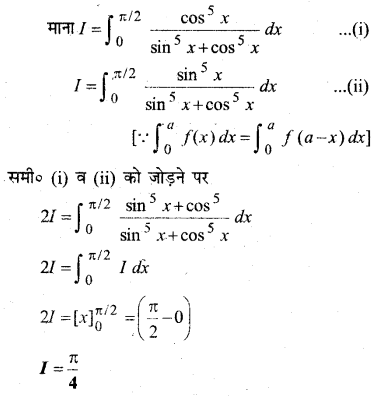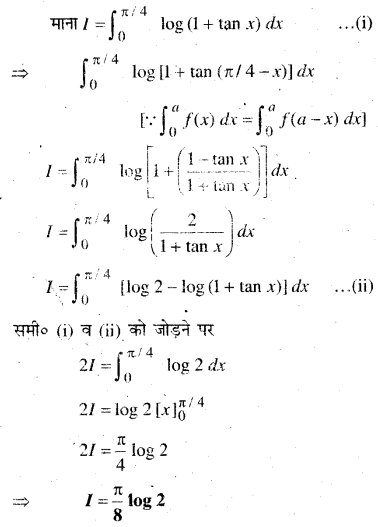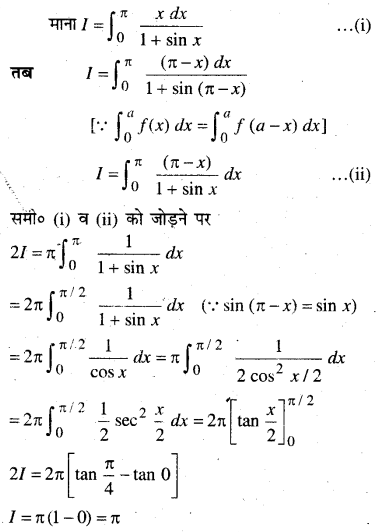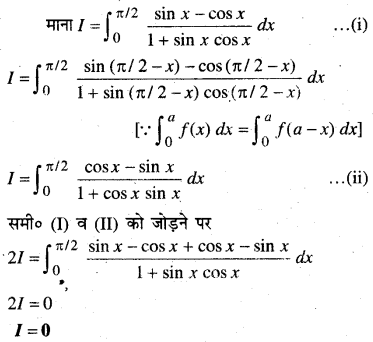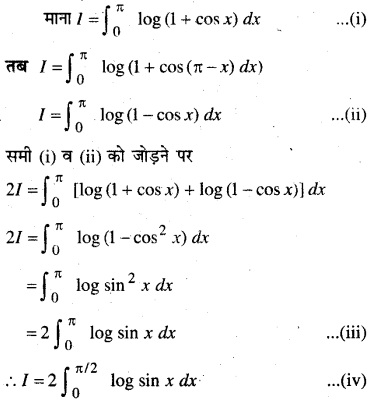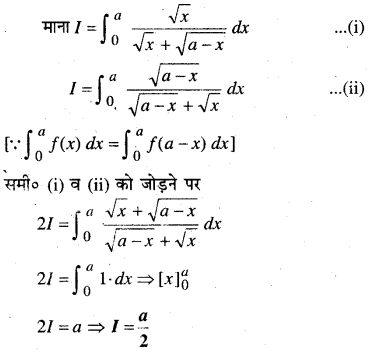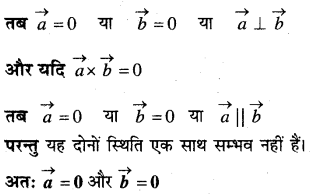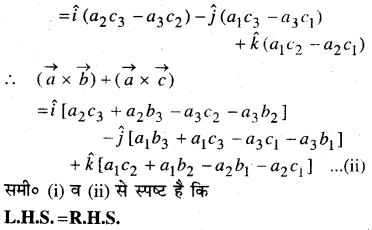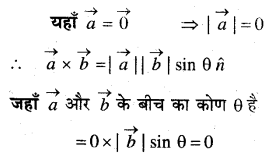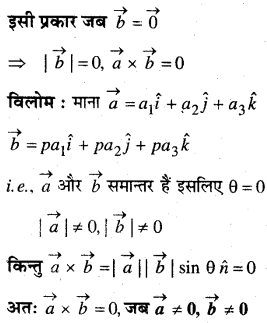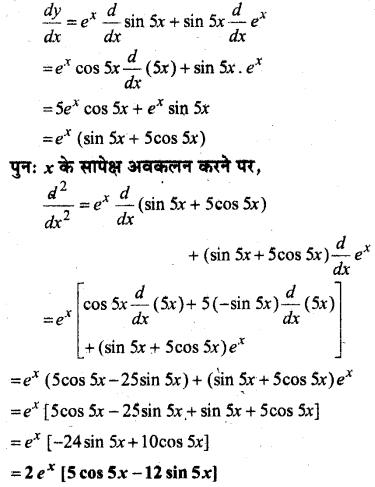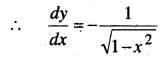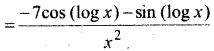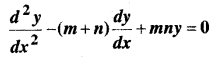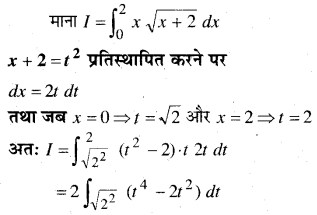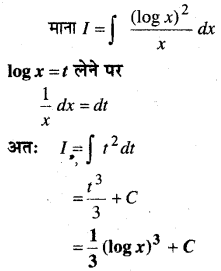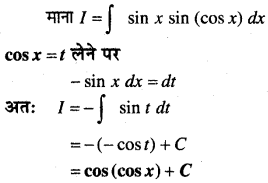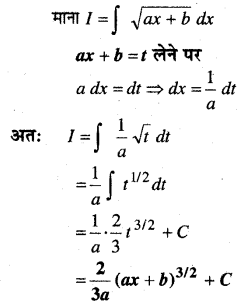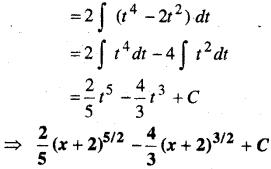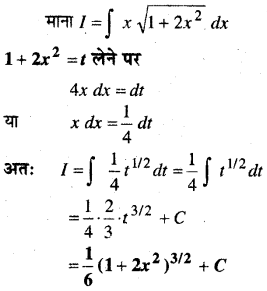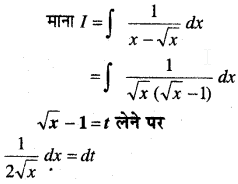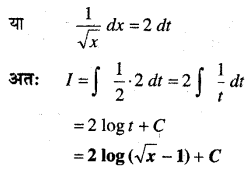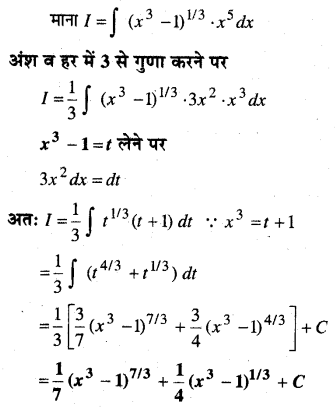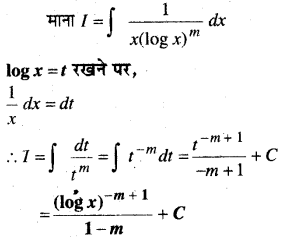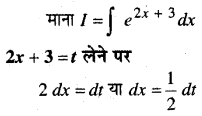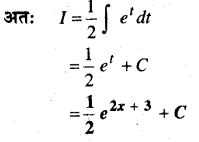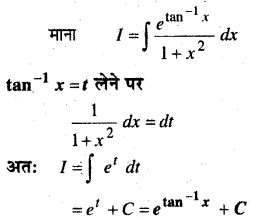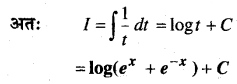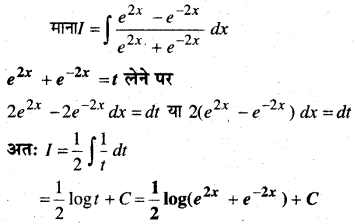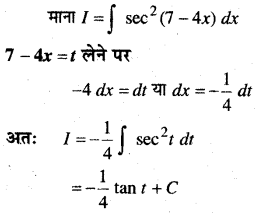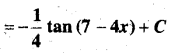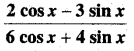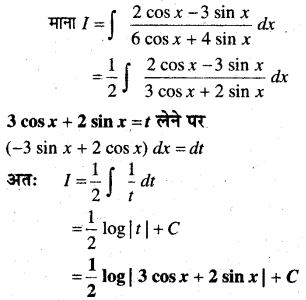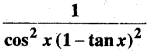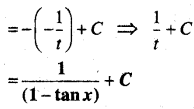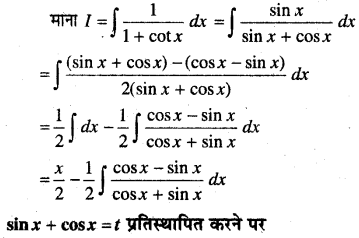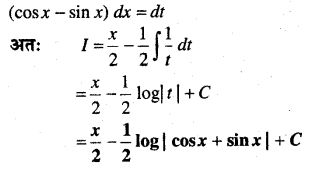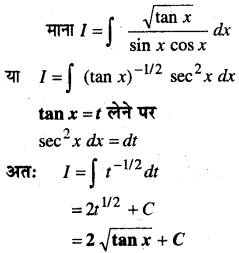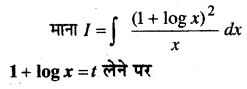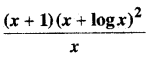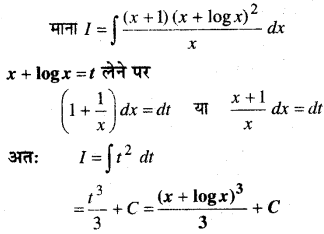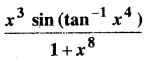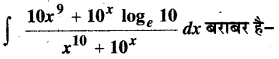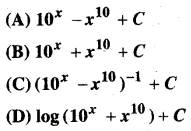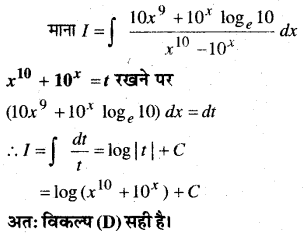In this article, we share MP Board Class 12th Maths Book Solutions Chapter 10 सदिश बीजगणित विविध प्रश्नावली Pdf, These solutions are solved by subject experts from the latest MP Board books.

MP Board Class 12th Maths Book Solutions Chapter 10 सदिश बीजगणित विविध प्रश्नावली

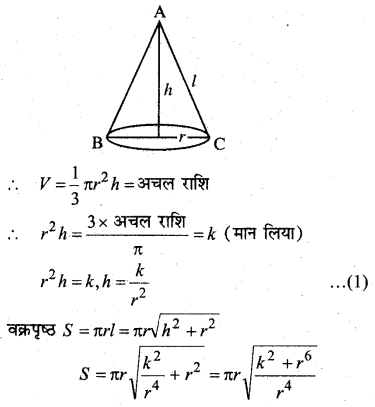
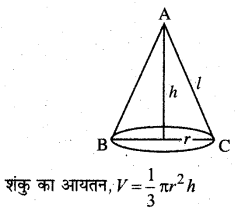
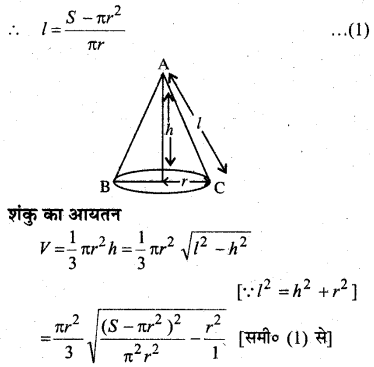
प्रश्न 1.
XY-तल में, x-अक्ष की धनात्मक दिशा के साथ वामावर्त दिशा में 30° का कोण बनाने वाला मात्रक सदिश लिखिए।
हल:

प्रश्न 2.
बिन्दु P (x₁, y₁, z₁) और Q (x₂, y₃, z₃) को मिलाने वाले सदिश के अदिश घटक और परिमाण ज्ञात कीजिए।
हल:

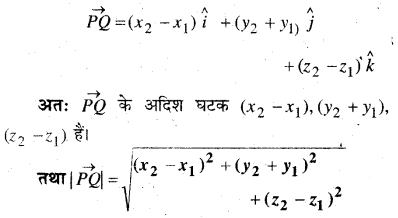
प्रश्न 3.
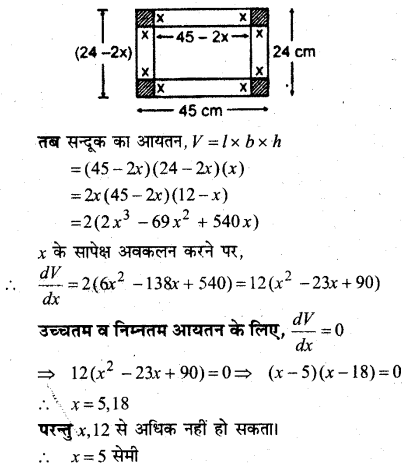
एक लड़की पश्चिम दिशा में 4 km चलती है। उसके पश्चात् वह उत्तर से 30° पश्चिम की दिशा में 3 km चलती है और रुक जाती है। प्रस्थान के प्रारम्भिक बिन्दु से लड़की का विस्थापन ज्ञात कीजिए।
हल:
माना O बिन्दु से Ox की ओर OP (4 km) चलती है। इसे \(-4 \hat{i}\) सदिश निरूपित करते हैं। अतः \(\overrightarrow{O P}=-4 \hat{i}\) अब वह उत्तर से 30° पश्चिम की ओर 3 km चलती है, वह Q बिन्दु जा पहुँचती है।
PQ ऊर्ध्वाधर से 30° का कोण बनाती है और OX’ के साथ 60° का कोण बनाती है।
PQ का OX’ पर प्रक्षेप PM है।

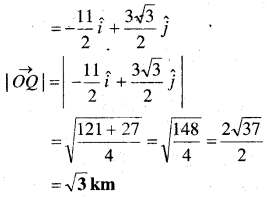
प्रश्न 4.
यदि \(\vec{a}=\vec{b}+\vec{c}\), तब क्या यह सत्य है कि \(|\vec{a}|=|\vec{b}|+|\vec{c}|\)? अपने उत्तर की पुष्टि कीजिए।
हल:
दिया है : \(\vec{a}=\vec{b}+\vec{c}\)
\(|\vec{a}|=|\vec{b}+\vec{c}|\)

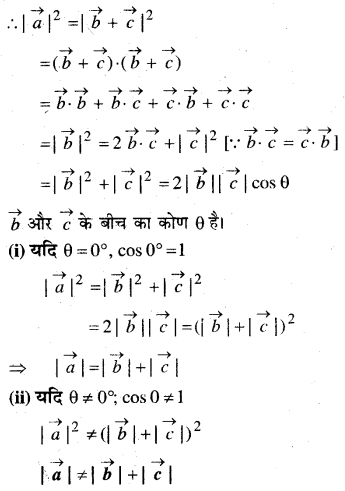
प्रश्न 5.
x का वह मान ज्ञात कीजिए जिसके लिए \(x(\hat{i}+\hat{j}+\hat{k})\) एक मात्रक सदिश है।
हल:
\(x(\hat{i}+\hat{j}+\hat{k})\) एक मात्रक सदिश है।

प्रश्न 6.
सदिशों \(\vec{a}=2 \hat{i}+3 \hat{j}-\hat{k}\) और \(\vec{b}=\hat{i}-2 \hat{j}+\hat{k}\) के परिणामी के समान्तर एक ऐसा सदिश ज्ञात कीजिए जिसका परिणाम 5 इकाई है।
हल:
माना \(\vec{P}\) सदिश \(\vec{a}\) तथा \(\vec{b}\) का परिणामी सदिश हैं।

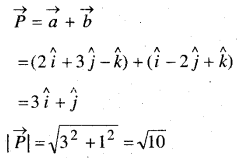
प्रश्न 7.
यदि \(\vec{a}=\hat{i}+\hat{j}+\hat{k}, \vec{b}=2 \hat{i}-\hat{j}+3 \hat{k}\) और \(\vec{c}=\hat{i}-2 \hat{j}+\hat{k}\), तो सदिश \(2 \vec{a}-\vec{b}+3 \vec{c}\) के समान्तर एक मात्रक सदिश ज्ञात कीजिए।
हल:

प्रश्न 8.
दर्शाइए कि बिन्दु A (1, -2, -8), B (5, 0, -2) और C (11, 3, 7)संरेख हैं और B द्वारा AC को विभाजित करने वाला अनुपात ज्ञात कीजिए।
हल:
बिन्दु A, B, C के स्थिति सदिश इस प्रकार हैं-
A(1, -2, -8), B (5, 0, -2), C (11, 3, 7)

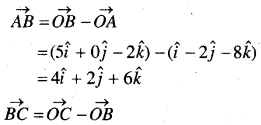
प्रश्न 9.
दो बिन्दुओं \(P(2 \vec{a}+\vec{b})\) और \(Q(\vec{a}-3 \vec{b})\) को मिलाने वाली रेखा को 1 : 2 के अनुपात में बाह्य विभाजित करने वाले बिन्दु R का स्थिति सदिश ज्ञात कीजिए। यह भी दर्शाइए कि बिन्दु P रेखाखण्ड RQ का मध्य बिन्दु है।
हल:
बिन्दु P, Q के स्थिति सदिश क्रमश: \(2 \vec{a}+\vec{b}\) और \(\vec{a}-3 \vec{b}\) हैं।
बिन्दु R, PQ को बाह्य 1 : 2 के अनुपात में विभाजित करता है।


जो P का स्थिति सदिश है।
अतः P, RQ का मध्य बिन्दु है।

प्रश्न 10.
एक समान्तर चतुर्भुज की संलग्न भुजाएँ \(2 \hat{i}-4 \hat{j}+5 \hat{k}\) और \(\hat{i}-2 \hat{j}-3 \hat{k}\) हैं। इसके विकर्ण के समान्तर एक मात्रक सदिश ज्ञात कीजिए। इसका क्षेत्रफल भी ज्ञात कीजिए।
हल:
माना ABCD एक समान्तर चतुर्भुज इस प्रकार है कि

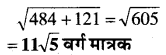
प्रश्न 11.
दर्शाइए कि OX, OY एवं OZ अक्षों के साथ बराबर झुके हुए सदिश की दिक-कोसाइन कोज्याएँ \(\pm\left(\frac{1}{\sqrt{3}}, \frac{1}{\sqrt{3}}, \frac{1}{\sqrt{3}}\right)\) हैं|
हल:
∵ सदिश अक्ष OX, OY तथा OZ के साथ बराबर झुके हैं
∴ α = β = γ
⇒ cos α = cos β = cos γ
परन्तु cos² α + cos² β + cos² γ = 1
⇒ cos² α + cos² α + cos² α = 1
3 cos²α = 1
cos² α = \(\frac{1}{3}\)
cos α = \(\frac{1}{\sqrt{3}}\)
∴ cos α = cos β = cos γ = 1
अतः दिक्-कोज्याएँ \(\frac{1}{\sqrt{3}}, \frac{1}{\sqrt{3}}, \frac{1}{\sqrt{3}}\) हैं।

प्रश्न 12.
मान लीजिए \(\vec{a}=\hat{i}+4 \hat{j}+2 \hat{k}\), \(\vec{b}=3 \hat{i}-2 \hat{j}+7 \hat{k}\) और \(\vec{c}=2 \hat{i}-\hat{j}+4 \hat{k}\) एक ऐसा सदिश \(\vec{d}\) ज्ञात कीजिए जो \(\vec{a}\) और \(\vec{b}\) के दोनों पर लम्ब है और \(\vec{c} \cdot \vec{d}\) = 15
हल:
माना \(\vec{a}\) और \(\vec{b}\) है पर कोई लम्ब सदिश \(\vec{a} \times \vec{b}\) है।

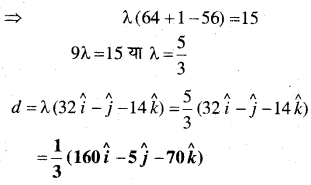
प्रश्न 13.
सदिश \(\hat{i}+\hat{j}+\hat{k}\) का, सदिशों \(2 \hat{i}+4 \hat{j}-5 \hat{k}\) और \(\lambda \hat{i}+2 \hat{j}+3 \hat{k}\) के योगफल की दिशा में मात्रक सदिश के साथ अदिश गुणनफल 1 के बराबर है, तो λ का मान ज्ञात कीजिए।
हल:

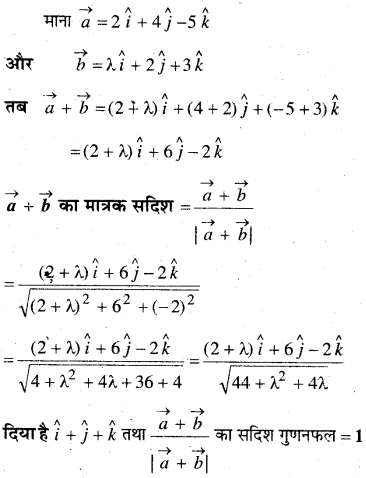
प्रश्न 14.
यदि \(\vec{a}, \vec{b}, \vec{c}\) समान परिमाणों वाले परस्पर लम्बवत् सदिश हैं तो दर्शाइए कि सदिश \(\vec{a}+\vec{b}+\vec{c}\) सदिशों \(\vec{a}, \vec{b}\) तथा \(\vec{c}\) के साथ बराबर झुका हुआ है।
हल:
दिया है \(\vec{a}, \vec{b}, \vec{c}\) सदिश परस्पर लम्बवत् हैं अतः

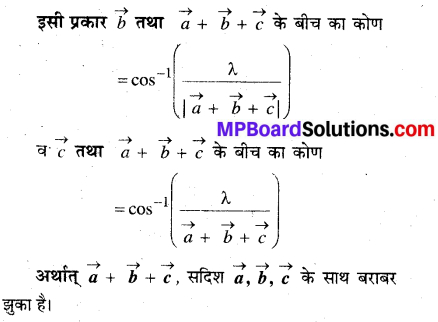
प्रश्न 15.
सिद्ध कीजिए कि \((\vec{a}+\vec{b})\)\((\vec{a}+\vec{b})=|\vec{a}|^{2}+|\vec{b}|^{2}\) यदि और केवल यदि \(\vec{a}, \vec{b}\) लम्बवत् हैं। यह दिया हुआ है कि \(\vec{a} \neq \overrightarrow{0}, \vec{b} \neq \overrightarrow{0}\) है
हल:

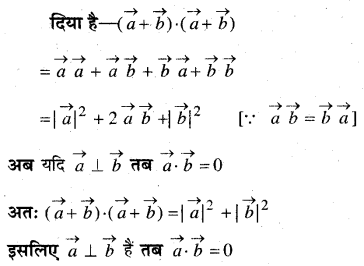
16 से 19 तक के प्रश्नों में सही उत्तर का चयन कीजिए।
प्रश्न 16.
यदि दो सदिशों \(\vec{a}\) और \(\vec{b}\) के बीच का कोण है तो \(\overrightarrow{\boldsymbol{a}} \cdot \overrightarrow{\boldsymbol{b}} \geq \boldsymbol{0}\) होगा यदि-
(A) 0 < θ < \(\frac{\pi}{2}\)
(B) 0 ≤ θ ≤ \(\frac{\pi}{2}\)
(C) 0 < θ < π
(D) 0 ≤ θ ≤ π
हल:

अतः विकल्प (B) सही है।

प्रश्न 17.
मान लीजिए \(\vec{a}\) और \(\vec{b}\) दो मात्रक सदिश हैं और उनके बीच का कोण θ है तो \(\vec{a}+\vec{b}\) के एक मात्रक सदिश है, यदि-

हल:


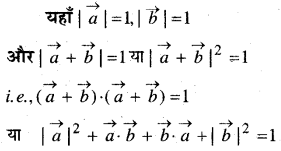
अतः विकल्प (D) सही है।

प्रश्न 18.
\(\hat{\boldsymbol{i}}(\hat{\boldsymbol{j}} \times \hat{\boldsymbol{k}})+\hat{\boldsymbol{j}} \cdot(\hat{\boldsymbol{i}} \times \hat{\boldsymbol{k}})+\hat{\boldsymbol{k}} \cdot(\hat{\boldsymbol{i}} \times \hat{\boldsymbol{j}})\) का मान है-
(A) 0
(B) -1
(C) 1
(D) 3
हल:
\(\{\hat{i} \hat{j} \hat{k}\}\) परस्पर लम्बवत् मात्रक सदिश हैं।

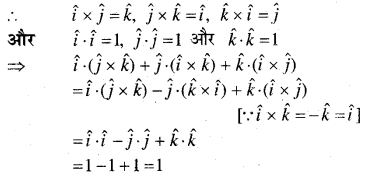
अतः विकल्प (C) सही है।

प्रश्न 19.
यदि दो सदिशों \(\vec{a}\) और \(\vec{b}\) के बीच का कोण 0 है तो \(|\vec{a} \cdot \vec{b}|=|\vec{a} \times \vec{b}|\) जब θ बराबर है
(A) 0
(B) \(\frac{\pi}{4}\)
(C) \(\frac{\pi}{2}\)
(D) π
हल:

अतः विकल्प (B) सही है।

In this article, we share MP Board Class 12th Maths Book Solutions Chapter 13 प्रायिकता Ex 13.3 Pdf, These solutions are solved by subject experts from the latest MP Board books.

MP Board Class 12th Maths Book Solutions Chapter 13 प्रायिकता Ex 13.3

प्रश्न 1.
एक कलश में 5 लाल और 5 काली गेंदें हैं। यादृच्छया एक गेंद निकाली जाती है, इसका रंग नोट करने के बाद पुनः कलश में रख दी जाती है। पुनः निकाले गए रंग की 2 अतिरिक्त गेंदें कलश में रख दी जाती हैं तथा कलश में से एक गेंद निकाली जाती है दूसरी गेंद की लाल होने की प्रायिकता क्या है?
हल:
एक कलश में 5 लाल और 5 काली गेंदें हैं।
(i) माना एक लाल गेंद निकाली जाती है।
∴ लाल गेंद निकालने की प्रायिकता = \(\frac{5}{10}=\frac{1}{2}\)
अब दो लाल गेंदें कलश में रख दी जाती हैं।
⇒ कलश में 7 लाल और 5 काली गेंदें हैं।
लाल गेंद निकालने की प्रायिकता = \(\frac{7}{12}\)
(ii) माना पहले काली गेंद निकाली जाती है।
काली गेंद निकालने की प्रायिकता = \(\frac{5}{10}=\frac{1}{2}\)
फिर दो काली गेंदें कलश में रख दी जाती हैं।
अब कलश में 5 लाल और 7 काली गेंदें हैं।
एक लाल गेंद होने की प्रायिकता = \(\frac{5}{12}\)
दूसरी लाल गेंद होने की प्रायिकता
= \(\frac{1}{2} \times \frac{7}{12}+\frac{1}{2} \times \frac{5}{12}\)
= \(\frac{7}{24}+\frac{5}{24}=\frac{12}{24}=\frac{1}{2}\)

प्रश्न 2.
एक थैले में 4 लाल और 4 काली गेंदें हैं और एक अन्य थैले में 2 लाल और 6 काली गेंदें हैं दोनों थैलों में से एक को यादृच्छया चुना जाता है और उसमें से 1 गेंद निकाली जाती है जो कि लाल है। इस बात की क्या प्रायिकता है कि गेंद पहले थैले से निकाली गई है?
हल:
माना पहले थैले चुनने की घटना E₁ व दूसरे थैले को चुनना E₂ है
∴1 थैले चुनने की प्रायिकता = \(\frac{1}{2}\)
⇒ P(E₁) = P(EE₂) = \(\frac{1}{2}\)
∵ पहले थैले में 4 लाल व 4 काली गेंद हैं
∴ इनमें से लाल गेंद चुनने की प्रायिकता
= \(\frac{4}{8}=\frac{1}{2}\)
माना लाल गेंद R से प्रदर्शित है
∴ \(P\left(\frac{R}{E_{1}}\right)=\frac{1}{2}\)
चूँकि दूसरे थैले में 2 लाल व 6 काली गेंद हैं।
∴ इसमें से लाल गेंद चुनने की प्रायिकता

अतः पडले शैले से लाल गोट निकाले जाने की परिकता

अतः पडले शैले से लाल गोट निकाले की परिकता
= \(\frac{2}{3}\)

प्रश्न 3.
यह ज्ञात है कि महाविद्यालय के छात्रों में से 60% छात्रावास में रहते हैं और 40% छात्रावास में नहीं रहते हैं। पूर्ववर्ती वर्ष के परिणाम सूचित करते हैं कि छात्रावास में रहने वाले छात्रों में से 30% और छात्रावास में न रहने वाले छात्रों में से 20% छात्रों ने A- ग्रेड लिया। वर्ष के अन्त में महाविद्यालय के एक छात्र को यादृच्छया चुना गया और यह पाया गया कि उसे A- ग्रेड मिला है। इस बात की क्या प्रायिकता है कि वह छात्र छात्रावास में रहने वाला है?
हल:
माना छात्रावास में रहने वाले और न रहने वाले छात्रों की घटनाएँ क्रमश: E₁ तथा E₁ हैं।
छात्रावास में रहने वाले छात्रों की प्रायिकता = 60% = 0.6
छात्रावास में न रहने वाले छात्रों की प्रायिकता = 40% = 0.4
A- ग्रेड छात्रावास में रहने वाले छात्रों की प्रायिकता = 30%
= 0.3 = P \(\left(\frac{A}{E_{1}}\right)\)
A- ग्रेड छात्रावास में न रहने वाले छात्रों की प्रायिकता
P\(\left(\frac{A}{E_{2}}\right)\) = 20% = 0.2
A- ग्रेड छात्रावास में रहने की प्रायिकता

प्रश्न 4.
एक बहुविकल्पीय प्रश्न का उत्तर देने में एक विद्यार्थी या तो प्रश्न का उत्तर जानता है या वह अनुमान लगाता है। मान लें कि उसके उत्तर जानने की प्रायिकता \(\frac{3}{4}\) है और अनुमान लगाने की प्रायिकता \(\frac{1}{4}\) है। मान लें कि छात्र के प्रश्न के उत्तर का अनुमान लगाने पर सही उत्तर देने की प्रायिकता \(\frac{1}{4}\)है तो इस बात की क्या प्रायिकता है कि कोई छात्र प्रश्न का उत्तर जानता है यदि यह ज्ञात है कि उसने सही उत्तर दिया है?
हल:
माना घटनाएँ
E₁ = विद्यार्थी के उत्तर जानने की
E₂ = वह अनुमान लगाता है।
P(E₁) = \(\frac{3}{4}\), P(E₂) = \(\frac{1}{4}\)
माना A उत्तर सही होने की घटना है।
यदि विद्यार्थी उत्तर जातना है
⇒ उत्तर सही है।
\(P\left(\frac{A}{E_{1}}\right)\) = 1
जब अनुमान लगाता है, P\(P\left(\frac{A}{E_{2}}\right)\) = \(\frac{1}{4}\)
∴ इस बात की प्रायिकता कि कोई छात्र प्रश्न का उत्तर जानता है यदि यह ज्ञात है कि उसने सही उत्तर दिया है —

प्रश्न 5.
किसी विशेष रोग के सही निदान के लिए रक्त की जाँच 99% असरदार है, जब वास्तव में रोगी उस रोग से ग्रस्त होता है। किन्तु 0.5% बार किसी स्वस्थ व्यक्ति की रक्त जाँच करने पर निदान गलत रिपोर्ट देता है यानी व्यक्ति को रोग से ग्रस्त बतलाता है। यदि किसी जनसमुदाय में 0.1% लोग उस रोग से ग्रस्त हैं तो क्या प्रायिकता है कि कोई यादृच्छया चुना गया व्यक्ति उस रोग से ग्रस्त होगा यदि उसके रक्त की जाँच में यह बताया जाता है कि उसे यह रोग है?
हल:
माना घटनाएँ E = रोग से ग्रस्त व्यक्ति
E’ = रोग से ग्रस्त नहीं व्यक्ति
A = रक्त की जाँच में रोग
रोग से ग्रस्त व्यक्ति की प्रायिकता
P(E) = 0.1% = 0.001
रोग से ग्रस्त नहीं व्यक्ति की प्रायिकता
P(E’) =1 – P(E)
=1 – 0.001 = 0.999
उन व्यक्तियों की प्रायिकता जो रोगी तथा रक्त की जाँच में रोग हो
P\(\left(\frac{A}{E}\right)\) = 99% = 0.99
किसी स्वस्थ व्यक्ति के रक्त की जाँच करने पर निदान गलत रिपोर्ट देता हैं यानि व्यक्ति को रोग से ग्रस्त बताने की प्रायिकता
P\(\left(\frac{A}{E^{\prime}}\right)\) = 0.005
कोई यादृच्छया चुना गया व्यक्ति उस रोग से ग्रस्त होगा यदि उसके रक्त की जाँच में पाये जाने की प्रायिकता

प्रश्न 6.
तीन सिक्के दिए गए हैं। एक सिक्के के दोनों ओर चित ही है। दूसरा सिक्का अभिनत है जिसमें चित 75% बार प्रकट होता है और तीसरा अनभिनत सिक्का है। तीनों में से एक सिक्के को यादृच्छया चुना गया और उसे उछाला गया है। यदि सिक्के पर चित प्रकट हो तो क्या प्रायिकता है कि वह दोनों चित वाला सिक्का है?
हल:
कुल सिक्कों की संख्या = 3
∴ तीनों सिक्कों में से 1 सिक्का चुनने की प्रायिकता = \(\frac{1}{3}\)
माना तीनों सिक्कों की घटनाएँ E₁, E₂ व E₃ हैं तथा चित आने की घटना A है
∴ P(E₁) = P(E₂) = P(E₃) = \(\frac{1}{3}\) = \(\frac{1}{3}\)
∵ एक सिक्के के दोनों और चित है
∴ P \(\left(\frac{A}{E_{1}}\right)\) = 1
∵ दूसरा सिक्का अभिनत है जिसमें चित 75% बार प्रकट होता है
∴ P\(\left(\frac{A}{E_{2}}\right)\) = 1
∴ P\(\left(\frac{A}{E_{2}}\right)\) = 0.75% = \(\frac{3}{4}\)
तथा तीसरा सिक्का अनभिनत है।
∴ P\(\left(\frac{A}{E_{2}}\right)\) = \(\frac{1}{2}\)

प्रश्न 7.
एक बीमा कम्पनी 2000 स्कूटर चालकों, 4000 कार चालकों और 6000 ट्रक चालकों का बीमा करती है। दुर्घटनाओं की प्रायिकताएँ क्रमशः 0.01, 0.03 और 0.15 हैं। बीमाकृत व्यक्तियों (चालकों) में से एक दुर्घटनाग्रस्त हो जाता है। उस व्यक्ति के स्कूटर चालक होने की प्रायिकता क्या है?
हल:
माना
E₁ = स्कूटर चालक का बीमा होना
E₂ = कार चालक का बीमा होना
E₃ = ट्रक चालक का बीमा होना
एक बीमा कम्पनी 2000 स्कूटर चालकों 4000 चालकों और 6000 ट्रक चालकों का बीमा करती है।
कुल चालकों की संख्या
= 2000 + 4000 + 6000 = 12000
माना स्कूटर चालकों के होने की प्रायिकता
=P(E₁) = \(\frac{2000}{12000}=\frac{1}{6}\)
कार चालकों के होने की प्रायिकता
= P(E₂) = \(\frac{4000}{12000}=\frac{1}{3}\)
ट्रक चालकों के होने की प्रायिकता
= P(E₃) = \(\frac{6000}{12000}=\frac{1}{2}\)
स्कूटर चालकों के दुर्घटना की प्रायिकता
= P\(\left(\frac{A}{E_{1}}\right)\) = 0.01 (जहाँ दुर्घटाओं की घटना A से प्रदर्शित है।)
कार चालकों के दुर्घटना की प्रायिकता
=P\(\left(\frac{A}{E_{2}}\right)\) = 0.03
ट्रक चालकों के दुर्घटना की प्रायिकता
=P\(\left(\frac{A}{E_{3}}\right)\) = 0.15
बीमाकृत चालकों में से एक दुर्घटनाग्रस्त हो जाता है। उस व्यक्ति के स्कूटर चालक होने की प्रायिकता

प्रश्न 8.
एक कारखाने में A और B दो मशीने लगी हैं। पूर्व विवरण से पता चलता है कि कुल उत्पादन का 60% मशीन A और 40% मशीन B द्वारा किया जाता है। इसके अतिरिक्त मशीन A का 2% मशीन B का 1% उत्पादन खराब है। यदि कुल उत्पादन का एक ढेर बना लिया जाता है और उस ढेर से यादृच्छया निकाली गई वस्तु खराब हो तो इस वस्तु के ‘मशीन A द्वारा बने होने की प्रायिकता क्या होगी?
हल:
माना मशीन A द्वारा उत्पादन की घटना = E₁
तथा मशीन B द्वारा उत्पादन की घटना = E₂
माना C खराब उत्पादन को प्रदर्शित करते हैं
∴ मशीन A द्वारा उत्पादन की गई वस्तु की प्रायिकता
P(E₁) = 60%
= 0.6
तथा मशीन B द्वारा उत्पादन की गई वस्तु की प्रायिकता
= 0.4
तथा मशीन A द्वारा खराब उत्पादन की प्रायिकता
P\(\left(\frac{c}{E_{1}}\right)\) = 2% = 0.02
तथा मशीन B द्वारा खराब उत्पादन की प्रायिकता
P\(\left(\frac{c}{E_{1}}\right)\) =1% = 0.01
∵ कुल उत्पादन के ढेर से निकाली खराब वस्तु के मशीन A द्वारा बने होने की प्रायिकता

प्रश्न 9.
दो दल एक निगम के निदेशक मंडल में स्थान पाने की प्रतिस्पर्धा में हैं। पहले तथा दूसरे दल के जीतने की प्रायिकताएँ क्रमशः 0.6 तथा 0.4 हैं। इसके अतिरिक्त यदि पहला दल जीतता है तो एक नए उत्पाद के प्रारम्भ होने की प्रायिकता 0.7 है और यदि दूसरा दल जीतता है तो इस बात की संगत प्रायिकता 0.3 है। इसकी प्रायिकता ज्ञात कीजिए कि नया उत्पादन दूसरा दल द्वारा प्रारम्भ किया गया था।
हल:
माना
E₁ = पहले दल के जीतने की घटना
E₂ = दूसरे दल के जीतने की घटना
A/E₁ = पहला दल नया उत्पाद प्रारम्भ करेगा
A/E₂ = दूसरा दल नया उत्पाद प्रारम्भ करेगा
पहले दल के जीतने की प्रायिकता = P(E₁) = 0.6
दूसरे दल के जीतने की प्रायिकता = P(E₂) = 0.4
पहला दल जीतता है तो एक नये उत्पाद के प्रारम्भ होने की प्रायिकता
=P \(\left(\frac{A}{E_{1}}\right)\) = 0.7
दूसरा दल जीतता है तो इस बात की संगत प्रायिकता
=P \(\left(\frac{A}{E_{2}}\right)\) = 0.3
i.e., P(E₁) = 0.6, P(E₂) = 0.4
अब नया उत्पादन दूसरे दल द्वारा प्रारम्भ किए गए, की प्रायिकता

प्रश्न 10.
मान लीजिए कि कोई लड़की एक पासा उछालती है। यदि उसे 5 या 6 की संख्या प्राप्त होती है तो वह एक सिक्के को तीन बार उछालती है और ‘चितों’ की संख्या नोट करती है। यदि उसे 1,2,3 या 4 की संख्या प्राप्त होती है तो वह एक सिक्के को एक बार उछालती है और यह नोट करती है कि उस पर ‘चित’ या ‘पट’ प्राप्त हुआ। यदि उसे ठीक एक चित प्राप्त होता है तो उसके द्वारा उछाले गए पासे पर 1,2,3 या 4 प्राप्त होने की प्रायिकता क्या है?
हल:
5 या 6 की संख्या प्राप्त होने की प्रायिकता
P(E₁) = \(\frac{2}{6}=\frac{1}{3}\)
1, 2, 3, 4 की संख्या प्राप्त होने की प्रायिकता
P(E₂) = \(\frac{4}{6}=\frac{2}{3}\)
जब वह 5 या 6 प्राप्त करती है, तब वह सिक्का तीन बार उछालती है।
∴ [HHH, HHT, HTH, THH, HTT, THT, TTH, TTT}
एक चित प्राप्त होने के तरीके [HTT, THT, TTH] यानी तीन तरीके
एक चित प्राप्त होने की प्रायिकता = \(\frac{3}{8}\)
∴ \(P\left(\frac{A}{E_{1}}\right)=\frac{3}{8}\)
जब वह 1, 2, 3, 4 प्राप्त करती है तब वह एक सिक्के को एक बार उछालती है।
एक चित प्राप्त होने की प्रायिकता = \(\frac{1}{2}\)
i.e., P\(\left(\frac{A}{E_{2}}\right)=\frac{1}{2}\)
यदि उसे ठीक एक चित प्राप्त होता है तो उसके द्वारा उछाले गए पासों पर 1, 2, 3 या 4 प्राप्त होने की प्रायिकता

प्रश्न 11.
एक व्यावसायिक निर्माता के पास A, B तथा C मशीन ऑपरेटर हैं। प्रथम ऑपरेटर A 1% खराब सामग्री उत्पादित करता है तथा ऑपरेटर B और C क्रमश: 5% और 7% खराब सामग्री उत्पादित करता है। कार्य पर A कुल समय का 50% लगाता है, B कुल समय का 30% तथा C कुल समय का 20% लगाता है। यदि एक खराब सामग्री उत्पादित है तो इसे A द्वारा उत्पादित किए जाने की प्रायिकता क्या है?
हल:
माना तीन मशीनों द्वारा समय के अनुसार घटनाएँ E₁, E₂, E₃ घटती हैं।
P(E₁) =50% = 0.5,
P(E₂) =30% = 0.3,
P(E₃) = 20% = 0.2
माना A खराब उत्पाद की घटना है।
प्रथम ऑपरेटर 1% खराब वस्तुएँ बनाता है।
⇒ \(P\left(\frac{A}{E_{1}}\right)=0.01\)
दूसरा ऑपरेटर 5% खराब वस्तुएँ बनाता है।
⇒ \(P\left(\frac{A}{E_{2}}\right)=0.05\)
तीसरा ऑपरेटर 7% खराब वस्तुएँ बनाता है।
⇒ \(P\left(\frac{A}{E_{3}}\right)=0.07\)
इस प्रकार, P(E₁) = 0.5,
P(E₂) = 0.3,
P(E₃) = 0.2
P\(\left(\frac{A}{E_{1}}\right)\) = 0.01,
P\(\left(\frac{A}{E_{2}}\right)\) = 0.05,
P\(\left(\frac{A}{E_{3}}\right)\) = 0.07
यदि एक खराब सामग्री उत्पादित है तो A द्वारा उत्पादित किए जाने की प्रायिकता

प्रश्न 12.
52 ताशों की गड्डी से एक पत्ता खो जाता है। शेष पत्तों से दो पत्ते निकाले जाते हैं जो ईंट के पत्ते हैं। खो गए पत्ते की ईंट होने की प्रायिकता क्या है?
हल:
E₁ = खो गए पत्ते ईंट की घटना है।
E₂ = खो गए पत्ते ईंट न होने की घटना है।
यहाँ 52 ताशों की गड्डी में से 13 पत्ते ईंट के हैं।
P(E₁) = \(\frac{13}{52} \mathrm{C}_{1}=\frac{13}{52}=\frac{1}{4}\)
यहाँ 39 पत्ते हैं जिसमें ईंट के पत्ते नहीं हैं।
P(E₂) = \(\frac{39}{52}=\frac{3}{4}\)
(i) जब ईंट का पत्ता खो गया हो तब 51 पत्तों में से 12 पत्ते ईंट के रह जाएंगे।
P\left(\frac{A}{E_{1}}\right)=\frac{^{12} C_{2}}{^{51} C_{2}}=\frac{12 \times 11}{51 \times 50}
यहाँ A खो गए पत्तों को प्रदर्शित करता है।
जब ईट के पत्ते खोए नहीं हैं, तब यहाँ 13 ईंट के पत्ते हैं।
दो ईंट के पत्ते खींचने की प्रायिकता
= \(\frac{^{13} C_{2}}{^{51} C_{2}}=\frac{13 \times 12}{51 \times 50}\)
खो गए पत्ते की ईंट होने की प्रायिकता

प्रश्न 13.
A द्वारा सत्य बोलने की प्रायिकता \(\frac{4}{5}\) है। एक सिक्का उछाला जाता है तथा A बताता है कि चित प्रदर्शित हुआ। वास्तविक रूप में चित प्रकट होने की प्रायिकता है –
(A) \(\frac{4}{5}\)
(B) \(\frac{1}{2}\)
(C) \(\frac{1}{5}\)
(D) \(\frac{2}{5}\)
हल:
माना E₁ = A सत्य बोलने की घटना
E₂ = A सत्य न बोलने की घटना
∴ P(E₁) = \(\frac{4}{5}\) (दिया है)
∴ P(E₂) =1 – P(E₁)
= \(1-\frac{4}{5}=\frac{1}{5}\)
चित प्रदर्शित होने की घटना A है।
∴ P \(\left(\frac{A}{E_{1}}\right)\) = \(\frac{1}{2}\)
जब A सत्य नहीं बोलता, तब यह चित है।
चित प्रकट होने की प्रायिकता
P \(\left(\frac{A}{E_{2}}\right)\) = \(\frac{1}{2}\)
वास्तविक रूप में चित प्रकट होने की प्रायिकता

अतः विकल्प (A) सही है।

प्रश्न 14.
यदि A और B ऐसी घटनाएँ हैं कि A⊂B तथा P(B) ≠ 0 तो निम्न में से कौन ठीक है –
(A) \(P\left(\frac{A}{B}\right)=\frac{P(B)}{P(A)}\)
(B) \(P\left(\frac{A}{B}\right)<P(A)\)
(C) \(P\left(\frac{A}{B}\right) \geq P(A)\)
(D) इनमें से कोई नहीं।
हल:
A ⊂ B ⇒ A ∩B = A

अत: विकल्प (C) सही है।

In this article, we share MP Board Class 12th Maths Book Solutions Chapter 12 प्रायिकता Ex 12.1 Pdf, These solutions are solved by subject experts from the latest MP Board books.

MP Board Class 12th Maths Book Solutions Chapter 12 प्रायिकता Ex 12.1

ग्राफीय विधि से निम्न रैखिक प्रोग्रामन समस्याओं को हल कीजिए।
प्रश्न 1.
निम्न अवरोधों के अन्तर्गत Z = 3x + 4y का अधिकतमीकरण कीजिए-
x + y ≤ 4, x ≥ 0, y ≥ 0
हल:
अधिकतम
Z = 3x +4y
x + y ≤ 4
x ≥ 0, y ≥ 0

पहले सभी समस्याओं को समीकरण के रूप में लिखने पर
x + y = 4
x = 0   ….(ii)
y = 0   …(iii)
अब ग्राफ बनाने पर सुसंगत क्षेत्र OAB प्राप्त होता है।
Z के मान की गणना प्रत्येक कोणीय बिन्दु पर करने पर

अतः Z का अधिकतम मान 16 बिन्दु (0, 4) पर है।

प्रश्न 2.
निम्न अवरोधों के अन्तर्गत Z = – 3x + 4y का न्यूनतमीकरण कीजिए-
x + 2y ≤ 8, 3x + 2y ≤ 12, x ≥ 0, y ≥ 0
हल:
सर्वप्रथम सभी असमीकरणों को समीकरण के रूप में लिखने पर
x + 2y =  8 ……(i)
3x + 2y = 12 ……(ii)
x = 0, y = 0 ……(iii)
अब आलेख बनाने पर सुसंगत क्षेत्र OABC प्राप्त होता है।
समी०
(i) व
(ii) को हल करने पर
x = 2, y = 3 प्राप्त होता है।
∵ रेखा
(i) व
(ii) बिन्दु (2, 3) पर मिलती हैं।

अतः बिन्दु (4,0) पर Z का मान न्यूनतम है।

प्रश्न 3:
निम्न अवरोधों के अन्तर्गत Z = 5x + 3y का अधिकतमीकरण कीजिए
3x + 5y ≤ 15, 5x + 2y ≤ 10, x ≥ 0, y ≥ 0
हल:
सर्वप्रथम असमीकरणों को समीकरणों के रूप में लिखने पर,
3x + 5y =15 ….(i)
5x + 2y=10 …(ii)
x = 0 …(iii)
y = 0 …(iv)
अब समीकरणों का ग्राफ बनाने पर सुसंगत क्षेत्र OABC प्राप्त होता है।

अब Z का मान प्रत्येक कोणीय बिन्दु पर ज्ञात करने पर

अतः बिन्दु Z का अधिकतम मान \(\frac{245}{19}\) है।
\(\left(\frac{20}{19}, \frac{45}{19}\right)\)

प्रश्न 4.
निम्न अवरोधों के अन्तर्गत z = 3x + 5y का न्यूनतमीकरण कीजिए-
x + 3y ≥ 3, x + y ≥ 2, x ≥ 0, y ≥ 0
हल:
सर्वप्रथम सभी असमीकरणों को समीकरणों के रूप में लिखने पर,
x + 3y =3 …(i)
x + y=2 …(ii)
x = 0 …(iii)
y = 0 …(iv)
अब ग्राफ बनाने पर सुसंगत क्षेत्र X ABCY प्राप्त होता हो।

सारणी से Z का न्यूनतम मान बिन्दु B\(\left(\frac{3}{2}, \frac{1}{2}\right)\) पर 7 है।

प्रश्न 5.
निम्न अवरोधों के अन्तर्गत Z = 3x +2y का अधिकतमीकरण कीजिए-
x + 2y ≤ 10, 3x + y ≤ 15, x, y ≥ 0
हल:
सर्वप्रथम असमीकरणों को समीकरणों के रूप में लिखने पर
x + 2y = 10 …(i)
3x + y = 15 …(ii)
x = 0, y = 0 …(iii)
अब ग्राफ बनाने पर सुसंगत क्षेत्र OABC प्राप्त होता है।
समीकरण (i) व (ii) को हल करने पर,
x =4, y=3
ये रेखाएँ बिन्दु B(4,3) पर प्रतिच्छेदित करती हैं।

सारणी से बिन्दु (4,3) पर Z का अधिकतम मान 18 है।

प्रश्न 6.
निम्न अवरोधों के अन्तर्गत Z = x+2y का न्यूनतमीकरण कीजिए-
2x+y ≥ 3, x+2y ≥ 6, x,y ≥ 0
हल:
सर्वप्रथम असमीकरणों को समीकरणों के रूप में लिखने पर
2x + y =3 ….(i)
x + 2y =6 …(ii)
x = 0, y = 0 …(iii)

ग्राफ बनाने पर सुसंगत क्षेत्र XABY प्राप्त होता है।
z का मान प्रत्येक कोणीय बिन्दु पर ज्ञात करने पर

यहाँ z का प्रत्येक मान 6 है।।
अतः बिन्दुओं (6,0) और (0,3) को मिलाने वाली रेखा खण्ड पर स्थित सभी बिन्दुओं पर Z का न्यूनतम मान 6 है।

दिखाइए कि z का न्यूनतम मान दो बिन्दुओं से अधिक बिन्दुओं पर घटित होता है।

प्रश्न 7.
निम्न अवरोधों के अन्तर्गत Z = 5x + 10y का न्यूनतमीकरण तथा अधिकतमीकरण कीजिए-
x + 2y ≤ 120; x + y ≥ 60, x – 2y ≥ 0, x, y ≥ 0
हल:
दिया है : उद्देश्य फलन : Z = 5x + 10y
अवरोध : x + 2y ≤ 120, x + y ≥ 60
x – 2y ≥ 0, x, y ≥ 0

(1) x +2y ≤ 120 का आरेख,
रेखा x + 2y =120, बिन्दु A(120, 0) और बिन्दु B(0, 60) से होकर जाती है।
∴ x + 2y =120 का आरेख रेखा AB है।
x + 2y ≤ 120 में x = 0, y = 0 रखने पर,
0 ≤ 120, जो सत्य है।
∴ x +2y ≤ 120 के क्षेत्र में बिन्दु रेखा AB पर और उसके नीचे मूल बिन्दु की ओर स्थित है।
(2) x + y ≥ 60 का आरेख
रेखा x + y = 60, बिन्दु P(60, 0), B(0, 60) से होकर जाती है।
∴ x + y = 60 का आरेख रेखा PB है।
x + y ≥ 60 में x = 0, y = 0 रखने पर, 0 ≥ 60 जो सत्य नहीं है।
⇒ x +y ≥ 60 क्षेत्र के बिन्दु रेखा PB पर और उसके ऊपर होते हैं।
(3) x – 2y ≥ 0 का आरेख
रेखा x – 2y = 0 मूल बिन्दु 0 और Q(120, 60) से होकर जाती है।
∴ x – 2y ≥ 0 का आरेख रेखा OQ है।
x – 2y ≥ 0 में x =1, y = 0 रखने पर 1 ≥ 0 जो सत्य है।
⇒ (1, 0) इस क्षेत्र में स्थित है। x – 2y ≤ 0 क्षेत्र के बिन्दु रेखा OQ पर और इसके नीचे (1, 0) की ओर हैं।
(4) x ≥ 0 क्षेत्र के बिन्दु y- अक्ष पर और y- अक्ष के दायीं ओर है।
(5) y ≥ 0 क्षेत्र के बिन्दु x- अक्ष पर और इसके ऊपर हैं।
इस समस्या का सुसंगत क्षेत्र PSRA है।
जबकि बिन्दु S(40, 20) PB: x + y = 60 और OQ: x – 2y = 0 का प्रतिच्छेद बिन्दु है।
और R(60, 30), AB: x + 2y =120 और x – 2y = 0 का प्रतिच्छेद बिन्दु है।
उद्देश्य फलन : Z = 5x + 10y
बिन्दु A(120, 0) पर,
Z = 5 x 120 + 10 x 0 = 600
बिन्दु R(60, 30) पर,
Z = 5 x 60 + 10 x 30
= 300 + 300 = 600
बिन्दु S(40, 20) पर,
Z = 5 x 40 + 10x 20
= 200 + 200 = 400
बिन्दु P(60, 0) पर,
Z = 5 x 60 + 10 x 0
= 300 + 0 = 300
⇒ Z का न्यूनतम मान P(60, 0) पर 300 है।
और Z का अधिकतम मान RA के सभी बिन्दुओं पर 600 है।

प्रश्न 8.
निम्न अवरोधों के अन्तर्गत Z = x + 2y का न्यूनतमीकरण तथा अधिकतमीकरण कीजिए-
x + 2y ≥ 100, 2x – y ≤ 0, 2x +y ≤ 200, x, y ≥ 0
हल:
सर्वप्रथम असमीकरणों को समीकरणों के रूप में लिखने पर
x + 2y = 100
2x – y = 0
2x + y = 200
x = 0 y=0
ग्राफ बनाने पर सुसंगत क्षेत्र BEDC प्राप्त होता है।
समी० 2x + y = 200 तथा 2x – y = 0 को हल करने पर x = 50, y = 100 प्राप्त होता है।
⇒ D(50,100)
पुनः समी० x + 2y = 100 तथा 2x – y = 0 को हल करने पर, x = 20, y = 40 प्राप्त होता है।

अतः Z का न्यूनतम मान 100 है तथा अधिकतम मान बिन्दु (0, 200) पर 400 है।

प्रश्न 9.
निम्न अवरोधों के अन्तर्गत Z = – x + 2y का अधिकतमीकरण कीजिए-
x ≥ 3, x + y ≥ 5, x + 2y ≥ 6, y ≥ 0
हल:
दिया है : उद्देश्य फलन :
Z = – x + 2y
(1) x + y ≥ 5 का आरेख
रेखा x + y =5, बिन्दु A(5, 0) और B(0, 5) से होकर जाती है।
∴ x + y =5 का आरेख रेखा AB है।
x + y ≥ 5 में x =0, y=0 रखने पर,
0 ≥ 5 जो सत्य नहीं है।
∴ x + y ≥ 5 क्षेत्र के बिन्दु रेखा AB पर और उसके ऊपर है।

(2) x + 2y ≥ 6 का आरेख
रेखा x + 2y = 6, बिन्दु C (6, 0) और D (0, 3) से होकर जाती है।
∴ x + 2y = 6 रेखा का आरेख रेखा CD है।
⇒ x + 2y ≥ 6 में x =0, y = 0 रखने पर, 0 ≤ 6 जो सत्य नहीं है।
∴ x + 2y ≥ 6 का क्षेत्र के बिन्दु CD पर या उसके ऊपर है।
(3) x ≥ 3 क्षेत्र के बिन्दु रेखा PQ: x =3 पर या उसके दायीं ओर है।
(4) y ≥ 0 क्षेत्र के बिन्दु x- अक्ष पर और उसके ऊपर होते हैं। समस्या का सुसंगत क्षेत्र PQRCX है।
बिन्दु रेखा PQ =3 और AB: x + y =5 का प्रतिच्छेदन बिन्दु Q के निर्देशांक (3, 2) है।
बिन्दु R रेखा CD: x + 2y = 6 और AB: x + y =5 का प्रतिच्छेदन बिन्दु (4, 1) है।
उद्देश्य फलन : Z = – x + 2y
अब, बिन्दु Q (3, 2) पर,
Z = – 3 + 2 x 2 = – 3 + 4 =1
बिन्दु R(4, 1) पर,
Z = – 4 + 2 x 1 = – 4 + 2 = – 2
बिन्दु C(6, 0) पर,
Z = – 6 + 0 = – 6
⇒ z का अधिकतम मान 1 है परन्तु सुसंगत क्षेत्र अपरिबद्ध है तो – x + 2y > 1 क्षेत्र पर विचार करें। .
– x + 2y > 1 तथा सुसंगत क्षेत्र में अनेकों बिन्दु उभयनिष्ठ है।
अतः Zका कोई अधिकतम मान नहीं है।

प्रश्न 10.
निम्न अवरोधों के अन्तर्गत Z = x + y का अधिकतमीकरण कीजिए-
x – y ≤ – 1, – x + y ≤ 0, x, y ≥ 0
हल:
(i) x – y ≤ -1 का क्षेत्र
रेखा x – y = – 1 बिन्दु A(-1,0), B(0, 1) से होकर जाती है, जो AB आरेख है।
x – y ≤ – 1 में x =0, y = 0 रखने पर,
0 ≤ -1 जो सत्य नहीं है।
⇒ x – y ≤ – 1 के क्षेत्र बिन्दु रेखा AB पर और उसके ऊपर है।
(ii) – x + y ≤ का क्षेत्र
रेखा – x + y = 0, मूल बिन्दु O और C(1, 1) से होकर जाती है।
– x + y ≤ 0 में x = 1, y = 0 रखने पर, -1 ≤ 0 जो सत्य है।
⇒ – x + y ≤ 0 के क्षेत्र बिन्दु OC पर या उसके नीचे (1,0) ओर हैं।

(iii) x ≥ 0 क्षेत्र के बिन्दु y- अक्ष पर और -अक्ष के दायीं ओर हैं।
(iv) y ≥ 0 क्षेत्र के बिन्दु x- अक्ष पर और x- अक्ष के ऊपर स्थित हैं।
इस समस्या का कोई सुसंगत क्षेत्र नहीं है।
अतः Z का अधिकतम मान नहीं है।

In this article, we share MP Board Class 12th Maths Book Solutions Chapter 6 अवकलज के अनुप्रयोग Ex 6.5 Pdf, These solutions are solved by subject experts from the latest MP Board books.

MP Board Class 12th Maths Book Solutions Chapter 6 अवकलज के अनुप्रयोग Ex 6.5

प्रश्न 1.
निम्नलिखित दिए गए फलनों के उच्चतम या निम्नतम मान, यदि कोई हो तो ज्ञात कीजिए
(i) f (x) = (2x – 1)² + 3
(ii) f (x) = 9x² + 12x + 2
(iii) f (x) = – (x – 1)² + 10
(iv) g (x) = x² + 1
हल:
(i) f (x) = (2x – 1)² + 3
(2x – 1)² का कम – से – कम मान = 0
∴ f(x) का निम्नतम मान = 3

(ii) f (x) = 9x² + 12x + 2 = 9x² + 12x + 4 – 2
= (3x + 2)² – 2
(3x + 2)² का निम्नतम मान = 0
∴ f (x) का निम्नतम मान = – 2

(iii) f (x) = – (x – 1)² + 10
– (x – 1)² का अधिकतम मान = 0
∴ f का उच्चतम मान = 10

(iv) g (x) = x³ + 1
g'(x) = 3x² जो x ϵ R के लिए धनात्मक है।
∴ g एक वर्धमान फलन है; अतः इसका कोई न्यूनतम तथा अधिकतम मान नहीं है।

प्रश्न 2.
निम्नलिखित दिए गए फलनों के उच्चतम मान या निम्नतम मान, यदि कोई हो तो ज्ञात कीजिए
(i) f (x) |x + 2| – 1
(ii) g (x) = – |x + 1| + 3
(iii) h (x) = sin (2x) + 5
(iv) f (x) = |sin 4x + 3|
(v) h(x) = x + 1, x ϵ ( – 1, 1)
हल:
(i) f(x) = |x + 2| – 1
|x + 2| का न्यूनतम मान 0 है।
∴ f का निम्नतम मान = – 1
अतः उच्चतम मान का अस्तित्व नहीं है।

(ii) g (x) = -|x + 1| + 3
– |x + 1| का अधिकतम मान = 0
∴ g (x) = – |x + 1| + 3 का उच्चतम मान 0 + 3 = 3
निम्नतम मान का अस्तित्व नहीं है।

(iii) h (x) = sin (2x) + 5
sin 2x का अधिकतम मान = 1
∴ h(x) = sin 2x + 5 का उच्चतम मान, 1 + 5 = 6
sin 2x का न्यूनतम मान = – 1
∴ h (x) = sin 2x + 5 का निम्नतम मान = – 1 + 5 = 4

(iv) f (x) = |sin 4x + 3|
sin 4x का अधिकतम मान = 1
f(x) = |sin 4x + 3| का उच्चतम मान = |1 + 3| = 4
तथा sin 4x का निम्नतम मान = – 1
f (x) = |sin 4x + 3| का निम्नतम मान = |- 1 + 3| = 2

(v) h (x) = x + 1 .
h'(x) = 1 = धनात्मक
h वर्धमान फलन है।
इसका कोई उच्चतम या निम्नतम मान नहीं है।

प्रश्न 3.
निम्नलिखित फलनों के स्थानीय उच्चतम या निम्नतम, यदि कोई हो तो ज्ञात कीजिए तथा स्थानीय उच्चतम या स्थानीय निम्नतम मान,जैसी स्थिति हो, भी ज्ञात कीजिए।
(i) f (x) = x²
(ii) g (x) = x³ – 3x
(iii) h(x) = sin x + cos x, o < x < \(\frac{\pi}{2}\)
(iv) f (x) = sin x – cos x, 0 < x < 2π
(v) f (x) = x³ – 6x² + 9x + 15
(vi) g (x) = \(\frac{x}{2}+\frac{2}{x}\), x > 0
(vii) g (x) = \(\frac{1}{x^{2}+2}\)
(viii) f (x) = \(x \sqrt{1-x}\), x > 0
हल:
(i) f (x) = x²
f'(x) = 2x
यदि f'(x) = 0 तब 2x = 0 या x = 0
f'(x) जैसे ही x = 0 से होकर आगे बढ़ता है तो इसका चिह्न ऋणात्मक से धनात्मक में बदल जाता है।
∴ x = 0 पर f स्थानीय निम्नतम है।
स्थानीय निम्नतम मान = f (0) = 0

(ii) g(x) = x³ – 3x
∴ g'(x) = 3x² – 3 = 3 (x² – 1) = 3 (x – 1) (x + 1)
यदि g’ (x) = 0 तब 3x² – 3 = 0
⇒ x² – 1 = 0 ⇒ x = ± 1
x = – 1 पर g'(x) का चित – – = +
– + = –
जैसे ही x, x = – 1 से होकर आगे बढ़ता है, g’ का चिह्न + ve से – ve में परिवर्तित होता है।
∴ x = – 1 पर g उच्चतम है।
उच्चतम मान = g (- 1) = (- 1)³ – 3 (- 1) = – 1 + 3 = 2
x = 1 पर g'(x) के चिह्न जैसे ही x, x = 1 से होकर आगे बढ़ता है,
– + = –
+ + = +
g’ (x), ऋणात्मक से धनात्मक में परिवर्तित हो जाता है।
x = 1 पर g निम्नतम है।
निम्नतम मान = g(1) = 1³ – 3 = – 2

(iii) h(x) = sin x + cos x, 0 < x < \(\frac{\pi}{2}\)
h'(x) = cos x – sin x = cos x(1 – tan x)
यदि h'(x) = 0 तब 1 – tan x = 0 या tan x = 1 या x = \(\frac{\pi}{4}\)
x = \(\frac{\pi}{4}\) पर x का मान \(\frac{\pi}{4}\) से थोड़ा कम करने से tan x, 1 से कम होगा और x का मान \(\frac{\pi}{4}\) से थोड़ा अधिक रखने पर tan x, 1 से अधिक होगा।
इस प्रकार 1 – tan x का चिह्न + ve से – ve में परिवर्तित होता है। cos x में चिह्न में कोई परिवर्तन नहीं होता।
∴ x = \(\frac{\pi}{4}\) उच्चतम है।
स्थानीय उच्चतम मान

(v) f (x) = x³ – 6x² + 9x + 15
∴ f'(x) = 3x² – 12x + 9 = 3 (x² – 4x + 3)
= 3(x – 1)(x – 3)
यदि f'(x) = 0 ⇒ x – 1 = 0 या x – 3 = 0
∴ x = 1 .या x = 3

x का मान 1 से थोड़ा कम रखने पर
x का मान 1 से थोड़ा अधिक रखने पर
इस प्रकार f'(x) का चिह्न, जैसे ही x, x = 1 से होकर आगे बढ़ता है, + ve से – ve में परिवर्तित होता है।
⇒ x = 1, पर स्थानीय उच्चतम बिन्दु है।
स्थानीय उच्चतम मान = f (1) = 1 – 6 + 9 + 15 = 19

x का मान 3 से थोड़ा कम रखने पर,
x का मान 3 से थोड़ा अधिक रखने पर,
∴ f'(x) का चिह्न धनात्मक से ऋणात्मक में परिवर्तित होता है, जब x, x = 3 बिन्दु से होकर जाता है।
∴ x = 3 पर स्थानीय निम्नतम बिन्दु है।
∴ स्थानीय निम्नतम मान = f (3) = 27 – 54 + 27 + 15
= 69 – 54 = 15

x का मान 2 से थोड़ा कम रखने पर,
x का मान 2 से थोड़ा अधिक रखने पर,
g'(x) का चिह्न – – ve से + ve में परिवर्तित होता है, जब x,x = 2 से होकर आगे बढ़ता है।
∴ f, x = 2 पर स्थानीय निम्नतम है।
स्थानीय निम्नतम मान = g (2) = \(\frac{2}{2}+\frac{2}{2}=2\)

प्रश्न 4.
सिद्ध कीजिए कि निम्नलिखित फलनों का उच्चतम यो निम्नतम मान नहीं है
(i) f (x) = e^x
(ii) g (x) = log x
(iii) h(x) = x³ + x² + x + 1
हल:
(i) f(x) = e^x

अतः दिया गया फलन न तो उच्चतम है और न ही न्यूनतम
(iii) h(x) = x³ + x² + x + 1
= h'(x) = 3x² + 2x + 1
यदि h'(x) = 0
⇒ 3x² + 2x + 1 = 0
⇒ \(\frac{-2 \pm \sqrt{4-12}}{6}=\frac{-1 \pm \sqrt{-2}}{3}\)
जो कि काल्पनिक संख्या है
अत: ∀ x ϵ R, h'(x) ≠0
अतः h का कोई भी मान उच्चतम या निम्नतम नहीं है।

प्रश्न 5.
प्रदत्त अन्तरालों में निम्नलिखित फलनों के निरपेक्ष उच्चतम मान और निरपेक्ष निम्नतम मान ज्ञात कीजिए।
(i) f (x) = x³, x ϵ [- 2,2]
(ii) f (x) = sin x + cos x x ϵ [0, 1]
(iii) f (x) = 4x – \(\frac{1}{2}\)x², x ϵ [-2, \(\frac{9}{2}\)]
(iv) f (x) = (x – 1)² + 3, x ϵ [- 3, 1]
हल:
(i) f (x) = x³, अन्तराल [ – 2, 2]
∴ (x) = 3x²
यदि f’ (x) = 0, तब 3x² = 0 ∴ x = 0
f(- 2) = (- 2)³ = – 8
f (0) = (0)³ = 0
तथा f (2) = (2)³ = 8
निरपेक्ष उच्चतम मान = 8
निरपेक्ष निम्नतम मान = – 8

(ii) f(x) = sinx + cosx, x ϵ [0, π]
⇒ f'(x) = cosx – sin x
उच्चतम व निम्नतम मान के लिए
f'(x) = 0
⇒ cosx – sin x = 0
⇒ tan x = 1
⇒ x = π/4
अब x = \(\frac{\pi}{4}\), 0, π पर f(x) का मान ज्ञात करना है।

f(0) = sin 0° + cos0° = 0 + 1 = 1
f(π) = sin π + cos π = 0 – 1 = – 1
अत: फलन f(x) का निरपेक्ष उच्चतम मान x = \(\frac{\pi}{4}\) पर \( \sqrt{{2}} \) है।
तथा x = π पर f(x) का निरपेक्ष निम्नतम मान – 1 है।

अंत: x = 4 पर f(x) का निरपेक्ष उच्चतम मान = 8
तथा x = – 2 पर f(x) का निरपेक्ष निम्नतम मान = – 10

(iv) यहाँ f (x) = (x – 1)² + 3, [- 3, 1]
∴ f'(x) = 2(x – 1)
यदि f'(x) = 0, 2(x – 1) = 0, x = 1
f(1) = (1 – 1)² + 3 = 0 + 3 = 3
f(- 3) = (- 3 – 1)² + 3 = 16 + 3 = 19
अतः निरपेक्ष उच्चतम मान = 19
तथा निरपेक्ष निम्नतम मान = 3

प्रश्न 6.
यदि लाभ फलन P(x) = 41 – 72x – 18x² से प्रदत्त है तो किसी कम्पनी द्वारा अर्जित उच्चतम लाभ ज्ञात कीजिए।
हल:
दिया है लाभ फलन
P(x) = 41 – 72x – 18x²

⇒ 36x = – 72
x = – 2
∴ x = – 2 पर
\(\frac{d^{2} P}{d x^{2}}\) = – 36 < 0
अतः x = – 2 पर लाभ फलन का मान उच्चतम है।
अतः उच्चतम लाभ = P( – 2)
= 41 – 72(- 2) – 18(- 2)²
= 41 + 144 – 72
= 113

प्रश्न 7.
अन्तराल [0, 3] पर 3x⁴ – 8x³ + 12x² – 48x + 25 के उच्चतम मान और निम्नतम मान ज्ञात कीजिए।
हल:
यहाँ f(x) = 3x⁴ – 8x² + 12x² – 48x + 25
∴ f'(x) = 12x³ – 24x² + 24x – 48
= 12[x³ – 2x² + 2x – 4] = 12[x² (x – 2) + 2(x – 2)]
= 12(x – 2)(x² + 2)
यदि f'(x) = 0, तब
x – 2 = 0 ∴ x = 2
अन्तराल (0, 3) पर,
f (0) = 25
f(2) = 3(2)⁴ – 8(2)³ + 12(2)² – 48(2) + 25
= 3 × 16 – 8 × 8 + 12 × 4 – 48 × 2 + 25
= 48 – 64 + 48 – 96 + 25 = – 39
तथा f(3) = 3(3)⁴ – 8(3)³ + 12(3)² – 48(3) + 25
= 3 × 81 – 8 × 27 + 12 × 9 – 48 × 3 + 25
= 243 – 216 + 108 – 144 + 25 = 16
∴ निरपेक्ष उच्चतम मान = 25
निरपेक्ष निम्नतम मान = – 39

प्रश्न 8.
अन्तराल [0, 2 π] के किन बिन्दुओं पर फलन sin 2x अपना उच्चतम मान प्राप्त करता है।
हल:
यहाँ f (x) = sin 2x,[0, π] पर
∴ (x) = 2cos 2x
यदि f'(x) = 0 ⇒ 2cos 2x = 0

प्रश्न 9.
फलन sin x + cos x का उच्चतम मान क्या है?
हल:
यहाँ f(x) = sin x + cos x, [0, 2π] पर,
∴ f(x) = cos x – sin x
f'(x) = 0 = cos x – sin x = 0 ⇒ tan x = 1

प्रश्न 10.
अन्तराल [1,3] में 2x³ – 24x + 107 का महत्तम मान ज्ञात कीजिए।इसी फलन का अन्तराल [- 3, – 1]में भी महत्तम मान ज्ञात कीजिए।
हल:
यहाँ f (x) = 2x³ – 24x + 107, [1, 3]
∴ f(x) = 6x² – 24
उच्चतम व निम्नतम मान के लिए,
f'(x) = 0
⇒ 6x² – 24 = 0 ⇒ 6x² = 24 ⇒ x² = 4 ∴ x = ± 2
अन्तराल [1, 3] के लिए,
f(1) = 2(1)³ – 24 (1) + 107 = 2 – 24 + 107 = 85
f(2) = 2(2)³ – 24 (2) + 107 = 16 – 48 + 107 = 75
f(3) = 2(3)³ – 24 (3) + 107 = 54 – 72 + 107 = 89
इस प्रकार अधिकतम f (x) = 89, x = 3 पर, अन्तराल [- 3, – 1] के लिए हम x = – 3, – 2, – 1 पर f (x) का मान ज्ञात करते हैं।
f(- 3) = 2(- 3)³ – 24(- 3) + 107
= – 54 + 72 + 107 = – 54 + 179 = 125
f(- 2) = 2(- 2)³ – 24 (- 2) + 107
= – 16 + 48 + 107 = 139
f(- 1) = 2(- 1)³ – 24(- 1) + 107 = – 2 + 24 + 107 = 129
इस प्रकार अधिकतम मान f (x) = 139, x = – 2 पर

प्रश्न 11.
यदि दिया है कि अन्तराल [0, 2] में x = 1 पर फलन x⁴ – 62x³ + ax + 9 उच्चतम मान प्राप्त करता है तो a का मान ज्ञात कीजिए।
हल:
यहाँ f (x) = x⁴ – 62x³ + ax + 9
∴ f'(x) = 4x³ – 124x + a
उच्चतम व निम्नतम मान के लिए, f'(x) = 0
⇒ 4x³ – 124x + a = 0
x = 1, पर f उच्चतम है ⇒ f (1) = 0
∴ 4 × – 124 × 1 + a = 0 ⇒ 4 – 124 + a = 0
⇒ – 120 + a = 0
∴ a = 120
f(x) = 4x³ = 124x + a
f(x) = 12x² – 124
f(1) = 12 – 124 = – 112 < 0
अतः x = 1, उच्चतम है जब a = 120

प्रश्न 12.
[0, 2π] पर x + sin 2x का उच्चतम और निम्नतम मान ज्ञात कीजिए।
हल:
माना f(x) = x + sin 2x
∴ f(x) = 1 + 2cos 2x
उच्चतम व निम्नतम बिन्दु के लिए, f'(x) = 0
⇒ 1 + cos 2x = 0 ⇒ cos 2x = – 1


f(x) का उच्चतम मान = 2π
f (x) का उच्चतम मान = 0

प्रश्न 13.
ऐसी दो संख्याएँ ज्ञात कीजिए जिनका योग 24 है और जिनका गुणनफल उच्चतम हो।
हल:
माना अभीष्ट संख्याएँ x तथा 24 – x हैं।
माना उनका गुणनफल P है।
∴ P = x(24 – x)
P = 24x – x²

अतः x = 12 के लिए P (संख्याओं का गुणनफल) उच्चतम है।

प्रश्न 14.
ऐसी दो धन संख्याएँ x और y ज्ञात कीजिए ताकि x + y = 60 और xy³ उच्चतम हो।
हल:
∵ x + y = 60
माना P = xy³
⇒ P = (60 – y) y³
(∵ x + y = 60
⇒ x = 60 – y)
⇒ P = 60y³ – y⁴


अत: x = 15, y = 45 के लिए P = xy³ उच्चतम है।

प्रश्न 15.
ऐसी दो धन संख्याएँ x और y ज्ञात कीजिए जिनका योग 35 हो और गुणनफल x²y² उच्चतम हो।
हल:
दो धन संख्याएँ x, y हैं।
x + y – 35
∴ y = 35 – x
गुणनफल P = x²y⁵
y का मान समी० (2) में रखने पर
P = x² (35 – x)⁵
x के सापेक्ष अवकलन करने पर

केवल 10 स्वीकृत मान है जैसे कि x = 0, 35 अस्वीकृत कर दिए जाते हैं।
x = 10 पर,
जब x, 10 के निकट और 10 की बाईं ओर हो तो
\(\frac{d P}{d x}\) = (1)(+ 1)(+ 1) = + ve
जब x, 10 के निकट और 10 की दाई ओर हो तो
\(\frac{d P}{d x}\) = (+)(+)(-) = – ve
इस प्रकार x, 10 से होता हुआ आगे बढ़ता है
\(\frac{d P}{d x}\) + ve से – ve को परिवर्तित होता है।
x = 10 पर P उच्चतम है।
∴ y = 35 – 10 = 25
अतः अभीष्ट संख्याएँ 10 और 25 हैं।

प्रश्न 16.
ऐसी दो धन संख्याएँ ज्ञात कीजिए जिनका योग 16 हो और जिनके घनों का योग निम्नतम हो।
हल:
माना x और 16 – x दो धन संख्याएँ हैं।
प्रश्नानुसार, घनों का योग S = x³ + (16 – x)³
अवकलन करने पर,
\(\frac{d S}{d x}\) = 3x² + 3(16 – x)² ( – 1)
= 3x² – 3(16 – x)²
= 3x² – 3(256 + x² – 32x)
= 3x² – 3 × 256 – 3x² + 3 × 32x
= 3(32x – 256)
उच्चतम व निम्नतम बिन्दु के लिए,

अतः अभीष्ट संख्याएँ 8 और (16 – 8)अर्थात् 8 और 8 हैं।

प्रश्न 17.
18 cm भुजा के टिन के किसी वर्गाकार टुकड़े से प्रत्येक कोने पर एक वर्ग काटकर तथा इस प्रकार बने टिन के फलकों को मोड़कर ढक्कन रहित एक सन्दूक बनाना है। काटे जाने वाले वर्ग की भुजा कितनी होगी जिससे सन्दूक का आयतन उच्चतम हो?
हल:
माना वर्ग की प्रत्येक भुजा x सेमी काटी गई है।
∴ सन्दूक के लिए,
लम्बाई = 18 – 2x
चौड़ाई = 18 – 2x
ऊँचाई = x
∴ आयतन V = ल० × चौ० × ॐ
= x (18 – 2x)(18 – 2x) = x (18 – 2x)².1


∴ x = 3 पर आयतन अधिकतम होगा। अर्थात् वर्ग की भुजा प्रत्येक कोने से 3 सेमी काटी गई है तो आयतन उच्चतम होगा।

प्रश्न 18.
45 cm × 24 cm की टिन की आयताकार चादर के कोनों पर वर्ग काटकर तथा इस प्रकार बने टिन के फलकों को मोड़कर ढक्कन रहित एक सन्दूक बनाना है। काटे जाने वाले वर्ग की भुजा कितनी होगी जिससे सन्दूक का आयतन उच्चतम हो?
हल:
माना प्रत्येक कोने से x सेमी भुजा काटी गई है।
∴ आयताकार सन्दूक की भुजाएँ
l = 45 – 2x
b = 24 – 2x
h = x सेमी


अतः x = 5 के लिए आयतन उच्चतम है।

प्रश्न 19.
सिद्ध कीजिए कि एक दिए वृत्त के अन्तर्गत सभी आयतों में वर्ग का क्षेत्रफल उच्चतम होता है।
हल:
माना a त्रिज्या के वृत्त के अन्तर्गत आयतन की लम्बाई x तथा चौड़ाई y है।

∴ x² + y² = (2a)²
⇒ x² + y² = 4a² …(1)
∴ आयतन का क्षेत्रफल = xy

जब x बिन्दु x = \( \sqrt{{2}} \) a से होकर जाता है तो A’ (x) का चिह्न धनात्मक से ऋणात्मक में बदल जाता है। अतः आयत का क्षेत्रफल उच्चतम होगा, जब x = \( \sqrt{{2}} \)a और y = \( \sqrt{{2}} \)a होगा। अर्थात् आयत वर्ग होगा।

प्रश्न 20.
सिद्ध कीजिए कि प्रदत्त पृष्ठ एवं महत्तम आयतन के बेलन की ऊँचाई आधार के व्यास के बराबर होती है।
हल:
माना बेलन का पृष्ठीय क्षेत्रफल = S
त्रिज्या = r
ऊँचाई = h
आयतन = V
पृष्ठीय क्षेत्रफल S = 2πr² + 2πrh


अतः जब बेलन की ऊँचाई आधार के व्यास के बराबर है तो आयतन अधिकतम होता है।

प्रश्न 21.
100 cm³ आयतन वाले डिब्बे सभी बंद बेलनाकार (लम्ब वृत्तीय) डिब्बों में से न्यूनतम पृष्ठ क्षेत्रफल वाले डिब्बे की विमाएँ ज्ञात कीजिए।
हल:
माना बेलनाकार डिब्बों की त्रिज्या और ऊँचाई क्रमश: r और h है।
आयतन = πr²h = 100 cm³


⇒ S न्यूनतम होगा।
अतः कुल पृष्ठीय क्षेत्रफल न्यूनतम होगा।

प्रश्न 22.
एक 28 cm लम्बे तार को दो टुकड़ों में विभक्त किया जाना है। एक टुकड़े से वर्ग तथा दूसरे से वृत्त बनाया जाना है। दोनों टुकड़ों की लम्बाई कितनी होनी चाहिए जिससे वर्ग एवं वृस का सम्मिलित क्षेत्रफल न्यूनतम हो?
हल:
माना तार के एक भाग की लम्बाई x सेमी है तब दूसरा भाग = (28 – x) सेमी होगा।
माना x लम्बाई वाला भाग । त्रिज्या वाले वृत्त में बदला गया है।

प्रश्न 23.
सिद्ध कीजिए कि R त्रिज्या के गोले के अन्तर्गत विशालतम शंकु का आयतन गोले के आयतन का \(\frac{8}{27}\) होता है।
हल:
माना V AB गोले के अन्तर्गत विशालतम शंकु का आयतन है।
स्पष्टतयाः अधिकतम आयतन के लिए शंकु का अक्ष गोले . की ऊँचाई के साथ होना चाहिए।

प्रश्न 24.
सिद्ध कीजिए कि न्यूनतम पृष्ठ पर दिए आयतन के लम्ब वृत्तीय शंकु की ऊँचाई, आधार की त्रिज्या की 72 गुनी होती है।
हल:
माना शंकु की त्रिज्या = r
शंकु की ऊँचाई = h


∴ S न्यूनतम है जब h = \( \sqrt{{2}} \)r
अतः न्यूनतम वक्र पृष्ठ वाला लम्ब वृत्तीय शंकु की ऊँचाई, त्रिज्या की \( \sqrt{{2}} \) गुनी है।

प्रश्न 25.
सिद्ध कीजिए कि दी हुई तिर्यक ऊँचाई और महत्तम आयतन वाले शंकु का अर्थ शीर्ष कोण tan^-1\( \sqrt{{2}} \) होता है।
हल:
माना शंकु की त्रिज्या = r
ऊँचाई = l
ऊर्ध्वाधर ऊँचाई = AM = lcosθ
शंकु की त्रिज्या = MC = lsinθ

प्रश्न 26.
सिद्ध कीजिए कि दिए हुए पृष्ठ और महत्तम आयतन वाले लम्ब वृत्तीय शंकु का अर्द्ध शीर्ष कोण sin^-1\(\left(\frac{1}{3}\right)\) होता है।
हल:
माना शंकु का पृष्ठीय क्षेत्रफल S तथा आयतन V है। शंकु की त्रिज्या , ऊँचाई h तथा तिर्यक ऊँचाई l है।
शंकु का पृष्ठीय क्षेत्रफल = πrl + πr²

नोट – प्रश्न संख्या 27 से 29 में सही उत्तर का चुनाव कीजिए।
प्रश्न 27.
वक्र x² = 2y पर (0, 5) से न्यूनतम दूरी पर स्थित बिन्दु है
(A) (2\( \sqrt{{2}} \), 4)
(B) (2\( \sqrt{{2}} \), 0)
(C) (0, 0)
(D) (2, 2)
हल:
माना वक्र x² = 2y पर कोई बिन्दु P (x, y) है।
दिया हुआ बिन्दु A (0, 5) है।
PA² = (x – 0) + (y – 5)² = Z (माना)
∴ Z = x² + (y – 5) …(1)
तथा वक्र x² = 2y …(2)
x² का मान समी० (1) में रखने पर,
Z = 2y + (y – 5)² = 2y + y² + 25 – 10y
= y² + 25 – 8y
अवकलन करने पर,

अतः विकल्प (A) सही है।

प्रश्न 28.
x के सभी वास्तविक मानों के लिए \(\frac{1-x+x^{2}}{1+x+x^{2}}\) का न्यूनतम मान है
(A) 0
(B) 1
(C) 3
(D) \(\frac{1}{3}\)
हल:

प्रश्न 29.
[x(x – 1) + 1]^1/3, 0 ≤ x ≤ 1का उच्चतम मान है-
(A) \(\left(\frac{1}{3}\right)^{\frac{1}{3}}\)
(B) \(\frac{1}{2}\)
(C) 1
(D) 0
हल:
यहाँ y = [x(x – 1) + 1]^1/3
x के सापेक्ष अवकलन करने पर,

उच्चतम मान = 1
अतः विकल्प (C) सही है।

In this article, we share MP Board Class 12th Maths Book Solutions Chapter 7 समाकलन Ex 7.11 Pdf, These solutions are solved by subject experts from the latest MP Board books.

MP Board Class 12th Maths Book Solutions Chapter 7 समाकलन Ex 7.11

निश्चित समाकलनों में गुणधर्मों का उपयोग करते हुए 1 से 19 तक के प्रश्नों में समाकलनों का मान ज्ञात कीजिए-
प्रश्न 1.
\(\int_{0}^{\pi / 2} \cos ^{2} x d x\)
हल:

प्रश्न 2.
\(\int_{0}^{\pi / 2} \frac{\sqrt{\sin x}}{\sqrt{\sin x}+\sqrt{\cos x}} d x\)
हल:

प्रश्न 3.
\(\int_{0}^{\pi / 2} \frac{\sin ^{3 / 2} x d x}{\sin ^{3 / 2} x+\cos ^{3 / 2} x} d x\)
हल:

प्रश्न 4.
\(\int_{0}^{\pi / 2} \frac{\cos ^{5} x}{\sin ^{5} x+\cos ^{5} x} d x\)
हल:

प्रश्न 5.
\(\int_{-5}^{5}|x+2| d x\)
हल:
\(\int_{-5}^{5}|x+2| d x\)

प्रश्न 6.
\(\int_{2}^{8}|x-5| d x\)
हल:

प्रश्न 7.
\(\int_{0}^{1} x(1-x)^{n} d x\)
हल:

प्रश्न 8.
\(\int_{0}^{\pi / 4} \log (1+\tan x) d x\)
हल:

प्रश्न 9.
\(\int_{0}^{2} x \sqrt{2-x} d x\)
हल:

प्रश्न 10.
\(\int_{0}^{\pi / 2}(2 \log \sin x-\log \sin 2 x) d x\)
हल:

प्रश्न 11.
\(\int_{-\pi / 2}^{\pi / 2} \sin ^{2} x d x\)
हल:

प्रश्न 12.
\(\int_{0}^{\pi} \frac{x d x}{1+\sin x}\)
हल:

प्रश्न 13.
\(\int_{-\pi / 2}^{\pi / 2} \sin ^{7} x d x\)
हल:
माना \(\int_{-\pi / 2}^{\pi / 2} \sin ^{7} x d x\)
क्योंकि sin⁷ x एक विषम फलन है।
अतः I = 0.

प्रश्न 14.
\(\int_{0}^{2 \pi} \cos ^{5} x d x\)
हल:
माना I = \(\int_{0}^{2 \pi} \cos ^{5} x d x\)
माना f (x) = cos⁵ x तब
f(2π – x) = [cos (2π – x)]⁵ = cos⁵ x = f (x)

प्रश्न 15.
\(\int_{0}^{\pi / 2} \frac{\sin x-\cos x}{1+\sin x \cos x} d x\)
हल:

प्रश्न 16.
\(\int_{0}^{\pi} \log (1+\cos x) d x\)
हल:

प्रश्न 17.
\(\int_{0}^{a} \frac{\sqrt{x}}{\sqrt{x}+\sqrt{a-x}} d x\)
हल:

प्रश्न 18.
\(\int_{0}^{4}|x-1| d x\)
हल:
\(\int_{0}^{4}|x-1| d x\)

प्रश्न 19.
\(\int_{0}^{a} f(x) g(x) d x=2 \int_{0}^{a} f(x) d x\)
यदि f और g को f(x) = f(a – x) एवं g(x) + g(x – a) = 4 के रूप में परिभाषित किया गया है।
हल:

प्रश्न 20 एवं 21 में सही उत्तर का चयन कीजिए।
प्रश्न 20.
\(\int_{-\pi / 2}^{\pi / 2}\left(x^{3}+x \cos x+\tan ^{5} x+1\right) d x\) का मान है-
(A) 0
(B) 2
(C) π
(D) 1
हल:


अतः विकल्प (C) सही है।

प्रश्न 21.
\(\int_{0}^{\pi / 2} \log \left(\frac{4+3 \sin x}{4+3 \cos x}\right)\) का मान है
(A) 2
(B) \(\frac{3}{4}\)
(C) 0
(D) -2
हल:

अतः l = 0
अतः विकल्प (C) सही है।

In this article, we share MP Board Class 12th Maths Book Solutions Chapter 10 सदिश बीजगणित Ex 10.4 Pdf, These solutions are solved by subject experts from the latest MP Board books.

MP Board Class 12th Maths Book Solutions Chapter 10 सदिश बीजगणित Ex 10.4

प्रश्न 1. यदि \(\vec{a}=\hat{i}-7 \hat{j}+7 \hat{k}\) और \(\vec{b}=3 \hat{i}-2 \hat{j}+2 \hat{k}\) हो तो \(|\vec{a} \times \vec{b}|\) ज्ञात कीजिए।
हल:

प्रश्न 2.
सदिश \(\vec{a}+\vec{b}\) और \(\vec{a}-\vec{b}\) की लम्ब दिशा में मात्रक सदिश ज्ञात कीजिए जहाँ \(\vec{a}=3 \hat{i}+2 \hat{j}+2 \hat{k}\) और \(\vec{b}=\hat{i}+2 \hat{j}-2 \hat{k}\) है।
हल:

प्रश्न 3.
यदि एक मात्रक सदिश \(\vec{a}, \hat{i}\) के साथ π/3, \(\hat{j}\) के साथ π/4 और \(\hat{k}\) के साथ एक न्यून कोण 8 बनाता है तो 0 का मान ज्ञात कीजिए और इसकी सहायता से \(\hat{a}\) के घटक भी ज्ञात कीजिए।
हल:

प्रश्न 4.
दर्शाइए कि
\((\vec{a}-\vec{b}) \times(\vec{a}+\vec{b})=2(\vec{a} \times \vec{b})\)
हल:
L.H.S. \((\vec{a}-\vec{b}) \times(\vec{a}+\vec{b})\)

प्रश्न 5.
λ और μ ज्ञात कीजिए यदि
\((2 \hat{i}+6 \hat{j}+27 \hat{k}) \times(\hat{i}+\lambda \hat{j}+\mu \hat{k})=\overrightarrow{0}\)
हल:
दिया है

प्रश्न 6.
दिया हुआ है कि \(\vec{a} \cdot \vec{b}=0\) और \(\vec{a} \times \vec{b}=\overrightarrow{0}\) सदिश \(\vec{a}\) और \(\vec{b}\) के बारे में आप क्या निष्कर्ष निकाल सकते हैं|
हल:
दिया है \(\vec{a} \cdot \vec{b}=0\)

प्रश्न 7.
मान लीजिए सदिश \(\vec{a}, \vec{b}, \vec{c}\) क्रमशः \(a_{1} \hat{i}+a_{2} \hat{j}+a_{3} \hat{k}, b_{1} \hat{i}+b_{2} \hat{j}+b_{3} \hat{k}, c_{1} \hat{i}+c_{2} \hat{j}+c_{3} \hat{k}\) के रूप में दिए हुए हैं तब दर्शाइए कि
\(\vec{a} \times(\vec{b}+\vec{c})=\vec{a} \times \vec{b}+\vec{a} \times \vec{c}\)
हल:
सिद्ध करना है-

प्रश्न 8.
यदि \(\vec{a}=\overrightarrow{0}\) अथवा \(\vec{b}=\overrightarrow{0}\) तब \(\vec{a} \times \vec{b}=\overrightarrow{0}\) होता है। क्या विलोम सत्य है? उदाहरण सहित अपने उत्तर की पुष्टि कीजिए।
हल:

प्रश्न 9.
एक त्रिभुज का क्षेत्रफल ज्ञात कीजिए जिसके शीर्ष A (1, 1, 2), B(2, 3, 5) और C (1, 5, 5) हैं।
हल:
दिया है A (1, 1, 2), B (2, 3, 5) और C (1, 5, 5)

प्रश्न 10.
एक समान्तर चतुर्भुज का क्षेत्रफल ज्ञात कीजिए जिसकी संलग्न भुजाएँ सदिश \(\vec{a}=\hat{i}-\hat{j}+3 \hat{k}\) और \(\vec{b}=2 \hat{i}-7 \hat{j}+\hat{k}\) द्वारा निर्धारित हैं।
हल:
समान्तर चतुर्भुज का क्षेत्रफल जिसकी संगत भुजाएँ सदिश \(\vec{a}\) तथा \(\vec{b}\) हैं = \(|\vec{a} \times \vec{b}|\)

प्रश्न 11.
मान लीजिए सदिश \(\vec{a}\) और \(\vec{b}\) इस प्रकार हैं कि \(|\vec{a}|=3\) और| \(|\vec{b}|=\frac{\sqrt{2}}{3}\) तब \(\vec{a} \times \vec{b}\) एक मात्रक सदिश है। तब \(\vec{a}\) और \(\vec{b}\) के बीच का कोण है-

हल:

अतः विकल्प (B) सही है।

प्रश्न 12.
एक आयत के शीर्ष A, B, C और D जिनके स्थिति सदिश क्रमशः \(-\hat{i}+\frac{1}{2} \hat{j}+4 \hat{k}, \quad \hat{i}+\frac{1}{2} \hat{j}+4 \hat{k}\) \(\hat{i}-\frac{1}{2} \hat{j}+4 \hat{k}\) और \(-\hat{i}-\frac{1}{2} \hat{j}+4 \hat{k}\) हैं, का क्षेत्रफल है

हल:

अतः विकल्प (C) सही है।

In this article, we share MP Board Class 12th Maths Book Solutions Chapter 5 सांतत्य तथा अवकलनीयता Ex 5.7 Pdf, These solutions are solved by subject experts from the latest MP Board books.

MP Board Class 12th Maths Book Solutions Chapter 5 सांतत्य तथा अवकलनीयता Ex 5.7

प्रश्न संख्या 1 से 10 तक में दिए फलनों के द्वितीय कोटि के अवकलज ज्ञात कीजिए-
प्रश्न 1.
x² + 3x + 2
हल:
माना y = x² + 3x + 2

प्रश्न 2.
x²⁰
हल:
माना y = x²⁰
x के सापेक्ष अवकलन करने पर,

प्रश्न 3.
xcosx
हल:
माना y = x cosx

प्रश्न 4.
log x
हल:
y = logx
x के सापेक्ष अवकलन करने पर,

प्रश्न 5.
x³ log x
हल:
माना y = x³ logx

प्रश्न 6.
e^x sin 5x
हल:
माना y = e^xsin 5x
x के सापेक्ष अवकलन करने पर,

प्रश्न 7.
e^6x cos 3x
हल:
माना y = e^6x cos 3x
x के सापेक्ष अवकलन करने पर,

= e^6x [-6sin 3x. 3 – 3cos 3x. 3] + [6cos 3x – 3sin 3x] × e^6x . 6
= e^6x[-18sin 3x – 9cos 3x] + e^6x[36cos 3x – 18sin 3x]
= e^6x[-18sin 3x – 9cos 3x + 36cos 3x – 18sin 3x]
= e^6x[-36sin 3x + 27cos 3x]
= 9e^6x[3 cos 3x – 4sin 3x]

प्रश्न 8.
tan^-1x
हल:
माना y = tan^-1 x
x के सापेक्ष अवकलन करने पर,

प्रश्न 9.
log (log x)
हल:
माना y = log (log x)

प्रश्न 10.
sin (log x)
हल:
माना y = sin (log x)
x के सापेक्ष अवकलन करने पर,

प्रश्न 11.
यदि y = 5 cosx – 3 sin x है तो सिद्ध कीजिए कि \(\frac{d^{2} y}{d x^{2}}\) + y = 0
हल:
∵ y = 5cosx – 3sin x

प्रश्न 12.
यदि y = cos^-1x है तो \(\frac{d^{2} y}{d x^{2}}\) पदों में ज्ञात कीजिए-
हल:
∵ y = cos^-1x

प्रश्न 13.
यदि y = 3 cos (log x) + 4 sin (log x) है तो दर्शाइए कि x²y₂ + xy₁ + y = 0
हल:
∵ y = 3 cos (log x) + 4 sin (log x)


इसलिए
x²y₂ + xy₁ + y = – 7cos (log x) – sin log x – 3sin (log x) + 4cos (cosx) + 3cos (log x) + 4 sin (log x)
= -7cos (log x) – sin (logx) + sin (log x) + 7cos (log x)
= 0
अत: x²y₂ + xy₁ + y = 0

प्रश्न 14.
यदि y = Ae^mx + Be^nx है तो दर्शाइए कि

हल:
∵ y = Ae^mx + Be^nx

प्रश्न 15.
यदि y = 500e^7x + 600^-7x है तो दर्शाइए कि
\(\frac{d^{2} y}{d x^{2}}\) = 49 y है।
हल:
y = 500e^7x + 600^-7x
x के सापेक्ष अवकलन करने पर,

= 3500e^7x – 4200e^-7x
पुनः x के सापेक्ष अवकलन करने पर,
\(\frac{d^{2} y}{d x^{2}}=3500 \frac{d}{d x} e^{7 x}-4200 \frac{d}{d x} e^{-7 x}\)
=3500 × e^7x × 7 – 4200 × e^-7x x (-7)
= 500 × 49e^7x + 600 × 49e^-7x
= 49(500e^7x + 600e^-7x)
= 49y

प्रश्न 16.
यदि e^y (x + 1) = 1 है तो दर्शाइए कि \(\frac{d^{2} y}{d x^{2}}=\left(\frac{d y}{d x}\right)^{2}\) है|
हल:
e^y (x + 1) = 1

प्रश्न 17.
यदि y = (tan^-1x)² है तो दर्शाइए कि (x² + 1²)y₂ + 2x (x² + 1) y₂ = 2 है।
हल:
y = (tan^-1x)²
x के सापेक्ष अवकलन करने पर,

In this article, we share MP Board Class 12th Maths Book Solutions Chapter 7 समाकलन Ex 7.10 Pdf, These solutions are solved by subject experts from the latest MP Board books.

MP Board Class 12th Maths Book Solutions Chapter 7 समाकलन Ex 7.10

1 से 8 तक के प्रश्नों में समाकलनों का मान प्रतिस्थापन का उपयोग करते हुए ज्ञात कीजिए-
प्रश्न 1.
\(\int_{0}^{1} \frac{x}{x^{2}+1} d x\)
हल:

प्रश्न 2.
\(\int_{0}^{\pi / 2} \sqrt{\sin \phi} \cos ^{5} \phi d \phi\)
हल:

प्रश्न 3.
\(\int_{0}^{1} \sin ^{-1}\left(\frac{2 x}{1+x^{2}}\right) d x\)
हल:

प्रश्न 4.
\(\int_{0}^{2} x \sqrt{x+2} d x\)
हल:

प्रश्न 5.
\(\int_{0}^{\pi / 2} \frac{\sin x}{1+\cos ^{2} x} d x\)
हल:

प्रश्न 6.
\(\int_{0}^{2} \frac{d x}{x+4-x^{2}}\)
हल:

प्रश्न 7.
\(\int_{-1}^{1} \frac{d x}{x^{2}+2 x+5}\)
हल:

प्रश्न 8.
\(\int_{1}^{2}\left(\frac{1}{x}-\frac{1}{2 x^{2}}\right) e^{2 x} d x\)
हल:

प्रश्न 9 एवं 10 में सही उत्तर का चयन कीजिए
प्रश्न 9.
समाकलन \(\int_{1 / 3}^{1} \frac{\left(x-x^{3}\right)^{1 / 3}}{x^{4}} d x\) का मान है-
(A) 6
(B) 0
(C) 3
(D) 4
हल:
x = sin θ रखने पर
dx = cos θ dθ

पुनः cot θ = t प्रतिस्थापित करने पर
-cosec²θ dθ = dt


अतः विकल्प (A) सही है।

प्रश्न 10.
यदि f(x) = \(\int_{0}^{x} t \sin t d t\) है, तब f'(x) है-
(A) cos x + x sin x
(B) x sin x
(C) x cos x
(D) sin x + x cos x
हल:
f(x) = \(\int_{0}^{x} t \sin t d t\)

अतः f'(x) = -[cos x – x sin x] + cos x
= – cos x + x sin x + cos x
= x sin x
अतः विकल्प (B) सही है।

In this article, we share MP Board Class 12th Maths Book Solutions Chapter 9 अवकल समीकरण Ex 9.1 Pdf, These solutions are solved by subject experts from the latest MP Board books.

MP Board Class 12th Maths Book Solutions Chapter 9 अवकल समीकरण Ex 9.1

1 से 10 तक के प्रश्नों में प्रत्येक अवकल समीकरण की कोटि एवं घात ( यदि परिभाषित हो) ज्ञात कीजिए
प्रश्न 1.
\(\frac{d^{4} y}{d x^{4}}\) + sin (y”’) = 0
हल:
इस अवकल समीकरण में उच्चतम अवकलज कोटि \(\frac{d^{4} y}{d x^{4}}\) है इसलिए समीकरण की कोटि 4 है। इस समीकरण का बायाँ पक्ष अवकलजों में बहुपद नहीं है इसलिए इसकी घात परिभाषित नहीं है।

प्रश्न 2.
y’ + 5y = 0
हल:
कोटि → 1
घात → 1

प्रश्न 3.
\(\left(\frac{d s}{d t}\right)^{4}+3 s \frac{d^{2} s}{d t^{2}}=0\)
हल:
ये कोटि 2 है तथा घात 1 है।

प्रश्न 4.

हल:
\(\left(\frac{d^{2} y}{d x^{2}}\right)^{2}+\cos \left(\frac{d y}{d x}\right)=0\) की कोटि 2 है तथा इसके बायें पद में कोई फलन नहीं है।
अतः इसकी घात परिभाषित नहीं है।

प्रश्न 5.
\(\frac{d^{2} y}{d x^{2}}\) = cos 3x + sin 3x
हल:
∵ उच्चतम अवकलज \(\frac{d^{2} y}{d x^{2}}\) है।
∴ इसकी कोटि 2 है तथा दायें पद में बहुपद की उच्चतम घात 1 है।
इसलिए समीकरण की घात 1 है।

प्रश्न 6. (y”’)² (y”)³ + (y’)⁴ + y⁵ = 0
हल:
⇒ \(\left(\frac{d^{3} y}{d x^{3}}\right)^{2}+\left(\frac{d^{2} y}{d x^{2}}\right)^{3}+\left(\frac{d y}{d x}\right)^{4}\) + y⁵ = 0
उपरोक्त समीकरण में उच्चतम अवकलज \(\left(\frac{d^{3} y}{d x^{3}}\right)^{2}\) है।
∴ समी० की कोटि 3 है।
तथा घात 5 है।

प्रश्न 7.
y” + 2y” + y = 0
हल:
अवकल समीकरण की कोटि-3 परिभाषित नहीं है।

प्रश्न 8.
y + y = e^x
हल:
अवकल समीकरण की कोटि 1 परिभाषित नहीं है।

प्रश्न 9.
y” + (y’)² + 2y = 0
हल:
अवकल समीकरण की कोटि 2 परिभाषित नहीं है।

प्रश्न 10.
y’ + 2y’ + sin y = 0
हल:
अवकल समीकरण की कोटि 2 परिभाषित नहीं है।

प्रश्न 11.
अवकल समीकरण
\(\left(\frac{d^{2} y}{d x^{2}}\right)^{3}+\left(\frac{d y}{d x}\right)^{2}+\sin \left(\frac{d y}{d x}\right)+1=0\) की घात है-
(A) 3
(B) 2
(C) 1
(D) परिभाषित नहीं है
हल:
यह समीकरण अवकलज़ में बहुपदीय नहीं है; अतः यह परिभाषित नहीं है।
अतः विकल्प (D) सही है।

प्रश्न 12.
अवकल समीकरण \(2 x^{2} \frac{d^{2} y}{d x^{2}} \cdot 3 \frac{d y}{d x}+y=0\) की कोटि है
(A) 2
(B) 1
(C) 0
(D) परिभाषित नहीं है
हल:
अवकल समीकरण \(2 x^{2} \frac{d^{2} y}{d x^{2}} \cdot 3 \frac{d y}{d x}+y=0\) की कोटि 2 है।
अतः विकल्प (A) सही है।

In this article, we share MP Board Class 12th Maths Book Solutions Chapter 7 समाकलन Ex 7.2 Pdf, These solutions are solved by subject experts from the latest MP Board books.

MP Board Class 12th Maths Book Solutions Chapter 7 समाकलन Ex 7.2

प्रश्न 1 से 37 तक के प्रश्नों में प्रत्येक फलन का समाकलन ज्ञात कीजिए-
प्रश्न 1.
\(\frac{2 x}{1+x^{2}}\)
हल:

प्रश्न 2.
\(\frac{(\log x)^{2}}{x}\)
हल:

प्रश्न 3.
\(\frac{1}{x+x \log x}\)
हल:

प्रश्न 4.
sin x sin (cosx)
हल:

प्रश्न 5.
sin (ax + b) cos (ax + b)
हल:

प्रश्न 6.
\(\sqrt{a x+b}\)
हल:

प्रश्न 7.
\(x \sqrt{x+2}\)
हल:

प्रश्न 8.
\(x \sqrt{1+2 x^{2}}\)
हल:

प्रश्न 9.
(4x + 2) \(\sqrt{x^{2}+x+1}\)
हल:

प्रश्न 10.
\(\frac{1}{x-\sqrt{x}}\)
हल:

प्रश्न 11.
\(\frac{x}{\sqrt{x+4}}\), x > 0
हल:

प्रश्न 12.
(x³ – 1)^1/3 . x⁵
हल:

प्रश्न 13.
\(\frac{x^{2}}{\left(2+3 x^{3}\right)^{3}}\)
हल:

प्रश्न 14.
\(\frac{1}{x(\log x)^{m}}\), x > 0, m ≠ 1
हल:

प्रश्न 15.
\(\frac{x}{9-4 x^{2}}\)
हल:

प्रश्न 16.
e^2x+3
हल:

प्रश्न 17.
\(\frac{x}{e^{x^{2}}}\)
हल:

प्रश्न 18.
\(\frac{e^{\tan ^{-1} x}}{1+x^{2}}\)
हल:

प्रश्न 19.
\(\frac{e^{2 x}-1}{e^{2 x}+1}\)
हल:

प्रश्न 20.
\(\frac{e^{2 x}-e^{-2 x}}{e^{2 x}+e^{-2 x}}\)
हल:

प्रश्न 21.
tan²(2x – 3)
हल:

प्रश्न 22.
sec² (7 – 4x)
हल:

प्रश्न 23.
\(\frac{\sin ^{-1} x}{\sqrt{1-x^{2}}}\)
हल:

प्रश्न 24.

हल:

प्रश्न 25.

हल:

प्रश्न 26.
\(\frac{\cos \sqrt{x}}{\sqrt{x}}\)
हल:

प्रश्न 27.
\(\sqrt{\sin 2 x} \cdot \cos 2 x\)
हल:

प्रश्न 28.
\(\frac{\cos x}{\sqrt{1+\sin x}}\)
हल:

प्रश्न 29.
cot x log sin x
हल:

प्रश्न 30.
\(\frac{\sin x}{1+\cos x}\)
हल:

प्रश्न 31.
\(\frac{\sin x}{(1+\cos x)^{2}}\)
हल:

प्रश्न 32.
\(\frac{1}{1+\cot x}\)
हल:

प्रश्न 33.
\(\frac{1}{1-\tan x}\)
हल:

प्रश्न 34.
\(\frac{\sqrt{\tan x}}{\sin x \cos x}\)
हल:

प्रश्न 35.
\(\frac{(1+\log x)^{2}}{x}\)
हल:

प्रश्न 36.

हल:

प्रश्न 37.

हल:

प्रश्न 38 व 39 में सही उत्तर का चयन कीजिए
प्रश्न 38.


हल:

प्रश्न 39.
\(\int \frac{d x}{\sin ^{2} x \cos ^{2} x}\) बराबर है-
(A) tan x + cot x + C
(B) tan x – cotx + C
(C) tan x cot x + C
(D) tan x – cot 2x + C
हल: