Bhagya

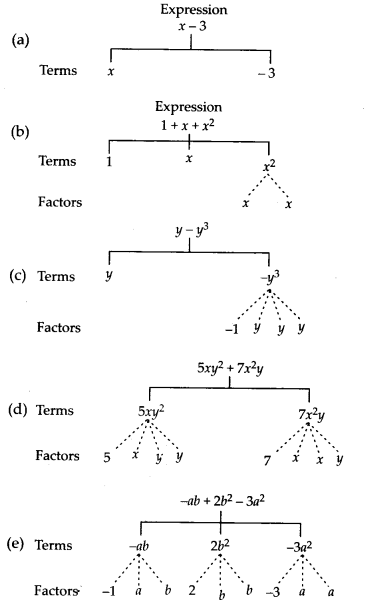
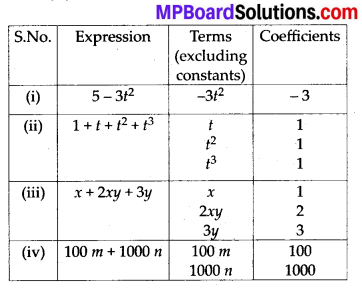
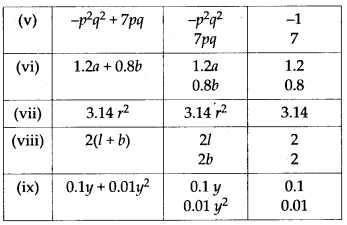
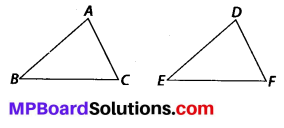
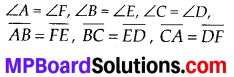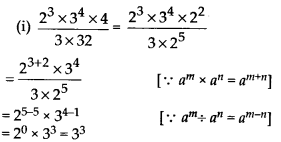MP Board Class 7th Maths Solutions Chapter 7 Congruence of Triangles Ex 7.2

Question 1.
Which congruence criterion do you use in the following?
(a) Given: AC = DF
AB = DE
BC = EF
So, ∆ABC ≅ ∆DEF

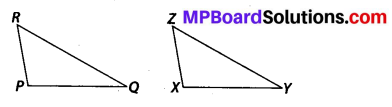
(b) Given: ZX = RP
RQ = ZY
∠PRQ = ∠XZY
So, ∆PQR ≅ ∆XYZ

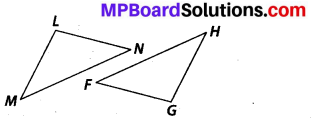
(c) Given: ∠MLN = ∠FGH
∠NML = ∠HFG
ML = FG
So, ∆LMN ≅ ∆GFH

(d) Given EB = BD

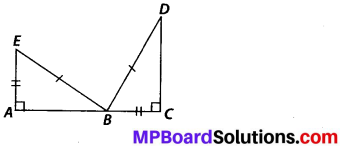
AE = CB
∠A = ∠C = 90°
So, ∆ABE ≅ ∆CDB
Solution:
(a) SSS, as all three sides of AABC are equal to the corresponding sides of ∆DEF.
(b) SAS, as two sides and the angle included between these sides of ∆PQR are equal to the corresponding sides and included angle of ∆XYZ.
(c) ASA, as two angles and the side included between these angles of ∆LMN are equal to the corresponding angles and included side of ∆GFH.
(d) RHS, as in the given two right-angled triangles, one side and the hypotenuse are respectively equal.

Question 2.
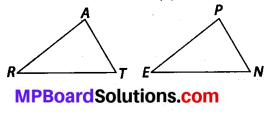
You want to show that ∆ART ≅ ∆PEN,
(a) If you have to use SSS criterion, then you need to show
(i) AR =
(ii) RT =
(iii) AT =
(b) If it is given that ∠T = ∠N and you are to use SAS criterion, you need to have
(i) RT = and
(ii) PN =
(c) If it is given that AT = PN and you are to use ASA criterion, you need to have

Solution:
(a) (i) AR = PE
(ii) RT = EN
(iii) AT = PN

(b) (i) RT = EN
(ii) PN = AT

(c) (i) ∠ATR = ∠PNE
(ii) ∠RAT = ∠EPN

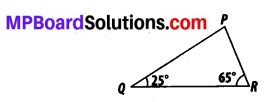
Question 3.
You have to show that ∆AMP ≅ ∆AMQ
In the following proof, supply the missing reasons.

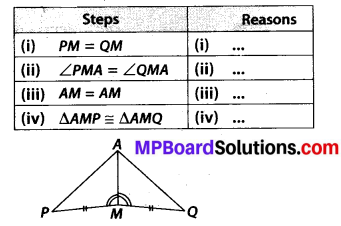
Solution:
(i) Given
(ii) Given
(iii) Common
(iv) SAS congruence criterion, as the two sides and the angle included between these sides of ∆AMP are equal to corresponding sides and included angle of ∆AMQ.

Question 4.
In ∆ABC, ∠A = 30°, ∠B = 40° and ∠C = 110°
In ∆PQR, ∠P = 30°, ∠Q = 40° and ∠R = 110°
A student says that ∆ABC ≅ ∆PQR by AAA congruence criterion. Is he justified? Why or why not?
Solution:
No. This property represents that these triangles have their respective angles of equal measure. However, this does not give any information about their sides. The sides of these triangles may have a ratio different from 1 : 1. Therefore, AAA property does not prove that two triangles are congruent.

Question 5.
In the figure, the two triangles are congruent. The corresponding parts are marked. We can write ∆RAT ≅ ?

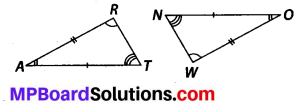
Solution:
It can be observed that,
∠RAT = ∠WON
∠ART = ∠OWN
AR = OW
Therefore, ∆RAT ≅ ∆WON, by ASA criterion.

Question 6.
Complete the congruence statement:

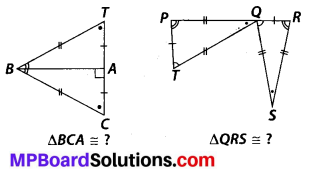
Solution:
In ∆BCA and ∆BTA,
BC = BT (given)
TA = CA (given)
BA is common.
Therefore, ∆BCA ≅ ∆BTA
(by SSS congruence criterion)
Now, in AQRS and ATPQ,
∠RQS = ∠PTQ (given)
RQ = PT (given)
∠SRQ = ∠QPT (given)
Therefore, ∆QRS = ∆TPQ
(by ASA congruence criterion)

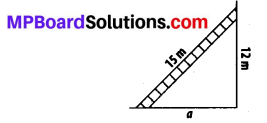
Question 7.
In a squared sheet, draw two triangles of equal areas such that
(i) the triangles are congruent.
(ii) the triangles are not congruent. What can you say about their perimeters?
Solution:

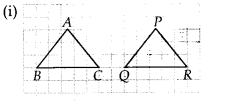
Here, ∆ABC and ∆PQR have the same area and are congruent to each other also. Also the perimeter of both the triangles will be the same.

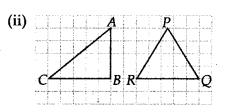
Here, ∆ABC and ∆PQR have the same height and same base. Thus, their areas are equal. However, these triangles are not congruent to each other. Also, the perimeter of both the triangles will not be the same.

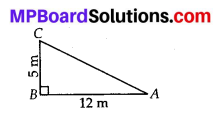
Question 8.
Draw a rough sketch of two triangles such that they have five pairs of congruent parts but still the triangles are not congruent.

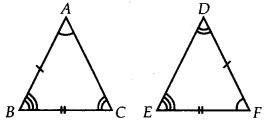
Solution:
∆ABC & ∆DEF are not congruent to each other but have five congruent parts i.e., ∠BAC = ∠EFD, ∠ABC = ∠DEF, ∠BCA = ∠EDF, AB = DF and BC = EF

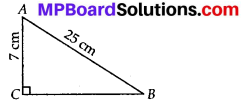
Question 9.
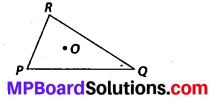
If ∆ABC and ∆PQR are to be congruent, name one additional pair of corresponding parts. What criterion did you use?

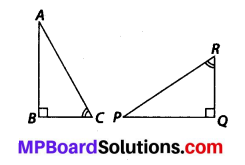
Solution:
∠ABC = ∠PQR = 90° and
∠BCA = ∠QRP (Given)
For triangles to be congruent, BC = QR
∆ABC ≅ ∆PQR (ASA congruence criterion)

Question 10.
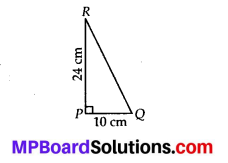
Explain, why ∆ABC ≅ ∆FED

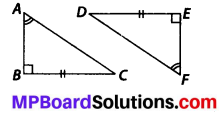
Solution:
Given that, ∠ABC = ∠FED = 90° and ∠BAC = ∠EFD
The two angles of ∆ABC are equal to the two respective angles of ∆FED. Also, the sum of all interior angles of a triangle is 180°. Therefore, third angle of both triangles will also be equal in measure.
∴ ∠BCA = ∠EDF
Now, in ∆ABC and ∆FED,
∠ABC = ∠FED, BC = ED and ∠BCA = ∠EDF
⇒ ∆ABC = ∆FED
(ASA congruence criterion)

MP Board Class 7th Maths Solutions

MP Board Class 7th Maths Solutions Chapter 12 Algebraic Expressions Ex 12.2

Question 1.
Simplify by combining like terms:
(i) 21b – 32 +7b – 20b
(ii) -z² + 13z² – 5z + 7z³ – 15z
(iii) p – (p – q) – q – (q – p)
(iv) 3a – 2b – ab – (a – b + ab) + 3ab + b – a
(v) 5x²y – 5x² + 3yx² – 3y² + x² – y² + 8xy² – 3y²
(vi) (3y² + 5y – 4) – (8y – y² – 4)
Solution:
(i) 21b – 32 + 7b – 20b
= 21b + 7b – 20b – 32
= (21 + 7 – 20)b – 32
= 8b – 32

(ii) -z² + 13z² – 5z + 7z³ – 15z
= 7z³ + (-1 + 13) z² + (-5 -15) z
= 7z³ + 12z² – 20z

(iii) p – (p – q) – q – (q – p)
= p – p + q – q – q + p
= p – q

(iv) 3a – 2b – ab – (a – b + ab) + 3ab + b – a
= 3a – 2b – ab – a + b – ab + 3 ab + b – a
= (3 – 1 – 1)a + (-2 + 1 + 1)b + (-1 – 1 + 3)ab
= a + ab

(v) 5x²y – 5x² + 3yx² – 3y² + x² – y² + 8xy² – 3y²
= (5 + 3) x²y + (-5 + 1) x² + (- 3 – 1 – 3 )y² + 8xy²
= 8x²y – 4x² – 7y² + 8xy²

(vi) (3y² + 5y – 4) – (8y – y² – 4)
= 3y² + 5y – 4 – 8y + y² + 4
= (3 + 1) y² + (5 – 8) y + 4 – 4
= 4y² – 3y

Question 2.
Add:
(i) 3mn, -5mn, 8mn, -4mn
(ii) t – 8tz, 3tz – z, z – 1
(iii) -7mn + 5, 12mn + 2, 9mn – 8, -2mn – 3
(iv) a + b – 3, b – a + 3, a – b + 3
(v) 14x + 10y – 12xy – 13, 18 – 7x – 10y + 8xy, 4xy
(vi) 5m – 7n, 3n – 4m + 2, 2m – 3mn – 5
(vii) 4x²y, -3xy², 5xy², 5x²y
(viii) 3 p²q² – 4pq + 5, -10p²q², 15 + 9pq + 7p²q²
(ix) ab – 4a, 4b – ab, 4a – 4b
(x) x² – y² – 1, y² – 1 – x², 1 – x² – y².
Solution:
(i) 3 mn + (-5 mn) + 8 mn + (-4 mn)
= (3 – 5 + 8 – 4 )mn = 2 mn

(ii) (t – 8tz) + (3tz – z) + (z – t)
= t – 8tz + 3tz – z + z – t
= (1 – 1)t + (- 8 + 3)tz + (-1 + 1)z
= -5 tz

(iii) (-7mn + 5) + (12mn + 2) + (9mn – 8) + (-2mn – 3)
=-7mn + 5 + 12mn + 2 + 9mn – 8 – 2mn – 3
= (-7 + 12 + 9 – 2)mn + (5 + 2 – 8 – 3)
= 12mn – 4

(iv) (a + b – 3) + (b – a + 3) + (a – b + 3)
= a + b – 3 + b – a + 3 + a – b + 3
= (1 -1 + 1)a + (1 + 1 – 1)b + (- 3 + 3 + 3)
= a + b + 3

(v) (14x + 10y – 12xy – 13) + (18 – 7x – 10y + 8xy) + 4xy
= 14x + 10y – 12xy – 13 + 18 – 7x – 10y + 8xy + 4xy
= (14 – 7)x + (10 – 10)y + (12 + 8 + 4 )xy + (-13 + 18)
= 7x + 5

(vi) (5m – 7n) + (3n – 4m + 2) + (2m – 3mn – 5)
= 5m – 7n + 3n – 4m + 2 + 2m – 3mn – 5
= (5 – 4 + 2)m + (- 7 + 3)n – 3mn + (2 – 5)
= 3m – 4n – 3mn – 3

(vii) (4x²y) + (-3xy²) + (-5xy²) + (5x²y)
= 4x²y – 3xy² – 5xy² + 5x²y
= (4 + 5) x²y + (-3 – 5) xy²
= 9x²y – 8xy²

(viii) (3p²q² – 4pq + 5) + (-10p²q²) + (15 + 9pq +7p²q²)
= 3p²q² – 4pq + 5 – 10p²q² + 15 + 9pq + 7p²q²
= (3 – 10 + 7) p²q² + (-4 + 9)pq + (5 + 15)
= 5pq + 20

(ix) (ab – 4a) +(4 b – ab) + (4a- 4b)
= ab – 4a + 4b – ab + 4a – 4b
= (1 – 1)ab + (-4 + 4 )a + (4 – 4)b = 0

(x) (x² – y² – 1) + (y² – 1 – x²) + (1 – x² – y²)
= x² – y² – 1 + y² – 1 – x² + 1 – x² – y²
= (1 – 1 – 1)x² + (-1 + 1 – 1)y² + (-1 – 1 + 1)
= -x² – y² – 1

Question 3.
Subtract:
(i) -5y² from y²
(ii) 6xy from -12xy
(iii) (a – b) from (a + b)
(iv) a(b – 5) from b (5 – a)
(v) – m2 + 5 mn from 4mi2 – 3mn + 8
(vi) -x² + 10x – 5 from 5x – 10
(vii) 5a² – 7ab + 5b² from 3ab – 2a² – 2b²
(viii) 4pq – 5q² – 3p² from 5p² + 3q² – pq
Solution:
(i) y² – (-5y²) = y² + 5y² = 6y²
(ii) -12xy – (6xy) = -12xy – 6xy = -18xy
(iii) (a + b) – (a – b) = a + b – a + b = 2b

(iv) b(5 – a) – a(b – 5)
= 5b – ab – ab + 5a
= 5a + 5b – 2ab

(v) (4m² – 3mn + 8) – (- m² + 5mn)
= 4m² – 3mn + 8 + m² – 5mn
= (4 + 1)m² + (- 3 – 5 )mn + 8
= 5m² – 8mn + 8

(vi) (5x – 10) – (-x² + 10x – 5)
= 5x – 10 + x² – 10x + 5
= x² + (5 – 10)x + (-10 + 5)
= x² – 5x – 5

(vii) (3ab – 2a² – 2b²) – (5a² – 7ab + 5b²)
= 3ab – 2a² – 2b² – 5a² + 7ab – 5b²
= (3 + 7)ab + (- 2 – 5)a² + (- 2 – 5 )b²
= 10ab – 7a² – 7b²

(viii) (5p² + 3q² – pq) – (4pq – 5a² – 3p²)
= 5p² + 3q² – pq – 4pq + 5q² + 3p²
= (5 + 3 )p² + (3 + 5 )q² + (-1 – 4 )pq
= 8p² + 8q² – 5pq

Question 4.
(a) What should be added to x² + xy + y² to obtain 2x² + 3xy?
(b) What should be subtracted from 2a + 8b + 10 to get – 3a + 7b + 16?
Solution:
(a) Let a be the required term.
∴ a + (x² + y² + xy) = 2x² + 3xy
⇒ a = 2x² + 3xy – (x² + y² + xy)
= 2x² + 3xy – x² – y² – xy
= (2 – 1) x² – y² + (3 – 1)xy
= x² – y² + 2xy

(b) Let p be the required term.
∴ (2a + 8b + 10) -p = -3a + 7b + 16
⇒ p = 2a + 8b + 10 – (- 3a + 7b + 16)
= 2a + 8b + 10 + 3a – 7b – 16
= (2 + 3)a + (8 – 7)b + (10 – 16)
= 5a + b – 6

Question 5.
What should be taken away from 3x² – 4y² + 5xy + 20 to obtain -x² – y² + 6xy + 20 ?
Solution:
Required term
= (3x² – 4y² + 5xy + 20) – (-x² – y² + 6xy + 20)
= 3x² – 4y² + 5xy + 20 + x² + y² – 6xy – 20
= (3 + 1)x² + (- 4 + 1) y² + (5 – 6)xy + (20 – 20)
= 4x² – 3y² – xy

Question 6.
(a) From the sum of 3x – y + 11 and -y – 11, subtract 3x – y – 11.
(b) From the sum of 4 + 3x and 5 – 4x + 2x², subtract the sum of 3x² – 5x and -x² + 2x + 5.
Solution:
(a) Sum of 3x – y + 11 and – y – 11
= (3x – y + 11) + (-y – 11)
= 3x – y + 11 – y – 11
= 3x + (- 1 – 1) y + (11 – 11)
= 3x – 2y
Now, required difference
= (3x – 2y) – (3x – y – 11)
= 3x – 2y – 3x + y + 11
= (3 – 3)x + (- 2 + 1) y + 11
= -y + 11

(b) Sum of 4 + 3x and 5 – 4x + 2x²
= (4 + 3x) + (5 – 4x + 2x²)
= 4 + 3x + 5 – 4x + 2x²
= (3 – 4)x + 2x² + 4 + 5
= – x + 2x² + 9
Now, sum of 3x² – 5x and -x² + 2x + 5
= (3x² – 5x) + (-x² + 2x + 5)
= 3x² – 5x – x² + 2x + 5
= (3 – 1) x² + (- 5 + 2)x + 5
= 2x² – 3x + 5
Required difference
= (- x + 2x² + 9) – (2x² – 3x + 5)
= -x + 2x² + 9 – 2x² + 3x – 5
= (-1 + 3)x + (2 – 2) x² + (9 – 5)
= 2x + 4

MP Board Class 7th Maths Solutions

MP Board Class 6th Hindi Bhasha Bharti Solutions विविध प्रश्नावली 1

प्रश्न 1.
निम्नलिखित विकल्पों में से सही चुनकर। लिखिए
(क) चीनी दार्शनिक थे
(i) लुकमान,
(ii) कन्फ्यू शस,
(iii) शास्त्री जी,
(iv) न्यूटन।
उत्तर-
(ii) कन्फ्यू शस,

(ख) महानगरों में गगन चूमते खड़े हैं
(i) पहाड़,
(ii) वृक्ष,
(iii) भवन,
(iv) खम्बे।
उत्तर-
(iii) भवन,

(ग) उज्जयिनी के सम्राट का नाम था
(i) कालिदास,
(ii) विक्रमादित्य,
(iii) शिवाजी,
(iv) राजा भोज।
उत्तर-
(ii) विक्रमादित्य,

(घ) सफलता शब्द में ‘ता’ है
(i) उपसर्ग,
(ii) प्रत्यय,
(iii) क्रिया,
(iv) सर्वनाम।
उत्तर-
(ii) प्रत्यय,

(ङ) ‘सूर्य’ का पर्यायवाची शब्द है
(i) मयंक,
(ii) भास्कर,
(iii) इन्दु,
(iv) रज।
उत्तर-
(ii) भास्कर।

प्रश्न 2.
रिक्त स्थानों की पूर्ति कीजिए
(क) ………………………” युद्ध वाणी के प्रयोग का ही परिणाम था।
(ख) बाबा भारती अपने घोड़े को ……………………… कहकर पुकारते थे।
(ग) धन के कोष भरने के बाद भी मनुष्य को ……………………… नहीं है।
(घ) ‘विशेष’ शब्द में ……………………… उपसर्ग है।
(ङ) मीठी बोली’ शब्द में ……………………… विशेषण है।
उत्तर-
(क) महाभारत,
(ख) सुलतान,
(ग) सन्तोष,
(घ) ‘वि’,
(ङ) मीठी।

प्रश्न 3.
निम्नलिखित प्रश्नों के उत्तर दीजिए

(क) स्वतन्त्रता संग्राम में शत्रु की दशा कैसी थी?
उत्तर-
स्वतन्त्रता संग्राम में माँ भारती के वीर सपूतों के साहस व पराक्रम को देखकर शत्रु काँपने लगते हैं।

(ख) अपना घोड़ा वापस पाकर बाबा भारती ने क्या कहा?
उत्तर-
अपना घोड़ा वापस पाकर बाबा भारती ने सन्तोष की साँस ली और बोले कि अब कोई गरीबों की सहायता से मुँह नहीं मोड़ेगा।

(ग) जन-सेवा का भाव क्यों समाप्त हो रहा है?
उत्तर-
जन-सेवा का भाव इसलिए समाप्त हो रहा है, क्योंकि जो शिक्षा दी जा रही है वह संस्कारविहीन है जिससे लोगों में चिन्तन की गहराई और विस्तृतता नहीं है।

(घ) संज्ञानन्द की पत्नी का नाम क्या था?
उत्तर-
संज्ञानन्द की पत्नी का नाम क्रियादेवी था।

(ङ) खाई-कुएँ से कवि का क्या आशय है?
उत्तर-
खाई-कुएँ से आशय है श्रेष्ठ वीरों के मार्ग में सब – ओर कठिनाई और बाधाएँ होती हैं।

(च) पतित-पावनी किसे कहा गया है?
उत्तर-
पतित-पावनी शब्द ‘गंगा माता’ के लिए कहा गया

प्रश्न 4.
निम्नलिखित प्रश्नों के उत्तर तीन से पाँच वाक्यों में दीजिए

(क) शास्त्रीजी ने अपनी पत्नी को कौन-कौन सी पंक्तियाँ सुनायीं और क्यों?
उत्तर-
शास्त्रीजी ने अपनी पत्नी को निम्नलिखित पंक्तियाँ सुनायीं “कुदरत को नापसन्द है सख्ती जबान में, इसलिए तो दी नहीं हड्डी जबान में, जो बात कहो, साफ हो, सुथरी हो, भली हो। कड़वी न हो, खट्टी न हो, मिश्री की डली हो।”

इन पंक्तियों को सुनकर उनकी पत्नी का क्रोध सदा के लिए समाप्त हो गया। इसी उद्देश्य से शास्त्रीजी ने उपर्युक्त पंक्तियाँ अपनी पत्नी को सुनायीं।।

(ख) खड्गसिंह ने बाबा भारती का घोड़ा वापिस क्यों कर दिया? समझाइए।
उत्तर-
खड्गसिंह के ऊपर बाबा भारती के इस कथन का कि “लोगों के सामने इस घटना को प्रकट न करना क्योंकि उन्हें इस घटना का पता लग गया, तो वे किसी गरीब पर विश्वास नहीं करेंगे।” बहुत प्रभाव पड़ा। वह सोचने लगा कि बाबा को घोड़े के छीन लेने का कोई कष्ट नहीं है, उन्हें तो केवल यही ख्याल रहा कि कहीं लोग गरीबों पर विश्वास करना न छोड़ दें। यह बात खड्गसिंह के कानों में बराबर गूंजती थी। इस बात से प्रभावित होकर कि बाबा भारती कोई सामान्य आदमी नहीं, यह तो निश्चय ही कोई देवता हैं, बाबा भारती के घोड़े को वापिस कर दिया। खड्गसिंह का हृदय परिवर्तन हो चुका था। उसकी आँखों में नेकी के आँसू भर आए।

(ग) अगस्त्य ऋषि का उल्लेख कवि ने क्यों किया है?
उत्तर-
कवि ने भारतीय वीरों में अपने निश्चय की दृढ़ता को बनाए रखने और अपने उद्देश्य से न डिगने के लिए अगस्त्य ऋषि का उल्लेख किया है। अगस्त्य ऋषि ने अपने हाथों की अंजलि जैसे छोटे साधन से विशाल समुद्र को पीकर उसके घमण्ड को चूर कर दिया था, अत: पक्के इरादों वाले हे वीरवरो ! तुम भी विपत्तियों पर विजय पाकर अपने लक्ष्य को प्राप्त कर सकते हो।

(घ) ‘अपना हिन्दुस्तान कहाँ है?’ कवि ने यह प्रश्न क्यों किया?
उत्तर-
अपना हिन्दुस्तान कहाँ है? यह प्रश्न कवि ने उचित ही किया है क्योंकि भूमण्डलीकरण के इस युग में हिन्दुस्तानीपन, अपनी जीवन शैली, अपनी सोच, अपनी शैक्षिक-प्रणाली, शिक्षा की विस्तृतता, गम्भीरता इत्यादि सभी समाप्त हो चुकी हैं। पारिवारिकता, संघीय सोच, वैवाहिक संस्थाएँ सब की सब बदल चुकी हैं। धन के लालच में लोगों के पारिवारिक सम्बन्ध टूट चुके हैं। टेलीफोन पर बातचीत करके ही किसी भी तरह की जानकारी ली जाती है। भारत से वैदिककालीन शिक्षा समाप्त है। मन्त्रों की घोष यन्त्रों की आवाज तले लुप्त हो गयी है। हमारी चिन्तन शैली भी सीमित हो चुकी है। शिक्षा संस्कारविहीन हो चुकी है। हनुमान की योगपरक शक्ति, राम की मर्यादा को भुला दिया है। कवियों और साहित्यकारों को समाज और शासन द्वारा सम्मान प्राप्त नहीं है। देश में तुलसी, सूर, निराला, दिनकर, रहीम और रसखान जैसे जनकवियों का अभाव है। गीतों और कविता में मधुमास की सरसता, श्रेष्ठ, काव्य सृजन की शक्ति का ह्रास हो चुका है। इन सभी बातों को सोचकर कवि ने अपना हिन्दुस्तान कहाँ है?’ कहकर उचित समय पर प्रश्न उठाया है। हिन्दुस्तानीयत की रक्षा के सवाल का उत्तर ही भारत राष्ट्र को सुदृढ़ता, सुसम्पन्नता से संयुक्त कर सकता है।

प्रश्न 5.
निम्नांकित पंक्तियों का भाव स्पष्ट कीजिए

(क) हो अगस्त्य, क्या कठिन सुखाना, बाधा का दुर्दम सागर। सम्हल-सम्हल कर चलो वीरवर, तलवारों की धारों पर।
उत्तर-
हे वीरो! तुम्हें किसी भी तरह का मोह भी छू न सके, इसके लिए तुम्हें एक तपस्वी बन जाना चाहिए। तुम्हें लोहे के हृदय वाला हो जाना चाहिए जिससे काल भी भयभीत हो उठे। तुम्हें अत्यन्त पक्के इरादों वाला हो जाना चाहिए। हे वीरवरो! तुम्हें अगस्त्य ऋषि के समान बन जाना चाहिए जिससे बाधाओं के  र्दमनीय (कठिनाई से वश में किए जाने वाला) सागर को भी वश में करना तुम्हारे लिए बिल्कुल भी कठिन नहीं होगा। अतः हे श्रेष्ठ वीरो! तुम्हें सम्हल कर तलवार की धार पर चलना है (चुनौतीपूर्ण कार्य करना है।)

(ख) कविकुल गुरु की सृजन शक्ति का, वह पांवन संस्कार कहाँ है?
फूहड़ गीतों में खोया जो, वह मधुरस शृंगार कहाँ है?
उत्तर-
आज कविकुल गुरु कालिदास की सी काव्य रचना करने की शक्ति पैदा करने के पवित्र संस्कार कहाँ छिप गए हैं। मिठास भरा श्रृंगार रस तो आज के फूहड़ गीतों में खो गया है। मन में उत्साह भर देने वाली कविता की धारा ही कहीं विलुप्त हो गयी है। साथ ही, राजा भोज जैसे साहित्य प्रेमी भी नहीं दीखते जिन्होंने कविता के साहित्यिक विकास को विस्तार दिया था। आज तुलसीदास, सूरदास, सूर्यकान्त त्रिपाठी ‘निराला’ और रामधारी सिंह ‘दिनकर’ जैसे महान कवि भी जन्म नहीं ले रहे जिन्होंने जन-जन में परस्पर आदर्श प्रेम, समता, महानता और राष्ट्रीय एकता के भाव लोगों में भरने के लिए काव्य रचना की। रहीम और रसखान जैसे आदर्श एवं जनकवियों का सर्वत्र अभाव . (कमी) दीख रहा है। आज वास्तव में, ऐसे अपने हिन्दुस्तान की विश्वभर में खोज करनी है कि वे अब कहाँ है ?

प्रश्न 6.
निम्नांकित पंक्तियों का आशय स्पष्ट कीजिए

(क) वाणी तो सभी को मिली हुई है, परन्तु बोलना किसी-किसी को ही आता है।
उत्तर-
लेखक का कथन है कि वाणी (जीभ) सभी को प्राप्त है परन्तु उससे बोलना तो किसी-किसी को ही आता है। बहुत कम लोग बोलना जानते हैं। वाणी का प्रयोग हर कोई ठीक से नहीं कर पाता। ऐसा देखा जाता है कि कुछ लोगों की वाणी से प्रेम झलकता है, तो किसी की बात इतनी चुभने वाली होती है कि झगड़ा हो जाता है। कड़वी बात संसार में कितने ही झगड़े पैदा कर देती है और उसका प्रभाव बहुत ही कष्टकारक होता है। बोलने में मात्र तीन इंच की छोटी जीभ का प्रयोग करते हैं परन्तु उसका प्रभाव इतना विनाशकारी होता है कि उससे छः फीट का लम्बा मनुष्य मर जाता है।

(ख) बाबाजी भी मनुष्य ही थे। अपनी वस्तु की प्रशंसा दूसरे के मुख से सुनने के लिए उनका हृदय अधीर हो गया।
उत्तर-
बाबा भारती भले ही संन्यासी थे लेकिन थे तो मनुष्य ही। अपनी चीज की तारीफ सबको अच्छी लगती है। खड्ग सिंह के मुख से अपने घोड़े की तारीफ सुनने की चाह उनके मन में जाग उठी।

(ग) अब संसार की कोई आकांक्षा मुझे इस स्थान से नहीं हटा सकती, क्योंकि यह मेरा प्यारा देश है और यही मेरी मातृभूमि है। बस, मेरी उत्कट इच्छा यही है कि मैं अपनी प्यारी मातृभूमि 1 में ही अपने प्राण विसर्जन करूँ।
उत्तर-
लेखक का मन अपनी मातृभूमि के प्रेम में रंग गया है। उसके अन्दर किसी भी अन्य वस्तु को याद करने की अब कोई | इच्छा नहीं रह गई है, जिसे प्राप्त करने के लिए वह अपनी मातृभूमि का त्याग कर सके। उसे उसकी मातृभूमि मिल गई है। वह उसकी मातृभूमि ही उसका प्यारा मातृदेश है। उसकी यह हार्दिक इच्छा है कि वह अपने जीवन के शेष समय को यहीं रहकर व्यतीत करे तथा जिस मातृभूमि ने उसे जन्म दिया, जिसका अन्न-जल खा-पीकर बड़ा हुआ, उसी मातृभूमि की पवित्र गोद में रहकर अपने जीवन की इह-लीला समाप्त करे। अपनी प्यारी भूमि में जन्म लेकर उसी की गोद में अपने प्राण त्याग करे।

प्रश्न 7.
‘हार की जीत’ कहानी के अनुरूप हृदय परिवर्तन करने वाली कोई कहानी लिखिए।
उत्तर-
विद्यार्थी स्वयं लिखें।

प्रश्न 8.
निम्नलिखित अपठित गद्यांश को ध्यानपूर्वक पढ़िए और प्रश्नों के उत्तर दीजिए “हिन्दू होते हुए भी शिवा के लिए सभी धर्म पूज्य हैं। इस्लाम के पवित्र स्थान, उसके पवित्र ग्रन्थ सम्मान की वस्तुएँ हैं। शिवा, हिन्दू और मुसलमान प्रजा में कोई भेद नहीं समझता। वह देश में हिन्दू राज्य नहीं, सच्चे स्वराज्य की स्थापना चाहता है। आतताइयों से सत्ता का अपहरण कर उदारचेताओं के हाथों में अधिकार देना चाहता है। फिर पर-स्त्री ! अरे ! पर-स्त्री तो हर एक के लिए माता के समान है।”

1. सभी धर्म किसे पूज्य हैं?
2. शिवा कैसे राज्य की स्थापना करना चाहता है?
3. उपर्युक्त गद्यांश का उचित शीर्षक लिखिए।

उत्तर-

1. शिवा हिन्दू है। लेकिन उसके लिए सभी धर्म पूज्य हैं।
2. शिवा सच्चे स्वराज्य की स्थापना करना चाहता है।
3. ‘शिवा की उदारता’।

MP Board Class 6th Hindi Solutions

MP Board Class 7th Maths Solutions Chapter 12 Algebraic Expressions Ex 12.1

Question 1.
Get the algebraic expressions in the following cases using variables, constants and arithmetic operations.
(i) Subtraction of z from y.
(ii) One-half of the sum of numbers x and y.
(iii) The number z multiplied by itself.
(iv) One-fourth of the product of numbers p and Q.
(v) Numbers x and y both squared and added.
(vi) Number 5 added to three times the product of numbers m and n.
(vii) Product of numbers y and z subtracted from 10.
(viii) Sum of numbers a and b subtracted from their product.
Solution:
(i) y – z
(ii) \(\frac{1}{2}\)(x + y)
(iii) z²
(iv) \(\frac{1}{4}\)(pq)
(v) x² + y²
(vi) 5 + 3 (mn)
(viii) ab – (a + b)

Question 2.
(i) Identify the terms and their factors in the following expressions. Show the terms and factors by tree diagrams.
(a) x – 3
(b) 1 + x + x²
(c) y – y³
(d) 5xy² + 7x²y
(e) -ab + 2b² – 3a²

(ii) Identify terms and factors in the expressions given below:
(a) -4x + 5
(b) -4x + 5y
(c) 5y + 3y²
(d) xy + 2x²y²
(e) pq + q
(f) 1.2ab – 2.4b + 3.6a
(g) \(\frac{3}{4}\)x + \(\frac{1}{4}\)
(h) 0.1p² + 0.2q²
Solution:
(i)

Question 3.
Identify the numerical coefficients of terms (other than constants) in the following expressions:
(i) 5 – 3t²
(ii) 1 + t + t² + t³
(iii) x + 2xy + 3y
(iv) 100m + 1000n
(v) -p²q² + 7pq
(vi) 1.2a + 0.8b
(vii) 3.14 r²
(viii) 2(l + b)
(ix) 0.1y + 0.01y²
Solution:

Question 4.
(a) Identify terms which contains x and give the coefficient of x.
(i) y²x + y
(ii) 13y² – 8yx
(iii) x + y + 2
(iv) 5 + z + zx
(v) 1 + x + xy
(vi) 12xy² + 25
(vii) 7x + xy²
(b) identify terms which contains y² and give the coefficient of y².
(i) 8 – xy²
(ii) 5y² + 7x
(iii) 2x²y – 15xy² + 7y²
Solution:
(a)

Question 5.
Classify into trinomials.
(i) 4y – 7z
(ii) y²
(iii) x + y – xy
(iv) 100
(v) ab – a – b
(vi) 5 – 3t
(vii) 4p²q – 4pq²
(viii) 7mn
(ix) z² – 3z + 8
(x) a² + b²
(xi) z² + z
(xii) 1 + x + x²
Solution:
The monomials, binomials and trinomials have 1, 2 and 3 unlike terms in it respectively.
(i) 4y – 7z Binomial
(ii) y² Monomial
(iii) x + y – xy Trinomial
(iv) 100 Monomial
(v) ab – a – b Trinomial
(vi) 5 – 3t Binomial
(vii) 4p²q – 4pq² Binomial
(viii) 7mn Monomial
(ix) z² – 3z + 8 Trinomial
(x) a² + b² Binomial
(xi) z² + z Binomial
(xii) 1 + x + x² Trinomial

Question 6.
State whether a given pair of terms is of like or unlike terms.
(i) 1,100
(ii) -7x, \(\frac{5}{2}\)x
(iii) -29x, -29y
(iv) 14xy, 42yx
(v) 4m²p, 4mp²
(vi) 12xz, 12x²z²
Solution:
The terms which have same algebraic factors are called like terms. However, when terms have different algebraic factors, these are called unlike terms.
(i) 1,100 Like
(ii) -7x, \(\frac{5}{2}\)x Like
(iii) -29x, -29y Unlike
(iv) 14xy, 42yx Like
(v) 4m²p, 4mp² Unlike
(vi) 12xz, 12x²z² Unlike

Question 7.
Identify like terms in the following:
(a) -xy², -4yx², 8x², 2xy², 7y, -11x², -100x, -11yx, 20x²y, -6x², y, 2xy, 3x
(b) 10pg, 7p, 8q, -p²q², -7qp, – 100q, -23, 12q²p², – 5p², 41, 2405p, 78qp, 13p²g, qp²,701p²
Solution:
(a) -xy² and 2xy²; -4yx² and 20x²y; 8x², -11x² and -6x²; 7y and y, -100x and 3x; -11yx and 2xy

(b) 10pq, -7qp and 78qp; 7p and 2405p; 8q and -100y; -p²q² and 12q²p², -23 and 41; -5p² and 701 p²; 13p2²q and qp²

MP Board Class 7th Maths Solutions

MP Board Class 7th Maths Solutions Chapter 7 Congruence of Triangles Ex 7.1

Question 1.
Complete the following statements:
(a) Two line segments are congruent if ___ .
(b) Among two congruent angles, one has a measure of 70°; the measure of the other angle is ___.
(c) When we write ∠A = ∠B, we actually mean ___.
Solution:
(a) They have the same length.
(b) 70°
(c) m∠A = m∠B

Question 2.
Give any two real-life examples for congruent shapes.
Solution:
(i) Sheets of same letter pad.
(ii) Biscuits in the same packet.

Question 3.
If ∆ABC ≅ ∆FED under the correspondence ABC ⟷ FED, write all the corresponding congruent parts of the triangles.
Solution:
If ∆ABC ≅ ∆FED, then the corresponding angles and sides will be equal to each other.

Question 4.
If ∆DEF ⟷ ∆BCA, write the part(s) of ∆BCA that correspond to
(i) ∠E
(ii) \(\overline{E F}\)
(iii) ∠F
(iv) \(\overline{D F}\)
Solution:
(i) ∠C
(ii) \(\overline{C A}\)
(iii) ∠A
(iv) \(\overline{B A}\)

MP Board Class 7th Maths Solutions

MP Board Class 7th Maths Solutions Chapter 6 The Triangles and Its Properties Ex 6.5

Question 1.
PQR is a triangle, right-angled at P. If PQ= 10 cm and PR = 24 cm, find QR.
Solution:
By applying Pythagoras theorem in ∆PQR,
(PQ)² + (PR)² = (QR)²
⇒ (10)² + (24)² = (QR)2²
⇒ (QR)² = 100 + 576
= 676 = (26)²
∴ QR = 26 cm

Question 2.
ABC is a triangle, right-angled at C. If AB = 25 cm and AC = 7 cm, find BC.
Solution:
By applying Pythagoras theorem in AABC,
(AC)² + (BC)² = (AB)²
⇒ (BC)² = (AB)² – (AC)²
= (25)² – (7)²
= 625 – 49 = 576
= (24)²
∴ BC = 24 cm

Question 3.
A 15 m long ladder reached a window 12 m high from the ground on placing it against a wall at a distance a. Find the distance of the foot of the ladder from the wall.

Solution:
By applying Pythagoras theorem,
(15)² = (12)² + a²
⇒ 225 = 144 + a²
⇒ a² = 225 – 144 = 81 = 9²
⇒ a = 9 m
Therefore, the distance of the foot of the ladder from the wall is 9 m.

Question 4.
Which of the following can be the sides of a right triangle?
(i) 2.5 cm, 6.5 cm, 6 cm.
(ii) 2 cm, 2 cm, 5 cm.
(iii) 1.5 cm, 2 cm, 2.5 cm.
In the case of right-angled triangles, identify the right angles.
Solution:
(i) 2.5 cm, 6.5 cm, 6 cm
∴ (2.5)² = 6.25, (6.5)² = 42.25 and (6)² = 36
It can be observed that,
36 + 6.25 = 42.25
⇒ (6)² + (2.5)² = (6.5)²
The square of the length of one side is the sum of the squares of the lengths of the remaining two sides. Hence, these are the sides of a right-angled triangle. Right angle will be in front of the side of measure 6.5 cm.

(ii) 2 cm, 2 cm, 5 cm
∴ (2)² = 4, (2)² = 4 and (5)² = 25
Here, (2)² + (2)² ≠ (5)²
The square of the length of one side is not equal to the sum of the squares of the lengths of the remaining two sides. Hence, these sides are not of a right-angled triangle.

(iii) 1.5 cm, 2 cm, 2.5 cm
∴ (1.5)² = 2.25, (2)² = 4 and (2.5)² = 6.25
Here, 2.25 + 4 = 6.25
⇒ (1.5)² + (2)² = (2.5)²
The square of the length of one side is the sum of the squares of the lengths of the remaining
two sides. Hence, these are the sides of a right-angled triangle.
Right angle will be in front of the side of measure 2.5 cm.

Question 5.
A tree is broken at a height of 5 m from the ground and its top touches the ground at a distance of 12 m from the base of the tree. Find the original height of the tree.
Solution:
In the drawn figure, BC represents the unbroken part of the tree. Point C represents the point where the tree broke and CA represents the broken part of the tree. Triangle ABC, thus formed, is right-angled at B.

Applying Pythagoras C theorem in ∆ABC,
AC² = BC² + AB²
= (5)²+ (12)² BL
= 25 + 144 = 169
= (13)²
∴ AC = 13 m
Thus, original height of the tree = AC + CB = 13m + 5m = 18m

Question 6.
Angles Q and R of a ∆PQR are 25° and 65°. Write which of the following is true:
(i) PQ² + QR² = RP²
(ii) PQ² + RP² = QR²
(iii) RP² + QR² = PQ²

Solution:
The sum of the measures of all interior angles of a triangle is 180°.
∠P + ∠Q + ∠R = 180°
∠P + 25°+ 65° = 180°
∠P + 90° = 180°
∠P = 180° – 90° = 90°
Therefore, ∆PQR is right-angled at point P. Hence, (PR)² + (PQ)² = (QR)²
∴ (ii) is true.

Question 7.
Find the perimeter of the rectangle whose length is 40 cm and a diagonal is 41 cm.
Solution:
Let ABCD be the given rectangle with length AB = 40 cm and diagonal AC = 41 cm.
In ∆ABC,
(AC)² = (AB)² + (BC)²
⇒ (4)² = (40)²+ (BQ)²
⇒ (BC)² = 1681 – 1600 = 81 = 9²
∴ BC = 9 cm

∴ Perimeter of rectangle = 2(40 + 9)
= 2(49) = 98 cm.

Question 8.
The diagonals of a rhombus measure 16 cm and 30 cm. Find its perimeter.
Solution:
Let ABCD be the given rhombus with diagonals AC = 16 cm and BD = 30 cm.
We know that diagonals of a rhombus bisect each other at right angle.
Let diagonals AC and BD bisects at O.

Hence, perimeter of rhombus = 4 × (17) = 68 cm

MP Board Class 7th Maths Solutions

MP Board Class 7th Maths Solutions Chapter 13 Exponents and Powers Ex 13.3

Question 1.
Write the following numbers in the expanded forms:
279404, 3006194, 2806196, 120719, 20068
Solution:
279404 = 2 × 10⁵ + 7 × 10⁴ + 9 × 10³ + 4 × 10² + 0 × 10¹ + 4 × 10⁰
3006194 = 3 × 10⁶ + 0 × 10⁵ + 0 × 10⁴ + 6 × 10³ + 1 × 10² + 9 × 10¹ + 4 × 10⁰
2806196 = 2 × 10⁶ + 8 × 10⁵ + 0 × 10⁴ + 6 × 10³ + 1 × 10² + 9 × 10¹ + 6 × 10⁰
120719 = 1 × 10⁵ + 2 × 10⁴ + 0 × 10³ + 7 × 10² + 1 × 10¹ + 9 × 10⁰
20068 = 2 × 10⁴ + 0 × 10³ + 0 × 10² + 6 × 10¹ + 8 × 10⁰

Question 2.
Find the number from each of the following expanded forms:
(a) 8 × 10⁴ + 6 × 10³ + 0 × 10² + 4 × 10¹ + 5 × 10⁰
(b) 4 × 10⁵ + 5 × 10³ + 3 × 10² + 2 × 10⁰
(c) 3 × 10⁴ + 7 × 10² + 5 × 10⁰
(d) 9 × 10⁵ + 2 × 10² + 3 × 10¹
Solution:
(a) 8 × 10⁴ + 6 × 10³ + 0 × 10² + 4 × 10¹ + 5 × 10⁰ = 86045
(b) 4 × 10⁵ + 5 × 10³ + 3 × 10² + 2 × 10⁰ = 405302
(c) 3 × 10⁴ + 7 × 10² + 5 × 10⁰ = 30705
(d) 9 × 10⁵ + 2 × 10² + 3 × 10¹ = 900230

Question 3.
Express the following numbers in standard form:
(i) 5,00,00,000
(ii) 70,00,000
(iii) 3,18,65,00,000
(iv) 3,90,878
(v) 39087.8
(vi) 3908.78
Solution:
(i) 50000000 = 5 × 10⁷
(ii) 7000000 = 7 × 10⁶
(iii) 3186500000 = 3.1865 × 10⁹
(iv) 390878 = 3.90878 × 10⁵
(v) 39087.8 = 3.90878 × 10⁴
(vi) 3908.78 = 3.90878 × 1³

Question 4.
Express the number appearing in the following statements in standard form.
(a) The distance between Earth and Moon is 384.0. 000 m.
(b) Speed of light in vacuum is 300,000,000 m/s
(c) Diameter of the Earth is 1,27,56,000 m.
(d) Diameter of the Sun is 1,400,000,000 m.
(e) In a gala×y there are on an average 100,000,000,000 stars.
(f) The universe is estimated to be about 12,0,000,000 years old.
(g) The distance of the Sun from the centre of the Milky Way Gala×y is estimated to be 300,000,000,000,000,000,000 m.
(h) 60, 230, 000, 000, 000, 000, 000, 000 molecules are contained in a drop of water weighing 1.8 gm.
(i) The earth has 1, 353, 000,000 cubic km of sea water.
(j) The population of India was about 1,027,0,000 in March, 2001.
Solution:
(a) 3.84 × 10⁸ m
(b) 3 × 10⁸ m/s
(c) 1.2756 × 10⁷ m
(d) 1.4 × 10⁹ m
(e) 1 × 10¹¹ stars
(f) 1.2 × 10¹¹ years
(g) 3 × 10²⁰ m
(h) 6.023 × 10²² molecules
(i) 1.353 × 10⁹ cubic km
(j) 1.027 × 10⁹

MP Board Class 7th Maths Solutions

MP Board Class 6th Hindi Sugam Bharti Solutions Chapter 19 मीरा पदावली

MP Board Class 6th Hindi Sugam Bharti Chapter 19 प्रश्न अभ्यास

वस्तुनिष्ठ प्रश्न

प्रश्न 1.
(क) सही जोड़ी बनाइए.
1. सांवरी – (क) मूरत
2. कंगना के – (ख) कंवल।
3. मोहनी – (ग) सूरत
4. चरण – (घ) झनकारे
उत्तर-
1. (ग),
2. (घ),
3. (क),
4. (ख)

प्रश्न (ख)
दिए गए शब्दों में से उपयुक्त शब्द चुनकर रिक्त स्थानों की पूर्ति कीजिए-
1. बसो मोरे नैनन में …………………………..। (गोपाल/नंदलाल)
2. उठो लालजी ………………………….. भयो है। (भोर/शोर)
3. द्रोपदी की लाज रखी तुम ………………………….. चीर। (बढ़ायो/चलायो)
4. छुद्र घंटिका ………………………….. तट शोभित। (कटि/बैनी),
उत्तर-
1. नंदलाल,
2. भोर,
3. बढ़ायो,
4. कटि।

MP Board Class 6th Hindi Sugam Bharti Chapter 19 अति लघु उत्तरीय प्रश्न

प्रश्न 2.
निम्नलिखित प्रश्नों के उत्तर एक-एक वाक्य में दीजिए

(क) गोपी सुबह-सुबह क्या मथती है?
उत्तर-
गोपी सुबह-सुबह दही मथती है।

(ख) मीरा हरि से क्या कहने के लिए कह रही है?
उत्तर-
मीरा हरि से लोगों के कष्ट हरने के लिए कह रही है।

(ग) भक्त के कारण हरि ने कौन-सा रूप धारण किया था?
उत्तर-
भक्त के कारण हरि ने नरहरि का रूप धारण किया था।

(घ) ग्वाल-बाल किन शब्द का उच्चारण कर रहे हैं?
उत्तर-
ग्वाल-बाल जय-जय शब्द का उच्चारण कर रहे हैं?

(ङ) मीरा नंदलाल को कहाँ बसाना चाहती है?
उत्तर-
मीरा नंदलाल को अपनी आँखों में बसाना चाहती हैं।

MP Board Class 6th Hindi Sugam Bharti Chapter 19 लघु उत्तरीय प्रश्न

प्रश्न 3.
निम्नलिखित प्रश्नों के उत्तर तीन-से-पाँच वाक्यों में दीजिए

(क) मीरा ने वंशीवाले को जगाने के लिए भोर के किन-किन क्रियाकलापों का वर्णन किया है?
उत्तर-
मीरा ने वंशी वाले को जगाने के लिए कहा है कि घरों के द्वार खुल गए हैं। गोपियों के दही मथने से उनके कंगन की आवाज आ रही है। द्वार पर देवता और मनुष्य खड़े हैं। ग्वाल-बाल जय-जय शब्द का उच्चारण करते हुए कोलाहल मचा रहे हैं।

(ख) मीरा के पद के आधार पर श्रीकृष्ण के रूप सौंदर्य का वर्णन कीजिए।
उत्तर-
कृष्ण की बड़ी-बड़ी आँखें, सांवरी सूरत और मूरत मन मोहने वाली है। उनके होठों पर सुशोभित मुरली अमृत रस बरसा रही है। उनके हृदय पर वैजयंती माला और कमर में छोटी-सी घंटी सुशोभित है। उनकी पायल मधुर ध्वनि कर रही है।

(ग) मीरा ने प्रभु से ‘संतन सुखदाई’ क्यों कहा है?
उत्तर-
मीरा के प्रभु भक्त वत्सल हैं। वे संतों को सुख देने वाले हैं। इसलिए मीरा ने प्रभु से ‘संतन सुखदाई’ कहा है।

(घ) द्रोपदी की लाज कृष्ण भगवान ने किस तरह बचाई थी?
उत्तर-
कृष्ण भगवान ने द्रोपदी के वस्त्र बढ़ा कर उनकी लाज बचाई थी। दुःशासन उनके वस्त्र खींचते-खींचते थक कर चूर हो गया, परंतु ईश्वर की कृपा से द्रौपदी के वस्त्र कम नहीं हुए, बढ़ते ही गए।

(ङ) कौन-कौन से उदाहरण देकर मीरा मनुष्यों की पीर दूर करने की प्रार्थना कर रही है?
उत्तर-
मीरा उदाहरण देती हैं कि प्रभु ने वस्त्र बढ़ाकर द्रौपदी की लाज रख ली। भक्त के कारण नरहरि का रूप धरा। हिरण्यकशिपु का वध किया। ऐसे ही तुम मनुष्यों की पीर दूर करो।

भाषा की बात

प्रश्न 4.
निम्नलिखित शब्दों का शुद्ध उच्चारण कीजिए
कंगन, मुरली, नूपुर, सुधारस, प्रभु, क्षुद्र, वैजन्तीमाला, हिरण्यकश्यपु।
उत्तर-
छात्र स्वयं करें।

प्रश्न 5.
निम्नलिखित शब्दों की वर्तनी शुद्ध कीजिए-
सूखदाई, कंगना, गिरीधर, मुरत, वीसाल, दोपदी।
उत्तर-
सुखदाई, कंगना, गिरिधर, मूरत, विशाल, द्रौपदी

प्रश्न 6.
निम्नलिखित शब्दों के दो-दो पर्यायवाची लिखिएरजनी, भोर, सुर, नर, नैन, कंवल
उत्तर-
पर्यायवाची-निशा, रैन, उषा, प्रातः, देव, देवता, मनुष्य, मानव, नेत्र, लोचन, सरोज, जलज

प्रश्न 7.
निम्नलिखित शब्दों के मानक रूप लिखिए-
मोरे, ठाढ़े, सबद, उचारे, छुद्र, सोभित
उत्तर-
मानक शब्द-मेरे, खड़े, शब्द, बोले, अच्छा, शोभायमान।

प्रश्न 8.
निम्नलिखित शब्दों के तत्सम रूप लिखिएदही, दूध, नैन, कान, ओठ
उत्तर-
तत्सम-दधि, दुग्ध, नेत्र, कण, ओष्ठ। निम्नलिखित गद्यांश को पढ़िए “आत्मा व परमात्मा ज्योति स्वरूप है। यह स्मरण रखने के लिए शुभ कार्यों में सर्वप्रथम दीपक प्रज्जवलित किया जाता है। इसकी लौ कर एकटक ध्यान करने से एकाग्रता व स्मरण शक्ति बढ़ती है। और यह प्रेरणा मिलती है कि ऊपर की ओर उठती हुई लौ के समान हम भी उच्च कर्म करें और चारों ओर ऊर्जा और ज्ञान का प्रकाश बिखेरें। दीपक स्वयं जलकर त्याग और बलिदान की प्रेरणा देता है।”।

प्रश्न 9.
उपर्युक्त गद्यांश में से संज्ञा, सर्वनाम, क्रिया एवं विशेषण शब्दों को छाँटकर लिखें-
उत्तर-

मीरा पदावली प्रसंग सहित व्याख्या

1. जागो बंसी बारे ललना, जागो मोरे प्यारे।
रजनी बीती भोर भयो है, घर-घर खुले किनारे।
गोपी दही मथत सुनियत हैं, कंगना के झनकारे।।
उठो लालजी भोर भयो है, सुर-नर ठाढ़े द्वारे।
ग्वाल बाल सब करत कुलाहल, जय जय सबद उचारे॥

शब्दार्थ-जागो-उठो। ललना-प्यारा बच्चा। बंसी= बांसुरी। रजनी = रात। भोर = सुबह। किवारे दरवाजे। झनकारे = झनकार, आवाज। सुर = देव। सबद-शबद। उचारे उच्चारित किए, बोले।

प्रसंग-प्रस्तुत पंक्तियाँ हमारी पाठ्य पुस्तक सुगम भारती-6 में संकलित ‘मीरा पदावली’ से ली गई हैं। इन पंदों में मीरा कृष्ण को जगा रही हैं।

व्याख्या-मीरा कहती हैं मेरे बंसी वाले प्यारे बाल कृष्ण, जागो। रात बीत चुकी है, सुबह हो गयी है और घर-घर के दरवाजे खुल गए हैं। गोपियों के कंगन की झनकार से लगता है वे दही मथ रहीं हैं। सुबह हो गई है। देवता-मनुष्य द्वारा पर खड़े हैं। ग्वाल-बाल सब शोर कर रहे हैं और जय-जय शब्द का उच्चारण कर रहे हैं।

विशेष-
1. भक्ति भाव की महत्ता है।
2. पद लयात्मक तथा संगीतात्मक है।

2. बसो मोरे नैनन में नंदलाल।
मोहनी मूरत सांवरी सूरत, नैना बने बिसाल।
अधर सुधारस मुरली राजति, उर बैजनीमाल।
छुद्र घटिका कटि तट शोभित, नूपुर सबद रसाल।
मीरा प्रभु संतन सुखदाई, भगत-बछल गोपाल॥

शब्दार्थ–बसो-निवास करो। मोरे मेरे। मोहनी-मन को मोहने वाली। सांवरी-सांवली.। बिसाल-सुशोभित। उर हृदय। कटि=कमर। तट-किनारा। नूपुर-पायल। सबद:शब्द। रसाल-मधुर। भगन-बछल-भक्त -वत्सल।

प्रसंग-पूर्ववत्

व्याख्या-मीरा कृष्ण को अपनी आंखों में बस जाने के लिए कहती हैं। कृष्ण के बड़े-बड़े नैन, सांवरी सूरत और मूरत मन मोहने वाली है। उनके होंठों पर सुशोभित – मुरली अमृतरस बरसा रही है। उनके हृदय पर वैजयंतीमाला और कमर पर छोटी-सी घंटी सुशोभित है। उनकी पायल मधुर ध्वनि कर रही है। मीरा के प्रभु संतों को सुख देने वाले और भक्त-वत्सल गोपाल हैं।

विशेष-
1. ईश्वर के रूप का वर्णन है।
2. वृत्यनुप्रास अलंकार का प्रयोग है।
3. पद लयात्मक तथा संगीतात्मक हैं।

MP Board Class 6th Hindi Solutions

MP Board Class 7th Maths Solutions Chapter 6 The Triangles and Its Properties Ex 6.4

Question 1.
Is it possible to have a triangle with the following sides?
(i) 2 cm, 3 cm, 5 cm
(ii) 3 cm, 6 cm, 7 cm
(iii) 6 cm, 3 cm, 2 cm
Solution:
In a triangle, the sum of the lengths of either two sides is always greater than the third side.
(i) Given that, the sides of the triangle are 2 cm, 3 cm, 5 cm.
It can be observed that,
(2 + 3) cm = 5 cm
However, 5 cm = 5 cm
Hence, this triangle is not possible.

(ii) Given that, the sides of the triangle are
3 cm, 6 cm, 7 cm.
Here, (3 + 6) cm = 9 cm > 7 cm
(6 + 7) cm = 13 cm > 3 cm
(3 + 7) cm = 10 cm > 6 cm
Hence, this triangle is possible.

(iii) Given that, the sides of the triangle are
6 cm, 3 cm, 2 cm.
Here, (6 + 3) cm = 9 cm > 2 cm
However, (3 + 2) cm = 5 cm < 6 cm Hence, this triangle is not possible.

Question 2.
Take any point 0 in the interior of a triangle PQR. Is

(i) OP + OQ > PQ?
(ii) OQ + OR > QR?
(iii) OR + OP > RP?
Solution:
If O is a point in the interior of a given triangle, then three triangles ∆OPQ, ∆OQR and ∆ORP can be constructed. In a triangle, the sum of the lengths of either two sides is always greater than the third side.
(i) Yes, as OQR is a triangle with sides OR, OQ and QR.

∴ OQ + OR> QR

(ii) Yes, as OQR is a triangle sides OR, OQ and QR.
∴ OQ + OR > QR

(iii) Yes, as A ORP is a triangle with sides OR, OP and PR.
∴ OR + OP > PR

Question 3.
AM is a median of a triangle ABC.
Is AB + BC + CA > 2AM?
(Consider the sides of ∆ABM and ∆AMC.)

Solution:
In a triangle, the sum of the lengths of either two sides is always greater than the third side.
In ∆ABM,
AB + BM > AM …(i)
Similarly, in ∆ACM,
AC + CM > AM …(ii)
Adding (i) and (ii), we obtain
AB + BM + MC +AC > AM + AM
AB + BC + AC > 2AM
Yes, the given expression is true.

Question 4.
ABCD is a quadrilateral.

Is AB + BC + CD + DA > AC + BD ?
Solution:
In a triangle, the sum of the lengths of either two sides is always greater than the third side.
In ∆ABC; AB + BC > CA …(i)
In ∆BCD; BC + CD > DB …(ii)
In ∆CDA; CD + DA > AC …(iii)
In ∆DAB; DA + AB > DB …(iv)
Adding (i), (ii), (iii) and (iv), we obtain
AB + BC + BC + CD + CD + DA + DA+ AB > AC + BD + AC + BD
⇒ 2AB + 2BC + 2CD + 2DA > 2AC + 2BD ⇒ 2{AB + BC + CD + DA) > 2(AC+BD)
⇒ (AB + BC + CD + DA) > (AC + BD)
Yes, the given expression is true.

Question 5.
ABCD is a quadrilateral.

Is AB + BC + CD + DA < 2(AC + BD)?
Solution:
In a triangle, the sum of the lengths of either two sides is always greater than the third side.
Let diagonals AC and BD of the quadrilateral ABCD intersects at O.

In ∆OAB, OA + OB > AB … (i)
In ∆OBC, OB + OC > BC … (ii)
In ∆OCD, OC + CD > CD … (iii)
In ∆ODA, OD + OA > DA … (iv)
OA + OB + OB + OC + OC + OD + OD + OA > AB + BC + CD + DA
⇒ 20A + 20B + 20C + 20D > AB + BC + CD + DA
⇒ 2(OA + OC) + 2(OB + OD) > AB + BC + CD + DA
⇒ 2(AC) + 2(BD) > AB + BC + CD + DA
⇒ 2(AC + BD) > AB + BC + CD + DA
Yes, the given expression is true.

Question 6.
The lengths of two sides of a triangle are 12 cm and 15 cm. Between what two measures should the length of the third side fall?
Solution:
In a triangle, the Sum of the lengths of either two side is always greater than the third side.
Lengths of two sides of a triangle are 12 cm and 15 cm.
Let the third side be x cm.
∴ x + 12 > 15 ⇒ x > 3
x + 15 > 12 ⇒ x > – 3 but side length never be negative.
and 12 + 15 > x ⇒ 27 > x
Hence, third side can measure between 3 and 27.

MP Board Class 7th Maths Solutions

MP Board Class 7th Maths Solutions Chapter 13 Exponents and Powers Ex 13.2

Question 1.
Using laws of exponents, simplify and write the answer in exponential form:
(i) 3² × 3⁴ × 3⁸
(ii) 6¹⁵ ÷ 6¹⁰
(iii) a³ × a²
(iv) 7^x × 7²
(v) (5²)³ 4 5³
(vi) 2⁵ × 5⁵
(vii) a⁴ × b⁴
(viii) (3⁴)³
(ix) (2²⁰ ÷ 2¹⁵) × 2³
(x) (8^t ÷ 8²)
Solution:
(i) 3² × 3⁴ × 3⁸ = (3)^{2 + 4 + 8} = 3¹⁴ [∵ a^m × aⁿ = a^m+n]
(ii) 6¹⁵ ÷ 6¹⁰ = (6)^{15 – 10} = 6⁵ [∵ a^m ÷ aⁿ = a^{m – n}]
(iii) a³ × a² = a^{3 + 2} = a⁵[∵ a^m × aⁿ = a^m+n]
(iv) 7^x × 7² = 7^{x + 2}[∵ a^m × aⁿ = a^m+n]
(v) (5²)³ ÷ 5³ = 5^{2 × 3} ÷ 5³ [∵ (a^m)ⁿ = a^mn]
= 5⁶ ÷ 5³ = 5^{(6 – 3)} [∵ a^m ÷ aⁿ = a^{m – n}]
= 5³
(vi) 2⁵ × 5⁵ = (2 × 5)⁵      [∵ a^m × b^m = (a × b)^m]
= 10⁵
(vii) a⁴ × b⁴ = (ab)⁴
(viii) (3⁴)³ = 3^{4 × 3} = 3¹²       [∵ (a^m)ⁿ = a^mn]
(ix) (2²⁰ ÷ 2¹⁵) × 2³ = (2^{20 – 15}) × 2³     [∵ a^m ÷ aⁿ = a^{m – n}]
= 2⁵ × 2³ = 2^{5 + 3} [∵ a^m × aⁿ = a^m+n]
(x) 8^t ÷ 8² = 8^{(t – 2)}    [∵ a^m ÷ aⁿ = a^{m – n}]

Question 2.
Simplify and express each of the following in exponential form:

Solution:

(ii) [(5²)³ × 5⁴] ÷ 5⁷
= [5^{2 × 3} × 5⁴] ÷ 5⁷ [∵ (a^m)ⁿ = a^mn]
= [5⁶ × 5⁴] ÷ 5⁷ [∵ a^m × aⁿ = a^{m + n}]
= [5^{6 + 4}] ÷ 5⁷
= 5¹⁰ ÷ 5⁷
= 5^{10 – 7} [∵ a^m ÷ aⁿ = a^{m – n}]
= 5³

(iii) 25⁴ ÷ 5³ = (5 × 5)⁴ ÷ 5³
= (5²)⁴ ÷ 5³ = 5^{2 × 4} ÷ 5³ [∵ (a^m)ⁿ = a^mn]
= 5⁸ ÷ 5³ = 5^{8 – 3} [∵ a^m ÷ aⁿ = a^{m – n}]
= 5⁵

(vi) 2⁰ + 3⁰ + 4⁰ = 1 + 1 + 1 = 3     [∵ a⁰ = 1]
(vii) 2⁰ × 3⁰ × 4⁰ = 1 × 1 × 1 = 1
(viii) (3⁰ + 2⁰) × 5⁰ = (1 + 1) × 1 = 2

Question 3.
Say true or false and justify your answer:
(i) 10 × 10¹¹ = 100¹¹
(ii) 2³ > 5²
(iii) 2³ × 3² = 6⁵
(iv) 3⁰ = (1000)⁰
Solution:
(i) L.H.S = 10 × 10¹¹
= 10^{1 + 11} = 10¹²
R.H.S = 100¹¹ = (10 × 10)¹¹ = (10⁰)¹¹ = 10^{2 × 11} = 10²²
⇒ L.H.S. ≠ R.H.S.
Hence, the given statement is false.

(ii) 2³ > 5²
L.H.S. = 2³ = 2 × 2 × 2 = 8
R.H.S. = 5³ = 5 × 5 = 25
⇒ L.H.S ≠ R.H.S
Hence, the given statement is false.

(iii) 2³ × 3² = 6⁵
L.H.S. = 2³ × 3² = 2 × 2 × 2 × 3 × 3 = 72
R.H.S. = 6⁵ = 6 × 6 × 6 × 6 × 6 = 7776
⇒ L.H.S. ≠ R.H.S.
Hence, the given statement is false.

(iv) 3⁰ = (1000)⁰
L.H.S. = 3⁰ = 1
R.H.S. = (1000)⁰ = 1
⇒ L.H.S. = R.H.S.
Hence, the given statement is true.

Question 4.
Express each of the following as a product of prime factors only in exponential form:
(i) 108 × 192
(ii) 270
(iii) 729 × 64
(iv) 768
Solution:
(i) 108 × 192
= (2 × 2 × 3 × 3 × 3) × (2 × 2 × 2 × 2 × 2 × 2 × 3)
= (2² × 3³) × (2⁶ × 3)
= 2²⁺⁶ × 3³⁺¹ = 2⁸ × 3⁴
(ii) 270 = 2 × 3 × 3 × 3 × 5 = 2 × 3³ × 5
(iii) 729 × 64 = (3 × 3 × 3 × 3 × 3 × 3) × (2 × 2 × 2 × 2 × 2 × 2) = 3⁶ × 2⁶
(iv) 768 = 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 3 = 2⁸ × 3

Question 5.
Simplify:

Solution:

MP Board Class 7th Maths Solutions