MP Board Class 8th Maths Solutions Chapter 7 Cube and Cube Roots Ex 7.1
Question 1.
Which of the following numbers are not perfect cubes?
(i) 216
(ii) 128
(iii) 1000
(iv) 100
(v) 46656
Solution:
(i) 216 = 2 × 2 × 2 × 3 × 3 × 3
Since, all the prime factors of 216 appear in a group of three.
∴ 216 is a perfect cube.
(ii) 128 = 2 × 2 × 2 × 2 × 2 × 2 × 2
Since, all the prime factors of 128 doesn’t appear in a group of three.
∴ 128 is not a perfect cube.
(iii) 1000 = 2 × 2 × 2 × 5 × 5 × 5
Since, all the prime factors of 1000 appear in a group of three.
∴ 1000 is a perfect cube.
(iv) 100 = 2 × 2 × 5 × 5.
Since, all the prime factors of 100 doesn’t appear in group of three.
∴ 100 is not a perfect cube.
(v) 46656 = 2 × 2 × 2 × 2 × 2 × 2 × 3 × 3 × 3 × 3 × 3 × 3
Since, all the prime factors of 46656 appear in a group of three.
∴ 46656 is a perfect cube.
![]()
Question 2.
Find the smallest number by which each of the following numbers must be multiplied to obtain a perfect cube.
(i) 243
(ii) 256
(iii) 72
(iv) 675
(v) 100
Solution:
(i) 243 = 3 × 3 × 3 × 3 × 3
Clearly, the prime factor 3 doesn’t appear in a group of three.
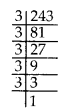
∴ 243 is not a perfect cube.
So, to make 243 a perfect cube, we multiply it by 3.
In that case
243 × 3 = 3 × 3 × 3 × 3 × 3 × 3 = 729, which is a perfect cube.
(ii) 256 = 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2
Clearly, the prime factor 2 doesn’t appear in a group of three.
256 is not a perfect cube.

So, to make 256 a perfect cube, we multiply it by 2.
In that case
256 × 2 = 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 = 512, which is a perfect cube.
(iii) 72 = 2 × 2 × 2 × 3 × 3
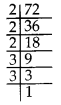
Clearly, the prime factor 3 doesn’t appear in a group of three.
∴ 72 is not a perfect cube.
So, to make 72 a perfect cube, we multiply it by 3.
In that case
72 × 3 = 2 × 2 × 2 × 3 × 3 × 3 = 216, which is a perfect cube.
(iv) 675 = 3 × 3× 3 × 5 × 5
Clearly, the prime factor 5 doesn’t appear in a group of three.
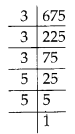
∴ 675 is not a perfect cube.
So, to make 675 a perfect cube, we multiply it by 5.
In that case
675 × 5 = 3 × 3× 3 × 5 × 5 × 5
= 3375, which is a perfect cube.
(v) 100 = 2 × 2 × 5 × 5
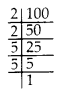
Clearly, both the prime factors 2 and 5 doesn’t appear in a group of three.
∴ 100 is not a perfect cube.
So, to make 100 a perfect cube, we multiply it by 2 × 5 = 10.
In that case
100 × 2 × 5 = 2 × 2 × 2 × 5 × 5 × 5 = 1000, which is a perfect cube.
![]()
Question 3.
Find the smallest number by which each of the following numbers must be divided to obtain a perfect cube.
(i) 81
(ii) 128
(iii) 135
(iv) 192
(v) 704.
Solution:
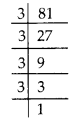
(i) 81 = 3 × 3 × 3 × 3
Clearly, the prime factor 3 doesn’t appear in a group of three.
∴ 81 is not a perfect cube.
So, to make it a perfect cube, we must divide it by 3.
![]()
which is a perfect cube.
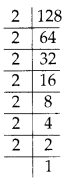
(ii) 128 = 2 × 2 × 2 × 2 × 2 × 2 × 2
Clearly, the prime factor 2 doesn’t appear in a group of three.
∴ 128 is not a perfect cube.
So, to make it a perfect cube, we must divide it by 2.
![]()
= 64,
which is a perfect cube.
(iii) 135 = 3 × 3 × 3 × 5
Clearly, the prime factor 5 doesn’t appear in a group of three.
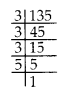
∴ 135 is not a perfect cube.
So, to make it a perfect cube, we must divide it by 5.
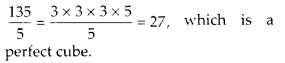
Thus the smallest number is 5 by which 135 must be divided.
(iv) 192 = 2 × 2 × 2 × 2 × 2 × 2 × 3
Clearly, the prime factor 3 doesn’t appear in a group of three.
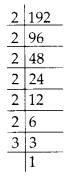
∴ 192 is not a perfect cube.
So, to make it a perfect cube, we must divide it by 3.
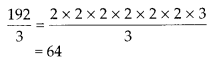
which is a perfect cube.
(v) 704 = 2 × 2 × 2 × 2 × 2 × 2 × 11
Clearly, the prime factor 11 doesn’t appear in a group of three.
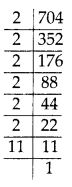
∴ 704 is not a perfect cube.
So, to make it a perfect cube, we must divide it by 11.
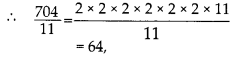
which is a perfect cube.
![]()
Question 4.
Parikshit makes a cuboid of plasticine of sides 5 cm, 2 cm, 5 cm. How many such cuboids will he need to form a cube?
Solution:
We have cuboid of dimensions 2 × 5 × 5
Clearly, in above, the prime factors 2 and 5 both doesn’t appear in a group of three,
∴ To make it a perfect cube, we need to multiply it by 2 × 2 × 5.
2 × 5 × 5 × 2 × 2 × 5 = 2 × 2 × 2 × 5 × 5 × 5
= 1000, which is a perfect cube.
Thus, Prikshit need 20 cuboids to form a cube.