MP Board Class 7th Maths Solutions Chapter 2 Fractions and Decimals Ex 2.1
Question 1.
Solve:
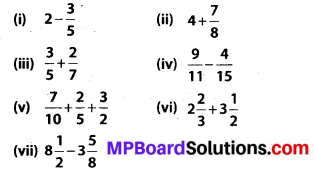
Solution:
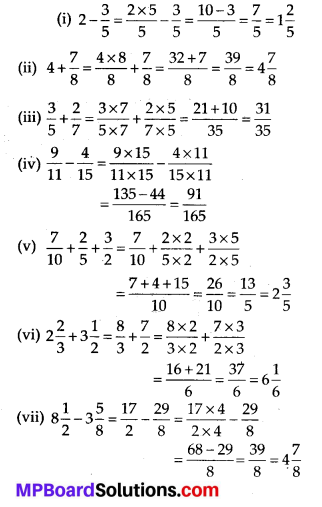
Question 2.
Arrange the following in descending order:

Solution:
(i)
\(\frac{2}{9}, \frac{2}{3}, \frac{8}{21}\)
Converting them into like fractions, we obtain

Converting them into like fractions, we obtain

Question 3.
In a “magic square”, the sum of the numbers in each row, in each column and along the diagonals is the same. Is this a magic square?
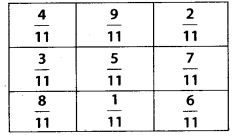
(Along the first row \(\frac{4}{11}+\frac{9}{11}+\frac{2}{11}=\frac{15}{11}\)).
Solution:
Sum along the first row

Since, the sum of the numbers in each row, in each column and along the diagonals is the same.
Yes, it is a magic square.
![]()
Question 4.
A rectangular sheet of paper is \(12 \frac{1}{2}\) cm long and \(10 \frac{2}{3}\) cm wide. Find its perimeter.
Solution:
Length = \(12 \frac{1}{2}\) cm = \(\frac{25}{2}\) cm and
Breadth \(=10 \frac{2}{3} \mathrm{cm}=\frac{32}{3} \mathrm{cm}\)
Perimeter = 2 × (Length + Breadth)

Question 5.
Find the perimeters of
(i) ∆ABE
(ii) the rectangle BCDE in this figure. Whose perimeter is greater?
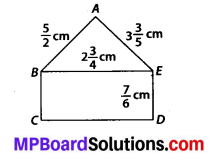
Solution:
(i) Perimeter of rectangle
∆ABE = AB + BE + EA
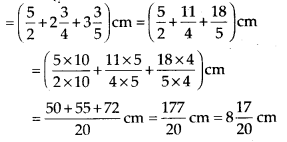
(ii) Perimeter of rectangle BCDE = 2(BE+DE)


So, \(\frac{177}{20}>\frac{47}{6}\)
Thus, perimeter of ∆ABE is greater
![]()
Question 6.
Salil wants to put a picture in a frame. The picture is \(7 \frac{3}{5}\) cm wide. To fit in the frame the picture cannot be more than \(7 \frac{3}{10}\) cm wide. How much should the picture be trimmed?
Solution:

Question 7.
Ritu ate 2 part of an apple and the remaining apple was eaten by her brother Somu. How much part of the apple did Somu eat? Who had the larger share? By how much?
Solution:
Part of an apple eaten by Ritu = \(\frac{3}{5}\)
Part of an apple eaten by Somu = 1 – (Part of an apple eaten by Ritu)

![]()
Question 8.
Michael finished colouring a picture in \(\frac{7}{12}\) hour. Vaibhav finished colouring the same picture in \(\frac{3}{4}\) hour. Who worked longer?
Solution:
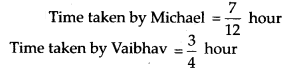
Converting these fractions into like fractions, we obtain
