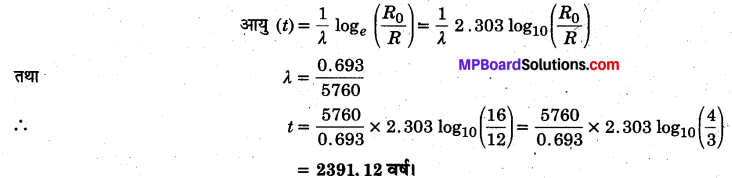MP Board Class 12th Physics Solutions Chapter 13 नाभिक
नाभिक NCERT पाठ्यपुस्तक के अध्याय में पाठ्यनिहित प्रश्न एवं उनके उत्तर
• अभ्यास के प्रश्न हल करने में निम्नलिखित आँकड़े आपके लिए उपयोगी सिद्ध होंगे :
e = 1.6×10-19 कूलॉम,
N = 6.023x 1023 प्रति मोल,
\(\frac{1}{4 \pi \varepsilon_{0}}\) = 9 x 109 न्यूटन-मीटर2/कूलॉम’2,
k= 1.381 x 1023 जूल/केल्विन,
1 मिलियन इलेक्ट्रॉन-वोल्ट = 1.6 x 10-13 जूल
1u = 931 मिलियन इलेक्ट्रॉन-वोल्ट,
1 year = 3.154 x 107 सेकण्ड,
mp = 1.007825
mH = 1.007823u
mn = 1.008665 u,
m(_{2}^{4} \mathrm{He}) = 4.002603u,
me = 0.000548u.
प्रश्न 1.
(a) लीथियम के दो स्थायी समस्थानिकों को \(_{3}^{6} \mathbf{L i}\) एवं \(_{3}^{7} \mathbf{L i}\) की बहुलता का प्रतिशत क्रमशः 7.5 एवं 92.5 है। इन समस्थानिकों के द्रव्यमान क्रमशः 6.01512 u एवं 7.01600 u हैं। लीथियम का परमाणु द्रव्यमान ज्ञात कीजिए।
(b) बोरॉन के दो स्थायी समस्थानिक \(\begin{array}{c}{10} \\ {5}\end{array}\)B एवं \(\begin{array}{l}{11} \\ {5}\end{array}\)B हैं। उनके द्रव्यमान क्रमशः 10.01294u एवं 11.00931u एवं बोरॉन का परमाणु भार 10.811u है। Bएवं VB की बहुलता ज्ञात कीजिए।
हल
(a) माना लीथियम के किसी नमूने में 100 परमाणु लिए गए हैं, तब इनमें 7.5 परमाणु \(_{3}^{6} \mathbf{L i}\) के तथा 92.5 परमाणु \(_{3}^{7} \mathbf{L i}\) के होंगे। .
∴ 100 परमाणुओं का द्रव्यमान = (7.5 x 6.01512+ 92.5 x 7.01600)u
= (45.1134 + 648.98)u= 694.0934u
∴ लीथियम का औसत परमाणु द्रव्यमान =
![]()
\(\frac { 694.0934 }{ 100 }\) = 6.940934u
≈ 6.941u
(b) माना बोरॉन के दो समस्थानिकों की बहुलता क्रमश: x% तथा y% है, तब
x+ y= 100
यदि बोरॉन के 100 परमाणु लिए जाएँ तो इनमें x परमाणु \(\begin{array}{c}{10} \\ {5}\end{array}\)B के तथा y परमाणु \(\begin{array}{l}{11} \\ {5}\end{array}\)B के होंगे।
∴ बोरॉन का परमाणु द्रव्यमान =
![]()
⇒ 10.811 = \(\frac { x×10.01294 + y × 11.00931 }{ 100 }\)
था 10.811×100 = 10.01294x + 11.00931 (100-x) [∵ x+ y = 100]
⇒ 1081.1-1100.931 = 10.01294x – 11.00931x
⇒ -19.831= – 0.99637x
∴ x = \(\frac { -19.831 }{ -0.99637 }\) = 19.9 .
∴ y = 100-x= 100 – 19.9 = 80.1
अत: बोरॉन में \(\begin{array}{c}{10} \\ {5}\end{array}\)B तथा \(\begin{array}{l}{11} \\ {5}\end{array}\)B समस्थानिकों की बहुलता प्रतिशत क्रमश: 19.9 तथा 80.1 हैं।
![]()
प्रश्न 2.
नियॉन के तीन स्थायी समस्थानिकों की बहुलता क्रमशः 90.51%, 0.27% एवं 9.22% है। इन समस्थानिकों के परमाणु द्रव्यमान क्रमशः 19.99u, 20.99u एवं 21.99u हैं। नियॉन का औसत परमाणु द्रव्यमान ज्ञात कीजिए।
हल
यदि नियॉन के 100 परमाणु लिए जाएँ तो उनमें नियॉन के तीन समस्थानिकों के क्रमश: 90.51 परमाणु, 0.27 परमाणु तथा 9.22 परमाणु होंगे।
∴ नियॉन का औसत परमाणु द्रव्यमान = \(\frac { (90.51 × 19.99 + 0.27 × 20.99+9.22 × 21.99)u }{ 100 }\)
= \(\frac { (1809.2949+ 5.6673+ 202.7478)u }{ 100 }\) = \(\frac { 2017.71 }{ 100 }\)
= 20.177u ≈ 20. 18u
प्रश्न 3.
नाइट्रोजन नाभिक (\(_{7}^{14} \mathrm{N}\)) की बन्धन ऊर्जा मिलियन इलेक्ट्रॉन-ऊर्जा में ज्ञात कीजिए। mr = 14.00307u
हल
दिया है : न्यूट्रॉन का द्रव्यमान mn = 1.00867u, प्रोटॉन का द्रव्यमान mp = 1.00783u
\(_{7}^{14} \mathrm{N}\) नाभिक का द्रव्यमान mN = 14.00307u
∴ \(_{7}^{14} \mathrm{N}\) नाभिक 7 प्रोटॉनों तथा 7 न्यूट्रॉनों से मिलकर बना है।
∴ \(_{7}^{14} \mathrm{N}\) नाभिक में उपस्थित न्यूक्लिऑनों का द्रव्यमान
= 7mp + 7mn
= 7 × 1.00783 + 7 × 1.00867
= 14.1155u
∴ \(_{7}^{14} \mathrm{N}\) की द्रव्यमान क्षति Δ m = न्यूक्लिऑनों का द्रव्यमान — नाभिक का द्रव्यमान
= 14.11550- 14.00307 = 0.11243u
1u = 931 MeV
∴ \(_{7}^{14} \mathrm{N}\) नाभिक की बन्धन ऊर्जा = Δ m × 931 = 0.11243 × 931
= 104.67
≈ 104.7 मिलियन इलेक्ट्रॉन-वोल्ट।
प्रश्न 4.
निम्नलिखित आँकड़ों के आधार पर \(\begin{array}{l}{56} \\ {26}\end{array} \mathbf{F} \mathbf{e}\) एवं \(\begin{array}{l}{209} \\ {83}\end{array}\)Bi नाभिकों की बन्धन ऊर्जा प्रति न्यूक्लिऑन मिलियन इलेक्ट्रॉन-वोल्ट में ज्ञात कीजिए। m (\(\begin{array}{l}{56} \\ {26}\end{array} \mathbf{F} \mathbf{e}\)) = 55.934939u, m (\(\begin{array}{l}{209} \\ {83}\end{array}\)Bi) = 208.980388u.
हल
दिया है, प्रोटॉन का द्रव्यमान mp = 1.007825u
न्यूट्रॉन का द्रव्यमान mn = 1.008665u
(i) \(\begin{array}{l}{56} \\ {26}\end{array} \mathbf{F} \mathbf{e}\) नाभिक का द्रव्यमान mFe = 55.934939u
इस नाभिक में 26 प्रोटॉन तथा (56- 26) = 30 न्यूट्रॉन हैं।
∴ न्यूक्लिऑनों का द्रव्यमान = 26mp + 30mn
= 26 x 1.007825+ 30 x 1.008665
= 26.20345 + 30.25995 = 56.4634u
द्रव्यमान क्षति Δm = न्यूक्लिऑनों का द्रव्यमान – नाभिक का द्रव्यमान
= 56.4634 – 55.934939 = 0.528461u
∴\(\begin{array}{l}{56} \\ {26}\end{array} \mathbf{F} \mathbf{e}\) नाभिक की बन्धन ऊर्जा = Δm x 931
= 0.528461x 931.5 मिलियन इलेक्ट्रॉन-वोल्ट
= 492.26 मिलियन इलेक्ट्रॉन-वोल्ट
∴ बन्धन ऊर्जा प्रति न्यूक्लिऑन = \(\frac { 496.26 }{ 56 }\)
= 8.79 मिलियन इलेक्ट्रॉन-वोल्ट/न्यूक्लिऑन।
(ii) \(\begin{array}{l}{209} \\ {83}\end{array}\)Bi नाभिक का द्रव्यमान mBi = 208.980388u
इस नाभिक में 83 प्रोटॉन तथा 126 न्यूट्रॉन हैं। .
∴ न्यूक्लिऑनों का द्रव्यमान = 83mp + 126mn
= 83×1.007825+ 126×1.008665
= 83.649475+127.091790
= 210.741260 u
∴ नाभिक की द्रव्यमान क्षति Δm = 210.741260 – 208.980388
= 1.760872 u
∴ नाभिक की बन्धन ऊर्जा = Δm x 931.5 मिलियन इलेक्ट्रॉन-वोल्ट
= 1.760872 x 931.5
= 1640.26 मिलियन इलेक्ट्रॉन-वोल्ट
∴ बन्धन ऊर्जा प्रति न्यूक्लिऑन = \(\frac { 1640.26 }{ 209 }\)
= 7.85 मिलियन इलेक्ट्रॉन-वोल्ट/न्यूक्लिऑन।
प्रश्न 5.
एक दिए गए सिक्के का द्रव्यमान 3.0 ग्राम है। उस ऊर्जा की गणना कीजिए जो इस सिक्के के सभी न्यूट्रॉनों एवं प्रोटॉनों को एक-दूसरे से अलग करने के लिए आवश्यक हो। सरलता के लिए मान लीजिए कि सिक्का पूर्णत: \(\begin{array}{l}{63} \\ {29}\end{array} \mathbf{C u}\) परमाणुओं का बना है। ( \(\begin{array}{l}{63} \\ {29}\end{array} \mathbf{C u}\) का द्रव्यमान = 62.9260u)
हल
दिया है, न्यूट्रॉन का द्रव्यमान mn = 1.008665u
प्रोटॉन का द्रव्यमान mp = 1.007825u 68
\(\begin{array}{l}{63} \\ {29}\end{array} \mathbf{C u}\) नाभिक का द्रव्यमान m = 62.9260u
\(\begin{array}{l}{63} \\ {29}\end{array} \mathbf{C u}\) का ग्राम परमाणु द्रव्यमान = 63 ग्राम
∴ 63 ग्राम कॉपर में परमाणुओं की संख्या
N = 6.02 x 1023
∴ 3 ग्राम कॉपर में परमाणुओं की संख्या = \(\frac{6.02 \times 10^{23}}{63}\) × 3
= 2.868x 1022 परमाणु
\(\begin{array}{l}{63} \\ {29}\end{array} \mathbf{C u}\) के एक नाभिक में 29 प्रोटॉन तथा 63-29 = 34 न्यूट्रॉन हैं।
∴ एक नाभिक के न्यूक्लिऑनों का द्रव्यमान = 29mp + 34 mn
= 29 x 1.007825+ 34×1.008665
= 29.226925+ 34.294610
= 63.521535u
∴ एक नाभिक पर द्रव्यमान क्षति = 63.521535 – 62.9260 = 0.595535u
∴ 3 ग्राम कॉपर के लिए कुल द्रव्यमान क्षति
Δm = 0.595635 x 2.868 x 1022
= 1.70x 1022u
∴ 3 ग्राम कॉपर की बन्धन ऊर्जा = Δm x 931.5 मिलियन इलेक्ट्रॉन-वोल्ट
= 1.70 x 1022 x 931.5
= 1583.5 x 1022 मिलियन इलेक्ट्रॉन-वोल्ट
=1.584 x 1025 मिलियन इलेक्ट्रॉन-वोल्ट
अथवा
बन्धन ऊर्जा = 1.584 x 1025 x 1.6 x 10-13 जूल
= 2.535 x 1012 जूल ।
अतः सभी न्यूट्रॉनों एवं प्रोटॉनों को अलग करने के लिए आवश्यक ऊर्जा
= 1.584 x 1025 मिलियन इलेक्ट्रॉन-वोल्ट
= 2.535 x 1012 जूल।
![]()
प्रश्न 6.
निम्नलिखित के लिए नाभिकीय समीकरण लिखिए-

उत्तर
दी गई अभिक्रियाओं के लिए नाभिकीय समीकरण निम्नलिखित हैं

प्रश्न 7.
एक रेडियोऐक्टिव समस्थानिक की अर्द्ध-आयु T वर्ष है। कितने समय के बाद इसकी ऐक्टिवता, प्रारम्भिक ऐक्टिवता की
(a) 3. 125%, तथा
(b) 1% रह जाएगी? ।
हल
(a) माना समस्थानिक की प्रारम्भिक रेडियोऐक्टिवता = R0
माना समयान्तराल n अर्धायुकालों के पश्चात् शेष रेडियोऐक्टिवता = R
प्रश्नानुसार, R= R0 का 3.125%
⇒ R = \(\frac{3.125}{100} R_{0}\)

अभीष्ट समयान्तराल = n × एक अर्द्ध-आयु
= 5T वर्ष।
(b) इस बार R = R0 का 1% = \(\frac { 1 }{ 100 }\) Ro
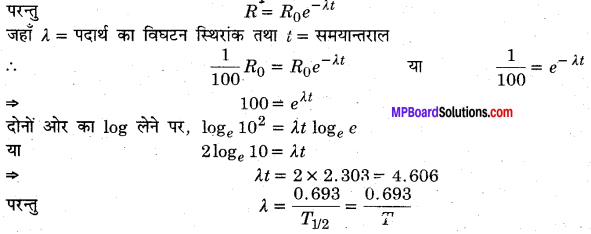

प्रश्न 8.
जीवित कार्बनयुक्त द्रव्य की सामान्य ऐक्टिवता, प्रति ग्राम कार्बन के लिए 15 क्षय प्रति मिनट है यह ऐक्टिवता, स्थायी समस्थानिक \(_{6}^{14} \mathbf{c}\) के साथ-साथ अल्प मात्रा में विद्यमान रेडियोऐक्टिव \(_{6}^{12} \mathbf{C}\) के कारण होती है। जीव की मृत्यु होने पर वायुमण्डल के साथ इसकी अन्योन्य क्रिया (जो उपर्युक्त सन्तुलित ऐक्टिवता को बनाए रखती है) समाप्त हो जाती है तथा इसकी ऐक्टिवता कम होनी शुरू हो जाती है। \(_{6}^{14} \mathbf{c}\) की ज्ञात अर्द्ध-आयु (5730 वर्ष) और नमूने की मापी गई ऐक्टिवता के आधार पर इसकी सन्निकट आयु की गणना की जा सकती है। यही पुरातत्व विज्ञान में प्रयुक्त होने वाली \(_{6}^{14} \mathbf{c}\) कालनिर्धारण (dating) पद्धति का सिद्धान्त है। यह मानकर कि मोहनजोदड़ो से प्राप्त किसी नमूने की ऐक्टिवता 9 क्षय प्रति मिनट प्रति ग्राम कार्बन है। सिन्धु घाटी सभ्यता की सन्निकट आयु का आकलन कीजिए।
हल
दिया है, R0 = 15 क्षय प्रति मिनट, R= 9 क्षय प्रति मिनट, T1/2 = 5730 वर्ष
सूत्र R = R0e-λt से, 9= 15e-λt
⇒ \(\frac { 5 }{ 3 }\) eλt या 1.6667 = eλt
दोनों पक्षों का log लेने पर,
loge(1.6667) = λt logee
या 2.303 log10 1.6667 = λt
⇒ λt = 2.3025×0.22185 = 0.5108
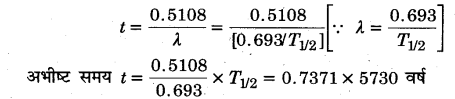
= 4224 वर्ष।
![]()
प्रश्न 9.
8.0 मिलीक्यूरी सक्रियता का रेडियोऐक्टिव स्रोत प्राप्त करने के लिए \(\begin{array}{l}{60} \\ {27}\end{array}\)Co की कितनी मात्रा की आवश्यकता होगी? \(\begin{array}{l}{60} \\ {27}\end{array}\)Co की अर्द्ध-आयु 5.3 वर्ष है।
हल
दिया है, सक्रियता R= 8.0 मिलीक्यूरी = 8.0×10-3 x 3.7 x 1010 विघटन/सेकण्ड
= 29.6 x 107 विघटन/सेकण्ड
तथा T1/2 = 5.3 वर्ष (∵ 1 क्यूरी = 3.7×1010 विघटन/सेकण्ड)
= 5.3 x 365 x 24 x 60 x 60 सेकण्ड .
सक्रियता R=-\(\frac { dN }{ dt }\) = – \(\frac { d }{ dt }\) (N0e-λt) [:: N = N0e-λt]
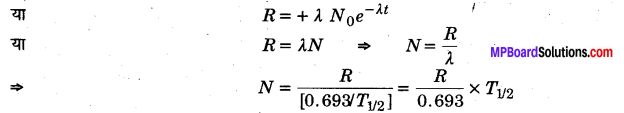
∴ आवश्यक परमाणुओं की संख्या N= \(\frac{29.6 \times 10^{7} \times 5.3 \times 365 \times 24 \times 60 \times 60}{0.693}\)
= 7.133 x 1016 परमाणु
∵ \(\begin{array}{l}{60} \\ {27}\end{array}\)Co का ग्राम परमाणु द्रव्यमान = 60
∴ 60 ग्राम Co में परमाणुओं की संख्या = NA = 6.02 x 1023
∴ 7.133 x 1016 परमाणु ओं का द्रव्यमान = \(\frac{60}{6.02 \times 10^{23}} \times 7.133 \times 10^{16}\)
= 7.109 x 10-6 ग्राम
= 7.11 माइक्रोग्राम।
प्रश्न 10.
\(\begin{array}{l}{90} \\ {38}\end{array} \mathbf{S} \mathbf{r}\) की अर्द्ध-आयु 28 वर्ष है। इस समस्थानिक के 15 मिलीग्राम की विघटन दर क्या है?
हल
दिया है : पदार्थ का द्रव्यमान = 15 × 10-3 ग्राम तथा
T1/2 = 28 वर्ष
= 28 × 365 × 24 × 60 × 60 सेकण्ड
= 88.3 × 107 सेकण्ड
∴
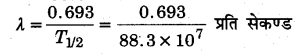
∴ \(\begin{array}{l}{90} \\ {38}\end{array} \mathbf{S} \mathbf{r}\) का ग्राम परमाणु द्रव्यमान = 90 ग्राम ∴ 90 ग्राम Sr में परमाणुओं की संख्या = 6.02 × 1023
∴ 15 × 10-3 ग्राम में परमाणुओं की संख्या .
\(=\frac{6.02 \times 10^{23}}{90} \times 15 \times 10^{-3}\)
= 1.004 × 1020
∴ पदार्थ की विघटन दर (सक्रियता) R= λN (देखें प्रश्न 9)
⇒ \(R=\frac{0.693}{88.3 \times 10^{7}} \times 1.004 \times 10^{20}\)
= 7.879 x 1010 विघटन/सेकण्ड
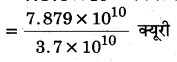
= 2.13 क्यूरी।
प्रश्न 11.
स्वर्ण के समस्थानिक \(\begin{array}{l}{197} \\ {79}\end{array}\)Au एवं रजत के समस्थानिक \(\begin{array}{l}{107} \\ {47}\end{array}\)Ag की नाभिकीय त्रिज्या के अनुपात का सन्निकट मान ज्ञात कीजिए।
हल
किसी नाभिक की त्रिज्या निम्नलिखित सूत्र द्वारा प्राप्त होती है
R= R0A1/3
जहाँ A= परमाणु द्रव्यमान जबकि R0 = नियतांक
यहाँ \(\begin{array}{l}{197} \\ {79}\end{array}\)Au के लिए, A1 = 197
तथा \(\begin{array}{l}{107} \\ {47}\end{array}\)Ag के लिए, A2 = 107
∴\(\frac{R_{1}}{R_{2}}=\frac{\left(A_{1}\right)^{1 / 3}}{\left(A_{2}\right)^{1 / 3}}=\left(\frac{A_{1}}{A_{2}}\right)^{1 / 3}=\left(\frac{197}{107}\right)^{1 / 3}\)
⇒ \(\frac{R_{1}}{R_{2}}=(1.84)^{1 / 3}=1.23\)
∴ त्रिज्याओं का अनुपात R1: R2 = 1. 23 : 1
प्रश्न 12.
(a) \(\begin{array}{l}{226} \\ {88}\end{array}\)Ra एवं
(b) \(\begin{array}{l}{220} \\ {86}\end{array}\)Rn नाभिकों के -क्षय में उत्सर्जित -कणों का Q-मान एवं गतिज ऊर्जा ज्ञात कीजिए। दिया है
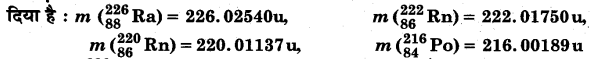
हल
(a) \(\begin{array}{l}{226} \\ {88}\end{array}\)Ra नाभिक के α-क्षय का समीकरण निम्नलिखित है
![]()
जहाँ Q अभिक्रिया में उत्पन्न ऊर्जा है।
उक्त अभिक्रिया में द्रव्यमान क्षति Δm = [बाएँ पक्ष का द्रव्यमान – दाएँ पक्ष का द्रव्यमान]
= [226.02540- (222.01750+ 4.002603)]u [दिया है, mα = 4.002603u]
= 0.005297u
∴ अभिक्रिया का Q मान = Δ m × 931.5 मिलियन इलेक्ट्रॉन-वोल्ट
= 0.005297 × 931.5 मिलियन इलेक्ट्रॉन-वोल्ट
= 4.9342 मिलियन इलेक्ट्रॉन-वोल्ट
मूल नाभिक का परमाणु द्रव्यमान Z = 226
Rn का परमाणु द्रव्यमान = Z-4
α – कण का परमाणु द्रव्यमान = 4.
माना विघटन के बाद उक्त कणों के संवेग क्रमश: pR व pα हैं।
तब संवेग संरक्षण से, Pα + PR = 0 (∵ मूल परमाणु का संवेग = 0)
⇒ PR = -Pα

Kα= 4.85 मिलियन इलेक्ट्रॉन-वोल्टा.
(b) \(\begin{array}{l}{226} \\ {88}\end{array}\)Ra के -क्षय का समीकरण निम्नलिखित है
![]()
द्रव्यमान क्षति Δm = [बाएँ पक्ष का द्रव्यमान – दाएँ पक्ष का द्रव्यमान]
= [220.01137- (216.00189+ 4.002603)]u
= 0.006877u
∴ अभिक्रिया का Q मान = Δm × 931.5 मिलियन इलेक्ट्रॉन-वोल्ट
= 0.006877 × 931.5 मिलियन इलेक्ट्रॉन-वोल्ट
= 6.41 मिलियन इलेक्ट्रॉन-वोल्ट।
भाग (a) के अनुसार,
α- कण की गतिज ऊर्जा Kα = \(\frac{m_{P_{0}}}{m_{\alpha}+m_{P_{0}}} Q\)
= \(\frac { Z-4 }{ Z }\) Q = \(\frac { 220-4 }{ 220 }\) × 0.641
Kα= 0.629 मिलियन इलेक्ट्रॉन-वोल्ट।
![]()
प्रश्न 13.
रेडियोन्यूक्लाइड 11c का क्षय निम्नलिखित समीकरण के अनुसार होता है
![]()
उत्सर्जित पॉजिट्रॉन की अधिकतम ऊर्जा 0.960 मिलियन इलेक्ट्रॉन-वोल्ट है। द्रव्यमानों के निम्नलिखित मान दिए गए हैं
तथा 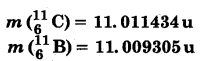
Q-मान की गणना कीजिए एवं उत्सर्जित पॉजिट्रॉन की अधिकतम गतिज ऊर्जा के मान से इसकी तुलना कीजिए।
हल
दिया गया समीकरण :
![]()
∴ Δm
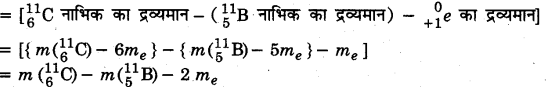
= 11.011434 – 11.009305-2 × 0.000548
= 0.001033u
∴ Q=Δm × 931 = 0.001033 × 931
= 0.961मिलियन इलेक्ट्रॉन-वोल्ट।
उत्सर्जित पॉजिट्रॉन की महत्तम गतिज ऊर्जा 0.960 मिलियन इलेक्ट्रॉन-वोल्ट है जो कि Q-मान के तुल्य है।
∴ उत्पाद नाभिक पॉजिट्रॉन की तुलना में अत्यधिक भारी है, अतः इसकी गतिज ऊर्जा लगभग शून्य होगी, पुनः चूँकि पॉजिट्रॉन की अधिकतम गतिज ऊर्जा २-मान के तुल्य है, अत: न्यूट्रिनो भी लगभग शून्य ऊर्जा के साथ उत्सर्जित होगा।
प्रश्न 14.
\(\begin{array}{l}{23} \\ {10}\end{array} \mathrm{Ne}\) का नाभिक, β– उत्सर्जन के साथ क्षयित होता है। इस β -क्षय के लिए समीकरण लिखिए और उत्सर्जित इलेक्ट्रॉनों की अधिकतम गतिज ऊर्जा ज्ञात कीजिए।
(m\(\begin{array}{l}{23} \\ {10}\end{array} \mathrm{Ne}\)) = 22.994466u, (m\(\begin{array}{l}{23} \\ {11}\end{array} \mathrm{Na}\)) = 22.989770u
हल
\(\begin{array}{l}{23} \\ {10}\end{array} \mathrm{Ne}\) नाभिक के β-क्षय का समीकरण निम्नलिखित है
![]()
द्रव्यमान क्षति Δm
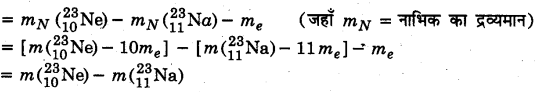
= [22.994466 – 22.989770] u= 0.004696u
∴ Q-मान = Δm × 931 मिलियन इलेक्ट्रॉन-वोल्ट
= 0.04696×931.5 मिलियन इलेक्ट्रॉन-वोल्ट
Q= 4.37 मिलियन इलेक्ट्रॉन-वोल्ट
∵ \(\begin{array}{l}{23} \\ {10}\end{array} \mathrm{Na}\) नाभिक, \(\begin{array}{c}{0} \\ {-1}\end{array} \beta\) तथा ऐन्टिन्यूट्रिनो की तुलना में अत्यधिक भारी है, अतः इसकी गतिज ऊर्जा लगभग शून्य होगी। β-कण की ऊर्जा अधिकतम होगी यदि ऐन्टिन्यूट्रिनो शून्य ऊर्जा के साथ उत्सर्जित हो। इस दशा में β-कण की ऊर्जा अधिकतम होगी यदि ऐन्टिन्यूट्रिनो शून्य ऊर्जा के साथ उत्सर्जित हो। इस दशा में β-कण की अधिकतम ऊर्जा Q-मान के बराबर अर्थात् 4.37 मिलियन इलेक्ट्रॉन-वोल्ट होगी।
![]()
प्रश्न 15.
किसी नाभिकीय अभिक्रिया A+ b → C+d का Q-मान निम्नलिखित समीकरण द्वारा परिभाषित होता है
![]()
जहाँ दिए गए द्रव्यमान, नाभिकीय विराम द्रव्यमान (rest mass) हैं। दिए गए आँकड़ों के आधार पर बताइए कि निम्नलिखित अभिक्रियाएँ ऊष्माक्षेपी हैं या ऊष्माशोषी।

उत्तर
(i) दी गई अभिक्रिया निम्नलिखित है
\(_{1}^{1} \mathrm{H}+_{1}^{3} \mathrm{H} \longrightarrow_{1}^{2} \mathrm{H}+_{1}^{2} \mathrm{H}\)
इस अभिक्रिया का Q-मान निम्नलिखित है

= 1.007825 + 3.016049- 2.014102 – 2.014102
= – 0.004339u
= – 0.004339x 1.66×10-27 किग्रा ।
[∵ m \(\left(_{1}^{1} \mathrm{H}\right)\) = 1.007825u व 1u = 1.66 x 10-27 किग्रा]
Q= – 0.004339×1.66×10-27x (3×108)2 जूल
= – 6.46 x 10-13 जूल
∵ इस अभिक्रिया का Q-मान ऋणात्मक है, अत: यह ऊष्माशोषी अभिक्रिया है।
(ii)
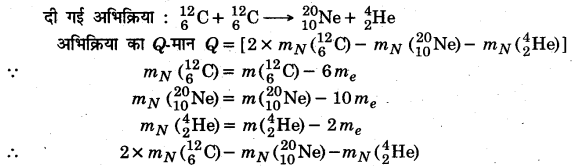
= 2 × 12.000000 -19.992439 – 4.002603 [∵ m \(\left(_{2}^{4} \mathrm{He}\right)\) = 4.002603]
= 0.004958u= 0.004958×1.66 × 10-27 किग्रा
∴ Q = 0.004958 × 1.66 x 10-27 × (3 × 108)2 जूल
= 7.41 × 10-13 जूल
∴ Qमान धनात्मक है, अतः यह अभिक्रिया ऊष्माक्षेपी अभिक्रिया है।
प्रश्न 16.
माना कि हम \(\begin{array}{l}{56} \\ {26}\end{array}\)Fe नाभिक के दो समान अवयवों \(\begin{array}{l}{28} \\ {13}\end{array} \mathbf{A} \mathbf{l}\) में विखण्डन पर विचार करें। क्या ऊर्जा की दृष्टि से यह विखण्डन सम्भव है? इस प्रक्रम का Q-मान ज्ञात करके अपना तर्क प्रस्तुत करें।
दिया है : m (\(\begin{array}{l}{56} \\ {26}\end{array}\)Fe) = 55.93494u एवं m(\(\begin{array}{l}{28} \\ {13}\end{array} \mathbf{A} \mathbf{l}\)) = 27.98191u
उत्तर
सम्भावित अभिक्रिया का समीकरण निम्नलिखित है- .
\(\begin{array}{l}{56} \\ {26}\end{array}\)Fe→ m\(\begin{array}{l}{28} \\ {13}\end{array} \mathbf{A} \mathbf{l}\)+ m\(\begin{array}{l}{28} \\ {13}\end{array} \mathbf{A} \mathbf{l}\)+Q
इस अभिक्रिया का Q-मान निम्नलिखित है
Q= [m(\(\begin{array}{l}{56} \\ {26}\end{array}\)Fe)- 2 × m(m(\(\begin{array}{l}{28} \\ {13}\end{array} \mathbf{A} \mathbf{l}\))] × 931.5 मिलियन इलेक्ट्रॉन-वोल्ट
= [55.93494 – 2 × 27.98191] × 931.5 मिलियन इलेक्ट्रॉन-वोल्ट
= – 0.02888×931.5
= – 26.90 मिलियन इलेक्ट्रॉन-वोल्ट।
∵ अभिक्रिया का Q-मान ऋणात्मक है, अतः यह अभिक्रिया सम्भव नहीं है।
प्रश्न 17.
\(\begin{array}{l}{239} \\ {94}\end{array} \mathbf{P} \mathbf{u}\) के विखण्डन गुण बहुत कुछ \(\begin{array}{l}{235} \\ {92}\end{array}\)U से मिलते-जुलते हैं। प्रति विखण्डन विमुक्त औसत ऊर्जा 180 मिलियन इलेक्ट्रॉन-वोल्ट है। यदि 1 किग्रा शुद्ध \(\begin{array}{l}{239} \\ {94}\end{array} \mathbf{P} \mathbf{u}\)के सभी परमाणु विखण्डित हों तो कितनी मिलियन इलेक्ट्रॉन-वोल्ट ऊर्जा विमुक्त होगी? ।
हल
यहाँ \(\begin{array}{l}{239} \\ {94}\end{array} \mathbf{P} \mathbf{u}\) के विखण्डन से मुक्त ऊर्जा = 180 मिलियन इलेक्ट्रॉन-वोल्ट
∵ \(\begin{array}{l}{239} \\ {94}\end{array} \mathbf{P} \mathbf{u}\) का ग्राम परमाणु द्रव्यमान = 239 ग्राम
∴ 239 ग्राम प्लूटोनियम में उपस्थित परमाणुओं की संख्या = 6.02 × 1023
∴ 1 किग्रा (= 1000 ग्राम) में उपस्थित परमाणुओं की संख्या = \(\frac{6.02 \times 10^{23}}{239} \times 1000\)
= 2.52 × 1024
∵ 1 परमाणु के विखण्डन से मुक्त ऊर्जा = 180 मिलियन इलेक्ट्रॉन-वोल्ट
∴ 1 किग्रा अर्थात् 2.52 × 1024 परमाणुओं के विखण्डन से मुक्त ऊर्जा
= 180 × 2.52 × 1024
= 4.536 × 1026 मिलियन इलेक्ट्रॉन-वोल्ट।
![]()
प्रश्न 18.
किसी 1000 मेगावाट विखण्डन रिऐक्टर के आधे ईंधन का 5.00 वर्ष में व्यय हो जाता है। प्रारम्भ में इसमें कितना \(\begin{array}{l}{235} \\ {92}\end{array}\)U था? मान लीजिए कि रिऐक्टर 80% समय कार्यरत रहता है, इसकी सम्पूर्ण ऊर्जा \(\begin{array}{l}{235} \\ {92}\end{array}\)U के विखण्डन से ही उत्पन्न हुई है तथा \(\begin{array}{l}{235} \\ {92}\end{array}\)U न्यूक्लाइड केवल विखण्डन प्रक्रिया में ही व्यय होता है।
हल
रिऐक्टर की शक्ति P= 1000 मिलियन इलेक्ट्रॉन-वोल्ट
= 1000 × 106 जूल/सेकण्ड
= 109 जूल/सेकण्ड
समय t = 5.00 वर्ष
= 5 × 365 × 24x 60 × 60 सेकण्ड = 1.577 × 108 सेकण्ड
∴ 5 वर्ष में रिऐक्टर में उत्पन्न ऊर्जा (जबकि यह 80% समय ही कार्य करता है)
E = 80% t × P
= \(\frac { 80 }{ 100 }\) × 1.577×108 × 109
= 1.2616×1017 जूल
∵ 235U के एक परमाणु के विखण्डन से औसतन 200 मिलियन इलेक्ट्रॉन-वोल्ट ऊर्जा उत्पन्न होती है।
∴ 100 मिलियन इलेक्ट्रॉन-वोल्ट ऊर्जा उत्पन्न होती है = 1 परमाणु से
या 200 × 1.6×10-13 जूल ऊर्जा उत्पन्न होती है = 1 परमाणु से
1 जूल ऊर्जा उत्पन्न होगी = \(\frac{1}{200 \times 1.6 \times 10^{-13}}\) परमाणु से
∴ 1.2616 × 1017 जूल ऊर्जा उत्पन्न होगी = \(\frac{1.2616 \times 10^{17}}{200 \times 1.6 \times 10^{-13}}\) परमाणु से
= 3.94 × 1027
∴ 5.0 वर्ष में विखण्डित नाभिकों की संख्या n= 3.94 × 1027 6.0 × 1023 परमाणु उपस्थित हैं
= 235 ग्राम यूरेनियम में ।
∴ 3.94 × 1027 परमाण उपस्थित होंगे = \(\frac{235 \times 3.94 \times 10^{27}}{6.0 \times 10^{23}}\) ग्राम में …
= 1.544 x 106 ग्राम में = 1.544 x 103 किग्रा
= 1544 किग्रा .
∵ 5.0 वर्ष में आधी माग विघटित होती है,
∴ रिऐक्टर में \(\begin{array}{l}{235} \\ {92}\end{array}\)U की प्रारम्भिक मात्रा = 2x 1544 = 3088 किग्रा।
प्रश्न 19.
2.0 किग्रा ड्यूटीरियम के संलयन से एक 100 वाट का विद्युत लैम्प कितनी देर प्रकाशित रखा जा सकता है? संलयन अभिक्रिया निम्नवत् ली जा सकती है
![]()
हल
लैम्प की शक्ति P = 100W, ड्यूटीरियम का द्रव्यमान m= 2.0 किग्रा
दी गई समीकरण- image 28
इस समीकरण से स्पष्ट है कि इस अभिक्रिया में \(_{1}^{2} \mathrm{H}\) के दो नाभिकों के संलयन से 3.27 मिलियन इलेक्ट्रॉन वोल्ट ऊर्जा उत्पन्न होती है।
∵ 2 ग्राम ड्यूटीरियम में उपस्थित नाभिकों की संख्या = 6.02 × 1023
∴ 2.0 किग्रा (= 2000 ग्राम) में उपस्थित नाभिकों की संख्या \(\begin{array}{l}{=\frac{6.02 \times 10^{23} \times 2000}{2}} \\ {=6.02 \times 10^{26}}\end{array}\)
दो नाभिकों के संलयन से उत्पन्न ऊर्जा = 3.27 मिलियन इलेक्ट्रॉन-वोल्ट
= 3.27 × 1.6 × 10-13 जूल
∴ 2 किग्रा अथवा 6.02 × 1026 नाभिकों के संलयन से उत्पन्न ऊर्जा
= 3.27 ×1.6 × 10-13 × 6.02 × 1026 जल
= 3.27 × 1.6 × 6.02 × 1013 जूल
माना इस ऊर्जा से लैम्प को t सेकण्ड तक प्रकाशित रखा जा सकता है, तब
लैम्प द्वारा व्यय ऊर्जा = 100 वाट × t सेकण्ड
= 100 t जूल
100 t = 3.27 × 1.6 × 6.02 × 1013
t = 3.27 × 1.6 × 6.02 × 1011
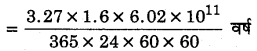
= 4.9 × 104 वर्ष
अर्थात् लैम्प को 4.9 × 104 वर्ष तक प्रकाशित रखा जा सकता है।
प्रश्न 20.
दो ड्यूट्रॉनों के आमने-सामने की टक्कर के लिए कूलॉम अवरोध की ऊँचाई ज्ञात कीजिए। (संकेत-कूलॉम अवरोध वह न्यूनतम गतिज ऊर्जा है जिसके द्वारा उन्हें एक-दूसरे की ओर भेजे जाने पर वे कूलॉमीय बल के विरुद्ध परस्पर संलयित हो सकें। यह मान सकते हैं कि ड्यूट्रॉन 2.0 फैम्टो मीटर प्रभावी त्रिज्या वाले दृढ़ गोले हैं।)
हल
प्रत्येक ड्यूट्रॉन पर आवेश q1= q2 = + 1.6 × 10-19 कूलॉम
ऊर्जा के पदों में कूलॉम अवरोध (विभव प्राचीर)
माना प्रारम्भ में प्रत्येक ड्यूट्रॉन की गतिज ऊर्जा K है। जब ये दोनों एक-दूसरे के सम्पर्क में आते हैं तो सम्पूर्ण ऊर्जा विद्युत स्थितिज ऊर्जा में बदल जाती है। ∴ ऊर्जा संरक्षण से, U= 2K ⇒ \(\frac{1}{4 \pi \varepsilon_{0}} \cdot \frac{q_{1} q_{2}}{r}=2 K\)
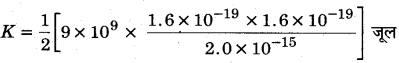
= 5.76x 10-14 जुल
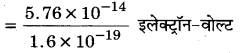
= 3.6 × 105 इलेक्ट्रॉन-वोल्ट
विभव प्राचीर K = 360 किलो इलेक्ट्रॉन-वोल्ट।
प्रश्न 21.
समीकरण R = \(\boldsymbol{R}_{0} \boldsymbol{A}^{1 / 3}\) के आधार पर, दर्शाइए कि नाभिकीय द्रव्य का घनत्व लगभग अचर है (अर्थात् A पर निर्भर नहीं करता है)। यहाँ R. एक नियतांक है एवं A नाभिक की द्रव्यमान संख्या है।
उत्तर
∵ नाभिक की द्रव्यमान संख्या = A
∴ नाभिक का द्रव्यमान m = Au = A × 1.66 × 10-27 किग्रा
पुन: नाभिक का आयतन V \(\begin{array}{l}{=\frac{4}{3} \pi R^{3}=\frac{4}{3} \pi\left(R_{0} A^{1 / 3}\right)^{3}} \\ {=\frac{4}{3} \pi R_{0}^{3} A}\end{array}\)
∴ नाभिक का घनत्व p \(\begin{aligned}=& \frac{m}{V}=\frac{A \times 1.66 \times 10^{-27}}{\frac{4}{3} \times \pi R_{0}^{3} A} \\=& \frac{3 \times 1.66 \times 10^{-27}}{4 \pi R_{0}^{3}} \end{aligned}\)
∵ यह घनत्व नाभिक की द्रव्यमान संख्या A से मुक्त है, अत: हम कह सकते हैं कि नाभिकीय द्रव्य का घनत्व लगभग अचर है।
प्रश्न 22.
किसी नाभिक से β+ (पॉजिट्रॉन) उत्सर्जन की एक अन्य प्रतियोगी प्रक्रिया है जिसे इलेक्ट्रॉन परिग्रहण (Capture) कहते हैं (इसमें परमाणु की आन्तरिक कक्षा, जैसे कि K-कक्षा, से नाभिक एक इलेक्ट्रॉन परिगृहीत कर लेता है और एक न्यूट्रिनो, v उत्सर्जित करता है)।
![]()
दर्शाइए कि यदि β+ उत्सर्जन ऊर्जा विचार से अनुमत है कि इलेक्ट्रॉन परिग्रहण भी आवश्यक रूप से अनुमत है, परन्तु इसका विलोम अनुमत नहीं है।
उत्तर
पॉजिट्रॉन उत्सर्जन की अभिक्रिया का समीकरण निम्नलिखित है
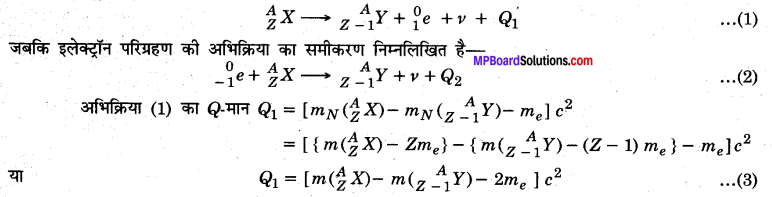
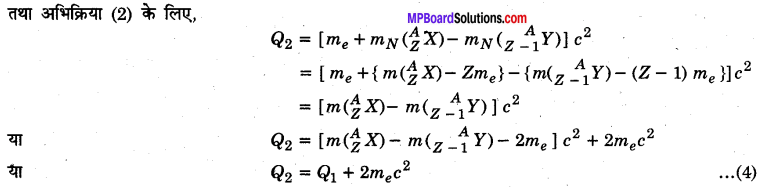
समीकरण (3) व (4) से स्पष्ट है कि Q1 < Q2
यदि पॉजिट्रॉन उत्सर्जन [अभिक्रिया (1)] ऊर्जा दृष्टि से अनुमत है तो इस अभिक्रिया का Q-मान अर्थात् Q1 धनात्मक होगा।
अर्थात् Q1>0
∵ Q2>Q1, अतः Q1>0 ⇒ Q2>0
अर्थात् तब अभिक्रिया (2) का Q-मान भी धनात्मक होगा अर्थात् ऊर्जा दृष्टि से इलेक्ट्रॉन परिग्रहण भी अनुमत है। अब इस अभिक्रिया के विलोम पर विचार कीजिए,
स्पष्ट है कि इस अभिक्रिया का Q-मान – Q2 के बराबर होगा।
∴ Q20, अतः Q3 = -Q2 < 0
∵ इस अभिक्रिया का Q-मान ऋणात्मक है, अत: यह अभिक्रिया ऊर्जा दृष्टि से अनुमत नहीं है।
![]()
प्रश्न 23.
आवर्त सारणी में मैग्नीशियम का औसत परमाणु द्रव्यमान 24.312u दिया गया है। यह औसत मान, पृथ्वी पर इसके समस्थानिकों की सापेक्ष बहुलता के आधार पर दिया गया है। मैग्नीशियम के तीनों समस्थानिक तथा उनके द्रव्यमान इस प्रकार हैं –\(\begin{array}{l}{24} \\ {12}\end{array} Mg\)(23. 98504u), \(\begin{array}{l}{25} \\ {12}\end{array} Mg\)(24.98584) एवं \(\begin{array}{l}{26} \\ {12}\end{array} Mg\) (25.98259u)। प्रकृति में प्राप्त मैग्नीशियम में \(\begin{array}{l}{24} \\ {12}\end{array} Mg\) की (द्रव्यमान के अनुसार) बहुलता 78.99% है। अन्य दोनों समस्थानिकों की बहुलता का परिकलन कीजिए।
हल
दिया है, मैग्नीशियम का औसत परमाणु द्रव्यमान = 24.312u
\(\begin{array}{l}{24} \\ {12}\end{array} Mg\) समस्थानिक की बहुलता = 78.99%
माना समस्थानिक \(\begin{array}{l}{25} \\ {12}\end{array} Mg\) की बहुलता α% है।
तब \(\begin{array}{l}{26} \\ {12}\end{array} Mg\) समस्थानिक की बहुलता
= 100 – 78.99 – α = (21.01-a) %
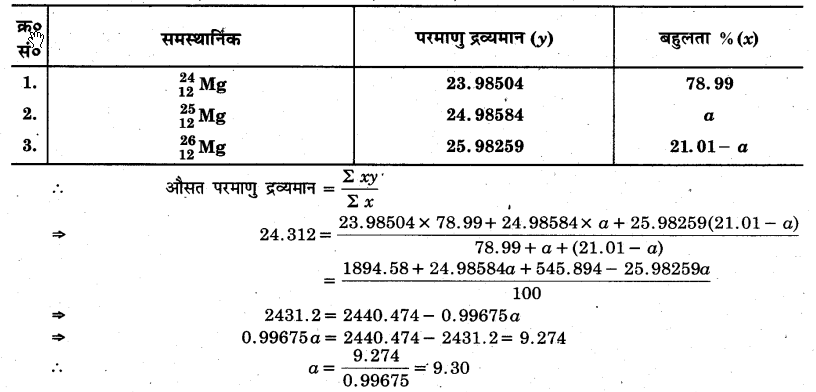
तथा 21.01 – a = 21.01- 9.30 = 11.70
अत: \(\begin{array}{l}{25} \\ {12}\end{array} Mg\) की बहुलता 9. 30% तथा \(\begin{array}{l}{26} \\ {12}\end{array} Mg\) की बहुलता 11.70% है।
प्रश्न 24.
न्यूट्रॉन पृथक्करण ऊर्जा (Separation energy), परिभाषा के अनुसार वह ऊर्जा है, जो किसी नाभिक से एक न्यूट्रॉन को निकालने के लिए आवश्यक होती है। नीचे दिए गए आँकड़ों का इस्तेमाल करके \(_{20}^{41} \mathrm{Ca}\) एवं \(_{13}^{27} \mathrm{Al}\) नाभिकों की न्यूट्रॉन पृथक्करण ऊर्जा ज्ञात कीजिए।
m(\(_{20}^{40} \mathrm{Ca}\)) = 39.962591u
m (\(_{20}^{41} \mathrm{Ca}\)) = 40.962278u
(\(\begin{array}{l}{26} \\ {13}\end{array} \mathrm{Al}\)) = 25. 98689
m(\(_{13}^{27} \mathrm{Al}\)) = 26.981541u
हल
(i) \(_{20}^{41} \mathrm{Ca}\) की न्यूट्रॉन पृथक्करण ऊर्जा
न्यूट्रॉन पृथक्करण अभिक्रिया का समीकरण निम्नलिखित है
\(_{20}^{41} \mathrm{Ca} \longrightarrow_{20}^{40} \mathrm{Ca}+_{0}^{1} n+Q\)
Q = [m(\(_{20}^{41} \mathrm{Ca}\))- m(\(_{20}^{40} \mathrm{Ca}\))- mn ] x 931.5 मिलियन इलेक्ट्रॉन-वोल्ट
= [40.962278- 39.962591-1.008665] x 931.5 मिलियन इलेक्ट्रॉन-वोल्ट [∵mn = 1.008665u]
= – 0.008978×931.5
= – 8.36 मिलियन इलेक्ट्रॉन-वोल्ट
∵ Q का मान ऋणात्मक है अर्थात् उक्त अभिक्रिया ऊष्माशोषी है।
∴ न्यूट्रॉन पृथक्करण ऊर्जा 8. 36 मिलियन इलेक्ट्रॉन-वोल्ट है।
(ii) \(_{13}^{27} \mathrm{Al}\) की न्यूट्रॉन पृथक्करण ऊर्जाTAI की न्यूट्रॉन पृथक्करण समीकरण निम्नलिखित है
![]()
Q = [m(\(_{13}^{27} \mathrm{Al}\)Al) – mn (\(\begin{array}{l}{26} \\ {13}\end{array} \mathrm{Al}\))- mn ] x 931.5 मिलियन इलेक्ट्रॉन-वोल्ट
= [26.981541- 25.986895-1.008665] x 931.5 मिलियन इलेक्ट्रॉन-वोल्ट
= -0.014019 x 931.5 मिलियन इलेक्ट्रॉन-वोल्ट .
= – 13.06 मिलियन इलेक्ट्रॉन-वोल्ट
∵ Q का मान ऋणात्मक है, अतः उक्त अभिक्रिया ऊष्माशोषी है।
∴ \(_{13}^{27} \mathrm{Al}\) की न्यूट्रॉन पृथक्करण ऊर्जा 13.06 मिलियन इलेक्ट्रॉन-वोल्ट है।
![]()
प्रश्न 25.
किसी स्रोत में फॉस्फोरस के दो रेडियो न्यूक्लाइड निहित हैं \(\begin{array}{l}{32}\\{15}\end{array}\)P(T1/2 = 14.3 दिन) एवं \(\begin{array}{l}{32}\\{15}\end{array}\)P(T1/2 = 25.3 दिन)। प्रारम्भ में \(\begin{array}{l}{32}\\{15}\end{array}\)P से 10% क्षय प्राप्त होता है। इससे 90% क्षय प्राप्त करने के लिए कितने समय प्रतीक्षा करनी होगी?
हल
माना प्रारम्भ में \(\begin{array}{l}{33}\\{15}\end{array}\) तथा \(\begin{array}{l}{32}\\{15}\end{array}\) की रेडियोऐक्टिवताएँ R01 व R02 हैं तथा + समय पश्चात् इनकी रेडियोऐक्टिवताएँ R1 व R2 हैं।
तब प्रारम्भ में, पदार्थ की कुल सक्रियता = R01 + R02
परन्तु R01 = 10% प्रारम्भिक सक्रियता = \(\frac { 10 }{100 }\)(R01 + R02)
⇒ 10 R01 = R01 + R02
या 9R01 = R02 ….(1)
पुनः t समय पश्चात् कुल सक्रियता = R1 + R2
परन्तु R1 = 90% कुल सक्रियता = \(\frac { 90 }{100 }\)(R1 + R2)
10R1 = 9R1 + 9R2
R1 = 9R2 ….(2)


प्रश्न 26.
कुछ विशिष्ट परिस्थितियों में एक नाभिक, -कण से अधिक द्रव्यमान वाला एक कण उत्सर्जित करके क्षयित होता है। निम्नलिखित क्षय-प्रक्रियाओं पर विचार कीजिए|
![]()
इन दोनों क्षय प्रक्रियाओं के लिए Q-मान की गणना कीजिए और दर्शाइए कि दोनों प्रक्रियाएँ ऊर्जा की दृष्टि से सम्भव हैं। \
उत्तर
दी गई पहली समीकरण निम्नलिखित है
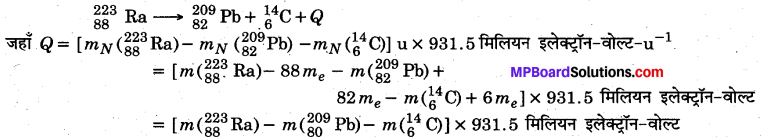
= [223.01850- 208.98107-14.00324] × 931.5 मिलियन इलेक्ट्रॉन-वोल्ट
= 0.03419 × 931.5
= 31.85 मिलियन इलेक्ट्रॉन-वोल्ट।
दूसरी समीकरण निम्नलिखित है
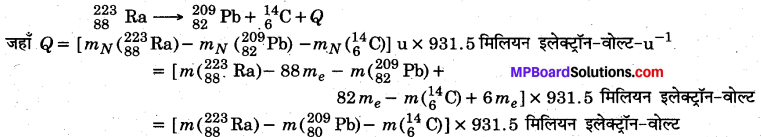
![]()
= [223.01850- 219.00948- 4.00260] × 931.5 मिलियन इलेक्ट्रॉन-वोल्ट
या Q= 0.00642 × 931.5
= 5.98 मिलियन इलेक्ट्रॉन-वोल्ट।
∵ दोनों अभिक्रियाओं के Q-मान धनात्मक हैं, अत: ऊर्जा दृष्टि से दोनों अभिक्रियाएँ सम्भव हैं।
प्रश्न 27.
तीव्र न्यूट्रॉनों द्वारा \(\begin{array}{c}{238} \\ {92}\end{array} \mathbf{U}\) के विखण्डन पर विचार कीजिए। किसी विखण्डन प्रक्रिया में प्राथमिक अंशों (Primary fragments) के बीटा-क्षय के पश्चात् कोई न्यूट्रॉन उत्सर्जित नहीं होता तथा \(\begin{array}{c}{140} \\ {58}\end{array} \mathbf{C} \mathbf{e}\) तथा । \(\begin{array}{l}{99} \\ {34}\end{array} \mathbf{R} \mathbf{u}\) अन्तिम उत्पाद प्राप्त होते हैं। विखण्डन प्रक्रिया के लिए Q के मान का परिकलन कीजिए। आवश्यक आँकड़े इस प्रकार हैं
m(\(\begin{array}{c}{238} \\ {92}\end{array} \mathbf{U}\)) = 238.05079u
m(\(\begin{array}{c}{140} \\ {58}\end{array} \mathbf{C} \mathbf{e}\)) = 139.90543u
m(\(\begin{array}{l}{99} \\ {34}\end{array} \mathbf{R} \mathbf{u}\)) = 98.90594u
हल
\(\begin{array}{c}{238} \\ {92}\end{array} \mathbf{U}\) की विखण्डन अभिक्रिया का समीकरण निम्नलिखित है
\(_{92}^{238} \mathrm{U}+\frac{1}{0} n \longrightarrow_{58}^{140} \mathrm{Ce}+_{34}^{99} \mathrm{Ru}+Q\)
इस समीकरण का Q-मान निम्नलिखित है
![]()
= [238.05079+1.00867- 139.90543- 98.90594] x 931.5मिलियन इलेक्ट्रॉन-वोल्ट
= 0.24809 x 931.5
= 231 मिलियन इलेक्ट्रॉन-वोल्ट।
![]()
प्रश्न 28.
D-T अभिक्रिया (ड्यूटीरियम- ट्राइटियम संलयन),\(_{1}^{2} H+_{1}^{3} H \rightarrow \begin{array}{l}{4} \\ {2}\end{array} H e+n\) पर विचार कीजिए। .
(a) नीचे दिए गए आँकड़ों के आधार पर अभिक्रिया में विमुक्त ऊर्जा का मान मिलियन इलेक्ट्रॉन-वोल्ट में ज्ञात कीजिए
![]()
(b) ड्यूटीरियम एवं ट्राइटियम दोनों की त्रिज्या लगभग 1.5 फैमटोमीटर मान लीजिए। इस अभिक्रिया में, दोनों नाभिकों के मध्य कूलॉम प्रतिकर्षण से पार पाने के लिए कितनी गतिज ऊर्जा की आवश्यकता है? अभिक्रिया प्रारम्भ करने के लिए गैसों (D तथा T गैसें) को किस ताप तक ऊष्मित किया जाना चाहिए?
(संकेत : किसी संलयन क्रिया के लिए आवश्यक गतिज ऊर्जा = संलयन क्रिया में संलग्न कणों की औसत तापीय गतिज ऊर्जा = \(\mathbf{2}\left(\frac{3 \boldsymbol{k} \boldsymbol{T}}{\mathbf{2}}\right) ; \boldsymbol{k}:\) बोल्ट्जमान नियतांक तथा T = परम ताप)
हल
(a) दी गई अभिक्रिया का समीकरण निम्नलिखित है
\(_{1}^{2} \mathrm{H}+_{1}^{3} \mathrm{H} \longrightarrow_{2}^{4} \mathrm{He}+_{0}^{1} n+Q\)
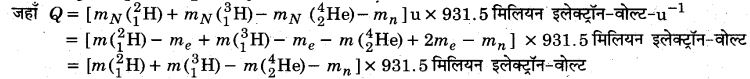
= [2.014102 + 3.016049- 4.002603-1.008665] x 931.5
= 0.018883x 931.5
= 17.59 मिलियन इलेक्ट्रॉन-वोल्ट।
(b) ड्यूटीरियम तथा ट्राइटियम प्रत्येक पर आवेश.
q1 + q2 = + 1.6 x 10-19 कूलॉम .
प्रत्येक की त्रिज्या r = 1.5 फैमटोमीटर
= 1.5×10-15 मीटर
दोनों के बीच कूलॉम अवरोध U = निकाय की विद्युत स्थितिज ऊर्जा जबकि दोनों परस्पर सम्पर्क में हैं।

माना उक्त कूलॉम अवरोध को पार करने के लिए प्रत्येक कण को K गतिज ऊर्जा की आवश्यकता होती है।
तब K+ K=U
⇒ 2K =U
अतः कुल गतिज ऊर्जा \(=\frac{7.68 \times 10^{-14}}{1: 6 \times 10^{-19}}\) इलेक्ट्रॉन-वोल्ट
= 480.0 किलो इलेक्ट्रॉन-वोल्ट।
परन्तु कण की तापीय गतिज ऊर्जा
K = \(\frac{3}{2} k T\)
\(\frac{3}{2} k T=\frac{1}{2} U \quad \Rightarrow \quad T=\frac{U}{3 k}\)
अभीष्ट परम ताप T = \(\frac{7.68 \times 10^{-14}}{3 \times 1.38 \times 10^{-23}}\)
= 1.85x 109K
प्रश्न 29.
नीचे दी गई क्षय-योजना में, १-क्षयों की विकिरण आवृत्तियाँ एवं -कणों की अधिकतम गतिज ऊर्जाएँ ज्ञात कीजिए। दिया है :
m (198Au) = 197.968233u
m (198Hg) = 197.966760u
हल
चित्र से, E1 = \(\begin{array}{l}{198} \\ {80}\end{array} \mathrm{Hg}\) की निम्नतम अवस्था में ऊर्जा = 0 मिलियन इलेक्ट्रॉन-वोल्ट
E2 = \(\begin{array}{l}{198} \\ {80}\end{array} \mathrm{Hg}\) की प्रथम उत्तेजित अवस्था में ऊर्जा = 0.412 मिलियन इलेक्ट्रॉन-वोल्ट
E3 = \(\begin{array}{l}{198} \\ {80}\end{array} \mathrm{Hg}\) की द्वितीय उत्तेजित अवस्था में ऊर्जा = 1.088 मिलियन इलेक्ट्रॉन-वोल्ट
माना उत्सर्जित γ फोटॉनों (γ1,γ2 व γ3) की आवृत्तियाँ क्रमशः ν1,ν2 व ν3 हैं। –
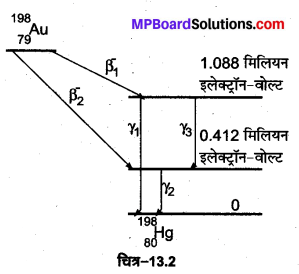
तब
ν1 = \(\frac { ΔE }{ h }\) = \(\frac{E_{3}-E_{1}}{h}\)
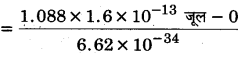
= 2.63 x 1020 हर्ट्स।
ν2 = \(\frac{E_{2}-E_{1}}{h}\)
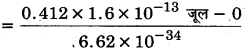
= 9.96 x 1019 हर्ट्स।
ν3 = \(\frac{E_{3}-E_{2}}{h}\)
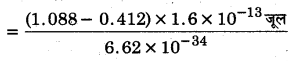
6.62x 10-34
= 1.63x 1020 हर्ट्स।
जबकि इन फोटॉनों की ऊर्जाएँ निम्नलिखित हैं –
E(γ1) = E3 – E1
= 1.088 मिलियन इलेक्ट्रॉन-वोल्ट ।
E(γ2)= E2 – E1
= 0.412 मिलियन इलेक्ट्रॉन-वोल्ट
E(γ3) = E3 – E2= 1.088-0.412 .
= 0.676 मिलियन इलेक्ट्रॉन-वोल्ट
\(\begin{array}{l}{198} \\ {79}\end{array} \mathrm{Au}\) के β1–-क्षय में Au नाभिक पहले एक β कण उत्सर्जित करता है तत्पश्चात् 11-फोटॉन को उत्सर्जित करके \(\begin{array}{l}{198} \\ {80}\end{array} \mathrm{Hg}\) नाभिक में बदल जाता है, अत: \(\begin{array}{l}{198} \\ {80}\end{array} \mathrm{Au}\) के E(β1–) -क्षय का समीकरण निम्नलिखित है
\(_{79}^{198} \mathrm{Au} \longrightarrow_{80}^{198} \mathrm{Hg}+_{-1}^{0} e+\cdot E\left(\beta_{1}^{-}\right)+E\left(y_{1}\right)\)
यहाँ E(β1–) तथा E(γ1) इन कणों की ऊर्जाएँ हैं। स्पष्ट है कि E(β1–) का मान अधिकतम होमा यदि \(\begin{array}{l}{198} \\ {80}\end{array} \mathrm{Hg}\) की गतिज ऊर्जा शून्य हो। अर्थात् अभिक्रिया की सम्पूर्ण ऊर्जा केवल 8-कण तथा y-फोटॉन की ऊर्जा के रूप में निकले।
β-कण की महत्तम गतिज ऊर्जा

\(\begin{array}{l}{198} \\ {79}\end{array} \mathrm{Au}\) के β2–-क्षय में Au नाभिक पहले β-कण उत्सर्जित करता है तत्पश्चात् γ2 फोटॉन उत्सर्जित करता हुआ \(\begin{array}{l}{198} \\ {80}\end{array} \mathrm{Hg}\) नाभिक में बदल जाता है।
इस क्षय का समीकरण निम्नलिखित है-
\(_{79}^{198} \mathrm{Au} \longrightarrow_{80}^{198} \mathrm{Hg}+_{-1}^{0} e+E\left(\beta_{2}^{-}\right)+E\left(\gamma_{2}\right)\)
∴ उत्सर्जित β2– -कण की महत्तम गतिज ऊर्जा .

प्रश्न 30.
सूर्य के अभ्यन्तर में (a) 1 किग्रा हाइड्रोजन के संलयन के समय विमुक्त ऊर्जा का परिकलन कीजिए। (b) विखण्डन रिऐक्टर में 1.0 किग्रा 235U के विखण्डन में विमुक्त ऊर्जा का परिकलन कीजिए। (c) प्रश्न के खण्ड (a) तथा (b) में विमुक्त ऊर्जाओं की तुलना कीजिए।
हल :
(a) सूर्य के अभ्यन्तर में हाइड्रोजन के 4 परमाणु निम्नलिखित अभिक्रिया के अनुसार संलयित होकर . हीलियम परमाणु का निर्माण करते हैं तथा लगभग 26 मिलियन इलेक्ट्रॉन-वोल्ट ऊर्जा उत्पन्न होती है।
![]()
∵ हाइड्रोजन का ग्राम परमाणु द्रव्यमान = 1 ग्राम
∴ 1 ग्राम हाइड्रोजन में उपस्थित परमाणुओं की संख्या = 6.02 × 1023
∴ 1 किग्रा (= 1000 ग्राम) में उपस्थित परमाणुओं की संख्या = 6.02 × 1026
∵ हाइड्रोजन के 4 परमाणुओं से उत्पन्न ऊर्जा = 26 मिलियन इलेक्ट्रॉन-वोल्ट
∴ 1 परमाणु से उत्पन्न ऊर्जा = \(\frac { 26 }{4 }\) मिलियन. इलेक्ट्रॉन-वोल्ट
∴ 6.02 × 1026 परमाणुओं से उत्पन्न ऊर्जा = \(\frac{26 \times 6.02 \times 10^{26}}{4}\)
= 39.13 × 1026 मिलियन इलेक्ट्रॉन-वोल्ट
∴ सूर्य के अभ्यन्तर में ‘1 किग्रा हाइड्रोजन के संलयन से उत्पन्न ऊर्जा
.. = 39.13 × 1026 मिलियन इलेक्ट्रॉन-वोल्ट। .
(b) हम जानते हैं कि विखण्डन रिऐक्टर में निम्न अभिक्रिया के अनुसार \(\begin{array}{l}{235} \\ {92}\end{array} \mathrm{u}\) के एक परमाणु के विखण्डन से. लगभग 200 मिलियन इलेक्ट्रॉन-वोल्ट ऊर्जा उत्पन्न होती है।
\(_{92}^{235} \mathrm{U}+_{0}^{1} n \longrightarrow_{56}^{141} \mathrm{Ba}+_{36}^{92} \mathrm{Kr}+3_{0}^{1} n+200\) मिलियन इलेक्ट्रॉन-वोल्ट ऊर्जा
∵ 235 ग्राम यूरेनियम में परमाणुओं की संख्या = 6.02 × 1023
∴ 1 ग्राम यरेनियम में परमाणओं की संख्या = \(\frac{6.02 \times 10^{23}}{235}\)
∴ 1 किग्रा (= 1000 ग्राम) यूरेनियम में परमाणुओं की संख्या = \(\frac{6.02 \times 10^{23} \times 1000}{235}\)
= 25.62 × 1023
1 परमाणु के विखण्डन से प्राप्त ऊर्जा = 200 मिलियन इलेक्ट्रॉन-वोल्ट
∴ 25.62 × 1023 परमाणुओं से प्राप्त ऊर्जा = 200 × 25.62 × 1023
= 5.124 × 1026 मिलियन इलेक्ट्रॉन-वोल्ट
या 1 किग्रा \(\begin{array}{l}{235} \\ {92}\end{array} \mathrm{u}\) के विखण्डन से प्राप्त ऊर्जा = 5.12 × 1026 मिलियन इलेक्ट्रॉन-वोल्ट।
(c)

= 7.64≈8
अर्थात् 1 किग्रा हाइड्रोजन के संलयन से प्राप्त ऊर्जा, 1 किग्रा 235U के विखण्डन से प्राप्त ऊर्जा की लगभग 8 गुनी है।
![]()
प्रश्न 31.
मान लीजिए कि भारत का लक्ष्य 2020 तक 200,000 मेगावाट विद्युत शक्ति जनन का है। इसका 10% नाभिकीय शक्ति संयंत्रों से प्राप्त होना है। माना कि रिऐक्टर की औसत उपयोग दक्षता (ऊष्मा को विद्युत में परिवर्तन करने की क्षमता) 25% है। 2020 के अन्त तक हमारे देश को प्रति वर्ष कितने विखण्डनीय यूरेनियम की आवश्यकता होगी? 2350 प्रति विखण्डन उत्सर्जित ऊर्जा 200 मिलियन इलेक्ट्रॉन-वोल्ट है। ..
हल
कुल ऊर्जा लक्ष्य = 200,000 मिलियन/वाट
∴ नाभिकीय संयंत्रों से प्राप्त शक्ति = 10% × 200,000 मेगावाट
= \(\frac { 10 }{100 }\) × 200,000 × 106 वाट = 2 × 1010 वाट
∴ प्रतिवर्ष नाभिकीय संयंत्रों से प्राप्त ऊर्जा
= 2x 1010 जूल/सेकण्ड × 1 × 365 × 24 × 60 × 60 सेकण्ड
= 6.31x 1017 जूल
माना संयंत्रों में विखण्डन हेतु – किग्रा 235U की प्रतिवर्ष आवश्यकता होती है।
∵ 235 ग्राम 235U में परमाणुओं की संख्या = 6.02 × 1023
∴ 1 ग्राम 235U में परमाणुओं की संख्या = \(\frac{6.02 \times 10^{23}}{235}\)
∴ x किग्रा (= x × 1000 ग्राम) यूरेनियम में परमाणुओं की संख्य = \(\frac{6.02 \times 10^{23} \times x \times 10^{3}}{235}\)
= 25.62 x × x 1023
235U के एक परमाणु के विखण्डन से प्राप्त ऊर्जा = 200 मिलियन इलेक्ट्रॉन-वोल्ट
∴ x किग्रा 235U के परमाणुओं के विखण्डन से प्राप्त ऊर्जा
= 25.62 x × x 1023 × 200 मिलियन इलेक्ट्रॉन-वोल्ट
= 51.24 x × x 1025 मिलियन इलेक्ट्रॉन-वोल्ट
= 51.24 x × x 1025 × 1.6 × 10-13 जूल
= 81.98 x × x 1012 जूल
∵ संयंत्रों की दक्षता 25% है, अत: संयंत्रों से प्राप्त उपयोगी ऊर्जा
= η x 81.98 x × x 1012
= \(\frac { 25 }{100 }\) × 81.98 x × x 1012 जूल
∴ \(\frac { 25 }{100 }\) × 81.98 x × x 1012 = 6.31 x 1017
\( x=\frac{6.31 \times 10^{17} \times 100}{25 \times 81.98 \times 10^{12}}\)
= 3.078x 104 किग्रा।
नाभिक NCERT भौतिक विज्ञान प्रश्न प्रदर्शिका (Physics Exemplar LO Problems) पुस्तक से चयनित महत्त्वपूर्ण प्रश्नों के हल
नाभिक बहुविकल्पीय प्रश्नोत्तर
प्रश्न 1.
मान लीजिए हम ऐसे बहुत से पात्रों पर विचार करते हैं जिनमें प्रत्येक में प्रारम्भ में 1 वर्ष अर्द्ध-आयु वाले रेडियोऐक्टिव पदार्थ के 10000 परमाणु हैं। 1 वर्ष के पश्चात्
(a) सभी पात्रों में इस पदार्थ के 5000 परमाणु होंगे ।
(b) सभी पात्रों में इस पदार्थ के परमाणुओं की संख्या समान होगी, परन्तु यह लगभग 5000 होगी
(c) सामान्य तौर पर इन पात्रों में इस पदार्थ के परमाणुओं की संख्या समान होगी, परन्तु इनका औसत 5000 के निकट होगा
(d) किसी भी पात्र में इस पदार्थ के 5000 परमाणुओं से अधिक नहीं होंगे।
उत्तर
(c) सामान्य तौर पर इन पात्रों में इस पदार्थ के परमाणुओं की संख्या समान होगी, परन्तु इनका औसत 5000 के निकट होगा
प्रश्न 2.
किसी हाइड्रोजन परमाणु तथा m द्रव्यमान के किसी अन्य कण के मध्य गुरुत्वीय बल को न्यूटन के नियम द्वारा निरूपित किया जाएगा
\(\boldsymbol{F}=\boldsymbol{G} \frac{\boldsymbol{M} \cdot \boldsymbol{m}}{\boldsymbol{r}^{2}}\) यहाँ r किलोमीटर में है तथा
(a) M = mप्रोटॉन + mइलेक्ट्रॉन
(b) M = mप्रोटॉन + mइलेक्ट्रॉन \(-\frac{B}{c^{2}}\)(B= 18.6ev)
(c) M हाइड्रोजन परमाणु के द्रव्यमान से सम्बन्धित नहीं है
(d) M = mप्रोटॉन + mइलेक्टॉन \(-\frac{|V|}{c^{2}}\) (V = H-परमाणु में इलेक्ट्रॉन की स्थितिज ऊर्जा का परिमाण)।
उत्तर
(b) M = mप्रोटॉन + mइलेक्ट्रॉन \(-\frac{B}{c^{2}}\)(B= 18.6ev)
प्रश्न 3.
जब किसी परमाणु के नाभिक का रेडियोऐक्टिव विघटन होता है तो परमाणु के इलेक्ट्रॉनिक ऊर्जा स्तरों में
(a) किसी भी प्रकार की रेडियोऐक्टिवता के लिए कोई परिवर्तन नहीं होता
(b) α एवं β रेडियोऐक्टिवता के लिए परिवर्तन होते हैं, परन्तु γ रेडियोऐक्टिवता के लिए कोई परिवर्तन नहीं होते .
(c) α रेडियोऐक्टिवता के लिए परिवर्तन होते हैं, परन्तु अन्य के लिए नहीं
(d) β रेडियोऐक्टिवता के लिए परिवर्तन होते हैं, परन्तु अन्य के लिए नहीं।
उत्तर
(b) α एवं β रेडियोऐक्टिवता के लिए परिवर्तन होते हैं, परन्तु γ रेडियोऐक्टिवता के लिए कोई परिवर्तन नहीं होते .
प्रश्न 4.
ट्राइटियम हाइड्रोजन का एक समस्थानिक है जिसके नाभिक टाइटॉन में दो न्यूट्रॉन और एक प्रोटॉन है। मुक्त न्यूट्रॉन \(p+\bar{e}+\bar{v}\) में विघटित हो जाते हैं। यदि ट्राइटॉन के दो न्यूट्रॉनों में किसी एक न्यूट्रॉन का विघटन होता है, तो यह He3 नाभिक में रूपान्तरित हो जाता, परन्तु ऐसा नहीं होता क्योंकि
(a) ट्राइटॉन की ऊर्जा He3 नाभिक की ऊर्जा से कम होती है
(b) β-विघटन प्रक्रिया में उत्पन्न इलेक्ट्रॉन नाभिक के भीतर नहीं रह सकता
(c) ट्राइटॉन में दोनों न्यूट्रॉन साथ-साथ विघटित होते हैं, जिसके फलस्वरूप तीन प्रोटॉनों का एक नाभिक बनता है . जो He3 नाभिक नहीं होता
(d) क्योंकि मुक्त न्यूट्रॉन बाह्म क्षोभ के कारण विघटित होते हैं और ट्राइटॉन नाभिक में मुक्त न्यूट्रॉन नहीं होते।
उत्तर
(a) ट्राइटॉन की ऊर्जा He3 नाभिक की ऊर्जा से कम होती है
प्रश्न 5.
स्थायी भारी नाभिकों में न्यूट्रॉनों की संख्या प्रोटॉनों से अधिक होती है। इसका कारण यह है कि
(a) न्यूट्रॉन, प्रोटॉन से अधिक भारी होते हैं।
(b) प्रोटॉनों के बीच स्थिर विद्युत बल प्रतिकर्षणात्मक होता है
(c) β विघटन द्वारा न्यूट्रॉन, प्रोटॉनों में विघटित हो जाते हैं
(d) न्यूट्रॉनों के बीच नाभिकीय बल प्रोटॉन के बीच नाभिकीय बल की अपेक्षा दुर्बल होता है।
उत्तर
(b) प्रोटॉनों के बीच स्थिर विद्युत बल प्रतिकर्षणात्मक होता है
प्रश्न 6.
किसी नाभिकीय रिऐक्टर में अवमन्दक विखण्डन प्रक्रिया में मुक्त न्यूट्रॉनों की गति को मन्द कर देते हैं। अवमन्दक के रूप में हल्के नाभिकों का प्रयोग किया जाता है। भारी नाभिक यह उद्देश्य पूरा नहीं कर सकते, क्योंकि
(a) वे टूट जाएँगे
(b) भारी नाभिकों के साथ न्यूट्रॉनों का प्रत्यास्थ संघट्ट उन्हें धीमा नहीं करेगा
(c) रिऐक्टर का नेट भार अत्यधिक हो जाएगा
(d) भारी नाभिकों वाले पदार्थ कक्ष-ताप पर द्रव अथवा गैसीय अवस्था में नहीं पाए जाते।
उत्तर
(b) भारी नाभिकों के साथ न्यूट्रॉनों का प्रत्यास्थ संघट्ट उन्हें धीमा नहीं करेगा
![]()
नाभिक अति लघु उत्तरीय प्रश्नोत्तर
प्रश्न 1.
\(\begin{array}{l}{3} \\ {2}\end{array} \mathbf{H} \mathbf{e}\) तथा \(\begin{array}{l}{3} \\ {1}\end{array} \mathbf{H} \mathbf{e}\) नाभिकों की द्रव्यमान संख्याएँ समान हैं। क्या इनकी बन्धन ऊर्जाएँ भी समान हैं?
उत्तर
नहीं, \(\begin{array}{l}{3} \\ {2}\end{array} \mathbf{H} \mathbf{e}\) नाभिक की बन्धन ऊर्जाएँ तुलनात्मक रूप में अधिक होंगी।
प्रश्न 2.
सक्रिय नाभिकों की संख्या में परिवर्तन के साथ विघटन की दर में परिवर्तन । दर्शाने वाला ग्राफ खींचिए।
उत्तर :
सक्रिय नाभिकों की संख्या में विघटन की \(\left(-\frac{d N}{d t}\right) \propto N\)
प्रश्न 3.
चित्र-13.4 में दर्शाए दो नमूनों A तथा B में किसकी औसत आयु कम
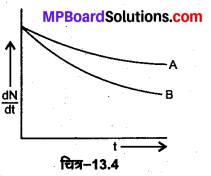
उत्तर
नमूने B के विघटन की दर अधिक है, अत: B की औसत आयु A की | तुलना में कम है।
प्रश्न 4.
निम्न में से कौन -विकिरण उत्सर्जित नहीं कर सकता और क्योंउत्तेजित नाभिक, उत्तेजित इलेक्ट्रॉन?
उत्तर
उत्तेजित इलेक्ट्रॉन γ-विकिरण उत्सर्जित नहीं कर सकता है क्योंकि इलेक्ट्रॉनिक ऊर्जा-स्तरों का ऊर्जा परास eV कोटि का होता है जबकि γ-विकिरण की ऊर्जा MeV कोटि की होती है।
प्रश्न 5.
युग्म विलोपन में एक इलेक्ट्रॉन तथा एक पॉजिट्रॉन एक-दूसरे का अस्तित्व समाप्त कर गामा विकिरण उत्पन्न करते हैं। इसमें संवेग संरक्षण कैसे होता है?
उत्तर
युग्म विलोपन में एक इलेक्ट्रॉन तथा एक पॉजिट्रॉन एक-दूसरे का अस्तित्व समाप्त कर दो गामा फोटॉन उत्पन्न करते हैं जो संवेग संरक्षण के लिए परस्पर विपरीत दिशाओं में गति करते हैं।
लघु उत्तरीय प्रश्नोत्तर
प्रश्न 1.
स्थायी नाभिकों में प्रोटॉनों की संख्या न्यूट्रॉनों की संख्या से कदापि अधिक नहीं हो सकती, क्यों?
उत्तर
नाभिक में उपस्थित प्रोटॉनों के बीच वैद्युत प्रतिकर्षण बल कार्य करता है। 10 से अधिक प्रोटॉन वाले नाभिक में यह प्रतिकर्षण बल इतना अधिक हो जाता है कि नाभिक के स्थायित्व के लिए न्यूट्रॉनों की संख्या, प्रोटॉनों की संख्या से अधिक होनी चाहिए।
प्रश्न 2.
यदि Z1 = N2 तथा Z2 = N1 हो तो किसी नाभिक को किसी दूसरे नाभिक का दर्पण समभारिक कहा जाता है।
(a) \(_{11}^{23} \mathrm{Na}\) का दर्पण समभारिक नाभिक क्या है?
(b) दो दर्पण समभारिकों में से किस नाभिक की बन्धन ऊर्जा अधिक है और क्यों? .
उत्तर
(a) \(_{11}^{23} \mathrm{Na}\) का दर्पण समभारिक नाभिक \(_{12}^{23} \mathrm{Na}\) है।
(b) यहाँ Z2 > Z1, अतः Mg नाभिक की बन्धन ऊर्जा Na नाभिक से अधिक है।
![]()
नाभिक आंकिक प्रश्नोत्तर
प्रश्न 1.
किसी प्राचीन इमारत के खण्डहर से प्राप्त लकड़ी के एक टुकड़े में 14C की सक्रियता इसके कार्बन अंश की 12 विघटन प्रति मिनट प्रति ग्राम पायी जाती है। किसी सजीव लकड़ी की 14C की सक्रियता 16 विघटन प्रति मिनट प्रति ग्राम होती है। कितने समय से पूर्व वह वृक्ष जिसकी लकड़ी का यह प्राप्त नमूना है, काटा गया था?
14C की अर्द्ध-आयु 5760 वर्ष है।
हल
दिया है, R= 12 विघटन प्रति मिनट प्रति ग्राम
R0 = 16 विघटन प्रति मिनट प्रति ग्राम .
अर्द्ध-आयु (T) = 5760 वर्ष ।