In this article, we share MP Board Class 12th Maths Book Solutions Chapter 5 सांतत्य तथा अवकलनीयता Ex 5.8 Pdf, These solutions are solved by subject experts from the latest MP Board books.
MP Board Class 12th Maths Book Solutions Chapter 5 सांतत्य तथा अवकलनीयता Ex 5.8
प्रश्न 1.
फलन f(x) = x2 + 2x – 8, x ϵ [-4, 2] के लिए रोले के प्रमेय को सत्यापित कीजिए।
हल:
फलन f(x) = x2 + 2x – 8, अंतराल [-4, 2] में संतत तथा अंतराल (-4, 2) में अवकलनीय है।
तथा f(-4) = 16 – 8 – 8 = 0
f(2) = 4 + 4 – 8 = 0
⇒ f(-4) = f(2)
अत: रोले के प्रमेय की सभी शर्ते सन्तुष्ट हैं तब रोले के प्रमेय के अनुसार एक बिन्दु CE(-4, 2), जहाँ f’ (c) = 0
⇒ f'(c) = 0
⇒ 2c + 2 =0 (::f’ (x) = 2x + 2)
⇒ c = -1
इसलिए c = -1 पर f’ (c) = 0 और c = -1 ϵ (-4, 2)
प्रश्न 2.
जाँच कीजिए कि क्या रोले का प्रमेय निम्नलिखित फलनों में से किन-किन पर लागू होता है। इन उदाहरणों से क्या आप रोले के प्रमेय के विलोम के बारे में कुछ कह सकते हैं?
(i) f(x) = |x| के लिए x ϵ [5, 9]
(ii) f(x) = |x| के लिए x ϵ [-2, 2]
(iii) f(x) = x2 – 1 के लिए x ϵ [1, 2]
हल:
(i) f(x) = [x] के लिए x ϵ [5, 9]
f(x) = [x], बिन्दु x = 6, 7, 8 पर न तो संतत है और न ही अवकलनीय है।
अतः रोले प्रमेय लागू नहीं है।
(ii) f(x) = [x], x ϵ [-2, 2]
f(x) = [x], बिन्दु x = -1, 0, 1 पर न तो संतत है और न ही अवकलनीय है।
अतः रोले प्रमेय लागू नहीं है।
(iii) f(x) = (x2 – 1), x ϵ [1, 2] के लिए
f(1) = 1 – 1 = 0 f(2) = 22 – 1 = 4 – 1 = 3
f(1) ≠ f(2)
यद्धपि f[1, 2] में संतत है तथा फलन (1, 2) अवकलनीय भी है परन्तु f(1) ≠ f(2).
अतः रोले प्रमेय लागू नहीं है।
प्रश्न 3.
यदि f: [-5, 5] → R एक संतत फलन है और यदि f’ (x) किसी भी बिन्दु पर शून्य नहीं होता है तो सिद्ध कीजिए कि f(-5) ≠ f(5).
हल:
यहाँ f : [-5, 5] →R
f संतत है तथा अवकलनीय है परन्तु f'(x) ≠ 0
अन्तराल (-5, 5) में रोले प्रमेय के लिए आवश्यक है-
यदि (i) [a, b] में f संतत है।
(ii) (a, b) में f अवकलित होता है।
(iii) f(a) = f(b)
तब f'(c) = 0, c ϵ (a, b)
यहाँ f'(c) ≠ 0 ⇒ f(a) ≠ f(b)
अतः f(-5) ≠ f(5)
![]()
प्रश्न 4.
माध्यमान प्रमेय सत्यापित कीजिए, यदि अंतराल [a, b] में f(x) = x2 – 4x – 3, जहाँ a = 1 और b = 4 है।
हल:
∵ f'(x) = x2 – 4x – 3 एक बहुपद है जो कि प्रत्येक बिन्दु पर संतत होगा।
∴ f'(x) = 2x – 4
⇒ f(x) का अस्तित्व है ∀ x ϵ (1, 4)
⇒ f(x), अंतराल (1, 4) में अवकलनीय है
माध्यमान प्रमेय द्वारा

अतः माध्यमान प्रमेय सत्यापित है।
प्रश्न 5.
माध्यमान प्रमेय सत्यापित कीजिए. यदि अन्तराल [a, b] में f(x) = x3 – 5x2 – 3x, जहाँ a = 1 और b= 3 है। f'(c)= 0 के लिए c ϵ (1, 3) को ज्ञात कीजिए।
हल:
यहाँ f(x) = x3 – 5x2 – 3x
[1, 3] में f संतत है तथा (1, 3) में अवकलनीय है क्योंकि यह बहुपदीय है।
f(1) = (1)3 – 5(1)2 – 3 x 1
= 1 – 5 – 3 = 1 – 8 = -7
f(3) = (3)3 – 5(3)2 – 3 x 3
= 27 – 45 – 9 = – 27
f(x) = 3x2 – 10x – 3
f(c)= 3c2 – 10c – 3
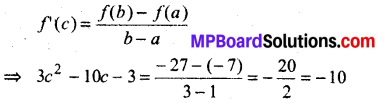
⇒ 3c2 – 10c – 3 = \(\)
⇒ 3c2 – 10c + 7= 0
⇒ (c – 1)(3c – 7) = 0
∴ c ≠ 1 c = \(\frac{7}{3}\) ϵ (1, 3)
यदि f'(c)= 0
तब 3c2 – 10c – 3 = 0
⇒ (3c – 1)(c – 3) = 0 ⇒ c = \(\frac{1}{3}\), 3 + c ∉ (1, 3)
![]()
प्रश्न 6.
प्रश्न संख्या 2 में उपर्युक्त दिए तीनों फलनों के लिए माध्यमान प्रमेय की अनुपयोगिता की जाँच कीजिए।
हल:
(i) f(x)=[x], x ϵ [5, 9].
अन्तराल (5, 9) में f(x) = [x] बिन्दु x = 6, 7, 8 पर न तो संतत है और न ही अवकलनीय है।
अतः माध्यमान प्रमेय लागू नहीं है।
(ii) f(x) ⊂ [x], x ϵ [-2, 2]
अन्तराल [-2, 2] में | बिन्दु x= -1, 0, 1 पर न तो संतत है और न ही अवकलनीय है।
अतः माध्यमान प्रमेय लागू नहीं है।.
(iii) f(x) = x2 – 1, x ϵ [1, 2]
एक बहुदीय है। यह अन्तराल [1, 2] में संतत है तथा (1, 2) में अवकलनीय है।
f(1) = (1)2 – 1 = 1 – 1 = 0
f(2) = (2)2 – 1 = 4 – 1 = 3
f'(x) = 2x
f'(c) = 2c
