MP Board Class 11th Maths Solutions Chapter 10 सरल रेखाएँ विविध प्रश्नावली
प्रश्न 1.
k के मान । ज्ञात कीजिए जब कि रेखा (k – 3)x – (4 – k2)y + K2 – 7k + 6 = 0
(a) x-अक्ष के समान्तर है।
(b) y-अक्ष के समान्तर है।
(c) मूल बिन्दु से जाती है।
हल:
(i) x-अक्ष के समान्तर y = a
∴ प्रश्न में दिए गए समीकरण में x का गुणांक = 0 या k – 3 = 0 अर्थात् k = 3.
(ii) xy-अक्ष के समान्तर रेखा x =q
दिए गए समीकरण में y का गुणांक = 0 या 4 – k2 = 0 अर्थात् k = ± 2.
(iii) यदि रेखा मूल बिन्दु से जाती है तो (0, 0) इसके समीकरण को संतुष्ट करेगा।
0 – 0 + K2 – 7k + 6 = 0 या (k – 6) (k – 1) = 0 या k = 1, 6.
![]()
प्रश्न 2.
θ और p के मान ज्ञात कीजिए यदि समीकरण x cos θ + y sin θ = p रेखा \(\sqrt{3}\)x + y + 2 = 0 का लम्ब रूप है।
हल:

प्रश्न 3.
उन रेखाओं के समीकरण ज्ञात कीजिए जिनके अक्षों से कटे अंतःखण्डों का योग और गुणनफल क्रमशः 1 और – 6 हैं।
हल:
मान लीजिए अक्षों पर कटे अतः खण्ड a और b हैं।
दिया है : a + b = 1, ab = – 6
b = 1 – a
∴ a(1 – a) = – 6
या a – a2 = – 6
a2 – a – 6 = 0
या (a – 3) (a + 2) = 0
∴ a = 3, – 2
∴ b = – 2, 3
3, – 2 अंत:खण्ड वाली रेखा का समीकरण,
\(\frac{x}{3}+\frac{y}{-2}\) = 1
या 2x – 3y = 6.
और – 2, 3 अंत:खण्ड वाली रेखा का समीकरण,
\(\frac{x}{-2}+\frac{y}{3}\) = 1
या – 3x + 2y = 6.
प्रश्न 4.
y-अक्ष पर कौन से बिन्दु ऐसे हैं, जिनकी रेखा \(\frac{x}{3}+\frac{y}{4}\) = 1 से दूरी 4 इकाई है।
हल:
मान लीजिए y-अक्ष पर बिन्दु (0, y1) है।
(0, y1) की रेखा 4x + 3y = 12 से दूरी
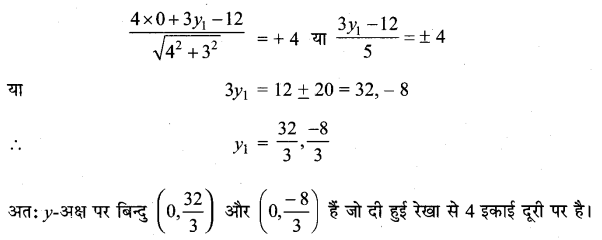
प्रश्न 5.
मूल बिन्दु से बिन्दुओं (cos θ, sin θ) और (cos ϕ, sin ϕ) को मिलाने वाली रेखा की लांबिक दूरी ज्ञात कीजिए।
हल:
(cos θ, sin θ), (cos ϕ, sin ϕ) को मिलाने वाली रेखा का समीकरण,

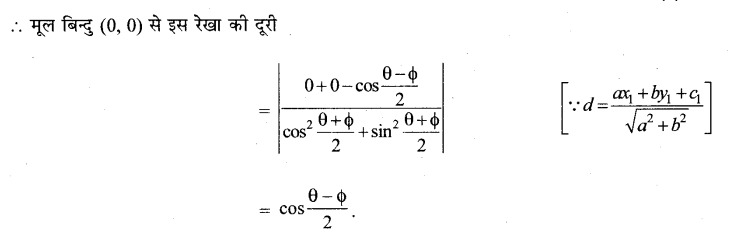
प्रश्न 6.
रेखाओं x – 7y + 5 = 0 और 3x + y = 0 के प्रतिच्छेद बिन्दु से खीची गई और y-अक्ष के समान्तर रेखा का समीकरण ज्ञात कीजिए।
हल:
दी गयी रेखाएँ
x – 7y + 5 = 0 …(1)
3x + y = 0 …(2)
समी (2) से,
y = – 3x
y का मान समी (1) में रखने पर,
x – 7(- 3x) + 5 = 0
या 22x + 5 = 0
x = \(\frac{-5}{22}\)
अब y = – 3x = – \(3\left(\frac{-5}{22}\right)\) = \(\frac{15}{22}\)
वह रेखा का जो \(\left(-\frac{5}{22}, \frac{15}{22}\right)\) से जाती है और y-अक्ष के समान्तर है, समीकरण x = – \(\frac{5}{22}\) या 22x + 5 = 0.
![]()
प्रश्न 7.
रेखा \(\frac{x}{4}+\frac{y}{6}\) = 1 पर लंब उस बिन्दु से खींची गई रेखा का समीकरण ज्ञात कीजिए जहाँ यह रेखा y-अक्ष से मिलती है।
हल:
रेखा AB का समीकरण,
\(\frac{x}{4}+\frac{y}{6}\) = 1 या 3x + 2y = 12,
2y = – 3x + 12
y = \(\frac{-3}{2} x+\frac{12}{2}\)
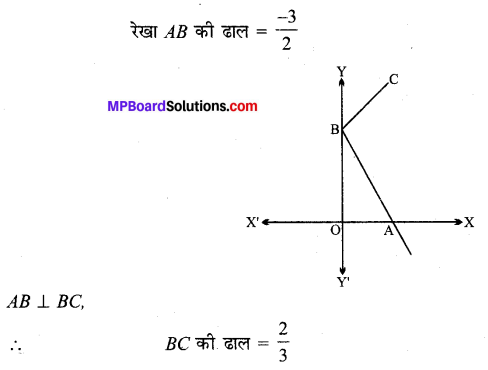
∵ रेखा y-अक्ष पर प्रतिच्छेद करती है, इसलिए बिन्दु B(0, 6) है।
∴ BC रेखा का समीकरण
y – 6 = \(\frac{2}{3}\)(x – 0)
या 3y – 18 = 2x
या 2x – 3y + 18 = 0.
प्रश्न 8.
रेखाओं y – x = 0, x + y = 0, और x – k = 0 से बने त्रिभुज का क्षेत्रफल ज्ञात कीजिए।
हल:
y – x = 0 और y + x = 0 बिन्दु (0, 0) पर मिलते हैं।
x = k को y – x = 0 में रखने से, y – k = 0 या y = k
x – k = 0 और y – x = 0 बिन्दु (k, k) पर मिलते हैं।
x = k को y + x = 0 में रखने से,
y + k = 0 या y = – k
x = k और y + x = 0 बिन्दु (k, – k) पर मिलते हैं।
अब बिन्दु (0, 0), (k, k) और (k, – k) से बने त्रिभुज का क्षेत्रफल
= \(\left|\frac{1}{2}[0 .(-2 k)+k(-k)+k(-k)]\right|\)
= \(\left|\frac{1}{2}\left(-k^{2}-k^{2}\right)\right|\)
= k2 वर्ग इकाई।
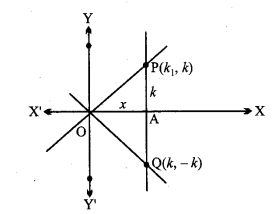
दूसरी विधि : त्रिभुज OPQ का क्षेत्रफल
= 2 × क्षेत्रफल ∆OAP
= 2 × [\(\frac{1}{2}\) × k × k] = k2 वर्ग इकाई।
प्रश्न 9.
p का मान ज्ञात कीजिए जिससे तीन रेखाएँ 3x + y – 2 = 0, px + 2y – 3 = 0 और 2x – y – 3 = 0 एक बिन्दु पर प्रतिच्छेद करें।
हल:
दी गयी रेखाएँ
3x + y = 2 …(1)
2x – y = 3 …(2)
समी (1) और (2) को जोड़ने पर,
5x = 5 या x = 1
∴ y = 2 – 3x = 2 – 3 = – 1
∴ समी (1) और (2) वाली रेखाएँ बिन्दु (1, – 1) पर प्रतिच्छेद करती हैं।
तीसरी रेखा px + 2y – 3 = 0 भी इसी बिन्दु से जाती है इसलिए (1, – 1) इस समीकरण को संतुष्ट करेगा।
p × 1 + 2 × (- 1) – 3 = 0
p – 2 – 3 = 0
∴ p = 5
अतः दी गयी रेखाएँ संगामी हैं यदि p = 5.
प्रश्न 10.
यदि तीन रेखाएँ जिनके समीकरण y = m1x + c1, y = m2x + c2 और y =m3x + c3 हैं, संगामी हैं, तो दिखाइए कि m1(c2 – c3) + m2(c3 – c1) + m3(c1 – c2) = 0.
हल:
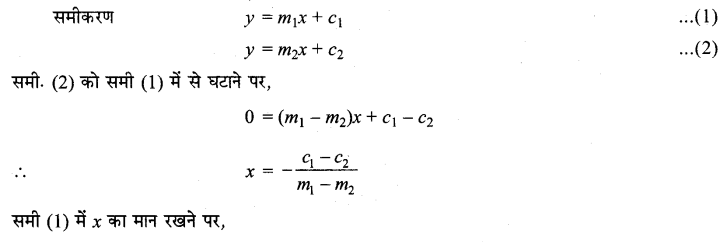

प्रश्न 11.
बिन्दु (3, 2) से जाने वाली उस रेखा का समीकरण ज्ञात कीजिए जो रेखा x – 2y = 3 से 45° का कोण बनाती है।
हल:
माना रेखा AB का समीकरण : x – 2y = 3
या y = \(\frac{1}{2}\)x – 3
तब रेखा AB की ढाल = \(\frac{1}{2}\)
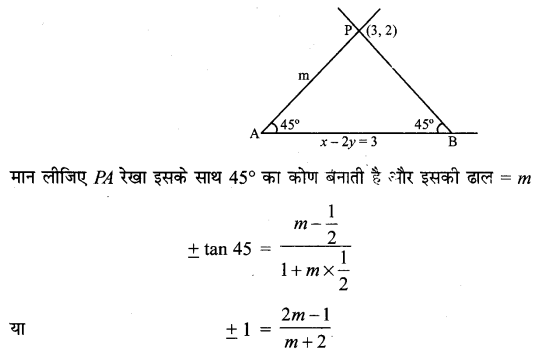
+ve चिन्ह लेने पर, 1 = \(\frac{2 m-1}{m+2}\)
या 2m – 1 = m + 2
∴ m = 3
2m -1
– ve चिन्ह लेने पर, – 1 = \(\frac{2 m-1}{m+2}\)
या 2m – 1 = – m – 2
∴ 3m = – 1
या m = \(\frac{-1}{3}\)
अतः रेखा PA का समीकरण जहाँ बिन्दु P = (3, 2) हो और m = \(\frac{-1}{3}\) हो।
y – 2 = – \(\frac{-1}{3}\)(x – 3)
3y – 6 = – x + 3
या x + 3y – 9 = 0
अब जब ढाल m = 3 हो, तब बिन्दु P(3, 2) से रेखा का समीकरण,
y – 2 = 3(x – 3)
y – 2 = 3x – 9
या 3x – y – 7 = 0.
![]()
प्रश्न 12.
रेखाओं 4x + 7y – 3 = 0 और 2x – 3y + 1 = 0 के प्रतिच्छेद बिन्दु से जाने वाली रेखा का समीकरण ज्ञात कीजिए जो अक्षों से समान अंतः खण्ड बनाती हैं।
हल:
4x + 7y = 3 …(1)
2x – 3y = – 1 …(2)
समी (2) को 2 से गुणा करने पर,
4x – 6y = – 2 …(3)
समी (3) को (1) में से घटाने पर
13y = 5
∴ y = \(\frac{5}{13}\)
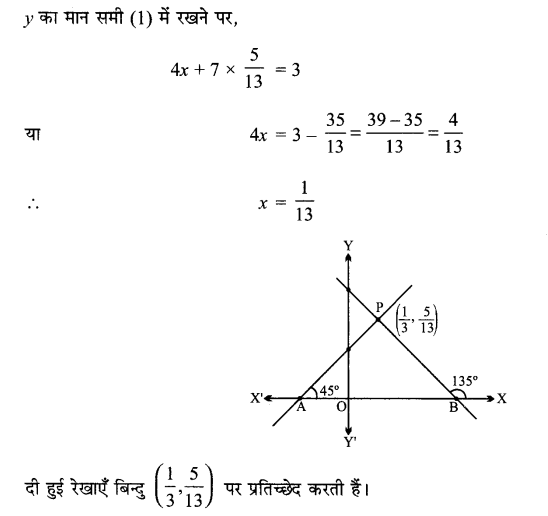
जो रेखा अक्षों पर बने अंतः खण्ड समान हैं तो वह धन x-अक्ष के साथ 45° या 135° का कोण बनाती हैं। इसलिए उसकी ढाल ±1 होगी।
∴ PA और PB रेखाओं के समीकरण
y – y1 = m(x – x1)
(i) जब m = 1 हो, तब y – \(\frac{5}{13}\) = 1 \(\left(x-\frac{1}{13}\right)\)
या 13y – 5 = 13 x – 1 या 13x – 13y + 4 = 0.
(i) जब m = – 1 हो, तब y – \(\frac{5}{13}\) = 1 \(\left(x-\frac{1}{13}\right)\)
13y – 5 = – 13x + 1
∴ 13x + 13y – 6 = 0.
प्रश्न 13.
दर्शाइए कि मूल बिन्दु से जाने वाली और रेखा y = mx + c से θ कोण बनाने वाली उस रेखा का समीकरण \(\frac{y}{x}=\pm \frac{m+\tan \theta}{1-m \tan \theta}\) हैं।
हल:
रेखा PA का समीकरण y = mx + c है
यह रेखा OP के साथ कोण θ बनाती है।
रेखा PA की ढाल = m
मान लीजिए OP की ढाल = m1 है।
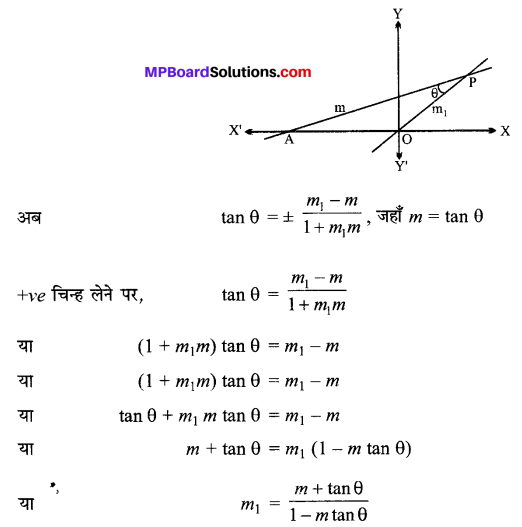

या \(\frac{y}{x}\) = m1
∴ अभीष्ट रेखाओं का समीकरण
\(\frac{y}{x}\) = \(\frac{m \pm \tan \theta}{1 \mp m \tan \theta}\)
प्रश्न 14.
(- 1, 1) और (5, 7) को मिलाने वाली रेखाखण्ड को रेखा x + y = 4 किस अनुपात में विभाजित करती है ?
हल:
मान लीजिए बिन्दु P रेखाखण्ड AB को k : 1 के अनुपात में विभाजित करता है। जबकि A और B के क्रमशः (- 1, 1) और (5, 7) निर्देशांक हैं।

अतः बिन्दु P रेखाखण्ड AB को 1 : 2 के अनुपात में विभाजित करता है। .
प्रश्न 15.
बिन्दु (1, 2) से रेखा 4x + 7y + 5 = 0 की 2x – y = 0 के अनुदिश दूरी ज्ञात करो।
हल:
माना रेखा PC का समीकरण, 2x – y = 0 जिस पर बिन्दु P(1, 2) स्थित है।
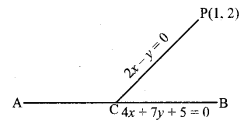
रेखा AB का समीकरण 4x + 7y + 5 = 0 और 2x – y = 0 को हल करने पर,
∴ x = \(\frac{-5}{18}\)
और y = \(-\frac{5}{9}\)
प्रश्न 16.
बिन्दु (- 1, 2) से खींची जा सकने वाली उस रेखा की दिशा ज्ञात कीजिए जिसका रेखा x + y = 4 से प्रतिच्छेदन बिन्दु दिए बिन्दु से 3 इकाई की दूरी पर है।
हल:
मान लीजिए अभीष्ट रेखा PQ की ढाल m है
रेखा PQ जो बिन्दु P(- 1, 2) से होकर जाती है और ढाल m है, का समीकरण
y – y1 = m(x – x1)
y – 2 = m(x + 1)
या mx – y + m + 2 = 0 …(1)
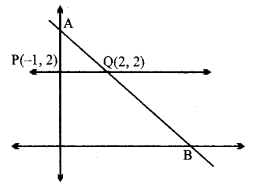
रेखा AB का समीकरण x+ y = 4
∴ y = 4 – x
y का मान समी (1) में रखने पर,
mx – (4 – x) + m + 2 = 0
या (m + 1) x + m – 2 = 0
∴ x = – \(\frac{m-2}{m+1}\)
अब y = 4 – x = 4 + \(\frac{m-2}{m+1}\)

अतः रेखा PQ की ढाल 0 है अर्थात् रेखा x-अक्ष के समांतर है।
प्रश्न 17.
समकोण त्रिभुज के कर्ण के अंत्य बिन्दु (1, 3) और (- 4, 1) हैं। त्रिभुज के पाद (leg) (समकोणीय भुजाओ) का एक समीकरण ज्ञात कीजिए।
हल:
माना त्रिभुज ABC एक समकोणीय त्रिभुज है जिसका कर्ण AB है। A और B के निर्देशांक क्रमशः (1, 3) और (- 4, 1) हैं।
मान लीजिए BC की ढाल m है।
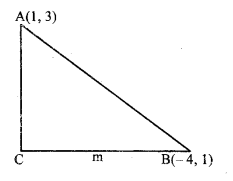
AC ⊥ BC
∴ AC की ढाल = – \(\frac{1}{m}\)
रेखा BC का समीकरण,
y – y1 = m(x – x1)
y – 1 = m(x + 4)
या mx – y + 4m + 1 = 0 …(1)
रेखा AC का समीकरण
y – 3 = – \(\frac{1}{m}\)(x – 1)
या my – 3m = – x + 1
या x + my – 3m – 1 = 0 …(2)
यह दोनों रेखाएँ m के दिए मान से इन का समीकरण ज्ञात कर सकते हैं। यदि BC भुजा x-अक्ष के समांतर हो तो m = 0.
BC का समीकरण, y – 1 = 0
या y = 1
∴ AC, y-अक्ष के समांतर हो और यह A(1, 3) से जाती है। अतः AC का समीकरण x = 1
अत: BC और AC के समीकरण y = 1 और x = 1 हैं।
![]()
प्रश्न 18.
किसी बिन्दु के लिए रेखा को दर्पण मानते हुए बिन्दु (3, 8) का रेखा x + 3y = 7 में प्रतिबिंब ज्ञात कीजिए।
हल:
माना रेखा AB का समीकरण x + 3y = 7 है और बिन्दु P के निर्देशांक (3, 8) हैं।
y = – \(\frac{1}{3} x +\frac{7}{3}\)
बिन्दु P का प्रतिबिंब Q होगा यदि PQ ⊥ AB, PQ और AB बिन्दु M पर इस प्रकार प्रतिच्छेद करते हैं कि
PM = QM
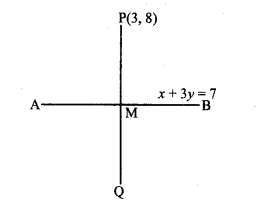
रेखा AB की ढाल = – \(\frac{1}{3}\)
और PQ की ढाल = 3
∴ PQ रेखा का समीकरण,
y – 8 = 3(x – 3)
= 3x – 9
या 3x – y = 1 …(1)
AB का समीकरण x + 3y = 7 …(2)
समी (1) को 3 से गुणा करके समी (2) में जोड़ने पर,
10x = 10 या x = 1
समी (1) से y = 3x – 1 = 3 – 1 = 2
∴ बिन्दु M के निर्देशांक (1, 2) हैं।
मान लीजिए Q के निर्देशांक (x1, y1) हैं
बिन्दु M रेखाखण्ड PQ का मध्य बिन्दु है
∴ जबकि P(3, 8) है।
∴ \(\frac{x_{1}+3}{2}\) = 1 या x1 = – 1
\(\frac{y_{1}+8}{2}\) = 2 या y1 = – 4
∴ P का प्रतिबिंब (- 1, – 4) हैं।
प्रश्न 19.
यदि रेखाएँ y = 3x + 1 और 2y = x + 3, रेखा y = mx + 4 पर समान रूप से आनत हो तो m का मान ज्ञात कीजिए।
हल:
रेखा AB का समीकरण, y = 3x + 1 की ढाल = 3
रेखा BC का समीकरण, y = mx + 4 को ढाल = m
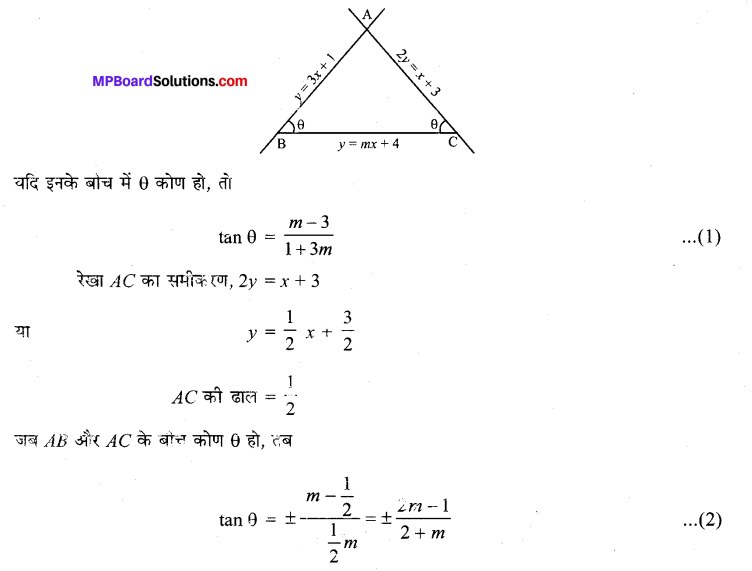

अतः m का अभीष्ट मान = \(\frac{1 \pm 5 \sqrt{2}}{7}\).
प्रश्न 20.
यदि एक वर बिन्दु P(x, y) की रेखाओं x + y – 5 = 0 और 3x – 2y + 7 = 0 से लांबिक दूरियों का योग सदैव 10 रहे तो दर्शाइए कि P अनिवार्य रूप से एक रेखा पर गमन करता है।
हल:
P(x, y) से रेखा x + y – 5 = 0 की दूरी
= \(\frac{x+y-5}{\sqrt{2}}\)
P(x, y) से रेखा 3x – 2y + 7 = 0 की दूरी
= \(\frac{3 x-2 y+7}{\sqrt{9+4}}\)
दोनों दूरियों का योग = 10 (दिया है)
∴ \(\sqrt{13}\)(x + y – 5) + \(\sqrt{2}\)(3x – 2y + 7) = 10\(\sqrt{26}\)
या \((\sqrt{13}+3 \sqrt{2}) x+(\sqrt{13}-2 \sqrt{2}) y-5 \sqrt{13}+7 \sqrt{2}-10 \sqrt{26}\) = 0
जो कि एक सरल रेखा का समीकरण है।
अत: P एक अनिवार्य रूप से एक रेखा पर गमन करता है।
![]()
प्रश्न 21.
समांतर रखाओं 9x + 6y – 7 = 0 और 3x + 2y + 6 = 0 से समदूरस्थ रेखा का समीकरण ज्ञात कीजिए।
हल:
दी गयी समांतर रेखाएँ
9x + 6y – 7 = 0 …(1)
और 3x + 2y + 6 = 0
या 9x + 6y + 18 = 0 …(2)
एक रेखा जो इसके समांतर है, उसका समीकरण
9x + 6y + c = 0 …(3)
रेखा (1) और (3) के बीच दूरी
\(\frac{(c+7)}{\sqrt{81+36}}=\frac{(c+7)}{\sqrt{117}}\) …(4)
रेखा (2) और (3) के बीच दूरी
\(\frac{(c-18)}{\sqrt{81+36}}=\frac{c-18}{\sqrt{117}}\) ….(5)
दूरियाँ (4) और (5) आपस में समान हैं।
\(\frac{(c+7)}{\sqrt{117}}=\pm \frac{c-18}{\sqrt{117}}\) [+ve चिन्ह मान्य नहीं है।]
c + 7 = – (c – 18)
= – c + 18
2c = 18 – 7 = 11
या c = \(\frac{11}{2}\)
c का मान समी (3) में रखने पर,
9x + 6y + \(\frac{11}{2}\) = 0
या 18x + 12y + 11 = 0.
प्रश्न 22.
बिन्दु (1, 2) से होकर जाने वाली एक प्रकाश किरण x-अक्ष के बिन्दु A से परावर्तित होती है और परावर्तित किरण बिन्दु (5, 3) से होकर जाती है। A के निर्देशांक ज्ञात कीजिए।
हल:
मान लीजिए BC, x-अक्ष के अनुदिश उस बिन्दु के निर्देशांक A (a, 0) है। AN इस पर लंब है। PA एक आपतित किरण है और AQ परावर्तित किरण है।
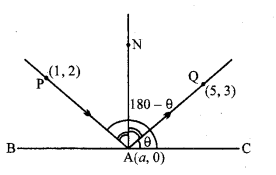
⇒ आपतित कोण PAN = परावर्तित कोण NAQ
⇒ ∠PAB = ∠QAC
⇒ यदि QA का झुकाव 0 हो तो PA का झुकाव 180 – θ होगा।
QA की ढाल जबकि Q(5, 3) और A(a, 0) हो, तो

प्रश्न 23.
दिखाइए कि (\(\sqrt{a^{2}-b^{2}}\), 0) और (-\(\sqrt{a^{2}-b^{2}}\),0) बिन्दुओं से रेखा \(\frac{x}{a}\)cosθ + \(\frac{y}{b}\)sinθ = 1 पर खींचे गए लम्बों की लंबाइयों का गुणनफल b2 है।
हल:

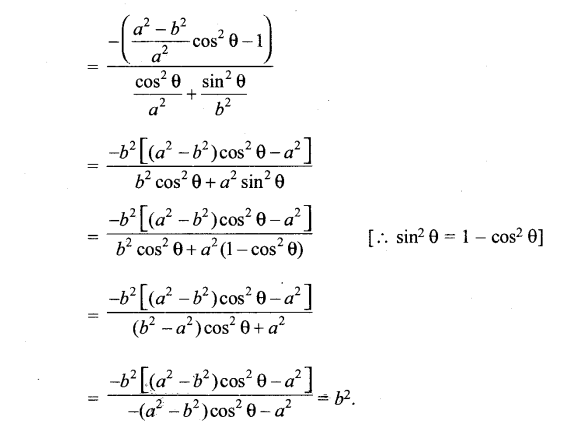
![]()
प्रश्न 24.
एक व्यक्ति समीकरणों 2x – 3y + 4= 0 और 3x + 4y – 5 = 0 से निरूपित सरल रेखीय पथों के संधि बिन्दुओं (junction/crosing) पर खड़ा है और समीकरण 6x – 7y + 8 = 0 से निरूपित पथ पर न्यूनतम समय में पहुँचना चाहता है। उसके द्वारा अनुसरित पथ का समीकरण ज्ञात कीजिए।
हल:
AB और BC दो रेखीय पथ हैं। AB व BC रेखाओं के समीकरण
2x – 3y + 4 = 0 …(1)
और 3x + 4y – 5 = 0 …(2)
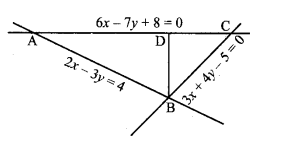
AB और BC बिन्दु B पर मिलते हैं।
समी (1) को 3 से तथा समी (2) को 2 से गुणा करने पर
6x – 9y = – 12 ….(3)
6x + 8y = 10 ….(4)
समी (3) को समी (4) में से घटाने पर,
17y = 10 + 12 = 22
∴ y = \(\frac{22}{17}\)
y का मान समी (1) में रखने पर,

B से AC तक न्यूनतम समय में पहुंचने के लिए कम से कम दूरी BD ( BD ⊥ AC) तय करनी है।
रेखा AC का समीकरण, 6x – 7y + 8= 0 की ढाल = \(\frac{6}{7}\)
BD की ढाल = – \(\frac{7}{6}\)
BD बिन्दु B \(\left(\frac{-1}{17}, \frac{22}{17}\right)\) से होकर जाती है।
∴ रेखा BD का समीकरण
y – y1 = m(x – x1)
\(y-\frac{22}{17}=-\frac{7}{6}\left(x+\frac{1}{17}\right)\)
102 से गुणा करने पर,
102y – 132 = – 119x – 7
119x + 102y – 125 = 0 .
अतः B से AC तक पहुँचने के लिए BD पथ अपनाना है जिसका समीकरण 119x + 102y – 125 = 0 है।