MP Board Class 10th Maths Solutions Chapter 8 Introduction to Trigonometry Ex 8.1

In this article, we will share MP Board Class 10th Maths Book Solutions Chapter 8 Introduction to Trigonometry Ex 8.1 Pdf, These solutions are solved subject experts from the latest edition books.

MP Board Class 10th Maths Solutions Chapter 8 Introduction to Trigonometry Ex 8.1

Question 1.
In ∆ABC, right-angled at B, AB = 24 cm, BC = 7 cm. Determine:
(i) sin A, cos A
(ii) sin C, cos C
Solution:
In right angle ∆ABC, we have
AB = 24 cm, BC = 7 cm

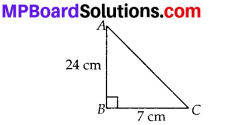
∴ Using Pythagoras theorem,
AC² = AB² + BC²
⇒ AC² = 24² + 7² = 576 + 49 = 625 = 25²
⇒ AC = 25 cm

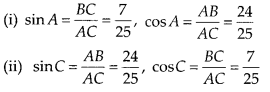
Question 2.
In the figure, find tan P – cotR?

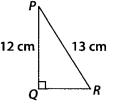
Solution:
In right angle ∆PQR
Using the Pythagoras theorem, we get
QR² = PR² – PQ²
⇒ QR² = 13² – 12² = (13 – 12)(13 + 12) = 1 × 25 = 25
∴ QR = \(\sqrt{25}\) = 5 cm
Now, tanP = \(\frac{Q R}{P Q}=\frac{5}{12}\) , cotR = \(\frac{Q R}{P Q}=\frac{5}{12}\)
∴ tanP – cotR = \(\frac{5}{12}-\frac{5}{12}\) = 0.

Question 3.
If sinA = \(\frac{3}{4}\), calculate cosA and tanA.
Solution:
Let us consider, the right angle ∆ABC, we have
Perpendicular = BC and Hypotenuse = AC

Question 4.
Given 15 cot A = 8, find sin A and sec A.
Solution:
In the right angle triangle ABC, we have 15 cot A = 8

Question 5.
Given sec θ = \(\frac { 13 }{ 12 } \), calculate all other trigonometric ratios.
Solution:

Question 6.
If ∠A and ∠B are acute angles such that cos A = cos B, then show that ∠A = ∠B.
Solution:

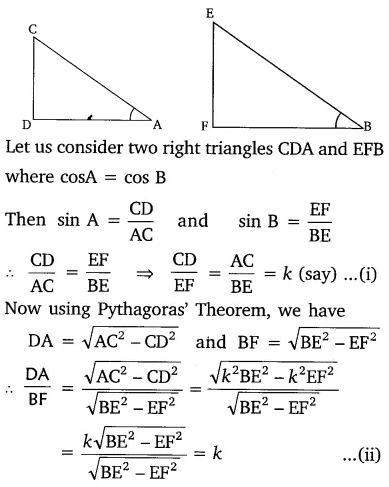
From equations (i) and (ii) we get:
\(\frac{\mathrm{CD}}{\mathrm{EF}}=\frac{\mathrm{AC}}{\mathrm{BE}}=\frac{\mathrm{AD}}{\mathrm{BF}}\)
⇒ ∆CDA ~ ∆EFB [By SSS similarity]
⇒ ∠A = ∠B Hence Proved

Question 7.
If cot θ = \(\frac { 7 }{ 8 }\), evaluate:
(i) \(\frac { \left( 1+sin\theta \right) \left( 1-sin\theta \right) }{ \left( 1+cos\theta \right) \left( 1-cos\theta \right)}\)
(ii) cot²θ
Solution:

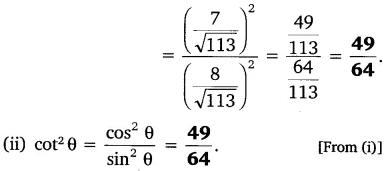
Question 8.
If 3 cot A = 4, check whether \(\frac { 1-tan^{ 2 }A }{ 1+tan^{ 2 }A }\) = cos² A – sin² A or not.
Solution:
In right angled ∆ABC, ∠B = 90°
For ∠A, we have:
Base = AB and perpendicular = BC. Also, Hypotenuse = AC

Question 9.
In triangle ABC, right angled at B, if tan A = \(\frac{1}{\sqrt{3}}\) find the value of:
(i) sin A cos C + cos A sin C
(ii) cos A cos C – sin A sin C
Solution:
In right ∆ABC, ∠B = 90°
For ∠A, we have
Base = AB, Perpendicular = BC,
Hypotenuse = AC

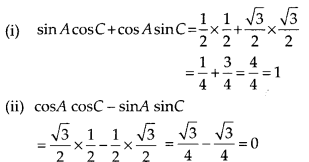
Question 10.
In ∆PQR, right-angled at Q, PR + QR = 25 cm and PQ = 5 cm. Determine the values of sinP, cosP and tanP.
Solution:
In right ∆PQR, Q = 90°

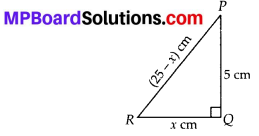
PR + QR = 25 cm and PQ = 5 cm
Let QR = x cm ⇒ PR = (25 – x) cm
∴ By Pythagoras theorem, we have
PR² = QR² + PQ²
⇒ (25 – x)² = x² + 5²
⇒ 625 – 50x + x² = x² + 25
⇒ – 50x = – 600
⇒ x = \(\frac{-600}{-50}\) = 12 i.e., QR = 12 cm
⇒ RP = 25 – 12 = 13 cm

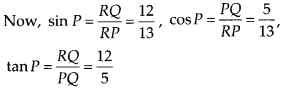
Question 11.
State whether the following are true or false. Justify your answer.
(i) The value of tan A is always less than 1.
(ii) secA = \(\frac{12}{5}\) for some value of angle A.
(iii) cosA is the abbreviation used for the cosecant of angle A.
(iv) cot A is the product of cot and A.
(v) sinθ = \(\frac{4}{3}\) for some angle θ.
Solution:
(i) False
∵ A tangent of an angle is the ratio of sides other than hypotenuse, which may be equal or unequal to each other.
(ii) True
∵ cos A is always less than 1.
∴ \(\frac{1}{\cos A}\) i.e., sec A will always be greater than 1.
(iii) False
∵ ‘cosine A’ is abbreviated as ‘cosA’
(iv) False
∵ ‘cot A’ is a single and meaningful term whereas ‘cot’ alone has no meaning.
(v) False
∵ \(\frac{4}{3}\) is greater than 1 and sinθ cannot be greater than 1