In this article, we will share MP Board Class 10th Maths Book Solutions Chapter 1 Real Numbers Ex 1.4 Pdf, These solutions are solved subject experts from the latest edition books.
MP Board Class 10th Maths Solutions Chapter 1 Real Numbers Ex 1.4
Question 1.
Without actually performing the long divison, state whether the following rational numbers will have a terminating decimal expansion or a non-terminating repeating decimal expansion:


Solution:




![]()
Question 2.
Write down the decimal expansions of those rational numbers in Question 1 above which have terminating decimal expansions.
Solution:
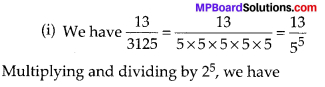
Multiplying and dividing by 25, we have


![]()
Question 3.
The following real numbers have decimal expansions as given below. In each case, decide whether they are rational or not. If they are rational, and of the form \(\frac{p}{q}\), what can you say about the prime factors of q?
(i) 43.123456789
(ii) 0.120120012000120000….
(iii) \(43 . \overline{123456789}\)
Solution:
(i) 43.123456789
∴ The given decimal expansion terminates.
∴ It is rational of the form \(\frac{p}{q}\)

Hence, p = 43123456789 and q = 29 × 59
Prime factors of q are 29 and 59.
(ii) 0.120120012000120000…
∵ The given decimal expansion is neither terminating nor repeating.
∴ It is irrational number, hence cannot be written in p/q form.
(iii) \(43 . \overline{123456789}\)
∵ The given decimal expansion is non-terminating repeating.
∴ It is rational number.
![]()
Multiplying both sides by 1000000000, we have
1OOOOOOOOOx = 43123456789.123456789…
… (2)
Subtracting (1) from (2), we have
(1000000000x) – x
= (43123456789.123456789 ) – 43.123456789…
⇒ 999999999x = 43123456746
![]()
Here, p = 4791495194 and q = 111111111, which is not of the form 2m × 5n i.e., the prime factors of q are not of the form 2m × 5n.