MP Board Class 11th Hindi Makrand Solutions Chapter 2 शिक्षा (निबंध, स्वामी विवेकानन्द)
शिक्षा पाठ्य-पुस्तक के प्रश्नोत्तर
शिक्षा लघु उत्तरीय प्रश्नोत्तर
प्रश्न 1.
ज्ञान का मूल उद्गम स्थान कौन-सा है?
उत्तर:
ज्ञान का मूल उद्गम स्थान मन हैं। ज्ञान पर प्रायः पर्दा पड़ा रहता है। यह पर्दा जब धीरे-धीरे हटता है, तब हम कुछ सीखने लगते हैं। इससे हमारे ज्ञान की वृद्धि होती जाती है।
प्रश्न 2.
व्यक्ति सर्वज्ञ सर्वदर्शी कब बनता है?
उत्तर:
व्यक्ति सर्वज्ञ सर्वदर्शी तब बनता है, जब उसके मन में मौजूद ज्ञान पर पड़ा हुआ पर्दा पूरी तरह से हट जाता है। जब तक यह पर्दा पड़ा रहता है, तब तक वह अज्ञानी बना रहता है।
प्रश्न 3.
शिक्षा में शिक्षक की क्या भूमिका है? पाठ के आधार पर स्पष्ट कीजिए।
उत्तर:
शिक्षा में शिक्षक की बहुत बड़ी भूमिका है। शिक्षक यह भली प्रकार जानता है कि मनुष्य के भीतर सारे ज्ञान का भण्डार भरा हुआ है। उसे केवल प्रबोध देने और जागृति ला देने की आवश्यकता है। इससे वह किसी की भी जीवनधारा को बिल्कुल बदल देता है।
प्रश्न 4.
विवेकानन्द ने आविष्कार का क्या अर्थ बतलाया है?
उत्तर:
विवेकानन्द ने आविष्कार का अर्थ मनुष्य का अपने अनन्त ज्ञान-स्वरूप: आत्मा के ऊपर से पड़े हुए पर्दे को हटा लेना बतलाया है।
प्रश्न 5.
काँच के समान पारदर्शी किसे कहा गया है?
उत्तर:
अनेक मनुष्यों के अन्दर दिव्य ज्योति होती है। वह अज्ञान के अन्धकार से ढकी रहती है। उसे जब पवित्रता और निःस्वार्थता के द्वारा हटाने का प्रयास किया जाता है, तब वह चमकने लगती है। इसे ही काँच के समान पारदर्शी कहा गया है।
![]()
शिक्षा दीर्घ उत्तरीय प्रश्न
प्रश्न 1.
शिक्षा मनुष्य में अन्तर्निहित पूर्णता को किस प्रकार अभिव्यक्त करती है?
उत्तर:
मनुष्य के मन में ज्ञान मौजूद होता है। वह स्वभाव-सिद्ध होता है। वह चाहे किसी प्रकार का क्यों न हो, वह उसके भीतर ही होता है। वह कहीं बाहर से उसमें नहीं आता है। उस पर अज्ञान का पर्दा पड़ा होता है। मनुष्य उसे खोज अर्थात् कुछ सीख-समझकर हटाता है। इस प्रकार मनुष्य की अन्तर्निहित पूर्णता को अभिव्यक्त करना ही शिक्षा है।
प्रश्न 2.
सुधार के लिए बलात् उद्योग करने का परिणाम सदैव उल्टा ही क्यों होता है?
उत्तर:
सुधार के लिए बलात् उद्योग करने का परिणाम हमेशा उल्टा ही होता है जिसमें कोई क्षमता और योग्यता न हो। अगर उसे कोई योग्य बनाना चाहे तो वह जो कुछ भी है, वह भी नहीं रह पाएगा। हम यह प्रायः देखते हैं कि माता-पिता या अभिभावक अपने बच्चों को लिखने-पढ़ने के लिए उनके पीछे हमेशा लगे रहते हैं। उन्हें कोसते रहते हैं कि वे अपने जीवन में कुछ भी न सीख सकते हैं और न बन सकते हैं। इसका परिणाम यह निकलता है कि उनके बच्चे उस हीनभावना का शिकार होकर सचमुच में कभी न कुछ सीख पाते हैं और न कुछ बन पाते हैं।
प्रश्न 3.
मनुष्य-निर्माण, जीवन-निर्माण और चरित्र-निर्माण कैसे किया जा सकता है?
उत्तर:
मनुष्य के भीतर सभी प्रकार का ज्ञान भरा हआ है। उसे केवल जगाने या प्रबोध देने की आवश्यकता होती है। यह काम शिक्षा ही करती है। शिक्षा के द्वारा हम अपने भीतर के ज्ञान का अनुभव करते हैं। अगर हमें जीवन-निर्माण, मनुष्य-निर्माण और चरित्र-निर्माण करना है, तो हमें ऐसे विचारों की अनुभूति कर लेनी चाहिए, जो इनके लिए सहायक या अनुकूल हों। इसके लिए यह बेहद आवश्यक है कि हम जीवन-निर्माण, मनुष्य- निर्माण और चरित्र-निर्माण में सहायक चुने हुए विचारों को ही अनुभूति करके अपना कदम बढ़ाएँ। इस प्रकार ही मनुष्य-निर्माण, जीवन-निर्माण और चरित्र-निर्माण किया जा सकता है।
प्रश्न 4.
“तुम केवल बाधाओं को हटा सकते हो और ज्ञान अपने स्वाभाविक रूप से प्रकट हो जाएगा।” इस उक्ति का आशय स्पष्ट कीजिए।
उत्तर:
आशय-“तुम केवल बाधाओं को हटा सकते हो और ज्ञान अपने स्वाभाविक रूप से प्रकट हो जाएगा।
उपर्युक्त वाक्य का आशय यह है कि किसी को खासतौर से बालक को शिक्षित करना बहुत ही कठिन होता है। यह इसलिए कि वह अपनी प्रकृति के ही अनुसार अपना विकास कर लेता है। इस प्रकार वह स्वयं को स्वयं ही शिक्षित करता है। उसे अपने विकास में किसी दूसरे का हस्तक्षेप करना उसके लिए हानिकारक सिद्ध होता है। इस सम्बन्ध में इतना अवश्य कहा जा सकता है कि अगर कोई उसे शिक्षित करना। चाहता है, तो वह उसे उसके अपने ही तौर-तरीके से विकास करने में उसका साथ – दे। उसकी इच्छानुसारं उसकी सहायता करे। इस प्रकार के सकारात्मक कदम उठाकर ही कोई किसी बालक को शिक्षित कर सकता है। उसके विकास के मार्ग में आने वाली कठिनाइयों को दूर कर सकता है। ऐसा करने से ही उसके भीतर का सोया’ हुआ ज्ञान अपने आप जग जाएगा।
प्रश्न 5.
पाठ के आधार पर ज्ञानी और अज्ञानी में अन्तर स्पष्ट कीजिए।
उत्तर:
मनुष्य के भीतर हरेक प्रकारका ज्ञान भरा होता है। उसमें लौकिक या आध्यात्मिक दोनों ही होता है। उसके भीतर के ज्ञान पर अज्ञान का पर्दा पड़ा रहता है। जब वह किसी से कुछ सीखता-समझता है, तब वह पर्दा धीरे-धीरे हटने लगता है। इससे उसका ज्ञान बढ़ता जाता है। फिर वह औरों की अपेक्षा अधिक ज्ञानी और विवेकी हो जाता है। इसके विपरीत जिस पर अज्ञान का पर्दा पड़ा ही रहता है, वह अज्ञानी और मूर्ख होता है। इस प्रकार मनुष्य के भीतर ज्ञान-अज्ञान दोनों ही होता है।
शिक्षा भाव विस्तार/पल्लवन
प्रश्न 1.
निम्नलिखित पंक्तियों का भाव-विस्तार कीजिए।
(क) “कार्य को पूजा की भावना से करो”।
(ख) अतीत जीवनों ने हमारी प्रवृत्तियों को गढ़ा है।
(ग) स्वाधीनता विकास की पहली शर्त है।
(घ) जो जहाँ पर है उसे वहीं से आगे बढ़ाओ।
उत्तर:
(क) “कार्य को पूजा की भावना से करो”। हमें किसी काम को सच्चाई और लगन से करना चाहिए। इससे ही सफलता मिलती है। दूसरी बात यह हमें अपने काम के उचित-अनुचित पर भी अवश्य ध्यान देना चाहिए। जो काम हमारे लिए उचित है उसे ही हमें करना चाहिए। जो काम हमारे लिए अनचित है, उस हमें विल्कल ही नहीं करना चाहिए। शिक्षक का काम शिक्षार्थी को शिक्षा देना है न कि उसे उपदेश देना। उसका केवल इतना ही काम होता है कि वह शिक्षार्थी के भीतर के सोए हुए ज्ञान को जगा दे। दूसरी ओर शिक्षार्थी का यह काम होता है कि वह अपने शिक्षा के द्वारा दी गई शिक्षा को ग्रहण करें। दोनों को ही अपना-अपना काम पूजा की भावना से करना चाहिए। इस प्रकार से काम करने से निश्चय ही सफलता मिलती है। इसीलिए किसी अंग्रेजी कवि ने कहा है-
‘Work is worship
(ख) ‘अतीत जीवनों ने हमारी प्रवृत्तियों को गढ़ा है।’
अतीत का हमारे जीवन पर गहरा प्रभाव पड़ता है। हम जो कुछ अनुभव करते हैं, अतीत से करते हैं। इसलिए अतीत को भूलाकर हम वर्तमान को सफल नहीं बना सकते हैं। हमारे युग महापुरुष और मार्गदर्शक अतीत की ऐसी जीवन ज्योति हैं, जिनसे हम अपने अज्ञान के अन्धकार को दूर कर अपने जीवन को खुशहाल और सम्पन्न बना सकते हैं। अगर हम अपने जीवन में सफलता की सीढ़ियों पर चढ़ते जा रहे हैं, तो इसका श्रेय अतीत जीवनों को दिया जा सकता है। ऐसा इसलिए कि अतीत जीवनों ने हमारी ऐसी प्रवृत्तियों को गढ़ा है, जिनसे हम अपने जीवन की सब बातों को बहुत अधिक सुन्दर ढंग से कर सकते हैं।
(ग) ‘स्वाधीनता विकास की पहली शर्त है।’
स्वाधीनता का महत्त्व सबके के लिए होता है। जिसका जीवन स्वाधीन नहीं है, वह अपना विकास नहीं कर सकता है। इसलिए किसी को विकसित होने या करने के लिए यह सबसे पहले आवश्यक तत्त्व है। उसकी स्वाधीनता पर किसी प्रकार आँच न आने दें। ऐसा करके हम किसी का मार्गदर्शक बन सकते हैं। इसके विपरीत कदम उठाने से विकास का प्रवाह रुक जाता है। इससे बड़ी-बड़ी कठिनाइयाँ खड़ी हो जाती हैं। चारों ओर अव्यवस्था और अशान्ति फैखने लगती है। सदियों तक स्वाधीन न होने के कारण हमारे देश का विकास नहीं हो सकीर उसमें कभी चैन-शान्ति का वातावरण नहीं बन सका। लेकिन जैसे ही वह स्वाधीन हुआ, वैसे उसमें विकास के नए-नए द्वार खुलने लगे। देखते-देखते वह विकासशील देशों से आगे बढ़कर विकसित देशों के करीब-करीब पहुँच गया है।
(घ) ‘जो जहाँ पर है, उसे वहीं से आगे बढ़ाओ।’
हमें किसी का विकास करने के लिए उसकी कमजोरियों के लिए उसे नहीं कोसना चाहिए। उसे तो उत्साहित करना चाहिए। अच्छाइयों को बढ़ा-चढ़ाकर उसे बताना चाहिए। इस प्रकार हमें किसी को आत्मनिर्भर बनाने के लिए उसके कमजोर विचारों, हीनभावनाओं और उसके द्वारा उठाए गये अनुचित कदमों को उसे नहीं बताना चाहिए। उसे तो उत्साहित करते हुए उसकी आवश्यकता के अनुसार ही उसे आगे बढ़ाना चाहिए। इससे वह उन सभी बातों को और अधिक अच्छी तरह से कर सकता है, जिनकी उसे आवश्यकता है। इस प्रकार किसी का विकास करने के लिए उसे और हौसला देकर उसे आगे ही बढ़ाना चाहिए।
![]()
शिक्षा भाषा अध्ययन
प्रश्न 1.
निम्नांकित शब्दों की सन्धि कीजिए और सन्धि का नाम भी लिखिए-
अन्तर्निहित, गुरुत्वाकर्षण, प्रतित्ये, खाद्यान्न, जीवाणु।
उत्तर:

प्रश्न 2.
निम्नलिखित शब्दों के विलोम शब्द लिखिए।
शिक्षा, ज्ञानी, व्यक्त, लौकिक, समर्थ, शुद्ध, धर्म।
उत्तर:

प्रश्न 3.
निम्नलिखित वाक्यांशों के लिए एक शब्द लिखिए
- प्रेरणां देने वाला।
- जिसे सब विषयों का ज्ञान हो।
- जिसकी सीमा न हो।
- जिसकी मृत्यु न हो।
- दूर की बातों को सोचने वाला।
उत्तर:
- प्रेरक
- सर्वज्ञ
- असीम
- अमर,
- दूरदर्शी
प्रश्न 4.
निम्नलिखित वाक्यों की रचना एवं शब्द के आधार पर शुद्ध करके लिखिए
- न्यूटन ने गुरुत्वाकर्षण का आविष्कार की।
- विसाल बुद्धि एक छोटी जीवानकोश में है।
- सभी ज्ञान और सभी शक्तियाँ आतमा के भीतर हैं।
- मृत्यु का सामना ही क्यों न करना पडे साक्षात।
- शायद हम लोग कानपुर अवश्यक जाँएग।
उत्तर:
- न्यूटन ने गुरुत्वाकार्पण का आविष्कार किया।
- विशाल बुद्धि एक छोटे-से जीवाणुकोश में है।
- सभी ज्ञान और शक्तियाँ आत्मा के भीतर हैं।
- साक्षात् मृत्यु का ही सामना क्यों न करना पड़े।
- हम लोग कानपुर अवश्य जाएँगे।
शिक्षा अपठित गद्यांश
राष्ट्रनिर्माण का दायित्व उसके नागरिकों पर होता है। इस दृष्टि से भारत के नव-निर्माण का दायित्व विद्यार्थियों के ऊपर भी है क्योंकि आज का विद्यार्थी कल का नागरिक है। राष्ट्र के विकास का अर्थ है उसके नागरिकों का विकास। अतः प्रत्येक छात्र-छात्रा को अपने भावी जीवन का निर्माण बड़ी सतर्कता के साथ करना चाहिए। उन्हें अपने राष्ट्र, समाज, धर्म-संस्कृति के विकास का लक्ष्य एक क्षण के लिए भी तिरोहित नहीं होने देना चाहिए। विद्यार्थियों को अपने जीवन का निर्माण राष्ट्रीय हित को दृष्टिगत रखते हुए करना चाहिए। यदि वे ऐसा नहीं करते हैं तो उनकी उन्नति राष्ट्र और समाज के लिए भार-स्वरूप होगी।
प्रश्न 1.
इस गद्यांश का उचित शीर्षक लिखिए।
उत्तर:
आज के विद्यार्थी का दायित्व।
प्रश्न 2.
गद्यांश के सार को अपने शब्दों में लिखिए।
उपर्युक्त गद्यांश को पढ़कर निम्नलिखित प्रश्नों के उत्तर दीजिए
उत्तर:
राष्ट्र के नव-निर्माण का दायित्व आज के विद्यार्थियों के ऊपर है। इसलिए हरेक विद्यार्थी को अपने राष्ट्र, समाज, धर्म-संस्कृति के विकास के प्रति हमेशा ही तत्पर रहना चाहिए। वे ऐसा करके ही अपने जीवन को महान बना सकते हैं।
प्रश्न 3.
राष्ट्र के विकास का क्या अर्थ है?
उत्तर:
राष्ट्र विकास का अर्थ है-राष्ट्र के नागरिकों का विकास।
प्रश्न 4.
छात्रों को अपने जीवन का निर्माण किसको दृष्टिगत रखकर करना चाहिए।
उत्तर:
छात्रों को अपने जीवन का निर्माण अपने राष्ट्र, समाज, धर्म और संस्कृति के विकास को दृष्टिगत रखकर करना चाहिए।
![]()
शिक्षा योग्यता विस्तार
प्रश्न 1.
अपने परिवेश के विभिन्न दो शिक्षाविद्/कवि लेखक की संक्षिप्त जानकारी एकत्रित कर जीवनी लिखिए।
उत्तर:
उपर्युक्त प्रश्नों को छात्र-छात्रा अपने अध्यापक की सहायता से हल करें।
प्रश्न 2.
“मातृभाषा ही सर्वश्रेष्ठ है” विषय पर अपने मत को स्पष्ट करते हुए दो अनुच्छेद लिखिए।
उत्तर:
उपर्युक्त प्रश्नों को छात्र-छात्रा अपने अध्यापक की सहायता से हल करें।
प्रश्न 3.
शिक्षा विषय से जुड़ी किसी लघु नाटिका को खोजकर वार्षिक उत्सव में उसका अभिनय कीजिए।
उत्तर:
उपर्युक्त प्रश्नों को छात्र-छात्रा अपने अध्यापक की सहायता से हल करें।
शिक्षा परीक्षोपयोगी अन्य महत्त्वपूर्ण प्रश्नोत्तर
शिक्षा लघु उत्तरीय प्रश्नोत्तर
प्रश्न 1.
आविष्कार का क्या अर्थ है?
उत्तर:
आविष्कार का अर्थ है-मनुष्य का अपनी अनन्त ज्ञानस्वरूप आत्मा के । ऊपर से पड़े हुए पर्दे को उठाना।
प्रश्न 2.
हमारे मन में ज्ञान किस प्रकार छिपा हुआ है?
उत्तर:
हमारे मन में ज्ञान चकमक पत्थर के टुकड़े में आग के समान छिपा हुआ है। वह किसी सुझाव या शिक्षा रूपी घर्षण के द्वारा देखते-देखते ही प्रकाशित होने लगता है।
प्रश्न 3.
लड़कों को ठोक-पीटकर शिक्षित बनाने की प्रणाली का क्यों अन्त कर देना चाहिए।
उत्तर:
लड़कों को ठोक-पीटकर शिक्षित बनाने की प्रणाली का अन्त कर देना चाहिए। यह इसलिए कि वे अपने माता-पिता के अनुचित दबाव के कारण अपने विकास का स्वतन्त्र अवसर प्राप्त नहीं कर पाते हैं।
प्रश्न 4.
श्री रामकृष्णदेव ने किस प्रकार निकम्मों की जीवन धारा को बदल दिया?
उत्तर:
श्री रामकृष्णदेव ने निकम्मों के प्रति आशा और उत्साह के भावों को. भरा। इस प्रकार उन्होंने उनकी जीवनधारा को बिल्कुल ही बदल दिया।
प्रश्न 5.
विदेशी भाषा की शिक्षा से क्या हानि होती है?
उत्तर:
विदेशी भाषा की शिक्षा से बहुत बड़ी हानि होती है। इससे समाज और समाज के लोगों का अभाव दूर नहीं हो पाता है। उनका चारित्रिक विकास भी नहीं हो पाता।
शिक्षा दीर्घ उत्तरीय प्रश्नोत्तर
प्रश्न 1.
मनुष्य के अन्दर ज्ञान का स्वरूप क्या है?
उत्तर:
मनुष्य के अन्दर सभी प्रकार का ज्ञान भरा होता है। लेकिन वह अज्ञान के पर्दे से ढका रहता है। इसलिए वह प्रायः प्रकाशित नहीं हो पाता है। जब उस पर पड़ा हुआ पर्दा ज्ञान के प्रभाव से धीरे-धीरे हटने लगता है। तब वह प्रकाशित होने लगता है। इसे हम सीखना कहते हैं। सीखने की यह प्रक्रिया जैसे-जैसे बढ़ती । जाती है, वैसे-वैसे ज्ञान की वृद्धि होती जाती है। इस प्रकार जिस पर अज्ञान का पड़ा हआ पर्दा उठता जाता है, वह औरों की अपेक्षा अधिक ज्ञानी हो जाता है। जिस पर यह पर्दा पड़ा रहता है, वह अज्ञानी ही बना रहता है।
प्रश्न 2.
शिक्षक का क्या कार्य होता है?
उत्तर:
शिक्षक को यह समझकर शिक्षा नहीं देना चाहिए कि वह शिक्षा दे रहा है। अगर वह ऐसा समझकर किसी को शिक्षा दे रहा है, तो उसे सफलता नहीं मिल सकती है। उसे तो यह समझकर शिक्षा देनी चाहिए कि जिसे वह शिक्षा दे रहा है, उसके अन्दर सारा ज्ञान भरा हुआ है। उसे केवल जगाने या प्रबोध देने की आवश्यकता . है। इस प्रकार उसे केवल इतना ही करना है कि वह जिसे शिक्षा दे रहा है, वह अपने पैरों पर खड़ा होकर अपना विकास करना सीख ले।
प्रश्न 3.
विद्यार्थियों की शिक्षा में किस प्रकार का परिवर्तन होना चाहिए?
उत्तर:
विद्यार्थियों की शिक्षा में उनकी आवश्यकता के ही अनुसार परिवर्तन होना चाहिए। ऐसा करते समय हमें यह नहीं भूलना चाहिए कि अतीत-जीवनों से उनकी प्रवृत्तियों को गढ़ा है। इसलिए उनकी प्रवृत्तियों के अनुसार उन्हें शिक्षा देनी चाहिए। उनकी कभी भी किसी विशेष प्रवृत्तियों को नहीं नष्ट करना चाहिए। किसी प्रकार के मन्द और निकम्मे विद्यार्थियों को नहीं कोसना चाहिए। ऐसे विद्यार्थियों के भी प्रति आशा और उत्साह भरी शिक्षा देनी चाहिए। इस प्रकार परम्परागत या रूढ़िगत विचारों से हमें हटकर विद्यार्थियों की शिक्षा में युग की माँग के अनुसार परिवर्तन करना चाहिए।
प्रश्न 4.
आज की शिक्षा कैसी होनी चाहिए?
उत्तर:
आज की शिक्षा आज की आवश्यकता के ही अनुसार होनी चाहिए। आज हममें चरित्र बल, मानसिक बल, बुद्धि बल आदि की बहुत कमी हो गई है। इसके साथ ही हमारे देश में उद्योग-धन्धों की भी अधिक कमी है। फलस्वरूप हमारे यहाँ बेरोजगारी बहुत बढ़ गई है। इससे हम और देशों की तुलना में बहुत पीछे हैं। इस प्रकार कमियों को दूर करने वाली हमें आज एक ऐसी शिक्षा चाहिए, जो हमें विदेशी भाषा और विज्ञान की जानकारी दे सके और हमें विदेशी प्रभाव से मुक्त रखे। हमारे ज्ञान-भण्डार की शाखाओं को विकसित करे। हमारी विभिन्न आवश्यकताओं को पूरा करने के लिए अधिक साधनों को बढ़ाए। इसके साथ-ही-साथ भविष्य के लिए कुछ बचाए रखने का भी ज्ञान दे सके।
प्रश्न 5.
सभी प्रकार की शिक्षा का क्या उद्देश्य होना चाहिए?
उत्तर:
सभी प्रकार की शिक्षा का उद्देश्य निम्नलिखित होना चाहिए-
- सभी प्रकार की शिक्षा का उद्देश्य मनुष्य का निर्माण होना चाहिए।
- सभी प्रकार की शिक्षा का उद्देश्य मनुष्य का विकास करना होना चाहिए।
- सभी प्रकार की शिक्षा का उद्देश्य मनुष्य की इच्छाशक्ति को प्रवाहित और प्रकाशित कर कल्याणकारी बनाने का होना चाहिए।
- सभी प्रकार की शिक्षा का उद्देश्य मनुष्य बनाने वाली होनी चाहिए।
- सभी प्रकार की शिक्षा का उद्देश्य परस्पर मेल-मिलाप के भावों को पैदा करना होना चाहिए।
![]()
शिक्षा लेखक-परिचय
प्रश्न.
स्वामी विवेकानन्द का संक्षिप्त जीवन-परिचय देते हुए उनके महत्त्व पर प्रकाश डालिए।
उत्तर:
जीवन-परिचय-स्वामी विवेकानन्द संसार के महापुरुषों में से एक हैं। उनका जन्म 12 जनवरी, 1863 को कोलकाता में हुआ था। उनके बचपन का नाम नरेन्द्र नाथ था। उनके पिता विश्वनाथ दत्त और माता भुवनेश्वरी देवी थीं। कुछ समय बाद नरेन्द्र नाथ विवेकानन्द के नाम से संसार में प्रसिद्ध हुए। नरेन्द्र नाथ बचपन से ही मेधावी, बुद्धिमान, निर्भीक, साहसी और स्मृतिधर थे। अपनी प्रारम्भिक शिक्षा समाप्त करने के बाद बी.ए. में प्रवेश लेकर पढ़ाई आरम्भ की, तो उनके पिता का स्वर्गवास हो गया। इससे उनके पारिवारिक जीवन में महासंकट आ गया। इसे देखकर उन्होंने नौकरी की तलाश की, लेकिन उन्हें इस दिशा में कोई सफलता नहीं मिली।
उनके अन्दर एक ओर भूख से तड़पते अपने परिवार को भरपेट भोजन-पानी जुटाने की जिम्मेदारी जोर मार रही थी, तो दूसरी ओर विश्व-कल्याण के लिए. धर्म-प्रचार और सेवा की भावना प्रवाहित हो रही थी। उन्होंने जनवरी, 1887 में संन्यास लेकर अपने विवेक से धर्म प्रचार और जन सेवा का व्रत लिया। अपने साथियों को लेकर उन्होंने कोलकाता के उत्तर प्रान्त के बराह नगर में बराह नगर मठ और रामकृष्ण संघ की स्थापना की। उन्होंने देश-विदेश के अनेक स्थानों का भ्रमण कर धर्म प्रचार किया। 4 जुलाई, 1902 में उनका निधन मात्र 39 वर्ष की आयु में हो गया।
महत्त्व :
स्वामी विवेकानन्द ने धर्म का प्रचार-प्रसार करते हुए सन् 1893 में अमेरिका के शिकागो शहर में आयोजित विश्व धर्म परिपद् में भाग लिया। इसके बाद पाश्चात्य देशों में सनातन धर्म और भारतीय संस्कृति का जोरदार प्रचार किया। इसके बाद उन्होंने भारतीय युवकों को प्रज्ञावान, दृढ़ निश्चयी, तेजस्वी, निर्भीक और आत्मनिर्भर बनने के लिए उत्साहित किया। उन्होंने उन्हें प्रेरित करते हुए कहा
“ गर्व से कहो कि मैं भारतीय हूँ। और प्रत्येक भारतवासी मेरा भाई है, भारत के कल्याण में मेरा कल्याण है।”
इस प्रकार स्वामी विवेकानन्द ने ‘वसुधैव कुटुम्बकम्’ की भावना को पूरे संसार में प्रसारित किया।
शिक्षा पाठ का सारांश
प्रश्न.
स्वामी विवेकानन्द द्वारा लिखित निबन्ध ‘शिक्षा’ का सारांश अपने शब्दों में लिखिए।
उत्तर:
स्वामी विवेकानन्द द्वारा लिखित निबन्ध ‘शिक्षा’ में शिक्षा के स्वरूप और उसके उद्देश्य पर सीधा प्रकाश डाला गया है। लेखक का यह मानना है कि हमारा मन ज्ञान का भण्डार है। उसे शिक्षा ही प्रकट करती है। हम जो कुछ सीखते हैं, वह वास्तव में हम आविष्कार करते हैं। अपनी अनन्त ज्ञानस्वरूप आत्मा के ऊपर से अज्ञान के पर्दे को हटा लेना ही आविष्कार है। इसी प्रकार न्यूटन ने गुरुत्वाकर्षण का आविष्कार किया था। जैसे-जैसे आविष्कार की प्रक्रिया बढ़ती जाती है, वैसे-वैसे हमारे अज्ञान का पर्दा हटने से ज्ञान की वृद्धि होती जाती है। जब अज्ञान का पर्दा पूरी तरह से हट जाता है, तब हम सर्वज्ञ, सर्वदर्शी हो जाते हैं। इस आधार पर यह कहा जा सकता है कि चकमक पत्थर के समान हमारे मन में ही ज्ञान की ज्योति छिपी हुई है। उसे किसी प्रकार के सुझाव या शिक्षा देखते-देखते प्रकाशित कर देती है। यह तभी सम्भव है, जब हम अपने अनुभव और अपनी विचार-शक्ति के द्वारा इसे अच्छी तरह से समझकर ग्रहण करें। दूसरी बात यह कि एक फैले हुए विशाल वट वृक्ष की एक छोटे से बीज में छिपी हुई शक्ति के समान हमारी आत्मा में अनन्त शक्ति है। इसको जामना ही उसका प्रकट होना है।
पौधे की तरह बालक का भी विकास अपनी प्रकृति के ही अनुसार होता है। इससे बालक स्वयं को शिक्षित करता है। इसलिए उसे दी गई शिक्षा उसमें स्वाभाविक रूप से ही प्रकट होगी। इस दृष्टि से शिक्षक को इस भ्रम में नहीं पड़ना चाहिए कि वह उसे शिक्षा दे रहा है। अगर वह ऐसा भ्रम रखता है तो इससे उसे सफलता नहीं मिल सकती है। उसे यह बोध होना चाहिए कि सारा ज्ञान मनुष्य के भीतर मौजूद है। उसे केवल जगाने की आवश्यकता है। बालकों में मौजूद इस ज्ञान को जगाने के लिए शिक्षक को ऐसा प्रयास करना चाहिए कि वह अपने हाथ, पैर, कान और आँखों के उचित उपयोग के लिए अपनी बुद्धि का प्रयोग करना सीख ले। इसलिए किसी बालक को अनुचित दबाव से शिक्षित बनाने की परिपाटी को त्याग देना चाहिए। उसे तो स्वतन्त्र रूप से विकास करने का मौका देना चाहिए।
इससे वह भले ही महान न बने, लेकिन वह महान बनाने का प्रयास तो कर सकता है। अगर हम अपने बच्चों को डाँट-फटकार कर और उन्हें हीन दृष्टि से योग्य बनाने की कोशिश करते हैं, तो वे कभी योग्य नहीं बन सकते हैं। वे तो अयोग्य ही बनकर रह जाएंगे। इसलिए हमें उन्हें हौसला देकर आत्मनिर्भर बनाने का प्रयास करना चाहिए। एक आदर्श विद्यार्थी के लिए आवश्यक है कि उसे समय की आवश्यकता के अनुसार शिक्षा दी जाए। उसकी प्रवृत्तियों के अनुसार उसे मार्ग मिले। इस आधार पर ही किसी को आगे बढ़ाया जा सकता है। श्री रामकृष्ण देव ने जीवन भर यही किया। उन्होंने निराश और दुःखी मनुष्यों में भी आशा और उत्साह की ज्योति जलाकर उन्हें आत्मनिर्भर बनाने का प्रयास किया।
हमें शिक्षा को विविध प्रकार के ज्ञान का ढेर नहीं समझना चाहिए। हमें जीवन-निर्माण, मनुष्य-निर्माण और चरित्र-निर्माण में सहायक विचारों को ही ग्रहण करना चाहिए। ऐसे विचारों के द्वारा अपने जीवन और चरित्र-निर्माण कर लेने वाला किसी ग्रन्थालय को कण्ठस्थ करने वाले से कहीं अधिक शिक्षित और योग्य कहा जा सकता है। शिक्षा का उद्देश्य बड़ी-बड़ी उपाधियाँ लेकर वकील या इससे बड़ा कोई पदाधिकारी वन जाना बिल्कुल नहीं है। ऐसा इसलिए कि इससे देश का कुछ भी भला नहीं हो ‘सकता है। देश का भला तो उस शिक्षा से होगा, जो देश के दीन-दुखियों की पुकार सुन सके। देश के अभाव को दूर करने के लिए देशवासियों में चरित्र-बल पैदा करे। उनमें अपार बुद्धि और साहस को जगा सके।
इस प्रकार की शिक्षा से हम आत्मनिर्भर होकर पराधीनता से मुक्त होकर विविध प्रकार के ज्ञान-विज्ञान का अध्ययन-मनन कर सकते हैं। अपने देश में छोटे-बड़े उद्योग-धन्धों का विकास करके बढ़ती हुई बेरोजगारी पर लगाम कस सकते हैं। यही नहीं, अपने भविष्य को उज्ज्वल बनाने के लिए कुछ बचाकर रख सकते हैं। मनुष्य का निर्माण करना ही शिक्षा का एकमात्र उद्देश्य होना चाहिए। वास्तविक शिक्षा वही होती है, जो मनुष्य की सोई हुई इच्छा-शक्ति को जगाकर उसे कल्याणकारी बनाती है। आज हमारे देश को हर प्रकार से मनुष्य बनाने वाली शिक्षा की सबसे बड़ी आवश्यकता है।
![]()
शिक्षा संदर्भ-प्रसंगसहित व्याख्या
1. मनुष्य की अन्तर्निहित पूर्णता को अभिव्यक्त करना ही शिक्षा है। ज्ञान मनुष्य में स्वभाव-सिद्ध है; कोई भी ज्ञान बाहर से नहीं आता, सब अन्दर ही है। हम जो कहते हैं कि मनुष्य ‘जानता’ है, यथार्थ में, मानसशास्त्र-संगत भाषा में हमें कहना चाहिए कि वह-आविष्कार करता है, ‘अनावृत’ या ‘प्रकट’ करता है। मनुष्य जो कुछ ‘सीखता है, वह वास्तव में ‘आविष्कार करना ही है। ‘आविष्कार’ का अर्थ है-मनुष्य का अपनी अनन्त ज्ञानस्वरूप आत्मा के ऊपर से आवरण को हटा लेना।
शब्दार्थ :
अन्तर्निहित-मन में मौजूद। अभिव्यक्त-प्रकट। यथार्थ-वास्तव। आविष्कार-खोज ।अनावृत-ढका हुआ, पर्दा पड़ा हुआ।अनन्त-अन्त रहित। आवरण-पर्दा, ढक्कन।
प्रसंग :
प्रस्तुत गद्यांश हमारी पाठ्य पुस्तक ‘हिन्दी सामान्य भाग-1’ में संकलित तथा स्वामी विवेकानन्द लिखित निबन्ध ‘शिक्षा’ से अवतरित है। इसमें लेखक ने यह बतलाना चाहा है कि मनुष्य के अन्दर ही ज्ञान होता है।
व्याख्या :
स्वामी विवेकानन्द का कहना है कि शिक्षा का अर्थ है-मनुष्य के मन में मौजूद ज्ञान के भण्डार को प्रकट करना। दूसरे शब्दों में मनुष्य के भीतर भरे हुए ज्ञान को बाहर शिक्षा ही प्रकट करती है। इसलिए हमें इस भ्रम में नहीं पड़ना चाहिए कि मनुष्य को ज्ञान बाहर से आता है। उसमें तो सभी प्रकार के ज्ञान उसके स्वभाव के अनुसार ही भरे होते हैं। अगर कोई यह कहता है कि मनुष्य सब कुछ जानता-समझता है, यह शत-प्रतिशत सही है। इसे हम मानस-शास्त्र-संगत भाषा में कहना चाहें, तो यह कह सकते हैं कि वह खोज करता है। अपने भीतर के ज्ञान के ऊपर पड़े हुए, पर्दे को हटाता हैं। इस प्रकार वह जो कुछ जानता-समझता है, वह सब कुछ उसकी खोज करना ही होता है। इस आधार पर हम यह कह सकते हैं कि मनुष्य का अपने भीतर मौजूद अपार और अनन्त ज्ञान के भण्डार के ऊपर पड़े पर्दे को हटा लेना ही उसकी खोज है।
विशेष :
- प्रस्तुत पंक्तियों में लेखक ने शिक्षा और खोज का अर्थ बतलाया है।
- भापा सरल और सुबोध है।
- शैली वर्णनात्मक है।
- यह अंश ज्ञानवर्द्धक है।
- यह अंश ज्ञानवर्द्धक है।
गद्यांश पर आधारित अर्थ-ग्रहण सम्बन्धी प्रश्नोत्तर-
प्रश्न.
(i) ज्ञान मनुष्य में किस प्रकार है?
(ii) आविष्कार का दूसरा अर्थ क्या है?
(iii) मनुष्य की आत्मा क्या है?
उत्तर:
(i) ज्ञान मनुष्य में स्वभाव सिद्ध है, क्योंकि वह बाहर से उसमें नहीं आता है। वह तो उसके भीतर उसके जन्म से ही होता है।
(ii) आविष्कार का दूसरा अर्थ है-सीखना, समझना।
(iii) मनुष्य की आत्मा अपार और अनन्त ज्ञान स्वरूप है।
गद्यांश पर आधारित बोधात्मक प्रश्नोत्तर
प्रश्न.
(i) शिक्षा क्या करती है?
(ii) हमारा जानना क्या है?
(iii) मनुष्य को कुछ सीखने-समझने से क्या लाभ होता है?
उत्तर:
(i) शिक्षा. मनुष्य के मन में मौजूद ज्ञान के ऊपर पड़े हुए अज्ञान के पर्दे को हटाती है।
(i) हमारा जीनना हमारे ज्ञान के ऊपर अज्ञान के पर्दे को हटाना है।
(iii) मनुष्य को सीखने-समझने से उसके ज्ञान का विस्तार होता है और अज्ञान का अन्त होने लगता है।
2. यह आवरण तह-पर-तह पड़ा है, वह अज्ञानी है। जिस पर से यह आवरण पूरा हट जाता है, वह सर्वज्ञ सर्वदर्शी हो जाता है। चकमक पत्थर के टुकड़े में अग्नि के समान, ज्ञान मन में निहित है और सुझाव या उद्दीपक-कारण ही वह घर्षण है, जो उस ज्ञानाग्नि को प्रकाशित कर देता है। सभी ज्ञान और सभी शक्तियाँ भीतर हैं। हम जिन्हें शक्तियाँ, प्रकृति के रहस्य या बल कहते हैं, वे सब भीतर ही हैं। मनुष्य की आत्मा से ही सारा ज्ञान आता है जो ज्ञान सनातन काल से मनुष्य के भीतर निहित है, उसी को वह बाहर प्रकट करता है, अपने भीतर ‘देख पाता है।
शब्दार्थ :
आवरण-पर्दा। सर्वदर्शी-सब कुछ देखने वाला। चकमक पत्थर-एक विशेष प्रकार का पत्थर। अग्नि-आग। निहित-छिपा हुआ। उद्दीपक-उत्तेजित करने वाला। ज्ञानाग्नि-ज्ञान की आग। सनातन-जो हमेशा से चला आ रहा है।
प्रसंग :
प्रस्तुत गद्यांश हमारी पाठ्य-पुस्तक ‘हिन्दी सामान्य भाग-1’ में संकलित तथा स्वामी विवेकानन्द लिखित ‘शिक्षा’ से अवतरित है। इसमें लेखक ने मनुष्य के मन में मौजूद ज्ञान के स्वरूप को बतलाने का प्रयास किया है।
व्याख्या :
लेखक का कहना है कि जिस मनुष्य पर से अज्ञान का पर्दा उठ जाता है, वह और मनुष्यों की अपेक्षा अधिक ज्ञानी बन जाता है। इससे ठीक विपरीत जिस मनुष्य पर अज्ञान का पर्दा पड़ा रहता है, वह अज्ञानी ही बना रहता है। इस प्रकार अज्ञान के पर्दे में रहने वाला मनुष्य मूर्ख होता है और अज्ञान के पर्दे से बाहर रहने वाला मनुष्य सर्वज्ञ और सर्वदर्शी होता है। हमें यह अच्छी प्रकार से समझ लेना चाहिए कि मनुष्य के मन में ज्ञान चकमक पत्थर में छिपी हुई आग के समान होता है। वह किसी प्रकार की शिक्षा या सुझाव के द्वारा प्रकट होता है। इसके लिए मनुष्य को सत्संगति या सद्गुरु की शरण लेनी चाहिए। इससे उसे यह अच्छी प्रकार से समझ आ जाती है कि सभी प्रकार के ज्ञान और सभी प्रकार के बल मनुष्य के मन में ही मौजूद है। इस तरह मनुष्य के मन में सनातन काल से ही ज्ञान मौजूद है। उसे वह किसी सद्गुरु या सदुपदेश के द्वारा अपने भीतर होने का अनुभव कर पाता है। यही नहीं, वह उसे सबके सामने भी प्रकट कर देता है।
विशेष :
- मनुष्य के मन में मौजूद ज्ञान की दशा का उल्लेख किया गया है।
- मनुष्य के मन में मौजूद ज्ञान की उपमा चकमक पत्थर के टुकड़े से दी गई है इसलिए इसमें उपमा अलंकार है।
- तत्सम शब्दावली है।
- शैली सुबोध है।।
गद्यांश पर आधारित अर्थ-ग्रहण सम्बन्धी प्रश्नोत्तर-
प्रश्न.
(i) कौन-सा आवरण तह पर पड़ा रहता है?
(ii) लेखक ने ‘चकमक पत्थर’ का क्यों उदाहरण दिया है?
(iii) अज्ञानी और सर्वज्ञ कौन होता है?
उत्तर:
(i) मनुष्य के मन में ज्ञान का भण्डार भरा होता है। लेकिन उसके तह पर अज्ञान का आवरण पड़ा रहता है।
(ii) लेखक ने ‘चकमक पत्थर’ का उदाहरण मनुष्य के भीतर छिपे हुए ज्ञान को समझाने के लिए दिया है। उसका यह मानना है कि जिस प्रकार चकमक पत्थर में आग छिपी रहती है, उसी प्रकार मनुष्य के भीतर ज्ञान छिपा हुआ है।
(iii) जिस मनुष्य पर अज्ञान का पदों पड़ा रहता है, वह अज्ञानी होता है। इसके विपरीत जिस मनुष्य पर से अज्ञान का पर्दा हट जाता है, वह सर्वज्ञ होता है।
गद्यांश पर आधारित बोधात्मक प्रश्नोत्तर-
प्रश्न.
(i) मनुष्य के भीतर कौन-कौन-सी शक्तियाँ होती हैं?
(ii) सुझाव का क्या फल होता है?
(iii) मनुष्य अपने भीतर किससे क्या देख पाता है?
उत्तर:
(i) मनुष्य के अपने भीतर सभी प्रकार के ज्ञान, प्रकृति के रहस्य और सभी प्रकार की शक्तियाँ होती हैं।
(ii) सुझाव का फल बहुत सुखद और लाभप्रद होता है, सुझाव वह घर्षण है, जो मनुष्य के भीतर छिपी हुई ज्ञान की आग को प्रकाशित कर देता है।
(iii) मनुष्य अपने भीतर छिपे हुए ज्ञान को अपनी आत्मा से देख पाता है।
![]()
3. हमें विधायक विचार सामने रखने चाहिए। निषेधात्मक विचार लोगों को दुर्बल बना देते हैं। क्या तुमने यह नहीं देखा कि जहाँ माता-पिता पढ़ने-लिखने के लिए अपने बालकों के सदा पीछे लगे रहते हैं और कहा करते हैं कि तुम कभी कुछ सीख नहीं सकते, तुम गधे बने रहोगे, वहाँ बालक यथार्थ में वैसे ही बन जाते हैं यदि तुम उनसे सहानुभूति-भरी बातें करो और उन्हें उत्साह दो, तो समय पाकर उनकी उन्नति होना निश्चित है। यदि तुम उनके सामने विधायक विचार रखो, तो उनमें मनुष्यत्व आएगा और वे अपने पैरों पर खड़ा होना सीखेंगे। भाषा और साहित्य काव्य और कला, हर एक विषय में हमें मनुष्यों को उनके विचार और कार्य की भूलें नहीं बतानी चाहिए, वरन् उन्हें वह मार्ग दिखां देना चाहिए, जिससे वे इन सब बातों को और भी सुचारु रूप से कर सकें।
शब्दार्थ :
विधायक-सकारात्मक, निर्णयात्मक। निषेधात्मक/नकारात्मक/ दुर्बल-कमजोर । यथार्थ-वास्तव । मनुष्यत्व-मनुप्यता। पैरों पर खड़ा होना-आत्मनिर्भर होना। वरन्-बल्कि, अपितु। सुचारु-सुन्दर।
प्रसंग :
पूर्ववत्। इसमें लेखक ने बालकों को आत्मनिर्भर और योग्य बनाने के तौर-तरीकों को बतलाने का प्रयास किया है।
व्याख्या :
लेखक का कहना है कि बच्चों को शिक्षित करने के लिए उनके माता-पिता या अभिभावक को सकारात्मक अर्थात् अपनापन का विचार-भाव रखना चाहिए। उनके प्रति किसी प्रकार के नकारात्मक अर्थात् पराएपन का व्यवहार नहीं करना चाहिए। इस प्रकार के दुर्व्यवहार उनके प्रति किए जाने से वे कुछ सीख-समझ नहीं पाएंगे। यह प्रायः देखा जाता है कि जो माता-पिता या अभिभावक अपने बच्चों को उनकी इच्छा के विपरीत पढ़ने-लिखने के लिए दबाव डालते रहते हैं। उन्हें कोसते रहते हैं, वे वास्तव में पढ़-लिख नहीं पाते हैं। वे उनकी हीनता के शिकार होकर अयोग्य और दुर्बल बन जाते हैं। इसलिए हमें बच्चों की भावनाओं का आदर करना चाहिए। उनके प्रति सहानुभूति और सद्भावना रखनी चाहिए। उन्हें उत्साहित करना चाहिए। ऐसा करके ही हम उन्हें सुशिक्षित और सुयोग्य बना सकते हैं फिर उनमें मानवता आ जाएगी। वे आत्मनिर्भर होकर देश और समाज का बहुत बड़ा कल्याण करेंगे। इससे आने वाली पीढ़ी भी बहुत कुछ सीख-समझ सकती है।
लेखक का पुनः कहना है कि बच्चों को शिक्षित कर उन्हें योग्य बनाने के लिए उन्हें विविध प्रकार की भाषा, साहित्य, काव्य और कला के बारे में ज्ञान देना चाहिए। ऐसा करते समय हमें इस ओर ध्यान देना चाहिए कि वे इन विषयों में आए हुए मनुष्य के दोषों को न जान पाएं। हमारा तो यह प्रयास होना चाहिए कि वे इन विषयों में आए हुए मनुष्यों के गुणों-अच्छाइयों को अच्छी तरह से समझकर ग्रहण कर सके। इससे वे आदर्श विद्यार्थी की भूमिका निभाकर एक श्रेष्ठ नागरिक कहलाएँ।
विशेष :
- बच्चों को आदर्श विद्यार्थी बनाने के सुझाव दिए गए हैं।
- यह अंश शिक्षाप्रद है।
- भाषा की शब्दावली तत्सम शब्दों की है।
- शैली उपदेशात्मक है।
- ‘पैरों पर खड़ा होना’ मुहावरे का सार्थक प्रयोग है।
गद्यांश पर आधारित अर्थ-ग्रहण सम्बन्धी प्रश्नोत्तर-
प्रश्न.
(i) हमें विधायक विचार क्यों रखने चाहिए?
(ii) बच्चे कुछ नहीं सीख पाते हैं, ऐसा लेखक ने क्यों कहा हैं?
(iii) बच्चों के प्रति कैसा व्यवहार करना चाहिए?
उत्तर:
(i) हमें विधायक विचार ही बच्चों के सामने रखना चाहिए। यह इसलिए कि निषेधात्मक विचार दर्बल बना देते हैं।
(ii) बच्चे अपने माता-पिता से कुछ सीख नहीं पाते हैं। इसका कारण यह है कि उनके माता-पिता उन्हें हमेशा कोसते रहते हैं। वे उन्हें हीन और अयोग्य ही समझते हैं। वे उनमें छिपी हुई उनकी अच्छाइयों और सम्भावनाओं को नहीं देख पाते
(iii) बच्चों के प्रति हमें सरस, आत्मीयतापूर्ण और सहानुभूतिपूर्ण व्यवहार करना चाहिए।
गद्यांश पर आधारित बोधात्मक प्रश्नोत्तर-
प्रश्न.
(i) बालक यथार्थ में कैसे बन जाते हैं?
(ii) बच्चों की उन्नति होना कैसे निश्चित है?
(iii) बच्चे आत्मनिर्भर होना कब सीखेंगे?
उत्तर:
(i) बालक यथार्थ में वैसे ही बन जाते हैं, जैसे उनके माता-पिता उन्हें चाहते हैं।
(ii) बच्चों की उन्नति होना तभी निश्चित है, जब उनके माता-पिता उनसे सहानुभूति-भरी बातें करें और उन्हें उत्साहित करते रहें।
(iii) बच्चे आत्मनिर्भर होना तभी सीखेंगे, जब उनमें मनुष्यता आएगी। उनमें मनुष्यता लाने के लिए विधायक विचारों को ही उनके सामने रखने होंगे।
4. विद्यार्थी की आवश्यकता के अनुसार शिक्षा में परिवर्तन होना चाहिए। अतीत जीवनों ने हमारी प्रवृत्तियों को गढ़ा है, इसलिए विद्यार्थी को उसकी प्रवृत्तियों के अनुसार मार्ग दिखाना चाहिए। जो जहाँ पर है, उसे वहीं से आगे बढ़ाओ। हमने देखा है कि जिनको हम निकम्मा समझते थे, उनको भी श्रीरामकृष्णदेव ने किस प्रकार उत्साहित किया और उनके जीवन का प्रवाह बिल्कुल बदल दिया। उन्होंने कभी भी किसी मनुष्य की विशेष प्रवृत्तियों को नष्ट नहीं किया। पन्होंने अत्यन्त पतित मनुष्यों के प्रति भी आशा और उत्साहपूर्ण वचन कहे और उन्हें ऊपर उठा दिया।
शब्दार्थ :
अतीत-बीते हुए। निकम्मा-निठल्ला, कामचोर। पतित-पापी, भ्रष्ट।
प्रसंग :
पूर्ववत्। इसमें लेखक ने विद्यार्थी को किस प्रकार शिक्षित करके योग्य बनाना चाहिए, इसे बतलाने का प्रयास किया है।
व्याख्या :
लेखक का कहना है कि विद्यार्थी को शिक्षा देने से पहले यह अच्छी तरह से समझ लेना चाहिए कि उसे किस प्रकार की शिक्षा की आवश्यकता है। इस प्रकार उसकी आवश्यकता के अनुसार शिक्षा देनी चाहिए। आवश्यकतानुसार उसकी शिक्षा में हेर-फेर करने से हमें संकोच या देर नहीं करनी चाहिए। इस प्रकार का कदम उठाते समय हमें अतीतकालीन जीवनादर्शों को नहीं भूलना चाहिए। ऐसा इसलिए कि उसने हमारी प्रवृत्तियों को बनाया है। उससे हम आज आगे बढ़ रहे हैं। अगर हम अपने विद्यार्थियों को उन्हीं प्रवृत्तियों के अनुसार शिक्षा देंगे, तो वे निश्चय ही एक आदर्श विद्यार्थी बनकर एक श्रेष्ठ नागरिक की भूमिका निभा सकेंगे। अपने समाज और अपने देश को महान बनाने के लिए हमें यह अवश्य प्रयास करना चाहिए कि जो कोई जिस दिशा में विकास कर रहा है, उसे उसी दिशा में विकास करने दें। उसमें किसी प्रकार का. फेर-बदल न करें।
लेखक का पुनः कहना है कि हमें किसी का निठल्ला या कामचोर समझना नहीं चाहिए। अगर कोई ऐसा है, तो उसे कोसना नहीं चाहिए। उसे हीन भावना से नहीं देखना चाहिए। उसे हतोत्साहित करने के वजाय उसे उत्साहित ही करना चाहिए। यह हम अच्छी प्रकार से जानते हैं कि निठल्लों या कामचोरों को श्रीरामकृष्णदेव ने कभी न तो कोसा और न ही उन्हें हतोत्साहित किया। उन्होंने तो ऐसे व्यक्तियों को खूब उत्साहित किया। उससे उनकी जीवन धारा ऐसी वदल गई कि वे एक श्रेष्ठ नागरिक बनकर समाज और देश का कल्याण करने लगे। इस प्रकार श्रीरामकृष्णदेव ने किसी भी प्रकार के मनुष्य के जीवन को उच्च और श्रेष्ठ बनाने के लिए उसकी विशेप प्रवृत्तियों को कभी नहीं दवाया। उन्हें वैसे ही बढ़ने दिया। उन्होंने तो एक-से-एक अधम और गिरे हुए मनुप्य को उत्साहित कर और आशा दे-देकर ऊपर उठाने का सफल प्रयास किया।
विशेष :
- विद्यार्थी को उसकी आवश्यकतानुसार शिक्षा देने का सुझाव दिया गया
- श्रीरामकृष्णदेव के उल्लेख से विषय को स्पष्ट करने का सफल प्रयास है।
- हिन्दी-उर्दू की मिश्रित शब्दावली है।
- भाषा सरल है।
- यह अंश प्रेरणादायक रूप में है।
गद्यांश पर आधारित अर्थ-ग्रहण सम्बन्धी प्रश्नोत्तर-
प्रश्न.
(i) शिक्षा में किस प्रकार का परिवर्तन होना चाहिए?
(ii) विद्यार्थियों को किस प्रकार दिशा-निर्देश देना चाहिए?
(iii) ‘जो जहाँ पर है, उसे वहाँ से आगे बढ़ाओ।’ ऐसा लेखक ने क्यों कहा है?
उत्तर:
(i) शिक्षा में युग को ध्यान में रखकर विद्यार्थियों की आवश्यकता के अनुसार परिवर्तन होना चाहिए।
(ii) विद्यार्थियों को उनकी प्रवृत्तियों के अनुसार दिशा-निर्देश देना चाहिए।
(iii) ‘जो जहाँ पर है, उसे वहाँ से आगे बढ़ओ।’ ऐसा लेखक ने कहा है। ऐसा इसलिए कि जो जिस दिशा में आगे बढ़ रहा है, उस दिशा में उसके विकास की और सम्भावमाएँ बनी रहती हैं। अगर उसे विपरीत दिशा में बढ़ने के लिए उस पर दबाव डाला जाएगा, तो उसका हुआ विकास बिखर जाएगा। उसकी और सम्भावनाएँ भी समाप्त हो जाएँगी।
गद्यांश पर आधारित बोधात्मक प्रश्नोत्तर-
प्रश्न.
(i) श्रीरामकृष्णदेव ने किस प्रकार निकम्मों को आगे बढ़ाया?
(ii) गिरे हुए मनुष्यों को कैसे ऊपर उठाना चाहिए?
उत्तर:
(i) श्रीरामकृष्णदेव ने उत्साहित और प्रेरित करके निकम्मों को आगे बढ़ाया।
(ii) गिरे हुए मनुष्यों को ऊपर उठाने के लिए उनमें आशा और विश्वास भरना चाहिए।
![]()
5. विदेशी भाषा में दूसरे के विचारों को रटकर, अपने मस्तिष्क में उन्हें दूंसकर और विश्वविद्यालयों की कुछ पदवियाँ प्राप्त करके, तुम अपने को शिक्षित समझते हो। क्या यही शिक्षा है? तुम्हारी शिक्षा का उद्देश्य क्या है? या तो मुन्शीगिरी करना, या वकील हो जानाध्या अधिक-से-अधिक डिप्टी मैजिस्ट्रेट बन जाना, जो मुन्शीगिरी का ही दूसरा रूप है। बस यही न? इससे तुमको या तुम्हारे देश को क्या लाभ होगा? आँखें खोलकर देखों, जो भारतखण्ड अन्न का अक्षय भण्डार रहा है, आज वही उसी अन्न के लिए कैसी करुण पुकार उठ रही है! क्या तुम्हारी शिक्षा इस अभाव की पूर्ति करेगी? वह शिक्षा जो जनसमुदाय को जीवन-संग्राम के उपयुक्त नहीं बनाती, जो उनकी चारित्र्य-शक्ति का विकास नहीं करती, जो उनमें दया का भाव और सिंह का साहस पैदा नहीं करती, क्या उसे भी हम ‘शिक्षा’ का नाम दे सकते हैं?
शब्दार्थ :
रटकर-कण्ठस्थ कर। पदवियाँ-उपाधियाँ (डिग्रियाँ)। डिप्टीमैजिस्ट्रेट-उप जिलाधीश। करुण-दुखद। अभाव-कमी। उपयुक्त-उचित। चारित्र्य-चरित्र की। भूत-प्राणी, जीव।
प्रसंग :
पूर्ववत्। इसमें लेखक ने आधुनिक शिक्षा को आड़े हाथ लेते हुए जीवनोपयोगी शिक्षा की आवश्यकता पर बल दिया है।
व्याख्या :
लेखक का कहना है कि हमारी आज की शिक्षा अनुपयोगी सिद्ध हो रही है। वह अपने उद्देश्य से भटक चुकी है। आज के विद्यार्थी की रुचि स्वदेशी भाषा के प्रति न होकर विदेशी भाषा के ही प्रति हो रही है। इससे वह विदेशी संस्कृति को बेहिचक अपना रहा है। उसके मन-मस्तिष्क में विदेशीपन इस तरह घुस गया है कि उसे निकाल पाना कठिन हो गया है। देखा जाए तो आज की शिक्षा का एकमात्र उद्देश्य विश्वविद्यालय की उपाधियाँ प्राप्त करना रह गया है। इसके द्वारा मुन्शीगिरी या डिप्टी मैजिस्ट्रेट जैसे पद को प्राप्त कर लेने तक सिमटकर रह गया है। इस प्रकार के शिक्षकों से अगर पूछा जाए कि क्या इससे वे समाज और देश का कोई भला कर सकेंगे; तो वे हाँ नहीं कह सकते हैं। ऐसा इसलिए उनमें इस प्रकार की शिक्षा लेकर समाज और देश का भला करने की कोई योग्यता-क्षमता है ही नहीं।
लेखक आज के शिक्षित नवजवानों को फटकारते हुए कह रहा है-हे आज शिक्षित नवजवानो! अपने इस देश की दुर्दशा को देखो। यह याद करो कि तुम्हारा यह देश कृषि प्रधान देश है। इसकी धरती अपार और अक्षय अन्न को उत्पन्न करने वाली रही है। लेकिन बड़े अफसोस के साथ यह कहना पड़ता है कि आज यहाँ के लोगों को भरपेट अन्न नहीं मिल रहा है। बार-बार अन्न की कमी से यहाँ के लोग बिलबिला रहे हैं। देश की इस दुर्दशा को दूर करने के लिए तुम्हारी शिक्षा क्या कारगर कदम उठा सकती है? शायद नहीं। इसलिए उस शिक्षा को सौ बार धिक्कार है, जो अपने देश और समाज को आत्मनिर्भर नहीं बनाती है। ऐसी शिक्षा किस काम की, जो सहानुभूति और कुछ कर गुजरने के भावों को नहीं पैदा करती है।
विशेष :
- आधुनिक शिक्षा की कमजोरियों पर सीधा प्रकाश डाला गया है।
- देश और समाज के लिए उपयोगी शिक्षा को महत्त्व दिया गया है।
- मिश्रित शब्दावली है।
- शैली रोचक है।
गद्यांश पर आधारित अर्थ-ग्रहण सम्बन्धी प्रश्नोत्तर-
प्रश्न.
(i) विदेशी भाषा और संस्कृति के प्रति लेखक ने क्या कहा है?
(ii) आज की शिक्षा का स्वरूप क्या है?
उत्तर:
(i) विदेशी भाषा और संस्कृति के प्रति लेखक का यह कहना है कि उससे हमारी भाषा और संस्कृति धूमिल और शक्तिहीन होती जा रही है। फलस्वरूप हमारा देश तन-मन से पुनः पराधीन होने के करीब आ चुका है।
(ii) आज की शिक्षा विदेशी शिक्षा के चंगुल में फंस गई है। इससे वह आत्मविवेक और मौलिक दृष्टिकोण देने में असमर्थ हो चुकी है।
गद्यांश पर आधारित बोधात्मक प्रश्नोत्तर-
प्रश्न.
(i) शिक्षा का क्या उद्देश्य होना चाहिए?
(ii) हम किस शिक्षा को ‘शिक्षा’ कह सकते हैं?
उत्तर:
(i) शिक्षा का यही उद्देश्य होना चाहिए कि वह अपने देश के नागरिकों
को अधिक-से-अधिक अन्न, वस्त्र और आवास प्रदान कर सके। दूसरे शब्दों में देश को आत्मनिर्भर बना सके।
(ii) हम उस शिक्षा को ‘शिक्षा’ कह सकते हैं, जो हमारी चारित्रिक शक्ति का विकास करती है। जो हर प्राणी के प्रति दयाभाव और कठिनाइयों का सामना करने के लिए साहस प्रदान करती है, वही सच्ची शिक्षा है।
6. हमें तो ऐसी शिक्षा चाहिए, जिससे चरित्र बने, मानसिक बल बढ़ेबुद्धि का विकास हो और जिससे मनुष्य अपने पैरों पर खड़ा हो सके। हमें आवश्यकता इस बात की है कि हम विदेशी अधिकार से स्वतन्त्र रहकर अपने निजी ज्ञान भण्डार की विभिन्न शाखाओं का और उसके साथ ही अंग्रेजी भाषा और पाश्चात्य विज्ञान का अध्ययन करें। हमें यान्त्रिक और ऐसी सभी शिक्षाओं की आवश्यकता है, जिनसे उद्योग-धन्धों की वृद्धि और विकास हो, जिससे मनुष्य नौकरी के लिए मारा-मारा फिरने के बदले अपनी आवश्यकताओं की पूर्ति के लिए पर्याप्त कमाई कर सके और आपत्काल के लिए कुछ संचय भी कर सके।
शब्दार्थ :
पाश्चात्य-पश्चिमी। यान्त्रिक यन्त्र सम्बन्धित। पर्याप्त अधिक। कमाई-धन प्राप्त करना। आपत्काल-संकट के समय। संचय-बचत।
प्रसंग :
पूर्ववत्। इसमें आज किस प्रकार की शिक्षा की आवश्यकता है, लेखक ने इसे बतलाने का प्रयास किया है।
व्याख्या :
लेखक का कहना है कि आज विद्यार्थियों को वही शिक्षा देनी चाहिए, जिससे उनका चारित्रिक विकास हो। उनका मन-मस्तिष्क अधिक विकसित हो। उनकी बल-बुद्धि अधिक आगे बढ़े। हरेक मनुष्य आत्मनिर्भर बन सके। आज की शिक्षा ऐसी होनी चाहिए कि वह हमें विदेशी संस्कृति के प्रभाव से मुक्त रखे। हमें स्वदेशीपन को अपनाने के लिए प्रेरित करे। हमें स्वतन्त्र जीवन जीने की दृष्टि दे। हमारी निजी समझ को अच्छी तरह से बढ़ावे। इसके बाद ही अंग्रेजी भाषा और पश्चिमी ज्ञान-विज्ञान को समझे और समझने का प्रयास करे। हमें इस प्रकार की शिक्षा ही आज के इस विज्ञान के युग में चाहिए। ऐसा इसलिए कि इस प्रकार की शिक्षा से ही हमारे देश में विविध प्रकार के कल-कारखानों का विस्तार हो सकेगा। इससे बेरोजगारों को नौकरी मिल सकेगी। वे अपनी रोज की जरूरतों को पूरा कर सकेंगे। यही नहीं, वे अपने उज्ज्वल भविष्य के लिए भी कुछ बचा सकेंगे।
विशेष :
- आज के युग में किस प्रकार की शिक्षा होनी चाहिए, इसे समझाया गया है।
- जीवनोपयोगी शिक्षा की विशेषताएँ बतलाई गई हैं।
- वाक्य गठन बड़े-बड़े हैं।
- सामासिक शब्दावली है।
- शैली वर्णनात्मक है।
गद्यांश पर आधारित अर्थ-ग्रहण सम्बन्धी प्रश्नोत्तर
प्रश्न.
(i) शिक्षा का स्वरूप कैसा होना चाहिए?
(ii) आज हमारी सबसे बड़ी क्या आवश्यकता है?
उत्तर:
(i)शिक्षा का स्वरूप विविध होना चाहिए! दूसरे शब्दों में मानसिक, चारित्रिक व बौद्धिक बल को बढ़ाकर आत्मनिर्भर बनाने वाली शिक्षा का स्वरूप होना चाहिए।
(ii) आज हमारी सबसे बड़ी आवश्यकता है-बेरोजगारी के चंगुल से मुक्त होना। इसके चंगुल से मुक्त होने के लिए अपने निजी ज्ञान को बढ़ाने की बहुत जरूरत है। इससे ज्ञान-विज्ञान की समझ उपजेगी और हमारे देश में विविध प्रकार के कलकारखानों का विस्तार होगा और बेरोजगारों को नौकरी मिलेगी।
गद्यांश पर आधारित बोधात्मक प्रश्नोत्तर-
प्रश्न.
(i) हमें आज सभी शिक्षाओं की क्यों आवश्यकता है?
(ii) उपर्युक्त गद्यांश का मुख्य भाव क्या है?
उत्तर:
(i) हमें आज सभी प्रकार की शिक्षाओं की आवश्यकता है। यह इसलिए कि उनसे हमारा देश विकासशील से विकसित बन सकेगा। फिर हमें किसी देश पर किसी प्रकार निर्भर होने के लिए मजबूर नहीं होना पड़ेगा।
(ii) उपर्युक्त गद्यांश का मुख्य भाव है-‘आज हमें वैविध्यपूर्ण शिक्षा की आवश्यकता है। इससे हमारा वर्तमान और भविष्य दोनों ही सुखद और उज्ज्वल हो सकेगा।
![]()
7. सभी प्रकार की शिक्षा और अभ्यास का उद्देश्य ‘मनुष्य’ निर्माण ही हो। सारे प्रशिक्षणों का अन्तिम ध्येय मनुष्य का विकास करना ही है। जिन प्रक्रिया से.. मनुष्य की इच्छा शक्ति का प्रवाह और प्रकाश संयमित होकर फलदायी बन सके, उसी का नाम है शिक्षा। आज हमारे देश को जिस चीज की आवश्यकता है, वह है लोहे की मांसपेशियां और फौलाद के स्नायु, दुर्दमनीय प्रचण्ड इच्छाशक्ति जो सृष्टि के गुप्त तथ्यों और रहस्यों को भेद सके और जिस उपाय से भी हो अपने उद्देश्य की पूर्ति करने में समर्थ हो, फिर चाहे उसके लिए समुद्र-तल में ही क्यों न जाना पड़े-साक्षात् मृत्यु का ही सामना क्यों न करना पड़े। हम ‘मनुष्य’ बनानेवाला धर्म ही चाहते हैं। हम ‘मनुष्य’ बनानेवाला सिद्धान्त ही चाहते हैं। हम सर्वत्र, सभी क्षेत्रों में ‘मनुष्य’ बनानेवाली शिक्षा ही चाहते हैं।
शब्दार्थ-ध्येय :
उद्देश्य। स्नायु-नाड़ी संस्थान। दुर्दमनीय-जिसका दमन करना कठिन हो। गुप्त-अप्रकट, छिपे हुए। साक्षात्-प्रत्यक्ष। प्रचण्ड-अत्यधिक।
प्रसंग :
पूर्ववत्। इसमें लेखक ने सभी प्रकार की शिक्षा का उद्देश्य मनुष्य का विकास करना बतलाते हुए कहा है कि
व्याख्या :
चाहे कोई भी शिक्षा हो, उसका एकमात्र उद्देश्य मनुष्य बनाना होना चाहिए। दूसरे शब्दों में यह कि मनुष्य को बनाना या विकास करना ही शिक्षा का उद्देश्य होना चाहिए। इस उद्देश्य से विपरीत होने वाली शिक्षा सार्थक नहीं हो सकती है। उसे हम शिक्षा न कहकर अशिक्षा ही कहेंगे। इस प्रकार वास्तविक शिक्षा मनुष्य के साए हुए मजबूत भावों को जगाती है। उसमें तेजी लाती है। फिर उसे प्रभावशाली वनाती हुई उसे लोककल्याणकारी रूप दे डालती है। इस प्रकार की शिक्षा ही हमारे समाज और देश को आज चाहिए। हमारे समाज और देश को आज ऐसी शिक्षा की आवश्यकता है, जो लोहे की तरह मजबूत मांसपेशियां और फौलादी नाड़ी संस्थानों के साथ अत्यधिक दृढ़ इच्छाशक्ति को ला सके। इससे ही सभी प्रकार के छिपे हुए भेदों को जाना जा सकता है।
आज हमें एक ऐसी ही शिक्षा की बहुत बड़ी आवश्यकता है जो मनुष्य बनाने के उद्देश्य को पूरा करने के लिए किसी प्रकार की मुसीबत का सामना करने से पीछे न हटे। वह अपने उद्देश्य को पूरा करने के लिए समुद्र की गहराइयों में जाने का साहस दे सके। यही नहीं, सामने आई हुई मौत को भी ललकारने की हिम्मत दे सके। इस तरह आज हमें वही शिक्षा चाहिए जो मनुष्य को बनाने का धर्म हमें सिखा सके। इस प्रकार का मत-सिद्धान्त हमें बता सके। कहने का भाव यह है कि आज के युग की माँग मनुष्य बनाने वाली या मनुष्य का विकास करने वाली शिक्षा अत्यधिक है।
विशेष :
- आधुनिक युग की माँग मनुष्य बनाने वाली शिक्षा की है, इसे सुस्पष्ट किया गया है।
- शब्द उच्चस्तरीय हैं।
- शैली वर्णनात्मक है।
- वाक्य बड़े-बड़े हैं।
- यह अंश बोधगम्य है।
गद्यांश पर आधारित अर्थ-ग्रहण सम्बन्धी प्रश्नोत्तर-
प्रश्न.
(i) ‘मनुष्य’ निर्माण से लेखक का क्या आशय है?
(ii) किस प्रकार मनुष्य की इच्छाशक्ति प्रवाहित होकर फलदायी बन सकती है?
उत्तर:
(i) ‘मनुष्य’ निर्माण से लेखक का बहुत बड़ा आशय है। इसके द्वारा चारों ओर अपनापन, भाईचारा और आत्मीयता का वह वातावरण तैयार होगा, जिसमें सुख-शान्ति और आनन्द के अपेक्षित फूल खिलेंगे।
(ii) मनुष्य की इच्छाशक्ति सशिक्षा की प्रक्रिया से ही प्रवाहित होकर फलदायी बन सकती है।
गद्यांश पर आधारित बोधात्मक प्रश्नोत्तर-
प्रश्न.
(i) आज हमारे देश को किस चीज की आवश्यकता है?
(ii) लेखक ने बार-बार ‘मनुष्य’ निर्माण का उल्लेख क्यों किया है?
उत्तर:
(i) आज हमारे देश की अनेक प्रकार की आवश्यकताएँ हैं। उसे आज ऐसी शिक्षा की आवश्यकता है, जो उसके नागरिकों में फौलादी इच्छाशक्ति भर दे, जिससे सृष्टि के सभी गुप्त रहस्यों और तथ्यों का खुलासा कर सके। यही नहीं, उसे आज वही शिक्षा चाहिए, जो जीवन के हरेक क्षेत्रों में ‘मनुष्यता’ ला सके।
(ii) ‘मनुष्य’ निर्माण से चारों ओर अपनापन, भाईचारा, आत्मीयता का वातावरण निर्मित होता है जिससे मनुष्य को सुख-शान्ति और आनन्द के अपेक्षित फूल खिलेंगे।




















































































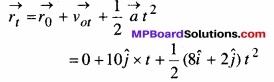
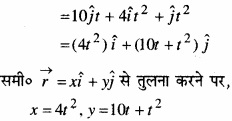


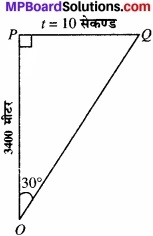
 = \(\frac{1963}{10}\)
= \(\frac{1963}{10}\)