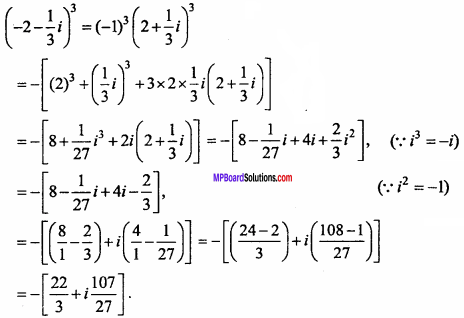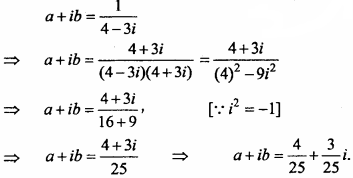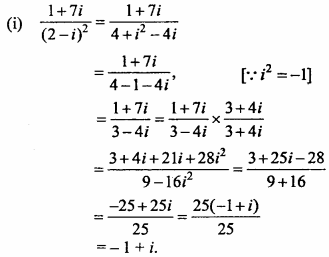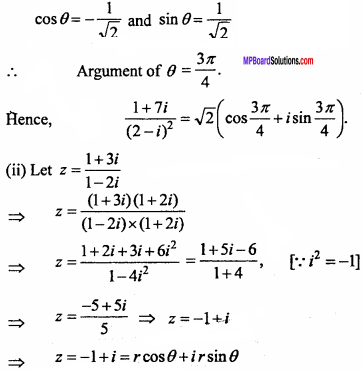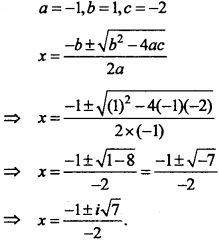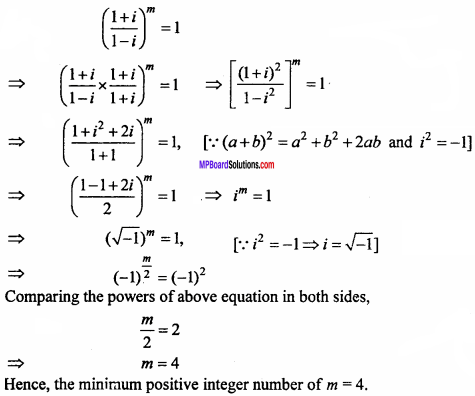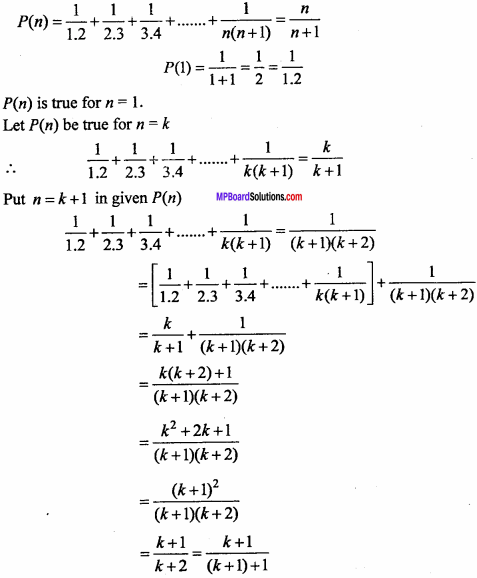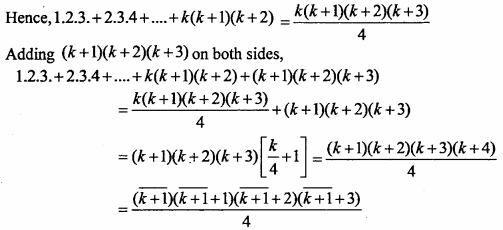Category: Class 11

MP Board Class 11th Maths Important Questions Chapter 12 Introduction to Three Dimensional Geometry

Introduction to Three Dimensional Geometry Important Questions

Introduction to Three Dimensional Geometry Objective Type Questions

(A) Choose the correct option :

Question 1.
Distance of a point (3,4, 5) from origin:
(a) 3
(b) 4
(c) 5
(d) 5\(\sqrt {2}\)
Answer:
(d) 5\(\sqrt {2}\)

Question 2.
The perpendicular distance of the point P (x, y, z) from X – axis is:
(a) \(\sqrt { { x }^{ 2 } + { z }^{ 2 } }\)
(b) \(\sqrt { { y }^{ 2 } + { z }^{ 2 } }\)
(c) \(\sqrt { { x }^{ 2 } + { y }^{ 2 } }\)
(d) \(\sqrt { { x }^{ 2 } + { y }^{ 2 } + { z }^{ 2 } }\)
Answer:
(b) \(\sqrt { { y }^{ 2 } + { z }^{ 2 } }\)

Question 3.
Distance of a point (3, 2, 5) from X – axis is:
(a) \(\sqrt {28}\)
(b)\(\sqrt {30}\)
(c) \(\sqrt {29}\)
(d) 3
Answer:
(c) \(\sqrt {29}\)

Question 4.
The YZ – plane divides the line segment joining the points (2, 3, 4) and (3, 5, – 4) in the ratio:
(a) 2 : 3 internally
(b) 1 : 2
(c) 2 : 3 externally
(d) 1 : 3
Answer:
(c) 2 : 3 externally

Question 5.
Distance between the points (1, 2,3) and (1,3, -2) is :
(a) \(\sqrt {- 26}\)
(b) \(\sqrt {26}\)
(c) 26
(d) ± \(\sqrt {24}\)
Answer:
(b) \(\sqrt {26}\)

Question 6.
Coordinate of a point on Z – axis, equidistant from the points (1, 5, 7) and (5, 1, – 4) is :
(a) (0, 0, \(\frac { 3 }{ 2 }\)
(b) (o, \(\frac { 3 }{ 2 }\), 0)
(c) (\(\frac { 3 }{ 2 }\), 0, 0)
(d) (4, – 4, – 11)
Answer:
(a) (0, 0, \(\frac { 3 }{ 2 }\)

Question 7.
Distance of a point (2, 1, 4) from Y – axis is:
(a) \(\sqrt {20}\)
(b) 1
(c) \(\sqrt {12}\)
(d) \(\sqrt {10}\)
Answer:
(a) \(\sqrt {20}\)

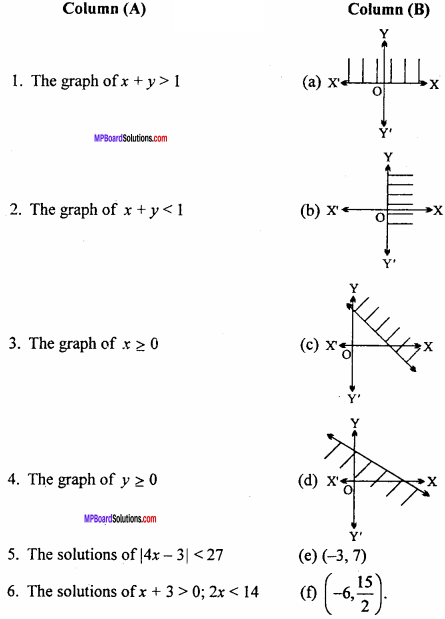
(B) Match the following :

Answer:

1. (e)
2. (d)
3. (b)
4. (a)
5. (c)

(C) Fill in the blanks :

1. If the points (- 1, 3, 2), (- 4, 2, – 2) and (5, 5, λ ) are collinear, then value of λ is …………….
2. The perpendicular distance of point P(x, y, z) from YZ – plane is …………….
3. XY – plane divides the line segment joining the points (- 3, 4, 8) and (5, – 6, 4) in the ratio …………….
4. Distance between the points (1, – 3, 4) and (3, 11, – 6) is …………….
5. Perpendicular distance of a point P (3,4, 5) from YZ – plane is …………….

Answer:

1. 10
2. x
3. 2 : 1
4. 10\(\sqrt {3}\)
5. 3

(D) Write true / false :

1. Distance of a point (4, 3, 5) from Y – axis is \(\sqrt {40}\).
2. Distance of a point (5, 12, 13) from YZ – axis is \(\sqrt {313}\).
3. The coordinate of a point where YZ – plane divides the join of the points (3, 5, – 7) and (- 2, 1, 8) are (0, \(\frac { 13 }{ 5 }\), 2).
4. Coordinate of mid point of the line segment joining the points (- 3, 4, – 8) and (5, – 6, 4) are (1, – 1, 2).
5. Points A(1, 2, 3), B(4, 0, 4) and C (- 2, 4, 2) are collinear.

Answer:

1. False
2. True
3. True
4. False
5. True

(E) Write answer in one word / sentence :

1. A point R lies on the line segment joining the points P (2, – 3, 4) and Q(8, 0, 10) whose x coordinate is 4, then the coordinate of R will be.
2. In what ratio does the plane 2x + y – z = 3 divide the line segment joining the points A (2, 1, 3) and 5(4, – 2, 5)?
3. If the origin is the centroid of the triangle ABC with vertices A (a, 1, 3), B (- 2, b, – 5), C (4, 7, c) then write the value of a, b and c.
4. Find the locus of the point, which is equidistant to the points (3, 4, – 5) and (- 2, 1, 4).
5. In which ratio the XY – plane divides the line joining the points (2, 4, 2) and (2, 5, – 4)?

Answer:

1. (4, – 2, 6)
2. 1 : 2 externally
3. – 2, – 8, – 2
4. 10x + 6y – 18z – 29 = 0
5. 1 : 2 internally.

Introduction to Three Dimensional Geometry Very Short Answer Type Questions

Question 1.
A point is on X – axis. What are its y – co – ordinate and z – co – ordinate?
Answer:
y – co – ordinate and z – co – ordinate of point on X – axis is 0, 0 is (x, 0, 0).

Question 2.
A point is in the xz – plane. What can you say about is y – co – ordinate?
Answer:
On xz – plane the y – co – ordinate will be zero.

Question 3.
The X – axis and Y – axis taken together to form a plane, name of the plane is.
Answer:
The plane is known as xy – plane.

Question 4.
Co – ordinate of any point on xy – plane is.
Answer:
The co – ordinate of any point on xy – plane is (x, y, 0).

Question 5.
Length of perpendicular of point P(x, y, z) from X – axis is.
Answer:
Length of perpendicular = \(\sqrt { { y }^{ 2 } + { z }^{ 2 } }\)

Question 6.
Length of perpendicular of point P(x, y, z) from yz – plane is.
Answer:
Length of perpendicular of point P(x, y, z) from yz – plane is x.

Question 7.
Find the distance of point (3, 4, 5) from xz – plane.
Answer:
Distance of point (3, 4, 5) from xz – plane M(3, 0, 5) = \(\sqrt {0 + 16 + 0}\) = 4.

Question 8.
What is the centroid of ∆ABC whose vertices A(x₁, y₁, z₁), B(x₂, y₂, Z₂) and C(x₃, y₃, z₃)?
Answer:
Centroid of ∆ABC is

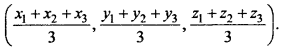
Question 9.
Find distance between points (2,3, 5) and (4,3,1).
Solution:
Distance between two points A(x₁, y₁, z₁) and B(x₂, y₂, Z₂):

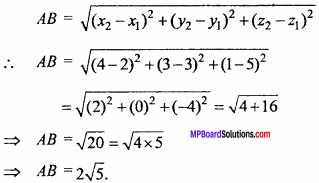
Question 10.
Find the distance between points (- 3, 7, 2) and (2, 4, – 1).
Solution:

Question 11.
Find the distance of the point (3, 2, 5) from X – axis.
Solution:
Point on X – axis (3, 0, 0)

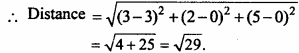
Question 12.
Find the distance of the point (2, 1, 4) from Y – axis.
Solution:
Point on Y – axis (0, 1, 0)

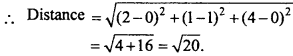
Question 13.
The three dimensional planes divides the space in how many octants?
Answer:
Three dimensional plane divides the space in eight octants.

Introduction to Three Dimensional Geometry Short Answer Type Questions

Question 1.
Prove that the points (- 2, 3, 5) (1, 2, 3) and (7, 0, – 1) are collinear. (NCERT)
Solution:
Given point are A (- 2, 3, 5), B(1, 2, 3) and C (7, 0, – 1).

Hence points A, B, Care collinear.

Question 2.
Find the co – ordinates of the point which divides the line segment joining the points (- 2, 3, 5) and (1, – 4, 6) in the ratio 2 : 3 internally. (NCERT)
Solution:
Required co – ordinates are :

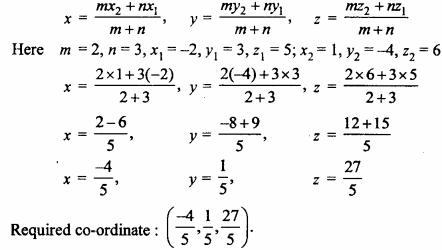
Question 3.
Given that P (3, 2, – 4), Q (5, 4, – 6) and R (9, 8, – 10) are collinear. Find the ratio in which Q divides PR. (NCERT)
Solution:

⇒ 5k + 5 = 9k + 3
⇒ 4k = 2
⇒ k = \(\frac { 1 }{ 2 }\)
Hence, point Q divides PR internally in ratio 1 : 2.

Question 4.
Find the ratio in which the YZ – plane divides the line segment formed by joining the points (- 2, 4, 7) and (3, – 5, 8).
Solution:
Let the point R (0, y, z) on YZ – plane divides the points P (- 2, 4, 7) and Q (3, – 5, 8) in the ratio m : n.
x = \(\frac{m x_{2}+n x_{1}}{m+n}\)
⇒ 0 = \(\frac { m × 3 + n( – 2) }{ m + n }\)
⇒ 3m – 2n = 0
⇒ 3m = 2n
⇒ \(\frac { m }{ n }\) = \(\frac { 2 }{ 3 }\)
⇒ m : n = 2 : 3
YZ – plane divides the line PQ internally in ratio 2:3.

Question 5.
If the origin is the centroid of the ∆PQR with vertices P(2a, 2, 6), Q(- 4, 3b, – 10) and R (8, 14, 2c) then find the value of a, b and c. (NCERT)
Solution:
Centroid of APQR is :
x = \(\frac{x_{1} + x_{2} + x_{3}}{3}\), y = \(\frac{y_{1} + y_{2} + y_{3}}{3}\), z = \(\frac{z_{1} + z_{2} + z_{3}}{3}\)
Co – ordinate of centroid are (0, 0, 0),

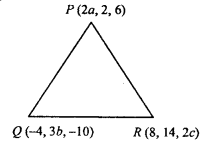
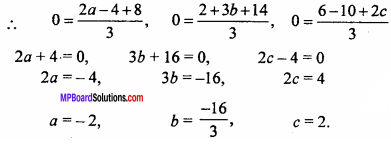
Question 6.
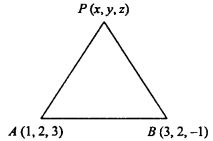
Find the co – ordinates of a point on Y – axis which are at a distance of 5\(\sqrt {2}\) from the point P(3, – 2, 5).
Solution:
Let A (0, y, 0) be any point on Y – axis.
Given : PA = 5\(\sqrt {2}\)
PA² = 50
⇒ (3 – 0)² + (- 2 – y)² + (5 – 0)² = 50
⇒ 9 + 4 + y² + 4y + 25 = 50
⇒ y² + 4y + 38 – 50 = 0
⇒ y² + 4y – 12 = 0
⇒ y² + 6y – 2y – 12 = 0
⇒ y(y + 6) – 2(y + 6) = 0
⇒ (y – 2)(y + 6) = 0
⇒ y = 2, – 6
The co – ordinate on Y – axis is (0, 2, 0) or (0, – 6, 0).

Question 7.
A point R with x co – ordinate 4 lies on the line segment joining the points P (2, – 3, 4) and Q (8, 0, 10). Find the co – ordinate of the point R.
Solution:
Let the point R (x, y, z) divides PQ in ratio m : n.

Co – ordinate of R (4, – 2, 6).

Question 8.
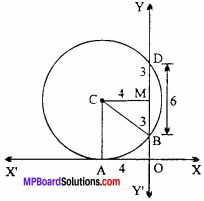
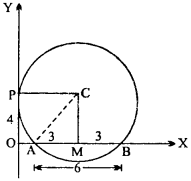
Find the equation of set of points which are equidistant from the points (1, 2, 3) and (3, 2, – 1). (NCERT)
Solution:
Let point P (x, y, z) be equidistant from points A (1, 2, 3) and B (3, 2, – 1).
∴ PA = PB

⇒ PA² = PB²
⇒ (x – 1)² + (y – 2)² + (z – 3)² = (x – 3)² + (y – 2)² + (z +1)²
⇒ x² – 2x + 1 + z² – 6z + 9
– 2x – 6z + 10 = – 6x + 2z + 10
⇒ 4x – 8z = 0
⇒ x – 2z = 0.
This is the required equation.

Question 9.
In which ratio the point (1, 1, 1) divides the line joining the points (3, – 2, 4) and (- 1, 4, 2)?
Solution:
Let point R (1,1,1), divides the line joining the points P (3, – 2, 4) and Q(- 1, 4, 2) in ratio λ : 1.
By formula:
x = \(\frac{m x_{2}+n x_{1}}{m+n}\)
Here x₁ = 3, x₂ = – 1, x = 1, m = λ and n = 1.
∴ 1 = \(\frac { λ(- 1) + 1 × 3 }{ λ + 1}\)
⇒ λ + 1 = – λ + 3
⇒ 2λ = 2
∴ λ = 1
Hence, required ratio is 1 : 1.

MP Board Class 11th Maths Important Questions

MP Board Class 11th Maths Important Questions Chapter 11 Conic Sections

Conic Sections Important Questions

Conic Sections Objective Type Questions

(A) Choose the correct option :

Question 1.
Coordinates of the focus of the parabola y = 2x² + x are:
(a) (0, 0)
(b) (\(\frac { 1 }{ 2 }\), \(\frac { 1 }{ 4 }\))
(c) (- \(\frac { 1 }{ 4 }\), 0)
(d) ( – \(\frac { 1 }{ 4 }\), \(\frac { 1 }{ 8 }\))
Answer:
(c) (- \(\frac { 1 }{ 4 }\), 0)

Question 2.
In a ellipse \(\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}\) = 1 a > b, the relation between a, b an eccentricity e is:
(a) b² = a²(1 – e²)
(b) b² = a²(e² – 1)
(c) a² = b²(1 – e²)
(d) a² = b²(e² – 1)
Answer:
(a) b² = a²(1 – e²)

Question 3.
The length of latus rectum of ellipse \(\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}\) = 1, represent a circle then its eccentricity will be:
(a) \(\frac { { 2a }^{ 2 } }{ b }\)
(b) \(\frac { { 2b }^{ 2 } }{ a }\)
(c) \(\frac { { a }^{ 2 } }{ b }\)
(d) \(\frac { { b }^{ 2 } }{ a }\)
Answer:
(b) \(\frac { { 2b }^{ 2 } }{ a }\)

Question 4.
The eccentricity of the parabola is:
(a) Less than 1
(b) Greater than 1
(c) 0
(d) 1
Answer:
(d) 1

Question 5.
The eccentricity of the ellipse is:
(a) Less than 1
(b) Greater than 1
(c) 0
(d) 1
Answer:
(a) Less than 1

Question 6.
The eccentricity of the hyperbola is:
(a) Less than 1
(b) Greater than 1
(c) 0
(d) 1
Answer:
(b) Greater than 1

Question 7.
In a ellipse \(\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}\) = 1, represent a circle then its eccentricity will be:
(a) Less than 1
(b) Greater than 1
(c) 0
(d) 1
Answer:
(c) 0

Question 8.
The sum of focal distances from any point on the ellipse is:
(a) Equal to major axis
(b) Equal to minor axis
(c) The distance between two foci
(d) Equal to latus rectum.
Answer:
(a) Equal to major axis

Question 9.
The differecne of the focal distances from any point on the hyperbola is:
(a) Equal to its conjugate axis
(b) Equal to its transverse axis
(c) The distance between two foci
(d) Equal to its latus rectum.
Answer:
(b) Equal to its transverse axis

Question 10.
The value of the eccentricity of ellipse 25x² + 16y² = 400 is:
(a) \(\frac { 3 }{ 5 }\)
(b) \(\frac { 1 }{ 3 }\)
(c) \(\frac { 2 }{ 5 }\)
(d) \(\frac { 1 }{ 5}\)
Answer:
(a) \(\frac { 3 }{ 5 }\)

Question 11.
Equation ax² + 2hxy + by² + 2gx + 2fy + c = 0 represent a circle if:
(a) a = b, c = 0
(b) f = g, h = 0
(c) a = b, h = 0
(d) f = g, c = 0
Answer:
(a) a = b, c = 0

Question 12.
Area of triangle whose centre (1,2) and which is passes through the point (4,6) will be:
(a) 5π
(b) 10π
(c) 25π
(d) 25π²
Answer:
(c) 25π

Question 13.
The circle passing through (1, – 2) and touching the X – axis at (3,0), also passes through the point:
(a) (2, – 5)
(b) (5, – 2)
(c) (- 2, 5)
(d) (- 5, 2)
Answer:
(a) (2, – 5)

Question 14.
The length of the diameter of the circle which touches the X – axis at the point (1,0) and passes through the point (2,3) is:
(a) \(\frac { 10 }{ 3 }\)
(b) \(\frac { 3 }{ 5 }\)
(c) \(\frac { 6 }{ 5 }\)
(d) \(\frac { 5 }{ 3 }\)
Answer:
(a) \(\frac { 10 }{ 3 }\)

Question 15.
Eccentricity of the hyperbola 3x² – y² = 4 :
(a) 1
(b) 2
(c) – 2
(d) \(\sqrt {2}\)
Answer:
(b) 2

(B) Match the following :

Answer:

1. (c)
2. (e)
3. (b)
4. (a)
5. (d)
6. (i)
7. (h)
8. (f)
9. (j)
10. (g)

(C) Fill in the blanks :

1. The length of the latus rectum of the parabola y² = 4ax is ……………
2. The centre of the ellipse \(\frac { { (x-1) }^{ 2 } }{ 9 } +\frac { { (y-2) }^{ 2 } }{ 4 }\) = 1 will be ……………
3. The vertex of the parabola (y – 2)² = 4a(x -1) is ……………
4. The lines \(\frac { x }{ a }\) – \(\frac { y }{ b }\) = m and \(\frac { x }{ a }\) + \(\frac { y }{ b }\) = \(\frac { 1 }{ m }\) meets always at ……………
5. If an ellipse \(\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}\) = 1, a > b and its eccentricity is e, then the foci will be
6. Standard form of equation of parabola is ……………
7. Parametric equation of a circle x² + y² = 4 is ……………
8. A line y = x + a\(\sqrt {2}\) touches the circle x² + y² = a² point ……………
9. A line y = mx + c touches the circle x² + y² = a² if c = ……………
10. Vertex of the parabola 3y² + 6y – 4x + 11 = 0 is ……………
11. Equation 2x² + 2y² – 12x – 16y + 4 = 0 represent a point circle if k = ……………
12. Radius of circle 3x² + 3y² – 5x – 6y + 4 = 0 is ……………

Answer:

1. 4a
2. (1, 2)
3. (1, 2)
4. Hyperbola
5. (± ae, 0)
6. y² = 4ax
7. x = 2cosθ
8. (- \(\frac { a }{ \sqrt { 2 } }\), \(\frac { a }{ \sqrt { 2 } }\) )
9. ±a\(\sqrt { 1+{ m }^{ 2 } }\)
10. (5, 1)
11. 50, 12
12. \(\sqrt {61}\)

(D) Write true / false :

1. Conic section is a locus of the point whose the ratio between the distance from the fixed point and distance from the fixed line, this ratio is called eccentricity of the conic section.
2. The ellipse \(\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}\) = 1 has two directrics, the equation of directrics are x = ± \(\frac { a }{ e }\); Where a > b and y = ± \(\frac { b }{ e }\) ; where b > a.
3. The foci of the ellipse \(\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}\) = 1 are (0, ± be) where a < b.
4. A circle drawn by taking major axis of the ellipse as diameter is called auxiliary circle of the ellipse.
5. The locus of intersection point of the lines bx + ay = abt and bx – ay = \(\frac { ab}{ t }\) will be a ellipse.
6. The focus of a parabola x² = – 16y will be (0, – 4).
7. Equation x² + y² – 6x + 8y + 50 = 0 represent a circle.
8. Circle x² + y² = 9 and x² + y² + 8y + c = 0 touches externally if c = 15 .
9. Eccentricity of hyperbola is 1.
10. Minimum distance between line y – x = 1 and curve x = y² is \(\frac { 3\sqrt { 2 } }{ 8 }\)

Answer:

1. True
2. True
3. True
4. True
5. False
6. True
7. False
8. True
9. False
10. True

(E) Write answer in one word / sentence :

1. If the circle x² + y² + 2ax + 8y +16 = 0, touches X – axis, then the value of α will be.
2. Coordinate of focus of parabola x² = – 10y will be.
3. Write the equation of a circle whose centre is (2,2) and passes through the point (4, 5).
4. The centre of a circle is (5, 7) and touches Y – axis, then its radius will be.
5. If the radius of a circle x² + y² – 6x + ky – 25 = 0 is \(\sqrt {38}\) the value of k will be.
6. Vertex of the parabola y = x² – 2x + 3 will be.
7. Equation of a parabola whose vertex (0, 0) and focus (0, 3) will be.
8. Length of major axis of ellipse 9x² + 16y² = 144 will be.
9. Eccentricity of an ellipse whose latus rectum in half of its minor axis will be.
10. Equation of hyperbola whose one focus in (4, 0 ) and corresponding equation of directrix x = 1 will be.

Answer:

1. ± 4
2. (0, \(\frac { – 5 }{ 2 }\))
3. x² + y² – 4x – 4y – 5 = 0
4. 7, 5
5. ± 4
6. (1, 2)
7. x² = 12y
8. 6
9. \(\frac { \sqrt { 3 } }{ 2 }\)
10. \(\frac { x^{ 2 } }{ 4 } -\frac { y^{ 2 } }{ 12 } \) = 1

Conic Sections Long Answer Type Questions

Question 1.
Find the equation of circle which touches the X – axis at a distance of 4 units in the negative direction and makes intercept of 6 units on positive direction of Y – axis.
Solution:
Here OA = CM = 4, BD = 6.
Length of perpendicular drawn from centre C on BD.
Then, BM = MD = 3
In right angled ∆ CMB,
CB² = CM² + BM²
= 4² + 3²
= 16 + 9 =25
⇒ CB = 5

∴ CA = Radius of circle = CB = 5
∴ Centre of circle (- 4, 5) and radius = 5
Hence, equation of circle :
(x + 4)² + (y – 5)² = 5²
⇒ x² + 8x + 16 + y² – 10y + 25 = 25
⇒ x² + y² + 8x – 10y + 16 = 0

Question 2.
Find the equation of circle which touches Y – axis at a distance of 4 units and makes intercept of 6 units on Y – axis?
Solution:
Given : OP = 4, AB = 6, PC = AC = radius.
CM ⊥ AB ∴ AM = BM = \(\frac { 6 }{ 2 }\) = 3
OP = CM = 4
In right angled ∆ AMC,

AC² = AM² + CM²
= (3)² + (4)² = 9 + 16 = 25
∴ AC = 5
From figure PC – OM= 5 = radius
Centre of circle is (5, 4) and radius = 5.
Hence, required equation of circle :
(x – 5)² + (y – 4)² = (5)²
x² – 10x + 25 + y² – 8y + 16 = 25
x² + y² – 10x – 8y + 16 = 0.

Question 3.
ABCD is a square. Supposing AB and AD as the coordinate axes. Find the equation of the circle circumscribing the square if each side of square is of length l.
Solution:
Taking AB and AD as X – axis and Y – axis respectively
Given : AB = BC = CD = DA = 1
M is mid point of AB.
N is mid point of AD.
AM = \(\frac { l }{ 2 }\), AN = \(\frac { l }{ 2 }\) = OM
In ∆OAM,
OA² = AM² + OM²
= \(\frac { l }{ 2 }\)² + \(\frac { l }{ 2 }\)²
= \(\frac{l^{2}}{4}+\frac{l^{2}}{4} = \frac{l^{2}}{2}\)
∴ Radius = OA = \(\frac{l}{\sqrt{2}}\)
Centre of circle (AM, OM) = ( \(\frac { l }{ 2 }\), \(\frac { l }{ 2 }\) )

Required equation of circle is :
(x – \(\frac { l }{ 2 }\) )² + (y – \(\frac { l }{ 2 }\) )² = \(\frac{l^{2}}{2}\)
Centre of circle (AM, OM) = (\(\frac { l }{ 2 }\), \(\frac { l }{ 2 }\))
Required equation of circle is :
(x – \(\frac { l }{ 2 }\))² + (y – \(\frac { l }{ 2 }\))² = \(\frac{l^{2}}{2}\)
⇒ x² – lx + \(\frac{l^{2}}{4}\) + y² – ly + \(\frac{l^{2}}{4}\) = \(\frac{l^{2}}{2}\)
⇒ x² + y² – l(x + y) = 0
⇒ x² + y² = l(x + y)

Question 4.
Find the equation of the circle passing through the points (4, 1) and (6, 5). Whose centre lies on line 4x + y = 16. (NCERT)
Solution:
Let the equation of circle be
x² + y² + 2gx + 2 fy + c = 0 …. (1)
It passes through points (4, 1) and (6, 5).
∴ 8g + 2f + c + 17 = 0 …. (2)
and 12g + 10f + c + 61 = 0 …. (3)
Centre of circle (1) is (- g, – f) which lies on line 4x + y = 16.
∴ – 4g – f – 16 = 0
⇒ 4g + f + 16 – 0 …. (4)
Subtracting equation (2) from equation (3), we get
4g + 8f + 44 = 0
⇒ g + 2f + 11 = 0 …. (5)
On solving equation (4) and (5), g = – 3, f = – 4
Put g = – 3 and f = – 4 in equation (2),
– 24 – 8 + C + 17 = 0
⇒ c = 15
Put values of g, f and c in equation (1), then required equation of circle is :
x² + y² – 6x – 8y + 15 = 0.

Question 5.
Find the equation of the circle which passes through the points (2, 3) and (- 1, 1) whose centre lies on line x – 3y – 11 = 0. (NCERT)
Solution:
Let the equation of circle is :
x² + y² + 2gx + 2fy + c = 0 …. (1)
∵Points (2, 3) and (- 1, 1) lies on equation (1),
∴ (2)² + (3)² + 2g(2) + 2f(3) + c = 0
⇒ 4 + 9 + 4g + 6f + c + 13 = 0
4g + 6f + c + 13 = 0 …. (2)
and (-1)² + (l)² – 2g + 2f + c = 0
⇒ 1 + 1 – 2g + 2f + c = 0
⇒ – 2g + 2f + c + 2 = 0 …. (3)

Putting the value of g, f and c in equation (1), then required equation of circle will be :
x² + y² + 2(\(\frac { -7 }{ 2 }\))x + 2(\(\frac { 5 }{ 2 }\))y + c = 0 …. (1)
x² + y² – 7x + 5y -14 = 0.

Question 6.
Find the equation of circle whose radius is 5, centre is on Y – axis and which passes through point (2, 3).
Solution:
Centre of circle is on X – axis, so k = 0.
Let the equation of circle be :
(x – h)² + (y – k)² = a²
Here a = 5
(x – h)² + (y – 0)² = (5)²
(x – h)² + y² = 25
Circle (1) passes through point (2, 3),
∴ (2 – h)² + (3)² = 25
⇒ (2 – h)² = 25 – 9 = 16 = (4)²
⇒ 2 – h = ± 4

Question 7.
y = mx is a chord of the circle whose radius is ‘a’ and its diameter is X – axis. Origin is one of the limiting points of the chord. Show that the equation to a circle whose diameter is the given chord is given by the equation (1 + m²) (x² + y² ) – 2a (x + my) = 0. Solution:
Equation of circle whose radius is a and centre is (a, 0) will be
(x – a)² + y² = a²
⇒ x² – 2ax + y² + a² = a²
⇒ x² – 2ax + y² = 0 …. (1)
Equation of given line is :
y = mx …. (2)
Now, equation of circle passing through the intersection of eqns. (1) and (2) will be :
x² + y² – 2ax + λ(y – mx) = 0 … (3)
Centre of co – ordinate of circle (3) are (\(\frac { λm + 2a }{ 2 }\), \(\frac { λ }{ 2 }\))
∵ Centre lies on line y = mx.
∴ – \(\frac { λ }{ 2 }\) = m\(\frac { λm + 2a }{ 2 }\)
⇒ λ = \(\frac{-2 a m}{1+m^{2}}\)

Put the value of λ in Equation (3),
x² + y² – 2ax + \(\frac{-2 a m}{1+m^{2}}\) (y – mx) = 0
⇒ (l + m²)(x² + y²) = 2ax + 2am²x + 2amy – 2am²x
⇒ (l + m²)(x² + y²) = 2a(x + my)
⇒ (l + m²)(x² + y²) – 2a(x + my) = 0
Which is required equation of circle.

Question 8.
If the straight line x cos α + y sin α = p cuts a circle x² + y² = a² in two points M and N, then show that the equation of the circle whose diameter is MN will be x² + y² – a² = 2p(x cos α + y sin α – p).
Solution:
Given : Equation of line is :
x cos α + y sin α = p …. (1)
and Equation of circle is
x² + y² = a² …. (2)
Now, equation of circle passing through the intersection of line (1) and circle (2) at points M and N is :
x² + y² – a² + λ(x cos α + y sin α – p) = 0 …. (3)
If MN is diameter of above circle then centre is :
(- \(\frac { λ }{ 2 }\)cos α, – \(\frac { λ }{ 2 }\)sin α)
Which is lies on line x cos α + y sin α = p.
– ( \(\frac { λ }{ 2 }\)cos α )cos α + (- \(\frac { λ }{ 2 }\)sin α)sin α = p
⇒ – \(\frac { λ }{ 2 }\)[cos² α + sin² α] = p
⇒ λ = – 2p
Put the value of λ in equation (3), then required equation of circle is
x² + y² – a² – 2p(x cos α + y sin α – p) = 0
⇒ x² + y² – a² = 2p(x cos α + y sin α – p)

Question 9.
Find the following equation of parabola : (i) co – ordinates of focus, (ii) axis, (iii) equation of directrix, (iv) length of Iatus rectum. (NCERT)
(A) y² = 12x
Solution:
Equation of parabola : y² = 12x
Comparing with y² = 4 ax,
4a = 12 ⇒ a = 3
∴Co – ordinates of focus (a, 0) = (3, 0).
Axis of parabola = X – axis.
Equation of directrix is x = – a ⇒ x = – 3.
Length of latus rectum = 4a = 4 x 3 = 12.

(B) x² = 6y.
Solution:
Equation of parabola: x² = 6y
Comparing with x² = 4ay
4a = 6 a ⇒ 3/2
∴ Co – ordinate of focus (0, a) = (0, 3/2).
Axis of parabola = Y – axis.
Equation of directrix is y = – a ⇒ y = – 3/2.

(C) y² = – 8x
Solution:
Equation of parabola : y² = – 8x
Comparing with y² = – 4ax
– 4a – = – 8 ⇒ a = 2
∴ Co – ordinates of focus (- a, 0) = (- 2, 0).
Axis of parabola = X – axis.
Equation of directrix is x = a ⇒ x = 2.
Length of latus rectum 4a = 4 x 2 = 8.

(D) x² = – 16y
Solution:
Equation of parabola : x² = – 16y
Comparing with x² = – 4ay
– 4a = – 16 ⇒ a = 4
∴ Co – ordinate of focus (0, – a) = (0, – 4)
Axis of parabola = Y – axis
Equation of directrix is y = a ⇒ y = 4
Length of latus rectum = 4a = 16.

Question 10.
An equilateral triangle inscribed in the parabola y² = 4ax, where one vertex is at the vertex of parabola. Find the length of the side of triangle. (NCERT)
Solution:
Let the equation of parabola is y² = 4ax.
Let APQ be the equilateral triangle whose vertex A(0, 0), P(h, k) and Q(h, – k).
AP² = (h – 0)² + (k – 0)²
= h² + k²
⇒ AP = \(\sqrt{h^{2}+k^{2}}\)
Similarly, AQ = \(\sqrt{h^{2}+k^{2}}\)

Again, PQ = \(\sqrt{(h-k)^{2}+(k+h)^{2}}\)
= \(\sqrt{(2k)^{2}}\) = 2k
∴ AP = PQ
⇒ \(\sqrt{h^{2}+k^{2}}\) = 2k
⇒ h² + k² = 4k²
⇒ h² = 3k²
⇒ h = \(\sqrt {3}\).k
∵ Point P(h, k) lies on parabola y² = 4ax.
k² = 4ah = 4a.\(\sqrt {3}\)k
⇒ k = 4a\(\sqrt {3}\), [∵ k ≠ 0]
Hence, length of side PQ = 2k = 2.(4a\(\sqrt {3}\)) = 8a\(\sqrt {3}\).

Question 11.
If a parabola reflector is 20 cm in diameter and 5 cm deep. Find the focus. (NCERT)
Solution:
Taking vertex of parabola reflector at origin and X – axis along the axis of parabola.

Equation of parabola y² = 4ax …. (1)
Given : OS = 5 cm, AB = 20 cm, AS = 10 cm
∴ Co – ordinate of A will be (5, 10).
∴ (10)² = 4a x 5
⇒ 100 = 20a
⇒ a = 5
∴ OS = 5 cm
Co – ordinates of focus S will be (5, 0).

Question 12.
An arch is in the form of a parabola with its vertical axis. The arch is 10 m high and 5 m wide at the base. How wide it is 2 m vertex of the parabola. (NCERT)
Solution:
Let the equation of parabola is :
x² = 4 ay …. (1)
Given : AB = 5 metre
AF = BF = \(\frac { 5 }{ 2 }\) metre
OE = 2 metre
OF = 10 metre
Co – ordinate of A will be (\(\frac { 5 }{ 2 }\), 10)
This point lies on parabola, hence it will be satisfy equation (1),
∴ \(\frac { 5 }{ 2 }\)² = 4a x 10
⇒ \(\frac { 25 }{ 4 }\) = 4 x a x 10
⇒ a = \(\frac { 25 }{ 4 × 4 × 10 }\)
⇒ a = \(\frac { 5 }{ 32 }\)

Put the value of a in Equation (1),
∴ x² = 4 x \(\frac { 5 }{ 32 }\)y
⇒ x² = \(\frac { 5 }{ 8 }\)y
Let EC = k
OE = 2
Co – ordinate of C will be (k, 2) and it will satisfy equation of parabola.
We get k² =\(\frac { 5 }{ 8 }\) x 2
⇒ k² = \(\frac { 5 }{ 4 }\)
⇒ k = \(\frac{\sqrt{5}}{2}\)
DE = 2EC
2 x \(\frac{\sqrt{5}}{2}\) = \(\sqrt {5}\)
= 2.23 metre (approx.)

Question 13.
In each of the following ellipse. Find the co – ordinates of the foci and vertices, the length of major axis and minor axis, the eccentricity and the length of latus rectum of the ellipse. (NCERT)
(A) = \(\frac{x^{2}}{36}+\frac{y^{2}}{16}\) = 1.
Solution:
Comparing with standard form of ellipse, \(\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}\) = 1
We get, a² = 36 ⇒ a = 6, b² = 16 ⇒ b = 4
Here a > b.
∴ b² = a²(1 – e²)
⇒ 16 = 36(1 – e²)
⇒ 1 – e² = \(\frac { 16 }{ 36 }\) = \(\frac { 4 }{ 9 }\)
⇒ e² = 1 – \(\frac { 4}{9 }\) = \(\frac { 5 }{ 9 }\)
∴ Eccentricity e = \(\frac{\sqrt{5}}{3}\)
Foci (± ae, o) = (± 6 × \(\frac{\sqrt{5}}{3}\), o)
= (± 2\(\sqrt {5}\), 0)
Vertices (± a, 0) = (± 6, 0)
Length of major axis = 2a = 2 x 6 = 12.
Length of minor axis = 2b = 2 x 4 = 8.
Length of latus rectum = \(\frac{2 b^{2}}{a}\) = \(\frac { 2 × 16 }{ 6 }\) = \(\frac { 16 }{ 3 }\).

(B) \(\frac{x^{2}}{4}+\frac{y^{2}}{25}\) = 1.
Solution:
Comparing with standard form of ellipse, \(\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}\) = 1
We get, a² = 36 ⇒ a = 6, b² = 16 ⇒ b = 4
Here a < b.
∴ a² = b²(1 – e²)
⇒ 4 = 25(1 – e²)
⇒ 1 – e² = \(\frac { 4 }{ 25 }\)
⇒ e² = 1 – \(\frac { 4}{25 }\) = \(\frac { 21 }{ 25 }\)
∴ Eccentricity e = \(\frac{\sqrt{21}}{5}\)
Foci (0, ± b) = (0, ± 5 × \(\frac{\sqrt{21}}{5}\))
= (0, ± \(\sqrt {21}\))
Vertices (0, ± b) = (0, ± 5)
Length of major axis = 2b = 2 x 5 = 12.
Length of minor axis = 2a = 2 x 2 = 8.
Length of latus rectum = \(\frac{2 a^{2}}{b}\) = \(\frac{2 \times 2^{2}}{5}\) = \(\frac { 2 × 4 }{ 5 }\) = \(\frac { 8 }{ 5 }\).

Question 14.
Find the equation of hyperbola whose foci is (± 4, 0) and length of latus rectum is 12. (NCERT)
Solution:
Foci of hyperbola (± 4, 0).
Hence equation of hyperbola will be :
\(\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}\) = 1
Foci (±ae, 0) = (± 4, 0)
∴ ae = 4
Length of latus rectum = \(\frac{2 b^{2}}{a}\) = 12
⇒ b² = 6a
We know, b² = a²(e² – 1)
⇒ 6a = a²e² – a²
⇒ 6a = 4² – a²
⇒ 6a = 16 – a²
⇒ 6a = 16 – a²
⇒ a² + 6a – 16 = 0
⇒ a² + 8a – 2a – 16 = 0
⇒ a(a – 2)(a + 8) = 0
⇒ a = 2, a = – 8, (∵ a cannot be negative)
∴ a = 2
b² = 6a = 6 x 2 = 12
⇒ b = \(\sqrt {12}\)
Putting values of a and b in equation (1), then required equation of hyperbola will be :
\(\frac{x^{2}}{2^{2}}-\frac{y^{2}}{(\sqrt{12})^{2}}\) = 1
⇒ \(\frac{x^{2}}{4}+\frac{y^{2}}{12}\) = 1
⇒ 3x² – y² = 12.

Question 15.
Find the axis, foci, directrix, eccentricity and the latus rectum of the ellipse 9x² + 4y² = 36.
Solution:
Given equation of ellipse
9x² + 4y² = 36
⇒ \(\frac{x^{2}}{4}+\frac{y^{2}}{9}\) = 1
Here, b² > a² or b > a
∴ Major axis = 2.3 = 6
Minor axis = 2.2 = 4
Now,
a² = b²(1 – e²)
(2)² = (3)²(1 – e²)
⇒ 4 = 9(1 – e²)
⇒ \(\frac { 4 }{ 9 }\) = 1 – e²
⇒ e² = 1 – \(\frac { 4 }{ 9 }\) = \(\frac { 9 – 4 }{ 9 }\) = \(\frac { 5 }{ 9 }\)
∴ e = \(\frac{\sqrt{5}}{3}\)
Co – ordinate of foci = (0, ± be )
= (0, ± 3. \(\frac{\sqrt{5}}{3}\))
= (0, ± \(\sqrt {5}\)).
Co – ordinate of vertex = (0, ± b )
= (0 ± 3 ).
Length of latus rectum = \(\frac{2 a^{2}}{b}\)
= \(\frac { 2.4 }{ 3 }\) = \(\frac { 8 }{ 3 }\).

Question 16.
(A) Find the equation of ellipse whose vertices are (± 5, 0) and foci (± 4, 0).
Solution:
Given : Vertices are (± 5, 0) and foci are (± 4, 0)
∴ a = 5
and ae = 4
⇒ 5e = 4
⇒ e = \(\frac { 4 }{ 5 }\)
Let the equation of ellipse is :
\(\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}\) = 1, where a > b …. (1)
∴ From b² = a²(1 – e²),
b² = 5²(1 – (\(\frac { 4 }{ 5 }\))²)
b² = 25(1 – \(\frac { 16 }{ 25 }\))
b² = 25 x \(\frac { 9 }{ 25 }\) = 9
Putting values of a and b in equation (1), the required equation of ellipse will be :
\(\frac{x^{2}}{25}+\frac{y^{2}}{9}\) = 1
⇒ 9x² + 25y² = 225

(B) Find the equation of ellipse whose vertices are (0, ± 13) and foci is (0, ± 5).
Solution:
Let the equation of ellipse is :
\(\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}\) = 1, where a < b …. (1)
Vertices of ellipse = (0, ± b) = (0, ± be)
∴ b = 13
Foci = (0, ± 5) = (0, ± be)
∴ be = 15
⇒ 13 x 3 = 5
⇒ e = \(\frac { 5 }{ 13 }\)
Now, a² = b²(1 – e²)
⇒ a² = 13²[1 – ( \(\frac { 5 }{ 13 }\))² ]
⇒ a² = 169[1 – \(\frac { 25 }{ 169 }\) ]
⇒ a² = 169\(\frac { 169 – 25 }{ 169 }\)
⇒ a² = 144
⇒ a = 12.
Putting values of a and b in equation (1), then required equation of ellipse will be :
\(\frac{x^{2}}{(12)^{2}}-\frac{y^{2}}{(13)^{2}}\) = 1
⇒ \(\frac{x^{2}}{144}+\frac{y^{2}}{169}\) = 1

Question 17.
Find the equation of ellipse whose centre is at (0, 0), major axis on the Y – axis passing through the points (3, 2) and (1, 6).
Solution:
Let the equation of ellipse is :
\(\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}\) = 1, where a < b …. (1)
∵ Equation (1) passes through points(3, 2) and (1, 6)
∴ \(\frac{9}{a^{2}}+\frac{4}{b^{2}}\) = 1 …. (2)
and \(\frac{1}{a^{2}}+\frac{36}{b^{2}}\) = 1 …. (3)
Multiply equation (2) by 9, we get

Putting value of a² in equation (2), we get
\(\frac { 9 }{ 10 }\) + \(\frac{4}{b^{2}}\) = 1
⇒ \(\frac{4}{b^{2}}\) 1 – \(\frac { 9 }{ 10 }\)
⇒ \(\frac{4}{b^{2}}\) = \(\frac { 1}{ 10 }\)
⇒ b² = 40
Putting values of a² and b² in equation (1), then required equation of ellipse will be :
\(\frac{x^{2}}{10}+\frac{y^{2}}{40}\) = 1

Question 18.
Find the equation of ellipse whose major axis on the X – axis which passes through the points (4, 3) and (6, 2).
Solution:
Let the equation of ellipse is :
\(\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}\) = 1 …. (1)
∵ It passes through points(4, 3) and (6, 2)
∴\(\frac{36}{a^{2}}+\frac{4}{b^{2}}\) = 1 …. (2)
and \(\frac{16}{a^{2}}+\frac{9}{b^{2}}\) = 1 …. (3)
Subtracting equation (3) from equation (2), we get
\(\frac{20}{a^{2}}-\frac{5}{b^{2}}\) = 1
⇒ \(\frac{4}{a^{2}}-\frac{1}{b^{2}}\) = 1
⇒ \(\frac{4}{a^{2}} = \frac{1}{b^{2}}\)
⇒ a² = 4b²
Putting value of a² in equation (2), we get
\(\frac{36}{4b^{2}}+\frac{4}{b^{2}}\) = 1
⇒ \(\frac{9}{b^{2}}+\frac{4}{b^{2}}\) = 1
⇒ 9 + 4 = b²
⇒ b² = 13
Putting values of a² and b² in equation (1), hence
Required equation of ellipse \(\frac{x^{2}}{52}+\frac{y^{2}}{13}\) = 1

Question 19.
An arch is the form of a semi ellipse. It is 8 m wide and 2 m high of the centre. Find the height of the arch at a point 1-5 m from one end. (NCERT)
Solution:
Let the equation of ellipse is :
\(\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}\) = 1 …. (1)
Here 2a = 8 ⇒ a = 4, b = 2
Putting the values of a and b, we get

\(\frac{x^{2}}{4^{2}}-\frac{y^{2}}{2^{2}}\) = 1 …. (1)
\(\frac{x^{2}}{16}+\frac{y^{2}}{4}\) = 1
Given :
AP = 1.5m, OA = \(\frac { 8 }{ 2 }\) = 4m,
OP = OA – AP = 4 – 1.5 = 2.5m.
Let PQ = k
∴ Co – ordinate of Q will be (2.5, k), which will satisfy ellipse’s equation.
Hence,
\(\frac{(2.5)^{2}}{16}+\frac{k^{2}}{4}\) = 1
⇒ \(\frac { 6.25}{ 16 }\) + \(\frac{k^{2}}{4}\) = 1
⇒ \(\frac{k^{2}}{4}\) = 1 – \(\frac { 6.25 }{ 16 }\)
⇒ \(\frac{k^{2}}{4}\) = \(\frac { 16 – 6.25 }{ 16 }\)
⇒ k² = \(\frac { 9.75 }{ 4 }\)
⇒ k² = 2.437
⇒ k = 1.56metre (approx).

Question 20.
A rod of length 12 cm moves with its ends always touching the co – ordinate axes. Determine the equation of the locus of a point P on the rod, which is 3 cm from the end in contact with the X – axis. (NCERT)
Solution:
Let AB be the rod of length 12 cm which make an angle θ with X – axis.
∴ ∠BAO = θ
AB = 12 cm
AP = 3 cm, then PB = 9 cm

In ∆PNA,
sin θ = \(\frac {PN }{ PA }\) = \(\frac { y }{ 3 }\)
In ∆PMB,
cos θ = \(\frac { PM }{ PB }\) = \(\frac { x }{ 9 }\)
sin²θ + cos²θ = \(\frac { y }{ 3 }\)² + \(\frac { x }{ 9 }\)²
⇒ 1 = \(\frac{y^{2}}{9}+\frac{x^{2}}{81}\)
Hence required equation is :
\(\frac{x^{2}}{81}+\frac{y^{2}}{9}\) = 1

Question 21.
Find the eccentricity, co – ordinate of foci, equation of directrix and length of Iatus rectum of ellipse 4x² + y² – 8x + 2y + 1 = 0.
Solution:
4x² + y² – 8x + 2y + 1 = 0
⇒ 4x² – 8x + y² + 2y +1 = 0
⇒ 4x² – 8x + (y + 1)² = 0
⇒ 4(x² – 2x) + (y + 1)² = 0
⇒ 4(x² – 2x + 1) + (y + 1)² = 4
⇒ 4(x² – 2x + 1) + (y + 1)² = 4
⇒ \(\frac{(x-1)^{2}}{1}+\frac{(y+1)^{2}}{4}\) or \(\frac{X^{2}}{1}+\frac{Y^{2}}{4}\) = 1
Here, b > a
a² = b²(1 – e²)
⇒ 1 = (1 – e²)
⇒ \(\frac { 1 }{ 4}\) = 1 – e²
⇒ e² = 1 – \(\frac { 1 }{ 4}\) = \(\frac { 3 }{ 4}\)
⇒ Eccentricity e = \(\frac{\sqrt{3}}{2}\)
Co – ordinate of foci (0, ± be)
= (0, ±2. \(\frac{\sqrt{3}}{2}\)
= (0, ± \(\sqrt {3}\) )
Here X = 0, Y = ± \(\sqrt {3}\)
∴ x – 1 = 0, y + 1 = ± \(\sqrt {3}\)
⇒ x = 1, y = – 1 ± \(\sqrt {3}\)
foci = (1 ± \(\sqrt {3}\) – 1)
Equation of directrix Y = ± \(\frac { b }{ e}\)
⇒ Y = ± \(\frac{2}{\sqrt{3}}\).2
⇒ Y = ± \(\frac{4}{\sqrt{3}}\)
Y + 1 = \(\frac{4}{\sqrt{3}}\), (∵ Y = y+1)
⇒ y = ± \(\frac{4}{\sqrt{3}}\) – 1
Length of latus rectum = \(\frac{2 a^{2}}{b}\)
= 2. \(\frac { 1 }{ 2 }\) = 1.

Question 22.
Find the vertices, co-ordinate of foci, eccentricity and length of latus rectum of hyperbola :
(A) 9y² – 4x² = 36.
Solution:
Given : 9y² – 4x² = 36
⇒ \(\frac{9 y^{2}}{36}-\frac{4 x^{2}}{36}\) = 1
⇒ \(\frac{y^{2}}{4}-\frac{x^{2}}{9}\) = 1
Comparing the above equation with the standard form of hyperbola
\(\frac{y^{2}}{b^{2}}-\frac{x^{2}}{a^{2}}\) = 1 …. (1)
b² = 4 ⇒ b = 2, a² = 9 ⇒ a = 3
Let e is the eccentricity of hyperbola.
Then, a² = b²(e² – 1)
⇒ 9 = (e² – 1)
⇒ \(\frac { 9 }{ 4 }\) = e² – 1
⇒ e² = \(\frac { 9 }{ 4 }\) + 1 = \(\frac { 13 }{ 4 }\)
∴ Eccentricity e = \(\frac{\sqrt{3}}{2}\)
Vertices = (0, ± b) = (0, ± 2)
Foci = (0, ± be) = (0, ± 2 x \(\frac{\sqrt{3}}{2}\)) = (0, ±\(\sqrt {3}\))
Length of latus rectum = \(\frac{2 a^{2}}{b}\) = \(\frac { 2 x 9 }{ 2 }\) = 9

(B) 16x² – 9y² = 576.
Solution:
Given : 16x² – 9y² = 576
⇒ \(\frac{16 x^{2}}{576}-\frac{9 y^{2}}{576}\) = 1
⇒ \(\frac{x^{2}}{36}-\frac{y^{2}}{64}\) = 1
Comparing the above equation with the standard form of hyperbola
\(\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}\) = 1 …. (1)
Here, a² = 36 ⇒ a = 6, b² = 64 ⇒ b = 3
We Know that, b² = a²(e² – 1)
64 = 36(e² – 1)
⇒ \(\frac { 64 }{ 36 }\) = e² – 1
⇒ \(\frac { 16 }{ 9 }\) = e² – 1
⇒ e² = \(\frac { 16 }{ 9 }\) + 1 = \(\frac { 25 }{ 9 }\)
∴ Eccentricity e = \(\frac{5}{3}\)
Vertices = (± a, 0) = (± 6, 0)
Foci = (± ae, 0) = (± 6 x \(\frac { 5 }{ 3 }\)) = (± 10, 0)
Length of latus rectum = \(\frac{2 b^{2}}{a}\) = \(\frac { 2 x 64 }{ 6 }\) = \(\frac { 64 }{ 3 }\).

(c) 5y² – 9x² = 36.
Solution:
Given : 5y² – 9x² = 36
⇒ \(\frac{5 y^{2}}{36}-\frac{9 x^{2}}{36}\) = 1
\(\frac{y^{2}}{\frac{36}{5}}-\frac{x^{2}}{4}\) = 1
Comparing the above equation with the standard form of hyperbola
\(\frac{y^{2}}{b^{2}}-\frac{x^{2}}{a^{2}}\) = 1 …. (1)
Here b² = \(\frac { 36 }{ 5 }\) ⇒ b = \(\frac{\sqrt{6}}{5}\), a² = 4 ⇒ a = 2
We know that, a² = b²(e² – 1)
⇒ 4 = \(\frac{\sqrt{36}}{5}\)(e² – 1)
⇒ e² – 1 = \(\frac { 20 }{ 36 }\) = \(\frac { 5 }{ 9 }\)
⇒ e² = 1 + \(\frac { 5 }{ 9 }\) = \(\frac { 14 }{ 9 }\)

Question 23.
Find the equation of hyperbola whose foci are (0, ± \(\sqrt {10}\)) and which passes through point (2,3).
Solution:
Foci of hyperbola are (0, ±\(\sqrt {10}\)).
∴Form of hyperbola is :
\(\frac{y^{2}}{b^{2}}-\frac{x^{2}}{a^{2}}\) = 1 …. (1)
Foci (0, ± be) = (0, ± \(\sqrt {10}\))
be = \(\sqrt {10}\)
Equation (1) passes through point (2, 3).
∴ \(\frac{9}{b^{2}}-\frac{4}{a^{2}}\)
⇒ 9a² – 4b² = a²b²
We know that, a² = b² (e² – 1)
⇒ a² = b²e² – b²
a² = ( \(\sqrt {10}\))² – b²
⇒ a² = 10 – b²
⇒ b² = 10 – a²
Putting value of b² in equation (2),
9a² – 4(10 – a²) = a² (10 – a²)
⇒ 9a² – 40 + 4a² = 10a² – a⁴
⇒ 13a² – 40 = 10a² – a⁴
⇒ a⁴ + 13a² – 10a² – 40 = 0
⇒ a⁴ + 3a² – 40 = 0
⇒ a⁴ + 8a² – 5a² – 40 = 0
⇒ a²(a² + 8) – 5(a² + 8) = 0
⇒ (a² – 5)(a² + 8) = 0
a² = 5, a² = – 8
∵ The value of a cannot be negative.
∴ a² = 5
b² = 10 – a²
⇒ b²  = 10 – 5
⇒  b² = 5
Putting values of a² and b² in equation (1), then required equation of hyperbola will be :
\(\frac{y^{2}}{5}-\frac{x^{2}}{5}\) = 1
⇒ y² – x² = 5.

Question 24.
Find the equation of hyperbola in which the distance between foci is 8 and distance between directrix is 6.
Solution:
Let the equation of hyperbola is :
\(\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}\) … (1)
and Eccentricity of hyperbola is e and foci are (ae, 0) and (- ae, 0) and latus rectum
are x = \(\frac { a }{ e }\) and x = – \(\frac { a }{ e }\)
Distance between foci = 2ae
Distance between latus rectum = \(\frac { 2a }{ e }\)
According to question, 2ae = 8
and \(\frac { 2a }{ e }\) = 6
Multiplying equation (2) and (3),
4a² = 48 ⇒ a² = 12
⇒ a = 2\(\sqrt {3}\)
Putting value of a in equation (2),
2.2\(\sqrt {3}\)e = 8 ⇒ e = \(\frac{2}{\sqrt{3}}\)
b² = a²(e² – 1)
= 12( \(\frac { 4 }{ 3 }\) – 1) = 4
Putting values of a² and b² in equation (1), the required equation of hyperbola is :
\(\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}\)
⇒ x² – 3y² = 12.

Question 25.
Find the centre, eccentricity, foci and length of latus rectum of hyperbola 9x² – 16y² + 18x + 32y – 151 = 0.
Solution:
Equation of hyperbola is :
9x² – 16y² + 18x + 32y – 151 = 0
⇒ 9x² + 18x – 16y² + 32y = 151
⇒ 9(x² + 2x) – 16(y² – 2y) = 151
⇒ 9(x + 1)² – 16(y – 1)² = 151 – 16 + 9
⇒ 9(x + 1)² – 16(y – 1)² = 144
⇒ \(\frac{9(x+1)^{2}}{144}-\frac{16(y-1)^{2}}{144}\)
⇒ \(\frac{(x+1)^{2}}{16}-\frac{(y-1)^{2}}{9}\) = 1
Let x + 1 = X and y – 1 = Y, then equation of hyperbola is
\(\frac{X^{2}}{16} – \frac{Y^{2}}{9}\) = 1
∴ a² = 16 ⇒ a = 4 and b² = 9 ⇒ b = 3.
∴ Centre is (- 1, 1).
For eccentricity = e
b² = a²(e² – 1)
⇒ 9 = 16(e² – 1)
⇒ \(\frac { 9 }{ 16 }\) = e² – 1
⇒ e² = 1 + \(\frac { 9 }{ 16 }\) = \(\frac { 25 }{ 16 }\)
⇒ e = \(\frac { 5 }{ 4 }\)
For foci, X = ± ae, Y = 0
⇒ x +1 = ± 4 x \(\frac { 5 }{ 4 }\), y – 1 = 0
⇒ x + 1 = ± 5, y = 1
⇒ x = 4, – 6, y = 1
∴ Foci are (4, 1) and (6, 1).
Equation of directrix is X = ± \(\frac { a }{ e }\)
⇒ x +1 = ± \(\frac { 4 }{ 5/4 }\)
⇒ x = ± \(\frac { 16 }{ 5 }\) – 1
⇒ x = ± \(\frac { 11 }{ 5 }\) and x = – \(\frac { 21 }{ 5 }\)
⇒ 5x = 11 and 5x + 21 = 0.

Question 26.
If e and ex are the eccentricity of hyperbola \(\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}\) and \(\frac{y^{2}}{b^{2}}-\frac{x^{2}}{a^{2}}\) = 1, then prove that: \(\frac{1}{e^{2}}+\frac{1}{e_{1}^{2}}\) = 1.
Solution:
Equation of hyperbola is
\(\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}\) = 1
and
\(\frac{y^{2}}{b^{2}}-\frac{x^{2}}{a^{2}}\) = 1
For eccentricity e of equation (1),
b² = a²(e² – 1)
⇒ \(\frac{b^{2}}{a^{2}}\) = (e² – 1)
⇒ e ² = 1 + \(\frac{b^{2}}{a^{2}}\) = \(\frac{a^{2}+b^{2}}{b^{2}}\)
⇒ \(\frac{1}{e_{1}^{2}}\) = \(\frac{a^{2}}{a^{2}+b^{2}}\)
Again for eccentricity e of equation (2),

Question 27.
On a level plain the crack of the rifle and the thud of the ball striking the target are heard at the same instant, prove that the locus of the hearer is a hyperbola.
Solution:
Let P be the situation of hearer and T be the situation of the rifle and S is target. Let the velocity of the ball be v₁ and the velocity of sound be v₂.

Then,
Time to reach the ball from T to S = \(\frac{T S}{v_{1}}\)
Time to reach the sound from S to P = \(\frac{S P}{v_{2}}\)
and Time to reach the sound from T to P = \(\frac{T P}{v_{2}}\)
∴ The crack of the rifle and the thud of the ball are heard at the same instant.
∴ \(\frac{T S}{v_{1}}\) + \(\frac{S P}{v_{2}}\) = \(\frac{T P}{v_{2}}\)
⇒ \(\frac{T P}{v_{2}}\) – \(\frac{S P}{v_{2}}\) = \(\frac{T S}{v_{1}}\)
⇒ TP – SP = \(\frac{v_{2}}{v_{1}}\)
⇒ PT – PS = A constant (∵ v₂, v₂, TS are constant)
Hence locus of point P is hyperbola whose foci is T and S.

MP Board Class 11th Maths Important Questions

MP Board Class 11th Maths Important Questions Chapter 8 Binomial Theorem

Binomial Theorem Important Questions

Binomial Theorem Objective Type Questions

(A) Choose the correct option :

Question 1.
The total number of terms in the expansion of
(a) 7
(b) 12
(c) 13
(d) 6.
Answer:
(c) 13

Question 2.
If y = 3x + 6x² + 10x³ + …………… ∞, then the correct relation will be :
(a) x = 1 – (1 + y)^{–\(\frac { 1 }{ 3 }\)}
(b) x = (1 + y)^{–\(\frac { 1 }{ 3 }\)}
(c) y = 1 – (1 – x)^-3
(d) x = 1 + (1 + y)^{–\(\frac { 1 }{ 3 }\)}
Answer:
(a) x = 1 – (1 + y)^{–\(\frac { 1 }{ 3 }\)}

Question 3.
The total number of terms in the expansion of (1+ x)^-1 will be :
(a) 0
(b) ∞
(c) 2
(d) It can not be expand
Answer:
(b) ∞

Question 4.
The mid – term in the expansion of (x – \(\frac { 1 }{ x }\))¹⁰ will be :
(a) – ¹⁰C₅
(b) ¹⁰C₅
(c) 251
(d) 252
Answer:
(a) – ¹⁰C₅

Question 5.
For all positive integer of n, n(n – 1) is :
(a) Integer
(b) Natural number
(c) Even positive integer
(d) Odd positive integer.
Answer:
(c) Even positive integer

Question 6.
Expansion of (a + x)ⁿ is :
(a) aⁿ + ⁿC₁a^n-1x + ⁿC₂a^n-2x² + ……….. + ⁿC_ra^n-rx^r + ………… + aⁿ
(b) xⁿ + ⁿC₁x^n-1a +ⁿC₂x^n-2a² + ……….. + ⁿC_rx^n-ra^r + ………… + aⁿ
(c) aⁿ – ⁿC₁a^n-1x + ⁿC₂a^n-2x² + ……….. + (-1)^rnC_ra^n-rx^r + ………… + (-1)ⁿaⁿ
(d) xⁿ – ⁿC₁a^n-1a + ⁿC₂a^n-2a² + ……….. + (-1)^rnC_ra^n-rx^r + ………… + (-1)ⁿxⁿ
Answer:
(a) aⁿ + ⁿC₁a^n-1x +ⁿC₂a^n-2x² + ……….. + ⁿC_ra^n-rx^r + ………… + aⁿ

Question 7.
The fifth term in the expansion of ( x – \(\frac { 1 }{ x }\) )¹⁰ from the end, will be :
(a) \(\frac { ^{ 10 }{ C }_{ 6 } }{ x }\)
(b) \(\frac { 105 }{ 32{ x }^{ 2 } }\)
(c) \(\frac { ^{ 10 }{ C }_{ 6 } }{ { x }^{ 2 } }\)
(d) \(\frac { ^{ 10 }{ C }_{ 6 } }{ { x }^{ 10 } }\)
Answer:
(a) \(\frac { ^{ 10 }{ C }_{ 6 } }{ x }\)
[Hint: The total number of terms be 11 in the expansion of it.
∵ The 5^th term from end = (11 – 5)^th = 7^th term from the beginning.]

Question 8.
The number of mid – terms in the expansion of ( x – \(\frac { 1 }{ x }\) )¹⁰
(a) 1
(b) 2
(c) – \(\frac { ^{ 13 }{ C }_{ 7 } }{ x }\)
(d) 1716x
Answer:
(b) 2

Question 9.
The value of ⁿC₀ + ⁿC₁ + ⁿC₂ + …………….. + ⁿC_n :
(a) 2ⁿ + 1
(b) 2^{n – 1}
(c) 2ⁿ – 1
(d) 2ⁿ
Answer:
(d) 2ⁿ

Question 10.
The value of ⁿC₀ + ⁿC₂ + ⁿC₄ + …………….. = ⁿC₁ + ⁿC₃ + ……………. will be :
(a) 2ⁿ + 1
(b) 2^{n – 1}
(c) 2ⁿ – 1
(d) 2ⁿ
Answer:
(b) 2^{n – 1}

Question 11.
The total number of terms in the expansion of (a + b + c + d)ⁿ will be :
(a) \(\frac { (n+1)(n+2) }{ 2 }\)
(b) \(\frac { n(n+1) }{ 2 }\)
(c) \(\frac { (n+1)(n+2)(n+3) }{ 6 }\)
(d) \(\frac { (n+1)(n+2) }{ 6 }\)
Answer:
(c) \(\frac { (n+1)(n+2)(n+3) }{ 6 }\)

Question 12.
The necessary condition for expansion of (1 + x)^-1 is :
(a) | x | < 1
(b) | x | > 1
(c) | x | = 1
(d) | x | = – 1.
Answer:
(a) | x | < 1

Question 13.
The general term in the expansion of (x + a)ⁿ will be :
(a) r^th
(b) (r+1)^thterm
(c) (r-1)^th
(d) (r+2)^thterm
Answer:
(b) (r+1)^thterm

Question 14.
In the expansion of ( 2x + \(\frac { 1 }{ { 3x }^{ 2 } }\) )⁹, then term independent of x will be :
(a) \(\frac { 8 }{ 127 }\)
(b) \(\frac { 124 }{ 81 }\)
(c) \(\frac { 1792 }{ 9 }\)
(d) \(\frac { 256 }{ 243 }\)
Answer:
(c) \(\frac { 1792 }{ 9 }\)

Question 15.
The coefficient of x3 in the expansion of ( x – \(\frac { 1 }{ x }\) )¹⁵ is :
(a) 14
(b) 21
(c) 28
(d) 35
Answer:
(b) 21

Question 16.
The independent term in the expansion of (x² – \(\frac { 2 }{ { x }^{ 3 } }\))¹⁵ is :
(a) 5^th
(b) 6^th
(c) 7^th
(d) 8^th
Answer:
(c) 7^th

Question 17.
The value of ⁿC₀ + ⁿC₁ + ⁿC₂ + …………….. = ⁿC_n the expansion of (l + x)ⁿ is :
(a) 2ⁿ – 1
(b) 2ⁿ – 2
(c) 2ⁿ
(d) 2^n-1
Answer:
(c) 2ⁿ

Question 18.
The value of ¹⁵C₀ + ¹⁵C₂ + ¹⁵C₄ + ¹⁵C₆ + …………….. = ¹⁵C₁₄ is :
(a) 2¹⁴
(b) 2¹⁵
(c) 2¹⁵ – 1
(d) None of these
Answer:
(a) 2¹⁴

(B) Match the following :

Answer:

1. (d)
2. (a)
3. (e)
4. (c)
5. (b)
6. (g)
7. (f)
8. (i)
9. (b)

(C) Fill in the blanks :

1. By binomial theorem the value of (102)⁴ is ……………..
2. The value of second term in the expansion of (1 – x)^-3/2 is ……………..
3. The 5^th term from the end in the expansion of (x – \(\frac { 1 }{ 2x }\) )¹⁰ is ……………..
4. The constant term will be …………….. in the expansion of ( x² – 2 + \(\frac { 1 }{ { x }^{ 2 } }\) )⁶
5. The value of C₁ + 2C₂ + 3C₃ + ………….. + nC_n will be ……………..
6. The value of ⁿC₀ – ⁿC₁ + ⁿC₂ – ⁿC₃ + ………….. will be ……………..
7. The value of is ……………..
8. The value of is ……………..
9. The value of is ……………..
10. (2x + 3y)⁵ = …………….. up to three terms.
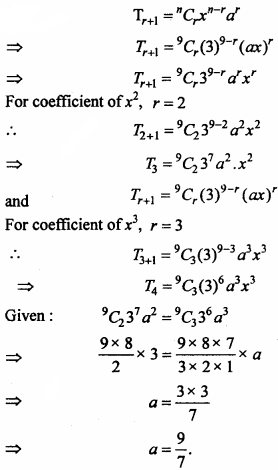
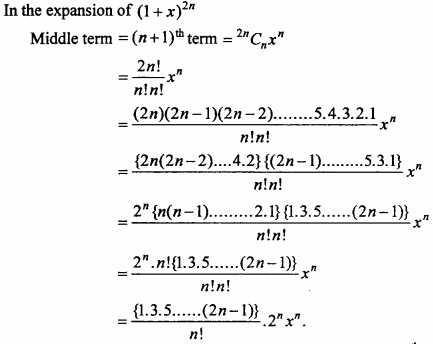
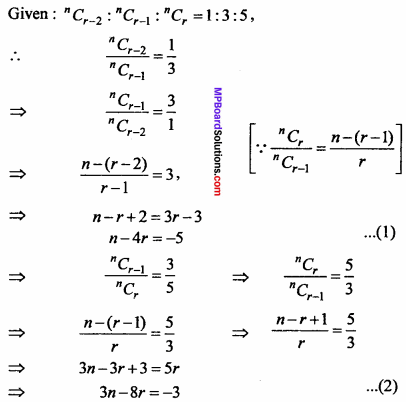
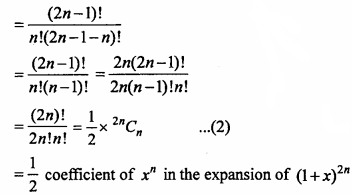
11. The coefficient of x⁷ in the expansion of (x² + \(\frac { 1 }{ x }\) )¹¹ will be …………….
12. In the expansion of (1 – x)¹⁰ the value of middle term is ……………..
13. Third (3^rd) term in the expansion of e^-3x will be ……………..
14. If n is odd, in the expansion of (x + a)ⁿ, then number of middle terms are ……………..
15. The middle term in the expansion of (\(\frac { x }{ a }\) + \(\frac { a }{ x }\) )¹⁰
16. The coefficient of xⁿ in the expansion of (1 + x) (1 – x)ⁿ will be ……………..

Answer:

1. 08243216
2. \(\frac { { x }^{ 3 } }{ 16 }\)
3. \(\frac { 105 }{ 32{ x }^{ 2 } }\)
4. 924
5. n.2^n-1
6. 0
7. \(\frac { n(n+1) }{ 2 }\)
8. \(\frac { n(n+1)(2n+1) }{ 6 }\)
9. [ \(\frac { n(n+1) }{ 2 }\) ]²
10. 32x⁵ + 240x⁴y + 720x³y²
11. 462
12. – 252 x^-5
13. \(\frac { 1 }{ 2 }\)
14. Two
15. 252
16. (- 1)ⁿ(1 – n)

(D) Write true / false :

1. The expansion of (1 + x)^-3 is 1 – 3x + 6x² – 10x³ + ………….. + \(\frac { (- 1)(r + 1)(r +2) }{ 2! }\)x^r + ……………..
2. The expansion of (1 – x)^-3 is 1 + 3x + 6x² + 10x³ + ………….. + \(\frac { (- 1)^r(r + 1)(r +2) }{ 2! }\)x^r + ……………..
3. The expansion of (1 – x)^-2 is 1 + 2x + 3x² + (r + 1) x^r+ ………….. +
4. The (r + 1 )^th term in the expansion of (1 – x)^-2 is (- 1)^r(r + 1) x^r+ ………….. +
5. The (r + 1 )^th term in the expansion of (1 – x)ⁿ will be x^r
6. The total number of terms in the expansion of (a + b + c)ⁿ is \(\frac { (n + 1)(n + 1) }{ 2 }\)
7. In the expansion of ( 3x – \(\frac { { x }^{ 3 } }{ 9 } \) )⁹, No . of terms is 9.
8. The number of term in the expansion of ( 3x – \(\frac { { x }^{ 3 } }{ 9 } \) )⁹ is 8.
9. In the expansion of (x + a)ⁿ then sum of powers of x and α in any term is n.
10. The coefficient of x in the expansion of (1 – 2x)^-3 is 6.
11. The second term in the expansion of (2x + 3y)⁵ is 240x⁴y.
12. The value of second term in the expansion of (1 – x)^-3/2 is \(\frac { 3 }{ 2 }\)x.

Answer:

1. True
2. True
3. True
4. True
5. False
6. True
7. False
8. False
9. True
10. False
11. True
12. True.

(E) Write answer in one word / sentence :

1. Find the value of 999³ by the binomial theorem
2. Find the middle term in expansion of (x² – \(\frac { 1 }{ x }\))⁶
3. General term in the expansion of (x + a)ⁿ will be.
4. If in the expansion of (1+x)⁵¹ the coefficient of x^r and x^{r – 5} are equal, then the value of r will be.
5. Find the coefficient of xⁿ in the expansion of (1 + x + x² + …………… ∞)², if | x | < 1.
6. In the expansion of (\(\frac { x }{ 3 }\) – \(\frac { 2 }{ { x }^{ 2 } }\))¹⁰, x⁴ comes in r^th term, then the value of r will be.
7. The 5^th term in the expansion of (1 – 2x)^{– 1} will be.

Answer:

1. 997002999
2. – 20 x⁵
3. ⁿC_r x^{n – r} a^r
4. 28
5. (n + 1)
6. 3
7. 16x²

Binomial Theorem Long Answer Type Questions

Question 1.
Expand : (\(\frac { 2 }{ x }\) – \(\frac { x }{ 2 }\))⁵ (NCERT)
Solution:

Question 2.
Expand : (2x – 3)⁶ (NCERT)
Solution:

Question 3.
Expand : (\(\frac { x }{ 3 }\) + \(\frac { 1 }{ x }\))⁵ (NCERT)
Solution:

Question 4.
Expand : (x + \(\frac { 1 }{ x }\))⁶. (NCERT)
Solution:

Question 5.
find 13^th term in the expansion of ( 9x – \(\frac { 1 }{ 3\sqrt { x } }\) )¹⁸. (NCERT)
Solution:

Question 6.
Find the middle term of (3 – \(\frac { { x }^{ 3 } }{ 6 }\))⁷
Solution:

Question 7.
Find the middle term in the expansion of (\(\frac { x }{ 3 }\) + 9y)¹⁰
Solution:
Here n =10
Total number of terms = n + 1 = 10 + 1 = 11 (odd)
Here, the term will be middle term.

Question 8.
If coefficient of x² and x³ in the expansion of (3 + ax)⁹ are equal, the value of a.
Solution:

Question 9.
Find the coefficient of x⁵ in the expansion of (x + 3)⁸
Solution:
Suppose x⁵ appears in (r + 1)^th term T_r+1 = nC₁x^n-ra^r
Here n = 8, x = x, a = 3
T_r+1 = ⁸C_r(x)^{8 – r}(3)^r
For the coefficient of x⁵,
8 – r = 5
=> r = 3
T₃₊₁ = ⁸C₃(3)³
= \(\frac { 8 × 7 × 6 }{ 3 × 2 × 1}\) × 3 × 3 × 3 × x⁵
= 1512 × x⁵
Hence coefficient of x⁵ is 1512.

Question 10.
Find the coefficient of a⁵b⁷ in the expansion of (a – 2b)¹².
Solution:

Question 11.
If the 17^th and 18^th terms in the expansion of (2 + a)⁵⁰ are equal, then find the value of a. (NCERT)
Solution:
In the expansion of (x + a)ⁿ
T_r+1 = ⁿC_r x^{n – r} a^r
Here n = 50, x = 2, a = a
T₁₇ = T_{16 + 1} = ⁵⁰C₁₆ (2)^{50 – 16} (a)¹⁶
⇒ T₁₇ = ⁵⁰C₁₆ (2)³⁴ (a)¹⁶
and T₁₈ = T_{17 + 1} = ⁵⁰C₁₇ (2)^{50 – 17} (a)¹⁷
= ⁵⁰C₁₇ (2)³³ (a)¹⁷

Question 12.
Prove that the value of the middle term in the expansion of (1+x)²ⁿ is \(\frac { { 1.3.5 …….. (2n – 1)} }{ n! }\).2ⁿ xⁿ
Solution:

Question 13.
In the expansion of (x + 1)ⁿ, the coefficient of the (r – 1)^th, r^th and (r + 1)^th terms are in the ratio 1 : 3 : 5, then find the value of n and r.
Solution:
In the expansion of (x + 1)ⁿ,
T_{r + 1} = ⁿC_rx^{n – r}(1)^r
T_{r – 1} = T_{r – 2 + 1} = ⁿC_{r – 2}(x)^{n – (r – 2)}(1)^{r – 2}
Coefficient of T_{r – 1}^th term = ⁿC_{r – 2}
T_r = T_{r – 1 + 1} = ⁿC_{r – 1}(x)^{n – (r – 1)}(1)^{r – 1}
Coefficient of T_r^thterm = ⁿC_{r – 1}
T_{r + 1} = ⁿC_r x^{n – r} (1)^r
Coefficient of T_r+1^th term = ⁿC_r

Put n = 4r – 5 from equation (1) in equation (2),
3(4r – 5) – 8r = – 3
⇒ 12r – 15 – 8r = – 3
⇒ 4r = 12
∴ r = 3
Put r = 3 in equation (2),
n – 4 x 3 = – 5
⇒ n = 12 – 5
⇒ n = l
n = 7, r = 3

Question 14.
Prove that the coefficient of xⁿ in the expansion of (1 + x)²ⁿ of in the expansion of (1 + x)^{2n – 1}.
Solution:
In the expansion of (x + a)ⁿ
T_r+1 = ⁿC_r x^{n – r} a^r
Here x = 1, a = x, n = 2n
T_r+1 = ²ⁿC_r(1)^{2n – r}(x)^r
For the coefficient of xⁿ, put r = n,
T_n+1 = ²ⁿC_n(a)^{2n – n}(x)ⁿ
and T₁₈ = T_{17 + 1} = ⁵⁰C₁₇ (2)^{50 – 17} (a)¹⁷
= (²ⁿC_n) xⁿ
∴ In the expansion of (1 + x)²ⁿ, the coefficient of xⁿ = ²ⁿC_n …. (1)
and in the expansion of (1 + x)^{2n – 1}, x = 1, a = x, n = 2n – 1
∴ T_r+1 = ²ⁿC_r (1)^{2n – 1  -r} (x)ⁿ
For the coefficient of xⁿ, put r = n, ‘
We get T_n+1 = ^{2n – 1}C_n xⁿ
The coefficient of xⁿ in the expansion of (1 + x)^{2n – 1} = ^{n – 1}C_n

∴ The coefficient of xⁿ in the expansion of (1 + x)²ⁿ
= 2 x The coefficient of xⁿ in the expansion of (1 + x)²ⁿ, [from equation (1) and (2)]

Question 15.
Find the constant term in the expansion of (\(\frac { 3 }{ 2 }\)x² – \(\frac { 1 }{ 3x }\))⁶
Solution:

MP Board Class 11th Maths Important Questions

MP Board Class 11th Maths Important Questions Chapter 7 Permutations and Combinations

Permutations and Combinations Important Questions

Permutations and Combinations Objective Type Questions

(A) Choose the correct option :

Question 1.
The correct relation between ⁿP_r and ⁿC_r is :
(a) ⁿC_r = \(\frac{[r}{^{n} P_{r}}\)
(b) ⁿC_r.ⁿP_r= 1
(c) ⁿC_r = \(^{n} P_{r} \times\lfloor r\)
(d) \(^{n} C_{r} \times\left\lfloor r=^{n} P_{r}\right.\)
Answer:
(d) \(^{n} C_{r} \times\left\lfloor r=^{n} P_{r}\right.\)

Question 2.
If ⁿC₂:ⁿC₄ = 2 : 1, then n = …………..
(a) 3
(b) 4
(c) 5
(d) 6
Answer:
(c) 5

Question 3.
How many words can be made by the letter of the word ‘COMMITEE’:

Answer:

Question 4.
If ⁿP₄ = 20 x ⁿP₃, then n =
(a) 20
(b) 21
(c) 18
(d) 23
Answer:
(d) 23

Question 5.
The number of different words that can be formed from the letter of the word ‘TRIANGLE’:
(a) 7200
(b) 36000
(c) 144000
(d) 1240.
Answer:
(b) 36000

Question 6.
In how many ways three person can be seated in 4 chairs :
(a) 42
(b) 20
(c) 24
(d) 12.
Answer:
(c) 24

Question 7.
If ¹⁵C_r = ¹⁵C_{r – 3} , then the value of ^rC₆ will be :
(a) 84
(b) 83
(c) 82
(d) 80.
Answer:
(a) 84

Question 8.
⁵C₀ + ⁵C₁ + ⁵C₂ + ⁵C₃ + ⁵C₄ + ⁵C₅ = ……………..
(a) 30
(b) 32
(c) 23
(d) 42
Answer:
(b) 32

Question 9.
The value of : \(\frac{1}{\lfloor- 4}\) will be :
(a) 0
(b) ∞
(c) 4
(d) 1.
Answer:
(a) 0

Question 10.
If ¹⁰P_r = 720, then the value of r will be :
(a) 4
(b) 5
(c) 6
(d) 3
Answer:
(d) 3

(B) Match the following :

Answer:

1. (d)
2. (a)
3. (f)
4. (b)
5. (c)
6. (e)

(C) Fill in the blanks :

1. The number of words can be made by the letters of the word ‘INDIA’ ……………
2. In order to invite 6 friends, the number of ways to send 3 servant is ……………
3. If ²⁰C_r = ²⁰C_y; x ≠ y, then the value of x + y will be ……………
4. The numbers of ways greater than 4000 can be made by the digits 2, 4, 5, 7 is ……………
5. If ¹²P_r = 1320, then r will be ……………
6. The number of ways can 8 friends be seated in a circular table is ……………
7. If ⁿC₈ = ⁿC₁₂, then n will be ……………

Answer:

1. 60
2. 4⁶
3. 20
4. 48
5. 3
6. 5040
7. 20

(D) Write true / false :

1. If ⁿC_r + ⁿC_{r + 1} = ^{n + 1}C_x, then x will be 6.
2. 5 letters be posted in 4 letter boxes in 5⁴ ways.
3. Fruit can be chosen from 5 guavas, 3 apples and 4 mangoes in 60 ways.
4. The number of ways can 8 friends stands in a row is 8.
5. The value of ⁿC_r ÷ ^{n – 1}C_ris \(\frac { n }{ r – 1 }\)

Answer:

1. True
2. False
3. False
4. True
5. False.

(E) Write answer in one word / sentence :

1. How many four digit numbers can be formed with the digits 2, 3, 4, 5 in these number divisible by 2?
2. How many ways can a garland be prepared with 6 flowers?
3. If 2.ⁿC₅ = 9.^{n – 2}C₅, then the value of n will be
4. Five points out of 15 points are collinear. If these points be joined, then how many triangles can be formed?
5. The value of will be?

Answer:

1. 12
2. 60
3. 10
4. 30
5. ⁵⁶C₄

Permutations and Combinations Short Answer Type Questions

Question 1.
If \(\frac{1}{\lfloor6}\) + \(\frac{1}{\lfloor7}\) = \(\frac{x}{\lfloor8}\), then find the value of x.
Solution:

Question 2.
Find the value of

(i) n = 6, r = 2 (ii) n = 9, r = 5
Solution:

Question 3.
If ^n-1P₃ : ⁿP₄ = 1 : 9, then find the value of n.
Solution:

Question 4.
IF ⁿP₅ : 42.ⁿP₃, then find the value of n.
Solution:
IF ⁿP₅ = 42.ⁿP₃, then find the value of n.
Solution:
Given:  ⁿP₅ = 42.ⁿP₃
⇒ n(n – 1)(n – 2)(n – 3)(n – 4) = 42n(n – 1)(n – 2)
⇒ (n – 3)(n – 4) = 42
⇒ n² – 7n – 30 = 0
⇒ n² – 10n + 3n – 30 = 00
⇒ (n – 10) (n + 3) = 0
n = 10, n ≠ – 3.

Question 5.
IF \(\frac{^{n} P_{4}}{^{n-1} P_{4}}\) = \(\frac { 5 }{ 3 }\), then find the value of n.
Solution:
Given : \(\frac{^{n} P_{4}}{^{n-1} P_{4}}\) = \(\frac { 5 }{ 3 }\)
⇒ 3.ⁿP₃ = 5.^n-1P₄
⇒ 3n(n – 1)(n – 2)(n – 3) = 5 (n – 1)(n – 2)(n – 3)(n – 4)
⇒ 3n = 5 (n – 4)
⇒ n = 10.

Question 6.
If ⁿC₉ = ⁿC₈, then find the value of ⁿC₁₇.
Solution:

Question 7.
If ⁿP_n-2 = 60, then find the value of n.
Solution:

Question 8.
If ¹²P_r = 1320, then find the value of r.
Solution:

Question 9.
If ⁿC₁₄ = ⁿC₁₆, then find the value of ³²C_n.
Solution:
Given : ⁿC₁₄ = ⁿC₁₆
⇒ ⁿC₁₄ = ⁿC_16-1
⇒ 14 = n – 16
⇒ n = 30
∴ ³²C_n = ³²C₃₀ = ³²C₂
= \(\frac { 32.31 }{ 2 }\) = 496.

Question 10.
If ²⁰C_x = ²⁰C_y, then find the value of x + y.
Solution:
Given :
⇒ ²⁰C_x = ²⁰C_y
⇒ ²⁰C_x = ²⁰C_20-y
⇒ x = 20 – y
⇒ x + y = 20

Question 11.
In how many ways can 8 friends sit around a round table?
Solution:
Total number of ways of sitting 8 friends around table = \(\lfloor 8 – 1\) = \(\lfloor 7\)
= 7 x 6 x 5 x 4 x 3 x 2 x 1
= 5040.

Question 12.
In how many ways can a garland be prepared with 6 flowers?
Solution:
Ways of preparing the garlands with 6 flowers = \(\frac { 1 }{ 2 }\) \(\lfloor 6 – 1\)
= \(\frac { 1 }{ 2 }\) \(\lfloor 5\)
= \(\frac { 1 }{ 2 }\).5.4.3.2.1 = 60.

Question 13.
How many numbers between 100 and 1000 can be formed with the digits 2, 3, 0, 4, 8, 9 if repetition of digits is not allowed in the same number?
Solution:
The numbers between 100 and 1000 are of three digits.
∴Number of three digits made from 6 digits will be ⁶P₃.
In this number which begins with 0 will be ⁵P₂.
∴Required number = ²⁰C_y – ⁵P₂ = 120 – 20 = 100.

Question 14.
How many words, with or without meaning can be formed using all the letters of the word EQUATION? (NCERT)
Solution:

Question 15.
How many chords can be drawn through 21 points on a circle? (NCERT)
Solution:
By joining two points we get one chord.
∴ No. of chords = ²¹C₂
= \(\frac { 21 x 20 }{ 2 x 1 }\)
= 210.

Question 16.
In how many ways can a team of 3 boys and 3 girls can be selected from 5 boys and 4 girls? (NCERT)
Solution:
Number of ways of selecting 3 boys from 5 boys and 3 girls from 4 girls will be
= ⁵C₃ × ⁴C₃
= \(\frac { 5 × 4 × 3 }{ 3 × 2 × 1}\) × \(\frac { 4 × 3 × 2 }{ 3 × 2 × 1 }\)
= 10 x 4 = 40.

Permutations and Combinations Long Answers Type Questions

Question 1.
Find the number of ways of selecting 9 balls from 6 red balls, 5 white balls and 5 blue balls if each selection consists of 3 balls of each colour. (NCERT)
Solution:
Since, 3 red balls out of 6 red balls can be selected
= ⁶C₃ = \(\frac { 6 × 5 × 4 }{ 3 × 2 × 1}\) = 20
3 white balls out of 5 white balls = ⁵C₃ = \(\frac { 5 × 4 × 3 }{ 3 × 2 × 1}\) = 10
and 3 blue balls out of 5 blue balls = ⁵C₃ = \(\frac { 5 × 4 × 3 }{ 3 × 2 × 1}\) = 10
Total number of ways of selecting 9 balls = 20 x 10 x 10

Question 2.
Determine the number of 5 cards combinations out of a deck of 52 cards, if there is exactly one ace in each combination (NCERT)
Solution:
Number of ways of selecting one ace from 4 ace = ⁴C₁
Number of selecting 4 cards from 48 cards = ⁴⁸C₄
= \(\frac { 48 × 47 × 46 × 45 }{ 4 × 3 × 2 × 1}\)
Total number of ways = ⁴C₁ x ⁴⁸C₄
= 4 × = \(\frac { 48 × 47 × 46 × 45 }{ 4 × 3 × 2 × 1}\)
= 7, 78, 320.

Question 3.
In how many ways can one select a cricket team of eleven players from 17 players. In which only 5 players can bowl, if each cricket team of 11 must include exactly 4 bowlers? (NCERT)
Solution:
Out of 17 players, to select 11 players in which 5 bowlers and 12 batsman.
Out of 5 bowlers to select 4 bowlers = ⁵C₄ = 5
Out of 12 batsman to select 7 batsman = ¹²C₇
= \(\frac { 12 × 11 × 10 × 9 × 8 × 7 × 6 }{ 7 × 6 × 5 × 4 × 3 × 2 × 1 }\)
= 11 × 9 × 8 = 792
∴ Number of ways selecting 11 players = 5 x 792 = 3960.

Question 4.
A bag contains 5 black and 6 red balls, determine the number of ways in which 2 black and 3 red balls can be selected. (NCERT)
Solution:
There are 5 black and 6 red balls.
Out of 5 black balls, 2 black balls can be =⁵C₂ = \(\frac { 5 × 4 }{ 2 × 1 }\) = 10
Out of 6 red balls, 3 red balls can be = ⁶C₃ = \(\frac { 6 × 5 × 4 }{ 3 × 2 × 1 }\) = 20
∴ Total No. of ways = 10 x 20 = 200.

Question 5.
In how many ways can a student choose a program of 5 courses, if 9 courses are available and 2 specific courses are compulsory for each students? (NCERT)
Solution:
Number of available courses = 9.
Number of courses to choose = 5.
Compulsory courses = 2.
∴ Required number of ways = ^9-2C_5-2 = ⁷C₃
= \(\frac { 7 × 6 × 5 }{ 3 × 2 × 1 }\) = 35.

Question 6.
How many words, with or without meaning each of 2 vowels and 3 consonants can be formed from the letters of the word DAUGHTER? (NCERT)
Solution:
There are 3 vowels and 5 consonants in DAUGHTER.
2 vowels out of 3 vowels = ³C₂ = \(\frac { 3! }{ 1!2! }\) = \(\frac { 3 × 2 }{ 2 × 1 }\)
3 consonants out of 5 consonats = ⁵C₃ = \(\frac { 5! }{ 2!3! }\) = \(\frac { 5 × 4 × 3 }{ 3 × 2 × 1 }\) = 10
Arrangement of 2 vowels and 3 consonants = 5!
= 5 × 4 × 3 × 2 × 1 = 120

Question 7.
How many words, with or without menning can be formed using all the letters of the word EQUATION at a time so that the vowels and consonants occur together?
Solution:
Given word is EQUATION.
Vowels – E, U, A, I, O
Consonants – T, Q, N.
Arrangement of 5 vowels = 5! = 5 x 4 x 3 x 2 x 1 = 120
Arrangement of 3 consonants = 3! = 3 x 2 x 1 = 6
Arrangements of vowels and consonants = 2!
∴ Total No. of ways = 120 x 6 x 2! = 720 x 2 = 1440.

Question 8.
A committee of 7 members has to be formed from 9 boys and 4 girls. In how many ways can this be done when the committee consists of: (NCERT)

1. Exactly 3 girls
2. At least 3 girls
3. At most 3 girls.

Solution:
Total members in committee = 7
1. Selection of 3 girls and 4 boys in committee
= ⁴C₃ x ⁹C₄
= \(\frac { 4 × 3 × 2 × 1 }{ 3 × 2 × 1 }\) x \(\frac { 9 × 8 × 7 × 6 }{ 4 × 3 × 2 × 1 }\)
= 9 x 8 x 7 = 504.

2. Selection of minimum 3 girls in committee
= ⁴C₃ x ⁹C₄ + ⁴C₄ x ⁹C₃
= 504 + 1 x \(\frac { 9 × 8 × 7 }{ 3 × 2 × 1 }\) = 504 + 84 = 588.

3. Selection of maximum 3 girls in a committee

Question 9.
How many different words can be formed by using the letters of the word ALLAHABAD, out of which in how many words vowels will come in even places? (NCERT)
Solution:
Total number of letters in ALLAHABAD = 9.
In which A = 4 times, L = 2 times.

= 9.8.7.3.5 = 7560.
Number of even places are = 4 and odd places = 5. Hence we can put A only in 4 places and rest 5 letters L, L, H, B, D in 5 odd places inways.

Question 10.
In how many ways can a cricket team of eleven can be formed from 14 players? Which win always have :

1. Captain is always taken.
2. When two fast bowlers are always taken?

Solution:
1. When captain is always taken (11 – 1) from (14 – 1) players.
= ¹³C₁₀ = ¹³C₃
= \(\frac { 13.12.11 }{ 3.2.1 }\) = 286.

2. When two fast bowlers are always taken = ¹²C₉ = ¹²C₃
= \(\frac { 12.11.10 }{ 3.2.1}\)

Question 11.
In how many ways committee of 5 members can be formed out of 6 men and 4 women ? If the committee has : (i) Only one woman, (ii) At least one woman.
Solution:
(i) Only one woman out of 4 women and 4 men out of 6 men.
No. of ways = ⁶C₄ x ⁴C₁
= ⁶C₂ x 4
= \(\frac { 6 × 5 × 4 }{ 2.1 }\) = 60

(ii) Atleast one woman :

Hence, total No. of ways = 60 + 120 + 60 + 6 = 246.

Question 12.
If ²ⁿC₃ : ⁿC₂ = 12 : 1,then find the value of it. (NCERT)
Solution:

Question 13.
If ²ⁿC₃ : ⁿC₃ = 11 : 1, then find the value of it. (NCERT)
Solution:

Question 14.
Prove that:

Solution:

Question 15.
Prove that:
²ⁿP_n = 2ⁿ{1.3.5 …………. (2n – 1)}.
Solution:

MP Board Class 11th Maths Important Questions

MP Board Class 11th Maths Important Questions Chapter 6 Linear Inequalities

Linear Inequalities Important Questions

Linear Inequalities Objective Type Questions

(A) Choose the correct option :

Question 1.
If x is a real number, then the solution of inequality 3x + 1 < 5x + 7 is :
(a) (- ∞, 3)
(b) (- 3,∞)
(c) (3, ∞)
(d) None of these.
Answer:
(b) (- 3,∞)

Question 2.
If x is a real number, then the solution of inequality \(\frac { 1 }{ 2 }\) (3x – 1) ≥ \(\frac { 1 }{ 3 }\)(4x + 3) – 1 is :
(a) (- ∞, 3)
(b) (3, ∞)
(c) (3, ∞)
(d) None of these.
Answer:
(c) (3, ∞)

Question 3.
The graph of x ≤ 2 and y ≥ 2 is situated in the :
(a) First and second quadrant
(b) Second and Third quadrant
(c) First and third quadrant
(d) None of these.
Answer:
(a) First and second quadrant

Question 4.
In linear programming problems, the objective function will be :
(a) One of the constraints
(b) A linear function which gives optimum solution
(c) Relation between varivable
(d) None of these.
Answer:
(b) A linear function which gives optimum solution

Question 5.
In linear constraints the maximum value of objective function will be :
(a) At the centre of feasible region
(b) At (0, 0)
(c) At one of the vertices of the feasible region
(d) At the vertex which is situated at maximum distance from (0, 0)
Answer:
(c) At one of the vertices of the feasible region

Question 6.
Which word is not used in linear programming problems :
(a) Slack variable
(b) Objective function
(c) Concave region
(d) Feasible solution.
Answer:
(a) Slack variable

Question 7.
The minimum value of p = 6x + 16y when constraints are x ≤ 40 and y ≥ 20 and x, y ≥ 0 is :
(a) 240
(b) 320
(c) 0
(d) None of these.
Answer:
(b) 320

Question 8.
At which point the value of 3x + 2y is maximum under the constraints x + y ≤ 2, x ≥ 0 y ≥ 0 :
(a) (0, 0)
(b) (1.5, 1.5)
(c) (2, 0)
(d) (0, 2).
Answer:
(c) (2, 0)

Question 9.
Under constraints x ≥ 0, y ≥ 0, x + y ≤ 4, maximum value of P = 3x + y is :
(a) 8
(b) 12
(c) 6
(d) 10.
Answer:
(b) 12

Question 10.
Under constraints x – 2y ≥ 6, x + 2y ≥ 0, x ≤ 6 , maximum value of P = x + 3y is :
(a) 16
(b) 17
(c) 18
(d) 19.
Answer:
(c) 18

Question 11.
Feasible solution of linear programming is in :
(a) Second quadrant only
(b) First and third quadrant
(c) First and second quadrant
(d) First quadrant only.
Answer:
(d) First quadrant only.

Question 12.
If x is a real number and |x| < 4, then :
(a) x ≥ 4
(b) – 4 < x < 4
(c) x ≤ – 4
(d) – 4 ≤ x ≤ 4
Answer:
(b) – 4 < x < 4

Question 13.
Solution of inequality 3x – 2 < 0 will be :
(a) [3, ∞]
(b) [- ∞, \(\frac { 2 }{ 3 }\)]
(c) [3, 2]
(d) [2, 3]
Answer:
(b) [- ∞, \(\frac { 2 }{ 3 }\)]

Question 14.
The set of solutions of inequality 4x – 12 ≥ 0 is :
(a) (4, 2)
(b) [4, 12]
(c) [3, ∞]
(d) [3, ∞]
Answer:
(c) [3, ∞]

Question 15.
The solution of inequality |4x – 3| < 27 is :
(a) (- 6, \(\frac { 15 }{ 2 }\))
(b) [ – 6, \(\frac { 15 }{ 2 }\) ]
(c) [ – 6, \(\frac { 15 }{ 2 }\) )
(d) ( – 6, \(\frac { 15 }{ 2 }\) ]
Answer:
(a) (- 6, \(\frac { 15 }{ 2 }\))

Question 16.
Solution of inequality x > 2 is :

Answer:

Question 17.
Sawant has a space to store at most 13 boxes of apples and oranges. If he bought x boxes of oranges and y boxes of apples, then correct inequality will be :
(a) x + y < 13
(b) x + y > 13
(c) x + y < 13
(d) x + y = 13.
Answer:
(c) x + y < 13

Question 18.
In which point the maximum of objective function P = 10x + 6y in the following points:
(a) (0, 0)
(b) (8, 4)
(c) (10, 0)
(d) (0, 0).
Answer:
(b) (8, 4)

Question 19.
The graph of inequality x +y > 2 is :

Answer:

Question 20.
The solution of inequality 3x – 7 ≥ x + 1 is :
(a) [4, ∞]
(b) (4, ∞]
(c) (4, ∞)
(d) [4, ∞).
Answer:
(d) [4, ∞).

Question 21.
The solution of inequality 3x – 6 > 0; 2x – 6 > 0 is :
(a) [3, ∞]
(b) (3, ∞)
(c) [2, ∞)
(d) (2, ∞).
Answer:
(b) (3, ∞)

Question 22.
The solution of inequality 2x + 6 = 0; 4x – 8 < 0 is :
(a) [- 3, ∞)
(b) (3, 2)
(c) [- 3, 2)
(d)[- 3, 2].
Answer:
(c) [- 3, 2)

Question 23.
The set of solution of inequality x ≥ 0 is :
(a) All points of X – axis and first, fourth quadrants
(b) All points of first and fourth quadrants
(c) All points of first and second quadrants
(d) All points of Y – axis and first, fourth quadrants.
Answer:
(d) All points of Y – axis and first, fourth quadrants.

Question 24.
Variables of the objective function of linear Programming problem are :
(a) Negative
(b) Zero or Negative
(c) Zero
(d) Zero or Positive.
Answer:
(d) Zero or Positive.

(B) Match the following :

Answer:

1. (c)
2. (d)
3. (a)
4. (f)
5. (e)

(C) Fill in the blanks :

1. The maximum or minimum value of objective function is called ……………….
2. The graph of x ≥ 0 is situated in the ………………. quadrant.
3. The graph of y ≤ 0 is situated in the ………………. quadrant.
4. Solution of inequality 3x + 1 < 5x + 7 is (where x is an integer) ……………….
5. Solution of inequality 3x – 4 < 5 is (where x is an integer) ……………….
6. Solution of inequality 4x + 3 > – 13 is (where x is a real number) ……………….
7. Solution of inequality 7x – 2 < 5x + 4 is (where x is a real number) ……………….
8. Solution of inequality 20x < 90 is (where x is a natural number) ……………….
9. Solution of inequality 3x – 2 < x + 4 is ……………….
10. The inequality of one variable is ……………….
11. The set of solutions of y > 0 are in the ………………. and ………………. quadrant.
12. x ≥ 2 and y ≥ 2 will be situated in the graph ……………….
13. The domain of inequality 3x – 15 ≤ 0 is ……………….
14. A function whose maximum and minimum value is to be found subject to the given constrains is known as ……………….

Answer:

1. Optimum value
2. First and fourth
3. Third and fourth
4. (- 3, ∞)
5. {… – 3, – 2, -1, 0, 1, 2}
6. (- 4, ∞)
7. (- ∞, 3)
8. {1, 2, 3, 4}
9. (- ∞, 3)
10. ax + b ≥ c or ax + b ≤ c; where a ≠ 0
11. First and second
12. First and second quadrant
13. (- ∞, \(\frac { 15 }{ 3 }\))
14. Objective function

(D) Write true / false :

1. If the variable x is such that its value lies between two fixed point a and b, then {x : a < x < b} is called a closed interval.
2. The function whose maximum or minimum value is to be found is called objective function.
3. The set of values of the variable satisfying all constraint is called feasible solution of the problem.
4. The process of doing certain specified steps in a given order is called programming.
5. The set {x : a < x < b} which consists of both a and b is called open interval.
6. The solution of inequality 6x – 30 ≥ 0 will be x ≤ 5
7. The solution of inequality – 2x + 7 < – 13 will be (10, ∞).
8. The linear inequality of one variable is ax + b = 0; a ≠ 0, ∀a, b ∈
9. R. The line inequality of two variables is ax + by + c = 0; a ≠ 0, b ≠ 0, ∀a, b, c ∈ R.
10. The graph of inequality x > 0 is :
    
11. The graph of inequality y ≤ 0 is :
    
12. The solution of inequality 5x – 30 ≤ 0 is :
    

Answer:

1. False
2. True
3. True
4. True
5. False
6. False
7. True
8. True
9. True
10. True
11. True
12. False.

(E) Write answer in one word / sentence :

1. In which quadrant lies the solution of x ≥ 0 and y ≥ 0?
2. In which quadrant lies the solution of x ≤ 2 and y ≥ 2?
3. Write the solution of 3(2 – x) ≥ 2(1 – x) .
4. Write the solution of \(\frac { x }{ 3 }\) > \(\frac { x }{ 2 }\) + 1.
5. Write the solution of \(\frac { x – 4 }{ x + 2 }\) ≤ 2.

Answer:

1. First quadrant
2. First and second quadrant
3. (- ∞, 4]
4. (- ∞, – 6)
5. (- ∞, – 8]∪(- 2, ∞)

Linear Inequalities Long Answer Type Questions

Question 1.
Draw the graph of inequality 2x + y ≥ 6 in two – dimensional plane. (NCERT)
Solution:
Given inequality is 2 x + y ≥ 6
Consider this as an equation 2x + y = 6.
For this equation following values of x and y are given in the table :

Plot the graph using the above table. Take a point (0, 0) and put in given inequality,
2x + y ≥ 6
⇒ 2 x 0 + 0 ≥ 6
⇒ 0 ≥ 6 Which is false.
Hence, shaded portion will be opposite of origin.

∴ The shaded region represents the inequality 2x + y ≥ 6.

Question 2.
Draw the graph of inequality 3x + 4y ≤ 12 in two – dimensional plane. (NCERT)
Solution:
Given inequality : 3x + 4y = 12
Consider this as an equation 3x + 4y = 12.
For this equation the following values of x and y are given in the table :

Plot the above points in a graph paper and join them.
Put (0, 0) in given inequality,
⇒ 3x + 4y ≤ 12
⇒ 3 x 0 + 4 x 0 ≤ 12
⇒ 0 ≤ 12
Which is true.
Hence, shaded portion will be towards origin as shown in figure.

∴ The shaded region represents the inequality 3x + 4y ≤ 12

Question 3.
Draw the graph of inequality y + 8 ≥ 2x in two – dimensional plane. (NCERT)
Solution:
Given inequality : y+8 > 2x Consider this as an equation 2x – y = 8
For this equation following values of x and y are given in the table :

Plot the above points in graph paper and join them.
Put (0, 0) in the given inequality,
y + 8 ≥ 2x
⇒ 0 + 8 ≥ 2 x 0
⇒ 8 ≥ 0 Which is true.
Hence, the shaded portion will be towards origin.

∴ Shaded portion represents the inequality y + 8 ≥ 2x.

Draw the graph of following inequality in two – dimensional plane :

Question 4.
2x – 3y > 6.
Solution:
Given inequality is :
2x – 3y > 6
Consider this as an equation 2x – 3y = 6
Following table is prepared for different values of x and y :

Plot the above points on xy – plane and join them.
Put x = 0, y = 0 in given inequality,
2x – 3y > 6
⇒ 2 x 0 – 3 x 0 > 6
⇒ 0 > 6 Which is false.
Hence, the shaded portion will be opposite of origin.

∴The shaded region represents the inequality 2x – 3y > 6

Question 5.
– 3x + 2y ≥ – 6.
Solution:
Given inequality is : – 3x + 2y ≥ – 6.
Consider this as an equation – 3x + 2y = – 6.
Following table is prepared for different values of x and y :

Plotting the above points on xy – plane and join them. Put x = 0, y = 0 in given inequality,
– 3x + 2y ≥ – 6
⇒ – 3(0) + 2(0) ≥ – 6
⇒ 0 ≥ – 6 Which is true.
∴ Shaded portion will be towards origin.

Hence, the shaded portion represents the inequality – 3x + 2y ≥ – 6.

Question 6.
3y – 5x < 30.
Solution:
Given inequality: y – 5x < 30.
Consider this as an equation 3y – 5x = 30.
Following table is prepared for different values of x and y :

Ploting the above points on xy – plane and join them.
Put x = 0, y = 0 in given inequality,
3y – 5x < 30
⇒ 3(0) – 5(0) < 30
⇒ 0 < 30
Which is true.
Hence, the shaded region will be towards origin.

∴ Shaded region represents the inequality 3y – 5x < 30

Question 7.
2x + y ≥ 6, 3x + 4y ≤ 12. (NCERT)
Solution:
Given inequalities are :
2x + y ≥ 6
and 3x + 4y ≤ 12
For the equation 2x+y = 6.
Following table is prepared for different values of x and y :

Plotting the above points on xy – plane to get straight line.
Put x = 0, y = 0 in the inequality,
2x + y ≥ 6
⇒ 2 x 0 + 0 ≥ 6
⇒ 0 ≥ 6
Which is false.
∴ The shaded region will be opposite of origin.
For the equation 3x + 4y = 12.
Following table is prepared for different values of x and y :

Plotting the above points on xy – plane to get straight line.
Put x = 0, y = 0 in given inequality,
3x + 4y ≤ 12
⇒ 3 x (0) + 4(0) ≤ 12
⇒ 0 ≤ 12
Which is true.
Hence, the shaded portion will be towards origin.

∴ The common shaded region is the required solution of the given inequalities.

Question 8.
Solve the following inequalities graphically in two – dimensional plane : x + y ≥ 4, 2x – y >0. (NCERT)
Solution:
Given inequalities are :
x + y ≥ 4
and 2x – y > 0
For the equation x + y = 4, following table is prepared for different values of x and y:

Plotting the above points on xy – plane to get straight line.
Put x = 0, y = 0 in the inequality,
x + y ≥ 4
⇒ 0 + 0 ≥ 4
⇒ 0 ≥ 4
Which is false.
Hence, the shaded region will be opposite of origin.
Preparing table for different value of x and y of the equation 2x – y = 0 :

Plotting the above points in xy – plane to get straight line.
Put x = 1 and y = 0 in given inequality,
2x – y > 0
⇒ 2(1) – 0 > 0
⇒ 2 > 0
Which is true.
Hence, the shaded region will be towards of point (1,0).

The common shaded region is the required solution of the given inequalities.

Question 9.
Solve the following inequalities graphically in two – dimensional plane :
5x + 4y ≤ 20, x ≥ 1, y ≥ 2 (NCERT)
Solution:
The given inequalities are :
5x + 4y ≤ 20
x ≥ 1
y ≥ 2
Prepared table for different values of x and y of the equation 5x +4y = 20 :

Plotting the points of the above table on xy – plane to get straight line.
Then, put x = 0, y = 0 in the inequality,
5x + 4y ≤ 20
⇒ 0 + 0 ≤ 20
⇒ 0 < 20
Which is true.
∴Shaded region will be towards origin.
For equation x + O.y = 1 to get different values of x and y are in the table :

Plotting the points from table on xy plane to get straight line.
Putting x = 0, y = 0 in the inequality,
x ≥ 1
⇒ 0 ≥ 1
Which is false.
Hence, the shaded region will be opposite side of origin.
For equation 0.x + y = 2, the different values of x and y are given in the table :

Plotting the points on xy plane to get straight line.
Then, put x = 0, y = 0 (0,0) in the inequality,
y ≥ 2
⇒ 0 ≥ 2
Which is false.
Hence, the shaded region will be opposite side of origin.

∴ The common shaded region is the required solution of the given inequalities.

Question 10.
Solve the following inequalities graphically :
3x + 4y ≤ 60, x + 3y ≤ 30, x ≥ 0, y ≥ 0. (NCERT)
Solution:
The given inequalities are :
3x + 4y ≤ 60
x + 3y ≤ 30
x ≥ 0
y ≥ 0
Prepared table for values of x and y of equation 3x + 4y = 60 :

Plotting the above points on xy – plane to get straight line.
Then, put x = 0, y = 0 in the inequality,
3x + 4y ≤ 60
⇒ 0 + 0 ≤ 60
⇒ 0 ≤ 60
Which is true.
Hence, the shaded portion will be towards origin.
Prepared table for values of x and y of equation x + 3y = 30:

Plotting the above points on xy – plane to get straight line.
Then, put x = 0, y = 0 in the inequality,
x + 3y ≤ 30
⇒ 0 + 0 ≤ 30
⇒ 0 ≤ 30
Which is true.
Hence, the shaded region will be towards origin.
The graph of x = 0 is y – axis and graph of y = 0 is x – axis.

The common shaded region is the required solution set of the given inequalities.

MP Board Class 11th Maths Important Questions

MP Board Class 11th Maths Important Questions Chapter 5 Complex Numbers and Quadratic Equations

Relations and Functions Important Questions

Relations and Functions Objective Type Questions

(A) Choose the correct option :

Question 1.
If x + iy = 2 + 3i, then (x, y) will be :
(a) (3, 2)
(b) (2, 3)
(c) (- 2,- 3)
(d) (3, 3)
Answer:
(b) (2, 3)

Question 2.
The simplest form of \(\frac { 1 + i }{ 1 – i }\) :
(a) – i
(b) i
(c) ± i
(d) None of these.
Answer:
(b) i

Question 3.
If z is a complex number, then z + z is :
(a) Real number
(b) Imaginary number
(c) Nothing can be said
(d) None of these.
Answer:
(a) Real number

Question 4.
The value of \(\sqrt {i}\) = ……………..
(a) ± \(\frac { 1 – i }{ \sqrt { 2 } }\)
(b) ± \(\frac { 1 + i }{ \sqrt { 2 } }\)
(c) ± (1 + i)
(d) ± (1 – i)
Answer:
(b) ± \(\frac { 1 + i }{ \sqrt { 2 } }\)

Question 5.
Number of solution of the equation z + z = 0 is :
(a) 1
(b) 2
(c) 3
(d) 4
Answer:
(d) 4

Question 6.
Argument of complex number 0 is :
(a) 0
(b) π
(c) 2π
(d) Not defined
Answer:
(d) Not defined

Question 7.
Conjugate of \(\frac { 1 – i }{ 1 + i }\) is :
(a) \(\frac { 1 – i }{ 1 + i }\)
(b) \(\frac { 1 – i }{ 1 – i }\)
(c) i
(d) – i
Answer:
(c) i

Question 8.
Argument (z₁.z₂) = ………………
(a) arg (z₁) – arg (z₂)
(b) arg (z₁) + arg (z₂)
(c) arg (z₁). arg (z₂)
(d) None of these
Answer:
(b) arg (z₁) + arg (z₂)

Question 9.
The least positive integer n for which \(\frac { 1 – i }{ 1 + i }\)ⁿ = 1 is :
(a) 2
(b) 4
(c) 8
(d) 12
Answer:
(b) 4

Question 10.
If |z – \(\frac { 4}{ z}\)| = 2, then |z| has maximum value:
(a) \(\sqrt {3}\) + 1
(b) \(\sqrt {5}\) + 1
(c) 2
(d) 2 + \(\sqrt {2}\)
Answer:
(b) \(\sqrt {5}\) + 1

(B) Match the following :

Answer:

1. (d)
2. (a)
3. (f)
4. (b)
5. (c)
6. (e)

(c) Fill in the blanks :

1. The value of (1 + i)⁴ (1 + \(\frac {1}{i}\))⁴ is ……………….
2. The value of \(\frac {1}{i}\) is ……………….
3. The value of z – \(\bar { z }\) is ……………….
4. Argument of – 1 – i is ……………….
5. polar form of i³ is ……………….
6. Argument of complex number is \(\frac { 1+\sqrt { 3i } }{ \sqrt { 3 } +i }\) is ……………….
7. If |\(\frac { z – i }{ z + i }\)| = 1, then locus of z will be ……………….
8. If x + \(\frac {1}{x}\) = 2cosθ, then the value of xⁿ = \(\frac { 1 }{ { x }^{ n } }\) will be ……………….
9. If z = 2 – 3i, then the value of z. \(\bar { z }\) is ……………….
10. If 2 + (x + yi) = 3 – i, the x = ……………… and y = ……………….

Answer:

1. 16
2. – i
3. Imaginary number
4. \(\frac {5π}{4}\)
5. cos\(\frac {π}{2}\) – i sin\(\frac {π}{2}\)
6. \(\frac {π}{6}\)
7. X – axis
8. 2cos nθ
9. 13
10. 1, – 1

(D) Write true / false :

1. Additive inverse of complex number – 2 + 5i is 2 – 5 i.
2. If | z² – 1 |= z² + 1, then z lies on a circle.
3. If | z₁ | = 12 and | z₂ – 3 – 4i | = 5, then the least value of | z₁ – z₂ | is 7.
4. If arg(z) < 0, then arg(- z) – arg(z) = π.
5. Polar form of 1 + \(\sqrt {- 1}\) is \(\sqrt {2}\)(cos\(\frac {π}{4}\) + isin\(\frac {π}{4}\)).
6. If z is a complex number such that | z | ≥ 2, then the minimum value of |z + \(\frac { 1 }{ 2 }\) | equal \(\frac { 5 }{ 2 }\)

Answer:

1. True
2. False
3. False
4. True
5. True
6. False.

(E) Write answer in one word / sentence :

1. If Z₁ = 2 – i, z₂ = 1 + i, them find the value \(\frac { { { z }_{ 1 }+{ z }_{ 2 }+1 } }{ { z }_{ 1 }-{ z }_{ 2 }+1 }\)
2. Modulus of \(\frac {1 – i }{ 1 + i }\) – \(\frac { 1 – i }{ 1 + i }\) will be.
3. Polar form of complex number \(\sqrt {3}\) + i will be.
4. If Z₁ = 2 – i and z₂ = – 2 + i, then Re(\(\frac { { { z }_{ 1 }{ z }_{ 2 } } }{ { z }_{ 1 } }\)) will be
5. If the number \(\frac { z – 1 }{ z + 1 }\) is purly imaginary, then the value of |z| will be.

Answer:

1. \(\sqrt {2}\)
2. 2
3. 2(cos\(\frac {π}{6}\) + isin\(\frac {π}{6}\))
4. \(\frac { – 2 }{ 5 }\)
5. 1

Complex Numbers and Quadratic Equations Very Short Answer Type Questions

Question 1.
If 1, ω, ω² are the cube root of unity then find the value of ω³ⁿ.
Solution:
Since ω³ = 1
ω³ⁿ = (ω³)ⁿ = (1)ⁿ = 1.

Question 2.
Find the value of i⁴ⁿ.
Solution:
i⁴ⁿ = (i⁴)ⁿ = (i².i²)ⁿ = [(- 1)(- 1)]ⁿ = (1)ⁿ = 1.

Question 3.
Find the condition of two complex numbers x + iy and a + ib are compaired.
Solution:
If x + iy = a + ib
Then, x = a, y = b.

Question 4.
Write conjugate of a complex number z = a – ib.
Solution:
z = conjugate of a – ib = a – (- ib)
= a + ib.

Question 5.
Write the complex number – 6₃ in ordered form.
Solution:
Ordered form of z = a + ib is (a, b).
Given: z = 0 – 6i
Ordered pair (0, – 6).

Question 6.
Write the complex number 3 – \(\sqrt { 7i }\) in ordered form.
Solution:
Ordered pair of z = a + ib is (a, b).
∴Ordered pair of 3 – \(\sqrt { 7i }\) = (3, – \(\sqrt { 7i }\))

Question 7.
Find the value of i + \(\frac { 1 }{ i }\).
Solution:
i + \(\frac { 1 }{ i }\) = \(\frac { { i }^{ 2 }+1 }{ i }\) = \(\frac { – 1 + i }{ i }\) = 0.

Question 8.
Find the value of i^-19.
Solution:
i^-19 = \(\frac { 1 }{ { i }^{ 19 } }\) = \(\frac { 1 }{ { i }^{ 18 }i } \) = \(\frac { 1 }{ (i^{ 2 })^{ 9 }.i }\)
= \(\frac { 1 }{ -1.i }\) = \(\frac { – 1 }{ i }\)
= \(\frac { – 1.i }{ { i }^{ 2 } }\) = i.

Question 9.
Write (1 – i)⁴ in form of a + ib.
Solution:
(1 – i)⁴ = [ (1 – i)² ]² (NCERT)
= [1 + i² – 2i]² = [1 – 1 – 2i]², [∵ i² = – 1]
= (- 2i)² = 4i² = 4(- 1) = – 4
= – 4 + 0i.

Question 10.
Find the modulus of complex number z = – 1 – i \(\sqrt {3}\) .
Solution:
Z = – 1 – i\(\sqrt {3}\)
a = – 1, b = \(\sqrt {3}\)
Modulus = \(\sqrt { { a }^{ 2 }+{ b }^{ 2 } }\) = \(\sqrt {1 + 3}\) = \(\sqrt {2}\)

Question 11.
Find the modulus of complex number 1 – i.
Solution:
z = 1 – i
a = 1, b = – 1
Modulus = \(\sqrt { { a }^{ 2 }+{ b }^{ 2 } }\) = \(\sqrt {1 + 1}\) = \(\sqrt {2}\)

Question 12.
Find the sum of 2 – 3i and its conjugate.
Solution:
z = 2 – 3i and \(\bar { z }\) = 2 + 3i
z + \(\bar { z }\) = 2 – 3i + 2 + 3i = 4.

Question 13.
Solve the quadratic equation x² + 2 = 0. (NCERT)
Solution:
x² + 2 = 0
⇒ x² = – 2
⇒ x² = – 1 x 2
= 2i² [∵ i² = – 1]
x = ± \(\sqrt {2i}\) or + \(\sqrt {2}\)i, – \(\sqrt {2}\)i

Question 14.
Solve the quadratic equation x² + 3 = 0. (NCERT)
Solution:
x² + 3 = 0
⇒ x² = – 3 = – 1 x 3
⇒ x² = 3i², [∵ i² = – 1]
x² = ± \(\sqrt {3i}\) or + \(\sqrt {3}\)i, – \(\sqrt {3}\)i

Question 15.
Write the triangle inequality for the two complex number Z₁ and z₂.
Solution:
| Z₁| and | z₂| are the two sides of any triangle
Then, | z₀ + z₂| ≤ | z₁| +| z₂|

Question 16.
If T and 9 are the modulus and argument of the complex number a + ib, then write its polar form.
Solution:
Polar form of a + ib is r(cosθ + i sinθ).

Question 17.
If z = cosθ + i sinθ where |z| = 1, then find \(\frac { 1 }{ z }\).
Solution:
\(\frac { 1 }{ z }\) = cosθ – isinθ.

Question 18.
Write the statement of De – moivre’s theorem.
Solution:
If polar form of z = a + ib is r(cosθ + isinθ), then De – moivre’s theorem is
(cosθ + isinθ)n = cos nθ + i sin nθ.

Question 19.
Write polar form of i.
Solution:
a + ib = 0 + i. 1
r = \(\sqrt { { a }^{ 2 }+{ b }^{ 2 } }\) =1, θ = tan^-1\(\frac { b }{ a}\) = tan^-1∞ = \(\frac { π }{ 2}\)
Polar form of i = (cos\(\frac { π }{ 2}\) + i sin \(\frac { π }{ 2}\)).

Question 20.
Find the polar form of (- 2 + 2i).
Solution:

Complex Numbers and Quadratic Equations Long Answer Type Questions

Question 1.
Convert (\(\frac { 1 }{ 3}\) + 3i)³ in form of a + ib. (NCERT)
Solution:

Question 2.
Write ( – 2 – \(\frac { 1 }{ 3}\)i)³ in form of a + ib. (NCERT)
Solution:

Question 3.
Write (5 – 3i)³ in the form of a + ib.
Solution:
(5 – 3i)³ = (5)³ – (3i)³ – 3(5².3i) + 3.5(3i)²
= 125 – 27.i³ – 75.3i + 15.9i²
= 125 – 27i.i² – 225i + 15(- 9)
= 125 + 27i – 225i – 135
= – 10 – 198i.

Find the multiplicative inverse of following complex number :

Question 4.
4 – 3i
Solution:
Let the multiplicative inverse of 4 – 3i is a + ib.
Then, (4 – 3i) x (a + ib) = 1

Question 5.
\(\sqrt {5}\) + 3i
Solution:
Let z = \(\sqrt {5}\) + 3i
Be multiplicative inverse

Question 6.
Find the polar form of the following :
(i) \(\frac { 1 + 7i }{ { 2 – i }^{ 2 } }\), (ii) \(\frac { 1 + 3i }{ 1 – 2i }\)
Solution:

Now, let – 1 + i = r(cosθ + i sinθ),
Then, r cosθ = – 1 …. (1)
and r sinθ = 1 …. (2)
Squaring and adding equation (1) and (2),
r² = 1 + 1 = 2
⇒ r = \(\sqrt {2}\)
Put value of r in equation (1) and (2),

Comparing the real and imaginary parts,
r cosθ = – 1
r sinθ = 1

Squaring and adding equation (1) and (2),

∵ Real part is negative and imaginary part is positive of z, hence θ will lie in 4^th quadrant

Question 7.
Find modulus and argument of complex number z = – 1 – i\(\sqrt {3}\) (NCERT)
Solution:
Let z = – 1 – i\(\sqrt {3}\) = rcosθ + ir sinθ

Comparing the real and imaginary parts,
rcosθ = – 1 …. (1)
rsinθ = – \(\sqrt {3}\) …. (2)
Squaring and adding equation (1) and (2),

Since both the real and imaginary part of z are negative.
∴ θ lies in third quadrant

Question 8.
Find the modulus and argument of z = – \(\sqrt {3}\)+ i.
Solution:
Let z = – \(\sqrt {3}\)+ i = rcosθ + ir sinθ

Comparing the real and imaginary parts,
r cosθ = – \(\sqrt {3}\)
rsinθ = 1
Squaring and adding eqns. (1) and (2),
rcosθ = – \(\sqrt {3}\) …. (1)
rsinθ = 1 …. (2)
Squaring and adding equation (1) and (2),

Since both the real and imaginary part of z are negative and positive respectively.
∴ θ lies in 2^2nd quadrant

Question 9.
Find the modulus and argument of 1 – i.
Solution:
Let z = 1 – i = rcosθ + ir smθ
Comparing the real and imaginary parts,
1 = r cosθ
and – 1 = rsinθ
Squaring and adding equation (1) and (2),
(1)² + (- 1)² = r² cos²0 + r² sin²0
⇒ r²(cos²0 + sin²0) = 1 + 1,
⇒ r²= 2 ⇒ r = \(\sqrt {2}\) (modulus)
Dividing equation (2) by equation (1),

Question 10.
Find square root of complex number 3 + 4i.
Solution:
Let \(\sqrt {3 + 4i}\) = x + iy
On squaring,
3 + 4 i = (x + iy)²
⇒ 3 + 4i = x² + 2ixy + i²y²
⇒ 3 + 4i = x² + 2ixy – y²
⇒ 3 + 4i = (x² – y²) + i(2xy)
x² – y² = 3 …. (1)
2xy = 4 …. (2)
(x² + y²)² = (x² – y²)² + 4x²y²
= (3)² + (4)²
= 25
∴ x² + y² = 5 …. (3)
Now adding eqns. (1) and (3),
2x² = 8
⇒ x² = 4
⇒ x = ± 2
From equation (2), 2(± 2)y = 4
∴ y = ± 1
\(\sqrt { x + iy }\) = ± 2 ± i.

Question 11.
Find square root of complex number 8 – 6i.
Solution:
Let \(\sqrt { 8 – 6i }\) = x + iy
On squaring,
8 – 6i = (x + iy)²
⇒ 8 – 6i = x² + 2ixy + i²y² .
⇒ 8 – 6i = (x² – y²) + 2ixy
∴ 8 = x² – y² …. (1)
and – 6 = 2 xy …. (2)
(x² + y²)² = (x² – y²)² + 4x²y²
(x²+y²)² = (8)² + (- 6)²
= 64 + 36 = 100
∴ x² + y² = 10 …. (3)
Now adding equation (1) and (3),
2x² = 18
⇒ x² = 9
⇒ x = ±3
From equation (3), y² = 10 – 9 = 1
∴ y = ± 1
\(\sqrt { 8 – 6i}\) = ± 3 ± i.

Question 12.
x² + 3x + 9 = 0.
Solution:
Given : x² + 3x + 9 = 0
Comparing the above equation by ax² + bx + c = 0,
a = 1, b = 3, c = 9
Now, D = b² – 4ac
= 3² – 4 x 1 x 9 = 9 – 36 = – 27 < 0

Question 13.
– x² + x – 2 = 0.
Solution:
Given : – x² + x – 2 = 0
Comparing the above equation by ax² + bx + c = 0,

Question 14.
x² + 3x + 5 = 0.
Solution:
Given : x² + 3x + 5 = 0
Comparing the above equation by ax² + bx+c = 0,
a = 1, b = 3, c = 5

Question 15.
x² – x + 2 = 0
Solution:
Given : x² – x + 2 = 0
Comparing the above equation by ax² + bx + c = 0,
a = 1, b = – 1, c = 2
Now, D = b² – 4ac
= (- 1)² – 4 x 1 x 2 = 1 – 8 = – 7 < 0

Question 16.
If (\(\frac { 1 + i }{ 1 – i }\)) = 1, then And the minimum positive integer number of m. (NCERT)
Solution:

MP Board Class 11th Maths Important Questions

MP Board Class 11th Maths Important Questions Chapter 4 Principle of Mathematical Induction

Principle of Mathematical Induction Important Questions

Principle of Mathematical Induction Long Answer Type Questions

Question 1.
For n > 1, prove that with the help of principle of mathematical induction :
1² + 2² + 3² + 4² + …………. + n² = \(\frac { n(n + 1)(2n + 1) }{ 6 }\). (NCERT)
Solution:

∴ p(n) is true for n = k + 1.
Hence, p(n) is true for all values of n ∈ N.

Question 2.
For n ≥ 1 prove that :
\(\frac { 1 }{ 1.2 }\) + \(\frac { 1 }{ 2.3 }\) + \(\frac { 1 }{ 3.4 }\) + …………. + \(\frac { 1 }{ n(n + 1) }\) = \(\frac { n }{ n + 1 }\)
Solution:
Let

∴ p(n) is true for n = k + 1.
Hence, p(n) is true for all values of n ∈ N.
Instruction:
All questions from 3 to 7 when n∈N prove the statement by using principle of mathematical induction :

Question 3.
1³ + 2³ + 3³ + …………. + n³ = \(\frac { { n }^{ 2 }{ (n+1) }^{ 2 } }{ 4 }\) (NCERT)
Solution:

∴ Given function is true for n = m + 1.
Hence, p(n) is true for all values of n ∈ N.

Question 4.
1 + \(\frac { 1 }{ 1 + 2 }\) + \(\frac { 1 }{ 1 + 2 + 3 }\) + ……….. + \(\frac { 1 }{ 1 + 2 + 3 + ………. + n }\) + …………. + = \(\frac { 2n }{ n + 1 }\).
Solution:
For n = 1, L.H.S = 1
and R.H.S. = \(\frac { 2 x 1 }{ 1 + 1 }\) = 1
The given function is true for n = 1.
Let the function be true for n = m

∴ The Given function is true for n = m + 1.
Hence, p(n) is true for all values of n ∈ N.

Question 5.
1.2 + 2.3 + 3.4 + ………….. + n(n + 1) = \(\frac { n(n + 1)(n + 2) }{ 3 }\)
Solution:
Let p(n) = 1.2 + 2.3 + 3.4 + ………….. + n(n + 1) = \(\frac { n(n + 1)(n + 2) }{ 3 }\)
If n = 1, L.H.S. = 1.2 = 2
R.H.S = \(\frac { n(n + 1)(n + 2) }{ 3 }\) = \(\frac { 1.2.3 }{ 3 }\) = 2
∴ p(n) is true for n = 1.
Let p(n) be true for n = k

∴ p(n) is true for n = k + 1.
Hence, p(n) is true for all values of n ∈ N.

Question 6.
\(\frac { 1 }{ 2.5}\) + \(\frac { 1 }{ 5.8 }\) + \(\frac { 1 }{ 8.11}\) + …………. + \(\frac { 1 }{ (3n – 1)(3n + 2) }\) = \(\frac { n }{ 6n + 4 }\)
Solution:
Let p(n) = \(\frac { 1 }{ 2.5}\) + \(\frac { 1 }{ 5.8 }\) + \(\frac { 1 }{ 8.11}\) + …………. + \(\frac { 1 }{ (3n – 1)(3n + 2) }\) = \(\frac { n }{ 6n + 4 }\)
∴ For n = 1, L.H.S = \(\frac { 1 }{ 2.5}\) = \(\frac { 1 }{ 10}\)
and R.H.S = \(\frac { 1 }{ 6.1 + 4}\) = \(\frac { 1 }{ 10}\)
∴ p(n) is true for n = 1.
Let p(n) be true for n = k

∴ p(n) is true for n = k + 1.
Hence, p(n) is true for all values of n ∈ N.

Question 7.
1.2.3. + 2.3.4 + …………. + n(n+1)(n+2) = \(\frac { n(n + 1)(n + 2)(n + 3) }{ 4 }\). (NCERT)
Solution:
For n = 1, L.H.S = 1.2.3 = 6
And R.H.S. = \(\frac { 1(1 + 1)(1 + 2)(1 + 3) }{ 4 }\) = \(\frac { 2.3.4 }{ 4 }\) = 6
∴ Given function is true for n = 1.
Let the function be true for n = k

∴ The given function is true for n = k + 1. Hence the given function is true for all values of n ∈ N.

Question 8.
Prove that (41)ⁿ – (14)ⁿ is a multiple of 27 with the help of principle of mathematical induction. (NCERT)
Solution:
Let P(n) = (41)ⁿ – (14)ⁿ
For n = 1,
P(1) = (41)¹ – (14)¹= 27
Which is multiple of 27.
Let P(ri) be true for n = k.
Then, (41)^k – (14)^k = 27m
Put n = k +1 in P(n)
(41)^k+1 – (14)^k+1 = (41)^k.41 – (14)^k. 14
= (41)^k.41 – 41.(14)^k + 41.(14)^k – (14)^k.14
= 41[(41)^k – (14)^k]+(14)^k [41 – 14]
= 41 x 27m + (14)^k x 27 = 27[41 x m + (14)^k]
Which is multiple of 27.
If the given function P(n) is true for n = k then P(n) will be true for U n = k +1 also.
Hence the given function is true for all values of n ∈ N.

MP Board Class 11th Maths Important Questions

MP Board Class 11th Hindi Swati Solutions गद्य महत्त्वपूर्ण वस्तुनिष्ठ प्रश्न

बहु-विकल्पीय प्रश्न

प्रश्न 1.
सच्चे उत्साही कहलाते हैं (2008)
(i) पलायनवादी
(ii) कायर
(iii) कर्म सौन्दर्य के उपासक
(iv) कर्म से विरक्त।
उत्तर:
(iii) कर्म सौन्दर्य के उपासक

प्रश्न 2.
साहसपूर्ण आनन्द की उमंग का नाम है- (2008)
(i) भय
(ii) क्रोध
(iii) उत्साह
(iv) घृणा।
उत्तर:
(iii) उत्साही

प्रश्न 3.
शिरीष फूलता है
(i) शरद ऋतु में
(ii) वर्षा ऋतु में
(iii) जेठ मास में
(iv) बसंत में।
उत्तर:
(ii) जेठ मास में

प्रश्न 4.
आजादी की लड़ाई में बड़े घर से आशय था (2009)
(i) महल
(ii) जेलखाना
(iii) बहुत बड़ी हवेली
(iv) विशाल मकान।
उत्तर:
(ii) जेलखाना

प्रश्न 5.
स्नेहबन्ध कहानी में सास का हृदय परिवर्तन होता है (2008)
(i) मीता की सम्पन्नता देखकर
(ii) मीता का सौन्दर्य देखकर
(iii) मीता की सामाजिक प्रतिष्ठा देखकर,
(iv) मीता की सेवा सुश्रूषा तथा कर्त्तव्य भावना देखकर।
उत्तर:
(iv) मीता की सेवा सुश्रूषा तथा कर्त्तव्य भावना देखकर।

प्रश्न 6.
स्नेहबन्ध कहानी में किया गया है (2008)
(i) सास-बहू की अनबन का चित्रण
(ii) सास-बहू के सम्बन्धों का मर्मस्पर्शी चित्रण
(iii) सास-बहू के अस्तित्व का चित्रण,
(iv) सास-बहू के बीच श्रेष्ठता का चित्रण।
उत्तर:
(ii) सास-बहू के सम्बन्धों का मर्मस्पर्शी चित्रण

प्रश्न 7.
‘मर्यादा’ एकांकी में निहित है (2009, 13)
(i) पारिवारिक आदर्श
(ii) सामाजिक आदर्श
(iii) धार्मिक आदर्श
(iv) ऐतिहासिक आदर्श।
उत्तर:
(i) पारिवारिक आदर्श

प्रश्न 8.
‘जननी जन्मभूमिश्च’ निबन्ध में मिश्रजी ने मातृभूमि का महत्व बताया है (2012)
(i) कल्पना के द्वारा
(ii) ऐतिहासिक प्रसंगों के द्वारा
(ii) परम्पराओं के द्वारा
(iv) नकल के द्वारा।
उत्तर:
(ii) ऐतिहासिक प्रसंगों के द्वारा

प्रश्न 9.
जननी जन्मभूमिश्च में लेखक ने जन्मभूमि को निरूपित किया है- (2008)
(i) स्वर्ग के समान
(ii) स्वर्ग से भी श्रेष्ठ
(iii) सबसे सुन्दर
(iv) सबसे महत्त्वपूर्ण।
उत्तर:
(ii) स्वर्ग से भी श्रेष्ठ

प्रश्न 10.
सतपुड़ा पर्वत की सबसे ऊँची चोटी है (2008)
(i) एवरेस्ट
(ii) माउण्ट आबू
(ii) कारगिल
(iv) धूपगढ़।
उत्तर:
(iv) धूपगढ़।

प्रश्न 11.
धूपगढ़ स्थित है (2010, 15)
(i) पचमढ़ी
(ii) भोजपुर
(iii) साँची
(iv) रायगढ़।
उत्तर:
(i) पचमढ़ी

प्रश्न 12.
नीरा के पिता को पढ़ने का शौक था (2008, 11,14)
(i) अखबार
(ii) पत्रिका
(iii) पत्र
(iv) उपन्यास।
उत्तर:
(i) अखबार

प्रश्न 13.
अवतार का अर्थ है
(i) जीवमात्र
(ii) विशिष्ट पुरुष
(iii) सामान्यजन
(iv) भगवान।
उत्तर:
(ii) विशिष्ट पुरुष

प्रश्न 14.
भोलाराम का जीव ढूँढ़ने धरती पर कौन गया? (2013)
(i) बच्चे
(ii) यमदूत
(iii) स्त्री
(iv) नारद।
उत्तर:
(iv) नारद।

प्रश्न 15.
संयुक्त परिवार की नींव है (2016)
(i) सद्भावना और त्याग
(ii) भाईचारा
(iii) सूझ-बूझ से
(iv) इन सबके सामंजस्य से।
उत्तर:
(iv) इन सबके सामंजस्य से।

प्रश्न 16.
कोणार्क मंदिर किस देवता से सम्बन्धित है? (2017)
(i) सूर्य
(1) चन्द्रमा
(ii) श्रीराम
(iv) श्रीकृष्ण।
उत्तर:
(i) सूर्य

प्रश्न 17.
शंकर की माताजी का नाम था
(i) उभय भारती
(ii) आर्यम्बा
(iii) अहिल्या
(iv) आत्री।
उत्तर:
(ii) आर्यम्बा

प्रश्न 18.
शंकराचार्य ने किस मत का प्रचार किया?
(i) अद्वैत
(ii) सनातन
(iii) द्वैत
(iv) हिन्दू।
उत्तर:
(i) अद्वैत

रिक्त स्थान पूर्ति

1. उत्साह के बीच …………. संचरण होता है। (2009)
2. शिरीष अपना पोषण …………. से प्राप्त करता है। (2009)
3. सतपुड़ा पर्वत की सबसे ऊँची चोटी………… है। (2014)
4. धूपगढ़ ………… में स्थित है। (2008, 09)
5. महादेवी वर्मा ने पहली पुस्तक ………… पढ़ी थी। (2009)
6. नीरा के पिता कुली बनकर ……….. गये थे। (2008, 09)
7. कोणार्क मन्दिर …………. देवता से सम्बन्धित है। (2008)
8. कोणार्क के मन्दिर में कलश की स्थापना ………. के सहयोग से सम्भव हो सकी। (2008)
9. सुमन जगदीश के घर …………. सुनने के लिए आई थी। (2010)
10. भोलाराम ने दरख्वास्तों पर …………. नहीं रखा था।
11. यमदूत को चकमा ………… के जीव ने दिया था। (2016)
12. शिरीष की तुलना ……….. से की गई है। (2011)
13. शिरीष …………. के आगमन से फूलना प्रारम्भ हो जाता है। (2013, 17)
14. ‘नीरा’ एक …………. है। (2013)
15. ‘गंगा और गंगा के कछार को मेरा सलाम कहें’ कथन ………. है। (2012)
16. शंकर के गुरु …………. थे।
17. भारत की आत्मा …………. में निवास करती है।

उत्तर:

1. साहस का
2. वायुमण्डल
3. धूपगढ़
4. पचमढ़ी
5. पंचतन्त्र
6. मॉरीशस,
7. सूर्य
8. धर्मपद
9. रामायण
10. वजन
11. भोलाराम
12. अवधूत
13. बसन्त ऋतु
14. कहानी
15. परदेशी का
16. गोविन्दपाद
17. वाराणसी।

सत्य / असत्य

1. उत्साह की गिनती दुर्गुण में होती है। (2011)
2. अवधूतों के मुख से संसार की सबसे सरस रचनाएँ निकली हैं। (2009)
3. फूल की अभिलाषा देवताओं पर चढ़ाए जाने की होती है।
4. नीरा के पिता को गीता पढ़ने का शौक था। (2015)
5. नीरा के पिता को अपनी बेटी के भविष्य की चिन्ता थी। (2009)
6. ‘स्नेहबंध’ कहानी में नारी हृदय के परिवर्तन का स्वाभाविक अंकन हुआ है। (2013)
7. ‘मेरे बचपन के दिन’ रेखाचित्र विधा से सम्बन्धित है। (2009)
8. भोलाराम का जीव पेंशन की दरख्वास्तों में अटका था। (2009)
9. कला के सम्बन्ध में आचार्य विशु और धर्मपद के विचारों में अन्तर है। (2008)
10. भोलाराम हृदयगति रुकने के कारण मरा। (2009)
11. भोलाराम का जीव ढूँढ़ने के लिए धरती पर यमराज आये। (2017)
12. श्रीमती मालती जोशी सुप्रसिद्ध आलोचक हैं। (2012)
13. संयुक्त परिवार की नींव धन पर आधारित होती है। (2012, 14)
14. ‘जननी जन्मभूमिश्च’ निबन्ध में लेखक ने स्वर्ग को श्रेष्ठ माना है। (2013)
15. सतपुड़ा की सबसे ऊँची चोटी एवरेस्ट है। (2013)
16. धूपगढ़ पचमढ़ी पर स्थित है। (2016)
17. शंकर के गुरु गौड़पादाचार्य थे।
18. शंकर ने शास्त्रार्थ में मंडन मिश्र और उनकी विदुषी पत्नी उभय भारती को पराजित किया था।

उत्तर:

1. असत्य
2. सत्य
3. असत्य
4. असत्य
5. सत्य
6. सत्य
7. असत्य
8. सत्य
9. सत्य
10. असत्य
11. असत्य
12. असत्य
13. असत्य
14. असत्य
15. असत्य
16. सत्य
17. असत्य
18. सत्य।

जोड़ी मिलाइए

I.

उत्तर:
1. → (ङ)
2. → (क)
3. → (घ)
4. → (ग)
5. → (ख)
6. → (च)।

II.

1. → (ख)
2. → (क)
3. → (घ)
4. → (ग)
5. → (च)
6. → (ङ)।

एक शब्द / वाक्य में उत्तर

प्रश्न 1.
उत्साह के बीच किसका संचरण होता है?
उत्तर:
धृति और साहस का

प्रश्न 2.
जननी और जन्मभूमि किससे अधिक श्रेष्ठ हैं? (2009, 15)
उत्तर:
स्वर्ग से

प्रश्न 3.
माँ का दूध कैसा होता है?
उत्तर:
अनमोल

प्रश्न 4.
यमदूत को किसने चकमा दिया था? (2014)
भोलाराम के जीव ने

प्रश्न 5.
महादेवी वर्मा अपने जेब खर्च के पैसे क्यों बचाती थीं?
उत्तर:
देश के लिए

प्रश्न 6.
धर्मपद कौन था? (2009)
उत्तर:
आशुशिल्पी युवक

प्रश्न 7.
साँझ की आँखों में करुणा किस रूप में प्रकट होती है?
उत्तर:
ओस कणों के रूप में

प्रश्न 8.
नीरा की माँ का क्या नाम था? (2017)
उत्तर:
कुलसम

प्रश्न 9.
विदेश न जाने के पीछे मीता का क्या भाव था? (2009)
उत्तर:
खर्च बचाना

प्रश्न 10.
‘मर्यादा’ एकांकी में परिवार की किस व्यवस्था का समर्थन हुआ है?
उत्तर:
संयुक्त परिवार

प्रश्न 11.
गीता का प्रमुख उद्देश्य क्या है?
उत्तर:
आत्मार्थी को आत्मदर्शन का एक अद्वितीय उपाय बताना

प्रश्न 12.
कोणार्क मन्दिर कहाँ स्थित है? (2012)
उत्तर:
उड़ीसा प्रान्त में पुरी के निकट समुद्र तट पर

प्रश्न 13.
‘मेरे बचपन के दिन’ पाठ किस विधा में लिखा गया है? (2012)
उत्तर:
संस्मरण

प्रश्न 14.
शिरीष अपना पोषण रस किससे खींचता है? (2013)
उत्तर:
वायुमण्डल से

प्रश्न 15.
शंकर ने किस नाम से पाँच श्लोकों की रचना की?
उत्तर:
मनीषपंचक

प्रश्न 16.
अपने लक्ष्य की पूर्ति के लिए अन्त में शंकराचार्य कहाँ पहुँचे?
उत्तर:
केदारनाथ

MP Board Class 11th Hindi Solutions

MP Board Class 11th Hindi Swati Solutions पद्य Chapter 3 प्रेम और सौन्दर्य

प्रेम और सौन्दर्य अभ्यास

प्रेम और सौन्दर्य अति लघु उत्तरीय प्रश्न

प्रश्न 2.
पदमाकर की गोपियों को सुबह-शाम और घर-बाहर अच्छा क्यों नहीं लगता है?
उत्तर:
पद्माकर की गोपियों को सुबह-शाम और घर-बाहर अच्छा नहीं लगता क्योंकि उनका मन श्रीकृष्ण से लग गया है। अत: उनके बिना गोपियों को संसार की कोई भी वस्तु अच्छी नहीं लगती है।

प्रश्न 3.
गोप-सुता पार्वती माँ से क्या वरदान माँगती है? (2016)
उत्तर:
गोप-सुता पार्वती माँ से यह वरदान माँगती है कि उसे सुन्दर, साँवला नन्दकुमार (अर्थात् कृष्ण) वर के रूप में चाहिए।

प्रश्न 4.
“वा मुख की मधुराई कहाँ-कहौ ?” में मतिराम ने किस मुख की ओर संकेत किया है?
उत्तर:
उक्त पद में मतिराम ने श्रीकृष्ण के सुन्दर मुख की ओर संकेत किया है।

प्रश्न 5.
श्रीकृष्ण के मुकुट में कौन-सी वस्तु लगी है?
उत्तर:
श्रीकृष्ण के मुकुट में मोर का पंख लगा हुआ है।

प्रेम और सौन्दर्य लघु उत्तरीय प्रश्न

प्रश्न 1.
गोपियों पर श्रीकृष्ण की वंशी का क्या प्रभाव पड़ता है?
उत्तर:
गोपियाँ श्रीकृष्ण की वंशी के मधुर स्वर को सुनकर अपनी सुध-बुध को भूल गयीं उन्हें अपने बूंघट का भी ध्यान न रहा। वे न तो घाट की रहीं और न अपने घर की।

प्रश्न 2.
‘मान रहोई नहीं मनमोहन मानिनी होय सो मानै मनायो’ का आशय स्पष्ट कीजिए। (2014)
उत्तर:
आशय- यहाँ पर पूर्ण समर्पित रूठी हुई नायिका नायक श्रीकृष्ण के देर से आने पर उन्हें उपालम्भ देती हुई कहती है कि उन्हें कसमें खाने की कोई आवश्यकता नहीं है क्योंकि वह तो कभी कोई अपराध नहीं करते। उसे तो कोई मानगुमान नहीं है। जो कोई मानिनी हो उसे मनाया जाए, वह तो मानिनी नहीं है। उसका तो मान रह ही नहीं गया इसलिए उसे मनाने की क्या आवश्यकता है।

प्रश्न 3.
मतिराम के शब्दों में श्रीकृष्ण की छवि का मोहक वर्णन कीजिए।
उत्तर:
मतिराम ने श्रीकृष्ण के रंग को सोने से भी अधिक सुन्दर बताया है। उनके मुकुट में मोर का पंख है। गले में सुन्दर माला है। कानों में गोल कुण्डल पहने हैं। जब कुण्डल हिलते हैं तो कृष्ण के गालों की सुन्दरता बढ़ जाती है। उनके नेत्र लाल रंग के हैं। वे सदैव मुस्कराते हैं। अतः हमारे नेत्रों को प्रिय लगते हैं।

प्रेम और सौन्दर्य दीर्घ उत्तरीय प्रश्न

प्रश्न 1.
गोपिका श्रीकृष्ण की छवि को नेत्रों से बाहर निकालने में क्यों असमर्थ है? (2009)
उत्तर:
गोपिका श्रीकृष्ण की छवि को नेत्रों से बाहर निकालने में इसलिए असमर्थ है, क्योंकि गोपिका के नेत्रों में गुलाल व नन्दलाल दोनों ही समाए हुए हैं। मैं तो जल द्वारा नेत्रों को धो-धोकर परेशान हो गयी हूँ। मैं कहाँ जाऊँ और किस प्रकार का प्रयास करूं, क्योंकि आँखें बार-बार धोने से मेरी पीड़ा बढ़ रही है। अतः इस कृष्ण को जो कि मेरे नेत्रों में समा गया है, उसे निकालना मेरी सामर्थ्य के परे हैं।

प्रश्न 2.
‘को बिन मोल बिकात नहीं कवि ने ऐसा क्यों कहा है? समझाइए। (2009)
उत्तर:
मतिराम कवि ने श्रीकृष्ण के अनुपम सौन्दर्य का वर्णन किया है। उन्होंने यह बताने का प्रयास किया है कि कृष्ण का रूप मन को प्रसन्न करने वाला है। श्रीकृष्ण का सुन्दर रूप नेत्रों में बस गया है। कुछ वस्तुएँ तो बिकाऊ होती हैं और व्यक्ति उन वस्तुओं का मूल्य चुकाकर उन्हें खरीद सकता है, लेकिन कृष्ण का यह अद्भुत सौन्दर्य बिना मूल्य का है। इसको कभी भी बेचा नहीं जा सकता है, लेकिन फिर भी यह मूल्यवान है। ईश्वर का कोई मूल्य नहीं है। वह तो अनमोल है। इस प्रकार कवि ने ईश्वर की महिमा का वर्णन किया है।

प्रश्न 3.
आशय स्पष्ट कीजिए
(क) कुन्दन को रंग फीको लागै झलकै अति अंगन चारु गुराई।
उत्तर:
आशय-नायिका गौर वर्ण की है। उसका सौन्दर्य अभूतपूर्व है। उसके सौन्दर्य के समक्ष सोना भी तुच्छ प्रतीत होता है। अंग से झलकने वाली सुषमा मन को मोहित करने वाली है।

(ख) एक पग भीतर औ एक देहरी पै धरै।
एक कर कंज, एक कर है किबार पर।।
उत्तर:
आशय-नायिका नायक के लिए प्रतीक्षारत है। वह अपनी सुध-बुध भूलकर नायक की प्रतीक्षा में व्याकुल है। उसका एक पैर घर के भीतर है, दूसरा दरवाजे पर है। उसके एक हाथ में कमल का पुष्प है और दूसरा हाथ किवाड़ पर रखे हुए वह विरह में विदग्धा नायिका खड़ी हुई है।

(ग) नेह सरसावन में मेह बरसावन में,
सावन में झूलियों सुहावनो लगत है।
उत्तर:
आशय-यहाँ नायिका सावन में झूला झूलने के आनन्द का वर्णन करती हुई कहती है कि हृदय में प्रेम रस हिलोरे ले रहा है, मेघ बरस रहे हैं। ऐसे में हे सखी ! झूला झूलना अत्यन्त सुखकर प्रतीत होता है।

प्रश्न 4.
निम्नलिखित काव्यांश की प्रसंग सहित व्याख्या कीजिए
(अ) कैसी करो कहाँ जाऊँ कासौं कहौं कौन सुने,
कोउ तौ निकासौ जाते दरद बढ़े नहीं।
एरी मेरी वीर ! जैसे तैसे इन आँखिन तें
कढ़िगो अबीर पै अहीर तो कढ़े नहीं।
(आ) कुन्दन को रंग फीको लागै, छलके अति अंगन चारु गुराई,
आँखिन में अलसनि चितौन में मंजु विलासन की सरसाई।
को बिन मोल बिकात नहीं, मतिराम लहै मुसकानि मिठाई,
ज्यौं-ज्यौं निहारिए नेरे कै नैनहिं, त्यों-त्यौं खरी निकरै सी निकाई।।
उत्तर:
(अ) सन्दर्भ :
प्रस्तुत छन्द हमारी पाठ्य-पुस्तक के ‘प्रेम और सौन्दर्य’ पाठ के ‘पद्माकर के छन्द’ शीर्षक से अवतरित हैं। इसके रचयिता पद्माकर हैं।

प्रसंग :
प्रस्तुत पद्य में गोपियों एवं श्रीकृष्ण के फाग (होली) खेलने का वर्णन किया गया है।

व्याख्या :
फाग खेलते समय गुलाल उड़ रहा है। इसके फलस्वरूप श्रीकृष्ण एवं गुलाल चारों ओर धूम मचा रहे हैं। नेत्रों में जो आनन्द भर गया है। वह समा नहीं रहा है। गोपी कह रही है कि हे सखी ! तुम्हारी शपथ खाकर कहती हूँ कि आँखों को धो-धोकर हार गई और अब तो कोई उपाय शेष नहीं बचा है। अब मैं अपनी व्यथा को कैसे दूर करूँ, किस स्थान पर जाऊँ, किससे कहूँ, कोई सुनने वाला भी नहीं है। अब कोई तो मेरी आँखों से इसे निकाले जिससे दर्द नहीं बढ़े। हे मेरी सखी ! मैंने यत्न करके किसी प्रकार आँखों से गुलाल को तो निकाल लिया किन्तु जो आँखों में बसा हुआ अहीर अर्थात् श्रीकृष्ण है वह किसी भाँति नहीं निकल रहा।

(आ) सन्दर्भ :
प्रस्तुत पद्य ‘प्रेम और सौन्दर्य’ पाठ के ‘मतिराम के छन्द’ शीर्षक से उद्धत है। इसके रचयिता मतिराम हैं।

प्रसंग :
प्रस्तुत पद में कवि ने नायिका के शारीरिक सौष्ठव का वर्णन किया है।

व्याख्या :
कवि कहता है कि नायिका के अंग-अंग में झलकने वाले सौन्दर्य के आगे स्वर्ण (सोने) की छवि भी फीकी लगती है। उसके नेत्र अलसाए हुए हैं और उसकी चितवन में मधुर विलास का सौन्दर्य है। मतिराम कहते हैं कि उसकी मुस्कान इतनी मधुर है कि देखने वाला ऐसा कौन है जो बिना मोल नहीं बिक जाता है अर्थात् जो उसके सौन्दर्य को देखता है वही मोहित हो जाता है। जैसे-जैसे निकट जाकर उसके नेत्रों को निहारो वैसे-वैसे ही उसकी सुन्दरता और अधिक बढ़ती जाती है।

प्रेम और सौन्दर्य काव्य सौन्दर्य

प्रश्न 1.
निम्नलिखित शब्दों के तत्सम रूप लिखिए
मोल, नेरे, मूरति, सनेह, घरी, देहरी, किबार, सौंह, घूघट।
उत्तर:
तत्सम शब्द-मूल्य, निकट, मूर्ति, स्नेह, घड़ी, देहली, किबाड़, सौं, चूंघट।

प्रश्न 2.
निम्नलिखित पंक्तियों में प्रयुक्त अलंकार, उनके सामने दिए गए विकल्पों में से छाँटकर लिखिए
(अ) घट की न औघट की, घाट की न घर की। (यमक, श्लेष, अनुमास)
उत्तर:
अनुप्रास।

(आ) छाजत छबीले छिति छहरि हरा के छोर। (अनुप्रास, यमक, श्लेष)
उत्तर:
अनुप्रास।

(इ) ज्यों-ज्यों निहारिए नेरे डै नैनहिं। त्यों-त्यों खरी निकरै सी निकाई। (उपमा, पुनरुक्ति, रूपक)
उत्तर:
पुनरुक्ति।

(ई) एक घरी घन से तन सौं, अँखियान घनो घनसार सौ दैगो। (उपमा, रूपक, उत्प्रेक्षा)
उत्तर:
उपमा।

प्रश्न 3.
काव्य में भाव-सौन्दर्य और शब्द विन्यास का अन्योन्याश्रित सम्बन्ध रहता है, एक के बिना दूसरे की कल्पना करना कठिन हो जाता है। ऐसे स्थल मतिराम जैसे कवियों की रचनाओं में कलात्मक उपलब्धि की दृष्टि से बहुत श्रेष्ठ बन पड़े हैं। ऐसा ही भाव सौन्दर्य और शब्द सौन्दर्य का उदाहरण देखिए-
“मान रहोई नहीं मनमोहन मानिनी होय सो मनायो।”
इस प्रकार के अन्य उदाहरण इस संकलन से चुनकर लिखिए।
उत्तर:
(1) को बिन मोल बिकात नहीं मतिराम लहै मुसकानि मिठाई।
(2) काहे को सौंहे हजार करौ, तुम तो कबहूँ अपराध न ठायो।
सोवन दीजै, न दीजै हमें दु:ख, यों ही कहा रसवाद बढ़ायो।।
(3) लाल विलोचनि कौलनि सौं मुसकाइ इतै अरुझाइ चितैगो।
एक घरी घन से तन सौं अँखियान घनो घनसार सो दैगो।
(4) वा मुख की मधुराई कहा कहाँ ? मीठी लगै अँखियान लुनाई।

प्रश्न 4.
पद्माकर के संकलित छन्दों में से रूप घनाक्षरी छन्द को पहचानकर लिखिए।
उत्तर:
लक्षण-वर्ण संख्या 32 चरण के अन्त में गुरु और लघु (51) तथा यति 16, 16 पद।
भौरन को गुंजन विहार वन कुंजन में,
मंजुल मलहारन को गावनो लगत है।
कहैं ‘पद्माकर’ गुमान हूँ ते मानहूँ ते
प्राण हूँ नैं प्यारो मनभावनो लगत है।
भौरन कौ सोर घनघोर चहुँ ओर न।
हिंडोरन को वृन्द छवि छावनो लगत है।
नेह सरसावन में मेह बरसावन में,
सावन में झूलियों सुहावनो लगत है।।

पद्माकर के छन्द भाव सारांश

प्रस्तुत पदों में पद्माकर ने श्रीकृष्ण और राधा को प्रेमी-प्रेमिका के रूप में चित्रित करके उनकी शृंगारिक चेष्टाओं का हृदयस्पर्शी वर्णन किया है। यहाँ बताया गया है कि श्रीकृष्ण फाग खेलते हैं, राधा वह दृश्य देखती हैं। फाग का अबीर तो झड़ जाता है किन्तु कृष्ण की छवि आँखों से धोए नहीं धुलती। मोहन की बाँसुरी सुनकर राधा सुध-बुध खो बैठती है। सावन के झूलों में राधा-कृष्ण का प्रेम विकसित होता है। पद्माकर ने राधा-कृष्ण के प्रेम की दशा का अत्यन्त मनोवैज्ञानिक, सूक्ष्म और हृदयग्राही चित्र प्रस्तुत किया है।

पद्माकर के छन्द संदर्भ-प्रसंग सहित व्याख्या

[1] एकै संग धाय नन्दलाल औ गुलाल दोऊ।
दृगनि गए जुभरि आनन्द मढ़े नहीं।
धो-धोइ हारी पद्माकर, तिहारी सौं।
अब तो उपाय एकौ चित पै चट्टै नहीं।
कैसी करो कहाँ जाऊँ, कासौ कहौं कौन सुने।
कोऊ तो निकासौ जासौ दरद बढ़े नहीं॥
ऐरी मेरी वीर ! जैसे तैसे इन आँखनि तें।
कढिगो अबीर पै अहीर तो कट्टै नहीं। (2010, 13)

शब्दार्थ :
संग = साथ; धाय = दौड़कर; गुलाल = अबीर; दोऊ = दोनों; दुगनि = नेत्रों में, आँखों में; तिहारी = तुम्हारी; कासौ = किससे; कोऊ = कोई; निकासौ = निकाले; जासौ = जिससे; दरद = पीड़ा; कढ़िगो = निकलेगा।

सन्दर्भ :
प्रस्तुत छन्द हमारी पाठ्य-पुस्तक के ‘प्रेम और सौन्दर्य’ पाठ के ‘पद्माकर के छन्द’ शीर्षक से अवतरित हैं। इसके रचयिता पद्माकर हैं।

प्रसंग :
प्रस्तुत पद्य में गोपियों एवं श्रीकृष्ण के फाग (होली) खेलने का वर्णन किया गया है।

व्याख्या :
फाग खेलते समय गुलाल उड़ रहा है। इसके फलस्वरूप श्रीकृष्ण एवं गुलाल चारों ओर धूम मचा रहे हैं। नेत्रों में जो आनन्द भर गया है। वह समा नहीं रहा है। गोपी कह रही है कि हे सखी ! तुम्हारी शपथ खाकर कहती हूँ कि आँखों को धो-धोकर हार गई और अब तो कोई उपाय शेष नहीं बचा है। अब मैं अपनी व्यथा को कैसे दूर करूँ, किस स्थान पर जाऊँ, किससे कहूँ, कोई सुनने वाला भी नहीं है। अब कोई तो मेरी आँखों से इसे निकाले जिससे दर्द नहीं बढ़े। हे मेरी सखी ! मैंने यत्न करके किसी प्रकार आँखों से गुलाल को तो निकाल लिया किन्तु जो आँखों में बसा हुआ अहीर अर्थात् श्रीकृष्ण है वह किसी भाँति नहीं निकल रहा।

काव्य सौन्दर्य :

1. शृंगार रस, ब्रजभाषा, माधुर्य गुण, सरस और ललित शब्दावली का प्रयोग।
2. कैसी करो-पंक्ति में अनुप्रास अलंकार है।

[2] आई संग आलिन के ननद पठाई नीठि।
सोहति सुहाई सीस ईडुरी सुघट की।
कहै पद्माकर गम्भीर, जमुना के तीर।
नीर लागी भरन नवेली नेह अरकी।
ताही समै मोहन सु बाँसुरी बजाई।
तामै मधुर मलार गाई ओर बंसीवट की।
तल लगि लटकी रहीं न सुधि पूंघट की।
घट की न औघट की घाट की न घर की।

शब्दार्थ :
आलिन = सखियों; सोहति = सुन्दर लगती है, सुशोभित होती है; सीस= सिर; ईडुरी= सिर पर रखने की; नीर = जल; नवेली = नई; नेह = स्नेह; ताही = उस; समै = समय, तामै = उसमें; मलार = गीत; सुधि = याद, स्मृति।

सन्दर्भ :
पूर्ववत्।

प्रसंग :
यहाँ पर कवि ने यमुना तट पर पानी भरने आई गोपिका की कृष्ण की बाँसुरी सुनने के बाद हुई मनोदशा का वर्णन किया है।

व्याख्या :
हे सखी ! मैं सखियों के साथ पनघट पर आई हूँ, मुझे मेरी ननद ने समझा-बुझाकर भेजा है। सिर पर घट रखने की ईडुरी शोभित हो रही है। पद्माकर कहते हैं कि गहरी यमुना के किनारे नई नवेली नवयुवती पानी भरने लगी उसका हृदय कृष्ण के प्रेम से भरा हुआ था। उसी समय श्रीकृष्ण ने मधुर स्वरों में बाँसुरी बजाई। उन्होंने वंशीवट की ओर मुँह करके मधुर मल्हार गाना शुरू किया। तब वह गोपी जैसी स्थिति में थी वैसी ही रह गई। उसने अपने घूघट को भी नहीं सम्भाला, न तो उसे घट भरने की सुध रही, न ही घाट की और न घर का ही ज्ञान रह गया। वह तो बंशी की धुन में मग्न हो गयी।

काव्य सौन्दर्य :

1. शृंगार रस, माधुर्य गुण, ब्रजभाषा।
2. सोहति सुहाइ………..और घट की न और घर की…………पंक्तियों में अनुप्रास अलंकार है।
3. कोमलकान्त पदावली का प्रयोग है।

[3] भौरन को गुंजन विहार वन कुंजन में।
मंजुल मलहारन को गावनो लगत हैं।
कहै पद्माकर गुमान हूँ तो मानहुँ ते।
प्राण हूँ मैं प्यारो मन भावनों लगत है।
भोरन को सोर घनघोर चहुँ ओरन।
हिंडोरन को वृन्द छवि छावनो लगत है।
नेह सरसावन में मेह बरसावन में।
सावन में झूलियों सुहावनो लगत है।।

शब्दार्थ :
भौरन = भँवरे; गुंजन = आवाज; विहार = विचरण करना; वन कुंजन = उपवन में; मंजुल = सुन्दर; मलहारन = एक प्रकार के गीत; गावनो = गाते हैं; मन भावनों = मन को अच्छा लगने वाला; भोरन = प्रातः; सोर = शोर, कोलाहल; चहुँ = चारों; ओरन = ओर; हिंडोरन = झूले वृन्द= समूह; मेह= वर्षा; सावन = एक माह का नाम; सुहावनो लगतं = सुन्दर लगना, अच्छा लगना।

सन्दर्भ :
पूर्ववत्।

प्रसंग:
यहाँ पर कवि ने सावन के माह में गोपियों के झूला झूलने का चित्रण किया है।

व्याख्या :
गोपियाँ कहती हैं कि भौरों का गूंजना, कुञ्जवनों में विहार करना, सुन्दर मधुर मल्हारों को गाना अच्छा लगता है। पद्माकर कहते हैं कि अपने स्वाभिमान अथवा मान-सम्मान की अपेक्षा मनभावन कृष्ण प्यारा लगता है जो प्राणों से भी प्यारा है। भ्रमरों का गुंजन और बादलों का घनघोर गर्जन है। ऐसे मनमोहक वातावरण में झूलों के समूह अत्यधिक सुन्दर प्रतीत हो रहे हैं। सावन के महीने में जबकि स्नेह की वर्षा हो रही हो और मेघों की वर्षा हो रही है, ऐसे समय में झूला-झूलना अत्यन्त सुखकर लगता है।

काव्य सौन्दर्य :

1. शृंगार रस, माधुर्य गुण, ब्रजभाषा कोमलकान्त पदावली।
2. मंजुल मलहारन में अनुप्रास अलंकार है।
3. प्रिय की मनोदशा का मनोवैज्ञानिक चित्रण है।

[4] घर न सुहात न सुहात वन बाहिर है।
बागन सुहात जो खुसाल सुख बोही सों।
कहै पद्माकर घनेरे धन धाम त्यौं ही।
चैन न सुहात चाँदनी हूँ जोग जोही सों।
साँझ हूँ सुहात न सुहात दिन माँझ कछु।
ब्याही यह बात सो बखानत हो तोही सों।
साँझ हूँ सुहात न सुहात परभात आली।
जब मन लागि जात काई निरमोही सौं।।

शब्दार्थ :
सुहात = अच्छा; बागन = बगीचा; खुसाल = प्रसन्न; सुख बोही = प्रसन्नता से सराबोर; धन = सम्पत्ति; धाम = घर; जोग = योग; बखानत = वर्णन करना; तोही = तुझसे; परभात = प्रातः, आली = सखि; काई = कोई; निरमोही = निष्ठुर।

सन्दर्भ :
पूर्ववत्।

प्रसंग :
यहाँ पर कवि ने बताया है कि श्रीकृष्ण के प्रेम में गोपियाँ आकण्ठ निमग्न हैं। उनकी मनोदशा इस प्रकार है।

व्याख्या :
गोपियाँ कहती हैं कि श्रीकृष्ण के प्रेम के समक्ष उन्हें न घर, न बाहर, कहीं अच्छा नहीं लगता है। जो बाग पहले प्रसन्नता देते थे जिनमें बहुत सुख प्राप्त होता था वह अब नहीं मिलता। पद्माकर कहते हैं कि इसी प्रकार न तो धन सुहाता है और न आलीशान महल ही सुहाते हैं। चाँदनी में भी सुख का अनुभव नहीं होता है। न संध्या काल रुचिकर लगता है और न दिन अच्छा लगता है। हे सखी ! यह बात मैं तुझसे ही कहती हूँ कि न साँझ सुहाती है, न प्रभात सुहाता है जब मन किसी निष्ठुर से लग जाता है अर्थात् मेरा मन उस निष्ठुर श्रीकृष्ण से लग गया है। अब उसके बिना मुझे संसार की कोई वस्तु अच्छी नहीं लगती है।

काव्य सौन्दर्य :

1. शृंगार रस है। माधुर्य गुण तथा ब्रजभाषा के ललित शब्दों का प्रयोग है।
2. साँझ हूँ सुहात न पंक्ति में अनुप्रास अलंकार है।
3. विरह की मनोदशा का मनोवैज्ञानिक चित्रण है।

[5] “आरस सो आरत सम्हारत न सीस-पट,
गजब गुजारति गरीवन की धार पर।
कहें पद्माकर सुरासो सरसार तैसे,
बिथुरि बिराजै बार हीरन के हार पर।
छाजत छबीले छिति छहरि हरा के छोर,
भोर उठि आई केलि-मन्दिर के द्वार पर।
एक पग भीतर औ एक देहरी पै धरै,
एक कर कंज, एक कर है किबार पर।।”

शब्दार्थ :
आरस = आलस्य; आरत = आर्त्त; सीस = सिर; पट = वस्त्र; बिथुरि = बिखरा हुआ; गजब = अनोखा, अद्भुत; गुजारति = व्यतीत करती; हीरन = हीरा एक रत्न; हार = माला, छिति = भूमि; भोर = प्रात:काल; केलि = क्रीड़ा; पग = पाँव; देहरी = देहली; कर = हाथ; किबार = किबाड़।

सन्दर्भ :
पूर्ववत्। प्रसंग-यहाँ कवि ने नायिका की विरह अवस्था का वर्णन किया है।

व्याख्या :
नायिका नायक के विरह में इतनी व्यग्र है कि उसे अपने तन की सुध-बुध नहीं रही है। दुःख के कारण निढाल हुई नायिका अपने शीश के वस्त्र को नहीं सम्भाल पा रही है। वह बेचारी अपने समय को अत्यन्त दुःखावस्था में व्यतीत करती है। पद्माकर कहते हैं कि नायिका जैसे मद्य के रस में डूबी हुई हो। उसे अपने शरीर का होश नहीं रहा है। उसके बाल बिखरे हुए हैं और हीरे के हार पर अस्त-व्यस्त से पड़े हुए हैं। उसके बाल पृथ्वी के छोर तक पहुंच रहे हैं। वह प्रातः होते ही अपने क्रीड़ा-मन्दिर के द्वार पर आकर खड़ी हो गई है। उसका एक पैर घर के भीतर है और एक देहली पर रखा हुआ है। उसके एक हाथ में कमल का फूल है और दूसरा हाथ उसने किबाड़ पर रखा हुआ है।

काव्य सौन्दर्य :

1. प्रस्तुत पद्य में प्रोषितपतिका नायिका की विदग्धावस्था का मार्मिक और मनोवैज्ञानिक चित्रण किया गया है।
2. ब्रजभाषा है, माधुर्य गुण और शृंगार रस के विरह पक्ष की व्यंजना हुई है।
3. आरस सो आरत, गजब गुजारति, गरीवन, सुरासो सरसार, बिथुरि बिराजै बार, छाजतछबीले, छिति-छहरि आदि में अनुप्रास अलंकार है।

मतिराम के छन्द भाव सारांश

प्रेम और शृंगार के वर्णन में मतिराम अद्वितीय हैं। उन्होंने अपने काव्य में राधा-कृष्ण के प्रेम, सौन्दर्य, शील, चेष्टाओं अनुरागमयी लीलाओं और परस्पर मान-मनुहार का हृदयग्राही चित्र प्रस्तुत किया है। नायक-नायिका के मिलन-वियोग का छवि ने सूक्ष्म और एकान्तिक चित्रण किया है।

मतिराम के छन्द संदर्भ-प्रसंग सहित व्याख्या

[1] कुन्दन को रंग फीको लागै, झलकै अति अंगन चारु गुराई।
आँखिन में अलसानि चितौन में मंजु बिलासन की सरसाई।।
को बिन मोल बिकात नहीं मतिराम लहै मुसकानि मिठाई।
ज्यों ज्यों निहारिए नेरे है नैनहि, त्यों त्यों खरी निकरै सी निकाई।। (2009, 17)

शब्दार्थ :
कुन्दन = सोना; फीकौ = रंगहीन, प्रभावहीन, कान्तिहीन; झलकै = कुछ आभास होना, दिखलाना; चारु = सुन्दर; गुराई = गोरापन; आँखिन = नेत्रों में; अलसानि = आलस्य होना; चितौन = चितवन, मंजु = सुन्दर; बिलासन = शोभा देना, योग देना; सरसाई = सुन्दरता, शोभा; बिन = बिना; मोल = मूल्य; बिकात = बिक जाना होना; निहारिए = देखिए; नेरे = समीप; नैनहिं = नेत्रों को, निकाई = सुन्दरता, अच्छाई।

सन्दर्भ :
प्रस्तुत पद्य ‘प्रेम और सौन्दर्य’ पाठ के ‘मतिराम के छन्द’ शीर्षक से उद्धत है। इसके रचयिता मतिराम हैं।

प्रसंग :
प्रस्तुत पद में कवि ने नायिका के शारीरिक सौष्ठव का वर्णन किया है।

व्याख्या :
कवि कहता है कि नायिका के अंग-अंग में झलकने वाले सौन्दर्य के आगे स्वर्ण (सोने) की छवि भी फीकी लगती है। उसके नेत्र अलसाए हुए हैं और उसकी चितवन में मधुर विलास का सौन्दर्य है। मतिराम कहते हैं कि उसकी मुस्कान इतनी मधुर है कि देखने वाला ऐसा कौन है जो बिना मोल नहीं बिक जाता है अर्थात् जो उसके सौन्दर्य को देखता है वही मोहित हो जाता है। जैसे-जैसे निकट जाकर उसके नेत्रों को निहारो वैसे-वैसे ही उसकी सुन्दरता और अधिक बढ़ती जाती है।

काव्य सौन्दर्य :

1. शृंगार रस, माधुर्य गुण, ब्रजभाषा है।
2. कुन्दन को रंग फीकौ लगै………में व्यतिरेक अलंकार है।
3. आँखिन अलसान ज्यों-ज्यों, त्यों-त्यों में अनुप्रास अलंकार है।
4. बिन मोल बिकात’ में लोकोक्ति का प्रयोग है।

[2] कोऊ नहीं बरजै मतिराम रहो तितही जितही मन भायो।
काहे कौ सौहे हजार करो, तुम तो कबहूँ अपराध न ठायो।।
सोवन दीजै, न दीजै हमें दुःख, यों ही कहा रसवाद बढ़ायो।
मान रहोई नहीं मनमोहन मानिनी होय सो मानै मनायो।। (2009)

शब्दार्थ :
बरजै = मना करना, रोकना; मन भायो = मन को अच्छा लगना; कबहूँ = कभी; अपराध = अनुचित कार्य; सोवन = सोने का भाव; दीजै = देना; दुःख = अवसाद; मान = मर्यादा; मनमोहन = मन को अच्छा लगना; मानिनी = हठी।

सन्दर्भ :
पूर्ववत्।

प्रसंग :
यहाँ कवि ने मानिनी नायिका का वर्णन किया है जो श्रीकृष्ण को उपालम्भ दे रही है।

व्याख्या :
मतिराम कहते हैं कि नायिका नायक से कह रही है कि तुम्हें कोई भी नहीं रोक रहा है। तुम्हारी जहाँ इच्छा हो तुम वहीं निवास करो। तुम व्यर्थ में हजारों शपथ क्यों खा रहे हो ? तुमने तो कभी कोई अपराध ही नहीं किया है। आप हमें सोने दीजिए हमें कोई दु:ख मत पहुँचाइए। तुम व्यर्थ में ही प्रेम में विवाद क्यों बढ़ा रहे हो। हे मनमोहन ! जब हमने तुम्हारे प्रेम में समर्पण कर दिया है तो मान तो पहले ही नहीं रहा। ये तो कोई मानिनी हो उसे मनाया जाए। मैं कोई मानिनी नहीं हूँ।

काव्य सौन्दर्य :

1. नायिका की नायक के प्रति खीझ का मनोवैज्ञानिक चित्रण है।
2. मनमोहन मानिनी में अनुप्रास अलंकार है।
3. वक्रोक्ति अलंकार का सुन्दर प्रयोग है।
4. माधुर्य गुण, ब्रजभाषा में कोमलकान्त पदावली का प्रयोग किया है।

[3] मोर-पखा ‘मतिराम’ किरीट मनोहर मूरति सौ मन लैगो।
कुण्डल डोलनि, गोल कपोलनि बोल सनेह के बीज से बैगो।।
लाल बिलोचनि कौलनि सो मुसकाइ इतै अरुझाइ चितैगो।
एक घरी घन से तन सौं अँखियान घनो घनसार सो दैगो।।

शब्दार्थ :
किरीट = मुकुट; मनोहर = सुन्दर; कुण्डल = कान का आभूषण; डोलनि = हिलना; कपोलनि = गालों पर; सनेह = प्रेम; मुसकाइ = मुस्कराना; इतै = यहाँ, अरुझाइ = उलझाना; घरी = घड़ी; घन = मेघ; घनो = गहरा; तन = शरीर; अँखियान = आँखों से।

सन्दर्भ :
पूर्ववत्।

प्रसंग :
यहाँ नायिका का श्रीकृष्ण के प्रति अनन्य प्रेम का चित्रण है।

व्याख्या :
नायिका कहती है कि वह श्रीकृष्ण जिन के सिर पर मोरपंखी से युक्त मुकुट सुशोभित है, वह मनोहर मूर्ति वाले श्रीकृष्ण मेरा मन ले गये हैं। उनके कानों में कुण्डल हिल रहे हैं, गाल गोलाकार हैं। वे बोलकर मानो स्नेह के बीज बो गये हैं। लाल नेत्रों के विलास से मुस्कराकर वह मेरा चित्त अपने में उलझा गये हैं। एक घड़ी के मिलन से मेघ के सदृश आनन्द देकर वह मेरे नेत्रों को घनघोर वर्षा से पूर्ण कर गये हैं अर्थात् उसके विरह में मेरी आँखें निरन्तर बरसती रहती हैं।

काव्य सौन्दर्य :

1. वियोग शृंगार का वर्णन है। नायिका की विरह व्यथा का भावपूर्ण चित्रण है।
2. ब्रजभाषा सरल, सरस एवं मधुर पदावली से युक्त है।
3. घनो घनसार …….. अनुप्रास अलंकार है।

[4] मोर-पखा ‘मतिराम’ किरीट में कण्ठ बनी वनमाल सुहाई।
मोहन की मुसकानि मनोहर कुण्डल डोलनि मैं छवि छाई।।
लोचन लोल बिसाल बिलोकनि को न बिलोकि भयो बस माई।
वा मुख की मधुराई कहाँ कहौं? मीठी लगै अँखियान लुनाई।। (2008)

शब्दार्थ :
कण्ठ = गले; सुहाई = अच्छी लगी; मोहन = श्रीकृष्ण; मनोहर = सुन्दर; छवि = रूप; छाई = फैली; लोचन = नेत्र; बिसाल = बड़े; बिलोकनि = देखना; मुख = मुँह; वा = उस; मीठी = मधुर।

MP Board Class 11th Hindi Solutions

MP Board Class 11th Hindi Swati Solutions गद्य Chapter 12 आदि शंकराचार्य

आदि शंकराचार्य अभ्यास

आदि शंकराचार्य अति लघु उत्तरीय प्रश्न

प्रश्न 1.
शंकर का जन्म कहाँ हुआ था?
उत्तर:
शंकर का जन्म भारत के केरल प्रान्त में पूर्णा नदी के किनारे बसे एक छोटे से गाँव कालड़ी में हुआ था।

प्रश्न 2.
शंकर के माता-पिता का नाम बताइए।
उत्तर:
शंकर की माताजी का नाम ‘आर्यम्बा’ तथा पिताजी का नाम ‘शिवगुरु’ था।

प्रश्न 3.
ओंकारेश्वर में शंकर ने किससे दीक्षा ली?
उत्तर:
मध्य प्रदेश के प्रसिद्ध तीर्थस्थल ओंकारेश्वर में शंकर ने गौड़पादाचार्य के शिष्य गोविन्दपाद से दीक्षा ली।

प्रश्न 4.
‘तत्वोपदेश’ नामक ग्रन्थ में किसके उपदेश संग्रहीत हैं?
उत्तर:
‘तत्वोपदेश’ नामक ग्रन्थ में शंकराचार्य द्वारा दीक्षा के समय मंडन मिश्र को दिये गये उपदेश संग्रहीत हैं।

प्रश्न 5.
शंकराचार्य और मण्डन मिश्र के बीच हुए शास्त्रार्थ का निर्णायक कौन था?
उत्तर:
शंकराचार्य और मण्डन मिश्र के बीच हुए शास्त्रार्थ का निर्णायक मंडन मिश्र की विदुषी पत्नी उभय भारती थीं।

आदि शंकराचार्य लघु उत्तरीय प्रश्नोत्तर

प्रश्न 1.
कनकधारा स्त्रोत किसके लिए और क्यों प्रसिद्ध है?
उत्तर:
एक दिन गुरुकुल में अध्ययन के समय ब्रह्मचारी शंकर भिक्षा के लिए निकले। एक झोंपड़ी के सामने पहुँचकर जब उन्होंने भिक्षा की गुहार लगायी तो गृहिणी के पास ब्रह्मचारी को दान में देने के लिए घर में मात्र एक सूखा आंवला था। गृहिणी ने दीनतापूर्वक वह सूखा आंवला शंकर के भिक्षा पात्र में रख दिया। भिक्षा पाकर शंकर को उस घर की दयनीय अवस्था का ज्ञान हो गया। उन्होंने धन और सम्पत्ति की अधिष्ठात्री देवी माँ महालक्ष्मी से प्रार्थना की। लक्ष्मीजी शंकर की स्तुति से प्रसन्न हुईं। कहा जाता है कि आकाश से सोने के आंवलों की वर्षा होने लगी। वह स्तुति कनकधारा स्त्रोत के रूप में प्रसिद्ध है।

प्रश्न 2.
शंकर को संन्यास ग्रहण करने की आज्ञा माँ से कब, किस स्थिति में प्राप्त हुई?
उत्तर:
एक दिन माँ के साथ स्नानादि के लिए शंकर पूर्णा नदी गये थे। माँ स्नान कर किनारे पर खड़ी थी कि उसने शंकर की चीख सुनी। माँ, ने देखा कि कमर तक पानी में डूबे शंकर को कोई अन्दर की ओर खींच रहा है। शंकर ने कहा माँ, मगर मुझे पानी में खींच रहा है, लगता है भगवान मुझे आपसे दूर कर रहे हैं। आप मुझे संन्यास ग्रहण करने की आज्ञा दें, संभव है मगर मेरा पैर छोड़ दे। तब माँ ने शंकर को संन्यास ग्रहण करने की आज्ञा दी।

प्रश्न 3.
अद्वैत का सार लिखिए।
उत्तर:
एक बार योगाचार्य गोविन्दपाद द्वारा शंकर से उसका परिचय पूछने पर शंकर ने उत्तर दिया-“मैं पृथ्वी नहीं हूँ, जल भी नहीं, तेज भी नहीं, न आकाश, न कोई इन्द्रिय अथवा उनका समूह भी। मैं तो इन सबसे अवशिष्ट केवल जो परम तत्व शिव है, वहीं हूँ।” वास्तव में यह मात्र शंकर का परिचय नहीं अपितु अद्वैत का सार ही है।

प्रश्न 4.
शंकर ने ‘मनीषपंचक’ नाम से विख्यात पाँच श्लोकों की रचना किन परिस्थितियों में की थी?
उत्तर:
वाराणसी में एक दिन शंकर से शंकराचार्य बन चुके शंकर अपने शिष्यों के साथ गंगा स्नान को जा रहे थे। अचानक एक चांडाल अपनी पत्नी व चार कुत्तों के साथ सामने से आ रहा था। उसे देखते ही शिष्यों ने उसे एक ओर हट जाने के लिए कहा, ताकि उसका किसी से स्पर्श न हो जाये। यह सुनकर चांडाल सपरिवार वहीं खड़ा हो गया। उसने पूछा-महात्मा आप किसे दूर हटने की आज्ञा दे रहे हैं? मेरे शरीर को या मेरी आत्मा को? शरीर तो नश्वर है, आत्मा सर्वव्यापी है। आप अद्वैत सिद्धान्त में यही उपदेश दे रहे हैं कि ब्राह्मण और चांडाल में कोई अंतर नहीं है। तब आपमें और मुझमें अन्तर कैसा?

शंकराचार्य शांति से चांडाल की बात सुनते रहे। उनको अपने शिष्य की भूल पर बड़ा पश्चाताप हुआ। उसी समय उन्होंने मनीषपंचक नाम से प्रसिद्ध पाँच श्लोकों की रचना की।

प्रश्न 5.
शंकर ने किस विद्वान और विदुषी (पति-पत्नी) से शास्त्रार्थ किया था? उसका क्या परिणाम हुआ?
उत्तर:
शंकर ने माहिष्मति निवासी विश्वनाथ मिश्र उर्फ मंडन मिश्र और उनकी विदुषी पत्नी उभय भारती से शास्त्रार्थ किया। परिणामस्वरूप शंकर से ये दोनों पराजित हो गये और दोनों ने शंकर से संन्यास की दीक्षा ले ली।

आदि शंकराचार्य दीर्घ उत्तरीय प्रश्नोत्तर

प्रश्न 1.
शंकर ने संन्यास मार्ग अपनाने का निश्चय क्यों किया?
उत्तर:
शंकर के गुरुकुल में अध्ययन करते समय ही उनके पिता शिवगुरु का देहान्त हो गया। पिता की मृत्यु से दुःखी शंकर के मन में विचार आया कि जब एक दिन यह नाशवान शरीर छूटना ही है तो कीड़े-मकोड़ों की तरह साधारण जीवन क्यों जिया जाए क्यों न किसी महान लक्ष्य को लेकर सत्य के मार्ग पर चला जाए। फलस्वरूप सांसारिक बंधनों से मुक्त रहकर शंकर ने समाज जागरण के लिए संन्यास मार्ग पर चलने का निश्चय किया।

प्रश्न 2.
आदि शंकराचार्य द्वारा स्थापित मठों के नाम लिखिए।
उत्तर:
आदि शंकराचार्य ने देश में वेदाध्ययन की परम्परा को पुनः जीवंत करने के उद्देश्य से देश की चारों दिशाओं में चार मठों-काञ्ची, बद्रीनाथ, जगन्नाथपुरी और शारदामठ की स्थापना की। वेदों के प्रचार-प्रसार के निमित्त प्रत्येक मठ को एक वेद के अध्ययन-अध्यापन का दायित्व सौंपा। प्रत्येक मठ का एक देवी-देवता निश्चित किया।

प्रश्न 3.
गोविन्दपाद कौन थे? उन्होंने किसे विधिवत संन्यास की दीक्षा दी थी?
उत्तर:
गुरुकुल में शिक्षा ग्रहण करने के बाद शंकर देश की परिस्थितियों का अवलोकन करते हुए उत्तर दिशा में चल पड़े। पैदल यात्रा करते हुए वह मध्य प्रदेश के सुविख्यात तीर्थस्थल ओंकारेश्वर पहुंचे।

ज्योतिर्लिंग के दर्शन कर वे माँ नर्मदा के घाट पर बैठे थे कि उन्हें सूचना मिली कि समीप ही एक गुफा में गौड़पादाचार्य के परमशिष्य एवं महान संत गोविन्दपाद तपस्यारत हैं। समाधिमग्न गोविन्दपादाचार्य के दर्शन से शंकर को अद्भुत शांति मिली। इस प्रकार यह कहा जा सकता है कि गोविन्दपाद महान आचार्य गौड़पादाचार्य के शिष्य थे और उन्होंने शंकर की असाधारण प्रतिभा को पहचाना और उन्हें अपना शिष्य स्वीकार कर विधिवत संन्यास की दीक्षा दी।

प्रश्न 4.
शृंगेरीमठ का प्रथम आचार्य किसे नियुक्त किया और क्यों?
उत्तर:
कुमारिलभट्ट के निर्देश पर शंकराचार्य उनके शिष्य मंडन मिश्र से शास्त्रार्थ करने माहिष्मती पहुँचे। वहाँ पर उन्होंने वेदों के प्रकाण्ड पण्डित मंडन मिश्र एवं उनकी विदुषी पत्नी उभय भारती को शास्त्रार्थ में पराजित किया। प्रतिज्ञानुसार पति-पत्नी दोनों ने शंकराचार्य से दीक्षा ली। दीक्षा के बाद मंडन मिश्र का नाम सुरेश्वराचार्य हो गया। शंकराचार्य ने मंडन मिश्र उर्फ सुरेश्वराचार्य की विद्वता के चलते उन्हें काञ्ची पीठ से सम्बद्ध शृंगेरी मठ का प्रथम अधिपति अर्थात् आचार्य नियुक्त किया।

प्रश्न 5.
शंकराचार्य के चरित्र की विशेषताओं का उल्लेख कीजिए।
उत्तर:
शंकराचार्य की प्रमुख चारित्रिक विशेषताएँ निम्नलिखित हैं-
(1) मेधावी शंकर बचपन से ही अत्यन्त अद्भुत मेधा के धनी थे। उनकी इस विलक्षण प्रतिभा से ऐसा प्रतीत होता था कि मानो वे शीघ्र ही ‘होनहार विरवान के होत चीकने पात’ वाली कहावत को चरितार्थ करेंगे। माता-पिता ने उन्हें अध्ययन के लिए गुरुकुल भेजा। वहाँ भी शंकर ने ‘अल्पकाल बहु विद्या पाई’ जैसी उक्ति को चरितार्थ किया। उनके सम्पर्क में आने वाले उनकी प्रतिभा और तेजस्वी व्यक्तित्व को देखते ही हतप्रभ हो जाते थे। मात्र 5 वर्ष की आयु में ही उन्हें वेदों के अध्ययन के लिए गुरुकुल भेजा गया था।

(2) तीव्र स्मरण शक्ति-गुरुकुल में शंकर पढ़ाये गये पाठ इत्यादि को एक बार में समझ जाते थे और उसे लम्बे समय तक स्मृति में अंकित कर लेते थे। वास्तव में, वे श्रुतिधर थे अर्थात कोई भी बात मात्र सनने पर ही उन्हें कण्ठस्थ हो जाती थी।

(3) करुणामयी व्यवहार-एक बार गुरुकुल के दिनों में जब वह भिक्षा प्राप्ति के लिए एक निर्धन की झोंपड़ी के द्वार पर पहुँचे और भिक्षा के लिए गुहार लगाई तो उस झोंपड़ी की गृहिणी ने उन्हें देखा और उन्हें कुछ न कुछ दान देना चाहा। किन्तु निर्धनता के कारण उसके पास एक सूखे आंवले के अतिरिक्त भिक्षा देने के लिए कुछ भी न था। उसने वह सूखा आंवला शंकर के भिक्षा-पात्र में रख दिया। भिक्षा पाकर शंकर को उस घर की दयनीय अवस्था का भान हुआ। वह करुणा से भर उठे। उन्होंने लक्ष्मी से प्रार्थना की ताकि उस झोंपड़ी की निर्धनता दूर हो सके। इस प्रकार यह कह सकते हैं कि उनका मन अत्यंत करुणामयी था।

(4) आज्ञाकारी एवं सेवाकारी सुपुत्र शंकर अपने माता-पिता के आज्ञाकारी सुपुत्र थे। बचपन में ही उनके सिर से उनके पिता का साया उठ गया। पिता की असमय मृत्यु पर विचलित हो बालक शंकर ने सांसारिक बंधनों में न बँधकर समाज के जागरण के लिए संन्यासी बनने की ठानी और इसके लिए उन्होंने अपनी माँ की अनुमति लेना ही श्रेष्ठ माना। संन्यासी जीवन के दौरान जब उन्हें अपनी माँ की अस्वस्थता का पता चला तब वह एक सेवाकारी सुपुत्र की तरह अविलम्ब अपनी माँ के पास लौट आये और अन्तिम समय तक अपनी माँ की सेवा-सुश्रुषा की। माँ के देहान्त होने पर प्रचलित मान्यताओं के विपरीत एक संन्यासी होने के बाद भी उन्होंने अपनी माँ का अन्तिम संस्कार स्वयं किया।

(5) प्रकाण्ड ज्ञानी-शंकर को अत्यन्त छोटी आयु से ही वेदों का पूर्ण ज्ञान हो गया था। उन्होंने गोविन्दपाद को अपना गुरु बनाया और ज्ञान की ज्योति चारों ओर फैलाने के ध्येय के साथ सम्पूर्ण भारतवर्ष की यात्रा की। बड़े-बड़े विद्वान पंडित भी इनकी विद्वता से प्रभावित शंकर से शंकराचार्य के रूप में प्रतिष्ठित हुए। मात्र 12 वर्ष की अल्पायु में ही वे कई नामचीन विद्वानों से शास्त्रार्थ करने लगे थे। इसी क्रम में उन्होंने मंडन मिश्र और उनकी विदुषी पत्नी उभय भारती को शास्त्रार्थ में पराजित किया और दोनों को दीक्षा दी। उज्जैन प्रवास के समय शंकराचार्य ने कापालिकों के अमर्यादित आचरण को देखकर उनसे शास्त्रार्थ किया और उन्हें पराजित किया।

(6) महान वेद-प्रचारक वेदों के प्रचार-प्रसार के लिए उन्होंने देश के चार कोनों में मठों की स्थापना की और स्वयं आदि शंकराचार्य कहलाये। प्रत्येक मठ को एक वेद के अध्ययन-अध्यापन का दायित्व सौंपा गया। प्रत्येक मठ का एक प्रमुख देवी-देवता का निर्धारित किया। उनके शिष्यों की संख्या सहस्त्रों में थी। वे सभी सनातन धर्म के प्रचार के साथ-साथ सम्पूर्ण भारतवर्ष को एकता के सूत्र में बाँधने में रत रहे।

(7) ग्रंथों के रचनाकार-उन्होंने कई महान ग्रन्थों की रचना की और अनेक भक्ति स्त्रोतों को लिखा। इनमें कनकधारा स्त्रोत, मनीषपंचक तत्वोपदेश, प्रस्थान त्रयी भाष्य, नर्मदाष्टकम् इत्यादि प्रमुख हैं।

(8) निरहंकारी तथा विनम्र-एक बार शंकर वाराणसी में जब गंगा स्नान के लिए जा रहे थे तब अचानक एक चांडाल अपनी पत्नी व चार कुत्तों के साथ सामने से आ रहा था। शंकर के शिष्यों ने यह सोचकर कि वह कहीं किसी से छू न जाये, उसे एक ओर हटने के लिए कहा। इस पर शंकर ने अपने शिष्यों के द्वारा किये गये व्यवहार पर खेद प्रकट करते हुए चांडाल को अपना गुरु कहा। वास्तव में, कितना निरहंकारी तथा विनम्र था शंकराचार्य का स्वभाव। वह छोटे-से-छोटे को भी अपनाने को तैयार रहते थे, उससे सीख लेते थे और उसे उचित आदर देते थे।

आदि शंकराचार्य भाषा अध्ययन

प्रश्न 1.
निम्नलिखित शब्दों में से उपसर्ग और प्रत्यय बाँटकर लिखिएअसाधारण, दयनीय, अश्रद्धा, विनम्र, प्रखर, निश्चयी, सांसारिक, अलौकिक।
उत्तर:

प्रश्न 2.
निम्नलिखित पदों में समास पहचान कर लिखिएपति-पत्नी, स्वर्गवास, प्रत्येक।
उत्तर:

प्रश्न 3.
दिए गए शब्दों का संधि-विच्छेद कर संधि का नाम लिखिएवेदाध्ययन, संन्यास, चिंतातुर, संकल्प।
उत्तर:

प्रश्न 4.
निम्नलिखित मुहावरों का वाक्यों में प्रयोग कीजिए-
हाथ बंटाना, खाली हाथ न लौटना, महासमाधि में लीन होना।
उत्तर:
हाथ बंटाना (सहयोग करना) – प्रत्येक विद्यार्थी को विद्यालय के कार्यों में हाथ बँटाना चाहिए।
खाली हाथ न लौटना (बिना कुछ लिए वापिस न होना) – प्रत्येक सद् गृहस्थ की इच्छा होती है कि याचक उसके घर से खाली हाथ न लौटे।
महासमाधि में लीन होना (प्राणांत) – शंकर अपने शिष्यों को उपदेश देते हुए महासमाधि में लीन हो गए।

प्रश्न 5.
निम्नलिखित वाक्यांशों के लिए दिए गए विकल्पों में से सही एक शब्द लिखिए-
(अ) जो क्रम के अनुसार हो-
(1) यथाक्रम
(2) क्रमबद्ध
(3) सूची
(4) तालिका।
उत्तर:
(1) यथाक्रम

(ब) आदि से अन्त तक-
(1) अन्तिम
(2) आद्यक्षर
(3) आद्यन्त
(4) आद्यादस्तक।
उत्तर:
(3) आद्यन्त

(स) जो छिपाने योग्य है-
(1) छिद्र
(2) गलती
(3) चरित्र
(4) गोपनीय।
उत्तर:
(4) गोपनीय।

(द) जो किए गए उपकार को नहीं मानता-
(1) कृतज्ञ
(2) कृतघ्न
(3) उपकारी
(4) अनुपकारी।
उत्तर:
(2) कृतघ्न

आदि शंकराचार्य पाठ का सारांश

‘आदि शंकराचार्य’ सुविख्यात साहित्यकार ‘श्रीधर पराड़कर’ की प्रयल लेखनी द्वारा जीवनी विधा में लिखित एक अत्यन्त मार्मिक, प्रेरक एवं प्रभावशाली रचना है। प्रस्तुत आलेख आदि शंकराचार्य और उनके जीवन-दर्शन का प्रतिबिम्ब है।

अनादिकाल से वेद-वेदान्त के प्रख्यात विद्वानों की जन्मस्थली एवं निवास स्थान रहे, भारत के केरल प्रान्त में पूर्णा नदी के किनारे बसे एक छोटे से गाँव कालड़ी’ में शंकर का जन्म हुआ। उनके पिता का नाम शिवगुरु एवं माता का नाम आर्यम्बा था। शंकर के दादाजी विद्याराम नंबूदरी वेदों के धुरंधर विद्वान थे।

शंकर बचपन से ही प्रतिभासम्पन्न एवं मेधावी थे। मात्र 5 वर्ष की बाल्यावस्था में ही उन्हें वेदों के अध्ययन के लिए गुरुकुल भेजा गया। शंकर श्रुतिधर थे। वह एक बार बताने पर ही पाठ समझ लेते थे। उन्होंने गुरुकुल में अल्पकाल में ही बहुत ज्ञान अर्जित कर लिया था। जो भी एक बार उनके सम्पर्क में आता था वह बिना उनसे प्रभावित हुए नहीं रहता था। गुरुकुल में शिक्षा प्राप्त करते हुए ही शंकर यह तथ्य जान चुके थे कि समाज ज्ञान के भण्डार वेदों के अनुसार आचरण नहीं कर रहा है। छोटी आयु में ही उनके पिता का देहान्त हो गया। इससे शंकर बहुत दुःखी हुए। उनके मन में विचार आया कि पिता की तरह उनका भी एक दिन जब यह नश्वर शरीर छूटना ही है तो क्यूँ न इसे किसी महान ध्येय की प्राप्ति के लिए लगाया जाये।

इन्होंने समाज के जागरण के लिए संन्यास मार्ग पर चलने का व्रत लिया। एकाकी जीवन जी रही माता आर्यम्बा से संन्यासी जीवन की अनुमति प्राप्त कर वे योग्य गुरु की खोज में देशाटन पर निकल गये। ओंकारेश्वर में उन्होंने गौड़पादाचार्य के शिष्य गोविन्दपाद को अपना गुरु बनाया और उनसे विधिवत् संन्यास की दीक्षा ली। गुरु गोविन्दपाद ने अपने प्रतिभावान शिष्य को ब्रह्मसूत्र, महावाक्य चतुष्टय एवं वेदान्त धर्म की सांगोपांग शिक्षा प्रदान कर धर्म प्रचार के सर्वथा योग्य बनाया। गुरु ने उन्हें अद्वैत का प्रचार करने की आज्ञा दी। इस बीच उन्हें माता की अस्वस्थता का समाचार ज्ञात हुआ। वे तुरन्त अपने गाँव कालड़ी के लिए चल पड़े। माताजी की अस्वस्थता में सेवा-सुश्रुषा की और उनके स्वर्गवास पर उनका अंतिम संस्कार किया। उन्होंने राष्ट्र कल्याण की भावना से कार्य कर रहे लोगों को संगठित करने का प्रण किया। इसकी शुरुआत के लिए उन्होंने भारत की आत्मा कहे जाने वाले नगर वाराणसी को चुना।

वाराणसी में विद्वान इनकी विद्वता से प्रभावित हुए। वे शंकर से शंकराचार्य के रूप में प्रतिष्ठित हुए। इस समय उनकी आयु मात्र 12 वर्ष की थी। यहीं उन्होंने ‘मनीषपंचक’ नाम से विख्यात पाँच श्लोकों की रचना की। अपनी विद्वता का परिचय देते हुए उन्होंने मंडन मिश्र और उनकी धर्मपत्नी विदुषी उभय भारती को शास्त्रार्थ में हराया। देशाटन करते हुए शंकराचार्य ने प्रमुख तीर्थों के दर्शन किये तथा सर्वस्य अद्वैत मत की विजय पताका फहरायी। शंकराचार्य सम्पूर्ण भारत को एकता के सूत्र में बाँधना चाहते थे। उन्होंने वेदान्त का भक्ति के साथ समन्वय कर अद्भुत कार्य किया।

आदि शंकराचार्य का देश के हृदयस्थल मध्यप्रदेश से गहरा सम्बन्ध रहा। ओंकारेश्वर में उन्होंने प्रस्थान त्रयी’ भाष्य तथा ‘नर्मदाष्टकम्’ स्त्रोत की रचना की। शंकराचार्य ने देश की चारों दिशाओं के कोनों में चार मठों की स्थापना की। अन्त में अपने लक्ष्य की पूर्ति करते हुए वे केदारनाथ पहुंचे और यहीं पर मात्र 32 वर्ष की अल्पायु में महासमाधि में लीन हो गये।

आदि शंकराचार्य कठिन शब्दार्थ

हरित = हरा। शस्य श्यामल = धनधान्य सम्पन्न। तट = किनारे। अनादिकाल = प्राचीन समय। प्रख्यात = प्रसिद्ध। धुरंधर = श्रेष्ठ गुणवान। धर्मनिष्ठ = धर्म में निष्ठा रखने वाले। कामना = इच्छा। मेधावी = बुद्धिमान। आह्लाद = हर्ष। प्रतीति = विश्वास। श्रुतिधर = सुनते ही याद करने वाले। नश्वर = नाशवान। ध्येय = लक्ष्य। ग्रहण = स्वीकार। अनुमति = आज्ञा। देशाटन = भ्रमण। आश्वस्त = विश्वास दिलाना। अवलोकन = देखना। दृष्टिक्षेप = नजर डालना। अवशिष्ट = अवशेष। गहन = गहरी। सांगोपांग = अंग व उपांगों सहित, पूर्ण। भासित = प्रतीत। प्रखर = तीव्र। आकांक्षा = इच्छा। अविलम्ब = शीघ्र ही। प्रतिष्ठित = स्थापित। निरहंकार = अभिमान रहित। दिग्विजय = दिशाएँ जीतने। दग्ध = जला हुआ। विदुषी = ज्ञानवान। अनुगत = अनुयायी। महत् = महान।

आदि शंकराचार्य संदर्भ-प्रसंग सहित व्याख्या

1. शंकर बचपन से ही मेधावी थे। उसकी प्रतिभा धीरे-धीरे प्रकट होने लगी। आर्यम्बा पुत्र की बुद्धिमत्ता की बातें सुनती तो उसका हृदय आह्वलाद से परिपूर्ण हो जाता। इसकी प्रतीति तब अधिक हुई जब 5 वर्ष का होने पर उन्हें वेदाध्ययन के लिये गुरुकुल भेजा गया। शंकर श्रुतिधर थे। एक बार बताने पर वे पाठ समझ लेते थे।

सन्दर्भ :
प्रस्तुत गद्यांश हमारी पाठ्य-पुस्तक के ‘शंकराचार्य’ नामक पाठ से अवतरित है। इसके रचयिता ‘श्रीधर पराड़कर’ हैं।

प्रसंग :
बाल शंकराचार्य की अकूत प्रतिभा का वर्णन किया गया है।

व्याख्या :
बाल्यावस्था से ही शंकर अत्यन्त प्रतिभाशाली थे। विभिन्न माध्यमों से इस मेधावी बालक के अन्दर छिपी मेधा के दर्शन उनके आसपास रहने वाले लोगों को होने लगे थे। शंकर की माता आर्यम्बा अपने होनहार सुपुत्र की वाहवाही की चर्चा जब सुनतीं तो उनका हृदय प्रसन्नता के भावों से भर उठता था। मात्र 5 वर्ष की अल्पायु में ही जब शंकर को ज्ञान के अनन्त स्त्रोत वेदों का अध्ययन करने के लिये गुरुकुल भेजा गया तो उनके बुद्धि-कौशल एवं प्रतिभा पर सहज विश्वास हुआ। शंकर बचपन से ही तेज मस्तिष्क के थे। वे मात्र एक बार सुनने अथवा बताने पर ही सम्बन्धित पाठ को न सिर्फ समझ लेते थे अपितु उसे स्मरण भी कर लेते थे। इसीलिए उन्हें श्रुतिधर कहा गया है।

विशेष :

1. भाषा सरल, बोधगम्य एवं सहज है।
2. वाक्य विन्यास लघु है।
3. शंकर की विलक्षण प्रतिभा का सुन्दर वर्णन किया गया है।

2. गुरुकुल में शिक्षा प्राप्त करते हुए शंकर जान चुके थे कि उन्होंने जिन वेदों का अध्ययन किया है समाज में उसके अनुसार आचरण नहीं हो रहा है। केवल वेद अध्ययन करने मात्र से कुछ नहीं होगा। वेदों के प्रति समाज की अश्रद्धा को दूर करना होगा।

सन्दर्भ :
पूर्ववत्।

प्रसंग :
प्रस्तुत गद्यांश में बताया गया है कि शंकर अपने अध्ययन काल में ही समझ चुके थे कि समाज में वेदों के प्रति श्रद्धा का भाव नहीं है, उसे समाप्त करना आवश्यक है।

व्याख्या :
शंकर जब गुरुकुल में पड़ते थे तब ही उन्हें इस बात का अनुभव हो गया था कि जिन वेदों का अध्ययन हम कर रहे हैं, समाज उनके अनुरूप आचरण नहीं करता है। समाज में वेदों के प्रति श्रद्धा का अभाव है। वे समझ गये थे कि वेदों को पढ़ने मात्र से कोई लाभ नहीं होगा। अपितु यह आवश्यक है कि समाज में वेदों के प्रति श्रद्धा भाव जगाया जाए। समाज को वेदों के अनुसार व्यवहार करना सिखाना होगा।

विशेष :

1. समाज में वेदों के प्रति श्रद्धा का जो अभाव है, उसे दूर करना आवश्यक है।
2. सरल, सुबोध भाषा-शैली में समझाया गया है।

3. संन्यास का अर्थ संसार को छोड़कर वन में तपस्या करना नहीं अपितु देश व धर्म के कर्म करना था जो मनुष्य को कर्मबंधन में नहीं बाँधते।

सन्दर्भ :
पूर्ववत्।

प्रसंग :
प्रस्तुत गद्यांश में संन्यास का वास्तविक अर्थ बताया गया है।

व्याख्या :
सामान्यतः लोग मानते हैं कि संन्यास अर्थ संसार को त्यागकर जंगल में जाकर तपस्या करना है। शंकर ने गुरुकुल में पढ़ते समय ही जान लिया था कि समाज वेदों के अनुसार आचरण नहीं कर रहा है। इसलिए उन्होंने संन्यास ग्रहण का अर्थ संसार छोड़कर वन में तपस्या करना स्वीकार नहीं किया। उन्होंने माना कि संन्यास का अर्थ देश और धर्म के लिए ऐसे कर्म करना है जो मनुष्य को कर्मबंधन में नहीं बाँधते हों। उन्होंने समाज कल्याण के लिए इसी प्रकार का संन्यासी बनना स्वीकार किया।

विशेष :

1. यहाँ संन्यास के वास्तविक अर्थ को स्पष्ट किया गया है।
2. सरल, सुबोध भाषा-शैली का प्रयोग हुआ है।

4. परमगुरु को भी शंकर में अलौकिक प्रतिभा भासित हुई। उससे भी अधिक उन्होंने देखा कि उसके पास अपने देश और धर्म की दशा को देखकर रोने वाला हृदय भी है तथा इसा दशा को दूर करने की एक अत्यन्त प्रखर आकांक्षा भी दिखाई दी।

सन्दर्भ :
पूर्ववत्।

प्रसंग :
यहाँ पर परमगुरु गौड़पादाचार्य ने जो विशेषताएँ शंकर में देखीं, उनका वर्णन किया गया है।

व्याख्या :
शंकर को शिक्षा देने के बाद गुरु गोविन्दपादाचार्य शंकर को अपने गुरु गौड़पादाचार्य से मिलाने बदरीनाथ ले गये। परमगुरु गौड़पादाचार्य ने जब शंकर को देखा तो उन्हें इस बात का आभास हुआ कि उस बालक में अद्भुत प्रतिभा विद्यमान है। इसके साथ ही उन्हें उस बालक के पास देश तथा धर्म की दयनीय दशा देखकर दु:खी होने वाला हृदय होने का भी अनुभव हुआ। उन्हें यह भी आभास हुआ कि इस बालक में देश और धर्म की दयनीय स्थिति से छुटकारा दिलाने वाली तीव्र इच्छा भी मौजूद है। उन्हें शंकर में विवेक, संवेदना तथा कार्यक्षमता की विद्यमानता का भी आभास हुआ।

विशेष :

1. इसमें बालक शंकर की असाधारण प्रतिभा, संवेदन की अनुभूति तथा उत्कट कर्मठता पर प्रकाश डाला गया है।
2. सहज, सरल भाषा तथा विवेचनात्मक शैली में विषय को प्रस्तुत किया गया है।

5. वे तो सम्पूर्ण भारतवर्ष को एकता के सूत्र में बाँधना चाहते थे। समाज को अद्वैत का पाठ पढ़ाना चाहते थे। उन्होंने वेदान्त और भक्ति का समन्वय किया। उन्होंने किसी भी देवता का खण्डन नहीं किया, लोगों की श्रद्धा को नष्ट न करते हुए केवल श्रद्धा का केन्द्र बदल दिया।

सन्दर्भ :
पूर्ववत्। प्रसंग-उपरोक्त गद्यांश में शंकराचार्य जी के कार्यों के बारे में बताया गया है।

व्याख्या :
शंकराचार्य का लक्ष्य महान था। उनकी इच्छा थी कि समस्त भारत एकता के सूत्र में बँधा हो। वे समाज को अद्वैत की दीक्षा देने के इच्छुक थे। उन्होंने इसके लिए बड़ा सहज उपाय खोज निकाला। उन्होंने वेदान्त और भक्ति में समन्वय स्थापित करने का अनूठा कार्य किया। लोग भिन्न देवताओं के पुजारी थे, इसलिए उन्होंने किसी भी देवता का निषेध नहीं किया। सभी देवताओं की पूजा का समर्थन करते हुए लोगों के हृदय में अद्वैत के प्रति श्रद्धा जाग्रत कर दी। इस तरह वे लोगों का श्रद्धा-केन्द्र बदलकर अपने उद्देश्य की प्राप्ति में सफल रहे।

विशेष :

1. इसमें शंकराचार्य द्वारा भारत की एकता, अद्वैत की शिक्षा तथा वेदान्त व भक्ति के समन्वय सम्बन्धी कार्यों को स्पष्ट किया गया है।
2. सरल, सुबोध भाषा तथा विवेचनात्मक शैली में विषय को प्रस्तुत किया गया है।

MP Board Class 11th Hindi Solutions