Prasanna

 MP Board Class 6th Maths Solutions Chapter 4 आधारभूत ज्यामितीय अवधारणाएँ Ex 4.4

पाठ्य-पुस्तक पृष्ठ संख्या # 88

प्रश्न 1.
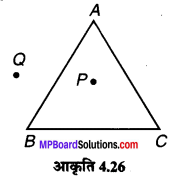
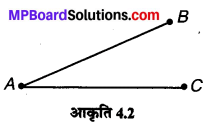
त्रिभुज ABC का एक रफ चित्र खींचिए। इस त्रिभुज के अभ्यन्तर में एक बिन्दु P अंकित कीजिए और उसके बहिर्भाग में एक बिन्दु Q अंकित कीजिए। बिन्दु A इसके अभ्यन्तर में स्थित है या बहिर्भाग में स्थित है ?
हल :
संलग्न चित्र में ABC एक त्रिभुज है।
(i) बिन्दु P, ∆ABC के अभ्यन्तर में है।
(ii) बिन्दु Q त्रिभुज के बहिर्भाग में है।
(iii) नहीं, बिन्दु A न तो इसके अभ्यन्तर में स्थित है और न ही इसके बहिर्भाग में।

प्रश्न 2.
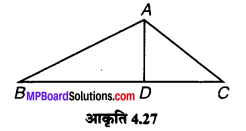
(a) संलग्न आकृति में तीन त्रिभुजों की पहचान कीजिए।
(b) ज्ञात कोणों के नाम लिखिए।
(c) इसी आकृति में छः रेखाखण्डों के नाम लिखिए।
(d) किन दो त्रिभुजों में ∠B उभयनिष्ठ है ?

हल :
(a) तीन त्रिभुज- ∆ABC, ∆ABD, ∆ADC
(b) सात कोण- ∠B, ∠C, ∠BAC, ∠BAD, ∠CAD, ∠ADB, ∠ADC
(c) छः रेखाखण्ड- \(\overline{A B}, \overline{A C}, \overline{B C}, \overline{A D}, \overline{B D}, \overline{D C}\)
(d) ∆ABC और ∆ABD में ∠B उभयनिष्ठ है।

MP Board Class 6th Maths Solutions

MP Board Class 6th Maths Solutions Chapter 4 आधारभूत ज्यामितीय अवधारणाएँ Ex 4.3

पाठ्य-पुस्तक पृष्ठ संख्या # 87

प्रश्न 1.
नीचे दी आकृति में, कोणों के नाम लिखिए :

हल :
∠A अथवा ∠DAB ; ∠B अथवा ∠ABC ; ∠C अथवा ∠BCD; ∠D अथवा ∠CDA

प्रश्न 2.
संलग्न आकृति में, वे बिन्दु लिखिए जो
(a) ∠DOE के अभ्यन्तर में स्थित हैं।
(b) ∠EOF के बहिर्भाग में स्थित हैं।
(c) ∠EOF पर स्थित हैं।

हल :
(a) ∠DOE के अभ्यंतर में बिन्दु A है।
(b) ∠EOF के बहिर्भाग में बिन्दु A,C और D हैं।
(c) ∠EOF पर स्थित बिन्दु हैं, E,B,O और F।

प्रश्न 3.
दो कोणों की रफ आकृतियाँ खींचिए जिससे
(a) उनमें एक बिन्दु उभयनिष्ठ हो।
(b) उनमें दो बिन्दु उभयनिष्ठ हों।
(c) उनमें तीन बिन्दु उभयनिष्ठ हों।
(d) उनमें चार बिन्दु उभयनिष्ठ हों।
(e) उनमें एक किरण उभयनिष्ठ हो।
हल :
(a) ∠PQS और ∠RQS में एक बिन्दु Q उभयनिष्ठ है।

(b) ∠AOB और ∠ODC में दो बिन्दु O तथा D उभयनिष्ठ है।

(c) ∠ABC और ∠QPR में तीन बिन्दु D, E तथा F उभयनिष्ठ हैं। .

(d) ∠BAC और ∠PQR में चार बिन्दु E, F G तथा H उभयनिष्ठ हैं।

(e) ∠RQS और ∠PQS में किरण QS उभयनिष्ठ है।

MP Board Class 6th Maths Solutions

MP Board Class 6th Maths Solutions Chapter 4 आधारभूत ज्यामितीय अवधारणाएँ Ex 4.2

पाठ्य-पुस्तक पृष्ठ संख्या # 84-85

प्रश्न 1.
पाठ्य-पुस्तक में दी हुई वक्रों को
(i) खुली या
(ii) बंद वक्रों के रूप में वर्गीकृत कीजिए :
हल :
(i) खुली वक्र – (a) व (c)
(ii) बन्द वक्र – (b), (b) व (e)

प्रश्न 2.
निम्न को स्पष्ट करने के लिए रफ आकृतियाँ बनाइए:
(a) खुला वक्र
(b) बन्द वक्र
हल :

प्रश्न 3.
कोई भी बहुभुज खींचिए और उसके अभ्यन्तर को छायांकित (Shade) कीजिए।
हल :
ABCDE एक बहुभुज है जिसके अभ्यंतर को छायांकित किया गया है।

प्रश्न 4.
संलग्न आकृति को देखकर निम्न प्रश्नों के उत्तर दीजिए :
(a) क्या यह एक वक्र है ?
(b) क्या यह बन्द है?

हल :
(a) हाँ, यह एक वक्र है।
(b) हाँ, यह बन्द वक्र है।

प्रश्न 5.
रफ आकृतियाँ बनाकर, यदि सम्भव हो, तो निम्न को स्पष्ट कीजिए :
(a) एक बन्द आकृति जो बहुभुज नहीं है।
(b) केवल रेखाखण्डों से बनी हुई खुली वक्र
(c) दो भुजाओं वाला एक बहुभुज।
हल :
(a) बन्द आकृति जो बहुभुज नहीं है।

(b) रेखाखण्डों से बनी हुई खुली वक्र

(c) दो भुजाओं वाला बहुभुज असम्भव है।

MP Board Class 6th Maths Solutions

MP Board Class 6th Maths Solutions Chapter 4 आधारभूत ज्यामितीय अवधारणाएँ Ex 4.1

पाठ्य-पुस्तक पृष्ठ संख्या # 80-81

प्रश्न 1.
संलग्न आकृति का प्रयोग करके, निम्न के नाम लिखिए :
(a) पाँच बिन्दु
(b) एक रेखा
(c) चार किरणें
(d) पाँच रेखाखण्ड

हल :
(a) पाँच बिन्दु-O, B, C, D, E
(b) एक रेखा-इसमें कई रेखाएँ हो सकती हैं \(\stackrel{\leftrightarrow}{D E}, \stackrel{\leftrightarrow}{D O}, \stackrel{\leftrightarrow}{D B}, \overrightarrow{E O}\) आदि।
(c) चार किरणें- \(\overrightarrow{D B}, \overrightarrow{D E}, \overrightarrow{E B}, \overrightarrow{O E}\) आदि (अनेक किरणें हो सकती हैं)।
(d) पाँच रेखाखण्ड- \(\overline{D E}, \overline{D O}, \overline{E O}, \overline{O B}, \overline{E B}\) आदि (अनेक रेखाखण्ड हो सकते हैं)।

प्रश्न 2.
संलग्न आकृति में दी हुई रेखा के सभी सम्भव प्रकारों के नाम लिखिए। आप इन चार बिन्दुओं में से किसी भी बिन्दु का प्रयोग कर सकते हैं।

हल :
रेखाओं को निम्न नामों से व्यक्त कर सकते हैं
\(\stackrel{\leftrightarrow}{AB}, \stackrel{\leftrightarrow}{AC}, \stackrel{\leftrightarrow}{AD}, \stackrel{\leftrightarrow}{BA}, \stackrel{\leftrightarrow}{BC}, \stackrel{\leftrightarrow}{BD}, \stackrel{\leftrightarrow}{CA}, \stackrel{\leftrightarrow}{CB}, \stackrel{\leftrightarrow}{CD}, \stackrel{\leftrightarrow}{DA}, \stackrel{\leftrightarrow}{DB}, \stackrel{\leftrightarrow}{DC}\)

प्रश्न 3.
संलग्न आकृति को देखकर नाम लिखिए :
(a) रेखाएँ जिसमें बिन्दु E सम्मिलित हैं
(b) A से होकर जाने वाली रेखा
(c) वह रेखा जिस पर O स्थित है
(d) प्रतिच्छेदी रेखाओं के दो युग्म

हल :
(a) ऐसी बहुत सी रेखाएँ है, जिनमें से एक है, \(\stackrel{\leftrightarrow}{EF}\) (या \(\stackrel{\leftrightarrow}{AE}\) )
(b) ऐसी बहुत सी रेखाएँ है, जिनमें से एक है, \(\stackrel{\leftrightarrow}{AE}\)
(c) \(\stackrel{\leftrightarrow}{CO}\) या \(\stackrel{\leftrightarrow}{CO}\)
(d) \(\stackrel{\leftrightarrow}{AE}\) और \(\stackrel{\leftrightarrow}{CO}\); \(\stackrel{\leftrightarrow}{AE}\) और \(\stackrel{\leftrightarrow}{EF}\)

प्रश्न 4.
निम्नलिखित से होकर कितनी रेखाएँ खींची जा सकती हैं ?
(a) एक बिन्दु
(b) दो बिन्दु
हल :
(a) एक बिन्दु से अनगिनत रेखाएँ खींची जा सकती हैं।
(b) दो बिन्दुओं से केवल एक रेखा खींची जा सकती है।

प्रश्न 5.
निम्नलिखित स्थितियों में से प्रत्येक के लिए एक रफ (Rough) आकृति बनाइए और चित रूप से उसे नामांकित कीजिए :
(a) बिन्दु P रेखाखण्ड \(\overline{A B}\) पर स्थित है।
(b) रेखाएँ XY और PQ बिन्दु M पर प्रतिच्छेद करती हैं।
(c) रेखा l पर E और F स्थित हैं, परन्तु D स्थित नहीं है।
(d) \(\stackrel{\leftrightarrow}{OP}\) और \(\stackrel{\leftrightarrow}{OQ}\) बिन्दु O पर मिलती हैं।
हल:

प्रश्न 6.
रेखा \(\stackrel{\leftrightarrow}{MN}\) की संलग्न आकृति को देखिए। इस आकृति के सन्दर्भ में बताइए कि निम्नलिखित कथन सत्य हैं या असत्य :

(a) Q, M, O और P रेखा \(\stackrel{\leftrightarrow}{MN}\) पर स्थित बिन्दु हैं।
(b) M, O और N रेखाखण्ड \(\overline{MN}\) पर स्थित बिन्दु हैं।
(c) M और N रेखाखण्ड \(\overline{MN}\) के अन्त बिन्दु हैं।
(d) O और N रेखाखण्ड \(\overline{OP}\) के अन्त बिन्दु हैं।
(e) M रेखाखण्ड \(\overline{QO}\) को दोनों अन्त बिन्दुओं में से एक बिन्दु है।
(f) M किरण \(\overrightarrow{OP}\) पर एक बिन्दु है।
(g) किरण \(\overrightarrow{OP}\) किरण \(\overrightarrow{QP}\) से भिन्न है।
(h) किरण \(\overrightarrow{O P}\) वही है जो किरण \(\overrightarrow{O M}\) है।
(i) किरण \(\overrightarrow{O M}\) किरण \(\overrightarrow{O P}\) के विपरीत (opposite) नहीं है।
(j) O किरण \(\overrightarrow{O P}\) का प्रारम्भिक बिन्दु नहीं है।
(k) N किरण \(\overrightarrow{N P}\) और \(\overrightarrow{N M}\) का प्रारम्भिक बिन्दु है।
उत्तर-
(a) सत्य,
(b) सत्य,
(c) सत्य
(d) असत्य,
(e) असत्य,
(f) भसत्य,
(g) सत्य,
(h) असत्य,
(i) असत्य,
(j) असत्य,
(k) सत्य।

पाठ्य-पुस्तक पृष्ठ संख्या # 83

इन्हें कीजिए

प्रश्न 1.
निम्न की सहायता से बहुभुज बनाने का प्रयत्न कीजिए :
1. माचिस की पाँच तीलियाँ
2. माचिस की चार तीलियाँ
3. माचिस की तीन तीलियाँ
4. माचिस की दो तीलियाँ
उपर्युक्त में से किस स्थिति में यह सम्भव नहीं हुआ ? क्यों?
हल :

4. माचिस की दो तीलियाँ-कोई बहुभुज सम्भव नहीं। चूँकि बहुभुज रेखाखण्डों से घिरी बन्द आकृति है। यह सम्भव नहीं कि दो रेखाखण्डों से एक बन्द घिरी हुई आकृति बनाई जाए। इसलिए दो माचिस की तीलियों से बहुभुज बनाना सम्भव नहीं है।

पाठ्य-पुस्तक पृष्ठ संख्या # 84

प्रश्न 1.
B और C इसके अन्य दो शीर्ष हैं। क्या आप इन बिन्दुओं पर मिलने वाली भुजाओं के नाम लिख सकते हैं?
हल :
इन भुजाओं के नाम हैं जिनके शीर्ष B और C हैं :
AB और BC, BC और CD

प्रश्न 2.
क्या AB और BC आसन्न भुजाएँ हैं? AE और DC के बारे में आप क्या कह सकते हैं?
हल :
चूँकि AB और BC में एक उभयनिष्ठ अंत बिन्दु है, इसलिए ये बहुभुज की आसन्न भुजाएँ हैं। AE और DC आसन्न भुजाएँ नहीं हैं। क्योंकि इनका उभयनिष्ठ अन्त बिन्दु नहीं है।

प्रश्न 3.
क्या रेखाखण्ड \(\overline{B C}\) एक विकर्ण है? क्यों या क्यों नहीं?
हल :
नहीं, रेखाखण्ड \(\overline{B C}\) विकर्ण नहीं है क्योंकि BC आसन्न शीर्षों को मिलाने वाला रेखाखण्ड है।

प्रश्न 4.
क्या आप आसन्न शीर्षों को जोड़कर विकर्ण प्राप्त कर सकते हैं?
हल :
नहीं, हम आसन्न शीर्षों को जोड़कर विकर्ण प्राप्त नहीं कर सकते हैं।

MP Board Class 6th Maths Solutions

MP Board Class 6th Maths Solutions Chapter 4 आधारभूत ज्यामितीय अवधारणाएँ Intext Questions

पाठ्य-पुस्तक पृष्ठ संख्या # 75

प्रयास कीजिए

प्रश्न 1.
अपनी पेंसिल के नुकीले सिरे से एक कागज पर चार बिन्दु अंकित कीजिए तथा उन्हें नाम A, C, P और H दीजिए। इन बिन्दुओं को विभिन्न प्रकार से नाम दीजिए। नाम देने का एक प्रकार संलग्न आकृति के अनुसार हो सकता है।

हल :
हम इन बिन्दुओं को निम्न प्रकार से नाम दे सकते हैं :

प्रश्न 2.
आसमान में एक तारा हमें एक बिन्दु के अवधारण का आभास कराता है। अपने दैनिक जीवन से इसी प्रकार की पाँच स्थितियाँ चुनकर दीजिए।
हल :
पेंसिल की नोंक, सुई की नोंक, कागज का कोना, डेस्क का कोना, वर्ग का कोना।

पाठ्य-पुस्तक पृष्ठ संख्या # 76-77

रेखाखण्ड के कुछ उदाहरण – मेज का किनारा, किसी आयत/वर्ग की भुजा, घन/ घनाभ का किनारा, दोनों सिरों पर कसा हुआ धागा, A, B को जोड़ने वाला सबसे छोटा रास्ता।

प्रयास कीजिए

प्रश्न 1.
संलग्न आकृति में दिए रेखाखण्डों को नाम दीजिए। क्या A प्रत्येक रेखाखण्ड का एक अन्त बिन्दु है ?

हल :
दी हुई आकृति में \(\overline{A B}\) (या \(\overline{B A}\) ) तथा \(\overline{A C}\) (या \(\overline{C A}\) ) रेखाखण्ड हैं।
हाँ, A प्रत्येक रेखाखण्ड का अन्त बिन्दु है।

प्रतिच्छेदी रेखा युग्मों के उदाहरण – घन के आसन्न किनारे, श्यामपट की आसन्न भुजाएँ, अंग्रेजी वर्णमाला के अक्षर V तथा L

पाठ्य-पुस्तक पृष्ठ संख्या # 78

इन्हें कीजिए

प्रश्न 1.
एक कागज लीजिए। इसे दो बार मोडिए (और मोड़ के निशान बनाइए) ताकि दो प्रतिच्छेदी रेखाएँ प्राप्त हो जाएँ और चर्चा कीजिए :
(a) क्या दो रेखाएँ एक से अधिक बिन्दुओं पर प्रतिच्छेद कर सकती हैं?
(b) क्या दो से अधिक रेखाएँ एक ही बिन्दु पर प्रतिच्छेद कर सकती हैं?
हल :
(a) नहीं, दो रेखाएँ एक से अधिक बिन्दुओं पर प्रतिच्छेद नहीं कर सकती हैं।
(b) हाँ, दो से अधिक रेखाएँ एक ही बिन्दु पर प्रतिच्छेद कर सकती हैं।

सोचिए, चर्चा कीजिए एवं लिखिए

आप समान्तर रेखाओं को और कहाँ देखते हैं ? इनके 10 उदाहरण ज्ञात करने का प्रयत्न कीजिए।
हल :
हम समान्तर रेखाओं को निम्नांकित में देख सकते हैं
पैमाने के सम्मुख किनारे, आयत के सम्मुख किनारे, श्यामपट के सम्मुख किनारे, खिड़की की सलाखें, रेल की पटरी, मेज के किनारे, घनाभ के किनारे, घन के किनारे, पेज के किनारे, अभ्यास-पुस्तिका/किताब के सम्मुख किनारे आदि।

पाठ्य-पुस्तक पृष्ठ संख्या # 79

सोचिए, चर्चा कीजिए एवं लिखिए

प्रश्न 1.
यदि \(\overrightarrow{P Q}\) एक किरण है, तो
(a) इसका प्रारम्भिक बिन्दु क्या है ?
(b) बिन्दु ए किरण पर कहाँ स्थित है ?
(c) क्या हम कह सकते हैं कि ए इस किरण का Q प्रारम्भिक बिन्दु है ?

हल :
\(\overrightarrow{P Q}\) एक किरण है :
(a) इसका प्रारम्भिक बिन्दु P है।
(b) बिन्दु Q, किरण \(\overrightarrow{P Q}\) पर स्थित है।
(c) नहीं, Q इस किरण का प्रारम्भिक बिन्दु नहीं है।
(Q, \(\overrightarrow{Q P}\) का प्रारम्भिक बिन्दु हो सकता है।)

पाठ्य-पुस्तक पृष्ठ संख्या # 80

प्रयास कीजिए

प्रश्न 1.
संलग्न दी आकृति में दर्शाई गई किरणों के नाम लिखिए।

हल :
संलग्न चित्र में \(\overrightarrow{T A}, \overrightarrow{T N}, \overrightarrow{T B}\) और \(\overrightarrow{N B}\) किरणें हैं।

प्रश्न 2.
क्या T इन सभी किरणों का प्रारम्भिक बिन्दु है ?
हल :
नहीं, T किरण \(\overrightarrow{N B}\) का प्रारम्भिक बिन्दु नहीं है।

संलग्न आकृति में एक किरण OA दी है। यह O से प्रारम्भ होती है और A से होकर जाती है। यह किरण बिन्दु B से होकर भी जाती है।

प्रश्न a.
(i) क्या आप इसे \(\overrightarrow{O B}\) भी कह सकते हैं ? क्यों? यहाँ \(\overrightarrow{O A}\) और \(\overrightarrow{O B}\) एक ही किरण को दर्शाते हैं।
(ii) क्या हम किरण \(\overrightarrow{O A}\) को किरण \(\overrightarrow{A O}\) लिख सकते हैं ? क्यों ? या क्यों नहीं ?
(iii) पाँच किरणें खींचिए और उनके उचित नाम लिखिए।
इन किरणों के सिरे पर लगे तीर क्या दर्शाते हैं ?
हल :
(i) हाँ, हम इसे \(\overrightarrow{O B}\) भी कह सकते हैं। क्योंकि एक किरण की कोई निश्चित लम्बाई नहीं होती है। किरण को अनिश्चित रूप से बढ़ाया जा सकता है। इसलिए \(\overrightarrow{O A}\) और \(\overrightarrow{O B}\) समान किरणें हैं।

(ii) यहाँ, \(\overrightarrow{O A}\) एक किरण है, जिसका प्रारम्भिक बिन्दु O हैं। इसे O से A की दिशा में अनिश्चित रूप से बढ़ाया गया है। दूसरी किरण \(\overrightarrow{A O}\) है, जिसका प्रारम्भिक बिन्दु A है। इसे A से O की दिशा में अनिश्चित रूप से बढ़ाया गया है।
अतः \(\overrightarrow{A O}\) और \(\overrightarrow{O A}\) अलग-अलग किरणें हैं। इस प्रकार \(\overrightarrow{O A}\) को \(\overrightarrow{A O}\) नहीं लिखा जा सकता है।

(iii) पाँच किरणें निम्नलिखित हैं

किरणों के सिरों पर लगे तीर दर्शाते हैं कि इन किरणों को तीर की दिशा में अनिश्चित रूप से बढ़ाया जा सकता है।

MP Board Class 6th Maths Solutions

MP Board Class 6th Maths Solutions Chapter 3 संख्याओं के साथ खेलना Ex 3.7

पाठ्य-पुस्तक पृष्ठ संख्या # 72

प्रश्न 1.
रेणु 75 किग्रा और 69 किग्रा भारों वाली दो खाद की बोरियाँ खरीदती है। भार के उस बट्टे का अधिकतम मान ज्ञात कीजिए जो दोनों बोरियों के भारों को पूरा-पूरा माप ले।
हल :
दोनों बोरियों के भारों को पूरा-पूरा मापने के लिए अधिकतम भार म. स. होगा।
∴75 = 3 x 5 x 5
69 = 3 x 23
∴सार्व गुणनखण्ड = 3, अत : म. स. = 3
अतः अधिकतम भार = 3 किग्रा

प्रश्न 2.
तीन लड़के एक ही स्थान से एक साथ कदम उठाकर चलना प्रारम्भ करते हैं। उनके कदमों की माप क्रमश: 63 सेमी, 70 सेमी और 77 सेमी है। इनमें से प्रत्येक कितनी न्यूनतम दूरी तय करे कि वह दूरी पूरे-पूरे कदमों में तय हो जाए?
हल :
प्रत्येक द्वारा तय की गई दूरी उनके कदमों का ल. स. होगी।
अतः

∴ल. स. = 2 x 3 x 3 x 5 x 7 x 11 = 6930
∴अभीष्ट न्यूनतम दूरी = 6930 सेमी

प्रश्न 3.
किसी कमरे की लम्बाई, चौड़ाई और ऊँचाई क्रमश: 825 सेमी, 675 सेमी और 450 सेमी हैं। ऐसा सबसे लम्बा फीता (tape) ज्ञात कीजिए जो कमरे की तीनों विमाओं (dimensions) को पूरा-पूरा माप ले।
हल :
फीते की अधिकतम लम्बाई 825, 675 और 450 का म. स. होगी।
∴825 = 3 x 5 x 5 x 11
675 = 3 x 3 x 3 x 5 x 5
450 = 2 x 3 x 3 x 5 x 5

∴म. स. = 3 x 5 x 5 = 75
अत: फीते की अधिकतम लम्बाई = 75 सेमी

प्रश्न 4.
6,8 और 12 से विभाज्य तीन अंकों की सबसे छोटी संख्या ज्ञात कीजिए।
हल :
तीन अंकों की सबसे छोटी संख्या = 100
तीन अंकों की सबसे छोटी संख्या जो 6, 8 और 12 से पूर्णतः विभाजित हो उनका ल. स. है।

∴ल. स. = 2 x 2 x 2 x 3 = 24
24 के सभी गुणज 6, 8 और 12 से विभाज्य होंगे। लेकिन हमें 3 अंकों का 24 का सबसे छोटा गुणज चाहिए।

अब 100 से बड़ी और 24 से पूर्णतया विभाज्य संख्या = (100 – 4) + 24 = 120
अत: अभीष्ट संख्या = 120

प्रश्न 5.
8, 10 और 12 से विभाज्य तीन अंकों की सबसे बड़ी संख्या ज्ञात कीजिए।
हल :
8, 10 और 12 का ल. स. :

∴ल. स. = 2 x 2 x 2 x 3 x 5 = 120
चूँकि 120 के सभी गुणज 8, 10 और 12 से भी विभाज्य होंगे।
अब 3 अंकों की सबसे बड़ी संख्या = 999

∴999 – 39 = 960 जो कि 120 का गुणज है।
अत : अभीष्ट संख्या = 960

प्रश्न 6.
तीन विभिन्न चौराहों की ट्रैफिक लाइट (traffic lights) क्रमशः प्रत्येक 48 सेकण्ड, 72 सेकण्ड और 108 सेकण्ड बाद बदलती है। यदि वे एक साथ प्रातः 7 बजे बदलें, तो वें पुनः एक साथ कब बदलेंगी?
हल :
अभीष्ट समय 48,72 और 108 का ल. स. होगा।

ल. स. = 2 x 2 x 2 x 2 x 3 x 3 x 3 = 432 सेकण्ड
अत : अभीष्ट न्यूनतम समय जब लाइटें दोबारा अपने आप बदलेंगी = 432 सेकण्ड = 7 मिनट 12 सेकण्ड
इसलिए वे दोबारा 7 बजकर 7 मिनट और 12 सेकण्ड पर बदलेंगी।

प्रश्न 7.
तीन टैंकरों में क्रमशः 403 लीटर, 434 लीटर और 465 लीटर डीजल है। उस बर्तन की अधिकतम धारिता ज्ञात कीजिए जो इन तीनों टैंकरों के डीजल को पूरा-पूरा माप देगा।
हल:
403 = 13 x 31
434 = 2 x 7 x 31
645 = 3 x 5 x 31
∴म. स. = सार्व गुणनखण्ड = 31
अत: बर्तन की अधिकतम अभीष्ट धारिता = 31 लीटर

प्रश्न 8.
वह सबसे छोटी संख्या ज्ञात कीजिए जिसे 6, 15 और 18 से भाग देने पर प्रत्येक दशा में 5 शेष रहे।
हल:

∴ल. स. = 2 x 3 x 3 x 5 = 90
अत : अभीष्ट संख्या = 90 + 5 = 95

प्रश्न 9.
चार अंकों की सबसे छोटी संख्या ज्ञात कीजिए जो 18, 24 और 32 से विभाज्य है।
हल:

∴ल. स. = 2 x 2 x 2 x 2 x 2 x 3 x 3 = 288
चार अंकों की सबसे छोटी संख्या = 1000
∴4 अंकों की सबसे छोटी संख्या जो 288 से विभाज्य हो
= 1000 – 136 + 288
= 1152

अत : अभीष्ट संख्या = 1152

प्रश्न 10.
निम्नलिखित संख्याओं का ल. स. ज्ञात कीजिए जिनमें एक संख्या सदैव 3 का गुणज है :
(a) 9 और 4
(b) 12 और 5
(c) 6 और 5
(d) 15 और 4
प्राप्त ल. स. में एक सामान्य गुण का अवलोकन कीजिए। क्या ल. स. प्रत्येक स्थिति में दोनों संख्याओं का गुणनफल है? क्या हम यह निष्कर्ष निकाल सकते हैं कि दो संख्याओं का ल. स. सदैव 3 का एक गुणज है।
हल :
(a)

∴ल. स. = 2 x 2 x 3 x 3 = 36
9 और 4 का गुणनफल = 9 x 4 = 36
∴4 और 9 का ल. स.= 9 और 4 का गुणनफल

(b)

∴ल. स.= 2 x 2 x 3 x 5 = 60
12 और 5 का गुणनफल = 12 x 5 = 60
∴12 और 5 का ल. स. = 12 और 5 का गुणनफल

(c)

∴ल. स. = 2 x 3 x 5 = 30
6 और 5 का गुणनफल = 6 x 5 = 30
∴6 और 5 का ल. स. = 6 और 5 का गुणनफल

(d)

∴ल. स. = 2 x 2 x 3 x 5 = 60
15 और 4 का गुणनफल = 15 x 4 = 60
∴15 और 4 का ल. स. = 15 और 4 का गुणनफल
हम पाते हैं कि
36 = 3 x 12,
60 = 3 x 20,
30 = 3 x 10
यहाँ प्रत्येक स्थिति ल. स. 3 का गुणज है।
हाँ, प्रत्येक स्थिति में ल. स. = दो संख्याओं का गुणनफल
हम यह निष्कर्ष नहीं निकाल सकते कि दो संख्याओं का ल. स. सदैव 3 का गुणज होता है।

प्रश्न 11.
निम्नलिखित संख्याओं का ल. स. ज्ञात कीजिए जिनमें एक संख्या दूसरी संख्या का एक गुणनखण्ड
(a) 5, 20
(b) 6, 18
(c) 12, 48
(d) 9, 45
प्राप्त परिणामों में आप क्या देखते हैं?
हल :
(a)

∴ल. स. = 2 x 2 x 5 = 20

(b)

∴ल. स. = 2 x 3 x 3 = 18

(c)

∴ल. स. = 2 x 2 x 2 x 2 x 3 = 48

(d)

∴ल. स. = 3 x 3 x 5 = 45
प्राप्त परिणामों से स्पष्ट है कि प्रत्येक स्थिति में दी हुई नंख्याओं का ल. स. उन दोनों में से बड़ी संख्या है।

MP Board Class 6th Maths Solutions

MP Board Class 6th Maths Solutions Chapter 3 संख्याओं के साथ खेलना Ex 3.6

प्रश्न 1.
निम्नलिखित संख्याओं के म. स. ज्ञात कीजिए :
(a) 18, 48
(b) 30, 42
(c) 18, 60
(d) 27, 63
(e) 36, 84
(f) 34, 102
(g) 70, 105, 175
(h) 91, 112, 49
(i) 18, 54, 81
(j) 12, 45, 75
हल :
(a) ∵18 = 2 x 3 x 3
48 = 2 x 2 x 2 x 2 x 3
∴म. स. = 2 x 3 = 6

(b) ∵30 = 2 x 3 x 5
42 = 2 x 3 x 7
∴म. स. = 2 x 3 = 6

(c)∵18 = 2 x 3 x 3
60 = 2 x 2 x 3 x 5
∴म. स. = 2 x 3 = 6

(d)∵27 = 3 x 3 x 3
63 = 3 x 3 x 7
∴म. स. = 3 x 3 = 9

(e) ∵36 = 2 x 2 x 3 x 3
84 = 2 x 2 x 3 x 7
∴म. स. = 2 x 2 x 3 = 12

(f)∵34 = 2 x 17
102 = 2 x 3 x 17
∴म. स. = 2 x 17 = 34

(g)∵70 = 2 x 5 x 7
105 = 3 x 5 x 7
175 = 5 x 5 x 7
∴म. स. = 5 x 7 = 35

(h)∵91 = 7 x 13
112 = 2 x 2 x 2 x 2 x 7
49 = 7 x 7
∴म. स. = 7

(i)∵18 = 2 x 3 x 3
54 = 2 x 3 x 3 x 3
81 = 3 x 3 x 3 x 3
∴म. स. = 3 x 3 = 9

(j) ∵12 = 2 x 2 x 3
45 = 3 x 3 x 5
75 = 3 x 5 x 5
∴म. स. = 3

प्रश्न 2.
निम्न का म. स. क्या है?
(a) दो क्रमागत संख्याएँ
(b) दो क्रमागत सम संख्याएँ
(c) दो क्रमागत विषम संख्याएँ।
उत्तर-
(a) 1,
(b) 2,
(c) 1

प्रश्न 3.
अभाज्य गुणनखण्डन द्वारा दो सह-अभाज्य संख्याओं 4 और 15 का म. स. इस प्रकार ज्ञात किया गयाः
4 = 2 x 2 और 15 = 3 x 5
चूँकि इन गुणनखण्डों में कोई अभाज्य सार्व गुणनखण्ड नहीं है, इसलिए 4 और 15 का म. स. शून्य है। क्या यह उत्तर सही है ? यदि नहीं तो सही म. स. क्या है ?
उत्तर-
∵ शून्य किसी भी संख्या का गुणनखण्ड नहीं हो सकता है।
1 प्रत्येक संख्या का गुणनखण्ड है। अत: 1 सार्व गुणनखण्ड है।
अतः शून्य उत्तर सही नहीं है। सही म. स. 1 है।

MP Board Class 6th Maths Solutions

MP Board Class 6th Maths Solutions Chapter 3 संख्याओं के साथ खेलना Ex 3.5

पाठ्य-पुस्तक पृष्ठ संख्या # 66-67

प्रश्न 1.
निम्नलिखित में कौन-से कथन सत्य हैं ?
(a) यदि कोई संख्या 3 से विभाज्य है, तो वह 9 से भी विभाज्य होती है।
(b) यदि कोई संख्या 9 से विभाज्य है, तो वह 3 से भी अवश्य विभाज्य होगी।
(c) एक संख्या 18 से भी विभाज्य होती है, यदि वह 3 और 6 दोनों से विभाज्य हो।
(d) यदि एक संख्या 9 और 10 दोनों से विभाज्य हो, तो वह 90 से भी विभाज्य होगी।
(e) यदि दो संख्याएँ सह-अभाज्य हों, तो इनमें से कम-से-कम एक अवश्य ही अभाज्य संख्या होगी।
(f) 4 से विभाज्य सभी संख्याएँ 8 से भी अवश्य विभाज्य होनी चाहिए।
(g) 8 से विभाज्य सभी संख्याएँ 4 से विभाज्य होनी चाहिए।
(h) यदि कोई संख्या दो संख्याओं को अलग-अलग पूरा-पूरा विभाजित करती है, तो वह उनके योग को भी पूरा-पूरा विभाजित करेगी।
(i) यदि कोई संख्या दो संख्याओं के योग को पूरी तरह विभाजित करती है, तो वह उन दोनों संख्याओं को अलग-अलग भी विभाजित करेगी।
उत्तर-
(a) असत्य,
(b) सत्य,
(c) असत्य,
(d) सत्य,
(e) असत्य,
(f) असत्य,
(g) सत्य,
(h) सत्य,
(i) असत्य

प्रश्न 2.
यहाँ 60 के लिए दो भिन्न-भिन्न गुणनखण्ड वृक्ष दिए हैं। इनमें अज्ञात संख्याएँ लिखिए।
हल :

प्रश्न 3.
एक भाज्य संख्या के अभाज्य गुणनखण्डन में किन गुणनखण्डों को सम्मिलित नहीं किया जाता है?
उत्तर-
1 और स्वयं संख्या को भाज्य संख्या के अभाज्य गुणनखण्डन में सम्मिलित नहीं किया जाता है।

प्रश्न 4.
चार अंकों की सबसे बड़ी संख्या लिखिए और उसे अभाज्य गुणनखण्डन के रूप में व्यक्त कीजिए।
हल :
चार अंकों की सबसे बड़ी संख्या = 9999

∴ 9999 = 3 x 3 x 11 x 101

प्रश्न 5.
पाँच अंकों की सबसे छोटी संख्या लिखिए और उसे अभाज्य गुणनखण्डन के रूप में व्यक्त कीजिए।
हल :
पाँच अंकों की सबसे छोटी संख्या = 10000

∴ 10000 = 2 x 2 x 2 x 2 x 5 x 5 x 5 x 5

प्रश्न 6.
1729 के सभी अभाज्य गुणनखण्ड ज्ञात कीजिए और उन्हें आरोही क्रम में व्यवस्थित कीजिए। अब दो क्रमागत अभाज्य गुणनखण्डों में यदि कोई सम्बन्ध है तो लिखिए।
हल :

∴1729 = 7 x 13 x 19
स्पष्ट है कि दो क्रमागत गुणनखण्डों में 6 का अन्तर है।

प्रश्न 7.
तीन क्रमागत संख्याओं का गुणनफल सदैव 6 से विभाज्य होता है। इस कथन को कुछ उदाहरणों की सहायता से स्पष्ट कीजिए।
हल :
तीन क्रमागत संख्याओं के गुणनफल
(i) 11 x 12 x 13 = 1716
गुणनफल के अंकों का योग = 1 + 7 + 1 + 6 = 15

(ii) 15 x 16 x 17 = 4080
गुणनफल के अंकों का योग = 4 + 0 + 8 + 0 = 12

(iii) 25 x 26 x 27 = 17550
गुणनफल के अंकों का योग = 1 + 7 + 5 + 5 + 0 = 18
(a) प्रत्येक गुणनफल में इकाई का अंक 6, 4 और 0 है अतः गुणनफल 2 से विभाज्य है।
(b) प्रत्येक गुणनफल के अंकों का योग 3 से विभाज्य है
∴2 और 3 सह-अभाज्य संख्याएँ हैं इसलिए 2 x 3 = 6
प्रत्येक गुणनफल को विभाजित करेगा।
∴अतः तीन क्रमागत संख्याओं का गुणनफल सदैव 6 से विभाज्य होता है।

प्रश्न 8.
दो क्रमागत विषम संख्याओं का योग 4 से विभाज्य होता है। कुछ उदाहरण लेकर इस कथन का सत्यापन कीजिए।
हल :
माना कि विषम संख्याओं का योग निम्न है
(i) 211 + 213 = 424
(ii) 405 + 407 = 812
(iii) 541 + 543 = 1084
(iv) 101 + 103 = 204
योगों के दायें से इकाई और दहाई के दो अंक क्रमश: 24, 12, 48 और 04 हैं जो कि 4 से विभाज्य हैं।
अत: दो क्रमागत विषम संख्याओं का योग 4 से विभाज्य होता है।

प्रश्न 9.
निम्न में से किन व्यंजकों में अभाज्य गुणनखण्डन किए गए हैं :
(a) 24 = 2 x 3 x 4
(b) 56 = 1 x 7 x 2 x 2 x 2
(c) 70 = 2 x 5 x 7
(d) 54 = 2 x 3 x 9
हल :
(a) और (d) में क्रमशः 4 और 9 के अभाज्य गुणनखण्डन नहीं हैं।
∴(b) और (c) व्यंजकों में अभाज्य गुणनखण्डन किये गये हैं।

प्रश्न 10.
बिना भाग किए ज्ञात कीजिए कि क्या 25110 संख्या 45 से विभाज्य है।
[संकेत : 5 और 9 सह-अभाज्य संख्याएँ हैं। दी हुई संख्या की 5 और 9 से विभाज्यता की जाँच कीजिए।]
हल :
∵संख्या 25110 में इकाई के स्थान पर 0 है। अतः संख्या 25110, 5 से विभाज्य है।
पुनः संख्या के अंकों का योग = 2 + 5 + 1 + 1 + 0 = 9, जो कि 9 से विभाज्य है।
इसलिए संख्या 25110, 9 से विभाज्य है।
अतः संख्या 25110, 45 से विभाज्य है।

प्रश्न 11.
संख्या 18, 2 और 3 से विभाज्य है। यह 2 x 3 = 6 से भी विभाज्य है। इसी प्रकार एक संख्या 4 और 6 दोनों से विभाज्य है। क्या हम कह सकते हैं कि वह संख्या 4 x 6 = 24 से भी विभाज्य होगी। यदि नहीं, तो अपने उत्तर की पुष्टि के लिए एक उदाहरण दीजिए।
हल :
यह आवश्यक नहीं है कि जो संख्या 4 और 6 से विभाज्य होगी वह उनके गुणनफल 4 x 6 = 24 से भी विभाज्य होगी।
क्योंकि 4 और 6 सह-अभाज्य संख्याएँ नहीं हैं।
संख्या 36, 4 और 6 दोनों से विभाज्य है, परन्तु संख्या 36 संख्या 24 से विभाज्य नहीं है।

प्रश्न 12.
मैं चार भिन्न-भिन्न अभाज्य गुणनखण्डों वाली सबसे छोटी संख्या हूँ। क्या आप मुझे ज्ञात कर सकते
हल :
चार भिन्न-भिन्न अभाज्य संख्याएँ 2, 3, 5 और 7 हैं।
∴अभीष्ट संख्या = 2 x 3 x 5 x 7 = 210

पाठ्य-पुस्तक पृष्ठ संख्या # 68

प्रयास कीजिए

प्रश्न 1.
निम्न का म. स. ज्ञात कीजिए :
(i) 24 और 36
(ii) 15, 25 और 30
(iii) 8 और 12
(iv) 12, 16 और 28
हल :
(i)

इस प्रकार 24 = 2 x 2 x 2 x 3.
36 = 2 x 2 x 3 x 3
24 और 36 के सार्व गुणनखण्ड 2, 2 और 3 हैं।
अतः 24 और 36 का म. स. = 2 x 2 x 3 = 12

(ii) ∵15 = 3 x 5
25 = 5 x 5
30 = 2 x 3 x 5
∴ म. स. = 5

(iii) ∵8 = 2 x 2 x 2
12 = 2 x 2 x 3
∴म. स. = 2 x 2 =4

(iv) ∵12 = 2 x 2 x 3
16 = 2 x 2 x 2 x 2
28 = 2 x 2 x 7
∴म. स. = 2 x 2 = 4

MP Board Class 6th Maths Solutions

MP Board Class 6th Maths Solutions Chapter 3 संख्याओं के साथ खेलना Ex 3.4

पाठ्य-पुस्तक पृष्ठ संख्या # 63

प्रश्नावली 3.4

प्रश्न 1.
निम्न के सार्व गुणनखण्ड ज्ञात कीजिए :
(a) 20 और 28
(b) 15 और 25
(c) 35 और 50
(d) 56 और 120
हल :
(a) 20 के सभी गुणनखण्ड
= 1, 2, 4, 5, 10, और 20 …(1)
28 के सभी गुणनखण्ड = 1, 2, 4, 7, 14 और 28 …(2)
∴20 और 28 के सार्व गुणनखण्ड = 1, 2 और 4

(b) 15 के सभी गुणनखण्ड = 1, 3, 5 और 15 …(1)
∴25 के सभी गुणनखण्ड = 1, 5 और 25 …(2)
∴15 और 25 के सार्व गुणनखण्ड = 1 और 5

(c) 35 के सभी गुणनखण्ड = 1, 5, 7 और 35 …(1)
50 के सभी गुणनखण्ड = 1, 2, 5, 10, 25 और 50 …(2)
∴35 और 50 के सार्व गुणनखण्ड = 1 और 5

(d) 56 सभी गुणनखण्ड = 1, 2, 4, 7, 8, 14, 28 और 56 ….(1)
120 के सभी गुणनखण्ड = 1, 2, 3, 4, 5, 6, 8, 10, 12, 15, 20, 24, 30, 40, 60 और 120 …(2)
∴56 और 120 के सार्व गुणनखण्ड = 1, 2, 4, और 8

प्रश्न 2.
निम्न के सार्व गुणनखण्ड ज्ञात कीजिए :
(a) 4, 8 और 12
(b) 5, 15 और 25
हल :
(a) 4 के सभी गुणनखण्ड = 1, 2 और 4
8 के सभी गुणनखण्ड = 1, 2, 4 और 8
12 के सभी गुणनखण्ड = 1, 2, 3, 4, 6 और 12
∴4,8 और 12 के सार्व गुणनखण्ड = 1,2 और 4

(b) 5 के सभी गुणनखण्ड =1 और 5
15 के सभी गुणनखण्ड = 1, 3, 5 और 15
25 के सभी गुणनखण्ड = 1, 5 और 25
∴5, 15 और 25 के सार्व गुणनखण्ड = 1 और 5

प्रश्न 3.
निम्न के प्रथम तीन सार्व गुणज ज्ञात कीजिए :
(a) 6 और 8
(b) 12 और 18
हल :
(a) 6 के गुणज = 6, 12, 18, [24], 30, 36, 42, [48], 54, 60, 66, [72] ,…..
8 के गुणज = 8, 16, [24], 32, 40, 48, 56, 64, [72],….
∴6 और 8 के प्रथम तीन सार्व गुणज =24, 48 और 72

(b) 12 के गुणज = 12, 24, [36], 48, 60, [72], 84, 96, [108], 120,…..
18 के गुणज = 18, [36], 54, [72], 90, [108], 126,……
∴12 और 18 के प्रथम तीन सार्व गुणज
= 36, 72 और 108

प्रश्न 4.
100 से छोटी ऐसी सभी संख्याएँ लिखिए जो 3 और 4 के सार्व गुणज हैं।
हल :
3 के गुणज = 3, 6, 9, [12], 15, 18, 21, 24, 27, 30, 33, [36], 39, 42, 45, [48], 51, 54, 57, [60], 63, 66, 69, [72], 75, 78, 81, [84], 87, 90, 93, [96], 99……
4 के गुणज = 4, 8, [12], 16, 20, [24], 28, 32, [36], 40, 44, [48], 52, 56, [60], 64, 68, [72], 76, 80, [84], 88, 92, [96] ,…..
∴3 और 4 के सार्व गुणज = 12, 24, 36,48, 60, 72, 84, 96,….

प्रश्न 5.
निम्नलिखित में से कौन-सी संख्याएँ सहअभाज्य हैं ?
(a) 18 और 35
(b) 15 और 37
(c) 30 और 415
(d) 17 और 68
(e) 216 और 215
(f) 81 और 16
हल :
(a) ∵18 के गुणनखण्ड = 1, 2, 3, 6, 9 और 18
35 के गुणनखण्ड = 1, 5, 7, और 35
चूँकि इनका सार्व गुणनखण्ड 1 है।
∴18 और 35 का 1 के अतिरिक्त सार्व गुणनखण्ड नहीं है।
अतः 18 और 35 सह-अभाज्य संख्याएँ हैं।

(b) ∵15 के गुणनखण्ड = 1, 3, 5 और 15
37 के गुणनखण्ड = 1 और 37
∴इनका सार्व गुणनखण्ड 1 है।
∴15 और 37 का 1 के अतिरिक्त सार्व गुणनखण्ड नहीं है।
अतः 15 और 37 सह-अभाज्य संख्याएँ हैं।

(c) ∵30 के गुणनखण्ड = 1, 2, 3, 5, 6, 10, 15 और 30
415 के गुणनखण्ड = 1, 5, 83 और 415
∴इनके सार्व गुणनखण्ड 1 और 5 हैं।
अत: 30 और 415 सह-अभाज्य संख्याएँ नहीं हैं।

(d) ∵17 के गुणनखण्ड = 1 और 17
68 के गुणनखण्ड = 1, 2, 4, 17, 34 और 68
∴17 और 68 के सार्व गुणनखण्ड = 1 और 17
अतः 17 और 68 सह-अभाज्य संख्याएँ नहीं हैं।

(e) ∵216 के गुणनखण्ड = 1, 2, 3, 4, 6, 8, 9, 12, 18, 24, 27, 36, 54, 72, 108 और 216
215 के गुणनखण्ड = 1, 5, 43 और 215
∴216 और 215 के सार्व गुणनखण्ड = 1
अत: 216 और 215 सह-अभाज्य संख्याएँ हैं।

(f) ∵81 के गुणनखण्ड = 1, 3, 9, 27 और 81
16 के गुणनखण्ड = 1, 2, 4, 8 और 16
∴81 और 16 के सार्व गुणनखण्ड = 1
अत : 81 और 16 सह-अभाज्य संख्याएँ हैं।

प्रश्न 6.
एक संख्या 5 और 12 दोनों से विभाज्य है। किस अन्य संख्या से यह संख्या सदैव विभाजित होगी?
हल :
दी हुई संख्या 5 और 12 के गुणनफल से विभाजित होगी।
अभीष्ट संख्या = 5 x 12 = 60
अतः संख्या 60 से सदैव विभाज्य होगी।

प्रश्न 7.
एक संख्या 12 से विभाज्य है। और कौन-सी संख्याएँ हैं जिनसे यह संख्या विभाज्य होगी?
हल :
12 के गुणनखण्ड = 1, 2, 3, 4, 6 और 12
∴संख्या 12 से विभाज्य है। इसलिए यह 12 के गुणनखण्डों से भी विभाज्य होगी।
अतः संख्या 2, 3, 4 और 6 से भी विभाज्य होगी।

पाठ्य-पुस्तक पृष्ठ संख्या # 65

प्रयास कीजिए

प्रश्न 1.
16, 28 और 38 के अभाज्य गुणनखण्डन लिखिए।
हल :
(i)

∴16 के अभाज्य गुणनखण्ड = 2 x 2 x 2 x 2

(ii)

∴28 के अभाज्य गुणनखण्डन = 2 x 2 x 7.

(iii)

∴38 के अभाज्य गुणनखण्ड = 2 x 19

पाठ्य-पुस्तक पृष्ठ संख्या # 66

प्रश्न 1.
ऐसा ही निम्न संख्याएँ लेकर कीजिए :
(a) 8
(b) 12
हल :

MP Board Class 6th Maths Solutions

MP Board Class 6th Social Science Solutions Chapter 8 The Realms of the Earth

MP Board Class 6th Social Science Chapter 8 Text Book Exercise

MP Board Class 6th Social Science Chapter 8 Short Answer Type Questions

Question 1.
Question (a)
How many realms of earth are there?
Answer:
There are three realms of earth.

Question (b)
What is meant by Lithosphere?
Answer:
The realm of the earth consisting of rocks, stones and soil is called lithosphere.

Question (c)
What are mountains?
Answer:
Mountains are highly elevated lands with steep slopes. They are higher than the surrounding areas. They have high peaks and deep valleys.

Question (d)
Define Biosphere?
Answer:
The zone of island, water and air which contains all forms of life is called plain and a plateau.

Plain:

1. Plains are mostly made of the slit, mud and sand carried by the rivers.
2. The plains offer most favourable living condition to the human being.
3. The plains are suitable for agriculture.

Plateau:

1. Plateaus are moderately elevated lands with flat tops.
2. The life in plateaus are not very comfortable.
3. The plateaus are not suitable for agriculture.

MP Board Class 6th Social Science Chapter 8 Long Answer Type Questions

Question 2.
Question (a)
What is lithosphere? Describe its different forms?
Answer:
1. The realm of the earth consisting of rocks, stones and soil is called lithosphere.

2. The small part of land surrounded by water are called islands and large masses of land are called continents. The surface of the land is not even.

3. Some parts are plain, others are rigid and some are very much elevated or too low. According to the shape of these parts, they are called mountains, plateaus and plains. These shapes are found in all the continents.

Question (b)
What is biosphere? How organisms depend on each other in the eco system?
Answer:
1. There is a very narrow zone on Earth where land, water and air come in contact with each other. This is called biosphere. All the living things such as plants, animals, and human being exist only in this zone (the biosphere). So biosphere is of great significance for all of us.

2. There are ten lakh species of animals in the animal kingdom. It includes microscopic organisms to large animals like the elephant and the whale fish.

3.The organisms in the animal kingdom move from one place to the other. Three lakh species of plants are found in the plant kingdom. It includes microscopic algae to large trees.

Question 3.
Give one term for the following:

1. The mixture of gases that envelopes the earth.
2. The large quantity of water collected in earth.
3. The part of land which rise high above the surrounding area.
4. The part of land which rise abruptly from the low land and stretch far.
5. Low – lying and relatively flat stretchs of land.
6. The zone made by the Lithosphere, Hydrosphere and Atmosphere.

Answer:

1. Air
2. Oceans
3. Mountain
4. Plateau
5. Plains
6. Biosphere.

Question 4.
Match the Column

Answer:

Question 5.
Fill in the blanks:

1. The land part of the earth is called ………………
2. Lithosphere, hydrosphere and atmosphere collectively form ………………..
3. Antarctica is spread on the …………… part of the earth.
4. The gas which is found in least quantity in the atmosphere is ……………..
5. The things given to us by nature should be used for …………….

Answer:

1. lithosphere
2. environment
3. southern
4. carbon – dioxide
5. human welfare.

Project Work

Question 1.
Make clay models of mountain, plateau and plain?
Answer:
Please do with the help of your teacher.

Question 2.
Look at the oceans in a map of the world and write their names as per their size?
Answer:
Please do with the help of your teacher.

Question 3.
Show the following in the given map?

1. Arctic Ocean
2. Indian Ocean
3. Australia
4. North America
5. Africa

Answer:

MP Board Class 6th Social Science Solutions