Bhagya

MP Board Class 8th Maths Solutions Chapter 15 Introduction to Graphs Ex 15.1

Question 1.
The following graph shows the temperature of a patient in a hospital, recorded every hour.

(a) What was the patient’s temperature at 1 p.m.?
(b) When was the patient’s temperature 38.5° C?
(c) The patient’s temperature was the same two times during the period given. What were these two times ?
(d) What was the temperature at 1.30 p.m. ? How did you arrive at your answer?
(e) During which periods did the patient’s temperature showed an upward trend?
Solution:
(a) At 1 p.m. patient’s temperature was 36.5°C.
(b) At 12 noon the patient’s temperature was 38.5°C.
(c) The patient’s temperature was 36.5°C at 1 p.m. and 2 p.m.
(d) The patient’s temperature was 36.5°C at 1.30 p.m. (because the temperature of the patient was constant from 1 p.m. to 2 p.m.). The point between 1 p.m. and 2 p.m. on the x-axis and equidistant from them will represent 1 : 30 p.m. Similarly, the point on the y-axis, between 36°C and 37°C and equidistant from them will represent 36.5° C.
(e) 9 a.m. to 10 a.m., 10 a.m. to 11 a.m. and 2 p.m. to 3 p.m.

Question 2.
The following line graph shows the yearly sales figures for a manufacturing company.
(a) What were the sales in
(i) 2002
(ii) 2006?
(b) What were the sales in
(i) 2003
(ii) 2005?
(c) Compute the difference between the sales in 2002 and 2006.
(d) In which year was there the greatest difference between the sales as compared to its previous year?

Solution:
(a) (i) In 2002 company’s sales were ₹ 4 crores.
(ii) In 2006 company’s sales were ₹ 8 crores.

(b) (i) The sales of a manufacturing company in 2003 were ₹ 7 crores.
(ii) The sales of a manufacturing company in 2005 were ₹ 10 crores.

(c) The difference between the sales in 2002 and 2006.
= Sales in 2006 – Sales in 2002
= ₹ 8 crores – ₹ 4 crores = ₹ 4 crores.

(d) In year 2005, the difference between the sales was greatest as compared to its previous year.

Question 3.
For an experiment in Botany, two different plants, plant A and plant B were grown under similar laboratory conditions. Their heights were measured at the end of each week for 3 weeks. The results are shown by the following graph.

(a) How high was Plant A after
(i) 2 weeks,
(ii) 3 weeks?
(b) How high was Plant B after
(i) 2 weeks,
(ii) 3 weeks?
(c) How much did Plant A grow during the 3rd week?
(d) How much did Plant B grow from the end of the 2nd week to the end of the 3rd week?
(e) During which week did Plant A grow most?
(f) During which week did Plant B grow least?
(g) Were the two plants of the same height during any week shown here? Specify.
Solution:
(a) (i) After 2 weeks the height of plant A was 7 cm.
(ii) After 3 weeks the height of plant A was 9 cm.

(b) (i) After 2 weeks the height of plant B was 7 cm.
(ii) After 3 weeks the height of plant B was 10 cm.
(c) During the 3rd week plant A grew (9 – 7) cm = 2 cm.
(d) The plant B grew from the end of 2nd week to the end of 3rd week
= 10 cm – 7 cm = 3 cm
(e) The plant A grew most during second week.
(f) The plant B grew least during first week.
(g) Yes, at the end of second week.

Question 4.
The following graph shows the temperature forecast and the actual temperature for each day of a week.
(a) On which days was the forecast temperature the same as the actual temperature?
(b) What was the maximum forecast temperature during the week?
(c) What was the minimum actual temperature during the week?
(d) On which day did the actual temperature differ the most from the forecast temperature?

Solution:
(a) The forecast temperature is the same as actual temperature on : Tuesday, Friday and Sunday.
(b) The maximum forecast temperature during the week was 35°C.
(c) The minimum actual temperature during the week was 15°C.
(d) On Thursday, the actual temperature differed the most from the forecast temperature.

Question 5.
Use the tables below to draw linear graphs.
(a) The number of days a hill side city received snow in different years

(b) Population (in thousands) of men and women in a village in different years.

Solution:
(a) By using a given information we draw a line graph, where the horizontal line i.e. x-axis shows the year and the vertical line i.e. y-axis shows the number of days.

(b) The horizontal line i.e. x-axis shows the year and the vertical line i.e. y-axis shows the number of men and number of women.

Question 6.
A courier-person cycles from a town to a neighbouring suburban area to deliver a parcel to a merchant. His distance from the town at different times is shown by the following graph.
(a) What is the scale taken for the time axis?
(b) How much time did the person take for the travel?
(c) How far is the place of the merchant from the town?
(d) Did the person stop on his way? Explain.
(e) During which period did he ride fastest?

Solution:
(a) 4 units = 1 hour is the scale taken for the time axis.
(b) Time taken by a person for the travel = (1 +1 + 1+ \(\frac{1}{2}\)) hours = 3\(\frac{1}{2}\) hours.
(c) The place of the merchant from the town is at a distance of 22 km.
(d) Yes, this is indicated by the horizontal part of the graph from 10 a.m. -10.30 a.m. where the stability of a distance has been shown.
(e) Between 8.00 a.m. – 9.00 a.m. he rode the fastest.

Question 7.
Can there be a time-temperature graph as follows? Justify your answer.


Solution:
Figure (i) shows temperature is increasing over time.
Figure (ii) shows temperature is decreasing over time.
Figure (iii) is not a possible time – temperature graph. because, at the same time, temperature can’t be different.
Figure (iv) shows temperature is constant over time

MP Board Class 8th Maths Solutions

MP Board Class 8th Hindi Bhasha Bharti Solutions Chapter 14 नव संवत्सर

नव संवत्सर बोध प्रश्न

प्रश्न 1.
निम्नलिखित शब्दों के अर्थ शब्दकोश से खोजकर लिखिए
उत्तर
नव संवत्सर = एक वर्ष की अवधि का समय; मत्स्य = मछली; उत्सव = पर्व, त्यौहार; कार्तिकादि = कार्तिक माह से प्रारम्भ होने वाला; अमान्त = अमावस्या को समाप्त होने वाला पक्ष; शृंगार = सजावट, सजना, सजाना; जयन्ती = जन्मदिन पीर=संत, महात्मा; सृष्टि रचना, जन्म देना, बनाना; वध = मार देना, नष्ट कर देना; चैत्रादि चैत्र माह से शुरू होने वाला; पूर्णिमान्त = पूर्णमासी को समाप्त होने वाला पक्ष; ऋतु  = मौसम; सम्वर्द्धन = विकास, वृद्धि, बढ़ोतरी; आततायी = कष्ट पहुँचाने वाला, अत्याचारी।

प्रश्न 2.
निम्नलिखित प्रश्नों के उत्तर संक्षेप में लिखिए

(क) नव संवत्सर से क्या तात्पर्य है ?
उत्तर
नव संवत्सर से तात्पर्य है-नये वर्ष का प्रारम्भ। यह नव संवत्सर चैत्र मास की शुक्ल पक्ष की प्रतिपदा से शुरू होता है।

(ख) गुड़ी पड़वा नाम का क्या अर्थ है ?
उत्तर
गुड़ी’ का अर्थ है ध्वज या झण्डी। पड़वा का अर्थ है प्रतिपदा। लोक में एक परम्परा व्याप्त है। उसके अनुसार यह माना जाता है कि इसी दिन श्री रामचन्द्रजी ने किष्किधा के राजा बाली का वध किया और उसके स्वेच्छाचारी राज्य का अन्त कर दिया। बाली वध के बाद वहाँ की प्रजा ने पताकाएँ फहराई और उत्सव मनाया। इन पताकाओं को महाराष्ट्र में गुड़ी कहते हैं। आज भी वहाँ इस दिन आँगन में बाँस के सहारे गुड़ी खड़ी की जाती है। इसलिए चैत्र शुक्ल प्रतिपदा को गुड़ी पड़वा कहा जाता है।

(ग) विक्रम संवत् किसने प्रारम्भ किया?
उत्तर
उज्जयिनी के महान् सम्राट् विक्रमादित्य ने विदेशी आक्रमणकारी शकों पर विजय प्राप्त की। इस विजय की खुशी में उन्होंने विक्रम संवत् आरम्भ किया। यह विक्रम संवत् ईसा के ईसवीय सन् से 57 वर्ष पूर्व प्रारम्भ किया गया।

(घ) बसन्त ऋतु का आगमन किस भारतीय माह में होता है ?
उत्तर
बसन्त ऋतु का आगमन चैत्र माह में होता है।

(ङ) दक्षिण भारत में विक्रम संवत् का प्रारम्भ किस भारतीय मास से होता है ?
उत्तर
दक्षिण भारत में विक्रम संवत् का प्रारम्भ कार्तिक मास से होता है।

प्रश्न 3.
रिक्त स्थानों की पूर्ति कीजिए
(क) चैती चाँद पर्व भगवान ……….. की जयन्ती के रूप में मनाते हैं।
(ख) प्रत्येक चार वर्ष बाद अतिरिक्त माह को ……………… माह तथा उसके वर्ष को …………… वर्ष कहते हैं।
(ग) नवरात्रि बासंतीय..”माह में तथा नवरात्रिशारदीय ………… माह में आती है।
उत्तर
(क) झूलेलाल
(ख) अधिक, चन्द्रमास,
(ग) चैत्र, कार्तिक।

प्रश्न 4.
निम्नलिखित प्रश्नों के उत्तर विस्तार से लिखिए
(क) संवत्सरों का नामकरण किस प्रकार किया जाता है ?
उत्तर
संवत्सर का उपयोग समय की गणना के लिए एक वर्ष की अवधि के अर्थ में किया जाता है। ऋग्वेद और अथर्ववेद आदि प्राचीन ग्रन्थों में भी संवत्सर का एक काल चक्र के रूप में उल्लेख है। इस प्रकार समय की गणना करने की विधि अति प्राचीन है। जिस तरह हमारे यहाँ दिनों और महीनों के नाम दिए गए हैं; उसी तरह संवत्सरों का भी नामकरण किया गया है। ये साठ वर्ष बाद पनः एक चक्र के रूप में आते रहते हैं। विक्रम संवत 2063 का नाम विकारी नामक संवत्सर है। इसके पहले के दो संवत्सरों के नाम ‘हेमलम्ब नाम’ और ‘विलम्ब नाम संवत्सर थे।

(ख) भगवान झूलेलाल की पूजा क्यों की जाती है ?
उत्तर
भगवान झूलेलाल की पूजा इसलिए की जाती है कि वे साम्प्रदायिक सद्भाव और एकता के प्रतीक हैं। उन्होंने सम्पूर्ण मानव जाति के कल्याण के लिए समानता के आधार पर स्थापित धर्म की सराहना की। उन्होंने धर्म के सच्चे स्वरूप का विवेचन कर लोगों को सही आचरण करने की सलाह दी। उन्होंने तत्कालीन मुस्लिम शासकों को कट्टरपंथी रुख न अपनाने के लिए विनती की। उन्होंने साम्प्रदायिक सद्भाव और एकता कायम रखने के लिए लोगों को बताया कि सत्य एक है, ईश्वर एक है, अल्लाह एक है। उसके नाम व रूप अनेक हैं। भगवान झूलेलाल ने सभी लोगों को विनम्रता और अपने कर्त्तव्य धर्म का पालन करने का उपदेश दिया। उन्होंने लोगों में सद्बुद्धि बनी रहे, इसके लिए समय-समय पर सभाएँ की। इनका जन्म संवत् 1007 वि. में नसरपुर में सूर्यवंशी क्षत्रियकुल में हुआ। इनके पिता का नाम रतन राय और माता का नाम देवकी था। कहते हैं कि इनके जन्म के समय से ही प्रत्येक हिन्दू घर में कलश पूजन (वरुण की पूजा) होने लगी। भगवान झूलेलाल की पूजा-अर्चना करने से मन की अभिलाषाएँ पूर्ण हो जाती हैं। ऐसा माना जाता है।

(ग) सौरवर्ष और चन्द्रवर्ष में क्या अन्तर है?
उत्तर
यह पृथ्वी सूर्य की परिक्रमा लगभग 365 दिन में करती है। यह अवधि एक नक्षत्र सौरवर्ष कहलाती है जबकि चन्द्रवर्ष लगभग 354 दिन का होता है। इसे 360 तिथियों में बाँटते हैं। सौरवर्ष और चन्द्रवर्ष में सामंजस्य बनाने के लिए प्रत्येक 32 या 33 चन्द्रमासों के बाद एक अतिरिक्त चन्द्रमास जोड़ दिया जाता है। इस अतिरिक्त मास को अधिक मास या मलमास या लौंद का महीना कहते हैं। जिस वर्ष लौद का महीना होता है, उस वर्ष चन्द्र वर्ष 13 महीने का होता है।

(घ) सौरवर्ष और चन्द्रवर्ष के सामंजस्य के लिए क्या विधि अपनाते हैं?
उत्तर
चन्द्रवर्ष में लगभग 354 दिन होते हैं। इसे 360 तिथियों में बाँटते हैं। सौरवर्ष और चन्द्रवर्ष में सामंजस्य बनाने के लिए प्रत्येक 32 या 33 चन्द्रमासों के बाद एक अतिरिक्त चन्द्रमास जोड़ दिया जाता है। सौरवर्ष में 365 दिन होते हैं। इस सौर वर्ष के ही कारण ऋतुओं में परिवर्तन होता है। सौरवर्ष में बारह महीने होते हैं जबकि चन्द्रवर्ष में तेरह महीने होते है।

(ङ) विक्रम संवत् के अनुसार वर्ष के महीनों के नाम लिखिए।
उत्तर
विक्रम संवत् के अनुसार वर्ष के महीनों के नाम निम्न प्रकार हैं

1. चैत्र
2. बैसाख
3. ज्येष्ठ
4. आषाढ़
5. श्रावण
6. भाद्रपद
7. आश्विन (क्वार)
8. कार्तिक
9. मार्गशीर्ष
10. पौष
11. माघ
12. फाल्गुन।

(च) विक्रम संवत् की प्रथम तिथि में कौन-कौन से प्रसंग जुड़े हैं ? लिखिए।
उत्तर
विक्रम संवत् को प्रथम तिथि को गुड़ी पड़वा कहते हैं। इस दिन से भारतीय नववर्ष या संवत्सर का प्रारम्भ होता है। इसे चैत्र शुक्ल प्रतिपदा भी कहते हैं। प्रजापति ब्रह्मा ने इसी तिथि को सृष्टि का सृजन किया। भगवान विष्णु ने भी इसी तिथि को मत्स्यावतार के रूप में अवतार लिया था। साथ ही यह भी कहा जाता है कि सतयुग का भी प्रारम्भ इसी तिथि को हुआ था। इसी प्रतिपदा के (पड़वा के) दिन भगवान श्री रामचन्द्रजी ने किष्किन्धा के राजा बाली का वध किया और उसके स्वेच्छाचारी राज्य का अन्त किया था। बाली वध के बाद प्रजा ने पताकाएँ बनाई, उन्हें फहराया गया और उत्सव मनाया गया, झण्डियों को गुड़ी कहते हैं। इसलिए इस तिथि को गुड़ी पड़वा कहते हैं। इस तरह इस तिथि से अनेक प्रसंग जुड़े हुए हैं।

नव संवत्सर भाषा-अध्ययन

प्रश्न 1.
निम्नलिखित शब्दों का उच्चारण कीजिए और अपने वाक्यों में प्रयोग कीजिए-
चैत्र, पौराणिक, किष्किंधा, ऋग्वेद, अथर्ववेद, पूर्णिमा, विक्रमादित्य, स्वेच्छाचारी।
उत्तर
विद्यार्थी उपर्युक्त शब्दों को ठीक-ठीक पढ़कर उनका शुद्ध उच्चारण करने का अभ्यास करें।
वाक्य प्रयोग-

1. चैत्र-चैत्र मास में बसन्ती हवाएँ चलती हैं।
2. पौराणिक-भारतवर्ष में अनेक पौराणिक कथाएँ प्रचलित हैं।
3. किष्किधा-किष्किधा में बाली का शासन था।
4. ऋग्वेद-ऋग्वेद सबसे प्राचीन ग्रन्थ है।
5. अथर्ववेद-अथर्ववेद पर अभी तक अधिक शोध नहीं
6. पूर्णिमा-पूर्णिमा के दिन हम सभी उपवास करते हैं।
7. विक्रमादित्य-विक्रमादित्य ने विक्रमी संवत् चलाया।
8. स्वेच्छाचारी-किष्किंधा राज्य का शासक स्वेच्छाचारी

प्रश्न 2.
निम्नलिखित शब्दों में ‘इक’ प्रत्यय का प्रयोग करके नए शब्द बनाइए
प्रसंग, समाज, परिवार, नीति, साहित्य, मूल।
उत्तर

1. प्रसंग + इक = प्रासंगिक
2. समाज + इक = सामाजिक
3. परिवार + इक = पारिवारिक
4. नीति + इक = नैतिक
5. साहित्य + इक = साहित्यिक
6. मूल + इक = मौलिक।

प्रश्न 3.
निम्नलिखित शब्दों की संधि विच्छेद कीजिए
स्वेच्छाचारी, विक्रमादित्य, सूर्योदय, पुस्तकालय, नरेन्द्र नीरोग, निष्कपट, प्रात:काल।
उत्तर

प्रश्न 4.
निम्नलिखित शब्दों के अर्थ शब्दकोश से खोजकर लिखिए और अपने वाक्य में प्रयोग कीजिए
पर्व, गणना, मलमास, उपलक्ष्य, प्रस्थान, सम्वर्द्धन।
उत्तर

प्रश्न 5.
निम्नलिखित शब्दों को वर्णक्रम के अनुसार लिखिए
शेखर, नव, पता, अखिल, चैत्र, उपयोग, ग्रंथों, ऋग्वेद, संवत्, विक्रम, बाद, रोचक, दक्षिण, और, तेरह, माह, कहा, आगमन।
उत्तर
अखिल, आगमन, उपयोग, और, ऋग्वेद, कहा, ग्रन्थों, चैत्र, तेरह, दक्षिण, नव, पता, बाद, माह, रोचक, विक्रम, शेखर, संवत्।

प्रश्न 6.
नीचे लिखे वाक्यों में विशेषण और विशेष्य छाँटकर तालिका में लिखिए
(क) नववर्ष बीते तो कितने दिन हो गए।
(ख) प्राचीन ग्रन्थों में भी संवत्सर का एक काल चक्र के रूप में उल्लेख है।
(ग) प्रत्येक माह के दो पक्ष होते हैं।
(घ) यह तो तुमने बड़ी रोचक बात बताई।
उत्तर

नव संवत्सर परीक्षोपयोगी गद्यांशों की व्याख्या 

(1) पौराणिक कथाओं के अनुसार प्रजापति ब्रह्मा ने इसी तिथि को सृष्टि का सृजन किया था, भगवान विष्णु भी मत्स्यावतार के रूप में इसी तिथि को प्रकट हुए थे और सतयुग के प्रारम्भ होने की भी यही तिथि है।’

शब्दार्थ-पौराणिक = पुराण सम्बन्धी; सृष्टि = सभी प्राणियों का; सृजन = निर्माण; मत्स्यावतार = मछली के अवतार; प्रकट = अवतरित; प्रारम्भ होने की = शुरू होने की।

सन्दर्भ-प्रस्तुत गद्यांश हमारी पाठ्य-पुस्तक भाषा-भारती के पाठ ‘ नव संवत्सर’ से अवतरित है।

प्रसंग-इसमें लेखकगण नव संवत्सर के शुरू होने और उसके महत्त्व को बताते हैं।

व्याख्या-पुराण की अनेक कथाओं में बताया गया है कि विश्व के सभी प्राणियों के स्वामी ब्रह्मा ने इसी तिथि को उनकी रचना की थी। भगवान विष्णु ने भी इसी तिथि (दिनांक) को मत्स्यावतार (मछली के रूप में जन्म लेना) के रूप में अवतरित हुए थे। साथ ही, इसी तिथि को सतयुग का प्रारम्भ हुआ था। यह तिथि चैत्र शुक्ल प्रतिपदा ही है जिस दिन से संवत्सर का प्रारम्भ होता है।

(2) गुडी का अर्थ है ‘ध्वज या झण्डी’ और पड़वा कहते हैं प्रतिपदा को। लोक परम्परा के अनुसार माना जाता है कि इसी दिन श्री रामचन्द्रजी ने किष्किंधा के राजा बाली का वध कर उसके स्वेच्छाचारो राज का अन्त किया था। बाली वध के पश्चात् वहाँ की प्रजा ने पताकाएँ, जिन्हें महाराष्ट्र में गुड़ी कहते हैं, फहराकर उत्सव मनाया था। आज वहाँ आँगन में बांस के सहारे गुड़ी खड़ी की जाती है। इसलिए चैत्र शुक्ल प्रतिपदा को गुड़ी प्रतिपदा कहते

शब्दार्थ-गुड़ी = झण्डी; परम्परा = रीति; वधकर = बाण से मारकर; स्वेच्छाचारी = अपनी इच्छा के अनुसार अन्त किया समाप्त किया; पताकाएँ = झण्डियाँ; उत्सव = त्योहार; पड़वा = प्रतिपदा

सन्दर्भ-पूर्व की तरह। प्रसंग-इसमें चैत्र प्रतिपदा से जुड़ी बातें बताई गई हैं।

व्याख्या-गुड़ी का अर्थ झण्डी अथवा ध्वज होता है। प्रतिपदा को पड़वा कहते हैं। लोक में प्रचलित एक परम्परा के अनुसार यह बात मानी जाती है कि किष्किन्धा का राजा बाली था। बाली का वध श्री रामचन्द्रजी ने इसी दिन (चैत्र शुक्ल प्रतिपदा को) किया था और इस प्रकार उसके राज्य का अन्त कर दिया था। वह अपने राज्य का संचालन अपनी इच्छा से करता था। जैसे ही राजा बाली का वध कर दिया गया, वैसे ही वहाँ की प्रजा ने खुशी मनाई और घर-घर पताकाएँ फहराई गई। इसी पड़वा या प्रतिपदा के दिन वहाँ उत्सव मनाया गया। महाराष्ट्र में पताकाओं को गुड़ी कहते हैं। वहीं इस प्रतिपदा के दिन आँगन में एक बाँस गाड़ दिया जाता है। उसके सहारे गुड़ी खड़ी की जाती है। इस कारण चैत्र शुक्ल प्रतिपदा को गुड़ी पड़वा कहते हैं।

(3) विक्रम संवत् का प्रचलन उज्जयिनी के महान् सम्राट विक्रमादित्य ने विदेशी आक्रमणकारी शक राजाओं पर अपनी विजय के उपलक्ष्य में ईसा पूर्व सन् 57 में किया

शब्दार्थ-प्रचलन = प्रारम्भ; उज्जयिनी = उज्जैन; आक्रमणकारी = आक्रमण करने वाले या आक्रान्ता; शक = शक जाति जो विदेशों के आक्रमण करने वाले थे; उपलक्ष्य में = सन्दर्भ में, विषय में; विजय = जीत।

सन्दर्भ-पूर्व की तरह।

प्रसंग-इन पंक्तियों में विक्रम संवत् के प्रारम्भ होने के विषय में बताया जा रहा है।

व्याख्या-उज्जयिनी के एक महान् सम्राट थे। उनका नाम विक्रमादित्य था। शक राजाओं ने विक्रमादित्य के राज्य पर आक्रमण कर दिया था। इन विदेशी आक्रमण करने वाले शक राजाओं को विक्रमादित्य ने परास्त कर दिया। उन पर जीत प्राप्त की। अपनी जीत के सन्दर्भ की खुशी में यह संवत् चलाया। यह संवत् ईसा सन् से सत्तावन बर्ष पूर्व प्रारम्भ किया गया। इस संवत् का नाम उनके नाम के आधार पर विक्रम संवत् किया गया।

(4) उत्तर भारत में विक्रम संवत् का प्रारम्भ चैत्र प्रतिपदा से होता है, इसे चैत्रादि कहते हैं जबकि दक्षिण भारत में संवत्सर का आरम्भ कार्तिक शुक्ल पक्ष की प्रतिपदा से माना जाता है, इसे कार्तिकादि कहते हैं। व्यापारी लोग भी कार्तिकादि नववर्ष मनाते हैं, इसलिए वे दीवाली पर नया बहीखाता प्रारम्भ करते हैं।

शब्दार्थ-प्रारम्भ = प्रचलन, शुरुआत; प्रतिपदा = पड़वा; चैत्रादि- चैत्र (चैत महीने) का प्रारम्भ; कार्तिकादि = कार्तिक महीने का प्रारम्भ; नववर्ष = नया साल; प्रारम्भ = शुरू।

सन्दर्भ-पूर्व की तरह।

प्रसंग-नव संवत्सर के प्रचलन के दो रूप बताये गये हैं।

व्याख्या-उत्तरी भारत में नव संवत्सर का प्रारम्भ चैत्र के शुक्ल पक्ष की प्रतिपदा (पड़वा) से माना जाता है। इसे | चैत्रादि कहते हैं। जबकि दक्षिण भारत में नव संवत्सर का प्रचलन कार्तिक महीने की शुक्ल पक्ष की प्रतिपदा से शुरू होना माना गया है। इसको कार्तिकादि कहते हैं। व्यापारी वर्ग कार्तिकादि नववर्ष का उत्सव मनाते हैं। यही कारण है कि वे दीपावली पर नया बहीखाता बनाते हैं और उसे प्रारम्भ करते हैं।

(5) चैत्र माह में बसन्त ऋतु का आगमन होता है। बसन्त . ऋतु में प्रकृति भी अपना नव श्रृंगार करती है। पेड़ अपने पुराने पत्ते गिराकर नए पत्ते धारण करते हैं। ऋतु परिवर्तन के अवसर पर हमारे यहाँ नवरात्रि पर्व मनाने की परम्परा है। चैत्र शुक्ल प्रतिपदा से प्रारम्भ होने वाली नवरात्रि वासन्तीय नवरात्रि एवं पितृमोक्ष अमावस्था के पश्चात् प्रारम्भ होने वाली नवरात्रि शारदीय कहलाती हैं। ‘वासन्तीय नवरात्रि’ का समापन रामनवमी और ‘शारदीय नवरात्रि’ का समापन दशहरा पर्व पर होता है।

शब्दार्थ-आगमन = आना या शुरू होना; नव श्रृंगार = नई सजावट, सजधज; धारण करते हैं = निकल आते हैं; परिवर्तन = बदलाव; परम्परा = रीति या रिवाज, प्रथा, प्रारम्भ = शुरू होना; वासन्तीय = वसन्त ऋतु की; समापन = समाप्ति, अन्त; शारदीय = शरद ऋतु की; पर्व = त्यौहार।

सन्दर्भ-पूर्व की तरह।

प्रसंग-शारदीय नवरात्रि और वासन्तीय नवरात्रि के प्रारम्भ होने की तिथि तथा उनके समापन की तिथि के विषय में बताया जा रहा है।

व्याख्या-चैत्र महीने में बसन्त ऋतु प्रारम्भ हो जाती है। बसन्त ऋतु के आने के साथ ही प्रकृति अपना नया शृंगार करती है। अपनी सजावट करती है। प्रकृति अपने स्वरूप को सजाती है। पेड़ों के पुराने पत्ते झड़ जाते हैं। उन पर नये पत्ते निकल आते हैं। प्रकृति में ऋतु सम्बन्धी परिवर्तन आ जाता है। ऋतु परिवर्तन के साथ ही हमारे यहाँ नवरात्रि का त्यौहार मनाये जाने की यह रीति है, परम्परा है। चैत्र मास की शुक्ल पक्षीय प्रतिपदा के दिन आरम्भ होने वाली नवरात्रि को वासन्तीय नवरात्रि कहा जाता है तथा पितृ पक्ष की समाप्ति पर अमावस्या के अगले – दिन से आरम्भ होने वाली नवरात्रि को शारदीय नवरात्रि कहते हैं। वासन्तीय नवरात्रि की समाप्ति रामनवमी को होती है तथा शारदीय नवरात्रि का समापन दशहरा के त्यौहार पर होता है।

MP Board Class 8th Hindi Solutions

MP Board Class 8th Maths Solutions Chapter 16 Playing with Numbers Ex 16.2

Question 1.
If 21y5 is a multiple of 9, where y is a digit, what is the value of y?
Solution:
The given number is 21y5
For this number to be multiple of 9, the sum of its digits should be a multiple of 9.
∴ 2 + 1 + y + 5 is a multiple of 9.
or 8 + y is a multiple of 9.
For y to be a single digit number,
8 + y = 9 ⇒ y = 1

Question 2.
If 31z5 is a multiple of 9, where z is a digit, what is the value of z? You will find that there are two answers for the last problem. Why is this so?
Solution:
The given number is 31z5.
For this number to be multiple of 9, the sum of its digits should be a multiple of 9.
∴ 3 + 1 + z + 5 is a multiple of 9.
or z + 9 is a multiple of 9.
∴ For z to be a single digit number,
z + 9 = 9 or z + 9 = 18
⇒ z = 0 or z = 9
Hence, z = 0, 9
We get two answers, because 9 and 18, both are multiples of 9.

Question 3.
If 24x is a multiple of 3, where x is a digit, what is the value of x? (Since 24x is a multiple of 3, its sum of digits 6 + x is a multiple of 3; so 6 + x is one of these numbers :0, 3, 6, 9, 12, 15, 18, But since x is a digit, it can only be that 6 + x = 6 or 9 o r12 or 15. Therefore, x = 0 or 3 or 6 or 9. Thus, x can have any of four different values).
Solution:
The given number 24x is a multiple of 3.
⇒ Sum of the digits of this number are also a multiple of 3.
∴ 2 + 4 + x = x + 6 is a multiple of 3.
For x to be a single digit number,
x + 6 = 6, 9, 12, 15 or x = 0, 3, 6, 9.

Question 4.
If 31z5 is a multiple of 3, where z is a digit, what might be the values of z?
Solution:
As the given number 31z5 is a multiple of 3, the sum of its digits should also be a multiple of 3.
∴ 3 + 1 + z + 5 is a multiple of 3.
or z + 9 is a multiple of 3.
Now, for z to be a single digit number,
z + 9 = 9, 12, 15, 18 or z = 0, 3, 6, 9

MP Board Class 8th Maths Solutions

MP Board Class 8th Maths Solutions Chapter 7 Cube and Cube Roots Ex 7.1

Question 1.
Which of the following numbers are not perfect cubes?
(i) 216
(ii) 128
(iii) 1000
(iv) 100
(v) 46656
Solution:
(i) 216 = 2 × 2 × 2 × 3 × 3 × 3
Since, all the prime factors of 216 appear in a group of three.
∴ 216 is a perfect cube.
(ii) 128 = 2 × 2 × 2 × 2 × 2 × 2 × 2
Since, all the prime factors of 128 doesn’t appear in a group of three.
∴ 128 is not a perfect cube.
(iii) 1000 = 2 × 2 × 2 × 5 × 5 × 5
Since, all the prime factors of 1000 appear in a group of three.
∴ 1000 is a perfect cube.
(iv) 100 = 2 × 2 × 5 × 5.
Since, all the prime factors of 100 doesn’t appear in group of three.
∴ 100 is not a perfect cube.
(v) 46656 = 2 × 2 × 2 × 2 × 2 × 2 × 3 × 3 × 3 × 3 × 3 × 3
Since, all the prime factors of 46656 appear in a group of three.
∴ 46656 is a perfect cube.

Question 2.
Find the smallest number by which each of the following numbers must be multiplied to obtain a perfect cube.
(i) 243
(ii) 256
(iii) 72
(iv) 675
(v) 100
Solution:
(i) 243 = 3 × 3 × 3 × 3 × 3
Clearly, the prime factor 3 doesn’t appear in a group of three.

∴ 243 is not a perfect cube.
So, to make 243 a perfect cube, we multiply it by 3.
In that case
243 × 3 = 3 × 3 × 3 × 3 × 3 × 3 = 729, which is a perfect cube.

(ii) 256 = 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2
Clearly, the prime factor 2 doesn’t appear in a group of three.
256 is not a perfect cube.

So, to make 256 a perfect cube, we multiply it by 2.
In that case
256 × 2 = 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 = 512, which is a perfect cube.

(iii) 72 = 2 × 2 × 2 × 3 × 3

Clearly, the prime factor 3 doesn’t appear in a group of three.
∴ 72 is not a perfect cube.
So, to make 72 a perfect cube, we multiply it by 3.
In that case
72 × 3 = 2 × 2 × 2 × 3 × 3 × 3 = 216, which is a perfect cube.

(iv) 675 = 3 × 3× 3 × 5 × 5
Clearly, the prime factor 5 doesn’t appear in a group of three.

∴ 675 is not a perfect cube.
So, to make 675 a perfect cube, we multiply it by 5.
In that case
675 × 5 = 3 × 3× 3 × 5 × 5 × 5
= 3375, which is a perfect cube.

(v) 100 = 2 × 2 × 5 × 5

Clearly, both the prime factors 2 and 5 doesn’t appear in a group of three.
∴ 100 is not a perfect cube.
So, to make 100 a perfect cube, we multiply it by 2 × 5 = 10.
In that case
100 × 2 × 5 = 2 × 2 × 2 × 5 × 5 × 5 = 1000, which is a perfect cube.

Question 3.
Find the smallest number by which each of the following numbers must be divided to obtain a perfect cube.
(i) 81
(ii) 128
(iii) 135
(iv) 192
(v) 704.
Solution:
(i) 81 = 3 × 3 × 3 × 3
Clearly, the prime factor 3 doesn’t appear in a group of three.
∴ 81 is not a perfect cube.
So, to make it a perfect cube, we must divide it by 3.


which is a perfect cube.

(ii) 128 = 2 × 2 × 2 × 2 × 2 × 2 × 2
Clearly, the prime factor 2 doesn’t appear in a group of three.
∴ 128 is not a perfect cube.
So, to make it a perfect cube, we must divide it by 2.


= 64,
which is a perfect cube.

(iii) 135 = 3 × 3 × 3 × 5
Clearly, the prime factor 5 doesn’t appear in a group of three.

∴ 135 is not a perfect cube.
So, to make it a perfect cube, we must divide it by 5.

Thus the smallest number is 5 by which 135 must be divided.

(iv) 192 = 2 × 2 × 2 × 2 × 2 × 2 × 3
Clearly, the prime factor 3 doesn’t appear in a group of three.

∴ 192 is not a perfect cube.
So, to make it a perfect cube, we must divide it by 3.

which is a perfect cube.

(v) 704 = 2 × 2 × 2 × 2 × 2 × 2 × 11
Clearly, the prime factor 11 doesn’t appear in a group of three.

∴ 704 is not a perfect cube.
So, to make it a perfect cube, we must divide it by 11.

which is a perfect cube.

Question 4.
Parikshit makes a cuboid of plasticine of sides 5 cm, 2 cm, 5 cm. How many such cuboids will he need to form a cube?
Solution:
We have cuboid of dimensions 2 × 5 × 5
Clearly, in above, the prime factors 2 and 5 both doesn’t appear in a group of three,
∴ To make it a perfect cube, we need to multiply it by 2 × 2 × 5.
2 × 5 × 5 × 2 × 2 × 5 = 2 × 2 × 2 × 5 × 5 × 5
= 1000, which is a perfect cube.
Thus, Prikshit need 20 cuboids to form a cube.

MP Board Class 8th Maths Solutions

MP Board Class 8th Maths Solutions Chapter 5 Data Handling Ex 5.3

Question 1.
List the outcomes you can see in these experiments.
(a) Spinning a wheel

(b) Tossing two coins together.
Solution:
(a) After spinning a wheel, we obtained total outcomes: A, B, C and D.
(b) After tossing two coins together, we get the following outcomes:
(i) HT i.e., Head on first coin and Tail on the second coin.
(ii) HH i.e., Head on both the coins.
(iii) TH i.e., Tail on first coin and Head on second coin.
(iv) TT i.e., Tail on both the coins.

Question 2.
When a die is thrown, list the outcomes of an event of getting
(i) (a) a prime number.
(b) not a prime number.
(ii) (a) a number greater than 5
(b) a number not greater than 5.
Solution:
Since, numbers on a die are 1, 2, 3, 4, 5 and 6. After throwing a die, we get
(i) (a) 2, 3, 5 are prime numbers.
(b) 1, 4, 6 are not prime numbers.
(ii) (a) 6 is a number greater than 5.
(b) 1, 2, 3, 4, 5 are not greater than 5.

Question 3.
Find the
(a) Probability of the pointer stopping on D in (Question 1-(a))?
(b) Probability of getting an ace from a well shuffled deck of 52 playing cards?
(c) Probability of getting a red apple. (See figure below).

Solution:
(a) Since total outcomes are A, A, B, C, D i.e., total 5 outcomes.
D occurs only once in a spinning wheel. Then, probability of the pointer stopping on D

(b) Number of aces = 4 Total number of cards = 52
∴ Probability of getting an ace from a well shuffled deck of 52 playing cards

(c) Number of red apples = 4
Total number of apples = 7
∴ Probability of getting a red apple

Question 4.
Numbers 1 to 10 are written on ten separate slips (one number on one slip), kept in a box and mixed well. One slip is chosen from the box without looking into it. What is the probability of
(i) getting a number 6?
(ii) getting a number less than 6?
(iii) getting a number greater than 6?
(iv) getting a 1-digit number?
Solution:
Total number of outcomes = 10
(i) Favourable outcomes of getting a number 6 = 10
∴ Probability of getting a number 6
Favourable outcomes of

(ii) Favourable outcomes of getting a number less than 6 = 5, i.e., 1, 2, 3, 4, 5
∴ Probability of getting a number less than 6
Favourable outcomes of

(iii) Favourable outcomes of getting a number greater than 6 = 4, i.e., 7, 8, 9, 10
∴ Probability of getting a number greater than 6
Favourable outcomes of

(iv) Favourable outcomes of getting a 1-digit number = 9, i.e, 1, 2, 3, 4, 5, 6, 7, 8, 9 ∴ Probability of getting a 1-digit number
Favourable outcomes of

Question 5.
If you have a spinning wheel with 3 green sectors, 1 blue sector and 1 red sector, what is the probability of getting a green sector? What is the probability of getting a non blue sector?
Solution:
Total number of outcomes = 5
Favourable number of outcomes of getting a green sector = 3
Favourable number of outcomes of getting a non-blue sector = 4
Thus, probability of getting a green sector
Favourable outcomes of

Probability of getting a non-blue sector
Favourable outcomes of getting

Question 6.
Find the probabilities of the events given in Question 2.
Solution:
If Total number of outcomes = 6
(i) (a) Probability of getting a prime number
Favourable outcomes of

(b) Probability of not getting a prime number
Favourable outcomes of

(ii) (a) Probability of getting a number greater than 5
Favourable outcomes of getting

(b) Probability of getting a number not greater than 5
Favourable outcomes of getting

MP Board Class 8th Maths Solutions

MP Board Class 11th Maths Solutions Chapter 1 समुच्चय Ex 1.6

प्रश्न 1.
यदि X और Y दो ऐसे समुच्चय हैं कि n(X) = 17, n(Y) = 23 तथा n(X ∪ Y) = 38, तो n(X ∩ Y) ज्ञात कीजिए।
हल:
दिया है: (A) = 17, n (Y) = 23
और n (X ∪ Y) = 38
∴ n(X ∪ Y) = n(X) + n(Y) – n(X ∩ Y)
38 = 17 + 23 – n(X ∩ Y)
= 40 – n (X ∩ Y)
n(X ∩ Y) = 40 – 38 = 2.

प्रश्न 2.
यदि X और Y दो ऐसे समुच्चय हैं कि X ∪ Yमें 18, X में 8 और Y में 15 अवयव हों तो X ∩ Y में कितने अवयव होंगे?
हल:
n(X) = 8, n(Y) = 15 और n(X ∪ Y) = 18
हम जानते हैं कि,
n(X ∪ Y) = n(X) + n(Y) – n (X ∩ Y)
18 = 8 + 15 – n(X ∩ Y)
= 23 – n(X ∩ Y )
या n(X ∩ Y) = 23 – 18 = 5.

प्रश्न 3.
400 व्यक्तियों के समूह में, 250 हिन्दी तथा 200 अंग्रेजी बोल सकते हैं। कितने व्यक्ति हिन्दी तथा अंग्रेजी दोनों बोल सकते हैं?
हल:
मान लीजिए कि H और E क्रमशः हिन्दी व अंग्रेजी बोलने वालों के समुच्चय हों, तब
n(H) = 250, n(E) = 200
और n(H ∪ E) = 400
अब n(H ∪ E) = n(H) + n(E) – n(H ∩ E)
∴ 400 = 250 + 200 – n(H ∩ E)
= 450 – n(H ∩ E)
∴ n (H ∩ E) = 450 – 400 = 50.

प्रश्न 4.
यदि S और T दो ऐसे समुच्चय हैं कि 5 में 21, T में 32 और S ∩ T में 11 अवयव हों तो S ∪ T में कितने अवयव होंगे?
हल:
यहाँ n(S) = 21, n (T) = 32, n(S ∩ T) = 11
n(S ∪ T) = n(S) + n(T) – n(S ∩ T)
= 21 + 32 – 11 = 53 – 11
= 42.

प्रश्न 5.
यदि और Y दो ऐसे समुच्चय हैं कि x में 40, X ∩ Y में 60 और X ∪ Y में 10 अवयव हों, तो Y में कितने अवयव होंगें?
हल:
n(X) = 40, n(X ∪ Y) = 60, n(X ∩ Y) = 10, n(Y) = ?
अब n(X ∪ Y) = n(X) + n(Y) – n (X ∩ Y)
60 = 40 + n (Y) – 10
n(Y) = 60 – 40 + 10 = 30.

प्रश्न 6.
70 व्यक्तियों के समूह में 37 कॉफी, 52 चाय पसंद करते हैं और प्रत्येक व्यक्ति दोनों मे से कम से कम एक पेय पसंद करता है, तो कितने व्यक्ति कॉफी और चाय दोनों पसंद करते हैं ?
हल:
मान लिया C, कॉफी पीने वाले लोगों के समुच्चय को और T, चाय पीने वाले लोगों के समुच्चय हों, तब
n(C ∪ T) = 70, n(C) = 37, n(T) = 52
n(C ∩ T) = n (C) + n(T) – n(C ∩ T)
70 = 37 + 52 – n(C ∩ T)
∴ n(C ∩ T) = 37 + 52 – 70
= 89 – 70 = 19.

प्रश्न 7.
65 व्यक्तियों के समूह में, 40 व्यक्ति क्रिकेट और 10 व्यक्ति क्रिकेट तथा टेनिस दोनों को पंसद करते हैं, तो कितने व्यक्ति केवल टेनिस को पंसद करते हैं किंतु क्रिकेट को नहीं? कितने व्यक्ति टेनिस को पंसद करते हैं?,
हल:
मान लीजिए C, क्रिकेट पंसद करने वाले लोगों का समुच्चय है और T टेनिस पंसद करने वालों का समुच्चय हो, तब
n(C ∪ T) = 65, n(C) = 40, n(C ∩ T) = 10
हम जानते हैं कि n(C ∪ T) = n(C) + n(T) – n(C ∩ T)
65 = 40 + n(T) – 10
= 30 + n(T)
n(T) = 65 – 30 = 35
केवल टेनिस पंसद करने वालो की संख्या = n(T) – n(C ∩ T)
= 35 – 10 = 25.
इस प्रकार टेनिस पंसद करने वालों की संख्या जो क्रिकेट पंसद नहीं करते = 25
अतः टेनिस पंसद करने वाले लोगों की संख्या = 35.

प्रश्न 8.
एक कमेटी में, 50 व्यक्ति फ्रैंच 20 व्यक्ति स्पेनिश और 10 व्यक्ति स्पेनिश और फ्रैंच दोनों ही . भाषाओं को बोल सकते हैं। कितने व्यक्ति इन दोनों ही भाषाओं में से कम से कम एक भाषा बोल सकते हैं?
हल:
मान लीजिए फ्रांसीसी बोलने वाले लोगों के समुच्चय को F से तथा स्पैनिश बोलने वाले लोगों के समुच्चय का S से निरुपित किया हो, तब
n(F) = 50, n(S) = 20, n(F ∩ S) = 10
अब n(F ∪ S) = n(F) + n (S) – n (F ∩ S)
= 50 + 20 – 10 = 60
कम से कम एक भाषा बोलने वाले लोगों की संख्या = 60

MP Board Class 11th Maths Solutions

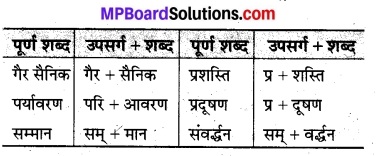
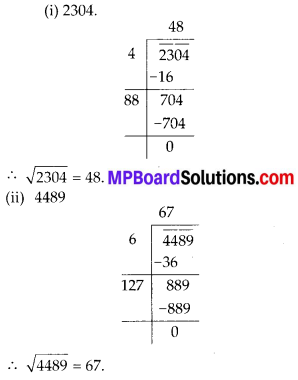
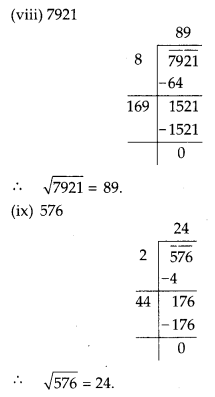
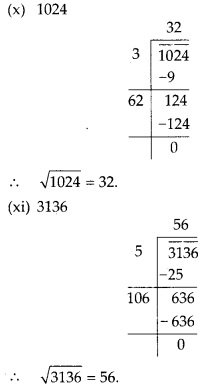
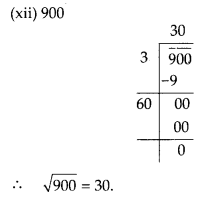
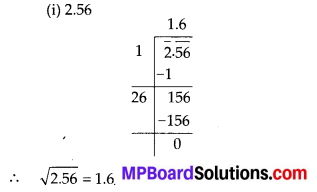
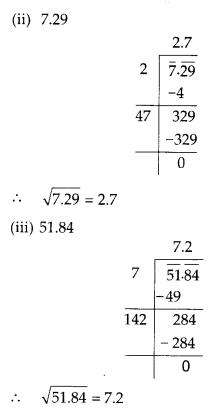
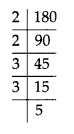
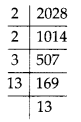
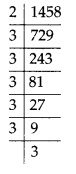
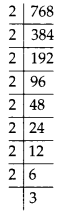
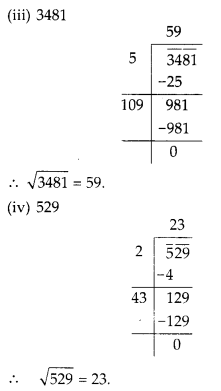MP Board Class 8th Maths Solutions Chapter 5 Data Handling Ex 5.2

Question 1.
A survey was made to find the type of music that a certain group of young people liked in a city. Adjoining pie chart shows the finding of this survey.

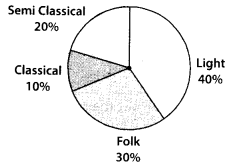
From this pie chart answer the following :
(i) If 20 people liked classical music, how many young people were surveyed?
(ii) Which type of music is liked by the maximum number of people?
(iii) If a cassette company were to make 1000 CD’s, how many of each type would they make?
Solution:
(i) Let total number of young people were surveyed be x.
According to question, \(x \times \frac{10}{100}\) = 20

Thus, 200 young people were surveyed.
(ii) Pie chart shows that the maximum number of people like light music.
(iii) Cassette company has to make 1000 CD’s.
∴ Number of CD’s of semi classical music

Number of CD’s of classical music

Number of CD’s of folk music

Number of CD’s of light music 40

Question 2.
A group of 360 people were asked to vote for their favourite season from the three seasons

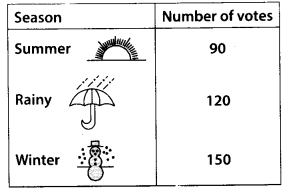
(i) Which season got the most votes?
(ii) Find the central angle of each sector.
(iii) Draw a pie chart to show this information.
Solution:
(i) Winter season got the most votes,
(ii) Total number of votes = 90 + 120 + 150
= 360
Total angle at the centre of a circle = 360°

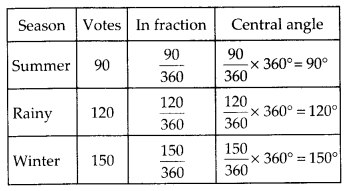
(iii) Now, we have to draw a pie chart to show the given information :

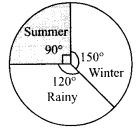
Question 3.
Draw a pie chart showing the following information. The table shows the colours preferred by a group of people.

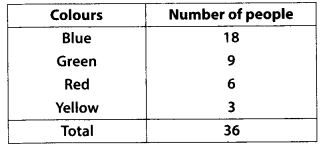
Find the proportion of each sector. For example,
Blue is \(\frac{18}{36}=\frac{1}{2}\) ; Green is \(\frac{9}{36}=\frac{1}{4}\) and so on. Use this to find the corresponding angles.
Solution:

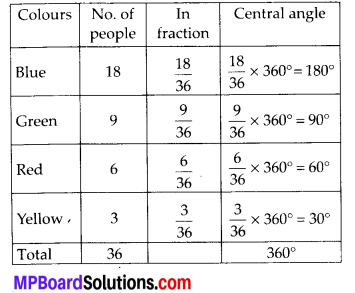
We have to draw a pie chart showing a given information :

Question 4.
The given pie chart gives the marks scored in an examination by a student in Hindi, English, Mathematics, Social Science and Science. If the total marks obtained by the students were 540, answer the following questions.

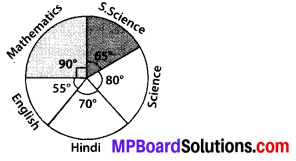
(i) In which subject did the student score 105 marks?
(Hint: For 540 marks, the central angle = 360°. So, for 105 marks, what is the central angle?)
(ii) How many more marks were obtained by the student in Mathematics than in Hindi?
(iii) Examine whether the sum of the marks obtained in Social Science and Mathematics is more than that in Science and Hindi. (Hint: Just study the central angles)
Solution:
(i) Total marks scored by students = 540
Central Angle

Since central angle is 70°, thus we found that in Hindi, the student scored 105 marks.
(ii) Marks scored in Mathematics

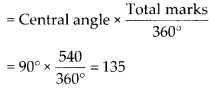
Thus, marks obtained by the student in Mathematics more than in Hindi = 135 – 105 = 30
(iii) Marks obtained in Social Science

So, marks obtained in Social Science and Mathematics = 97.5 + 135
= 232.5 …(i)
And marks obtained in Science and Hindi = 120+ 105 = 225 …(ii)
Thus, (i) and (ii) shows that marks obtained in Mathematics and Social Science is more than that in Science and Hindi.

Question 5.
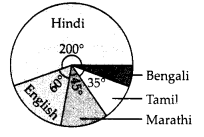
The number of students in a hostel, speaking different languages is given below. Display the data in a pie chart.

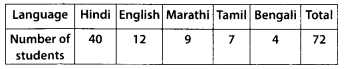
Solution:

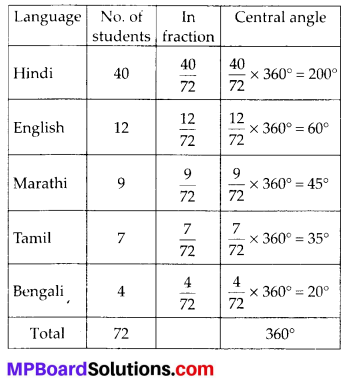
The pie chart is shown below :

MP Board Class 8th Maths Solutions

MP Board Class 11th Maths Solutions Chapter 1 समुच्चय Ex 1.5

प्रश्न 1.
मान लीजिए कि U = {1, 2, 3, 4, 5, 6, 7, 8, 9}, A = {1, 2, 3, 4}, B = {2, 4, 6, 8, और C = {3, 4, 5, 6} तो निम्नलिखित को ज्ञात कीजिए :
(i) A’
(ii) B’
(ii) (A ∪ C)
(iv) (A ∪ B)’
(v) (A’)’
(vi) (B – C)’
हल:
(i) A’ = U – A
= {1, 2, 3, 4, 5, 6, 7, 8, 9} – {1, 2, 3, 4}
= {5, 6, 7, 8, 9}.
(ii) B’ = U – B
= {1, 2, 3, 4, 5, 6, 7, 8, 9} – {2, 4, 6, 8}
= {1, 3, 5, 7, 9}.
(iii) A ∪ C = {1, 2, 3, 4} ∪ {3, 4, 5, 6}
= {1, 2, 3, 4, 5, 6}.
(A ∪ C) = U – (A ∪ C)
= {1, 2, 3, 4, 5, 6, 7, 8, 9} – {1, 2, 3, 4, 5, 6}
= {7, 8, 9}.
(vi) A ∪ B = {1, 2, 3, 4} ∪ {2, 4, 6, 8}
= {1, 2, 3, 4, 6, 8}.
(A ∪ B) = U – (A ∪ B)
= {1, 2, 3, 4, 5, 6, 7, 8, 9} – {1, 2, 3, 4, 6, 8}
= {5, 7, 9}.
(v) (A)’ = U – A
= {1, 2, 3, 4, 5, 6, 7, 8, 9} – {1, 2, 3, 4}
= {5, 6, 7, 8, 9}
(A’) = U – A
= {1, 2, 3, 4, 5, 6, 7, 8, 9} – {5, 6, 7, 8, 9}
= {1, 2, 3, 4}.
(vi) B – C = {2, 4, 6, 8} – {3, 4, 5, 6} = {2, 8}
(B – C) = U – (B – C)
= {1, 2, 3, 4, 5, 6, 7, 8, 9} – {2, 8}
= {1, 3, 4, 5, 6, 7, 9}.

प्रश्न 2.
यदि U = {a, b, c, d, e, f, g, h}, तो निम्नलिखित समुच्चयों के पूरक ज्ञात कीजिए:
(i) A = {a, b, c}
(ii) B = {d, e, f, g}
(iii) C = {a, c, e, g}
(iv) D = {f, g, h, a}
हल:
(i) A’ = U – A
= {a, b, c, d, e, f, g, h} – {a, b, c}
= {d, e, f, g, h}.
(ii) B’ = U – B = {a, b, c, d, e, f, g, h} – {d, e, f, g}
= {a, b, c, h}
(iii) C = U – C
= {a, b, c, d, e, f, g, h} – {a, c, e, g} = {b, d, f, h}
(iv) D’ =U – D
= {a, b, c, d, e, f, g, h} – {f, g, h, a} = {b, c, d, e}

प्रश्न 3.
प्राकृत संख्याओं के समुच्चय को सार्वत्रिक समुच्चय मानते हुए, निम्नलिखित समुच्चयों के पूरक लिखिए :
(i) {x : x एक प्राकृत सम संख्या है।
(ii) {x : x एक प्राकृत विषम संख्या है?
(iii) {x : x संख्या 3 का एक धन गुणज है
(iv) {x : x एक अभाज्य संख्या है?
(v) {x : x, 3 और 5 से विभाजित होने वाली एक संख्या है?
(vi) {x : x एक पूर्ण वर्ग संख्या है?
(vii) {x : x एक पूर्ण घन संख्या है?
(viii){x : x + 5 = 8}
(ix) {x : 2x + 5 = 9}
(x) {x : x ≥ 7}
(vi) {x : x ϵ N और 2x + 1 > 10}
हल:
(i) {x : x एक विषम प्राकृत संख्या है}
(ii) {x : x एक सम संख्या है?
(iii) {x : x ϵ N और x संख्या 3 का धन गुणज नहीं है।
(iv) {x : x = 1 और x एक धन भाज्य संख्या है?
(v) {x : x ϵ N और x, संख्या 3 व 5 किसी से भी विभाजित नहीं होती}
(vi) {x : x ϵ N तथा x एक पूण वर्ग संख्या नहीं है}
(vii) {x : x ϵ N तथा x एक पूर्ण वर्ग घन संख्या नहीं है}
(viii) {x : x ϵ N तथा x ≠ 3}
(ix) {x : x ϵ N तथा x ≠ 2}
(x) {x : x ϵ N तथा x < 7}
(xi) {x : x ϵ N तथा x < \(\frac{9}{2}\)}

प्रश्न 4.
यदि U = {1, 2, 3, 4, 5, 6, 7, 8, 9}, A = {2, 4, 6, 8} और B = {2, 3, 5, 7}, तो सत्यापित कीजिए कि:
(i) (A ∪ B)’ = A’ ∩ B’
(i) (A ∩ B)’ = A’ ∪ B’
हल:
(i) A ∪ B = {2, 4, 6, 8} ∪ {2, 3, 5, 7}
= {2, 3, 4, 5, 6, 7, 8}
बायाँ पक्ष = (A ∪ B)’ = U – (A ∪ B)
{1, 2, 3, 4, 5, 6, 7, 8, 9} – {2, 3, 4, 5, 6, 7, 8}
= {1, 9}
A’ = U – A
= {1, 2, 3, 4, 5, 6, 7, 8, 9} – {2, 4, 6, 8}
= {1, 3, 5, 7, 9}.
B’ = U – B
= {1, 2, 3, 4, 5, 6, 7, 8, 9} – {2, 3, 5, 7}
= {1, 4, 6, 8, 9}
दायाँ पक्ष = A’ ∩ B’
= {1, 3, 5, 7, 9} ∩ {1, 4, 6, 8, 9} = {1, 9}
अतः (A ∪ B)’ = A’ ∩ B’.
(ii) बायाँ पक्ष = (A ∩ B)’
(A ∩ B) = {2, 4, 6, 8} ∩ {2, 3, 5, 7} = {2}
(A ∩B)’ = {1, 2, 3, 4, 5, 6, 7, 8, 9} – {2}
= {1, 3, 4, 5, 6, 7, 8, 9}
दायाँ .पक्ष : A’ ∪ B’ = {1, 3, 5, 7,9} ∪ {1, 4, 6, 8, 9} [(i) और (ii)]
= {1, 3, 4, 5, 6, 7, 8, 9}
अतः (A ∩ B)’ = A’ ∪ B.

प्रश्न 5.
निम्नलिखित में से प्रत्येक के लिए उपयुक्त वेन आरेख खींचिए :
(i) (A ∪ B)’
(ii) A’ ∩ B’
(iii) (A ∩ B)’
(iv) (A’ ∪ B’)
हल:
छायांकित क्षेत्र को निम्नलिखित समुच्चयों द्वारा दर्शाते हैं :

प्रश्न 6.
मान लीजिए कि किसी समतल में स्थित सभी त्रिभुजों का समुच्चय सार्वत्रिक समुच्चय U है। यदि A उन सभी त्रिभुजों का समुच्चय हैं जिनमें कम से कम एक कोण 60° से भिन्न है, तो A’ क्या है?
हल:
U = {x : x समतल में एक त्रिभुज है}
A = {x : x एक त्रिभुज जिसका कम से कम एक कोण 60° का न हो}
A’ = {सभी समबाहु त्रिभुजों का समुच्चय है।

प्रश्न 7.
निम्नलिखित कथनों को सत्य बनाने के लिए रिक्त स्थान भरिए :
(i) A ∪ A’ = ……………
(ii) ϕ’ ∩ A = ……………..
(iii) A ∩ A’ = ………….
(iv) U’ ∩ A = …………
हल:
(i) A ∪ A’ = U
(ii) ϕ’ ∩ A = U ∩ A = A
(iii) A ∩ A’ = ϕ
(iv) U’ ∩ A = ϕ ∩ A = ϕ

MP Board Class 11th Maths Solutions

MP Board Class 8th Maths Solutions Chapter 5 Data Handling Ex 5.1

Question 1.
For which of these would you use a histogram to show the data?
(a) The number of letters for different area in a postman’s bag.
(b) The height of competitors in an athletics meet.
(c) The number of cassettes produced by 5 companies.
(d) The number of passengers boarding trains from 7:00 a.m. to 7:00 p.m. at a station. Give reasons for each.
Solution:
(a) We use pictograph for the given statement. Since, letters can be represented through appropriate picture or symbols, we will not use histogram.
(b) We use histogram for the given statement. Since, the height of competitors in an athletics meet can be divided into class intervals.
(c) We will not use histogram. We use pictograph for the given statement since the cassettes can be represented through appropriate picture or symbols.
(d) We use histogram for the given statement since the time of boarding trains from 7:00 a.m. to 7:00 p.m. can be divided into class intervals.

Question 2.
The shoppers who come to a departmental store are marked as : man (M), woman (W), boy (B) or girl (G). The following list gives the shoppers who came during the first hour in the morning:

WWWGBWWMGGMMWWWWGBMWB
GGMWWMMWWWMWBWGMWWWW
GWMMWWMWGWMGWMMBGGW
Make a frequency distribution table using tally marks. Draw a bar graph to illustrate it.
Solution:
Firstly by using a given information, we make a frequency distribution table using tally marks.
Shopper Tally marks Frequency

Question 3.
The weekly wages (in ₹) of 30 workers in a factory are:
830, 835, 890, 810, 835, 836, 869, 845, 898, 890,820,860,832,833,855,845,804,808,812, 840,885,835,835,836,878,840,868,890,806, 840.
Using tally marks make a frequency table with intervals as 800 – 810, 810 – 820 and so on.
Solution:
By using a given information, we have to make a frequency table :

Question 4.
Draw a histogram for the frequency table made for the data in Question 3, and answer the following questions.
(i) Which group has the maximum number of workers?
(ii) How many workers earn ? 850 and more?
(iii) How many workers earn less than ? 850?
Solution:
We have to draw a histogram :

(i) 830 – 840 is a group which has the maximum number of workers.
(ii) 10 workers earn ₹ 850 and more.
(iii) 20 workers earn less than ₹ 850.

Question 5.
The number of hours for which students of a particular class watched television during holidays is shown through the given graph. Answer the following:
(i) For how many hours did the maximum number of students watch TV?
(ii) How many students watched TV for less than 4 hours?
(iii) How many students spent more than 5 hours in watching TV?
Solution:

(i) The above given graph shows that in between 4-5 hours, maximum number of students used to watch TV.
(ii) Number of students watched TV for less than 4 hours = 4 + 8 + 22 = 34
(iii) Number of students spent more than 5 hours in watching TV = 8 + 6 = 14

MP Board Class 8th Maths Solutions

MP Board Class 8th Hindi Bhasha Bharti Solutions Chapter 10 प्राण जाएँ पर वृक्ष न जाए

MP Board Class 8th Hindi Bhasha Bharti Chapter 10 पाठ का अभ्यास

बोध प्रश्न

प्रश्न 1.
निम्नलिखित शब्दों के अर्थ शब्दकोश से खोजकर लिखिए
उत्तर
रक्षक = रक्षा करने वाले ताम्रपत्र = ताँबे का पत्तर, स्मृति पत्र; श्रद्धांजलि = मरने के बाद श्रद्धा प्रकट करने हेतु व्यक्त शब्द; संवर्द्धन = वृद्धि, विकास; शहीद = बलिदान; प्रशस्ति = प्रशंसा; उत्कृष्ट = उच्च कोटि का।

प्रश्न 2.
निम्नलिखित प्रश्नों के संक्षेप में उत्तर लिखिए

(क) सैनिकों की कुल्हड़ी का सबसे पहले विरोध किसने किया?
उत्तर
सैनिकों की कुल्हाड़ी का सबसे पहले विरोध एक महिला अमृता देवी विश्नोई ने किया। कुल्हाड़ी चलाना आरम्भ किए जाने पर अमृतादेवी विश्नोई पेड़ों से लिपट गई।

(ख) अमृता देवी का नारा क्या था?
उत्तर
पेड़ों से लिपटकर वह कहती रही “सिर साँटे पर  रूख रहे तो भी सस्तो जाण”। यही अमृतादेवी का नारा था।’

(ग) विश्नोई समाज की स्थापना किसने की थी ?
उत्तर
विश्नोई समाज की स्थापना आज से लगभग पाँच सौ वर्ष पहले सन् 1485 ई. में भगवान जम्भेश्वर ने की थी।

(घ) हिरणों की रक्षा में कौन शहीद हुआ था ?
उत्तर
सन् 1996 ई. में अक्टूबर माह में राजस्थान के चुरु जिले में हिरणों की रक्षा करते हुए श्री निहालचन्द विश्नोई शहीद हुए थे।

(ङ) राजा ने पेड़ काटने की क्या सजा घोषित की ?
उत्तर
राजा अभयसिंह ने सैनिकों के दुष्कृत्य के लिए क्षमा माँगी और ताम्रपत्र पर राजा की आज्ञा को जारी किया गया कि विश्नोई गाँवों में कोई भी पेड़ नहीं काटेगा। यदि काटेगा तो राजदण्ड का भागी होगा।

प्रश्न 3.
निम्नलिखित प्रश्नों के उत्तर विस्तार से लिखिए

(क) जोधपुर के राजा अभयसिंह को लकड़ी की आवश्यकता क्यों पड़ी? इसके लिए उन्होंने क्या किया ?
उत्तर
जोधपुर के राजा अभयसिंह ने अपना महल बनवाया। यह भादों का महीना था एवं शुक्ल पक्ष की दशमी का दिन था। इसके निर्माण के लिए राजा अभयसिंह को लकड़ी की आवश्यकता पड़ी। इसके लिए राजा अभयसिंह ने अपनी सेना के कुछ सैनिकों को लकड़ी काटकर लाने का आदेश दिया। इस तरह राजा के सैनिक जोधपुर के पास खेजड़ली गाँव पहुँचे। वहाँ वे पेड़ काटना चाहते थे। यह गाँव विश्नोइयों का था। विश्नोइयों ने कहा, “हम परम्परा से वनों के रक्षक हैं। हमारे रहते पेड़ नहीं कट सकते।” सैनिकों ने उनके विरोध की अनदेखी की। सैनिकों ने कुल्हाड़ी चला दी। अमृता देवी विश्नोई नामक महिला पेड़ों से लिपट गई और कहती रही, “सिर साँटे पर रूख रहे तो भी सस्तो जाण।” राजा की आज्ञा का पालन करना है, इस भाव से सैनिकों ने अमृता देवी को काट डाला।

(ख) अमृता देवी वृक्षों की रक्षा और किस प्रकार से कर सकती थीं ? सोचकर लिखिए।
उत्तर
राजा के आदेश से उनके सैनिक पेड़ काटने के लिए खेजड़ली गाँव पहुँचे। राजा की आज्ञा का पालन करना उन सैनिकों का धर्म हो गया था। अमृता देवी वृक्षों की रक्षा के लिए उन्हें काटने से रोकने के लिए, सैनिकों से निवेदन कर सकती थीं तथा अपनी बात को राजा के पास जाकर विरोध के रूप में कह सकती थीं और पेड़ों के न काटने के लिए अपनी परम्परा को स्पष्ट रूप से बता सकती थीं।

(ग) अमृतादेवी का नारा इस पाठ में किस तरह सार्थक हुआ?
उत्तर
अमृता देवी का नारा, “सिर साँटे पर रूख रहे तो भी सस्तो जाण” सार्थक हो गया। पेड़ों की आवश्यकता हम लोगों को है, पेड़ों को हमारी आवश्यकता नहीं है। दिन-प्रतिदिन बढ़ते प्रदूषण से अपनी रक्षा के लिए हमें पेड़ लगाने होंगे और उनकी रक्षा करनी होगी। अमृता देवी और तीन सौ बासठ शहीदों के बलिदान की स्मृति में भारत सरकार प्रति वर्ष राष्ट्रीय पर्यावरण पुरस्कार देती है। मध्य प्रदेश का वन विभाग प्रति वर्ष वन-संवर्द्धन एवं वन रक्षा के क्षेत्र में उल्लेखनीय कार्य करने वाली ग्राम पंचायत अथवा संस्था को शहीद अमृता देवी विश्नोई पुरस्कार और एक लाख रुपया नकद प्रदान करता है। मध्य प्रदेश सरकार शहीद अमृता देवी विश्नोई के नाम पर दो व्यक्तिगत पुरस्कार भी देती है। पचास हजार रुपया नगद और प्रशस्ति पत्र के पुरस्कार के रूप में वन सम्बर्द्धन और वन्य प्राणियों की रक्षा में उत्कृष्ट कार्य करने वाले व्यक्ति को प्रतिवर्ष दिए जाते हैं।

(घ) राजा अभयसिंह ने पश्चाताप किस प्रकार किया ?
उत्तर
जब जोधपुर के राजा अभयसिंह को विश्नोई समाज द्वारा किए गये बलिदान सम्बन्धी भीषण घटना का समाचार मिला तो उन्हें बड़ा दुःख हुआ। वे स्वयं खेजड़ली गाँव आए। अपनी सेना के द्वारा किए गये दुष्कृत्य के लिए क्षमा माँगी। उन्होंने ताम्रपत्र जारी किया। उसमें राजाज्ञा जारी की गई कि विश्नोई – गाँवों में कोई पेड़ नहीं काटेगा। यदि काटेगा तो राजदण्ड का भागी होगा। इस प्रकार राजा के द्वारा निर्णय लिया गया और पश्चाताप किया गया।

(ङ) अमृता देवी व अन्य शहीदों से आपको क्या प्रेरणा मिलती है?
उत्तर
अमृता देवी व अन्य शहीदों से यह प्रेरणा मिलती है कि हमें पर्यावरण की सुरक्षा के लिए वृक्षों और वनों को पूर्ण सुरक्षा देनी चाहिए। उनके सम्वर्द्धन और विकास में रुचि लेनी चाहिए। वन्य जीवों की सुरक्षा और उनकी प्रजातियों का विकास करना चाहिए। प्रत्येक राज्य सरकार को वृक्षारोपण और वन सम्पदा के विकास और सुरक्षा के लिए अपनी ओर से प्रोत्साहन पुरस्कार घोषित किये जाने चाहिए। ग्राम पंचायतों को भी वृक्षों का आरोपण करने के अभियान चलाने चाहिए।

प्रश्न 4.
सही विकल्प चुनिए
(क) विश्नोई समाज के नियम मुख्यतः आधारित थे
(अ) प्रकृति के पोषण पर
(आ) समाज की परम्परा पर
(इ) धर्म की मान्यता पर
(ई) जीव-जन्तुओं के प्रति करुणा पर,
(उ) इन सबके सम्मिलित प्रभाव वाली प्रथा पर।
उत्तर
उ) इन सबके सम्मिलित प्रभावशाली प्रथा पर

(ख) म. प्र. सरकार किसके नाम पर दो व्यक्तिगत पुरस्कार देती है?
(अ) विश्नोई समाज
(आ) अमृता देवी विश्नोई
(इ) निहालचन्द विश्नोई
(ई) शहीदों।
उत्तर
(आ) अमृता देवी विश्नोई

(ग) वृक्ष का पर्यायवाची शब्द है
(अ) काननं
(आ) तरु
(इ) गिरि
(ई) चक्षु
उत्तर
(आ) तरु

(घ) अमृता देवी के साथ शहीद विश्नोइयों की संख्या थी
(अ) 362
(आ) 365
(इ) 363
(ई) 364
(ङ) श्री निहाल चन्द विश्नोई को भारत सरकार ने
उत्तर
(अ) 362

(ङ) सम्मानित किया
(अ) पद्मश्री से
(आ) शौर्य चक्र से
(इ) परमवीर चक्र से
(ई) वीर चक्र से।
उत्तर
(आ) शौर्य चक्र से

भाषा-अध्ययन

प्रश्न 1.
नीचे लिखे शब्दों के विलोम शब्द उनके नीचे बनी वर्ग पहेली (पाठ्यपुस्तक में) में दिए गए हैं। आप उन्हें खोजकर लिखिए
वाचाल, राजा, अपमानित, भक्षक, हर्ष, क्षम्य, हिंसा, हित, दुःखी, विरोध।
उत्तर

1. मूक
2. रंक
3. सम्मानित
4. रक्षक
5. शोक
6. अक्षम्य
7. अहिंसा
8. अहित
9. सुखी
10. समर्थन

प्रश्न 2.
निम्नलिखित शब्दों के शुद्ध उच्चारण कीजिए और उन्हें वाक्यों में प्रयोग कीजिए।
श्रद्धांजलि, संकल्प, शौर्यचक्र, प्रासंगिक, जम्भेश्वर।
उत्तर
विद्यार्थी उपर्युक्त शब्दों को ठीक-ठीक पढ़कर उनका शुद्ध उच्चारण करने का अभ्यास करें।
वाक्यों में प्रयोग-

1. महापुरुषों के नियमों का पालन करना ही उनके प्रति सच्ची श्रद्धांजलि होती है।
2. हम देश की सेवा करने का संकल्प लेते हैं।
3. निहाल चन्द को मरणोपरान्त शौर्य चक्र से सम्मानित किया।
4. अमृता देवी का वृक्ष संरक्षण कार्यक्रम आज बहुत ही प्रासंगिक है।
5. जम्भेश्वर भगवान ने प्रकृति के नियमों के पालन का आदेश दिया।

प्रश्न 3.
निम्नलिखित शब्दों की सन्धि विच्छेद कीजिए और सन्धि का प्रकार लिखिए
वृक्षारोपण, एकमेव, राजाज्ञा, मरणोपरान्त, वातावरण।
उत्तर

प्रश्न 4.
निम्नलिखित शब्दों का समास विग्रह कीजिए
ताम्रपत्र, राजदण्ड, प्रतिवर्ष, ग्राम पंचायत, शौर्य चक्र।
उत्तर

प्रश्न 5.
निम्नलिखित शब्दों में उपसर्ग पहचानकर लिखिए
गैर सैनिक, पर्यावरण, सम्मान, प्रशस्ति, प्रदूषण, संवर्द्धन।
उत्तर

प्रश्न 6.
निम्नलिखित वाक्यों में उद्देश्य और विधेय छाँटकर लिखिए
(क) भगवान जम्भेश्वर द्वारा हरे-भरे वृक्षों को बनाए रखने की प्रेरणा दी गई थी।
(ख) विश्नोई समाज ने वनों की रक्षा के लिए महत्वपूर्ण योगदान दिया है।
(ग) भारत शासन प्रतिवर्ष राष्ट्रीय पुरस्कार देता है।
उत्तर

प्राण जाएँ पर वृक्ष न जाए परीक्षोपयोगी गद्यांशों की व्याख्या 

(1) इन दिनों वृक्षों की घटती संख्या और बिगड़ते पर्यावरण को देखकर समूचे विश्व में पर्यावरण की रक्षा की चिन्ता की जा रही है। वृक्षों की अंधाधुन्ध कटाई पर रोक लगाई जा रही है। वृक्षारोपण पर जोर दिया जा रहा है। आज से सैकड़ों वर्ष पूर्व जब चारों ओर वन-ही-वन थे, भगवान जम्भेश्वर द्वारा हरे-भरे वृक्षों की रक्षा करने की प्रेरणा देना सचमुच अद्भुत था। इन दिनों बिगड़ते प्रदूषण को देखते हुए यह प्रेरणा बहुत प्रासंगिक है।

शब्दार्थ-घटती संख्या कम होती संख्या; पर्यावरण = चारों ओर का वातावरण; अंधाधुन्ध = बिना सोचे-विचारे; वृक्षारोपण = पेड़-पौधे लगाना; प्रेरणा = उत्साहपूर्ण तीव्र इच्छा; अद्भुत = अनोखी; बिगड़ते = खराब होते; प्रदूषण = बहुत तीव्रता से फैलते हुए दोष; प्रासंगिक = उचित।

सन्दर्भ-प्रस्तुत गद्यांश हमारी पाठ्य-पुस्तक ‘भाषा-भारती’ के पाठ ‘प्राण जाएँ पर वृक्ष न जाए’ से अवतरित हैं।

प्रसंग-इसमें वृक्षों की अन्धाधुन्ध कटाई के दोष और पर्यावरण पर पड़ने वाले बुरे प्रभाव को बताया है।

व्याख्या-आजकल लोगों द्वारा वृक्षों को काटा जा रहा है। इससे वृक्षों की संख्या में बहुत कमी आ गई है। इसका सीधा प्रभाव यह हुआ है कि हमारे चारों ओर का वातावरण खराब होता जा रहा है। इसके दोषपूर्ण प्रभाव को देखते हुए विद्वानों को इस बात की चिन्ता लग गई है कि इस बिगड़ते वातावरण को किस तरह बचाया जाए। अत: विभिन्न देशों की सरकारों में वृक्षों की बिना सोचे-विचारे की जा रही कटाई पर रोक लगाने के लिए विचार किया जा रहा है। इसके अलावा नए वृक्ष लगाए जाने के “लिए लोगों को प्रेरित किया जा रहा है। आज से सैकड़ों वर्ष पहले हमारे चारों ओर घने जंगल बड़ी तादाद में थे। भगवान जम्भेश्वर का आज से लगभग पाँच सौ वर्ष पहले जन्म हुआ था। उन्होंने लोगों को प्रेरित किया कि वे हरे-भरे वृक्षों की रक्षा करें और नये पेड़-पौधे लगाएँ। इस तरह लोगों में उत्साह जागृत करना सभी के लिए एक अनोखी बात थी। आज के पर्यावरण को चारों ओर से प्रदूषित किए जाने के प्रसंग में उनके द्वारा दी गई प्रेरणा व उत्साह बहुत ही महत्वपूर्ण है।

(2) आज्ञा पालन विवेक के साथ करना है, इस बात का सैनिकों ने ध्यान नहीं रखा। इस बलिदान को देखकर सैकड़ों विश्नोई नर नारी आगे आकर पेड़ों की रक्षा करने के लिए पेड़ों से लिपट गए। पेड़ों को काटने से बचाने के लिए सभी अपना सिर कटवाने को तैयार थे। पेड़ों की रक्षा के लिए आत्म-बलिदान के लिए तत्पर विश्नोई नर-नारी “सिर साँटे पर रूख रहे” का नारा लगा रहे थे। सेना कुल्हाड़ी चलाती रही। एक-एक करके 362 विश्नोई नर-नारी स्वयं कट गए, परन्तु उन्होंने एक भी पेड़ नहीं कटने दिया।

शब्दार्थ-विवेक = अच्छी तरह विचार करके; आज्ञा पालन = आदेश का मानना; बलिदान = त्याग; नर-नारीपुरुष और स्त्री; रक्षा = बचाव; आत्मबलिदान = अपने जीवन का त्याग; तत्पर = तैयार; साँटे = कट जाए; रूख = वृक्ष।

सन्दर्भ-पूर्व की तरह।

प्रसंग-पेड़ों की रक्षा में विश्नाई समाज ने अपना बलिदान दिया; इस महान त्याग के विषय में बताया जा रहा है।

व्याख्या-जोधपुर के राजा अभयसिंह ने अपने सैनिकों को अपने महल के निर्माण के लिए खेजड़ली गाँव में जाकर पेड़ों को काटने के लिए आदेश दिया। उस गाँव के विश्नोई समाज के लोगों ने उन सैनिकों को पेड़ काटने से रोक दिया। सैनिक राजा की आज्ञा पालन करना ही उचित समझते रहे। उनके द्वारा राजा की आज्ञा का पालन सोच-विचार करके ही करना चाहिए था, लेकिन सैनिकों ने इस बात का ध्यान नहीं रखा। विश्नोई समाज के सैकड़ों लोग पेड़ों को कटने से बचाने के लिए आये और पेड़ों से लिपट गये। वे सभी अपने सिर कटवाने को तैयार थे परन्तु पेड़ नहीं कटने चाहिए। वे पेड़ों को काटे जाने से रोकने के लिए अपना बलिदान देने को तैयार थे। उन्होंने कहा था कि चाहे हमारे सिर कट जाएँ, पर वृक्षों को काटने से रोका जाए। उनकी रक्षा की जानी चाहिए। उनका यही नारा था। सेना अपनी कुल्हाड़ी चला रही थी। उधर एक-एक करके तीन सौ बासठ विश्नोई समाज के स्त्री-पुरुष अपने आप कट गए। उन्होंने इस तरह एक भी वृक्ष नहीं कटने दिया।

(3) स्मरण रहे, हमें पेड़ों की जरूरत है, पेड़ों को हमारी जरूरत नहीं है। वातावरण में दिन-प्रतिदिन बढ़ते प्रदूषण से बचने के लिए हमें पेड़ों की रक्षा करनी ही होगी तथा और पेड़ लगाने होंगे। वृक्ष रक्षा तथा जीवन रक्षा का संकल्प एवं नया वृक्षारोपण कार्य ही वृक्षों की रक्षा में शहीद हुए विश्नोइयों को हमारी सच्ची श्रद्धांजलि होगी।

शब्दार्थ-स्मरण रहे = याद रखना होगा; जरूरत = आवश्यकता; दिन-प्रतिदिन = रोजाना; प्रदूषण = बड़ी मात्रा में दोष; बचाने के लिए = रक्षा के लिए; और दूसरे लगाने होंगे रोपने होंगे; संकल्प = प्रतिज्ञा, प्रण; वृक्षारोपण कार्य = वृक्ष लागने का काम; शहीद हुए = अपनी बलि देने वाले।

सन्दर्भ-पूर्व की तरह।

प्रसंग-बलिदान करने वाले विश्नोइयों को श्रद्धांजलि देने के लिए हमें वृक्ष लगाने होंगे तथा वन के जीवों की रक्षा करनी -होगी।

व्याख्या-हमें यह याद रखना होगा कि हमारी आवश्यकता है कि पेड़ रहें। पेड़ों को हमारी कोई आवश्यकता नहीं है। हमारे चारों ओर के वातावरण में रोजाना प्रदूषण बढ़ रहा है। हमें अपनी रक्षा करनी है, तो हमें पेड़ों की रक्षा करनी होगी। क्योंकि प्रदूषण से हम अनेक तरह के रोगों से ग्रस्त हो जायेंगे। इसके लिए हमें पेड़ लगाने होंगे। वन के जीवों की रक्षा करने से और नये पेड़-पौधे लगाने से ही हम बलिदानी विश्नोइयों को सच्ची श्रद्धांजलि दे सकते हैं।

MP Board Class 8th Hindi Solutions