Bhagya

MP Board Class 11th Maths Solutions Chapter 2 संबंध एवं फलन विविध प्रश्नावली

प्रश्न 1.

दर्शाइए कि क्यों है एक फलन है और g फलन नहीं है।
हल:
(i) दिए गए अंतराल 0 ≤ x ≤ 3 में, f(x) = x² जो कि पूर्णतया परिभाषित है। इस प्रकार अन्तराल 3 ≤ x ≤ 10 में f(x) = 3x भी पूर्णतया परिभाषित है। x = 3, हो, तब x² = 9, और 3x = 9.
अत f(3) = 9
इस प्रकार f एक फलन है।
(ii) अंतराल 0 ≤ x ≤ 2 में g(x) = x² जो कि पूर्णतया परिभाषित है।
अंतराल 2 ≤ x ≤ 10 में g(x) = 3x पूर्णतया परिभाषित है।
x = 2 पर x² = 4 और 3x = 6
x = 2 पर g(x) के दो मान हैं।
अतः संबंध g एक फलन नहीं है।

प्रश्न 2.
यदि f(x) = x² तो \(\frac{f(1.1)-f(1)}{1.1-1}\) ज्ञात कीजिए।
हल:
f(x) = x²
∴ f(1.1) = (1.1)² = 1.21, और f(1) = 1² = 1

प्रश्न 3.
फलन f(x) = \(\frac{x^{2}+2 x+1}{x^{2}-8 x+12}\) का प्रान्त ज्ञात कीजिए।
हल:

x = 2 और x = 6 पर परिभाषित नहीं है।
अतः फलन का प्रान्त संख्याओं 6 और 2 को छोड़कर शेष वास्तविक संख्याओं का समुच्चय है।

प्रश्न 4.
f(x) = \(\sqrt{x-1}\) द्वारा परिभाषित वास्तविक फलन का प्रांत तथा परिसर ज्ञात कीजिए।
हल:
f(x) = \(\sqrt{x-1}\)
यदि x – 1 < 0 या x < 1, फलन परिभाषित नहीं है।
फलन का प्रांत = {x : x ϵ R, x ≥ 1) = [1, ∞)
(ii) मान लीजिए y = \(\sqrt{x-1}\) या y² = x – 1 या x = 1 + y²
अतः फलन का परिसर = {y : y ϵ R, Y ≥ 0} = [0, ∞).

प्रश्न 5.
f(x) = |x – 1| द्वारा परिभाषित वास्तविक फलन का प्रांत तथा परिसर ज्ञात कीजिए।
हल:
f(x) = |x – 1|
x के सभी वास्तविक मूल्यों के लिए फलन परिभाषित है
f का प्रांत = R
f(x) = |x – 1|, f का मान जब x ϵ R, एक धनात्मक संख्या है।
अतः f का परिसर = ऋणेत्तर वास्तविक संख्याएँ।

प्रश्न 6.
मान लीजिए कि f = \(\left\{\left(x, \frac{x^{2}}{1+x^{2}}\right) : x \in R\right\}\) R से R में एक फलन है।। f का परिसर निर्धारित कीजिए।
हल:
माना f(x) = \(\frac{x^{2}}{1+x^{2}}\) या y + yx² = x² या x² – x²y = y या x² (1 – y) = y तब x² = \(\frac{y}{1-y}\)
⇒ y ≠ 1
x की सभी वास्तविक मूल्यों के लिए y ≥ 0
f का अंश हर से सदैव कम है, y ≤ 1
∴ f का परिसर = कोई भी धन वास्तविक संख्या इस प्रकार कि 0 ≤ x ≤ 1.

प्रश्न 7.
मान लीजिए कि f, g : R → R क्रमशः f(x) = x + 1, g(x) = 2x – 3 द्वारा परिभाषित है। f + g, f – g और \(\frac{f}{g}\) ज्ञात कीजिए।
हल:
f(x) = x + 1, g(x) = 2x -3
(f + g) = f(x) + g(x) = x + 1 + 2x – 3 = 3x – 2.
(f – g) (x) = f(x) – g(x) = (x + 1) – (2x – 3) = x + 1 – 2x + 3 = – x + 4.

प्रश्न 8.
मान लीजिए कि f = {(1, 1), (2, 3), (0, -1), (-1, -3)} Z से Z में, f(x) = ax + b, द्वारा परिभाषित एक फलन है, जहाँ a, b कोई पूर्णांक हैं। a, b को निर्धारित कीजिए।
हल:
दिया है : f = {(1, 1). (2, 3), (0, -1), (- 1, -3)}
और f(x) = ax + b …(A)
जब x = 1, y = 1, हो तब a + b = 1 …(i)
और जब x = 2, y = 3, 2a + b = 3 …(ii)
समीकरण (i) और (ii) से,
a = 2, b = -1
a तथा b के इन मानों को समीकरण (A) में रखने पर,
f(x) = 2x – 1
जब x = 0, f(x) = -1
और जब x = – 1, f(x) = – 3
अतः f(x) = 2x – 1
तथा a = 2, b = – 1.

प्रश्न 9.
R = {(a, b) : a, b ϵ N तथा a = b²} द्वारा परिभाषित N से N में, एक संबंध R है। क्या निम्नलिखित कथन सत्य है।
(i) {a, a} ϵ R सभी a ϵ N
(ii) (a, b) ϵ R का तात्पर्य है कि (b, a) ϵ R
(ii) (a, b) ϵ R, (b, c) ϵ R का तात्पर्य है कि (a, c) ϵ R? प्रत्येक दशा में अपने उत्तर का औचित्य भी बताइए।
हल:
(i) a = a यह सत्य है जब a = 0. 0 ∉ N,
अत: यह एक संबंध नहीं है।
(ii) a = b², और b = a², यह a, b ϵ N, a, b के सभी मूल्यों के लिए सत्य नहीं है। अत: यह एक संबंध नहीं है।
(iii) जब a = b², b = c² तब a ≠ c²
∴ यह संबंध नहीं है।

प्रश्न 10.
मान लीजिए A = {1, 2, 3, 4}, B = {1, 5, 9, 11, 15, 16} और f= {(1, 5), (2, 9), (3, 1), (4, 5), (2, 11)}, क्या निम्नलिखित कथन सत्य है ?
(i) f, A से B में एक संबंध है।
(ii) f, A से B में एक फलन है। प्रत्येक दशा में अपने उत्तर का औचित्य बताइए।
हल:
(i) दिया है: A = {1, 2, 3, 4} तथा B = {1, 5, 9, 11, 15, 16}
∴ A × B = {(1, 1), (1, 5), (1, 9), (1, 11), (1, 15), (1, 16), (2, 1), (2, 5), (2, 9), (2, 11), (2, 15), (2, 16), (3, 1), (3, 5), (3, 9), (3, 11), (3, 15), (3,16), (4, 1), (4, 5), (4, 9), (4, 11), (4, 15), (4, 16)}
अवयव , A × B का उपसमुच्चय है।
अतः यह एक संबंध है।
(ii) f में (2, 9) और (2, 11) अवयव प्रथम घटक दोनों युग्मों में 2 है।
∴ यह फलन नहीं है।

प्रश्न 11.
मान लीजिए कि f, f= {{ab, a + b); a, b ϵ Z द्वारा परिभाषित Z × Z का एक उपसमुच्चय है। क्या f, Z से Z में एक फलन है ? अपने उत्तर का औचित्य भी स्पष्ट कीजिए।
हल:
मान लीजिए a = 0, b = 1 हो, तब
ab = 0 और a + b = 0 + 1 = 1
पुनः माना a = 0, b = 2 हो, तब
ab = 0, a + b = 2
अवयव 0 के दो प्रतिबिंब 1 और 2 हैं।
अतः f एक फलन नहीं है।

प्रश्न 12.
मान लीजिए कि A= {9, 10, 11, 12, 13} तथा f : A → N ,f(n) = n का महत्तम अभाज्य गुणक द्वारा परिभाषित है। का परिसर ज्ञात करो।
हल:
यदि n = 9 = 3 × 3 तो 3 इन गुणनखंडों में सबसे बड़ी अभाज्य संख्या है।
n = 10 = 2 × 5 तो 5 इन गुणनखंडों में सबसे बड़ी अभाज्य संख्या है।
n = 11 = 1 × 11 तो 11 इन गुणनखंडों में सबसे बड़ी अभाज्य संख्या है।
n = 12 = 2² × 3 तो 3 इन गुणनखंडों में सबसे बड़ी अभाज्य संख्या है।
n = 13 = 1 × 13 तो 13 इन गुणनखंडों में सबसे बड़ी अभाज्य संख्या है।
अतः f का परिसर = {3, 5, 11, 13}.

MP Board Class 11th Maths Solutions

MP Board Class 12th Maths Solutions Chapter 11 प्रायिकता Ex 11.3

प्रश्न 1.
निम्नलिखित प्रश्नों में से प्रत्येक में समतल के अभिलम्ब का दिक् कोसाइन और मूल बिन्दु से दूरी ज्ञात कीजिए-
(a) z = 2
(b) x + y + z = 1
(c) 2x + 3y – 2 = 5
(d) 5y + 8 = 0
हल:
माना दिये गये समतल का कार्तीय समीकरण ax + by + cz =d तथा अभिलम्ब के दिक् अनुपात a, b, c हैं।
तब मूल बिन्दु से लम्बवत् दूरी = \(\left|\frac{d}{\sqrt{a^{2}+b^{2}+c^{2}}}\right|\)
(a) समतल का समी० z = 2
∴ दिक् कोसाइन 0, 0, 1 हैं।
(b) समतल x + 1 + z = 1
दिक अनुपात 1, 1, 1 हैं।
तब दिक् कोसाइन

प्रश्न 2.
उस समतल का सदिश समी० ज्ञात कीजिए जो मूल बिन्दु से 7 मात्रक दूरी पर है और सदिश \(3 \hat{\mathbf{i}}+5 \hat{\mathbf{j}}-6 \hat{\mathbf{k}}\) पर अभिलम्ब है।
हल:

प्रश्न 3.
निम्नलिखित समतलों का कार्तीय समी० ज्ञात कीजिए–

हल:

प्रश्न 4.
निम्न स्थितियों में, मूल बिन्दु से खींचे गए लम्ब के पाद के निर्देशांक ज्ञात कीजिए–
(a) 2x + 3y + 4z – 12 = 0
(b) 3y + 4z – 6 = 0
(c) x + y + z = 1
(d) 5y + 8 = 0
हल:
(a) समतल का समीकरण
2x + 3y + 4z – 12 = 0 ……(i)

(b) समतल का समीकरण


(c) समतल का समीकरण

(d) समतल का समीकरण

प्रश्न 5.
निम्नलिखित प्रतिबंधों के अन्तर्गत समतलों का सदिश व कार्तीय समीकरण ज्ञात कीजिए जो-
(a) बिन्दु (1,0,-2) से जाता हो और \(\hat{i}+\hat{j}-\hat{k}\) समतल पर अभिलंब हो।
(b) बिन्दु (1, 4, 6) से जाता हो और \(\hat{\boldsymbol{i}}-2 \hat{\boldsymbol{j}}+\hat{\boldsymbol{k}}\) समतल पर अभिलम्ब सदिश है।
हल:
(a) बिन्दु (1, 0, – 2) का स्थिति सदिश

यही अभीष्ट कार्तीय समीकरण है।

यही अभीष्ट कार्तीय समीकरण है।

प्रश्न 6.
उन समतलों का समीकरण ज्ञात कीजिए जो निम्नलिखित तीन बिन्दुओं से गुजरता है।
(a) (1, 1, – 1), (6, 4, – 5), (- 4, – 2, 3)
(b) (1, 1, 0), (1, 2, 1), (- 2, 2, – 1)
हल:
(a) माना
(x₁, y₁, z₁) ≡ (1, 1, – 1)
(x₂, y₂, z₂) ≡ (6, 4, – 5)
(x₃, y₃, z₃) ≡ ( – 4, – 2, 3)
इन तीन बिन्दुओं से जाने वाले समतल का समी०

समीकरण (1), (2), (3) में से a, b, c को लुप्त करने से, समतल का समीकरण
\(\left|\begin{array}{ccc}{x-1} & {y-1} & {z} \\ {0} & {1} & {1} \\ {3} & {-1} & {1}\end{array}\right|\) = 0
⇒ 2(x – 1) + 3 (y – 1) – 3z = 0
⇒ 2x – 2 + 3y – 3 – 3z = 0
⇒ 2x + 3y – 3z = 5

प्रश्न 7.
समतल 2x + y – x = 5 द्वारा काटे गये अन्तः खण्डों को ज्ञात कीजिए।
हल:
दिया गया समतल 2x + y – z = 5 समी० को अन्तः खण्ड रूप में लिखने पर
\(\frac{x}{\frac{5}{2}}+\frac{y}{5}+\frac{2}{(-5)}\) = 1
जो कि \(\frac{x}{a}+\frac{y}{b}+\frac{z}{c}\) = 1 के रूप की हैं।
अत: अक्षों से कटे अन्तः खण्ड, \(\frac{5}{2}\), 5, – 5 हैं।

प्रश्न 8.
उस समतल का समी० ज्ञात कीजिए जिसका y- अक्ष पर
अंतः खण्ड 3 और जो तल ZOX के समांतर है।
हल:
अक्ष ZOX का समी० y = 0 है।
∴ इस समतल के समांतर समी० y = a
∵ समतल का -अक्ष पर अंत: खण्ड 3 है इसलिए समतल y- अक्ष पर (0, 3, 0) पर मिलता हैं।
∴ 3 = a
अतः समतल का समी० y = 3

प्रश्न 9.
उस समतल का समीकरण ज्ञात कीजिए जो समतलों 3x – y + 22 – 4 = 0 और x + y + z – 2 = 0 के प्रतिच्छेदन तथा बिन्दु (2, 2, 1) से होकर जाता है।
हल:
समतल तथा उसके प्रतिच्छेदन बिन्दु से जाने वाले तल का समीकरण
(3x – y + 2z – 4) + λ (x + y + z – 2) = 0 …(i)
परन्तु तल बिन्दु (2.2.1) से होकर जाता है तब
(6 – 2 + 2 – 4) + (2 + 2 + 1 – 2) = 0
2 + 3λ = 0
λ = – \(\frac{2}{3}\)
λ का यह मान समीकरण (i) में रखने पर
(3x – y + 2z – 4) – \(\frac{2}{3}\) (x + y + z – 2) = 0
(9x – 3y + 6z – 12) – (2x + 2y + 2z – 4) = 0
7x – 5y + 4z – 8 = 0

प्रश्न 10.
उस समतल का सदिश समीकरण ज्ञात कीजिए जो समतलो \(\vec{r} \cdot(2 \hat{i}+2 \hat{j}-\hat{3} \hat{k})=7\), \(\vec{r} \cdot(2 \hat{i}+5 \hat{j}+3 \hat{k})=9\) के प्रतिच्छेदन रेखा और (2, 1, 3) से होकर जाता है।
हल:

प्रश्न 11.
तलों x + y+ z = 1 और 2x + 3y + 4z = 5 के प्रतिच्छेदन रेखा से होकर जाने वाले तथा तल x – y + z = 0 पर लम्बवत् तल का समीकरण ज्ञात कीजिए।
हल:
समतल x + y + z = 1 और 2x + 3y + 4z = 5 के प्रतिच्छेदन रेखा से होकर जाने वाली समतल का समीकरण
(x + y + z – 1) + λ (2x + 3y + 4z – 5) = 0
या (1+ 2λ) x + (1+3λ) y+ (1+4λ) z – 1 – 5λ = 0
यह तल x – y + z = 0 पर लम्बवत् है
∴ (1 + 2λ) . 1 + (1 + 3λ)(- 1) + (1 + 4λ) . 1 = 0 (∵ a₁ a₂ + b₁ b₂ + c₁ c₂) = 0
या 1 = 2λ – 1 – 3λ + 1 + 4λ = 0
⇒ 1 + 3λ = 0
⇒ λ = – \(\frac{1}{3}\)
λ का मान समी० (i) में रखने पर,

x – z + 2 = 0

प्रश्न 12.
समतलों जिनके सदिश समीकरण \(\vec{r} \cdot(2 \hat{i}+2 \hat{j}-3 \hat{k})=5\) और \(\vec{r}(3 \hat{i}-3 \hat{j}+5 \hat{k})=3\) हैं के बीच का कोण ज्ञात करो।
हल:
माना

प्रश्न 13.
निम्नलिखित प्रश्नों में ज्ञात कीजिए कि क्या दिए गए समतलों के युग्म समान्तर हैं अथवा लम्बवत् हैं और उस स्थिति में, जब ये न तो समान्तर हैं और न ही लम्बवत्, उनके बीच का कोण ज्ञात कीजिए।
(a) 7x + 5y + 6z + 30 = 0 और 3x -y – 10z + 4 = 0
(b) 2x + y + 3z – 2 = 0 और x – 2y + 5 = 0
(c) 2x – 2y + 4x + 5 = 0 और 3x – 3y + 6z – 1 = 0
(d) 2x – y + 3z – 1 = 0 और 2x – y + 3x + 3 =0
(e) 4x + 8y + 7 – 8 = 0 और y + 2 – 4 = 0
हल:


(b) दिए गए समतल

प्रश्न 14.
निम्न प्रश्नों में प्रत्येक दिये गये बिन्दु से दिये गये संगत समतलों की दूरी ज्ञात कीजिए।

हल:

MP Board Class 12th Maths Solutions

MP Board Class 11th Maths Solutions Chapter 2 संबंध एवं फलन Ex 2.3

प्रश्न 1.
निम्नलिखित संबंधों में से कौन से फलन हैं ? कारण का उल्लेख कीजिए। यदि संबंध एक फलन है तो उसका परिसर निर्धारित कीजिए।
(i) {(2, 1), (5, 1), (8, 1), (11, 1), (14, 1), (17, 1)}
(ii) {(2, 1), (4, 2), (6, 3), (8, 4), (10, 5), (12, 6), (14, 7)}
(iii) {(1, 3), (1, 5), (2, 5)}
हल:
(i) माना R = {(2, 1), (5, 1), (8, 1), (11, 1), (14, 1), (17, 1)}
यह संबंध एक फलन है क्योंकि किसी भी दो क्रमित युग्म का पहला घटक बराबर नहीं है।
प्रान्त = {2, 6, 8, 11, 14, 17} तथा परिसर = {1}.
(ii) माना R = {(2, 1), (4, 2), (6, 3), (8, 4), (10, 5), (12, 6), (14, 7)}
यह एक फलन है क्योंकि किसी भी दो क्रमित युग्म का पहला घटक बराबर नहीं है।
अतः प्रांत = {2, 4, 6, 8, 10, 12, 14}, परिसर = {1, 2, 3, 4, 5, 6, 7}.
(iii) यह एक फलन नहीं है क्योंकि (1, 3), (1,5) में पहला घटक समान है।

प्रश्न 2.
निम्नलिखित वास्तविक फलनों के प्रांत तथा परिसर ज्ञात कीजिए।
(i) f(x) = – |x|
(ii) f(x) = \(\sqrt{9-x^{2}}\)
हल:
दिया है : f(x) = – |x |, f(x) ≤ 0 सभी x ⊂ R के लिए
f का प्रान्त = R
तथा f का परिसर = {y : y ϵ R, Y ≤ 0) = (-∞, 0]
(ii) (a) f(x) = \(\sqrt{9-x^{2}}\)
f(x) परिभाषित नहीं है जब 9 – x² < 0 या x² > 9
⇒ x > 3 और x < -3
∴ f परिभाषित है जब – 3 ≤ x ≤ 3.
f का प्रान्त = – 3 ≤ x ≤ 3, x ϵ R
अब मान लीजिए y = \(\sqrt{9-x^{2}}\) या y² = 9 – x²
x² = 9 – y², x = \(\sqrt{9-x^{2}}\)
f परिभाषित है यदि 9 ≥ y² 2 0 या y² ≤ 9
⇒ y ≤ 3, y ≠ – ve
(b) f का परिसर = y ≤ 3 और y ≥ 0
= {y : y ≤ R और 0 ≤ y ≤ 3}.

प्रश्न 3.
एक फलन f(x) = 2x – 5 द्वारा परिभाषित है। निम्नलिखित के मान लिखिए :
(i) f(0)
(ii) f(7)
(iii) f(-3)
हल:
f(x) = 2x – 5
(i) f(o) = 2 × 0 – 5 = -5
(ii) f(7) = 14 – 5 = 9
(iii) f(-3) = 2 × (-3) – 5 = – 6 – 5 = – 11.

प्रश्न 4.
फलन ‘t’ सेल्सियस तापमान का फारेनहाइट तापमान में प्रतिचित्रण करता है, जो t(C) = \(\frac{9 C}{5}+32\) द्वारा परिभाषित है। निम्नलिखित को ज्ञात कीजिए :
(i) t (0)
(ii) t (28)
(iii) t (-10)
(iv) C का मान, जब t(C) = 212
हल:

प्रश्न 5.
निम्नलिखित में से प्रत्येक फलन का परिसर ज्ञात कीजिए :
(i) f(x) = 2 – 3x, x ϵ R, x > 0.
(ii) f(x) = x + 2, x एक वास्तविक संख्या है।
(iii) f(x) = x, x एक वास्तविक संख्या है।
हल:
(i) दिया है : f(x) = 2 – 3x, x ϵ R, x > 0
= y (माना)
∴ 2 – 3x = y या 2 – y = 3x या x = \(\frac{2-y}{3}\)
दिया है: x > 0 अर्थात \(\frac{2-y}{3}\) > 0 या 2 – y > 0 या y < 2
अतः f का परिसर = y < 2 या (-∞, 2)
(ii) f(x) = y = x² + 2, x ϵ R
या x² = y – 2
या x = \(\sqrt{y-2}\)
अर्थात y – 2 ≤ 0 या y ≥ 2
अतः f का परिसर y = {y : y ϵ R और y ≥ 2}
= [2, ∞].
(iii) f(x) = y = x या x = y
∵ x ϵ R और x = y तब y ϵ R
अतः f का परिसर = {y : y ϵ R} = R.

MP Board Class 11th Maths Solutions

MP Board Class 11th Maths Solutions Chapter 2 संबंध एवं फलन Ex 2.2

प्रश्न 1.
मान लीजिए A= {1, 2, 3, ……. 14}, R = {(x, y): 3x – y = 0, जहाँ x, Y ϵ A) द्वारा A से A का एक संबंध R लिखिए। इसके प्रांत, सहप्रांत और परिसर लिखिए।
हल:
A = {1, 2, 3, ….., 14}, R : A जबकि
(i) R = {(x, y) : 3x – y = 0 या y = 3x}
= {(1, 3), (2, 6), (3, 9), (4, 12),….}
(ii) प्रांत : संबंध R के समुच्चयों में x के अवयव = {1, 2, 3, 4}.
सहप्रांत : {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14}.
परिसर : संबंध R के समुच्चयों में y के अवयव = {3, 6, 9, 12}.

प्रश्न 2.
प्राकृत संख्याओं के समुच्चय पर R = {x, y) : y = x + 5, x संख्या 4 से कम, एक प्राकृत संख्या है, x,y ϵ N} द्वारा एक संबंध R परिभाषित कीजिए। इस संबंध को
(i) रोस्टर रूप में इसके प्रांत और परिसर लिखिए।
हल:
संबंध R, दिया गया है।
R = {(x, y) : y = x + 5, x, y ϵ N तथा x < 4}
= {(1, 6), (2, 7), (3, 8)}.
(i) प्रान्त = {1, 2, 3}.
परिसर = {6, 7, 8}.

प्रश्न 3.
A = {1, 2, 3, 5} और B = {4, 6, 9}, A से B में एक सम्बन्ध
R = {x, y} : x और y का अंतर विषम है, x ϵ A, y ϵ B} द्वारा परिभाषित कीजिए। R को रोस्टर रूप में लिखिए।
हल:
दिया है: A = {1, 2, 3, 5} और B = {4, 6, 9}. A से B में संबंध,
R = {(x, y) : x, में अंतर विषम है, x ϵ A, y ϵ B}
= {1, 4,), (1, 6), (2, 9), (3, 4), (3, 6), (5, 4), (5, 6)}.

प्रश्न 4.
दी हुई आकृति समुच्चय P से Q का एक संबंध दर्शाती है। इस संबंध को (i) समुच्चय निर्माण रूप में (ii) रोस्टर रूप में लिखिए। इसके प्रांत व परिसर क्या हैं ?

हल:
(i) समुच्चय निर्माण रूप में, R = {(x, y) : y = x – 2, x = 5, 6, 7 के लिए}
(ii) रोस्टर रूप में, R = {(5, 3), (6, 4), (7, 5)}
प्रान्त = {5, 6, 7}
और परिसर = {3, 4, 5}.

प्रश्न 5.
मान लीजिए कि A= {1, 2, 3, 4, 6) मान लीजिए कि R, A पर {(a, b) : a, b ϵ A, संख्या a संख्या b को यथावथ विभाजित करती है} द्वारा परिभाषित एक संबंध है।
(i) R को रोस्टर रूप में लिखिए।
(ii) R का प्रांत ज्ञात कीजिए।
(iii) R का परिसर ज्ञात कीजिए।
हल:
दिया है :
A = {1, 2, 3, 4, 6}
R = {(a, b) : a, b ϵ A, a संख्या b को विभाजित करती है}
(i) रोस्टर रूप में, R = {(1, 1), (1, 2), (1, 3), (1, 4), (1, 6), (2, 2), (2, 4), (2, 6), (3, 3), (3, 6), (4,4), (6, 6)}
(ii) R का प्रांत = {1, 2, 3, 4, 5, 6}
(iii) R का परिसर = {1, 2, 3, 4, 5, 6}.

प्रश्न 6.
R = {(x, x + 5) : x ϵ {0, 1, 2, 3, 4, 5}} द्वारा परिभाषित संबंध R के प्रांत और परिसर ज्ञात कीजिए।
हल:
R = {(x, x + 5) : x ϵ {0, 1, 2, 3, 4, 5}}
= {(0, 5), (1, 6), (2, 7), (3, 8), (4, 9), (5, 10)}
R का प्रांत = {0, 1, 2, 3, 4, 5}
R का परिसर : {5, 6, 7, 8, 9, 10}.

प्रश्न 7.
संबंध R = {(x, x³) : x संख्या 10 से कम एक अभाज्य संख्या है} को रोस्टर रूप में लिखिए।
हल:
10 से कम अभाज्य संख्याएँ 2, 3, 5, 7
रोस्टर रूप में, R = {(x, x³) : x एक अभाज्य संख्या है जो 10 से कम है}
= {(2, 8), (3, 27), (5, 125), (7, 343)}.

प्रश्न 8.
मान लीजिए कि A = {x, y, } और B = {1, 2}, A से B के संबंधों की संख्या ज्ञात कीजिए।
हल:
दिया है: A = {x, y, z}, B = {1, 2}
A × B = {(x, 1), (x, 2), (y, 1), (y, 2), (z, 1), (z, 2)}
n(A × B) = 6
संबंधों की कुल संख्या = A × B के उपसमुच्चयों की संख्या
= 2⁶ = 64.

प्रश्न 9.
मान लीजिए कि R, Z पर, R = {(a, b) : a, b ϵ z, a – b एक पूर्णांक है}, द्वारा परिभाषित एक संबंध है। R के प्रांत व परिसर ज्ञात कीजिए।
हल:
R समुच्चय Z पर एक संबंध है तथा R = {(a, b), a ϵ Z, b ϵ Z, a – b एक पूर्णांक संख्या है।
∴ प्रांत (R) = Z
परिसर (R) = Z.

MP Board Class 11th Maths Solutions

MP Board Class 8th Hindi Bhasha Bharti Solutions Chapter 15 महेश्वर

महेश्वर बोध प्रश्न

प्रश्न 1.
निम्नलिखित शब्दों के अर्थ शब्दकोष से खोजकर लिखिए
उत्तर
संस्कृति = आचरणगत परम्परा, प्राचीन सभ्यता; पुराविद् = प्राचीन इतिहास आदि विषयों की जानकारी रखने वाला; सर्वतोन्मुखी = सभी तरह का प्रागैतिहासिक = इतिहास लिखे जाने से भी पहले के इतिहास से सम्बन्धित फलकपटल, तख्ता; अलंकरण = सजावट, पुरातात्विक = पुरातत्व सम्बन्धी उत्तरदायित्व-जिम्मेदारी; पाषाण पत्थर खननखुदाई: अवशेष = शेष भाग, वह जो बचा रहे।

प्रश्न 2.
निम्नलिखित प्रश्नों के उत्तर संक्षेप में लिखिए
(क) महेश्वर का प्राचीन नाम क्या है?
उत्तर
महेश्वर का प्राचीन नाम माहेश्वरी अथवा माहिष्मती

(ख) महेश्वर मध्य प्रदेश के किस जिले में स्थित है?
उत्तर
महेश्वर मध्य प्रदेश के इन्दौर जिले में स्थित है। यह इन्दौर से लगभग 105 किलोमीटर दूर है।

(ग) महेश्वर की खुदाई में किस प्रकार की वस्तुएँ प्राप्त
उत्तर
महेश्वर की खुदाई में पुरातात्विक महत्त्व की अनेक वस्तुएँ और अवशेष प्राप्त हुए हैं।

(घ) हैहय साम्राज्य की स्थापना किसने की थी?
उत्तर
हैहय साम्राज्य की स्थापना कीर्तिवीर्य सहस्रार्जुन ने की थी।

(ङ) नर्मदा के तट पर किला और शिव का मन्दिर किसने बनवाया था?
उत्तर
नर्मदा के तट पर किला और शिव का मन्दिर महारानी अहिल्याबाई ने बनवाया था।

प्रश्न 3.
निम्नलिखित प्रश्नों के उत्तर विस्तार से लिखिए
(क) सहस्त्रार्जुन के वध का क्या कारण था ?
उत्तर
महेश्वर नगर को सूर्यवंशी राजा मान्धाता ने बसाया था। उनके बाद इस नगर पर कीर्तिवीर्य सहलार्जुन ने अपना आधिपत्य जमा लिया था। उसका साम्राज्य हैहय कहलाया और इस नगर को अपने साम्राज्य की राजधानी बनाया था। सहस्त्रार्जुन ने परशुराम जी के पिता ऋषि जमदग्नि का वध कर दिया। इसका बदला लेने के लिए भगवान परशुराम ने सहस्रार्जुन का अन कर दिया। इसके बाद यह स्थान इतिहास के गर्त में खो गया।

(ख) महारानी अहिल्याबाई के किन-किन कार्यों से । महेश्वर प्रसिद्ध हुआ?
उत्तर
इन्दौर की महारानी अहिल्याबाई ने महेश्वर को एक बार फिर से प्रसिद्धि प्रदान की। उन्हें यह स्थान बहुत ही प्रिय था।
उन्होंने इस स्थान पर नर्मदा के तट पर एक किला और भगवान शिव का विशाल मन्दिर बनवाया। यहाँ स्थित पवित्र शिवलिंग महेश्वर के नाम से प्रसिद्ध है। मन्दिर में महारानी अहिल्याबाई द्वारा प्रज्वलित अखण्डदीप में यहाँ आने वाला प्रत्येक दर्शनार्थी घी डालकर स्वयं को धन्य समझता है। महेश्वर धार्मिक, पौरानिक, पुरातात्विक, सांस्कृतिक और ऐतिहासिक सम्पदा से सम्पन्न है। महारानी अहिल्याबाई ने मराठों के शासनकाल में यहाँ सुन्दर घाटों, मन्दिरों, धर्मशालाओं तथा भवनों का निर्माण कराया। इस काल में महेश्वर का सर्वतोन्मुखी विकास हुआ। यह नगर रेशमी – साड़ियों के निर्माण के लिए भी बहुत प्रसिद्ध है।

(ग) महारानी अहिल्याबाई को ‘लोकमाता’ के रूप में क्यों याद किया जाता है?
उत्तर
महारानी अहिल्याबाई ने महेश्वर नगर का सर्वतोन्मुखी विकास कराया। उन्होंने ही इसे प्रसिद्धि प्रदान करने के लिए महान् से महान् कार्य किए। नर्मदा के तटों पर सुन्दर घाटों का और मन्दिरों का निर्माण कराया। यहाँ का किला और शिवमन्दिर बहुत ही विशाल है। इस मन्दिर में दीप ज्योति निरनार जलती रहती है। इस दीप को महारानी अहिल्याबाई ने स्वयं प्रज्ज्वलित किया था। यहाँ पर देवदर्शन के लिए आने वाला प्रत्येक दर्शनार्थी परम शान्ति का अनुभव करता है। लोग प्रात: व सायं पवित्र जल वाली नर्मदा में स्नान करके नर नारी आरती की मधुर ध्वनि’ॐ नमः शिवाय:’ के मन्त्र में डूब से जाते हैं। यहाँ का वातावरण पवित्र है। यह प्राकृतिक सौन्दर्य से भरा है एवं मनोहारी है। इस सबके लिए वे महारानी अहिल्याबाई के ऋणी हैं। इसलिए उनें लोग ‘लोकमाता’ के रूप में मानते हैं।

(घ) पाषाणकालीन सभ्यता के लोग अपना जीवन किस प्रकार व्यतीत करते थे?
उत्तर
नर्मदा नदी की घाटी में पाषाणकालीन सभ्यता के पत्थर से निर्मित औजार मिले हैं। प्रागैतिहासिक काल के पुरा-अवशेषों से पता चलता है कि उस समय यहाँ के लोग घास-फूस के झोंपड़ों में या पेड़ों पर बने घरों में रहते थे। उस समय की पाई गई वस्तुओं में लाल और काले रंग के मिट्टी के बर्तनों और घड़ों के टुकड़े प्रमुख हैं। सम्भवतः वे अपनी सुरक्षा की दृष्टि से पेड़ों पर या ऊँची जमीन पर अपने घर बनाते थे। यह भी सत्य है कि पापणकाल के लोग नदियों, तालाबों आदि के किनारे ही असते रहे हैं, क्योंकि इन स्थानों पर उनकी आवश्यकता की सारी वस्तुएँ आसानी से प्राप्त हो जाती थी।

प्रश्न 4.
रिक्त स्थानों की पूर्ति उचित शब्दों द्वारा कीजिए
नर्मदा, रेशम, पुरातात्विक, महेश्वर।
(क) महेश्वर की खुदाई में ……. महत्व की वस्तुएँ
(ख) महारानी अहिल्याबाई ने ……… में किला और शिव मन्दिर बनवाया था।
(ग) महेश्वर की बनी ….. की साड़ियाँ प्रसिद्ध हैं।
(घ) महेश्वर ……….. नदी के किनारे बसा है।
उत्तर
(क) पुरातात्विक
(ख) महेश्वर
(ग) रेशमी
(घ) नर्मदा

महेश्वर भाषा-अध्ययन

प्रश्न 1.
निम्नलिखित शब्दों का शुद्ध उच्चारण कीजिए और वाक्यों में प्रयोग कीजिए
आशीवाद, सहस्रार्जुन, संस्कृति, ऋषि, जमदग्नि, दर्शनार्थी, प्रज्ज्वलित, पुरातात्विक।
उत्तर
विद्यार्थी उपर्युक्त शब्दों को वीक-ठीक पढ़कर उनका शुद्ध उच्चारण करने का अभ्यास करें।
वाक्य-प्रयोग-

1. देवदर्शन करके उनका आशीर्वाद प्राप्त करते हैं।
2. सहस्त्रार्जुन ने ऋषि जमदग्नि का वध कर दिया था।
3. भारतीय संस्कृति पूरे संसार में अपना प्रभाव जमाए
4. ऋषि धौम्य महान् त्यागी और लोकरंजक थे।
5. जमदग्नि, भगवान परशुराम के पिता थे।
6. शिव मन्दिर में दर्शनार्थियों की भीड़ लगी रहती है।
7. गाँवों में सायंकाल को घर-घर में दीप प्रज्ज्वलित किए जाते हैं।
8. महेश्वर पुरातात्विक महत्त्व का नगर है।

प्रश्न 2.
निम्नलिखित शब्दों का समास-विग्रह करके, उनके सामने समास का नाम लिखिए.
लोकमाता, मधुर ध्वनि, नर-नारी, विशाल मन्दिर, अखण्ड दीप, महारानी।
उत्तर

प्रश्न 3.
निम्नलिखित शब्दों में प्रयुक्त उपसर्ग छाँटकर लिखिए
अखण्ड, अवशेष, प्रसिद्ध, अनुशासन, विज्ञान।
उत्तर

प्रश्न 4.
निम्नलिखित शब्दों के सन्धि-विच्छेद कीजिए और उनके सामने सन्धि का नाम लिखिए
महेश्वर, मनोहर, आशीर्वाद, दर्शनार्थी।
उत्तर

प्रश्न 5.
निम्नलिखित वाक्यों में से उद्देश्य और विधेव छाँटकर लिखिए
(क) इन्दौर की महारानी अहिल्याबाई ने सुन्दर घाटों, मन्दिरों और धर्मशालाओं का निर्माण कराया था।
(ख) पाषाणकालीन सभ्यता के औजार नर्मदा के घाटों को खुदाई में मिले हैं।
(ग) महेश्वर की सिल्क साड़ियाँ बहुत प्रसिद्ध है।
उत्तर

प्रश्न 6.
सही जोड़ी बनाइए


उत्तर
(क) → (2), (ख) → (3), (ग) → (5), (घ)→ (1), (ङ)→(4)

प्रश्न 7.
प्रधानाध्यापक को एक पत्र लिखिए, जिसमें महेश्वर दर्शनीय स्थल पर भ्रमण-दल ले जाने का अनुरोध कीजिए।
उत्तर
विद्यार्थी स्वयं लिखें।

महेश्वर परीक्षोपयोगी गद्यांशों की व्याख्या  

(1) महेश्वर धार्मिक, पौराणिक, पुरातात्विक, सांस्कृतिक और ऐतिहासिक सम्पदा से सम्पन्न है। यहाँ नर्मदा – घाटी में पाषाणकालीन सभ्यता के औजार मिले हैं। प्रागैतिहासिक काल के पुरा-अवशेषों से पता चलता है कि उस समय यहाँ के लोग घास-फूस के झोंपड़ों में या पेड़ों पर बने घरों में रहते थे। उस समय की पाई गई वस्तुओं में लाल और काले रंग के मिट्टी के बरतनों और घड़ों के टुकड़े प्रमुख हैं। ईसा पूर्व की चौथी सदी से लेकर पहली सदी तक का समय महेश्वर के इतिहास में महत्त्वपूर्ण है। इस समय के भवनों के अवशेष यहाँ मिले हैं। इन भवनों में ईंटों का प्रयोग किया गया

शब्दार्थ-पुरातात्विक पुरातत्व सम्बन्धी ऐतिहासिक इतिहास सम्बन्धी; सम्पदा = सम्पत्ति; सम्पन्न – युक्त, सहित; प्रागैतिहासिक = लिखित इतिहास से पहले के इतिहास से सम्बन्धित काल-युग,समय;पुरा-प्राचीन काल के अवशेष = वह जो बचा रहे, शेष भाग;
प्रमुख = मुख्य भवनों = घरों।

सन्दर्भ-प्रस्तुत गद्यांश हमारी पाठ्य-पुस्तक ‘भाषा-भारती’ के पाठ ‘महेश्वर’ से अवतरित है।

प्रसंग-नर्मदा घाटी के महेश्वर नगर की प्रागैतिहासिक संस्कृति के विषय में वर्णन किया गया।

व्याख्या-महेश्वर नगर धर्म और पुराण सम्बन्धी सम्पदा से युक्त स्थान है। यह पुरातत्व सम्बन्धी, प्राचीन आचार-विचार सम्बन्धी एवं इतिहास से सम्बन्ध रखने वाली सम्पत्ति से भरपूर स्थान है। यह नर्मदा नदी के किनारे स्थित है। इस नदी की घाटी में पत्थर के युग (पाषाण युग) की सभ्यता से सम्बन्ध रखने वाले औजार प्राप्त हुए हैं। इतिहास लिखे जाने की पद्धति से भी पूर्व के इतिहास सम्बन्धी समय (युग) के अति प्राचीन शेष भाग से ज्ञात होता है कि उस समय में वहाँ के रहने वाले लोग घास और फंस से बनाए गए झोंपड़ों में रहते थे अथवा वे लोग उन घरों में रहते थे जो पेड़ों पर बनाए जाते थे। ये स्थान वे हैं जब लोग अपनी सुरक्षा के लिए पेड़ों पर अपने निवास बनाते थे। नगरीय सभ्यता या गाँवों में सामूहिक रूप में रहने की सभ्यता का उस समय तक विकास नहीं हुआ था। उस युग की पाई जाने वाली वस्तुओं में लाल और काले रंग के मिट्टी के बरतन तथा घड़ों के टुकड़ें मुख्य हैं। महेश्वर नगर का इतिहास ईसा पूर्व की चौथी सदी से लेकर पहली सदी तक अति महत्त्वपूर्ण है। उस काल के भवनों के खण्डहर अभी तक अवशेष के रूप में प्राप्त हुए हैं। इन भवनों का निर्माण ईंटों से किया गया है। .

(2) मराठों के शासनकाल में महारानी अहिल्याबाई ने यहाँ सुन्दरघाटों, मन्दिरों, धर्मशालाओं तथा भवनों का निर्माण कराया। उनके काल में महेश्वर का सर्वतोन्मुखी विकास हुआ। एक बार तो मैं भूला ही जा रहा था। यहाँ की बनी रेशमी साड़ियाँ महेश्वरी साड़ियों के नाम से प्रसिद्ध हैं। महेश्वर के बारे में जितना भी लिखू कम

शब्दार्थ-निर्माण कराया = बनवाये; सर्वतोन्मुखी = सभी तरह का; विकास = बढ़ोत्तरी।

सन्दर्भ-पूर्व की तरह।

प्रसंग-महारानी अहिल्याबाई के द्वारा महेश्वर नगर में कराए गए विकास कार्यों के बारे में बताया गया है।

व्याख्या-मराठों के शासन काल में जो निर्माण कार्य यहाँ किया गया है, वह बेजोड़ था। महारानी अहिल्याबाई ने नर्मदा नदी के घाटों, मन्दिरों तथा धर्मशालाओं का निर्माण कराया। इसके अलावा यहाँ बहुत ही अच्छे भवनों का निर्माण किया गया। महेश्वर नगर में अपने शासन काल में सभी तरह के विकास का कार्य किया गया। लेखक यहाँ बताना नहीं भूला है कि यहाँ पर रेशम की बनी साड़ियाँ बहुत अच्छी होती हैं। इन साड़ियों को महेश्वरी साड़ियाँ कहते हैं। महेश्वर नगर के विषय में जितना भी | लिखा जाय, वह कम ही है।

MP Board Class 8th Hindi Solutions

MP Board Class 8th Maths Solutions Chapter 15 Introduction to Graphs Ex 15.3

Question 1.
Draw the graphs for the following tables of values, with suitable scales on the axes.
(a) Cost of apples

(b) The horizontal line x-axis shows the time (in hours) and vertical line y-axis shows the distance (in km).

(i) How much distance did the car cover during the period 7.30 a.m. to 8 a.m.?
(ii) What was the time when the car had covered a distance of 100 km since it’s start?
(c) interest on deposits for a year.

(i) Does the graph pass through the origin?
(ii) Use the graph to find the interest on ₹ 2500 for a year.
(iii) To get an interest of ₹ 280 per year, how much money should be deposited?
Solution:
(a) The horizontal line x-axis shows the number of apples and vertical line y-axis shows the cost (in ₹) of apples.

(b) The horizontal line x-axis shows the time (in hours) and vertical line y-axis shows the distance (in km).

(i) The total distance covered by the car during the period 7.30 a.m. to 8 a.m. is (120 – 100) = 20 km.
(ii) At 7.30 a.m.car had covered a distance of 100 km since its start.
(c) The horizontal line x-axis shows deposit (in ₹) and vertical line y-axis shows simple interest (in ₹)

(i) Yes, graph passes through the origin.
(ii) Interest on ₹ 2500 is ₹ 200.
(iii) To get an interest of ₹ 280 per year, ₹ 3500 should be deposited.

Question 2.
Draw a graph for the following

Is it a linear graph?

Solution:
(i) The horizontal line x-axis shows a side of square (in cm) and the vertical line y-axis shows a perimeter (in cm).

Yes, it is a linear graph.
(ii) The horizontal line x-axis shows a side of a square (in cm) and the vertical line y-axis shows an area (in cm²).

No, it is not a linear graph.

MP Board Class 8th Maths Solutions

MP Board Class 11th Maths Solutions Chapter 2 संबंध एवं फलन Ex 2.1

प्रश्न 1.
यदि \(\left(\frac{x}{3}+1, y-\frac{2}{3}\right)=\left(\frac{5}{3}, \frac{1}{3}\right)\) तो तथा ज्ञात कीजिए।
हल:
दिया है : \(\left(\frac{x}{3}+1, y-\frac{2}{3}\right)=\left(\frac{5}{3}, \frac{1}{3}\right)\)
दोनों पक्षों के क्रमित अवयवों की तुलना से,

प्रश्न 2.
यदि समुच्चय A में 3 अवयव हैं तथा समुच्चय B = {3, 4, 5}, तो A × B में अवयवों की संख्या ज्ञात कीजिए।
हल:
समुच्चय A में 3 अवयव है और समुच्चय B में भी 3 अवयव हैं।
∴ A × B में अवयवों की संख्या = 3 × 3= 9.

प्रश्न 3.
यदि G = {7, 8} और H = {5, 4, 2}, तो G × H तथा H × G ज्ञात कीजिए।
हल:
G = {7, 8}, H = {5, 4, 2}
G × H = {7, 8} × {5, 4, 2}
= {(7, 5), (7, 4), (7, 2), (8, 5), (8, 4), (8, 2)}
तथा H × G = {5, 4, 2} × {7, 8}
= {(5, 7), (5, 8), (4, 7), (4, 8), (2, 7), (2, 8)}.

प्रश्न 4.
बताइए कि निम्नलिखित कथनों में से प्रत्येक सत्य है या असत्य है। यदि कथन असत्य है, तो दिए गए कथन को सही बनाकर लिखिए।
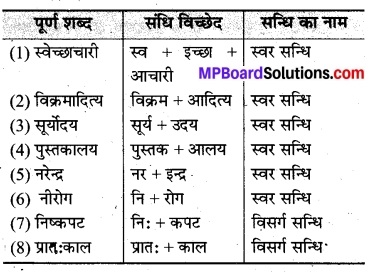
(i) यदि P = {m, n} और Q = {n, m} तो P × Q = {(m, n), (n, m)}.
(ii) यदि A और Bअरिक्त समुच्चय हैं, तो Ax B क्रमित युग्मों (x,y) का एक अरिक्त समुच्यय है इस प्रकार कि x E A तथा y E B.
(iii) यदि A = {1, 2}, B = {3, 4}, तो A × (B ∩ ϕ) = ϕ.
हल:
(i) दिया है :
P = {m, n} और Q = {n, m }
∴ P × Q = {m, n} × {n, m}
∴ = {(m, n), (m, m), (n, n), (n, m)}
अतः दिया गया P × Q = {(m, n), (n, m),} कथन असत्य है।
(ii) सत्य है क्योंकि A × B क्रमित युग्म (x, y) का अरिक्त समुच्चय है जिसमें
X ϵ A और Y ϵ B
(iii) सत्य है क्योंकि B ϵ ϕ = ϕ, ∴ A × (B ⊂ ϕ) = A × ϕ = ϕ.

प्रश्न 5.
यदि A = {-1, 1}, तो A × A × A ज्ञात कीजिए।
हल:
∵ A = {(-1, 1)}
∴ A × A = {- 1, 1} × {- 1, 1}
= {(- 1, – 1), (- 1, 1), (1, – 1), (1, 1)}
A × A × A = {- 1, 1} × {(-1, – 1), (- 1, 1), (1, – 1), (1, 1)}
= {(-1, – 1, – 1), (-1, – 1, 1), (- 1, 1, – 1), (-1, 1, 1), (1, – 1, – 1), (1, – 1, 1), (1, 1, -1), (1, 1, 1)}.

प्रश्न 6.
यदि A × B = {(a, x), (a, y), (b, x), (b, y)} तो A तथा B ज्ञात कीजिए।
हल:
A × B = {(a, x), (a, y), (b, x), (b, y)}
= {a, b} × {x, y}
अतः A = {a, b}, B = {x, y}.

प्रश्न 7.
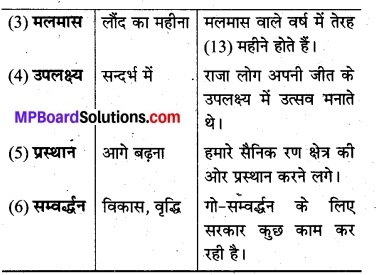
मान लीजिए कि A = {1, 2}, B = {1, 2, 3, 4}, C = {5, 6} तथा D = {5, 6, 7, 8} सत्यापित कीजिए कि
(i) A × (B ∩ C) = (A × B) ∩ (A × C)
(ii) A × C, B × D का एक उपसमुच्चय है।
हल:
दिया है : A = {1, 2}, B = {1, 2, 3, 4}, C = {5, 6}, D = {5, 6, 7, 8}
(i) बायाँ पक्ष = A × (B ∩ C)
= {1, 2} × ({1, 2, 3, 4} ∩ {5, 6})
= {1, 2} × ϕ = ϕ
दायाँ पक्ष = (A × B) (A × C)
= [{1, 2} × {1, 2, 3, 4}] ∩ [{1, 2} × {5, 6}]
= {(1, 1), (1, 2), (1, 3), (1, 4), (2, 1), (2, 2), (2, 3), (2, 4)} {(1, 5), (1, 6), (2, 5), (2, 6)}
= ϕ
अतः बायाँ पक्ष = दायाँ पक्ष।
A × C = {1, 2} × {5, 6} = {(1, 5), (1, 6), (2, 5), (2, 6)}
B × D = {1, 2, 3, 4} × {5, 6, 7, 8}
= {(1, 5), (1, 6), (1, 7), (1, 8), (2, 5), (2, 6), (2, 7), (2, 8), (3, 5), (3, 6), (3, 7), (3, 8), (4, 5), (4, 6), (4, 7), (4, 8)}
हम पाते हैं कि A × C के सभी अवयव समुच्चय B × D में स्थित हैं।
अतः A × C ⊂ B × D.

प्रश्न 8.
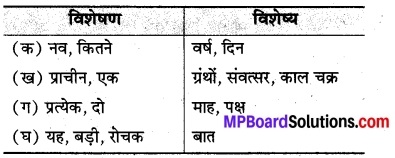
मान लीजिए कि A = {1, 2} और B = {3, 4}. A × B लिखिए। A × B के कितने उपसमुच्चय होंगें ? उनकी सूची बनाइए।
हल:
A × B = {1, 2} × {3, 4}
= {(1, 3), (1, 4), (2, 3), (2, 4)}
A × B के उपसमुच्चयों की संख्या = 24 = 16
A × B के उपसमुच्चयों के अवयव = h, {(1, 3)}, {(1, 4)}, {(2, 3)}, {(2, 4)}, {(1, 3), (1, 4)}, {(1, 3), (2, 3)},{(1, 3), (2, 4)}, {(1, 4), (2, 3)}, {(1,4), (2,4)}, {(2, 3), (2, 4)}, {(1, 3), (1, 4), (2, 3)}, {(1, 3), (1, 4), (2, 4)}, {(1, 3), (2, 3), (2, 4)}, {(1, 4), (2, 3), (2, 4)}, {(1, 3), (1, 4), (2, 3), (2,4)}.

प्रश्न 9.
मान लीजिए कि A और B दो समुच्चय हैं, जहाँ n (A) = 3 और n (B) = 2. यदि (x, 1), (y, 2), (z, 1), A × B में हैं, तो A और B को ज्ञात कीजिए, जहाँ x, y और z भिन्न-भिन्न अवयव हैं।
हल:
अवयव x, y, z ϵ A अर्थात् A = {x, y, z}
1, 2 ϵ B अर्थात् B = {1, 2}.

प्रश्न 10.
कार्तीय गुणन A × A में 9 अवयव हैं जिनमें (-1, 0) तथा (0, 1) भी हैं। समुच्चय A ज्ञात कीजिए तथा A × A के शेष अवयव भी ज्ञात कीजिए।
हल:
(-1, 0) ϵ A × A ⇒ -1 ϵ A और 0 ϵ A
⇒ -1, 0 ϵ A
और (0, 1) ϵ A ⇒ 0 ϵ A तथा 1 ϵ A
⇒ 0, 1 ϵ A
⇒ – 1, 0, 1 ϵ A
∴ A = {- 1, 0, 1}
∴ A × A = {- 1, 0, 1} × {- 1, 0, 1}
= {(-1, – 1), (-1, 0), (-1, 1), (0, – 1), (0, 0), (0, 1), (1, -1), (1, 0), (1, 1)}
जिसमें (- 1, 0), (0, 1) सम्मिलित है।
अतः A × A के शेष अवयव = (-1, – 1), (- 1, 1), (0, – 1), (0, 0), (1, – 1), (1, 0), (1, 1).

MP Board Class 11th Maths Solutions

MP Board Class 8th Maths Solutions Chapter 15 Introduction to Graphs Ex 15.2

Question 1.
Plot the following points on a graph sheet. Verify if they lie on a line
(a) A(4, 0), B(4, 2), C(4, 6), D(4, 2.5)
(b) P(1, 1), Q(2, 2), R(3, 3), S(4, 4)
(c) K(2, 3), L(5, 3), M(5, 5), N(2, 5).
Solution:
(a) A(4, 0), B(4, 2), C(4, 6), D(4, 2.5)

Yes, above all points lie on the same line,

(b) P(1, 1), Q(2, 2), R(3, 3), S(4, 4).

Yes, above all points lie on the same line.

(c) K(2, 3), L(5, 3), M(5, 5), N(2, 5).

No, above all points do not lie on the same line.

Question 2.
Draw the line passing through (2, 3) and (3, 2). Find the coordinates of the points at which this line meets the x-axis and y-axis.
Solution:
After drawing a graph the line passing through (2, 3) and (3, 2), then the co-ordinates of the points which meets the x-axis and y-axis are at (5, 0) and (0, 5) respectively.

Question 3.
Write the coordinates of the vertices of each of these adjoining figures.

Solution:
After observing a graph we find that O(0, 0), A(2, 0), B(2, 3), C(0, 3), P(4, 3), Q(6,1), R(6, 5), S(4, 7), L(7, 7), M(10, 8), K(10, 5).

Question 4.
State whether True or False. Correct that are false.
(i) A point whose x-coordinate is zero and y-coordinate is non-zero will lie on the y-axis.
(ii) A point whose y-coordinate is zero and x-coordinate is 5 will lie on y-axis.
(iii) The coordinates of the origin are (0, 0).
Solution:
(i) True
(ii) False, because it will lie on x-axis.
(iii) True.

MP Board Class 8th Maths Solutions

MP Board Class 8th Maths Solutions Chapter 7 Cube and Cube Roots Ex 7.2

Question 1.
Find the cube root of each of the following numbers by prime factorisation method.
(i) 64
(ii) 512
(iii) 10648
(v) 15625
(vi) 13824
(vii) 110592
(viii) 46656
(ix) 175616
(x) 91125
Solution:

Question 2.
State true or false.
(i) Cube of any odd number is even.
(ii) A perfect cube does not end with two zeros.
(iii) If square of a number ends with 5, then its cube ends with 25.
(iv) There is no perfect cube which ends with 8.
(v) The cube of a two digit number may be a three digit number.
(vi) The cube of a two digit number may have seven or more digits.
(vii) The cube of a single digit number may be a single digit number.
Solution:
(i) False
Because the cube of any odd number is odd.

(ii) True
Because to make a perfect cube, we need each and every factor to occur three times in a group.
So, we need 3, 6, 9, …. zeros to make a perfect cube.

(iii) False
15² = 225, which ends with 5.
and 15³ = 3375, which ends with 75.

(iv) False
∵ 12³ = 1728, which ends with 8.

(v) False
∵ 10³ = 1000, where 10 is the smallest two digit number, and its cube contains 4 digits.

(vi) False
∵ 99³ = 970299, where 99 is the largest two digit number and its cube contains 6 digits.

(vii) True
∵ 1³ = 1, Which is a single digit number.

Question 3.
You are told that 1,331 is a perfect cube. Can you guess without factorisation what is its cube root? Similarly, guess the cube roots of 4913, 12167, 32768.
Solution:
The given number is 1331.
Step-1: Start making groups of three digits starting from the right most digit of the, number we get 331 and 1 as two groups of three and one digits.
Step-2: First group, i.e., 331 will give the one’s digit (unit’s) of the required cube root. The number 331 ends with 1. We know that 1 comes at the unit’s place of a number only
when its cube root ends in 1.
So, we get 1 at the unit’s place of the cube root.
Step-3: Now take another group, i.e., 1
We know that 1³ = 1 and 2³ = 8. Also 1 ≤ 1 ≤ 8. We take the smaller number 1 as the ten’s place of the required cube root. So, we get
\(\sqrt[3]{1331}=11\)
Cube root of 4913
Step-1: Forming groups of three digits starting ’ from the right most digit of 4913 we get two groups 913 and 4.
Step-2: One’s place digit of first group is 3.
∴ We take one’s place digit of required cube root is 7(∵ 7³ = 343)
Step-3: Now the second group is 4.
1³ = 1, 2³ = 8
1 < 4 < 8, hence 1 is the ten’s place digit of required cube root.
So, we get \(\sqrt[3]{4913}\) = 17.
Cube root of 12167.
Step-1 : Forming groups of three digits starting from the right most digit of 12167 we get two groups 167 and 12.
Step-2 : First group is 167.
∴ unit’s place digit of required cube root is 3. (∵ 3³ = 27)
Step-3: Second group is 12
2³ = 8 and 3³ = 27, 8 < 12 < 27
⇒ 23 < 12 < 33
∴ 2 is the ten’s place digit of required cube root. So, we get \(\sqrt[3]{12167}\) = 23.
Cube root of 32768
Step-1: Forming groups of three digits starting from the right most digit of 32768 we get two groups 768 and 32.
Step-2: First group is 768.
∴ unit’s place digit of required cube root is 2
(∵ 2³ = 8).
Step-3: Second group is 32
3³ = 27 and 4³ = 64, 27 < 32 < 64
⇒ 33 < 32 < 43
∴ 3 is the ten’s place digit of required cube root. So, we get \(\sqrt[3]{32768}\) = 32.

MP Board Class 8th Maths Solutions

MP Board Class 11th Maths Solutions Chapter 1 समुच्चय विविध प्रश्नावली

प्रश्न 1.
निम्नलिखित समुच्चयों में से कौन किसका उपसमुच्चय है, इसका निर्णय कीजिए :
A = {x : x ϵ R तथा x² – 8x + 12 = 0 को संतुष्ट करने वाली सभी वास्तविक संख्याएं x}, B = {2, 4, 6}, C = {2, 4, 6, 8….}, D = {6}.
हल:
A = {x : x ϵ R, x समीकरण x² – 8x + 12 = 0 को संतुष्ट करता है}
अर्थात् A = {2, 6}
B = {2, 4, 6}
C = {2, 4, 6, 8….}
D = {6}
(i) समुच्चय A के अवयव 2, 6 समुच्चय B में भी हैं।
⇒ A ⊂ B.
(ii) इस प्रकार समुच्चय A के अवयव 2, 6 समुच्चय C में भी है
⇒ A ⊂ C.
(iii) समुच्चय B के अवयव 2, 4, 6 समुच्चय C में हैं।
⇒ B ⊂ C.
(iv) समुच्चय D का अवयव 6, समुच्चय A, B और C तीनों में हैं,
⇒ D ⊂ A, D ⊂ B, D ⊂ C.

प्रश्न 2.
ज्ञात कीजिए कि निम्नलिखित में से प्रत्येक कथन सत्य है या असत्य है। यदि सत्य है, तो उसे सिद्ध कीजिए। यदि असत्य है तो एक उदाहरण दीजिए।
(i) यदिx ϵ A तथा A ϵ B, तो x ϵ B
(ii) यदि A ⊂ B तथा B ϵ C, तो A ϵ C
(iii) यदि A ⊂ B तथा B ⊂ C, तो A ⊂ C
(iv) यदि A ⊄ B तथा B ⊄ C, तो A ⊄ C
(v) यदि x ϵ A तथा A ⊄ B, तो x ϵ B
(vi) यदि A ⊂ B तथा x ∉ B, तो x ∉ A
हल:
(i) असत्य : मान लीजिए A = {1}, B = {{1}, 2}
स्पष्ट है कि 1 ϵ A, A ϵ B परंतु 1 ∉ समुच्चय B क्योंकि 1 B में नहीं है। इस प्रकार दिया हुआ कथन सत्य नहीं
(ii) असत्य : मान लीजिए A = {1}, B = {1, 2} और C = {{1, 2}, 3}
समुच्चय A का अवयव समुच्चय B में हैं ∴ A ϵ B
अवयव {1, 2} समुच्चय C में हैं ” B ϵ C
पंरतु A = {1} समुच्चय C में नहीं है।
∴ कथन A ϵ C सत्य नहीं है।
(iii) सत्य : A ⊂ B ⇒ यदि x ϵ A तथा x ϵ B
परंतु B ⊂ C ⇒ यदि x ϵ B तब x ϵ C
∴ यदि x ϵ A तब x ϵ A तब x ϵ C ⇒ A ⊂ C
(iv) असत्य : मान लीजिए A = {1, 2}, B = {2, 3}, C = {1, 2, 5}
समुच्चय A के सभी अवयव 1, 2 समुच्चय B में नहीं हैं।
∴ A ⊄ D
समुच्चय B के सभी अवयव 2, 3 समुच्चय C में नहीं हैं।
∴ A ⊂ C
पंरतु समुच्चय A के सभी अवयव 1, 2 समुच्चय C में हैं।
∴ A ⊂ C
इस प्रकार दिया कथन सत्य नहीं है।
(v) समुच्चय A = {1, 2}, B = {2, 3, 4, 5}
समुच्चय A का अवयव 1, 2 समुच्चय B में नहीं है
∴ A ⊄ B
समुच्चय A का अवयव 1 समुच्चय B में नहीं हैं
∴ x ⊄ B
इस प्रकार दिया गया कथन सत्य नहीं है।
(vi) सत्य : A ⊂ B = यदि x ϵ A तब x ϵ B यदि x ∉ B तथा x ∉ A
इस प्रकार कथन A ⊂ B, x ∉ B तब x ∉A सत्य हैं।

प्रश्न 3.
मान लीजिए A, B और C ऐसे समुच्चय हैं कि A ∪ B = A ∪ C तथा A ∩ B = A ∩ C, तो दर्शाइए कि B = C.
हल:
दिया है : A ∪ B = A ∪ C
⇒ (A ∪ B) ∩ C = (A ∪ C) ∩ C
= C
⇒ [(A ∩ C) ∩ (B ∩ C) = C
⇒ (A ∩ B) ∪ (B ∩ C) = C (i) [A ∩ C= A ∩ B = दिया है]
और A ∪ B = A ∪ C
(A ∪ B) ∩ B = (A ∪ C) ∩ B
B = (A ∪ C) ∩ B
= (A ∩ B) (C ∩ B)
(A ∩ B) ∪ (B ∩ C) = B ….(ii)
(i) और (ii) से B = C प्राप्त होता है।

प्रश्न 4.
दिखाइए कि निम्नलिखित चार प्रतिबन्ध तुल्य हैं :
(i) A ⊂ B
(ii) A – B = ϕ
(iii) A ∪ B = B
(iv) A ∩ B = A
हल:
(i) A ⊂ B अर्थात् समुच्चय A के सभी अवयव B में हैं
⇒ A – B = ϕ अर्थात (i) ⇔ (ii)
(ii) A – B = ϕ ⇔ समुच्चय A के सभी अवयव B में हैं
⇔ A ∪ B = B
अर्थात (ii) ⇔ (iii)
(iii) A ∪ B = B ⇔ समुच्चय A के सभी अवयव B में है
समुच्चय A और B मे समुच्चय A के अवयव उभयनिष्ठ है
∴ A ∩ B = A
इससे स्पष्ट है सभी कथन समान हैं।

प्रश्न 5.
दिखाइए कि यदि A ⊂ B तो C – B ⊂ C – A.
हल:
मान लीजिए x ϵ C – B = x ϵ C पंरतु x ∉ B
दिया है : A ⊂ B ⇒ यदि x ∉ B ⇒ x ∉ A
अर्थात x ϵ C और x ∉ A ⇒ x ϵ C – A
यहाँ हम पाते हैं कि
यदि x ϵ C – B तब x ϵ C – A
⇒ C – B ⊂ C – A.

प्रश्न 6.
मान लीजिए कि P(A) = P(B), सिद्ध कीजिए कि A = B.
हल:
मान लीजिए x, समुच्चय A का कोई अवयव है। तब एक उपसमुच्चय X (मान लो) ऐसा होगा जिसमे x ϵ A जिसके अनुसार
∴ X ⊂ A X ϵ P(A)
⇒ X ϵ P(B) [∴ P(A) = P(B)]
∴ X ⊂ B या x ϵ B
अर्थात यदि x ϵ A तब x ϵ B D A ⊂ B
∵ y समुच्चय B का कोई अवयव हो, तब
समुच्चय B का कोई उपसमुच्चय Y (मान लो) होगा जिससे y ϵ Y
तब Y ⊂ B = Y ϵ P(B)
⇒ Y ϵ P(A) [∵ P(A) = P(B)]
⇒ Y ⊂ A
⇒ यदि y ϵ B तब Y ϵ A
⇒ B ⊂ A …(ii)
समीकरण (i) और (ii) से, हम पाते हैं

प्रश्न 7.
किन्हीं भी समुच्चयों A तथा B के लिए क्या यह सत्य है कि P(A) ∪ P(B) = P(A ∪ B) ? अपने उत्तर का औचित्य बताइए।
हल:
मान लीजिए
A = {a}, B = {b}, और A ∪ B = {a, b}
P(A) = {ϕ, {a}}, P(B) = {ϕ, {b}}
P(A) ∪ P(B) = {ϕ, {a}, {b}} …(i)
अब A ∪ B = {a, b}
∴ P(A ∪ B) = {ϕ, {a}, {b}, {a, b}} …(ii)
समी (i) और (ii) से हम देखते हैं कि
अतः P(A) ∪ P(B) ≠ P(A ∪ B).

प्रश्न 8.
किन्हीं दो समुच्चयों A तथा B के लिए सिद्ध कीजिए कि
A = (A ∩ B) ∪ (A – B) और A ∪ (B – A) = A ∪ B.
हल:
(i) दायाँ पक्ष = (A ∩ B) ∪ (A – B)
= (A ∩ B) ∪ (A ∩ B) [∴ A – B = A ∩ B’]
= (A ∩ (B ∪ B’) (वितरण गुण से)
= A ∩ U (यहाँ U सार्वत्रिक समुच्चय)
= A .
अतः (A ∩ B) (A – B) = A.
बायाँ पक्ष = A ∪ (B – A)
= A ∪ (B ∩ A’) [∴ B – A = B ∩ A’]
= (A ∪ B) ∩ (A ∪ A) (वितरण गुण से)
= (A ∪ B) ∩ U [यहाँ U सार्वत्रिक समुच्चय]
= A ∪ B
अतः A ∪ (B – A) = A ∪ B.

प्रश्न 9.
समुच्चयों के गुणधर्मों का प्रयोग करके सिद्ध कीजिए कि
(i) A ∪ (A ∩ B) = A
(ii) A ∩ (A ∪ B) = A.
हल:
(i) बायाँ पक्ष = A ∪ (A ∩ B)
= (A ∪ A) (A ∪ B) (वितरण गुण से)
= A ∩ (A ∪ B) (∴ A ∪ A = A)
= A [∴ A ⊂ A ∪ B]
∴ A ∪ (A ∩ B) = A.

(ii) बायाँ पक्ष = A ∩ (A ∪ B)
= (A ∩ A) ∪ (A ∩ B) [वितरण गुण से]
= A ∪ (A ∩ B) [∴ A ∩ A = A]
= A [∴ A ∩ B ⊂ A]
अतः A ∩ (A ∪ B) = A.

प्रश्न 10.
दिखलाइए कि A ∩ B = A ∩ C का तात्पर्य B = C आवश्यक रूप से नहीं होता।
हल:
मान लीजिए A = {1, 2}, B = {1, 7} तथा C = {1, 4} हो, तब
A ∩ B = {1, 2} ∩ {1, 7} = {1}
A ∩ C = {1, 2} ∩ {1, 4} = {1}
⇒ A ∩ B = A ∩ C
परंतु B ≠ C
⇒ यदि A ∩ B = A ∩ C तो आवश्यक नहीं है कि B = C.

प्रश्न 11.
मान लीजिए कि A और B समुच्चय हैं। यदि किसी समुच्चय x के लिए A ∪ X = B ∪ X = ϕ तथा A ∪ X = B ∪ X तो सिद्ध कीजिए कि A = B.
हल:
दिया है A ∪ X = B ∪ X, जब कि X कोई समुच्चय है।
⇒ A ∩ (A ∪ X) = A ∩ (B ∪ X) [A ⊂ A ∪ X, ∴ A ∩ (A ∪ X) = A]
⇒ A = A ∩ (B ⊂ X)
= (A ∩ B) ∪ (A ∩ A) [वितरण गुण से]
= (A∩ B) U ϕ (∴ दिया है, A ∩ x = ϕ)
= A ∩ B
⇒ A ⊂ B …(i)
पुनः A ∪ X = B ∪ X
⇒ B ∩ (A ∪ X) = B ∩ (B ∪ X)
⇒ B ∩ (A ∪ X) = B [∴ B ⊂ B ∪ X]
⇒ (B ∩ A) ∪ (B ∩ X) = B [वितरण गुण से]
⇒ (B ∩ A) ∪ ϕ = B [दिया है: B ∩ X = ϕ]
⇒ (B ∩ A) = B
⇒ B ⊂ A …..(ii)
समी. (i) और (ii) से, हम पाते हैं कि A = B.

प्रश्न 12.
ऐसे समुच्चय A, B और C ज्ञात कीजिए ताकि A ∩ B, B ∩ C तथा A ∩ C आरिक्त समुच्चय हों और A ∩ B ∩ C = ϕ.
हल:
मान लीजिए A = {1, 2}, B = {2, 3}, C = {1, 3}
A ∩ B = {1, 2} ∩ {2, 3} = {2}
B ∩ C = {2, 3} ∩ {1, 3} = {3}
C ∩ A = {1, 3} ∩ {1, 2} = {1}
अतः A ∩ B, B ∩ C, C ∩ A रिक्त समुच्चय नहीं हैं।
A ∩ B ∩ C = (A ∩ B) ∩ C
= {2} ∩ {1, 3} = ϕ.

प्रश्न 13.
किसी विद्यालय के 600 विद्यार्थियों के सर्वेक्षण से ज्ञात हुआ कि 150 विद्यार्थी चाय, 225 विद्यार्थी कॉफी तथा 100 विद्यार्थी चाय और कॉफी दोनों पीते हैं। ज्ञात कीजिए कि कितने विद्यार्थी न तो चाय पीते हैं और न कॉफी पीते हैं।
हल:
मान लीजिए T और C चाय तथा कॉफी पीने वाले विद्यार्थियों के समुच्चय हों, तब
n(T) = 150, n(C) = 225, n(T ∩ C) = 100
n(T ∪ C) = n(T) + n(C) – n(T ∩ C)
= 150 + 225 – 100
= 275
= उन विद्यार्थियों की संख्या जो चाय या कॉफी पीते हैं या चाय और कॉफी दोनों पीते हैं।
विद्यार्थियों की कुल संख्या = 600
∴ उन विद्यार्थियों की संख्या जो चाय या कॉफी कुछ भी नहीं पीते
= 600 – 275 = 325.

प्रश्न 14.
विद्यार्थियों के समूह में, 100 विद्यार्थी हिन्दी, 50 विद्यार्थी अंग्रेजी तथा 25 विद्यार्थी दोनों भाषाओं को जानते हैं। विद्यार्थियों में से प्रत्येक या तो हिन्दी या अंग्रेजी जानता है। समूह में कुल कितने विद्यार्थी हैं?
हल:
पाना H तथा E क्रमशः हिन्दी और अंग्रेजी जानने वालों के समुच्चय हों, तब
n(H) = 100, n(E) = 50, n(H ∩ E) = 25
∴ n(H ∪ E) = n(H) + n(E) – n(H ∩ E)
= 100 + 50 – 25
=125
उन विद्यार्थियों की संख्या जो हिन्दी या अंग्रेजी जानते हैं = 125.

प्रश्न 15.
60 लोगों के सर्वेक्षण में पाया गया कि 25 लोग समाचार पत्र H, 26 लोग समाचार पत्र T, 26 लोग समाचार पत्र I, 9 लोग H तथा I दोनों, 11 लोग H तथा T दोनों, 8 लोग T तथा । दोनों और 3 लोग तीनों ही समाचार पत्र पढ़ते हैं, तो निम्नलिखित ज्ञात कीजिए :
(i) कम से कम एक समाचार पत्र पढ़ने वालों की संख्या।
(ii) ठीक ठीक केवल एक समाचार पत्र पढ़ने वालों की संख्या।
हल:
कुल लोगों की संख्या जिनका सर्वेक्षण किया गया = 60
H समाचार पत्र पढ़ने वालों की संख्या, n (H) = 25
T समाचार पत्र पढ़ने वालों की संख्या, n (T) = 26
समाचार पत्र पढ़ने वालों की संख्या, n (I) = 26

H और I समाचार पत्र पढ़ने वालों की संख्या, n (H ∩ I) = 9
H और T समाचार पत्र पढ़ने वालों की संख्या, n (H ∩ T) = 11
T और I समाचार पत्र पढ़ने वालों की संख्या, n (T ∩ I) = 8
तीनों समाचार पत्र पढ़ने वालों की संख्या, n (H ∩ T ∩ I) = 3
H और I समाचार पत्र पढ़ने वाले तथा T समाचार पत्र न पढ़ने वालों की संख्या = 9 – 3 = 6
H और T समाचार पत्र पढ़ने वाले तथा I समाचार पत्र न पढ़ने वालों की संख्या = 11 – 3 = 8
T और I समाचार पत्र पढ़ने वाले तथा H समाचार पत्र न पढ़ने वालों की संख्या = 8 – 3 = 5
केवल H समाचार पत्र पढ़ने वालों की संख्या = 25 – 8 – 6 – 3 = 8
केवल T समाचार पत्र पढ़ने वालों की संख्या = 26 – 8 – 3 – 5 = 10
केवल I समाचार पत्र पढ़ने वालों की संख्या = 26 – 6 – 3 – 5 = 12
कम से कम एक समाचार पत्र पढ़ने वालों की संख्या
= केवल एक समाचार पत्र पढ़ने वालों की संख्या + केवल दो समाचार पत्र पढ़ने वालों की संख्या + तीनों समाचार पत्र पढ़ने वालों की संख्या
= (8 + 10 + 12) + (8 + 6 + 5) + 3 = 30 + 19 + 3
= 52
वैकल्पिक विधि :
n(H ∪ T ∪ I) = n(H) + n(T) + n(I) – n(H ∩ T) = n(T ∩ I)- n(H ∩ I) + n(H ∩ T ∩ I)
= 25 + 26 + 26 – 11 – 8 – 9 + 3
= 77 – 28 + 3 = 80 – 28 = 52
(ii) केवल H और T समाचार पत्र पढ़ने वालों की संख्या = 11 – 3 = 8
केवल T औरI समाचार पत्र पढ़ने वालों की संख्या = 8 – 3 = 5
केवल I और H समाचार पत्र पढ़ने वालों की संख्या = 9 – 3 = 6
तीनों समाचार पत्र पढ़ने वालों की संख्या = 3
केवल एक समाचार पत्र पढ़ने वालों की संख्या = 52 – (8 + 5 + 6 + 3)
= 52 – 22 = 30.

प्रश्न 16.
एक सर्वेक्षण में पाया गया कि 21 लोग उत्पाद A,26 लोग उत्पाद B, 29 लोग उत्पाद पसंद करते हैं। यदि 14 लोग उत्पाद A तथा B, 12 लोग उत्पाद C तथा A, 14 लोग उत्पाद B तथा C और 8 लोग तीनों ही उत्पादों को पसंद करते हैं ज्ञात कीजिए कि कितने लोग केवल उत्पाद C को पसंद करते हैं?
हल:
दिया है n(A) = 21, n(B) = 26
और n(C) = 29
n(A ∩ B) = 14, n(A ∩ C) = 12
n(B ∩ C) = 14, n(A ∩ B ∩ C) = 8
अब n(A ∪ C) = 12, n(A ∩ B ∩ C) = 8

∴ n(केवल A और C) = 12 – 8 = 4
∴ n(केवल B और C) = 14 – 8 = 6
∴ (केवल C) = n(C) – n (केवल A और C) – n (केवल B और C) – n(A ∩ B ∩ C)
= 29 – 4 – 6 – 8 = 29 – 18 = 11.

MP Board Class 11th Maths Solutions