MP Board Class 8th Maths Solutions Chapter 3 चतुर्भुजों को समझना Ex 3.3
प्रश्न 1.
ABCD एक समान्तर चतुर्भुज है। प्रत्येक कथन को परिभाषा या प्रयोग किए गए गुण द्वारा पूरा कीजिए –
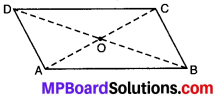
- AD = …..
- ∠DCB = …..
- OC = …..
- m∠DAB + m∠CDA = …..
हल:
- AD = BC; (सम्मुख भुजाएँ बराबर होती हैं।)
- ∠DCB = ∠DAB; (सम्मुख कोण बराबर होते हैं।)
- OC = OA; (विकर्ण परस्पर समद्विभाजित करते हैं।)
- m∠DAB + m∠CDA = 180°; तिर्यक रेखा के एक ही ओर के अन्तः कोण, क्योंकि \(\overline { AB } \) || \(\overline { CD } \).
प्रश्न 2.
निम्न समान्तर चतुर्भुजों में अज्ञात x, y, z के मानों को ज्ञात कीजिए –
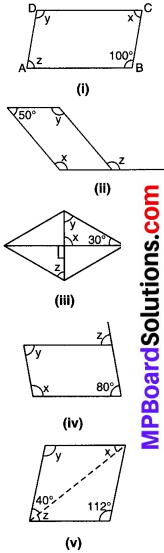
हल:
(i) समान्तर चतुर्भुज के किन्हीं दो आसन्न कोणों का योग 180° होता है, इसलिए,
x + 100° = 180°
या x = 180° – 100° = 80°
x + y = 180°
या y = 180° – x = 180 – 80°
= 100°
y + z = 180°
या 100° + z = 180°
या z = 180° – 100° = 80°
यहाँ, x = 80°, y= 100° और 2 = 80°
(ii) चूँकि ABCD एक समान्तर चतुर्भुज है, अतः AB || DC ओर AD = BC
अब, AB || DC और तिर्यक रेखा BC इन्हें प्रतिच्छेद करती है।
∴ z = y (∵ एकान्तर कोण बराबर होते हैं।)
और AD || BC और तिर्यक रेखा इन्हें काटती हैं।
∴ z =x (∵ संगत कोण बराबर होते हैं।)
∴ x = y =z
चूँकि समान्तर चतुर्भुज के किन्हीं दो संगत कोणों का योग = 180°
अतः y + 50° = 180°
y = 180° – 50° = 130°
इस प्रकार x = y = z = 130°
(iii) आकृति से स्पष्ट है कि,
x = 90°
∆DOC में, हम प्राप्त करते हैं,
∠DOC + ∠OCD + ∠CDO = 180°
या x + 30° + y = 180°
या 90° + 30° + y = 180°
या 120° + y = 180°
y = 180° – 120° = 60°
अब, समान्तर चतुर्भुज ABCD में, AB || DC और BD इन्हें प्रतिच्छेद करती है।
∴ z = y (एकान्तर कोण है)
z = 60° (∵ y = 60°)
अतः x = 90°, y = 60 और z = 60
(iv) ∵ ∠A + ∠B = 180° ⇒ x + 80° = 180°
या x = 180° – 80° = 100°
∠A + ∠D = 180° ⇒ x + y = 180°
y = 180° – x = 180° – 100° =80
∠D + ∠C = 180°
या y + ∠C = 180°
या 80° + ∠C = 180°
अब ∠C = 180 – 80 = 100°
∠C + z = 180°
100° + z = 180°
z = 180° – 100° = 80°
अतः x = 100°, y = 80° और z = 80°
(v) ∵ समान्तर चतुर्भुज में सम्मुख कोण बराबर माप के होते हैं।
इसलिए, y = 112°
∆ACD से,
x + y + 40° = 180°
x + 112° + 40° = 180°
x = 180° – 152° = 28°
समान्तर चतुर्भुज ABCD में, AB || DC और तिर्यक रेखा AC इन्हें प्रतिच्छेद करती है।
∴ z = x (एकान्तर कोण हैं।)
∴ z = 28°
अतः x = 28°
y= 112
z = 28°
![]()
प्रश्न 3.
क्या एक चतुर्भुज ABCD समान्तर चतुर्भुज हो सकता है, यदि –
- ∠D + ∠B = 180° ?
- AB = DC = 8cm, AD = 4cm और BC = 4.4cm?
- ∠A = 70° और ∠C = 65°
हल:
- ∠D + ∠B = 180° समान्तर चतुर्भुज हो सकता है, परन्तु यह आवश्यक नहीं है।
- AB = DC = 8 cm, AD = 4 cm, BC = 4.4 cm. यह समान्तर चतुर्भुज नहीं हो सकता है।
समान्तर चतुर्भुज में सम्मुख भुजाएँ बराबर होती हैं, परन्तु यहाँ AD ≠ BC. - ∠A = 70° और ∠C = 65°
समान्तर चतुर्भुज नहीं हो सकता है। समान्तर चतुर्भुज के सम्मुख कोण बराबर होते हैं, परन्तु यहाँ ∠A ≠∠C.
प्रश्न 4.
एक चतुर्भुज की कच्ची (Rough) आकृति खींचिए जो समान्तर चतुर्भुज न हो परन्तु जिसके दो सम्मुख कोणों की माप बराबर हो।
हल:
चतुर्भुज की कच्ची आकृति जो समान्तर चतुर्भुज नहीं है।
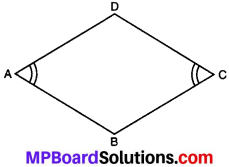
यहाँ, ∠A = ∠C, उदाहरण-पतंग आकृति का चतुर्भुज।
प्रश्न 5.
किसी समान्तर चतुर्भुज के दो आसन्न कोणों का अनुपात 3 : 2 है। समान्तर चतुर्भुज के सभी कोणों की माप ज्ञात कीजिए।
हल:
माना कि दो आसन्न कोण ∠A और ∠B हैं, जो 3 : 2 के अनुपात में हैं।
∴ ∠A = 3x
∠B = 2x
∴ समान्तर चतुर्भुज के आसन्न कोण सम्पूरक होते हैं।
∠A + ∠B = 180°
या 3x + 2x = 180°
या 5x= 180°
या x = \(\frac{180°}{5}\) = 36°
∴ ∠A = 3 x 36° = 108°
और ∠B = 2 x 36° = 72°
∴ समान्तर चतुर्भुज के सम्मुख कोण बराबर होते हैं।
∴ ∠C = ∠A = 108° और ∠D = ∠B = 72°
अत: ∠A = 108°, ∠B = 72°, ∠C = 108°, ∠D = 72°
![]()
प्रश्न 6.
किसी समान्तर चतुर्भुज के आसन्न कोणों की माप बराबर है। समान्तर चतुर्भुज के सभी कोणों की माप ज्ञात कीजिए।
हल:
मानाकि समान्तर चतुर्भुज ABCD के दो आसन्न कोण A और B में प्रत्येक की माप x है।
∴ समान्तर चतुर्भुज के आसन्न कोण सम्पूरक होते हैं।
∠A + ∠B = 180°
या x + x = 180°
या 2x = 180°
∴ x = \(\frac{180°}{2}\) = 90°
अर्थात् ∠A= ∠B = 90°
चूँकि समान्तर चतुर्भुज के सम्मुख कोण बराबर होते हैं।
∠C = ∠A = 90°
∠D = ∠B = 90°
अतः ∠A = ∠B = ∠C = ∠D = 90°
प्रश्न 7.
संलग्न आकृति HOPE एक समान्तर चतुर्भुज है। x,और कोणों की माप ज्ञात कीजिए। ज्ञात करने में प्रयोग किए गए गुणों को बताइए।
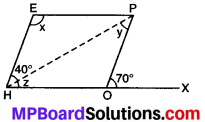
हल:
∴ HOPE एक समान्तर चतुर्भुज है।
∴ HE || OP और HO || EP
अब HE || OP और HO तिर्यक रेखा इन्हें काटती है।
∠EHO = ∠POX
(∵ संगत कोण बराबर होते हैं)
∴ 40° + z = 70°
या z = 70° – 40° = 30°
पुनः HE ||OP और तिर्यक रेखा इन्हें काटती है।
∠OPH = ∠EHP (∴ एकान्तर कोण बराबर होते हैं)
∴ y = 40°
∴ समान्तर चतुर्भुज के सम्मुख कोण बराबर होते हैं।
∴ ∠HEP = ∠HOP
या x = 180° – ∠POX
या x = 180° – 70° = 110°
अतः x = 110°, y= 40°, z = 30°
प्रश्न 8.
निम्न आकृतियाँ GUNS और RUNS समान्तर चतुर्भुज है। x तथा y ज्ञात कीजिए (लम्बाई cm में है)।
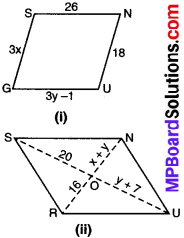
हल:
(i) ∴ चतुर्भुज GUNS समान्तर चतुर्भुज है। इसलिए इसकी सम्मुख भुजाएँ बराबर होंगी।
∴ 3x = 18
या x = \(\frac{18}{3}\) = 6 cm
ओर 3y – 1 = 26
या 3y = 26 + 1 = 27
या y = \(\frac{27}{3}\) = 9 cm
अतः x = 6 cm और y = 9 cm
(ii) ∴ समान्तर चतुर्भुज में विकर्ण एक-दूसरे को समद्विभाजित करते हैं।
∴ OR = ON
अर्थात् 16 = x + y ……(1)
और OU = OS
अर्थात् y + 7= 20 ……(2)
समीकरण (2) से,
y = 20 – 7 = 13
समीकरण (1) में, y = 13 रखने पर, हम प्राप्त करते हैं।
16 = x + 13
या x = 16 – 13 = 3
अतः x = 3 cm और y = 13 cm
![]()
प्रश्न 9.
दी हुई आकृति में RISK तथा CLUE दोनों समान्तर चतुर्भुज हैं, x का मान ज्ञात कीजिए।

हल:
समान्तर चतुर्भुज RISK से,
∠RIS = ∠RKS = 120°
(∴ सम्मुख कोण बराबर होते हैं)
और ∠RIS + ∠SIC = 180° (रेखीय युग्म)
या ∠SIC = 180° – 120° = 60° = ∠OIC
समान्तर चतुर्भुज CLUS से,
CE || LU और ICL इन्हें प्रतिच्छेद करती हैं।
∠OCI = ∠ULC (∴ संगत कोण है)
∠OCI = 70°
अब, ∆OLC से,
∠OIC + ∠OCI + ∠IOC = 180°
या 60° + 70° + ∠IOC = 180°
∠IOC = 180° – 130° = 50°
x = ∠IOC = 50°
(∴ शीर्षाभिमुख कोण हैं।)
प्रश्न 10.
बताइए कैसे यह आकृति एक समलम्ब है। इसकी कौन-सी दो भुजाएँ समान्तर हैं?
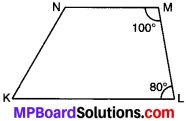
हल:
∴ ∠MLK + ∠NML = 180°
अर्थात् ये सम्पूरक कोणों का युग्म हैं।
अतः KL || NM
अतः KLMN एक समलम्ब है। .
प्रश्न 11.
संलग्न आकृति में m∠C ज्ञात कीजिए यदि AB || DC है।
हल:
∵ AB || DC और तिर्यक रेखा BC इन्हें प्रतिच्छेद करती है।
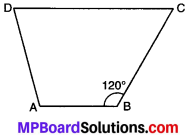
∠B + ∠C = 180°
या 120° + ∠C = 180°
∠C = 180° – 120° = 60°
अतः m∠C = 60°
प्रश्न 12.
संलग्न आकृति में ∠P तथा ∠S की माप ज्ञात कीजिए यदि \(\overline { SP } \) || \(\overline { RQ } \) (यदि आप m∠R ज्ञात करते हैं, तो क्या m∠P को ज्ञात करने की एक से अधिक विधि है?
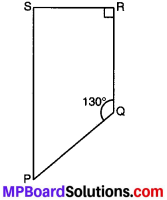
हल:
∴ \(\overline { SP } \) || \(\overline { RQ } \) और PQ एक तिर्यक रेखा है जो P और Q पर काटती है।
∠P + ∠Q = 180°
(∵ अंत:कोणों का योग = 180°)
या ∠P + 130° = 180°
∠P = 180° – 130° = 50°
पुनः \(\overline { SP } \) || \(\overline { RQ } \) और SR एक तिर्यक रेखा है जो इन्हें S और R पर काटती है।
∴ ∠S + ∠R = 180°
या∠S + 90° = 180°
या ∠S = 180° – 90° = 90°
हाँ, हम m∠P को दूसरी विधि से भी ज्ञात कर सकते हैं।
m∠P + m∠Q + m∠R + m∠S = 360°
या m∠P + 130° + 90° + 90° = 360°
या m∠P + 310° = 360°
या m∠P = 360° – 310° = 50°
![]()
पाठ्य-पुस्तक पृष्ठ संख्या # 57
इन्हें कीजिए
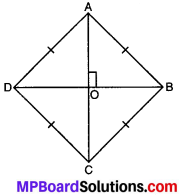
प्रश्न 1.
समचतुर्भुज की एक प्रतिलिपि लीजिए। पेपर को मोड़कर जाँच कीजिए कि क्या प्रतिच्छेदी बिन्दु प्रत्येक विकर्ण का मध्य बिन्दु है। आप एक सेट स्क्वेयर के किनारे का उपयोग करके जाँच कर सकते हैं कि वे एक दूसरे को समकोण पर प्रतिच्छेद करते हैं।
हल:
हाँ, प्रतिच्छेदी बिन्दु प्रत्येक विकर्ण का मध्य बिन्दु है। सेट स्क्वे यर का उपयोग करने पर हम पाते हैं कि समचतुर्भुज के विकर्ण समकोण पर प्रतिच्छेद करते हैं।
पाठ्य-पुस्तक पृष्ठ संख्या # 58
एक आयत
प्रश्न 1.
आयत एक समान्तर चतुर्भुज है जिसके सभीकोण समान माप के होते हैं। इस परिभाषा का पूर्ण अर्थ क्या है? इसकी चर्चा अपने मित्रों के साथ कीजिए। यदि आयत समकोणिक हो तो प्रत्येक कोण की माप क्या होगी?
हल:
आयत एक समान्तर चतुर्भुज है जो समकोणिक होता है। आयत का प्रत्येक कोण समकोण होता है। इसकी सम्मुख भुजाएँ समान लम्बाई की होती हैं तथा इसके विकर्ण एक दूसरे को समद्विभाजित करते हैं।
माना कि आयत के प्रत्येक कोण की माप =x° है।
तब 4x° = 360°
इसलिए x° = \(\frac{360°}{4}\) = 90°
अतः आयत का प्रत्येक कोण 90° का होता है।
पाठ्य-पुस्तक पृष्ठ संख्या # 60
इन्हें कीजिए
प्रश्न 1.
एक वर्गाकारशीट PQRS (आकृति : 3.39) लीजिए। दोनों विकर्णों के अनुदिश तह (fold) लगाइए क्या उनके मध्य बिन्दु समान ही हैं?
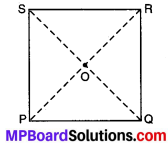
सेट स्क्वेयर का उपयोग करके जाँच कीजिए, क्या o पर बना कोण 90° का है? यह ऊपर बताए गुणधर्म को सिद्ध करता है।
हल:
हाँ, दोनों विकर्णों के मध्य बिन्दु समान हैं। हाँ, ‘o’ पर बना कोण 90° का है। हाँ, यह वर्ग के गुणधर्म को सिद्ध करता है कि –
- वर्ग की सभी भुजाएँ समान लम्बाई की होती है।
- विकर्ण समान लम्बाई के होते हैं तथा एक-दूसरे को समकोण पर समद्विभाजित करते हैं।