MP Board Class 8th Maths Solutions Chapter 3 चतुर्भुजों को समझना Ex 3.2
प्रश्न 1.
निम्नलिखित आकृतियों में x का मान ज्ञात कीजिए –
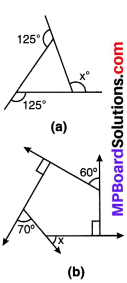
हल:
(a) सभी बाह्य कोणों की कुल माप = 360°
∴ x + 125° + 125° = 360°
या x + 250° = 360°
या x = 360° – 250° = 110°
(b) x + 90° + 60° + 90° + 70° = 360°
या x + 310° = 360°
या x = 360° – 310° = 50°
![]()
प्रश्न 2.
एक समबहुभुज के प्रत्येक बाह्य कोण का माप ज्ञात कीजिए जिसकी –
(i) 9 भुजाएँ
(ii) 15 भुजाएँ हों।
हल:
(i) ∴ प्रत्येक बाह्य कोण = \(\frac{360°}{n}\); यहाँ n = 9
∴ प्रत्येक बाह्य कोण = \(\frac{360°}{9}\) = 40°
(ii) यहाँ, n = 15
∴ प्रत्येक बाह्य कोण = \(\frac{360°}{15}\) = 24°
प्रश्न 3.
एक समबहुभुज की कितनी भुजाएँ होंगी यदि एक बाह्य कोण का मान 24° हो?
हल:

प्रश्न 4.
एक समबहुभुज की भुजाओं की संख्या ज्ञात कीजिए यदि इसका प्रत्येक अन्तःकोण 165° का हो।
हल:
माना कि समबहुभुज की भुजाओं की संख्या = n है।
तब, इसका प्रत्येक अन्त: कोण = \(\frac{(n-2)x180°}{n}\)
अब, प्रश्नानुसार, \(\frac{(n-2)x180°}{n}\) = 165°
या 180°n – 360° = 165°n
या 180°n – 165°n = 360°
या 15°n = 360°
या n = \(\frac{360°}{15}\) = 24
n = 24
अतः समबहुभुज में 24 भुजाएँ होंगी।
प्रश्न 5.
(a) क्या ऐसा समबहुभुज सम्भव है जिसके प्रत्येक बाह्य कोण का माप 22° हो?
(b) क्या यह किसी समबहुभुज का अन्तःकोण हो सकता है? क्यों?
हल:
(a) ∴ समबहुभुज की भुजाओं की संख्या

∴ ऐसा समबहुभुज सम्भव नहीं है, जिसके प्रत्येक बाह्य कोण की माप 22° हो।
(b) यदि अन्त: कोण 22° हो, तो बाह्य कोण = 180° – 22° = 158°
लेकिन 360° ÷ 158 पूर्णतः विभाजित नहीं है। इसलिए समबहुभुज सम्भव नहीं है।
अत: 22° किसी समबहुभुज का अन्त:कोण नहीं हो सकता है।
प्रश्न 6.
(a) किसी समबहुभुज में कम से कम कितने अंश का अन्तःकोण सम्भव है? क्यों?
(b) किसी समबहुभुज में अधिक से अधिक कितने अंश का बाह्य कोण सम्भव है ?
हल:
(a) समबाहु त्रिभुज कम से कम 3 भुजाओं का समबहुभुज है जिसके प्रत्येक अन्त:कोण की माप 60° होती है। अतः किसी समबहुभुज में कम से कम 60° का अन्त:कोण सम्भव है।
(b) ∴ किसी समबहुभुज के लिए कम से कम अन्त:कोण की माप = 60°
∴ अधिकतम बाह्य कोण की माप = 180° – 60° = 120°
![]()
पाठ्य-पुस्तक पृष्ठ संख्या # 115
इन्हें कीजिए
प्रश्न 1.
समान सर्वांगसम त्रिभुजों से कटे हुए भाग लीजिए जिनकी भुजाएँ3 cm,4cm, 5 cm हैं। इन्हें व्यवस्थित कीजिए जैसा कि आकृति में दर्शाया गया है (आकृति : 13.17)।
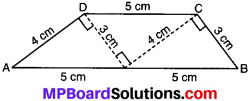
आपको एक समलम्ब प्राप्त होता है। (निरीक्षण कीजिए)। यहाँ पर कौन-सी भुजाएँ समान्तर हैं? क्या असमान्तर भुजाएँ बराबर माप की होनी चाहिए? इन समान त्रिभुजों के समूह का उपयोग कर आप दो और समलम्ब प्राप्त कर सकते हैं। उनको ढूँढ़िए और उनकी आकृतियों की चर्चा कीजिए।
हल:
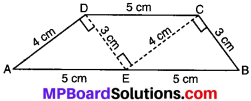
∠DEC = ∠ECB = 90°
DE || BC तथा DE = BC = 3 cm
और EB = DC = 5 cm
∴ ∠BCD एक समान्तर चतुर्भुज है।
इसलिए AB || DC
अत: ABCD एक समलम्ब है।
असमान्तर भुजाएँ AD और BC हैं। यह आवश्यक नहीं है कि असमान्तर भुजाएँ बराबर माप की हों।
दो अन्य समलम्ब ABCD एवं PQRS निम्नवत हैं –
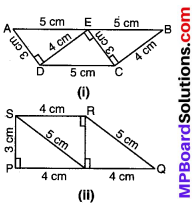
प्रश्न 2.
अपने तथा अपने मित्रों के ज्यामितीय बॉक्स से चार सेट स्क्वेयर लीजिए। इन्हें अलग-अलग संख्याओं में उपयोग कर साथ-साथ रखिए और अलग-अलग किस्म के समलम्ब प्राप्त कीजिए।
क्या आपने ऊपर किए गए अपने किसी निरीक्षण में कोई समद्विबाहु समलम्ब प्राप्त किया है?
हल:
हमने ज्यामितीय बॉक्स से चार सेटस्क्वेयर लेकर निम्न समलम्ब प्राप्त किए हैं –
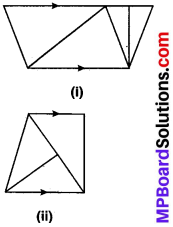
हाँ, हमने निरीक्षण में समद्विबाहु समलम्ब प्राप्त किया है।
पाठ्य-पुस्तक पृष्ठ संख्या # 50
इन्हें कीजिए
प्रश्न 1.
एक मोटे कागज की शीट लीजिए। इसे दोहरा मोड़िए। दो अलग-अलग लम्बाई वाले रेखाखण्डों को खींचिए। इन रेखाखण्डों के अनुदिश काटकर खोलिए। आपको एक पतंग की आकृति प्राप्त होती है।
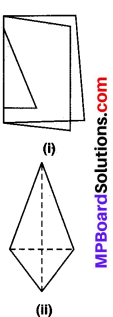
क्या पतंग में कोई सममित रेखा है?
पतंग को दोनों विकर्णों पर मोड़िए। सेट स्क्वेयर के उपयोग से जाँचिए कि क्या वे एक-दूसरे को समकोण पर काटते हैं। क्या विकर्ण बराबर लम्बाई के हैं?
जाँचिए (पेपर को मोड़ने या मापने द्वारा) कि क्या विकर्ण एक-दूसरे को समद्विभाजित करते हैं?
पतंग के एक कोण को एक विकर्ण के अनुदिश विपरीत मोड़ने पर बराबर माप वाले कोणों को जाँचिए।
विकर्ण पर पड़ी तह का निरीक्षण कीजिए क्या यह दर्शाता है कि विकर्ण एक कोण समद्विभाजक होता है?
अपनी जानकारी को साथियों में बाँटिए और सूची बनाइए। इन परिणामों का सारांश अध्याय में कहीं पर आपके लिए दिया गया है।
हल:
हाँ, पतंग में एक सममित रेखा (AC) है।
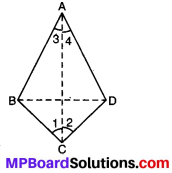
संलग्न आकृति में विकर्ण बिन्दुवत् रेखाओं AC तथा BD द्वारा दर्शाए गए हैं। हाँ, विकर्ण एक-दूसरे को समकोण पर काटते हैं। विकर्ण बराबर लम्बाई के नहीं है।
विकर्ण AC विकर्ण BD को समद्विभाजित करता है।
m∠1 = m∠2 और m∠3 = m∠4 हाँ, यह दर्शाता है कि विकर्ण एक समद्विभाजक होता है।
समान्तर चतुर्भुज:
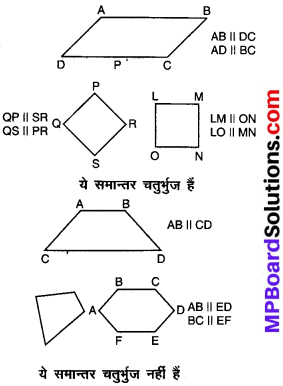
प्रश्न 2.
इन आकृतियों का अध्ययन कीजिए और अपने शब्दों में बताने का प्रयास कीजिए कि समान्तर चतुर्भुज क्या है? अपने निष्कर्ष अपने मित्रों के साथ बाँटिए।
हल:
समान्तर चतुर्भुज एक चतुर्भुज होता है जिसकी सम्मुख भुजाएँ समान्तर होती हैं। समान्तर चतुर्भुज में –
- सम्मुख भुजाएँ समान्तर होती हैं।
- सम्मुख भुजाएँ बराबर होती हैं।
- सम्मुख कोण बराबर होते हैं।
- विकर्ण एक-दूसरे को समद्विभाजित करते हैं।
- आसन्न कोण सम्पूरक होते हैं।
![]()
पाठ्य-पुस्तक पृष्ठ संख्या # 51
समान्तर चतुर्भुज के अवयव
प्रश्न 1.
क्या \(\overline { BC } \) और \(\overline { CD } \) आसन्न भुजाएँ हैं? दो और आसन्न भुजाओं के युग्मों को ढूँढ़ने का प्रयास कीजिए।
हल:
हाँ, \(\overline { BC } \) और \(\overline { CD } \) आसन्न भुजाएँ हैं।
आसन्न भुजाओं के दो अन्य युग्म – \(\overline { CD } \) और \(\overline { DA } \) तथा \(\overline { DA } \) और \(\overline { AB } \).
प्रश्न 2.
समान्तर चतुर्भुज के आसन्न कोणों के दूसरे युग्मों की पहचान कीजिए।
हल:
समान्तर चतुर्भुज के आसन्न कोणों के दूसरे युग्म – ∠C और ∠D तथा ∠D और ∠A.
पाठ्य-पुस्तक पृष्ठ संख्या # 52
इन्हें कीजिए
दो समान समान्तर चतुर्भुज के कटे हुए भाग ABCD तथा A’ B’ C’ D’ लीजिए। इनकी संगत भुजाएँ समान हैं।
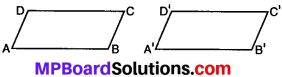
प्रश्न 1.
AB को DC के ऊपर रखिए। क्या वे एक-दूसरे को पूर्णतया ढकती हैं? अब आप \(\overline { AB } \) और \(\overline { DC } \) की लम्बाई के बारे में क्या कह सकते हैं?
उत्तर:
हाँ, \(\overline { A’B’ } \) एवं \(\overline { D’C’ } \) एक-दूसरे को पूर्णतया ढकती हैं। \(\overline { AB } \) तथा \(\overline { DC } \) की लम्बाई बराबर हैं।
![]()
प्रश्न 2.
इसी प्रकार AD और BC की लम्बाई की जाँच कीजिए। आप क्या पाते हैं?
उत्तर:
हम पाते हैं कि AD और BC की लम्बाई समान है। अतः हम कह सकते हैं कि समान्तर चतुर्भुज की सम्मुख भुजाएँ समान होती हैं।
प्रयास कीजिए (क्रमांक 3.2)
प्रश्न 1.
30° – 60° – 90° कोणों वाले दो समान सेट स्क्वेयर लीजिए। अब इन्हें आपस में इस प्रकार मिलाकर रखिए जिससे एक समान्तर चतुर्भुज बन जाए। क्या यह ऊपर बताए गए गुण की पुष्टि करने में आपकी सहायता करता है?
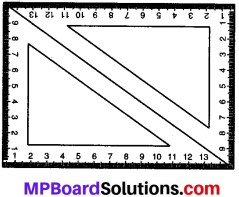
उत्तर:
हाँ, यह ऊपर बताए गए समान्तर चतुर्भुज के गुणं की पुष्टि करने में सहायता करता है। अर्थात् समान्तर चतुर्भुज की सम्मुख भुजाएँ बराबर माप की होती हैं।
पाठ्य-पुस्तक पृष्ठ संख्या # 53
इन्हें कीजिए
प्रश्न 1.
क्या यह कोण A तथा कोण C के मापों के बारे में आपको कुछ बताता है? कोण B तथा D के मापों के लिए जाँच कीजिए। अपने निष्कर्ष की चर्चा कीजिए।
उत्तर:
हाँ, यह कोण A तथा कोण C के बारे में बताता है कि कोण A तथा कोण C बराबर माप के हैं। कोण B तथा कोण D भी बराबर माप के हैं।
निष्कर्ष:
समान्तर चतुर्भुज के सम्मुख कोण बराबर माप के होते हैं।
समान्तर चतुर्भुज के कोण
प्रयास कीजिए (क्रमांक 3.3)
प्रश्न 1.
30° – 60° – 90° कोणों वाले दो समान सेट स्क्वे यर लेकर पहले की तरहही एक समान्तर चतुर्भुज बनाइए। क्या प्राप्त आकृति ऊपर बताए गुण की पुष्टि करने में आपकी सहायता करती है?
उत्तर
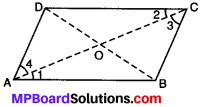
हाँ, प्राप्त आकृति यह पुष्टि करने में हमारी सहायता करती है कि समान्तर चतुर्भुज के सम्मुख कोण बराबर माप के होते हैं।
पाठ्य-पुस्तक पृष्ठ संख्या # 54
प्रश्न 1.
आकृति से दो और सम्पूरक कोणों के युग्म की पहचान कीजिए।
उत्तर:
सम्पूरक कोणों के युग्म – ∠B तथा ∠C और ∠C तथा ∠D।
सोचिए, चर्चा कीजिए और लिखिए
प्रश्न 1.
m∠R = m∠N = 70°; दर्शाने के उपरान्त क्या आप किसी अन्य विधि से m∠I और m∠G को ज्ञात कर सकते हैं?
हल:
समान्तर चतुर्भुज IRGN में, m∠R = m∠N
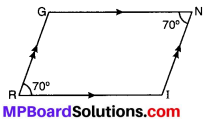
∴ RG || IN और RI एक तिर्यक रेखा है जो उन्हें क्रमशः R तथा I पर प्रतिच्छेद करती है।
इसलिए, ∴ ∠R + ∠I = 180°
(अन्तः सम्मुख कोण हैं)
70° + ∠I= 180°
I = 180° – 70° = 110°
पुनः RI || GN और RG तिर्यक रेखा इन्हें क्रमशः R तथा G पर प्रतिच्छेद करती है।
इसलिए ∠R + ∠G = 180°
70 + ∠G= 180° – 70° = 110°
अतः ∠I = ∠G.
![]()
पाठ्य-पुस्तक पृष्ठ संख्या # 55
समान्तर चतुर्भुज के विकर्ण
इन्हें कीजिए
प्रश्न 1.
समान्तर चतुर्भुज (माना ABCD) का एक कटा हुआ भाग लीजिए। माना इसके विकर्ण \(\overline { AB } \) और \(\overline { DB } \) एक दूसरे को ‘o’ पर प्रतिच्छेद करते हैं।
C को A पर रखकर एक तह (Fold) के द्वारा \(\overline { AC } \) का मध्य बिन्दु ज्ञात कीजिए। क्या मध्य बिन्दु o ही है? क्या यह दर्शाता है कि विकर्ण DB विकण AC को मध्य बिन्दु o पर समद्विभाजित करता है? अपने मित्रों के साथ इसकी चर्चा कीजिए। इस क्रियाकलाप को यह ज्ञात करने के लिए दोहराएँ कि \(\overline { DB } \) का मध्य बिन्दु कहाँ पर स्थित होगा?
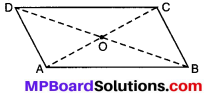
हल:
तह करने पर हम देखते हैं कि बिन्दु C बिन्दु A पर पड़ता है। स्पष्ट है कि \(\overline { AC } \) का मध्य बिन्दु o ही है।
यह दर्शाता है कि विकर्ण \(\overline { DB } \), विकर्ण \(\overline { AC } \) को समद्विभाजित करता है।
\(\overline { DB } \) का मध्य बिन्दु o पर ही होगा।
अतः समान्तर चतुर्भुज के विकर्ण एक दूसरे को समद्विभाजित करते हैं।
उत्तर