Category: Class 8

MP Board Class 8th Maths Solutions Chapter 6 Square and Square Roots Ex 6.3

Question 1.
What could be the possible ‘ones’ digits of the square root of each of the following numbers?
(i) 9801
(ii) 99856
(iii) 998001
(iv) 657666025
Solution:
(i) We know that the ‘ones’ place of the square of 1 and 9 is 1.
∴ The possible ‘ones’ digits of the square root of 9801 are 1 and 9.
(ii) We know that the ‘ones’ place of the square of 4 and 6 is 6.
∴ The possible ‘ones’ digits of the square root of 99856 are 4 and 6.
(iii) We know that the ‘ones’ place of the square of 1 and 9 is 1.
∴ The possible ‘ones’ digits of the square root of 998001 are 1 and 9.
(iv) We know that ‘ones’ place of the square of 5 is 5.
∴ The possible ‘ones’ digit of the square root of 657666025 is 5.

Question 2.
Without doing any calculation, find the numbers which are surely not perfect squares,
(i) 153
(ii) 257
(iii) 408
(iv) 441
Solution:
We know that the numbers ending with 2, 3, 7 or 8 are not perfect squares. So, (i), (ii) and (iii) are surly not perfect squares.
(iv) Since, the number 441 ends with 1. Thus, 441 may or may not be a perfect square.

Question 3.
Find the square root of 100 and 169 by the method of repeated subtraction.
Solution:
First consider 100.
(1) 100 – 1 = 99
(2) 99 – 3 = 96
(3) 96 – 5 = 91
(4) 91 – 7 = 84
(5) 84-9 = 75
(6) 75 – 11 = 64
(7) 64 – 13 = 51
(8) 51 – 15 = 36
(9) 36 – 17 = 19
(10) 19 – 19 = 0.
∴ \(\sqrt{100}\) = 10.
Now, consider 169
(1) 169 – 1 = 168
(2) 168 – 3 = 165
(3) 165 – 5 = 160
(4) 160 – 7 = 153
(5) 153 – 9 = 144
(6) 144 – 11 = 133
(7) 133 – 13 = 120
(8) 120 – 15 = 105
(9) 105-17 = 88
(10) 88 – 19 = 69
(11) 69 – 21 = 48
(12) 48 – 23 = 25
(13) 25 – 25 = 0.
∴ \(\sqrt{169}\) = 13.

Question 4.
Find the square roots of the following numbers by the Prime Factorisation Method.
(i) 729
(ii) 400
(iii) 1764
(iv) 4096
(v) 7744
(vi) 9604
(vii) 5929
(viii) 9216
(ix) 529
(x) 8100
Solution:

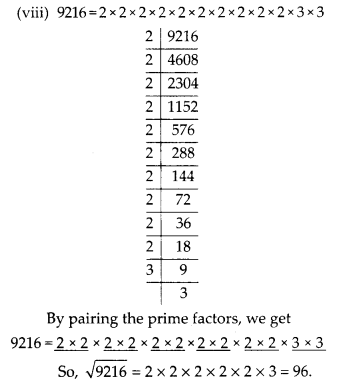
Question 5.
For each of the following numbers, find the smallest whole number by which it should be multiplied so as to get a perfect square number. Also find the square root of the square number so obtained.
(i) 252
(ii) 180
(iii) 1008
(iv) 2028
(v) 1458
(vi) 768
Solution:
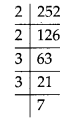
(i) We have, 252 = 2 × 2 × 3 × 3 × 7
The smallest whole number is 7 by which 252 should be multiplied so as to get a perfect square.
252 × 7 = 2 × 2 × 3 × 3 × 7 × 7
Now each prime factor is in a pair. Therefore, 252 × 7 = 1764 is a perfect square.

(ii) We have, 180 = 2 × 2 × 3 × 3 × 5

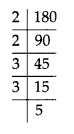
The smallest whole number is 5, by which 180 should be multiplied so as to get a perfect square.
180 × 5 = 2 × 2 × 3 × 3 × 5 × 5
So, \(\sqrt{900}\) = 2 × 3 × 5 = 30.

(iii)
We have,

1008 = 2 × 2 × 2 × 2 × 3 × 3 × 7
The smallest whole number is 7, by which 1008 should be multiplied so as to get a perfect square.
1008 × 7 = 2 × 2 × 2 × 2 × 3 × 3 × 7 × 7
Now each prime factor is in pair. Therefore,
1008 × 7 = 7056 is a perfect square.
So, \(\sqrt{7056}\) = 2 × 2 × 3 × 7 = 84.

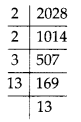
(iv) We have, 2028 = 2 × 2 × 3 × 13 × 13
The smallest whole number is 3 by which 2028 should be multiplied so as to get a perfect square.

2028 × 3 = 2 × 2 × 3 × 3 × 13 × 13
Now each prime factor is in pair. Therefore, 2028 × 3 = 6084 is a perfect square.
So, \(\sqrt{6084}\) = 2 × 3 × 13 = 78.

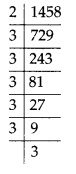
(v) We have, 1458 = 2 × 3 × 3 × 3 × 3 × 3 × 3
The smallest whole number is 2, by which 1458 should be multiplied so as to get a perfect square.
1458 × 2 = 2 × 2 × 3 × 3 × 3 × 3 × 3 × 3

Now each prime factor is in pair.
Therefore, 1458 × 2 = 2916 is a perfect square.
So, \(\sqrt{2916}\) = 2 × 3 × 3 × 3 = 54

(vi) We have, 768 = 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 3

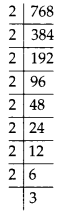
The smallest whole number is 3, by which 768 should be multiplied so as to get a perfect square.
768 × 3 = 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 3 × 3
Now each prime factor is in pair.
Therefore, 768 × 3 = 2304 is a perfect square.
So, \(\sqrt{2304}\) = 2 × 2 × 2 × 2 × 3 = 48.

Question 6.
For each of the following numbers, find the smallest whole number by which it should be divided so as to get a perfect square. Also find the square root of the square number so obtained,
(i) 252
(ii) 2925
(iii) 396
(iv) 2645
(v) 2800
(vi) 1620
Solution:
(i) We have 252 = 2 × 2 × 3 × 3 × 7

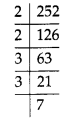
We find that 252 should be divided by 7, to get a perfect square.
252 ÷ 7 = 36 = 2 × 2 × 3 × 3
Therefore, the required smallest number is 7.

(ii) We find that 2925 = 3 × 3 × 5 × 5 × 13
We find that 2925 should be divided by 13, to get a perfect square.
2925 ÷ 13 = 225 = 3 × 3 × 5 × 5

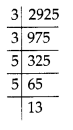
Therefore, the required smallest number is 13.
Also, \(\sqrt{225}\) = 3 × 5 = 15.

(iii) We have, 396 = 2 × 2 × 3 × 3 × 11
We find that 396 should be divided by 11, to get a perfect square.

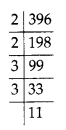
396 ÷ 11 = 36 = 2 × 2 × 3 × 3
Therefore, the required smallest number is 11.
Also, \(\sqrt{36}\) = 2 × 3 = 6.

(iv) We have, 2645 = 5 × 23 × 23

We find that 2645 should be divided by 5, to get a perfect square.
2645 ÷ 5 = 529 = 23 × 23
Therefore, the required smallest number is 5.
Also, \(\sqrt{529}\) = 23.

(v) We have, 2800 = 2 × 2 × 2 × 2 × 5 × 5 × 7
We find that 2800 should be divided by 7, to get a perfect square

2800 ÷ 7 = 400 = 2 × 2 × 2 × 2 × 5 × 5
Therefore, the required smallest number is 7.
Also, \(\sqrt{400}\) = 2 × 2 × 5 = 20.

(vi) We have,
1620 = 2 × 2 × 3 × 3 × 3 × 3 × 5

Question 7.
The students of Class VIII of a school donated ₹ 2401 in all, for the Prime Minister’s National Relief Fund. Each student donated as many rupees as the number of students in the class. Find the number of students in the class.
Solution:
We have, 2401 = 7 × 7 × 7 × 7

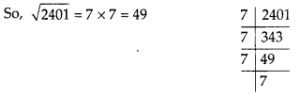
We find that the number of students in the class is 49.

Question 8.
2025 plants are to be planted in a garden in such a way that each row contains as many plants as the number of rows. Find the number of rows and the number of plants in each row.
Solution:
Total number of plants = 2025
The plants are planted in a garden in such a way that each row contains as many plants as the number of rows.

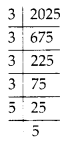
2025 = 3 × 3 × 3 × 3 × 5 × 5
∴ Number of plants in each row = \(\sqrt{2025}\) = 3 × 3 × 5 = 45
So, number of rows = number of plants.
Thus, the number of rows = 45
and number of plants in each row = 45.

Question 9.
Find the smallest square number that is divisible by each of the numbers 4,9 and 10.
Solution:
The smallest number divisible by each 4, 9 and 10 is their LCM.
The LCM of 4, 9 and 10 is 2 × 2 × 3 × 3 × 5 = 180.
Now, prime factorisation of 180 is
180 = 2 × 2 × 3 × 3 × 5

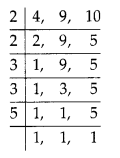
In order to get a perfect square, each factor of 180 must be paired.
So, we need to make pair of 5.
∴ 180 should be multiplied by 5.
Hence, the required number is 180 × 5 = 900.

Question 10.
Find the smallest square number that is divisible by each of the numbers 8, 15 and 20.
Solution:
The smallest number divisible by each 8, 15 and 20, is their LCM.
The LCM of 8, 15 and 20 is 2 × 2 × 2 × 3 × 5 = 120

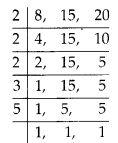
Now prime factorisation of 120 is
120 = 2 × 2 × 2 × 3 × 5 ….. (i)
In order to get a perfect square, each factor of 120 must be paired.
Thus we multiply (i) by 2 × 3 × 5 = 30, we get 120 × 30 = 3600.

MP Board Class 8th Maths Solutions

MP Board Class 8th Maths Solutions Chapter 13 सीधा और प्रतिलोम समानुपात Ex 13.1

प्रश्न 1.
एक रेलवे स्टेशन के निकट कार पार्किंग शुल्क इस प्रकार है –

• 4 घण्टों तक – ₹ 60
• 8 घण्टों तक – ₹ 100
• 12 घण्टों तक – ₹ 140
• 24 घण्टों तक – ₹180

जाँच कीजिए कि क्या कार पार्किंग शुल्क पार्किंग समय के प्रत्यक्ष अनुपात में है?
हल:
∴ \(\frac{4}{60}\) ≠ \(\frac{8}{100}\) ≠ \(\frac{12}{140}\) ≠ \(\frac{24}{180}\)
∴ कार पार्किंग शुल्क पार्किंग समय के प्रत्यक्ष अनुपात में नहीं है।

प्रश्न 2.
एक पेंट के मूल मिश्रण (base) के 8 भागों में लाल रंग के पदार्थ का 1 भाग मिलाकर मिश्रण तैयार किया जाता है। निम्नलिखित सारणी में, मूल मिश्रण के वे भाग ज्ञात कीजिए जिन्हें मिलाए जाने की आवश्यकता है –

हल:
यहाँ, माना कि लाल रंग के पदार्थ का भाग x, मूल मिश्रण के ” भाग में मिलाया जाता है, तथा x और y प्रत्यक्ष अनुपात में हैं।
अतः x और y का अनुपात अचर रहेगा।
तब \(\frac{x}{y}\) = \(\frac{1}{8}\)
अतः अभीष्ट अनुपात = \(\frac{4}{32}\), \(\frac{7}{56}\), \(\frac{12}{96}\), \(\frac{20}{160}\)
सारणी में रखने पर,

प्रश्न 3.
प्रश्न 2. में यदि लाल रंग पदार्थ के 1 भाग के लिए 75 mL मूल मिश्रण की आवश्यकता है, तो मूल मिश्रण के 1800 mL में हमें कितना लाल रंग का पदार्थ मिलाना चाहिए?
हल:
माना कि 1800 mL में x भाग लाल रंग का पदार्थ मिलाना चाहिए।
सारणी में रखने पर,

अतः मूल मिश्रण में हमें 24 भाग लाल रंग का पदार्थ मिलाना चाहिए।

प्रश्न 4.
किसी सॉफ्ट ड्रिंक फैक्ट्री में एक मशीन 840 बोतलें 6 घण्टे में भरती है। वह मशीन पाँच घण्टे में कितनी बोतलें भरेगी?
हल:
माना कि 5 घण्टे में x बोतलें भरी जा सकती हैं। तब सारणी के रूप में रखने पर,

अतः मशीन 5 घण्टे में 700 बोतलें भरेगी।

प्रश्न 5.
एक बैक्टीरिया या जीवाणु के फोटोग्राफ (चित्र) को 50,000 गुना आवर्धित करने पर उसकी लम्बाई 5 cm हो जाती है, जैसा कि संलग्न चित्र में दिखाया गया है। इस बैक्टीरिया की वास्तविक लम्बाई क्या है ? यदि फोटोग्राफ को केवल 20,000 गुना आवर्धित किया जाए, तो उसकी आवर्धित लम्बाई क्या होगी?

हल:
बैक्टीरिया की आवर्धित लम्बाई = 50,000 गुना
बैक्टीरिया की लम्बाई = 5 cm

अतः बैक्टीरिया की वास्तविक लम्बाई = 10_-4 cm
यहाँ, फोटोग्राफ की लम्बाई तथा आवर्धित लम्बाई अनुक्रमानुपाती हैं।
माना कि आवर्धित लम्बाई x cm है
सारणी के रूप में लिखने पर,

यहाँ आवर्धित लम्बाई तथा आवर्धित फोटोग्राफ परस्पर अनुक्रमानुपाती हैं।

अतः आवर्धित लम्बाई = 2 cm

प्रश्न 6.
एक जहाज के मॉडल में उसका मस्तूल (mast) 9 cm ऊँचा है, जबकि वास्तविक जहाज का मस्तूल 12 m ऊँचा है। यदि जहाज की लम्बाई 28 m है तो उसके मॉडल की लम्बाई कितनी है?
हल:

स्पष्ट है, मॉडल की लम्बाई और वास्तविक लम्बाई परस्पर – अनुक्रमानुपाती हैं।
\(\frac{9}{12}\) = \(\frac{x}{28}\)
x = \(\frac{9×28}{12}\) = 21
अतः जहाज के मॉडल की लम्बाई = 21 cm

प्रश्न 7.
मान लीजिए 2 kg चीनी में 9x 10 क्रिस्टल हैं। निम्नलिखित चीनी में कितने क्रिस्टल होंगे?

1. 5 kg
2. 1.2 kg.

हल:
माना कि 5 kg चीनी और 1.2 kg चीनी में क्रमशः x और y क्रिस्टल हैं। इन्हें सारणी रूप में लिखने पर,

स्पष्ट है कि यहाँ क्रिस्टल की संख्या और चीनी की मात्रा परस्पर अनुक्रमानुपाती हैं।
1.

अतः 5 kg चीनी में 2.25 x 10₇ क्रिस्टल होंगे।
2.

अतः 1.2 kg चीनी में 5.4 x 10₆ क्रिस्टल होंगे।

प्रश्न 8.
रश्मि के पास एक सड़क का मानचित्र है, जिसके पैमाने में 1 cm की दूरी 18 km निरूपित करती है। वह उस सड़क पर अपनी गाड़ी से 72 km की दूरी तय करती है। उसके द्वारा तय की गई दूरी मानचित्र में क्या होगी?
हल:
यहाँ, 1 cm की दूरी = 18 km.
माना कि रश्मि के द्वारा तय की गई दूरी मानचित्र में x cm है, तब दी हुई सूचना को सारणी के रूप में निरूपित करने पर,

यहाँ, मानचित्र में दूरी तथा वास्तविक दूरी परस्पर अनुक्रमानुपाती हैं।
\(\frac{1}{18}\) = \(\frac{x}{72}\)
या x = \(\frac{1×72}{18}\) cm = 4 cm
अतः मानचित्र में दूरी = 4 cm

प्रश्न 9.
एक 5 m 60 cm ऊँचे ऊर्ध्वाधर खम्भे की छाया की लम्बाई 3 m 20 cm है। उसी समय पर ज्ञात कीजिए –

1. 10 m 50 cm ऊँचे एक अन्य खम्भे की छाया की लम्बाई।
2. उस खम्भे की ऊँचाई जिसकी छाया की लम्बाई 5 m है।

हल:
1. माना कि x m उस खम्भे की लम्बाई है जिसकी छाया की लम्बाई 10 m 50 cm है। y m उस खम्भे की ऊँचाई है जिसकी छाया 5 m है।
इन्हें सारणी के रूप निरूपित करने पर,

यहाँ, यह स्पष्ट है कि खम्भे की ऊँचाई और छाया परस्पर अनुक्रमानुपाती हैं।

अतः छाया की लम्बाई = 6 m
2.

अतः खम्भे की ऊँचाई = 8 m 75 cm

प्रश्न 10.
माल से लदा हुआ एक ट्रक 25 मिनट में 14 km चलता है। यदि चाल वही रहे, तो वह 5 घण्टे में कितनी दूरी तय कर पाएगा?
हल:
माना कि ट्रक 5 घण्टे में x km दूरी तय करता है। तब इन्हें सारणी के रूप में निरूपित करने पर,

यहाँ, दूरी तथा समय परस्पर अनुक्रमानुपाती हैं।
\(\frac{14}{25/60}\) = \(\frac{x}{5}\)
या x = \(\frac{5x14x60}{25}\) = 168 km
अतः ट्रक द्वारा 5 घण्टे में तय की गई दूरी = 168 km

पाठ्य-पुस्तक पृष्ठ संख्या # 216-217

इन्हें कीजिए (क्रमांक 13.3)

प्रश्न 1.
एक वर्गांकित कागज पर भिन्न-भिन्न भुजाओं के पाँच वर्ग खींचिए। निम्नलिखित सूचना को एक सारणी के रूप में लिखिए –

ज्ञात कीजिए कि क्या भुजा की लम्बाई –

1. वर्ग के परिपाम के अनुक्रमानुपाती है।
2. वर्ग के क्षेत्रफल के अनुक्रमानुपाती है।

हल:

सूचना को सारणी के रूप में निरूपित करने पर,

यहाँ स्पष्ट है कि,

1. वर्ग की भुजा की लम्बाई वर्ग के परिमाप के अनुक्रमानुपाती है।
2. वर्ग की भुजा की लम्बाई वर्ग के क्षेत्रफल के अनुक्रमानुपाती नहीं है।

प्रश्न 2.
पाँच व्यक्तियों के लिए हलवा बनाने के लिए, निम्नलिखित सामग्री की आवश्यकता होती है: सूजी/रवा = 250 g, चीनी = 300 g, घी = 200 g, पानी = 200 g. समानुपात की अवधारणा का प्रयोग करते हुए, अपनी कक्षा के लिए हलवा बनाने के लिए इन सामग्रियों की मात्राओं में होने वाले परिवर्तनों का आकलन (estimate) कीजिए।
हल:
माना कि कक्षा में विद्यार्थियों की संख्या = 20 है।
स्पष्ट है कि यहाँ अनुक्रमानुपाती की स्थिति है।
अत: वांछित सामग्री \(\frac{20}{5}\) = 4 गुना होगी –
अर्थात् सूजी/रवा = 250 x 4g = 1000 g = 1 kg
चीनी = 300 x 4g = 1200 g = 1.200kg
घी = 200 x 4g = 800 g
पानी = 200 x 4g = 800 g.

प्रश्न 3.
एक पैमाने का चुनाव करते हुए, अपनी कक्षा के कमरे का मानचित्र खींचिए, जिसमें खिड़कियाँ, दरवाजे, ब्लैकबोर्ड इत्यादि दर्शाए गए हों (एक उदाहरण यहाँ दिया है।

हल: माना की पैमाना 1 : 40 है, तब
मानचित्र इस प्रकार है –

सोचिए, चर्चा कीजिए और लिखिए (क्रमांक 13.2)

प्रश्न 1.
सीधा समानुपात (विचरण) की अब तक हल की गई समस्याओं में से कुछ को लीजिए। क्या आप सोचते हैं कि इन समस्याओं को इकाई की विधि या ऐकिक विधि (unitary method) से हल किया जा सकता है?
हल:
हाँ, इन समस्याओं को ऐकिक विधि से हल किया जा सकता है।
हम यहाँ प्रश्नावली 13.1 से प्रश्न 4 एवं प्रश्न 10 को हल करते हैं –
प्रश्न 4 का हल:
∴ 6 घण्टे में भरी जाने वाली बोतलें = 840
∴ 1 घण्टे में भरी जाने वाली बोतलें = \(\frac{840}{6}\)
∴ 5 घण्टे में भरी जाने वाली बोतलें = \(\frac{840×5}{6}\)
= 140 x 5 = 700 बोतलें।
प्रश्न 10 का हल:
25 मिनट = \(\frac{25}{60}\) घण्टे
∴ \(\frac{25}{60}\) घण्टे में तय की गई दूरी = 14 km
∴ 1 घण्टे में तय की गई दूरी = \(\frac{14}{25/60}\) km
∴ 5 घण्टे में तय की गई दूरी = \(\frac{14x60x5}{25}\) km
= 168 km

पाठ्य-पुस्तक पृष्ठ संख्या # 219

इन्हें कीजिए (क्रमांक 13.4)

प्रश्न 1.
एक वर्गांकित कागज लीजिए और उस पर 48 काउंटरों (counters) को पंक्तियों की विभिन्न संख्याओं में नीचे दर्शाए अनुसार व्यवस्थित कीजिए –


आप क्या देखते हैं? जब R में वृद्धि होती है, तो C में कमी होती है।

1. क्या R₁ : R₂ = C₂ : C₁ है?
2. क्या R₃ : R₄ = C₄ : C₃
3. क्या R और C परस्पर व्युत्क्रमानुपाती है?

इस क्रियाकलाप को 36 काउंटरों के साथ प्रयास कीजिए।
हल:
C₁ → 24
C₂ → 16
C₅ → 6
हम यहाँ देखते हैं कि R में वृद्धि होती है तो C में कमी होती

1. R₁ : R₂ = 2 : 3 और
C₂ : C₁ = 16 : 24 = 2 : 3
R₁ : R₂ = C₂ : C₁

2. R₃ : R₄ = 4 : 6 = 2 : 3 और
C₄ : C₃ = 8 : 12 = 2 : 3
R₃ : R₄ = C₄ : C₃

3. हाँ, R और C परस्पर व्युत्क्रमानुपाती हैं। उत्तर अब, 36 काउण्टरों के साथ क्रियाकलाप।

सूचना को सारणी के रूप में लिखने पर, हम प्राप्त करते हैं –

हम देखते हैं कि R में वृद्धि होती है, तो C में कमी होती हैं।

1. R₁ : R₂ = 2 : 3 और C₂ : C₁ = 12 : 18 = 2 : 3
R₁ : R₂ = C₂ : C₁

2. R₃ : R₄ = 4 : 6 = 2 : 3 और C₄ : C₃ = 6 : 9 = 2 : 3
R₃ : R₄ = C₄ : C₃

3. हाँ, R और C परस्पर व्युत्क्रमानुपाती हैं।

प्रयास कीजिए (क्रमांक 14.2)

प्रश्न 1.
निम्नलिखित सारणियों को देखिए तथा ज्ञात कीजिए कि कौन-कौन से चरों (यहाँ x और y) के युग्म परस्पर प्रतिलोम समानुपात में हैं –

हल:
(i) हम देखते हैं कि
x × y = 50 x 5 ≠ 40 x 6 ≠ 30 x 7 ≠ 20 x 8
अतः x और y परस्पर प्रतिलोम समानुपात में नहीं हैं।

(ii) हम देखते हैं कि
x × y = 100 x 6 = 200 x 30 = 300 x 20
= 400 x 15 = अचर
अतः x और y परस्पर प्रतिलोम समानुपात में हैं।

(iii) हम देखते हैं कि
x × y = 90 x 10 = 60 x 15 = 45 x 20 ≠ 30 x 25 ≠ 20 x 30 ≠ 5 x 35
अतःx और , परस्पर प्रतिलोम समानुपात में नहीं हैं।

MP Board Class 8th Maths Solutions

MP Board Class 8th Maths Solutions Chapter 6 Square and Square Roots Ex 6.2

Question 1.
Find the square of the following numbers.
(i) 32
(ii) 35
(iii) 86
(iv) 93
(v) 71
(vi) 46
Solution:
(i) 32² = (30 + 2)² = (30 + 2) (30 + 2)
= 30 (30 + 2) + 2 (30 + 2)
= 900 + 60 + 60 + 4 = 1024.
(ii) 35² = (30 + 5)² = (30 + 5) (30 + 5)
= 30(30 + 5) + 5 (30 + 5)
= 900 + 150 + 150 + 25 = 1225.
(iii) 86² = (80 + 6)² = (80 + 6) (80 + 6)
= 80(80 + 6) + 6(80 + 6)
= 6400 + 480 + 480 + 36 = 7396.
(iv) 93² = (90 + 3)² = (90 + 3) (90 + 3)
= 90(90 + 3) + 3(90 + 3)
= 8100 + 270 + 270 + 9 = 8649.
(v) 71² = (70+ 1)² = (70 + 1) (70 + 1)
= 70(70 + 1) + 1 (70 + 1)
= 4900 + 70 + 70 + 1 = 5041.
(vi) 46² = (40 + 6)² = (40 + 6) (40 + 6)
= 40(40 + 6) + 6(40 + 6)
= 1600 + 240 + 240 + 36 = 2116.

Question 2.
Write a Pythagorean triplet whose one member is
(i) 6
(ii) 14
(iii) 16
(iv) 18
Solution:
We can get Pythagorean triplet by using general form 2m, m² – 1, m² + 1.
(i) Let us take 2m = 6 ⇒ m = 3
Thus, m² – 1 = 3² – 1 = 9 – 1 = 8 and m² + 1 = 3² + 1 = 9 + 1 = 10.
∴ The required triplet is 6, 8, 10

(ii) Let us take 2m = 14 ⇒ m = 7
Thus, m² – 1 = 7² – 1 = 49 – 1 = 48
and m² + 1 = 7² + 1 = 49 + 1 = 50
∴ The required triplet is 14, 48, 50.

(iii) Let us take 2m = 16 ⇒ m = 8
Thus, m² – 1 = 8² – 1 = 64 – 1 = 63
and m² + 1 = 8² + 1 = 64 + 1 = 65.
∴ The required triplet is 16, 63, 65.

(iv) Let us take 2m = 18 ⇒ m = 9
Thus, m² – 1 = 9² – 1 = 81 – 1 = 80
and m² + 1 = 9² + 1 = 81 + 1 = 82
∴ The required triplet is 18, 80, 82.

MP Board Class 8th Maths Solutions

MP Board Class 8th Maths Solutions Chapter 6 Square and Square Roots Ex 6.1

Question 1.
What will be the unit digit of the squares of the following numbers?
Solution:
(i) The unit digit of (81)² is 1. Because when we multiply digit 1 by itself, we get 1.
(ii) The unit digit of (272)² is 4. Because when we multiply digit 2 by itself, we get 4.
(iii) The unit digit of (799)² is 1. Because when we multiply digit 9 by itself, we get 81.
(iv) The unit digit of (3853)² is 9. Because when we multiply digit 3 by itself, we get 9.
(v) The unit digit of (1234)² is 6. Because when we multiply digit 4 by itself, we get 16.
(vi) The unit digit of (26387)² is 9. Because when we multiply digit 7 by itself, we get 49.
(vii) The unit digit of (52698)² is 4. Because when we multiply digit 8 by itself, we get 64.
(viii) The unit digit of (99880)² is 0. Because when we multiply digit 0 by itself, we get 0.
(ix) The unit digit of (12796)² is 6. Because when we multiply the unit digit 6 by itself, we get 36.
(x) The unit digit of (55555)² is 5. Because when we multiply the unit digit 5 by itself, we get 25.

Question 2.
The following numbers are obviously not perfect squares. Give reason.
(i) 1057
(ii) 23453
(iii) 7928
(iv) 222222
(v) 64000
(vi) 89722
(vii) 222000
(viii) 505050.
Solution:
We know that number ending in 2, 3, 7 or 8 are not perfect squares.
∴ (i) 1057,
(ii) 23453,
(iii) 7928,
(iv) 222222
and
(vi) 89722 are not perfect squares.
Since, for perfect squares, there should be even number of zeroes at the end.
∴ (v) 64000,
(vii) 222000 and
(viii) 505050. Are not perfect squares.

Question 3.
The square of which of the following would be odd numbers ?
(i) 431
(ii) 2826
(iii) 7779
(iv) 82004
Solution:
(i) When we multiply the unit digit 1 by itself, we get 1 at the end, which shows that the square of 431 is an odd number.
(ii) When we multiply the unit digit 6 by itself we get 36, i.e., we get 6 at the end, which shows that the square of 2826 is an even number.
(iii) When we multiply the unit digit 9 by itself we get 81, i.e., we get 1 at the end, which shows that the square of 7779 is an odd number.
(iv) When we multiply the unit digit 4 by itself we get 16, i.e., we get 6 at the end, which shows that the square of 82004 is an even number.

Question 4.
Observe the following pattern and find the missing digits.
11² = 121
101² = 10201
1001² = 1002001
100001² = 1 …… 2 …… 1 …….
10000001² = ……….
Solution:
100001² = 10000200001
10000001² = 100000020000001.

Question 5.
Observe the following pattern and supply the missing numbers.
11² = 121
101² = 10201
10101² = 102030201
1010101² = ……
…….² = 10203040504030201
Solution:
1010101² = 1020304030201
101010101² = 10203040504030201.

Question 6.
Using the given pattern, find the missing numbers.
1² + 2² + 2² = 3²
2² + 3² + 6² = 7²
3² +4² + 12² = 13²
4² + 5² + _² = 21²
5² + _² + 30² = 31²
6² + 7² + _² = _²
Solution:
In the pattern,
Third number = first number × second number and fourth number = third number + 1
4² + 5² + 20² = 21²
5² + 6² + 30² = 31²
6² + 7² + 42² = 43².

Question 7.
Without adding, find the sum.
(i) 1 + 3 + 5 + 7 + 9
(ii) 1 + 3 + 5 + 7 + 9 + 11 + 13 + 15 + 17 + 19
(iii) 1 + 3 + 5 + 7 + 9 + 11 + 13 + 15 + 17 + 19 + 21 +23.
Solution:
We have to find the sum of first 5 odd numbers,
1 + 3 + 5 + 7 + 9 = 5² = 25.
(ii) We have to find the sum of the first 10 odd numbers,
1 + 3 + 5 + 7 + 9 + 11 + 13 + 15 + 17 + 19 = 10² = 100.
(iii) We have to find the sum of first 12 odd numbers,
1 + 3 + 5 + 7 + 9 + 11 + 13 + 15 + 17 + 19 + 21 + 23 = 12² = 144.

Question 8.
(i) Express 49 as the sum of 7 odd numbers,
(ii) Express 121 as the sum of 11 odd numbers.
Solution:
(i) 49 = 7² = 1 + 3 + 5 + 7 + 9 + 11 + 13.
(ii) 121 = 11² = 1 + 3 + 5 + 7 + 9 + 11 + 13 + 15 + 17 + 19 + 21.

Question 9.
How many numbers lie between squares of the following numbers?
(i) 12 and 13
(ii) 25 and 26
(iii) 99 and 100.
Solution:
(i) We can find the number of terms between the squares of 12 and 13, by doubling the first term from 12 and 13. i.e., 2 × 12 = 24:
∴ Total number of terms = 24.
(ii) We can find the number of terms between the squares of 25 and 26, by doubling the first term from 25 and 26. i.e., 2 × 25 = 50.
∴ Total number of terms = 50.
(iii) We can find the number of terms between the squares of 99 and 100, by doubling the first term from 99 and 100. i.e., 2 × 99 = 198.
∴ Total number of terms = 198.

MP Board Class 8th Maths Solutions

MP Board Class 8th Maths Solutions Chapter 4 Practical Geometry Ex 4.5

Question 1.
Draw the following.
(i) The square READ with RE = 5.1 cm.
(ii) A rhombus whose diagonals are 5.2 cm and 6.4 cm long.
(iii) A rectangle with adjacent sides of lengths 5 cm and 4 cm.
(iv) A parallelogram OKAY where OK = 5.5 cm and KA = 4.2 cm.
Solution:
(i) Since, all 4 sides of a square are equal and each of 4 angles is equal to 90°.
Steps of Construction:
Step-1: Draw RE = 5.1 cm.
Step-2 : Draw ∠REX = 90°.
Step-3 : Cut off EA = 5.1 cm on \(\overrightarrow{E X}\)
Step-4: With R as centre and radius equal to 5.1 cm, draw an arc.
Step-5 : With A as centre and radius equal to 5.1 cm, cut off another arc on the arc drawn in step-4 at point D.
Step-6 : Join DA and DR.
Hence, READ is the required square.

(ii) We know that diagonals of a rhombus bisect each other at right angles. Let AC = 5.2 cm and BD = 6.4 cm.
Steps of Construction:
Step-1: Draw AC = 5.2 cm.
Step-2 : Draw perpendicular bisector XY of AC which cut AC at point O.
Step-3 : Cut off OD = 3.2 cm on OX and OB = 3.2 cm on \(\overrightarrow{O Y}\).
Step-4 : Join AD, CD, AB and CB.
Hence, ABCD is the required rhombus.

(iii) In a rectangle, opposite sides are equal and each of 4 angles is equal to 90°.
Let AB = 5 cm and BC = 4 cm
∴ AB = DC = 5 cm and BC = AD = 4 cm.
Also, ∠A = ∠B = ∠C = ∠D = 90°.
Steps of Construction:
Step-1: Draw AB = 5 cm.
Step-2 : Draw ∠ABX = 90°.
Step-3 : Cut off BC = 4 cm on BX .
Step-4: With A as centre and radius equal to 4 cm, cut off an arc.
Step-5 : With C as centre and radius equal to 5 cm cut off another arc on the arc drawn in step-4 at point D.
Step-6 : Join AD and CD.
Hence, ABCD is the required rectangle.

(iv) Here, data given is incomplete. Since we know that to draw a quadrilateral at least five parts are necessary. In the present case, OK = 5.5 cm & KA = 4.2 cm is given.
We know that opposite sides of a parallelogram are equal.
∴ OK = YA = 5.5 cm and KA = OY = 4.2 cm
Here, only four parts are given. This means that one more part is necessary.
So, either one angle or diagonal of a parallelogram is required to construct it.
Hence, parallelogram OKAY cannot be drawn.

MP Board Class 8th Maths Solutions

MP Board Class 8th Maths Solutions Chapter 4 Practical Geometry Ex 4.4

Question 1.
Construct the following quadrilaterals.
(i) Quadrilateral
DEAR
DE = 4 cm
EA = 5 cm
AR = 4.5 cm
∠E = 60°
∠A = 90°

(ii) Quadrilateral
TRUE
TR = 3.5 cm
RU = 3 cm
UE = 4 cm
∠R = 75°
∠U = 120°
Solution:
(i) Steps of Construction:
Step-1: Draw EA = 5 cm.
Step-2: Make ∠AEX = 60° and ∠EAY = 90°.
Step-3 : Cut off arcs AR = 4.5 cm on \(\overrightarrow{A Y}\) and ED = 4 cm on \(\overrightarrow{E X}\).
Step-4: Join DR.
Hence, DEAR is the required quadrilateral.

(ii) Steps of Construction :
Step-1: Draw RU = 3 cm.
Step-2 : Make ∠URX = 75° and ∠RUY = 120°
Step-3 : Cut off RT = 3.5 cm on \(\overrightarrow{R X}\) and UE = 4 cm on \(\overrightarrow{U Y}\).
Step-4: Join TE.
Hence, TRUE is the required quadrilateral.

MP Board Class 8th Maths Solutions

MP Board Class 8th Maths Solutions Chapter 4 Practical Geometry Ex 4.3

Question 1.
Construct the following quadrilaterals.
(i) Quadrilateral
MORE
MO = 6 cm
OR = 4.5 cm
∠M = 60°
∠O = 1050°
∠R = 105°

(ii) Quadrilateral
PLAN
PL = 4 cm
LA = 6.5 cm
∠P = 90°
∠A = 6.5 cm
∠N = 85°

(iii) Parallelogram
HEAR
HE =5 cm
EA = 6 cm
∠B = 85°

(iv) Rectangle
OKAY
OK = 7 cm
KA = 5 cm
Solution:
(i) Steps of Construction:
Step-1: Draw MO = 6 cm
Step-2 : Make ∠MOX = 105° and ∠OMY = 60°.
Step-3 : Cut off OR = 4.5 cm on OX.
Step-4 : At point R, draw ∠ORZ = 105° which cuts MY at E.
Hence, MORE is the required quadrilateral.

(ii) Here, ∠P = 90°, ∠A = 110°, ∠N = 85°
∴ ∠L = 360° – (∠P + ∠A + ∠N)
= 360° – (90° + 110° + 85°)
= 360°- 285° = 75° ….. (A)
Steps of Construction:
Step-1: Draw PL = 4 cm.
Step-2 : Make ∠LPX = 90° and ∠PLY = 75°. [From (A)]
Step-3 : Cut off LA = 6.5 cm on \(\overrightarrow{L Y}\).
Step-4: Draw ∠LAZ = 110° which cut \(\overrightarrow{P X}\) at point N.
Hence, PLAN is the required quadrilateral.

(iii) Since, opposite sides and angles of a parallelogram are equal i.e., ∠R = ∠E = 85°, HE = RA = 5 cm and EA = HR = 6 cm.
Steps of Construction:
Step-1: Draw HE = 5 cm.
Step-2 : Draw ∠HEX = 85°.
Step-3 : Cut off EA = 6 cm on \(\overrightarrow{E X}\)
Step-4: With H as centre and radius equal to 6 cm, draw an arc.
Step-5: With A as centre and radius equal to 5 cm, cut another arc on the arc drawn in step-4 at point R.
Step-6 : Join HR and RA.
Hence HEAR is the required parallelogram.

(iv) We know that each of the four angles of a rectangle is equal to 90° and opposite sides are also equal.
OK = YA and KA = OY
Steps of Construction:
Step-1: Draw OK = 7 cm.
Step-2 : Make ∠OKX = 90°.
Step-3 : Cut off KA = 5 cm on \(\overrightarrow{K X}\).
Step-4: With O as centre and radius equal to 5 cm, cut an arc.
Step-5: With A as centre and radius equal to 7 cm cut another arc on the arc drawn in step-4 at point Y.
Step-6 : Join OY and YA.
Hence, OKAY is the required rectangle.

MP Board Class 8th Maths Solutions

MP Board Class 8th Maths Solutions Chapter 4 Practical Geometry Ex 4.2

Question 1.
Construct the following quadrilaterals
(i) Quadrilateral
LIFT
LI = 4 cm
IF = 3 cm
TL = 2.5 cm
LF= 4.5 cm
IT =4 cm

(ii) Quadrilateral
GOLD
OL = 7.5 cm
GL = 6 cm
GD = 6 cm
LD = 5 cm
OD = 10 cm

(iii) Rhombus BEND
BN = 5.6 cm,
DE = 6.5 cm
Solution:
(i) Steps of Construction:
Step-1: Draw LI = 4 cm.
Step-2: With L as centre and radius equal to 2.5 cm, cut an arc.
Step-3: With I as centre and radius equal to 4 cm, cut another arc on the arc drawn in step-2 at point T.
Step-4 : With I as centre and radius equal to 3 cm, cut an arc.
Step-5: With L as centre and radius equal to 4.5 cm, cut another arc on the arc drawn in step-4 at point F.
Step-6 : Join LT, IT, LF, IF and TF.
Hence, LIFT is the required quadrilateral.

(ii) Steps of Construction:
Step-1: Draw OL = 7.5 cm.
Step-2: With L as centre and radius equal to 5 cm cut an arc.
Step-3 : With O as centre and radius equal to 10 cm, cut another arc on the arc drawn in step-2 at point D.
Step-4: With L as centre and radius equal to 6 cm, cut another arc.
Step-5: With D as centre and radius equal to 6 cm cut an arc on arc drawn in step-4 at point G.
Step-6 : Join LD, LG, OG, OD and DG. Hence, GOLD is the required quadrilateral.

(iii) Here, BN = 5.6 cm and DE = 6.5 cm are given. These two sides are diagonals of a rhombus BEND. We know that diagonals of a rhombus bisect each other at right angles.

Steps of Construction:
Step-1: Draw BN = 5.6 cm.
Step-2 : Draw perpendicular bisector XY of BN which intersect BN at O.
Step-3 : Cut off OD = OF = 3.25 cm on \(\overrightarrow{\mathrm{OX}}\) and \(\overrightarrow{\mathrm{OY}}\) respectively.
Step-4 : Join BD, ND, BE and NE.
Hence, BEND is the required rhombus.

MP Board Class 8th Maths Solutions

MP Board Class 8th Maths Solutions Chapter 4 Practical Geometry Ex 4.1

Question 1.
Construct the following quadrilaterals.
(i) Quadrilateral
ABCD
AB = 4.5 cm
BC= 5.5 cm
MP= 5 cm
AD = 6cm
AC = 7 cm

(ii) Quadrilateral
JUMP
JU = 3.5 cm
UM = 4 cm
MP = 5 cm
PJ = 4.5 cm
PU = 6.5 cm

(iii) Parallelogram
MORE
OR = 6 cm
RE = 4.5 cm
EO = 7.5 cm

(iv) Rhombus
BEST
BE = 4.5 cm
ET = 6 cm
Solution:
(i) Steps of Construction :
Step-1: Draw AB = 4.5 cm.
Step-2: With B as centre and radius equal to 5.5 cm, cut an arc.
Step-3 : With A as centre and radius equal to 7 cm, cut another arc on the arc drawn in step-2 at point C.
Step-4 : With C as centre and radius equal to 4 cm, cut off an arc. Also, with A as centre and. radius equal to 6 cm cut off another arc on the arc just drawn at point D.
Step-5 : Join BC, AC, CD and AD.
Hence, ABCD is the required quadrilateral.

(ii) Steps of Construction :
Step-1: Draw JU = 3.5 cm.
Step-2: With J as centre and radius equal to 4.5 cm, cut an arc.
Step-3 : With U as centre and radius equal to 6.5 cm, cut another arc on the arc drawn in step-2 at point P.
Step-4: With P as centre and radius equal to 5 cm, cut off an arc.
Step-5: With U as centre and radius equal to 4 cm, cut another arc on the arc drawn in step-4 at point M.
Step-6 : Join JP, UP, UM and PM. Thus, JUMP is the required quadrilateral.

(iii) We know that opposite sides of a parallelogram are equal and parallel to each other.
∴ OR = ME and MO = ER.
Steps of Construction:
Step-1: Draw OR = 6 cm.
Step-2 : With R as centre and radius equal to 4.5 cm, cut an arc.
Step-3 : With O as centre and radius equal to 7.5 cm, cut another arc on the arc drawn in step-2 at point E.
Step-4: With E as centre and radius equal to 6 cm, cut an arc.
Step-5 : With O as centre and radius equal to 4.5 cm, cut an arc on the arc drawn in step-4 at point M.
Step-6 : Join RE, OE, OM and ME.
Hence, MORE is the required parallelogram.

(iv) We know that all four sides of a rhombus are equal.
∴ BE = ES = ST = BT = 4.5 cm.
Steps of Construction:
Step-1: Draw BE = 4.5 cm.
Step-2: With B as centre and radius equal to 4.5 cm, draw an arc.
Step-3: With E as centre and radius equal to 6 cm, draw another arc, cutting the previous arc at point T.
Step-4: With E as centre and radius equal to 4.5 cm, cut an arc.
Step-5: With T as centre and radius equal to 4.5 cm, cut another arc on the previous arc at point S.
Step-6 : Join BT, ES, ET and ST.
Hence, BEST is the required rhombus.

MP Board Class 8th Maths Solutions

MP Board Class 8th Maths Solutions Chapter 3 Understanding Quadrilaterals Ex 3.4

Question 1.
State whether True or False.
(a) All rectangles are squares.
(b) All rhombuses are parallelograms.
(c) All squares are rhombuses and also rectangles.
(d) All squares are not parallelograms.
(e) All kites are rhombuses.
(f) All rhombuses are kites.
(g) All parallelograms are trapeziums.
(h) All squares are trapeziums.
Solution:
(a) No, because in a square all sides are equal, but it is not true in case of rectangle.
(b) Yes, because both diagonals bisect each other and opposite sides are equal.
(c) Yes, because in square all sides are equal.
(d) No, all squares are parallelograms. Because all squares satisfies the conditions of a parallelogram.
(e) No, because only two pairs of consecutive sides are equal in kite whereas in rhombus all sides are of equal length.
(f) Yes, all rhombuses are kites.
(g) Yes, because in trapezium, there is only one pair of parallel opposite sides and in parallelograms, two pairs of opposite sides are parallel.
(h) Yes, because in trapezium, there is only one pair of parallel opposite sides and in square, two pairs of opposite sides are parallel.

Question 2.
Identify all the quadrilaterals that have
(a) four sides of equal length
(b) four right angles
Solution:
(a) The quadrilaterals, those have four sides of equal length are square and rhombus.
(b) The quadrilaterals, those have four right angles, are square and rectangle.

Question 3.
Explain how a square is
(i) a quadrilateral
(ii) a parallelogram
(iii) a rhombus
(iv) a rectangle
Solution:
(i) A square is four sided, so it is a quadrilateral.
(ii) Since a square has opposite sides parallel and diagonals bisect each other, so it is a parallelogram.
(iii) Since square is a parallelogram with all 4 sides equal, so it is a rhombus.
(iv) Since square is a parallelogram with each angle a right angle, so it is a rectangle.

Question 4.
Name the quadrilaterals whose diagonals
(i) bisect each other
(ii) are perpendicular bisectors of each other
(iii) are equal
Solution:
(i) The quadrilaterals in which diagonals bisect each other are rhombus, rectangle, square and parallelogram.
(ii) The quadrilaterals in which diagonals are perpendicular bisectors of each other are rhombus and square.
(iii) The quadrilaterals in which diagonals are equal are square and rectangle.

Question 5.
Explain why a rectangle is a convex quadrilateral.
Solution:
When we draw the diagonals joining the end points of a rectangle it lies in its interior. So, it is a convex quadrilateral.

Question 6.
ABC is a right-angled triangle and O is the mid point of the side opposite to the right angle. Explain why O is equidistant from A, B and C. (The dotted lines are drawn additionally to help you).

Solution:
Since ∆ABC is right angled at B. So ∠D = 90°, \(\overline{A D} \| \overline{B C}\) and \(\overline{A B} \| \overline{C D}\)
⇒ ABCD is a rectangle where AB = CD and AD = BC
AC and BD are the diagonals which bisects each other.
Thus AO = OC and BO = OD, also BO = OC which shows that O is equidistant from A, B and C.

MP Board Class 8th Maths Solutions