Category: Class 6

MP Board Class 6th Maths Solutions Chapter 2 पूर्ण संख्याएँ Intext Questions

पाठ्य-पुस्तक पृष्ठ संख्या # 29

प्रयास कीजिए

प्रश्न 1.
19; 1997%; 12000; 49; 100000; 2440701; 100199; और 208090 के पूर्ववर्ती और परवर्ती लिखिए।
हल :
पूर्ववर्ती : 19 – 1 = 18; 1997 – 1 = 1996; 12000 – 1 = 11999; 49 – 1 = 48; 100000 – 1 = 99999; 2440701 – 1 = 2440700; 100199 – 1 = 100198; 208090 – 1 = 208089;
परवर्ती : 19 + 1 = 20; 1997 + 1 = 1998; 12000 + 1 = 12001; 49 + 1 = 50; 100000 + 1 = 100001; 2440701 + 1 = 2440702; 100199 + 1 = 100200; 208090 + 1 = 208091

प्रश्न 2.
क्या कोई ऐसी प्राकृत संख्या है जिसका कोई पूर्ववर्ती नहीं है ?
उत्तर-
हाँ, 1 ऐसी प्राकृत संख्या है जिसका कोई पूर्ववर्ती नहीं है।

प्रश्न 3.
क्या कोई ऐसी प्राकृत संख्या है जिसका कोई परवर्ती नहीं है ? क्या कोई अंतिम प्राकृत संख्या है ?
उत्तर-
नहीं, ऐसी प्राकृत संख्या नहीं है जिसका कोई परवर्ती नहीं।
नहीं, कोई संख्या अंतिम प्राकृत संख्या नहीं है।

पाठ्य-पुस्तक पृष्ठ संख्या # 30

प्रयास कीजिए

प्रश्न 1.
क्या सभी प्राकृत संख्याएँ पूर्ण संख्याएँ भी हैं ?
उत्तर-
हाँ, सभी प्रांकृत संख्याएँ पूर्ण संख्याएँ भी हैं।

प्रश्न 2.
क्या सभी पूर्ण संख्याएँ प्राकृत संख्याएँ भी हैं ?
उत्तर-
नहीं, सभी पूर्ण संख्याएँ प्राकृत संख्याएँ नहीं हैं। क्योंकि शून्य (0) पूर्ण संख्या है लेकिन यह प्राकृत संख्या नहीं है।

प्रश्न 3.
सबसे छोटी पूर्ण संख्या कौन-सी है ?
उत्तर-
सबसे छोटी पूर्ण संख्या शून्य (0) है।

प्रश्न 4.
सबसे बड़ी पूर्ण संख्या कौन-सी है ?
उत्तर-
कोई भी सबसे बड़ी पूर्ण संख्या नहीं है।

पाठ्य-पुस्तक पृष्ठ संख्या # 31

प्रश्न 1.
संख्या रेखा का प्रयोग करके, 4 + 5; 2 + 6; 3 + 5; और 1 + 6 को ज्ञात कीजिए।
हल :
(i) 4 + 5

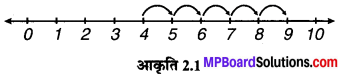
∴ 4 + 5 = 9

(ii) 2 + 6

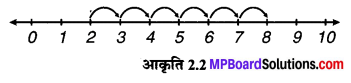
∴ 2 + 6 = 8

(iii) 3 + 5

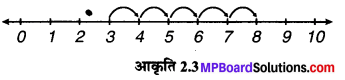
∴ 3 + 5 = 8

(iv) 1 + 6

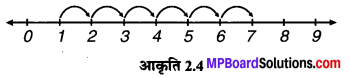
∴ 1 + 6 = 7

पाठ्य-पुस्तक पृष्ठ संख्या # 32

प्रयास कीजिए

प्रश्न 1.
संख्या रेखा का प्रयोग करके, 8 – 3; 6 – 2; और 9 – 6 ज्ञात कीजिए।
हल :
(i) 8 – 3

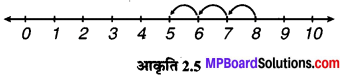
∴ 8 – 3 = 5

(ii) 6 – 2

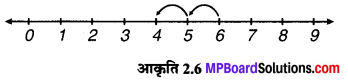
∴ 6 – 2 = 4

(iii) 9 – 6

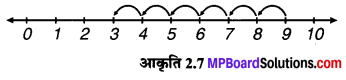
∴ 9 – 6 = 3

प्रयास कीजिए

प्रश्न 1.
संख्या रेखा का प्रयोग करके, 2 x 6; 3 x 3; और 4 x 2 ज्ञात कीजिए।
हल :
(i) 2 x 6

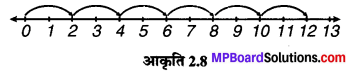
∴ 2 x 6 = 12

(ii) 3 x 3

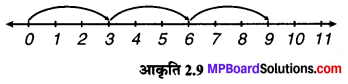
∴ 3 x 3 = 9

(iii)4 x 2

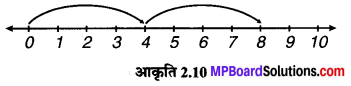
∴ 4 x 2 = 8

MP Board Class 6th Maths Solutions

MP Board Class 6th Maths Solutions Chapter 5 Understanding Elementary Shapes Ex 5.1

Question 1.
What is the disadvantage in comparing line segments by mere observation?
Solution:
There may be chance of error due to improper viewing.

Question 2.
Why is it better to use a divider than a ruler, while measuring the length of a line segment?
Solution:
It is better to use a divider than a ruler, because the thickness of the ruler may cause difficulties in reading of the length of a line segment. However, a divider gives accurate measurement.

Question 3.
Draw any line segment, say \(\overline{A B}\). Take any point C lying in between A and B. Measure the lengths of AB, BC and AC. Is AB = AC + CB? [Note : If A, B, C are any three points on a line such that AC + CB = AB, then we can be sure that C lies between A and B.]
Solution:

AB = 4 cm,
AC = 2 cm,
CB = 2 cm
Hence, AC + CB = 2 cm + 2 cm = 4 cm = AB
Yes, AB = AC + CB.

Question 4.
If A, B, C are three points on a line such that AB = 5 cm, BC = 3 cm and AC =8 cm, which one of them lies between the other two?
Solution:
Since, \(\overline { AC }\) is the longest line segment. Thus B is the point lying between A and C.

Question 5.
Verify, whether D is the mid point of AG.

Solution:
AD = 3 units,
DG = 3 units,
AD = DG
Thus, D is the mid-point of AG.

Question 6.
If B is the mid point of \(\overline { AC }\) and C is the mid point of \(\overline { BD }\), where A, B, C, D lie on a straight line, say why AB = CD?
Solution:
B is the mid point of \(\overline { AC }\).
∴ AB = BC … (i)
And C is the mid point of BD.
∴ BC = CD … (ii)
From (i) and (ii), we get
AB = CD

Question 7.
Draw five triangles and measure their sides. Check in each case, if the sum of the lengths of any two sides is always less than the third side.
Solution:
Sum of the lengths of any two sides of a triangle can never be less than length of the third side.

MP Board Class 6th Maths Solutions

MP Board Class 6th Maths Solutions Chapter 1 अपनी संख्याओं की जानकारी Ex 1.3

प्रश्न 1.
व्यापक नियम का प्रयोग करते हुए, निम्नलिखित में से प्रत्येक का आकलन कीजिए :
(a) 730 + 998
(b) 796 – 314
(c) 12,904 + 2,888
(d) 28,292 – 21,496
जोड़ने, घटाने और उनके परिणामों के आकलन के दस और उदाहरण बनाइए।
हल :
(a) 730 + 998
∵730 → 700 (सौ के सन्निकटित)
998 → 1000 (सौ के सन्निकटित)
∴आकलित योग = 700 + 1000 = 1700

(b) 796 – 314
∵796 → 800 (सौ के सन्निकटित)
314 → 300 (सौ के सन्निकटित)
∴आकलित अन्तर = 800 – 300 = 500

(c) ∵12,904 + 2,888
12,904 → 13,000 (सौ के सन्निकटित)
2,888 → 3,000 (सौ के सन्निकटित)
∴आकलित योग = 13000 + 3000 = 16000

(d) 28,292 – 21,496
∵28292 → 28000 (सौ के सन्निकटित)
21496 → 21000 (सौ के सन्निकटित)
∴आकलित अन्तर = 28000 – 21000 = 7000

10 अन्य उदाहरण
(i) 838 + 895
(ii) 890 – 210
(iii) 740 + 781
(iv) 980 – 688
(v) 13904 + 2868
(vi) 38394 – 31496
(vii) 14909 + 2675
(viii) 28283 – 21529
(ix) 25688 + 4213
(x) 28457 – 23624.
हल :
(i) ∵ 838 → 800; 895 → 900
∴आकलित योग = 800 + 900 = 1700

(ii) ∵ 890 → 900; 210 → 200
∴आकलित अन्तर = 900 – 200 = 700

(iii) ∵ 740 → 700; 781 → 800
∴आकलित योग = 700 + 800 = 1500

(iv) ∵ 980 → 1000; 688 → 700
∴आकलित अन्तर = 1000 – 700 = 300

(v) ∵ 13904 → 14000; 2868 → 3000
∴आकलित योग = 14000 + 3000 = 17000

(vi) ∵ 38394 → 40000; 31496 → 30000
∴आकलित अन्तर = 40000 – 30000 = 10000

(vii) ∵ 14909 → 15000; 2675 → 3000
∴आकलित योग = 15000 + 3000 = 18000

(viii) ∵ 28283 → 30000; 21529 → 20000
∴आकलित अन्तर = 30000 – 20000 = 10000

(ix) ∵ 25688 → 26000; 4213 → 4000
∴आकलित योग = 26000 + 4000 = 30000

(x) ∵ 28457 → 30000; 23624 → 20000
∴आकलित अंतर = 30000 – 20000 = 10000

प्रश्न 2.
एक मोटे तौर पर (Rough) आकलन (सौ तक सन्निकटन) और एक निकटतम आकलन (दस तक सन्निकटन) दीजिए:
(a) 439 + 334 + 4,317
(b) 1,08,734 – 74,599
(c) 8,325 – 491
(d) 4,89,348 – 48,365
ऐसे चार और उदाहरण बनाइए।
हल :
(a) 439 + 334 + 4,317
∵ 439 → 400
334 → 300
(प्रत्येक को सौ के सन्निकटन करने पर)
4317 → 74300
(प्रत्येक को सौ के सन्निकटन करने पर)
∵ रफ आकलन = 400 + 300 + 4300
= 5000
439 → 440
334 → 330
(प्रत्येक को दहाई के सन्निकटन करने पर)
∴4317 → 4320
निकटतम आकलन = 440 + 330 + 4320
= 5090

(b) 1,08,734 – 47,599
108734 → 108700
47599 → 47600 (सौ के सन्निकटन करने पर)
∴रफ आकलन = 108700 – 47600
= 61,100
पुनः 1,08,734 → 1,08,730
47,599 → 47,600
(दहाई के सन्निकटन करने पर)
∴निकटतम आकलन = 108730 – 47600
= 61,130

(c) 8325 – 491
8325 → 8300
491 → 500
(सौ के सन्निकटन करने पर)
∴रफ आकलन = 8300 – 500 = 7800
8325 → 8330
491 → 490
(दहाई के सन्निकटन करने पर)
∴निकटतम आकलन = 8330 – 490
= 7840

(d) 4,89,348 → 48,365
4,89,348 → 4,89,300
48,365 → 48,400
(सौ के सन्निकटन करने पर)
∴रफ आकलन = 489300 – 48400
= 4,40,900
पुनः
489348 → 489350
48365 → 48370
(दहाई के सन्निकटन करने पर)
∴निकटतम आकलन = 489350 – 48370
= 4,40,980

चार और उदाहरण
(i) 593 + 434 + 5317
(ii) 1,09,834 – 48,596
(iii) 7,625 – 591
(iv) 4,79,548 – 47,465
हल :
(i) 593 + 434 + 5317
593 → 600
434 →400
5317 → 5300 (सौ के सन्निकटन करने पर)
∴रफ आकलन = 600 + 400 + 5300 = 6300
पुनः 593 → 590
434 → 430
5317 → 5320
(दहाई के सन्निकटन करने पर)
∴निकटतम आकलन = 590 + 430 + 5320
= 6340

(ii) 1,09,834 – 48,596
1,09,834 → 1,09,800
(सौ के सन्निकटन करने पर)
48,596 → 48,600
∴रफ आकलन = 109800 – 48600
= 61,200
पुनः 109834 → 109830
48596 → 48600
(दहाई के सन्निकटन करने पर)
∴निकटतम आकलन = 109830 – 48600
= 61,230

(iii) 7,625 → 591
7,625 → 7,600
591 → 600 (सौ के सन्निकटन करने पर)
∴रफ आकलन = 7600 – 600
= 7,000
पुनः 7,625 → 7,630
591 → 600 (दहाई के सन्निकटन करने पर)
∴निकटतम आकलन = 7630 – 600
= 7,030

(iv) 4,79,548 – 47,465
4,79,548 → 4,79,500
47,465 → 47,500 (सौ के सन्निकटन करने पर)
∴रफ आकलन = 479500 – 47500
= 4,32,000
पुनः 4,79,548 → 4,79,550
47,465 → 47,470
(दहाई के सन्निकटन करने पर)
निकटतम आकलन = 4,79,550 – 47,470
= 4,32,080

प्रश्न 3.
व्यापक नियम का प्रयोग करते हुए, निम्नलिखित गुणनफलों का आकलन कीजिए :
(a) 578 x 161
(b) 5281 x 3419
(c) 1291 x 592
(d) 9250 x 29
ऐसे चार और उदाहरण बनाइए।
हल :
(a) 578 x 161
578 → 600
161 → 200 (सौ के सन्निकटन)
∴गुणनफल का आकलन = 600 x 200
= 1,20,000

(b) 5281 x 3491
5281 → 5000 (हजार के सन्निकटन)
3491 → 3500 (सौ के सन्निकटन)
∴गुणनफल का आकलन = 5000 x 3500
= 1,75,00,000

(c) 1291 x 592
1291 → 1300
592 + 600 (सौ के सन्निकटन)
∴गुणनफल का आकलन = 1300 x 600
= 7,80,000

(d) 9250 x 29
9250 → 9300 (सौ के सन्निकटन)
29 → 30 (दहाई के सन्निकटन)
∴गुणनफल का आकलन = 9300 x 30
= 2,79,000

चार और उदाहरण
(a) 680 x 271
(b) 2368 x 4483
(c) 7360 x 38
(d) 1487 x 697
हल :
(a) 680 x 271
∵680 → 700
271 → 300
∴गुणनफल का आकलन = 700 x 300
= 2,10,000

(b) 2368 x 4483
∵2368 → 2400
4483 → 4500
∴गुणनफल का आकलन = 2400 x 4500
= 1,08,00,000

(c) 7360 x 38
∵7360 → 7400
38 → 40
∴गुणनफल का आकलन = 7400 x 40
= 2,96,000

(d) 1487 x 697
∵1487 → 1500
697 → 700
∴गुणनफल का आकलन = 1500 x 700
= 10,50,000

पाठ्य-पुस्तक पृष्ठ संख्या # 25

प्रयास कीजिए

प्रश्न 1.
कोष्ठकों का प्रयोग करते हुए निम्नलिखित में मे प्रत्येक के लिए व्यंजक लिखिए :
(a) नौ और दो के योग का चार से गुणा।
(b) अठारह और छः के अन्तर को चार से भाग।
(c) पैंतालीस को तीन और दो के योग के तिगुने से भाग देना।
हल :
(a) 4 x (9 + 2)
(b) (18 – 6) ÷ 4
(c) 45 ÷ [3(3 + 2)]

प्रश्न 2.
(5 + 8) x 6 के लिए तीन विभिन्न स्थितियाँ लिखिए।
(ऐसी एक स्थिति है : सोहनी और रीता ने 6 दिन कार्य किया। सोहनी 5 घण्टे प्रतिदिन कार्य करती है और रीता 8 घण्टे प्रतिदिन कार्य करती है। दोनों ने एक सप्ताह में कुल कितने घण्टे कार्य किया ?
हल :
स्थिति 1-राहुल एक उपन्यास के 5 पृष्ठ प्रतिदिन सुबह और 8 पृष्ठ प्रतिदिन शाम को पढ़ता है। वह 6 दिन में कितने पृष्ठ पढ़ लेगा ?
स्थिति 2-राहुल प्रतिदिन 5 रुपये के अण्डे और 8 रुपये का दूध खरीदता है। वह 6 दिनों में कितने रुपए खर्च करेगा ?
स्थिति 3-मीनाक्षी और अनुपमा 6 दिन कार्य करती हैं। मीनाक्षी प्रतिदिन 5 रुपये और अनुपमा प्रतिदिन 8 रुपये कमाती हैं। दोनों मिलकर 6 दिन में कितना कमाएँगी?

प्रश्न 3.
निम्नलिखित के लिए पाँच स्थितियाँ लिखिए, जहाँ कोष्ठकों का प्रयोग आवश्यक हो :
(a) 7 (8 – 3)
(b) (7 + 2) (10 – 3)
हल :
(a) 7(8 – 3) स्थिति 1 – राम को प्रतिदिन जेब खर्च के लिए 8 रुपये मिलते हैं। उनमें से वह 3 रुपये बचाता है। 7 दिन में वह कितने रुपये खर्च करेगा?
स्थिति 2 – 8 और 3 के अन्तर को 7 से गुणा करने पर क्या प्राप्त होगा?
स्थिति 3 दूध से भरी 7 टंकियाँ हैं। प्रत्येक टंकी में 8 लीटर दूध भरा हुआ है। यदि प्रत्येक टंकी में से 3 लीटर दूध निकाल लें तो टंकियों में कितना दूध रह जाएगा?
स्थिति 4 – सात बालक बाजार गए। प्रत्येक बालक के पास 8 रुपये थे। उनमें से प्रत्येक ने 3 रुपये की गेंद खरीद ली। अब उनके पास कुल कितने रुपये शेष रहे?
स्थिति 5 – माना कि एक ड्राइवर 8 घण्टे कार्य करता है। लेकिन किसी कारणवश उसे प्रतिदिन 3 घण्टे के लिए घर जाना पड़ता है। 7 दिन में उसने कुल कितने घण्टे कार्य किया?

(b) (7 + 2) (10 – 3) स्थिति 1 – 7 और 2 योग को 10 और 3 के अन्तर से गुणा करने पर गुणनफल क्या होगा ?
स्थिति 2 – 7 सेल्स गर्ल्स और 2 मैनेजर की एक टीम एक गारमेण्ट्स की दुकान पर 10 घण्टे प्रतिदिन कार्य करती है।
रविवार को दुकान 3 घण्टे पहले बन्द हो गई। उस टीम ने कुल कितने घण्टे दुकान पर कार्य किया?
स्थिति 3 – 7 व्यक्तियों ने रेलवे स्टेशन जाने के लिए 10 रुपये प्रति व्यक्ति के हिसाब से एक वैन किराये पर ली। वैन चालक ने उसमें 2 सवारी और बैठा ली और उसने 3 रुपए प्रति सवारी किराया कम कर दिया। वैन चालक ने किराये से कुल कितनी धनराशि प्राप्त की?
स्थिति 4 – एक माली को एक महीने में 7 दिन कार्य करने के लिए रखा। प्रतिदिन उसे 10 घण्टे कार्य करना था। लेकिन उसने प्रतिदिन 3 घण्टे कम कार्य किया। लेकिन उसने दो दिन अधिक कार्य किया। उसने कुल कितने घण्टे कार्य किया?
स्थिति 5 – एक रेस्टोरेंट चालक 7 व्यक्ति और 2 बच्चों के लिए एक सोसाइटी के 10 घरों में लंच टिफिन भेजता है। रविवार को 3 घरों को उसने लंच टिफिन नहीं भेजा। रविवार को कितनों घरों में टिफिन भेजा गया?

पाठ्य-पुस्तक पृष्ठ संख्या # 27

प्रयास कीजिए

प्रश्न 1.
रोमन पद्धति में लिखिए :
1.73
2.92
हल :
1. 73 = 50 + 20 + 3
= LXXIII
2. 92 = 90 + 2 = (100 – 10) + 2
= XCII

MP Board Class 6th Maths Solutions

MP Board Class 6th Maths Solutions Chapter 4 Basic Geometrical Ideas Ex 4.6

Question 1.
From the figure, identify:

(a) the centre of circle
(b) three radii
(c) a diameter
(d) a chord
(e) two points in the interior
(f) a point in the exterior
(g) a sector
(h) a segment
Solution:
(a) O is the centre of circle.
(b) Three radii: \(\overline{O A}\), \(\overline{O B}\) and \(\overline{O C}\)
(c) A diameter : \(\overline{A C}\)
(d) A chord : \(\overline{E D}\)
(e) Two interior points : O and P
(f) Exterior point: Q
(g) A sector : OAB (shaded part)
(h) A segment: ED (shaded part)

Question 2.
(a) Is every diameter of a circle also a chord?
(b) Is every chord of a circle also a diameter?
Solution:
(a) Yes, every diameter of a circle is also a chord. It is the largest chord of a circle.
(b) No, every chord of a circle is not a diameter.

Question 3.
Draw any circle and mark
(a) its centre
(b) a radius
(c) a diameter
(d) a sector
(e) a segment
(f) a point in its interior
(g) a point in its exterior
Solution:

(a) O is the centre of the circle.
(b) \(\overline{O A}\) is the radius
(c) \(\overline{A B}\) is the diameter.
(d) OAC is the sector, (shaded part)
(e) EF is the segment, (shaded part)
(f) Q is a point in its interior.
(g) R is a point in its exterior.
(h) \(\widehat{A C}\) is an arc.

Question 4.
Say true or false:
(a) Two diameters of a circle will necessarily intersect.
(b) The centre of a circle is always in its interior.
Solution:
(a) True
(b) True

MP Board Class 6th Maths Solutions

MP Board Class 6th Maths Solutions Chapter 4 Basic Geometrical Ideas Ex 4.5

Question 1.
Draw a rough sketch of a quadrilateral PQRS. Draw its diagonals. Name them. Is the meeting point of the diagonals in the interior or exterior of the quadrilateral?
Solution:

Diagonal PR and diagonal SQ meet at point O, which is in the interior of the quadrilateral PQRS.

Question 2.
Draw a rough sketch of a quadrilateral KLMN. State,
(a) two pairs of opposite sides,
(b) two pairs of opposite angles,
Solution:

(a) Two pairs of opposite sides :
\(\overline{K L}\) and \(\overline{N M}\), \(\overline{K N}\) and \(\overline{L M}\)

(b) Two pairs of opposite angles :
∠K and ∠M, ∠L and ∠N

(c) Two pairs of adjacent sides :
\(\overline{K N}\) and \(\overline{N M}\) , \(\overline{K L}\) and \(\overline{L M}\)

(d) Two pairs of adjacent angles :
∠K and ∠N, ∠L and ∠M

Question 3.
Investigate :
Use strips and fasteners to make a triangle and a quadrilateral.
Try to push inward at any one vertex of the triangle. Do the same to the quadrilateral.
Is the triangle distorted? Is the quadrilateral distorted? Is the triangle rigid?
Why is it that structures like electric towers make use of triangular shapes and not quadrilaterals?
Solution:
No, the triangle is not distorted but the quadrilateral is distorted and also the triangle is rigid.
Structures like electric towers make use of triangular shape so that they could not be distorted and they could be rigid.

MP Board Class 6th Maths Solutions

MP Board Class 6th Maths Solutions Chapter 1 अपनी संख्याओं की जानकारी Ex 1.2

प्रश्न 1.
किसी स्कूल में चार दिन के लिए एक पुस्तक प्रदर्शनी आयोजित की गई। पहले, दूसरे, तीसरे और अन्तिम दिन खिड़की पर क्रमशः 1094, 1812, 2050 और 2751 टिकट बेचे गए। इन चार दिनों में बेचे गए टिकटों की कुल संख्या ज्ञात कीजिए।
हल :
चार दिनों में बेचे गए टिकटों की संख्या
= 1094 + 1812 + 2050 + 2751
= 7707

प्रश्न 2.
शेखर एक प्रसिद्ध क्रिकेट खिलाड़ी है। वह टैस्ट मैचों में अब तक 6980 रन बना चुका है। वह 10,000 रन पूरे करना चाहता है। उसे कितने और रनों की आवश्यकता है ?
हल :
∵ शेखर द्वारा बनाए गए रन = 6,980
उसे रन पूरे करने हैं = 10,000
∴ और आवश्यक रनों की संख्या = 10,000 – 6,980
= 3020

प्रश्न 3.
एक चुनाव में सफल प्रत्याशी ने 5,77,500 मत प्राप्त किए, जबकि उसके निकटतम प्रतिद्वन्द्वी ने 3,48,700 मत प्राप्त किए। सफल प्रत्याशी ने चुनाव कितने मतों से जीता?
हल :
∵सफल प्रत्याशी द्वारा प्राप्त मतों की
संख्या = 5,77,500
प्रतिद्वन्द्वी द्वारा प्राप्त मतों की संख्या = 3,48,700
सफल प्रत्याशी की जीत हुई = 577500 – 348700
= 2,28,800 मतों से

प्रश्न 4.
कीर्ति बुक-स्टोर ने जून के प्रथम सप्ताह में Rs 2,85,891 मूल्य की पुस्तकें बेचीं। इसी माह के दूसरे सप्ताह में Rs 4,00,768 मूल्य की पुस्तकें बेची गईं ? किस सप्ताह में बिक्री अधिक हुई और कितनी अधिक ?
हल :
प्रथम सप्ताह में पुस्तकों की बिक्री = Rs 2,85,891
दूसरे सप्ताह में पुस्तकों की बिक्री = Rs 4,00,768
दोनों सप्ताहों में पुस्तकों की कुल बिक्री
= 2,85,891 + 4,00,768
= Rs 6,86,659
स्पष्ट है कि दूसरे सप्ताह में पुस्तकों की अधिक बिक्री हुई
= 4,00,768 – 2,85,891
= Rs 1,14,877

प्रश्न 5.
अंकों 6, 2, 7, 4 और 3 में से प्रत्येक का केवल एक बार प्रयोग करते हुए बनाई जा सकने वाली सबसे बड़ी और सबसे छोटी संख्याओं का अन्तर ज्ञात कीजिए।
हल :
दिए हुए अंक हैं- 6, 2, 7, 4 और 3
इन अंकों से बनी सबसे बड़ी संख्या = 76,432
इन अंकों से बनी सबसे छोटी संख्या = 23,467
इन संख्याओं का अन्तर = 76,432 – 23,467
= 52,965

प्रश्न 6.
एक मशीन औसतन एक दिन में 2,825 पेंच बनाती है। जनवरी 2006 में उस मशीन ने कितने पेंच बनाए ?
हल :
जनवरी 2006 में दिनों की संख्या = 31
∵1 दिन में बने पेंचों की संख्या = 2,825
∴31 दिनों में बने पेंचों की संख्या = 31 x 2825
= 87,575
∴जनवरी 2006 में दिनों की संख्या = 87,575

प्रश्न 7.
एक व्यापारी के पास Rs 78,592 थे। उसने 40 रेडियो खरीदने का ऑर्डर दिया तथा प्रत्येक रेडियो का मूल्य Rs 1200 था। इस खरीदारी के बाद उसके पास कितनी धनराशि शेष रह जाएगी ?
हल :
खरीदे गए रेडियो की संख्या = 40
1 रेडियो का मूल्य = Rs 1200
∴40 रेडियो का मूल्य = 40 x 1200
= Rs 48,000
∵व्यापारी के पास कुल रुपए = Rs 78,592
∴रेडियो खरीदने के बाद व्यापारी के पास शेष धनराशि
= 78,592 – 48,000
= Rs 30,592

प्रश्न 8.
एक विद्यार्थी ने 7236 को 56 के स्थान पर 65 से गुण कर दिया। उसका उत्तर सही उत्तर से कितना अधिक था ? (संकेतः दोनों गुणा करना आवश्यक नहीं।)
हल :
अभीष्ट गुणनफल = 7236 x 56
विद्यार्थी द्वारा किया गुणनफल = 7236 x 65
दोनों गुणनफलों का अंतर = 7236 x 65 – 7236 x 56
= 7236 x (65 – 56)
= 7236 x 9
= 65124
अतः उसका उत्तर सही उत्तर से 65124 अधिक है।

प्रश्न 9.
एक कमीज सीने के लिए 2 मी 15 सेमी कपड़े की आवश्यकता है। 40 मीटर कपड़े में से कितनी कमीजें सी जा सकती हैं और कितना कपड़ा शेष बच जाएगा?
हल :
1 कमीज में लगा कपड़ा = 2 मी 15 सेमी.
= 200 सेमी + 15 सेमी
= 215 सेमी
कुल कपड़ा = 40 मीटर = 40 x 100 सेमी
= 4000 सेमी
कुल कपड़े में से सिली गई कमीजों की संख्या = \(\frac { 4000 }{ 215 }\)

अतः 40 मी कपड़े में से 18 कमीजें सिल सकती हैं और 130 सेमी (1 मी 30 सेमी) कपड़ा बच जाएगा।

प्रश्न 10.
दवाइयों को बक्सों में भरा गया है और ऐसे प्रत्येक बक्स का भार 4 किग्रा 500 ग्रा है। एक वैन (van) में जो 800 किग्रा से अधिक का भार नहीं ले जा सकती ऐसे कितने बक्से लादे जा सकते हैं ?
हल :
1 बक्से का भार = 4 किलो 500 ग्रा
= 4500 ग्रा
अधिकतम भार जो वैन में रखा जा सकता है = 800 किग्रा
= 800 x 1000 ग्राम = 800000 ग्राम

अतः वैन में 177 बक्से रखे जा सकते हैं।

प्रश्न 11.
एक स्कूल और किसी विद्यार्थी के घर के बीच की दूरी 1 किमी 875 मी है। प्रत्येक दिन यह दूरी दो बार तय की जाती है। 6 दिन में उस विद्यार्थी द्वारा तय की गई कुल दूरी ज्ञात कीजिए। हल :
स्कूल और घर के बीच की दूरी
= 1 किमी 875 मी
= 1000 मी + 875 मी
= 1875 मी
∵विद्यार्थी द्वारा एक दिन में तय की गई दूरी
= 2 x 1875 मी
= 3750 मी
अतः 6 दिन में विद्यार्थी द्वारा तय की गई दूरी
= 6 x 3750 मी
= 22500 मी
= 22 किमी 500 मी

प्रश्न 12.
एक बर्तन में 4 ली 500 मिली दही है। 25 मिली धारिता वाले कितने गिलासों में इसे भरा जा सकता है?
हल :
∵4 ली 500 मिली
= 4 x 1000 मिली + 500 मिली
= 4000 मिली + 500 मिली
= 4500 मिली
गिलास की धारिता = 25 मिली
∵भरे गए गिलासों की संख्या = \(\frac { 4500 }{ 25 }\) = 180

अतः 180 गिलास भरे जा सकते हैं।

पाठ्य-पुस्तक पृष्ठ संख्या # 19

प्रश्न 1.
(a) ज्ञात कीजिए कि कौन-से झण्डे 270 की तुलना में 260 के अधिक समीप हैं ?
(b) ज्ञात कीजिए कि कौन-से झण्डे 260 की तुलना में 270 के अधिक समीप हैं ?
हल :
(a) 261 और 263 झण्डे 260 के अधिक समीप हैं
(b) 267 और 269 झण्डे 270 के अधिक समीप हैं।

पाठ्य-पुस्तक पृष्ठ संख्या # 20

प्रयास कीजिए

प्रश्न a.
इन संख्याओं को निकटतम दहाई तक सन्निकटित कीजिए :
28 32 52 41 39 48
64 59 99 215 1453 2936
हल :

प्रश्न 1.
जाँच कीजिए कि निम्नलिखित सन्निकटन (सैकड़े तक) सही हैं या नहीं :
(i) 841 → 800
(ii) 9537 → 9500
(iii) 49730 → 49700
(iv) 2546 → 2500
(v) 286 → 300
(vi) 5750 → 5800
(vii) 168 → 200
(viii) 149 → 100
(ix) 9870 → 9800
उन्हें सही कीजिए जो गलत हैं।
उत्तर-
(i) सही,
(ii) सही,
(iii) सही,
(iv) सही,
(v) सही,
(vi) सही,
(vii) सही,
(viii) सही,
(ix) गलत है, सन्निकटन 9900 है।

प्रश्न 2.
निम्नलिखित सन्निकटनों की जाँच कीजिए और उन्हें सही कीजिए जो गलत हैं :
(i) 2573 → 3000
(ii) 53552 → 53000
(iii) 6404 → 6000
(iv) 65437 → 65000
(v) 7805 → 7000
(vi) 3499 → 4000
उत्तर-
(i) सही,
(ii) गलत, सही 53552 → 54000,
(iv) सही.
(v) गलत, सही 7805 → 7800;
(vi) गलत, सही 3499 → 30001

पाठ्य-पुस्तक पृष्ठ संख्या # 21

प्रयास कीजिए

प्रश्न 1.
दी हुई संख्या को निकटतम दहाई, सौ, हजार और दस हजार तक सन्निकटित कीजिए :
हल :

पाठ्य-पुस्तक पृष्ठ संख्या # 23

प्रयास कीजिए

प्रश्न 1.
निम्न गुणनफलों का आकलन कीजिए :
(a) 87 x 313
(b) 9 x 795
(c) 898 x 785
(d) 958 x 387
ऐसे ही पाँच और प्रश्न बनाइए और उन्हें हल कीजिए।
हल :
(a) 87 x 313
∵ 87 → 90 (दहाई के सन्निकटित)
313 → 300 (सौ के सन्निकटित)
∴ गुणनफल का आकलन = 90 x 300 = 27000

(b) 9 x 795
∵9 → 10 (दहाई के सन्निकटित)
795 → 800 (सौ के सन्निकटित)
∴गुणनफल का आकलन = 10 x 800 = 8000

(c) 898 x 785
∵898 → 900 (सौ के सन्निकटित)
785 → 800 (सौ के सन्निकटित)
∴गुणनफल का आकलन = 900 x 800 = 720000

(d) 958 x 387
∵958 → 1000 (सौ के सन्निकटित)
387 → 400 (सौ के सन्निकटित)
∴गुणनफल का आकलन = 1000 x 400 = 400000

पाँच और प्रश्न
(i) 78 x 412
(ii) 8 x 989
(iii) 789 x 876
(iv) 65 x 193
(v) 868 x 486
हल :
(i) ∵78 → 80 (दस के सन्निकटित)
412 → 400 (सौ के सन्निकटित)
∴गुणनफल का आकलन = 80 x 400 = 32000

(ii) ∵8 → 10 (दहाई के सन्निकटित)
989 → 1000 (सौ के सन्निकटित)
∴गुणनफल का आकलन = 10 x 1000 = 10000

(iii) ∵789 → 800 (सौ के सन्निकटित)
876 → 900 (सौ के सन्निकटित)
∴गुणनफल का आकलन = 800 x 900 = 720000

(iv) ∵65 → 70 (दहाई के सन्निकटित)
193 → 200 (सौ के सन्निकटित)
∴गुणनफल का आकलन = 70 x 200 = 14000

(v) ∵868 → 900 (सौ के सन्निकटित)
486 → 500 (सौ के सन्निकटित)
∴गुणनफल का आकलन = 900 x 500 = 450000

MP Board Class 6th Maths Solutions

MP Board Class 6th Social Science Solutions Chapter 6 Globe and Map

MP Board Class 6th Social Science Chapter 6 Globe and Map Text Book Exercise

MP Board Class 6th Social Science Chapter 6 Globe and Map Short Answer Type Questions 

Question 1.
Question (a)
What is a globe?
Answer:
Globe is a three dimensional model of earth or sphere, which gives us the correct idea of the shape of the earth.

Question (b)
What information can we get from a globe? Write any five?
Answer:
The following information we can get from a globe:

1. The earth is a bit flat at the poles.
2. The shape of earth is spheroid.
3. The earth is not straight on its axis but a little tilted.
4. The globe shows the location of oceans, islands, continents, main mountains and countries, etc.
5. The characteristics of the horizontal and vertical lines drawn on the globe.

Question (c)
What is a scale?
Answer:
1. The scale of the map is a measuring line with the help of which correct distance between various points on a map can be measured. The scale of map is, a ratio between any two points on the maps and actual distance on the land.

2. It can be a millimetre, a centimetre or an inch to represent a kilometre, a hundred kilometre or a thousand kilometre or even still larger distances. On some maps the scale is not given as a line but is mentioned in words. For instance, it may be given as 1 centimetre = 100 kilometre

3. It means that one centimetre on the map is equal to one hundred kilometre on the ground.

MP Board Class 6th Social Science Chapter 6 Globe and Map Long Answer Type Questions

Question 2.
Question (a)
What should we know to read a map? Explain any two.
Answer:
A map can be read and understand as a book is read and information is gathered from it. A map can be made and read on four basic points. These are:

1. Symbol
2. Direction
3. Headings
4. Scale

1. Symbol:
It is the third important component of any map. When an area or locality is shown on a map, it is not possible to show various features, e.g., roads, building, trees, railway lines in their actual shape and size. To overcome this difficulty, the features are shown by different symbols. The use of symbols saves space and a lot of information can be given in a single map.

Various colours in maps are chosen for the same purpose. All over the world there has been some kind of agreement regarding the use of symbols and colours. The symbols used all over the world in various maps are called conventional symbols.

2.  Direction:
It is another very important component of any map. A map has four directions i.e., north, south, east and west. While knowing any one direction on map we fan find all the remaining directions.

3.  Headings:
Heading is the one of the component of read a map. “Structure” to their code that identifies main headings and subheadings. Headings Map creates a visual heading structure of the webpage by generating an index or ‘map’ of the headings created by the author.

4.  Scale:
The scale of the map is a measuring line with the help of which correct distance between various points on a map can be measured. The scale of map is, a ratio between any two points on the maps and actual distance on the land.

5. It can be a millimetre, a centimetre or an inch to represent a kilometre, a hundred kilometre or a thousand kilometre or even still larger distances. On some maps the scale is not given as a line but is mentioned in words. For instance, it may be given as 1 centimetre = 100 kilometre

6. It means that one centimetre on the map is equal to one hundred kilometre on the ground.

Question (b)
Why are maps made?
Answer:
Maps are made to study any part of earth, about our country, our” state, the district in which we live or the town or the village etc.
The importance of a Globe in Geography:

1. To understand the phenomena related to the shape, inclination and movement of the planet and earth.
2. To understand the distribution of land and water on the earth.
3. To understand the extent of oceans and continents and their position on earth.
4. The globe can be rotated as the earth rotates on its axis.

The Importance of a Map in Geography:

1. Map helps us to find the exact location of the countries, states of the world.
2. Maps shows the roads and boundries of any state; district, town, city and village.
3. Maps showing physical features of the earth such as land forms of different elevations.

Question 3.
Fill in the blanks choosing the correct option given:
(seven, four, globe, map, blue)

1. The drawing of any part of the earth on a plane surface is called …………….
2. The model of the earth is called …………….
3. There are ……………… continents and oceans on earth.
4. The colour ………………… is seen most on the globe.

Answer:

1. map
2. globe
3. seven, four
4. blue

Question 4.
Match the column.

Answer:

Question 5.
Choose the correct names of the symbols given in the bracket and write in the blanks given in front of the symbol:
(district border, state border, railway line, metal road, well)

Answer:

1. State border
2. Railway line
3. District border
4. Well

Question 6.
The scale in a map is 1 cm = 20 km. What will be the actual distance shown in the map by 4 cm?
Answer:

• Here, 1 cm = 20 km
• ∴ The actual distance of 4 cm = 4 x 20 km = 80 km
  Thus, the actual distance shown in the map by 4 cm is 80 km.

Question 7.
Draw the picture of a globe below and show, equator, tropic of cancer and tropic of capricorn.
Answer:

Project Work

Question 1.
Make a list of continents, ocean, seas and islands using a globe or the map of the world. With the help of a globe write down the names of the main latitudes between the north and the south pole.
Answer:
List of Continents:

1. North America
2. South America
3. Asia
4. Europe
5. Africa
6. Australia
7. Antarctica

List of Oceans:

1. Pacific Ocean
2. Atlantic Ocean
3. Indian Ocean
4. Arctic Ocean

List of Seas:
1. Arabian sea

List of Islands:
1. Andaman and Nicobar Islands.

MP Board Class 6th Social Science Solutions

MP Board Class 6th Maths Solutions Chapter 4 Basic Geometrical Ideas Ex 4.4

Question 1.
Draw a rough sketch of a triangle ABC. Mark a point P in its interior and a point Q in its exterior. Is the point A in its exterior or in its interior?
Solution:
We have,

A is neither in the interior nor in the exterior of the triangle ABC. It is a vertex.

Question 2.
(a) Identify three triangles in the figure.
(b) Write the names of seven angles.
(c) Write the names of six line segments.
(d) Which two triangles have ∠B as common?

Solution:
(a) The three triangles are ∆ABC, ∆ABD, ∆ADC
(b) 7 angles are ∠ADB, ∠ADC, ∠ABD, ∠ACD, ∠BAD, ∠CAD, ∠BAC
(c) 6 line segments are \(\overline{A B}\), \(\overline{A C}\), \(\overline{A D}\), \(\overline{B D}\), \(\overline{D C}\), \(\overline{B C}\)
(d) Two triangles having ∠B as common are ∆ABC, ∆ABD

MP Board Class 6th Maths Solutions

MP Board Class 6th Maths Solutions Chapter 4 Basic Geometrical Ideas Ex 4.3

Question 1.
Name the angles in the given figure.

Solution:
There are four angles in the given figure i.c., ∠ABC, ∠CDA, ∠DAB, ∠DCB

Question 2.
In the given diagram, name the point(s)
(a) In the interior of ∠DOE
(b) In the exterior of ∠EOF
(c) On ∠EOF

Solution:
(a) Point in the interior of ∠DOE : A
(b) Points in the exterior of ∠EOF : C, A, D
(c) Points on ∠EOF : E, O, B, F

Question 3.
Draw rough diagrams of two angles such that they have
(a) One point in common.
(b) Two points in common.
(c) Three points in common.
(d) Four points in common.
(e) One ray in common.
Solution:

Here, two angles are ∠AOD and ∠BOC and point O is common.

(b)

Here, two angles are ∠AOB and ∠CDE and two points F and G are common.

Here, two angles are ∠AOB and ∠CDE and three points F, D and G are common.

Here, two angles are ∠AOB and ∠CDE and four points F, G, H and I are common.

Here, two angles are ∠AOB and ∠AOC and ray OA is common.

MP Board Class 6th Maths Solutions

MP Board Class 6th Maths Solutions Chapter 1 अपनी संख्याओं की जानकारी Ex 1.1

प्रश्न 1.
रिक्त स्थानों को भरिए :
(a) 1 लाख = ……… दस हजार
(b) 1 मिलियन = ……… सौ हजार
(c) 1 करोड़ = ……… दस लाख
(d) 1 करोड़ =………. मिलियन
(e) 1 मिलियन = ……… लाख।
उत्तर-
(a) 10,
(b) 10,
(c) 10,
(d) 10,
(e) 10

प्रश्न 2.
सही स्थानों पर अल्प विराम लगाते हुए, संख्यांकों को लिखिए :
(a) तिहत्तर लाख पचहत्तर हजार तीन सौ सात
(b) नौ करोड़ पाँच लाख इकतालीस
(c) सात करोड़ बावन लाख इक्कीस हजार तीन सौ दो
(d) अट्ठावन मिलियन चार सौ तेईस हजार दो सौ दो
(e) तेईस लाख तीस हजार दस।
उत्तर-
(a) 73,75,307
(b) 9,05,00,041
(c) 7,52,21,302
(d) 58,423,202
(e) 23,30,010

प्रश्न 3.
उपयुक्त स्थानों पर अल्प विराम लगाइए और संख्या नामों को भारतीय संख्यांकन पद्धति में लिखिए :
(a) 87595762
(b) 8546283
(c) 99900046
(d) 98432701.
हल :
(a) 8,75,95,762 – आठ करोड़ पचहत्तर लाख पिच्चानवे हजार सात सौ बासठ
(b) 85,46,283 – पिचासी लाख छियालीस हजार दो सौ तिरासी
(c) 9,99,00,046 – नौ करोड़ निन्यानवे लाख छियालीस
(d) 9,84,32,701 – नौ करोड़ चौरासी लाख बत्तीस हजार सात सौ एक।

प्रश्न 4.
उपयुक्त स्थानों पर अल्प विराम लगाइए और संख्या नामों को अन्तर्राष्ट्रीय संख्यांकन पद्धति में लिखिए :
(a) 78921092
(b) 7452283
(c) 99985102
(d) 48049831.
हल :
(a) 78,921,092 – अठहत्तर मिलियन नौ सौ इक्कीस हजार बानवे
(b) 7,452,283 – सात मिलियन चार सौ बावन हजार दो सौ तिरासी
(c) 99,985,102 – निन्यानवे मिलियन नौ सौ पिचासी हजार एक सौ दो
(d) 48,049,831 – अड़तालीस मिलियन उन्चास हजार आठ सौ इकतीस।

पाठ्य-पुस्तक पृष्ठ संख्या # 13

प्रयास कीजिए

प्रश्न 1.
कितने सेण्टीमीटरों से एक किलोमीटर बनता है?
हल :
∵1 किलोमीटर = 1000 मीटर
और . 1 मीटर = 100 सेण्टीमीटर
∴1 किलोमीटर = 1000 × 100 सेण्टीमीटर
= 100000 सेण्टीमीटर
अतः 1,00,000 सेण्टीमीटर से 1 किलोमीटर बनता है।

प्रश्न 2.
भारत के पाँच बड़े शहरों के नाम लिखिए। उनकी जनसंख्या पता कीजिए। इन शहरों में से प्रत्येक युग्म शहरों के बीच की दूरी भी किलोमीटर में पता कीजिए।
हल :

प्रयास कीजिए

प्रश्न 1.
कितने मिलीग्राम से एक किलोग्राम बनता है ?
हल :
∵1 किलोग्राम = 1000 ग्राम
1 ग्राम = 1000 मिलीग्राम
∴1 किलोग्राम = 1000 x 1000 मिलीग्राम
= 10,00,000 मिलीग्राम
= 10 लाख मिलीग्राम
अत: 10 लाख मिलीग्राम से 1 किलोग्राम बनता है।

प्रश्न 2.
दवाई की गोलियों के एक बक्से में 2,00,000 गोलियाँ हैं, जिनमें प्रत्येक का भार 20 मिग्रा है। इस बक्से में रखी सभी गालियों का कुल भार ग्रामों में कितना है और किलोग्राम में कितना है ? हल :
गोलियों की संख्या = 2,00,000;
1 गोली का भार = 20 मिग्रा
∴2,00,000 गोलियों का भार = 200000 x 20
= 4000000 मिग्रा
= \(\frac{4000000}{1000}\) ग्राम
= 4000 ग्राम
= \(\frac{4000}{1000}\)
= 4 किलोग्राम

पाठ्य-पुस्तक पृष्ठ संख्या # 14-15

प्रयास कीजिए

प्रश्न 1.
एक बस ने अपनी यात्रा प्रारम्भ की और 60 किमी/घण्टा की चाल से विभिन्न स्थानों पर पहुँची। इस यात्रा को नीचे दर्शाया गया है।
(i) A से D तक जाने में बस द्वारा तय की गई कुल दूरी ज्ञात कीजिए।

(ii) D से G तक जाने में बस द्वारा तय की गई कुल दूरी ज्ञात कीजिए।
(iii) बस द्वारा तय की गई कुल दूरी ज्ञात कीजिए।
(iv) क्या आप C से D तक और D से E तक दूरियों का अन्तर ज्ञात कर सकते हैं?
(v) बस द्वारा निम्नलिखित यात्रा में लिया गया समय ज्ञात कीजिए :
(a) A से B तक
(b) C से D तक
(c) E से G तक
(d) कुल यात्रा।
हल :
(i) बस द्वारा A से D तक जाने में तय की गई कुल दूरी
= 4170 किमी + 3410 किमी + 2160 किमी
= 9740 किमी

(ii) D से G तक जाने में बस द्वारा तय की गई कुल दूरी
= 8140 किमी + 4830 किमी + 2550 किमी
= 15520 किमी

(iii) बस द्वारा तय की गई कुल दरी
= 4170 किमी + 3410 किमी + 2160 किमी + 8140 किमी + 4830 किमी + 2550 किमी + 1290 किमी
= 26550 किमी

(iv) C से D तक की दूरी = 2160 किमी;
D से E तक की दूरी = 8140 किमी
∴C से D तथा D से E तक की दूरी का अन्तर
= 8140 किमी – 2160 किमी
= 5980 किमी

(v)

∴ बस द्वारा यात्रा में लिया गया समय
(a) A से B तक = \(\frac { 4170 }{ 60 }\) घण्टे
= \(69\frac { 1 }{ 2 }\) घण्टे

(b) C से D तक = \(\frac { 2160 }{ 60 }\) घण्टे
= 36 घण्टे

(c) E से G तक = \(\frac { 4830+2550 }{ 60 }\)
= \(\frac { 7380 }{ 60 }\) घण्टे
= 123 घण्टे

(d) कुल यात्रा = \(\frac { 26550 }{ 60 }\) घण्टे
= \(442\frac { 1 }{ 2 }\) घण्टे

प्रश्न 2.
रमन की दुकान


(a) क्या आप रमन द्वारा पिछले वर्ष बेचे गए सेब और संतरों का कुल भार ज्ञात कर सकते हैं?
सेबों का भार = ……. किग्रा
संतरों का भार = …… किग्रा
अतः कुल भार = ….. किग्रा + ….. किग्रा = ……किग्रा
उत्तर- संतरों और सेबों का कुल भार = ……
(b) क्या आप रमन द्वारा सेबों को बेचने से प्राप्त कुल धन राशि ज्ञात कर सकते हैं?
(c) क्या आप रमन द्वारा सेबों और सन्तरों को बेचने से प्राप्त कुल धनराशि प्राप्त कर सकते हैं?
(d) रमन द्वारा प्रत्येक वस्तु के बेचने से प्राप्त धनराशियों को दशाने वाली एक सारणी बनाइए। धनराशियों की इन प्रविष्टियों को अवरोही क्रम में व्यवस्थित कीजिए। वह कौन-सी वस्तु है जिससे रमन को सबसे अधिक धनराशि प्राप्त हुई ? यह धनराशि क्या है ?
हल :
(a) रमन द्वारा पिछले वर्ष बेचे गए सेबों और संतरों का भार
सेबों का भार = 2457 किग्रा
संतरों का भार = 3004 किग्रा
अतः कुल भार = 2457 किग्रा + 3004 किग्रा
= 5461 किग्रा
संतरों और सेबों का कुल भार = 5461 किग्रा

(b) 1 किग्रा सेब का मूल्य = Rs 40
बेचे गये सेबों का भार = 2457 किग्रा
सेबों को बेचने से रमन को प्राप्त कुल धनराशि
= 2457 x 40
= Rs 98,280

(c) बेचे गए संतरों का मार = 3004 किग्रा
1 किग्रा संतरों का विक्रय मूल्य = Rs 30
बेचे गये संतरों द्वारा रमन को प्राप्त कुल धनराशि
= 3004 x 30
= Rs 90120
∴सेबों और संतरों को बेचने से प्राप्त कुल धनराशि
= 98280 + 90120
= Rs 1,88,400

सारणी – रमन द्वारा प्रत्येक वस्तु को बेचने से प्राप्त धनराशि

प्राप्त धनराशि को अवरोही क्रम में रखने पर,
Rs 2,53,670, Rs 2,40,012, Rs 1,60,040, Rs 98,280, Rs 90,120, Rs 68,280, Rs 38,530
सबसे अधिक धनराशि दाँतों के बुश से प्राप्त हुई। यह धनराशि Rs 2,53,670 है।

MP Board Class 6th Maths Solutions