Category: Class 12

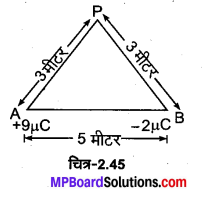
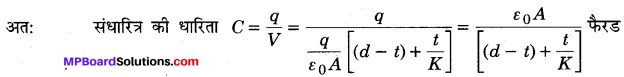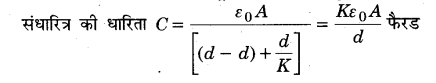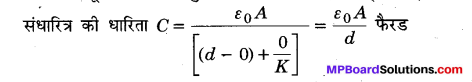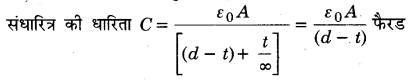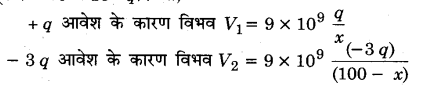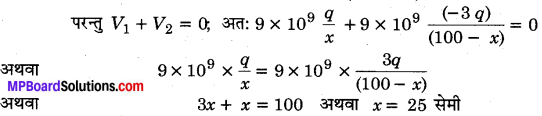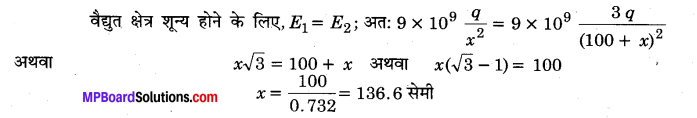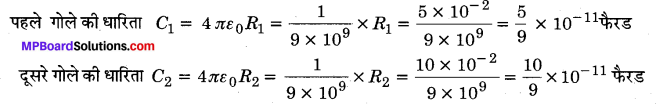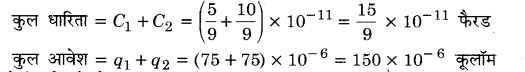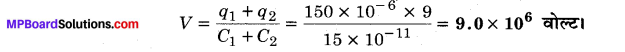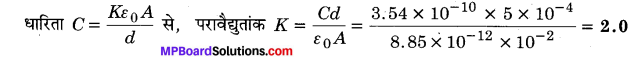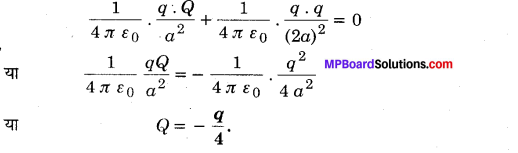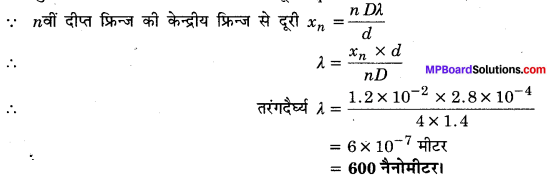MP Board Class 12th Physics Important Questions Chapter 14 अर्द्धचालक इलेक्ट्रॉनिकी: पदार्थ युक्तियाँ तथा सरल परिपथ

Students can also download MP Board 12th Model Papers to help you to revise the complete Syllabus and score more marks in your examinations.

अर्द्धचालक इलेक्ट्रॉनिकी: पदार्थ युक्तियाँ तथा सरल अन्य महत्त्वपूर्ण प्रश्नोत्तर

अर्द्धचालक इलेक्ट्रॉनिकी: पदार्थ युक्तियाँ तथा सरल विस्तृत उत्तरीय प्रश्नोत्तर

प्रश्न 1.
ऊर्जा बैण्ड क्या है? किसी क्रिस्टलीय ठोस में ऊर्जा बैण्डों के गठन की क्रिया विधि स्पष्ट कीजिए।
उत्तर :
ऊर्जा बैण्ड (Energy Band)-जब अनेक परमाणु मिलकर किसी ठोस की रचना करते हैं तो इन परमाणुओं के बीच अन्योन्य क्रियाओं के कारण उनके ऊर्जा-स्तरों में विक्षोभ उत्पन्न हो जाता है जिसके परिणामस्वरूप प्रत्येक ऊर्जा-स्तर अनेक ऊर्जा स्तरों में विभक्त होकर एक बैण्ड का रूप ले लेते हैं, जिसे ऊर्जा बैण्ड कहते हैं।

ठोसों में ऊर्जा बैण्ड (Energy Bands in Solids)-प्रत्येक पदार्थ परमाणुओं से मिलकर बना होता है। प्रत्येक परमाणु के केन्द्रीय भाग में धनावेशित नाभिक होता है जिसके चारों ओर ऋणावेशित इलेक्ट्रॉन कुछ निश्चित कक्षाओं में परिक्रमण करते रहते हैं। इस प्रकार किसी पृथक्कृत परमाणु में इलेक्ट्रॉनों के विविक्त (discrete) एवं सुस्पष्ट ऊर्जा-स्तर होते हैं। जब विभिन्न परमाणु एक-दूसरे के अत्यधिक निकट आकर ठोस की रचना करते हैं तब इन परमाणुओं की बाह्य कक्षाएँ एक-दूसरे को ढक लेती हैं।

इन कक्षाओं में इलेक्ट्रॉन की गति नाभिक-नाभिक, इलेक्ट्रॉन-नाभिक तथा इलेक्ट्रॉन-इलेक्ट्रॉन के बीच होने वाली अन्योन्य क्रियाओं के कारण, किसी पृथक्कृत परमाणु में इलेक्ट्रॉन की गति से भिन्न होती है। इस स्थिति में परमाणुओं के ऊर्जा-स्तरों में विक्षोभ उत्पन्न हो जाता है जिसके परिणामस्वरूप प्रत्येक. ऊर्जा-स्तर अनेक ऊर्जा-स्तरों में विभक्त हो जाता है जिनमें ऊर्जा का सतत परिवर्तन होता रहता है। ये ऊर्जा-स्तर एक-दूसरे के अत्यधिक निकट होने के कारण बैण्ड का रूप ले लेते हैं, जिन्हें ऊर्जा बैण्ड (energy band) कहते हैं।

वह ऊर्जा बैण्ड जिसमें संयोजक इलेक्ट्रॉनों (valence electrons) के ऊर्जा-स्तर उपस्थित होते हैं, संयोजी बैण्ड (valence band) कहलाता है। वह ऊर्जा-बैण्ड जिसमें चालक इलेक्ट्रॉनों (conduction electrons) के ऊर्जा-स्तर उपस्थित होते हैं, चालन बैण्ड (conduction band) कहलाता है। सामान्यत: चालन बैण्ड रिक्त होता है। संयोजी बैण्ड तथा चालन बैण्ड के बीच रिक्ति होती है, जिसे वर्जित ऊर्जा अन्तराल (forbidden energy gap) कहते हैं। इस रिक्ति में कभी कोई इलेक्ट्रॉन उपस्थित नहीं रहता है।

सिलिकन में ऊर्जा बैण्डों का निर्माण (Formation of Energy Bands in Silicon)-सिलिकन का परमाणु क्रमांक 14 है, अतः इसकी बाह्य कक्षा में 4 इलेक्ट्रॉन होते हैं तथा इसके सभी कोशों एवं उपकोशों में इलेक्ट्रॉनिक विन्यास 1s²,2s²,2p⁶,3s²3p² होता है। स्तर 1s,2s, 2p, 3p पूर्णतः भरे होते हैं जबकि स्तर 3p जिसमें अधिकतम 6 इलेक्ट्रॉन रह सकते हैं, में केवल 2 इलेक्ट्रॉन होते हैं।

सिलिकन (Si) के N परमाणु वाले क्रिस्टल की बाह्य कक्षा में उपस्थित इलेक्ट्रॉनों की संख्या 4N होगी। किसी एक परमाणु की बाह्यतम कक्षा में उपस्थित इलेक्ट्रॉनों की अधिकतम संख्या 8 हो सकती है। अत: N परमाणुओं के उपस्थित 4N संयोजी इलेक्ट्रॉनों के लिए उपलब्ध ऊर्जा-स्तर 8N होंगे। ये 8N ऊर्जा-स्तर क्रिस्टल में उपस्थित परमाणुओं के बीच की दूरी (7) के आधार पर कोई सतत बैण्ड बना सकते हैं अथवा इनका विभिन्न बैण्डों में समूहन हो . सकता है जिसे आगे स्पष्ट किया गया है

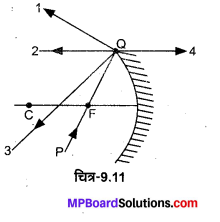
1. जब r =r₃ >> r₀ अर्थात् अन्तरपरमाण्विक दूरी (r), क्रिस्टल जालक दूरी r₀ से बहुत अधिक हो तो क्रिस्टल जालक में उपस्थित प्रत्येक परमाणु पृथक्कृत परमाणु की भाँति व्यवहार करता है, अत: प्रत्येक परमाणु के विविक्त एवं सुस्पष्ट ऊर्जा-स्तर होते हैं, जिन्हें चित्र-14.17 में परस्पर समान्तर रेखाओं द्वारा प्रदर्शित किया गया है।

2. जब r =r₂ >ro तब परमाणुओं के संयोजी इलेक्ट्रॉनों के मध्य अन्त:क्रिया (interaction) प्रभावी हो जाने के कारण 3s व 3p उपकोश अत्यधिक निकट स्थित दो ऊर्जा-स्तरों में विभक्त हो जाते हैं, जिनके बीच का ऊर्जा अन्तराल पहले की अपेक्षा कम होता है। अन्तरपरमाण्विक दूरी r के और घटने पर 3s व 3p स्तरों से सम्बद्ध ऊर्जा बैण्डों का फैलाव बढ़ता है तथा इनके बीच का ऊर्जा अन्तराल घटता है।

3. जब r = r₁ > r₀ तब 3s व 3p बैण्डों में अतिव्यापन (overlapping) के कारण उनके बीच ऊर्जा-अन्तराल समाप्त हो जाता है तथा सभी 8N स्तर अर्थात् 3 8 से सम्बद्ध 2N ऊर्जा-स्तर तथा 3p से सम्बद्ध 6N ऊर्जा-स्तर अब सतत रूप से वितरित होते हैं। 8N ऊर्जा-स्तरों में से 4N ऊर्जा-स्तर पूर्णतया भरे हुए तथा 4N ऊर्जा-स्तर रिक्त होते हैं।

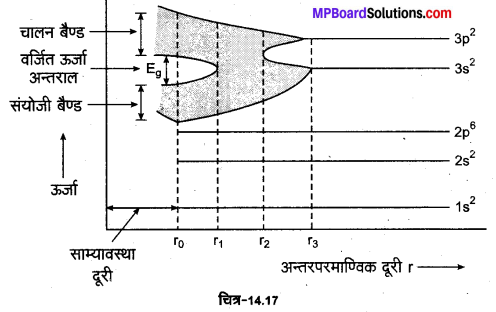
4. जब r = r_o अर्थात् अन्तरपरमाण्विक दूरी (r), क्रिस्टल जालक दूरी r₀ के बराबर हो तो पूर्णतया भरे हुए तथा रिक्त ऊर्जा-स्तर एक ऊर्जा अन्तराल से परस्पर पृथक्कृत हो जाते हैं। यह ऊर्जा अन्तराल वर्जित ऊर्जा अन्तराल (forbidden energy gap) कहलाता है। निचला पूर्णतया भरा हुआ ऊर्जा बैण्ड जिसमें केवल संयोजी इलेक्ट्रॉन रह सकते हैं, संयोजी बैण्ड (valence band) कहलाता है तथा ऊपरी रिक्त ऊर्जा बैण्ड जिसमें चालक इलेक्ट्रॉन रहते हैं, चालन बैण्ड (conduction band) कहलाता है।

प्रश्न 2.
ऊर्जा बैण्ड के आधार पर चालक, अचालक एवं अर्द्धचालकों का वर्गीकरण स्पष्ट कीजिए। [2017]
अथवा
ऊर्जा बैण्ड क्या है? चालक, अचालक और अर्द्धचालक में अन्तर इनके ऊर्जा बैण्ड आरेखों के आधार पर बताइए। [2018]
उत्तर :
ऊर्जा बैण्ड-जब अनेक परमाणु मिलकर किसी ठोस की रचना करते हैं तो इन परमाणुओं के बीच अन्योन्य, क्रियाओं के कारण उनके ऊर्जा-स्तरों में विक्षोभ उत्पन्न हो जाता है जिसके परिणामस्वरूप प्रत्येक ऊर्जा-स्तर अनेक ऊर्जा-स्तरों में विभक्त होकर एक बैण्ड का रूप ले लेता है, जिसे ऊर्जा बैण्ड कहते हैं।

ऊर्जा बैण्ड के आधार पर ठोसों (चालक, अचालक व अर्द्धचालकों में) का वर्गीकरण (Classification of Solids (in Conductors, Insulators and Semiconductors) on the Basis of Energy Bands)-ठोसों का उनके संयोजी बैण्ड एवं चालन बैण्ड के बीच वर्जित ऊर्जा अन्तराल के आधार पर चालक, अचालक एवं अर्द्धचालकों में वर्गीकरण किया जा सकता है।

1. चालक (Conductors)-चालक वे पदार्थ होते हैं जिनमें चालक इलेक्ट्रॉनों की पर्याप्त संख्या पायी जाती है तथा उनमें धारा प्रवाह सरलता से हो जाता है। उदाहरण-चाँदी, ताँबा, ऐलुमिनियम आदि। ऊर्जा बैण्ड संरचना के अनुसार चालक वे पदार्थ होते हैं जिनके चालन बैण्ड इलेक्ट्रॉनों से आंशिक रूप से भरे होते हैं तथा इनके संयोजी बैण्ड एवं चालन बैण्ड या तो परस्पर अतिव्यापित (overlapped) होते हैं या उनके बीच वर्जित ऊर्जा अन्तराल लगभग नगण्य होता है (चित्र-14.18)।

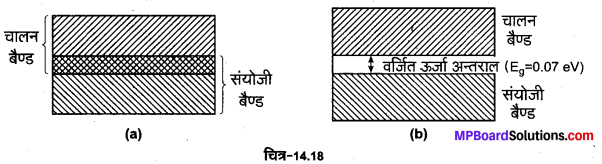
2. अचालक (Insulators)-अचालक वे पदार्थ होते हैं जिनमें चालक इलेक्ट्रॉन लगभग नगण्य संख्या में पाए जाते हैं, अत: इनमें धारा का प्रवाह नहीं होता है। उदाहरण-लकड़ी, ऐबोनाइट, काँच आदि। ऊर्जा बैण्ड संरचना के आधार पर अचालक वे पदार्थ होते हैं जिनके संयोजी बैण्ड पूर्णतः भरे हुए तथा चालन बैण्ड पूर्णतः रिक्त होते हैं तथा उनके बीच वर्जित ऊर्जा अन्तराल बहुत अधिक (E_g > 3 ev) होता है (चित्र-14.19)।

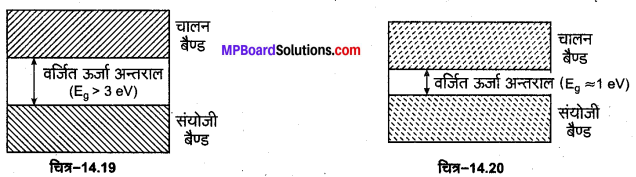
3. अर्द्धचालक (Semiconductors)-अर्द्धचालक वे पदार्थ होते हैं जिनकी चालकता चालकों से कम तथा अचालकों से अधिक होती है। उदाहरण–जर्मेनियम, सिलिकन, कार्बन आदि। ऊर्जा बैण्ड संरचना के आधार पर अर्द्धचालक वे पदार्थ होते हैं जिनके संयोजी बैण्ड पूर्ण रूप से भरे हुए होते हैं तथा चालन बैण्ड पूर्णत: रिक्त होते हैं परन्तु चालन बैण्ड एवं संयोजी बैण्ड के बीच वर्जित ऊर्जा अन्तराल बहुत कम (E_g ≈ 1 ev) होता है (चित्र-14.20)।

परम शून्य ताप (OK) पर अर्द्धचालकों का चालन बैण्ड पूर्णतया रिक्त होता है, अतः परम शून्य ताप पर अर्द्धचालक एक अचालक की भाँति व्यवहार करता है। जैसे-जैसे अर्द्धचालक का ताप बढ़ता है, वर्जित ऊर्जा अन्तराल घटता जाता है तथा संयोजी बैण्ड से कुछ इलेक्ट्रॉन चालन बैण्ड में पहुँच जाते हैं, जिसके फलस्वरूप अर्द्धचालक की चालकता बढ़ जाती है। इस प्रकार अर्द्धचालकों की चालकता ताप बढ़ाने पर बढ़ती है। अतः अर्द्धचालकों का प्रतिरोध ताप गुणांक (α) ऋणात्मक होता है।

प्रश्न 3.
अर्द्धचालक कितने प्रकार के होते हैं? निज अर्द्धचालकों में वैद्युत चालन किस प्रकार होता है? समझाइए।
उत्तर :
अर्द्धचालकों के प्रकार (Types of Semiconductors)-अर्द्धचालक दो प्रकार के होते हैं
1. निज अर्द्धचालक (Intrinsic Semiconductor)-एक शुद्ध अर्द्धचालक जिसमें कोई अशुद्धि (अपद्रव्य impurity) न मिली हो, निज अर्द्धचालक कहलाता है। इस प्रकार शुद्ध जर्मेनियम तथा शुद्ध सिलिकन अपनी प्राकृतिक अवस्था में निज अर्द्धचालक हैं।

2. बाह्य अर्द्धचालक (Extrinsic Semiconductors)-निज अर्द्धचालकों की वैद्युत चालकता बहुत कम होती है परन्तु यदि उसमें संयोजकता 5 अथवा 3 वाले किसी पदार्थ की अल्प मात्रा अपद्रव्य (impurity) के रूप में मिला दी जाए तो अर्द्धचालक की चालकता बहुत अधिक बढ़ जाती है। अपद्रव्य मिलाने की यह क्रिया अपमिश्रण (doping) कहलाती है तथा अपद्रव्य मिले ऐसे अर्द्धचालक को बाह्य अर्द्धचालक कहते हैं। बाह्य अर्द्धचालक दो प्रकार के होते हैं-(a) n-टाइप अर्द्धचालक, (b) pटाइप अर्द्धचालक

निज अर्द्धचालकों में वैद्युत चालन (Electric Conduction in Intrinsic Semiconductors)-जर्मेनियम (Ge³²) तथा सिलिकन (Si¹⁴) की संयोजकता 4 है। अत: Ge (अथवा Si) के पत्येक परमाणु में 4 संयोजक इलेक्ट्रॉन होते हैं। ये इलेक्ट्रॉन परमाणु के नाभिक तथा उससे दृढ़तापूर्वक बँधे आन्तरिक इलेक्ट्रॉनों के एक आन्तरिक क्रोड जिस पर +4 e आवेश होता है, के चारों ओर होते हैं।

जर्मेनियम क्रिस्टल में प्रत्येक परमाणु एक सम चतुष्फलक के किसी भी कोने पर स्थित होते हैं (चित्र-14.21)। परमाणु के चारों संयोजक इलेक्ट्रॉन, निकटवर्ती चार अन्य परमाणुओं के इलेक्ट्रॉनों में से एक-एक के साथ भागीदार होकर सहसंयोजक बन्धों (covalent bonds) की रचना करते हैं। इन बन्धों के कारण ही पड़ोसी परमाणुओं के बीच बन्धन बल उत्पन्न होता है। इस प्रकार परम शून्य ताप (0 K) पर शुद्ध जर्मेनियम क्रिस्टल में सभी संयोजक इलेक्ट्रॉन क्रोड के साथ दृढ़तापूर्वक बँधे होते हैं, अतः धारा चालन के लिए कोई मुक्त .. इलेक्ट्रॉन नहीं रहता है। सामान्य ताप पर ऊष्मीय विक्षोभ के कारण कुछ संयोजक बन्ध टूट जाते हैं, जिनके कारण कुछ इलेक्ट्रॉन धारा चालन के लिए मुक्त हो जाते हैं, ये इलेक्ट्रॉन मुक्त इलेक्ट्रॉन कहलाते हैं। क्रिस्टल को गर्म करने पर, अधिकाधिक इलेक्ट्रॉन मुक्त होने लगते हैं, जिससे क्रिस्टल की चालकता बढ़ने लगती है। वैद्युत क्षेत्र की अनुपस्थिति में ये मुक्त इलेक्ट्रॉन क्रिस्टल जालक के अन्दर गैस के अणुओं की भाँति अनियमित गति करते रहते हैं। जब क्रिस्टल पर वैद्युत क्षेत्र लगाया जाता है तो ये मुक्त इलेक्ट्रॉन वैद्युत क्षेत्र के विपरीत दिशा में यादृच्छिक गतियाँ करते हैं जिससे उनमें वैद्युत क्षेत्र के विपरीत दिशा में धारा बहती है।

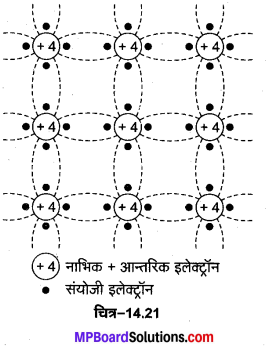
साधारण ताप पर जर्मेनियम के 10⁹ परमाणुओं में से केवल एक सहसंयोजक बन्ध टूटता है इसलिए निज अर्द्धचालकों की चालकता बहुत कम होती है, जिसके कारण इनका कोई व्यावहारिक उपयोग नहीं हो सकता है। जब जर्मेनियम के क्रिस्टल जालक में कोई सहसंयोजक बन्ध टूटकर इलेक्ट्रॉन मुक्त होता है तो उस परमाणु में एक इलेक्ट्रॉन की कमी हो जाती है। परमाणु में इलेक्ट्रॉन के मूल स्थान पर उत्पन्न यह रिक्ति ‘कोटर’ (hole) कहलाती. है। क्रिस्टल जालक में ऊष्मीय विक्षोभ के कारण जब किसी अन्य परमाणु का सहसंयोजक बन्ध इस कोटर के निकट आता है तो पहला परमाणु इस परमाणु के सहसंयोजक बन्ध से एक इलेक्ट्रॉन ग्रहण कर इस रिक्ति को पूरा कर लेता है।

अब इलेक्ट्रॉन की रिक्ति अर्थात् कोटर दूसरे परमाणु पर उत्पन्न हो जाता है। यह प्रक्रिया क्रिस्टल जालक में निरन्तर चलती रहती है और कोटर एक परमाणु से दूसरे परमाणु पर स्थानान्तरित होता रहता है। वैद्युत क्षेत्र की अनुपस्थिति में क्रिस्टल जालक में कोटर की गति यादृच्छिक (random) होती है। जब क्रिस्टल पर वैद्युत क्षेत्र लगाया जाता है तो ये कोटर यादृच्छिक गति के साथ-साथ वैद्युत क्षेत्र की दिशा में गति करते हैं जिसके परिणामस्वरूप क्रिस्टल में वैद्युत क्षेत्र की दिशा में वैद्युत धारा बहती है। इस प्रकार निज अर्द्धचालक क्रिस्टल में मुक्त इलेक्ट्रॉनों एवं कोटरों दोनों के कारण वैद्युत धारा बहती है।

किसी निश्चित ताप पर निज अर्द्धचालक में मुक्त इलेक्ट्रॉनों की सान्द्रता ne तथा कोटरों की सान्द्रता n परस्पर बराबर होती है।

प्रश्न 4.
(a) n-टाइप अर्द्धचालक से क्या तात्पर्य है? इसकी रचना समझाइए। [2007, 10, 12]]
(b) p-टाइप अर्द्धचालक से क्या तात्पर्य है? इसकी रचना समझाइए। [2007, 10, 12]
उत्तर :
(a) n-टाइप अर्द्धचालक (n-type Semiconductor)—जब शुद्ध जर्मेनियम (अथवा सिलिकन) क्रिस्टल में 5 संयोजकता वाले अपद्रव्य परमाणु, जैसे आर्सेनिक अथवा ऐन्टिमनी अल्प मात्रा में मिलाये जाते हैं तो प्रत्येक अपद्रव्य परमाणु के पाँच संयोजक इलेक्ट्रॉनों में से चार संयोजक इलेक्ट्रॉन, जर्मेनियम के चार निकटतम परमाणुओं के एक-एक संयोजक इलेक्ट्रॉन के साथ मिलकर सहसंयोजक बन्ध बना लेते हैं तथा आर्सेनिक अपद्रव्य का पाँचवाँ संयोजक इलेक्ट्रॉन क्रिस्टल में गति के लिए मुक्त रह जाता है (चित्र-14.22)। यह इलेक्ट्रॉन आवेश वाहक का कार्य करता है तथा इस पर ऋणावेश होता है।

इस प्रकार शुद्ध जर्मेनियम में अपद्रव्य मिलाने से मुक्त इलेक्ट्रॉनों की संख्या बढ़ जाती है. अर्थात् क्रिस्टल की चालकता बढ़ जाती है। इस प्रकार के अपद्रव्य मिले जर्मेनियम क्रिस्टल को n-टाइप अर्द्धचालक कहते हैं, क्योंकि इसमें आवेश वाहक (मुक्त इलेक्ट्रॉन) ऋणात्मक होते हैं। अपद्रव्य परमाणुओं को दाता (donor) परमाणु कहते हैं, क्योंकि ये क्रिस्टल को चालक इलेक्ट्रॉन प्रदान करते हैं।

उपर्युक्त व्याख्या से स्पष्ट है कि n-टाइप अर्द्धचालक क्रिस्टल में चलनशील आवेश वाहक (ऋणात्मक) इलेक्ट्रॉन होते हैं तथा इतनी ही संख्या में स्थिर (धनात्मक दाता) (donor) आयन होते हैं (चित्र-14.23)। इस प्रकार सम्पूर्ण क्रिस्टल उदासीन ही रहता है।
दाता परमाणु

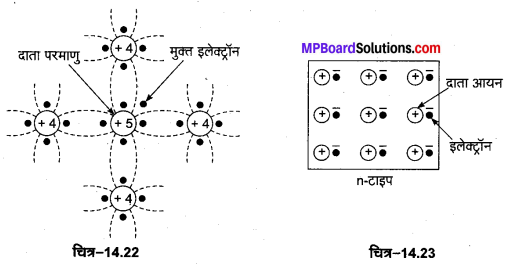
(b) p-टाइप अर्द्धचालक (p-type Semiconductor)-जब शुद्ध जर्मेनियम (अथवा सिलिकन) क्रिस्टल में 3 संयोजकता वाले अपद्रव्य परमाणु, जैसे ऐलुमिनियम (अथवा बोरॉन) अल्प मात्रा में मिलाए जाते हैं तो प्रत्येक अपद्रव्य परमाणु के तीन संयोजक इलेक्ट्रॉन, जर्मेनियम के तीन निकटतम परमाणुओं के एक-एक संयोजक इलेक्ट्रॉन के साथ मिलकर सहसंयोजक बन्ध बना लेते हैं तथा जर्मेनियम का एक संयोजक इलेक्ट्रॉन बन्ध नहीं बना पाता है, अत: क्रिस्टल में अपद्रव्य परमाणु के एक ओर रिक्त स्थान रह जाता है जिसे कोटर (hole) कहते हैं (चित्र-14.24)। वैद्युत क्षेत्र लगाने पर, इस कोटर में पड़ोसी परमाणु से एक इलेक्ट्रॉन आ जाता है, जिससे पड़ोसी परमाणु में एक स्थान रिक्त होकर कोटर बन जाता है।

इस प्रकार क्रिस्टल में कोटर एक स्थान से दूसरे स्थान तक की गति कर सकता है। इसकी गति की दिशा इलेक्ट्रॉन की गति की दिशा के विपरीत होती है। इस प्रकार कोटर एक धनावेशित कण के समान है, अत: अपद्रव्य मिले जर्मेनियम क्रिस्टल को p-टाइप अर्द्धचालक कहते हैं, क्योंकि इसमें आवेश वाहक (कोटर) धनात्मक होते हैं। अपद्रव्य परमाणुओं को ग्राही (acceptor) परमाणु कहते हैं, क्योंकि ये शुद्ध अर्द्धचालक से इलेक्ट्रॉनों को ग्रहण करते हैं।

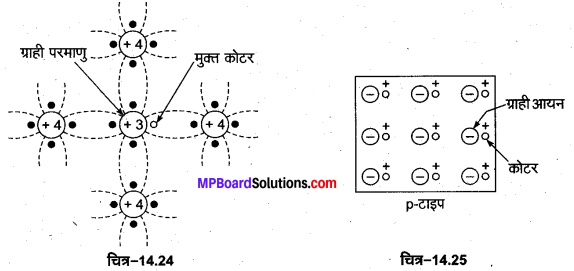
उपर्युक्त व्याख्या से स्पष्ट है कि p-टाइप अर्द्धचालक क्रिस्टल में चलनशील (धनात्मक) कोटर होते हैं तथा इतनी ही संख्या में स्थिर (ऋणात्मक) ग्राही आयन होते हैं (चित्र-14.25), परन्तु p-टाइप अर्द्धचालकों में कोटरों की गतिशीलता n-टाइप अर्द्धचालकों में इलेक्ट्रॉनों की गतिशीलता की तुलना में कम होती है।

प्रश्न 5.
p-n सन्धि डायोड का अग्र दिशिक (अभिनत) तथा उत्क्रम दिशिक (अभिनत) वैद्युत परिपथ खींचकर समझाइए। दोनों अवस्थाओं हेतु प्राप्त अभिलक्षण वक्रों को समझाइए। [2008, 11, 12, 15]
अथवा
p-8 सन्धि डायोड में अग्र-अभिनत और उत्क्रम-अभिनत से आप क्या समझते हैं? आवश्यक परिपथ आरेख बनाइए तथा दोनों विन्यासों को समझाइए। [2017, 18]
अथवा
p-n सन्धि डायोड क्या है? इसमें अवक्षय परत तथा विभव प्राचीर कैसे बनते हैं? [2006]
अथवा
उपयुक्त परिपथों की सहायता से prn सन्धि डायोड में वैद्युत धारा प्रवाह की व्याख्या कीजिए। [2013]
अथवा
p-n सन्धि डायोड क्या है? [2014, 16]
अथवा
पश्चदिशिक बायसित सन्धि डायोड में धारा कम क्यों बहती है? [2018]
अथवा
p-n सन्धि डायोड के लिए अग्रदिशिक परिपथ आरेख खींचिए। [2017]
उत्तर :
p.n सन्धि डायोड (p-n Junction Diode)-जब एक p-टाइप अर्द्धचालक क्रिस्टल को एक विशेष विधि द्वारा n-टाइप अर्द्धचालक क्रिस्टल के साथ जोड़ा जाता है तो इस संयोजन को जहाँ पर क्रिस्टल जुड़ते हैं उसे p-n सन्धि कहते हैं (चित्र-14.26)| p-टाइप क्षेत्र में कोटर बहुसंख्यक आवेश वाहक होते हैं तथा इतने ही स्थिर ऋणात्मक ग्राही आयन होते हैं जबकि n-टाइप क्षेत्र में इलेक्ट्रॉन बहुसंख्यक आवेश वाहक होते हैं तथा इतने ही स्थिर धनात्मक दाता आयन होते हैं। इस प्रकार दोनों क्षेत्र वैद्युत उदासीन होते हैं।

विभव प्राचीर अथवा p-n सन्धि पर अवक्षय परत का बनना-जैसे ही p-n सन्धि बनती है, ऊष्मीय विक्षोभ के कारण सन्धि के आर-पार आवेश वाहकों का विसरण प्रारम्भ हो जाता है। n-टाइप क्रिस्टल से कुछ इलेक्ट्रॉन p-टाइप क्रिस्टल में तथा p-टाइप क्रिस्टल से कुछ कोटर n-टाइप क्रिस्टल में विसरित हो जाते हैं। विसरण के बाद, ये आवेश वाहक अपने-अपने पूरकों से मिलकर परस्पर उदासीन हो जाते हैं। इस प्रकार सन्धि के समीप n-क्षेत्र में धनावेशित दाताओं की अधिकता तथा p-क्षेत्र में ऋणावेशित ग्राहियों की अधिकता हो जाती है (चित्र-14.27)। इससे सन्धि पर एक आन्तरिक वैद्युत क्षेत्र E; स्थापित हो जाता है जो धन n-क्षेत्र से, ऋण p-क्षेत्र की ओर दिष्ट होता है। कुछ समय पश्चात् यह क्षेत्र इतना प्रबल हो जाता है कि आवेश वाहकों का और आगे विसरण रुक जाता है, क्योंकि इलेक्ट्रॉन क्षेत्र के विपरीत दिशा में चलते हैं तथा कोटर क्षेत्र की दिशा में चलते हैं, अत: वैद्युत क्षेत्र E_i इन्हें चलने से रोक देता है।

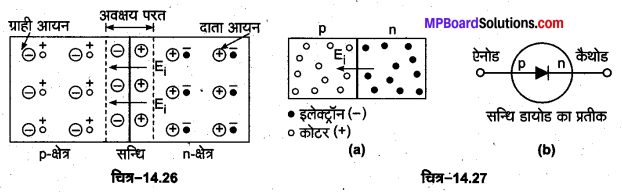
इस प्रकार सन्धि के दोनों ओर एक बहुत पतली परत बन जाती है, जिसमें आवेश वाहक नहीं रहते हैं। इस परत को अवक्षय परत (depletion layer) कहते हैं। इसकी मोटाई 10^-6 मीटर कोटि की होती है। इस अवक्षय परत के सिरों के बीच उत्पन्न वैद्युत वाहक बल को सम्पर्क विभव अथवा विभव प्राचीर कहते हैं। सम्पर्क विभव सन्धि के ताप पर निर्भर करता है तथा इसका मान 0.1 से लेकर 0.5 वोल्ट के बीच होता है। सन्धि डायोड का प्रतीक चित्र-14.28 में प्रदर्शित किया गया है। इसमें p को ऐनोड तथा n को कैथोड कहते हैं।

p-n सन्धि डायोड में वैद्युत धारा का प्रवाह-किसी बाह्य बैटरी की अनुपस्थिति में सन्धि डायोड में कोई धारा नहीं बहती है [चित्र-14.28 (a)]| जब इस सन्धि के सिरों को किसी बैटरी के ध्रुवों से जोड़कर इस पर कोई वोल्टता लगाई जाती है तो इसमें वैद्युत धारा प्रवाहित हो जाती है। p-n सन्धि डायोड पर बैटरी को दो प्रकार से जोड़ा जा सकता है-

1. अग्र अभिनत (Forward Bias)-“जब p-n सन्धि डायोड के p-टाइप क्रिस्टल को बाह्य बैटरी के धन सिरे से तथा n-टाइप क्रिस्टल को बैटरी के ऋण सिरे से जोड़ते हैं तो यह सन्धि अग्र अभिनत या फॉरवर्ड बायस कहलाती है” [चित्र-14.28 (a)]। इस दशा में pn सन्धि डायोड · में p-क्षेत्र से n-क्षेत्र की ओर एक बाह्य वैद्युत क्षेत्र E स्थापित हो जाता है। यह क्षेत्र आन्तरिक वैद्युत क्षेत्र E; से कहीं अधिक शक्तिशाली होता है। इस प्रकार सन्धि डायोड में वैद्युत क्षेत्र E के कारण कोटर क्षेत्र से n-क्षेत्र की ओर वैद्युत क्षेत्र E की दिशा में चलने लगते हैं जबकि इलेक्ट्रॉन n-क्षेत्र से p क्षेत्र की ओर वैद्युत क्षेत्र E की विपरीत दिशा में चलने लगते हैं। सन्धि के समीप पहुँचकर ये कोटर तथा . इलेक्ट्रॉन परस्पर संयोग करके विलुप्त हो जाते हैं।

प्रत्येक इलेक्ट्रॉन कोटर संयोग के लिए pक्षेत्र में बैटरी के धन सिरे के समीप एक सहसंयोजक बन्ध टूट जाता है। इससे उत्पन्न कोटर तो सन्धि की ओर चलने लगता है जबकि इलेक्ट्रॉन संयोजक तार में से होकर बैटरी के धन सिरे में प्रवेश कर जाता है। ठीक इसी क्षण बैटरी के ऋण सिरे से एक इलेक्ट्रॉन निकलकर n-क्षेत्र में प्रवेश कर जाता है तथा सन्धि के समीप इलेक्ट्रॉन-कोटर संयोग प्रक्रिया में लुप्त इलेक्ट्रॉन का स्थान ले लेता है। इस प्रकार p-n सन्धि डायोड में बहुसंख्यक आवेश वाहकों की गति के कारण उच्च वैद्युत धारा बहने लगती है। इस उच्च वैद्युत धारा को ही अग्र धारा कहते हैं। इस उच्च धारा के अतिरिक्त अल्पसंख्यक वाहकों की गति के कारण भी एक अल्प उत्क्रम धारा बहती है। परन्तु यह लगभग नगण्य होती है [चित्र-14.28 (b)]। इस प्रकार बाह्य परिपथ में केवल इलेक्ट्रॉनों की गति के कारण ही धारा बहती है। कोटर

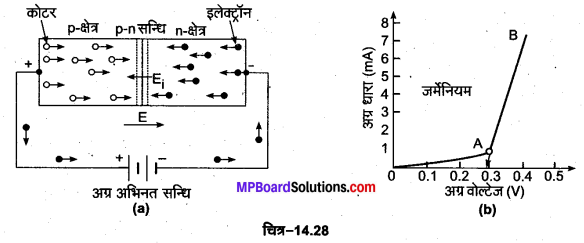
चूँकि अग्र अभिनत में आरोपित वैद्युत क्षेत्र E आन्तरिक वैद्युत क्षेत्र E₁ से अधिक शक्तिशाली होता है। इस कारण बहुसंख्यक आवेश वाहक (pक्षेत्र में कोटर तथा n-क्षेत्र में इलेक्ट्रॉन) सन्धि की ओर आकर्षित होते हैं जिसके कारण. अवक्षय परत की मोटाई कम हो जाती है। इसीलिए अग्र अभिनत सन्धि डायोड का धारा प्रवाह के लिए प्रतिरोध कम होता है। चित्र-14.28 में p-n सन्धि पर आरोपित अग्र वोल्टेज तथा अग्र धारा के बीच खींचा गया ग्राफ प्रदर्शित है। प्रारम्भ में जर्मेनियम के लिए 0.3 वोल्ट पर विरोधी विभव प्राचीर के कारण धारा लगभग शून्य रहती है। आरोपित वोल्टेज के बढ़ाने पर, धारा बहुत धीरे-धीरे एवं अरैखिक रूप से तब तक बढ़ती है जब तक कि आरोपित वोल्टेज, विभव प्राचीर से अधिक नहीं हो जाती है [चित्र-14.28 (b) में OA भाग]। जब आरोपित वोल्टेज को और बढ़ाया जाता है तो धारा रैखिक रूप में आगे बढ़ती है (AB भाग)। यदि रेखा AB को पीछे की ओर बढ़ाया जाए तो यह वोल्टेज अक्ष को विभव प्राचीर वोल्टेज पर काटती है।

2. उत्क्रम अभिनत (Reverse Bias)-“जब p-n सन्धि डायोड के p-टाइप क्रिस्टल को बैटरी के ऋण सिरे से तथा n-टाइप क्रिस्टल को बैटरी के धन सिरे से जोड़ते हैं तो यह सन्धि उत्क्रम अभिनत या रिवर्स बायस कहलाती है” [चित्र-14.29 (a)]। इस दशा में p-n सन्धि डायोड में n से p की ओर एक बाह्य वैद्युत क्षेत्र E उत्पन्न हो जाता है, जो आन्तरिक वैद्युत क्षेत्र E; की सहायता करता है। अत: p-क्षेत्र के कोटर बैटरी के ऋण सिरे की ओर तथा n-क्षेत्र के इलेक्ट्रॉन बैटरी के धन सिरे की ओर आकर्षित होकर p-n सन्धि से दूर हो जाते हैं, जिसके कारण धारा प्रवाह पूर्णत: बन्द हो जाता है।

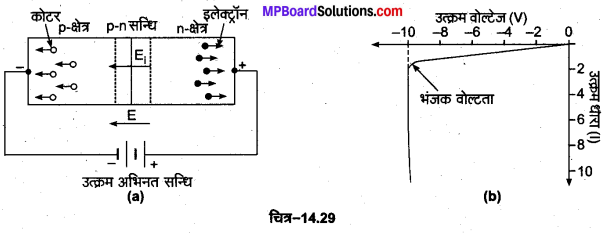
जब p-n सन्धि उत्क्रम अभिनत होती है तो बहुत क्षीण उत्क्रम धारा परिपथ में बहती है, क्योंकि p तथा n-क्षेत्रों में ऊष्मीय विक्षोभ के कारण क्रमश: कुछ इलेक्ट्रॉन तथा कुछ कोटर विद्यमान रहते हैं. इनको अल्पसंख्यक वाहक कहते हैं। उत्क्रम अभिनत में ये बहुसंख्यक वाहकों की गति का विरोध करते हैं, परन्तु अल्पसंख्यक वाहकों को सन्धि के आर-पार जाने में सहायता करते हैं, जिस कारण बहुत क्षीण उत्क्रम धारा परिपथ में बहने लगती है [चित्र-14.29 (b)]।

इस प्रकार उत्क्रम वोल्टेज (V) तथा उत्क्रम धारा (I) के बीच खींचा गया ग्राफ p-n. सन्धि डायोड का उत्क्रम अभिनत अभिलाक्षणिक वक्र कहलाता है। इससे स्पष्ट है कि उत्क्रम वोल्टेज बढ़ाने पर, उत्क्रम धारा प्रारम्भ में लगभग स्थिर रहती है, परन्तु वोल्टेज बहुत अधिक होने पर, सन्धि के निकट सहसंयोजक बन्ध टूट जाते हैं, जिससे इलेक्ट्रॉन-कोटर युग्म अधिक संख्या में मुक्त हो जाते हैं, इस कारण उत्क्रम धारा एकदम बहुत बढ़ जाती है। इस स्थिति को ऐवेलांश भंजन (avalanche breakdown) कहते हैं।

प्रश्न 6.
p-n सन्धि डायोड को अर्द्ध-तरंग दिष्टकारी के रूप में कैसे प्रयुक्त किया जाता है? सरल परिपथ बनाकर इसकी कार्य-विधि समझाइए। निवेशी तथा निर्गत वोल्टताओं के तरंग रूप दिखाइए। [2009, 14, 16]
अथवा
सन्धि डायोड का प्रयोग कर अर्द्ध-तरंग दिष्टकारी का परिपथ आरेख बनाइए। [2017]
उत्तर :
p-n सन्धि डायोड अर्द्ध-तरंग दिष्टकारी के रूप में (p-n Junction Diode as a Half Wave Rectifier)-p-n सन्धि डायोड, अग्र अभिनत स्थिति में धारा को एक ‘दिशा में प्रवाहित करने के लिए इसके मार्ग में बहुत कम प्रतिरोध लगाता है तथा उत्क्रम अभिनत में धारा को विपरीत दिशा में प्रवाहित करने के लिए इसके मार्ग में बहुत अधिक प्रतिरोध लगाता है। इस गुण के आधार पर p-n सन्धि डायोड, डायोड वाल्व की भाँति दिष्टकारी के रूप में प्रयुक्त किया जाता है। p-n सन्धि डायोड का अर्द्ध-तरंग दिष्टकारी परिपथ चित्र-14.30 (a) में तथा इसके निवेशी व निर्गत तरंग रूपों को चित्र-14.30 (b) में प्रदर्शित किया गया है।

जिस प्रत्यावर्ती वोल्टता को दिष्टीकृत करना होता है अर्थात् निवेशी प्रत्यावर्ती वोल्टेज को एक उच्चायी ट्रांसफॉर्मर की प्राथमिक कुण्डली (P) के सिरों के बीच लगा देते हैं। सन्धि डायोड के pक्षेत्र को ट्रांसफॉर्मर की द्वितीयक कुण्डली S के एक सिरे A से जोड़ देते हैं तथा n-क्षेत्र को एक लोड प्रतिरोध R_L के सिरे C से जोड़ देते हैं। लोड प्रतिरोध R_L का दूसरा सिरा D द्वितीयक कुण्डली के दूसरे सिरे B से जोड़ देते हैं। निर्गत दिष्ट वोल्टेज (या विभव) को लोड प्रतिरोध R_L के सिरों पर प्राप्त किया जाता है।

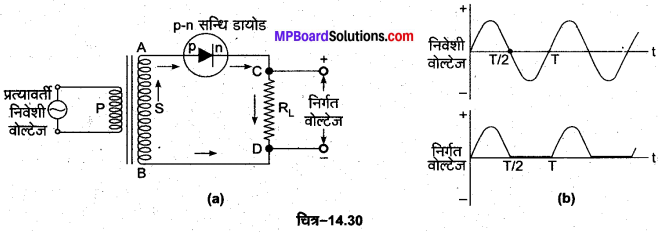
कार्य-विधि-निवेशी प्रत्यावर्ती वोल्टेज के पहले आधे चक्र में, जब द्वितीयक कुण्डली का A सिरा B सिरे के सापेक्ष धनात्मक है (अर्थात् सन्धि डायोड का p-क्षेत्र धनात्मक तथा n-क्षेत्र ऋणात्मक विभव पर होता है) तो p-nसन्धि डायोड अग्र अभिनत होता है, अत: इसमें से होकर धारा प्रवाहित होती है। इस प्रकार से लोड प्रतिरोध R_L में धारा C से D की ओर बहती है। इसके विपरीत निवेशी प्रत्यावर्ती वोल्टेज के दूसरे आधे चक्र में, जब द्वितीयक कुण्डली का A सिरा B सिरे के सापेक्ष ऋणात्मक है (अथवा सन्धि डायोड का p-क्षेत्र ऋणात्मक तथा n-क्षेत्र धनात्मक विभव पर होता है) तो p-n सन्धि डायोड उत्क्रम अभिनत होता है।

इस दशा में लोड प्रतिरोध R_L में धारा शून्य होती है। इस प्रकार निर्गत धारा केवल निवेशी वोल्टता के पहले आधे चक्रों में प्रवाहित होती है शेष आधे चक्र कट जाते हैं। चित्र-14.30 (b) के निचले भाग में धारा का तरंग रूप दिखाया गया है जिसमें थोड़ी-थोड़ी दूर पर (अर्थात् थोड़ी-थोड़ी देर में) धारा के एकदिशीय स्पन्द प्रदर्शित हैं। इस प्रकार p-n सन्धि डायोड अर्द्ध-तरंग दिष्टकारी की भाँति कार्य करता है।

प्रश्न 7.
p-n सन्धि डायोड को पूर्ण-तरंग दिष्टकारी के रूप में कैसे प्रयुक्त किया जाता है? सरल परिपथ बनाकर इसकी कार्यविधि समझाइए। निवेशी तथा निर्गत तरंग रूप भी प्रदर्शित कीजिए। [2010, 11, 12, 13, 15, 17]
अथवा
p-n सन्धि डायोड का प्रयोग कर पूर्ण-तरंग दिष्टकारी का परिपथ आरेख बनाइए। निर्गत तरंग-रूपों को प्रदर्शित कीजिए। [2014, 18]
अथवा
दो p-n सन्धि डायोडों को पूर्ण तरंग दिष्टकारी के रूप में कैसे प्रयुक्त किया जाता है? निवेशी तथा निर्गत
वोल्टताओं के तरंग रूपों को देते हुए, सरल परिपथ आरेख बनाकर इसकी कार्य-विधि समझाइए। [2014]
अथवा
प्रत्यावर्ती धारा को दिष्ट धारा में परिवर्तित करने हेतु आवश्यक परिपथ का नामांकित आरेख बनाइए। निर्गत धारा का चित्रांकन भी कीजिए। [2018]
उत्तर :
p-n सन्धि डायोड पूर्ण-तरंग दिष्टकारी के रूप में (p-n Junction Diode as Full Wave Rectifier)पूर्ण-तरंग दिष्टीकरण क्रिया में निवेशी प्रत्यावर्ती वोल्टेज के दोनों अर्द्धचक्रों के समय निर्गत धारा एक ही दिशा में प्राप्त . होती है। इसके लिए दो सन्धि डायोड D₁ व D₂ इस प्रकार प्रयुक्त किए जाते हैं कि एक डायोड तरंग के पहले आधे चक्र का तथा दूसरा डायोड तरंग के दूसरे आधे चक्र का दिष्टीकरण करता है। p-n सन्धि डायोड का पूर्ण-तरंग दिष्टकारी परिपथ चित्र-14.31 (a) में दिखाया गया है तथा इसके निवेशी व निर्गत तरंग रूपों को चित्र-14.31 (b) में प्रदर्शित किया गया है।

जिस प्रत्यावर्ती वोल्टता का दिष्टकरण करना होता है (अर्थात् निवेशी प्रत्यावर्ती वोल्टेज) उसे एक ट्रांसफॉर्मर की प्राथमिक कुण्डली P के सिरों के बीच जोड़ते हैं। ट्रांसफॉर्मर की द्वितीयक कुण्डली के A व B सिरों को दो p-n सन्धि डायोडों के p क्षेत्रों से जोड़ते हैं तथा n-सिरों को परस्पर जोड़कर इनके उभयनिष्ठ बिन्दु M तथा द्वितीयक कुण्डली S₁S₂ के केन्द्रीय अंश निष्कासित बिन्दु (central tapping point) T के बीच एक लोड प्रतिरोध R_L जोड़ देते हैं। निर्गत दिष्ट वोल्टेज को बाह्य. प्रतिरोध R_L के सिरों पर प्राप्त किया जाता है।

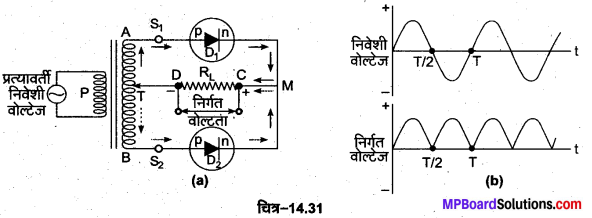
कार्य-विधि-निवेशी प्रत्यावर्ती वोल्टेज के पहले आधे चक्र में, जब द्वितीयक कुण्डली का A सिरा मध्य-बिन्दु T के सापेक्ष धनात्मक तथा B सिरा मध्य-बिन्दु T के सापेक्ष ऋणात्मक होता है तो सन्धि डायोड D₁ अग्र अभिनत हो जाता है और इसमें धारा प्रवाहित होने लगती है, जबकि इस समय सन्धि डायोड D₂ उत्क्रम अभिनत होता है और इसमें धारा नहीं बहती है। सन्धि डायोड D₁ से धारा, लोड प्रतिरोध R_L में C से D की ओर बहती है, जिससे निर्गत विभव प्राप्त होता है।

निवेशी वोल्टेज के अगले आधे चक्र में, जब ट्रांसफॉर्मर का A सिरा T के सापेक्ष ऋणात्मक तथा B सिरा धनात्मक होता है तो इस समय सन्धि डायोड D₁ उत्क्रम अभिनत हो जाता है और इसमें धारा नहीं बहती है, जबकि इस समय सन्धि डायोड D₂ अग्र अभिनत हो जाता है और उसमें धारा प्रवाहित होने लगती है। डायोड D₂ से धारा, लोड प्रतिरोध R_L में पुन: C से D की ओर बहती है, जिससे निर्गत विभव प्राप्त होता है।

इस प्रकार निवेशी विभव के पूर्ण चक्र के लिए बाह्य प्रतिरोध R7 में धारा C से D की ओर प्रवाहित होती है अर्थात् लोड प्रतिरोध में प्रवाहित धारा दिष्ट धारा है। यह निर्गत धारा एकदिशीय स्पन्दों के रूप में होती है, जिसे समकारी फिल्टरों के द्वारा लगभग स्थायी धारा के.रूप में बदला जा सकता है।

प्रश्न 8.
प्रकाश उत्सर्जक डायोड ‘LED’ क्या है? एक परिपथ आरेख खींचिए तथा इसकी क्रिया-विधि समझाइए। प्रचलित लैम्पों की तुलना में इसके लाभ बताइए। [2016]]
अथवा
LED क्या होता है? इसका सिद्धान्त समझाइए। LED में प्रयोग में आने वाली किसी अर्द्धचालक का नाम लिखिए। [2018]
उत्तर :
प्रकाश उत्सर्जक डायोड (Light Emitting Diode : ‘LED’)-प्रकाश उत्सर्जक डायोड एक विशिष्ट प्रकार का अधिक अपमिश्रित (highly doped) p-n सन्धि डायोड होता है जो अग्र-अभिनति (forward biasing) में प्रकाश उत्सर्जित करता है।

प्रकाश उत्सर्जक डायोड (LED) सेल एक ऐसी युक्ति है जो अभिनत बैटरी से प्राप्त वैद्युत ऊर्जा को विकिरण ऊर्जा में परिवर्तित करती है। LED का प्रतीक चिह्न तथा परिपथ आरेख चित्र-14.32 में प्रदर्शित किया गया है। LED बनाने के लिए गैलियम आर्सेनाइड (GaAs), गैलियम फॉस्फाइड (GaP), गैलियम आर्सेनाइड फॉस्फाइड (GaAsP) आदि पदार्थ प्रयुक्त किये जाते हैं। LED के p-क्षेत्र को अभिनत बैटरी के धन सिरे से तथा n-क्षेत्र को बैटरी के ऋण सिरे से सम्बन्धित किया जाता है। परिपथ में एक धारा सीमक (current limiting) प्रतिरोध R लगाते हैं जो LED में प्रवाहित धारा को सुरक्षित सीमा से बढ़ जाने पर क्षतिग्रस्त होने से बचाता है। hv उत्सर्जित विकिरण (दृश्य अथवा अदृश्य) की ऊर्जा है।

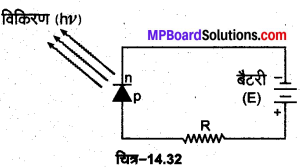
कार्यविधि (Working)-जब LED को अग्र-अभिनत किया जाता है तो n-क्षेत्र के बहुसंख्यक आवेश वाहक अर्थात् इलेक्ट्रॉन तथा p-क्षेत्र के बहुसंख्यक आवेश वाहक अर्थात् कोटर सन्धि की ओर गति करते हैं तथा सन्धि क्षेत्र में परस्पर संयोजित हो जाते हैं। संयोजन की इस क्रिया में मुक्त हुई ऊर्जा, वैद्युतचुम्बकीय तरंगों के रूप में सन्धि पर उत्पन्न हो जाती है। ऐसे वैद्युतचुम्बकीय फोटॉन जिनकी ऊर्जा LED के पदार्थ के वर्जित ऊर्जा अन्तराल (forbidden energy gap) के बराबर या उससे कम होती है, LED की सन्धि से बाहर प्रकाश के रूप में आ जाती है। जैसे-जैसे अग्र धारा का मान बढ़ता है LED से उत्सर्जित प्रकाश की तीव्रता भी बढ़ती जाती है और अन्ततः अपना महत्तम मान प्राप्त कर लेती है। यदि अग्र धारा का मान और अधिक बढ़ाएँ तो उत्सर्जित प्रकाश की तीव्रता पुनः घटने लगती है, अत: LED की अभिनति इस प्रकार समायोजित की जाती है कि वह अधिकतम प्रकाश उत्सर्जित करे अर्थात् उसकी दक्षता (efficiency) महत्तम हो।

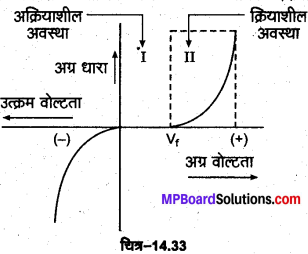
LED के अभिलक्षण (Characteristics of LED)-LED अवस्था । का वोल्टता-धारा (V-I) अभिलाक्षणिक वक्र, किसी सामान्य p-n. अग्र धारा सन्धि डायोड की भाँति ही होता है, जिसे चित्र-14.33 में प्रदर्शित किया गया है। वक्र में V_f, LED की आन्तरिक अवरोध वोल्टता को प्रदर्शित करता है जिसका मान बैटरी की उस वोल्टता के बराबर होता है जिस पर या जिससे अधिक वोल्टता पर LED में सुचारु रूप से धारा का प्रवाह होता है। अतः वक्र में क्षेत्र-I LED की अक्रियाशील अवस्था (non-active state) को तथा क्षेत्र-II, LED की क्रियाशील अवस्था (active state) को प्रदर्शित करता है।

LED की परम्परागत प्रदीप्त लैम्पों से तुलना (Comparison of LED’s with Common Incandescent Lamps)-

1. LED के संचालन के लिए प्रदीप्त लैम्पों की तुलना में बहुत कम वैद्युत वोल्टता एवं शक्ति की आवश्यकता होती है।
2. LED की दक्षता परम्परागत प्रदीप्त लैम्पों से कई गुना अधिक होती है।
3. LED का आकार परम्परागत लैम्पों के आकार की अपेक्षा बहुत छोटा होता है।
4. LED का जीवनकाल, परम्परागत प्रदीप्त लैम्पों की तुलना में बहुत अधिक होता है।
5. LED के पूर्ण-प्रदीपन के लिए परम्परागत प्रदीप्त लैम्पों की तुलना में बहुत कम समय की आवश्यकता होती है।
6. LED से उत्सर्जित प्रकाश में ऊष्मीय ऊर्जा लगभग नगण्य होती है, अत: ये ठण्डा प्रकाश उत्सर्जित करते हैं जबकि . परम्परागत प्रदीप्त लैम्प से उत्सर्जित प्रकाश में ऊष्मीय ऊर्जा भी सम्मिलित रहती है।
7. LED पर्यावरण तथा पारिस्थितिक तन्त्र (ecosystem) को बहुत कम क्षति पहुँचाते हैं। अत: ये अधिक पारिस्थितिक मित्र (eco-friendly) युक्ति है।

LED के उपयोग (Uses of LED)-इसके निम्नलिखित उपयोग हैं

• कम्प्यूटर तथा कैलकुलेटर के अंक व शब्द प्रदर्शन (alpha numeric display) में LED का प्रयोग किया जाता है।
• चोर सूचक घण्टी (burglar alarm) बनाने में LED का प्रयोग किया जाता है।
• प्रकाशीय कम्प्यूटर मैमोरी में सूचना प्रवेश के लिए LED का प्रयोग किया जाता है।
• LED का उपयोग टी०वी०, डी०वी०डी० प्लेयर, म्यूजिक प्लेयर आदि के रिमोट में अवरक्त विकिरण के उत्सर्जन के लिए किया जाता है।

प्रश्न 9.
फोटो डायोड प्रकाश संसूचक की भाँति कार्य करता है। स्पष्ट कीजिए। [2017]
अथवा
फोटो डायोड में p-n सन्धि डायोड किस प्रकार से संयोजित किया जाता है? इसका क्या उपयोग है? [2016]
अथवा
फोटो डायोड क्या है? प्रकाश संसूचक के रूप में इसके अनुप्रयोग को समझाइए। [2018]
उत्तर :
फोटो डायोड (Photo Diode)-फोटो डायोड एक, ऐसी युक्ति है जो प्रकाशित संकेतों के संसूचन में : प्रयुक्त की जाती है। फोटो डायोड एक प्रकाश संवेदनशील (photosensitive) अर्द्धचालक से बना p-n सन्धि डायोड है जो उत्क्रम अभिनति (reverse biasing) अथवा पश्च-दिशिक में कार्य करता है। यह डायोड सन्धि प्रकाश-प्रभाव पर आधारित है।

रचना- फोटो डायोड का निर्माण करने हेतु एक p-n सन्धि को, जिसका p-क्षेत्र बहुत पतला व पारदर्शी हो, एक काँच अथवा प्लास्टिक के आवरण में इस प्रकार रखा जाता है कि सन्धि के ऊपरी भाग पर प्रकाश सरलतापूर्वक पहुँच जाए। आवरण में प्रयुक्त प्लास्टिक के शेष भागों पर काला पेन्ट कर देते हैं।

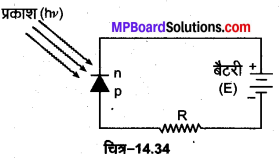
कार्यविधि-फोटो डायोड का विद्युतीय परिपथ चित्र-14.34 में प्रदर्शित है। जब p-n सन्धि पर बिना प्रकाश डाले पर्याप्त वोल्टेज (0.1 वोल्ट) लगाकर उत्क्रम अभिनत किया जाता है तो सन्धि के दोनों ओर के अल्पसंख्यक वाहक सन्धि को पार कर जाते हैं, जिसके कारण एक संतृप्त परन्तु लघु धारा (कुछ µA की) का प्रवाह आरम्भ हो जाता है। इस धारा को अदीप्त धारा (dark current) कहते हैं। इस धारा की दिशा सन्धि पर क्षेत्र n से p की ओर होती है। यदि p-n सन्धि पर इतनी ऊर्जा का प्रकाश डाला जाए जिसका परिमाण सन्धि के निषिद्ध ऊर्जा अन्तराल E_g से अधिक (hv > E_g) हो तो, सन्धि के समीप अल्पसंख्यक वाहकों का घनत्व बढ़ जाता है।

सन्धि के उत्क्रम अभिनत होने के कारण जब ये वाहक सन्धि को पार करते हैं तो ये सन्धि पर उत्पन्न धारा की प्रबलता को बढ़ा देते हैं। इस कारण परिपथ की कुल धारा का मान बढ़ जाता है, इस धारा को प्रकाश धारा कहते हैं। फोटो डायोड की सन्धि को प्रदीप्त करने के बाद सन्धि पर पहले से ही मौजूद संतृप्त धारा के मान में हुए परिवर्तन को ज्ञात करके सन्धि पर आपतित प्रकाश की तीव्रता की गणना कर ली जाती है। इस प्रकार यह डायोड प्रकाश संसूचक (light detector) की भाँति कार्य कक्षाएँ।

उपयोग

• इसका उपयोग प्रकाश संचालित कुँजियों में किया जाता है।
• कम्प्यूटर पंच कार्डों आदि को पढ़ने में किया जाता है।

प्रश्न 10.
सौर सेल की कार्य-विधि उपयुक्त आरेख की सहायता से समझाइए। इसके उपयोग भी लिखिए।
अथवा
सोलर सेल की संरचना तथा कार्य-विधि समझाइए। [2018]
उत्तर :
सौर सेल (Solar Cell)-सौर सेल एक विशिष्ट प्रकार का अनअभिनत (unbiased) p-n सन्धि डायोड होता है जो सौर ऊर्जा को वैद्युत ऊर्जा में परिवर्तित करता है। सौर सेल में p-n सन्धि डायोड का p-टाइप क्षेत्र काफी पतला (लगभग 0.2 um) होता है जिससे इस पर आपतित प्रकाशफोटॉन बिना अधिक अवशोषित हुए p-n सन्धि पर पहुँच जाते हैं। p-टाइप क्षेत्र से एक धात्विक अंगुलीनुमा इलेक्ट्रोड (finger electrode) सम्बन्धित रहता है जो ऐनोड का कार्य करता है। डायोड के n-टाइप क्षेत्र के पदार्थ की प्रकृति, p-टाइप क्षेत्र के पदार्थ की प्रकृति के समान होती है परन्तु इसकी मोटाई p-टाइप क्षेत्र की अपेक्षा बहुत अधिक (लगभग 300 um) होती है। इसके नीचे एक धातु की परत होती है जो कैथोड की भाँति कार्य करती है। सौर सेल की संरचना को चित्र-14.35 (a) तथा इसके प्रतीक को चित्र-14.35 (b) में प्रदर्शित किया गया है।

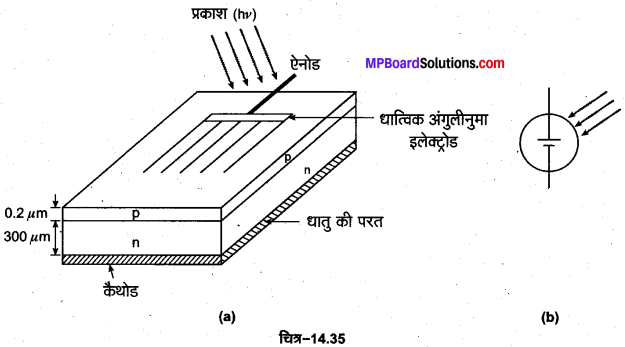
कार्य-विधि- सौर सेल बनाने के लिए सिलिकन अर्द्धचालक (E_g = 1.2 ev) तथा गैलियम आर्सेनाइड अर्द्धचालक (GaAs, E_g ≈1:53 ev) का प्रयोग किया जाता है क्योंकि सौर-विकिरण की अधिकतम ऊर्जा लगभग 1.5 ev कोटि की होती है। गैलियम आर्सेनाइड की फोटॉन अवशोषण क्षमता (अवशोषण गुणांक) लगभग 10⁴ प्रति सेमी अति उच्च होती है। अत: यह सौर सेल बनाने के लिए सिलिकन की तुलना में श्रेष्ठ है। जब सूर्य का प्रकाश सौर सेल पर आपतित होता है तो यह p-टाइप क्षेत्र को पार कर p-n सन्धि पर पहुँच जाता है, जहाँ पर यह सहसंयोजी बन्धों को तोड़कर इलेक्ट्रॉन-कोटर युग्म उत्पन्न कर देता है।

अवक्षय परत में n-क्षेत्र से p-क्षेत्र की ओर विद्यमान वैद्युत क्षेत्र E; के कारण p-क्षेत्र में उत्पन्न इलेक्ट्रॉन-कोटर युग्म के इलेक्ट्रॉन n-क्षेत्र की ओर गति करते हैं और शेष बचे कोटर p-क्षेत्र में रह जाते हैं। n-क्षेत्र में उत्पन्न इलेक्ट्रॉन-कोटर युग्म के कोटर वैद्युत क्षेत्र E; के कारण p क्षेत्र की ओर गति करते हैं और शेष बचे इलेक्ट्रॉन n क्षेत्र में रह जाते हैं। इस प्रकार p-क्षेत्र में अतिरिक्त कोटर एवं n-क्षेत्र में अतिरिक्त इलेक्ट्रॉनों के कारण यह युक्ति एक बैटरी की भाँति व्यवहार करती है।

एक सौर सेल से लगभग 0.4 वोल्ट से 0.5 वोल्ट पर लगभग 60 मिलीऐम्पियर धारा प्राप्त होती है। अतः व्यावहारिक उपयोग के लिए अनेक सौर सेलों को एक विशेष श्रेणीक्रम एवं समान्तर-क्रम संयोजन में व्यवस्थित कर. प्रयुक्त करते हैं। सौर सेलों के संयोजन से बनी यह युक्ति सोलर पैनल (solar panel) कहलाती है।

सौर सेल के उपयोग (Uses of Solar Cell)-
1. सौर सेलों से बने सोलर पैनलों का प्रयोग सुदूर क्षेत्रों (remote areas) में जहाँ वैद्युत ऊर्जा के कोई भी स्रोत उपलब्ध नहीं होते हैं, स्ट्रीट लाइट, रेडियो, टेलीविजन आदि उपकरणों को चलाने में किया जाता है।

2. सौर सेलों से बने सोलर पैनलों का प्रयोग सोलर वाटर हीटर के रूप में किया जाता है।

3. कृत्रिम उपग्रहों में लगी बैटरियों के आवेशन के लिए सोलर पैनलों का उपयोग किया जाता है।

प्रश्न 11.
जेनर डायोड क्या है? इसकी धारा-वोल्टता अभिलाक्षणिक खींचिए तथा समझाइए कि यह वोल्टता . नियन्त्रक के रूप में कैसे कार्य करता है? [2015]
अथवा
जेनर डायोड क्या होता है? इसका प्रतीक चिह्न प्रदर्शित कीजिए। जेनर डायोड का वोल्टता नियन्त्रक के रूप में प्रयोग परिपथ बनाकर समझाइए। [2015]
अथवा
जेनर डायोड क्या है? एक परिपथ आरेख की सहायता से जेनर डायोड का उपयोग, वोल्टता नियन्त्रक के रूप में समझाइए। [2015, 16]
अथवा
जेनर डायोड क्या है? जेनर डायोड का उपयोग वोल्टेज रेगुलेटर (stablizer) के रूप में परिपथ आरेख की सहायता से समझाइए। [2014, 15, 17, 18]
अथवा
उचित परिपथ आरेख की सहायता से विभव नियन्त्रक के रूप में जेनर डायोड की क्रियाविधि समझाइए। [2016]]
अथवा
वोल्टता-नियन्त्रक के रूप में जेनर डायोड की उपयोगिता उपयुक्त परिपथ द्वारा स्पष्ट कीजिए। [2017, 18]
उत्तर :
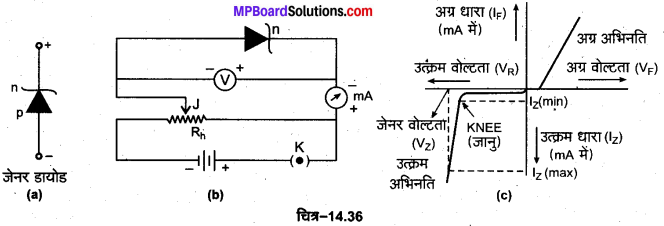
जेनर डायोड अथवा भंजक डायोड (Zener Diode or Breakdown Diode)—“जेनर डायोड विशेष रूप से निर्मित अधिक अपमिश्रित (heavily doped) p-n सन्धि डायोड होता है जो उत्क्रम अभिनति में भंजक वोल्टता (breakdown voltage) पर बिना खराब हुए निरन्तर कार्य कर सकता है।” जेनर डायोड का प्रतीक [चित्र-14.36 (a)] से प्रदर्शित है।

जेनर डायोड में p-n सन्धि डायोड के अधिक अपमिश्रित होने के कारण p-क्षेत्र में ग्राही तथा n-क्षेत्र में दाता अशुद्धियों के उच्च घनत्व के कारण अवक्षय परत की चौड़ाई बहुत कम (लगभग 1 µm) हो जाती है जिसके फलस्वरूप बाह्य बैटरी द्वारा आरोपित सूक्ष्म उत्क्रम वोल्टता (5 वोल्ट) के संगत सन्धि क्षेत्र में वैद्युत क्षेत्र बहुत अधिक हो जाता है। यह प्रबल वैद्युत क्षेत्र संयोजी बैण्ड में उपस्थित इलेक्ट्रॉन को चालन बैण्ड में जाने के लिए पर्याप्त ऊर्जा दे देता है।

यह इलेक्ट्रॉन अवक्षय परत से होकर n-क्षेत्र की ओर गति करता है। ये इलेक्ट्रॉन ही भंजन के समय उच्च धारा के लिए उत्तरदायी होते हैं। उच्च वैद्युत क्षेत्र के कारण इलेक्ट्रॉनों का उत्सर्जित होना आन्तरिक क्षेत्रीय उत्सर्जन अथवा क्षेत्रीय आयनन कहलाता है। एक निश्चित उत्क्रम वोल्टता (V_z) के पश्चात् उत्क्रम धारा I_z का मान वोल्टता परिवर्तन के सापेक्ष बहुत तेजी से बढ़ता है। यह निश्चित उत्क्रम वोल्टता, जेनर वोल्टेज (zener voltage) कहलाता है तथा पश्च धारा का अनियन्त्रित रूप से तेजी से बढ़ना जेनर भंजन (zener breakdown) कहलाता है।

जेनर डायोड का धारा-वोल्टता अभिलाक्षणिक वक्र- जेनर डायोड की धारा-वोल्टता अभिलक्षण का विद्युत परिपथ आरेख चित्र-14.36 (b) में प्रदर्शित है। सर्वप्रथम कुंजी K को लगाकर धारा नियन्त्रक R_h की सपी कुंजी J को इस प्रकार व्यवस्थित करते हैं कि इसके समान्तर क्रम में जुड़े वोल्टमीटर V का पाठ्यांक न्यूनतम हो जाए। इस स्थिति में वोल्टमीटर V तथा मिलीमीटर mA का पाठ्यांक नोट कर लेते हैं। पश्च वोल्टता को धीरे-धीरे बढ़ाकर उसके संगत वोल्टमीटर V तथा मिलीअमीटर (mA) के पाठ्यांक नोट कर लेते हैं।

इस पश्च वोल्टता को तब तक बढ़ाते जाते हैं जब तक कि मिलीअमीटर mA के पाठ्यांकों में अचानक से वृद्धि न हो जाए। जिस क्षण ऐसा होता है उस क्षण वोल्टमीटर का पाठ्यांक जेनर भंजक वोल्टता V_z को. निरूपित करेगा। पश्च वोल्टता V_z को थोड़ा सा बढ़ाकर, उसके संगत पश्च धारा के मानों को नोट कर लेते हैं। इन पाठ्यांकों की सहायता धारा i व वोल्टता में ग्राफ खींचते है। यही ग्राफ जेनर डायोड का धारा वोल्टता अभिलक्षण ग्राफ कहलाता है [चित्र-14.36(c)]]

जेनर डायोड से प्रवाहित होने वाली धारा में अत्यधिक परिवर्तन होने पर भी जेनर वोल्टता नियत रहती है। इसी गुण के कारण जेनर डायोड को दिष्ट वोल्टता नियन्त्रक (dc voltage regulator) के रूप में प्रयोग किया जाता है।

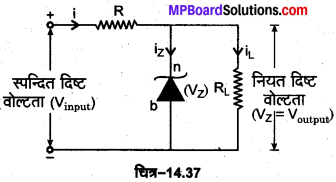
जेनर डायोड वोल्टता नियन्त्रक के रूप में (Zener Diode as Voltage Stabilizer)- जेनर डायोड को वोल्टता नियन्त्रक के रूप में प्रयुक्त करने के लिए आवश्यक परिपथ को चित्र-14.37 में प्रदर्शित किया गया है। जेनर डायोड पर एक स्पन्दित दिष्ट वोल्टता V_input को श्रेणीक्रम में संयोजित प्रतिरोध R से होते हुए जेनर डायोड से इस प्रकार संयोजित करते हैं कि जेनर डायोड उत्क्रम अभिनत हो। जब निवेशी वोल्टता में वृद्धि होती है तो जेनर डायोड तथा प्रतिरोध R से प्रवाहित होने वाली धारा में वृद्धि हो जाती है। यदि जेनर डायोड के सिरों पर वोल्टता V_input का मान जेनर डायोड के जेनर वोल्टता (V_z) से अधिक है तो डायोड भंजन स्थिति में होता है तथा जेनर डायोड की जेनर वोल्टता नियत रहती है, अत: जेनर डायोड के सिरों पर वोल्टता में कोई परिवर्तन हुए बिना ही R के सिरों पर वोल्टता में वृद्धि हो जाती है।

इसी प्रकार जब निवेशी वोल्टता घटती है तो जेनर डायोड व प्रतिरोध R से प्रवाहित होने वाली धारा में कमी हो जाती है। अब जेनर डायोड के सिरों पर वोल्टता में कोई परिवर्तन हुए बिना ही R के सिरों पर वोल्टता में कमी हो जाती है। इस पर निवेशी वोल्टता के बढ़ने या घटने पर जेनर डायोड के सिरों पर वोल्टता में कोई परिवर्तन हुए बिना प्रतिरोध R के सिरों पर वोल्टता में वृद्धि अथवा कमी हो जाती है। इस प्रकार जेनर डायोड वोल्टता नियन्त्रक के रूप में कार्य करता है।

प्रश्न 12.
ट्रांजिस्टर क्या होता है? आवश्यक चित्र की सहायता से p-n-p ट्रांजिस्टर की रचना तथा कार्यविधि समझाइए।
अथवा
p-n-p ट्रांजिस्टर की रचना एवं कार्य-विधि का वर्णन कीजिए। [2017]
उत्तर :
ट्रांजिस्टर (Transistor)-सन्धि ट्रांजिस्टर p तथा n प्रकार के अर्द्धचालकों से बनी एक इलेक्ट्रॉनिक युक्ति है, जो ट्रायोड वाल्व के स्थान पर प्रयुक्त की जाती है। ट्रांजिस्टर दो प्रकार के होते हैं

• p-n-p ट्रांजिस्टर,
• n-p-n ट्रांजिस्टर।

1. P-n-p ट्रांजिस्टर की रचना-इसमें n-टाइप अर्द्धचालक की एक बहुत पतली परत को दो p-टाइप अर्द्धचालकों के छोटे-छोटे क्रिस्टलों के बीच दबाकर रखते हैं [चित्र-14.38 (a)]। इस बहुत पतली n परत को आधार (base) तथा इसके बाएँ व दाएँ क्रिस्टलों को क्रमशः उत्सर्जक (emitter) व संग्राहक (collector) कहते हैं। इन्हें क्रमश: B, E तथा C से प्रदर्शित करते हैं। उत्सर्जक को आधार के सापेक्ष, धन विभव तथा संग्राहक को आधार के सापेक्ष, ऋण विभव दिया जाता है। इस प्रकार बायीं ओर की.उत्सर्जक आधार (p-n) संधि अग्र अभिनत (अल्प प्रतिरोध वाली) है तथा दायीं ओर की आधार संग्राहक (n-p) संधि उत्क्रम अभिनत (उच्च प्रतिरोध वाली) है। इसका प्रतीक चित्र-14.38 (b) में दिखाया गया है, जिसमें बाण की दिशा वैद्युत धारा की दिशा (कोटरों के चलने की दिशा) को प्रदर्शित करती है।

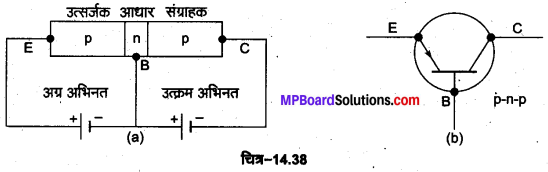
p-n-p ट्रांजिस्टर की कार्य-विधि- चित्र-14.39 में p-n-p ट्रांजिस्टर का उभयनिष्ठ आधार परिपथ दिखाया. गया है। इसके दोनों p-क्षेत्रों में आवेश वाहक (धन) कोटर होते हैं, जबकि n-क्षेत्र में आवेश वाहक इलेक्ट्रॉन होते हैं। इसमें बायीं ओर की उत्सर्जक-आधार (p-n) सन्धि को बैटरी से थोड़ा-सा अग्र अभिनत विभव V_EB देते हैं, जबकि दायीं ओर की आधार-संग्राहक (n-p) सन्धि को बैटरी से बड़ा उत्क्रम अभिनत विभव V_CB देते हैं।

उत्सर्जक-आधार (p-n) सन्धि के अग्र अभिनत होने के कारण, p-क्षेत्र में उपस्थित कोटर आधार की ओर गति करते हैं, जबकि n-क्षेत्र में उपस्थित इलेक्ट्रॉन p-क्षेत्र (उत्सर्जक) की ओर गति करते हैं। चूँकि आधार बहुत पतला है

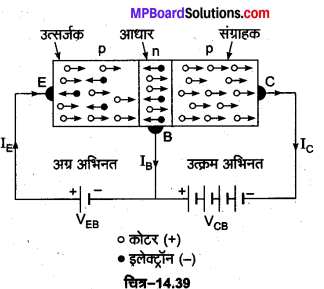
इस कारण इसमें प्रवेश करने वाले अधिकतर कोटर (लगभग 98%) इसे पार करके संग्राहक C तक पहुँच जाते हैं, जबकि उनमें से बहुत कम (लगभग 2%) आधार में उपस्थित इलेक्ट्रॉनों से संयोग करते हैं। जैसे ही कोई कोटर इलेक्ट्रॉन से संयोग करता है वैसे ही उत्सर्जक में बैटरी के धन ध्रुव के निकट एक सहसंयोजक बन्ध टूट जाता है। बन्ध टूटने से उत्पन्न इलेक्ट्रॉन बैटरी के धन ध्रुव से बैटरी में प्रवेश कर जाता है। ठीक इसी क्षण एक नया इलेक्ट्रॉन बैटरी V_EB के ऋण सिरे से निकलकर आधार B में प्रवेश करता है। ठीक इसी क्षण एक इलेक्ट्रॉन उत्सर्जक E में से निकलकर बैटरी V_EB के धन सिरे पर पहुँचता है। इस कारण उत्सर्जक E में एक कोटर उत्पन्न हो जाता है, जो आधार की ओर चलना प्रारम्भ कर देता है। इस प्रकार आधार उत्सर्जक परिपथ में एक क्षीण आधार धारा (I_B) बहने लगती है।

जो कोटर संग्राहक में प्रवेश कर जाते हैं, वे उत्क्रम अभिनत के कारण टर्मिनल C पर पहुँच जाते हैं। जैसे ही कोई कोटर टर्मिनल C पर पहुँचता है, बैटरी V_CB के ऋण सिरे से एक इलेक्ट्रॉन आकर उसे उदासीन कर देता है, पुनः ठीक इसी क्षण एक इलेक्ट्रॉन उत्सर्जक E से निकलकर बैटरी V_EB के धन सिरे पर पहुँच जाता है। इस कारण उत्सर्जक में एक कोटर उत्पन्न हो जाता है जो आधार की ओर चलना प्रारम्भ कर देता है। इस प्रकार संग्राहक उत्सर्जक परिपथ में सग्राहक धारा I_c बहने लगती है। आधार टर्मिनल B से चलने वाली धारा को आधार धारा I_B तथा संग्राहक टर्मिनल C से बाहर जाने वाली धारा को संग्राहक धारा I_C कहते हैं। धाराएँ I_B तथा I_C मिलकर उत्सर्जक E में प्रवेश करती हैं, अतः इसे उत्सर्जक धारा I_E कहते हैं।
अत: I_E = I_B +I_c
इस प्रकार p-n-p ट्रांजिस्टर के अन्दर धारा प्रवाह कोटरों के उत्सर्जक से संग्राहक की ओर चलने के कारण होता है, जबकि बाहरी परिपथ में इलेक्ट्रॉनों के चलने के कारण होता है।

आधार के बहुत पतला होने के कारण आधार में संयोजित होने वाले कोटर-इलेक्ट्रॉनों की संख्या बहुत कम होती है। इस कारण लगभग सभी कोटर, जो उत्सर्जक से आधार में प्रवेश करते हैं, संग्राहक तक पहुँच जाते हैं इसलिए संग्राहक धारा I_c, उत्सर्जक धारा I_E से कुछ ही कम होती है।

प्रश्न 13.
आवश्यक चित्र की सहायता से n-p-n ट्रांजिस्टर की रचना तथा कार्यविधि समझाइए। [2012]
अथवा
n-p-n ट्रांजिस्टर में वैद्युत चालन की क्रिया को समझाइए। इसमें आधार पतला क्यों होता है? p-n-p ट्रांजिस्टर की तुलना में यह अधिक उपयोगी क्यों है? [2018]
उत्तर :
n-p-n ट्रांजिस्टर की रचना-इसमें p-टाइप अर्द्धचालक की एक बहुत पतली परत को दो n-टाइप अर्द्धचालकों के छोटे-छोटे क्रिस्टलों के बीच दबाकर रखते हैं। इस पतली परत p को आधार (base) तथा इसके बाएँ व दाएँ क्रिस्टलों को क्रमश: उत्सर्जक (emitter) व संग्राहक (collector) कहते हैं। इन्हें क्रमश: B, E तथा C से प्रदर्शित करते हैं। उत्सर्जक को आधार के सापेक्ष, ऋण विभव तथा संग्राहक को आधार के सापेक्ष धन विभव दिया जाता है। इस प्रकार बायीं ओर की उत्सर्जक-आधार (n-p) सन्धि अग्र अभिनत है तथा दायीं ओर की आधार-संग्राहक (p-n) सन्धि उत्क्रम अभिनत है। इसका प्रतीक चित्र-14.40 (b) में दिखाया गया है, जिसमें बाण की दिशा वैद्युत धारा की दिशा .(इलेक्ट्रॉनों के प्रवाह की विपरीत दिशा) को प्रदर्शित करती है।

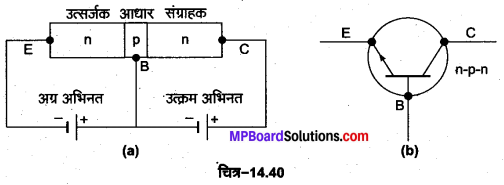
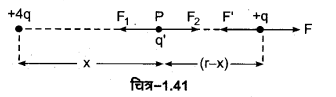
n-p-n ट्रांजिस्टर की कार्यविधि-n-p-n ट्रांजिस्टर का उभयनिष्ठ आधार परिपथ [चित्र-14.41] में दिखाया गया है। इसके दोनों n-क्षेत्रों में आवेश वाहक इलेक्ट्रॉन होते हैं, जबकि मध्य के पतले p-क्षेत्र में आवेश वाहक (धन) कोटर होते हैं। इसमें बायीं ओर के उत्सर्जक आधार (n-p) सन्धि को बैटरी से थोड़ा-सा अग्र अभिनत विभव V_BE दिया जाता है, जबकि दायीं ओर की आधार संग्राहक (p-n) सन्धि को बैटरी से बड़ा उत्क्रम अभिनत विभव V_Bc दिया जाता है।

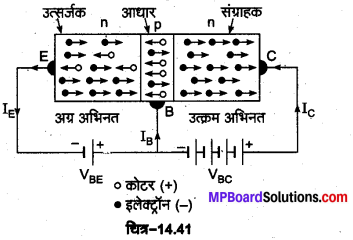
उत्सर्जक-आधार (p-n) सन्धि के अग्र अभिनत होने के कारण, उत्सर्जक , आधार उत्सर्जक (n-क्षेत्र) में उपस्थित इलेक्ट्रॉन आधार की ओर गति करते हैं, जबकि आधार (p-क्षेत्र से) कोटर उत्सर्जक की ओर गति करते हैं। चूँकि आधार बहुत पतला है। इस कारण इसमें प्रवेश करने वाले अधिकतर इलेक्ट्रॉन (लगभग 98%), इसे पार करके संग्राहक C तक पहुँच जाते हैं जबकि उनमें से बहुत कम (लगभग 2%) आधार में | उपस्थित कोटरों से संयोग करते हैं। जैसे ही कोई इलेक्ट्रॉन कोटर से संयोग करता है वैसे ही बैटरी V_EB के धन सिरे के निकट आधार में एक सहसंयोजक बन्ध टूट जाता है। बन्ध टूटने से आधार में उत्पन्न इलेक्ट्रॉन टर्मिनल B से बैटरी V_EB के धन सिरे से बैटरी में प्रवेश करता है। ठीक इसी क्षण एक इलेक्ट्रॉन बैटरी V_EB के ऋण सिरे से निकलकर टर्मिनल E के द्वारा उत्सर्जक में प्रवेश करता है। आधार से. एक इलेक्ट्रॉन के बैटरी V_EB में प्रवेश करने पर आधार में एक कोटर उत्पन्न हो जाता है जो संयोग के कारण नष्ट हुए कोटर की क्षतिपूर्ति करता है। इस प्रकार आधार उत्सर्जक परिपथ में आधार धारा (I_B) बहने लगती है।

जो इलेक्ट्रॉन संग्राहक में प्रवेश कर जाते हैं, वे उत्क्रम अभिनत के कारण टर्मिनल C पर पहुँच जाते हैं। जैसे ही कोई इलेक्ट्रॉन टर्मिनल C को छोड़कर बैटरी V_BC के धन सिरे में प्रवेश करता है, वैसे ही बैटरी V_BE के ऋण सिरे से एक इलेक्ट्रॉन उत्सर्जक में प्रवेश करता है। इस प्रकार संग्राहक-उत्सर्जक परिपथ में धारा बहने लगती है।

आधार टर्मिनल B में प्रवेश करने वाली क्षीण धारा को आधार धारा I_B तथा संग्राहक टर्मिनल C में प्रवेश करने वाली संग्राहक धारा I_c मिलकर उत्सर्जक टर्मिनल E से निकलती हैं, अत: इसे उत्सर्जक धारा I_E कहते हैं।
अतः I_E = I_B + I_c

इस प्रकार n-p-n ट्रांजिस्टर के अन्दर तथा बाह्य परिपथ में धारा प्रवाह इलेक्ट्रॉनों के कारण होता है।
ट्रांजिस्टर में आधार पतला रखे जाने का कारण-ट्रांजिस्टर के आधार क्षेत्र में कोटरों तथा इलेक्ट्रॉनों के संयोजन को कम करने के लिए आधार को पतला बनाया जाता है। n-p-n ट्रांजिस्टर, p-n-p ट्रांजिस्टर की तुलना में अधिक उपयोगी होता है क्योंकि इसमें धारा वाहक इलेक्ट्रॉन होते हैं, जबकि p-n-p ट्रांजिस्टर में धारा वाहक कोटर होते हैं। धारा वाहक इलेक्ट्रॉन, कोटर की अपेक्षा अधिक गतिशील होते हैं।

प्रश्न 14.
ट्रांजिस्टर परिपथ के विन्यास कितने प्रकार के होते हैं?
उत्तर :
ट्रांजिस्टर परिपथ के विन्यास-ट्रांजिस्टर में तीन टर्मिनल उत्सर्जक (E), आधार (B) तथा संग्राहक (C) होते हैं। अतः किसी परिपथ में निवेशी तथा निर्गत का संयोजन इस प्रकार होना चाहिए कि तीनों टर्मिनलों में से कोई एक (E या B या C) निवेशी तथा निर्गत में उभयनिष्ठ हो। इस आधार पर ट्रांजिस्टर को तीन विन्यासों में संयोजित किया जा सकता है।
1. उभयनिष्ठ आधार विन्यास- इस विन्यास में ट्रांजिस्टंर के आधार टर्मिनल (B) को निर्गत तथा निवेशी परिपथों के मध्य उभयनिष्ठ करके भू-सम्पर्कित कर देते हैं

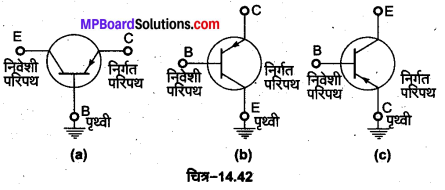
2. उभयनिष्ठ उत्सर्जक विन्यास-इस विन्यास में उत्सर्जक टर्मिनल (E) को निर्गत तथा निवेशी परिपथों के मध्य उभयनिष्ठ करके भू-सम्पर्कित कर देते हैं [चित्र-14.42 (b)]।

3. उभयनिष्ठ संग्राहक विन्यास–इस विन्यास में संग्राहक टर्मिनल (C) को निर्गत तथा निवेशी परिपथों के मध्य उभयनिष्ठ करके भू-सम्पर्कित कर देते हैं [चित्र-14.42 (c)]|

प्रश्न 15.
ट्रांजिस्टर के अभिलक्षण वक्र क्या हैं? ये कितने प्रकार के होते हैं? उभयनिष्ठ उत्सर्जक विन्यास में n-p-n ट्रांजिस्टर के अभिलाक्षणिक वक्र परिपथ आरेख बनाकर समझाइए।
अथवा
उभयनिष्ठ उत्सर्जक विन्यास में n-p-n ट्रांजिस्टर का अभिलाक्षणिक वक्र प्राप्त करने हेतु आवश्यक परिपथ आरेख बनाइए। निवेशी एवं निर्गत अभिलाक्षणिक वक्रों से प्राप्त निष्कर्षों का उल्लेख कीजिए। [2017]
उत्तर :
ट्रांजिस्टर के अभिलक्षण वक्र (Characteristics Curves of Transistor)-किसी ट्रांजिस्टर परिपथ में निर्गत तथा निवेशी धारा के मान में वोल्टता के साथ होने वाले परिवर्तन को निरूपित करने वाले वक्र ट्रांजिस्टर के अभिलाक्षणिक वक्र कहलाते ये तीन प्रकार के होते हैं

• निवेशी अभिलाक्षणिक वक्र,
• निर्गत अभिलाक्षणिक वक्र तथा
• अन्तरण अभिलाक्षणिक वक्र।

उभयनिष्ठ उत्सर्जक विन्यास में ट्रांजिस्टर के अभिलाक्षणिक वक्र (Characteristic Curves of a Transistor in Common Emitter Configuration)-किसी n-p-n ट्रांजिस्टर के उभयनिष्ठ उत्सर्जक विन्यास को चित्र-14.43 में प्रदर्शित किया गया है। इस विन्यास में आधार-उत्सर्जक परिपथ को निम्न विभव बैटरी V_BB की सहायता से अग्र अभिनत तथा संग्राहक-उत्सर्जक परिपथ को उच्च विभव बैटरी V_cc की सहायता से उत्क्रम अभिनत करते हैं। इस विन्यास में संग्राहक टर्मिनल का विभव सर्वाधिक, उत्सर्जक टर्मिनल का विभव सबसे कम तथा आधार टर्मिनल का विभव इन दोनों टर्मिनलों के विभवों के मध्य होना चाहिए। इस विन्यास में निवेशी (input) आधार तथा उत्सर्जक के बीच लगाते हैं तथा निर्गत (output) संग्राहक व उत्सर्जक के बीच प्राप्त होता है।

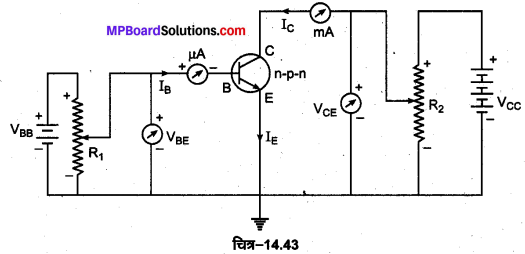
निवेशी अभिलाक्षणिक वक्र (Input Characteristics Curve)- ट्रांजिस्टर के उभयनिष्ठ उत्सर्जक विन्यास में आधार-उत्सर्जक वोल्टता (V_BE) में परिवर्तन के संगत आधार धारा (I_B) में परिवर्तन होना निवेशी अभिलाक्षणिक कहलाता है। उभयनिष्ठ उत्सर्जक विन्यास में नियत संग्राहक-उत्सर्जक वोल्टता के लिए आधार धारा (I_B) तथा आधार-उत्सर्जक वोल्टता (V_BE) के बीच खींचा गया वक्र, निवेशी अभिलाक्षणिक वक्र कहलाता है। इसके लिए संग्राहक-उत्सर्जक वोल्टता (V_BE ) को 1 वोल्ट पर नियत रखकर आधार-उत्सर्जक वोल्टता (V_BE) को धीरे-धीरे बढ़ाते हुए उनके संगत आधार धारा (I_B) का मान पढ़ते हैं। इस प्रकार I_B तथा V_BE के बीच खींचा गया वक्र, निवेशी अभिलाक्षणिक वक्र है। इसी प्रकार अन्य वक्र V_CE को 10 वोल्ट पर स्थिर रखकर प्राप्त किया जा सकता है (चित्र-14.44)।

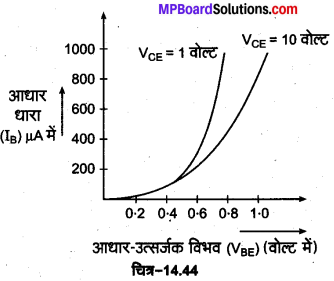
निर्गत अभिलाक्षणिक वक्र (Output Characteristics Curve)-ट ्रांजिस्टर के उभयनिष्ठ उत्सर्जक विन्यास में संग्राहक-उत्सर्जक वोल्टता (V_CE) में परिवर्तन के साथ संग्राहक धारा (I_C) में परिवर्तन होना निर्गत अभिलाक्षणिक वक्र कहलाता है तथा नियत आधार धारा । (I_B) के लिए. संग्राहक-उत्सर्जक वोल्टता (V_CE) तथा संग्राहक धारा (I_c) के बीच खींचा गया वक्र, निर्गत अभिलाक्षणिक वक्र कहलाता है।

आधार-उत्सर्जक वोल्टता (V_BE) में सूक्ष्म वृद्धि करने पर उत्सर्जक क्षेत्र से कोटर धारा तथा आधार क्षेत्र से इलेक्ट्रॉन धारा दोनों में वृद्धि होती है, जिसके परिणामस्वरूप आधार धारा I_B तथा संग्राहक धारा I_C में अनुपातिक रूप से वद्धि हो जाती है। अतः स्पष्ट है कि आधार धारा I_B में वृद्धि होने पर संग्राहक धारा I_C में भी वृद्धि हो जाती है। आधार धारा को 10 µA मान पर नियत रखते हुए संग्राहक-उत्सर्जकं वोल्टता को धीरे-धीरे बढ़ाते हए संगत संग्राहक-उत्सर्जक वोल्टता (V_CE) (वोल्ट में) संग्राहक धारा का मान पढ़ते हैं।

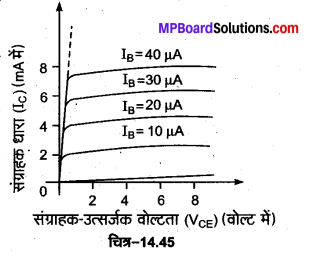
इस प्रकार संग्राहक-उत्सर्जक वोल्टता तथा संग्राहक धारा के बीच प्राप्त वक्र ही निर्गत अभिलाक्षणिक वक्र है। इसी प्रकार अन्य वक्र आधार धारा को 20 µA, 30 µA,… आदि मानों पर स्थिर रखकर प्राप्त किए जा सकते हैं [चित्र-14.45]।

प्रश्न 16.
ट्रांजिस्टर प्रवर्धक के रूप में किस प्रकार कार्य करता है?.p-n-p तथा n-p-n ट्रांजिस्टर उभयनिष्ठ उत्सर्जक प्रवर्धक की भाँति किस प्रकार कार्य करता है? समझाइए।
अथवा
p-n-p ट्रांजिस्टर के उभयनिष्ठ उत्सर्जक प्रवर्धन की कार्य-विधि परिपथ आरेख खींचकर समझाइए। [2014, 16, 17]
अथवा
n-p-n ट्रांजिस्टर ट्रांजिस्टर प्रवर्धक के रूप में किस प्रकार कार्य करता है? समझाइए। [2015]
अथवा
n-p-n ट्रांजिस्टर के उभयनिष्ठ उत्सर्जक प्रवर्धन क्रिया परिपथ आरेख बनाकर समझाइए। हुए। [2016]
अथवा
उभयनिष्ठ उत्सर्जक (CE) प्रवर्धक के रूप में प्रयुक्त ट्रांजिस्टर को परिपथ चित्र द्वारा प्रदर्शित कीजिए। इसके धारा लाभ तथा वोल्टेज लाभ का सूत्र प्राप्त कीजिए। स्पष्ट कीजिए कि निवेशी तथा निर्गत सिग्नल एक-दूसरे के विपरीत कला में होते हैं। [2017, 18]
उत्तर :
ट्रांजिस्टर प्रवर्धक के रूप में (Transistor as an Amplifier)-किसी दुर्बल प्रत्यावर्ती संकेत को . उसकी तरंग प्रकृति को अपरिवर्तित रखते हुए उसकी क्षमता में वृद्धि करने की प्रक्रिया को प्रवर्धन (amplification) तथा इस कार्य के लिए प्रयुक्त होने वाली युक्ति को प्रवर्धक (amplifier) कहते हैं। ट्रांजिस्टर को प्रवर्धक के रूप में निम्न तीन विन्यासों में प्रयुक्त किया जा सकता है

1. उभयनिष्ठ आधार प्रवर्धक
2. उभयनिष्ठ उत्सर्जक प्रवर्धक
3. उभयनिष्ठ संग्राहक प्रवर्धक

P-n-p ट्रांजिस्टर उभयनिष्ठ उत्सर्जक प्रवर्धक की भाँति (p-n-p Transistor as Common Emitter Amplifier)-चित्र-14.46 में p-n-p ट्रांजिस्टर प्रवर्धक का उभयनिष्ठ उत्सर्जक परिपथ प्रदर्शित है। यहाँ उत्सर्जक E के सापेक्ष, आधार ऋणात्मक है तथा उत्सर्जक E व आधार B दोनों के सापेक्ष, संग्राहक ऋणात्मक हैं। उत्सर्जक टर्मिनल उभयनिष्ठ होने के साथ-साथ भू-सम्पर्कित है। इसमें निवेशी सिग्नल को आधार B पर लगाया जाता है और निर्गत सिग्नल को संग्राहक C पर प्राप्त किया जाता है। चूँकि ट्रांजिस्टर में क्षीण आधार धारा के संगत प्रबल संग्राहक धारा प्राप्त होती है, अतः निवेशी सिग्नल को आधार पर लगाने से आधार धारा में अल्प परिवर्तन, संग्राहक धारा में बहुत अधिक परिवर्तन कर देता है। इस प्रकार इस परिपथ से पर्याप्त ‘धारा प्रवर्धन’ प्राप्त होता है, जबकि उभयनिष्ठ आधार परिपथ में धारा की हानि होती है।

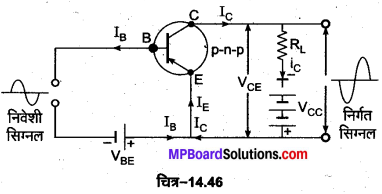
p-n-p ट्रांजिस्टर उभयनिष्ठ उत्सर्जक प्रवर्धक के लाभ-p-n-p ट्रांजिस्टर उभयनिष्ठ उत्सर्जक प्रवर्धक से प्राप्त विभिन्न लाभ निम्नलिखित हैं

1. ac धारा लाभ (ac Current Gain)-“एक नियत संग्राहक-उत्सर्जक वोल्टेज पर, संग्राहक धारा में परिवर्तन Δl_c तथा इसके संगत आधार धारा में परिवर्तन ΔI_B के अनुपात को ट्रांजिस्टर का ac धारा लाभ कहते हैं।” इसे ‘β’ से प्रदर्शित करते हैं।

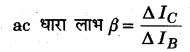
सामान्यत: β का मान 20 से 200 तक होता है।

2. ac वोल्टेज लाभ (ac Voltage Gain)-“निर्गत वोल्टेज में परिवर्तन तथा निवेशी वोल्टेज में परिवर्तन के अनुपात को वोल्टेज लाभ अथवा वोल्टेज प्रवर्धन कहते हैं।” इसे ‘A_v‘ से प्रदर्शित करते हैं।
ac वोल्टेज लाभ A_v = \(\beta \times \frac{R_{2}}{R_{1}}\) [जहाँ R₁ व R₂ क्रमशः निवेशी तथा निर्गत प्रतिरोध हैं।]

3. ac शक्ति लाभ (ac Power gain)-“वोल्टेज लाभ तथा धारा लाभ के गुणनफल को शक्ति लाभ कहते हैं।” इसे ‘A_P‘ से प्रदर्शित करते हैं।
अतः शक्ति लाभ = धारा लाभ × वोल्टेज लाभ अथवा A^p = \(\beta^{2} \times \frac{R_{2}}{R_{1}}\)

4. कला सम्बन्ध (Phase Relationship) उभयनिष्ठ उत्सर्जक प्रवर्धक में, निर्गत वोल्टेज सिग्नल तथा निवेशी वोल्टेज सिग्नल विपरीत कलाओं में होते हैं, अर्थात् इनके बीच 180° का कलान्तर होता है।

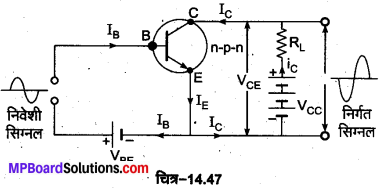
n-p-n ट्रांजिस्टर उभयनिष्ठ उत्सर्जक प्रवर्धक की भाँति (n-p-n Transistor as a Common Emitter Amplifier)-चित्र-14.47 में n-p-n ट्रांजिस्टर प्रवर्धक का उभयनिष्ठ उत्सर्जक परिपथ प्रदर्शित है। इसमें आधार B, उत्सर्जक E के सापेक्ष धनात्मक है तथा संग्राहक C, उत्सर्जक E तथा आधार B दोनों के सापेक्ष धनात्मक है। उत्सर्जक टर्मिनल उभयनिष्ठ होने के साथ-साथ भू-सम्पर्कित है। इसमें निवेशी सिग्नल को आधार B पर लगाया जाता है तथा निर्गत सिग्नल को संग्राहक C पर प्राप्त किया जाता है। चूँकि । ट्रांजिस्टर में क्षीण आधार धारा के संगत प्रबल संग्राहक धारा 8 प्राप्त होती है। अत: निवेशी सिग्नल को आधार पर लगाने से आधार धारा में अल्प परिवर्तन संग्राहक धारा में बहुत बड़ा परिवर्तन कर देता है। इस प्रकार इस परिपथ में पर्याप्त धारा प्रवर्धन, प्राप्त होता है, जबकि उभयनिष्ठ आधार परिपथ में धारा की हानि होती है।

प्रश्न 17.
दोलित्र क्या है? ट्रांजिस्टर दोलित्र की भाँति किस प्रकार कार्य करता है? चित्र बनाकर समझाइए।
अथवा
परिपथ चित्र की सहायता से n-p-n ट्रांजिस्टर की दोलनी क्रिया समझाइए। [2014]
अथवा
n-p-n ट्रांजिस्टर का दोलित्र के रूप में प्रयोग परिपथ बनाकर समझाइए। [2017]
अथवा
n-p-n ट्रांजिस्टर दोलित्र की भाँति कैसे कार्य करता है? परिपथ चित्र द्वारा समझाइए। [2018]
उत्तर :
दोलित्र (Oscillator)-दोलित्र एक ऐसी युक्ति है जो दिष्ट धारा स्रोत की ऊर्जा का उपयोग करके नियत आवृत्तिः तथा आयाम की प्रत्यावर्ती वोल्टता का उत्पादन करती है।

ट्रांजिस्टर एक दोलित्र की भाँति (Transistor as an E परिपथ Oscillator)-दोलित्र एक धनात्मक पुनर्भरण (feedback) के साथ स्वयं पोषित ट्रांजिस्टर प्रवर्धक होता है (चित्र-14.48)। ट्रांजिस्टर दोलित्र के तीन प्रमुख भाग होते हैं

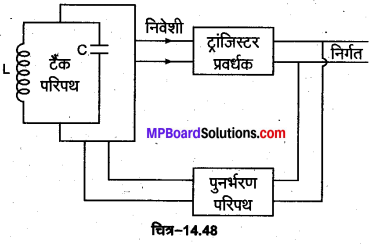
1. टैंक परिपथ (Tank Circuit)-यह परिपथ एक प्रेरकत्व (L) तथा धारिता (C) का समान्तर क्रम संयोजन होता है। यह परिपथ \(f=\frac{1}{2 \pi \sqrt{L C}}\) आवृत्ति के अवमन्दित वैद्युत
दोलन उत्पन्न करता है।

2. ट्रांजिस्टर प्रवर्धक (Transistor Amplifier)-टैंक परिपथ से प्राप्त वैद्युत दोलनों की ट्रांजिस्टर प्रवर्धक पर निवेशी के रूप में आरोपित कर देते हैं, जिससे निर्गत के रूप में प्रवर्धित दोलन प्राप्त होते हैं।

3. पुनर्भरण परिपथ (Feedback Circuit)-ट्रांजिस्टर प्रवर्धक के निर्गत का एक भाग टैंक परिपथ को निवेशी सिग्नल की कला में लौटा देते हैं जो टैंक परिपथ में होने वाली ऊर्जा-हानि की पूर्ति करता है। यह क्रिया धनात्मक पुनर्भरण (positive feedback) कहलाती है। धनात्मक पुनर्भरण के परिणामस्वरूप नियम आयाम के वैद्युत दोलन प्राप्त होते हैं।

परिपथ आरेख- ट्रांजिस्टर को दोलित्र के रूप में प्रयुक्त करने के लिए एक p-n-p ट्रांजिस्टर को उभयनिष्ठ उत्सर्जक विन्यास में चित्र-14.49 में प्रदर्शित किया गया है। चित्र में L₁C₁ एक टैंक परिपथ तथा L₂ एक पुनर्भरण कुंडली है। संधारित्र C₂ दोलन के सिरा निम्न प्रतिघात पथ प्रदान करता है। ट्रांजिस्टर का आवश्यक अभिनति श्रेणीक्रम में जुड़े दो प्रतिरोधों R₁ व R₂ की सहायता से दी जाती है। ट्रांजिस्टर सन्धि के ताप को R_E, उत्सर्जक प्रतिरोध से नियन्त्रित करते हैं। प्रवर्धित संकेतों का आधार-उत्सर्जक परिपथ में ऋणात्मक पुनर्भरण रोकने के लिए संधारित्र C_E को प्रयुक्त किया जाता है। बैटरी V_cc के द्वारा पूरे परिपथ को DC शक्ति दी जाती है तथा परिपथ में उत्पन्न दोलनों को प्रेरण कुंडली L₃ के सिरों पर प्राप्त किया जाता है।

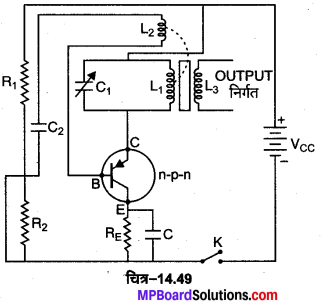
कार्यविधि-जैसे ही कुंजी K को जोड़ते हैं वैसे ही टैंक परिपथ के संधारित्र C₁ को आवेशन प्रारम्भ हो जाता है। जब यह संधारित्र पूर्ण आवेशित हो जाता है तो प्रेरण कुंडली L₁ इसे अनावेशित करना प्रारम्भ कर देती है। इसके फलस्वरूप L₁C₁ टैंक परिपथ में अवमन्दित दोलन उत्पन्न होने लगते हैं। ये दोलन पुनर्भरण कुंडली L₂ में L₁C₁, टैंक परिपथ के समान आवृत्ति का एक विद्युत वाहक बल उत्पन्न कर देते हैं। पुनर्भरण कुंडली L2 में उत्पन्न विद्युत वाहक बल का परिमाण कुंडली में फेरों की संख्या तथा इस कुंडली का प्रेरण कुंडली L₁ के सापेक्ष कपलिंग पर निर्भर करता है। अब पुनर्भरण कुंडली L₂ के सिरों पर उत्पन्न इस विभवान्तर को ट्रांजिस्टर प्रवर्धक के आधार व उत्सर्जक (B-E) टर्मिनलों के बीच लगा देते हैं। इस प्रकार यह प्रवर्धित होकर पुनर्भरण की प्रक्रिया द्वारा टैंक परिपथ L₁C₁ को पुन: प्राप्त हो जाता है।

इस प्रकार परिपथ बिना अवमन्दित हुए दोलन करता रहता है। इसके दोलनों की आवृत्ति \(f=\frac{1}{2 \pi \sqrt{L_{1} C_{1}}}\) की जाती है।

प्रश्न 18.
ट्रांजिस्टर स्विच के रूप में किस प्रकार कार्य करता है? चित्र बनाकर समझाइए।
अथवा
n-p-n ट्रांजिस्टर स्विच के रूप में कैसे कार्य करता है? आवश्यक परिपथ चित्र द्वारा कार्य-विधि स्पष्ट कीजिए। [2015, 18]
उत्तर :
ट्रांजिस्टर एक स्विच के रूप में (Transistor as a Switch)-स्विच एक ऐसी युक्ति है जिसका प्रयोग किसी परिपथ में धारा को प्रवाहित करने या रोकने के लिए किया जाता है। ट्रांजिस्टर को एक स्विच के रूप में प्रयुक्त करने के लिए एक n-p-n ट्रांजिस्टर का उभयनिष्ठ उत्सर्जक परिपथ चित्र-14.50 में प्रदर्शित किया गया है। परिपथ में धारा प्रवाह को प्रदर्शित किया गया है।

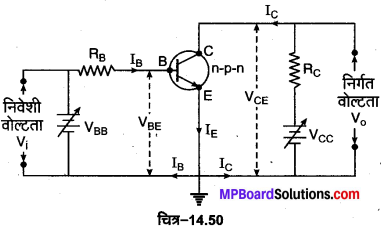
आधार-उत्सर्जक परिपथ में, V_BB = I_BRB + V_BE …(1)
संग्राहक-उत्सर्जक परिपथ में,
V_cc = I_c R_c + V_CE अथवा V_CE = V_cc – I_cR_c …..(2)
यदि आधार-उत्सर्जक परिपथ में लगाया गया निवेशी विभव V_i हो तब V_BB = V_i
तथा निर्गत विभव V₀ हो तब V_CE = V₀
अत: समीकरण (1) व (2) से,
V_i = I _BR_B + V_BE …….(3)
तथा V₀ = V_CC – I_CR_C ……(4)
सिलिकन ट्रांजिस्टर के लिए विभव प्राचीर 0.6 वोल्ट होता है। अत: सिलिकन ट्रांजिस्टर के लिए

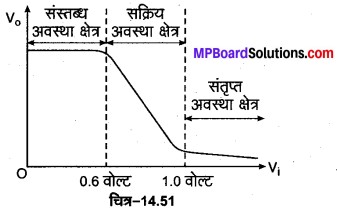
1. जब V_i < 0.6 वोल्ट है, अर्थात् निवेशी विभव ट्रांजिस्टर के विभव प्राचीर से कम हो परिपथ में कोई संग्राहक धारा नहीं बहती है अर्थात्
I_C = 0 अत: V₀ = V_CC
यह स्थिति ट्रांजिस्टर की संस्तब्ध अथवा अंतक अवस्था (cut off state) कहलाती है। इस स्थिति में ट्रांजिस्टर से होकर कोई धारा नहीं बहती है, अतः ट्रांजिस्टर एक खुले स्विच (OFF Switch) की भाँति कार्य करता है।

2. जब 1.0 वोल्ट >V_i > 0.6 वोल्ट है अर्थात् निवेशी विभव, विभव प्राचीर से अधिक परन्तु 1.0 वोल्ट से कम हो तो परिपथ में संग्राहक धारा बहती है। निवेशी विभव के 0.6 वोल्ट आगे धीरे-धीरे बहने पर संग्राहक धारा I_C सरल रेखीय रूप में बढ़ती है जिसके परिणामस्वरूप निर्गत वोल्टता V₀ भी सरल रेखीय रूप से घटती है। यह स्थिति ट्रांजिस्टर की सक्रिय अवस्था (active state) कहलाती है।

3. जब V_i > 1.0 वोल्ट है अर्थात् निवेशी विभव 1.0 वोल्ट से अधिक हो तो V_i में वृद्धि के साथ V₀ अरेखीय रूप में घटता है परन्तु शून्य कभी नहीं होता है। इस स्थिति में संग्राहक धारा अधिकतम हो जाती है तथा यह स्थिति ट्रांजिस्टर की संतृप्त अवस्था (saturation state) कहलाती है।

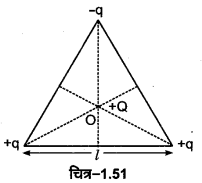
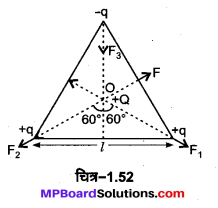
निवेशी वोल्टता (V_i) के साथ निर्गत वोल्टता (V₀) के इन सभी क्षेत्रों में परिवर्तन को चित्र-14.51 में प्रदर्शित किया गया है। इस प्रकार स्पष्ट है कि जब तक निवेशी वोल्टता (V_i) कम है (0.6 वोल्ट से कम) तब तक परिपथ में निर्गत वोल्टता (V₀) अधिकतम है तथा संग्राहक धारा (I_C) शून्य है। अत: ट्रांजिस्टर अपनी संस्तब्ध अवस्था में है। अतः ट्रांजिस्टर खुले स्विच की भाँति कार्य करता है। जब निवेशी वोल्टता (V_i) उच्च (1.0 वोल्ट से अधिक) है तब संग्राहक धारा अधिकतम अथवा नियत होती है तथा निर्गत वोल्टता (V₀) लगभग शून्य होती है।
अत: ट्रांजिस्टर अपनी संतृप्त अवस्था में होता है और यह एक बन्द (ON) स्विच की भाँति कार्य करता है।

इस प्रकार कोई लघु निवेशी वोल्टता, उच्च निर्गत वोल्टता प्रदान कर ट्रांजिस्टर का स्विच खुला (OFF) कर देती है जबकि उच्च निवेशी वोल्टता, लघु निर्गत वोल्टता प्रदान कर ट्रांजिस्टर का स्विच बन्द (ON) कर देती है। ट्रांजिस्टर को स्विच के रूप में प्रयुक्त करते समय परिपथ इस प्रकार से बनाए जाते हैं कि ट्रांजिस्टर कभी भी अपनी सक्रिय अवस्था में न हो।

प्रश्न 19.
ऐनालोग तथा डिजिटल परिपथ क्या है? ऐनालोग परिपथों की तुलना में डिजिटल परिपथों के लाभ बताइए।
उत्तर :
ऐनालोग परिपथ (Analog Circuit)–“ऐसा वैद्युत परिपथ जिस पर आरोपित वोल्टेज अथवा जिसमें प्रवाहित धारा समय के साथ निरन्तर परिवर्तित होती हैं, ऐनालोग परिपथ कहलाता है” तथा “समय के साथ निरन्तर परिवर्तनशील वोल्टेज अथवा धारा को ऐनालोग सिग्नल कहते हैं।” चित्र-14.52 में एक ऐनालोग वोल्टेज सिग्नल को प्रदर्शित किया गया है जो 0 तथा ±5 वोल्ट के बीच ज्या वक्रीय रूप से निरन्तर बदल रहा है।

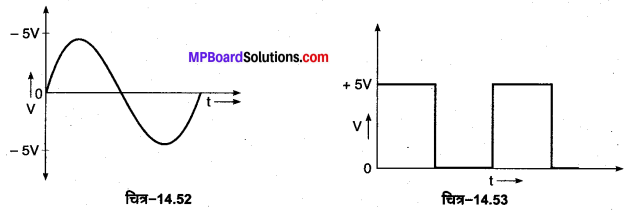
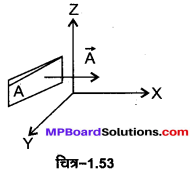
डिजिटल परिपथ (Digital Circuits)-“ऐसा वैद्युत परिपथ जिस पर आरोपित वोल्टेज अथवा जिसमें प्रवाहित धारा केवल दो मान (शून्य तथा कोई निश्चित मान) ग्रहण कर सकती है, डिजिटल परिपथ कहलाता है’ तथा “उस वोल्टेज अथवा धारा को जो केवल दो मान ग्रहण कर सकती है, डिजिटल सिग्नल कहते हैं।” चित्र-14.53 में एक डिजिटल सिग्नल को प्रदर्शित किया गया है, जिसमें वोल्टेज केवल दो मान 0 वोल्ट अथवा +5 वोल्ट ग्रहण कर सकती है। अडिजिटल परिपथों में द्विआधारी संख्या पद्धति (binary number system) प्रयुक्त की जाती है, जिसमें डिजिटल सिग्नल के दो मान 0 तथा 1 से प्रदर्शित किए जाते हैं। इस परिपथ का उपयोग इलेक्ट्रॉनिक घड़ियों, कम्प्यूटरों, धुलाई की मशीनों, टी० वी० आदि में किया जाता है। इलेक्ट्रॉनिक स्विच भी डिजीटल युक्ति है जिसमें दो अवस्थाएँ ON अथवा OFF होती हैं।

डिजिटल परिपथों के लाभ (Advantages of Digital Circuits)- ऐनालोग परिपथों की तुलना में डिजिटल परिपथों के निम्नलिखित लाभ होते हैं

1. डिजिटल परिपथों को एकीकृत परिपथों (integrated circuits) IC’s में संविरचित (fabricate) किया जा सकता है। इनका उपयोग टेलीविजन, अन्तरिक्ष यानों, श्रवण यन्त्रों, कम्प्यूटरों इत्यादि में किया जाता है।
2. डिजिटल परिपथों की सहायता से सूचनाएँ संग्रह करना सरल है। IC’s पर सूचनाएँ थोड़े समय के लिए अथवा सदैव के लिए संचित की जा सकती हैं। .
3. इनमें यथार्थता तथा परिशुद्धता (accuracy and precision) अधिक है।
4. डिजिटल परिपथ उपयुक्त लॉजिक द्वार (logic gates) का उपयोग करके सरलता से बनाए जा सकते हैं।
5. डिजिटल परिपथ को एक उपयोग से दूसरे उपयोग के लिए आसानी से बदला जा सकता है।
6. डिजिटल परिपथों से उपलब्ध आँकड़े (data) परिशुद्ध (precise) परिकलनों में प्रयुक्त किए जा सकते हैं।
7. डिजिटल परिपथ प्रोग्रामिंग (programming) में प्रयुक्त होते हैं।
8. डिजिटल परिपथ शोर से कम प्रभावित होते हैं। वास्तव में जिन सिग्नलों को हम निर्गत सिग्नल में नहीं चाहते, उन्हें ‘शोर’ कहते हैं। इन अवांछित सिग्नलों को डिजिटल परिपथ में से आसानी से हटाया जा सकता है क्योंकि यहाँ वोल्टेज के यथार्थ मान के ज्ञान की आवश्यकता नहीं होती है।
9. जिटल परिपथ सस्ते, हल्के, सूक्ष्म व सरल आकार के विश्वसनीय तथा स्थायी होते हैं।

प्रश्न 20.
लॉजिक गेट क्या है? मूल लॉजिक गेट कितने प्रकार के होते हैं? सत्यता सारणी एवं बूलियन व्यंजक को समझाइए।
उत्तर :
लॉजिक गेट अथवा तर्क द्वार (Logic Gates)-लॉजिक गेट ऐसे इलेक्ट्रॉनिक परिपथ हैं जिसमें निवेशी सिग्नल (input signal) एक या एक से अधिक परन्तु निर्गत सिग्नल (output signal) केवल एक ही होता है। इन परिपथों से निर्गत सिग्नल केवल तभी प्राप्त होता है जबकि निवेशी सिग्नलों के बीच कुछ तर्कपूर्ण शर्ते (logic conditions) सन्तुष्ट होती हैं, अतः वे डिजिटल परिपथ, जिनके निवेशी तथा निर्गत सिग्नलों के बीच एक तर्कपूर्ण सम्बन्ध होता है लॉजिक गेट अथवा तर्क द्वार कहलाते हैं।
मूल लॉजिक गेट तीन प्रकार के होते हैं

1. OR गेट
2. AND गेट तथा .
3. NOT गेट

सत्यता सारणी (Truth Table)-किसी लॉजिक गेट का एक अथवा एक से अधिक निवेशी सिग्नल तथा केवल एक निर्गत सिग्नल होता है। किसी लॉजिक गेट के सभी सम्भव निवेशी संयोगों (input combinations) तथा उनके संगत निर्गतों को प्रदर्शित करने वाली सारणी, उस लॉजिक गेट की सत्यता सारणी कहलाती है।

बूलियन व्यंजक (Boolean Expression)—प्रत्येक लॉजिक गेट का एक तर्कयुक्त प्रतीक (Logical symbol) . होता है। जॉर्ज बूल (George Boole) ने सन् 1854 ई० में एक भिन्न प्रकार का बीजगणित विकसित किया जिसका उपयोग इलेक्ट्रॉनिक डिजिटल परिपथों को सरल रूप देने में किया जाता है। यह बीजगणित ऐसे तर्कसंगत कथनों (logical statements) पर आधारित है जिनके केवल दो अर्थ अथवा मान हो सकते हैं-सत्य (true) मान अथवा असत्य (false) मान। ये तर्कसंगत कथन बूलियन चर (Boolean variables) कहलाते हैं। बूलियन चर के सत्य मान को द्विआधारी (binary) अंक ” से तथा असत्य मान को द्विआधारी अंक ‘0’ से प्रदर्शित करते हैं।

अत: एक ऐसा व्यंजक जो दो बूलियन चरों के ऐसे संयोग को प्रदर्शित करता है जिससे एक नया बूलियन चर प्राप्त होता है, बूलियन व्यंजक कहलाता है जैसे यदि एक बूलियन चर A तथा दूसरा बूलियन चर B है तो Y = A. B तथा Y = A+ B आदि बूलियन व्यंजक हैं।

प्रश्न 21.
मूल लॉजिक गेटों की संक्रियाएँ स्पष्ट कीजिए।
उत्तर :
मूल लॉजिक गेटों की संक्रियाएँ (Operations in Basic Logic Gates)-मूल लॉजिक गेटों में निम्न तीन संक्रियाएँ प्रयुक्त होती हैं-
1. OR संक्रिया (OR Operation)- बूलियन बीजगणित (Boolean Algebra) में OR संक्रिया को योग चिह्न (+) से प्रदर्शित किया जाता है। इसका बूलियन व्यंजक A+ B = Y होता है तथा इसे ‘A OR Bequals Y’ पढ़ा जाता है, जहाँ A तथा B निवेशी सिग्नल तथा Y निर्गत सिग्नल है। इसमें दो निवेशियों A तथा B से, व्यंजक के अनुसार निर्गत Y प्राप्त होता है।

2. AND संक्रिया (AND Operation)-बूलियन बीजगणित में AND संक्रिया को गुणन चिन्ह (.) से प्रदर्शित किया जाता है। इसका बूलियन व्यंजक A. B = Y होता है तथा इसे ‘A AND B equals Y’ पढ़ा जाता है, जहाँ A तथा B निवेशी सिग्नल तथा Y निर्गत सिग्नल है। इसमें दो निवेशियों A तथा B को, व्यंजक के अनुसार संयुक्त करके निर्गत Y प्राप्त होता है।

3. NOT संक्रिया (NOT operation)-बूलियन बीजगणित में NOT संक्रिया को चर राशि के ऊपर बार चिह्न (-) लगाकर प्रदर्शित किया जाता है। इसका बूलियन व्यंजक \(\overline{\boldsymbol{A}}\) = Y होता है तथा इसे ‘NOT A equals Y’ पढ़ा जाता है, जहाँ A निवेशी सिग्नल तथा Y निर्गत सिग्नल है। NOT संक्रिया को ऋणक्रमण (negation) अथवा उत्क्रमण (inversion) भी कहते हैं। इसमें केवल एक निवेशी (input) होता है तथा इससे उत्पन्न निर्गत (output) निवेशी का ऋणक्रमण होता है।

प्रश्न 22.
OR गेट का प्रतीक बनाइए तथा इसकी सत्यता सारणी बनाइए। सन्धि डायोड का प्रयोग करके इसे दो निवेशी सिग्नलों वाला OR गेट किस प्रकार बनाया जा सकता है? समझाइए।
अथवा OR गेट के लिए लॉजिक प्रतीक, सत्यता सारणी, परिपथ आरेख तथा बूलियन व्यंजक दीजिए। [2015]
उत्तर :
OR गेट की परिभाषा-OR गेट एक ऐसी युक्ति है जिसमें दो या दो से अधिक निवेश चर (input variables) अथवा सिग्नल A व B होते हैं जबकि एक निर्गत चर (output variables) अथवा सिग्नल Y होता है। चित्र-14.54 (a) में दो निवेशी चर A तथा B वाले OR गेट के प्रतीक को प्रदर्शित किया गया है। इसका बुलियन व्यंजक A+ B= Y होता है जिसे ‘A OR B equals Y पढ़ा जाता है। इसकी सत्यता सारणी चित्र-14.54 (c) में प्रदर्शित है।

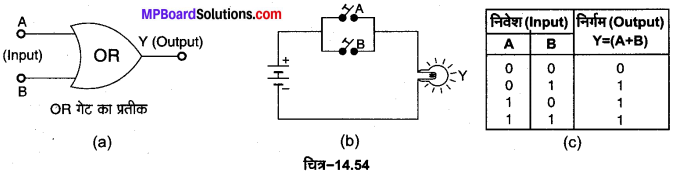
OR गेट की क्रिया पद्धति को चित्र-14.54 (b) में प्रदर्शित वैद्युत परिपथ की सहायता से समझा जा सकता है। इस परिपथ में एक बैटरी, एक बल्ब व दो स्विचों के समान्तर संयोजन को श्रेणीक्रम में जोड़ा गया है। स्पष्ट है कि स्विचों के खुले अथवा बन्द होने का परिणाम हमें बल्ब में देखने को मिलता है, अतः दोनों स्विच A, B निवेशी टर्मिनल हैं तथा बल्ब Y निर्गत टर्मिनल है। जब कोई स्विच बन्द (ON) होता है अर्थात् धारा को गुजरने देता है तो उसकी अवस्था को बाइनरी अंक 1 से प्रदर्शित किया जाता है तथा जब कोई स्विच खुला (OFF) होता है अर्थात् धारा के प्रवाह को रोक देता है तो उसकी अवस्था को बाइनरी अंक 0 से प्रदर्शित किया जाता है। इसी प्रकार जब बल्ब जला होता है तो उसकी अवस्था Y = 1 होगी जबकि बल्ब के बुझे होने पर उसकी अवस्था Y = 0 होगी।
परिपथ से स्पष्ट है कि यदि

1. A = 0, B= 0; दोनों स्विच खुले (OFF ) हैं तो बल्ब बुझा रहेगा अर्थात् Y = 0
2. A = 1, B = 0; A बन्द (ON) है, B खुला (OFF ) है तो बल्ब जल जाएगा अर्थात् Y = 1
3. A = 0, B= 1; A खुला (OFF ) है, B बन्द (ON) है तो बल्ब जल जाएगा अर्थात् Y = 1
4. A = 1, B= 1 ; दोनों स्विच बन्द (ON) है तो बल्ब जल जाएगा अर्थात् Y = 1

इस प्रकार इस परिपथ का निर्गम Y = 1 होता है, जबकि कम-से-कम एक निवेश 1 है, अत: इस परिपथ के निर्गम और निवेश में OR गेट के समान सम्बन्ध हैं, इसलिए यह OR गेट का तुल्य परिपथ है।

OR गेट प्राप्त करना (Realisation of OR Gate)-इस गेट को दो p-n सन्धि डायोडों को चित्र-14.55 के अनुसार प्रयोग करके प्राप्त किया जा सकता है। इस परिपथ में एक +5 वोल्ट की बैटरी का ऋण सिरा भू-सम्पर्कित रखा गया है, जो 0 स्थिति को तथा धन सिरा (+5 वोल्ट) 1 स्थिति को प्रदर्शित करता है। सत्यता सारणी के अनुसार निवेश के चार सम्भव संयोजन हैं जिन्हें बारी-बारी से आगे समझाया गया है।

1. प्रथम स्थिति, A = 0, B= 0-यदि दोनों निवेश शून्य हैं अर्थात् दोनों डायोडों के सिरों A तथा B को भू-सम्पर्कित रखा जाए (अर्थात् A = B = 0) तो दोनों में से कोई भी डायोड अग्र अभिनत नहीं होगा; अतः प्रतिरोध R में कोई धारा नहीं बहेगी तथा निर्गत विभव Y शून्य होगा (अर्थात् Y = 0)।
अर्थात् 0 + 0 = 0

2. द्वितीय स्थिति, A = 1, B = 0–यदि B को भू-सम्पर्कित करें (B = 0) तथा A को बैटरी के धन सिरे से जोड़ें तो A पर +5 वोल्ट का विभव होगा अर्थात् (A = 1), तब डायोड D₁ अग्र अभिनत होगा, जबकि डायोड D₂ पश्च अभिनत होगा। D₁ से धारा प्रवाहित होगी तथा अग्र अभिनति के कारण D₁ का प्रतिरोध लगभग नगण्य होगा। प्रतिरोध R में धारा प्रवाहित होने के कारण इसके सिरों के बीच 5 वोल्ट का विभवान्तर होगा;
अतः Y पर निर्गत विभव 5 वोल्ट होगा (अर्थात् Y = 1)|
अर्थात् 1 + 0 =1

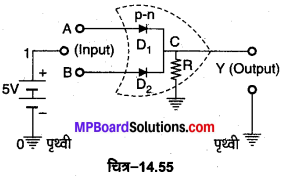
3. तृतीय स्थिति, A = 0, B = 1-यह स्थिति A को भू-सम्पर्कित करके तथा B को बैटरी के धन सिरे से जोड़कर प्राप्त होगी। इस स्थिति में केवल डायोड D₂ से धारा प्रवाहित होगी। द्वितीय स्थिति के समान ही इस स्थिति में भी निर्गत विभव 5 वोल्ट होगा (अर्थात् Y = 1)। .
अर्थात् 0+1 = 1

4. चतुर्थ स्थिति, A = 1,B = 1–यह स्थिति A तथा B दोनों को बैटरी के धन सिरे से जोड़ने पर प्राप्त होती है। इस स्थिति में दोनों डायोड D₁ तथा D₂ अग्र अभिनत होते है; अत: बैटरी से चलने वाली धारा अब D₁ व D₂ में बँट जाती है तथा पुन: संयुक्त होकर प्रतिरोध R से होकर गुजरती है। R के सिरों के बीच पुन: 5 वोल्ट का विभवान्तर उत्पन्न होता है; अत: निर्गत विभव पुन : +5 वोल्ट होगा, (अर्थात् Y = 1)
अर्थात् 1+1 = 1
इस प्रकार OR गेट में यदि दोनों निवेशी 0 हैं तो निर्गत 0 होगा, अन्यथा निर्गत 1 होगा।
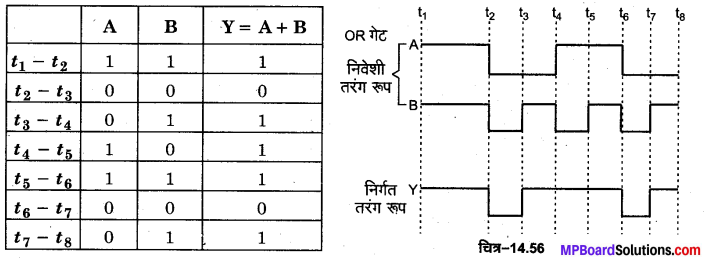
OR गेट का तरंग रूप

प्रश्न 23.
AND गेट का प्रतीक बनाइए तथा इसकी सत्यता सारणी बनाइए। सन्धि डायोड का प्रयोग करके इसे दो निवेशी सिग्नलों वाला AND गेट कैसे बनाया जा सकता है? समझाइए। [2013]
उत्तर :
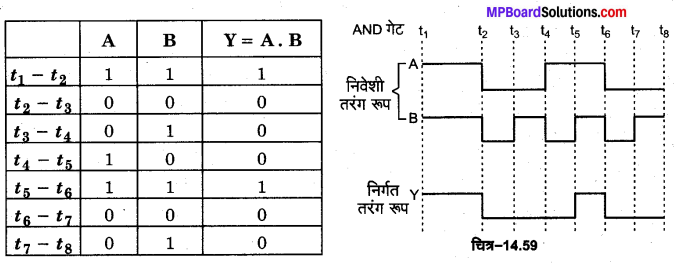
AND गेट की. परिभाषा-AND गेट एक ऐसी युक्ति है जिसमें दो निवेशी चरों A व B को संयुक्त करके एक निर्गत चर Y प्राप्त होता है। चित्र-14.57 (a) में दो निवेशों A तथा B वाले AND गेट का प्रतीक प्रदर्शित किया गया है इसका बूलियन व्यंजक A. B= Y होता है जिसे ‘A AND B equals Y’ पढ़ा जाता है। इसकी सत्यता सारणी चित्र-14.57 (c) में प्रदर्शित है।

AND गेट की क्रिया-पद्धति को चित्र-14.57 (b) में प्रदर्शित वैद्युत परिपथ की सहायता से समझा जा सकता है। इस परिपथ में एक बैटरी, एक बल्ब व दो स्विचों A तथा B को श्रेणीक्रम में जोड़ा गया है। दोनों स्विच निवेश का निर्माण करते हैं, जबकि बल्ब निर्गम Y को प्रदर्शित करेगा। जब कोई स्विच बन्द (ON) होगा तो उसकी स्थिति 1 होगी तथा खुले (OFF) होने पर स्थिति 0 होगी।
इसी प्रकार बल्ब के जले होने पर Y = 1 होगा अन्यथा Y = 0 होगा। परिपथ से स्पष्ट है कि यदि
1. A = 0, B= 0, दोनों स्विच खुले (OFF ) हैं तो बल्ब बुझा रहेगा अर्थात् Y = 0
2. A= 1, B= 0, स्विच A बन्द (ON) तथा स्विच B खुला (OFF ) है तो बल्ब बुझा रहेगा अर्थात् Y = 0

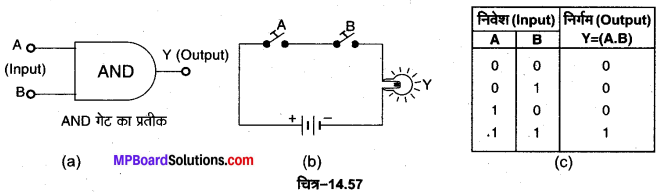
3. A = 0, B= 1, स्विच A खुला (OFF ) तथा स्विच B बन्द (ON) है तो बल्ब बुझा रहेगा अर्थात् Y = 0
4. A = 1, B = 1, दोनों स्विच बन्द (ON) हैं तो बल्ब जल जाएगा अर्थात् Y = 1
इस गेट का निर्गम Y = 1 (उच्च) केवल तभी होता है जबकि इसके सभी निवेश 1 (उच्च) हों। यही AND गेट की विशेषता है।

AND गेट प्राप्त करना (Realisation of AND Gate)-इस गेट को दो p-n सन्धि डायोडों का चित्र-14.58 के अनुसार प्रयोग करके प्राप्त । किया जा सकता है। इस परिपथ में एक + 5 वोल्ट की दो बैटरियों का ऋण सिरा भू-सम्पर्कित रखा गया है। प्रथम बैटरी का भू-सम्पर्कित सिरा 0 25V स्थिति को धन सिरा (+ 5 वोल्ट) स्थिति को प्रदर्शित करता है। सत्यता सारणी के अनुसार निवेश के चार सम्भव संयोजन हैं, जिन्हें बारी-बारी से 03 पृथ्वी नीचे समझाया गया है।

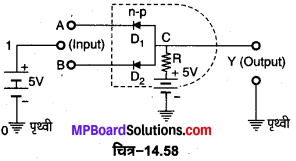
1. प्रथम स्थिति, A = 0,B= 0–यह स्थिति A तथा B दोनों निवेश टर्मिनलों को भू-सम्पर्कित करने पर प्राप्त होती है। इस स्थिति में दोनों डायोड अग्र अभिनत होंगे तथा दोनों से धारा प्रवाहित होगी किन्तु अग्र अभिनति में दोनों का प्रतिरोध शून्य होगा; अतः प्रत्येक डायोड का विभवान्तर शून्य होगा, अत: Y पर निर्गत विभव भी शून्य होगा।
अर्थात् जब A = B = 0 (निम्न) तब Y = 0 (निम्न)
अर्थात् 0.0 = 0

2. द्वितीय स्थिति, A = 1,B = 0 -यह स्थिति A को 5 वोल्ट की बैटरी के धन सिरे से जोड़कर तथा B को भू-सम्पर्कित करने पर प्राप्त होती है। इस स्थिति में A पर +5 वोल्ट का विभव (उच्च स्थिति A = 1) तथा B पर 0 विभव (निम्न स्थिति B = 0) है। इस स्थिति में केवल डायोड D₂ अग्र अभिनत है, अत: केवल इसी में धारा प्रवाहित होती है। अग्र अभिनति के कारण इसका प्रतिरोध शून्य होगा, अतः इसके सिरों के बीच विभवान्तर शून्य होगा अर्थात् Y पर निर्गत विभव शून्य होगा (Y = 0 निम्न स्थिति)।
अर्थात् जब A = 1, B = 0, तब Y = 0.
अर्थात् Y = 1. 0 = 0

3. तृतीय स्थिति, A = 0,B = 1–यह स्थिति द्वितीय स्थिति के विपरीत है। इस स्थिति में केवल डायोड D₁ में धारा प्रवाहित होती है D₂ में नहीं। इस स्थिति में भी Y पर निर्गत विभव शून्य है अर्थात् Y = 0 (निम्न स्थिति)।
अर्थात् Y = 0.1 = 0

4. चतुर्थ स्थिति, A = B = 1- यह स्थिति A तथा B दोनों को 5 वोल्ट की बैटरी के धन सिरे से जोड़ने पर प्राप्त होती है। इस स्थिति में A तथा B दोनों पर + 5 वोल्ट का विभव होता है अर्थात् A = B = 1 (उच्च स्थिति)। इस स्थिति में दोनों डायोड D₁ व D₂, में से कोई भी अग्र अभिनत नहीं है, अत: किसी में भी धारा प्रवाहित नहीं होती। इस स्थिति में Y पर उपलब्ध विभव प्रतिरोध R से जुड़ी बैटरी के धन सिरे के विभव +5 वोल्ट के बराबर होगा अर्थात् Y = 1 (उच्च स्थिति)।
अर्थात् Y = 1.1 = 1
इस प्रकार AND गेट में, यदि दोनों निवेशी 1 हैं तो निर्गत 1 होगा, अन्यथा निर्गत 0 होगा।
AND गेट का निर्गत तरंग रूप

प्रश्न 24.
NOT गेट का प्रतीक तथा सत्यता सारणी बनाइए। इस गेट को डिजिटल परिपथ के रूप में कैसे प्राप्त किया जा सकता है? समझाइए।
अथवा
NOT गेट का उपयुक्त आरेख की सत्यता से सत्यता सारणी बनाइए। [2013]
अथवा
NOT गेट के लिए लॉजिक प्रतीक, बूलियन व्यंजक, परिपथ आरेख तथा सत्यता सारणी बनाइए। [2015]
अथवा
NOT गेट के लिए लॉजिक प्रतीक, सत्यता सारणी तथा बूलियन व्यंजक दीजिए। परिपथ आरेख के साथ समझाइए कि यह गेट किस प्रकार प्राप्त किया जा सकता है? [2018]
उत्तर :
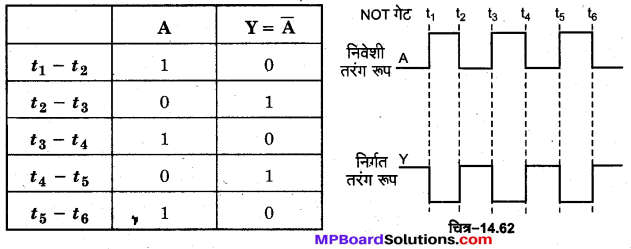
NOT गेट की परिभाषा–यह एक ऐसी युक्ति है जिसमें एक निवेशी चर (सिग्नल) तथा एक ही निर्गत चर (सिग्नल) Y होता है। चित्र-14.60 (a) में एक निवेशी सिग्नल A तथा एक निर्गत सिग्नल वाला NOT गेट का प्रतीक प्रदर्शित किया गया है। इसका बूलियन व्यंजक \(\bar{A}\) = Y होता है। जिसे ‘NOT A equals Y’ पढ़ा जाता है। इसकी सत्यता सारणी चित्र-14.60 (c) में प्रदर्शित है।

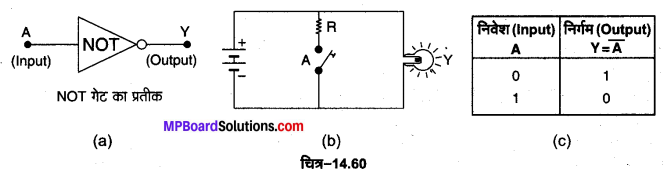
NOT गेट की क्रिया पद्धति को चित्र-14.60 (b) में प्रदर्शित वैद्युत परिपथ की सहायता से समझा जा सकता है। इस परिपथ में एक बल्ब Y को एक बैटरी के श्रेणीक्रम में जोड़ा गया है तथा एक स्विच A को बल्ब के समान्तर क्रम मे जोड़ा गया है। स्पष्ट है कि स्विच A को खोलने अथवा बन्द करने का प्रभाव बल्ब Y पर देखने को मिलता है । अर्थात् स्विच A निवेश तथा बल्ब Y निर्गत है। जब स्विच A खुला (OFF ) अर्थात् A = 0 होता है तो बल्ब में धारा. प्रवाहित होती रहती है। अत: बल्ब जला रहता है अर्थात् निर्गम Y = 1 होता है। इसके विपरीत जब स्विच A को बन्द (ON) कर देते हैं अर्थात् जब A = 1 होता है तो बैटरी लघुपथित (short circuit) हो जाती है, जिससे बैटरी के सिरों का विभवान्तर शून्य हो जाता है। अत: बल्ब में धारा शून्य हो जाती है अर्थात् बल्ब बुझ जाता है, जिससे Y = 0 हो जाता है। अतः इस परिपथ में हम पाते हैं कि

यदि निवेश A = 0 है तो निर्गम Y = 1
तथा यदि निवेश A = 1 है तो निर्गम Y = 0
यही NOT गेट की विशेषता है, अतः उपर्युक्त परिपथ NOT गेट का तुल्य परिपथ है।

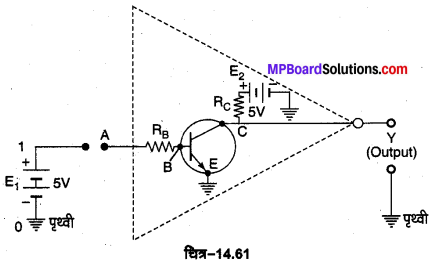
NOT गेट प्राप्त करना (Realisation of NOT Gate)-इस गेट को n-p-n ट्रांजिस्टर की सहायता से चित्र-14.61 के अनुसार परिपथ तैयार करके प्राप्त किया जा सकता है। ट्रांजिस्टर के आधार B को एक प्रतिरोध R_B के द्वारा निवेशी टर्मिनल A से जोड़कर उत्सर्जक E को भू-सम्पर्कित कर देते हैं। संग्राहक को एक अन्य प्रतिरोध R_c तथा 5 वोल्ट की बैटरी के द्वारा भू-सम्पर्कित कर देते हैं। निर्गत Y संग्राहक C का पृथ्वी के सापेक्ष वोल्टेज है।

सत्यता सारणी के अनुसार निवेश के लिए केवल दो सम्भावनाएँ हैं जिनके संगत निर्गमों को बारी-बारी से नीचे समझाया गया है

1. प्रथम स्थिति, A=0-यह स्थिति A को भू-सम्पर्कित करके प्राप्त होती है। इस स्थिति में A पर निवेशी विभव शून्य है (निम्न स्थिति A = 0), अत: उत्सर्जक आधार सन्धि अग्र अभिनति में नहीं है, अत: इस स्थिति में ट्रांजिस्टर में कोई धारा प्रवाहित नहीं होती। इस स्थिति में बैटरी E₂ खुले परिपथ पर है, अत: Y पर उपलब्ध विभव E₂ के वैद्युत वाहक बल (5 वोल्ट) के बराबर होगा अर्थात् Y = 1 होगा।
यदि A = 0 तब Y = 1 = \(\bar{0}\) = \(\bar{A}\)

2. द्वितीय स्थिति, A= 1–यह स्थिति A को बैटरी E, के धन सिरे से जोड़ने पर प्राप्त होती है। इस स्थिति में A पर निवेशी विभव +5 वोल्ट होगा (अर्थात् A = 1); अत: उत्सर्जक-आधार सन्धि अग्र अभिनत होगी। ट्रांजिस्टर में उच्च उत्सर्जक धारा प्रवाहित होगी, जिसका अधिकांश भाग संग्राहक से गुजरेगा, इसलिए R_c के सिरों के बीच लगभग 5 वोल्ट का विभवान्तर उत्पन्न हो जाएगा, अत: Y पर उपलब्ध विभव E₂ के वैद्युत वाहक बल तथा R_c के विभवान्तर के परिणामी के बराबर होगा।

चूँकि R_C में धारा संग्राहक टर्मिनल से बाहर निकलती है, अत: R_C के सिरों के बीच विभवान्तर बैटरी E₂ के वैद्युत वाहक बल के विपरीत दिशा में होगा, इसलिए R_c के Y से जुड़े सिरे पर उपलब्ध विभव शून्य होगा अर्थात् Y = 0 (निम्न स्थिति)।
अर्थात् \(Y=0 \neq 1=\overline{1}=\bar{A}\)
इस प्रकार NOT गेट में यदि निवेशी 0 है तब निर्गत 1 होगा तथा इसका उल्टा भी होगा।
NOT गेट का निर्गत तरंग रूप-

प्रश्न 25.
लॉजिक गेटों के संयोजन को स्पष्ट कीजिए।
उत्तर :
लॉजिक गेटों का संयोजन (Combination of Logic Gates)-कम्प्यूटर, कैलकुलेटर आदि उपकरणों में प्रयुक्त होने वाले जटिल परिपथों में तीन मूल लॉजिक गेटों (OR, AND तथा NOT) के अतिरिक्त इनके संयोजनों से प्राप्त विभिन्न गेट भी प्रयुक्त किए जाते हैं। लॉजिक गेटों के सबसे अधिक प्रचलित संयोजन गेट NOR गेट तथा NAND गेट हैं। इन लॉजिक गेटों को सार्वत्रिक गेट (universal gate) भी कहते हैं, क्योंकि इनको बार-बार विभिन्न क्रमों में प्रयुक्त कर तीनों मूल लॉजिक गेटों को प्राप्त किया जा सकता है।

NOR गेट -NOR गेट को OR गेट तथा NOT गेट के संयोजन से प्राप्त किया जाता है। यदि OR गेट के निर्गत टर्मिनल Y’ को NOT गेट के निवेशी टर्मिनल से जोड़ दें [चित्र-14.63 (a)] तो यह पूर्ण संयोजन NOR गेट कहलाता है, NOR गेट का लॉजिक प्रतीक चित्र-14.63 (b) में प्रदर्शित है।

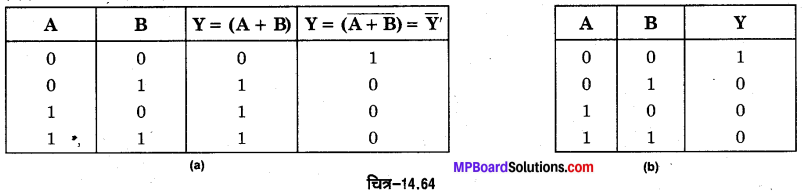
NOR गेट का बूलियन व्यंजक \(\overline{A+B}=Y\) है तथा इसे ‘A OR B negated equals Y’ पढ़ा जाता है। NOR गेट की सत्यता सारणी OR तथा NOT गेटों की सत्यता सारणियों को तर्कसंगत संयोजित करके प्राप्त की जा सकती है चित्र-14.64 (a) व (b)।

इसके लिए प्रदर्शित परिपथ में दो स्विच A व B एक लघु प्रतिरोध, एक बैटरी तथा एक बल्ब Y को चित्र-14.65 के अनुसार जोड़ते हैं। जब दोनों स्विच खुले हैं अर्थात् A = 0, B= 0 तो बल्ब Y जलता । है। जब स्विच A खुला है तथा स्विच B बन्द है अर्थात् A = 0, B= 1 तो बल्ब Y बुझ जाता है।

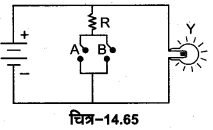
जब स्विच A बन्द है तथा स्विच B खुला है अर्थात् A = 1, B= 0 तो बल्ब Y बुझ जाता है। जब दोनों स्विच बन्द हैं अर्थात् A = 1, B= 1 तो बल्ब Y बुझा रहता है।
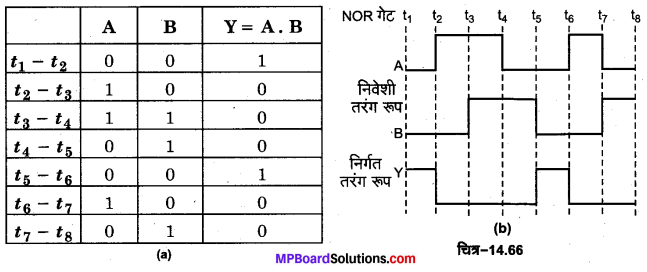
NOR गेट का निर्गत तरंग रूप

NAND गेट-NAND गेट को AND गेट तथा NOT गेट के संयोजन से प्राप्त किया जाता है। यदि AND गेट के निर्गत टर्मिनल Y’ को NOT गेट के निवेशी टर्मिनल से जोड़ दें [चित्र-14.67(a)] तो यह पूर्ण संयोजन NAND गेट कहलाता है। इसका लॉजिक प्रतीक [चित्र-14.67 (b)] में प्रदर्शित है।

NAND गेट का बूलियन व्यंजक \(\overline{A \cdot B}=Y\) है तथा इसे ‘A AND B negated equals Y ‘ पढ़ा जाता है। NAND गेट की सत्यता सारणी AND तथा NOT गेटों की सत्यता सारणियों को तर्कसंगत संयोजित करके प्राप्त की जा सकती है चित्र-14.68

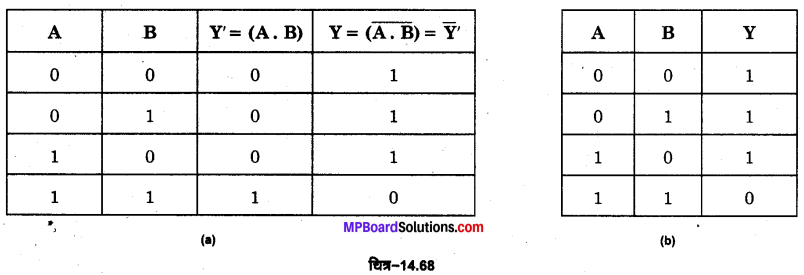
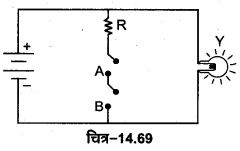
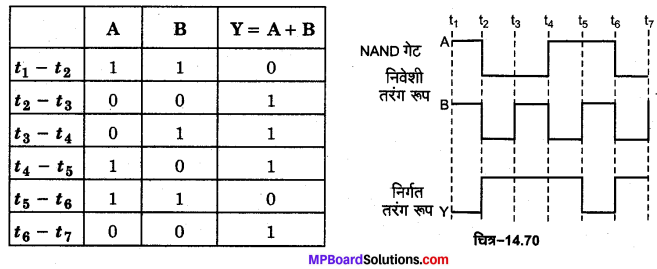
इसके लिए प्रदर्शित परिपथ में दो स्विच A व B एक लघु प्रतिरोध R, एक बैटरी तथा एक बल्ब Y को चित्र-14.70 के अनुसार जोड़ते हैं। जब दोनों स्विच A व B खुले हैं अर्थात् A = 0, B= 0 तो बल्ब Y जलता है। जब केवल स्विच A खुला है अर्थात् A = 0, B= 1 है तो बल्ब Y जल जाता है। जब स्विच A व B दोनों बन्द हैं अर्थात् A = 1, B= 1 तो बल्ब Y बुझा रहता है।

प्रश्न 26.
OR गेट, AND गेट, NOT गेट NAND तथा NOR गेट की तुलनात्मक सारणी बनाइए।
अथवा
AND, NOR तथा NOT गेट के लिए लॉजिक प्रतीक, बुलियन व्यंजक तथा सत्यता सारणी बनाइए। [2014]
अथवा
NAND गेट का लॉजिक प्रतीक बनाइए। [2016]
उत्तर :
OR, AND, NOT, NAND तथा NOR गेट की तुलनात्मक सारणी

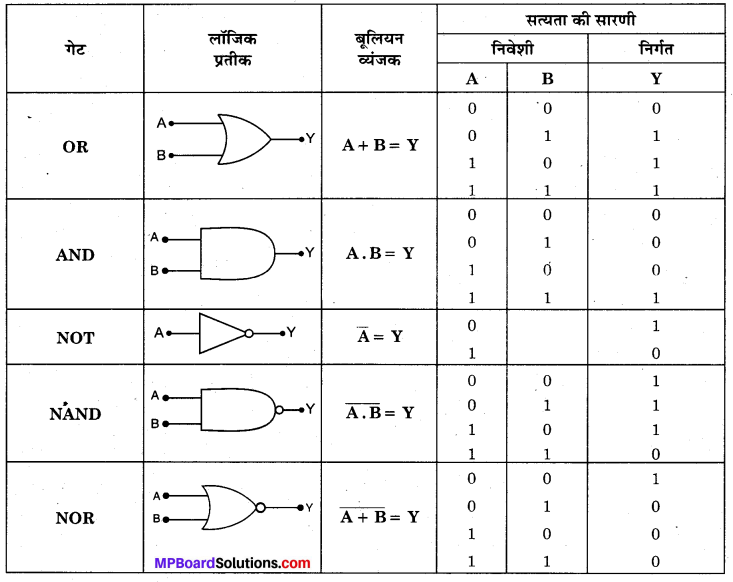
प्रश्न 27.
NAND गेटों का प्रयोग कर (i) AND गेट, (ii) OR गेट, किस प्रकार बना सकते हैं? चित्र बनाकर समझाइए।[2018]
अथवा
NAND गेट द्वारा AND गेट किस प्रकार बनाया जाता है? इसकी सत्यता सारणी बनाइए तथा बूलियन व्यंजक लिखिए। [2018]
हल :
1. NAND गेट से AND गेट की प्राप्तिNAND गेट से AND गेट की प्राप्ति का परिपथ चित्र 14.71 में दर्शाया गया है। यदि NAND गेट के दोनों निवेशी B टर्मिनलों पर सिग्नल A व B लगाएँ तथा निर्गत सिग्नल Y₁ को दूसरे NAND गेट के दोनों निवेशी टर्मिनलों पर संयुक्त
चित्र-14.71 रूप से लगाएँ तो यह पूर्ण संयोजन AND गेट की भाँति कार्य करता है।

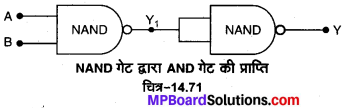
यहाँ \(\mathrm{Y}_{1}=\overline{\mathrm{A} . \mathrm{B}}\)
तथा \(\mathrm{Y}=\overline{\mathrm{Y}_{1}}=\overline{\mathrm{A} \cdot \mathrm{B}}=\mathrm{A} \cdot \mathrm{B}\)
सत्यता सारणी :

2. NAND गेट से OR गेट की प्राप्ति

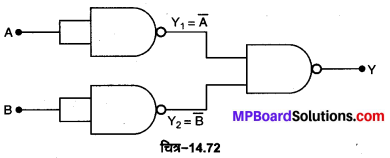
यहाँ Y₁= \(\overline{\mathbf{A}}\) तथा Y₂ = \(\overline{\mathbf{B}}\)
तथा \(\mathrm{Y}=\overline{\mathrm{Y}_{1} \cdot \mathrm{Y}_{2}}=\overline{\overline{\mathrm{A}} \cdot \overline{\mathrm{B}}}=\overline{\overline{\mathrm{A}}}+\overline{\overline{\mathrm{B}}}=\mathrm{A}+\mathrm{B}\)
इस प्रकार NAND गेटों का उपर्युक्त संयोजन OR गेट की भाँति कार्य करता है।

अर्द्धचालक इलेक्ट्रॉनिकी: पदार्थ युक्तियाँ तथा सरल लघु उत्तरीय प्रश्नोत्तर

प्रश्न 1.
बताइए कि किसी p-टाइप जर्मेनियम अर्द्धचालक के लिए तीन संयोजकता वाला अपद्रव्य क्यों मिलाया जाता है? [2001]
उत्तर :
तीन संयोजकता वाला अपद्रव्य पदार्थ मिलाने से अपद्रव्य परमाणु क्रिस्टल जालक में एक जर्मेनियम परमाणु । का स्थान ले लेता है। इसके समीप के तीन जर्मेनियम परमाणुओं के इलेक्ट्रॉन अपद्रव्य परमाणु के इलेक्ट्रॉनों के साथ बन्ध बना लेते हैं तथा चौथे जर्मेनियम परमाणु के साथ बन्ध बनाने के लिए इलेक्ट्रॉन की कमी रह जाती है। यह इलेक्ट्रॉन रिक्तिका एक धनावेशित कण के तुल्य है, जिसे कोटर कहते हैं। इस प्रकार जालक में धनावेशित कोटर उत्पन्न हो जाते हैं।

प्रश्न 2.
अर्द्धचालक में डोपिंग का क्या अर्थ है? इसे क्यों किया जाता है? [2002]
अथवा
किसी निज अर्द्धचालक को मादित (डोपिंग) करने से क्या तात्पर्य है? यह क्रिया अर्द्धचालक की चालकता को किस प्रकार प्रभावित करती है? [2003, 15]]
उत्तर :
डोपिंग (मादित) किसी निज अर्द्धचालक में 3 संयोजी अथवा 5 संयोजी इलेक्ट्रॉन वाली अशुद्धि मिलाकर उसे बाह्य अर्द्धचालक में बदलने की क्रियां डोपिंग (मादित) कहलाती है। ऐसा करने से निज अर्द्धचालक की चालकता बढ़ जाती है।

प्रश्न 3.
सन्धि-डायोड में विभव प्राचीर से क्या तात्पर्य है? [2005, 18]]
उत्तर :
विभव प्राचीर-p-n सन्धि के दोनों ओर बनी अवक्षय परत के सिरों के बीच उत्पन्न विभवान्तर. को विभव प्राचीर अथवा सम्पर्क विभव कहते हैं। इसका मान 0.1 से लेकर 0.5 वोल्ट तक होता है तथा इसका मान सन्धि के ताप पर निर्भर करता है।

प्रश्न 4.
p-n सन्धि को अग्र अभिनत करने का अवक्षय परत तथा विभव प्राचीर पर क्या प्रभाव पड़ेगा? [2002, 07, 13]
उत्तर :
p-n सन्धि को अग्र अभिनत करने पर अवक्षय परत की चौड़ाई कम हो जाती है तथा विभव प्राचीर भी कम हो जाता है।

प्रश्न 5.
ट्रांजिस्टर में आधार क्षेत्र को अपेक्षाकृत पतला क्यों रखा जाता है? [2002, 06, 08, 09]
उत्तर :
आधार क्षेत्र में कोटरों तथा इलेक्ट्रॉनों के संयोजनों को कम करने के लिए आधार को बहुत पतला बनाया जाता है। इस दशा में उत्सर्जक से आने वाले अधिकांश कोटर (अथवा इलेक्ट्रॉन) आधार के आर-पार विसरित होकर संग्राहक पर पहुँच जाते हैं. अतः संग्राहक धारा. उत्सर्जक धारा के लगभग बराबर हो जाती है. आधार धारा अपेक्षाकत बहुत क्षीण होती है। ट्रांजिस्टर द्वारा शक्ति प्रवर्धन तथा वोल्टता प्रवर्धन का भी यही मुख्य कारण है। यदि आधार क्षेत्र मोटा बनाया जाता तो उत्सर्जक से आने वाले अधिकतर आवेश वाहक आधार में ही उदासीन हो जाते तथा संग्राहक धारा बहुत क्षीण हो जाती; अत: ट्रांजिस्टर का उपयोग नहीं हो पाता।

प्रश्न 6.
p-n-p तथा n-p-n प्रकार के ट्रांजिस्टर में से कौन अधिक उपयोगी है तथा क्यों? [2010, 12, 17]
उत्तर :
n-p-n ट्रांजिस्टर अधिक उपयोगी है; क्योंकि इसमें धारावाहक इलेक्ट्रॉन होते हैं, जबकि p-n-p ट्रांजिस्टर में धारावाहक कोटर होते हैं। धारावाहक इलेक्ट्रॉन, कोटर की अपेक्षा अधिक गतिशील होते हैं।

प्रश्न 7.
ताप बढ़ाने पर अर्द्धचालक के प्रतिरोध में क्या परिवर्तन होता है? [2004]]
उत्तर :
ताप बढ़ाने से अर्द्धचालक का प्रतिरोध घट जाता है; क्योंकि सहसंयोजक बन्ध टूटने के कारण चालक इलेक्ट्रॉन अधिक संख्या में उत्पन्न हो जाते हैं।

प्रश्न 8.
p-n सन्धि के अग्र अभिनत तथा पश्च अभिनत के बीच अन्तर बताइए। [2005]
उत्तर :
अग्र अभिनत सन्धि में, सन्धि का p-क्षेत्र बाह्य बैटरी के धन सिरे से तथा n-क्षेत्र बैटरी के ऋण सिरे से जोड़ा जाता है जबकि पश्च अभिनत सन्धि में, सन्धि का p-क्षेत्र बैटरी के ऋण सिरे से तथा n-क्षेत्र बैटरी के धन सिरे से जोड़ा जाता है।

प्रश्न 9.
अग्र धारा तथा पश्च धारा की उत्पत्ति कैसे होती है? [2005]
उत्तर :
अग्र धारा की उत्पत्ति—यह बैटरी द्वारा स्थापित बाह्य वैद्युत क्षेत्र में बहुसंख्यक वाहकों (p-क्षेत्र में कोटर तथा n-क्षेत्र में इलेक्ट्रॉन) की सन्धि के आर-पार गति के कारण उत्पन्न होती है।
पश्च धारा की उत्पत्ति- यह अल्पसंख्यक वाहकों (p-क्षेत्र में इलेक्ट्रॉन तथा n-क्षेत्र में कोटर) की गति के कारण उत्पन्न होती है। यह धारा अत्यल्प होती है।

प्रश्न 10.
उत्क्रम अभिनत p-n सन्धि डायोड में ऐवेलांश भंजन का क्या अर्थ है? [2012]
उत्तर :
ऐवेलांश भंजन-जब उत्क्रम वोल्टेज बढ़ाई जाती है तो प्रारम्भ में उत्क्रम धारा स्थिर रहती है, परन्तु वोल्टेज अधिक होने पर सन्धि के निकट सहसंयोजक बन्ध टूट जाते हैं जिसके कारण इलेक्ट्रॉन-कोटर युग्म अधिक संख्या में मुक्त हो जाते हैं तथा उत्क्रम धारा एकदम बहुत बढ़ जाती है। इस स्थिति को ऐवेलांश भंजन कहते हैं।

प्रश्न 11.
उत्क्रम अभिनत सन्धि डायोड द्वारा अल्प धारा क्यों प्रवाहित होती है? [2014]
उत्तर :
उत्क्रम अभिनत सन्धि डायोड में धारा अल्पसंख्यक वाहकों की गति से उत्पन्न होती है जोकि बाह्य व आन्तरिक दोनों वैद्युत क्षेत्रों के अन्तर्गत सन्धि को पार कर जाते हैं। इसीलिए यह धारा अति अल्प होती है।

प्रश्न 12.
n-प्रकार तथा p प्रकार के अर्द्धचालकों में बहुसंख्यक तथा अल्पसंख्यक आवेश वाहकों की उत्पत्ति को समझाइए।
उत्तर :
बहुसंख्यक तथा अल्पसंख्यक आवेश वाहक (Majority and Minority Charge Carriers)n-टाइप अर्द्धचालक मिलाई गई पाँच इलेक्ट्रॉन वाली अशुद्धि का प्रत्येक परमाणु क्रिस्टल को एक चलनशील इलेक्ट्रॉन प्रदान करता है। n-टाइप अर्द्धचालक में मिश्रित अशुद्धि द्वारा प्रदान किए गए ये इलेक्ट्रॉन ही बहुसंख्यक आवेश वाहक हैं। इसी प्रकार p-टाइप अर्द्धचालक में मिश्रित अशुद्धि द्वारा प्रदान किए गए कोटर बहुसंख्यक आवेश वाहक हैं।

बहुसंख्यक आवेश वाहकों के अतिरिक्त n-टाइप तथा pटाइप अर्द्धचालकों के भीतर ऊष्मीय विक्षोभ से उत्पन्न कुछ इलेक्ट्रॉन व कोटर उपस्थित रहते हैं जिनकी उत्पत्ति सामान्य ताप पर कुछ सहसंयोजक बन्धों के टूटने से होती है अल्पसंख्यक वाहक कहलाते हैं। n-टाइप क्रिस्टल में अल्प कोटरों में तथा pटाइप क्रिस्टल में अल्प इलेक्ट्रॉनों को अल्पसंख्यक वाहक कहते हैं।

प्रश्न 13.
दो समान आदर्श सन्धि डायोड, चित्र (a) तथा (b) के अनुसार जोड़े गए हैं। प्रत्येक में प्रतिरोध R में होकर प्रवाहित होने वाली धारा ज्ञात कीजिए। [2018]

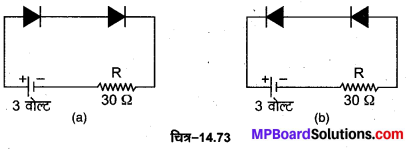
हल :
[चित्र-14.73 (a)] में दोनों सन्धि डायोड अग्र अभिनत हैं। अतः परिपथ में धारा बहेगी।
प्रतिरोध R में प्रवाहित धारा (i) = \(\frac { V }{ R }\)
= \(\frac { 30 }{ 30 }\) = 0.1 ऐम्पियर।
[चित्र-14.73 (b)] में दोनों सन्धि डायोड उत्क्रम अभिनत हैं। अत: परिपथ में कोई धारा नहीं बहेगी।
∴ प्रतिरोध R में प्रवाहित धारा = शून्य।

प्रश्न 14.
ट्रांजिस्टर में किस जंक्शन को अग्र अभिनत तथा किस जंक्शन को उत्क्रम अभिनत किया जाता है तथा क्यों? [2006] .
उत्तर :
ट्रांजिस्टर में उत्सर्जक-आधार जंक्शन को अग्र अभिनत तथा संग्राहक-आधार जंक्शन को उत्क्रम अभिनत रखा जाता है। ऐसा करने से अल्प उत्सर्जक वोल्टता से ही पर्याप्त उत्सर्जक धारा उत्पन्न होती है, अतः इसमें निवेशी सिरों पर सिग्नल वोल्टता में अल्प परिवर्तन उत्सर्जक धारा में बहुत बड़ा परिवर्तन उत्पन्न कर देता है।

आधार-संग्राहक सन्धि को उत्क्रम अभिनत करने से आधार से विसरित होने वाले सभी आवेश वाहक संग्राहक में पहुँच जाते हैं और प्रबल संग्राहक धारा प्राप्त होती है। यदि आधार-संग्राहक सन्धि को भी अग्र अभिनत कर दिया जाए तो उत्सर्जक से आने वाले आवेश वाहक संग्राहक तक नहीं पहुंचेंगे तथा ट्रांजिस्टर दो अलग-अलग परिपथों (उत्सर्जक-आधार परिपथ तथा संग्राहक-आधार परिपथ) के रूप में कार्य करेगा।

प्रश्न 15.
ऐनालोग सिग्नल क्या है? उदाहरण दीजिए। . .
उत्तर :
ऐनालोग सिग्नल-“वह सिग्नल जो एक दिए गए परिसर में कोई भी मान ग्रहण कर सकता है ऐनालोग सिग्नल कहलाता है। उदाहरण-ज्या वक्रीय सिग्नल तथा आयाम मॉडुलित सिग्नल।

प्रश्न 16.
डिजिटल सिग्नल क्या है? उदाहरण दीजिए। [2003]
उत्तर :
डिजिटल सिग्नल-“वह सिग्नल जो केवल दो सम्भव मान ग्रहण कर सकता है डिजिटल सिग्नलल कहलाता है।” उदाहरण-वोल्टेज स्तर 0 व 5V तथा लैम्प की ON व OFF की अवस्थाएँ।

प्रश्न 17.
ऐनालोग परिपथ से क्या तात्पर्य है? उदाहरण दीजिए।[2003, 07]
उत्तर :
ऐनालोग परिपथ–“जो इलेक्ट्रॉनिक परिपथ ऐनालोग सिग्नलों को क्रियान्वित करने के लिए बनाया जाता है ऐनालोग परिपथ कहलाता है।” जैसे-प्रवर्धक तथा T.V. ग्राही।

प्रश्न 18.
डिजिटल परिपथ से क्या तात्पर्य है? [2007]
उत्तर :
डिजिटल परिपथ-“जो इलेक्ट्रॉनिक परिपथ डिजिटल सिग्नलों को क्रियान्वित करने के लिए बनाया जाता है डिजिटल परिपथ कहलाता है।” जैसे-डिजिटल घड़ी, कैलकुलेटर।

प्रश्न 19.
सार्वत्रिक गेट से क्या तात्पर्य है? [2005, 07, 08]
उत्तर :
सार्वत्रिक गेट-वह गेट, जिसे बारम्बार प्रयुक्त करके तीनों मूल गेट OR, AND तथा NOT प्राप्त किए जा सकते हैं, सार्वत्रिक गेट कहलाता है; जैसे–NAND, NOR तथा EXOR या XOR गेट। NAND गेट का अर्थ है NOT-AND, NOR गेट का अर्थ है NOT-OR तथा EXOR गेट का अर्थ है Exclusive OR गेट।

प्रश्न 20.
लॉजिक गेट क्या है? मूल लॉजिक गेटों के नाम बताइए।[2013, 16]
उत्तर :
लॉजिक गेट–“वे डिजिटल परिपथ, जिनके निवेशी तथा निर्गत सिग्नलों के बीच एक तर्कपूर्ण सम्बन्ध होता है, लॉजिक गेट कहलाते हैं।” यह किसी सिग्नल को या तो अपने अन्दर से होकर गुजरने देता है या उसे रोक देता है। मूल लॉजिक गेट

• OR गेट,
• AND गेट तथा
• NOT गेट हैं।

प्रश्न 21.
बूलियन व्यंजक से क्या तात्पर्य है?
उत्तर :
बूलियन व्यंजक-एक ऐसा व्यंजक जो दो बूलियन चरों के ऐसे संयोग को प्रदर्शित करता है जिससे एक नया बूलियन चर प्राप्त होता है, बूलियन व्यंजक कहलाता है। इसके केवल दो मान 1 तथा 0 हो सकते हैं

प्रश्न 22.
लॉजिक गेट की सत्यता सारणी क्या है?
उत्तर :
सत्यता सारणी-“किसी लॉजिक गेट के सभी सम्भव निवेशी सिग्नल संयोजनों तथा निर्गत सिग्नल संयोजनों को एकसाथ प्रदर्शित करने वाली सारणी लॉजिक गेट की सत्यता सारणी कहलाती है।”

प्रश्न 23.
OR गेट, AND गेट तथा NOT गेट क्या हैं? इनके बूलियन व्यंजक लिखिए तथा प्रतीकों के चित्र बनाइए। [2010, 12, 13, 14, 16]
अथवा
लॉजिक गेटों NOT तथा OR के प्रतीक बनाइए। [2009, 10, 13]
अथवा
AND तथा OR गेट का लॉजिक प्रतीक बनाइए। [2014, 15]
उत्तर :
OR गेट-इस गेट के दो या दो से अधिक निवेश होते हैं जबकि एक निर्गत होता है। चित्र-14.74 (a) में दो निवेशी सिग्नल A तथा B वाले OR गेट के प्रतीक को प्रदर्शित किया गया है। इस गेट का निर्गत सिग्नल Y है। इसका बूलियन व्यंजक A+ B= Y होता है। इसे ‘A OR B equals Y’ पढ़ा जाता है।

AND गेट-यह एक ऐसा गेट है जिसमें दो अथवा दो से अधिक निवेशी चर A व B होते हैं तथा एक निर्गत चर Y होता है चित्र-14.74 (b) में दो निवेशों A तथा B वाले AND गेट का प्रतीक प्रदर्शित किया गया है जिसका निर्गम Y है। इसका बूलियन व्यंजक A. B= Y होता है। इसे ‘A AND B equals Y’ पढ़ा जाता है।

NOT गेट-यह एक ऐसा गेट है जिसमें एक निवेशी चर A तथा एक ही निर्गत चर Y होता है। इस गेट का निर्गम 1 उच्च होता यदि और केवल यदि इसका निवेश निम्न हो। चित्र-14.74 (c) में NOT गेट का प्रतीक प्रदर्शित किया गया है जिसका निवेश A तथा निर्गत Y है। इसका बूलियन व्यंजक \(\bar{A}\) = Y होता है। इसे ‘NOT A equals Y’ पढ़ा जाता है।

प्रश्न 24.
OR गेट, AND गेट व NOT गेट की सत्यता सारणी बनाइए। [2010, 12, 13, 16]
हल :

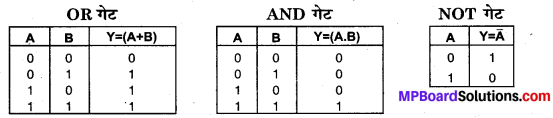
प्रश्न 25.
संलग्न सत्यता सारणी एक 2-निवेशी तर्क (लॉजिक) गेट के निर्गम को दर्शाती है
प्रयुक्त तर्क गेट को पहचानिए और इसका तर्क प्रतीक बनाइए। [2003]
उत्तर :
सत्यता सारणी से हम देखते हैं कि निर्गम Y केवल तभी 1 के बराबर है जबकि दोनों निवेश A तथा B, 1 के बराबर हैं अन्यथा निर्गम Y शून्य है। यह विशेषता AND गेट की है। अतः प्रयुक्त गेट AND गेट है जिसका प्रतीक प्रश्न 23 के उत्तर में चित्र-14.74 (b) में प्रदर्शित है।

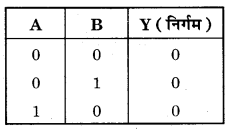
प्रश्न 26.
दिए गए लॉजिक परिपथ चित्र-17.75 में लॉजिक गेटों 1 20-.Y व 2 के नाम लिखिए। [2004, 09, 10] B P
उत्तर :
लॉजिक गेट-
(1) OR गेट तथा लॉजिक गेट
(2) NOT

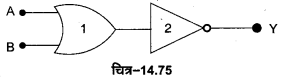
प्रश्न 27.
यदि A = 1 तथा B = 0 हो तो नीचे दिए गए लॉजिक परिपथों में 11 तथा 12 के मान ज्ञात कीजिए। [2008, 18]

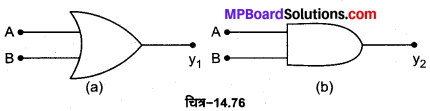
हल
प्रथम चित्र-14.76
(a) OR गेट है जिसके बूलियन व्यंजक A+ B= y₁ A = 1, B= 0 रखने पर, y₁ = 1 द्वितीय चित्र-14.76
(b) AND गेट है जिसके बूलियन व्यंजक A. B= y₂ में A = 1, B= 0 रखने पर, y₂ = 0.

प्रश्न 28.
दिए गए लॉजिक परिपथ का बूलियन व्यंजक तथा सम्पूर्ण सत्यता सारणी लिखिए। [2018]

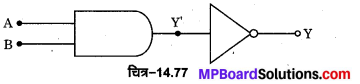
हल :
दिए गए परिपथ का बूलियन व्यंजक Y = A . B (Y equals negated of A and B)
सत्यता सारणी:

प्रश्न 29.
चित्र में एक लॉजिक परिपथ दिया गया है। दिखाइए कि यह परिपथ OR गेट की तरह कार्य करता है।[2018]

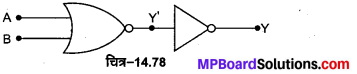
हल :
दिए गए परिपथ में, Y’ =\(\overline{\mathrm{A}+\mathrm{B}}\)
तथा Y = Y’ = \(\overline{\mathrm{Y}^{\prime}}=\overline{\overline{\mathrm{A}+\mathrm{B}}}\) या Y = A+ B
अत: दिया गया परिपथ OR गेट की तरह कार्य करता है।

प्रश्न 30.
बुलियन व्यंजक Y = \(\overline{A B}+\overline{B A}\) में यदि
(i) A = 0 व B = 1 तथा
(ii) A = 1 व B = 1 तब Y का मान क्या होगा? [2012, 14]
हल
(i) A = 0, \(\bar{A}\)= 1 तथा B = 1, \(\bar{B}\) = 0
∴ Y = \(\overline{A B}+\overline{B A}\) = 0.0 + 1.1 = 0+ 1 = 1.

(ii) A = 1, \(\bar{A}\) = 0 तथा B= 1, \(\bar{B}\) = 0 .
∴ Y = \(\overline{A B}+\overline{B A}\) = 1.0+ 1.0 = 0+ 0= 0.

प्रश्न 31.

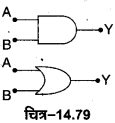
• निर्गत तभी 1 होता है जबकि और केवल जब सभी निवेशी 1 हों।
• निर्गत तभी होता है जबकि और केवल जब सभी निवेशी 0 हों।

हल :

• AND गेट A. B= Y
• OR गेट A+ B= Y

प्रश्न 32.
तीन निवेशी AND गेट का (i) लॉजिक प्रतीक, (ii) बूलियन व्यंजक तथा (iii) सत्यता सारणी दीजिए। [2013]

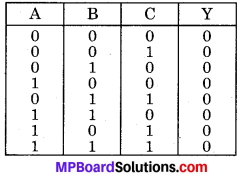
उत्तर :
1.

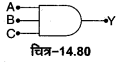
2. बूलियन व्यंजक Y = A. B.C
3. सत्यता सारणी।

प्रश्न 33.
A तथा B, OR गेट तथा NAND गेट के निवेशी तरंग प्रतिरूप चित्र-14.81 में प्रदर्शित है। दोनों गेटों के निर्गत प्रतिरूप (Y) अपनी । उत्तर-पुस्तिका में दर्शाइए। [2014] ।

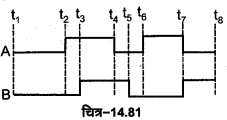
हल :
OR गेट तथा NAND गेट के निर्गत तरंग प्रतिरूप चित्र-14.82 में B प्रदर्शित है

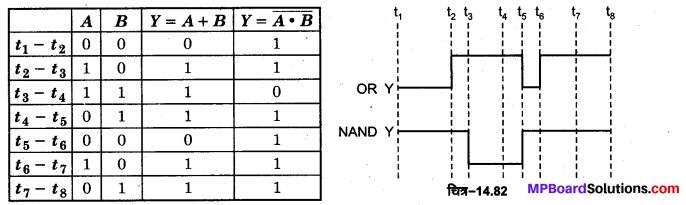
प्रश्न 34.
निम्न चित्र-14.83 में प्रदर्शित निवेश A तथा B के लिए NAND गेट के निर्गत तरंग रूप को स्केच कीजिए। [2016]

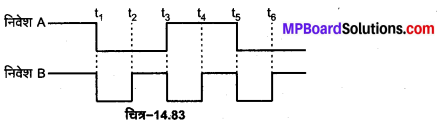
उत्तर :
NAND गेट का निर्गत तरंग रूप चित्र-14.84 में प्रदर्शित है

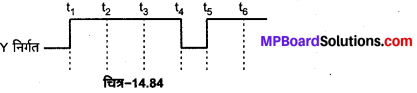
अर्द्धचालक इलेक्ट्रॉनिकी: पदार्थ युक्तियाँ तथा सरल अति लघु उत्तरीय प्रश्नोत्तर

प्रश्न 1.
ठोसों में उपस्थित ऊर्जा बैण्डों के नाम लिखिए। [2014, 15,17]
उत्तर:
चालन बैण्ड, संयोजी बैण्ड तथा वर्जित ऊर्जा अन्तराल।

प्रश्न 2.
संयोजी बैण्ड किसे कहते हैं?
उत्तर :
संयोजी बैण्ड–वह ऊर्जा बैण्ड जिसमें संयोजक इलेक्ट्रॉनों के ऊर्जा-स्तर उपस्थित होते हैं, संयोजी बैण्ड कहलाते हैं।

प्रश्न 3.
चालन बैण्ड से क्या तात्पर्य है?
उत्तर :
चालन बैण्ड-वह ऊर्जा बैण्ड जिसमें चालक इलेक्ट्रॉनों के ऊर्जा-स्तर उपस्थित होते हैं, चालन बैण्ड कहलाता है।

प्रश्न 4.
वर्जित ऊर्जा अन्तराल क्या है?
उत्तर :
वर्जित ऊर्जा अन्तराल-संयोजी बैण्ड तथा चालन बैण्ड के बीच एक रिक्ति होती है जिसमें कोई इलेक्ट्रॉन उपस्थित नहीं रहता है, इसे वर्जित ऊर्जा अन्तराल (forbidden energy gap) कहते हैं।

प्रश्न 5.
अर्द्धचालक क्या होता है? दो अर्द्धचालकों के नाम लिखिए।[2007, 09]
उत्तर :
अर्द्धचालक-“वे पदार्थ जिनकी चालकता चालक एवं अचालक के बीच होती है, अर्द्धचालक कहलाते हैं।” जैसे-सिलिकन तथा जर्मेनियम।

प्रश्न 6.
ऐसे तीन पदार्थों के नाम लिखिए जिनकी प्रतिरोधकता ताप बढ़ाने पर घटती है।
उत्तर :
कार्बन, सिलिकन तथा जर्मेनियम।

प्रश्न 7.
कोटर किसे कहते हैं? यह किस प्रकार का व्यवहार करता है? [2003]
उत्तर :
कोटर-“p-टाइप अर्द्धचालक में अपद्रव्य परमाणु के एक ओर इलेक्ट्रॉन की जो रिक्ति होती है वह कोटर कहलाता है।” यह धनावेशित कण के समान व्यवहार करता है।

प्रश्न 8.
दाता अपद्रव्यों से क्या तात्पर्य है? किन्हीं दो दाता अपद्रव्यों के नाम लिखिए।
उत्तर :
दाता अपद्रव्य–“जो अपद्रव्य, अर्द्धचालक को चालक इलेक्ट्रॉन प्रदान करते हैं, दाता अपद्रव्य कहलाते हैं।” जैसे-आर्सेनिक तथा ऐन्टिमनी। .

प्रश्न 9.
p-टाइप अर्द्धचालक से क्या तात्पर्य है? इसमें आवेश वाहक क्या होते हैं?[2007, 10]
उत्तर :
pटाइप अर्द्धचालक-“वह अर्द्धचालक जो शुद्ध अर्द्धचालक में 3 संयोजकता वाला अपद्रव्य अपमिश्रित करके बनाया जाता है, p-टाइप अर्द्धचालक कहलाता है।” इसमें बहुसंख्यक आवेश वाहक कोटर (धनात्मक) तथा अल्पसंख्यक आवेश वाहक इलेक्ट्रॉन (ऋणात्मक) होते हैं।

प्रश्न 10.
n-टाइप अर्द्धचालक से क्या तात्पर्य है? इसमें आवेश वाहक क्या होते हैं?[2003, 10]
उत्तर :
n-टाइप अर्द्धचालक–“वह अर्द्धचालक जो शुद्ध अर्द्धचालक में 5 संयोजकता वाला अपद्रव्य अपमिश्रित करके बनाया जाता है, n-टाइप अर्द्धचालक कहलाता है।” इसमें बहुसंख्यक आवेश वाहक इलेक्ट्रॉन (ऋणात्मक) तथा अल्पसंख्यक आवेश वाहक कोटर (धनात्मक) होते हैं।

प्रश्न 11.
n-प्रकार के अर्द्धचालक में बहुसंख्यक तथा अल्पसंख्यक धारा वाहकों के नाम लिखिए। [2003, 07, 08]
उत्तर :
n-प्रकार के अर्द्धचालक में बहुसंख्यक धारा वाहक इलेक्ट्रॉन तथा अल्पसंख्यक धारा वाहक कोटर होते हैं।

प्रश्न 12.
किन्हीं दो गुणों से एक चालक तथा एक अर्द्धचालक का भेद बताइए। [2004]
उत्तर :

• अर्द्धचालक की चालकता चालक से कम होती है।
• अर्द्धचालक का प्रतिरोध ताप गुणांक ऋणात्मक व चालक का धनात्मक होता है।

प्रश्न 13.
n-प्रकार के अर्द्धचालक बनाने के लिए कौन-सी अशुद्धि शुद्ध जर्मेनियम में मिलाई जाती है?
उत्तर :
5 संयोजकता वाला अपद्रव्य परमाणु; जैसे-आर्सेनिक (As) अल्प मात्रा में मिलाया जाता है।

प्रश्न 14.
जर्मेनियम को किस प्रकार p प्रकार का अर्द्धचालक बनाया जाता है? [2006]
उत्तर :
3 संयोजकता वाला अपद्रव्य परमाणु; जैसे-ऐलुमिनियम (AI) अल्प मात्रा में मिलाने पर p-प्रकार का अर्द्धचालक बनता है।

प्रश्न 15.
दो ऐसे अपद्रव्यों के नाम लिखिए जो शुद्ध सिलिकन को अर्द्धचालक बना देते हैं। [2002, 08]
उत्तर :
आर्सेनिक, ऐलुमिनियम, फॉस्फोरस, बोरॉन।

प्रश्न 16.
निज अर्द्धचालक में अपद्रव्य मिलाकर बाह्य अर्द्धचालक बनाने का उद्देश्य लिखिए। [2000]
अथवा
शुद्ध अर्द्धचालक में जब कोई अपद्रव्य मिलाया जाता है तो क्या होता है? [2009]
उत्तर :
चूँकि निज अर्द्धचालक की वैद्युत चालकता बहुत कम होती है, अत: अपद्रव्य मिलाने से बाह्य अर्द्धचालक की वैद्युत चालकता बढ़ जाती है।

प्रश्न 17.
सिलिकन में वर्जित बैण्ड की ऊर्जा कितनी होती है? [2001]
उत्तर :
सिलिकन में वर्जित बैण्ड की ऊर्जा 1.1 ev होती है।

प्रश्न 18.
जर्मेनियम, लोहा, निकिल तथा सिलिकन में कौन अर्द्धचालक हैं?
अथवा
किन्हीं दो अर्द्धचालकों के नाम लिखिए। [2001]
अथवा
ट्रांजिस्टर की रचना में सामान्यतया प्रयुक्त होने वाले किन्हीं दो पदार्थों के नाम लिखिए। [2006]
उत्तर :
जर्मेनियम तथा सिलिकन।

प्रश्न 19.
n-टाइप तथा Pटाइप अर्द्धचालकों में आवेश वाहक कौन-कौन होते हैं?[2013]
उत्तर :
n-टाइप में मुक्त इलेक्ट्रॉन (ऋणात्मक) तथा p-टाइप में कोटर (धनात्मक) आवेश वाहक होते हैं।

प्रश्न 20.
सिलिकन में गैलियम मिलाने पर किस प्रकार का अर्द्धचालक बनेगा?[2002]
उत्तर :
p-टाइप अर्द्धचालक।

प्रश्न 21.
अर्द्धचालक को ‘n’ तथा ‘ प्रकार का अर्द्धचालक कैसे बनाया जाता है?[2004]
अथवा
शुद्ध सिलिकन को ‘n’ तथा ‘ प्रकार के अर्द्धचालक बनाने के लिए इसमें कैसे अपद्रव्य मिलाए जाएँगे?[2009]
उत्तर :
अर्द्धचालक में 5 संयोजकता वाला अपद्रव्य (आर्सेनिक) मिलाकर n-टाइप का तथा 3 संयोजकता वाला अपद्रव्य (ऐलुमिनियम) मिलाकर pटाइप का अर्द्धचालक बनाया जाता है।

प्रश्न 22.
ताप बढ़ाने पर अर्द्धचालक की चालकता एवं प्रतिरोध पर क्या प्रभाव पड़ता है?[2004]
उत्तर :
ताप बढ़ाने पर अर्द्धचालक की चालकता बढ़ जाती है तथा प्रतिरोध घट जाता है।

प्रश्न 23.
सामान्यतः pn सन्धि डायोड किस कार्य के लिए प्रयुक्त किया जाता है? [2000]
उत्तर :
प्रत्यावर्ती धारा के दिष्टकरण के लिए प्रयुक्त किया जाता है।

प्रश्न 24.
p-n सन्धि डायोड में अवक्षय परत से क्या तात्पर्य है?[2005, 10, 11, 17]
उत्तर :
अवक्षय परत-“p-n सन्धि के दोनों ओर की उस परत को जिसमें आवेश वाहक नहीं रहते, अवक्षय परत कहते हैं।”

प्रश्न 25.
P-n सन्धि डायोड के लिए अग्र अभिनत तथा उत्क्रम अभिनत अवस्था में परिपथ बनाइए। [2003, 07, 09]
उत्तर

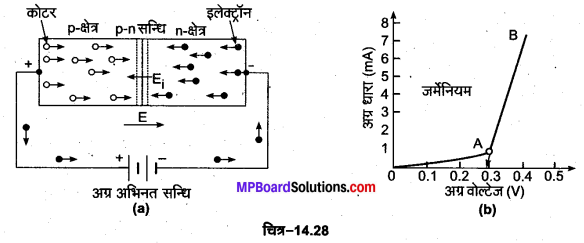
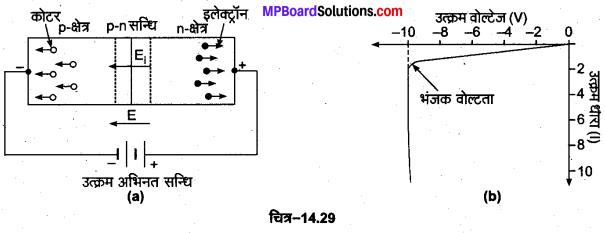
प्रश्न 26.
p-n सन्धि डायोड का प्रतीक बनाइए।[2002]
उत्तर :

प्रश्न 27.
pn सन्धि डायोड को प्रयुक्त करके एक अर्द्ध-तरंग दिष्टकारी का केवल परिपथ चित्र बनाइए।[2002]
उत्तर :

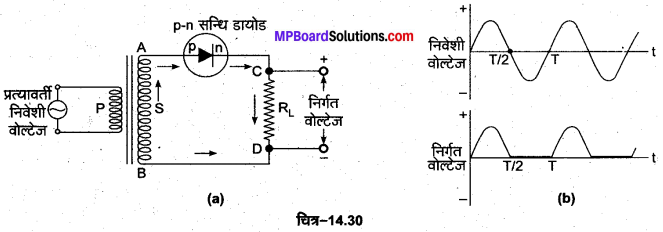
प्रश्न 28.
सन्धि डायोड द्वारा किसी तरंग के पूर्ण दिष्टीकरण हेतु परिपथ बनाइए। [2003]
उत्तर :

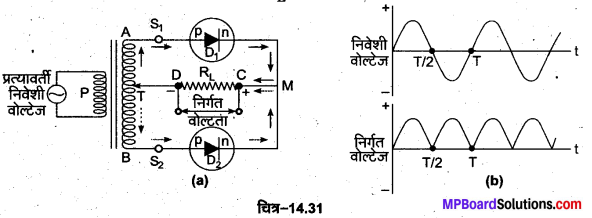
प्रश्न 29.
p-n सन्धि डायोड का पश्चदिशिक परिपथ बनाइए।[2018]
उत्तर :

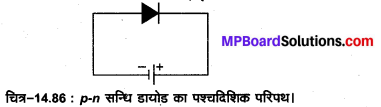
चित्र-14.86 : p.n सन्धि डायोड़ का पश्चदिशिक परिपथ।

प्रश्न 30.
अर्द्ध तरंग दिष्टकारी में यदि निवेशी आवृत्ति 50 हर्ट्स है तो निर्गत आवृत्ति क्या होगी? पूर्ण तरंग दिष्टकारी में इसी निवेशी आवृत्ति के लिए निर्गत आवृत्ति कितनी होगी?[2018]
उत्तर :
अर्द्ध तरंग दिष्टकारी में निर्गत आवृत्ति = 50 हर्ट्स, पूर्ण तरंग दिष्टकारी में निर्गत आवृत्ति = 100 हर्ट्स।

प्रश्न 31.
ट्रांजिस्टर की संग्राहक धारा, आधार धारा एवं उत्सर्जक धारा में क्या सम्बन्ध होता है? [2013,.16]
उत्तर :
उत्सर्जक धारा I_E = IB + I_C.

प्रश्न 32.
चित्र-14.87 में ट्रांजिस्टरों के प्रकार बताइए तथा प्रत्येक में उत्सर्जक, आधार व संग्राहक अंकित कीजिए।

अथवा
p-n-p तथा n-p-n ट्रांजिस्टर के नामांकित प्रतीक चिह्न बनाइए। [2007, 08, 10, 12, 14, 16]
उत्तर :
(a) p-n-p ट्रांजिस्टर चित्र-14.88(a) तथा (b) n-p-n ट्रांजिस्टर चित्र-14.88(b)।

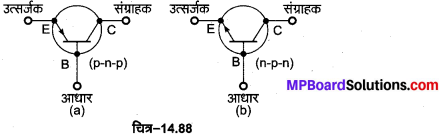
प्रश्न 33.
संलग्न चित्र-14.89 में प्रदर्शित ट्रांजिस्टर किस प्रकार का है? इसमें

• उत्सर्जक एवं आधार तथा
• धार एवं संग्राहक के बीच दो p-n सन्धियाँ हैं। इन दोनों में से कौन-सी सन्धि अग्र अभिनत (फॉरवर्ड बायस) तथा कौन-सी सन्धि उत्क्रम अभिनत (रिवर्स बायस) है?

उत्तर :
ट्रांजिस्टर p-n-p प्रकार का है। उत्सर्जक-आधार (p-n) सन्धि अग्र अभिनत है, जबकि आधार-संग्राहक (n-p) सन्धि उत्क्रम अभिनत है।

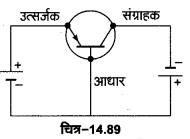
प्रश्न 34.
p-n-p ट्रांजिस्टर का नामांकित संकेत चित्र बनाइए।
उत्तर

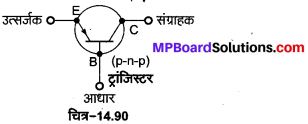
प्रश्न 35.
ट्रांजिस्टर से आप क्या समझते हैं?[2004, 05]
उत्तर :
ट्रांजिस्टर-ट्रांजिस्टर p तथा n-टाइप के अर्द्धचालकों से बनी एक इलेक्ट्रॉनिक युक्ति है, जो ट्रायोड वाल्व के स्थान पर प्रयुक्त की जाती है।

प्रश्न 36.
ट्रांजिस्टर की रचना कैसे की जाती है?
उत्तर :
दो समान प्रकार के अर्द्धचालक; जैसे p-टाइप (अथवा n-टाइप) क्रिस्टलों के बीच एक विपरीत प्रकार के अर्द्धचालक जैसे n-टाइप (अथवा p-टाइप) क्रिस्टल की पतली परत को दबाकर ट्रांजिस्टर की रचना की जाती है।

प्रश्न 37.
ट्रांजिस्टर के एक उपयोग का नाम लिखिए।
उत्तर :
ट्रांजिस्टर प्रवर्धक के रूप में प्रयुक्त होता है। प्रश्न 38. ट्रांजिस्टर के शक्ति लाभ का व्यंजक लिखिए। उत्तर : शक्ति लाभ = वोल्टेज लाभ x धारा लाभ।

प्रश्न 39.
क्या दो pn सन्धि डायोडों को p-n a n-p क्रम में मिलाकर रखने पर p-n-p ट्रांजिस्टर का कार्य कर सकते हैं?
उत्तर :
नहीं; क्योंकि इस दशा में n-क्षेत्र (जो आधार का कार्य करेगा) बहुत मोटा हो जाएगा।

प्रश्न 40.
p-n-p ट्रांजिस्टर में उत्सर्जक तथा संग्राहक दोनों टाइप के होते हुए भी वे कैसे समान नहीं हैं? [2004]
उत्तर :
उत्सर्जक अधिक अपमिश्रित तथा संग्राहक अपेक्षाकृत कम अपमिश्रित होता है।

प्रश्न 41.
LED का पूरा नाम लिखिए। [2015]
उत्तर :
Light Emitting Diode.

प्रश्न 42.
LED क्या है?
अथवा
परिपथ बनाकर इसके.V-I अभिलाक्षणिक वक्र को प्रदर्शित कीजिए। [2017]
उत्तर :
LED-प्रकाश उत्सर्जक डायोड (LED) अधिक अपमिश्रित p-n सन्धि डायोड होता है जो अग्र अभिनति में प्रयुक्त किया जाता है तथा अभिनत बैटरी से प्राप्त वैद्युत ऊर्जा को प्रकाश के रूप में उत्सर्जित करता है।

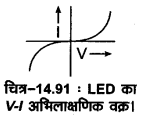
प्रश्न 43.
सौर सेल क्या है?
उत्तर :
सौर सेल-सौर सेल एक विशिष्ट प्रकार का अवअभिनत (unbiased) p-n सन्धि डायोड होता है जो सौर ऊर्जा को वैद्युत ऊर्जा में परिवर्तित करता है।

प्रश्न 44.
जेनर डायोड क्या है? इसका परिपथ चिह्न बनाइए। [2014, 17]
उत्तर :
जेनर डायोड-जेनर डायोड अधिक अनमिश्रित p-n सन्धि डायोड होता है जो उत्क्रम अभिनति में भंजक वोल्टता पर बिना खराब हुए निरन्तर कार्य कर सकता है।

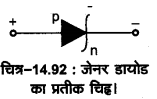
प्रश्न 45.
जेनर डायोड का उपयोग क्या है?
उत्तर :
जेनर डायोड वोल्टता नियन्त्रक के रूप में प्रयुक्त होता है।

प्रश्न 46.
क्या दिए गए चित्र-14.93 में सन्धि डायोड D अग्र-अभिनत है
अथवा
उत्क्रम-अभिनत है?
उत्तर :
सन्धि डायोड D उत्क्रम-अभिनत है।

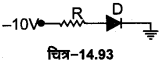
प्रश्न 47.
ऐनालोग तथा डिजिटल सिग्नलों में क्या अन्तर है? –
उत्तर :
ऐनालोग सिग्नल दिए गए परिसर में कोई भी मान ग्रहण कर सकता है क्योंकि यह सतत होता है जबकि डिजिटल सिग्नल केवल दो विविक्त मान ग्रहण कर सकता है।

प्रश्न 48.
ऐनालोग तथा डिजिटल परिपथों में क्या अन्तर है?[2007]
उत्तर :
ऐनालोग परिपथ में वोल्टेज (अथवा धारा) समय के साथ निरन्तर बदलता रहता है जबकि डिजिटल परिपथ में वोल्टेज (अथवा धारा) के केवल दो स्तर होते हैं।

प्रश्न 49.
मूल लॉजिक गेटों के नाम बताइए।[2003, 10]
उत्तर :
OR गेट, AND गेट तथा NOT गेट।

प्रश्न 50.
AND गेट को व्यवहार में कैसे प्रयुक्त करते हैं?
उत्तर :
AND गेट का बूलियन व्यंजक A. B= Y है। यदि A = 0, B= 0 तो Y = 0; यदि A = 0, B= 1 तो Y = 0; यदि A = 1, B= 0 तो Y = 0; यदि A = 1, B= 1 तो Y = 1.

प्रश्न 51.
NOT गेट को व्यवहार में कैसे प्रयुक्त करते हैं?[2007]
उत्तर :
NOT गेट का बूलियन व्यंजक \(\bar{A}\) = Y है। बाइनरी पद्धति में केवल दो अंक 0 व 1 होते हैं। यदि निवेशी A = 0 तो निर्गत Y = 1 होगा। इसके विपरीत यदि निवेशी A = 1 तो निर्गत Y = 0 होगा।

प्रश्न 52.
AND गेट का बूलियन एक्सप्रेशन लिखिए।[2008]]
अथवा
AND द्वारक हेतु बूलियन व्यंजक लिखिए तथा इसकी सत्यता सारणी भी लिखिए।[2018]
उत्तर :
दो निवेशों A तथा B वाले AND गेट का बूलियन एक्सप्रेशन A. B = Y है।
AND द्वारक की सत्यता सारणी

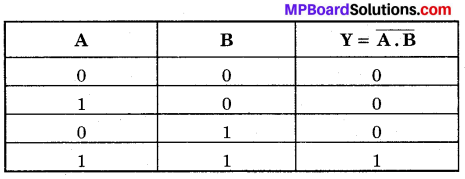
प्रश्न 53.
NOT गेट का बूलियन व्यंजक लिखिए।
अथवा
NOT गेट के लिए लॉजिक प्रतीक तथा बूलियन व्यंजक दीजिए। [2018]
उत्तर
एक निवेशी सिग्नल A वाले NOT गेट का बूलियन व्यंजक Y = \(\bar{A}\) है।

प्रश्न 54.
OR गेट का बूलियन व्यंजक लिखिए।
उत्तर :
दो निवेशी सिग्नलों A व B वाले OR गेट का बूलियन व्यंजक Y = A+ B है।

प्रश्न 55.
AND गेट किस नियम पर कार्य करता है?
उत्तर :
AND गेट का निर्गत स्तर 1 केवल तब होता है जब दोनों निवेशियों का स्तर 1 हो।

प्रश्न 56.
NOT गेट किस नियम पर कार्य करता है?
उत्तर :
यदि NOT गेट का एकल निवेशी का स्तर 0 हो तो उसका निर्गत स्तर 1 होता है।

प्रश्न 57.
लॉजिक गेट को लॉजिक गेट क्यों कहा जाता है?
उत्तर
लॉजिक गेट को लॉजिक गेट इसलिए कहा जाता है क्योंकि यह या तो किसी डिजिटल सिग्नल को रोकता है अथवा गुजरने देता है तथा इसके निर्गत तथा निवेश के बीच एक तर्कपूर्ण सम्बन्ध (logical relation) होता है।

प्रश्न 58.
चित्र-14.95 में प्रदर्शित लॉजिक गेट का नाम लिखिए। [2009]
उत्तर :
AND गेट।

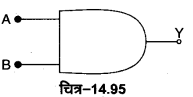
प्रश्न 59.
प्रदर्शित लॉजिक परिपथ के लिए निर्गत सिग्नल Y का बूलियन व्यंजक लिखिए। [2018]

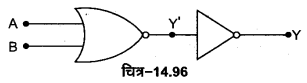
हल :
यहाँ y’ = \(\overline{\mathrm{A}+\mathrm{B}}\) तथा Y= \(\overline{\mathbf{Y}}^{\prime}\)

अर्द्धचालक इलेक्ट्रॉनिकी: पदार्थ युक्तियाँ तथा सरल आंकिक प्रश्नोत्तर

प्रश्न 1.
एक p-n सन्धि डायोड का अग्र अभिनत में प्रतिरोध 10 ओम है। यदि अग्र वोल्टेज में 0•025 वोल्ट का परिवर्तन करें तो डायोड धारा में कितना परिवर्तन होगा? [2010, 14]
हल :
दिया है, R= 10 ओम, ΔV = 0.025 वोल्ट, ΔI = ?
डायोड धारा में परिवर्तन ΔI = \(\frac { ΔV }{ R }\) = \(\frac { 0.025 }{ 10 }\) = 2.5 x 10^-3 ऐम्पियर।

प्रश्न 2.
उभयनिष्ठ उत्सर्जक ट्रांजिस्टर का धारा लाभ 5.0 है। यदि इसकी आधार धारा का मान 0.4 मिलीऐम्पियर हो, तो उत्सर्जक धारा का मान ज्ञात कीजिए। [2018]
हल :
दिया है, β = 5.0, ΔI_B = 0.4 मिलीऐम्पियर, Δl_c = ?
\(\beta=\frac{\Delta I_{C}}{\Delta I_{B}}\)
∴ ΔI_c = β × ΔI_B = 5.0 × 0.4 = 2.0 मिलीऐम्पियर
उत्सर्जक धारा ΔI_E = ΔI_B + ΔI_C = 0.4+ 2.0 = 2.4 मिलीऐम्पियर।

प्रश्न 3.
उभयनिष्ठ उत्सर्जक प्रवर्धक के लिए धारा लाभ 59 है। यदि उत्सर्जक धारा 6.0 मिलीऐम्पियर हो तब आधार धारा का मान ज्ञात कीजिए। [2018]
हल :
दिया है, β = 59, ΔI_E = 6.0 मिलीऐम्पियर, ΔI_B = ?
β = \(\frac{\Delta I_{C}}{\Delta I_{B}}\) या ΔI_c = 59 (ΔI_B)
उत्सर्जक धारा ΔI_E = ΔI_B + ΔI_c
6.0 = ΔI_B + 59(ΔI_B)
6.0 = 60(ΔI_B)
या ΔI_B = \(\frac { 6.0 }{ 60 }\) = 0.1 मिलीऐम्पियर।

प्रश्न 4.
एक p-n सन्धि डायोड का अग्र अभिनत की स्थिति में प्रतिरोध 250 है। अग्र अभिनत विभव में कितना परिवर्तन किया जाए कि धारा में 2 मिलीऐम्पियर का परिवर्तन हो जाए?
[2003]
हल :
दिया है, R = 25Ω, ΔI = 2 मिलीऐम्पियर,
अग्र अभिनत विभव ΔV = R × ΔI = 25 × 2 = 50 मिलीवोल्ट।

प्रश्न 5.
उभयनिष्ठ आधार परिपथ में किसी ट्रांजिस्टर का धारा लाभ 0.98 है। यदि उत्सर्जक धारा में 5.0 मिलीऐम्पियर का परिवर्तन हो तो संग्राहक धारा में परिवर्तन ज्ञात कीजिए।
[2015]
हल :
दिया है, a = 0.98, ΔI_E = 5.0 मिलीऐम्पियर, Δl_c = ?
संग्राहक धारा में परिवर्तन ΔI_C = a × ΔI_E = 0.98 × 5 = 4.9 मिलीऐम्पियर।

प्रश्न 6.
एक B = 19 धारा लाभ वाले ट्रांजिस्टर की उभयनिष्ठ उत्सर्जक व्यवस्था में यदि आधार धारा में 0.4 मिलीऐम्पियर का परिवर्तन किया जाए तो संग्राहक धारा में कितना परिवर्तन होगा? उत्सर्जक धारा में क्या परिवर्तन होगा? [2001]
हल :
दिया है, β = 19, ΔI_B = 0.4 मिलीऐम्पियर, Δl_c = ?
सूत्र β = \(\frac{\Delta I_{C}}{\Delta I_{B}}\) से,
संग्राहक धारा में परिवर्तन ΔI = β × ΔI_B = 19 × 0.4 = 7.6
मिलीऐम्पियर। उत्सर्जक धारा में परिवर्तन ΔI_E = ΔI_B + Δl_c = 0.4+ 7.6 = 8.0 मिलीऐम्पियर।

प्रश्न 7.
एक n-p-n ट्रांजिस्टर में 10-6 सेकण्ड में 1010 इलेक्ट्रॉन उत्सर्जक में प्रवेश करते हैं। 2% इलेक्ट्रॉन आधार में क्षय हो जाते हैं। उत्सर्जक धारा (IF) तथा आधार धारा (IB) के मान ज्ञात कीजिए। धारा परिणमन अनुपात तथा धारा प्रवर्धन गुणांक की गणना कीजिए। [2005, 06]
हल :
दिया है, t= 10^-6 सेकण्ड,

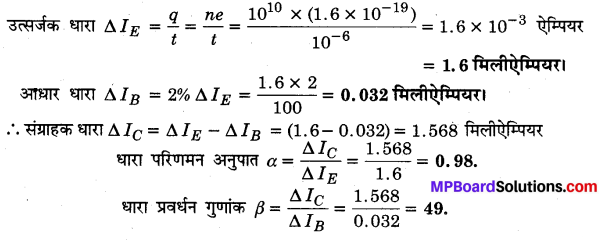
प्रश्न 8.
n-p-n सिलिकन ट्रांजिस्टर का निवेशी प्रतिरोध 665 2 है। आधार-धारा में 15 माइक्रोएम्पियर का परिवर्तन करने पर संग्राहक धारा में 2 मिलीऐम्पियर का परिवर्तन होता है। ट्रांजिस्टर का उपयोग उभयनिष्ठ उत्सर्जक का उपयोग उभयनिष्ठ उत्सर्जक प्रवर्धक के रूप में किया जाता, जिसका लोड प्रतिरोध 5 किलोओम है। प्रवर्धक का वोल्टेज लाभ ज्ञात कीजिए। [2018]
हल :
दिया है, R₁ = 665 Ω, ΔI_B = 15 माइक्रोएम्पियर = 0.015 मिली ऐम्पियर, ΔI_C = 2 मिलीऐम्पियर
R₂ = 5 किलोओम = 5000 Ω, A = ?
धारा लाभ \(\beta=\frac{\Delta I_{C}}{\Delta I_{B}}=\frac{2}{0.15}=\frac{2000}{15}=\frac{400}{3}\)
प्रवर्धक का वोल्टेज लाभ (A) = \(\beta \cdot \frac{R_{2}}{R_{1}}=\frac{400}{3} \times \frac{5000}{665}=1002.5\)

प्रश्न 9.
एक सिलिकन ट्रांजिस्टर में, उत्सर्जक धारा में 8.89 मिलीऐम्पियर के परिवर्तन से संग्राहक धारा में 8.80 मिलीऐम्पियर का परिवर्तन होता है। संग्राहक धारा में इतने ही परिवर्तन के लिए आधार-धारा में कितना परिवर्तन करना होगा?
हल :
दिया है, ΔI_E = 8.89 मिलीऐम्पियर, Δl_c = 8.80 मिलीऐम्पियर, Δl_B = ?
आधार-धारा ΔI_B = ΔI_E – ΔI_c = 8.89- 8.80 = 0.09 मिलीऐम्पियर

प्रश्न 10.
एक ट्रांजिस्टर प्रवर्धक के लिए β = 30, लोड प्रतिरोध R_L = 4 किलीओम तथा निवेशी प्रतिरोध R_i = 4002 है। इसका वोल्टेज प्रवर्धन ज्ञात कीजिए।
हल :
वोल्टेज प्रवर्धन A_v = \(\beta\left(\frac{R_{L}}{R_{i}}\right)=30 \times \frac{4000}{400}=300\)

प्रश्न 11.
एक ट्रांजिस्टर परिपथ में संग्राहक धारा 13.4 मिलीऐम्पियर तथा आधार-धारा 150 माइक्रोएम्पियर है। परिपथ में उत्सर्जक धारा ज्ञात कीजिए।
हल :
दिया है,ΔI_C= 13.4 माइक्रोएम्पियर, ΔI_B = 150 माइक्रोएम्पियर = 0.150 मिली ऐम्पियर, ΔI_E = ?
उत्सर्जक धारा ΔI_E = Δl_C + ΔI_B = 13.4+ 0.150 = 13.55 मिलीऐम्पियर।

प्रश्न 12.
एक ट्रांजिस्टर परिपथ की उत्सर्जक धारा में 1.8 मिलीऐम्पियर का परिवर्तन करने पर संग्राहक धारा में 1.6 मिलीऐम्पियर का परिवर्तन होता है। इसके लिए परिपथ की आधार धारा में परिवर्तन का मान ज्ञात कीजिए। [2012]
हल :
दिया है, ΔI_E = 1.8 मिलीऐम्पियर, Δl_C = 1.6 मिलीऐम्पियर
सूत्र ΔI_E = ΔL_c + ΔI_B से
Δl_B = ΔI_E – Δl_C = 1.8 – 1.6 = 0.2 मिलीऐम्पियर।

प्रश्न 13.
संलग्न चित्र 14.97 में प्रदर्शित अमीटर A, तथा A में मापी गई विद्युत धाराएँ क्या हैं? यदि उनके प्रतिरोध नगण्य तथा (p-n) सन्धि डायोड आदर्श हों? [2013]
हल :

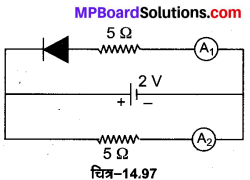
दिया गया p-n सन्धि डायोड उत्क्रम अभिनति में है, अत: इसका प्रतिरोध अनन्त होगा तथा उस शाखा में कोई धारा नहीं बहेगी।
∴ अमीटर A₁ से मापी गई वैद्युत धारा I₁ = 0
अमीटर A₂ से मापी गई वैद्युत धारा I₂ = \(\frac { V }{ R }\) = \(\frac { 2 }{ 5 }\)= 0.4 ऐम्पियर।

प्रश्न 14.
दिए गए p-n सन्धि डायोड से प्रवाहित धारा की गणना कीजिए।
हल :

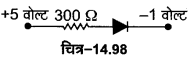
परिपथ के सिरों पर विभवान्तर = 5 – (-1) = 6 वोल्ट
परिपथ में प्रवाहित धारा I = \(\frac { V }{ R }\) = \(\frac { 6 }{ 300 }\)= 0.02 ऐम्पियर।

प्रश्न 15.
संलग्न चित्र-14.99 में लॉजिक परिपथ की सम्पूर्ण सत्य सारणी लिखिए।

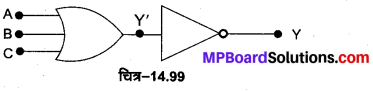
हल :
प्रथम AND गेट तथा द्वितीय NOT गेट है, अतः यह NAND गेट होगा। इसका बूलियन व्यंजक Y’=A. B. C है

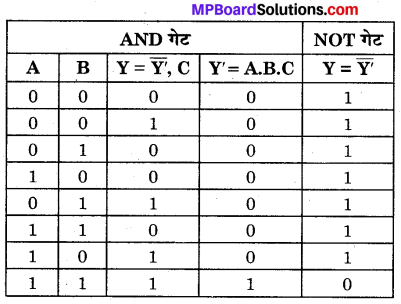
प्रश्न 16.
संलग्न चित्र 14.100 में लॉजिक परिपथ के लिए सत्य सारणी बनाइए तथा इसका बूलियन व्यंज़क लिखिए [2008, 12]

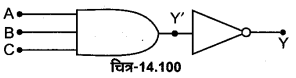
हल :
प्रथम OR गेट तथा द्वितीय NOT गेट है। अत: यह NOR गेट है। इसका बूलियन व्यंजक Y’= A+ B+ C

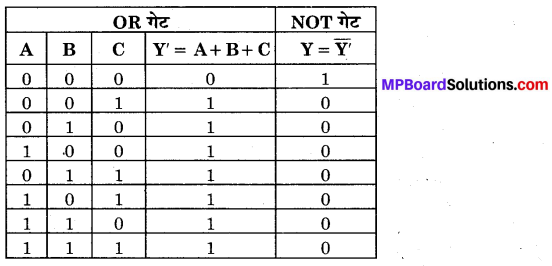
प्रश्न 17.
चित्र में प्रदर्शित लॉजिक गेट का संकेत चित्र दिया गया है-

1. लॉजिक गेट का नाम तथा सत्यता सारणी लिखिए।
2. A व B को दिए गए निवेशी सिग्नलों का निर्गत सिग्नल प्रदर्शित कीजिए।

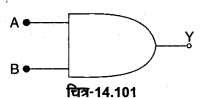
उत्तर :
1. दिया गया लॉजिक गेट AND गेट है। AND गेट की सत्यता सारणी

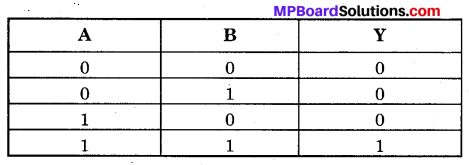
2.

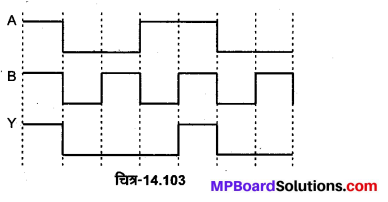
अर्द्धचालक इलेक्ट्रॉनिकी: पदार्थ युक्तियाँ तथा सरल बहुविकल्पीय प्रश्नोत्तर

• निम्नलिखित प्रश्नों के चार विकल्प दिए गए हैं। सही विकल्प का चयन कीजिए

1. Pटाइप का अर्द्धचालक बनाने के लिए शुद्ध जर्मेनियम में मिलाया जाने वाला अपद्रव्य है- [2003, 11,17]
(a) फॉस्फोरस
(b) ऐन्टिमनी
(c) ऐलुमिनियम
(d) नाइट्रोजन।
उत्तर :
(c) ऐलुमिनियम

2. n-टाइप का अर्द्धचालक बनाने के लिए शुद्ध सिलिकन में जो अपद्रव्य मिलाया जाता है, वह है [2004]
(a) बोरॉन
(b) फॉस्फोरस
(c) ऐन्टिमनी
(d) ऐलुमिनियम।
उत्तर :
(b) फॉस्फोरस
(c) ऐन्टिमनी

3. n-टाइप का अर्द्धचालक वैद्युत से होता है[2005]
(a) धनात्मक आवेशित
(b) उदासीन
(c) ऋणात्मक आवेशित
(d) इनमें से कोई नहीं।
उत्तर :
(b) उदासीन

4. एक p-टाइप अर्द्धचालक होता है [2018]
(a) धनावेशित
(b) ऋणावेशित
(c) उदासीन
(d) धनावेशित या ऋणावेशित कोई भी।
उत्तर :
(c) उदासीन

5. n-टाइप के अर्द्धचालक में वैद्युत चालन का कारण है [2005, 16]
(a) इलेक्ट्रॉन .
(b) प्रोटॉन
(c) कोटर
(d) पॉजिट्रॉन।
उत्तर :
(a) इलेक्ट्रॉन

6. n-टाइप अर्द्धचालक में आवेश वाहक होते हैं [2005, 06, 08, 11]
(a) केवल इलेक्ट्रॉन
(b) केवल कोटर
(c) दोनों, अल्प संख्या में इलेक्ट्रॉन तथा अधिक संख्या में कोटर
(d) दोनों, अधिक संख्या में इलेक्ट्रॉन तथा अल्प संख्या में कोटर।
उत्तर :
(d) दोनों, अधिक संख्या में इलेक्ट्रॉन तथा अल्प संख्या में कोटर।

7. p-टाइप का अर्द्धचालक बनता है [2007]
(a) जब एक जर्मेनियम क्रिस्टल में 3 संयोजी अपद्रव्य पदार्थ मिलाए जाते हैं
(b) जब एक जर्मेनियम क्रिस्टल में 5 संयोजी अपद्रव्य पदार्थ मिलाए जाते हैं
(c) शुद्ध जर्मेनियम से
(d) शुद्ध ताँबे से।
उत्तर :
(a) जब एक जर्मेनियम क्रिस्टल में 3 संयोजी अपद्रव्य पदार्थ मिलाए जाते हैं

8. p-टाइप चालक प्राप्त करने के लिए जर्मेनियम में थोड़ा अपद्रव्य मिलाया जाता। अपद्रव्य की संयोजकता है- [2018]
(a) 1
(b) 2
(c) 3
(d) 5.
उत्तर :
(c) 3

9. Pटाइप के अर्द्धचालक में आवेश वाहक होते हैं
(a) केवल कोटर
(b) इलेक्ट्रॉनों तथा कोटरों की समान संख्या
(c) इलेक्ट्रॉनों की अधिक संख्या और कोटरों की कम संख्या
(d) कोटरों की अधिक संख्या तथा इलेक्ट्रॉनों की कम संख्या।
उत्तर :
(d) कोटरों की अधिक संख्या तथा इलेक्ट्रॉनों की कम संख्या।

10. अर्द्धचालकों में वैद्युत चालन होता है[2010, 17]
(a) कोटरों से
(b) इलेक्ट्रॉनों से
(c) कोटरों तथा इलेक्ट्रॉनों से
(d) न तो कोटरों से और न ही इलेक्ट्रॉनों से।
उत्तर :
(c) कोटरों तथा इलेक्ट्रॉनों से

11. अर्द्धचालकों की चालकता [2017]
(a) ताप पर निर्भर नहीं करती
(b) ताप बढ़ने पर घटती है
(c) ताप बढ़ने पर बढ़ती है
(d) ताप घटने पर बढ़ती है।
उत्तर :
(c) ताप बढ़ने पर बढ़ती है

12. कोटर (छिद्र) अधिसंख्य आवेश वाहक होते हैं[2017]
(a) नैज अर्द्धचालकों में
(b) n-प्रकार के अर्द्धचालकों में
(c) p-प्रकार के अर्द्धचालकों में ।
(c) धातुओं में।
उत्तर :
(c) p-प्रकार के अर्द्धचालकों में ।

13. n-टाइप के अर्द्धचालक में अल्पसंख्यक आवेश वाहक होते हैं [2010]
(a) इलेक्ट्रॉन
(b) होल
(c) इलेक्ट्रॉन तथा होल
(d) इनमें में से कोई नहीं।
उत्तर :
(b) होल

14. किसी जर्मेनियम क्रिस्टलों को pटाइप अर्द्धचालक में परिवर्तित करने के लिए अपद्रव्य तत्व की संयोजकता है [2012]
(a)6
(b) 5
(c) 4
(d) 3
उत्तर :
(d) 3

15. परम शून्य ताप पर शुद्ध जर्मेनियम का क्रिस्टल व्यवहार करता है [2010, 12, 13]
(a) पूर्ण चालक की भाँति
(b) पूर्ण अचालक की भाँति
(c) अर्द्धचालक की भाँति
(d) इनमें से कोई नहीं।
उत्तर :
(b) पूर्ण अचालक की भाँति

16. शुद्ध सिलिकन के n-टाइप अर्द्धचालक बनाने के लिए इसमें अपद्रव्य पदार्थ मिलाते हैं [2014]
(a) ऐलुमिनियम
(b) लोहा
(c) बोरॉन
(d) ऐन्टिमनी।
उत्तर :
(d) ऐन्टिमनी।

17. शुद्ध जर्मेनियम में कौन-सा अपद्रव्य परमाणु मिश्रित कर दें कि यह एक Pटाइप अर्द्धचालक हो जाए
(a) फॉस्फोरस
(b) एण्टीमनी
(c) ऐलुमिनियम
(d) बिस्मथ।
उत्तर :
(c) ऐलुमिनियम

18. निम्न में से कौन-सा कथन सत्य नहीं है? [2018]
(a) अर्द्धचालक का प्रतिरोध तापमान बढ़ाने पर कम हो जाता है
(b) वैद्युत क्षेत्र में कोटर (होल) इलेक्ट्रॉन की गति के विपरीत दिशा में गति करता है
(c) धातु का प्रतिरोध तापमान बढ़ाने पर कम हो जाता है .
(d) n-टाइप के अर्द्धचालक उदासीन होते हैं।
उत्तर :
(c) धातु का प्रतिरोध तापमान बढ़ाने पर कम हो जाता है .

19. चालन एवं संयोजी बैण्डों की ऊर्जाओं में अन्तर [2018]
(a) चालकों में अधिकतम होता है
(b) चालकों में न्यूनतम होता है
(c) अर्द्धचालकों में चालकों से कम होता है
(d) कुचालकों में चालकों से कम होता है।
उत्तर :
(b) चालकों में न्यूनतम होता है

20. तीन पदार्थों के ऊर्जा बैण्ड चित्र-14.104 में दिए गए हैं, जहाँ V संयोजी बैण्ड तथा Cचालन बैन्ड हैं। ये पदार्थ क्रमशः हैं [2014] |

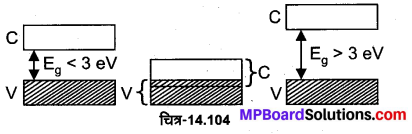
(a) चालक, अर्द्धचालक, कुचालक
(b) अर्द्धचालक, कुचालक, चालक
(c) कुचालक, चालक, अर्द्धचालक
(d) अर्द्धचालक, चालक, कुचालक।
उत्तर :
(d) अर्द्धचालक, चालक, कुचालक।

21. एक अर्द्धचालक डायोड के p-सिरे को भू-सम्पर्कित किया गया है तथा n-सिरे पर-2 वोल्ट का विभव लगाया गया है। डायोड में [2004]
(a) चालन होगा
(b) चालन नहीं होगा
(c) आंशिक चालन होगा
(d) भंजन हो जाएगा।
उत्तर :
(a) चालन होगा

22. pn सन्धि डायोड के अवक्षय परत में होते हैं [2007, 12, 17]
(a) केवल कोटर
(b) केवल इलेक्ट्रॉन
(c) इलेक्ट्रॉन तथा कोटर
(d) न इलेक्ट्रॉन न कोटर।
उत्तर :
(d) न इलेक्ट्रॉन न कोटर।

23. p-n सन्धि डायोड में उत्क्रम संतृप्त धारा का कारण है, केवल [2009]
(a) अल्पसंख्यक वाहक
(b) बहुसंख्यक वाहक
(c) ग्राही आयन
(d) दाता आयन।
उत्तर :
(a) अल्पसंख्यक वाहक

24. एक अर्द्धचालक डायोड में विभव प्राचीर विरोध करता है, मात्र [2009]
(a) n-क्षेत्र में बहुसंख्यक वाहकों को
(b) p-क्षेत्र में बहुसंख्यक वाहकों को
(c) दोनों क्षेत्रों के बहुसंख्यक वाहकों को .
(d) दोनों क्षेत्रों के अल्पसंख्यक वाहकों को।
उत्तर :
(c) दोनों क्षेत्रों के बहुसंख्यक वाहकों को .

25. जर्मेनियम डायोड का प्राचीर विभव लगभग है[2009]
(a) 0.1 वोल्ट
(b) 0.3 वोल्ट
(c) 0.5 वोल्ट
(d) 0.7 वोल्ट।
उत्तर :
(b) 0.3 वोल्ट

26. सिलिकन डायोड में सन्धि विभव का मान होता है [2008]
(a) 0.2 वोल्ट
(b) 0.4 वोल्ट
(c) 0.3 वोल्ट
(d) 0.6 वोल्ट।
उत्तर :
(d) 0.6 वोल्ट।

27. ट्रांजिस्टर मूल रूप से एक [2003, 06]
(a) शक्ति चालित साधन है
(b) विभव चालित साधन है
(c) प्रतिरोध चालित साधन है
(d) धारा चालित साधन है।
उत्तर :
(d) धारा चालित साधन है।

28. n-p-n ट्रांजिस्टर का परिपथ प्रतीक है [2006]

उत्तर :

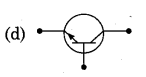
29. एक ट्रांजिस्टर में [2013]
(a) उत्सर्जक के अपद्रव्य का सान्द्रण न्यूनतम होता है
(b) संग्राहक के अपद्रव्य का सान्द्रण न्यूनतम होता है
(c) आधार के अपद्रव्य का सान्द्रण न्यूनतम होता है .
(d) तीनों क्षेत्रों के अपद्रव्य का सान्द्रण समान होता है।
उत्तर :
(c) आधार के अपद्रव्य का सान्द्रण न्यूनतम होता है .

30. एक n-p-n ट्रांजिस्टर में संग्राहक धारा 10 मिलीऐम्पियर है। यदि इलेक्ट्रॉनों में से 90% संग्राहक पर पहुँचते हैं तो[2013]
(a) उत्सर्जक धारा 9 मिलीऐम्पियर होगी
(b) उत्सर्जक धारा 10 मिलीऐम्पियर होंगी
(c) आधारा धारा 1 मिलीऐम्पियर होगी
(d) आधार धारा 11 मिलीऐम्पियर होगी।
उत्तर :
(c) आधारा धारा 1 मिलीऐम्पियर होगी

31. धारा लाभ β = 19 वाले ट्रांजिस्टर की उभयनिष्ठ उत्सर्जक व्यवस्था में यदि आधार धारा में 0.4 मिलीऐम्पियर का परिवर्तन किया जाए तो संग्राही धारा में परिवर्तन होगा
[2007]
(a) 7.6 मिलीऐम्पियर
(b) 4.75 मिलीऐम्पियर
(c) 1.31 मिलीऐम्पियर
(d) 0.21 मिलीऐम्पियर।
उत्तर :
(a) 7.6 मिलीऐम्पियर

32. एक ट्रांजिस्टर के आधार धारा में 25 µA का परिवर्तन करने पर संग्राहक धारा में 0.55 मिलीऐम्पियर का परिवर्तन होता है। β (ac) का मान होगा [2009]
(a) 22 .
(b) 0.045
(c) 20
(d) 0.09.
उत्तर :
(a) 22 .

33. एक ट्रांजिस्टर के उभयनिष्ठ उत्सर्जक प्रवर्धक के लिए शक्ति प्रवर्धन A_P तथा वोल्टेज प्रवर्धन A_V हो, तो धारा प्रवर्धन होगा [2018]
(a) A_p × A_V
(b) A_P / A_V
(c) A_V / A_p
(d) \(\sqrt{A_{P} \times A_{V}}\)
उत्तर :
(b) A_P / A_V

34.
एक ट्रांजिस्टर की आधार धारा 100 मिलीऐम्पियर तथा संग्राहक धारा 2.15 मिलीऐम्पियर है। 8 का मान होगा [2009]
(a) 21.5
(b) 0.0465
(c) 2.15 × 105
(d) 10.
उत्तर :
(a) 21.5

35. एक n-p-n ट्रांजिस्टर में संग्राहक धारा 24 mA है। यदि संग्राहक की ओर 80% इलेक्ट्रॉन पहुँचते हों तो आधार धारा [2014]
(a) 3 मिली ऐम्पियर
(b) 16 मिली ऐम्पियर
(c) 6 मिली ऐम्पियर
(d) 36 मिली ऐम्पियर।
उत्तर :
(c) 6 मिली ऐम्पियर

36. डिजिटल निकाय जिस संख्या पद्धति पर कार्य करते हैं, वह है
(a) दशमलव
(b) बाइनरी
(c) अष्ट
(d) षट्दशमलव।
उत्तर :
(b) बाइनरी

37. डिजिटल परिपथ कार्य करता है-.
(a) केवल एक अवस्था में
(b) केवल दो अवस्थाओं में
(c) सभी अवस्थाओं में
(d) कुछ निश्चित नहीं।
उत्तर :
(b) केवल दो अवस्थाओं में

38. दी गई सत्यता सारणी किस गेट की है [2004, 09, 10] |
(a) NAND गेट
(b) AND गेट
(c) OR गेट
(d) NOT गेट।
उत्तर :
(b) AND गेट

39. AND गेट में उच्च (1) निर्गत प्राप्त करने के लिए निवेशी A व B होने चाहिए [2004, 05, 11]
अथवा दो निवेशों A तथा B वाले AND गेट को निर्गत 1 होने के लिए यह आवश्यक है कि [2006]

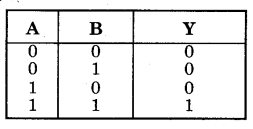
(a) A= 0, B= 0
(b) A = 1, B= 0
(c) A = 0, B= 1
(d) A = 1, B = 1.
उत्तर :
(d) A = 1, B = 1.

40. दिया गया लॉजिक प्रतीक निरूपित करता है [2004, 06]

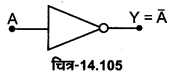
(a) AND गेट
(b) OR गेट
(c) NAND गेट
(d) NOT गेट।
उत्तर :
(d) NOT गेट।

41. निवेशियों A तथा B के लिए निर्गत C का बूलियन व्यंजक A+ B = C से दिया गया है। इस समीकरण के संगत गेट होगा [2004, 05, 06]
(a) AND
(b) OR
(c) NOT
(d) NOR.
उत्तर :
(b) OR

42. दो निवेश A तथा B वाले OR गेट का निर्गत शून्य होने के लिए आवश्यक है कि [2011]
(a) A = 0, B= 0
(b) A = 1, B= 0
(c) A = 0, B= 1 .
(d) A = 1, B= 1.
उत्तर :
(a) A = 0, B= 0

43. दिया गया लॉजिक प्रतीक निरूपित करता है [2005, 06]

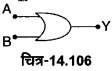
(a) AND गेट
(b) NAND गेट
(c) OR गेट
(d) NOT गेट।
उत्तर :
(c) OR गेट

44. दिया गया लॉजिक प्रतीक निरूपित करता है [2005, 06]

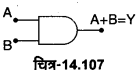
(a) AND
(b) OR
(c) NOT
(d) इनमें से कोई नहीं।
उत्तर :
(a) AND

45. बूलियन व्यंजक Y = \(A \bar{B}+B \bar{A}\) दिया गया है। यदि A = 1 तथा B = 1 हो तो Y का मान होगा [2006, 11, 12]
(a) 0
(b) 1
(c) 11
(d) 10.
[संकेत : ∵ A = 1, B= 1 है तो \(\bar{A}\) = 0, \(\bar{B}\) = 0 ∴ \(A \bar{B}+B \bar{A}\) = (1) (0) + (1) (0) = 0+ 0 = 0]
उत्तर :
(a) 0

46. OR गेट में एक निवेशी ‘0’ तथा दूसरा ‘1’ है। निर्गत होगा [2006]
(a) 0
(b) 1
(c) 0 अथवा 1
(d) अनिश्चित।
उत्तर :
(b) 1

47. दी गई सत्यता सारणी किस गेट की है [2008, 09, 10, 11]

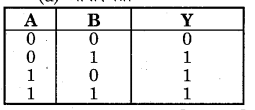
(a) OR गेट की
(b) NOT गेट की
(c) NOR गेट की
(d) AND गेट की।
उत्तर :
(a) OR गेट की

48. दो निवेशी टर्मिनलों वाले OR गेट का निर्गत केवल तब 0 होता है, जब [2013, 16]
(a) कोई एक निवेशी 1 हो
(b) दोनों निवेशी 1 हों
(c) कोई एक निवेशी 0 हो
(d) इसके दोनों निवेशी 0 हों।
उत्तर :
(d) इसके दोनों निवेशी 0 हों।

49. AND गेट में एक निवेशी 0 तथा दूसरा 1 है। निर्गत होगा
(a) 0
(b) 1
(c) अनन्त
(d) इनमें से कोई नहीं।
उत्तर :
(a) 0

50. चित्र-14.108 में प्रदर्शित गेटों के संयोजन से, निर्गत Y = 1प्राप्त करने के लिए [2015, 16]

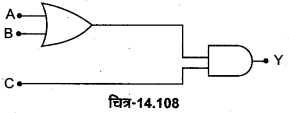
(a) A = 1, B= 0, C = 1
(b) A = 1, B= 1, C= 0
(c) A = 0, B= 1, C = 0
(d) A= 1, B= 0, C = 0.
उत्तर :
(a) A = 1, B= 0, C = 1

51. दिए गए लॉजिक गेटों के संयोजन का बूलियन व्यंजक है

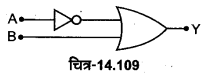
(a)Y = A + \(\bar{B}\)
(b) Y = \(\overline{A+B}\)
(c) Y = \(\bar{A}\) + \(\bar{B}\)
(d) Y = \(\bar{A}\) + B.
उत्तर :
(d) Y = \(\bar{A}\) + B.

52. चित्र-14.110 में प्रदर्शित लॉजिक निकाय निरूपित करता है- [2016]

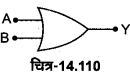
(a) NAND गेट
(b) OR गेट
(c) AND गेट
(d) NOT गेट।
चित्र-14.110
उत्तर :
(b) OR गेट

MP Board Class 12th Physics Important Questions

MP Board Class 12th Physics Important Questions Chapter 2 स्थिरवैद्युत विभव तथा धारिता

स्थिरवैद्युत विभव तथा धारिता अन्य महत्त्वपूर्ण प्रश्नोत्तर

प्रश्न 1.
वैद्युत विभव से क्या तात्पर्य है? किसी बिन्दु आवेश के कारण किसी बिन्दु पर वैद्युत विभव के लिए व्यंजक प्राप्त कीजिए। [2001, 02, 06, 15, 17]
अथवा
किसी बिन्दु आवेश के कारण उससे µ दूरी पर वैद्युत विभव के लिए सूत्र की गणना कीजिए। [2010]
उत्तर :
बिन्दु आवेश के कारण किसी बिन्दु पर वैद्युत विभव (Electric Potential at a Point due to a Point Charge) – माना +q कूलॉम का बिन्दु आवेश, K परावैद्युतांक वाले माध्यम में बिन्दु 0 पर स्थित है (चित्र-2.19)। बिन्दु आवेश + q के कारण उत्पन्न वैद्युत क्षेत्र में बिन्दु O से r मीटर दूरी पर कोई बिन्दु A है, जहाँ पर वैद्युत विभव ज्ञात करना है।।

माना रेखा OA पर, बिन्दु O से x मीटर की दूरी पर कोई बिन्दु B है, जिस पर परीक्षण आवेश +qp स्थित है। .. कूलॉम के नियमानुसार बिन्दु आवेश + q के कारण, परीक्षण आवेश +q_o पर लगने वाला वैद्युत बल
\(F=\frac{1}{4 \pi \varepsilon_{0} K} \frac{q q_{0}}{x^{2}}\)

वैद्युत विभव-वैद्युत क्षेत्र में, किसी धन परीक्षण आवेश (+ q_o) को अनन्त से किसी बिन्दु तक लाने में किए गए कार्य (W) तथा परीक्षण आवेश के अनुपात को उस बिन्दु पर वैद्युत विभव कहते हैं। इसे ‘V’ से प्रदर्शित करते हैं।

वैद्युत विभव V = \(\frac{W}{q_{0}}\)

इसका मात्रक ‘जूल/कूलॉम’ या ‘वोल्ट’ है। यह एक अदिश राशि हैं।
परीक्षण आवेश +q_o को बल F के विरुद्ध, बिन्दु B से बिन्दु C तक अनन्त सूक्ष्म दूरी dx लाने में किया गया अल्पांश कार्य

प्रश्न 2.
बिन्दु आवेशों के निकाय के कारण किसी बिन्दु पर वैद्युत विभव का व्यंजक प्राप्त कीजिए।
उत्तर :
बिन्दु आवेशों के निकाय के कारण किसी बिन्दु पर वैद्युत विभव-वैद्युत विभव अदिश राशि है। इसकी दिशा नहीं होती है; अत: किसी बिन्दु पर कई आवेशों के कारण विभव को बीजगणितीय विधि से जोड़कर प्राप्त कर सकते हैं। यदि कोई बिन्दु, + q₁,-q₂,- -q₃ तथा + q₄ कूलॉम के बिन्दु आवेशों से क्रमशः r₁ , r₂ , r₃ तथा r₄ मीटर की दूरी पर हों तो उस बिन्दु पर परिणामी वैद्युत विभव, पृथक्-पृथक् वैद्युत आवेशों के कारण उत्पन्न वैद्युत विभवों के बीजगणितीय योग के बराबर होगा।

प्रश्न 3.
वैद्युत द्विध्रुव से क्या तात्पर्य है? किसी वैद्युत द्विधुव के कारण अक्षीय स्थिति में उत्पन्न वैद्युत विभव के लिए व्यंजक प्राप्त कीजिए। [2007, 08, 14, 18]
अथवा
किसी वैद्युत द्विध्रुव की अक्ष (अनुदैर्ध्य स्थिति) पर स्थित किसी बिन्दु पर वैद्युत विभव का सूत्र स्थापित कीजिए। [2012, 14, 15, 16, 17]
उत्तर :
वैद्युत द्विध्रुव-दो समान परिमाण एवं विपरीत प्रकृति के बिन्दु आवेशों को अत्यन्त निकट रखने पर बना निकाय, वैद्युत द्विध्रुव कहलाता है।
उदाहरण-HCl का अणु, H₂O का अणु आदि।
वैद्युत द्विध्रुव की अक्ष पर स्थित किसी बिन्दु पर वैद्युत विभव (Electric Potential at a Point on the . Axis of the Electric Dipole) (अक्षीय अथवा अनुदैर्ध्य स्थिति : End-on Position)-माना AB वैद्युत द्विध्रुव K परावैद्युतांक के माध्यम में स्थित है, जिसके A सिरे पर + q आवेश तथा B सिरे पर -q आवेश एक-दूसरे से 21 दूरी पर स्थित हैं (चित्र 2.20)। इस वैद्युत द्विध्रुव के मध्य-बिन्दु 0 से 7 मीटर की दूरी पर इसकी अक्षीय स्थिति में कोई बिन्दु P है, जहाँ पर वैद्युत विभव ज्ञात करना है। बिन्दु P की +q आवेश से दूरी (r – 1) तथा – q आवेश से दूरी (r + 1) है। यदि इनके संगत विभव क्रमश: V₁ व V₂ हों तो


चूँकि वैद्युत विभव एक अदिश राशि है; अत: वैद्युत द्विध्रुव के कारण बिन्दु P पर परिणामी वैद्युत विभव v; दोनों विभवों V, तथा V, के बीजगणितीय योग (चिह्न सहित) के बराबर होगा।
अतः बिन्दु P पर परिणामी वैद्युत विभव

परन्तु 2 ql = p (वैद्युत द्विध्रुव का आघूर्ण) रखने पर, V \(V=\frac{1}{4 \pi \varepsilon_{0} K} \frac{p}{\left(r^{2}-l^{2}\right)}\) वोल्ट
यदि l का मान r के सापेक्ष बहुत कम हो (l <<r) तो l² का मान r² की तुलना में नगण्य माना जा सकता है।
अत: वैद्युत द्विध्रुव के कारण बिन्दु P पर वैद्युत विभव \(V=\frac{1}{4 \pi \varepsilon_{0} K} \frac{p}{r^{2}}\) वोल्ट
यदि माध्यम वायु अथवा निर्वात हो तो K = 1; अत: वैद्युत द्विध्रुव के कारण बिन्दु P पर वैद्युत विभव
\(V=\frac{1}{4 \pi \varepsilon_{0} K} \frac{p}{r^{2}}\) वोल्ट।

प्रश्न 4.
वैद्युत द्विध्रुव-आघूर्ण से आप क्या समझते हैं? सिद्ध कीजिए कि किसी वैद्युत द्विध्रुव की अनुप्रस्थ (निरक्षीय) स्थिति में किसी बिन्दु पर वैद्युत विभव शून्य होता है।
[2012, 13, 16]
उत्तर :
वैद्युत द्विध्रुव-आघूर्ण-वैद्युत द्विध्रुव के किसी एक आवेश के परिमाण तथा आवेशों के बीच की दूरी के गुणनफल को वैद्युत द्विध्रुव-आघूर्ण कहते हैं। इसे ‘p से प्रदर्शित करते हैं।
\(\overrightarrow{\mathrm{p}}=q \times 2 \vec{l}\)
इसका मात्रक ‘कूलॉम-मीटर’ है। यह एक सदिश राशि है जिसकी दिशा ऋणावेश से धनावेश की ओर होती है।
वैद्युत द्विध्रुव की निरक्षीय रेखा पर स्थित किसी बिन्दु पर वैद्युत विभव (Electric Potential due to an Electric Dipole on Equatorial Line)-माना AB वैद्युत द्विध्रुव K परावैद्युतांक के माध्यम में स्थित है, जिसके A सिरे पर +q आवेश तथा B सिरे पर – q आवेश एक-दूसरे से 2l दूरी पर स्थित हैं (चित्र 2.21)। वैद्युत द्विध्रुव के मध्य-बिन्दु O से r मीटर की दूरी पर निरक्षीय स्थिति में कोई बिन्दु P है, जहाँ पर वैद्युत विभव ज्ञात करना है। संलग्न चित्र से स्पष्ट है कि बिन्दु P की + q व -q दोनों आवेशों से दूरी \(\sqrt{r^{2}+l^{2}}\) के बराबर है।


अतः वैद्युत द्विध्रुव के कारण निरक्षीय स्थिति में किसी बिन्दु पर वैद्युत विभव शून्य होता है (वैद्युत क्षेत्र की तीव्रता शून्य नहीं होती है)।

प्रश्न 5.
किसी वैद्युत द्विध्रुव के कारण किसी व्यापक बिन्दु पर उत्पन्न वैद्युत विभव के लिए व्यंजक प्राप्त कीजिए।
उत्तर :
किसी वैद्युत द्विध्रुव के कारण किसी व्यापक हिन्दु पर वैद्युत विभव-माना एक वैद्युत द्विध्रुव AB, दो बिन्दु आवेशों +q तथा -q से मिलकर बना है, जिनके बीच की दूरी 2l है। हमें वैद्युत द्विध्रुव के केन्द्र O से r दूरी पर स्थित बिन्दु P, जिसके ध्रुवीय निर्देशांक (r,θ) हैं, पर वैद्युत विभव ज्ञात करना है।
अत: OP = r तथा ∠AOP = θ
बिन्दु A से रेखा OP पर तथा बिन्दु B से बढ़ती हुई रेखा OP पर
लम्ब क्रमश: AM व BN डालते हैं (चित्र-2.22)।

Δ OMA तथा Δ ONB mem ,
OM = ON = I cosθ
अतः AP = MP = (r – l cos θ)
तथा BN = NP = (r + l cos तथा)

प्रश्न 6.
आवेश q को a तथा b (b > a) त्रिज्या वाले दो संकेन्द्री खोखले गोलों पर इस प्रकार वितरित किया .. गया है कि तलीय आवेश घनत्व समान हैं। इन दोनों गोलों के उभयनिष्ठ केन्द्र पर विभव की गणना कीजिए। [2012]
हल :
माना गोलों को दिया गया आवेश q उन पर क्रमशः q₁ व q₂ के रूप में वितरित हो जाता है।
अतः q= q₁ + q₂ ………………(1)
दोनों गोलों के पृष्ठीय आवेश घनत्व समान हैं।

q₂ का मान समीकरण (1) में रखने पर,

प्रश्न 7.
विभव प्रवणता से क्या तात्पर्य है? वैद्युत क्षेत्र की तीव्रता तथा विभव प्रवणता में सम्बन्ध स्थापित कीजिए। [2012]
उत्तर :
विभव प्रवणता (Potential Gradient)—किसी वैद्युत क्षेत्र में दूरी के सापेक्ष विभव परिवर्तन की दर को विभव प्रवणता कहते हैं। विभव प्रवणता का मात्रक वोल्ट/मीटर है। यह एक सदिश राशि है जिसकी दिशा उच्च विभव से निम्न विभव की ओर होती है।
माना बिन्दु 0 पर स्थित बिन्दु आवेश +q के कारण X-अक्ष के अनुदिश वैद्युत क्षेत्र E की दिशा में बिन्दु 0 से x तथा (x + Ax) दूरियों पर दो बिन्दु क्रमश: A तथा B स्थित हैं, जिन पर वैद्युत विभव क्रमश: V तथा (V-ΔV) हैं।

अतः विभव प्रवणता \(\frac{(V-\Delta V)-V}{(x+\Delta x)-x}=-\frac{\Delta V}{\Delta x}\)
वैद्युत क्षेत्र की तीव्रता तथा विभव प्रवणता में सम्बन्ध (Relation between Intensity of Electric Field and Potential Gradient)—माना वैद्युत क्षेत्र E में, परीक्षण धन आवेश +q_o को बिन्दु B से बिन्दु A तक लाया जाता है तथा इस परीक्षण आवेश +q_o पर एक वैद्युत बल F वैद्युत क्षेत्र E की दिशा में कार्य करता है।
अतः F=q_o x E ……………(1)
माना परीक्षण आवेश +q_o को बिन्दु B से बिन्दु A तक ले जाने में बाह्य कर्ता द्वारा वैद्युत बल F के विरुद्ध किया गया कार्य ΔW है तो

समीकरण (2) तथा समीकरण (3) की तुलना करने पर,
– E x Δx = ΔV
अतः वैद्युत क्षेत्र की तीव्रता E=-\frac{\Delta V}{\Delta x} वोल्ट/मीटर
ΔV/Δx को ही विभव प्रवणता कहते हैं। इससे स्पष्ट होता है कि वैद्युत क्षेत्र की तीव्रता, ऋणात्मक विभव प्रवणता के बराबर होती है। यहाँ पर ऋण चिह्न यह प्रदर्शित करता है कि वैद्युत क्षेत्र की दिशा में वैद्युत विभव का मान घटता है।

प्रश्न 8.
एक आवेशित इलेक्ट्रॉन किसी एकसमान वैद्युत क्षेत्र में, क्षेत्र के लम्बवत् दिशा में गति करता हुआ प्रवेश करता है। दिखाइए कि वैद्युत क्षेत्र के भीतर इस इलेक्ट्रॉन का गमन पथ परवलयाकार होगा।
उत्तर :
एकसमान वैद्युत क्षेत्र में एक आवेशित इलेक्ट्रॉन का गमन-पथ (Path of a Charged Electron in an Uniform Electric Field) –
(i) जब इलेक्ट्रॉन का प्रारम्भिक वेग वैद्युत क्षेत्र की दिशा के लम्बवत् है (When initial velocity of an electron is perpendicular to electric field)—mana धातु की दो समान्तर प्लेटें जिन पर विपरीत आवेश हैं, एक-दूसरे से कुछ दूरी पर स्थित हैं। इन प्लेटों के बीच के स्थान में वैद्युत क्षेत्र एकसमान है। माना ऊपरी प्लेटधनावेशित है, जबकि नीचे की प्लेट ऋणावेशित है; अतः वैद्युत क्षेत्र E कागज के तल में नीचे की ओर दिष्ट होगा (चित्र 2.25)।

माना एक इलेक्ट्रॉन जिस पर आवेश – e तथा द्रव्यमान m है जो X-अक्ष के अनुदिश गतिमान है तथा v वेग से वैद्युत क्षेत्र E में प्रवेश करता है। चूँकि वैद्युत क्षेत्र Y-अक्ष की ऋणात्मक दिशा में नीचे की ओर है; अत: इलेक्ट्रॉन पर Y-अक्ष के अनुदिश लगने वाला बल F = eE.

‘इलेक्ट्रॉन पर X-अक्ष के अनुदिश कोई बल कार्य नहीं करेगा।
इस बल के कारण इलेक्ट्रॉन की गति में उत्पन्न तवरण \(a=\frac{F}{m}=\frac{e E}{m}\)
चूँकि इलेक्ट्रॉन का X-अक्ष के अनुदिश प्रारम्भिक वेग v तथा त्वरण शून्य है; अत: X-अक्ष के अनुदिश t सेकण्ड में चली गई दूरी
x= vt
चूँकि इलेक्ट्रॉन का Y-अक्ष के अनुदिश प्रारम्भिक वेग शून्य तथा त्वरण a है; अत: Y-अक्ष के अनुदिश t सेकण्ड में चली गई दूरी

यह समीकरण y = cx² के समरूप है तथा परवलय निरूपित करती है। अत: वैद्युत क्षेत्र में अभिलम्बवत् प्रवेश करने वाले आवेशित इलेक्ट्रॉन का गमन-पथ परवलयाकार होता है।
(ii) जब इलेक्ट्रॉन का प्रारम्भिक वेग वैद्युत क्षेत्र की दिशा के अनुदिश है-इस स्थिति में वैद्युत क्षेत्र द्वारा उत्पन्न त्वरण अथवा मन्दन इलेक्ट्रॉन के प्रारम्भिक वेग की ही दिशा में होता है; अत: आवेशित इलेक्ट्रॉन का गमन-पथ ऋजुरेखीय होता है।

प्रश्न 9.
वैद्युत स्थितिज ऊर्जा से क्या अभिप्राय है? q₁ व q₂ कूलॉम के दो आवेशों की स्थितिज ऊर्जा ज्ञात कीजिए , जबकि उनके बीच की दूरी r मीटर है।
उत्तर :
वैद्युत स्थितिज ऊर्जा (Electric Potential Energy)—“किन्हीं दो अथवा दो से अधिक बिन्दु आवेशों को अनन्त से एक-दूसरे के समीप लाकर निकाय की रचना करने में कृत कार्य उन आवेशों से बने निकाय में स्थितिज ऊर्जा के रूप में संचित हो जाता है। इस ऊर्जा को ही निकाय की वैद्युत स्थितिज ऊर्जा कहते हैं।” इसे प्रायः ‘U’ से प्रदर्शित करते हैं।
अत: “दो या दो से अधिक बिन्दु आवेशों के किसी निकाय की वैद्युत स्थितिज ऊर्जा उस कार्य के बराबर होती है जो उन आवेशों को अनन्त दूरी से
परस्पर निकट लाकर निकाय की रचना करने में किया जाता है।

दो वैद्युत आवेशों से बने निकाय की वैद्युत स्थितिज ऊर्जा का व्यंजक-माना एक आवेश निकाय AB दो बिन्दु आवेशों + q₁ व + q₂ से मिलकर बना है जो कि एक-दूसरे से । दूरी पर निर्वात अथवा वायु में स्थित हैं (चित्र 2.26)।
माना +q₂ आवेश, बिन्दु B पर न होकर अनन्त पर स्थित है, तब आवेश + q₁ के कारण बिन्दु B पर

वैद्युत विभव की परिभाषानुसार आवेश +q₂ को अनन्त से बिन्दु B तक लाने में किया गया कार्य
W = आवेश × बिन्दु B का विभव

यह कार्य W ही +q₁ व +q₂ से बने वैद्युत निकाय की वैद्युत स्थितिज ऊर्जा U है।
अत: निकाय (q₁ + q₂) की वैद्युत स्थितिज ऊर्जा \(U=\frac{1}{4 \pi \varepsilon_{0}} \frac{q_{1} q_{2}}{r}\) जल। ……….(2)
यदि दोनों आवेश समान प्रकार के हों तो वे एक-दूसरे को प्रतिकर्षित करेंगे; अत: उन्हें एक-दूसरे के समीप लाने में क्षेत्र के विरुद्ध कार्य करना पड़ेगा; अत: ऐसे निकाय की ऊर्जा धनात्मक होगी। इसके विपरीत विजातीय आवेशों को परस्पर समीप लाकर निकाय की रचना करने में, कार्य क्षेत्र के द्वारा किया जाएगा; अत: ऐसे निकाय की ऊर्जा ऋणात्मक होगी; अत: ऊर्जा का चिह्न सहित मान ज्ञात करने के लिए उपयुक्त सूत्र (2) में q₁ व q₂ के मान चिह्नसहित रखने चाहिए।

प्रश्न 10.
यदि किसी वैद्युत द्विध्रुव को एक समरूप वैद्युत क्षेत्र में 4 कोण से घुमाया जाता है तो इस क्रिया में किए गए कार्य का परिकलन कीजिए।
उत्तर :
एकसमान वैद्युत क्षेत्र में वैद्युत द्विध्रुव को घुमाने में कृत कार्य (Work Done in Rotating an Electric Dipole in an Uniform Electric Field)—माना p वैद्युत द्विध्रुव-आघूर्ण का एक वैद्युत द्विध्रुव AB किसी एकसमान वैद्युत क्षेत्र E में रखा है तथा वैद्युत द्विध्रुव को वैद्युत क्षेत्र के भीतर घुमाया जा रहा है (चित्र 2.27)। माना किसी क्षण वैद्युत द्विध्रुव-आघूर्ण p की दिशा वैद्युत क्षेत्र की दिशा से θ कोण बनाती है, तब वैद्युत द्विध्रुव पर वैद्युत क्षेत्र के कारण कार्य करने वाले बलयुग्म का आघूर्ण

t = pE sinθ
वैद्युत द्विध्रुव AB को इस स्थिति से आगे अल्पांश कोण dθ द्वारा घुमाने में वैद्युत क्षेत्र के विरुद्ध कृत कार्य
dw = बल-युग्म का आघूर्ण x कोणीय विस्थापन
= t x dθ = pE sin θ x dθ
अत: वैद्युत द्विध्रुव को प्रारम्भिक स्थिति θ = θ₁ से अन्तिम स्थिति θ = θ₂ तक घुमाने में कृत कार्य

यदि प्रारम्भ में वैद्युत द्विध्रुव बाह्य क्षेत्र की दिशा में अनुरेखित है अर्थात् θ₁ = 0°,
तब वैद्युत द्विध्रुव को θ कोण से घुमाने में कृत कार्य W = pE (cos 0° – cosθ) [∵ θ₂= θ]
अतः W = pE(1 – cos θ)
विशेष स्थितियाँ-1. यदि θ = 90° है अर्थात् वैद्युत द्विध्रुव को क्षेत्र की दिशा से 90° घुमाया जाए तो
W = pE (1 – cos 90°) = pE (1 – 0)= PE .
2. यदि θ = 180° है अर्थात् वैद्युत द्विध्रुव को क्षेत्र की दिशा से 180° घुमाया जाए तो
W = pE (1 – cos 180°) = pE [1 – (-1)] = 2pE.

प्रश्न 11.
एकसमान वैद्युत क्षेत्र में स्थित वैद्युत द्विध्रुव की वैद्युत स्थितिज ऊर्जा की गणना कीजिए। वैद्युत द्विध्रुव को क्षेत्र के लम्बवत् रखने पर वैद्युत स्थितिज ऊर्जा क्या होगी?
उत्तर :
एकसमान वैद्युत क्षेत्र में वैद्युत द्विध्रुव की स्थितिज ऊर्जा (Potential Energy of an Electric Dipole in an Uniform Electric Field)—“वैद्युत क्षेत्र में किसी वैद्युत द्विध्रुव की स्थितिज ऊर्जा उस कार्य के बराबर होती है जो कि वैद्युत द्विध्रुव को अनन्त से वैद्युत क्षेत्र के भीतर लाने में करना पड़ता है।”

माना AB वैद्युत द्विध्रुव + q तथा -q आवेशों से मिलकर बना है जिनके बीच की दूरी 2l है। इस वैद्युत द्विध्रुव को अनन्त से किसी एकसमान वैद्युत क्षेत्र E में इस प्रकार लाया जाता है कि वैद्युत द्विध्रुव के आघूर्ण p की दिशा सदैव वैद्युत क्षेत्र E की दिशा के समान्तर रहे (चित्र-2.28)। वैद्युत क्षेत्र E के कारण + q आवेश पर बल F = qE क्षेत्र की दिशा में तथा -q आवेश पर बल F = qE क्षेत्र की विपरीत दिशा में लगता है; अत: वैद्युत
द्विध्रुव को अनन्त से वैद्युत क्षेत्र में लाने के लिए +q आवेश पर बाह्य कर्ता द्वारा कार्य किया जाएगा, जबकि -q आवेश पर स्वयं वैद्युत क्षेत्र कार्य करेगा। वैद्युत द्विध्रुव को अनन्त से वैद्युत क्षेत्र के भीतर लाने में -q आवेश; + q आवेश से 2l दूरी अधिक चलता है। इस कारण -q आवेश पर वैद्युत क्षेत्र द्वारा किया गया कार्य अधिक होगा तथा इसका मान ऋणात्मक होगा; अत: वैद्युत द्विध्रुव को अनन्त से वैद्युत क्षेत्र के भीतर लाने में वैद्युत क्षेत्र द्वारा किया गया नैट कार्य
W₁= आवेश (-q) पर बल.x आवेश द्वारा चली गई अतिरिक्त दूरी (AB)
= – qE x 2l = – pE
जहाँ q x 2l =p वैद्युत द्विध्रुव-आघूर्ण है। यह कार्य ही वैद्युत क्षेत्र में क्षेत्र के समान्तर रखे वैद्युत द्विध्रुव की स्थितिज ऊर्जा है। इसे ‘U₀‘ से प्रदर्शित करते हैं।
अतः U_o = – pE
वैद्युत द्विध्रुव की इस स्थिति को स्थायी सन्तुलन (stable equilibrium) की स्थिति कहते हैं।
यदि वैद्युत द्विध्रुव को वैद्युत क्षेत्र के भीतर θ कोण से घुमाएँ तो वैद्युत द्विध्रुव पर किया गया कार्य
W₂ = pE (1 – cos θ)
इसके कारण वैद्युत द्विध्रुव की स्थितिज ऊर्जा बढ़ जाएगी; अत: θ कोण की स्थिति में वैद्युत द्विध्रुव की स्थितिज ऊर्जा .
U_θ = U_o + W₂ = – pE + pE (1 – cos θ) = – pE cos θ
यह वैद्युत द्विध्रुव की स्थितिज ऊर्जा का व्यापक समीकरण है।
विशेष स्थितियाँ-1. यदि θ = 0° है अर्थात् वैद्युत द्विध्रुव, वैद्युत क्षेत्र की दिशा में है, तब स्थितिज ऊर्जा
U_o = – pE
इस स्थिति में वैद्युत द्विध्रुव स्थायी सन्तुलन (stable equilibrium) में होगा; अत: स्थितिज ऊर्जा न्यूनतम होगी।
2. यदि θ = 90° है अर्थात् वैद्युत द्विध्रुव, वैद्युत क्षेत्र E के लम्बवत् है, तब स्थितिज ऊर्जा
U_90°= – pE cos 90° = 0
अर्थात् यदि वैद्युत द्विध्रुव को वैद्युत क्षेत्र E के लम्बवत् रखकर अनन्त से लाएँ तो वैद्युत द्विध्रुव पर कोई कार्य नहीं करना पड़ेगा।
3. यदि θ = 180° है अर्थात् वैद्युत द्विध्रुव को स्थायी सन्तुलन से 180° घुमाने पर स्थितिज ऊर्जा
U_180° = – pE cos 180° = + pE
इस स्थिति में, वैद्युत द्विध्रुव अस्थायी सन्तुलन (unstable equilibrium) में होगा।

प्रश्न 12.
किसी आवेशित चालक में संगृहीत स्थितिज ऊर्जा के लिए व्यंजक प्राप्त कीजिए।
अथवा
सिद्ध कीजिए कि किसी आवेशित चालक की स्थितिज ऊर्जा \(U=\frac{1}{2} C V^{2}\) अथवा \(\frac{1}{2} \frac{q^{2}}{C}\) होती है, जहाँ c चालक की धारिता, q चालक पर आवेश तथा V उसका विभव है। [2011]
उत्तर :
आवेशित चालक की स्थितिज ऊर्जा (Potential Energy of a Charged Conductor)- “किसी चालक को आवेशित करने में किए गए सम्पूर्ण कार्य को आवेशित चालक की वैद्युत स्थितिज ऊर्जा कहते हैं।”
माना C धारिता वाले किसी चालक को आवेशित किया जा रहा है। माना आवेशन की क्रिया में किसी क्षण चालक . . पर उपस्थित आवेश की मात्रा 41 है तथा चालक का विभव V₁ है, तब
सूत्र q₁ = CV₁ से, V₁ = q₁/C
अब अनन्त सूक्ष्म आवेश dq को अनन्त से लाकर, V₁ विभव पर चालक को देने में किया गया कार्य
dW = V₁ x dq = (q₁/C) x dq
माना आवेशन की क्रिया में चालक को कुल q आवेश दिया जाता है, तब चालक को q₁ = 0 से q₁ = q

विशेष स्थितियाँ-1. चालक की स्थितिज ऊर्जा सदैव धनात्मक होती है चाहे चालक को धन आवेश देकर आवेशित किया जाए अथवा ऋण आवेश देकर।
2. यदि आवेशित चालक के सम्पूर्ण आवेश को किसी चालक तार अथवा प्रतिरोध में प्रवाहित करके इसे निरावेशित कर दिया जाए तो उसकी सम्पूर्ण वैद्युत स्थितिज ऊर्जा चालक तार में ऊष्मा में बदल जाती है।

प्रश्न 13.
(i) सिद्ध कीजिए कि दो आवेशित चालकों को परस्पर स्पर्श कराके अलग कर देने से उन पर आवेश, चालकों की धारिताओं के अनुपात में बँट जाएगा।. – (ii) सिद्ध कीजिए कि आवेशों के पुनर्वितरण में ऊर्जा का ह्रास होता है। यह ऊर्जा किस रूप में लुप्त होती है? अथवा दो आवेशित चालकों को तार द्वारा जोड़ने पर ऊर्जा हानि के सूत्र का निगमन कीजिए। [2008, 17]
अथवा सिद्ध कीजिए कि दो आवेशित चालकों को तार से जोड़ने पर आवेश के पूर्ण वितरण के दौरान सदैव ऊर्जा की हानि होती है तथा ऊर्जा-हानि का व्यंजक प्राप्त कीजिए। [2018]
उत्तर :
(i) आवेशों का पुनर्वितरण (Redistribution of Charges)- माना दो पृथक्कृत चालकों A तथा B की धारिताएँ क्रमश: C₁ व C₂ हैं। जब इन चालकों को q₁ व q₂ आवेश दिया जाता है तो इनके विभव क्रमश: V₁ व V₂ हो जाते हैं।
अत: चालक A पर आवेश q₁ = C₁V₁ तथा चालक B पर आवेश q₂ = C₂V₂
यदि इन चालकों को एक चालक तार द्वारा जोड़ दें तो धन आवेश उच्च विभव वाले चालक से निम्न विभव वाले चालक की ओर तब तक बहता है जब तक कि दोनों चालकों का विभव समान नहीं हो जाता है (चित्र 2.29)। इस विभव को उभयनिष्ठ विभव (V) कहते हैं। इस प्रकार दो आवेशित चालकों को आपस में जोड़ने पर आवेश का पुनर्वितरण होता है, यद्यपि आवेश की कुल मात्रा (q₁ +q₂) ही रहती है।

माना दोनों चालक एक-दूसरे से पर्याप्त दूरी पर हैं तथा जोड़ने वाले चालक तार की वैद्युत धारिता नगण्य है।
चूँकि q₁= C₁V₁ तथा q₂ = C₂V₂ अतः चालकों पर कुल आवेश q = q₁ + q₂ = C₁V₁ + C₂V₂ ………………(1)
माना चालकों को तार द्वारा जोड़ने के बाद उन पर आवेश क्रमशः q₁‘ व q₂‘ तथा दोनों का उभयनिष्ठ विभव V हो जाता है, तब
प्रथम च (क पर आवेश q’₁ = C₁V ………………(2)
तथा दूसरे चालक पर आवेश q’₂ = C₂V ………………(3)
समीकरण (2) को समीकरण (3) से भाग देने पर,
\(\frac{q_{1}^{\prime}}{q_{2}^{\prime}}=\frac{C_{1} V}{C_{2} V}=\frac{C_{1}}{C_{2}}\)
अर्थात् दो आवेशित चालकों को परस्पर जोड़ने पर, चालकों पर आवेश का पुनर्वितरण उनकी धारिताओं के अनुपात में होता है।
अब संयोजन पर कुल आवेशq = q’₁ + q’₂ = q₁ + q₂
अथवा C₁V + C₂V = C₁V₂ +C₂V₂
अथवा
V(C₁ + C₂) = C₁V₁ + C₂V₂
अतः उभयनिष्ठ विभव \(V=\frac{C_{1} V_{1}+C_{2} V_{2}}{C_{1}+C_{2}}=\frac{q_{1}+q_{2}}{C_{1}+C_{2}}\) ………….(4)
स्थानान्तरित आवेश की मात्रा (Quantity of Transferred Charge)-चूँकि चालकों को परस्पर जोड़ने से पहले, चालक A पर आवेश q₁ है तथा चालक तार द्वारा जोड़ने के पश्चात् इस पर आवेश q’₁ रह जाता है।
अत: चालक A से चालक B पर स्थानान्तरित आवेश की मात्रा

(ii) आवेशों के पुनर्वितरण में ऊर्जा का ह्रास (Loss of Energy in Redistribution of Charges)—आवेशों के पुनर्वितरण की प्रक्रिया में जब आवेश चालक तार में प्रवाहित होता है तो इस क्रिया में कुछ कार्य किया जाता है। यह कार्य ऊष्मा के रूप में क्षय होता है। इस प्रकार दोनों चालकों के आवेश की कुल मात्रा तो वही रहती है, परन्तु चालकों की कुल स्थितिज ऊर्जा कम हो जाती है। जोड़ने से पूर्व
पहले चालक A की स्थितिज ऊर्जा U₁ = = \(\frac { 1 }{ 2 }\)C₁V₁²
दूसरे चालक B की स्थितिज ऊर्जा U₂ = = \(\frac { 1 }{ 2 }\)C₂V₂²
अत: जोड़ने से पूर्व दोनों चालकों की कुल स्थितिज ऊर्जा U = U₁ + U₂ = \(\frac { 1 }{ 2 }\)C₁V₁² + \(\frac { 1 }{ 2 }\)C₂V₂²)

इस समीकरण में C₁ व C₂ दोनों धनात्मक हैं तथा (V₁~V₂)² पूर्ण वर्ग होने के कारण एक धनात्मक संख्या है; अत: ∆U = (U – U’) भी धनात्मक संख्या है। यह तभी सम्भव है जबकि U’

प्रश्न 14.
समान्तर प्लेट संधारित्र की धारिता के लिए सूत्र का निगमन कीजिए। इसकी धारिता को किस प्रकार बढ़ाया जा सकता है? [2013, 14, 15, 16, 17]
अथवा
किसी समान्तर प्लेट वायु संधारित्र की धारिता का व्यंजक व्युत्पन्न कीजिए। [2011, 18]
उत्तर :
समान्तर प्लेट संधारित्र की धारिता का व्यंजक (Expression for Capacitance of a Parallel Plate Capacitor)-दो समतल तथा समान्तर धातु की प्लेटों एवं उनके बीच स्थित वैद्युतरोधी माध्यम से बने संकाय को समान्तर प्लेट संधारित्र कहते हैं।
माना P₁ व P₂ धातु की दो समतल प्लेटें हैं, जिनके बीच की दूरी d तथा प्रत्येक प्लेट का क्षेत्रफल A है। माना प्लेटों के बीच भरे माध्यम का परावैद्युतांक K है। जब प्लेट P₁ को + q आवेश दिया जाता है तो प्लेट P₂ पर प्रेरण के कारण -q आवेश उत्पन्न हो जाता है। चूंकि प्लेट P₂ पृथ्वी से जुड़ी है इसीलिए इसके बाह्य तल का + q आवेश पृथ्वी से आने वाले इलेक्ट्रॉनों द्वारा निरावेशित हो जाता है। इस प्रकार प्लेटों P व P₂ पर बराबर तथा विपरीत प्रकार के आवेश होंगे; अतः प्रत्येक प्लेट पर आवेश का पृष्ठ घनत्व

समीकरण (2) से स्पष्ट है कि समान्तर प्लेट संधारित्र की धारिता निम्नलिखित बातों पर निर्भर करती है –
1. प्लेटों के क्षेत्रफल A पर – C ∝ A अर्थात् धारिता प्लेटों के क्षेत्रफल के अनुक्रमानुपाती होती है; अत: संधारित्र की धारिता बढ़ाने के लिए प्लेटों का क्षेत्रफल A अधिक होना चाहिए अर्थात् प्लेटें बड़े क्षेत्रफल की लेनी चाहिए।
2. प्लेटों के बीच की दूरी d पर-C ∝ 1/d अर्थात् धारिता प्लेटों के बीच की दूरी के व्युत्क्रमानुपाती होती है; अतः संधारित्र की धारिता बढ़ाने के लिए प्लेटों के बीच की दूरी d कम होनी चाहिए अर्थात् प्लेटें एक-दूसरे के समीप रखनी चाहिए।
3. प्लेटों के बीच के माध्यम पर-C ∝ K अर्थात् धारिता माध्यम के परावैद्युतांक के अनुक्रमानुपाती होती है; अतः संधारित्र की धारिता बढ़ाने के लिए प्लेटों के बीच ऐसा माध्यम अर्थात् पदार्थ रखना चाहिए जिसका परावैद्युतांक (K) अधिक हो।

समान्तर प्लेट वायु संधारित्र की धारिता–यदि प्लेटों के बीच निर्वात (अथवा वायु ) हो अर्थात् K = 1 तो संधारित्र की धारिता
\(C_{0}=\frac{\varepsilon_{0} A}{d}\)फैरड
संधारित्र की धारिता के पद में परावैद्युतांक की परिभाषा–जब समान्तर प्लेट संधारित्र की प्लेटों के बीच परावैद्युत माध्यम भरा है तो संधारित्र की धारिता \(C_{0}=\frac{K\varepsilon_{0} A}{d}\) जब समान्तर प्लेट संधारित्र की प्लेटों के बीच वायु अथवा निर्वात है तो संधारित्र की धारिता \(C_{0}=\frac{\varepsilon_{0} A}{d}\)
अत: \(\frac{C}{C_{0}}=\frac{K \varepsilon_{0} A / d}{\varepsilon_{0} A / d}=K\) अथवा C = KC₀
अत: यदि प्लेटों के बीच निर्वात के स्थान पर परावैद्युत माध्यम हो तो संधारित्र की धारिता K गुना बढ़ जाएगी।
अतः “किसी माध्यम का परावैद्युतांक (dielectric constant) उस माध्यम से युक्त संधारित्र की धारिता तथा उसी आकार के निर्वात अथवा वायु. संधारित्र की धारिता के अनुपात के बराबर होता है (अर्थात् K = C/C₀)

प्रश्न 15.
समान्तर प्लेट संधारित्र की धारिता के लिए सूत्र का निगमन कीजिए , जब इसकी प्लेटों के बीच आंशिक रूप से परावैद्युत पदार्थ रखा हो।[2013]]
अथवा
t मोटाई तथा K परावैद्युतांक वाले पदार्थ से आंशिक रूप से भरे एक समान्तर प्लेट संधारित्र की धारिता के लिए व्यंजक व्युत्पन्न कीजिए।[2005, 09]
उत्तर :
समान्तर प्लेट संधारित्र की धारिता, जब उसकी प्लेटों के बीच आंशिक रूप से परावैद्युतांक रखा हो (Capacity of Parallel Plate Capacitor when Partially Filled with Dielectric)-माना P₁ व P₂ समान्तर प्लेट संधारित्र की दो प्लेटें हैं, जिनके बीच की दूरी d है एवं प्रत्येक प्लेट का क्षेत्रफल A है। माना t मोटाई की परावैद्युत पदार्थ की एक प्लेट संधारित्र की प्लेटों के बीच रखी है। इस प्रकार प्लेटों के बीच (d – t) मोटाई में वायु तथा t मोटाई में परावैद्युत माध्यम है। प्लेट P₁ को +q आवेश देने पर प्रेरण के कारण प्लेट P₂ पर -q आवेश उत्पन्न हो जाता है,


चूँकि K का मान सदैव 1 से अधिक होता है; अतः प्लेटों के बीच प्रभावी दूरी d से कुछ कम हो जाती है, जिससे संधारित्र की धारिता बढ़ जाती है।
विशेष स्थितियाँ-1. यदि प्लेटों के बीच पूरे स्थान में परावैद्युतांक भरा हो (अर्थात् t = d) तो

2. यदि प्लेटों के बीच पूरे स्थान में वायु अथवा निर्वात हो (अर्थात् t = 0) तो

3. यदि प्लेटों के बीच 1 मोटाई की धातु की पट्टी हो (K = ∞) तो

4. यदि प्लेटों के बीच K₁, K₂, K₃,…., K_n परावैद्युतांकों की पट्टियाँ रखी हों, जिनकी मोटाइयाँ क्रमशः t₁ , t₂ , t₃, ….. , t_n हों तो

5. यदि प्लेटों के बीच पूरे स्थान में परावैद्युत की पट्टियाँ भरी हों तो d = t₁ + t₂ + t₃ + …. + t_n

प्रश्न 16.
श्रेणीक्रम में जुड़े तीन संधारित्रों की तुल्य धारिता के लिए व्यंजक प्राप्त कीजिए।
उत्तर :
श्रेणीक्रम में (In Series) जुड़े संधारित्र—माना तीन संधारित्रों को, जिनकी धारिताएँ C₁, C₂ व C₃ हैं, श्रेणीक्रम में चित्रानुसार जोड़ा गया है।

जब किसी वैद्युत स्रोत द्वारा संधारित्र C₁की पहली प्लेट को +q आवेश देते हैं। प्रेरण द्वारा इसकी दूसरी प्लेट पर -q आवेश उत्पन्न हो जाता है तथा इस प्लेट का स्वतन्त्र आवेश + q; दूसरे संधारित्र C₂ की पहली प्लेट पर चला जाता है और संधारित्र C₂ की दूसरी प्लेट पर -q आवेश उत्पन्न हो जाता है।

अतः “श्रेणीक्रम में जुड़े संधारित्रों की तुल्य धारिता का व्युत्क्रम, उन संधारित्रों की अलग-अलग धारिताओं के व्युत्क्रमों के योग के बराबर होता है।” वास्तव में तुल्य धारिता का मान श्रेणीक्रम में जुड़े सबसे कम धारिता वाले संधारित्र की धारिता से भी कम होता है।
श्रेणीक्रम में जडे संधारित्रों के लिए-1. सभी संधारित्रों पर आवेश की मात्रा समान रहती है।
2. संयोजन के सिरों के बीच आरोपित कुल विभवान्तर, अलग-अलग संधारित्रों की प्लेटों के बीच उत्पन्न विभवान्तर के योग के बराबर होता है अर्थात् V = V₁ + V₂ +V₃
इसीलिए श्रेणीक्रम संयोग का प्रयोग तब करते हैं, जबकि किसी ऊँचे वोल्टेज को (जिसे अकेला संधारित्र सहन न कर सके), अनेक संधारित्रों पर विभाजित करना होता है।
3. इस संयोजन में न्यूनतम धारिता वाले संधारित्र की प्लेटों के बीच विभवान्तर अधिकतम होता है।

प्रश्न 17.
समान्तर क्रम में जुड़े तीन संधारित्रों की तुल्य धारिता के लिए व्यंजक प्राप्त कीजिए। अथवा संधारित्रों के समान्तर संयोजन के तुल्य संधारित्र की धारिता के लिए व्यंजक प्राप्त कीजिए। [2004]
उत्तर :

समान्तर क्रम में (In Parallel) जुड़े संधारित्र-माना तीन संधारित्रों को, जिनकी धारिताएँ C₁,C₂ व C₃ हैं, समान्तर क्रम में बिन्दु A व B के बीच जोड़ा गया है। इसमें सभी संधारित्रों की पहली प्लेटों को एक बिन्दु A से तथा दूसरी प्लेटों को दूसरे बिन्दु B से जोड़ते हैं और बिन्दु B को पृथ्वी से जोड़ देते हैं। यदि किसी वैद्युत स्रोत द्वारा बिन्दु A को + q आवेश दिया जाता है तो यह आवेश तीनों संधारित्रों पर उनकी धारिताओं के अनुपात में बँट जाता है। प्रेरण की क्रिया से संधारित्रों की दूसरी प्लेटों के अन्दर वाले तलों पर बराबर व विपरीत ऋण आवेश उत्पन्न हो जाता है तथा बाहरी तलों पर उत्पन्न धन आवेश पृथ्वी से आने वाले इलेक्ट्रॉनों द्वारा निरावेशित हो जाता है। चूँकि तीनों संधारित्र बिन्दुओं A व B के बीच जुड़े हैं; अत: प्रत्येक संधारित्र की प्लेटों के बीच विभवान्तर समान होगा। माना यह विभवान्तर V है तथा संधारित्रों पर आवेश क्रमश: q₁; q₂व q₃ हैं, तब q₁ = C₁V, q₂ = C₂V तथा q₃ = C₃V तीनों संधारित्रों पर कुल आवेश
q= q₁ + q₂ + q₃
= C₁V + C₂V + C₃V
= V (C₁ + C₂+ C₃)………..(1)
यदि इन तीनों संधारित्रों के स्थान पर एक ऐसा संधारित्र लगाया जाए जिसे 4 आवेश देने पर उसकी प्लेटों के बीच विभवान्तर V हो जाए, तो वह तुल्य संधारित्र होगा। यदि इस संधारित्र की धारिता C हो तो
समीकरण (1) व समीकरण (2) की तुलना करने पर,
VC = V(C₁ + C₂ + C₃)
अतः C = C₁ + C₂ + C₃
अत: “समान्तर क्रम में जुड़े संधारित्रों की तुल्य धारिता, उन संधारित्रों की अलग-अलग धारिताओं के योग के बराबर होती है।” इस प्रकार संधारित्रों को जोड़कर धारिता बढ़ाई जा सकती है।
समान्तर क्रम में जुड़े संधारित्रों के लिए –
1. सभी संधारित्रों की प्लेटों के बीच विभवान्तर (V) समान रहता है।
2. संधारित्रों के निकाय का कुल आवेश, उनके अलग-अलग आवेशों के योग के बराबर होता है।
अर्थात् q= q₁ + q₂ + q₃
संधारित्रों पर अलग-अलग आवेश, उनकी धारिताओं के अनुपात में होता है।
4. समान्तर-संयोजन का प्रयोग तब करते हैं, जबकि कम विभव पर अधिक धारिता की आवश्यकता होती है।

प्रश्न 18.
किसी आवेशित संधारित्र की ऊर्जा से क्या तात्पर्य है? किसी आवेशित संधारित्र की ऊर्जा के लिए व्यंजक प्राप्त कीजिए। यह ऊर्जा कहाँ रहती है?
अथवा
सिद्ध कीजिए कि आवेशित संधारित्र की स्थितिज ऊर्जा U = \(\frac { 1 }{ 2 }\)CV²जहाँ C संधारित्र की धारिता तथा V विभवान्तर हैं। [2016, 17]
उत्तर :
आवेशित संधारित्र की स्थितिज ऊर्जा का व्यंजक (Expression for Potential Energy of a Charged Capacitor)—किसी संधारित्र को आवेशित करने में जो कार्य करना पड़ता. है, वह संधारित्र में वैद्युत स्थितिज ऊर्जा के रूप में संचित हो जाता है, जब संधारित्र को किसी प्रतिरोध तार से जोड़ा जाता है तो आवेश का प्रवाह तार में हो जाता है, जिस कारण संधारित्र विसर्जित हो जाता है तथा संधारित्र द्वारा संचित ऊर्जा ऊष्मा के रूप में प्रकट होती है।
माना C धारिता के संधारित्र को आवेशित किया जा रहा है। माना किसी क्षण संधारित्र पर q₁ आवेश है तथा इसकी प्लेटों के बीच विभवान्तर V₁ है।
अत: संधारित्र की प्लेटों के बीच विभवान्तर V₁ = q₁/C
संधारित्र को और एक अनन्त सूक्ष्म आवेश dq देने में किया गया कार्य अर्थात् संधारित्र में संचित स्थितिज ऊर्जा
dU = V₁ x dq = (q₁/C) x dq
अतः संधारित्र को शून्य से q आवेश देने में संचित कुल ऊर्जा

अत: आवेशित संधारित्र की ऊर्जा उसकी प्लेटों के बीच स्थित माध्यम में उत्पन्न वैद्युत क्षेत्र में रहती है।

प्रश्न 19.
आवेशित संधारित्र के ऊर्जा घनत्व से क्या तात्पर्य है? समान्तर पट्ट संधारित्र के ऊर्जा घनत्व का सूत्र ज्ञात कीजिए।
अथवा
सिद्ध कीजिए कि संधारित्र का ऊर्जा घनत्व – \(\frac { 1 }{ 2 }\)ε₀E² के बराबर होता है जहाँ ε₀ निर्वात की वैद्युतशीलता तथा E संधारित्र की दोनों प्लेटों के मध्य उत्पन्न वैद्युत क्षेत्र की तीव्रता है। [2013]
अथवा
सिद्ध कीजिए कि एकांक आयतन में किसी समान्तर प्लेट संधारित्र में संचित ऊर्जा \(\frac { 1 }{ 2 }\)ε₀E² है। प्रतीकों के सामान्य अर्थ हैं।
उत्तर :
आवेशित संधारित्र का ऊर्जा घनत्व (Energy Density of a Charged Capacitor)-जब किसी
[2015] संधारित्र को आवेशित किया जाता है तो संधारित्र में ऊर्जा संचित हो जाती है जो प्लेटों के बीच के आयतन में वैद्युत क्षेत्र की ऊर्जा के रूप में संचित रहती है। अत: “संधारित्र के एकांक आयतन में संचित ऊर्जा को संधारित्र का ऊर्जा घनत्व कहते हैं।”
माना किसी समान्तर पट्ट संधारित्र का प्लेट क्षेत्रफल A तथा उनके बीच की दूरी d है, प्लेटों के बीच का स्थान परावैद्युत माध्यम K द्वारा भरा है तथा प्लेटों के बीच का विभवान्तर V है।

प्रश्न 20.
वान डे ग्राफ जनित्र का सिद्धान्त बताइए तथा चित्र की सहायता से इसकी रचना एवं कार्यविधि समझाइए। [2011, 15, 17]
अथवा
उपयुक्त चित्र की सहायता से वान डे ग्राफ जनित्र की कार्यविधि स्पष्ट कीजिए। [2018]
अथवा
वान डे ग्राफ जेनरेटर का नामांकित चित्र बनाइए। इसके कार्य करने का सिद्धान्त बताइए। बताइए यह किस तरह से उच्च वोल्टेज उत्पन्न करता है?
[2018]
उत्तर :
वान डे ग्राफ जनित्र (Van de Graff Generator)—वैज्ञानिक रॉबर्ट जे० वान डे ग्राफ ने सन् 1931 ई० में एक स्थिर वैद्युत जनित्र की रचना की जिसकी सहायता से कुछ मिलियन वोल्ट के उच्च विभव को उत्पन्न किया जा सकता है। इस उच्च विभव से प्राप्त प्रबल वैद्युत क्षेत्र का प्रयोग आवेशित कणों जैसे इलेक्ट्रॉन, प्रोटॉन आदि को त्वरित कर उनकी ऊर्जा में वृद्धि करने में किया जाता है।
सिद्धान्त (Principle)-इस जनित्र का सिद्धान्त दो प्रमुख स्थिर वैद्युत घटनाओं पर आधारित है. –

(i) किसी खोखले चालक को दिया गया आवेश केवल उसके बाहरी पृष्ठ पर विद्यमान रहता है तथा एकसमान रूप से वितरित रहता है।
यदि r त्रिज्या के खोखले गोलीय चालक को q आवेश दिया जाए तब उसका वैद्युत विभव
\(V=\frac{1}{4 \pi \varepsilon_{0}} \frac{q}{r}\) वोल्ट

(ii) किसी आवेशित चालक से वायु में वैद्युत विसर्जन उसके तीक्ष्ण नुकीले सिरों (sharp points) से प्राथमिकता से होता है।
गोले का आवेश पृष्ठ घनत्व \(\sigma=\frac{q}{A}\)

तीक्ष्ण नुकीले सिरों का क्षेत्रफल बहुत कम होने के कारण वहाँ आवेश पृष्ठ घनत्व बहुत अधिक होता है, जिस कारण उनसे वायु में आवेश का क्षरण होने लगता है। .
संरचना (Construction)-इसमें एक धातु का एक बड़ा गोला S, दो अचालक स्तम्भों A व B पर सधा होता है तथा इसमें एक रबर अथवा सिल्क की सिरेहीन बैल्ट (endless string) होती है जो दो घिरनियों P₁ व P₂ द्वारा एक वैद्युत मोटर की सहायता से चलायी जा सकती है। घिरनी P₁ पृथ्वी के तल में तथा घिरनी P₂ गोले के केन्द्र से तल पर होती है। इसमें दो तीक्ष्ण नुकीले सिरों वाले धातु के चालक (conductor) होते हैं। निचला चालक (कंघा) C₁ अति उच्च विभव वाले स्रोत (High Tension Source, HTS ) (≈ 10⁴ वोल्ट) के धन टर्मिनल से तथा ऊपरी चालक (कंघा) C₂ खोखले गोले S के आन्तरिक पृष्ठ से सम्बन्धित रहता है। इन्हें क्रमश: फुहार चालक (spray conductor) तथा संग्राहक चालक (collecting conductor) कहते हैं। एक विसर्जन नलिका गतिमान डोरी के समान्तर लगी होती है इस नलिका का ऊपरी सिरा गोले S के केन्द्र पर होता है, जहाँ आयन स्रोत स्थित होता है तथा नलिका का दूसरा सिरा पृथ्वी से सम्बन्धित रहता है।

कार्यविधि (Working)-जब चालक (कंघे) C₁ को अति उच्च विभव (HTS) दिया जाता है तो तीक्ष्ण बिन्दुओं की क्रिया के फलस्वरूप यह अपने चारों ओर के स्थान में आयन उत्पन्न करता है। धन-आयनों व चालक (कंघे) C₁ के बीच प्रतिकर्षण के कारण ये धन-आयन गति करती बैल्ट पर चले जाते हैं। गतिमान बैल्ट द्वारा ये आयन ऊपर ले जाए जाते हैं। चालक (कंघे) C₂ के तीक्ष्ण सिरे बैल्ट को ठीक छूते हैं। इस प्रकार चालक(कंघा) C₂ बैल्ट के धन आवेश को एकत्रित करता है। यह धन-आवेश शीघ्र ही गोले S के बाहरी पृष्ठ पर स्थानान्तरित हो जाता है। चूंकि बैल्ट घूमती रहती है। अत: यह धन आवेश को ऊपर की ओर ले जाती है जो चालक (कंघे) C₂ द्वारा एकत्रित कर लिया जाता है तथा गोले S के बाहरी पृष्ठ पर स्थानान्तरित हो जाता है। इस प्रकार गोले S का बाहरी पृष्ठ निरन्तर धन आवेश प्राप्त करता है तथा इसका विभव अति उच्च हो जाता है।

जब गोले S का विभव बहुत अधिक (लगभग 3 x 10⁶ वोल्ट/मीटर) हो जाता है, तो निकटवर्ती वायु की परावैद्युत तीव्रता (dielectric strength) टूट जाती है तथा आवेश का निकटवर्ती वायु में क्षरण (leakage) हो जाता है। अधिकतम विभव की स्थिति में आवेश के क्षरण होने की दर गोले पर स्थानान्तरित आवेश की दर के बराबर हो जाती है। गोले से आवेश का क्षरण रोकने के लिए, जनित्र को स्टील के आवरण से घिरे एक टैंक में रखा जाता है जिसमें उच्च दाब LED पर नाइट्रोजन अथवा मेथेन गैस भरी होती है।
वान डे ग्राफ जनित्र धन आवेशित कणों को अति उच्च वेग तक त्वरित करने के लिए प्रयोग किया जाता है।

स्थिरवैद्युत विभव तथा धारिता लघु उत्तरीय प्रश्नोत्तर

प्रश्न 1.
वैद्युत विभव से क्या तात्पर्य है? [2015]
उत्तर :
वैद्युत विभव-किसी बिन्दु आवेश q को अनन्त से वैद्युत क्षेत्र के भीतर किसी बिन्दु तक लाने में क्षेत्र के विरुद्ध किए गए कार्य W तथा बिन्दु आवेश q के अनुपात को उस बिन्दु का वैद्युत विभव कहते हैं, इसे ‘V’ से प्रदर्शित करते हैं।
अतः वैद्युत विभव V = \(\frac{W}{q}\) जूल/कूलॉम अथवा वोल्ट।

प्रश्न 2.
वैद्युत विभवान्तर को परिभाषित कीजिए।
उत्तर :
वैद्युत विभवान्तर–वैद्युत क्षेत्र में, किसी बिन्दु आवेश q को एक बिन्दु A से दूसरे बिन्दु B तक लाने में क्षेत्र के विरुद्ध किए गए कार्य (W) तथा बिन्दु आवेश के अनुपात को उन बिन्दुओं के बीच वैद्युत विभवान्तर कहते हैं।”
अतः बिन्दुओं A व B के बीच वैद्युत विभवान्तर V_B – V_A = \(\frac{W}{q}\) जूल/कूलॉम अथवा वोल्ट।

प्रश्न 3.
वैद्युत विभव तथा विभवान्तर का मात्रक बताइए तथा इसकी परिभाषा लिखिए।
उत्तर :
वैद्युत विभव तथा विभवान्तर का मात्रक वोल्ट है।
सूत्र V = \(\frac{W}{q}\) से, यदि q= 1 कूलॉम तथा W = 1 जूल हो तो V = 1 वोल्ट।
वोल्ट की परिभाषा–यदि + 1 कूलॉम के आवेश को अनन्त से किसी बिन्दु तक लाने में 1 जूल कार्य करना पड़ता है तो उस बिन्दु का वैद्युत विभव 1 वोल्ट होगा।

प्रश्न 4.
समविभव पृष्ठ से क्या तात्पर्य है? [2015, 18]]
उत्तर :
समविभव पृष्ठ-किसी वैद्युत क्षेत्र में स्थित कोई ऐसा पृष्ठ, जिस पर स्थित किन्हीं दो बिन्दुओं के बीच वैद्युत विभवान्तर शून्य है, समविभव पृष्ठ कहलाता है। परिभाषा से स्पष्ट है कि समविभव पृष्ठ पर स्थित सभी बिन्दु एक ही विभव पर होते हैं।

प्रश्न 5.
सिद्ध कीजिए कि विद्युत बल रेखाएँ समविभव सतह के लम्वबत् होती हैं। [2018]
उत्तर :
यदि, विद्युत क्षेत्र समविभव पृष्ठ के लम्बवत् नहीं है तो वैद्युत क्षेत्र का समविभव पृष्ठ के अनुदिश कोई शून्येतर (non-zero) घटक होगा। अतः किसी परीक्षण आवेश को समविभव पृष्ठ पर इस घटक के विरुद्ध गति कराने में कुछ कार्य करना होगा? जबकि समविभव पृष्ठ पर परीक्षण आवेश को एक बिन्दु से दूसरे बिन्दु तक ले जाने में किया गया कार्य शून्य होता है। अत: विद्युत क्षेत्र एवं विद्युत बल रेखाएँ समविभव सतह के लम्बवत् होती हैं।

प्रश्न 6.
दो समविभव पृष्ठ परस्पर काटते क्यों नहीं हैं?
उत्तर :
समविभव पृष्ठ पर वैद्युत क्षेत्र की दिशा पृष्ठ पर लम्ब होती है। यदि दो समविभव पृष्ठ एक-दूसरे को काटते हैं तो कटान बिन्दु पर दो लम्ब खींचे जा सकेंगे; अत: वैद्युत क्षेत्र की भी दो दिशाएँ होंगी, जोकि असम्भव है।

प्रश्न 7.
इलेक्ट्रॉन-वोल्ट किस भौतिक राशि का मात्रक है? इसकी परिभाषा लिखिए।
उत्तर :
इलेक्ट्रॉन-वोल्ट, ऊर्जा का मात्रक है। 1 इलेक्ट्रॉन-वोल्ट, ऊर्जा की उस मात्रा के बराबर होता है, जो एक इलेक्ट्रॉन, 1 वोल्ट के विभवान्तर से त्वरित किए जाने पर अर्जित करता है। .

प्रश्न 8.
आवेशों के निकाय की वैद्युत स्थितिज ऊर्जा से क्या तात्पर्य है?
उत्तर :
वैद्युत स्थितिज ऊर्जा-आवेशों के निकाय की वैद्युत स्थितिज ऊर्जा आवेशों को परस्पर अनन्त दूरी से उनकी वर्तमान स्थिति में लाकर निकाय की रचना करने में बाह्य स्रोत द्वारा किए गए कार्य के बराबर होती है।

प्रश्न 9.
चित्र-2.35 में प्रदर्शित आवेशों के निकाय की वैद्युत स्थितिज ऊर्जा ज्ञात कीजिए। [2014]
हल :
निकाय की वैद्युत स्थितिज ऊर्जा

प्रश्न 10.
1 MeV को जूल में व्यक्त कीजिए। [2007]
हल :
∵ 1eV = 1.6 x 10^-19 जूल
अतः 1MeV = 10⁶ eV = 10⁶ x 1.6 x 10^-19 जूल = 1.6 x 10^-13जूल।

प्रश्न 11.
दो बिन्दुओं के बीच विभवान्तर 50 वोल्ट हैं। एक बिन्दु से दूसरे बिन्दु तक 2 x 10^-5 कूलॉम आवेश को ले जाने पर कितना कार्य करना होगा? [2011, 12]
हल :
दिया है, q= 2 x 10^-5 कूलॉम, ∆V = 50 वोल्ट, W = ?
अतः कृत कार्य W = q∆V = 2 x 10^-5 x 50 = 10^-3 जूल।

प्रश्न 12.
5 सेमी की दूरी पर स्थित दो बिन्दुओं A व B के विभव +10 वोल्ट तथा -10 वोल्ट हैं। 1.0 कूलॉम आवेश को A से B तक ले जाने में कितना कार्य करना होगा? [2012]
हल :
दिया है, q= 1.0 कूलॉम, ∆V = 10-(-10) = 20 वोल्ट, W = ?
अतः किया गया कार्य W = q∆V = 1.0 x 20 = 20 जूल।

प्रश्न 13.
5 सेमी की दूरी पर दो बिन्दुओं A और B में से प्रत्येक 10 वोल्ट के विभव पर है। 10 कूलॉम के धन आवेश को बिन्दु A से बिन्दु B तक ले जाने में कितना कार्य करना होगा? [2010]
हल :
किया गया कार्य W = q (V_B – V_A) = q x 0 [∵ VB = VA = 10 वोल्ट]

प्रश्न 14.
निर्वात में किसी बिन्दु (x, Y, 2 सभी मीटर में) पर वैद्युत विभव V = 4x² वोल्ट है। बिन्दु (1 मीटर, 0 मीटर,.2 मीटर) पर वैद्युत क्षेत्र की तीव्रता ज्ञात कीजिए। [2012]
हल :
बिन्दु (x, y, 2) पर वैद्युत विभव V = 4x²
इससे स्पष्ट है कि विभव केवल x पर निर्भर करता है y अथवा z पर नहीं।

इसमें x = 1 मीटर, y = 0 मीटर, 2 = 2 मीटर रखने पर, बिन्दु (1 मीटर, 0 मीटर, 2 मीटर) पर
वैद्युत क्षेत्र की तीव्रता E = -8 x 1 = -8 वोल्ट/मीटर।
ऋण चिह्न यह प्रदर्शित करता है कि वैद्युत क्षेत्र ऋण X-अक्ष की ओर दिष्ट है।

प्रश्न 15.
चित्र-2.36 के अनुसार दो प्लेटें A तथा B परस्पर 2 मिमी की दूरी पर रखी हैं। प्लेट A का विभव 10,000 वोल्ट है, प्लेट B पृथ्वी से सम्बन्धित है। इन प्लेटों के बीच वैद्युत क्षेत्र की तीव्रता ज्ञात कीजिए।[2001]

हल :
दिया है, d = 2 मिमी = 2 x 10^-3 मीटर,
V_A = +10,000 वोल्ट, V_B = 0, E = ?
सूत्र \(E=\frac{V_{A}-V_{B}}{d}\)
प्लेटों के बीच वैद्युत क्षेत्र की तीव्रता \(E=\frac{10,000-0}{2 \times 10^{-3}}=5 \times 10^{6}\) वोल्ट/मीटर।

प्रश्न 16.
दो बिन्दुओं A तथा B के विभव क्रमशः +V तथा – V वोल्ट हैं। यदि उनके बीच की दूरीr मीटर है। तो ज्ञात कीजिए-
(i) A व B के बीच औसत वैद्युत क्षेत्र तथा
(ii) -q कूलॉम आवेश को A से B तक ले जाने में उसकी स्थितिज ऊर्जा में परिवर्तन।
हल :
(i) A व B के बीच औसत वैद्युत क्षेत्र

(ii) स्थितिज ऊर्जा में वृद्धि = 2qV जूल।

प्रश्न 17.
आवेश q को a तथा b(b> a) त्रिज्या वाले दो संकेन्द्री खोखले गोलों पर इस प्रकार वितरित किया गया है कि पृष्ठीय आवेश घनत्व समान हैं। इन दोनों गोलों के उभयनिष्ठ केन्द्र पर विभव की गणना कीजिए। [2012]
हल :
माना a तथा b त्रिज्याओं वाले संकेन्द्री खोखले गोलों पर आवेश q₁ व q₂ हैं।
अतः q= q₁ + q₂

प्रश्न 18.
यदि दो वैद्युत द्विध्रुवों के केन्द्रों के बीच की दूरी दोगुनी कर दी जाए तो
(i) उनके बीच लगने वाले बल तथा
(ii) उनकी स्थितिज ऊर्जा का मान कितने गुना परिवर्तित हो जाएँगे? [2005]
हल :

प्रश्न 19.
चित्र-2.37 में प्रदर्शित A व B बिन्दुओं के बीच विभवान्तर ज्ञात कीजिए।

हल :
सूत्र V = iR से,
V_AB = 2 × 2 + 3+ 2 × 1- 2 + 2 × 1 ,
= 9 वोल्ट।

प्रश्न 20.
संधारित्र से क्या तात्पर्य है? [2004, 14, 16]
उत्तर :
संधारित्र-संधारित्र किसी भी प्रकार के दो ऐसे चालकों का युग्म है जो कि एक-दूसरे के समीप हों, जिन पर बराबर व विपरीत आवेश हों तथा जिसकी एक प्लेट पृथ्वी से जुड़ी हो।

प्रश्न 21.
संधारित्रों के उपयोग लिखिए। [2016]
उत्तर :
संधारित्रों के उपयोग-निम्नलिखित में संधारित्रों का उपयोग किया जाता है –

1. आवेश का संचय करने में
2. ऊर्जा का संचय करने में
3. वैद्युत उपकरणों में
4. इलेक्ट्रॉनिक परिपथों में
5. वैज्ञानिक अध्ययन में
6. प्रत्यावर्ती धारा नियन्त्रण में।

प्रश्न 22.
फैरड क्या है? एक फैरड में कितने पिकोफैरड होते हैं?
उत्तर :
फैरड की परिभाषा-सूत्र C = q/V में,q = 1 कूलॉम, V = 1 वोल्ट रखने पर, C=1 फैरड।
“1 फैरड उस चालक की धारिता है, जिसको 1 कूलॉम का आवेश देने पर उसके विभव में 1 वोल्ट की वृद्धि हो।”
1 पिकोफैरड = 10^-12 फैरड; अत: 1 फैरड = 10¹² पिकोफैरड।

प्रश्न 23.
परावैद्युत पदार्थ से आप क्या समझते हैं? (1) जर्मेनियम, (2) अभ्रक, (3) कार्बन में से कौन-सा परावैद्युत है? [2010, 12]
उत्तर :
परावैद्युत पदार्थ—“वे पदार्थ, जिनके अणुओं में इलेक्ट्रॉन नाभिक के साथ दृढ़तापूर्वक बँधे होते हैं, परावैद्युत पदार्थ कहलाते हैं।” जैसे-काँच, मोम, अभ्रक आदि। जर्मेनियम, अभ्रक तथा कार्बन में अभ्रक परावैद्युत पदार्थ है।

प्रश्न 24.
संधारित्र में परावैद्युत का क्या कार्य है? [2006]
उत्तर :
संधारित्र में परावैद्युत का कार्य-संधारित्र में परावैद्युत इसकी प्लेटों के बीच उपस्थित वैद्युत क्षेत्र की दिशा के विपरीत दिशा में ध्रुवित होकर प्लेटों के बीच के वैद्युत क्षेत्र को कम कर देता है, जिसके कारण प्लेटों के बीच विभवान्तर कम हो जाता है; अत: संधारित्र की धारिता बढ़ जाती है।

प्रश्न 25.
संधारित्र की प्लेटों के बीच परावैद्युत भरने अथवा उपयोग से धारिता क्यों बढ़ जाती है? [2000, 06]
अथवा
किसी संधारित्र की प्लेटों के बीच परावैद्युत पदार्थ भरने पर उसकी धारिता पर क्या प्रभाव पड़ता है? [2014, 17]
उत्तर :
आवेशित संधारित्र की प्लेटों के बीच परावैद्युत माध्यम भरने से उसके अणु ध्रुवित हो जाते हैं तथा माध्यम के अन्दर एक वैद्युत क्षेत्र, मुख्य वैद्युत क्षेत्र की विपरीत दिशा में उत्पन्न हो जाता है। इस कारण दोनों प्लेटों के बीच वैद्युत क्षेत्र की तीव्रता कम हो जाती है। तीव्रता कम होने के कारण प्लेटों के बीच उत्पन्न विभवान्तर कम हो जाता है। विभवान्तर के कम होने से संधारित्र की धारिता बढ़ जाती है।

प्रश्न 26.
क्या आप एक फैरड धारिता वाले समान्तर प्लेट धारित्र को एक अलमारी में रख सकते हैं? स्पष्ट कीजिए। [2018]
उत्तर :
समान्तर प्लेट धारित्र की धारिता \(C=\frac{A \varepsilon_{0}}{d}\)
या \(\frac{A}{d}=\frac{C}{\varepsilon_{0}}=\frac{1}{8.85 \times 10^{-12}}\)
= 1.13 x 10¹¹
सामान्य संधारित्रों के लिए d मिमी कोटि का होता है।
∴ A = 1.13 x 10¹¹ x 10^-3
= 113 x 10⁸ मीटर²
इस आकार के संधारित्र को अलमारी में रख पाना सम्भव नहीं है।

प्रश्न 27.
एक आवेशित संधारित्र की प्लेटों को एक वोल्टमीटर से जोड़ा गया है। यदि संधारित्र की प्लेटों को परस्पर दूर हटाया जाए तो वोल्टमीटर के पाठ्यांक पर क्या प्रभाव पड़ेगा?
उत्तर :
सूत्र C ∝ 1/d से, प्लेटों के बीच की दूरी d बढ़ाने पर धारिता C घट जाएगी। निश्चित आवेश के लिए . प्लेटों के बीच विभवान्तर V ∝ 1/C से, धारिता C के घटने पर विभवान्तर V बढ़ जाएगा; अत: वोल्टमीटर का पाठ्यांक बढ़ जाएगा।

प्रश्न 28.
सिद्ध कीजिए कि कूलॉम /न्यूटन-मीटर तथा फैरड/मीटर एक ही भौतिक राशि के मात्रक हैं। [2010]
उत्तर :

प्रश्न 29.
C₁ तथा C₂ धारिता वाले दो संधारित्रों पर आवेश क्रमशः q₁ व q₂ हैं तथा विभव क्रमशः V₁ व V₂ हैं। इनको स्पर्श कराकर फिर अलग करने के पश्चात् संधारित्रों का आवेश q’₁ व q’₂ एवं विभव में परिवर्तन क्रमशः ΔV₁ तथा ΔV₂ हो जाता है। सिद्ध कीजिए – [2006]
(i) \(\frac{q^{\prime}_{1}}{q_{2}^{\prime}}=\frac{C_{1}}{C_{2}}\) तथा
(ii) C₁ΔV₁ = C₂ΔV₂
हल :
(i) पहले संधारित्र पर आवेश q₁ = C₁V₁ तथा दूसरे संधारित्र पर आवेश q₂ = C₂V₂
दोनों पर कुल आवेश q = q₁ + q₂ = C₁V₁ + C₂V₂
स्पर्श कराने के बाद माना दोनों का उभयनिष्ठ विभव V है तो
q’₁=C₁V तथा q’₂ = C₂V ।
अत: \(\frac{q_{1}^{\prime}}{q_{2}^{\prime}} \doteq \frac{C_{1} V}{C_{2} V}=\frac{C_{1}}{C_{2}}\)

(ii) जोड़ने से पहले कुल आवेश q = q₁ + q₂ = C₁V₁ + C₂V₂| चूँकि जोड़ने पर दोनों का विभव समान हो जाता है; अत: एक का विभव बढ़ेगा तथा दूसरे का घटेगा। इसलिए जोड़ने के बाद कुल आवेश
q = C₁(V₁ + ∆V₁) + C₂ (V₂ – ∆V₂)

चूँकि जोड़ने से पहले तथा बाद में कुल आवेश वही रहता है।
1. C₁(V₁ + ∆V₁) + C₂ (V₂– ∆V₂) = C₁V₁ + C₂V₂
अथवा [C₁V₁ + C₁∆V₁] + C₂V₂ – C₂∆V₂ = C₁V₁ + C₂V₂.
अथवा C₁∆V₁ – C₂∆V₂ = 0
अतः C₁∆V₁ = C₂∆V₂

प्रश्न 30.
C₁ व C₂ धारिताओं वाले दो संधारित्रों को समान्तर क्रम में जोड़कर q आवेश दिया गया है। प्रत्येक संधारित्र का विभवान्तर तथा आवेश बताइए।
हल :
समान्तर क्रम में जुड़े होने के कारण विभवान्तर समान होगा। प्रत्येक संधारित्र का विभवान्तर V = q/ (C₁ + C₂)

प्रश्न 31.
धातु की चार एकसमान प्लेटों में प्रत्येक की एक तरफ की सतह का क्षेत्रफल A है। ये प्लेटें वायु में एक-दूसरे से d दूरी पर रखी हैं। इन्हें चित्र 2.38 के अनुसार आपस में जोड़ दिया गया है। A तथा B के बीच तुल्य धारिता ज्ञात कीजिए। [2002]]
हल :

दिए गए परिपथ में प्लेटें 1 व 2 एक संधारित्र तथा प्लेटें 3 व 4 दूसरा संधारित्र बनाती हैं। इनके तुल्य परिपथ संलग्न चित्रों (2.38) में प्रदर्शित हैं। स्पष्ट है कि दोनों संधारित्र समान्तरक्रम में जुड़े हैं।

प्रत्येक संधारित्र की धारिता C₁ = C₂ = \(\frac{\varepsilon_{0} A}{d}\)
अतः बिन्दुओं A व B के बीच तुल्य धारिता C = C₁ + C₂
\(=\frac{\varepsilon_{0} A}{d}+\frac{\varepsilon_{0} A}{d}=\frac{2 \varepsilon_{0} A}{d}\)

प्रश्न 32.
संलग्न चित्र-2.40 में दिखाई गई चार प्लेटों में प्रत्येक प्लेट का क्षेत्रफल A मीटर² तथा संलग्न प्लेटों के बीच दूरी d मीटर है। एकान्तर प्लेटें पतले तारों से जोड़ी गई हैं। बिन्दुओं A व B के बीच तुल्य धारिता ज्ञात कीजिए। [2004]

हल :
यह तीन संधारित्रों (1, 2); (2, 3) व (3, 4) का समान्तर संयोजन है। प्लेट 2, पहले व दूसरे संधारित्रों की दूसरी उभयनिष्ठ प्लेट है तथा प्लेट 3, दूसरे व तीसरे संधारित्रों की पहली उभयनिष्ठ प्लेट है।
अतः बिन्दुओं A व B के बीच तुल्य धारिता C = C₁ + C₂ + C₃
\(=\frac{\varepsilon_{0} A}{d}+\frac{\varepsilon_{0} A}{d}+\frac{\varepsilon_{0} A}{d}=\frac{3 \varepsilon_{0} A}{d}\) फैरड

प्रश्न 33.
एक समान्तर प्लेट संधारित्र की प्रत्येक प्लेट का क्षेत्रफल A तथा प्लेटों के बीच की दूरी d है। इसकी दोनों प्लेटों के बीच t मोटाई की एक धातु की प्लेट खिसकाई जाती है। इससे निकाय की धारिता पर क्या प्रभाव पड़ेगा?
उत्तर :
पट्टी रखने से पहले धारिता \(C_{0}=\frac{\varepsilon_{0} A}{d}\)

अत: निकाय की धारिता बढ़ जाएगी।

प्रश्न 34.
एक समान्तर पट्ट संधारित्र की प्लेटों के बीच की दूरी d है। प्लेटों के बीच d/2 मोटाई की एक धातु की पट्टी रख दी जाती है। धारिता पर इसका क्या प्रभाव पड़ेगा?
हल :
t मोटाई की पट्टी रखने से पहले धारिता \(C_{0}=\frac{\varepsilon_{0} A}{d}\)

प्रश्न 35.
R₁ व R₂ त्रिज्याओं वाले दो गोलीय चालकों को आवेशित किया गया है। यदि इन्हें एक तार द्वारा जोड़ा जाए तो उनके पृष्ठ आवेश घनत्वों का अनुपात क्या होगा? किस गोले पर पृष्ठ आवेश घनत्व अधिक होगा? [2005, 06]
हल :
चूँकि दोनों गोलीय चालकों पर विभव V समान है; अत: गोलों के आवेशों का अनुपात

पृष्ठ आवेश घनत्व छोटे गोले (जिसकी त्रिज्या R₂ है) पर अधिक होगा।

प्रश्न 36.
एक समान्तर प्लेट संधारित्र को बैटरी से आवेशित किया जाता है। बैटरी का सम्बन्ध संधारित्र से विच्छेदित करने के उपरान्त प्लेटों के बीच की दूरी दोगुनी करने पर संधारित्र की
(i) धारिता तथा (ii) संगृहीत ऊर्जा पर क्या प्रभाव पड़ेगा? [2012]
हल :
(i) माना d₁ = d अत: d₂ = 2d सूत्र C ∝ 1/ d से, संधारित्र की धारिता आधी हो जाएगी।
(ii) सूत्र U ∝ 1/C से, संगृहित ऊर्जा दोगुनी हो जाएगी।

प्रश्न 37.
स्थैतिक वैद्युत ऊर्जा में क्या परिवर्तन होगा तथा क्यों, जब एक आवेशित समान्तर प्लेट धारित्र की प्लेटों के बीच एक परावैद्युतांक K वाला परावैद्युतांक स्लैब डाला जाता है, जब धारित्र को बैटरी से अलग कर दिया जाता है? [2018]
हल :
धारित्र को बैटरी से अलग कर देने पर उसकी प्लेटों पर आवेश अपरिवर्तित रहेगा।
संधारित्र की धारिता \(C=\frac{A \varepsilon_{0}}{d}\)
संधारित्र में संचित स्थैतिक वैद्युत ऊर्जा \(U=\frac{1}{2} \frac{q^{2}}{C}\)
संधारित्र की प्लेटों के बीच परावैद्युतांक स्लैब रखने पर,

प्रश्न 38.
धातु का एक बड़ा गोला, एक दूसरे बाहरी छोटे गोले से तार द्वारा जुड़ा है। इस समायोजन को कुछ आवेश दिया जाता है। (i) किस गोले पर अधिक आवेश होगा? (ii) किस गोले पर पृष्ठ आवेश घनत्व अधिक होगा? [2006]
उत्तर :
(i) चूँकि बड़े गोले की त्रिज्या अधिक है; अत: इसकी धारिता भी अधिक होगी जिसके कारण बड़े गोले के पृष्ठ पर अधिक आवेश होगा।
(ii) पृष्ठ आवेश घनत्व छोटे गोले पर अधिक होगा।

प्रश्न 39.
दो विभिन्न धारिता वाले गोले भिन्न-भिन्न विभवों तक आवेशित किए जाते हैं। अब इन गोलों को एक तार द्वारा जोड़ दिया जाता है। बताइए कि उनकी कुल ऊर्जा पहली स्थिति से बढ़ेगी, घटेगी अथवा समान रहेगी। ऊर्जा में यह अन्तर किस रूप में होता है?
उत्तर :
आवेश के पुनर्वितरण से सदैव ऊर्जा का ह्रास होता है; अत: कुल ऊर्जा घटेगी। ऊर्जा में यह अन्तर संयोजक तार में ऊष्मा के रूप में क्षय होगा।

प्रश्न 40.
किसी आवेशित चालक के चारों ओर परावैद्युत पदार्थ रखने पर उसके विभव तथा धारिता पर क्या प्रभाव पड़ता है?
उत्तर :
किसी आवेशित चालक के चारों ओर K परावैद्युतांक वाला पदार्थ रखने पर उसका विभव V से घटकर V/K रह जाता है तथा धारिता C से बढ़कर KC हो जाती है।

प्रश्न 41.
दिए गए ग्राफ में एक संधारित्र की कुल संचित ऊर्जा (U) तथा धारिता (C) का परिवर्तन प्रदर्शित है। संधारित्र की प्लेटों पर आवेश (q) तथा प्लेटों के बीच विभवान्तर (V) में से कौन-सी राशि नियत है? [2013]

उत्तर :
दिए गए ग्राफ से स्पष्ट है कि U ∝ 1/C
संधारित्र में संचित कुल ऊर्जा \(\frac{1}{2} \frac{q^{2}}{C}\)
U व C के बीच ग्राफ अतिपरवलय है।
यदि q नियत है तो U ∝ 1/C
अत: संधारित्र की प्लेटों पर आवेश (q) नियत है।

प्रश्न 42.
n समरूप संधारित्र (प्रत्येक की धारिता C) समान्तर क्रम में जुड़े हैं, जिन्हें V विभव तक आवेशित किया गया है। इस संयोजन का कुल आवेश, कुल विभवान्तर तथा कुल ऊर्जा बताइए। यदि इन्हें अलग-अलग करके श्रेणीक्रम में जोड़ें तब उपर्युक्त मान बताइए। [2013]
हल :
समान्तर क्रम में, प्रत्येक संधारित्र पर आवेश = CV
अतः कुल आवेश = n x CV = nCV
कुल विभवान्तर V है; अत: कुल ऊर्जा = \(\frac { 1 }{ 2 }\) (nC)V² = \(\frac { 1 }{ 2 }\) nCV²
श्रेणीक्रम में, कुल आवेश = प्रत्येक संधारित्र पर आवेश = CV
कुल विभवान्तर = nv
कुल ऊर्जा = \(\frac{1}{2}\left(\frac{C}{n}\right)\)(nV)² = InCV²

प्रश्न 43.
N समान आवेशित छोटी बूंदें मिलकर बड़ी बूँद बनाती हैं। बड़ी बूंद तथा छोटी बूंद के लिए निम्न का अनुपात ज्ञात कीजिए-(i) धारिता, (ii) विभव, (iii) आवेश, (iv) स्थैतिक वैद्युत ऊर्जा। [2018]
उत्तर :
माना प्रत्येक छोटी बूंद की त्रिज्या 7 व उस पर आवेश q है।
बड़ी बूंद पर आवेश (Q) = Nq
बड़ी बूंद का आयतन = N x छोटी बूंद का आयतन

प्रश्न 44.
यदि वायु की परावैद्युत सामर्थ्य 3.0 x 10⁶ वोल्ट/मीटर हो तो दर्शाइए कि वान डे ग्राफ जनित्र के 0.1 मीटर त्रिज्या वाले गोले का विभव 3.0 x 10⁵ वोल्ट से अधिक नहीं बढ़ाया जा सकता। [2018]
उत्तर :
किसी माध्यम का परावैद्युत सामर्थ्य, वैद्युत क्षेत्र का वह अधिकतम मान है जो वह अपना परावैद्युत भंजन हुए बिना सहन कर सकता है।
अतः E_max = 3.0 x 10⁶ वोल्ट/मीटर, r = 0.1 मीटर
गोले के पृष्ठ पर वैद्युत क्षेत्र, \(E=\frac{1}{4 \pi \varepsilon_{0}} \cdot \frac{q}{r^{2}}\)
गोले के पृष्ठ पर वैद्युत विभव, \(V=\frac{1}{4 \pi \varepsilon_{0}} \frac{q}{r}\)
∴ \(\frac{E}{V}=\frac{1}{r}\) या V= E.r
या V_max = E_max.r = 3.0 x 10⁶ x 0.1
= 3.0 x 10⁵ वोल्ट।
अतः वान डे ग्राफ जनित्र के गोले का विभव 3.0 x 10⁵ वोल्ट से अधिक नहीं बढ़ाया जा सकता है।

स्थिरवैद्युत विभव तथा धारिता अति लघु उत्तरीय प्रश्नोत्तर

प्रश्न 1.
S.I. पद्धति में वैद्युत विभव का मात्रक लिखिए।
उत्तर :
S.I. पद्धति में वैद्युत विभव का मात्रक वोल्ट है।

प्रश्न 2.
वैद्युत विभवान्तर तथा वैद्युत विभव की विमा लिखिए।
उत्तर :
वैद्युत विभवान्तर तथा वैद्युत विभव दोनों की विमा [ML²T^-3A^-1] है।

प्रश्न 3.
उस भौतिक राशि का नाम बताइए जिसका S.I. मात्रक ‘जूल/कूलॉम’ होता है। यह एक अदिश राशि है अथवा सदिश राशि?
उत्तर :
‘जूल/कूलॉम’ वैद्युत विभव अथवा विभवान्तर का मात्रक है। यह एक अदिश राशि है।

प्रश्न 4.
बताइए वैद्यत क्षेत्र तथा वैद्यत विभव सदिश राशियाँ हैं अथवा अदिश राशियाँ।
उत्तर :
वैद्युत क्षेत्र सदिश राशि है, जबकि वैद्युत विभव अदिश राशि है।

प्रश्न 5.
एक बिन्दु आवेश q सेr दूरी पर वैद्युत विभव के लिए सूत्र लिखिए।
हल :
वैद्युत विभव \(V=\frac{1}{4 \pi \varepsilon_{0}} \frac{q}{r}\)

प्रश्न 6.
एक वैद्युत द्विध्रुव के कारण उसकी अक्षीय एवं निरक्षीय स्थिति में वैद्युत विभव का व्यंजक लिखिए। [2018]
हल :
अक्षीय स्थिति में, \(V=\frac{1}{4 \pi \varepsilon_{0}} \frac{p}{r^{2}}\) तथा निरक्षीय स्थिति में, V = 0

प्रश्न 7.
विभव प्रवणता तथा वैद्युत क्षेत्र की तीव्रता के बीच सम्बन्ध लिखिए। [2003, 05, 13]
उत्तर :
वैद्युत क्षेत्र की ताजता \(E=-\frac{d V}{d r}\)
अर्थात् वैद्युत क्षेत्र की तीव्रता ऋणात्मक विभव प्रवणता के बराबर होती है।

प्रश्न 8.
यदि दो समान्तर प्लेटों के बीच की दूरी d हो तथा उनके बीच विभवान्तर V हो तो प्लेटों के बीच विभव प्रवणता एवं वैद्युत क्षेत्र की तीव्रता कितनी होगी?
उत्तर :
विभव प्रवणता तथा वैद्युत क्षेत्र की तीव्रता अर्थात् दोनों का आंकिक मान E =V/d होगा।

प्रश्न 9.
विभव प्रवणता का मात्रक क्या है?
उत्तर :
विभव प्रवणता का मात्रक वोल्ट/मीटर है।

प्रश्न 10.
किसी सम वैद्युत क्षेत्र में वैद्युत क्षेत्र की तीव्रता तथा विभवान्तर में सम्बन्ध लिखिए। [2009]]
उत्तर :
वैद्युत क्षेत्र की तीव्रता E = (V₁ – V₂)/d वोल्ट/मीटर।

प्रश्न 11.
दो बिन्दुओं A तथा B पर वैद्युत विभव क्रमशः +V वोल्ट तथा – V वोल्ट हैं। यदि उनके बीच की दूरी r मीटर हो तो A और B के बीच औसत वैद्युत क्षेत्र ज्ञात कीजिए। [2018]
हल :
बिन्दु A व B के बीच विभवान्तर = V_B – V_A = – V – (V) = – 2V
A व B के बीच वैद्यत क्षेत्र की तीव्रता \(E=\frac{-d V}{d r}=\frac{-(-2 V)}{r}=\frac{2 V}{r}\)

प्रश्न 12.
कोई आवेशित कण एकसमान स्थिर वैद्युत क्षेत्र में, क्षेत्र के लम्बवत् प्रवेश करता है। कण का पथ क्या होगा?
उत्तर :
आवेशित कण का पथ परवलयाकार होगा।

प्रश्न 13.
क्षैतिज दिशा में एकसमान वेग v से गति करती हुई कैथोड किरण एक ऊर्ध्वाधर वैद्युत क्षेत्र E से गुजर रही है। किरण के ऊर्ध्वाधर विक्षेप के लिए व्यंजक लिखिए।
उत्तर :
कैथोड किरण पर आवेश q= e है; अतः कैथोड किरण का ऊर्ध्वाधर दिशा में विक्षेप \(y=\left(\frac{e E}{2 m v^{2}}\right) x^{2}\) जहाँ x क्षैतिज दिशा में चली गई दूरी है।

प्रश्न 14.
वैद्युत क्षेत्र रेखा के अनुदिश वैद्युत विभव बढ़ता है अथवा घटता है?
उत्तर :
वैद्युत क्षेत्र रेखा के अनुदिश वैद्युत विभव घटता है।

प्रश्न 15.
एक प्रोटॉन को दूसरे प्रोटॉन की ओर लाने पर, निकाय की वैद्युत स्थितिज ऊर्जा में क्या परिवर्तन होता है? [2006]
उत्तर :
निकाय की वैद्युत स्थितिज ऊर्जा बढ़ जाएगी।

प्रश्न 16.
किसी समविभवी पृष्ठ के दो बिन्दुओं के बीच 500 माइक्रोकूलॉम आवेश को गति कराने में कितना कार्य किया जाता है? [2003, 13]
हल :
कार्य W = qΔV = q x 0 = 0 (∵ ΔV = 0)

प्रश्न 17.
वैद्युत क्षेत्र में इलेक्ट्रॉन उच्च विभव से निम्न विभव की ओर अथवा निम्न विभव से उच्च विभव में से किस ओर गति करता है? इसी क्षेत्र में प्रोटॉन किस ओर गति करेगा?.
उत्तर :
इलेक्ट्रॉन निम्न विभव से उच्च विभव की ओर गति करता है, जबकि प्रोटॉन उच्च विभव से निम्न विभव की ओर गति करेगा।

प्रश्न 18.
क्या ऐसा सम्भव है कि किसी बिन्दु पर वैद्युत क्षेत्र शून्य हो परन्तु वैद्युत विभव शून्य न हो? उदाहरण दीजिए।
उत्तर :
हाँ, किसी खोखले आवेशित चालक के अन्दर वैद्युत क्षेत्र शून्य होता है, परन्तु वैद्युत विभव शून्य नहीं होता

प्रश्न 19.
क्या ऐसा सम्भव है कि किसी बिन्दु पर वैद्युत विभव शून्य हो परन्तु वैद्युत क्षेत्र शून्य न हो? उदाहरण दीजिए।
उत्तर :
हाँ, किसी वैद्युत द्विध्रव की निरक्ष पर वैद्युत विभव शून्य होता है, जबकि वैद्युत क्षेत्र शून्य नहीं होता

प्रश्न 20.
किसी बिन्दु आवेश q को एक अन्य आवेश Q के परितः r त्रिज्या के वृत्तीय पथ में घूर्णन कराया जाता है। किया गया कार्य ज्ञात कीजिए।
उत्तर :
बिन्दु आवेश एक समविभव पृष्ठ पर गति करता है; अत: किया गया कार्य शून्य होगा।

प्रश्न 21.
किसी धन बिन्दु आवेश के लिए दो समविभव खींचिए। .
उत्तर :

चित्र 2.42 में प्रदर्शित गोलीय पृष्ठ S₁ व S₁ धन बिन्दु आवेश के समविभव पृष्ठ हैं।

प्रश्न 22.
एक खोखले आवेशित चालक के बाहरी पृष्ठ पर वैद्युत बल क्षेत्र लम्बवत् चित्र-2.42 क्यों होता है?
उत्तर :
आवेशित चालक का बाहरी पृष्ठ समविभव पृष्ठ होता है इसीलिए उसके बाहरी पृष्ठ पर वैद्युत बल क्षेत्र .. लम्बवत् होता है।

प्रश्न 23.
समविभव पृष्ठ के सापेक्ष वैद्युत बल रेखाओं की दिशा बताइए।
उत्तर :
समविभव पृष्ठ पर वैद्युत बल रेखाएँ अभिलम्बवत् होती हैं।

प्रश्न 24.
\([latex][latex]\overrightarrow{\mathbf{p}}\)[/latex][/latex] वैद्युत द्विध्रुव आघूर्ण वाला एक वैद्युत द्विध्रुव एकसमान वैद्युत क्षेत्र \([latex][latex]\overrightarrow{\mathbf{E}}\)[/latex][/latex] में स्थायी सन्तुलन में रखा हुआ है। वैद्युत द्विध्रुव की स्थितिज ऊर्जा क्या होगी?
उत्तर :
स्थायी सन्तुलन की अवस्था में θ = 0°
अतः वैद्युत द्विध्रुव की वैद्युत स्थितिज ऊर्जा U = – pE cos 0° = pE

प्रश्न 25.
p वैद्युत द्विध्रुव आघूर्ण वाले एक वैद्युत द्विध्रुव को E तीव्रता के एकसमान वैद्युत क्षेत्र में स्थायी सन्तुलन की स्थिति से 90° तथा 180° विक्षेपित करने में कितना कार्य करना पड़ेगा?
हल :
स्थायी सन्तुलन की स्थिति से 90° विक्षेपित करने में किया गया कार्य
W₁ = pE (cos 0° – cos 90° ) = pE
स्थायी सन्तुलन की स्थिति से 180° विक्षेपित करने में किया गया कार्य
W₂ = pE (cos 0° – cos 180°) = 2 pE

प्रश्न 26.
एक इलेक्ट्रॉन तथा एक प्रोटॉन परस्पर 1Å की दूरी पर हैं। इस निकाय की वैद्युत स्थितिज ऊर्जा ज्ञात कीजिए।
हल :
दिया है, q₁ = -e तथा q₂ = e, r = 1Å = 10^-10 मीटर, U = ?

प्रश्न 27.
दो बिन्दु आवेशों के निकाय की वैद्युत स्थितिज ऊर्जा के लिए सूत्र लिखिए।
उत्तर :
परस्पर r दूरी पर निर्वात या वायु में स्थित बिन्दु आवेशों q₁ व q₂ के निकाय की
वैद्युत स्थितिज ऊर्जा \(U=\frac{1}{4 \pi \varepsilon_{0}} \frac{q_{1} q_{2}}{r}\)

प्रश्न 28.
दो समान बिन्दु आवेश q प्रत्येक कूलॉम, परस्पर r मीटर की दूरी पर हैं। इनकी वैद्युत स्थितिज ऊर्जा कितनी होगी? [2004]
उत्तर :
वैद्युत स्थितिज ऊर्जा \(U=\frac{1}{4 \pi \varepsilon_{0}} \frac{q^{2}}{r}\)जूल

प्रश्न 29.
दिखाइए कि मात्रक वोल्ट/मीटर तथा न्यूटन/कूलॉम एक ही भौतिक राशि के मात्रक हैं। ये मात्रक किस भौतिक राशि से सम्बद्ध हैं?
उत्तर :

ये दोनों मात्रक वैद्यत क्षेत्र की तीव्रता के हैं।

प्रश्न 30.
बिन्दु आवेश के कारण वैद्युत क्षेत्र की तीव्रता तथा वैद्युत विभव, दूरी r के साथ कैसे विचरण करते [2002]
उत्तर :
वैद्युत क्षेत्र की तीव्रता E, दूरी के वर्ग के व्युत्क्रमानुपाती होता है अर्थात् E ∝ 1/r²
वैद्युत विभव V, दूरी r के व्युत्क्रमानुपाती होता है अर्थात् V ∝ 1/r ; अत: वैद्युत विभव की तुलना में, वैद्युत क्षेत्र की तीव्रता, दूरी r के बढ़ने पर तेजी से घटती है।

प्रश्न 31.
बिन्दु आवेश तथा रेखीय आवेश के कारण वैद्युत क्षेत्र दूरी के साथ कैसे परिवर्तित होता है? [2005]
उत्तर :
बिन्दु आवेश के लिए वैद्युत क्षेत्र E ∝ 1/r² तथा रेखीय आवेश के लिए वैद्युत क्षेत्र E & 1/r होता है।

प्रश्न 32.
एकसमान वैद्युत क्षेत्र में क्षेत्र की दिशा से θ कोण पर संरेखित वैद्युत द्विध्रुव की वैद्युत स्थितिज ऊर्जा के लिए, सूत्र लिखिए।
उत्तर :
एकसमान वैद्युत क्षेत्र \overrightarrow{\mathrm{E}} से θ कोण पर संरेखित द्विध्रुव की स्थितिज ऊर्जा
U_θ = – \(\overrightarrow{\mathrm{P}}\).\(\overrightarrow{\mathrm{E}}\) = – pE cosθ

प्रश्न 33.
1 सेमी त्रिज्या के गोले को 1 कूलॉम आवेश देने से गोले के पृष्ठ पर वैद्युत विभव ज्ञात कीजिए। [2016]
हल :
दिया है, r = 1 सेमी = 10^-2 मीटर, q= 1 कूलॉम, V = ?
वैद्युत विभव V = 9 x 10⁹ x \(\frac{q}{r}\) = 9 x 10⁹ x \(\frac{1}{10^{-2}}\) = 9 x 10¹¹ वोल्ट।

प्रश्न 34.
धारिता का विमीय सूत्र तथा मात्रक लिखिए। [2014]
उत्तर :
धारिता का विमीय सूत्र = [M^-1L^-2T⁴A²] तथा मात्रक फैरड है।

प्रश्न 35.
M.K.S.A. पद्धति में R त्रिज्या के धातु के खोखले गोले की धारिता का सूत्र लिखिए। अथवा विलगित गोलीय चालक की धारिता का सूत्र लिखिए।
[2001, 03]
उत्तर :
R त्रिज्या के धातु के खोखले गोले की धारिता C = 4 πε₀R फैरड।

प्रश्न 36.
संधारित्र के श्रेणी संयोजन का सूत्र लिखिए।
उत्तर :
संधारित्र के श्रेणी संयोजन का सूत्र
\(\frac{1}{C}=\frac{1}{C_{1}}+\frac{1}{C_{2}}\)

प्रश्न 37.
किसी आवेशित संधारित्र की ऊर्जा के लिए सूत्र लिखिए।
उत्तर :
आवेशित संधारित्र की ऊर्जा = \(\frac{1}{2} \frac{q^{2}}{C}\) जूल अथवा \(\frac{1}{2} C V^{2}\) जूल।।

प्रश्न 38.
संधारित्र में साधारणतया प्रयुक्त होने वाले किन्हीं दो परावैद्युत पदार्थों के नाम लिखिए। [2002]
उत्तर :
अभ्रक, मोम, कागज।

प्रश्न 39.
समान्तर प्लेट संधारित्र में दूसरी प्लेट का क्या कार्य है?
उत्तर :
संधारित्र में दूसरी प्लेट का कार्य, प्लेटों का आकार स्थिर रखते हुए पहली प्लेट के विभव को कम करना है, जिससे कि उसे अधिक आवेश दिया जा सके तथा धारिता बढ़ाई जा सके।

प्रश्न 40.
किसी आवेशित चालक की धारिता C फैरड तथा आवेश q के कारण उसमें संचित स्थितिज ऊर्जा U जूल है। चालक पर उपस्थित आवेश का व्यंजक लिखिए।
उत्तर :
चालक की स्थितिज ऊर्जा U = q²/2C; अत: चालक पर आवेश \(q=\sqrt{2 U C}\)

प्रश्न 41.
एक नियत विभवान्तर के लिए कौन-सा संधारित्र अधिक आवेश संगृहीत करेगा? (i) परावैद्युत से भरा संधारित्र या (ii) वायु संधारित्र।
[2018] .
उत्तर :
संधारित्र में संगृहीत आवेश q= CV = \(\frac{K A \varepsilon_{0}}{d} V\)
अत: परावैद्युत से भरा संधारित्र अधिक आवेश संगृहीत करेगा।

प्रश्न 42.
एक आवेशित छड़ के निकट एक अनावेशित धातु की छड़ रखने पर प्रथम छड़ के विभव पर क्या प्रभाव पड़ेगा?
उत्तर :
प्रथम छड़ का विभव घट जाएगा।

प्रश्न 43.
सिद्ध कीजिए कि दो आवेशित चालकों को परस्पर स्पर्श कराके अलग कर देने से उन पर आवेश, चालकों की धारिताओं के अनुपात में बँट जाता है।
उत्तर :
दो आवेशित चालकों को स्पर्श कराने पर उनका विभव V समान हो जाएगा इसलिए उन पर आवेश क्रमशः
q₁ = C₁V व q₂ = C₂V हो जाएगा।
अतः .
\(\frac{q_{1}}{q_{2}}=\frac{C_{1}}{C_{2}}\)

प्रश्न 44.
एक अनावेशित वैद्युतरोधी चालक A एक-दूसरे आवेशित वैद्युतरोधी चालक B के समीप लाया जाता है तो चालक B के आवेश तथा विभव में क्या परिवर्तन होगा? [2010]
उत्तर :
चालक B पर आवेश में कोई परिवर्तन नहीं होगा परन्तु विभव कम हो जाएगा क्योंकि यह चालक A पर अपने से विपरीत आवेश प्रेरित करता है।

प्रश्न 45.
किसी आवेशित संधारित्र पर नैट आवेश कितना होता है?
उत्तर :
शून्य।

प्रश्न 46.
किसी माध्यम के परावैद्युतांक से क्या तात्पर्य है?[2010]
उत्तर :
परावैद्युतांक-“किसी माध्यम की निरपेक्ष वैद्युतशीलता ६ तथा निर्वात की वैद्युतशीलता ६० के अनुपात को उस माध्यम का परावैद्युतांक K कहते हैं।” अर्थात् ε/ε₀ = K

प्रश्न 47.
किसी संधारित्र की धारिता को कैसे बढ़ाया जा सकता है? [2004]
उत्तर :
संधारित्र प्लेटों का क्षेत्रफल बढ़ाकर, प्लेटों के बीच की दूरी कम करके तथा प्लेटों के बीच परावैद्युत पदार्थ रखकर संधारित्र की धारिता को बढ़ाया जा सकता है।

प्रश्न 48.
आवेशित संधारित्र में ऊर्जा किस रूप में कहाँ संचित रहती है? [2002, 04]
उत्तर :
आवेशित संधारित्र की ऊर्जा, संधारित्र की प्लेटों के बीच स्थित परावैद्युत माध्यम में वैद्युत क्षेत्र की ऊर्जा के रूप में संचित रहती है।

प्रश्न 49.
यदि आवेशित संधारित्र की प्लेटों के बीच की दूरी को बढ़ाया जाए तो उनके बीच विभवान्तर पर क्या प्रभाव पड़ेगा? [2005]
उत्तर :
सूत्र V ∝ d से, विभवान्तर बढ़ जाएगा।

प्रश्न 50.
यदि आवेशित समान्तर पट्ट संधारित्र की प्लेटों को परस्पर निकट लाया जाए तो उनके विभवान्तर में क्या परिवर्तन होगा? [2003]
उत्तर :
सूत्र C ∝ 1/d से, दूरी d के कम होने से धारिता C बढ़ जाएगी तथा सूत्र V ∝ 1/C से, धारिता C के बढ़ने से विभवान्तर V कम हो जाएगा।

प्रश्न 51.
किसी संधारित्र की धारिता की परिभाषा व मात्रक लिखिए। [2014, 15, 16]
उत्तर :
संधारित्र की धारिता–“संधारित्र की एक प्लेट को दिए गए आवेश तथा दोनों प्लेटों के बीच उत्पन्न विभवान्तर के अनुपात को संधारित्र की धारिता कहते हैं।” इसका मात्रक फैरड है।

प्रश्न 52.
किसी संधारित्र की धारिता किन-किन बातों पर निर्भर करती है?
उत्तर :
संधारित्र की धारिता प्लेटों के क्षेत्रफल, प्लेटों के बीच की दूरी तथा प्लेटों के बीच रखे परावैद्युत माध्यम पर निर्भर करती है।

प्रश्न 53.
तीन संधारित्रों के संयोग से अधिकतम तथा न्यूनतम धारिता कैसे प्राप्त करेंगे?
उत्तर :
तीनों संधारित्रों को समान्तर क्रम में जोड़कर अधिकतम धारिता तथा श्रेणीक्रम में जोड़कर न्यूनतम धारिता प्राप्त कर सकते हैं।

प्रश्न 54.
तीन समान धारिता C के संधारित्र श्रेणीक्रम में जुड़े हुए हैं। इनकी परिणामी धारिता कितनी होगी? यदि संधारित्र समान्तर क्रम में जुड़े हों, तब?
उत्तर :
श्रेणीक्रम में परिणामी धारिता = C/3 तथा समान्तर क्रम में परिणामी धारिता = 3C

प्रश्न 55.
किसी आवेशित चालक में संचित स्थितिज ऊर्जा का व्यंजक धारिता तथा विभव के पदों में लिखिए। [2001]
अथवा
किसी चालक का विभव V तथा धारिता C है, चालक की वैद्युत स्थितिज ऊर्जा का सूत्र बताइए। [2004]
उत्तर :
संचित स्थितिज ऊर्जा \(U=\frac{1}{2} C V^{2}\) जूल; जहाँ C धारिता तथा V विभव है।

प्रश्न 56.
किसी संधारित्र की धारिता C है। यदि इस पर Q आवेश हो तो इस पर संगृहीत ऊर्जा कितनी होगी? [2004]
उत्तर :
संचित स्थितिज ऊर्जा \(U=\frac{1}{2} \frac{Q^{2}}{C}\) जूल।

प्रश्न 57.
C धारिता के संधारित्र को q आवेश देने पर संचित ऊर्जा U है। यदि आवेश बढ़ाकर 24 कर दिया जाए तो संचित ऊर्जा का मान क्या होगा? । [2006]
उत्तर :
सूत्र U ∝ q² से, संचित ऊर्जा 4U होगी।

प्रश्न 58.
संधारित्रों के संयोजन की समतुल्य धारिता से क्या तात्पर्य है? [2004]
उत्तर :
संयोजन की समतुल्य धारिता-संयोजन की समतुल्य धारिता, उस एकल संधारित्र की धारिता के तुल्य होती है जो किसी बैटरी से जोड़े जाने पर उतना ही आवेश संचित करे, जितना कि उस बैटरी से जोड़े जाने पर संयोजन करता है।

प्रश्न 59.
यदि एक परिवर्ती वायु संधारित्र में n प्लेटें हों तथा दो समीपवर्ती प्लेटों के बीच की दूरी d हो तो संधारित्र की धारिता कितनी होगी? ।
उत्तर :
संधारित्र की धारिता \(C=\frac{(n-1) \varepsilon_{0} A}{d}[latex] फैरड होगी।

प्रश्न 60.
समान्तर पट्ट संधारित्र की धारिता का सूत्र लिखिए , जब उसकी प्लेटों के बीच आंशिक रूप से परावैद्युत पदार्थ रखा हो। .
उत्तर :
समान्तर पट्ट संधारित्र की धारिता C=\frac{\varepsilon_{0} A}{[(d-t)+t / K]} फैरड

प्रश्न 61.
समान्तर प्लेट संधारित्र की धारिता का सूत्र लिखिए। प्रयुक्त संकेतों का अर्थ स्पष्ट कीजिए। [2009]
उत्तर :
समान्तर प्लेट संधारित्र की धारिता [latex]C=\frac{K \varepsilon_{0} A}{d}\) फैरड।
जहाँ d प्लेटों के बीच की दूरी, A प्लेटों का क्षेत्रफल तथा K प्लेटों के बीच के माध्यम का परावैद्युतांक है।

प्रश्न 62.
निर्वात की वैद्युतशीलता से क्या तात्पर्य है?
उत्तर :
सूत्र C = ε₀A/d से, यदि A = 1 मीटर², d = 1 मीटर है तो C = ε₀
अतः निर्वात की वैद्युतशीलता उस समान्तर प्लेट संधारित्र की धारिता के तुल्य होती है जिसकी प्लेटों का क्षेत्रफल 1 मीटर² तथा उनके बीच की दूरी 1 मीटर हो।

प्रश्न 63.
\(\frac{1}{2} \varepsilon_{0} E^{2}\) की विमा लिखिए, जहाँ , मुक्त स्थान की वैद्युतशीलता तथा E वैद्युत क्षेत्र की तीव्रता है।
[2002]
उत्तर :
व्यंजक \(\frac{1}{2} \varepsilon_{0} E^{2}\), प्रति एकांक आयतन में संचित ऊर्जा अर्थात् ऊर्जा घनत्व को प्रदर्शित करता है।

प्रश्न 64.
किसी संधारित्र को एक सीमा से अधिक आवेश देना सम्भव क्यों नहीं है? [2000]
उत्तर :
संधारित्र को लगातार आवेश देते रहने से उसकी प्लेटों के बीच वैद्युत क्षेत्र बढ़ता जाएगा। अन्त में एक स्थिति ऐसी आ जाएगी जब संधारित्र की प्लेटों के बीच के माध्यम का रोधन (insulation) टूट जाएगा और संधारित्र चिनगारी देकर निरावेशित हो जाएगा।

प्रश्न 65.
दो आवेशित चालकों को तार द्वारा जोड़ने पर ऊर्जा-हानि के लिए सूत्र लिखिए। [2005]
उत्तर :

प्रश्न 66.
पृथ्वी के वैद्युत विभव को शून्य माना जाता है, क्यों?
[2003]
उत्तर :
क्योंकि पृथ्वी की धारिता अनन्त होती है; अत: सूत्र V = q/C से, पृथ्वी का वैद्युत विभव V = \(\frac{q}{\infty}\)= 0 (शून्य) होगा।

प्रश्न 67.
क्या कोई ऐसा चालक है जिसे असीमित आवेश दिया जा सके?
उत्तर :
हाँ, पृथ्वी।

प्रश्न 68.
एक आवेशित समान्तर प्लेट संधारित्र किसी पदार्थ, जिसका परावैद्युतांक 2 है, में पूर्ण रूप से डुबो , दिया जाता है। इस संधारित्र की प्लेटों के बीच वैद्युत क्षेत्र की तीव्रता में क्या परिवर्तन होगा? [2001]
उत्तर :
सूत्र \(E=\frac{q}{K \varepsilon_{0} A}\) से, \(E \propto \frac{1}{K}\) अत: K= 2 रखने पर, वैद्युत क्षेत्र की तीव्रता आधी हो जाएगी।

प्रश्न 69.
धातु का परावैद्युतांक कितना होता है? स्पष्ट कीजिए।
उत्तर :
धातु का परावैद्युतांक अनन्त होता है; क्योंकि जब किसी धातु को वैद्युत क्षेत्र में रखते हैं तो धातु के भीतर वैद्युत क्षेत्र शून्य ही रहता है।

प्रश्न 70.
परावैद्युत सामर्थ्य से क्या अभिप्राय है? [2010, 13]
उत्तर :
परावैद्युत सामर्थ्य-किसी परावैद्युत पदार्थ के लिए वह महत्तम वैद्युत क्षेत्र जिसे वह बिना वैद्युत भंजन के सहन कर सकता है, परावैधत सामर्थ्य कहलाता है।

प्रश्न 71.
भंजक विभवान्तर से क्या तात्पर्य है? [2010, 13, 18]
उत्तर :
भंजक विभवान्तर—किसी संधारित्र की प्लेटों के बीच वह अधिकतम विभवान्तर जिस पर प्लेटों के बीच रखे परावैद्युत पदार्थ में वैद्युत भंजन होने लगता है, भंजक विभवान्तर कहलाता है।

प्रश्न 72.
एक आवेशित संधारित्र एवं एक वैद्युत सेल में मूल अन्तर क्या है?
उत्तर :
वैद्युत सेल से ली गई धारा नियत होती है जबकि आवेशित संधारित्र से ली गई धारा क्षीण होती जाती है।

प्रश्न 73.
किसी समान्तर प्लेट संधारित्र की धारिता पर, उसमें परावैद्युत पदार्थ भरने से क्या प्रभाव पड़ता है? [2004]
उत्तर :
ऐसा करने से संधारित्र की धारिता बढ़ जाएगी।

प्रश्न 74.
ऊर्जा घनत्व से क्या तात्पर्य है? अथवा आवेशित समान्तर पट्ट संधारित्र की प्लेटों के बीच वैद्युत क्षेत्र में ऊर्जा घनत्व का सूत्र लिखिए। [2013]
उत्तर :
ऊर्जा घनत्व-संधारित्र के एकांक आयतन में संचित ऊर्जा को संधारित्र का ऊर्जा घनत्व कहते हैं। इसे ‘u’ से प्रदर्शित करते हैं।
ऊर्जा घनत्व \(u=\frac{1}{2} \varepsilon_{0} E^{2}\)
यहाँ E प्लेटों के बीच वैद्युत क्षेत्र की तीव्रता तथा ε₀ निर्वात की वैद्युतशीलता है।

स्थिरवैद्युत विभव तथा धारिता आंकिक प्रश्नोत्तर

प्रश्न 1.
दो बिन्दुओं के बीच विभवान्तर 50 वोल्ट है। एक बिन्दु से दूसरे बिन्दु तक 3 x 10^-5 कूलॉम आवेश को ले जाने पर कितना कार्य करना होगा? [2018]
हल :
दिया है, विभवान्तर V = 50 वोल्ट, q= 3 x 10^-5 कूलॉम, W = ?
किया गया कार्य (W)= qV
= 3 x 10^-5 x 50
= 1.5 x 10^-3 जूल।

प्रश्न 2.
किसी α-कण को 10 वोल्ट के विभवान्तर से ले जाया जाता है। किए गए कार्य की गणना जूल में कीजिए। [2005]
हल :
दिया है, α= a-कण = 3.2 x 10^-19 कूलॉम, V = 10 वोल्ट, w = ?
किया गया कार्य W = q x V = 3.2 x 10^-19 x 10 = 3.2 x 10^-18 जूल।

प्रश्न 3.
5 कूलॉम वाले एक वैद्युत आवेश को एक वैद्युत क्षेत्र में एक बिन्दु से दूसरे बिन्दु तक ले जाने में 25 जूल ऊर्जा खर्च करनी पड़ती है। यदि पहले बिन्दु का विभव 10 वोल्ट हो तो दूसरे बिन्दु का विभव कितना होगा? [2010]
हल :
दिया है, q= 5 कूलॉम, W = 25 जूल, V_A = 10 वोल्ट, V_B = 0
सूत्र V_B – V_A = \(\frac{W}{q}\) से, V_B – 10 = \(\frac{25}{5}\); अत: दूसरे बिन्दु का विभव VB = 15 वोल्ट।

प्रश्न 4.
+ 40 μC के दो आवेश परस्पर 0.4 मीटर की दूरी पर स्थित हैं। इनके मध्य-बिन्दु पर विभव की गणना कीजिए। माध्यम का परावैद्युतांक 2 है।
[2004, 14]
हल :
दिया है, q₁ = q₂ = q = + 40 μC = 40 x 10^-6C, K = 2
मध्य-बिन्दु की प्रत्येक आवेश से दूरी r = 0.4/2 = 0.2 मीटर, V = ?
एक आवेश के कारण मध्य-बिन्दु पर वैद्युत विभव

प्रश्न 5.
दो बिन्दु आवेश +q तथा -2q एक-दूसरे से d दूरी पर स्थित हैं। दोनों आवेशों को मिलाने वाली रेखा पर ऐसे बिन्दुओं की स्थिति ज्ञात कीजिए, जहाँ पर आवेशों के इस निकाय के कारण विभव शून्य हो। [2017]
उत्तर :
माना बिन्दु आवेशों को मिलाने वाली रेखा पर +q से आवेश – 2q की ओर x दूरी पर वैद्युत विभव शून्य है। विभव के सूत्र

इस प्रकार आवेशों को मिलाने वाली रेखा पर +q से -2q की ओर, +q से d 13 दूरी पर वैद्युत विभव शून्य है। यदि आवेशों को मिलाने वाले रेखा पर आवेशों के बाहर x दूरी पर वैद्युत विभव शून्य है, तो

CLASSROOM EXPERIENCE

प्रश्न 6.
संलग्न चित्र 2.44 के अनुसार आवेशों को मिलाने वाली रेखा के किन बिन्दुओं पर (i) वैद्युत विभव तथा (ii) वैद्युत क्षेत्र शून्य होंगे? [2005]

(i) Step 1. माना + q आवेश से x सेमी दूरी पर वैद्युत विभव शून्य होगा।
सूत्र V = 9 x 10⁹ q/r से,

Step 2.

अतः = 25 सेमी की दूरी पर दोनों आवेशों के बीच में वैद्युत विभव शून्य होगा।

(ii) Step 3 माना +q आवेश से बायीं ओर × सेमी पर वैद्युत क्षेत्र शून्य होगा; अत:
सूत्र E = 9 × 10⁹ q/r² से,

Step 4.

अत: +q आवेश से बाहर की ओर x = 136.6 सेमी की दूरी पर वैद्युत क्षेत्र शून्य होगा।

प्रश्न 7.
एक 9μC के बिन्दु आवेश से 5 मीटर की दूरी पर – 2μC का दूसरा बिन्दु आवेश वायु में रखा हुआ है। इन दोनों आवेशों से 3 मीटर की दूरी पर स्थित बिन्दु पर वैद्युत विभव के मान की गणना कीजिए। (दिया है, 1/4πε^o = 9 × 10⁹ न्यूटन-मीटर/कूलॉम²) [2000]
हल :
दिया है, q₁ = 9 μC = 9 × 10^-6 कूलॉम, r₁ = 3 मीटर,
q₂ = -2μC = – 2 x 10^-6 कूलॉम, r₂ = 3 मीटर, V = ?

चित्र-2.45 से दोनों आवेशों से समान दूरी r₁ = r₂ = 3 मीटर पर वैद्युत विभव

प्रश्न 8.
एक वर्ग की प्रत्येक भुजा 60 सेमी लम्बी है। इसके कोनों पर क्रमशः -2, 3, -4 तथा 5 माइक्रोकूलॉम के आवेश रखे हैं। वर्ग के केन्द्र पर विभव ज्ञात कीजिए।
हल :
दिया है, q₁ = -2μ0 = – 2 × 10^-6 कूलॉम, q₂ = 3μC = 3 × 10^-6 कूलॉम,
q₃ = – 4μC = – 4 × 10^-6 कूलॉम, q₄ = 5μC = 5 × 10^-6 कूलॉम

प्रश्न 9.
चार बिन्दु आवेश 1.0 मीटर लम्बाई की भुजा वाले वर्ग ABCD के कोनों पर चित्र-2.47 के अनुसार रखे हैं। यदि वर्ग के विकर्णों के कटान बिन्दु O तथा भुजा BC का मध्य-बिन्दु E हो तो ज्ञात कीजिए –
(i) बिन्दु O पर वैद्युत क्षेत्र की तीव्रता का मान तथा दिशा,
(ii) बिन्दु O पर वैद्युत विभव का मान,
(iii) बिन्दु आवेश 1.0 C को बिन्दु O से बिन्दु E तक ले जाने के लिए आवश्यक ऊर्जा।
(दिया है, 1/4πε^o = 9 × 10⁹ न्यूटन-मीटर²/कूलॉम²) .

हल :

EXTRA SHOTS

• वैद्युत क्षेत्र की तीव्रता एक सदिश राशि है, अत: किसी बिन्दु पर अनेक बिन्दु आवेशों के कारण उत्पन्न परिणामी . वैद्युत क्षेत्र की तीव्रता, सभी आवेशों के कारण उत्पन्न वैद्युत क्षेत्र की तीव्रताओं के सदिश योग के बराबर होती है।
• वैद्युत विभव एक अदिश राशि है, अत: किसी बिन्दु पर परिणामी विभव, अनेक बिन्दु आवेशों के कारण उस
  बिन्दु पर उत्पन्न वैद्युत विभवों के बीजगणितीय योग के बराबर होता है।

बिन्दुओं A व C पर स्थित आवेशों के कारण बिन्दु O पर वैद्युत क्षेत्र की तीव्रता

इसी प्रकार बिन्दुओं B व D पर स्थित आवेशों के कारण बिन्दु O पर वैद्युत क्षेत्र की तीव्रता

अतः बिन्दु O पर परिणामी वैद्युत क्षेत्र की तीव्रता

(ii) चारों कोनों पर स्थित आवेशों के कारण बिन्दु O पर परिणामी वैद्युत विभव

परन्तु A0 = CO = BO = DO; अतः V₀ = 0 शून्य।

(iii) चारों कोनों पर स्थित आवेशों के कारण बिन्दु E पर परिणामी वैद्युत विभव

अत: बिन्दु O तथा बिन्दु E के बीच वैद्युत विभवान्तर ∆V = V₀ – V_E = 0 (शून्य)
अतः 1.0 कूलॉम आवेश को बिन्दु O से बिन्दु E तक ले जाने में किया गया कार्य
w= q × ∆V = 1.0 कूलॉम × 0 वोल्ट = 0 (शून्य)
अर्थात् 1.0 कूलॉम के आवेश को बिन्दु 0 से बिन्दु E तक ले जाने में किसी ऊर्जा की आवश्यकता नहीं होगी।

प्रश्न 10.
किसी बिन्दु P पर वैद्युत विभव दिया गया है –
V(x, y, 2) = 6x- 8xy² – 8y+ 6yz – 4z² मूलबिन्दु पर स्थित 2 कूलॉम बिन्दु आवेश पर वैद्युत बल की गणना कीजिए। [2007]
हल :
V(x, y, 2) = 6x – 8xy² – 8y + 6yz – 4z²

अत: 2 कूलॉम बिन्दु आवेश पर वैद्युत बल F = qE = 2 × 10 = 20 न्यूटन।

CLASSROOM EXPERIENCE

प्रश्न 11.
एक इलेक्ट्रॉन को 15 × 10³ वोल्ट विभवान्तर से त्वरित किया जाता है। इसकी ऊर्जा में वृद्धि जूल तथा इलेक्ट्रॉन-वोल्ट में ज्ञात कीजिए। यह कितनी चाल प्राप्त करेगा? (e = 1.6 × 10^-19 कूलॉम, m = 9.0 × 10^-31 किग्रा)
[2001, 14] ..
हल :
Step 1. सर्वप्रथम प्रश्न में दिए गए आँकड़े नोट कर लेते हैं।
दिया है, V = 15 × 10³ वोल्ट, q= e = 1.6 × 10^-19 कूलॉम, K = ?, y = ?
Step 2. V विभवान्तर से त्वरित इलेक्ट्रॉन की गतिज ऊर्जा वृद्धि
K = q × v = (1.6 × 10^-19) × (15 × 10³)= 2.4 × 10^-15 जूल।
Step 3. परन्तु 1.6 × 10^-19 जूल = 1 eV
∴ इलेक्ट्रॉन-वोल्ट में ऊर्जा वृद्धि K = \(\frac{2.4 \times 10^{-15}}{1.6 \times 10^{-19}}\) = 15 × 10³eV

Step 4.

प्रश्न 12.
एक समबाहु त्रिभुज के प्रत्येक कोने पर + 250 μC के आवेश वायु में रखे हैं। इस त्रिभुज के परिकेन्द्र पर जिसकी प्रत्येक कोने से दूरी 18 सेमी है, परिणामी वैद्युत विभव की गणना कीजिए।
हल :
दिया है, q= + 250 μC = + 250 × 10^-6 कूलॉम,
r = 18 सेमी = 18 × 10^-2 मीटर, V = ?
चित्र-2.48 से तीनों कोनों पर स्थित आवेशों के कारण त्रिभुज के परिकेन्द्र O पर वैद्युत विभव

प्रश्न 13.
एक तार को 10 सेमी त्रिज्या के वृत्त में मोड़कर उसे 250 μC आवेश दिया जाता है जो उस पर समान रूप से फैल जाता है। इसके केन्द्र पर वैद्युत क्षेत्र की तीव्रता तथा विभव ज्ञात कीजिए। –
हल :
दिया है, r = 10 सेमी = 10 × 10^-2 मीटर = 0.1 मीटर,
q= 250μC = 250 × 10^-6 कूलॉम, E = ?,V = ?
आवेश के वृत्त पर समान रूप से फैलने के कारण यह वृत्त एक सम विभव वृत्त होगा। चूँकि सम विभव के कारण वृत्त के भीतर प्रत्येक बिन्दु पर वैद्युत क्षेत्र शून्य होता है; अत: वृत्त के केन्द्र पर वैद्युत क्षेत्र की तीव्रता E = 0 (शून्य) होगी।
तथा वृत्त के केन्द्र पर वैद्युत विभव V = 9 × 10⁹\(\frac{q}{r}=\frac{9 \times 10^{9} \times 250 \times 10^{-6}}{0.1}\)
= 2.25 × 10⁷ वोल्ट। ,

प्रश्न 14.
+10μC तथा -10μC के दो बिन्दु आवेशों के बीच की दूरी 1 मीटर है। इनके मध्य-बिन्दु पर वैद्युत विभव ज्ञात कीजिए। [2004, 10]
हल :
दिया है, q₁ = + 10μC, q₂ = – 10μC, r = 1 मीटर, V = ?

अत: मध्य-बिन्दु पर परिणामी वैद्युत विभव V = V₁ + V₂ = 0

प्रश्न 15.
+5.0 × 10^-7 कूलॉम तथा – 5.0 × 10^-7 कूलॉम के दो बिन्दु आवेशों के बीच की दूरी 1.0 सेमी है। इन आवेशों से बने द्विध्रुव की अक्ष पर केन्द्र से 50 सेमी की दूरी पर स्थित बिन्दु पर वैद्युत विभव की गणना कीजिए। [2007]
हल :
दिया है, q= 5.0 × 10^-7 कूलॉम, 2l = 1.0 सेमी = 1.0 × 10^-2 मीटर,
r= 50 सेमी = 50 × 10^-2 मीटर, V= ?

प्रश्न 16.
दो समान्तर प्लेटें परस्पर 15 सेमी की दूरी पर हैं, उनके बीच 450 वोल्ट का विभवान्तर लगाने पर प्लेटों के बीच वैद्युत क्षेत्र की तीव्रता ज्ञात कीजिए। हल :
विभवान्तर V = 450 वोल्ट, दूरी d = 15 सेमी = 0.15 मीटर, E = ?
वैद्युत क्षेत्र की तीव्रता \(E=\frac{V}{d}=\frac{450}{0.15}=3000\) वोल्ट/मीटर।

प्रश्न 17.
एक वैद्युत क्षेत्र में किसी बिन्दु x पर विभव V = 5x² – 2x + 10 वोल्ट है जहाँ x मीटर में है। बिन्दु x= 1 मीटर पर वैद्युत क्षेत्र की तीव्रता तथा इसकी दिशा बताइए।
हल :
V = (5x² – 2x + 10) वोल्ट
E =- \(\frac{d V}{d x}\) = –\(\frac{d}{d x}\) (5x² – 2x + 10)
= – [5 × 2x – 2 × 1+ 0] = – 10x + 2 वोल्ट/मीटर
x = 1 मीटर रखने पर,
E = – 10 × 1+ 2 = – 8 वोल्ट/मीटर।
ऋण चिह्न प्रदर्शित करता है कि वैद्युत क्षेत्र ऋण X-अक्ष की ओर दिष्ट है।

प्रश्न 18.
U²³⁸ नाभिक में दो प्रोटॉन 6.0 × 10^-15 मीटर की दूरी पर हैं। उनकी पारस्परिक वैद्युत स्थितिज ऊर्जा की गणना कीजिए।
हल :
दिया है, r = 6.0 × 10^-15 मीटर, q₁ = q₂ = 1.6 × 10^-19 जूल, U = ?

= 3:84 × 10^-14 जूल।

प्रश्न 19.
6.0 × 10^-8 कूलॉम का एक बिन्दु आवेश निर्देशांक मूलबिन्दु पर स्थित है। एक इलेक्ट्रॉन को बिन्दु x = 3 मीटर से x= 6 मीटर तक ले जाने में कितना कार्य करना होगा?
हल :
मूलबिन्दु पर स्थित आवेश के कारण x = 3 मीटर पर,

प्रश्न 20.
हाइड्रोजन परमाणु में इलेक्ट्रॉन व प्रोटॉन के बीच की दूरी 0.5A है। इनकी पारस्परिक वैद्युत स्थितिज ऊर्जा क्या होगी?
हल :
दिया है, q₁ = +1.6 × 10^-19 कूलॉम, q₂ = -1.6 × 10^-19 कूलॉम,
r = 0.5 Å = 5 × 10^-11 मीटर, U = ?

प्रश्न 21.
+ 1 × 10^-6 कूलॉम और – 1 × 10^-6 कूलॉम के दो बिन्दु आवेश परस्पर 2.0 सेमी की दूरी पर स्थित हैं। यह वैद्युत द्विध्रुव 1 × 10⁵ वोल्ट/मीटर के एक समान वैद्युत क्षेत्र में स्थित है। द्विधुव की स्थायी सन्तुलन की स्थिति में स्थितिज ऊर्जा ज्ञात कीजिए। [2012, 18]
हल :
दिया है, q = 1 × 10^-6 कूलॉम, 2l = 2.0 सेमी = 2.0 × 10^-2 मीटर
E = 1 × 10⁵ वोल्ट/मीटर
वैद्युत क्षेत्र में वैद्युत द्विध्रुव की स्थितिज ऊर्जा U = – pE cos θ
स्थायी सन्तुलन की अवस्था में, θ = 0°
U = – pE = – (q × 2l) E –
= -1 × 10^-6 × 2 × 10^-2 × 1 × 10⁵
= – 2 × 10^-3 जूल।

प्रश्न 22.
एक गेंद जिसका द्रव्यमान 1 ग्राम है तथा जिस पर 10^-8C आवेश है, एक बिन्दु से दूसरे बिन्दु की ओर चलती है। यदि पहले बिन्दु का विभव 600 वोल्ट हो तथा दूसरे बिन्दु का विभव शून्य हो तथा दूसरे बिन्दु पर गेंद का वेग 20 सेमी/सेकण्ड हो तो पहले बिन्दु पर गेंद का वेग क्या होगा? [2009]
हल :
दिया है, m = 1 ग्राम = 10^-3 किग्रा, q = 10^-8C, V₁ = 600 वोल्ट, V₂ = 0,
V₂ = 20 सेमी/सेकण्ड = 0.2 मीटर/सेकण्ड, V₁ = ?
गतिज ऊर्जा में वृद्धि = किया गया कार्य

प्रश्न 23.
जब एक आवेशित कण को 100 वोल्ट विभव के बिन्दु से 200 वोल्ट विभव के बिन्दु तक ले जाया जाता है तो इसकी गतिज ऊर्जा 10 जूल कम हो जाती है। कण पर आवेश की गणना कीजिए।
हल :
दिया है, विभवान्तर V = (200-100) = 100 वोल्ट, K = 10 जूल, q= ?
सूत्र गतिज ऊर्जा K = qV से, कण पर आवेश \(q=\frac{K}{V}=\frac{10}{100}=0.1\) कूलॉम।
चूँकि उच्च विभव की ओर जाने में ऊर्जा में कमी होती है; अतः कण पर आवेश धनात्मक होगा।

प्रश्न 24.
एक प्रोटॉन 500 वोल्ट के विभवान्तर से त्वरित किया जाता है। प्रोटॉन का वेग ज्ञात कीजिए। [2018]
हल :
दिया है, V = 500 वोल्ट
प्रोटॉन का द्रव्यमान (m) = 1.66 × 10^-24 kg, q = 1.6 × 10^-19 कूलॉम

प्रश्न 25.
+ q, + 2q तथा + 4q आवेशों को a मीटर भुजा वाले एक समबाहु त्रिभुज के कोणों पर रखने में कितना कार्य करना होगा? निकाय की वैद्युत स्थितिज ऊर्जा क्या होगी?
हल :
+q व + 2q के निकाय की वैद्युत स्थितिज ऊर्जा

प्रश्न 26.
दो समान आवेश +q, 2 a दूरी पर रखे गए हैं। एक तीसरा आवेश – 2q इन दोनों के मध्य बिन्दु पर रखा जाता है। निकाय की स्थितिज ऊर्जा की गणना कीजिए। [2013]
हल :
माना q₁ = q₂ = q, 4₃ = – 2q

निकाय की स्थितिज ऊर्जा

प्रश्न 27.
दो समान आवेशों में प्रत्येक 2.0 × 10^-7 कूलॉम है। दोनों आवेश परस्पर 20 सेमी की दूरी पर हैं। उसी परिमाण का एक तीसरा आवेश दोनों आवेशों के ठीक बीच में स्थित है। इसे दोनों आवेशों से 20 सेमी दूर एक बिन्दु तक ले जाया जाता है। इस प्रक्रिया में वैद्युत क्षेत्र द्वारा कितना कार्य किया जाता है?
हल :
चित्र-2.50 से A व B पर स्थित बिन्दु आवेशों के कारण इनके मध्य-बिन्दु O पर परिणामी वैद्युत विभव

P एक ऐसा बिन्दु है जो दोनों आवेशों से समान दूरी 20 सेमी पर है; अत: A तथा B आवेशों के कारण बिन्दु P पर परिणामी वैद्युत विभव


एक अन्य समान परिमाण के आवेश को बिन्दु O से बिन्दु P तक ले जाने में वैद्युत क्षेत्र के विरुद्ध किया गया कार्य
W = q × (V_p  – V_o )
= 2.0 × 10^-7 × (18 – 36) × 10³ जूल
= -2.0 × 18 x 10^-4
=-3.6 × 10^-3 जूल।
ऋण चिह्न प्रदर्शित करता है कि कार्य वैद्युत क्षेत्र द्वारा किया गया है। अतः
अभीष्ट कार्य W = 3.6 × 10^-3 जूल।

प्रश्न 28.
दो इलेक्ट्रॉन 10⁶ मीटर/सेकण्ड के वेग से एक-दूसरे की ओर छोड़े गए। वे अधिक-से-अधिक एक-दूसरे के कितने समीप आ सकते हैं?
हल :
दिया है, q = 1.6 × 10^-19 कूलॉम, v = 10⁶ मीटर/सेकण्ड, m = 9.0 × 10^-31 किग्रा, r = ?
दो इलेक्ट्रॉनों की कुल गतिज ऊर्जा = अधिकतम समीप की स्थितिज ऊर्जा

प्रश्न 29.
विभवमापी के 10 मीटर लम्बे तार के सिरों के बीच 1.0 वोल्ट का विभवान्तर लगाया जाता है। तार में विभव प्रवणता तथा वैद्युत क्षेत्र का मान लिखिए।।
[2003]
हल :
दिया है, Δx= 10 मीटर, ΔV = 1.0 वोल्ट, E = ? ..
चूँकि विभव प्रवणता = वैद्युत क्षेत्र = ΔV/Δ x = 1.0/10 = 0.1वोल्ट/मीटर।

प्रश्न 30.
धातु की दो प्लेटें एक-दूसरे से 5 सेमी की दूरी पर समान्तर स्थित हैं। इनके बीच 200 वोल्ट की एक बैटरी जुड़ी है। गणना कीजिए-(i) इन प्लेटों के बीच गुजरने वाले -कण पर कार्यरत बल तथा (ii) एक प्लेट से दूसरी प्लेट तक पहुँचने में α-कण की गतिज ऊर्जा में वृद्धि। [2007]
हल :
दिया है, d = 5 सेमी = 0.05 मीटर, V = 200 वोल्ट
α-कण का आवेश q= + 2e = 2 × 1.6 × 10^-19 कूलॉम, F = ?, ΔK = ?

प्रश्न 31.
10⁷ मीटर/सेकण्ड की चाल से गतिमान इलेक्ट्रॉन की गतिज ऊर्जा, इलेक्ट्रॉन-वोल्ट (eV) में ज्ञात . कीजिए। (m = 9.1 × 10^-31 किग्रा)।[2004]
हल :
दिया है, v = 10⁷ मीटर/सेकण्ड, m = 9.1 × 10^-31 किग्रा, K = ?

प्रश्न 32.
एक इलेक्ट्रॉन 500 वोल्ट के विभवान्तर पर त्वरित किया जाता है। उसकी गतिज ऊर्जा की गणना कीजिए। वह कितनी चाल प्राप्त कर लेगा?
हल :
दिया है, (q) = 1.6 × 10^-19 कूलॉम, V = 500 वोल्ट, K = ?, v = ?
गतिज ऊर्जा K = V_q = 500 × 1.6 × 10^-19 जूल = 8.0 × 10^-17 जूल।

प्रश्न 33.
एक इलेक्ट्रॉन धारा में इलेक्ट्रॉन का वेग 2.0 × 10⁷ मीटर/सेकण्ड, 1.6 × 10³ वोल्ट/मीटर के वैद्युत क्षेत्र के लम्बवत् दिशा में 10 सेमी चलने में 3.4 मिमी विक्षेपित हो जाती है। इलेक्ट्रॉन का विशिष्ट आवेश (e/m) ज्ञात कीजिए। [2013]
हल :
दिया है, v = 2.0 × 10⁷ मीटर/सेकण्ड, E = 1.6 × 10³ वोल्ट/मीटर, e / m = ?
x = 10 सेमी = 10 × 10^-2 मीटर, y = 3.4 मिमी = 3.4 × 10^-3मीटर

प्रश्न 34.
आसुत जल की 64 छोटी बूंदें, प्रत्येक की त्रिज्या 0.1 मिमी तथा आवेश (2/3) × 10^-12 कूलॉम है, मिलकर एक बड़ी बूंद बनाती हैं। बड़ी बूंद पर विभव ज्ञात कीजिए। [2007]
हल :
दिया है, r = 0.1 मिमी = 10^-4 मीटर, q= (2/3) × 10^-12 कूलॉम, V= ?
एक बड़ी बूंद का आयतन = 64 × छोटी बूंदों का आयतन

प्रश्न 35.
समान रूप से आवेशित तथा समान त्रिज्या वाली जल की 64 छोटी बूंदें मिलकर एक बड़ी बूंद बनाती हैं। बड़ी बूंद के लिए-(i) त्रिज्या, (ii) विभव तथा (iii) स्थितिज ऊर्जा के मान एक छोटी बूँद की तुलना में कितने-कितने होंगे?.
[2005]
हल :
माना छोटी बूंद की त्रिज्या r तथा बड़ी बूंद की त्रिज्या R है।
(i) एक बड़ी बूंद का आयतन = 64 × छोटी बूंदों का आयतन

(ii)

(iii)

प्रश्न 36.
एक संधारित्र को 1000 वोल्ट से आवेशित करने पर वह 2 माइक्रोकूलॉम आवेश ग्रहण करता है। संधारित्र की धारिता ज्ञात कीजिए।
हल :
दिया है, V = 1000 वोल्ट, q= 2 माइक्रोकूलॉम = 2 × 10^-6 कूलॉम, C = ?

प्रश्न 37.
25 μF धारिता के संधारित्र की प्लेटों के बीच 250 वोल्ट का विभवान्तर लगाने से संधारित्र प्लेटों पर कितना आवेश एकत्रित होगा?
हल :
दिया है, C = 25 μF = 25 × 10^-6 फैरड़, V = 250 वोल्ट, q = ?
प्लेटों पर आवेश q= CV = 25 × 10^-6 × 250 = 6250 × 10^-6 कूलॉम ।
= 6.250 × 10^-3 कूलॉम।
अत: संधारित्र की पहली प्लेट पर + 6.250 × 10^-3 कूलॉम तथा दूसरी प्लेट पर -6.250 × 10^-3 कूलॉम आवेश होगा।

प्रश्न 38.
एक धातु के गोले को, जिसकी त्रिज्या 1 सेमी है, 1 कूलॉम का आवेश देने पर उसका विभव कितना हो जाएगा? [2001]
हल :
दिया है, q= 1 कूलॉम, R= 1 सेमी = 10^-2 मीटर, V = ?

प्रश्न 39.
पृथ्वी को 1.28 × 10⁴ किमी व्यास का गोलाकार चालक मानकर उसकी वैद्युत धारिता की गणना कीजिए। [2007]
हल :
दिया है, = 6.4 × 10³ किमी = 6.4 × 10⁶ मीटर, C = ?
गोलाकार चालक की धारिता C = 4 πε^oR = \(\frac{1}{9 \times 10^{9}}\) × 6.4 × 10⁶
= 711 × 10^-6 फैरड = 711μF.

प्रश्न 40.
0.9 मीटर त्रिज्या के एक धनावेशित गोले का विभव 960 वोल्ट है। गोले पर कितने इलेक्ट्रॉनों की कमी है?
हल :
दिया है, R= 0.9 मीटर, V = 960 वोल्ट, n= ? . माना
गोले पर n इलेक्ट्रॉनों की कमी है।
गोले की धारिता C = 4 πε_o R; अत: गोले पर आवेश q = CV = πε^oRV
परन्तु q= ne अत: ne = 4 πε_o RV

= 6.0 × 10¹¹ इलेक्ट्रॉनों की कमी।

प्रश्न 41.
धातु के दो गोलों के व्यास 12 सेमी तथा 8 सेमी हैं। इन्हें समान विभव तक आवेशित किया गया है। इन पर आवेश के पृष्ठ घनत्वों का अनुपात बताइए।
[2012]
हल :

प्रश्न 42.
धातु के दो आवेशित गोलों की त्रिज्याएँ 5 सेमी तथा 10 सेमी हैं। दोनों पर अलग-अलग 75 μC का आवेश है। किसी चालक तार द्वारा दोनों गोलों को जोड़ दिया जाता है। गणना कीजिए- (i) जोड़ने के पश्चात् गोलों का उभयनिष्ठ विभव, (ii) प्रत्येक गोले पर आवेश की मात्रा, (iii) तार में से होकर स्थानान्तरित आवेश की मात्रा तथा (iv) जोड़ने के बाद ऊर्जा में ह्रास (क्षय)। [2004, 05]
हल :
दिया है, R₁ = 5 सेमी = 5 × 10^-2 मीटर, R₂ = 10 सेमी = 10 × 10^-2 मीटर,q₁ = q₂ = 75 μC = 75 × 10^-6 कूलॉम


(i) दोनों गोलों को जोड़ने पर उभयनिष्ठ विभव

(ii) पहले गोले पर नया आवेश q’₁ = C₁V = \(\frac{5}{9}\) × 10^-11 × 9.0 × 10⁶ = 50 μC.
दूसरे गोले पर नया आवेश q’₂ = C₂V = \(\frac{10}{9}\) × 10^-11 × 9.0 × 10⁶ = 100 μC.

(iii) तार में होकर स्थानान्तरित आवेश की मात्रा = 75 – 50 = 25 μC छोटे गोले से।
(iv)

प्रश्न 43.
एक समान्तर प्लेट संधारित्र की प्रत्येक प्लेट का क्षेत्रफल 100 सेमी² है तथा दोनों प्लेटों के बीच की दूरी 0.05 सेमी है। इनके बीच एक परावैद्युत पदार्थ भर देने पर संधारित्र की धारिता 3.54 × 10¹⁰ फैरड हो । जाती है। पंदार्थ के परावैद्युतांक की गणना कीजिए।
हल :
दिया है, A = 100 सेमी ² = 1 × 10^-2 मीटर2, d = 0.05 सेमी = 5 × 10^-4 मीटर, C = 3.54 × 10^-10 फैरड, K = ?

प्रश्न 44.
एक वायु संधारित्र की धारिता 2.0μF है। यदि इसकी प्लेटों के बीच कोई अन्य माध्यम रखने पर धारिता 12 μF हो जाए तो माध्यम के परावैद्युतांक की गणना कीजिए।
हल :
दिया है, C_o = 2.0 μr, C = 12 μF, K = ?
अत: माध्यम का परावैद्युतांक K = \(\frac{C}{C_{0}}=\frac{12}{2}\) = 6

प्रश्न 45.
एक समान्तर प्लेट संधारित्र को 500 वोल्ट तक आवेशित किया जाता है, अब इसकी प्लेटों के बीच की . . दूरी को घटाकर आधा कर दिया जाता है। संधारित्र पर नए विभवान्तर की गणना कीजिए।
हल :
दिया है, V₁ = 500 वोल्ट, d₁ = d, d₂ = d/2, V₂ = ?

प्रश्न 46.
एक समान्तर प्लेट संधारित्र की प्लेटों का व्यास 8 सेमी है तथा उसमें परावैद्युत के रूप में वायु है। यदि इस संधारित्र की धारिता 100 सेमी त्रिज्या वाले गोले की धारिता के समान हो तो इसकी प्लेटों के बीच की दूरी ज्ञात कीजिए। [2010, 14]
हल :
दिया है, r = 4 सेमी = 4 × 10^-2 मीटर, R = 100 सेमी = 1 मीटर, d = ?
प्लेट का क्षेत्रफल A = Tr² = n × (4 × 10^-2)² = 16 n × 10^-4 मीटर²
समान्तर प्लेटसंधारित्र की धारिता C = Aε_o /d
तथा गोले की धारिता C = 4πε_o R

प्रश्न 47.
एक समान्तर प्लेट संधारित्र की प्लेटों के बीच की दूरी 1.0 सेमी तथा प्लेट क्षेत्रफल 0.01 मीटर² है। इसको 150 वोल्ट विभवान्तर से आवेशित किया गया है। आवेशन बैटरी को हटाकर संधारित्र की प्लेटों के बीच में 7 परावैद्युत स्थिरांक का एक गुटका रख दिया जाता है। परावैद्युत माध्यम में वैद्युत क्षेत्र की तीव्रता की गणना कीजिए।
[2007]
हल :
दिया है, V₀ = 150 वोल्ट, d = 1.0 सेमी = 1.0 × 10^-2 मीटर, A = 0.01 मीटर², K = 7, E = ?
चूँकि बैटरी हटा ली गई है; अतः आवेश नियत रहेगा।
अर्थात् q= C₀V₀ = CV अथवा C₀ V₀ = KC₀ V
[∵ C = KC₀]
अत: नया विभवान्तर V=\frac{V_{0}}{K}=\frac{150}{7} = 21.43 वोल्ट।
परावैद्युत माध्यम में वैद्युत क्षेत्र की तीव्रता
E=\frac{V}{d}=\frac{21.43}{10^{-2}}
= 2.143 × 10³ वोल्ट/मीटर।

प्रश्न 48.
एक समान्तर प्लेट संधारित्र की प्रत्येक प्लेट का क्षेत्रफल 3.0 × 10^-2 मीटर² है तथा प्लेटों के बीच की दूरी 0.6 मिमी है। इसे 1000 वोल्ट विभवान्तर तक आवेशित किया जाता है। इसमें कितनी ऊर्जा संचित होगी? [2009]]
हल :
दिया है, A = 3.0 × 10^-2 मीटर², d = 0.6 मिमी = 6 × 10^-4 मीटर, V_o = 1000 वोल्ट, U = ?

प्रश्न 49.
एक समान्तर प्लेट संधारित्र की प्रत्येक प्लेट का क्षेत्रफल 40 सेमी² है तथा दोनों प्लेटों के बीच वैद्युत क्षेत्र की तीव्रता 50 न्यूटन/कूलॉम है। प्रत्येक प्लेट पर कितना आवेश है? [2009, 14]
हल :
दिया है, A= 40 सेमी² = 40 × 10^-4 मीटर², E = 50 न्यूटन/कूलॉम, q= ?
सूत्र E = q/ε_oA से, q= E× ε_oA .
अतः प्रत्येक प्लेट पर आवेश q= 50 × (8.85 × 10^-12) × 40 × 10^-4
= 1.77 × 10^-12 कूलॉम।।

प्रश्न 50.
एक समान्तर प्लेट वायु संधारित्र की धारिता 2 μF है। जब इसकी प्लेटों के बीच, प्लेटों के बीच की दूरी की तीन-चौथाई मोटाई की K परावैद्युतांक की प्लेट रखी जाती है, तब संधारित्र की धारिता 4 μF हो जाती है। K का मान ज्ञात कीजिए जहाँ प्लेटों का तथा परावैद्युत प्लेट का क्षेत्रफल समान है। [2014]
हल :
दिया है, C_o = 2μF, C = 4 μF, \(t=\frac{3}{4} d\)
समान्तर प्लेट वायु संधारित्र की धारिता \(C_{0}=\frac{A \varepsilon_{0}}{d}\)
t मोटाई तथा K परावैद्युतांक की प्लेट संधारित्र के बीच रखने पर संधारित्र की धारिता

प्रश्न 51.
100μF समान्तर प्लेट संधारित्र 400 वोल्ट तक आवेशित है। यदि इसकी प्लेटों के बीच की दूरी आधी कर दी जाए तो प्लेटों के बीच नया विभवान्तर क्या होगा तथा इसकी संचित ऊर्जा में क्या परिवर्तन होगा? [2004, 06, 14]
हल :
दिया है, C = 100 μF = 100 × 10^-6 F = 10^-4F, V₁= 400 वोल्ट, d₁=d, d₂ = d/2, V₂= ? ∆U = ?

प्रश्न 52.
एक समान्तर प्लेट संधारित्र की प्रत्येक प्लेट का क्षेत्रफल 100 सेमी है तथा दोनों प्लेटों के बीच अन्तराल 0.025 सेमी है। यदि संधारित्र को 3.54 μC आवेश दिया जाए, तो इसकी प्लेटों के बीच विभवान्तर कितना होगा? यदि प्लेटों के बीच अन्तराल बढ़ाकर 0.05 सेमी कर दिया जाए तो नया विभवान्तर कितना होगा? [2018]
हल :
A = 100 सेमी² = 100 × 10^-4 मीटर², d = 0.025 सेमी = 2.5 × 10^-4 मीटर
q = 3.54 μC= 3.54 × 10^-6C, V= ?

प्रश्न 53.
एक समान्तर प्लेट संधारित्र 300pF है तथा इसकी दोनों प्लेटों के बीच 1 मिमी की दूरी है। प्लेटों के बीच वायु है—(i) यदि संधारित्र को 1200 वोल्ट तक आवेशित किया जाए तो इसकी ऊर्जा क्या होगी? (ii) यदि प्लेटों के बीच की दूरी दोगुनी कर दी जाए तो प्लेटों के बीच विभवान्तर कितना हो जाएगा? [2007]]
हल :
दिया है, C = 300pF = 300 × 10^-12F, d = 1 मिमी = 10^-3 मीटर,V = 1200 वोल्ट,U = ?,V = ?

प्रश्न 54.
20 μF के एक संधारित्र को, जिसे 500 वोल्ट तक आवेशित किया गया है, एक अन्य 10 uF के संधारित्र के साथ, जिसे 200 वोल्ट तक आवेशित किया गया है, समान्तर क्रम में जोड़ दिया जाता है। उनका उभयनिष्ठ विभव ज्ञात कीजिए।
हल :
दिया है, C₁= 20 μF, V₁ = 500 वोल्ट, C₂ = 10 μr, V₂ = 200 वोल्ट, V = ?

प्रश्न 55.
4 तथा 2 माइक्रोफैरड धारिता के दो संधारित्र 6 वोल्ट की बैटरी के समान्तर क्रम में जोड़ दिए गए हैं—
(i) प्रत्येक संधारित्र की प्लेटों के बीच विभवान्तर बताइए तथा
(ii) प्रत्येक संधारित्र पर आवेश ज्ञात कीजिए।
हल :
(i) चूँकि संधारित्र बैटरी के समान्तर क्रम में लगे हैं; अतः प्रत्येक संधारित्र की प्लेटों के बीच विभवान्तर बैटरी के विद्युत वाहक बल अर्थात् 6 वोल्ट के बराबर होगा।
(ii) 4μF धारिता वाले संधारित्र पर आवेश q₁ = 4 μF × 6V = 24 μC.
2 μF धारिता वाले संधारित्र पर आवेश q₂ = 2 μF × 6V = 12 μC.

प्रश्न 56.
दो संधारित्र, जिनकी धारिताएँ 4 μF तथा 12 μF हैं, 120 वोल्ट की लाइन से श्रेणीक्रम में जुड़े हैं। संयोजन की प्रभावी धारिता तथा प्रत्येक संधारित्र के विभवान्तर व आवेश की गणना कीजिए। ..
हल :
दिया है, C₁ = 4 uF, C₂ = 12 uF, V = 120 वोल्ट, C = ?, q= ?, V₁ = ?, V₂ = ?

प्रश्न 57.
तीन समरूप संधारित्र C₁,C₂तथा C₃ जिनकी प्रत्येक की धारिता 6 μF है, 12 वोल्ट की बैटरी से जुड़े हैं जो कि चित्र में प्रदर्शित है।

ज्ञात कीजिए-(i) प्रत्येक संधारित्र का आवेश,
(ii) परिपथ की समतुल्य धारिता। – [2018]
हल :
(i) संधारित्र C₁ व C₂ परस्पर श्रेणीक्रम में हैं। अत: इनकी तुल्य धारिता,

(ii) संधारित्र C’ व C₃ परस्पर समान्तर क्रम में हैं।
अतः इनकी समतुल्य धारिता C = C’ + C₃ = 3+ 6 = 9μF

प्रश्न 58.
दो संधारित्र जिनकी धारिताएँ क्रमशः 2 व 3 माइक्रोफैरड हैं, श्रेणीक्रम में लगे हैं। पहले संधारित्र की बाहरी प्लेट 1000 वोल्ट पर है और दूसरे संधारित्र की बाहरी प्लेट पृथ्वी से जुड़ी है। प्रत्येक संधारित्र की भीतरी प्लेट का विभव तथा आवेश ज्ञात कीजिए।
हल :

इस संधारित्र की भीतरी प्लेट 1000 वोल्ट पर है; अत: बाहरी प्लेट (1000 – 600)
= 400 वोल्ट पर होगी।
∵ दूसरे संधारित्र की भीतरी प्लेट पहले संधारित्र की बाहरी प्लेट से जुड़ी है। अत: दूसरे संधारित्र की भीतरी प्लेट भी 400 वोल्ट पर होगी।

प्रश्न 59.
20 वोल्ट की एक बैटरी को एक वायु संधारित्र से जोड़ने पर संधारित्र पर 30 µC आवेश आ जाता है। यदि प्लेटों के बीच तेल भर दिया जाए तो प्लेटों पर 75µC आवेश आ जाता है-(i) तेल का परावैद्युतांक तथा (ii) तेल से भरे संधारित्र में संचित ऊर्जा की गणना कीजिए।
हल :
(i) दिया है, V = 20 वोल्ट तथा q= 30 µC

(ii)

प्रश्न 60.
किसी वायु संधारित्र को 5 वोल्ट के स्रोत से आवेशित करके स्रोत से अलग कर दिया गया। अब संधारित्र की प्लेटों के बीच एक परावैद्युत भर दिया गया जिसका परावैद्युतांक 2 है। यदि वायु संधारित्र की धारिता 10 uF हो तो परावैद्युत पदार्थ भरने के पश्चात् इस संधारित्र में संचित ऊर्जा की गणना कीजिए।
[2006]
हल :
दिया है, V_o = 5 वोल्ट, C_o = 10 uF, K = 2, U = ?

प्रश्न 61.
एक समान्तर प्लेट संधारित्र की धारिता 50 पिकोफैरड व प्लेटों के बीच की दूरी 4 मिमी है। इसे बैटरी द्वारा 200 वोल्ट तक आवेशित करके बैटरी को हटा लिया जाता है। फिर प्लेटों के बीच 2 मिमी मोटी परावैद्युत की पट्टी (K = 4) रखी जाती है। ज्ञात कीजिए
(i) प्रत्येक प्लेट पर अन्तिम आवेश, (ii) प्लेटों के बीच अन्तिम विभवान्तर, (iii) ऊर्जा-हानि। [2018]
हल :
दिया है, C = 50 पिकोफैरड = 50 × 10^-12 फैरड, d = 4 मिमी = 4 × 10^-3 मीटर,
V= 200 वोल्ट, t = 2 मिमी = 2 × 10^-3 मीटर, K = 4
(i) संधारित्र को आवेशित कर बैटरी हटा ली गई है; अतः प्लेटों पर प्रारिम्भक आवेश
= प्लेटों पर अन्तिम आवेश
q= CV = 50 × 10^-12 × 200 कूलॉम
= 1 × 10^-8 कूलॉम।
(ii)

(iii)

प्रश्न 62.
समान धारिता के चार संधारित्र समान्तर क्रम में जुड़े हैं। जब इन्हें 1.5 वोल्ट के सेल से जोड़ते हैं तो प्रत्येक पर 1.5µC आवेश संचित हो जाता है। यदि इन्हें श्रेणीक्रम में जोड़कर उसी सेल से आवेशित किया जाए तब उन संधारित्रों पर कितना आवेश संचित होगा? [2009, 16]]
हल :
दिया है, V = 1.5 वोल्ट, q= 1.5 µC, Q= ?
प्रत्येक संधारित्र की धारिता \(C=\frac{q}{V}=\frac{1.5}{1.5}\)= 1 µF
श्रेणीक्रम में जोड़ने पर तुल्य धारिता C₁ = 0.25µF
अतः संधारित्रों पर आवेश Q = C₁ V = 0.25 × 1.5 = 0.375µc

प्रश्न 63.
एक 100 pF धारिता के संधारित्र को 100 वोल्ट के विभवान्तर तक आवेशित किया गया है। इसे एक-दूसरे संधारित्र के समान्तर क्रम में जोड़ा गया है। यदि अन्तिम वोल्टेज 30 वोल्ट हो तो संधारित्र की धारिता क्या होगी? कितनी ऊर्जा का ह्रास होगा और उसका क्या होगा? .
हल :
दिया है, C= 100 pF = 100 × 10^-12 F = 10^-10 F, V₁= 100 वोल्ट, .
V₂= 0, V = 30 वोल्ट, C₂ = ?

इस ऊर्जा का ऊष्मा के रूप में ह्रास होगा।

प्रश्न 64.
एक समान्तर प्लेट संधारित्र की धारिता 16 μF है तथा इस पर आवेश 3.2 × 10^-4 कूलॉम है। आवेश को अपरिवर्तित रखते हुए प्लेटों के बीच की दूरी दोगुनी करने के लिए कितना कार्य करना होगा? [2012]
हल :
दिया है , C₁ = 16 μF = 16 × 10^-6 F, q= 3.2 × 10^-4 कूलॉम,
d₁ = d, d₂ = 2 d, W = ?

प्रश्न 65.
एक 10 μF के संधारित्र का विभवान्तर 100 वोल्ट से 200 वोल्ट कर देने पर उसकी ऊर्जा में वृद्धि की गणना कीजिए।
[2007, 12, 13, 14]
हल :
दिया है, C = 10 μF = 10 × 10^-6 F, V₂ = 200 वोल्ट, V₁ = 100 वोल्ट, ΔU = ?

प्रश्न 66.
एक 8 माइक्रोफैरड के संधारित्र का विभवान्तर 20 वोल्ट से बढ़कर 25 वोल्ट कर देने पर उसकी स्थितिज ऊर्जा में हुई वृद्धि की गणना कीजिए। [2018]]
हल :
दिया है, C = 8 माइक्रोफैरड = 8 × 10^-6 फैरड, V₁ = 20 वोल्ट, V₂ = 25 वोल्ट
संधारित्र की स्थितिज ऊर्जा में वृद्धि ΔU = \(\frac{1}{2} C V_{2}^{2}-\frac{1}{2} C V_{1}^{2}\)
= \(\frac{1}{2}\) C(V₂² – V₁²
= \(\frac{1}{2}\) × 8 × 10^-6 [(25)² – (20)²] = 4 × 10^-6 [625 – 400]
= 4 × 10^{-6 ×} 225
= 9.0 × 10^-4 जूल।

प्रश्न 67.
0.5μF के संधारित्र को इतना आवेशित किया गया कि उसकी प्लेटों के बीच विभवान्तर 25 वोल्ट हो जाता है। संधारित्र में संचित ऊर्जा की गणना कीजिए।
[2005, 06, 09]
हल :
दिया है, C = 0.5μF = 5 × 10^-7F, V = 25 वोल्ट, U = ?
संचित ऊर्जा U = \(\frac { 1 }{ 2 }\)CV² ==\(\frac { 1 }{ 2 }\) × (5 x 10^-7) × (25)² = 1.5625 × 10^-4 जूल।

प्रश्न 68.
4.0 μF तथा 6.0 μF के दो संधारित्र 20 V की बैटरी के साथ श्रेणीक्रम में संयोजित हैं। 4.0 uF धारिता के संधारित्र में संगृहीत ऊर्जा तथा प्रति सेकण्ड बैटरी द्वारा दी गयी ऊर्जा का मान ज्ञात कीजिए। [2017]
हल :
4.0 μF व 6.0 μF श्रेणीक्रम में हैं।

प्रश्न 69.
एक आवेशित समान्तर प्लेट संधारित्र द्वारा संचित ऊर्जा घनत्व 17.70 जूल/मीटर³ है। संधारित्र की प्लेटों के बीच वैद्युत क्षेत्र की तीव्रता ज्ञात कीजिए। (ε_o = 8.85 x 10^-12 कूलॉम²/न्यूटन-मीटर²) [2000, 04]
हल :
दिया है, U = 17.70 जूल/मीटर³ ε_o = 8.85 × 10^-12 कूलॉम²/न्यूटन-मीटर², E = ?

प्रश्न 70.
3 μF, 3 μF और 6 μF धारिता के संधारित्रों को किस प्रकार संयुक्त करें कि तुल्य धारिता 5μF हो?
हल :
3 μF व 6 μF को श्रेणीक्रम में जोड़ने पर, तुल्य धारिता C = \(\frac{3 \times 6}{3+6}\) = 2 μF
2 μF व 3 μF को समान्तर क्रम में जोड़ने पर, तुल्य धारिता C = 2+ 3 = 5μF

प्रश्न 71.
दो संधारित्रों की तुल्य धारिता समान्तर क्रम में 24 μF तथा श्रेणीक्रम में 6μF है। उनकी अलग-अलग धारिताएँ क्या हैं?
हल :
समान्तर क्रम में, C = C₁+C₂; अतः 24 = C₁ + C₂ …………(1)

∴  C₁C₂ = 24 × 6 = 144
सूत्र (C₁ – C₂)² = (C₁+C₂)² – 4 C₁C₂ से,
(C₁ – C₂)² = (24)²-4 × 144 = 576 – 576 = 0
अतः C₁ = C₂
अतः दोनों संधारित्रों की धारिताएँ C₁ = C₂ = 12 μF.

प्रश्न 72.
बिन्दुओं A तथा B के बीच तुल्य धारिता ज्ञात कीजिए। [2017]

हल :
दिए गए चित्र को निम्न रूप में व्यवस्थित करने पर
2 μF, 3 μF व 6 μF समान्तर क्रम में हैं। अतः तुल्य धारिता
C₁ = 2+ 3+ 6 = 11 μF
4 μF व 5μF समान्तर-क्रम में हैं। अत: तुल्य धारिता ।
C₂ = 4+ 5 = 9 μF
8 μF, 11 μF व 9 μF श्रेणीक्रम में हैं। अतः तुल्य धारिता

प्रश्न 73.
संलग्न परिपथ चित्र-2.54 में यदि A तथा B बिन्दुओं के बीच 150 वोल्ट विभवान्तर लगाया जाए तो 6 μF के संधारित्र के प्लेटों के बीच उत्पन्न विभवान्तर एवं संचित ऊर्जा की गणना कीजिए। [2015]

हल :
(i) 2 μF व 3 μF के संधारित्र श्रेणीक्रम में हैं, अत: इनकी
तुल्य धारिता C₁ = \(\frac{2 \times 3}{2+3}\) = 1.2 μF
1.8uF व 1.2uF समान्तर क्रम में हैं, अत: इनकी तुल्य धारिता
C₂ = 1.8+ 1.2 = 3 μF
अब 3 μF व 6μF के संधारित्र श्रेणीक्रम में हैं; अत: A व B के बीच तुल्य धारिता
C = \(\frac{3 \times 6}{3+6}\) = 2 μF
(ii) सम्पूर्ण निकाय पर आवेश Q = CV = 2μF × 150 = 300 μC

प्रश्न 74.
3 μF की धारिता वाले तीन संधारित्रों को किस प्रकार जोड़ा जाए कि उनकी सम्मिलित धारिता-(i) 4.5 μF तथा (ii) 9 μF हो जाए? प्रत्येक का परिपथ आरेख भी खींचिए। [2010]

हल :
(i) दो संधारित्रों को श्रेणीक्रम में जोड़कर तीसरा संधारित्र इनके साथ समान्तरक्रम में जोड़ने पर [चित्र-2.55],
चित्र-2.55

अतः तुल्य धारिता C = 1.5+ 3 = 4.5 μF

(ii) तीनों संधारित्रों को समान्तर-क्रम में जोड़ने पर [चित्र-2.55]
तुल्य धारिता C = 3 + 3 +3 = 9 μF.

प्रश्न 75.
चित्रानुसार संयोजन के समतुल्य संधारित्र की गणना कीजिए। [2018]

हल :
संधारित्र C₁ व C₂ परस्पर श्रेणीक्रम में हैं।

प्रश्न 76.
संलग्न चित्र में संधारित्रों के जालक्रम में A तथा B बिन्दुओं के बीच तुल्य धारिता 1μF है। संधारित्र C की धारिता का मान ज्ञात कीजिए।[2017]

हल :
6 μF व 1 μF श्रेणीक्रम में हैं, अतः तुल्य धारिता

प्रश्न 77.
दिए गए चित्र में A तथा B के मध्य विभवान्तर 100 वोल्ट का लगाया गया है। C व D के मध्य विभवान्तर ज्ञात कीजिए।
[2018]

हल :
बिन्दु E व F के बीच संधारित्र C₂, C₃ तथा C₄ परस्पर श्रेणीक्रम में हैं।

संधारित्रों C₂,C₃ तथा C₄ पर समान आवेश q = C’V = 2 × 100 = 200μC
C व D के मध्य विभवान्तर, V = \(\frac{q}{C_{3}}=\frac{200}{6}\) वोल्ट = 33. 3 वोल्ट।

प्रश्न 78.
संलग्न परिपथ चित्र-2.62 में स्थिर अवस्था में दोनों संधारित्रों पर संचित आवेशों तथा विभव की गणना कीजिए।
[2002, 14]

हल;
4 μF व 6 μF के संधारित्रों के आवेशित हो जाने पर इनमें कोई धारा नहीं बहेगी; अत: 4 μF व 6 μF कार्य नहीं करेंगे। 4Ω, 5Ω व 1Ω श्रेणीक्रम में हैं; अत: इनका तुल्य प्रतिरोध R = 4+ 5 + 1 = 10Ω
4Ω, 5Ω व 1Ω में बहने वाली धारा

4Ω व 5Ω श्रेणीक्रम में हैं; अत: इनका तुल्य प्रतिरोध
R= 4 + 5 = 9Ω
9Ω के सिरों के बीच विभवान्तर V = iR = 2 × 9 = 18 वोल्ट
4 μF व 6 μF श्रेणीक्रम में हैं; अत: इनकी तुल्य धारिता

अतः 4 μF व 6 μF के संधारित्रों पर संचित आवेश q= CV = 2.4 × 18 = 43.2 μC.

प्रश्न 79.
संलग्न परिपथ चित्र-2.63 में प्रदर्शित संधारित्र में संचित ऊर्जा ज्ञात कीजिए। [2008]

हल :
संधारित्र के आवेशित हो जाने पर इसमें कोई धारा नहीं बहेगी; अत: 2 μF कार्य नहीं करेगा।
2Ω, 3Ω व 5Ω श्रेणीक्रम में हैं; अत: इनका तुल्य प्रतिरोध
R= 2 + 3 + 5 = 10Ω
परिपथ का विभवान्तर V = iR = 2 × 10 = 20 वोल्ट
अतः संधारित्र में संचित ऊर्जा U = \(\frac { 1 }{ 2 }\) CV²
=\(\frac { 1 }{ 2 }\) × 2 x 10^-6 × (20)² = 4 × 10^-4 जूल।

प्रश्न 80.
संलग्न परिपथ चित्र-2.64 में यदि B को पृथ्वी से जोड़ दिया जाए तथा A को 1500 वोल्ट विभव पर रखा जाए तो P पर विभव की गणना कीजिए।

हल :
5 μF व 5 μF श्रेणीक्रम में हैं; अत: इनकी तुल्य धारिता

2.5 μF व 1 μF समान्तर क्रम में हैं; अत: इनकी तुल्य धारिता
C₂ = 1+ 2.5 = 3.5 μF
3.5μF व 3.5 μF श्रेणीक्रम में हैं; अत: A व B के बीच तुल्य धारिता

अतः संधारित्रों पर आवेश q= CV = 1.75 × 10^-6 × 1500 = 2625 × 10^-6 कूलॉम

∵ B पृथ्वी से जुड़ा है; अत: V_B = 0 वोल्ट
अतः . बिन्दु P पर विभव V_P = V_B + 750 = 0+ 750 = 750 वोल्ट।

प्रश्न 81.
चित्र में प्रदर्शित संधारित्र C₂ में विभवान्तर व संचित ऊर्जा की गणना कीजिए। बिन्दु A पर विभव 90 वोल्ट है। C₁ = 20 μF, C₂ = 30μF और C = 15μF हैं। [2018]

हल :
संयोजन के सिरों पर विभवान्तर = 90 – 0 = 90 वोल्ट
संधारित्र C₁, C₂ व C₃ परस्पर श्रेणीक्रम में हैं। अत: इनकी तुल्य धारिता,

प्रश्न 82.
निम्नांकित परिपथ [चित्र-2.66 (a)] में प्रदर्शित परिपथ में बिन्दु A एवं B के बीच की कुल धारिता का मान इसका सरल समतुल्य परिपथ बनाकर ज्ञात कीजिए। [2000, 04, 06]]

हल :
चित्र-2.66 (a) में प्रत्येक संधारित्र की प्रथम प्लेट A बिन्दु से तथा द्वितीय प्लेट B बिन्दु से जुड़ी है। इस प्रकार तीनों संधारित्र समान्तर-क्रम में हैं चित्र-2.66 (b)। अतः इनकी तुल्य धारिता C = 3 + 4 + 5 = 12 μF.

प्रश्न 83.
निम्नांकित परिपथ चित्र-2.67 (a) में A व B के बीच तुल्य धारिता की गणना कीजिए। [2003]

हल:
सर्वप्रथम चित्र-2.67 (a) को चित्र-2.67 (b) के अनुसार प्रतिस्थापित करते हैं; अतः दिया गया परिपथ एक व्हीटस्टोन सेतु की व्यवस्था है। भुजाओं MN व NO की धारिताओं का अनुपात तथा भुजाओं MP व PO की धारिताओं का अनुपात समान है; अतः सेतु सन्तुलित है।
प्रत्येक श्रेणी की संयोजन की धारिता

प्रश्न 84.
निम्नांकित परिपथ चित्र-2.68 (a) में A और B बिन्दुओं के बीच तुल्य धारिता ज्ञात कीजिए। [2015]

हल :
सर्वप्रथम परिपथ-2.68 (a) को चित्र 2.64 (b) की भाँति व्यवस्थित करते हैं जो कि एक व्हीटस्टोन सेतु है। अत: 8 μF पर कोई आवेश संचित नहीं होगा। AC व CB के मध्य 3 μF व 6 μF श्रेणीक्रम में हैं तथा AD व DB के मध्य 3 μF व 6 μF श्रेणीक्रम में हैं।

प्रश्न 85.
तीन संधारित्र एक 30 वोल्ट की बैटरी से चित्र-2.69 के अनुसार जुड़े हैं। गणना कीजिए-
(i) संधारित्र की तुल्य धारिता तथा
(ii) 10 μF धारिता के संधारित्र द्वारा संचित ऊर्जा। [2011]

हल :
(i) 6 μF व 12 μF श्रेणीक्रम में हैं।
अत: इनकी तुल्य धारिता C₁= \frac{6 \times 12}{6+12} = 4 μF
4 μF व 10 μF समान्तर क्रम में हैं।
अत: इनकी तुल्य धारिता C = 4+ 10 = 14 μF

(ii) 10 μF में संचित ऊर्जा U = = \(\frac { 1 }{ 2 }\)C’V²
=\(\frac { 1 }{ 2 }\) × 10 × 10^-6 × (30)² = 4.5 × 10^-3 जूल।

प्रश्न 86.
संलग्न परिपथ चित्र-2.70 की सहायता से ज्ञात कीजिए –
C = 100 pF
(i) संयोजन की तुल्य धारिता
(ii) C₁ संधारित्र पर आवेश तथा
(iii) संयोजन की कुल संचित ऊर्जा।[2008, 13]

हल :
(i) 200pF व 200pF श्रेणीक्रम में हैं; अत: इनकी तुल्य धारिता

100pF व 100pF समान्तर क्रम में हैं। अत: इनकी तुल्य धारिता
C” ‘ = 100 + 100 = 200pF
200pF श्रेणीक्रम में हैं; अत: A व B के बीच तुल्य धारिता

(ii) संयोजन पर कुल आवेश q = CV = 100 × 200 = 20000 pC

(iii)

प्रश्न 87.
किसी समान्तर प्लेट संधारित्र की धारिता 2 μ F है, जब इसकी प्लेटों के बीच निर्वात रहता है। प्लेटों के बीच के स्थान को दो परावैद्युतों की बराबर-बराबर मात्राओं से चित्र-2.71 में प्रदर्शित गई दो विधियों से भरा जाता है। यदि उनके परावैद्युतांक 3 व 6 हों तो दोनों स्थितियों में संधारित्र की धारिता की गणना कीजिए। [2006]

हल :
दिया है, K₁ = 3, K₂ = 6, ε_oA/d = 2 μF
(i) जब संधारित्र समान्तर क्रम में हैं तो क्षेत्रफल A/2 होगा।

अतः प्रथम स्थिति में संधारित्र की तुल्य धारिता
C_I = C₁+C₂ = 3 + 6 = 9 μF

(ii) श्रेणीक्रम में दूरी d/2 होगी; अत:

प्रश्न 88.
किसी समान्तर प्लेट संधारित्र की धारिता 2 μF है। इसके आधे भाग को चित्रानुसार एक परावैद्युत पदार्थ से भरा जाता है तो इसकी धारिता 5 μF हो जाती है। परावैद्युतांक K का मान ज्ञात कीजिए। [2018]

हल :
माना समान्तर प्लेट संधारित्र की प्लेटों का क्षेत्रफल A तथा उनके बीच की दूरी d है।

स्थिरवैद्युत विभव तथा धारिता बहुविकल्पीय प्रश्नोत्तर

निम्नलिखित प्रश्नों के चार विकल्प दिए गए हैं। सही विकल्प का चयन कीजिए –

प्रश्न 1.
वैद्युत विभव का मात्रक है [2011]
(a) जूल/कूलॉम
(b) जूल-कूलॉम
(c) कूलॉम/जूल
(d) न्यूटन/कूलॉम।
उत्तर :
(a) जूल/कूलॉम

प्रश्न 2.
वैद्युत विभव का मात्रक [2014]
(a) जूल/कूलॉम
(b) वोल्ट/मीटर
(c) जूल-कूलॉम
(d) जूल/कूलॉम-मीटर।
उत्तर :
(a) जूल/कूलॉम

प्रश्न 3.
निम्नलिखित में से कौन वैद्युत विभव का मात्रक नहीं है [2013]
(a) वोल्ट
(b) जूल/कूलॉम
(c) न्यूटन/कूलॉम
(d) न्यूटन-मीटर/कूलॉम।
उत्तर :
(c) न्यूटन/कूलॉम

प्रश्न 4.
एक-दूसरे से 0.5 मीटर की दूरी पर स्थित दो बिन्दुओं के बीच विभवान्तर 50 वोल्ट है।2 कूलॉम आवेश को एक बिन्दु से दूसरे बिन्दु तक ले जाने में आवश्यक कार्य का मान होगा – [2004]
(a) 1 जूल
(b) 25 जूल
(c) 50 जूल
(d) 100 जूल।
उत्तर :
(d) 100 जूल।

प्रश्न 5.
0.45 मीटर त्रिज्या की एक अचालक वलय की परिधि पर एकसमान रूप से वितरित कुल आवेश 2 × 10^-10कूलॉम है। 2 कूलॉम आवेश को अनन्त से वलय के केन्द्र तक ले जाने में आवश्यक कार्य होगा – [2005]
(a) 4 जूल
(b) 8 जूल
(c) – 4 जूल
(d) शून्य।
उत्तर :
(b) 8 जूल

प्रश्न 6.
दो प्लेटें एक-दूसरे से 1 सेमी दूरी पर हैं और उनमें विभवान्तर 10 वोल्ट है। प्लेटों के बीच वैद्युत क्षेत्र की तीव्रता है – [2009]
(a) 10 न्यूटन/कूलॉम
(b) 500 न्यूटन/कूलॉम
(c) 1000 न्यूटन/कूलॉम
(d) 250 न्यूटन/कूलॉम।
उत्तर :
(c) 1000 न्यूटन/कूलॉम

प्रश्न 7.
1 वोल्ट विभवान्तर पर त्वरित करने पर इलेक्ट्रॉन की ऊर्जा होती है [2007]
(a) 1 जूल
(b) 1 इलेक्ट्रॉन-वोल्ट
(c) 1 अर्ग
(d) 1 वाट।
उत्तर :
(b) 1 इलेक्ट्रॉन-वोल्ट

प्रश्न 8.
1 इलेक्ट्रॉन-वोल्ट का मान होता है – [2004, 08, 13]
(a) 2 × 10^-18 जूल
(b) 1.6 × 10^-31 जूल
(c) 1.6 × 10^-19 जूल
(d) 3.1 × 10^-31 जूला
उत्तर :
(c) 1.6 × 10^-19 जूल

प्रश्न 9.
1 इलेक्ट्रॉन-वोल्ट (eV) मात्रक है [2005]
(a) ऊर्जा का
(b) वैद्युत विभव का
(c) वेग का
(d) कोणीय संवेग का।
उत्तर :
(a) ऊर्जा का

प्रश्न 10.
एक इलेक्ट्रॉन 5 वोल्ट विभवान्तर द्वारा त्वरित किया जाता है। इलेक्ट्रॉन द्वारा अर्जित ऊर्जा होगी- [2006, 07]
(a) 5 जूल
(b) 5 इलेक्ट्रॉन-वोल्ट
(c) 5 अर्ग
(d) 5 वाट।
उत्तर :
(b) 5 इलेक्ट्रॉन-वोल्ट

प्रश्न 11.
एक इलेक्ट्रॉन को दूसरे इलेक्ट्रॉन के अधिक समीप लाने पर निकाय की वैद्युत स्थितिज ऊर्जा [2010]
(a) घटती है
(b) बढ़ती है
(c) उतनी ही रहती है
(d) शून्य हो जाती है।
उत्तर :
(b) बढ़ती है

प्रश्न 12.
दो समान धनावेशित बिन्दु आवेशों, जिनमें प्रत्येक पर 1 μC का आवेश है, को 1 मीटर की दूरी पर वायु में रखा
जाता है। इसकी स्थितिज ऊर्जा है –
(a) 1 जूल
(b) 1 इलेक्ट्रॉन-वोल्ट
(c) 9 × 10^-3 जूल
(d) शून्य।
उत्तर :
(c) 9 × 10^-3 जूल

प्रश्न 13.
E = 0 तीव्रता वाले वैद्युत क्षेत्र में विभव V का दूरी r के साथ परिवर्तन होगा – [2012,17]
(a) V \propto \frac{1}{r}
(b) V ∝ r
(c) V \propto \frac{1}{r^{2}}
(d) V = नियत अर्थात् r पर निर्भर नहीं।
उत्तर :
(d) V = नियत अर्थात् r पर निर्भर नहीं।

प्रश्न 14.
निम्नलिखित में से कौन-सा तथ्य समविभव पृष्ठ के लिए सत्य नहीं है – [2009]
(a) पृष्ठ पर किन्हीं दो बिन्दुओं के बीच विभवान्तर शून्य होता है
(b) वैद्युत बल रेखाएँ पृष्ठ के सर्वथा लम्बवत् होती हैं
(c) पृष्ठ पर किसी आवेश को एक स्थान से दूसरे स्थान पर ले जाने पर कोई कार्य नहीं होता
(d) समविभव पृष्ठ सर्वदा गोलाकार होता है।
उत्तर :
(d) समविभव पृष्ठ सर्वदा गोलाकार होता है।

प्रश्न 15.
दूरी पर रखे वैद्युत द्विध्रुवों के बीच लगने वाला बल अनुक्रमानुपाती है – [2005]
(a) r² के
(b) r⁴ के
(c) r^-2के
(d) r^-4 के।
उत्तर :
(d) r^-4 के।

प्रश्न 16.
एक इलेक्ट्रॉन एक वैद्युत क्षेत्र में, क्षेत्र के अभिलम्बवत् प्रवेश करता है। इसका गमन पथ होगा – [2006]
(a) वृत्ताकार
(b) दीर्घवृत्ताकार
(c) कुण्डलिनी के आकार का
(d) परवलयाकार।
उत्तर :
(d) परवलयाकार।

प्रश्न 17.
क्षैतिज दिशा में गति करता हुआ इलेक्ट्रॉन एक ऐसे स्थान में प्रवेश करता है जहाँ ऊर्ध्वाधर दिशा में एकसमान वैद्युत क्षेत्र है। इस स्थान में इलेक्ट्रॉन का पथ होगा – [2008]
(a) क्षैतिज से 45° के कोण पर सीधी रेखा
(b) ऊर्ध्वाधर तल में एक वृत्त
(c) क्षैतिज तल में एक परवलय
(d) ऊर्ध्वाधर तल में एक परवलय।
उत्तर :
(d) ऊर्ध्वाधर तल में एक परवलय।

प्रश्न 18.
दो बिन्दु आवेश 8μC तथा 12μC एक-दूसरे से 10 सेमी की दूरी पर वायु में रखे गए हैं। इनके बीच की दूरी 6 सेमी परिवर्तित करने के लिए कार्य आवश्यक होगा – [2018]
(a) 5.8जूल
(b) 4.8जूल
(c) 3.8जूल
(d) 2.8 जूल।
उत्तर :
(a) 5.8जूल

प्रश्न 19.
एक समान वैद्युत क्षेत्र E में रखे वैद्युत द्विध्रुव आघूर्ण pवाले वैद्युत द्विध्रुव को 90° से घुमाने में कुल कार्य है- [2018]
(a) pE/2
(b) 2pE
(c) pE
(d) √2pE.
उत्तर :
(c) pE

प्रश्न 20.
एक धातु के गोले की धारिता 1.0 μF है। उसकी त्रिज्या लगभग होगी – [2011]
(a) 9 किमी
(b) 10 मीटर
(c) 1.11 मीटर
(d) 1.11 सेमी।
उत्तर :
(a) 9 किमी

प्रश्न 21.
एक गोलाकार चालक की त्रिज्या 9 मीटर है। इसकी विद्युत-धारिता है – [2018]
(a) 10⁹ फैरड
(b) 9 × 10⁹ फैरड
(c) 9 × 10^-9 फैरड
(d) 10^-9 फैरड।
उत्तर :
(d) 10^-9 फैरड।

प्रश्न 22.
दो गोलीय चालक A₁ तथा A₂ व उनकी त्रिज्याएँ क्रमशः तथाr हैं। चालक A₁ व A₂ पर क्रमशः r₁ तथा r₂
आवेश हैं। चित्र के अनुसार चालकों को हवा में एक ताँबे के तार द्वारा जोड़ा जाता है।

इस निकाय की तुल्य धारिता होगी
[2018]
(a) 4πε^or₁r₂/r₁ – r₂
(b) 4πε^o₁ + r₂
(c) 4πε^or₁
(d) 4πε^or₂
उत्तर :
(b) 4πε^o₁ + r₂

प्रश्न 23.
एक आवेशित वायुसंधारित्र में U_o ऊर्जा संचित है। एक परावैद्युत की पट्टी जिसका परावैद्युतांक K है, को इसमें प्रवेश कराने पर ऊर्जा U हो जाती है, तो – [2018]
(a) U = U_o.
(b) U = KU_o.
(c) U = K²U_o.
(d) U = \(\frac{u_{0}}{K}\)
उत्तर :
(d) U = \(\frac{u_{0}}{K}\)

प्रश्न 24.
संलग्न परिपथ चित्र-2.74 में बिन्दुओं PवQ के बीच तुल्य धारिता होगी – [2004]

(a) 4 μF
(b) 3/4 μF
(c) 4/3 μF
(d) 1/2 μF.
उत्तर :
(c) 4/3 μF

प्रश्न 25.
श्रेणीक्रम में जोड़े गए पाँच समान संधारित्रों की परिणामी धारिता 4 μF है। यदि इनको समान्तरक्रम में जोड़कर 400 वोल्ट तक आवेशित करें तो इसमें संगृहीत कुल ऊर्जा होगी – [2005]
(a) 80 जूल
(b) 16 जूल
(c) 8 जूल
(d) 4 जूल।
उत्तर :
(c) 8 जूल

प्रश्न 26.
एक आवेशित संधारित्र बैटरी से जुड़ा है। यदि इसकी प्लेटों के बीच परावैद्युत पदार्थ की एक पट्टी रखी जाए तो निम्नलिखित में से कौन-सी मात्रा अपरिवर्तित रहेगी [2005, 10]]
(a) आवेश
(b) विभवान्तर
(c) धारिता
(d) ऊर्जा।
उत्तर :
(b) विभवान्तर

प्रश्न 27.
संलग्न परिपथ चित्र-2.75 में यदि A व B के बीच तुल्य धारिता 5uF हो तब संधारित्र C .
की धारिता होगी –

(a) 3μF
(b) 6μF
(c) 9μF
(d) 12 μF.
उत्तर :
(b) 6μF

प्रश्न 28.
संलग्न चित्र-2.76 में बिन्दुओं A व B के बीच तुल्य धारिता है- [2009]

(a) \(\frac{2}{3} \mu \mathrm{F}\)
(b) \(\frac{3}{2} \mu \mathrm{F}\)
(c) \(\frac{11}{3} \mu \mathrm{F}\)
(d) 1 µF
उत्तर :
(b) \(\frac{3}{2} \mu \mathrm{F}\)

प्रश्न 29.
100 μF धारिता वाले संधारित्र को 10 वोल्ट तक आवेशित करने पर उसमें संचित ऊर्जा होगी – [2009,16]
(a) 5.0 × 10^-3 जूल
(b) 0.5 × 10^-3 जूल
(c) 0.5 जूल
(d) 5.0 जूल।
उत्तर :
(a) 5.0 × 10^-3 जूल

प्रश्न 30.
संलग्न चित्र-2.77 में बिन्दुओं A व B के बीच तुल्य धारिता है- [2009]

(a) 4 µF
(b) \(\frac{12}{7} \mu \mathrm{F}\)
(c) \(\frac{1}{4} \mu \mathrm{F}\)
(d) \(\frac{7}{12} \mu \mathrm{F}\)
उत्तर :
(a) 4 µF

प्रश्न 31.
60 μF धारिता वाले एक संधारित्र की प्रत्येक प्लेट पर 3 × 10^-8C आवेश है। संधारित्र में संचित ऊर्जा होगी [2009]
(a) 2.5 × 10^-15 जूल
(b) 1.5 × 10^-14 जूल
(c) 3.5 × 10^-13 जूल
(d) 7.5 × 10^-12 जूल।
उत्तर :
(d) 7.5 × 10^-12 जूल।

प्रश्न 32.
तीन बराबर धारिता वाले संधारित्रों को पहले समान्तर क्रम में तथा बाद में श्रेणीक्रम में जोड़ा जाता है। दोनों दशाओं में तुल्य धारिताओं का अनुपात होगा [2009]
(a) 9:1
(b) 6:1
(c) 3:1
(d) 1:9.
उत्तर :
(a) 9:1

प्रश्न 33.
एक संधारित्र जिसकी धारिता 100 μF है, 200 वोल्ट तक आवेशित किया जाता है। उसे 22 के प्रतिरोध द्वारा विसर्जित करने पर उत्पन्न हुई ऊष्मा है [2009]
(a) 1 जूल
(b) 2 जूल
(c) 3 जूल
(d) 4 जूल।
उत्तर :
(b) 2 जूल

प्रश्न 34.
संलग्न परिपथ चित्र-2.78 में प्रदर्शित संधारित्रों की तुल्य धारिता A व B के बीच है – [2015]

(a) 4 μF
(b) 2.5 μF
(c) 2 μF
(d) 0.25 μF.
उत्तर :
(b) 2.5 μF

MP Board Class 12th Physics Important Questions

MP Board Class 12th Physics Solutions Chapter 15 संचार व्यवस्था

संचार व्यवस्था  अन्य महत्त्वपूर्ण प्रश्नोत्तर

संचार व्यवस्था  विस्तृत उत्तरीय प्रश्नोत्तर

प्रश्न 1.
संचार व्यवस्था क्या है? इसके कितने मूल अवयव हैं? स्पष्ट कीजिए।
अथवा रेडियो संचार व्यवस्था का नामांकित ब्लॉक आरेख बनाइए। [2014, 16, 17]
अथवा संचार व्यवस्था के मुख्य अवयव कौन-कौन से हैं? एक ब्लॉक आरेख द्वारा प्रदर्शित कीजिए। [2017]
अथवा संचार व्यवस्था का योजनाबद्ध आरेख खींचिए तथा इसके विभिन्न अवयवों का उल्लेख कीजिए। [2016, 18]
उत्तर :
संचार व्यवस्था (Communication System)-“सूचनाओं अथवा सन्देशों के एक स्थान से दूसरे स्थान तक स्थानान्तरण की प्रक्रिया संचार कहलाती है।” इस प्रकार सन्देशों अथवा सूचनाओं को किसी विधि द्वारा (विद्युतचुम्बकीय तरंगों द्वारा अथवा केबिल्स द्वारा) एक स्थान से सम्प्रेषित करके दूसरे स्थान पर ग्रहण करने की व्यवस्था को संचार व्यवस्था कहते हैं।

संचार व्यवस्था के अवयव (Elements of a Communication System)-संचार व्यवस्था किसी भी प्रकृति की हो, इसके तीन प्रमुख अवयव होते हैं-

1. प्रेषित्र (transmitter),
2. संचार माध्यम (communication channel) तथा
3. अभिग्राही (receiver)।

1. प्रेषित्र (Transmitter)- इसे सम्प्रेषण चैनल भी कहते हैं क्योंकि यह मूल सन्देश (जैसे—भाषण, सूचना) सिग्नल को एक उचित सिग्नल में बदलता है। जब कोई वक्ता व श्रोता के बीच की दूरी बहुत अधिक होती है तो तारें (केबिल्स) सम्प्रेषण चैनल का कार्य नहीं कर पाती हैं। इस स्थिति में पहले ध्वनि को माइक्रोफोन द्वारा विद्युत सिग्नलों में बदलते हैं तथा इनकी शक्ति को ऐम्पिलीफायर द्वारा बढ़ाकर इनको रेडियो आवृत्ति की वाहक तरंगों के साथ मॉडुलित करके ऐन्टिना द्वारा विद्युतचुम्बकीय तरंगों के रूप में अन्तरिक्ष में प्रेषित कर देते हैं।

2. संचार माध्यम (Communication Channel)- संचार माध्यम ऐसा भौतिक माध्यम (अथवा मुक्त आकाश) है जिसके द्वारा प्रेषित्र से भेजी गई विद्युतचुम्बकीय तरंगों के रूप में सूचना अथवा भाषण अभिग्राही के ऐन्टिना पर पहुँचती है, संचार माध्यम कहलाता है। यह तारों का एक युग्म अर्थात् केबिल तथा बेतार अर्थात् मुक्त आकाश में से कुछ भी हो सकता है।

3. अभिग्राही (Receiver)- अभिग्राही प्रेषित्र द्वारा भेजे गए परिवर्तित सिग्नल को वास्तविक सिग्नल में बदलता है। इस प्रक्रिया को विमॉडुलन (demodulation) अथवा डिमॉडुलन कहते हैं। जब अभिग्राही के ऐन्टिना पर मॉडुलित तरंगें पहुँचती हैं तो वहाँ पर पहले श्रव्य तरंगों को अलग कर लेते हैं फिर इन्हें प्रवर्धित कर लाउडस्पीकर को भेज देते हैं। यहाँ पर इन्हें पुन: ध्वनि तरंगों में परिवर्तित कर देते हैं।

संचार व्यवस्था का नामांकित आरेख चित्र-15.3 में प्रदर्शित है

प्रश्न 2.
इलेक्ट्रॉनिक संचार व्यवस्था में प्रयुक्त होने वाली मूल शब्दावली को परिभाषित कीजिए।
उत्तर
इलेक्ट्रॉनिक संचार व्यवस्थाओं में उपयोग होने वाली मूल शब्दावली (Basic Terms Used in Electronic Telecommunication System)-किसी भी संचार व्यवस्था को समझने के लिए उसकी मूल शब्दावली को समझना आवश्यक है। संचार व्यवस्था की मूल शब्दावली में सम्मिलित मुख्य शब्द निम्न प्रकार हैं

1. ट्रान्सड्यूसर (Transducer)- ट्रान्सड्यूसर वह युक्ति है जो ऊर्जा के एक रूप को दूसरे रूप में परिवर्तित कर देती है। इलेक्ट्रॉनिक संचार व्यवस्थाओं में प्रायः ऐसी युक्तियाँ प्रयुक्त होती हैं जिनका निवेश (input) अथवा निर्गत (output) विद्युतीय रूप में होता है। विद्युतीय ट्रान्सड्यूसर एक ऐसी युक्ति है जो कुछ भौतिक चरों जैसे दाब, विस्थापन, बल, ताप आदि को अपने निर्गत (output) पर विद्युतीय सिग्नल में रूपान्तरित कर देती है।

2. सिग्नल (Signal)- प्रेषण के लिए उपयुक्त विद्युत रूप में रूपान्तरित सूचना को सिग्नल या संकेत कहते हैं। सिग्नल अनुरूप (analog) अथवा अंकीय (digital) प्रकार का हो सकता है। अनुरूप सिग्नल में वोल्टता तथा धारा निरन्तर परिवर्तित होते हैं जो अनिवार्यतः समय के एकल मान वाले फलन होते हैं। टेलीविजन के ध्वनि तथा दृश्य सिग्नल, अनुरूप सिग्नल होते हैं। अंकीय सिग्नल में वोल्टता तथा धारा क्रमवार विविक्त मान प्राप्त करते हैं। अंकीय इलेक्ट्रॉनिकी में मुख्य रूप से द्विआधारी पद्धति (binary system) प्रयुक्त होती है जिसमें किसी सिग्नल के केवल दो स्तर होते हैं। वोल्टता-धारा के निम्न स्तर को ‘0’ से तथा वोल्टता-धारा के उच्च स्तर को ‘1’ से प्रदर्शित किया जाता है।

3. शोर (Noise)- शोर का अर्थ है अवांछनीय सिग्नल जो किसी संचार व्यवस्था में सन्देश सिग्नलों के प्रेषण तथा अभिग्रहण में व्यवधान उत्पन्न करने का प्रयत्न करता है।

4. प्रेषित्र (प्रेषी) (Transmitter)- प्रेषित्र वह युक्ति है जो सूचनाओं के विद्युत सिग्नलों.को संसाधित कर वाहक तरंगों (carrier waves) पर अध्यारोपण के पश्चात् उसे संचार माध्यम से होकर प्रेषण तथा अभिग्राही पर अभिग्रहण के लिए उपयुक्त बनाती है।

5. अभिग्राही (Receiver)- अभिग्राही वह युक्ति है जो संचार माध्यम के निर्गत (output) पर प्राप्त सिग्नल से वांछनीय सन्देश सिग्नलों को प्राप्त करता है।

6. क्षीणता (Attenuation)- संचार माध्यम से संचरण के समय सिग्नल की प्रबलता में क्षति होने की प्रक्रिया क्षीणता कहलाती है।

7.प्रवर्धन (Amplification)- किसी इलेक्ट्रॉनिक परिपथ द्वारा सिग्नल की प्रबलता बढ़ाने की प्रक्रिया प्रवर्धन कहलाती है। संचार व्यवस्था में क्षीणता के कारण होने वाले क्षय की क्षतिपूर्ति के लिए प्रवर्धन आवश्यक है।

8. परास (Range)- प्रेषित्र तथा अभिग्राही के सिरों के बीच की वह अधिकतम दूरी है जहाँ तक सिग्नल को उसकी पर्याप्त प्रबलता के साथ अथवा मॉडुलेशन से प्राप्त किया जा सकता है, परास कहलाती है।

9. बैण्ड-चौड़ाई (Bandwidth)- बैण्ड-चौड़ाई से तात्पर्य उस आवृत्ति परास से है जिस पर कोई उपकरण कार्य करता है अथवा सिग्नल में उपस्थित तरंगों की आवृत्ति-परास को बैण्ड-चौड़ाई कहते हैं।

10. मॉडुलन अथवा मॉडुलेशन (Modulation)- निम्न आवृत्ति की विद्युतचुम्बकीय तरंगों को बहुत अधिक दूरियों तक प्रेषित नहीं किया जा सकता है। इसीलिए प्रेषित्र पर, निम्न आवृत्ति की विद्युतचुम्बकीय तरंगों को उच्च आवृत्ति की वाहक तरंगों पर अध्यारोपित कराया जाता है। इस प्रक्रिया को मॉडुलन अथवा मॉडुलेशन कहते हैं।

11. विमॉडुलन अथवा डिमॉडुलेशन (Demodulation)- वह प्रक्रिया जिसमें अभिग्राही से प्राप्त मॉडुलित तरंगों में से मूल विद्युतचुम्बकीय तरंगों को अलग किया जाता है, उन्हें विमॉडुलन अथवा डिमॉडुलेशन कहते हैं।

12. पुनरावर्तक (Repeater)- पुनरावर्तक अभिग्राही तथा प्रेषित्र का संयोजन होता है। पुनरावर्तक का उपयोग किसी संचार व्यवस्था का परास बढ़ाने के लिए किया जाता है। पुनरावर्तक प्रेषित से सिग्नल प्राप्त करके उसे प्रवर्धित करता है तथा उसे अभिग्राही को पुनः प्रेषित कर देता है।

प्रश्न 3.
सिग्नलों की बैण्ड-चौड़ाई से क्या तात्पर्य है? समझाइए।
उत्तर
सिग्नलों की बैण्ड-चौड़ाई (Bandwidth of Signals)-किसी संचार व्यवस्था द्वारा प्रेषित किया जाने वाला सन्देश सिग्नल, कोई आवाज, संगीत, दृश्य अथवा डिजिटल आँकड़ा हो सकता है। इन सिग्नलों में प्रत्येक का आवृत्ति परास भिन्न-भिन्न होता है। किसी दिए गए सिग्नल की संचार प्रक्रिया के लिए किस प्रकार की संचार व्यवस्था होनी चाहिए यह उस सिग्नल के आवृत्ति बैण्ड पर निर्भर करता है। किसी सिग्नल की आवृत्ति परास उस सिग्नल की आवृत्ति बैण्ड कहलाती है तथा बैण्ड में . सम्मिलित उच्चतम तथा न्यूनतम आवृत्तियों का अन्तर बैण्ड-चौड़ाई कहलाता है। बैण्ड-चौड़ाई के आधार पर सिग्नल दो प्रकार के होते हैं

1. वाक् सिग्नल (Speech Signals)-ध्वनि तरंगों की आवृत्ति का श्रव्य परिसर 20 हर्ट्स से 20 किलोहर्ट्स तक है। वाक् सिग्नलों के लिए उपयुक्त आवृत्ति परास 300 हर्ट्स से 3100 हर्ट्स है। अत: वाक् सिग्नलों के व्यापारिक टेलीफोन संचार के लिए बैण्ड-चौड़ाई 3100 हर्ट्स – 300 हर्ट्स = 2800 हर्ट्स है। वाद्य यन्त्र उच्च आवृत्तियों के स्वर उत्पन्न करते हैं, अत: संगीत के प्रेषण के लिए बैण्ड-चौड़ाई लगभग 20 किलोहर्ट्स होती है।

2. टी० वी० सिग्नल (T.V. Signals)-दृश्यों के प्रसारण (प्रेषण) के लिए वीडियो सिग्नलों को 4.2 मेगाहर्टस बैण्ड-चौड़ाई की आवश्यकता होती है। T.V. सिग्नलों में दृश्य तथा श्रव्य दोनों अवयव होते हैं तथा उनके प्रेषण के लिए प्रायः 6 मेगाहर्ट्स बैण्ड-चौड़ाई आवंटित की जाती है। विभिन्न सिग्नलों के आवृत्ति परास तथा बैण्ड-चौड़ाई सारणी-1 में दिए गए हैं

प्रश्न 4.
प्रेषण माध्यम की बैण्ड-चौड़ाई को समझाइए।
उत्तर
प्रेषण माध्यम की बैण्ड-चौड़ाई (Bandwidth of Transmission Mediator)-सन्देश सिग्नलों की ही भाँति अलग-अलग प्रकार के प्रेषण माध्यमों के लिए भिन्न-भिन्न बैण्ड-चौड़ाई की आवश्यकता होती है। सामान्यतया प्रेषण में प्रयुक्त होने वाले माध्यम-तार, मुक्त आकाश तथा प्रकाशिक तन्तु केबिल हैं।

1. तारें (Wires)-माध्यम के रूप में समाक्षी केबिल (coaxial cable) व्यापक रूप से प्रयुक्त किया जाता है जो सामान्यत: 18 गीगाहर्ट्स आवृत्ति से नीचे कार्य करता है तथा जिसके लिए बैण्ड-चौड़ाई लगभग 750 मेगाहर्ट्स है।

2. मुक्त आकाश (Free Space)-संचार माध्यम के रूप में मुक्त आकाश से रेडियो तरंगों का विस्तृत आवृत्ति परास संचरित होता है। रेडियो तरंगों के विभिन्न आवृत्ति परिसर को अलग-अलग सेवाएँ प्रदान करने के लिए आवंटित किया गया है जिन्हें सारणी-2 में प्रदर्शित किया गया है।

प्रश्न 5.
पृथ्वी के वायुमण्डल की विभिन्न परतों तथा उनका संचार में उपयोग समझाइए।
उत्तर
पृथ्वी का वायुमण्डल (Earth’s Atmosphere)-पृथ्वी के चारों ओर उपस्थित गैसों के आवरण को वायुमण्डल कहते हैं। वायुमण्डल में मुख्यत: नाइट्रोजन, ऑक्सीजन, गैसें तथा अल्प मात्रा में कार्बन डाइऑक्साइड, आर्गन गैसें व जलवाष्प तथा सल्फर के यौगिक तथा धूल के कण होते हैं। पृथ्वी तल से ऊँचाई के साथ वायुमण्डल का घनत्व धीरे-धीरे घटता जाता है। पृथ्वी के वायुमण्डल की कोई स्पष्ट सीमा रेखा नहीं है, फिर भी इसे विभिन्न परतों में विभाजित किया जाता है जो निम्न प्रकार हैं

1. क्षोभमण्डल (Troposphere)-इस भाग का विस्तार पृथ्वी तल से 10 किमी की ऊँचाई तक होता है। इस क्षेत्र में पृथ्वी तल से ऊँचाई के साथ ताप 15°C से -50°C तक घटता है। हमारे पर्यावरण को प्रभावित करने वाली अधिकांश मौसमी घटनाएँ इसी क्षेत्र में उत्पन्न होती हैं।

2. समतापमण्डल (Stratosphere)-इस भाग का विस्तार पृथ्वी तल से 10 किमी से 50 किमी तक होता है। यह भाग धूल रहित, जल-वाष्प रहित होता है। इस भाग में ऊपर की ओर चलने पर ताप – 50°C से बढ़कर 10°C तक हो जाता है तथा वायु का घनत्व घटकर पृथ्वी तल पर घनत्व की तुलना में 10-3 हो जाता है। समतापमण्डल में पृथ्वी तल से 30 किमी से लेकर 50 किमी तक के भाग को ओजोन परत (ozone layer) कहते हैं। यह परत सूर्य से आने वाले अधिकांश पराबैंगनी विकिरणों का अवशोषण कर लेता है और इस प्रकार पृथ्वी के लिए सुरक्षा कवच का कार्य करती है।

3. मध्यमण्डल (Mesosphere)-इस भाग का विस्तार पृथ्वी तल से 50 किमी ऊँचाई से 80 किमी ऊँचाई तक होता है। इस भाग में ऊपर की ओर जाने पर ताप एकसमान रूप से 10°C से घटकर -90°C हो जाता है तथा वायु का घनत्व घटकर पृथ्वी तल पर घनत्व की तुलना में 10-3 से 10- हो जाता है। यह क्षेत्र उच्च आवृत्ति (H.F.) की विद्युतचुम्बकीय तरंगों के एक भाग को अवशोषित कर शेष भाग को अपने में से होकर पृथ्वी की ओर आने देता है।

4. आयनमण्डल (Ionosphere)-इस भाग का विस्तार पृथ्वी तल से 80 किमी ऊँचाई से 400 किमी ऊँचाई तक होता है। इस भाग में ऊपर की ओर जाने पर ताप एकसमान रूप से -93°C से 427°C तक बढ़ता है तथा वायु का घनत्व पृथ्वी तल पर घनत्व की तुलना में 10-5 से घटकर 10-10 गुना रह जाता है। आयनमण्डल के इस भाग को तापमण्डल (thermosphere) कहते हैं। सूर्य से आने वाली पराबैंगनी तथा X-किरणें इस भाग में आयनन (ionisation) उत्पन्न करती हैं, इसी कारण इस भाग में अधिकांशत: मुक्त इलेक्ट्रॉन व धन आयन होते हैं।

इसी कारण इस भाग को आयनमण्डल कहते हैं। पृथ्वी तल से लगभग 110 किमी की ऊँचाई पर इलेक्ट्रॉनों की सान्द्रता बहुत अधिक हो जाती है तथा इसका विस्तार लगभग 150 किमी तक ऊपर की ओर होता है, इस परत को E परत अथवा कैनेली हैवीसाइड परत (Kennelly-Heaviside Layer) कहते हैं। इसके पश्चात् पृथ्वी तल से 250 किमी की ऊँचाई तक इलेक्ट्रॉनों की सान्द्रता काफी घट जाती है। इसके ऊपर इलेक्ट्रॉनों की अपेक्षाकृत अधिक सान्द्रता की एक ओर परत होती है, जिसे F-परत अथवा एपल्टन परत (Appleton layer) कहते हैं।

आयनमण्डल की E तथा F परतों से रेडियो तरंगों का परावर्तन होता है। वह अधिकतम आवृत्ति जो आयनमण्डल द्वारा परावर्तित हो सकती है, क्रान्तिक आवृत्ति (critical frequency) कहलाती है, इसे ‘f_c‘ से प्रदर्शित करते हैं।
क्रान्तिक आवृत्ति \(f_{c}=9 \sqrt{N_{\max }}\)
जहाँ N_max आयनमण्डल की उस परत का (जहाँ परावर्तन होता है) अधिकतम इलेक्ट्रॉन घनत्व है।

प्रश्न 6.
वायुमण्डल में वैद्युतचुम्बकीय तरंगों का संचरण किस प्रकार होता है? समझाइए।
अथवा व्योम तरंगें क्या हैं? इनके संचरण का संक्षिप्त विवरण दीजिए।  [2018]
अथवा व्योम तरंग संचरण तथा आकाश तरंग संचरण से क्या तात्पर्य है?  [2014]
अथवा आकाश तरंग संचरण की आवृत्ति परास लिखिए।समझाइए कि इन तरंगों का संचरण कितने प्रकार से किया जाता है? [2018]
अथवा व्योम तरंगों तथा आकाश तरंगों का वर्णन कीजिए।  [2018]
अथवा सिद्ध किजिए कि आकाश तरंगों के संचरण हेतु एक टी०वी० प्रेषी ऐन्टिना जो पृथ्वी तल से h ऊँचाई पर है, का प्रसारण परास \(d=\sqrt{2 R h}\) है, जहाँ R पृथ्वी की त्रिज्या है। [2015,17]
अथवा एक टी०वी० ऐन्टिना की ऊँचाई मीटर है। दर्शाइए कि इसके द्वारा पृथ्वी की सतह पर दूरी \(d_{T}=\sqrt{2 h R} \sqrt{10 h}\) तक सिग्नल प्रसारित किया जा सकता है, यहाँ R पृथ्वी की त्रिज्या है।  [2018]
उत्तर
वायुमण्डल में वैद्युतचुम्बकीय तरंगों का संचरण अथवा विभिन्न संचार विधियाँ (Propagation of Electromagnetic Waves in Atmosphere or Different Modes of Propagation)-विभिन्न आवृत्ति परास की सूचना सिग्नलों के संचार के लिए भिन्न-भिन्न संचार विधियाँ प्रयुक्त की जाती हैं जो अग्र प्रकार हैं

1. भू-तरंग संचरण (Ground Wave Propagation)- वह रेडियो तरंग जो पृथ्वी के पृष्ठ के अनुदिश एक बिन्दु से दूसरे बिन्दु तक गमन करती हैं, भू-तरंग (ground wave) कहलाती हैं। किसी भी सिग्नल को उच्च दक्षता से विकिरित करने के लिए ऐन्टिना का न्यूनतम आकार सिग्नल की तरंगदैर्घ्य (2) का एक चौथाई (214) होना चाहिए। विद्युतचुम्बकीय तरंगें (रेडियो तरंगें) जिनकी आवृत्ति 500 किलोहर्ट्स से 1500 किलोहर्ट्स तक होती है का संचरण प्रेषित्र से अभिग्राही तक पृथ्वी तल के समीप वायुमण्डल में पृथ्वी सतह की चालकता के कारण समान्तर होता है।

भू-तरंगें गमन करते समय पृथ्वी पर आवेश प्रेरित करती हैं, जो तरंग के साथ आगे बढ़ता है तथा पृथ्वी की सतह पर प्रेरित धारा उत्पन्न करता है। प्रेरित धाराओं के प्रवाह के कारण इन तरंगों की प्रबलता क्षीण होती जाती है। पृथ्वी के समीप संचरित तरंगें ऊर्ध्वाधर तल में ध्रुवित होती हैं, अत: इनका विद्युत क्षेत्र पृथ्वी तल के समान्तर होता है, जिसका अवशोषण, पृथ्वी तल के प्रतिरोध तथा वस्तुओं द्वारा विवर्तन होने के कारण बहुत अधिक होता है।

विवर्तन के कारण ही तरंगों के आगे बढ़ने के साथ उनका झुकाव कोण बढ़ता जाता है और कुछ दूरी तय करने के बाद तरंग नीचे आ जाती है तथा समाप्त हो जाती है। अत: ये बहुत दूरी तक संचरित नहीं होती है। अधिक आवृत्ति की तरंगों का अवशोषण अधिक होने के कारण, अधिक आवृत्ति की रेडियो तरंगों का संचरण इस विधि में नहीं होता है। भू-तरंग संचरण का परास रेडियो तरंगों की आवृत्ति तथा प्रेषित्र की शक्ति पर निर्भर करता है।

2. व्योम तरंग संचरण (Sky Wave Propagation)-वे रेडियो तरंगें जिनका संचरण वायुमण्डल में आयनमण्डल की उपस्थिति के कारण होता है, व्योम तरंगें कहलाती हैं। व्योम तरंगों (sky waves) की आवृत्ति 3 मेगाहर्ट्स से 30 मेगाहर्ट्स तक होती है। ये तरंगें वायुमण्डल के आयनमण्डल द्वारा परावर्तित हो जाती हैं तथा इनसे उच्च आवृत्ति की विद्युतचुम्बकीय तरंगें आयनमण्डल को भेदकर पलायन कर जाती हैं।

इनका प्रेषित्र ऐन्टिना द्वारा वायुमण्डल में प्रसारण होता है तथा वायुमण्डल के आयनमण्डल द्वारा पूर्ण आन्तरिक परावर्तन होने के बाद ये अभिग्राही ऐन्टिना में प्रेरित विद्युत वाहक बल उत्पन्न करती हैं। व्योम तरंग संचरण उच्च आवृत्तियों की लम्बी दूरी तक (4000 किमी तक) संचरित करने के उपयोग में लायी जाती है।

3. आकाश तरंग अथवा क्षोभमण्डलीय संचरण (Space Wave or Tropospheric Propagation)- आकाश तरंगों की आवृत्ति 40 मेगाहर्टस से 300 मेगाहर्टस होती है। आकाश तरंगें प्रेषित्र ऐन्टिना से सीधे, पृथ्वी तल से परावर्तन के पश्चात् अथवा क्षोभमण्डल (troposphere) से परावर्तन के पश्चात् अभिग्राही ऐन्टिना तक पहुँचती है। इसलिए इनके संचरण को क्षोभमण्डलीय संचरण (tropospheric propagation) भी कहते हैं।

आकाश तरंग संचरण में परा उच्च आवृत्ति (UHF), अति उच्च आवृत्ति (VHF) तथा माइक्रोवेव (microwave) तरंगों का उपयोग किया जाता है। उच्च आवृत्ति का संचरण भू-तरंग तथा व्योम तरंग के द्वारा नहीं हो सकता है क्योंकि पृथ्वी की सतह पर बहुत कम दूरी तय करने पर अति उच्च आवृत्ति तथा परा उच्च आवृत्ति की तरंगें पूर्णत: अवशोषित हो जाती हैं तथा ये तरंगें आयनमण्डल से परावर्तित नहीं होतीं वरन् उससे पारगमित हो जाती हैं। आकाश तरंग संचरण दृष्टि रेखा संचार (Line of Sight distance, LOS) तथा पृथ्वी की वक्रता (curvature of the earth) द्वारा सीमित होता है।

इन तरंगों का संचरण निम्न दो प्रकार से किया जा सकता है-

• भू-स्थिर संचार उपग्रहों के द्वारा संचार उपग्रह सिग्नलों को परावर्तित कर अभिग्राही ऐन्टिना तक प्रेषित कर देता है।
• सीधे प्रेषित्र ऐन्टिना के द्वारा-इन विधि में प्रेषित्र ऐन्टिना से प्रसारित सिग्नल सीधे अभिग्राही ऐन्टिना तक पहुँच जाता है। दीर्घ दूरी तक प्रसारण के लिए प्रेषित्र ऐन्टिना की ऊँचाई अधिक रखी जाती है।

(a) प्रेषित्र ऐन्टिना की पृथ्वी से ऊँचाई (h) तथा पृथ्वी पर उसके परास (d) में सम्बन्ध [Relation between Height of Transmitting Antenna from Earth (h) and its Range on Earth (d)]-माना प्रेषित्र ऐन्टिना (T) की पृथ्वी से ऊँचाई h है तथा पृथ्वी का केन्द्र 0 व त्रिज्या R है। पृथ्वी की वक्रता के कारण पृथ्वी सतह के बिन्दुओं A व B से दूर सिग्नल प्राप्त नहीं किए जा सकते। यहाँ AT व BT क्रमशः बिन्दुओं A व B पर स्पर्श रेखाएँ हैं। माना d ऐन्टिना के आधार से पृथ्वी की दूरी है जहाँ तक सिग्नल प्राप्त होते हैं।
त्रिभुज TOA में,
OT² = (OA)² + (AT)²
जहाँ OT = R+ h, OA = R, AP ≈ AT = d (:: h << R)
अत: (R+ h)² = R² +d²
अत: R² + h² +2 Rh = R² +d²
अथवा h² +2Rh = d²
अथवा 2 Rh = d²
प्रसारण परास \(d=\sqrt{2 R h}\)

d वह दूरी है जहाँ तक प्रेषित्र ऐन्टिना से पृथ्वी पर सिग्नल पहुँचता है। यह प्रेषित्र ऐन्टिना की ऊँचाई h पर निर्भर करता है अर्थात् ऊँचाई h अधिक होने पर अधिक तथा कम होने पर कम होता है। . A वह क्षेत्रफल है, जहाँ तक ऐन्टिना द्वारा प्रेषित टी०वी० प्रसारण देखा जा सकता है
A= πd² = 2πRh
इस क्षेत्र में प्रसारण से लाभान्वित जनसंख्या = जनसंख्या घनत्व – क्षेत्रफल जिनमें TV सिग्नल प्रसारित हो सकता है।

(b) प्रेषित्र ऐन्टिना की ऊँचाई (h_t) तथा अभिग्राही ऐन्टिना की ऊँचाई (h_R) हो तो इनके मध्य संचरण दृष्टि रेखा (Line of Sight distance, LOS) की अधिकतम

दूरी-40 मेगाह से अधिक आवृत्तियों पर संचार केवल दृष्टि रेखीय (LOS-Line of Sight) द्वारा ही सम्भव है। LOS प्रकृति का संचार चित्र-15.4 में दर्शाया गया है, जिसमें पृथ्वी की वक्रता के कारण सीधी तरंगें किसी बिन्दु P पर अवरोधित हो जाती हैं, यदि सिग्नल को क्षैतिज से आगे (दृष्टि बाधित क्षेत्र में) प्राप्त करना है तो अभिग्राही ऐन्टिना की ऊँचाई h_R अधिक रखनी होगी जिससे वह LOS तरंगों को प्राप्त कर सके। यदि प्रेषक ऐन्टिना की ऊँचाई h_T,उससे क्षितिज बिन्दु P की दूरी d_T तथा अभिग्राही ऐन्टिना की ऊँचाई h_R, उससे क्षितिज बिन्दु P की दूरी d_R हो (चित्र-15.5) तथा दोनों ऐन्टिनाओं के बीच की अधिकतम दृष्टि रेखा की दूरी d_M हो, तो
\(d_{M}=d_{T}+d_{R}=\sqrt{2 R h_{T}}+\sqrt{2 R h_{R}}\)

प्रश्न 7.
मॉडुलेशन से क्या तात्पर्य है? इसकी आवश्यकता क्यों पड़ती है? समझाइए। [2015]
अथवा तरंगों के ‘मॉडुलन’ से क्या तात्पर्य है? किसी माध्यम में तरंगों के संचरण में मॉडुलन की आवश्यकता पर प्रकाश डालिए। [2018]
अथवा दो कारणों को लिखिए जिससे किसी सिग्नल के मॉडुलन की आवश्यकता स्पष्ट होती है।  [2014]
अथवा सिग्नल संचरण के लिए मॉडुलेशन की आवश्यकता क्यों है?  [2015]
उत्तर
मॉडुलन अथवा मॉडुलेशन तथा इसकी आवश्यकता (Modulation and its Need)-निम्न आवृत्ति की वैद्युतचुम्बकीय तरंगों को उच्च आवृत्ति की वाहक तरंगों पर अध्यारोपित करने की प्रक्रिया को मॉडुलन अथवा मॉडुलेशन कहते हैं। … निम्न आवृत्ति की अध्यारोपित की जाने वाली तरंगों को मॉडुलेटिंग तरंग (modulating waves) उच्च आवृत्ति की तरंगों को जिन पर निम्न आवृत्ति की तरंगें अध्यारोपित की जाती हैं, को वाहक तरंगें (carrier waves) तथा मॉडुलेशन प्रक्रिया के फलस्वरूप प्राप्त परिणामी तरंग को मॉडुलित तरंग (modulated waves) कहते हैं।

संचार निकाय में सन्देश सिग्नल श्रव्य आवृत्ति परास (20 हर्ट्स से 20000 हर्ट्स) के होते हैं। प्रेषित करने से पूर्व इनकों . माइक्रोफोन द्वारा विद्युत सिग्नल में परिवर्तित किया जाता है जिनका आवृत्ति परास भी इतना ही होता है। इन तरंगों को लम्बी दूरी तक प्रसारित नहीं किया जा सकता है इनके निम्नलिखित कारण हैं

1. ऐन्टिना का आकार (Size of Antenna)- किसी सन्देश सिग्नल को प्रेषित करने के लिए ऐन्टिना की आवश्यकता होती है। किसी सिग्नल को प्रसारित करने के लिए ऐन्टिना की लम्बाई सिग्नल की तरंगदैर्घ्य की कोटि की न्यूनतम 21 4 होनी चाहिए। श्रव्य तरंगों की आवृत्ति परास 20 हर्ट्स से 20 किलोहर्ट्स होती है जिनके लिए न्यूनतम तरंगदैर्घ्य λ = \(\frac { c}{ v }\)

मीटर=15000 मीटर है। अतः श्रव्य तरंगों को ऐन्टिना से प्रेषित करने के लिए उसकी न्यूनतम लम्बाई \(\frac { 15000 }{ 4 }\) मीटर के क्रम की होनी चाहिए, परन्तु इतनी लम्बाई का ऐन्टिना बनाना व्यावहारिक नहीं है। अत: श्रव्य तरंगों को ऐन्टिना से प्रसारित नहीं किया जा सकता है। यदि इन तरंगों को उच्च आवृत्ति (लगभग 106 हर्ट्स) की वाहक तरंगों पर अध्यारोपित कर दिया जाए तब आवश्यक ऐन्टिना की न्यूनतम लम्बाई \(\frac{\lambda}{4}=\frac{3 \times 10^{8}}{4 \times 10^{6}}\) मीटर होगी जोकि व्यावहारिक है।
अतः प्रेषण से पूर्व निम्न आवृत्ति के सिग्नल को उच्च आवृत्ति की तरंगों के साथ अध्यारोपित करना आवश्यक है।

2. ऐन्टिना द्वारा प्रभावी शक्ति विकिरण (Effective Power Radiation by Antenna)-किसी / लम्बाई के रेखीय ऐन्टिना द्वारा विकिरित शक्ति P तरंगदैर्घ्य 2 के वर्ग के व्युत्क्रमानुपाती होती है, अर्थात्
\(P \propto \frac{1}{\lambda^{2}}\)
अत: निम्न आवृत्ति एवं दीर्घ तरंगदैर्घ्य के आधार बैण्ड सिग्नल द्वारा प्रभावी शक्ति का विकिरण कम होगा, अत: अच्छे एवं प्रभावी प्रेषण के लिए उच्च शक्ति चाहिए जो उच्च आवृत्ति एवं कम तरंगदैर्घ्य के आधार बैण्ड सिग्नल से ही सम्भव है। अतः स्पष्ट है कि निम्न आवृत्ति के सिग्नल का उच्च आवृत्ति की तरंगों के साथ मॉडुलेशन करना आवश्यक है।

3. विभिन्न प्रेषित्रों से प्राप्त सिग्नलों का मिश्रण (Mixing of Signals obtained from Different Transmitters)-जब एकसाथ कई आधार बैण्ड सिग्नल प्रेषित किए जाते हैं तो वे परस्पर मिश्रित हो जाते हैं जिनमें विभेद करना सरल नहीं होता है। अत: इस कठिनाई को दूर करने के लिए निम्न आवृत्तिं सिग्नलों को उच्च आवृत्ति की तरंगों के साथ मॉडुलित कर प्रेषित किया जाता है तथा प्रत्येक प्रसारण स्टेशन को एक अलग आवृत्ति बैण्ड आवंटित कर देते हैं।

इस प्रकार स्पष्ट है कि निम्न आवृत्ति के सन्देश सिग्नलों को प्रेषित करने से पूर्व उनका उच्च आवृत्ति की वाहक तरंगों के साथ मॉडुलेशन आवश्यक होता है।

प्रश्न 8.
मॉडुलन कितने प्रकार के होते हैं? प्रत्येक को समझाइए।
अथवा आयाम मॉडुलन से क्या तात्पर्य है? एक आयाम मॉडुलक का परिपथ आरेख बनाइए।  [2014, 15]
अथवा आयाम मॉडुलित तरंग के उत्पादन हेतु आवश्यक नामांकित परिपथ आरेख बनाइए।   [2015,17]
अथवा परिपथ चित्र की सहायता से रेडियो प्रसारण में मॉडुलन की प्रक्रिया समझाइए।           [2015]
उत्तर
मॉडुलन के प्रकार (Types of Modulation)-निम्न आवृत्ति के सन्देश सिग्नल को उच्च आवृत्ति की वाहक . तरंगों के किस गुण में परिवर्तन कर अध्यारोपित किया गया है, इस आधार पर मॉडुलेशन निम्नलिखित प्रकार का होता है

1. आयाम मॉडुलन (Amplitude Modulation)- जब उच्च आवृत्ति की वाहक तरंगों के आयाम को निम्न आवृत्ति के श्रव्य सिग्नलों के संगत आयामों के अनुरूप परिवर्तित किया जाता है तो उनके परस्पर अध्यारोपण की प्रक्रिया आयाम मॉडुलन कहलाती है। भारत में अधिकांश रेडियो प्रसारण तथा टेलीविजन प्रसारण में वीडियो संकेतों को आयाम मॉडुलित तरंगों द्वारा प्रसारित किया जाता है। आयाम मॉडुलक का परिपथ आरेख चित्र-16.6 में प्रदर्शित है।

2. आवृत्ति मॉडुलन (Frequency Modulation)- जब उच्च आवृत्ति की वाहक तरंगों की आवृत्ति को श्रव्य संकेतों के संगत आयामों के अनुरूप परिवर्तित किया जाता तो उनके परस्पर अध्यारोपण की प्रक्रिया आवृत्ति मॉडुलन कहलाती है। भारत में कुछ रेडियो स्टेशनों से तथा टेलीविजन प्रसारण में ध्वनि संकेतों को आवृत्ति मॉडुलित कर प्रसारित किया जाता है।

3. कला मॉडुलन (Phase Modulation)- जब उच्च आवृत्ति की वाहक तरंगों की कला (phase) को श्रव्य तरंगों के संगत आयामों के अनुरूप परिवर्तित किया जाता है तो उनके परस्पर अध्यारोपण की प्रक्रिया कला मॉडुलन कहलाती है।

प्रश्न 9.
आयाम मॉडुलन को स्पष्ट करके मॉडुलन सूचकांक अथवा गुणांक को समझाइए।
उत्तर
आयाम मॉडुलन (Amplitude Modulation)-माना किसी क्षण t पर सूचना सिग्नल (मॉडुलक सिग्नल) की वोल्टता समीकरण निम्नलिखित है –
e_m = E_m sinω_mt
जहाँ E_m = सिग्नल का आयाम, ω_m = सिग्नल की कोणीय आवृत्ति तथा ω_m = 2 πv_m
जहाँ ν_m सूचना सिग्नल की आवृत्ति है।
किसी क्षण t पर वाहक तरंग का वोल्टता समीकरण e_c = E_c sinω_ct
जहाँ E_c = वाहक तरंग का आयाम, ω_c = वाहक तरंग की कोणीय आवृत्ति तथा ω_c= 2 πV_c.
जहाँ ν_c वाहक तरंग की आवृत्ति है।
आयाम मॉडुलेशन में मॉडुलित तरंग का आयाम सूचना सिग्नल (मॉडुलक सिग्नल) के आयाम की भाँति समय के साथ बदलता है, अत: मॉडुलित तरंग का आयाम
E= E_c + e_m = E_c + E_m sinω_m t
चित्र-15.6 में परिणामी आयाम मॉडुलित तरंग प्रदर्शित है।
मॉडुलित तरंग का वोल्टता समीकरण
e = E sinω_ct = (E_c + E_m sinω_mt) sinω_ct
\(=E_{c}\left[1+\frac{E_{m}}{E_{c}} \sin \omega_{m} t\right] \sin \omega_{c} t\)
e= E_c(1+ m_α sinω_mt)sinω_ct

जहाँ mα \(\frac{E_{m}}{E_{c}}\) मॉडुलन गुणांक (modulation factor) अथवा मॉडुलन सूचकांक (modulation index)
अथवा मॉडुलन की गहराई (depth of modulation) अथवा मॉडुलन की मात्रा (degree of modulation) कहलाता है।

यह मॉडुलित तरंग का समीकरण है तथा इसके वोल्टेज स्वरूप को चित्र-15.6 में प्रदर्शित किया गया है। इस प्रकार आयाम मॉडुलित तरंग में तीन घटक तरंगें उपस्थित हैं

इस प्रकार स्पष्ट है कि मॉडुलित तरंग में मूल वाहक तरंग की आवृत्ति अपरिवर्तित रहती है। है तो दो अन्य आवृत्तियों (f_c-f_m)तथा (f_c+f_m) की तरंगें उत्पन्न होती है। इन आवृत्तियों को पार्श्व बैण्ड आवृत्तियाँ (side band frequency) कहते हैं। (f_c-f_m) को निम्न पार्श्व बैण्ड आवृत्ति (Lower Side Band Frequency अर्थात् LSB) तथा (f_c+f_m) को उच्च पार्श्व बैण्ड आवृत्ति (Upper Side Band Frequency अर्थात् USB) कहते हैं।

आयाम मॉडुलित तरंग का आवृत्ति स्पेक्ट्रम (Frequency Spectrum of Amplitude Modulated Wave)-आयाम मॉडुलित तरंग का आवृत्ति स्पेक्ट्रम चित्र-15.7 में प्रदर्शित किया गया है। जिससे स्पष्ट है कि मॉडुलित तरंग वाहक तरंग की आवृत्ति f_c के दोनों ओर समान आवृत्ति अन्तराल f_m पर स्थित है।
आयाम मॉडुलित तरंग की बैण्ड-चौड़ाई
= (f_c+f_m-f_c-f_m)= 2f_m
अतः आयाम मॉडुलित तरंग की बैण्ड-चौड़ाई सूचना सिग्नल (मॉडुलक सिग्नल) की आवृत्ति की दोगुनी होती है।

प्रश्न 10.
आयाम मॉडुलित तरंग का उत्पादन समझाइए। अथवा आयाम मॉडुलन क्या है? परिपथ आरेख द्वारा एक आयाम मॉडुलित तरंग कैसे प्राप्त करते हैं, समझाइए। [2018]
उत्तर
आयाम मॉडुलन-जब उच्च आवृत्ति की वाहक तरंगों के आयाम को निम्न आवृत्ति के श्रव्य सिग्नलों के संगत आयाम के अनुरूप परिवर्तित किया जाता है तो उनके परस्पर अध्यारोपण की प्रक्रिया आयाम मॉडुलन कहलाती है।

आयाम मॉडुलित तरंगों का उत्पादन (Production of Amplitude Modulation)- आयाम मॉडुलित तरंग के उत्पादन के लिए संयोजन को चित्र-15.8 में प्रदर्शित किया गया है। यह परिपथ n-p-n ट्रांजिस्टर वाहक तरंगों के लिए उभयनिष्ठ उत्सर्जक प्रवर्धक की भाँति कार्य करता है। इस परिपथ में वाहक तरंग को आधार B पर लगाया जाता है जोकि संधारित्र C से होकर जाता है। इस प्रकार संधारित्र C केवल AC घटकों को ही जाने देता है। इसके आधार पर मॉडुलक सिग्नल e_m = E_m sinω_mt को इस प्रकार लगाया जाता है कि आधार बायस वोल्टेज के साथ मॉडुलक सिग्नल भी निवेशित हो।

इस प्रकार आधार वोल्टता स्थिर नहीं,रहती बल्कि यह मॉडुलक सिग्नल के तात्कालिक मान के अनुसार परिवर्तित होती रहती है। अतः आधार उत्सर्जक के बीच निवेशी वोल्टता, मॉडुलक सिग्नल के अनुसार परिवर्तित होती है जिसके कारण निर्गत वोल्टता भी उसी के अनुसार प्रवर्धित होती है। इस प्रकार निर्गम में आयाम मॉडुलित तरंग प्राप्त हो जाती है।

प्रश्न 11.
आयाम मॉडुलित तरंग का संसूचन (अथवा विमॉडुलन) को स्पष्ट कीजिए।
उत्तर
आयाम मॉडुलित तरंग का संसूचन अथवा विमॉडुलन (Demodulation of Amplitude Modulated Wave)-अभिग्राही द्वारा मॉडुलित तरंग से श्रव्य सिग्नल (मूल सिग्नल) प्राप्त करने की प्रक्रिया को विमॉडुलन अथवा संसूचन
कहते हैं।
विमॉडुलन की आवश्यकता- संचार माध्यम से प्रसारित होते समय आयाम मॉडुलित संदेश क्षीण हो जाता है। अतः अभिग्राही ऐन्टिना द्वारा प्राप्त सिग्नल को प्रवर्धित एवं संसूचित करना पड़ता है। इस प्रक्रिया में निम्नलिखित दो क्रियाएँ होती हैं

• मॉडुलित तरंग का दिष्टकरण
• मॉडुलित तरंग से वाहक तरंग घटक को अलग करना।

आयाम मॉडुलित तरंग के लिए डायोड संसूचक- p-n सन्धि डायोड संसूचक सामान्यतया विमॉडुलन के लिए प्रयुक्त किया जाता है। इसका परिपथ चित्र-15.9 में प्रदर्शित है। इसके निवेशी परिपथ में स्वप्रेरकत्व L तथा परिवर्ती संधारित्र C परस्पर समान्तर क्रम में संयोजित होते हैं। इस परिपथ को स्वसरित परिपथ (tuned circuit) कहते हैं। ग्राही ऐन्टिना पर आने वाली विभिन्न रेडियो सिग्नलों में से वांछित रेडियो आवृत्ति सिग्नल को संधारित्र C को समायोजित करके अनुनाद के आधार पर चयन कर लिया जाता है।

p-n सन्धि डायोड इस सिग्नल का दिष्टकरण कर देता है। इस दिष्टकारी सिग्नल को उच्च प्रतिरोध के लोड प्रतिरोध R, तथा उपमार्गी संधारित्र CB (bypass condenser) के समान्तर-क्रम संयोजन पर लगाया जाता है। संधारित्र का प्रतिघात \(\left(X_{C}=\frac{1}{2 \pi f C_{B}}\right)\) उच्च आवृत्तियों के लिए कम तथा निम्न आवृत्तियों के लिए अधिक होता है। अतः संधारित्र का प्रतिघात वाहक तरंगों के लिए कम व श्रव्य तरंगों के लिए अधिक होता है। अत: उच्च आवृत्ति की वाहक रेडियो तरंगों के अवयव उपमार्गी संधारित्र से गुजरकर पृथ्वी में चले जाते हैं तथा निम्न आवृत्ति की श्रव्य तरंगों के अवयव लोड प्रतिरोध (R_L) के सिरों पर प्राप्त हो जाते हैं। यह श्रव्य तरंगें हैडफोन में धारा भेजते हैं जिनके संगत मूल श्रव्य सिग्नल उत्पन्न होते हैं।

संसूचन के लिए आवश्यक प्रतिबन्ध- फिल्टर परिपथ से जुड़े संधारित्र की धारिता इतनी होनी चाहिए कि
(1) जब रेडियो आवृत्ति f_c के लिए, प्रतिघात \(\left(x_{C}=\frac{1}{2 \pi f_{c} C_{B}}\right)\) प्रतिरोध R_L की तुलना में बहुत कम हो,
अर्थात् x_c << R_L अथवा \(\frac{1}{2 \pi f_{c} C_{B}}<<R_{L}\).

(2) जब श्रव्य आवृत्ति f_m के लिए, प्रतिघात, प्रतिरोध R_L की तुलना में बहुत अधिक हो,
अर्थात् \(\frac{1}{\omega_{m} C_{B}}>>R_{L}\) अथवा \(\frac{1}{2 \pi f_{m} C_{B}}>>R_{L}\)

संचार व्यवस्था  लघु उत्तरीय प्रश्नोत्तर

प्रश्न 1.
संचार व्यवस्था से क्या तात्पर्य है? इसके कौन-कौन से अवयव है?
उत्तर
संचार व्यवस्था-सन्देशों अथवा सूचनाओं को किसी विधि द्वारा एक स्थान से सम्प्रेषित करके दूसरे स्थान पर ग्रहण करने की व्यवस्था को संचार व्यवस्था कहते हैं। इसके तीन अवयव हैं-

• प्रेषित्र
• संचार चैनल तथा
• अभिग्राही।

प्रश्न 2.
ट्रान्सड्यूसर क्या है?
उत्तर
ट्रान्सड्यूसर-एक ऐसी युक्ति जो ऊर्जा के एक रूप को दूसरे में परिवर्तित कर देती है, ट्रान्सड्यूसर कहलाती है।

प्रश्न 3.
सिग्नल की बैण्ड-चौड़ाई से आप क्या समझते हैं? [2014, 17]
उत्तर
बैण्ड-चौड़ाई-अधिकतम तथा न्यूनतम आवृत्तियों के अन्तर को आवृत्ति परास अथवा सिग्नल की बैण्ड-चौड़ाई कहते हैं।

प्रश्न 4.
क्षीणता क्या होती है?
उत्तर
क्षीणता-संचार माध्यम में संचरण के समय सिग्नल की प्रबलता में क्षति होने की प्रक्रिया क्षीणता कहलाती है।

प्रश्न 5.
मॉडुलेशन से क्या तात्पर्य है? [2015]
अथवा मॉडुलन का क्या अर्थ है?[2015, 16, 17]
उत्तर
मॉडुलन अथवा मॉडुलेशन-वह क्रिया जिसमें प्रेषित्र (प्रेषी) पर, निम्न आवृत्ति की विद्युतचुम्बकीय तरंगों को उच्च आवृत्ति की वाहक तरंगों पर अध्यारोपित कराया जाता है, मॉडुलन अथवा मॉडुलेशन कहलाती है।

प्रश्न 6.
मॉडुलित तरंग क्या है? [2014]
उत्तर
मॉडुलित तरंग- मॉडुलन अथवा मॉडुलेशन की प्रक्रिया के फलस्वरूप प्राप्त परिणामी तरंग मॉडुलित तरंगा कहलाती है।

प्रश्न 7.
आयाम मॉडुलन का अर्थ स्पष्ट कीजिए। [2014, 16, 17]
उत्तर
आयाम मॉडुलन (AM)-किसी उच्च आवृत्ति की वाहक तरंग के आयाम को ध्वनि तरंग के आयाम के अनुसार, परिवर्तित कर अध्यारोपित करने की प्रक्रिया आयाम मॉडुलन कहलाती है।

प्रश्न 8.
आवृत्ति मॉडुलन (FM) से आप क्या समझते हैं? [2016]
उत्तर
आवृत्ति मॉडुलन (FM)—जब उच्च आवृत्ति की वाहक तरंगों की आवृत्ति को श्रव्य संकेतों के संगत आयामों के अनुरूप परिवर्तित किया जाता है तो उनके परस्पर अध्यारोपण की प्रक्रिया आवृत्ति मॉडुलन कहलाती है। भारत में कुछ रेडियो स्टेशनों से तथा टेलीविजन प्रसारण में ध्वनि संकेतों को आवृत्ति मॉडुलित कर प्रसारित किया जाता है।

प्रश्न 9.
विमॉडुलन का क्या अर्थ है? [2015,17]
उत्तर
विमॉडुलन अथवा डिमॉडुलेशन-वह प्रक्रिया जिसमें अभिग्राही से प्राप्त मॉडुलेटिड तरंगों में से मूल वैद्युतचुम्बकीय तरंगों को अलग कर दिया जाता है विमॉडुलन अथवा डिमॉडुलेशन कहलाती है।

प्रश्न 10.
आयाम मॉडुलेशन संचार व्यवस्था में बैण्ड-चौड़ाई का सूत्र क्या है? [2017]
उत्तर
आयाम मॉडुलित तरंग की बैण्ड-चौड़ाई = (f_c + f_m)- (f_c – f_m)= 2f_m.

प्रश्न 11.
वाहक तरंगें क्या होती हैं? समझाइए। [2018]
उत्तर
वाहक तरंगें उच्च आवृत्ति तथा नियत आयाम की वे विद्युतचुम्बकीय तरंगें जो पृथ्वी तल पर श्रव्य आवृत्ति की तरंगों को एक स्थान से दूसरे स्थान तक ले जाती हैं वाहक तरंगें कहलाती हैं। .

प्रश्न 12.
प्रसारण से पूर्व ध्वनि तरंगों को मॉडुलित करना क्यों आवश्यक है?
उत्तर
ध्वनि तरंगों को बिना मॉडुलित किए प्रसारित करने के लिए अधिक ऊँचाई (7.5 किमी) के प्रसारण ऐन्टिना की आवश्यकता होती है, जिसे लगा पाना असम्भव है। इसके अतिरिक्त इन तरंगों की ऊर्जा कुछ दूरी तक जाते-जाते समाप्त हो जाती है।

प्रश्न 13.
भू-तरंगें क्या हैं?
उत्तर
भू-तरंगें- यदि प्रेषित्र ऐन्टिना से कोई रेडियो तरंग अभिग्राही ऐन्टीना पर सीधे अथवा पृथ्वी से परावर्तित होकर पहुँचती है तो वे भू-तरंगें कहलाती हैं।

प्रश्न 14.
ट्रान्सपोंडर किसे कहते हैं?
उत्तर
ट्रान्सपोंडर-ट्रान्सपोंडर संचार उपग्रह में लगाई जाने वाली एक ऐसी युक्ति है जो सिग्नल को ग्रहण करके उन्हें प्रवर्धित करती है तथा उनका पुनः प्रसारण करती है।

प्रश्न 15.
भू-स्थैतिक (geo-stationary) अथवा तुल्यकाली उपग्रह का क्या अर्थ है?
उत्तर
भू-स्थैतिक अथवा तुल्यकाली उपग्रह- यह एक ऐसा उपग्रह होता है जो पृथ्वी के किसी एक स्थान के सापेक्ष स्थिर रहता है। इस उपग्रह का पृथ्वी के विषुवत् तल में परिक्रमण काल 24 घण्टा होता है। इसे तुल्यकाली उपग्रह (geo-synchronus satellite) भी कहते हैं।

प्रश्न 16.
क्या लम्बी दूरी के दूरदर्शन प्रसारण के लिए उपग्रह को प्रयोग करना आवश्यक है?
उत्तर
हाँ, दूरदर्शन प्रसारण में अति उच्च आवृत्ति की (UHF) तरंगों का प्रयोग किया जाता है। ये तरंगें पृथ्वी के आयनमण्डल को पार करके अन्तरिक्ष में निकल जाती हैं। अतः इन्हें पृथ्वी पर वापस भेजने के लिए उपग्रहों का उपयोग करना आवश्यक है।

प्रश्न 17.
अधिकतम दृष्टि रेखा दूरी के लिए सूत्र लिखिए।
उत्तर
अधिकतम दृष्टि रेखा दूरी d_m = d_T + d_R = \(\sqrt{2 R h_{T}}+\sqrt{2 R h_{R}}\)

प्रश्न 18.
आकाश तरंगों का संचरण किन विधियों से किया जाता है? [2017]
उत्तर

• भू-स्थिर संचार उपग्रहों के द्वारा तथा
• सीधे प्रेषित ऐन्टिना के द्वारा।

प्रश्न 19.
क्रान्तिक आवृत्ति से क्या तात्पर्य है?
उत्तर
क्रान्तिक आवृत्ति-वह अधिकतम आवृत्ति, जो आयनमण्डल द्वारा परावर्तित हो सकती है क्रान्तिक आवृत्ति कहलाती है। इसे ‘f_c‘ से प्रदर्शित करते हैं। \(f_{c}=9 \sqrt{N_{\mathrm{max}}}\)
जहाँ N_max आयनमण्डल की उस परत का (जहाँ पर परावर्तन होता है) अधिकतम इलेक्ट्रॉन घनत्व है।

प्रश्न 20. सिद्ध कीजिए कि आकाश तरंगों के संचरण हेतु एक टी०वी० प्रेषी ऐन्टिना जो पृथ्वी तल से ऊँचाई पर है, का प्रसारण परास \(d=\sqrt{2 R h}\) है, जहाँ R पृथ्वी की त्रिज्या है। [2015]
उत्तर
प्रेषित्र ऐन्टिना की पृथ्वी से ऊँचाई (h) तथा पृथ्वी पर उसके परास (d) में सम्बन्ध-माना प्रेषित्र ऐन्टिना (T) की । पृथ्वी से ऊँचाई h है तथा पृथ्वी का केन्द्र 0 व त्रिज्या R है। पृथ्वी की वक्रता के कारण पृथ्वी सतह के बिन्दुओं A व B से दूर सिग्नल प्राप्त नहीं किए जा सकते। यहाँ AT व BT क्रमशः बिन्दुओं A व B पर स्पर्श रेखाएँ हैं। माना d ऐन्टिना के आधार से पृथ्वी की दूरी है जहाँ तक सिग्नल प्राप्त होते हैं।
त्रिभुज TOA में,
OT² = (OA)² + (AT)²
जहाँ OT = R+ h, OA = R, AP ≈ AT = d ∵ h << R
अतः (R+ h)² = R² + d²
अतः R² + h² +2Rh = R² +d²
अथवा h² +2Rh = d²
अथवा  2Rh ≈ d²
प्रसारण परास \(d=\sqrt{2 R h}\)

संचार व्यवस्था  अति लघु उत्तरीय प्रश्नोत्तर

प्रश्न 1.
संचार से क्या तात्पर्य है?
उत्तर
संचार-सूचना के प्रसारण तथा अभिग्रहण की प्रक्रिया को संयुक्त रूप से संचार कहा जाता है।

प्रश्न 2.
संचार व्यवस्था का नाम बताइए जिसमें\

• सिग्नल, सूचना अथवा संदेश के समरूप तथा सतत होते हैं,
• सिग्नल, मूल सूचना के द्विआधारी पद्धति में परिवर्तित रूप में होते हैं।

उत्तर

• ऐनालोग (analog) संचार व्यवस्था,
• डिजिटल (digital) संचार व्यवस्था।

प्रश्न 3.
दिए गए ब्लॉक आरेख में संचार व्यवस्था के x तथा Y भागों को पहचानिए [2017]

उत्तर
X-सूचना स्रोत, Y-चैनल।

प्रश्न 4.
मॉडुलन सूचकांक क्या है? इसकी क्या महत्ता है? अथवा मॉडुलन गुणांक की परिभाषा दीजिए। [2017]
उत्तर
मॉडुलन सूचकांक अथवा गुणांक-मॉडुलक तरंग के आयाम (E_m) तथा वाहक तरंग के आयाम (E_c) के अनुपात को मॉडुलन सूचकांक अथवा गुणांक कहते हैं। इसे ‘m_a‘ से प्रदर्शित करते हैं।
\(m_{a}=\frac{E_{m}}{E_{c}}\)
महत्ता- मॉडुलन सूचकांक, मॉडुलन तरंग की गुणवत्ता को प्रदर्शित करता है।

प्रश्न 5.
मॉडुलक का अर्थ स्पष्ट कीजिए।
उत्तर
मॉडुलक- किसी उच्च आवृत्ति की वाहक तरंग को मॉडुलित करने वाली युक्ति मॉडुलक कहलाती है।

प्रश्न 6.
आयाम मॉडुलन का अर्थ स्पष्ट कीजिए। [2014, 16]
उत्तर
आयाम मॉडुलन- किसी उच्च आवृत्ति की वाहक तरंग के आयाम को ध्वनि तरंग के आयाम के अनुसार परिवर्तित कर अध्यारोपित करने की प्रक्रिया आयाम मॉडुलन कहलाती है।

प्रश्न 7.
ध्वनि सिग्नल के व्यापार प्रसारण में कौन-सा मॉडुलन प्रयोग किया जाता है?
उत्तर
आयाम मॉडुलन।

प्रश्न 8.
दूरदर्शन के प्रसारण में कौन-सा मॉडुलन प्रयोग किया जाता है?
उत्तर
आवृत्ति मॉडुलन।

प्रश्न 9.
ऐन्टिना का क्या कार्य है? इसकी न्यूनतम लम्बाई कितनी होती है? [2017]
उत्तर
ऐन्टिना का कार्य–ऐण्टिना तरंगों को प्रेषित व ग्रहण करने के लिए प्रेषित व अभिग्राही में प्रयुक्त किया जाता है। ऐन्टिना की न्यूनतम लम्बाई = \(\frac { λ }{ 4 }\)

प्रश्न 10.
ऐन्टिना द्वारा प्रभावी विकिरित शक्ति तरंगदैर्घ्य के साथ किस प्रकार परिवर्तित होती है?
उत्तर
\(P \propto \frac{1}{\lambda^{2}}\)

प्रश्न 11.
वाहक तरंगों की आवृत्ति कितनी होनी चाहिए?
उत्तर
वाहक तरंगों की आवृत्ति उच्च (किलोहर्ट्स से गीगाहर्ट्स की परास में) होनी चाहिए।

प्रश्न 12.
आयाम मॉडुलेशन संचार व्यवस्था में बैण्ड-चौड़ाई का सूत्र क्या है?
उत्तर
आयाम मॉडुलित तरंग की बैण्ड-चौड़ाई = (f_c + f_m) – (f_c – f_m)= 2f_m.

प्रश्न 13.
आयाम मॉडुलित तरंग में तीन आवृत्तियाँ कौन-सी हैं? अथवा आयाम मॉडुलित तरंगों में उपस्थित आवृत्तियों का उल्लेख कीजिए। [2016]
उत्तर
तीन आवृत्तियाँ हैं
निम्न पार्श्व बैण्ड आवृत्ति (f_c – f_m) उच्च पार्श्व बैण्ड आवृत्ति (f_c + f_m) तथा वाहक तरंग की आवृत्ति (f_c) जहाँ (f_m) मॉडुलन तरंग की आवृत्ति है।

प्रश्न 14.
LSB तथा USB क्या हैं?
उत्तर
निम्न पार्श्व बैण्ड आवृत्ति LSB = (f_c – f_m) तथा उच्च पार्श्व बैण्ड आवृत्ति USB = (f_c + f_m)

प्रश्न 15.
आवृत्ति मॉडुलन (FM) से आप क्या समझते हैं? [2016]
उत्तर
आवृत्ति मॉडुलन (FM)- जब उच्च आवृत्ति की वाहक तरंगों की आवृत्ति को श्रव्य संकेतों के संगत आयामों के अनुरूप परिवर्तित किया जाता तो उनके परस्पर अध्यारोपण की प्रक्रिया आवृत्ति मॉडुलन कहलाती है। भारत में कुछ रेडियो स्टेशनों से तथा टेलीविजन प्रसारण में ध्वनि संकेतों को आवृत्ति मॉडुलित कर प्रसारित किया जाता है।

प्रश्न 16.
विमॉडुलन का क्या अर्थ है? [2015]
उत्तर
विमॉडुलन अथवा डिमॉडुलेशन-वह प्रक्रिया जिसमें अभिग्राही से प्राप्त मॉडुलेटिड तरंगों में से मूल विद्युतचुम्बकीय तरंगों को अलग कर दिया जाता है विमॉडुलन अथवा डिमॉडुलेशन कहलाती है।

प्रश्न 17.
टी०वी० संकेतों का आवृत्ति परास कितना है इनका सम्प्रेषण किस प्रकार करते हैं?
उत्तर
30 मेगाहर्ट्स से 300 मेगाहर्ट्स तक। इनका सम्प्रेषण ऐनालोग की संचार विधि से करते हैं।

प्रश्न 18.
15 किलोहर्ट्स से उच्च आवृत्ति की तरंगों का प्रसारण भू-तरंगों द्वारा क्यों सम्भव नहीं है?
उत्तर
15 किलोह से उच्च आवृत्ति की तरंगें थोड़ी ही दूरी पर पृथ्वी की सतह द्वारा अवशोषित कर ली जाती हैं। अत: इनका प्रसारण भू-तरंगों द्वारा सम्भव नहीं है।

प्रश्न 19.
30 मेगाहर्ट से उच्च आवृत्ति की तरंगों का प्रसारण व्योम तरंगों द्वारा सम्भव नहीं है, क्यों?
उत्तर
30 मोगाहर्ट्स से उच्च आवृत्ति की तरंगें पृथ्वी के आयनमण्डल द्वारा वापस पृथ्वी की ओर परावर्तित नहीं होती, अपितु आयनमण्डल को पार करके अन्तरिक्ष से निकल जाती हैं। इसी कारण इनका प्रसारण व्योम तरंगों द्वारा सम्भव नहीं है।

प्रश्न 20.
व्योम तरंगें क्या है? इसकी आवृत्ति परास बताइए। [2014, 17]
उत्तर
व्योम तरंगें (Sky waves)-वे रेडियो तरंगें जो पृथ्वी के आयनमण्डल द्वारा वापस पृथ्वी की ओर परावर्तित कर दी जाती हैं, व्योम तरंगें कहलाती हैं। इनकी आवृत्ति 3 मेगाहर्ट्स से 30 मेगाहर्ट्स के बीच होती है।

प्रश्न 21.
व्योम तरंग का संचरण क्या है?
उत्तर
व्योम तरंग का संचरण-व्योम तरंगों का संचरण वायुमण्डल में उपस्थित आयनमण्डल के कारण होता है जिसके गुण समय के साथ-साथ बदलते रहते हैं। इस प्रकार व्योम तरंगों द्वारा संचरण अविश्वसनीय है। आयनमण्डल की ऊँचाई पृथ्वी की सतह से लगभग 80 किमी से 400 किमी तक होती है।

प्रश्न 22.
आकांश तरंगें क्या हैं? इन तरंगों के संचरण के लिए प्रयुक्त आवृत्ति परास क्या है? [2014, 15, 17]
उत्तर
आकाश तरंगें (Space Waves)-आकाश तरंगें प्रेषी ऐन्टिना से सीधे, पृथ्वी तल से परावर्तन के पश्चात् अभिग्राही पर लौट आती हैं, इसीलिए इनके संचरण को क्षोभमण्डलीय संचरण भी कहते हैं। इनकी आवृत्ति 40 मेगाहर्ट्स से 300 मेगाहर्ट्स होती है।

प्रश्न 23.
आकाश तरंग संचरण क्या है?
उत्तर
आकाश तरंग संचरण-तरंग संचरण की वह प्रक्रिया, जिसमें आकाश तरंगें, प्रेषण ऐन्टिना से अभिग्राही ऐन्टिना तक दृष्टि रेखा पथ पर गमन करती हैं, आकाश तरंग संचरण कहलाता है।

प्रश्न 24.
तरंगसंचरण में ‘दृष्टि रेखा पथ (LOS) से क्या तात्पर्य है? किन तरंगों में इसका प्रयोग होता है? [2008]
उत्तर
दृष्टि रेखा पथ (LOS)-प्रेषी से ग्राही तक तरंगों के सीधे सरल रेखीय पथ को दृष्टि रेखा पथ (LOS) कहते हैं। आकाश तरंग संचरण दृष्टि रेखा पथ (LOS) से सीमित होता है।

प्रश्न 25.
भू-तरंगों की आवृत्ति कितनी होती है?
उत्तर
500 किलोह से 1500 किलोहर्ट्स तक।

प्रश्न 26.
विद्युतचुम्बकीय तरंगों के संचरण की तीन विधियाँ लिखिए। [2015]
उत्तर

• भू-तरंगों का संचरण
• व्योम तरंगों का संचरण तथा
• आकाश तरंगों का संचरण।

प्रश्न 27.
सूक्ष्म तरंगों (microwaves) के संचार में बार-बार अभिग्रहण तथा पुनः प्रसारण की आवश्यकता क्यों होती है?
उत्तर
क्योंकि ये तरंगें दृष्टि रेखा संचार व्यवस्था द्वारा प्रसारित होती हैं।

प्रश्न 28.
सम्पूर्ण पृथ्वी को दूर संचार सिग्नलों से आच्छादित करने के लिए कितने भू-स्थैतिक उपग्रह आवश्यक हैं?
उत्तर
कम-से-कम तीन।

प्रश्न 29.
कौन-सी तरंगों का प्रसारण दृष्टि रेखा संचरण के द्वारा होता है?
उत्तर
आकाश तरंगों का।

प्रश्न 30.
प्रकाशिक तन्तु (optical fibre) का सिद्धान्त बताइए।
उत्तर
प्रकाशिक तन्तु पूर्ण आन्तरिक परावर्तन के सिद्धान्त पर कार्य करता है।

संचार व्यवस्था आंकिक प्रश्नोत्तर

प्रश्न 1.
एक दूरदर्शन टावर की ऊँचाई 75 मीटर है। अधिकतम दूरी क्या है जो यह दूरदर्शन प्रसारण ग्रहण कर सकता है? [2015]
हल
अधिकतम दूरी d = \(\sqrt{2 R h}=\sqrt{2 \times 6.4 \times 10^{6} \times 75}\)
= 30.98 × 10³ मीटर।

प्रश्न 2.
प्रेषण एन्टिना की ऊँचाई क्या होगी यदि टी०वी० प्रसारण 128 किमी तक पहुँचाना है? [2018]
हल
दिया है, d = 128 किमी = 128 × 10³ मीटर, R= 6.4 × 10⁶ मीटर

प्रश्न 3.
एक टी०वी० टावर की ऊँचाई 45 मीटर है। इसकी विस्तार दूरी क्या होगी? इन संकेतों को 40 किमी की दूरी पर प्राप्त करने के लिए अभिग्राही ऐन्टिना की न्यूनतम ऊँचाई क्या होगी? (पृथ्वी की त्रिज्या = 6400 किमी)
हल
दिया है, टी०वी० टावर की ऊँचाई (h_T) = 45 मीटर, पृथ्वी की त्रिज्या (R) = 6400 किमी = 6400 × 10³ मीटर

प्रश्न 4.
किसी प्रेषी एन्टिना की ऊँचाई 72 मीटर है। यदि पृथ्वी की त्रिज्या 6250 किमी ली जाए तो एन्टिना द्वारा प्रसारण के लिए प्रसारण क्षेत्रफल ज्ञात कीजिए। [2018]
हल :
प्रसारण क्षेत्रफल (A) = πd² = π × 2 Rh
= 3.14 × 2 × 6250 x 10³ × 72 = 2.826 × 10⁹ मीटर²
= 2826 किमी²।

प्रश्न 5.
एक टी०वी० टावर की ऊँचाई एक दिए गए स्थान पर 500 मीटर है। यदि पृथ्वी की त्रिज्या 6400 किमी हो, तो – इसके प्रसारण परास की गणना कीजिए। [2015, 17]
हल
दिया है, h = 500 मीटर, R= 6400 किमी = 6400 × 10³ मीटर
प्रसारण परास = \(\sqrt{2 h R}=\sqrt{2 \times 500 \times 6400 \times 10^{3}}\)
= 80 × 10³ मीटर = 80 किमी।

प्रश्न 6.
एक वाहक तरंग प्रदर्शित की जाती है
C(t) = 4 sin (8πt) वोल्ट
यदि मॉडुलक सिग्नल तरंग का आयाम 1.0 वोल्ट हो, तब मॉडुलन सूचकांक का मान क्या है?
उत्तर
दिया है, Em = 1.0 वोल्ट, E_c = 4.0 वोल्ट, m_α = ?
मॉडुलन सूचकांक m_α = \(\frac{E_{m}}{E_{c}}\) = \(\frac { 1 }{ 4 }\) ≈ 0.25.

प्रश्न 7.
किसी मॉडुलित वाहक तरंग का समीकरण e = 100 (1+ 0.5 cos 3000 π t) cos 4 × 10₆ π t है। ज्ञात कीजिए,

1. वाहक तरंग की आवृत्ति।
2. इस आवृत्ति पर आवश्यक एन्टिना की लम्बाई। [2018]]

हल
दी गई समीकरण की तुलना e = E_c (1+ m_α cos ω_mt) cos ω_ct से करने पर,
ω_c= 4 x 10⁶
1. वाहक तरंग की आवृत्ति (f_c) = \(\frac{\omega_{c}}{2 \pi}=\frac{4 \times 10^{6}}{2 \times 3.14}\)= 6. 37x 10⁵ हर्टस।

2. तरंग की तरंगदैर्घ्य λ = \(\frac{c}{f_{c}}=\frac{3 \times 10^{8}}{6.37 \times 10^{5}}\) = 471 मीटर
एन्टिना की लम्बाई l =\(\frac { λ }{ 4 }\)= \(\frac { 471 }{ 4 }\)= 117.75 मीटर।

प्रश्न 8.
2 × 10⁵ हर्ट आवृत्ति तथा अधिकतम वोल्टेज 60 वोल्ट के वाहक तरंग को श्रव्य तरंग e_m = 30 sin 2 π X 2500 t वोल्ट द्वारा मॉडुलित किया जाता है। ज्ञात कीजिए-

1. मॉडुलन प्रतिशतता तथा
2. मॉडुलित तरंग के घटकों की आवृत्ति। [2017]

हल
1. मॉडुलित प्रतिशतता = \(\frac{E_{m}}{E_{c}}\) x 100 = \(\frac { 30 }{ 60 }\) = 50%

2. f_c= 2×10⁵ हर्ट्स = 200 kHz
f_m = 2500 हर्ट्स = 2.5 kHz
USB= f_c + f_m = 200+ 2.5 = 202.5 kHz
LSB= f_c– f_m = 200 – 2.5 = 197.5 kHz.

प्रश्न 9.
आयाम मॉडुलित वोल्टेज का मान e = 150[1+0. 5cos 3250t]cos5x10⁵t से दिया जाता है। गणना कीजिए

1. मॉडुलन सूचकांक,
2. मॉडुलन आवृत्ति,
3. वाहक आवृत्ति तथा
4. वाहक आयाम। ‘

हल
आयाम मॉडुलित वोल्टेज की सामान्य समीकरण
e = E_c (1+ mα cosω_mt)cosω_ct से दी गयी समीकरण
e = 150 [1+ 0.5cos 3250 t]cos 5×10⁵t की तुलना करने पर,
E_c = 150 वोल्ट, m_α = 0.5, ω_m = 3250, ω_c= 5×10⁵

1. मॉडुलन सूचकांक ma = 0.5 = 50%.
2. मॉडुलन आवृत्ति (f_m) = \(\frac{\omega_{m}}{2 \pi}=\frac{3250}{2 \times 3.14}\)= 517.5 हर्ट्स।
3. वाहक आवृत्ति (f_c) = \(\frac{\omega_{c}}{2 \pi}=\frac{5 \times 10^{5}}{2 \times 3.14}\)= 79.6×10³ हर्ट्स = 79.6 किलोहर्ट्स।
4. वाहक आयाम E_c = 150 वोल्ट।

प्रश्न 10.
मॉडुलित वाहक तरंग के अधिकतम व न्यूनतम आयाम क्रमशः 900 मिर वोल्ट तथा 300 मिलीवोल्ट हैं। मॉडुलन प्रतिशत ज्ञात कीजिए। [2015]
हल
दिया है, मॉडुलित वाहक तरंग के लिए E_max = 900 मिलीवोल्ट, E_min = 300 मिलीवोल्ट
मॉडलन गणांक (m_α) =

∴ मॉडुलन प्रतिशत = 0.5 x 100 = 50%.

प्रश्न 11.
किसी दिन आयनमण्डल से परावर्तित अधिकतम आवृत्ति 10 मेगाहर्ट्स है। किसी दूसरे दिन यह घटकर 8 मेगाहर्ट्स पायी जाती है। इन दो दिनों में आयनमण्डल के अधिकतम इलेक्ट्रॉन घनत्वों की निष्पत्ति बताइए।
हल
क्रान्तिक आवृत्तियाँ (f_c)₁ = 10 मेगाहर्ट्स, (f_c)₂ = 8 मेगाहर्ट्स
क्रान्तिक आवृत्ति f_c = \(9 \sqrt{N_{\max }}\)

प्रश्न 12.
एक वाहक तरंग जिसकी शिखर वोल्टता 12 वोल्ट है किसी संदेश सिग्नल को प्रेषित करने के लिए उपयोग की जाती है। मॉडुलित सिग्नल की शिखर वोल्टता क्या होनी चाहिए जिससे मॉडुलन सूचकांक 75% प्राप्त हो? [2014]
हल
दिया है, वाहक तरंग की शिखर वोल्टता (E_c) = 12 वोल्ट
मॉडुलन सूचकांक (m_α) = 75% = 0.75
मॉडुलन सूचकांक (m_α)= \(\frac{E_{m}}{E_{c}}\)
मॉडुलन सिग्नल की शिखर वोल्टता E_m = m_α x E_c = 0.75 x 12 = 9 वोल्ट।

प्रश्न 13.
एक मॉडुलित तरंग का अधिकतम आयाम 11 वोल्ट तथा न्यूनतम आयाम 3 वोल्ट है। मॉडुलन सूचकांक ज्ञात कीजिए। [2014]
हल
दिया है, E_max = 11 वोल्ट, E_min = 3 वोल्ट, mα = ?
∴ E_max = E_c + E_m = 11 वोल्ट तथा E_min = E_c – E_m = 3 वोल्ट

प्रश्न 14.
एक आयाम मॉडुलित वाहक तरंग का अधिकतम एवं न्यूनतम आयाम क्रमशः 8 वोल्ट तथा 2 वोल्ट है। मॉडुलेशन सूचकांक का मान ज्ञात कीजिए। [2016]
हल
दिया है, E_max= 8 वोल्ट, E_min = 2 वोल्ट, mα = ?
मॉडलेशन सूचकांक (mα) = \(\frac{E_{\max }-E_{\min }}{E_{\max }+E_{\min }}\)
=\(\frac { 8-2 }{ 8+2 }\)= \(\frac { 6 }{ 10 }\) = 0.6.

प्रश्न 15.
एक वाहक तरंग का आयाम 500 मिलीवोल्ट है। मॉडुलक सिग्नल के कारण यह 200 मिलीवोल्ट से 800 मिलीवोल्ट तक बदलता है। मॉडुलन गुणांक तथा प्रतिशत मॉडुलन की गणना कीजिए। [2018]
हल
दिया है, E_c = 500 मिली वोल्ट, E_min = 200 मिलीवोल्ट, E_max = 800 मिली वोल्ट
E_max = E_c + E_m
E_m = E_max – E_c
= 800 – 500 = 300 मिलीवोल्ट
मॉडुलन गुणांक (m_α) =

प्रतिशत मॉडुलन = 0.6 x 100 = 60%
अथवा मॉडलेशन गणांक (m_α) = \(\frac{E_{\max }-E_{\min }}{E_{\max }+E_{\min }}\) = \(\frac { 800-200 }{ 800+200 }\) = \(\frac { 600 }{ 1000 }\) =0.6
प्रतिशत मॉडुलन = 0.6 × 100 = 60%.

प्रश्न 16.
एक मॉडुलक सिग्नल एक वर्गाकार तरंग है। वाहक तरंग e(t)= 2 sin (8πt) वोल्ट है। आयाम मॉडुलित तरंग का रेखाचित्र खींचिए। [2014]
हल
चित्र-15.11 में एक मॉडुलक सिग्नल एक वर्गाकार तरंग प्रदर्शित है
दिया है, e (t) = 2 sin (8πt)
यहाँ E_c = 2 वोल्ट
तथा E_m = 1 वोल्ट
अतः E_c + E_m = 2 + 1 = 3 वोल्ट
तथा E_c – E_m = 2 – 1 = 1 वोल्ट
ω_c = 8π, अत: 2 π f_c = 8π
अथवा f_c = 4 प्रति सेकण्ड।
आवर्तकाल T = \(\frac{1}{f_{c}}\) = \(\frac { 1 }{ 4 }\) = 0.25 सकण्ड।
अतः आयाम मॉडुलित तरंग चित्र-15.12 में प्रदर्शित है।

संचार व्यवस्था  बहुविकल्पीय प्रश्नोत्तर

• निम्नलिखित प्रश्नों के चार विकल्प दिए गए हैं। सही विकल्प का चयन कीजिए

1. उच्च आवृत्ति तरंगों पर सन्देश सिग्नल के अध्यारोपण की प्रक्रिया कहलाती है [2016]
(a) संचरण
(b) मॉडुलन
(c) संसूचन
(d) अभिग्रहण।
उत्तर
(b) मॉडुलन

2. किसी रेखीय ऐन्टिना द्वारा विकिरित शक्ति तरंगदैर्घ्य पर किस प्रकार निर्भर करती है [2014]
(a) P ∝ λ
(b) P∝ λ²
(c) P∝\(\frac { 1 }{ λ }\)
(d) P∝\(\frac{1}{\lambda^{2}}\)
उत्तर
(d) P∝\(\frac{1}{\lambda^{2}}\)

3. सन्देश सिग्नल को किसी ऐन्टिना द्वारा प्रेषित करने के लिए उसकी न्यूनतम लम्बाई होनी चाहिए
(a) λ
(b) \(\frac { λ }{ 2 }\)
(c) \(\frac { λ}{ 4 }\)
(d) \(\frac { λ }{ 8 }\)
उत्तर
(c) \(\frac { λ}{ 4 }\)

4. एक ऐन्टिना एक अनुनादी परिपथ की भाँति कार्य तभी करता है जबकि उसकी लम्बाई ( λ = तरंगदैर्घ्य ) हो
(a) \(\frac { λ }{ 8 }\)
(b) \(\frac { λ}{ 4 }\)
(c) \(\frac { λ }{ 2 }\) की पूर्णांक गुणज
(d) \(\frac { λ}{ 4 }\) की विषम गुणज।
उत्तर
(b) \(\frac { λ}{ 4 }\)

5. टी०वी० प्रसारण के लिए प्रयुक्त आवृत्ति परास होता है
(a) 30 मेगाहर्ट्स -300 मेगाहर्ट्स
(b) 30 गीगाहर्ट्स-300 गीगाहर्ट्स
(c) 30 किलोहर्ट्स-300 किलोहर्ट्स
(d) 30 हर्ट्स- 300 हर्ट्स।
उत्तर
(a) 30 मेगाहर्ट्स -300 मेगाहर्ट्स

6. वाहक तरंग की आवृत्ति f_m के साथ श्रव्य तरंग आवृत्ति f_m के आयाम मॉडुलेशन से प्राप्त बैण्ड-चौड़ाई का मान होगा [2015]
अथवा f_c आवृत्ति की वाहक तरंग f_m आवृत्ति की श्रव्य तरंग द्वारा आयाम मॉडुलित की जाती है। मॉडुलित तरंग की बैण्ड चौड़ाई होगी [2018]
(a) 2f_c
(b) 2f_m
(c) f_{c +} f_m
(d) f_c – f_m.
उत्तर
(b) 2f_m

7. आयाम मॉडुलित तरंग में मॉडुलन सूचकांक है
(a) सदैव शून्य .
(b) 0 तथा 1 के बीच
(c) 1 तथा अनन्त के बीच
(d) सदैव अनन्त।
उत्तर
(b) 0 तथा 1 के बीच

8. आयाम मॉडुलेशन तरंग निम्न के योग के समतुल्य है [2014]
(a) दो ज्यावक्रीय तरंगें
(b) तीन ज्यावक्रीय तरंगें
(c) चार ज्यावक्रीय तरंगें
(d) इनमें से कोई नहीं।
उत्तर
(b) तीन ज्यावक्रीय तरंगें

9. रेडियो तरंग के प्रसारण के लिए मॉडुलन है [2014]
(a) आयाम माडुलन
(b) कला मॉडुलन
(c) आवृत्ति मॉडुलन
(d) इनमें से कोई नहीं।।
उत्तर
(a) आयाम माडुलन

10. 3 x 10⁸ हर्ट्स आवृत्ति की वाहक तरंगों के लिए द्विधुवी ऐन्टिना की लम्बाई होनी चाहिए [2014] .
(a) 0.25 मीटर
(b) 0.50 मीटर
(c) 1.0 मीटर
(d) 4.0 मीटर।
उत्तर
(b) 0.50 मीटर

11. यदि संप्रेषी ऐन्टिना की ऊँचाई h तथा अभिग्राही ऐन्टिना की ऊँचाई h2 है तो दृष्टिरेखीय (LOS) संचरण विधि में संतोषजनक संचरण के लिए दोनों ऐन्टिनों के बीच की अधिकतम दूरी होती है। (पृथ्वी की त्रिज्या R है)- [2016]
(a) \(\sqrt{2 h_{1} R+2 h_{2} R}\)
(b) \(\sqrt{h_{1} R}+\sqrt{h_{2} R}\)
(c) \(\sqrt{\left(h_{1}+h_{2}\right) R}\)
(d) \(\sqrt{2 h_{1} R}+\sqrt{2 h_{2} R}\)
उत्तर
(d) \(\sqrt{2 h_{1} R}+\sqrt{2 h_{2} R}\)

12. 200 किलोहर्ट्स की वाहक आवृत्ति और 10 किलोहर्ट्स के मॉडुलन संकेत के लिए आयाम मॉडुलित (AM) सिग्नल की बैण्ड-चौड़ाई होगी [2016]
(a) 20 किलोहर्ट्स
(b) 210 किलोहर्ट्स
(c) 400 किलोहर्ट्स
(d) 190 किलोहर्ट्स।
उत्तर
(a) 20 किलोहर्ट्स

13. 10 किलोहर्ट्स आवृत्ति तथा 10 वोल्ट शिखर वोल्टता के संदेश सिग्नल का उपयोग किसी 1 मेगाहर्ट्स आवृत्ति तथा
20 वोल्ट शिखर वोल्टता की वाहक तरंगों को मॉडुलित करने में किया गया है। उत्पन्न पार्श्व बैण्ड की आवृत्तियाँ होंगी [2018]
(a) 1000 किलोहर्ट्स तथा 900 किलोहर्ट्स
(b) 1010 किलोहर्ट्स तथा 990 किलोहर्ट्स
(c) 1010 किलोहर्ट्स तथा 1020 किलोहर्ट्स
(d) 11 मेगाहर्ट्स तथा 9 मेगाहर्ट्स।
उत्तर
(b) 1010 किलोहर्ट्स तथा 990 किलोहर्ट्स

14. व्योम तरंगों द्वारा क्षितिज से पार संचार के लिए निम्न में से कौन-सी आवृत्ति उपयुक्त होगी [2018]
(a) 10 किलोहर्ट्स
(b) 10 मेगाहर्ट्स
(c) 1 गीगाहर्ट्स
(d) 1000 गीगाहर्ट्स।
उत्तर
(b) 10 मेगाहर्ट्स

15. UHF परिसर की आवृत्तियों का प्रसारण प्रायः किस प्रकार की तरंगों द्वारा होता है [2018]
(a) भू-तरंग
(b) व्योमतरंगें
(c) पृष्ठीय तरंगें
(d) आकाश तरंगें।
उत्तर
(d) आकाश तरंगें।

16. आयन मण्डल से निम्न में से कौन-सी आवृत्ति परावर्तित हो सकती है [2018]
(a) 5 किलोहर्ट्स
(b) 5 मेगाहर्ट्स
(c) 5 गीगाहर्ट्स
(d) 500 मेगाहर्ट्स।
उत्तर
(b) 5 मेगाहर्ट्स

MP Board Class 12th Physics Important Questions

MP Board Class 12th Physics Solutions Chapter 11 विकिरण तथा द्रव्य की द्वैत प्रकृति

विकिरण तथा द्रव्य की द्वैत प्रकृति NCERT पाठ्यपुस्तक के अध्याय में पाठ्यनिहित प्रश्न एवं उनके उत्तर

प्रश्न 1.
30 किलोवोल्ट इलेक्ट्रॉनों के द्वारा उत्पन्न x-किरणों की
(a) उच्चतम आवृत्ति तथा
(b) निम्नतम तरंगदैर्घ्य प्राप्त कीजिए।
हल
दिया है, V = 30 किलोवोल्ट = 30 × 10³ वोल्ट
∴ इलेक्ट्रॉनों की ऊर्जा E = eV
x-किरण उत्पादन में लक्ष्य से टकराने वाले इलेक्ट्रॉनों की ऊर्जा x-किरण फोटॉनों की ऊर्जा में बदल जाती है।

(a) यदि किसी फोटॉन की आवृत्ति ν है तो
फोटॉन की ऊर्जा E = hν
∴ ν = \(\frac { E }{ h }\)
स्पष्ट है कि यदि इलेक्ट्रॉन की सम्पूर्ण ऊर्जा एक x-किरण फोटॉन के रूप में विकिरित हो तो फोटॉन की आवृत्ति . महत्तम होगी।
∴ \(v_{\max }=\frac{e V}{h}=\frac{1.6 \times 10^{-19} \times 30 \times 10^{3}}{6.62 \times 10^{-34}}\)
⇒ ν_max. = 7.24 × 10¹⁸ हर्ट्स।

(b) ∵ X-किरणें प्रकाश के वेग से चलती हैं,
अतः c = νλ
⇒ λ = \(\frac { c }{ ν }\)
∴ λ_min = \(\frac{c}{\nu \max }\)

= 0.0414 नैनोमीटर।

प्रश्न 2.
सीज़ियम धातु का कार्य-फलन 2.14 इलेक्ट्रॉन वोल्ट है। जब 6 × 10¹⁴ हर्ट्स आवृत्ति का प्रकाश धातु-पृष्ठ पर आपतित होता है, इलेक्ट्रॉनों का प्रकाशिक उत्सर्जन होता है।
(a) उत्सर्जित इलेक्ट्रॉनों की उच्चतम गतिज ऊर्जा,
(b) निरोधी विभव और
(c) उत्सर्जित प्रकाशिक इलेक्ट्रॉनों की उच्चतम चाल कितनी है?
हल
दिया है, कार्य-फलन W या Φ_o= 2.14 इलेक्ट्रॉन-वोल्ट = 2.14 × 1.6 × 10^-19 जूल,
आपतित प्रकाश की आवृत्ति ν = 6 × 10¹⁴ हर्ट्स,
h = 6.6 × 10^-34 जूल-सेकण्ड

(a) आइन्स्टीन के सूत्र से,
उत्सर्जित इलेक्ट्रॉनों की महत्तम गतिज ऊर्जा
E_max = hν – W
= 6.6 × 10^-34 × 6 x 10¹⁴ – 2.14 × 1.6 × 10^-19
= 39.6 × 10^-20 जूल – 34.2 × 10^-20 जूल
= 5.4 × 10^-20 जूल
= \(\frac{5.4 \times 10^{-20}}{1.6 \times 10^{-19}}\) इलेक्ट्रॉन-वोल्ट
= 0.34 इलेक्ट्रॉन-वोल्ट।

(b) यदि निरोधी विभव V₀ है तो
eV_o = E_max (जूल में)
निरोधी विभव V₀ = \(\frac{E_{\max }}{e}\)

(c) यदि इलेक्ट्रॉनों की महत्तम चाल υ _max है तो
\(E_{\max }=\frac{1}{2} m v_{\max }^{2}\)
⇒

∴ इलेक्ट्रॉनों की महत्तम चाल
\(v_{\max }=\sqrt{\frac{2 \times 5.4 \times 10^{-20}}{9.1 \times 10^{-31}}}\) (∵ m= इलेक्ट्रॉनों का द्रव्यमान)
= 3.44 × 10⁵ मीटर/सेकण्ड।

प्रश्न 3.
एक विशिष्ट प्रयोग में प्रकाश-विद्युत प्रभाव की अन्तक वोल्टता 1.5 वोल्ट है। उत्सर्जित प्रकाशिक इलेक्ट्रॉनों की उच्चतम गतिज ऊर्जा कितनी है?
हल
दिया है, अन्तक वोल्टता V_o = 1.5 वोल्ट
∴ इलेक्ट्रॉनों की अधिकतम गतिज ऊर्जा
E_max = eV_o
= 1.6 × 10^-19 × 1.5 जूल
= 2.4 × 10^-19 जूल

= 1.5 इलेक्ट्रॉन-वोल्ट।

प्रश्न 4.
632.8 नैनोमीटर तरंगदैर्घ्य का एकवर्णी प्रकाश एक हीलियम-नियॉन लेसर के द्वारा उत्पन्न किया जाता है। उत्सर्जित शक्ति 9.42 मिलीवाट है।
(a) प्रकाश के किरण पुंज में प्रत्येक फोटॉन की ऊर्जा तथा संवेग प्राप्त कीजिए।
(b) इस किरण पुंज के द्वारा विकिरित किसी लक्ष्य पर औसतन कितने फोटॉन प्रति सेकण्ड पहुँचेंगे? (यह मान लीजिए कि किरण पुंज की अनुप्रस्थ काट एकसमान है जो लक्ष्य के क्षेत्रफल से कम है) तथा
(c) एक हाइड्रोजन परमाणु को फोटॉन के बराबर संवेग प्राप्त करने के लिए कितनी तेज चाल से चलना होगा?
हल
दिया है, उत्सर्जित शक्ति P= 9.42 मिलीवाट = 9.42 × 10^-3 वाट
फोटॉन की तरंगदैर्घ्य λ = 632.8 नैनोमीटर = 632.8 × 10^-9 मीटर

(a) प्रत्येक फोटॉन की ऊर्जा E = \(\frac { hc }{ λ }\)
=\(\frac{6.62 \times 10^{-34} \times 3 \times 10^{8}}{632.8 \times 10^{-9}}\) जूल
= 3.14 × 10^-19 जूल।

= 1.05 × 10^-27 किग्रा-मीटर/सेकण्ड।

(b) माना लक्ष्य पर प्रति सेकण्ड n फोटॉन पहुँचते हैं, तब
n × एक फोटॉन की ऊर्जा = उत्सर्जित शक्ति
⇒

\(=\frac{9.42 \times 10^{-3}}{3.14 \times 10^{-19}}=3 \times 10^{16}\)

(c) हाइड्रोजन परमाणु का द्रव्यमान
m= 1.67 × 10^-27 किग्रा
माना इसकी चाल υ है, तब हाइड्रोजन परमाणु का संवेग
mυ = 1.05 × 10^-27
⇒चाल υ = \(\frac{1.05 \times 10^{-27}}{1.67 \times 10^{-27}}\)
= 0.63 मीटर/सेकण्ड।

प्रश्न 5. पृथ्वी के पृष्ठ पर पहुँचने वाला सूर्य-प्रकाश का ऊर्जा-अभिवाह (फ्लक्स) 1.388 × 10³ वाट/मीटर है। लगभग कितने फोटॉन प्रति वर्ग मीटर प्रति सेकण्ड पृथ्वी पर आपतित होते हैं? यह मान लें कि सूर्य-प्रकाश में फोटॉन का औसत तरंगदैर्घ्य 550 नैनोमीटर है।
हल
दिया है, सूर्य-प्रकाश में फोटॉन का तरंगदैर्घ्य
λ = 550 नैनोमीटर = 550 × 10^-9 मीटर
प्रति मीटर² क्षेत्रफल पर ऊर्जा आपतन दर
Φ = 1.388 × 10³ वाट/मीटर²
प्रत्येक फोटॉन की ऊर्जा E= \(\frac { hc }{ λ }\)
= \(\frac{6.62 \times 10^{-34} \times 3 \times 10^{8}}{550 \times 10^{-9}}\)
= 3.6 × 10^-19 जूल।
माना प्रति मीटर² क्षेत्रफल पर n फोटॉन प्रति सेकण्ड गिरते हैं, तब
ऊर्जा फ्लक्स Φ = n × एक फोटॉन की ऊर्जा (E)
∴ \(n=\frac{\phi}{E}=\frac{1.388 \times 10^{3}}{3.6 \times 10^{-19}}\)
= 3.85 × 10²¹
≈ 4 × 10²¹.

प्रश्न 6.
प्रकाश-विद्युत प्रभाव के एक प्रयोग में, प्रकाश आवृत्ति के विरुद्ध अन्तक वोल्टता की ढलान 4.12 × 10^-15 वोल्ट-सेकण्ड प्राप्त होती है। प्लांक स्थिरांक का मान परिकलित कीजिए।
हल

∴आइन्स्टीन के प्रकाश-विद्युत समीकरण से,
\(e V_{0}=h\left(v-v_{0}\right) \quad \Rightarrow \quad V_{0}=\frac{h}{e}\left(v-v_{0}\right)\)
अतः अन्तक वोल्टता-आवृत्ति वक्र का ढाल m = \(\frac { h}{ e }\)
परन्तु दिया है, m = 4.12 × 10^-15 वोल्ट-सेकण्ड
अत: \(\frac { h}{ e }\) = 4.12 × 10^-15 वोल्ट-सेकण्ड
∴ प्लांक नियतांक h = e × 4.12 × 10^-15
=1.6 × 10^-19 × (4.12 × 10^-15)
h = 6.59 × 10^-34 जूल-सेकण्ड।

प्रश्न 7.
एक 100 वाट सोडियम बल्ब (लैम्प) सभी दिशाओं में एकसमान ऊर्जा विकिरित करता है। लैम्प को एक ऐसे बड़े गोले के केन्द्र पर रखा गया है जो इस पर आपतित सोडियम के सम्पूर्ण प्रकाश को अवशोषित करता है। सोडियम प्रकाश का तरंगदैर्घ्य 589 नैनोमीटर है।
(a) सोडियम प्रकाश से जुड़े प्रति फोटॉन की ऊर्जा कितनी है?
(b) गोले को किस दर से फोटॉन प्रदान किए जा रहे हैं?
हल
दिया है, λ = 589 × 10^-9 मीटर, बल्ब की विकिरित शक्ति P = 100 वाट
(a) प्रत्येक फोटॉन की ऊर्जा E = \(\frac { hc }{ λ }\)
\(=\frac{6.62 \times 10^{-34} \times 3 \times 10^{8}}{589 \times 10^{-9}}\) जूल
= 3. 38 × 10^-19 जूल।
अथवा E = \(\frac{3.38 \times 10^{-19}}{1.6 \times 10^{-19}}\) इलेक्ट्रॉन-वोल्ट।
= 2.1 इलेक्ट्रॉन-वोल्ट।

(b) माना गोले को फोटॉन प्रदान करने की दर n प्रति सेकण्ड है।
तब n x एक फोटॉन की ऊर्जा = बल्ब की विकिरित शक्ति
⇒

= \(\frac{100}{3.38 \times 10^{-19}}\)
= 3 × 10²⁰ फोटॉन/सेकण्ड।

प्रश्न 8.
किसी धातु की देहली आवृत्ति 3.3 × 10¹⁴ हर्ट्स है। यदि 8.2 × 10¹⁴ हर्ट्स आवृत्ति का प्रकाश धातु . पर आपतित हो तो प्रकाश-विद्युत उत्सर्जन के लिए अन्तक वोल्टता ज्ञात कीजिए।
हल
दिया है, देहली आवृत्ति ν = 3.3 × 10¹⁴ हर्ट्स,
आपतित प्रकाश की आवृत्ति ν = 8.2 × 10¹⁴ हर्ट्स,
अन्तक वोल्टता Vo = ?
उत्सर्जित इलेक्ट्रॉनों की महत्तम गतिज ऊर्जा
E_max = h (ν – ν_o) = 6.62 × 10^-34 (8.2 × 10¹⁴ – 3.3 × 10¹⁴)
= 32.44 × 10^-20 जूल
सूत्र eV_o = E_max से,
अन्तक वोल्टता V₀ = \(\frac{E_{\max }}{e}=\frac{32.44 \times 10^{-20}}{1.6 \times 10^{-19}}\)
= 2.0 वोल्ट।

प्रश्न 9.
किसी धातु के लिए कार्य-फलन 4.2 इलेक्ट्रॉन-वोल्ट है। क्या यह धातु 330 नैनोमीटर तरंगदैर्घ्य के आपतित विकिरण के लिए प्रकाश-विद्युत उत्सर्जन देगा?
उत्तर
दिया है : कार्य-फलन W = 4.2 इलेक्ट्रॉन-वोल्ट = 4.2 × 1.6 × 10^-19 जूल
आपतित तरंगदैर्घ्य λ = 330 नैनोमीटर
सूत्र w = \(\frac{h c}{\lambda_{0}}\) से
देहली तरंगदैर्घ्य λ₀ = \(\frac{h c}{W}=\frac{6.62 \times 10^{-34} \times 3 \times 10^{8}}{4.2 \times 1.6 \times 10^{-19}}\)
= 2.95 × 10^-7 मीटर
λ₀ = 295 × 10^-9 मीटर = 295 नैनोमीटर
∵ λ = 330 नैनोमीटर > λ₀ = 295 नैनोमीटर
अत: λ = 330 नैनोमीटर के विकिरण के लिए प्रकाश-विद्युत उत्सर्जन नहीं होगा।

प्रश्न 10.
7.21 × 10¹⁴ हर्ट्स आवृत्ति का प्रकाश एक धातु-पृष्ठ पर आपतित है। इस पृष्ठ से 6.0 × 10⁵ मीटर/सेकण्ड की उच्चतम गति से इलेक्ट्रॉन उत्सर्जित हो रहे हैं। इलेक्ट्रॉनों के प्रकाश उत्सर्जन के लिए देहली आवृत्ति क्या है?
हल
आपतित प्रकाश की आवृत्ति ν = 7.21 × 10¹⁴ हर्ट्स
इलेक्ट्रॉनों की अधिकतम चाल υ_max = 6.0 × 10⁵ मीटर/सेकण्ड
इलेक्ट्रॉनों का द्रव्यमान m = 9.1 × 10^-31 किग्रा
∴ इलेक्ट्रॉनों की अधिकतम गतिज ऊर्जा
\(E_{\max }=\frac{1}{2} m v_{\max }^{2}=\frac{1}{2} \times 9.1 \times 10^{-31} \times\left(6.0 \times 10^{5}\right)^{2}\)
= 1.64 × 10^-19 जूल
आपतित फोटॉन की ऊर्जा hν = 6.62 × 10^-34 × 7.21 × 10¹⁴
= 4.77 × 10^-19 जूल।
E_max = hν – hν_o से,
hν_o = hν – E_max
∴ देहली आवृत्ति ν₀ = \(\frac{E_{\max }-h v}{h}=\frac{(4.77-1.64) \times 10^{-19}}{6.62 \times 10^{-34}}\)
= 4.7 × 10¹⁴ हर्ट्स।

प्रश्न 11.
488 नैनोमीटर तरंगदैर्घ्य का प्रकाश एक आर्गन लेसर से उत्पन्न किया जाता है, जिसे प्रकाश-विद्युत प्रभाव के उपयोग में लाया जाता है। जब इस स्पेक्ट्रमी रेखा के प्रकाश को उत्सर्जक पर आपतित किया जाता है, तब प्रकाशिक इलेक्ट्रॉनों का निरोधी (अन्तक) विभव 0.38 वोल्ट है। उत्सर्जक के पदार्थ का कार्य-फलन ज्ञात कीजिए।
हल
दिया है, आपतित तरंगदैर्घ्य λ = 488 × 10^-9 मीटर
अन्तक विभव V_o = 0.38 वोल्ट, W = ?
फोटॉन की ऊर्जा. E = \(\frac { hc }{ λ }\) = \(\frac{6.6 \times 10^{-34} \times 3 \times 10^{8}}{488 \times 10^{-9}}\) = 4.07 × 10^-9 जूल
जबकि उत्सर्जित इलेक्ट्रॉनों की महत्तम गतिज ऊर्जा
E_max = eV_o = 1.6 × 10^-19 × 0.38
= 0.608 × 10^-19 जूल
∴E_max = hν – Φ₀ से,
कार्य-फलन W = hν – E_max
= 4.07 × 10^-19 – 0.608 × 10^-19
= 3.46 × 10^-19 जूल।
अथवा W = \(\frac{3.46 \times 10^{-19}}{1.6 \times 10^{-19}}\) इलेक्ट्रॉन-वोल्ट
= 2.16 इलेक्ट्रॉन-वोल्ट।

प्रश्न 12.
56 वोल्ट विभवान्तर के द्वारा त्वरित इलेक्ट्रॉनों का
(a) संवेग और
(b) दे-ब्रॉग्ली तरंगदैर्घ्य परिकलित कीजिए।
हल
दिया है, त्वरक विभव V = 56 वोल्ट, इलेक्ट्रॉन का द्रव्यमान m = 9.1 × 10^-31 किग्रा,
e= 1.6 × 10^-19 कूलॉम
(a) ∴ इलेक्ट्रॉन की ऊर्जा = \(\frac { 1 }{ 2 }\)mv² = eV
⇒ \(v=\sqrt{\frac{2 e V}{m}}=\sqrt{\frac{2 \times 1.6 \times 10^{-19} \times 56}{9.1 \times 10^{-31}}}\)
= 4.44 × 10⁶ मीटर/सेकण्ड
∴ इलेक्ट्रॉनों का संवेग p = mυ
= 9.1 × 10^-31 × 4.44 × 10⁶
= 4.04 × 10^-24 किग्रा-मीटर/सेकण्ड।

(b) इलेक्ट्रॉन से सम्बद्ध दे-ब्रॉग्ली तरंगदैर्घ्य
\(\lambda=\frac{12.27}{\sqrt{V}} \mathrm{A}=\frac{12.27}{\sqrt{56}} \mathrm{A}=1.64 \mathrm{A}\)
⇒ λ = 1.64 × 10^-10 मीटर
= 0.164 × 10^-9 मीटर
= 0.164 नैनोमीटर।
अथवा λ = \(\frac { h}{ p }\) = \(\frac{6.62 \times 10^{-34}}{4.04 \times 10^{-24}}\) मीटर
= 0.164 × 10^-9 मीटर
= 0.164 नैनोमीटर।

प्रश्न 13.
एक इलेक्ट्रॉन जिसकी गतिज ऊर्जा 120 इलेक्ट्रॉन-वोल्ट है, उसका
(a) संवेग,
(b) चाल और
(c) दे-ब्रॉग्ली तरंगदैर्घ्य क्या है?
हल
दिया है,
इलेक्ट्रॉन की ऊर्जा E = 120 इलेक्ट्रॉन-वोल्ट
(a) ∵ \(E=\frac{1}{2} m v^{2}=\frac{m^{2} v^{2}}{2 m}=\frac{p^{2}}{2 m}\)
∴ इलेक्ट्रॉन का संवेग p= \(\sqrt{2 m E}\)
= \(\left(2 \times 9.1 \times 10^{-31} \times 120 \times 1.6 \times 10^{-19}\right)^{1 / 2}\)
= 5.91 × 10^-24 किग्रा-मीटर/सेकण्ड।

(b) p= mυ से,
इलेक्ट्रॉन की चाल υ =\(\frac{p}{m}=\frac{5.91 \times 10^{-24}}{9.1 \times 10^{-31}}\)
= 6.5 × 10⁶ मीटर/सेकण्ड

(c) इलेक्ट्रॉन से सम्बद्ध दे-ब्रॉग्ली तरंगदैर्घ्य
λ = \(\frac { h}{ p }\) = \(\frac{6.62 \times 10^{-34}}{5.91 \times 10^{-24}}\)= 0.112 × 10^-9 मीटर
= 0.112 नैनोमीटर।

प्रश्न 14.
सोडियम के स्पेक्ट्रमी उत्सर्जन रेखा के प्रकाश का तरंगदैर्घ्य 589 नैनोमीटर है। वह गतिज ऊर्जा ज्ञात कीजिए जिस पर
(a) एक इलेक्ट्रॉन और
(b) एक न्यूट्रॉन का दे-ब्रॉग्ली तरंगदैर्घ्य समान होगा।
हल
दिया है, λ = 589 नैनोमीटर = 589 × 10^-9 मीटर, m_e = 9.1 × 10^-31 किग्रा,
m_n = 1.67 × 10^-27 किग्रा

(a) माना इलेक्ट्रॉन की अभीष्ट ऊर्जा E₁ है, तब
इलेक्ट्रॉन की ऊर्जा E₁ = \(\frac{\left(6.62 \times 10^{-34}\right)^{2}}{2 \times 9.1 \times 10^{-31} \times\left(589 \times 10^{-9}\right)^{2}}\) = 6.94 x 10^-25 जूल।
= \(\frac{6.94 \times 10^{-25}}{1.6 \times 10^{-19}}\) इलेक्ट्रॉन-वोल्ट = 4.34 × 10^-6 इलेक्ट्रॉन-वोल्ट।

(b) खण्ड (a) की भाँति, न्यूट्रॉन की ऊर्जा
\(E_{2}=\frac{h^{2}}{2 m_{n} \lambda^{2}}=\frac{\left(6.62 \times 10^{-34}\right)^{2}}{2 \times 1.67 \times 10^{-27} \times\left(589 \times 10^{-9}\right)^{2}}\)
= 3.782 × 10^-28 जूल।
= \(\frac{3.782 \times 10^{-28}}{1.6 \times 10^{-19}}\) इलेक्ट्रॉन-वोल्ट = 2.36 x 10^-9 इलेक्ट्रॉन-वोल्ट।

प्रश्न 15.
(a) एक 0.040 किग्रा द्रव्यमान का बुलेट जो 1.0 किमी/सेकण्ड की चाल से चल रहा है,
(b) एक 0.060 किग्रा द्रव्यमान की गेंद जो 1.0 मीटर/सेकण्ड की चाल से चल रही है और
(c) एक धूल-कण जिसका द्रव्यमान 1.0 × 10^-9 किग्रा और जो 2.2 मीटर/सेकण्ड की चाल से अनुगमित हो रहा है, का दे-ब्रॉग्ली तरंगदैर्घ्य कितना होगा?
हल
(a) दिया है, m = 0.040 किग्रा, υ = 1.0 किमी/सेकण्ड = 1000 मीटर/सेकण्ड
∴ दे-ब्रॉग्ली तरंगदैर्घ्य \(\lambda=\frac{h}{m v}=\frac{6.62 \times 10^{-34}}{0.040 \times 1000}\)
= 1.655 × 10^-35 मीटर
≈ 1.7 × 10^-35 मीटर।

(b) दिया है : m = 0.060 किग्रा, υ = 1.0 मीटर/सेकण्ड^-1
∴ दे-ब्रॉग्ली तरंगदैर्घ्य \(\lambda=\frac{h}{m v}=\frac{6.62 \times 10^{-34}}{0.060 \times 1.0}\)
= 1.1 × 10^-32 मीटर।

(c) दिया है, m = 1.0 x 10^-9 किग्रा, υ = 2.2 मीटर/सेकण्ड
∴ दे-ब्रॉग्ली तरंगदैर्घ्य \(\lambda=\frac{h}{m v}=\frac{6.62 \times 10^{-34}}{1.0 \times 10^{-9} \times 2.2}\)
= 3.01 × 10^-25 मीटर।।

प्रश्न 16.
एक इलेक्ट्रॉन और एक फोटॉन प्रत्येक का तरंगदैर्घ्य 1.00 नैनोमीटर है।
(a) इनका संवेग,
(b) फोटॉन की ऊर्जा और
(c) इलेक्ट्रॉन की गतिज ऊर्जा ज्ञात कीजिए।
हल
यहाँ λ = 1.00 नैनोमीटर = 1.0 × 10^-9 मीटर, h = 6.62 × 10^-34 जूल-सेकण्ड,
इलेक्ट्रॉन का द्रव्यमान m = 9.1 × 10^-31 किग्रा

(a) सूत्र λ = \(\frac { h}{ p }\) = से, p = \(\frac { h }{ λ }\)
∴ प्रत्येक का संवेग \(p=\frac{6.62 \times 10^{-34}}{1.0 \times 10^{-9}}\)
= 6.62 × 10^-25 किग्रा-मीटर/सेकण्ड।

(b) फोटॉन की ऊर्जा E = \(\frac { hc }{ λ }\) = pc .
= 6.62 × 10^-25 × 3 × 10⁸
= 19.86 × 10^-17 जूल।
अथवा \(E=\frac{19.86 \times 10^{-17}}{1.6 \times 10^{-19}}\) इलेक्ट्रॉन-वोल्ट
= 1.24 × 10³ इलेक्ट्रॉन-वोल्ट।

(c) इलेक्ट्रॉन की ऊर्जा \(E=\frac{p^{2}}{2 m}=\frac{\left(6.62 \times 10^{-25}\right)^{2}}{2 \times 9.1 \times 10^{-31}}\)
= 2.41 × 10^-19 जूल।
अथवा \(E=\frac{2.41 \times 10^{-19}}{1.6 \times 10^{-19}}\) इलेक्ट्रॉन-वोल्ट
= 1.51 इलेक्ट्रॉन-वोल्ट।

प्रश्न 17.
(a) न्यूट्रॉन की किस गतिज ऊर्जा के लिए दे-ब्रॉग्ली तरंगदैर्घ्य 1.40 × 10-10 मीटर होगा?
(b) एक न्यूट्रॉन, जो पदार्थ के साथ तापीय साम्य में है और जिसकी 300 K पर औसत गतिज ऊर्जा – kT है, का भी दे-ब्रॉग्ली तरंगदैर्घ्य ज्ञात कीजिए।
हल
(a) दिया है, न्यूट्रॉन की दे-ब्रॉग्ली तरंगदैर्घ्य 2 = 1.40 × 10^-10 मीटर .
न्यूट्रॉन का द्रव्यमान m = 1.67 × 10^-27 किग्रा
अब न्यटॉन की गतिज ऊर्जा E = \(\frac{p^{2}}{2 m}=\frac{h^{2}}{2 m \lambda^{2}}\) (∵p = \(\frac { h }{ λ }\))
\(=\frac{\left(6.62 \times 10^{-34}\right)^{2}}{2 \times 1.67 \times 10^{-27} \times\left(1.40 \times 10^{-10}\right)^{2}}\)
= 6.69 × 10^-21 जूल।
अथवा \(E=\frac{6.69 \times 10^{-21}}{1.6 \times 10^{-19}}\) इलेक्ट्रॉन-वोल्ट
= 4.18 × 10^-2 इलेक्ट्रॉन-वोल्ट।

(b) दिया है, T = 300 K, k = 1.38 × 10^-23 जूल-K^-1
∴ न्यूट्रॉन की गतिज ऊर्जा E = \(\frac{3}{2} k T=\frac{3}{2} \times 1.38 \times 10^{-23} \times 300\)
= 6.21 × 10^-21 जूल
∵ E = \(\frac{h^{2}}{2 m \lambda^{2}}\) ∴ λ = \(\frac{h}{\sqrt{2 m E}}\)
∴ दे-ब्रॉग्ली तरंगदैर्घ्य = \(\lambda=\frac{6.62 \times 10^{-34}}{\sqrt{2 \times 1.67 \times 10^{-27} \times 6.21 \times 10^{-21}}}=\frac{6.62 \times 10^{-34}}{4.55 \times 10^{-24}}\)
= 1.45 × 10^-10 मीटर = 0.145 नैनोमीटर।

प्रश्न 18.
यह दर्शाइए कि विद्युतचुम्बकीय विकिरण का तरंगदैर्घ्य इसके क्वाण्टम (फोटॉन) के तरंगदैर्ध्य के बराबर है।
उत्तर
माना किसी विद्युतचुम्बकीय विकिरण की तरंगदैर्घ्य 2 तथा आवृत्ति । है।
तब λ = \(\frac { c }{ v }\) (∵ c = vλ)
इस विकिरण के फोटॉन का गतिज द्रव्यमान
m = \(\frac { h }{ cλ }\)
∴ फोटॉन का संवेग p = mc (∵ फोटॉन का वेग = c)
\(=\frac{h}{c \lambda} \times c=\frac{h}{\lambda}\)
∴ फोटॉन का दे-ब्रॉग्ली तरंगदैर्घ्य
\(\lambda^{\prime}=\frac{h}{p}=\frac{h}{h / \lambda} \quad \Rightarrow \quad \lambda^{\prime}=\lambda\)
अतः फोटॉन की दे-ब्रॉग्ली तरंगदैर्घ्य = विकिरण की तरंगदैर्घ्य।

प्रश्न 19.
वायु में 300 K ताप पर एक नाइट्रोजन अणु का दे-ब्रॉग्ली तरंगदैर्घ्य कितना होगा? यह मानें कि अणु इस ताप पर अणुओं के वर्ग-माध्य चाल से गतिमान है। ( नाइट्रोजन का परमाणु द्रव्यमान = 14.0076 u)
हल
दिया है, T= 300 K, , k = 1.38 × 10^-23 जूल-K^-1
नाइट्रोजन के 1 अणु का द्रव्यमान m = 2 × 14.0076 u
= 2 × 14.0076 × 1.67 × 10^-27 किग्रा
= 46.78 × 10^-27 किग्रा [∵ 1u = 1.67 × 10^-27 किग्रा]
यदि अणु की वर्ग-माध्य-मूल चाल υ है तो
1 अणु की गतिज ऊर्जा \(\frac{1}{2} m v^{2}=\frac{3}{2} k T \Rightarrow v=\sqrt{\frac{3 k T}{m}}\)
∴ अणु की चाल \(v=\sqrt{\frac{3 \times 1.38 \times 10^{-23} \times 300}{46.78 \times 10^{-27}}}\)
= 515 मीटर/सेकण्ड।
∴ नाइट्रोजन अणु का दे-ब्रॉग्ली तरंगदैर्घ्य \(\lambda=\frac{h}{m v}=\frac{6.62 \times 10^{-34}}{46.78 \times 10^{-27} \times 515}\)
= 2.75 × 10^-11 मीटर
= 0.028 नैनोमीटर।

प्रश्न 20.
(a) एक निर्वात नली के तापित कैथोड से उत्सर्जित इलेक्ट्रॉनों की उस चाल का आकलन कीजिए, जिससे वे उत्सर्जक की तुलना में 500 वोल्ट के विभवान्तर पर रखे गए ऐनोड से टकराते हैं। इलेक्ट्रॉनों के लघु प्रारम्भिक चालों की उपेक्षा कर दें। इलेक्ट्रॉन का आपेक्षिक आवेश अर्थात् \(\frac { e }{ m }\) = 1.76 x 10¹¹ कूलॉम/किग्रा है।
(b) संग्राहक विभव 10 मेगावोल्ट के लिए इलेक्ट्रॉनों की चाल ज्ञात करने के लिए उसी सूत्र का प्रयोग करें, जो (a) में काम में लाया गया है। क्या आप इस सूत्र को गलत पाते हैं? इस सूत्र को किस प्रकार सुधारा जा सकता है?
हल
(a) त्वरक विभव V= 500 वोल्ट
इलेक्ट्रॉन का आपेक्षिक आवेश \(\frac { e }{ m }\) = 1.76 x 10¹¹ कूलॉम/किग्रा
माना ऐनोड से टकराते समय इलेक्ट्रॉनों का वेग υ है, तब
इलेक्ट्रॉनों की ऊर्जा में वृद्धि

= 13.26 × 10⁶ मीटर/सेकण्ड
∴ इलेक्ट्रॉनों की चाल υ ≈ 1.33 × 10⁷ मीटर/सेकण्ड।

(b) पुन: इलेक्ट्रॉन की चाल υ = \(=\sqrt{2 \times \frac{e}{m} \times V}\) [∵V= 10 मेगावोल्ट = 10 x 10⁶ V]
=\(\sqrt{2 \times 1.76 \times 10^{11} \times 10 \times 10^{6}}\)
= 18.76 × 10⁸ मीटर/सेकण्ड।
∵ इलेक्ट्रॉन की यह चाल निर्वात में प्रकाश की चाल c= 3 × 10⁸ मीटर/सेकण्ड से अधिक है तथा हम जानते हैं कि कोई द्रव्य कण निर्वात में प्रकाश के वेग के बराबर अथवा अधिक चाल से नहीं चल सकता।
इससे स्पष्ट है कि इस दशा में उक्त सूत्र \(\left(\mathrm{K.E}=\frac{1}{2} m v^{2}\right)\) सही नहीं हो सकता।
इस दशा में इलेक्ट्रॉन की सही चाल ज्ञात करने के लिए सापेक्षता के विशिष्ट सिद्धान्त का उपयोग करना होगा।
इस सिद्धान्त के अनुसार यदि कोई द्रव्य कण प्रकाश के वेग के तुलनीय वेग से गति करता है तो उसका गतिज द्रव्यमान निम्नलिखित होगा
\(m=\frac{m_{0}}{\sqrt{\left(1-\frac{v^{2}}{c^{2}}\right)}}\)
तब कण की गतिज ऊर्जा में वृद्धि निम्नलिखित सूत्र द्वारा प्राप्त होगी


∴ इलेक्ट्रॉन की चाल υ = 0.9988 × c
= 0.9988 × 3 × 10⁸
= 2.99 × 10⁸ मीटर/सेकण्ड।

प्रश्न 21.
(a) एक समोर्जी इलेक्ट्रॉन किरण-पुंज जिसमें इलेक्ट्रॉन की चाल 5.20 × 10⁶ मीटर/सेकण्ड है, पर एक चुम्बकीय क्षेत्र 1.30 × 10^-4 टेस्ला किरण-पुंज की चाल के लम्बवत् लगाया जाता है। किरण-पुंज द्वारा आरेखित वृत्त की त्रिज्या कितनी होगी, यदि इलेक्ट्रॉन के \(\frac { e }{ m }\) का मान 1.76 × 10¹¹ कूलॉम/किग्रा है।
(b) क्या जिस सूत्र को (a) में उपयोग में लाया गया है वह यहाँ भी एक 20 मिलियन इलेक्ट्रॉन-वोल्ट इलेक्ट्रॉन किरण-पुंज की त्रिज्या परिकलित करने के लिए युक्तिपरक है? यदि नहीं, तो किस प्रकार इसमें संशोधन किया जा सकता है?
[नोट : प्रश्न 20 (b) तथा 21 (b) आपको आपेक्षिकीय यान्त्रिकी तक ले जाते हैं जो पुस्तक के विषय के बाहर है। यहाँ पर इन्हें इस बिन्दु पर बल देने के लिए सम्मिलित किया गया है कि जिन सूत्रों को आप (a) में उपयोग में लाते हैं वे बहुत उच्च चालों अथवा ऊर्जाओं पर युक्तिपरक नहीं होते। यह जानने के लिए कि ‘बहुत उच्च चाल अथवा ऊर्जा’ का क्या अर्थ है? अन्त में दिए गए उत्तरों को देखें।]
हल
(a) दिया है, इलेक्ट्रॉन के लिए \(\frac{e}{m_{0}}\) = 1.76 x 10¹¹ कूलॉम/किग्रा
B= 1.30 × 10^-4 टेस्ला υ = 5.20 × 106 मीटर/सेकण्ड
यदि इलेक्ट्रॉन के पथ की त्रिज्या r है तो ।

अथवा r= 22.7 सेमी।

(b) यहाँ इलेक्ट्रॉन की ऊर्जा \(\frac { 1 }{ 2 }\)mυ² = 20 मिलियन इलेक्ट्रॉन-वोल्ट

इलेक्ट्रॉन की चाल v = 2.65 × 10⁹ मीटर/सेकण्ड
∵ इलेक्ट्रॉन की चाल निर्वात में प्रकाश की चाल से अधिक है। अत: पथ की त्रिज्या का परिकलन करने के लिए सामान्य सूत्र का प्रयोग नहीं किया जा सकता अपितु आपेक्षिकीय यान्त्रिकी का प्रयोग करना होगा।
अतः त्रिज्या के सूत्र \(r=\frac{m_{0} v}{e B}\) में m के स्थान पर इलेक्ट्रॉन का गतिज द्रव्यमान रखना होगा।
यहाँ इलेक्ट्रॉन गतिज द्रव्यमान \(m=\frac{m_{0}}{\sqrt{\left(1-v^{2} / c^{2}\right)}}\)
∴ \(r=\frac{m_{0}}{\sqrt{\left(1-v^{2} / c^{2}\right)}} \times \frac{v}{e B}=\frac{1}{\sqrt{\left(1-v^{2} / c^{2}\right)}}\left(\frac{m_{0}}{e} \times \frac{v}{B}\right)\)
उक्त सूत्र से पथ की त्रिज्या की गणना की जा सकती है।

प्रश्न 22.
एक इलेक्ट्रॉन गन जिसका संग्राहक 100 वोल्ट विभव पर है, एक कम दाब (~10^-2 मिमी Hg) पर हाइड्रोजन से भरे गोलाकार बल्ब में इलेक्ट्रॉन छोड़ती है। एक चुम्बकीय क्षेत्र जिसका मान 2.83 × 10^-4 टेस्ला है, इलेक्ट्रॉन के मार्ग को 12.0 सेमी त्रिज्या के वृत्तीय कक्षा में वक्रित कर देता है। (इस मार्ग को देखा जा सकता है क्योंकि मार्ग में गैस आयन किरण-पुंज को इलेक्ट्रॉनों को आकर्षित करके और इलेक्ट्रॉन ग्रहण के द्वारा प्रकाश . उत्सर्जन करके फोकस करते हैं; इस विधि को ‘परिष्कृत किरण-पुंज नली’ विधि कहते हैं।) आँकड़ों से \(\frac { e }{ m }\) का मान निर्धारित कीजिए।
हल
दिया है, इलेक्ट्रॉनों के लिए त्वरक विभव V = 100 वोल्ट, B= 2.83 × 10^-4 टेस्ला ,
पथ की त्रिज्या r = 12.0 सेमी = 0.12 मीटर
इलेक्ट्रॉन की गतिज ऊर्जा \(\frac { 1 }{ 2 }\)mυ₂ = ev

= 1.73 × 10¹¹ कलॉम/किग्रा।

प्रश्न 23.
(a) एक x-किरण नली विकिरण का एक सतत स्पेक्ट्रम जिसका लघु तरंगदैर्घ्य सिरा 0.45 A पर है, उत्पन्न करता है। विकिरण में किसी फोटॉन की उच्चतम ऊर्जा कितनी है?
(b) अपने (a) के उत्तर से अनुमान लगाइए कि किस कोटि की त्वरक वोल्टता (इलेक्ट्रॉन के लिए) की इस नली में आवश्यकता है?
हल
(a) X-किरण विकिरण में
λ_min = 0.45 A = 45 × 10^-12 मीटर
∴ विकिरण में फोटॉन की उच्चतम ऊर्जा
E_max = \(\frac{h c}{\lambda_{\min }}\)
\(=\frac{6.62 \times 10^{-34} \times 3 \times 10^{8}}{45 \times 10^{-12}}\)
= 4.42 × 10^-15 जूल।
अथवा E_max= \(\frac{4.42 \times 10^{-15}}{1.6 \times 10^{-19}}\) इलेक्ट्रॉन-वोल्ट
= 2.76 × 10⁴ इलेक्ट्रॉन-वोल्ट
= 27.6 किलोइलेक्ट्रॉन-वोल्ट।

(b) माना लक्ष्य से टकराने वाले इलेक्ट्रॉनों को उक्त ऊर्जा प्रदान करने के लिए त्वरक विभव V की आवश्यकता
तब इलेक्ट्रॉन की ऊर्जा E = eV
त्वरक विभव V = \(\frac{E}{e}=\frac{E_{\max }}{e}=\frac{4.42 \times 10^{-15}}{1.6 \times 10^{-19}}\)
∴ अभीष्ट त्वरक विभव V = 27.6 किलोवोल्ट।

प्रश्न 24.
एक त्वरित्र (accelerator) प्रयोग में पॉजिट्रॉनों (e⁺) के साथ इलेक्ट्रॉनों के उच्च-ऊर्जा संघट्टन पर, एक विशिष्ट घटना की व्याख्या कुल ऊर्जा 10.2 बिलियन इलेक्ट्रॉन-वोल्ट के इलेक्ट्रॉन-पॉजिट्रॉन युग्म के बराबर ऊर्जा की दो /-किरणों में विलोपन के रूप में की जाती है। प्रत्येक γ-किरण से सम्बन्धित तरंगदैर्यों के मान क्या होंगे? (1 बिलियन इलेक्ट्रॉन-वोल्ट= 10⁹ इलेक्ट्रॉन- वोल्ट)
हल
घटना में विलुप्त इलेक्ट्रॉन-पॉजिट्रॉन की कुल ऊर्जा = 10.2 × 10⁹ इलेक्ट्रॉन-वोल्ट
यह ऊर्जा दोनों γ-फोटॉनों में बराबर-बराबर बँट जाएगी।
∴ प्रत्येक γ-फोटॉन की ऊर्जा = \(\frac { 1 }{ 2 }\) x 10.2 × 10⁹ इलेक्ट्रॉन-वोल्ट
= \(\frac { 1 }{ 2 }\) x 10.2 x 10⁹ x 1.6 x 10^-19 जूल
= 8.16 × 10^-10 जूल
परन्तु E = \(\frac { hc }{ λ }\)
∴ फोटॉन की तरंगदैर्घ्य λ = \(\frac { hc }{ λ }\) = \(\frac{6.62 \times 10^{-34} \times 3 \times 10^{8}}{8.16 \times 10^{-10}}\) मीटर
या λ = 2.43 × 10^-16 मीटर।

प्रश्न 25.
आगे आने वाली दो संख्याओं का आकलन रोचक हो सकता है। पहली संख्या यह बताएगी कि रेडियो अभियान्त्रिक फोटॉन की अधिक चिन्ता क्यों नहीं करते। दूसरी संख्या आपको यह बताएगी कि हमारे नेत्र ‘फोटॉनों की गिनती’ क्यों नहीं कर सकते, भले ही प्रकाश साफ-साफ संसूचन योग्य हो?
(a) एक मध्य तरंग (medium wave) 10 किलोवाट सामर्थ्य के प्रेषी, जो 500 मीटर तरंगदैर्घ्य की रेडियो तरंग उत्सर्जित करता है, के द्वारा प्रति सेकण्ड उत्सर्जित फोटॉनों की संख्या।
(b) निम्नतम तीव्रता का श्वेत प्रकाश जिसे हम देख सकते हैं (~10-10 वाट/मीटर²) के संगत फोटॉनों की संख्या जो प्रति सेकण्ड हमारे नेत्रों की पुतली में प्रवेश करती है। पुतली का क्षेत्रफल लगभग 0.4 सेमी² और श्वेत प्रकाश की औसत आवृत्ति को लगभग 6 × 10¹⁴ हर्ट्स मानिए।
हल
(a) प्रेषी की शक्ति P = 10 किलोवाट = 10⁴ वाट
उत्सर्जित फोटॉनों की तरंगदैर्घ्य λ = 500 मीटर
∴ प्रत्येक फोटॉन की ऊर्जा E = \(\frac { hc }{ λ }\) = \(\frac{6.62 \times 10^{-34} \times 3 \times 10^{8}}{500}\)
= 3.98 × 10^-28 जूल
∴ प्रति सेकण्ड उत्सर्जित फोटॉनों की संख्या
\(n=\frac{P}{E}=\frac{10^{4}}{3.98 \times 10^{-28}}\)
= 2.51 × 10³¹ फोटॉन/सेकण्ड।

हम देख सकते हैं कि 10 किलोवाट सामर्थ्य के प्रेषी द्वारा प्रति सेकण्ड उत्सर्जित फोटॉनों की संख्या काफी अधिक है। अतः फोटॉनों की अलग-अलग ऊर्जा की उपेक्षा करके रेडियो तरंगों की कुल ऊर्जा को सतत माना जा सकता है।

(b) श्वेत प्रकाश की औसत आवृत्ति ν = 6 × 10¹⁴ हर्ट्स
∴ श्वेत प्रकाश की फोटॉन की ऊर्जा E = hν
= 6.62 × 10^-34 × 6 × 10¹⁴
= 3.97 × 10^-19 जूल
आँख द्वारा संसूचित न्यूनतम तीव्रता = 10^-10 वाट/मीटर²
इस स्थिति में आँख में प्रवेश करने वाले प्रकाश की न्यूनतम शक्ति
P= 10^-10 वाट/मीटर² × (0.4 × 10^-4) मीटर²
= 4 × 10^-15 वाट
∴ आँख में प्रति सेकण्ड प्रवेश करने वाले फोटॉनों की संख्या
\(n=\frac{P}{E}=\frac{4 \times 10^{-15}}{3.97 \times 10^{-19}}\)
= 1.01 × 10⁴ फोटॉन/सेकण्ड।
यद्यपि यह संख्या रेडियो प्रेषी द्वारा प्रति सेकण्ड उत्सर्जित फोटॉनों की संख्या से अत्यन्त कम है परन्तु आँख के सूक्ष्म क्षेत्रफल की दृष्टि से इतनी अधिक है कि हम आँख पर गिरने वाले फोटॉनों के अलग-अलग प्रभाव को संसूचित नहीं कर पाते अपितु प्रकाश के सतत प्रभाव का अनुभव करते हैं।

प्रश्न 26.
एक 100 वाट पारद (Mercury) स्रोत से उत्पन्न 2271A तरंगदैर्ध्य का पराबैंगनी प्रकाश एक मॉलिब्डेनम धातु से निर्मित प्रकाश सेल को विकिरित करता है। यदि निरोधी विभव – 1.3 वोल्ट हो तो धातु के कार्य-फलन का आकलन कीजिए। एक He-Ne लेसर द्वारा उत्पन्न 6328 A के उच्च तीव्रता (~10⁵वाट/मीटर²) के लाल प्रकाश के साथ प्रकाश सेल किस प्रकार अनुक्रिया करेगा?
हल
दिया है, λ¹ = 2271 A = 2271 × 10^-10 मीटर के लिए,
निरोधी विभव V₀ = – 1.3 वोल्ट, e= – 1.6 × 10^-19 कूलॉम
∴ आपतित फोटॉन की ऊर्जा E = \(\frac { hc }{ λ }\)
= \(\frac{6.62 \times 10^{-34} \times 3 \times 10^{8}}{2271 \times 10^{-10}}\)
= 8.745 × 10^-19 जूल
जबकि उत्सर्जित इलेक्ट्रॉनों की महत्तम गतिज ऊर्जा
E_max = eV₀
= (-1.6 × 10^-19) × (-1.3)
= 2.08 × 10^-19 जूल
∴ Φ₀ या W = \(\frac { hc }{ λ }\) – w से,
Φ₀ = \(\frac { hc }{ λ }\) – E_max
∴धातु का कार्यफलन W = \(\frac{h c}{\lambda_{1}}\) – E_max
= 8.745 × 10^-19 – 2.08 × 10^-19
W = 6.665 × 10^-19 जूल।
या W = \(\frac{6.665 \times 10^{-19}}{1.6 \times 10^{-19}}\) इलेक्ट्रॉन-वोल्ट
= 4.17 इलेक्ट्रॉन-वोल्ट।
पुन: W = \(\frac{h c}{\lambda_{0}}\) से,
देहली तरंगदैर्घ्य λ₀ = \(\frac { hc }{ w }\) = \(\frac{6.62 \times 10^{-34} \times 3 \times 10^{8}}{6.665 \times 10^{-19}}\)
= 2.979 × 10^-7 मीटर
λ₀ = 2979A
∵ दूसरी दशा में आपतित तरंगदैर्घ्य
λ₂ = 6328A > λ₀
अत: प्रकाश सेल इलेक्ट्रॉन उत्सर्जित नहीं करेगा और कोई धारा प्रवाहित नहीं होगी।

प्रश्न 27.
एक नियॉन लैम्प से उत्पन्न 640.2 नैनोमीटर (1 नैनोमीटर = 10^-9 मीटर) तरंगदैर्ध्य का एकवर्णी विकिरण टंगस्टन पर सीजियम से निर्मित प्रकाश-संवेदी पदार्थ को विकिरित करता है। निरोधी वोल्टता 0.54 वोल्ट मापी जाती है। स्रोत को एक लौह-स्रोत से बदल दिया जाता है। इसकी 427.2 नैनोमीटर वर्ण-रेखा उसी प्रकाश सेल को विकिरित करती है। नयी निरोधी वोल्टता ज्ञात कीजिए।
हल
दिया है, λ₁ = 640.2 नैनोमीटर = 640.2 × 10^-9 मीटर
निरोधी वोल्टता V₁ = 0.54 वोल्ट, λ₂ = 427.2 नैनोमीटर
= 427.2 × 10^-9 मीटर के लिए निरोधी विभव V₂ = ?
आइन्स्टीन के प्रकाश-विद्युत समीकरण से,
E_max = \(\frac { hc }{ λ }\) – W या eV₀ = \(\frac { hc }{ λ }\)-w [∵E_max = eV₀ ]
प्रथम दशा में, eV₁ = \(\frac{h c}{\lambda_{1}}\) – W ….(1)
दूसरी दशा में, eV₂ = \(\frac{h c}{\lambda_{2}}\) – W …(2) [ ∵ सेल वही है, अत: Φ₀ नियत है]
समीकरण (2) में से (1) को घटाने पर,

∴ अभीष्ट निरोधी विभव V₂ = V₁ + 0.97 = 1.51 वोल्ट।

प्रश्न 28.
एक पारद लैम्प, प्रकाश-विद्युत उत्सर्जन की आवृत्ति निर्भरता के अध्ययन के लिए एक सुविधाजनक स्रोत है क्योंकि यह दृश्य-स्पेक्ट्रम के पराबैंगनी (UV) से लाल छोर तक कई वर्ण-रेखाएँ उत्सर्जित करता है। रूबीडियम प्रकाश सेल के हमारे प्रयोग में, पारद (Mercury) स्रोत की निम्न वर्ण-रेखाओं का प्रयोग किया गया
λ₁ = 3650 A
λ₂ = 4047Ā
λ₃= 4358 A
λ₄ = 5461A
λ₅ = 6907A
निरोधी वोल्टताएँ, क्रमशः निम्न मापी गईं हैं
V_o1 = 1.28 वोल्ट,
V_o2 = 0.95 वोल्ट,
V_o3 = 0.74 वोल्ट,
V_o4 = 0.16 वोल्ट,
V_o5 = 0 वोल्ट
(a) प्लांक स्थिरांक का मान ज्ञात कीजिए।
(b) धातु के लिए देहली आवृत्ति तथा कार्यफलन का आकलन कीजिए।
[नोट-उपर्युक्त आँकड़ों से h का मान ज्ञात करने के लिए आपको e = 1.6 × 10^-19 कूलॉम की आवश्यकता होगी। इस प्रकार के प्रयोग Na, Li, K आदि के लिए मिलिकन ने किए थे। मिलिकन ने अपने तेल-बूंद प्रयोग से प्राप्त e के मान का उपयोग कर आइन्स्टीन के प्रकाश विद्युत समीकरण को सत्यापित किया तथा इन्हीं प्रेक्षणों से h के मान के लिए पृथक् अनुमान लगाया।]
हल
किसी दी गई तरंगदैर्घ्य λ के लिए संगत आवृत्ति

अब दिए गए आँकड़े निम्न प्रकार हैं1
ν₁ = 8.2 × 1014 हर्ट्स
ν₂ = 7.4 × 1014 हर्ट्स
ν₃ = 6.9 × 1014 हर्ट्स
ν₄ = 5.5 × 1014 हर्ट्स
ν₅= 4.3 × 1014 हर्ट्स

V_o1 = 1.28 वोल्ट
V_o2 = 0.95 वोल्ट
V_o3 = 0.74 वोल्ट
V_o4 = 0.16 वोल्ट
V_o5 = 0 वोल्ट

उपर्युक्त आँकड़ों के आधार पर ν तथा V₀ के बीच खींचा गया ग्राफ निम्नांकित चित्र में प्रदर्शित है।

उक्त ग्राफ से स्पष्ट है कि प्रथम चार बिन्दु एक सरल रेखा में हैं तथा ‘,
देहली आवृत्ति ν_o = 5.0 × 10₁₄ हर्ट्स
∵ पाँचवें बिन्दु के लिए, ν₅ < ν_o
अतः इस दशा में इलेक्ट्रॉन उत्सर्जन रोकने हेतु निरोधी विभव की आवश्यकता नहीं होती।

(a) ग्राफ का ढाल \(\frac{\Delta V_{0}}{\Delta v}=\frac{V_{A}-V_{B}}{v_{A}-v_{B}}\)

∴ प्लांक नियतांक h = e × ग्राफ का ढाल
= 1.6 × 10_-19 × 4.1 × 10_-15
≈ 6.6 × 10^-34 जूल-सेकण्ड।

(b) ग्राफ से देहली आवृत्ति ν_o = 5 × 10¹⁴ हर्ट्स।
कार्य-फलन W = hν₀
= 6.6 × 10^-34 × 5 × 10¹⁴ हर्ट्स
= 3.3 × 10^-19 जूल।
अथवा W = \(\frac{3.3 \times 10^{-19}}{1.6 \times 10^{-19}}\) इलेक्ट्रॉन-वोल्ट
= 2.06 इलेक्ट्रॉन-वोल्ट।
≈ 2.1 इलेक्ट्रॉन-वोल्ट।

प्रश्न 29.
कुछ धातुओं के कार्य-फलन निम्न प्रकार दिए गए हैं
Na : 2.75 इलेक्ट्रॉन-वोल्ट; K : 2.30 इलेक्ट्रॉन-वोल्ट; Mo : 4.17 इलेक्ट्रॉन-वोल्ट; Ni : 5.15 इलेक्ट्रॉन-वोल्ट। इनमें धातुओं में से कौन प्रकाश सेल से 1 मीटर दूर रखे गए He-Cd लेसर से उत्पन्न 3300 A तरंगदैर्घ्य के विकिरण के लिए प्रकाश-विद्युत उत्सर्जन नहीं देगा? लेसर को सेल के निकट 50 सेमी दूरी पर रखने पर क्या होगा?
हल
He-Cd लेसर से उत्पन्न तरंगदैर्घ्य
λ = 3300 A = 3.3 × 10^-7 मीटर
इस विकिरण के एक फोटॉन की ऊर्जा
E = \(\frac { hc }{ λ }\)
= \(\frac{6.6 \times 10^{-34} \times 3 \times 10^{8}}{3.3 \times 10^{-7}}\)
= 6 × 10^-19 जूल
= \(\frac{6 \times 10^{-19}}{1.6 \times 10^{-19}}\) इलेक्ट्रॉन-वोल्ट
= 3.75 इलेक्ट्रॉन-वोल्ट
∵ Mo तथा Ni के लिए कार्य-फलन, उक्त विकिरण के एक फोटॉन की ऊर्जा से अधिक है, अतः उक्त दोनों धातु प्रकाश विद्युत उत्सर्जन नहीं देंगे।

यदि लेसर को 1 मीटर के स्थान पर 50 सेमी दूरी पर रख दें तो भी उक्त परिणाम में कोई अन्तर नहीं आएगा, क्योंकि लेसर को समीप रखने पर धातु पर गिरने वाले प्रकाश की तीव्रता तो बढ़ जाएगी, परन्तु एक फोटॉन से सम्बद्ध ऊर्जा में कोई परिवर्तन नहीं होगा।

प्रश्न 30.
10^-5 वाट/मीटर² तीव्रता का प्रकाश सोडियम प्रकाश सेल के 2 सेमी² क्षेत्रफल के पृष्ठ पर पड़ता है। यह मान लें कि ऊपर की सोडियम की पाँच परतें आपतित ऊर्जा को अवशोषित करती हैं तो विकिरण के तरंग-चित्रण में प्रकाश-विद्युत उत्सर्जन के लिए आवश्यक समय का आकलन कीजिए। धातु के लिए कार्य-फलन लगभग 2 इलेक्ट्रॉन-वोल्ट दिया गया है। आपके उत्तर का क्या निहितार्थ है?
हल
दिया है, प्रकाश की तीव्रता I = 10^-5 वाट/मीटर²
सेल का क्षेत्रफल A = 2 × 10^-4 मीटर²,
कार्य-फलन W = 2 इलेक्ट्रॉन-वोल्ट
∵ सोडियम परमाणु की लगभग त्रिज्या
r= 10^-10 मीटर
∴ सोडियम परमाणु का लगभग क्षेत्रफल
πr² = 3.14 × 10^-20 ≈ 10^-20 मीटर²
∴ एक परत में उपस्थित सोडियम परमाणुओं की संख्या

∵ 5 परतों में परमाणुओं की संख्या n= 5 × 2 × 10¹⁶ = 10¹⁷
∵ सोडियम के एक परमाणु में एक चालन इलेक्ट्रॉन होता है, अत: इन n परमाणुओं में n चालन इलेक्ट्रॉन होंगे। सेल पर प्रति सेकण्ड आपतित प्रकाशिक ऊर्जा
= I × A
= 10^-5 × 2 × 10^-4
= 2 × 10^-9 वाट
∵ कुल ऊर्जा सोडियम की पाँच परतों द्वारा अवशोषित होती है, अत: तरंग सिद्धान्त के अनुसार यह ऊर्जा पाँच परतों के n इलेक्ट्रॉनों में समान रूप से बँट जाती है।
∴ एक इलेक्ट्रॉन को प्रति सेकण्ड प्राप्त होने वाली ऊर्जा

= 2 × 10^-26 जूल/सेकण्ड
∵ कार्य-फलन Φ₀ = 2 इलेक्ट्रॉन-वोल्ट
= 2 × 1.6 × 10^-19 जूल
अर्थात् 1 इलेक्ट्रॉन को उत्सर्जित कराने के लिए आवश्यक ऊर्जा = 3.2 × 10^-19 जूल
∴ किसी इलेक्ट्रॉन को उत्सर्जित होने में लगा समय t = पर्याप्त ऊर्जा प्राप्त करने में लगा समय

उत्तर का निहितार्थ- इस उत्तर से स्पष्ट है कि प्रकाश के तरंग सिद्धान्त के अनुसार प्रकाश विद्युत-उत्सर्जन की घटना में एक इलेक्ट्रॉन को उत्सर्जित होने में लगने वाला समय बहुत अधिक है जो कि इलेक्ट्रॉन उत्सर्जन में लगे प्रेक्षित समय (लगभग 10^-9 सेकण्ड) से मेल नहीं खाता। इससे स्पष्ट है कि प्रकाश का तरंग सिद्धान्त प्रकाश विद्युत उत्सर्जन की व्याख्या नहीं कर सकता।

प्रश्न 31.
x-किरणों के प्रयोग अथवा उपयुक्त वोल्टता से त्वरित इलेक्ट्रॉनों से क्रिस्टल-विवर्तन प्रयोग किए जा सकते हैं। कौन-सी जाँच अधिक ऊर्जा सम्बद्ध है? (परिमाणिक तुलना के लिए, जाँच के लिए तरंगदैर्घ्य को 1A लीजिए, जो कि जालक (लेटिस) में अन्तर-परमाणु अन्तरण की कोटि का है) (me = 9.11 × 10_-31 किग्रा)।
हल
दिया है, x-किरण फोटॉन तथा इलेक्ट्रॉन की तरंगदैर्घ्य λ= 1A = 10^-10 मीटर
∴ x-किरण फोटॉन की ऊर्जा E = \(\frac { hc }{ λ }\) = \(\frac{6.62 \times 10^{-34} \times 3 \times 10^{8}}{10^{-10}}\) = 1.986 x 10^-15 जूल
∵ इलेक्ट्रॉन की दे-ब्रॉग्ली तरंगदैर्घ्य λ = \(\frac { h}{ p }\)
∴ इलेक्ट्रॉन का संवेग p = \(\frac { h }{ λ }\)
इलेक्ट्रॉन की गतिज ऊर्जा \(E=\frac{1}{2} m v^{2}=\frac{m^{2} v^{2}}{2 m}\)
⇒ \(E=\frac{p^{2}}{2 m}=\frac{h^{2}}{2 m \lambda^{2}}\)
= \(\frac{\left(6.62 \times 10^{-34}\right)^{2}}{2 \times 9.1 \times 10^{-31} \times\left(10^{-10}\right)^{2}}\)
= 2.40 × 10^-17 जूल
स्पष्ट है कि x-किरण फोटॉन की ऊर्जा समान तरंगदैर्घ्य के इलेक्ट्रॉन की ऊर्जा से अधिक है।

(b) दिया है, कमरे का तापमान T = 27 + 273 = 300K
न्यूट्रॉन का द्रव्यमान m_n = 1.675 × 10^-27 किग्रा
बोल्ट्समान नियतांक k = 1.38 × 10^-23 जूल/मोल-K
कमरे के ताप पर न्यूट्रॉन की गतिज ऊर्जा

∴ न्यूट्रॉन का संवेग p= m_nυ =\(\sqrt{3 m_{n} k T}\)
अत: न्यूट्रॉन की दे-ब्रॉग्ली तरंगदैर्घ्य

= 1.45 A

स्पष्ट है कि 27°C के न्यूट्रॉन की दे-ब्रॉग्ली तरंगदैर्घ्य, क्रिस्टलों में अन्तरापरमाण्विक दूरी के साथ तुलनीय है। अत: यह न्यूट्रॉन क्रिस्टल विवर्तन प्रयोग के लिए उपयुक्त है।

इससे स्पष्ट है कि न्यूट्रॉनों को क्रिस्टल विवर्तन प्रयोगों में उपयोग में लाने के लिए उन्हें वातावरण के साथ तापीकृत करना चाहिए।

प्रश्न 33.
एक इलेक्ट्रॉन सूक्ष्मदर्शी में 50 किलोवोल्ट वोल्टता के द्वारा त्वरित इलेक्ट्रॉनों का उपयोग किया जाता है। इन इलेक्ट्रॉनों से जुड़े देब्रॉग्ली तरंगदैर्घ्य ज्ञात कीजिए। यदि अन्य बातों (जैसे कि संख्यात्मक द्वारक आदि) को लगभग समान लिया जाए, इलेक्ट्रॉन सूक्ष्मदर्शी की विभेदन क्षमता की तुलना पीले प्रकाश का प्रयोग करने वाले प्रकाश सूक्ष्मदर्शी से किस प्रकार होती है?
हल
दिया है, इलेक्ट्रॉनों का त्वरक विभवान्तर V= 50 किलोवोल्ट = 50 × 10³ वोल्ट
∴ इलेक्ट्रॉन की ऊर्जा E = eV जूल

∴ इलेक्ट्रॉन की दे-ब्रॉग्ली तरंगदैर्घ्य λ_e = \(\frac { h}{ p }\)

जबकि पीले प्रकाश की तरंगदैर्घ्य λ_y = 5900 A
∵ किसी प्रकाशिक यन्त्र की विभेदन क्षमता \(\propto \frac{1}{\lambda}\)

प्रकाशिक सूक्ष्मदर्शी की विभेदन क्षमता 0.05481
अर्थात् इलेक्ट्रॉन सूक्ष्मदर्शी की विभेदन क्षमता, प्रकाशिक सूक्ष्मदर्शी की विभेदन क्षमता की 10⁵ गुनी होती है।

प्रश्न 34.
किसी जाँच की तरंगदैर्घ्य उसके द्वारा कुछ विस्तार में जाँच की जा सकने वाली संरचना के आकार की लगभग आमाप है। प्रोटॉनों तथा न्यूट्रॉनों की क्वार्क (quark) संरचना 10^-15 मीटर या इससे भी कम लम्बाई के लघु पैमाने की है। इस संरचना को सर्वप्रथम 1970 दशक के प्रारम्भ में, एक रेखीय त्वरित्र (Linear accelerator) से उत्पन्न उच्च ऊर्जा इलेक्ट्रॉनों के किरण-पुंजों के उपयोग द्वारा, स्टैनफोर्ड, संयुक्त राज्य अमेरिका में जाँचा गया था। इन इलेक्ट्रॉन किरण-पुंजों की ऊर्जा की कोटि का अनुमान लगाइए। (इलेक्ट्रॉन की विराम द्रव्यमान ऊर्जा 0.511 मिलियन इलेक्ट्रॉन-वोल्ट है।)
हल
क्वार्क संरचना का आमाप, λ = 10^-15 मीटर,
इलेक्ट्रॉन का विराम द्रव्यमान m_o = 9.1 × 10^-31 किग्रा
∴ इलेक्ट्रॉन की विराम द्रव्यमान ऊर्जा
\(E_{0}=m_{0} c^{2}=9.1 \times 10^{-31} \times\left(3 \times 10^{8}\right)^{2}\)
= 8.19 × 10^-14 जूल
सूत्र λ = \(\frac { h}{ p }\) से, संवेग p=\(\frac { h}{ λ }\)
⇒\(p=\frac{6.62 \times 10^{-34}}{10^{-15}}\)
= 6.62 × 10^-34 जूल
∴ आपेक्षिक सिद्धान्त के अनुसार, \(E^{2}=\dot{m}_{0}^{2} c^{4}+p^{2} c^{2}=\left(m_{0} c^{2}\right)^{2}+p^{2} c^{2}\)

अत: रेखीय त्वरित्र से निकलने वाले इलेक्ट्रॉन की ऊर्जा 10⁹ इलेक्ट्रॉन-वोल्ट (अथवा बिलियन इलेक्ट्रॉन वोल्ट) की कोटि की है।

प्रश्न 35.
कमरे के ताप (27°C) और 1 वायुमण्डल दाब पर He परमाणु से जुड़े प्रारूपी दे-ब्रॉग्ली तरंगदैर्घ्य ज्ञात कीजिए और इन परिस्थितियों में इसकी तुलना दो परमाणुओं के बीच औसत दूरी से कीजिए।
हल
कमरे का ताप T = 27+ 273 = 300 K
He का परमाणु द्रव्यमान = 4 ग्राम
1 ग्राम मोल (4 ग्राम) हीलियम में परमाणुओं की संख्या = N_A = 6.02 × 10²³

= 0.7274 ≈ 0.73A.
यहाँ गैस का दाब P = 1.01 × 10⁵ पास्कल · तथा T = 300 K

= 3.4 × 10^-9 मीटर = 34 A.
इससे स्पष्ट है कि परमाणुओं के बीच की दूरी, दे-ब्रॉग्ली तरंगदैर्ध्य से लगभग 50 गुनी बड़ी है।

प्रश्न 36.
किसी धातु में 27°C पर एक इलेक्ट्रॉन का प्रारूपी दे-ब्रॉग्ली तरंगदैर्घ्य परिकलित कीजिए और इसकी तुलना धातु में दो इलेक्ट्रॉनों के बीच औसत पृथक्य से कीजिए जो लगभग 2 × 10^-10 मीटर दिया गया है।
[नोट-प्रश्न 35 और 36 प्रदर्शित करते हैं कि जहाँ सामान्य परिस्थितियों में गैसीय अणुओं से जुड़े तरंग पैकेट अ-अतिव्यापी हैं; किसी धातु में इलेक्ट्रॉन तरंग पैकेट प्रबल रूप से एक-दूसरे से अतिव्यापी हैं। यह सुझाता है कि जहाँ किसी सामान्य गैस में अणुओं की अलग पहचान हो सकती है, किसी धातु में इलेक्ट्रॉन की एक-दूसरे से अलग पहचान नहीं हो सकती। इस अप्रभेद्यता के कई मूल निहितार्थताएँ हैं जिन्हें आप भौतिकी के अधिक उच्च पाठ्यक्रमों में जानेंगे]
हल
परम ताप T = 27 + 273 = 300K
इस ताप पर इलेक्ट्रॉन की गतिज ऊर्जा \(E=\frac{1}{2} m v^{2}=\frac{3}{2} k T\)
⇒\(v=\sqrt{\frac{3 k T}{m}}\)
\(\lambda=\frac{h}{p}=\frac{h}{\sqrt{3 m k T}}\)
[m = 9.1 × 10^-31 किग्रा, k= 1.38 × 10^-23 जूल/मोल-K]
∴ इलेक्ट्रॉन की दे-ब्रॉग्ली तरंगदैर्घ्य \(\lambda=\frac{6.62 \times 10^{-34}}{\sqrt{\left(3 \times 9.1 \times 10^{-31} \times 1.38 \times 10^{-23} \times 300\right)}}\)
= 62  × 10^-10 मीटर = 62A.
जबकि दो इलेक्ट्रॉनों के बीच की दूरी r_o = 2 × 10^-10 मीटर
∴ \(\frac{\lambda}{r_{0}}=\frac{62}{2}=31\)
अर्थात् दे-ब्रॉग्ली तरंगदैर्घ्य, इलेक्ट्रॉनों के बीच की दूरी की 31 गुनी है।

प्रश्न 37.
निम्नलिखित प्रश्नों के उत्तर दीजिए-
(a) ऐसा विचार किया गया है कि प्रोटॉन और न्यूट्रॉन के भीतर क्वार्क पर आंशिक आवेश होते है \(\left[\left(+\frac{2}{3}\right) e ;\left(-\frac{1}{3}\right) e\right]\) यह मिलिकन तेल-बूंद प्रयोग में क्यों नहीं प्रकट होते?
(b) \(\frac { e }{ m }\) संयोग की क्या विशिष्टता है? हम e तथा m के विषय में अलग-अलग विचार क्यों नहीं करते?
(c) गैसें सामान्य दाब पर कुचालक होती हैं, परन्तु बहुत कम दाब पर चालन प्रारम्भ कर देती हैं। क्यों?
(d) प्रत्येक धातु का एक निश्चित कार्य-फलन होता है। यदि आपतित विकिरण एकवर्णी हो तो सभी प्रकाशिक इलेक्ट्रॉन समान ऊर्जा के साथ बाहर क्यों नहीं आते हैं? प्रकाशिक इलेक्ट्रॉनों का एक ऊर्जा वितरण क्यों होता है?
(e) एक इलेक्ट्रॉन की ऊर्जा तथा इसका संवेग इससे जुड़े पदार्थ-तरंग की आवृत्ति तथा इसके तरंगदैर्घ्य के साथ निम्न प्रकार सम्बन्धित होते हैं -E = hν, p = \(\frac { h }{ λ }\)

परन्तु λ का मान जहाँ भौतिक महत्त्व का है, ” के मान (और इसलिए कला चाल A का मान) का कोई भौतिक महत्त्व नहीं है। क्यों?
उत्तर
(a) भिन्नात्मक आवेश वाले क्वार्क न्यूट्रॉन तथा प्रोटॉन के भीतर इस प्रकार सीमित रहते हैं कि प्रोटॉन में उपस्थित क्वार्कों के आवेशों का योग +e तथा न्यूट्रॉन में उपस्थित क्वार्कों के आवेशों का योग शून्य बना रहता है तथा ये क्वार्क पारस्परिक आकर्षण बलों द्वारा बँधे रहते हैं। जब इन्हें अलग करने का प्रयास किया जाता है तो बल और अधिक शक्तिशाली हो जाते हैं और इसी कारण वे एक-साथ बने रहते हैं। इसीलिए प्रकृति में भिन्नात्मक आवेश मुक्त अवस्था में नहीं पाए जाते अपितु वे सदैव इलेक्ट्रॉनिक आवेश के पूर्ण गुणज के रूप में ही पाए जाते हैं।

(b) इलेक्ट्रॉन की गति समीकरणों eV= \(\frac { 1 }{ 2 }\) mv², eE = ma तथा evB= \(\frac{m v^{2}}{r}\) द्वारा निर्धारित होती है। इनमें से प्रत्येक में e तथा m दोनों एक साथ आए हैं। इससे स्पष्ट है कि इलेक्ट्रॉन की गति के लिए e अथवा m पर अकेले-अकेले विचार करने के स्थान पर \(\frac { e }{ m }\) पर विचार किया जाता है।

(c) सामान्य दाब पर गैसों में विसर्जन के कारण उत्पन्न आयन कुछ ही दूरी तय करने तक गैस के अन्य अणुओं से टकराकर उदासीन हो जाते हैं और इस कारण सामान्य दाब पर गैसों में विद्युत चालन नहीं हो पाता। इसके विपरीत अत्यन्त निम्न दाब पर गैस में अणुओं की संख्या बहुत कम रह जाती है। इस कारण उत्पन्न आयन अन्य अणुओं से टकराने से पूर्व ही विपरीत इलेक्ट्रॉड तक पहुँच जाते हैं।

(d) कार्य-फलन से, धातु में उच्चतम ऊर्जा स्तर अथवा चालन बैण्ड में उपस्थित इलेक्ट्रॉनों के उत्सर्जन के लिए आवश्यक न्यूनतम ऊर्जा का ज्ञान होता है। परन्तु प्रकाश विद्युत उत्सर्जन में इलेक्ट्रॉन अलग-अलग ऊर्जा स्तरों से निकल कर आते हैं। अत: उत्सर्जन के बाद उनके पास भिन्न-भिन्न ऊर्जाएँ होती हैं।

(e) किसी द्रव्य कण की ऊर्जा का निरपेक्ष मान (न कि संवेग) एक निरपेक्ष स्थिरांक के अधीन स्वेच्छ होता है। यही कारण है कि द्रव्य तरंगों से सम्बद्ध तरंगदैर्घ्य λ का ही भौतिक महत्त्व होता है न कि आवृत्ति ν का। इसी कारण कला वेग νλ. का भी कोई भौतिक महत्त्व नहीं होता।

विकिरण तथा द्रव्य की द्वैत प्रकृति NCERT भौतिक विज्ञान प्रश्न प्रदर्शिका (Physics Exemplar LO Problems) पुस्तक से चयनित महत्त्वपूर्ण प्रश्नों के हल

विकिरण तथा द्रव्य की द्वैत प्रकृति बहुविकल्पीय प्रश्नोत्तर

प्रश्न 1.
किसी कण को H ऊँचाई से गिराया जाता है। ऊँचाई के फलन के रूप में कण दे-ब्रॉग्ली तरंगदैर्घ्य निम्न में से किसके __ अनुक्रमानुपाती होती है
(a) H
(b) H^1/2
(c) H⁰
(d) H^-1/2
उत्तर
(d) H^-1/2

प्रश्न 2.
नाभिक से 1 Mev ऊर्जा द्वारा बन्धित प्रोटॉन को नाभिक से बाहर निकालने के लिए आवश्यक फोटॉन की तरंगदैर्घ्य लगभग कितनी होती है
(a) 1.2 नैनोमीटर
(b) 1.2 × 10^-3 नैनोमीटर
(c) 1.2 × 10^-6 नैनोमीटर
(d) 1.2 × 10¹ नैनोमीटर।
उत्तर
(b) 1.2 × 10^-3 नैनोमीटर

प्रश्न 3.
निर्वातित प्रकोष्ठ में रखे धातु के पृष्ठ पर आपतित इलेक्ट्रॉनों को किसी पुंज (जिसमें प्रत्येक इलेक्ट्रॉन की ऊर्जा E₀ है) पर विचार कीजिए। इस पृष्ठ से
(a) कोई इलेक्ट्रॉन उत्सर्जित नहीं होगा क्योंकि केवल फोटॉन ही इलेक्ट्रॉन उत्सर्जित कर सकते हैं
(b) इलेक्ट्रॉन उत्सर्जित हो सकते हैं परन्तु प्रत्येक की ऊर्जा E₀ होगी
(c) अधिकतम ऊर्जा E₀ – Φ + सहित, (Φ धातु का कार्य-फलन है) किसी भी ऊर्जा के इलेक्ट्रॉन उत्सर्जित हो सकते हैं
(d) अधिकतम ऊर्जा E₀ सहित किसी भी ऊर्जा के इलेक्ट्रॉन उत्सर्जित हो सकते हैं।
उत्तर
(d) अधिकतम ऊर्जा E₀ सहित किसी भी ऊर्जा के इलेक्ट्रॉन उत्सर्जित हो सकते हैं।

प्रश्न 4.
एक प्रोटॉन, एक न्यूट्रॉन, एक इलेक्ट्रॉन तथा एक a-कण की ऊर्जा परस्पर बराबर है तो उनकी दे-ब्रॉग्ली तरंगदैर्यों में तुलना इस प्रकार की जा सकती है
(a) λ_p = λ_n > λ_e > λ_α
(b) λ_α < λ_p = λ_n > h_e
(c) λ₂ < λp = λ_n > λ_α
(d) λ_e = λ_p = λn = λ_α.
उत्तर
(b) λ_α < λ_p = λ_n > h_e

प्रश्न 5.
कोई इलेक्ट्रॉन जिसका प्रारम्भिक वेग \(v=v_{0} \hat{\mathrm{i}}\) है किसी चुम्बकीय क्षेत्र \(\mathrm{B}=B_{0} \hat{\mathrm{j}}\) में गतिमान है। इस इलेक्ट्रॉन की
दे-ब्रॉग्ली तरंगदैर्घ्य
(a) अचर रहती है
(b) समय के साथ बढ़ती है
(c) समय के साथ घटती है।
(d) आवर्ती रूप से बढ़ती और घटती है।
उत्तर
(a) अचर रहती है

विकिरण तथा द्रव्य की द्वैत प्रकृति अति लघु उत्तरीय प्रश्नोत्तर

प्रश्न 1.
किसी प्रोटॉन और किसी -कण को समान विभवान्तर द्वारा त्वरित किया गया है। दे-ब्रॉग्ली तरंगदैर्घ्य λ_p एवं λ_α परस्पर किस प्रकार सम्बन्धित हैं? उत्तर

प्रश्न 2.
(i) प्रकाश-विद्युत प्रभाव की व्याख्या करते समय हमने यह माना था कि आवृत्ति का फोटॉन किसी इलेक्ट्रॉन से संघट्ट करता है और अपनी ऊर्जा उसको हस्तान्तरित कर देता है। इससे हमें उत्सर्जित इलेक्ट्रॉन की अधिकतम ऊर्जा, E _{अधिकतम} के लिए निम्न प्रकार का समीकरण प्राप्त होता है
E_{अधिकतम} = hν-Φ₀
जहाँ Φ₀ धातु का कार्य-फलन है। यदि कोई इलेक्ट्रॉन दो फोटॉन (प्रत्येक की आवृत्ति । है) अवशोषित करता है, तो उत्सर्जित इलेक्ट्रॉन की अधिकतम ऊर्जा क्या होगी?
(ii) निरोधी विभव सम्बन्धी हमारी विवेचना में दो फोटॉन अवशोषण के इस प्रकरण पर विचार क्यों नहीं किया गया?
उत्तर
(i) इलेक्ट्रॉन द्वारा दो फोटॉन अवशोषित करने पर उत्सर्जित इलेक्ट्रॉन की अधिकतम ऊर्जा,
E_{अधिकतम} = 2hν-Φ₀
(ii) एक ही इलेक्ट्रॉन द्वारा दो फोटॉन अवशोषित करने की प्रायिकता बहुत कम है। अत: इस प्रकरण पर विचार नहीं किया जाता है।

प्रश्न 3.
कुछ पदार्थ ऐसे होते हैं जो लघु तरंगदैर्घ्य के फोटॉन को अवशोषित करते हैं और दीर्घ तरंगदैर्घ्य के फोटॉन उत्सर्जित करते हैं। क्या ऐसे स्थायी पदार्थ भी हो सकते हैं जो दीर्घ तरंगदैर्घ्य के फोटॉन अवशोषित करके लघु तरंगदैर्यों का प्रकाश उत्सर्जित करें।
उत्तर
लघु तरंगदैर्घ्य के फोटॉन, जिनकी ऊर्जा उच्च होती है; को अवशोषित कर दीर्घ तरंगदैर्घ्य के फोटॉन, जिनकी ऊर्जा निम्न होती है; को उत्सर्जित करना सरलता से सम्भव है। दीर्घ तरंगदैर्घ्य के फोटॉन, जिनकी ऊर्जा कम होती है; को अवशोषित कर लघु तरंगदैर्घ्य के फोटॉन, जिनकी ऊर्जा अधिक होती है; को उत्सर्जित करने के लिए पदार्थ को ऊर्जा आपूर्ति करनी होगी तथा किसी भी स्थायी पदार्थ के लिए ऐसा करना सम्भव नहीं है।

प्रश्न 4.
क्या फोटॉन अवशोषित करने वाले सभी इलेक्ट्रॉन फोटो इलेक्ट्रॉनों के रूप में निष्क्रमित होते हैं?
उत्तर
नहीं, फोटॉन अवशोषित करने वाले सभी इलेक्ट्रॉन, फोटो इलेक्ट्रॉन के रूप में निष्क्रमित नहीं होते हैं क्योंकि अधिकांश इलेक्ट्रॉन धातु में ही प्रकीर्णित हो जाते हैं और केवल कुछ ही इलेक्ट्रॉन धातु से बाहर निष्क्रमित हो पाते हैं।

विकिरण तथा द्रव्य की द्वैत प्रकृति लघु उत्तरीय प्रश्नोत्तर

प्रश्न 1.
25 एवं 2, दे-ब्रॉग्ली तरंगदैर्घ्य के दो कण A एवं B मिलकर कोई कण C बनाते हैं। इस प्रक्रिया में संवेग संरक्षण होता है। कण C के दे-ब्रॉग्ली तरंगदैर्घ्य का परिकलन कीजिए (गति एकविमीय है)।
हल
कण C का संवेग = (कण A का संवेग) + (कण B का संवेग)
PC = P_A + P_B.
परन्तु संवेग p = \(\frac { h }{ λ }\), जहाँ λ. कण के संगत दे-ब्रॉग्ली तरंगदैर्घ्य है।

विकिरण तथा द्रव्य की द्वैत प्रकृति आंकिक प्रश्नोत्तर

प्रश्न 1.
दो प्रकाश स्रोत हैं जिनमें प्रत्येक 100 वाट शक्ति उत्सर्जित करता है। इनमें से एक 1 नैनोमीटर तरंगदैर्घ्य की x-किरणें और दूसरा 500 नैनोमीटर का दृश्य प्रकाश उत्सर्जित करता है। दी गई तरंगदैर्यों के लिए x-किरणों के फोटॉनों की संख्या तथा दृश्य प्रकाश के फोटॉनों की संख्या का अनुपात ज्ञात कीजिए।
हल
दिया है : शक्ति (P) = 100 वाट, λ₁ = 1 नैनोमीटर = 1 × 10^-9 मीटर,
λ₂ = 500 नैनोमीटर = 500 × 10^-9 मीटर
P= n₁ E₁=n₂ E₂
या \(n_{1} \frac{h c}{\lambda_{1}}=n_{2} \frac{h c}{\lambda_{2}}\)
या \(\frac{n_{1}}{n_{2}}=\frac{\lambda_{1}}{\lambda_{2}}=\frac{1 \times 10^{-9}}{500 \times 10^{-9}}=\frac{1}{500}\)
या n₁ : n₂ = 1 : 500.

प्रश्न 2.
600 नैनोमीटर की तरंगदैर्घ्य के प्रकाश से उद्भासित किसी धातु की सतह से उत्सर्जित इलेक्ट्रॉनों की अधिकतम ऊर्जा मापी गई। यह पाया गया कि 400 नैनोमीटर तरंगदैर्घ्य के प्रकाश का उपयोग करने पर इससे उत्सर्जित होने वाले इलेक्ट्रॉनों की अधिकतम ऊर्जा दोगुनी हो गई। धातु का कार्य-फलन (ev में) ज्ञात कीजिए।
हल
λ₁ = 600 नैनोमीटर, λ₂ = 400 नैनोमीटर
प्रकाश-इलेक्ट्रॉनों की अधिकतम गतिज ऊर्जा, E_k = E – W = \(\frac { hc }{ λ }\) – W

प्रश्न 3.
कोई विद्यार्थी दो पदार्थ A एवं B लेकर प्रकाश-विद्युत प्रभाव सम्बन्धी प्रयोग करता है। V_{नरोधी} तथा ν का ग्राफ चित्र-11.3 में (v)| दर्शाया गया है।
(i) A एवं B में किस पदार्थ का कार्य-फलन अधिक है?
(ii) इलेक्ट्रॉन का विद्युत आवेश = 1.6 × 10^-19 कूलॉम लेकर 15 प्रयोग से प्राप्त आँकड़ों के आधार पर A एवं B दोनों के लिए h का 1 मान ज्ञात कीजिए।
टिप्पणी कीजिए कि क्या यह आइन्स्टीन के सिद्धान्त के अनुरूप

हल
(i) पदार्थ B के लिए देहली आवृत्ति (ν_o) का मान पदार्थ A से अधिक है। अत: पदार्थ B का कार्य-फलन (W = hν_o) अधिक होगा।

(ii) दिए गए ग्राफ का ढलान = \(\frac { h }{ e }\)
पदार्थ A के लिए ग्राफ का ढलान = \(\frac { h }{ e }\)
\(=\frac{2}{(10-5) \times 10^{14}}=\frac{2}{5 \times 10^{14}}\)
∴ पदार्थ A के लिए, h = \(\frac{2}{5 \times 10^{14}} \times 1.6 \times 10^{-19}\)
= 6.04 × 10^-34 जूल-सेकण्ड
पदार्थ B के लिए ग्राफ का ढलान = \(\frac { h }{ e }\)
\(=\frac{2.5}{(15-10) \times 10^{14}}=\frac{2.5}{5 \times 10^{14}}\)
∴ पदार्थ B के लिए, h = \(\frac{2.5}{5 \times 10^{14}} \times 1.6 \times 10^{-19}\)
= 8 × 10^-34 जूल-सेकण्ड।
दोनों पदार्थों के लिए h के मान भिन्न-भिन्न हैं, अत: यह प्रयोग आइन्स्टीन के सिद्धान्त के अनुरूप नहीं है।

MP Board Class 12th Physics Solutions

MP Board Class 12th Physics Important Questions Chapter 1 वैद्युत आवेश तथा क्षेत्र

वैद्युत आवेश तथा क्षेत्र अन्य महत्त्वपूर्ण प्रश्नोत्तर

वैद्युत आवेश तथा क्षेत्र विस्तृत उत्तरीय प्रश्नोत्तर

प्रश्न 1.
किसी वैद्युत द्विध्रुव के कारण उसकी अक्षीय स्थिति (अनुदैर्ध्य स्थिति) में किसी बिन्दु पर वैद्युत क्षेत्र की तीव्रता के सूत्र का निगमन कीजिए। [2002, 11, 12, 13, 14]
अथवा
वैद्युत द्विध्रुव की अक्षीय दिशा में अत्यधिक दूरी पर स्थित बिन्दु पर वैद्युत क्षेत्र की तीव्रता का व्यंजक प्राप्त कीजिए। [2015, 16, 17]
उत्तर :
वैद्युत द्विध्रुव की अक्ष पर स्थित किसी बिन्दु पर वैद्युत क्षेत्र की तीव्रता (Intensity of the Electric Field at an Axial Point of an Electric Dipole) (अक्षीय अथवा अनुदैर्घ्य स्थिति :End-on Position) –  माना AB वैद्युत द्विध्रुव K परावैद्युतांक के माध्यम में स्थित है, जिसके A सिरे पर +q आवेश तथा B सिरे पर -q आवेश एक-दूसरे से 2l दूरी पर स्थित हैं (चित्र 1.23)। इस वैद्युत द्विध्रुव के मध्य-बिन्दु O से r मीटर की दूरी पर इसकी अक्षीय स्थिति में कोई बिन्दु P है, जहाँ पर वैद्युत क्षेत्र की तीव्रता ज्ञात करनी है।

बिन्दु P की आवेश +q से दूरी (r – l) और आवेश -q से दूरी (r + l) है। यदि इनके संगत तीव्रताएँ क्रमश: E₁ व E₂ हों तो
+q आवेश के कारण बिन्दु P पर वैद्युत क्षेत्र की तीव्रता E ₁ = \(\frac{1}{4 \pi \varepsilon_{0} K} \frac{q}{(r-l)^{2}}\) (A →P दिशा में)
-q आवेश के कारण बिन्दु P पर वैद्युत क्षेत्र की तीव्रता E₂ = \(\frac{1}{4 \pi \varepsilon_{0} K} \frac{q}{(r+l)^{2}}\) (P →B दिशा में)

E₁ व E₂ एक ही रेखा के अनुदिश विपरीत दिशाओं में कार्यरत हैं तथा E₁ का मान E₂ से अधिक है; अत: बिन्दु P पर परिणामी तीव्रता E इन दोनों तीव्रताओं के अन्तर के बराबर तथा \(\overrightarrow{\mathrm{E}}_{1}\) की दिशा में होगी।
अतः बिन्दु P पर वैद्युत द्विध्रुव के कारण परिणामी वैद्युत क्षेत्र की तीव्रता E = E₁ – E₂

यदि l का मान r की अपेक्षा बहुत कम हो (1 <<r) तो l² का मान r² की तुलना में नगण्य माना जा सकता है; अत: वैद्युत द्विध्रुव के कारण बिन्दु P पर वैद्युत क्षेत्र की तीव्रता

यदि वैद्युत द्विध्रुव निर्वात (अथवा वायु) में रखा है, तब निर्वात अथवा वायु के लिए K = 1, अतः वैद्युत द्विध्रुव के कारण बिन्दु P पर वैद्युत क्षेत्र की तीव्रता
E = \(\frac{1}{4 \pi \varepsilon_{0}} \frac{2 p}{r^{3}}\) न्यूटन/कूलॉम।
सदिश रूप में, \(\overrightarrow{\mathrm{E}}=\frac{1}{4 \pi \varepsilon_{0}} \frac{2 \overrightarrow{\mathrm{p}}}{r^{3}}\) न्यूटन/कूलॉम।
इस प्रकार अक्षीय स्थिति में वैद्युत क्षेत्र E की दिशा वैद्युत द्विध्रुव आघूर्ण के अनुदिश अर्थात् ऋण आवेश से धन . आवेश की ओर होती है।

प्रश्न 2.
किसी वैद्युत द्विध्रुव के कारण निरक्षीय (अनुप्रस्थ) स्थिति में किसी बिन्दु पर वैद्युत क्षेत्र की तीव्रता का व्यंजक प्राप्त कीजिए।
[2009, 14]
अथवा
किसी वैद्युत द्विध्रुव के कारण समद्विभाजक लम्ब अक्ष के किसी बिन्दु पर वैद्युत क्षेत्र की तीव्रता का व्यंजक प्राप्त कीजिए। [2008, 09]
उत्तर :
वैद्युत द्विध्रुव की निरक्षीय स्थिति पर स्थित किसी बिन्दु पर वैद्युत क्षेत्र की तीव्रता (Intensity of the Electric Field at an Equatorial point of an Electric Dipole) (निरक्षीय अथवा अनुप्रस्थ स्थिति : Equatorial Line)-माना AB वैद्युत द्विध्रुव K परावैद्युतांक के माध्यम में स्थित है, जिसके A सिरे पर + q आवेश तथा B सिरे पर – q आवेश एक-दूसरे से 2l दूरी पर स्थित हैं [चित्र 1.24 (a)]। इस वैद्युत द्विध्रुव के मध्य-बिन्दु O से r मीटर की दूरी पर इसकी निरक्षीय स्थिति में कोई बिन्दु P स्थित है, जहाँ पर वैद्युत क्षेत्र की तीव्रता ज्ञात करनी है। माना आवेशों + q तथा –q के कारण बिन्दु P पर वैद्युत क्षेत्र की तीव्रताएँ क्रमश: E₁ व E₂ हैं।

समकोण ∆ AOP तथा ∆ BOP से,
AP² = BP² = r²+l² अथवा AP = BP = \(\sqrt{r^{2}+l^{2}}\)
प्रत्येक आवेश से बिन्दु P की दूरी \(\sqrt{r^{2}+l^{2}}\) है; अतः
+q आवेश के कारण बिन्दु P पर वैद्युत क्षेत्र की तीव्रता E₁ =\(\frac{1}{4 \pi \varepsilon_{0} K} \frac{q}{\left(r^{2}+l^{2}\right)}\) (A→P दिशा में)
तथा -q आवेश के कारण बिन्दु P पर वैद्युत क्षेत्र की तीव्रता E₂ = \(\frac{1}{4 \pi \varepsilon_{0} K} \frac{q}{\left(r^{2}+l^{2}\right)}\) (P→B दिशा में)

चूँकि E₁ व E₂ के मान परस्पर बराबर हैं, परन्तु दिशाएँ भिन्न हैं; अत: E₁ व E₂ को AB के समान्तर तथा लम्बवत् घटकों में वियोजित करने पर AB के लम्बवत् घटक E₁ sin θ व E₂ sin θ बराबर व विपरीत होने के कारण एक-दूसरे को निरस्त (cancel) कर देंगे, जबकि AB के समान्तर घटक E₁ cos θ व E₂ cos θ एक ही दिशा में होने के कारण जुड़ जाएँगे चित्र 1.24 (b)]; अत: बिन्दु P पर वैद्युत द्विध्रुव के कारण परिणामी वैद्युत क्षेत्र की तीव्रता
E = E₁ cos θ + E₂ cos θ .

यदि l का मान 7 की अपेक्षा बहुत कम हो (1 <<r) तो 12 का मान 2 की तुलना में नगण्य माना जा सकता है; अत: वैद्युत द्विध्रुव के कारण बिन्दु P पर वैद्युत क्षेत्र की तीव्रता
E = \(\frac{1}{4 \pi \varepsilon_{0} K} \cdot \frac{p}{\left(r^{2}\right)^{3 / 2}}=\frac{1}{4 \pi \varepsilon_{0} K} \frac{p}{r^{3}}\) न्यूटन/कूलॉमा
यदि वैद्युत द्विध्रुव निर्वात अथवा वायु में रखा है; तब निर्वात अथवा वायु के लिए K = 1 रखने पर, वैद्युत द्विध्रुव के कारण बिन्दु P पर वैद्युत क्षेत्र की तीव्रता
E=\(\frac{1}{4 \pi \varepsilon_{0}} \frac{p}{r^{3}}\) न्यूटन/कूलॉम
सदिश रूप में, \(\overrightarrow{\mathrm{E}}=\frac{1}{4 \pi \varepsilon_{0}} \frac{-\overrightarrow{\mathrm{p}}}{r^{3}}\) न्यूटन/कूलॉम।
इस प्रकार निरक्षीय स्थिति में वैद्युत क्षेत्र E की दिशा वैद्युत द्विध्रुव की अक्ष के समान्तर परन्तु वैद्युत द्विध्रुव आघूर्ण के विपरीत दिशा में अर्थात् धन आवेश से ऋण आवेश की ओर होती है।

प्रश्न 3.
एकसमान रूप से आवेशित वलय के कारण वैद्युत क्षेत्र की तीव्रता का व्यंजक ज्ञात कीजिए। अथवा एक वृत्ताकार आवेशित धातु के वलय (छल्ले) की परिधि पर q आवेश है तथा a इसकी त्रिज्या है तो वलय के केन्द्र से इसकी अक्ष पर कितनी दूरी पर वैद्युत क्षेत्र की तीव्रता अधिकतम होगी? प्रयुक्त सूत्र को स्थापित कीजिए। [2004]
उत्तर :
एकसमान रूप से आवेशित वलय के कारण वैद्युत क्षेत्र की तीव्रता (Intensity of Electric Field due to a Uniformly Charged Ring)-माना a त्रिज्या का एक आवेशित वलय, जिसका केन्द्र O है, वायु में स्थित है। माना इस वलय पर +q आवेश एकसमान रूप से वितरित है। माना वलय की अक्ष पर इसके केन्द्र O से x दूरी पर कोई बिन्दु P है, जहाँ वैद्युत क्षेत्र की तीव्रता ज्ञात करनी है।
माना वलय छोटे-छोटे अल्पांशों में विभक्त है तथा इनमें से एक अल्पांश AB पर आवेश ∆q है। माना अल्पांश AB से बिन्दु P की दूरी में r है (चित्र-1.25)।

अत: ∆q आवेश के कारण बिन्दु P पर वैद्युत क्षेत्र की तीव्रता
∆E = \(\frac{1}{4 \pi \varepsilon_{0}} \frac{\Delta q}{r^{2}}\)
वैद्युत क्षेत्र की तीव्रता ∆ E को वलय की अक्ष के अनुदिश तथा लम्बवत् घटकों में वियोजित करने पर लम्बवत् । घटक ∆ E sin θ एक-दूसरे के विपरीत दिशा में होने के कारण निरस्त हो जाएँगे, जबकि अनुदिश घटक ∆ E cosθ एक ही दिशा में होने के कारण जुड़ जाएँगे।
अत: पूरी वलय के कारण बिन्दु P पर वैद्युत क्षेत्र की तीव्रता

वैद्युत क्षेत्र की तीव्रता E की दिशा 0 से P की ओर होगी।
विशेष स्थितियाँ-1. यदि बिन्दु P वलय के केन्द्र पर स्थित है तो x = 0; अतः वैद्युत क्षेत्र की तीव्रता E = 0. 2. यदि बिन्दु P वलय के केन्द्र से बहुत दूर स्थित है अर्थात् x >> a
इस स्थिति में उपर्युक्त सूत्र में x² की तुलना में a² को नगण्य माना जा सकता है।
अतः वैद्युत क्षेत्र की तीव्रता \(E=\frac{1}{4 \pi \varepsilon_{0}} \frac{q}{x^{2}}\) न्यूटन/कूलॉम।

वलय की अक्ष पर वैद्युत क्षेत्र की अधिकतम तीव्रता की स्थिति – वलय की अक्ष पर वैद्युत क्षेत्र की अधिकतम तीव्रता E, उस बिन्दु पर अधिकतम होगी जिसके लिए \(\frac{d E}{d x}=0\) होगा।

अत: x = ± a/√2 अर्थात् वलय की अक्ष पर, वलय के केन्द्र के दोनों ओर केन्द्र से a/√2 दूरी पर वैद्युत क्षेत्र की तीव्रता अधिकतम होगी।

प्रश्न 4.
स्थिर वैद्युतिकी में गाउस की प्रमेय का उल्लेख कीजिए तथा इसे सिद्ध कीजिए। [2014, 18]
अथवा
सिद्ध कीजिए कि किसी बन्द पृष्ठ से गुजरने वाला वैद्युत फ्लक्स Φ_E उस पृष्ठ द्वारा परिबद्ध कुल आवेश q का 1/ε₀ गुना होता है, जहाँ ε₀ मुक्त आकाश की वैद्युतशीलता है। [2008, 09]
उत्तर :
गाउस की प्रमेय (Gauss’s Theorem )-इस प्रमेय के अनुसार, “किसी बन्द पृष्ठ A से गुजरने वाला वैद्युत फ्लक्स Φ_E , उस पृष्ठ द्वारा परिबद्ध (घिरे हुए) कुल आवेश q का 1/e₀ गुना होता है।”
अतः वैद्युत फ्लक्स कई \(\phi_{E}=q \cdot\left(\frac{1}{\varepsilon_{0}}\right)=\frac{q}{\varepsilon_{0}}\)

परन्तु बन्द पृष्ठ A से बद्ध कुल वैद्युत फ्लक्स \(\phi_{E}=\oint \overrightarrow{\mathrm{E}} \cdot d \overrightarrow{\mathrm{A}}\)
अतः \(\int_{A} \overrightarrow{\mathrm{E}} \cdot d \overrightarrow{\mathrm{A}}=\frac{q}{\varepsilon_{0}}\)

जहाँ ε₀ निर्वात अथवा वायु की वैद्युतशीलता है। यह गाउस प्रमेय का समाकल रूप है।

उपपत्ति – माना कोई बिन्दु आवेश + q, किसी बन्द पृष्ठ A के भीतर किसी बिन्दु O पर स्थित है। माना पृष्ठ A पर कोई बिन्दु P है जिसकी बिन्दु O से दूरी r है। माना पृष्ठ A पर बिन्दु P के चारों ओर एक अल्पांश क्षेत्रफल dA है जिसके संगत क्षेत्रफल वेक्टर d \(\overrightarrow{\mathrm{A}}\) है जिसकी दिशा बिन्दु P पर अल्पांश क्षेत्रफल dA के बाहर की ओर खींचे गए अभिलम्ब के अनुदिश है (चित्र 1.26)।

माना बिन्दु O पर रखे बिन्दु आवेश + q के कारण बिन्दु P पर वैद्युत क्षेत्र \(\overrightarrow{\mathrm{E}}\) है जिसका परिमाण
\(E=\frac{1}{4 \pi \varepsilon_{0}} \frac{q}{r^{2}}\) …(1)
जिसकी दिशा त्रिज्य रेखा OP के अनुदिश है।
यदि वैद्युत वेक्टर \(\overrightarrow{\mathrm{E}}\) तथा क्षेत्रफल वेक्टर d \overrightarrow{\mathrm{A}} के बीच कोण θ है तो अल्पांश क्षेत्रफल dA से गुजरने वाला बाहर की ओर दिष्ट वैद्युत फ्लक्स
\(d \phi_{E}=\overrightarrow{\mathrm{E}} \cdot d \overrightarrow{\mathrm{A}}=E d A \cos \theta\)

समीकरण (1) से E का मान रखने पर,
\(d \phi_{E}=\frac{q}{4 \pi \varepsilon_{0} r^{2}} d A \cos \theta=\frac{q}{4 \pi \varepsilon_{0}} \frac{d A \cos \theta}{r^{2}}\)……………(2)
परन्तु \(\frac{d A \cos \theta}{r^{2}}=d \omega\)

जहाँ dω अल्पांश क्षेत्रफल dA द्वारा बिन्दु O पर अन्तरित घन कोण है।
तब समीकरण (2) से, \(d \phi_{E}=\frac{q}{4 \pi \varepsilon_{0}} d \omega\)
अत: बिन्दु आवेश q के कारण सम्पूर्ण पृष्ठ A से बाहर की ओर निकलने वाला वैद्युत फ्लक्स
\(\phi_{E}=\oint d \phi_{E}=\oint \frac{q}{4 \pi \varepsilon_{0}} d \omega=\frac{q}{4 \pi \varepsilon_{0}} \oint d \omega\)
परन्तु \(\oint d \omega\), सम्पूर्ण बन्द पृष्ठ क्षेत्रफल A द्वारा बिन्दु O पर अन्तरित कुल घन कोण है, अर्थात् \(\oint d \omega=4 \pi\)
अतः \(\phi_{E}=\frac{q}{\varepsilon_{0}}\)

यही गाउस का प्रमेय है।
यदि बन्द पृष्ठ क्षेत्रफल A के भीतर अनेक बिन्दु आवेश q1, q2, -q3, q4, …. आदि उपस्थित हैं तो पृष्ठ से गुजरने वाला बाहर की ओर दिष्ट कुल वैद्युत फ्लक्स, सभी बिन्दु आवेशों के कारण अलग-अलग वैद्युत फ्लक्सों के बीजगणितीय योग के बराबर होगा। जहाँ धन आवेशों के कारण वैद्युत फ्लक्स बाहर की ओर दिष्ट होगा वहीं ऋण आवेशों के कारण वैद्युत फ्लक्स भीतर की ओर दिष्ट होगा; अत: पृष्ठ से बाहर की ओर गुजरने वाला कुल (नेट) वैद्युत फ्लक्स
\(\phi_{E}=\frac{q_{1}}{\varepsilon_{0}}+\frac{q_{2}}{\varepsilon_{0}}-\frac{q_{3}}{\varepsilon_{0}}+\frac{q_{4}}{\varepsilon_{0}}+\ldots \ldots=\frac{1}{\varepsilon_{0}} \Sigma q\)
जहाँ Σq बन्द पृष्ठ के भीतर स्थित ओवेशों का बीजगणितीय योग है।

माना एक बिन्दु आवेश +q, किसी बन्द पृष्ठ A से बाहर बिन्दु O पर स्थित है। आवेश q को शीर्ष लेकर एक अत्यन्त सूक्ष्म घन कोण dω का शंक्वाकार क्षेत्र बनाते हैं जो बन्द पृष्ठ से चित्र-1.27 के अनुसार दो स्थानों से होकर गुजरता है तथा पृष्ठ पर क्रमश: dA₁ व dA ₂क्षेत्रफल काटता है।

आवेश +q के कारण dω कोण से होकर गुजरने वाला वैद्युत फ्लक्स dΦ= q/e
अतः सूक्ष्म क्षेत्रफल dA₁ से होकर प्रवेश करने वाला वैद्युत फ्लक्स \(\phi_{1}=+\frac{q}{\varepsilon_{0}} \frac{d \omega}{4 \pi}\)
तथा सूक्ष्म क्षेत्रफल dA से होकर बाहर आने वाला वैद्युत फ्लक्स \(\phi_{2}=-\frac{q}{\varepsilon_{0}} \frac{d \omega}{4 \pi}\)
६0 41 अतः बन्द पृष्ठ से गुजरने वाला कुल वैद्युत फ्लक्स \(\phi=\phi_{1}+\phi_{2}=+\frac{q}{\varepsilon_{0}} \frac{d \omega}{4 \pi}-\frac{q}{\varepsilon_{0}} \frac{d \omega}{4 \pi}=0\)

इस प्रकार किसी बन्द पृष्ठ से बाहर स्थित आवेश के कारण बन्द पृष्ठ से गुजरने वाला कुल वैद्युत फ्लक्स शून्य होता है। इससे स्पष्ट है कि यदि बन्द पृष्ठ से कोई आवेश परिबद्ध (घिरा हुआ) नहीं है. तो बन्द पृष्ठ से बद्ध वैद्युत फ्लक्स शून्य होगा।

प्रश्न 5.
स्थैतिक वैद्युत में गाउस के नियम का उल्लेख कीजिए तथा इसकी सहायता से कूलॉम के नियम का निगमन कीजिए।
[2018]
उत्तर :
गाउस का नियम : इस नियम के अनुसार किसी बन्द पृष्ठ A से गुजरने वाला वैद्युत फ्लक्स Φ_E उस पृष्ठ द्वारा परिबद्ध (घिरे हुए) कुल आवेश q का 1/ε₀ गुना होता है।
वैद्युत फ्लक्स \(\phi_{E}=\frac{q}{\varepsilon_{0}}\)

गाउस के नियम से कूलॉम के नियम की प्राप्ति – एक बिन्दु आवेश q को केन्द्र मानकर उसके चारों ओर r त्रिज्या का गोलीय गाउसीय पृष्ठ लेते हैं। गाउसीय पृष्ठ पर एक सूक्ष्म क्षेत्रफल अवयव dA लेते हैं, जिस पर वैद्युत क्षेत्र \(\overrightarrow{\mathrm{E}} व क्षेत्रफल सदिश d \overrightarrow{\mathrm{A}}\) दोनों की दिशा समान, त्रिज्यत: बाहर की ओर है।

यदि q आवेश से r दूरी पर परीक्षण आवेश q₀ स्थित हो तब उस पर कार्यरत बल,
\(F=q_{0} E=\frac{1}{4 \pi \varepsilon_{0}} \frac{q q_{0}}{r^{2}}\) या \(F \propto \frac{q q_{0}}{r^{2}}\)

यही कूलॉम का नियम है।

प्रश्न 6.
गाउस प्रमेय की सहायता से एकसमान रूप से आवेशित अनन्त लम्बाई के सीधे तार के निकट वैद्युत क्षेत्र की तीव्रता का व्यंजक प्राप्त कीजिए। [2012, 15]
अथवा
गाउस के नियम का उपयोग करके आवेशित लम्बे तार के निकट, जिसका रेखीय आवेश घनत्व λ कूलॉम/मीटर है, वैद्युत क्षेत्र की तीव्रता के लिए व्यंजक व्युत्पन्न कीजिए। [2007, 08]
उत्तर :
अनन्त लम्बाई के एकसमान आवेशित तार के कारण वैद्युत क्षेत्र की तीव्रता (Intensity of Electric Field due to a Uniformly Charged Wire of Infinite Length) –  माना अनन्त लम्बाई का एक तार YY’ है जिस पर धन आवेश एकसमान रूप से वितरित है। माना आवेश का रेखीय घनत्व λ कूलॉम/मीटर है। माना तार से r दूरी पर कोई बिन्दु P है जहाँ पर इस तार के कारण वैद्युत क्षेत्र की तीव्रता ज्ञात करनी है (चित्र 1.29)।

इसके लिए हम बिन्दु P से जाने वाले, त्रिज्या r तथा l लम्बाई के लम्बवृत्तीय बेलनाकार , पृष्ठ की कल्पना करते हैं, जिसकी अक्ष तार की अक्ष के साथ सम्पाती है। यह बेलनाकार । पृष्ठ, गाउसियन पृष्ठ की भाँति कार्य करेगा। चूँकि इस बेलन के वक्र पृष्ठ का प्रत्येक बिन्दु तार से समान दूरी पर है; अतः सममिति के कारण वक्र पृष्ठ के प्रत्येक बिन्दु पर वैद्युत क्षेत्र परिमाण में समान तथा उस बिन्दु पर त्रिज्यतः बाहर की ओर दिष्ट होगा। यदि वक्र पृष्ठ पर स्थित बिन्दु P पर कोई क्षेत्रफल वेक्टर \(d \overrightarrow{\mathrm{A}}\) लिया जाए तो उस बिन्दु पर वैद्युत क्षेत्र की तीव्रता \(\overrightarrow{\mathrm{E}}\) तथा क्षेत्रफल वेक्टर d \(\overrightarrow{\mathrm{A}}\) एक ही दिशा में होंगे अर्थात् इनके बीच कोण शून्य होगा।

अत: वक्र पृष्ठ पर स्थित सभी बिन्दुओं के लिए वैद्युत फ्लक्स
\(\phi_{P}=\overrightarrow{\mathrm{E}} \cdot d \overrightarrow{\mathrm{A}}=E d A \cos 0^{\circ}=E d A\)
यदि बेलन के वृत्तीय पृष्ठ पर स्थित किसी बिन्दु M पर क्षेत्रफल वेक्टर \(d \overrightarrow{\mathrm{A}}\) हो तो इस बिन्दु पर वैद्युत क्षेत्र की तीव्रता \(\overrightarrow{\mathrm{E}}\)  तथा क्षेत्रफल वेक्टर \(d \overrightarrow{\mathrm{A}}\) परस्पर लम्बवत् होंगे (चित्र 2.29)।

अत: वृत्तीय पृष्ठों के लिए वैद्युत फ्लक्स \(\phi_{M}=\overrightarrow{\mathrm{E}} \cdot d \overrightarrow{\mathrm{A}}=E d A \cos 90^{\circ}=0\)
अतः गाउसियन पृष्ठ से बाहर की ओर गुजरने वाला कुल वैद्युत फ्लक्स
Φ_E = वक्र पृष्ठ से बद्ध वैद्युत फ्लक्स (Φ_P) + वृत्तीय पृष्ठों से बद्ध वैद्युत फ्लक्स (Φ_M)

परन्तु गाउस प्रमेय से, Φ_E = \(\frac{1}{\varepsilon_{0}}\) (बेलनाकार पृष्ठ के भीतर स्थित कुल आवेश).
= \(\frac{1}{\varepsilon_{0}}\) (तार की ! लम्बाई पर स्थित आवेश) = \(\frac{1}{\varepsilon_{0}} λl\)
अतः E(2πrl) = \(\frac{1}{\varepsilon_{0}}λl\)

अत: आवेशित तार से r दूरी पर वैद्युत क्षेत्र की तीव्रता E=\(\frac{\lambda}{2 \pi \varepsilon_{0} r}=\frac{1}{4 \pi \varepsilon_{0}} \frac{2 \lambda}{r}\)

चूँकि तार धनावेशित है; अतः वैद्युत क्षेत्र की तीव्रता E की दिशा त्रिज्यत: बाहर की ओर वेक्टर \(\overrightarrow{\mathbf{r}}\) के अनुदिश होगी। यदि वेक्टर \overrightarrow{\mathbf{r}} की दिशा में एकांक वेक्टर \(\begin{array}{l}{\wedge} \\ {\mathbf{I}^{*}}\end{array}\) है तो वेक्टर रूप में
\(\overrightarrow{\mathrm{E}}=\frac{\lambda}{2 \pi \varepsilon_{0} r} \hat{\mathrm{r}}=\frac{1}{4 \pi \varepsilon_{0}} \frac{2 \lambda}{r} \hat{\mathrm{r}}\)

इस प्रकार रेखीय आवेश के कारण वैद्युत क्षेत्र की तीव्रता (E) रेखीय आवेश से बिन्दु की दूरी (r) के व्युत्क्रमानुपाती होती है। इसकी दिशा रेखीय आवेश के लम्बवत् बाहर की ओर होती है। दूरी r के साथ वैद्युत क्षेत्र की तीव्रता E में परिवर्तन का आरेख
चित्र-1.30 संलग्न चित्र 1.30 में प्रदर्शित है।

प्रश्न 7.
आवेश घनत्व σ कूलॉम/मीटर² के एक अनन्त विस्तार वाली समतल आवेशित ‘अचालक’ प्लेट के कारण किसी निकट बिन्दु पर वैद्युत क्षेत्र की तीव्रता के लिए व्यंजक प्राप्त कीजिए। [2008, 12]
अथवा अनन्त समतल आवेशित अचालक प्लेट के समीप वैद्युत क्षेत्र की तीव्रता का व्यंजक व्युत्पन्न कीजिए। [2009, 13]
अथवा
गाउस की प्रमेय के आधार पर असीमित विस्तार वाले आवेशित समतल चादर के निकट किसी बिन्दु पर वैद्युत क्षेत्र की तीव्रता का सूत्र स्थापित कीजिए। [2015, 16]
अथवा
एक समान आवेशित अचालक समतल प्लेट के कारण उसके निकट स्थित किसी बिन्दु पर वैद्युत क्षेत्र की तीव्रता का व्यंजक प्राप्त कीजिए।
उत्तर :
अनन्त विस्तार की समतल आवेशित अचालक प्लेट के कारण वैद्युत क्षेत्र की तीव्रता (Intensity of Electric Field near an Infinite Plane Charged Non-conducting Plate)-माना अनन्त विस्तार की समतल अचालक प्लेट ABCD के एक तल पर धन आवेश समान रूप से वितरित है। माना इस तल के एकांक क्षेत्रफल पर उपस्थित आवेश की मात्रा (आवेश का पृष्ठ घनत्व) σ है। माना समतल प्लेट की मोटाई नगण्य है तथा समतल प्लेट का यह तल, आवेश की एक समतल चादर के समान है (चित्र 1.31)1

माना आवेशित तल से r दूरी पर कोई बिन्दु P है जहाँ । वैद्युत क्षेत्र की तीव्रता ज्ञात करनी है। माना चादर के दूसरी
ओर, चादर से समान दूरी r पर एक अन्य बिन्दु Q इस प्रकार है कि रेखा PQ चादर के लम्बवत् है।

बिन्दु P पर वैद्युत क्षेत्र की तीव्रता ज्ञात करने के लिए हम एक ऐसे बेलनाकार पृष्ठ की कल्पना करते हैं जिसकी
अक्ष आवेशित चादर के लम्बवत् है तथा इसके समतल पृष्ठ बिन्दु P तथा २ से होकर गुजरते हैं। माना बेलन के प्रत्येक समतल पृष्ठ का क्षेत्रफल A है। चूँकि बिन्दु P तथा Q चादर से समान दूरी पर हैं; अत: दोनों बिन्दुओं पर वैद्युत क्षेत्र की तीव्रता परिमाण में समान होगी।

क्योंकि चादर का विस्तार अनन्त है; अत: चादर के समीप सभी बिन्दुओं पर वैद्युत क्षेत्र की दिशा चादर के लम्बवत् बाहर की ओर दिष्ट (धनावेश के कारण) होगी; अत: बेलन के समतल पृष्ठ पर वैद्युत क्षेत्र की दिशा पृष्ठ के लम्बवत् अर्थात् संगत क्षेत्रफल वेक्टर d \(\overrightarrow{\mathrm{A}}\) की दिशा में होगी, जबकि बेलन के वक्र पृष्ठ पर वैद्युत क्षेत्र \(\overrightarrow{\mathrm{E}}\) की दिशा पृष्ठ के समान्तर (अक्ष के अनुदिश) अर्थात् संगत क्षेत्रफल वेक्टर d \(\overrightarrow{\mathrm{A}}^{\prime}\) के लम्बवत् होगी (चित्र 1.31)।

अत: बेलन के समतल पृष्ठ हेतु वैद्युत फ्लक्स
\(d \phi_{P}=d \phi_{Q}=\overrightarrow{\mathrm{E}} \cdot d \overrightarrow{\mathrm{A}}=E d A \cos 0^{\circ}=E d A\)
तथा बेलन के वक्र पृष्ठ हेतु वैद्युत फ्लक्स \(d \phi_{N}=\overrightarrow{\mathrm{E}} \cdot d \overrightarrow{\mathrm{A}^{\prime}}=E d A^{\prime} \cos 90^{\circ}=0\)

अत: बेलनाकार गाउसियन पृष्ठ से गुजरने वाला कुल वैद्युत फ्लक्स

परन्तु गौस प्रमेय से कई \(\phi_{E}=\frac{1}{\varepsilon_{0}}\) (गाउसियन पृष्ठ के भीतर स्थित कुल आवेश)
= \(\frac{1}{\varepsilon_{0}}\) (चादर के क्षेत्रफल A पर आवेश) = \(\frac{1}{\varepsilon_{0}}(Aσ) = \frac{\sigma A}{\varepsilon_{0}}\)
अथवा \frac{\sigma A}{\varepsilon_{0}}=2 E A
अत: चादर के समीप वैद्युत क्षेत्र की तीव्रता E =\(\frac{\sigma}{2 \varepsilon_{0}}\)

चूँकि इस सूत्र में बिन्दु P की आवेशित चादर से दूरी नहीं है। इसका अर्थ है कि आवेशित समतल चादर के समीप सभी बिन्दुओं पर वैद्युत क्षेत्र की तीव्रता एकसमान होती है।

1. यदि समतल चादर धनावेशित है तो चादर के समीप किसी भी बिन्दु पर वैद्युत क्षेत्र E की दिशा चादर के लम्बवत् तथा चादर से दूर की ओर होती है।
2. यदि समतल चादर ऋणावेशित है तो चादर के समीप किसी भी बिन्दु पर वैद्युत क्षेत्र E की दिशा चादर के लम्बवत् तथा चादर की ओर होती है।

प्रश्न 8.
गाउस के प्रमेय की सहायता से एकसमान रूप से आवेशित गोलीय कोश के कारण-(i) कोश के बाहर, (ii) कोश के पृष्ठ पर तथा (iii) कोश के भीतर, वैद्युत क्षेत्र की तीव्रता ज्ञात कीजिए। [2009, 10, 13, 16]
अथवा
गाउस के प्रमेय की सहायता से एकसमान आवेशित पतले गोलीय कोश के बाहर किसी बिन्दु पर वैद्युत क्षेत्र की तीव्रता का सूत्र ज्ञात कीजिए। [2014, 15, 16, 18]
अथवा
एकसमान आवेशित गोलीय कोश के कारण उसके पृष्ठ के किसी बिन्दु पर वैद्युत क्षेत्र की तीव्रता का व्यंजक प्राप्त कीजिए। [2015]
अथवा
गाउस की प्रमेय से सिद्ध कीजिए कि किसी आवेशित गोलीय कोश के भीतर वैद्युत क्षेत्र की तीव्रता शून्य होती है तथा कोश के बाहर बिन्दुओं के लिए आवेशित कोश, केन्द्र पर स्थित बिन्दुवत् आवेश की भाँति व्यवहार करता है? [2005, 06, 18]
उत्तर :
एकसमान रूप से आवेशित गोलीय कोश के कारण वैद्युत क्षेत्र की तीव्रता (Electric Field Intensity due to a Uniformly Charged Spherical Shell)-माना R त्रिज्या के किसी विलगित गोलीय कोश को + q आवेश दिया गया है, जो उसके पृष्ठ पर समान रूप से वितरित है।

(i) गोलीय कोश के बाहर – माना गोलीय कोश का केन्द्र बिन्दु O पर है। इस कोश के केन्द्र O से r दूरी पर कोश से बाहर (r > R) स्थित किसी बिन्दु P पर वैद्युत क्षेत्र की तीव्रता ज्ञात करनी है।

इसके लिए हम बिन्दु P से जाने वाला त्रिज्या r का संकेन्द्रीय गोलीय पृष्ठ खींचते हैं (चित्र 1.32)। इस गोलीय पृष्ठ को ‘गाउसियन पृष्ठ’ कहते हैं। इस पृष्ठ
पर स्थित बिन्दु P के चारों ओर एक क्षेत्रफल अवयव dA लेते हैं जिसके संगत क्षेत्रफल वेक्टर d \(\overrightarrow{\mathrm{A}}\) है जिसकी दिशा क्षेत्रफल अवयव dA पर बाहर की ओर दिष्ट अभिलम्ब के अनुदिश होगी। चूँकि गाउसियन पृष्ठ तथा आवेशित गोलीय कोश संकेन्द्रीय हैं; अत: गाउसियन पृष्ठ के प्रत्येक बिन्दु पर वैद्युत क्षेत्र का परिमाण E समान तथा पृष्ठ पर बाहर की ओर खींचे अभिलम्ब की ओर दिष्ट होगा।

माना बिन्दु P पर वैद्युत क्षेत्र वेक्टर \(\overrightarrow{\mathrm{E}}\) है, जो क्षेत्रफल वेक्टर d \(\overrightarrow{\mathrm{A}}\) के समान्तर बाहर की ओर दिष्ट है अर्थात् इनके बीच कोण शून्य है।
अत: \(\overrightarrow{\mathrm{E}} \cdot d \overrightarrow{\mathrm{A}}=E \cdot d A \cos 0^{\circ}=E d A\)
अतः गाउसियन पृष्ठ से बाहर निकलने वाला कुल वैद्युत फ्लक्स
\(\phi_{E}=\oint \overrightarrow{\mathrm{E}} \cdot d \overrightarrow{\mathrm{A}}=\oint E d A\)
=\(E \Phi d A\) [∵ E पृष्ठ के प्रत्येक बिन्दु पर नियत है|
= E(4πr²) …………………..(1)
परन्तु गाउस प्रमेय से, \(\phi_{E}=q / \varepsilon_{0}\)
जहाँ q बन्द गाउसियन पृष्ठ द्वारा परिबद्ध सम्पूर्ण आवेश है।
∴ E (4πr²) = q/ε_o
अतः \(E=\frac{1}{4 \pi \varepsilon_{0}} \frac{q}{r^{2}}\) न्यूटन/कूलॉम

यह किसी बिन्दु आवेश q के कारण उससे r दूरी पर वैद्युत क्षेत्र की तीव्रता E के सूत्र के समान है; अतः समान रूप से आवेशित गोलीय कोश बाह्य बिन्दुओं के लिए ऐसे व्यवहार करती है जैसे कि उसका सम्पूर्ण आवेश उसके केन्द्र पर स्थित हो।

पुन: चूँकि आवेश + q, गोलीय कोश के सम्पूर्ण पृष्ठ 4πR² पर समान रूप से वितरित है।
अत: गोलीय कोश पर आवेश का पृष्ठ घनत्व \(\sigma=\frac{q}{4 \pi R^{2}}\) अथवा q = 4πR²σ
अतः आवेशित गोलीय कोश के बाहर उसके केन्द्र से r दूरी पर वैद्युत क्षेत्र की तीव्रता .
\(E=\frac{1}{\varepsilon_{0}} \frac{4 \pi R^{2} \sigma}{4 \pi r^{2}}=\frac{\sigma}{\varepsilon_{0}}\left(\frac{R}{r}\right)^{2}\) ………………(2)

(ii) गोलीय कोश के पृष्ठ पर-यदि हमें गोलीय कोश के पृष्ठ पर अर्थात् कोश के केन्द्र से R दूरी पर वैद्युत . क्षेत्र ज्ञात करना है तो इस बार गाउसियन पृष्ठ की त्रिज्या r = R लेनी होगी, तब समीकरण (2) में r = R रखने पर, वैद्युत क्षेत्र की तीव्रता
\(E=\frac{\sigma}{\varepsilon_{0}}\left(\frac{R}{R}\right)^{2}=\frac{\sigma}{\varepsilon_{0}}\)

(iii) गोलीय कोश के भीतर-माना गोलीय कोश के भीतर उसके केन्द्र से r (r < R) दूरी पर कोई बिन्दु P है जिस पर वैद्युत क्षेत्र की तीव्रता ज्ञात करनी है। इसके लिए हम बिन्दु O को केन्द्र मानकर, बिन्दु P से जाने वाला एक गोलीय पृष्ठ खींचते हैं, जो गाउसियन पृष्ठ कहलाएगा। (चित्र 1.33) से स्पष्ट है कि इस दशा में गाउसियन पृष्ठ पूर्णतः गोलीय कोश के भीतर है; अतः गाउसियन पृष्ठ के भीतर उपस्थित आवेश की मात्रा शून्य होगी।

तब गाउस प्रमेय से, Φ _E = q/ ε₀ = 0 [∵q = 0]
समीकरण (1) से, Φ _E = E (4πr²)= 0; अतः E = 0
अर्थात् आवेशित गोलीय कोश के भीतर प्रत्येक बिन्दु पर वैद्युत क्षेत्र की तीव्रता शून्य होती है।
आवेशित गोलीय कोश के कारण, दूरी के साथ वैद्युत क्षेत्र की तीव्रता का परिवर्तन चित्र 1.34 में प्रदर्शित किया गया है।

वैद्युत आवेश तथा क्षेत्र लघु उत्तरीय प्रश्नोत्तर

प्रश्न 1.
वैद्युत आवेश से आप क्या समझते हैं? [2000]
उत्तर :
वैद्युत आवेश – जिस मूल कारण की उपस्थिति से वस्तुओं में अन्य वस्तुओं को अपनी ओर आकर्षित करने का गुण आ जाता है, उसे वैद्युत आवेश कहते हैं।

प्रश्न 2.
आवेश की ई०एस०यू०, ई०एम०यू० तथा कूलॉम इकाई में सम्बन्ध बताइए। [2001]
उत्तर :
1 कूलॉम = 3 × 10⁹ e.s.u. अथवा 1e.s.u.=\(\frac{1}{3 \times 10^{9}}\)कूलॉम
तथा 1 कूलॉम = 10^-1e.m.u. अथवा 1e.m.u.= 10 कूलॉम।

प्रश्न 3.
‘एक धातु के गोले को वैधुत से आवेशित किया जाता है।’ इस कथन का क्या तात्पर्य है?
उत्तर :
इस कथन का अर्थ है-1. यदि गोला धनावेशित है तो उससे कुछ इलेक्ट्रॉन हटाए गए हैं।
2. यदि गोला ऋणावेशित है तो उसे कुछ अतिरिक्त इलेक्ट्रॉन दिए गए हैं। .

प्रश्न 4.
ठीक बराबर द्रव्यमान के दो सर्वसम धातु के गोले लिए गए हैं। एक को Q ऋण आवेश से तथा दूसरे को उतने ही धन आवेश से आवेशित किया जाता है। क्या दोनों गोलों के द्रव्यमानों में कोई अन्तर आ जाएगा और क्यों?
उत्तर :
दोनों गोलों के द्रव्यमानों में अन्तर आ जाएगा; क्योंकि धनावेशित गोले से इलेक्ट्रॉन निकल जाने से उसका द्रव्यमान कुछ कम हो जाएगा, जबकि ऋणावेशित गोले पर इलेक्ट्रॉन आ जाने से उसका द्रव्यमान कुछ बढ़ जाएगा।

प्रश्न 5.
‘मूल आवेश’ से आप क्या समझते हो? इसका मान कितना है?
उत्तर :
मूल आवेश-“वस्तुओं के बीच आवेश का आदान-प्रदान, आवेश की एक न्यूनतम मात्रा (e) के पूर्ण गुणजों के रूप में ही किया जा सकता है।” आवेश की इस न्यूनतम मात्रा को ही मूल आवेश कहते हैं। इसका मान 1.6 × 10^-19 कूलॉम होता है।

प्रश्न 6.
आवेश की परमाणुकता से आप क्या समझते हैं? [2001]
अथवा
वैद्युत आवेश के क्वाण्टीकरण से आप क्या समझते हैं? [2005]
उत्तर :
आवेश का क्वाण्टीकरण अथवा परमाणुकता—किसी वस्तु को आवेश, एक न्यूनतम इकाई (e) के पूर्ण गुणजों के रूप में ही दिया जा सकता है। अत: किसी वस्तु को दिया गया आवेश q = ± ne, जहाँ n कोई पूर्णांक है। इस प्रकार किसी वस्तु पर आवेश q = ± 1e, ± 2e, ± 3e,…. हो सकता है। इनके बीच में नहीं। आवेश के इस गुण को आवेश का क्वाण्टीकरण अथवा परमाणुकता (quantization or atomicity of charge) कहते हैं। .

प्रश्न 7.
कूलॉम का वैद्युत बल सम्बन्धी नियम लिखिए। [2016]
अथवा
दो बिन्दु आवेशों के बीच लगने वाले आकर्षण अथवा प्रतिकर्षण बल के लिए कूलॉम का सूत्र लिखिए। [2008]
उत्तर :
कूलॉम का नियम – इस नियमानुसार, “दो स्थिर बिन्दु आवेशों के बीच लगने वाला आकर्षण अथवा प्रतिकर्षण बल (F), दोनो आवेशों की मात्राओं (q₁ व q₂) के गुणनफल के अनुक्रमानुपाती तथा दोनों आवेशों के बीच की दूरी (7) के वर्ग के व्युत्क्रमानुपाती होता है।” यह बल दोनों आवेशों को मिलाने वाली रेखा के अनुदिश होता है।
\(F \propto \frac{q_{1} q_{2}}{r^{2}}\) अथवा \(F=\frac{1}{4 \pi \varepsilon_{0}} \frac{q_{1} q_{2}}{r^{2}}\) न्यूटन

प्रश्न 8.
दो बिन्दु आवेशों के मध्य लगने वाले आकर्षण अथवा प्रतिकर्षण बल के लिए कूलॉम का नियम वेक्टर स्वरूप में लिखिए। [2016]
अथवा कूलॉम के नियम का सदिश रूप लिखिए तथा इसका महत्त्व बताइए।
उत्तर :
कूलॉम के नियम का वेक्टर स्वरूप आवेश q₂ द्वारा आवेश q₁ पर आरोपित वैद्युत बल
\(\overrightarrow{\mathrm{F}}_{12}=\frac{1}{4 \pi \varepsilon_{0}} \frac{q_{1} q_{2}}{r_{21}^{3}} \overrightarrow{\mathrm{r}} 21\)
इसी प्रकार आवेश q₁ द्वारा आवेश q₂ पर आरोपित वैद्युत बल
\(\overrightarrow{\mathrm{F}}_{21}=\frac{1}{4 \pi \varepsilon_{0}} \frac{q_{1} q_{2}}{r_{12}^{3}} \overrightarrow{\mathrm{r}}_{12}\)

इस प्रकार \(\overrightarrow{\mathrm{F}}_{21}=\frac{1}{4 \pi \varepsilon_{0}} \frac{q_{1} q_{2}}{r_{12}^{3}} \overrightarrow{\mathrm{r}}_{12}\)

कूलॉम के नियम के सदिश स्वरूप से ज्ञात होता है कि दो बिन्दु आवेशों के बीच कार्यरत वैद्युत बल, केन्द्रीय बल है। अतः यह बल दोनों आवेशों को मिलाने वाली रेखा के अनुदिश, एक-दूसरे पर बराबर एवं परस्पर विपरीत दिशा में कार्य करता है।

प्रश्न 9.
‘आवेश के रेखीय घनत्व’ का अर्थ बताइए। [2012, 13]
उत्तर :
रेखीय आवेश वितरण की प्रति एकांक लम्बाई पर आवेश की मात्रा को रेखीय आवेश घनत्व कहते हैं। इसे λ से प्रदर्शित करते हैं।
यदि रेखीय आवेश वितरण के सूक्ष्म अवयव dl पर आवेश dq है तो
\(\lambda=\frac{d q}{d l}\)
इसका मात्रक ‘कूलॉम/मीटर’ है।

प्रश्न 10.
‘पृष्ठीय आवेश घनत्व’ का अर्थ बताइए। अथवा आवेश के पृष्ठ घनत्व से क्या तात्पर्य है? [2015]
उत्तर :
पृष्ठीय आवेश वितरण के प्रति एकांक क्षेत्रफल पर आवेश की मात्रा को पृष्ठीय आवेश घनत्व कहते हैं। इसे ‘o’ से प्रदर्शित करते हैं।
यदि पृष्ठीय आवेश वितरण के सूक्ष्म क्षेत्रफल अवयव dA पर आवेश dq है तो
\(\sigma=\frac{d q}{d A}\)
इसका मात्रक ‘कूलॉम/मीटर ² है।

प्रश्न 11.
‘आयतन आवेश घनत्व’ का अर्थ बताइए।
उत्तर :
आयतन आवेश वितरण के प्रति एकांक आयतन पर आवेश की मात्रा को आयतन आवेश घनत्व कहते हैं। इसे ‘ρ’ से प्रदर्शित करते हैं। यदि आयतन आवेश वितरण के सूक्ष्म आयतन अवयव dV पर आवेश dq है तो \(\rho=\frac{d q}{d V}\)
इसका मात्रक कूलॉम/मीटर ³ है।

प्रश्न 12.
वैद्युत क्षेत्र से क्या तात्पर्य है?
उत्तर :
वैद्युत क्षेत्र (Electric Field) – “किसी वैद्युत आवेश अथवा आवेश-समुदाय के चारों ओर स्थित वह क्षेत्र, जिसमें कोई अन्य आवेश आकर्षण अथवा प्रतिकर्षण के बल का अनुभव करता है, उस आवेश अथवा आवेशसमुदाय का वैद्युत क्षेत्र अथवा वैद्युत बल क्षेत्र कहलाता है।”

प्रश्न 13.
वैद्यत क्षेत्र की तीव्रता से क्या तात्पर्य है? इसका मात्रक भी लिखिए। [2015, 16, 17]
उत्तर :
वैद्युत क्षेत्र की तीव्रता (Intensity of Electric Field)—“वैद्युत क्षेत्र में किसी बिन्दु पर रखे परीक्षण-आवेश पर लगने वाले वैद्युत बल तथा परीक्षण-आवेश के अनुपात को उस बिन्दु पर वैद्युत क्षेत्र की तीव्रता कहते हैं।”
माना वैद्युत क्षेत्र में किसी बिन्दु पर रखे परीक्षण आवेश q⁰ पर लगने वाला बल \(\overrightarrow{\mathrm{F}}\) है तो उस बिन्दु पर
वैद्युत क्षेत्र की तीव्रता \(\overrightarrow{\mathrm{E}}=\frac{\overrightarrow{\mathrm{F}}}{q_{0}}\)
इसका मात्रक न्यूटन/कूलॉम (N/C) है।
यह एक सदिश राशि है तथा इसकी दिशा धनावेश पर कार्यरत बल की दिशा में होती है।

प्रश्न 14.
किसी बिन्दु आवेश के कारण वैद्युत क्षेत्र की तीव्रता का सूत्र लिखिए तथा स्पष्ट कीजिए कि बिन्दु आवेश के कारण वैद्युत क्षेत्र दूरी के साथ किस प्रकार बदलता है?
उत्तर :
किसी बिन्दु आवेश q के कारण उससे r दूरी पर वैद्युत क्षेत्र की तीव्रता
\(E=\frac{1}{4 \pi \varepsilon_{0}} \frac{q}{r^{2}}\) न्यूटन/कूलॉम; अत: \(E \propto \frac{1}{r^{2}}\)
अत: वैद्युत क्षेत्र की तीव्रता दूरी के वर्ग के व्युत्क्रमानुपाती होती है।

प्रश्न 15.
बिन्दु आवेश तथा रेखीय आवेश के कारण वैद्युत क्षेत्र दूरी के साथ कैसे परिवर्तित होता है? [2005]
उत्तर :
बिन्दु आवेश के लिए वैद्युत क्षेत्र E ∝ 1/r² तथा रेखीय आवेश के लिए वैद्युत क्षेत्र E ∝ 1/r होता है।

प्रश्न 16.
सूत्र \(E =\frac{1}{4 \pi \varepsilon} \frac{q}{r^{2}}\) से का मात्रक ज्ञात कीजिए।
उत्तर :

प्रश्न 17.
वैद्युत बल रेखाएँ किसे कहते हैं?
उत्तर :
वैद्युत क्षेत्र में खींची गईं वे काल्पनिक निष्कोण वक्र रेखाएँ जिन पर कोई स्वतन्त्र धन परीक्षण आवेश गति करता है, वैद्युत बल रेखाएँ कहलाती हैं।

प्रश्न 18.
वैद्युत बल रेखाएँ एक-दूसरे को क्यों नहीं काटतीं? [2001]
अथवा क्या किसी धन बिन्दु आवेश q से चलने वाली दो वैद्युत बल रेखाएँ एक-दूसरे को काट सकती हैं? कारण बताइए।
उत्तर :
दो वैद्युत बल रेखाएँ कभी एक-दूसरे को नहीं काट सकती क्योंकि इस स्थिति में कटान बिन्दु पर दो स्पर्श रेखाएँ खींची जाएँगी जो उस बिन्दु पर वैद्युत क्षेत्र की दो दिशाएँ प्रदर्शित करेंगी जो कि असम्भव है।

प्रश्न 19.
विलगित धन आवेश तथा ऋण आवेश के वैद्युत क्षेत्र की वैद्युत बल रेखाएँ खींचिए। अथवा किसी विलगित ऋण बिन्दु. आवेश के वैद्युत क्षेत्र को वैद्युत बल रेखाएँ खींचकर दर्शाइए।
[2002]
उत्तर :
चित्र 1.35 देखिए।

प्रश्न 20.
यदि बिन्दु आवेश पर वैद्युत बल रेखाएँ आकर मिलती हैं तो इस बिन्दु आवेश की प्रकृति कैसी होगी? [2004]
उत्तर :
बिन्दु आवेश की प्रकृति ऋणात्मक होगी क्योंकि वैद्युत बल रेखाएँ धन आवेश से ऋण आवेश की ओर चलती हैं।

प्रश्न 21.
वैद्युत द्विध्रुव से आप क्या समझते हो? दो उदाहरण दीजिए। [2014].
उत्तर :
दो समान परिमाण एवं विपरीत प्रकृति के बिन्दु आवेशों को अल्प दूरी पर रखने पर बना निकाय, वैद्युत द्विध्रुव कहलाता है।
उदाहरण-HCl का अणु, H₂O का अणु आदि।

प्रश्न 22.
वैद्युत द्विध्रुव आघूर्ण से क्या तात्पर्य है? इसका मात्रक एवं विमाएँ लिखिए। यह अदिश राशि है अथवा सदिश राशि? यदि सदिश राशि है तो इसकी दिशा भी बताइए। [2001, 02, 04, 08, 09]
उत्तर :
यह सदिश राशि है इसकी दिशा वैद्युत द्विध्रुव की अक्ष के अनुदिश ऋण आवेश से धन आवेश की ओर होती है।
वैद्युत द्विध्रुव आघूर्ण – वैद्युत द्विध्रुव के दोनों बिन्दु आवेशों में से किसी एक आवेश के परिमाण तथा दोनों आवेशों के बीच की दूरी के गुणनफल को वैद्युत द्विध्रुव आघूर्ण कहते हैं। इसे ‘p’ से प्रदर्शित करते हैं।
यदि वैद्युत द्विध्रुव में + q तथा – q बिन्दु आवेश 21 दूरी पर स्थित हों तब इसका वैद्युत द्विध्रुव आघूर्ण
\(\overrightarrow{\mathrm{p}}=q \times 2 \vec{l}\)
इसका मात्रक ‘कूलॉम-मीटर’ तथा विमा [LTA] है।

प्रश्न 23.
एक वैद्युत द्विध्रुव, एकसमान वैद्युत क्षेत्र में सन्तुलन की स्थिति में रखा है। किस स्थिति में यह सन्तुलन (i) स्थायी तथा (ii) अस्थायी होगा?
उत्तर :
(i) यदि वैद्युत द्विध्रुव आघूर्ण \(\overrightarrow{\mathrm{p}}, वैद्युत क्षेत्र \overrightarrow{\mathrm{E}}\) की दिशा में है तो सन्तुलन स्थायी होगा।
(ii) यदि वैद्युत द्विध्रुव आघूर्ण \(\overrightarrow{\mathrm{p}}\), वैद्युत क्षेत्र \(\overrightarrow{\mathrm{E}}\) के विपरीत दिशा में है तो सन्तुलन अस्थायी होगा।

प्रश्न 24.
वैद्युत द्विध्रुव द्वारा अक्षीय (अथवा अनुदैर्घ्य ) स्थिति में किसी बिन्दु पर वैद्युत क्षेत्र की तीव्रता का व्यंजक लिखिए। [2008]
उत्तर :
अक्षीय स्थिति में वैद्युत क्षेत्र की तीव्रता \(E=\frac{1}{4 \pi \varepsilon_{0}} \frac{2 p}{r^{3}}\) न्यूटन/कूलॉम।
जहाँ p वैद्युत द्विध्रुव का आघूर्ण तथा । वैद्युत द्विध्रुव के मध्य-बिन्दु से वह दूरी है, जहाँ पर वैद्युत क्षेत्र की तीव्रता ज्ञात करनी है।

प्रश्न 25.
वैद्युत द्विध्रुव के कारण निरक्षीय अथवा अनुप्रस्थ स्थिति में किसी बिन्दु पर वैद्युत क्षेत्र की तीव्रता का सूत्र प्रयुक्त संकेतों का अर्थ बताते हुए लिखिए।
[2008]
उत्तर :
अनुप्रस्थ स्थिति में वैद्युत क्षेत्र की तीव्रता \(E=\frac{1}{4 \pi \varepsilon_{0}} \frac{p}{r^{3}}\) न्यूटन/कूलॉम।
जहाँ p वैद्युत द्विध्रुव का आघूर्ण तथा । वैद्युत द्विध्रुव के मध्य-बिन्दु से वह दूरी है, जहाँ पर वैद्युत क्षेत्र की तीव्रता ज्ञात करनी है।

प्रश्न 26.
ज्वलनशील पदार्थों को ले जाने वाले वाहनों को हमेशा धात्विक चेन (chains) से जुड़े हुए रखा जाता है, जिनको गति के समय भूमि के सम्पर्क में रखा जाता है। समझाइए क्यों?
उत्तर :
जब वाहन गति करता है तब वायु से घर्षण के कारण वह आवेशित हो जाता है। वाहन पर अधिक आवेश संचित हो जाने पर चिंगारी उत्पन्न हो सकती है जिससे ज्वलनशील पदार्थ आग पकड़ सकते हैं। ऐसी दुर्घटना से बचने के लिए वाहन से धात्विक चेन जुड़ी रखते हैं जो गति के समय पृथ्वी के सम्पर्क में रहती है। इस चेन द्वारा वाहन पर संचित आवेश पृथ्वी को स्थानान्तरित होता रहता है।

प्रश्न 27.
वायुयान के टायरों का निर्माण करने के लिए एक विशेष प्रकार की रबड़ का प्रयोग किया जाता है जो आंशिक चालक होती है, क्यों?
उत्तर :
वायुयान उड़ान भरते समय अथवा नीचे उतरते समय धावन पथ (run way) पर गति करता है। गति करते समय टायरों तथा पथ के बीच घर्षण से टायरों पर आवेश प्रेरित हो जाता है। यदि टायरों की रबड़ आंशिक चालक है तो यह प्रेरित आवेश पृथ्वी में स्थानान्तरित हो जाता है। अत: आवेश के कारण वैद्युत चिंगारी के उत्पन्न होने की सम्भावना नहीं रहती है।

प्रश्न 28.
वैद्युत फ्लक्स की परिभाषा, मात्रक तथा विमा लिखिए। [2004, 06, 09, 12, 15]]
अथवा
वैद्युत फ्लक्स ऋणात्मक तथा धनात्मक कब होता है?
उत्तर :
वैद्युत फ्लक्स-“किसी वैद्युत क्षेत्र में स्थित किसी काल्पनिक पृष्ठ से, पृष्ठ के लम्बवत् दिशा में गुजरने वाली कुल वैद्युत बल रेखाओं की संख्या को उस पृष्ठ से बद्ध वैद्युत फ्लक्स कहते हैं।’ इसे Φ_E से प्रदर्शित करते हैं। इसका मात्रक न्यूटन-मीटर / कूलॉम अथवा वोल्ट-मीटर है। इसकी विमा [ML³T^-3A^-1] है।
यदि किसी बन्द पृष्ठ से नेट वैद्युत फ्लक्स भीतर प्रविष्ट हो रहा है तो वैद्युत फ्लक्स ऋणात्मक होता है अथवा यदि नेट वैद्युत फ्लक्स सतह से बाहर आ रहा है तो वैद्युत फ्लक्स धनात्मक होता है।

प्रश्न 29.
एक अचालक बेलन एकसमान वैद्युत क्षेत्र \(\overrightarrow{\mathbf{E}}\) में पूर्णत: भीतर स्थित है तथा बेलन की अक्ष वैद्युत क्षेत्र के समान्तर है। बेलन से गुजरने वाला वैद्युत फ्लक्स कितना होगा? [2005]
उत्तर :

सम्पूर्ण बेलन से गुजरने वाला वैद्युत फ्लक्स

चूँकि बाएँ फलक पर \(\overrightarrow{\mathbf{E}} व \overrightarrow{d A}\) के बीच कोण 180°, दाएँ फलक पर कोण शून्य तथा वक्र पृष्ठ पर कोण 90° है।

अतः बेलन से गुजरने वाला वैद्युत फ्लक्स शून्य होगा।

प्रश्न 30.
स्थिर वैद्युतिकी में गाउस के नियम का उल्लेख कीजिए। [2012, 13, 14, 15, 16]
अथवा
स्थिर वैद्युतिकी में गाउस के प्रमेय को गणितीय रूप में लिखिए। [2010]
उत्तर :
गाउस का नियम-इस नियम के अनुसार, “किसी बन्द पृष्ठ से गुजरने वाला कुल वैद्युत फ्लक्स Φ_E, उस पृष्ठ के भीतर स्थित कुल आवेश q का 1/e₀ गुना होता है।”
अर्थात् Φ_E =1/ε₀, जहाँ ε₀ निर्वात अथवा वायु की वैद्युतशीलता है।

प्रश्न 31.
गाउसियन पृष्ठ क्या है? स्थिर वैद्युतिकी में गाउसियन पृष्ठ की क्या उपयोगिता है?
उत्तर :
गाउसियन पृष्ठ-किसी दिए गए आवेश को परिबद्ध करने वाला कोई भी काल्पनिक बन्द पृष्ठ उस आवेश का गाउसियन पृष्ठ कहलाता है।
इसका उपयोग किसी बिन्दु पर वैद्युत क्षेत्र की तीव्रता ज्ञात करने के लिए किया जाता है, जहाँ सामान्य नियमों द्वारा वैद्युत क्षेत्र ज्ञात कर पाना कठिन होता है।

प्रश्न 32.
एकसमान पृष्ठ घनत्व σ कूलॉम/मीटर² तथा R मीटर त्रिज्या के गोलीय आवेश के कारण वैद्युत क्षेत्र के सूत्र लिखिए।
उत्तर :
गोले के केन्द्र से r दूरी पर वैद्युत क्षेत्र \(E=\frac{\sigma}{\varepsilon_{0}}\left(\frac{R}{r}\right)^{2}\) जबकि r>R
गोले के पृष्ठ पर वैद्युत क्षेत्र \(E=\frac{\sigma}{\varepsilon_{0}}\)
गोले के भीतर वैद्युत क्षेत्र E = 0.

प्रश्न 33.
गाउस के नियम का उपयोग करते हुए एक असीमित विस्तार वाली आवेशित समतल चादर के निकट वैद्युत क्षेत्र की तीव्रता की सहायता से समान्तर प्लेट संधारित्र की धारिता का सूत्र प्राप्त कीजिए। [2008, 11]
उत्तर :
असीमित विस्तार की एकसमान धनावेशित समतल चादर के समीप वैद्युत क्षेत्र की तीव्रता
\(E=\frac{\sigma}{2 \varepsilon_{0}}\) (जहाँ σ चादर पर आवेश का पृष्ठ घनत्व है।)
समान्तर प्लेट संधारित्र की दोनों प्लेटों के बीच वैद्युत क्षेत्र की तीव्रता
E = E₁ + E₁ = \(\frac{\sigma}{2 \varepsilon_{0}}+\frac{\sigma}{2 \varepsilon_{0}}=\frac{\sigma}{\varepsilon_{0}}\)
चूँकि E₁ व E₂ की दिशाएँ एक ही हैं; अत: इनके बीच विभवान्तर
\(V=E d=\frac{\sigma}{\varepsilon_{0}} d=\frac{q}{A} \frac{d}{\varepsilon_{0}}\)
अतः समान्तर प्लेट संधारित्र की धारिता \(C=\frac{q}{V}=\frac{\varepsilon_{0} A}{d}\)

प्रश्न 34.
एक खोखले बेलन के भीतर १ कूलॉम आवेश स्थित है। यदि बेलन के वक्रीय पृष्ठ से Φ वोल्ट-मीटर वैद्युत फ्लक्स सम्बन्धित हो तब बेलन के किसी एक समतल पृष्ठ से कितना वैद्युत फ्लक्स सम्बन्धित होगा? [2014]
हल :
गाउस की प्रमेय से, खोखले बेलन से बद्ध वैद्युत फ्लक्स = \(\frac{q}{\varepsilon_{0}}\)
बेलन के वक्रीय पृष्ठ का वैद्युत फ्लक्स = Φ वोल्ट-मीटर
अतः बेलन के पृष्ठ का कुल वैद्युत फ्लक्स = \(\phi+\phi_{p}+\phi_{p}=\frac{q}{\varepsilon_{0}}\)
अथवा Φ + 2Φ_p =\(\frac{q}{\varepsilon_{0}}\) अथवा 2 \(\phi_{p}=\frac{q}{\varepsilon_{0}}-\phi\)
अत: समतल पृष्ठ के लिए वैद्युत फ्लक्स \(\phi_{p}=\frac{1}{2}\left(\frac{q}{\dot{\varepsilon}_{0}}-\phi\right)\)

प्रश्न 35.
एक गाउसीय पृष्ठ के अन्दर 3q, – 2q, q तथा + 2q आवेश रखे हैं। पृष्ठ से परिबद्ध कुल वैद्युत फ्लक्स कितना होगा? [2016]
हल :

प्रश्न 36.
m द्रव्यमान की एक आवेशित तेल की बूँद दो क्षैतिज प्लेटों के बीच सन्तुलन में लटकी है। यदि प्रत्येक प्लेट का क्षेत्रफल A मीटर² तथा उन पर आवेश +q व – कूलॉम हो तो तेल की बूंद पर आवेश की मात्रा ज्ञात कीजिए।
हल :
माना तेल की बूंद पर आवेश q₁ कूलॉम है।
सन्तुलन की अवस्था में, q₁E = mg
जहाँ E दोनों प्लेटों के बीच वैद्युत क्षेत्र की तीव्रता है।

वैद्युत आवेश तथा क्षेत्र अति लघु उत्तरीय प्रश्नोत्तर

प्रश्न 1.
वैद्युत आवेश किसे कहते हैं?
उत्तर :
वैद्युत आवेश द्रव्य का वह गुण है जिसके कारण वह वैद्युत तथा चुम्बकीय प्रभाव उत्पन्न करता है तथा उनका अनुभव करता है।

प्रश्न 2.
एक धनावेशित चालक पर इलेक्ट्रॉनों की कमी होती है अथवा अधिकता, बताइए।
उत्तर :
एक धनावेशित चालक पर इलेक्ट्रॉनों की कमी होती है।

प्रश्न 3.
किसी चालक को धनावेशित करने पर उसके द्रव्यमान पर क्या प्रभाव पड़ेगा? कारण सहित बताइए।
उत्तर :
द्रव्यमान घट जाएगा, क्योंकि धनावेशित करने पर चालक से कुछ इलेक्ट्रॉन बाहर निकल जाएँगे।

प्रश्न 4.
3.2 कूलॉम आवेश कितने इलेक्ट्रॉनों द्वारा निर्मित होगा? [2010, 11, 12]
हल :
दिया है, q= 3.2 कूलॉम, n = ?
3.2 सूत्र q = ne से, इलेक्ट्रॉनों की संख्या n = \(\frac{q}{e}=\frac{3.2}{1.6 \times 10^{-19}}\) = 2 x 10¹⁹ इलेक्ट्रॉन।

प्रश्न 5.
एक निश्चित दूरी पर स्थित दो इलेक्ट्रॉनों के बीच वैद्युत बल F न्यूटन है। इतनी ही दूरी पर स्थित दो प्रोटॉनों के बीच वैद्युत बल ज्ञात कीजिए।
उत्तर :
चूँकि प्रोटॉन पर आवेश, इलेक्ट्रॉन के आवेश के बराबर होता है; अत: प्रोटॉन के बीच वैद्युत बल, इलेक्ट्रॉनों के बीच वैद्युत बल के बराबर होगा अर्थात् F न्यूटन ही होगा।

प्रश्न 6.
यदि दो बिन्दु आवेशों के बीच की दूरी आधी कर दी जाए तो उनके बीच लगने वाले वैद्युत बल पर क्या प्रभाव पड़ेगा? [2000, 01]
उत्तर :
\(F \propto 1 / r^{2}\) से, दूरी आधी करने पर बल चार गुना हो जाएगा।

प्रश्न 7.
एक निश्चित दूरी पर स्थित दो इलेक्ट्रॉनों के बीच वैद्युत बल F न्यूटन है। इससे आधी दूरी पर स्थित दो प्रोटॉनों के बीच वैद्युत बल कितना होगा?
[2011]
हल :

प्रश्न 8.
कुछ दूरी पर रखे गए +2 μ C तथा -2μ C के आवेश वाले दो एक जैसे चालकों के बीच 10 न्यूटन का आकर्षण बल क्रिया करता है। यदि इन्हें परस्पर स्पर्श कराकर पुनः उतनी ही दूरी पर रखा जाए तो उनके बीच बल कितना हो जाएगा? [2010]
उत्तर :
चालक एक जैसे हैं; अत: स्पर्श कराने पर प्रत्येक चालक पर
नया आवेश \(q_{1}^{\prime}=q_{2}^{\prime}=\frac{+2 \mu \mathrm{C}+(-2 \mu \mathrm{C})}{2}=0\) होगा।
क्योंकि बल, आवेशों के गुणनफल के अनुक्रमानुपाती होता है।
अतः दोनों के बीच लगने वाला नया बल भी शून्य हो जाएगा।

प्रश्न 9.
निर्वात की वैद्युतशीलता ε₀ का मात्रक लिखिए।
उत्तर :
_ε0 का मात्रक = कूलॉम²/(न्यूटन-मीटर) है।

प्रश्न 10.
S.I. पद्धति में निर्वात की वैद्युतशीलता ε₀ की विमाएँ लिखिए।
[2003]
उत्तर :
ε₀ की विमाएँ = [M^-1L^-3T⁴A²]

प्रश्न 11.
निर्वात की वैद्युतशीलता तथा किसी परावैद्युत माध्यम की वैद्युतशीलता में क्या सम्बन्ध है?
उत्तर :
ε = ε₀ K, जहाँ K माध्यम का परावैद्युतांक है।

प्रश्न 12.
वैद्युत क्षेत्र की तीव्रता का मांत्रक लिखिए। यह कैसी राशि है? ।
उत्तर :
वैद्युत क्षेत्र की तीव्रता का मात्रक = न्यूटन/कूलॉम। यह सदिश राशि है।

प्रश्न 13.
वैद्युत क्षेत्र की तीव्रता की विमा लिखिए। .
उत्तर :
वैद्युत क्षेत्र की तीव्रता की विमा = [MLT^-3A^-1]

प्रश्न 14.
एक वैद्युत क्षेत्र में इलेक्ट्रॉन तथा प्रोटॉन स्वतन्त्र रूप से स्थित हैं। क्या दोनों पर समान बल लगेंगे?
उत्तर :
दोनों पर आवेश समान परन्तु विपरीत प्रकृति के हैं; अतः F = qE से दोनों पर बलों के परिमाण समान होंगे परन्तु उनकी दिशाएँ विपरीत होंगी। .

प्रश्न 15.
एक वैद्युत क्षेत्र में एक इलेक्ट्रॉन तथा एक प्रोटॉन स्वतन्त्र रूप से स्थित हैं। इनमें से किस कण का त्वरण अधिक होगा और क्यों?
उत्तर :
दोनों के आवेश समान होने के कारण दोनों पर बल तो समान ही लगेगा, परन्तु सूत्र a= F/m से, इलेक्ट्रॉन का द्रव्यमान, प्रोटॉन की तुलना में कम होने के कारण इलेक्ट्रॉन का त्वरण अधिक होगा।

प्रश्न 16.
E तीव्रता वाले एकसमान वैद्युत क्षेत्र से θ कोण पर एक वैद्युत द्विध्रुव रखा है। द्विध्रुव पर लगने वाला शुद्ध स्थानान्तरण बल क्या होगा? [2007]
उत्तर :
द्विध्रुव पर लगने वाला स्थानान्तरण बल F = qE – qE = 0 (शून्य) होगा।

प्रश्न 17.
5.0 x 10^-8 कूलॉम बिन्दु आवेश से कितनी दूरी पर वैद्युत क्षेत्र की तीव्रता 450 वोल्ट/मीटर होगी? [2012]
हल :
दिया है, q = 5.0 x 10^-8 कूलॉम, E = 450 वोल्ट/मीटर, r = ?
सूत्र E = 9.0 x 10⁹ \frac{q}{r^{2}} से, 450 = 9.0 x 10⁹ x \(\frac{5 \times 10^{-8}}{r^{2}}\) अत: r = 1 मीटर।

प्रश्न 18.
परस्पर समान्तर वैद्युत बल रेखाएँ किस प्रकार के वैद्युत क्षेत्र को प्रदर्शित करती हैं?
उत्तर :
एकसमान वैद्युत क्षेत्र को।

प्रश्न 19.
वैद्युत द्विध्रुव से क्या समझते हो? दो उदाहरण दीजिए। [2005, 14]
उत्तर :
वैद्युत द्विध्रुव-“वह निकाय जिसमें दो बराबर, परन्तु विपरीत प्रकार के बिन्दु आवेश एक-दूसरे से अल्प दूरी पर स्थित हों, वैद्युत द्विध्रुव कहलाता है।” जैसे HCl, H₂O के अणु आदि।

प्रश्न 20.
वैद्युत द्विध्रुव आघूर्ण का S.I. मात्रक एवं विमा लिखिए।
उत्तर :
वैद्युत द्विध्रुव आघूर्ण का S.I. मात्रक कूलॉम-मीटर तथा विमा [LTA] है।

प्रश्न 21.
एकसमान वैद्युत क्षेत्र में स्थित वैद्युत द्विध्रुव पर लगने वाले बलयुग्म के आघूर्ण का व्यंजक लिखिए। यह बलयुग्म का आघूर्ण अधिकतम कब होगा? .
[2006, 08]
उत्तर :
बलयुग्म के आघूर्ण का व्यंजक t = pE sin θ, जब θ = 90° तो t _max = pE.

प्रश्न 22.
वैद्युत फ्लक्स तथा वैद्युत क्षेत्र में सम्बन्ध लिखिए। वैद्युत फ्लक्स का मात्रक बताइए। [2007]
उत्तर :
किसी पृष्ठ A से बद्ध वैद्युत फ्लक्स ।
\(\phi_{E}=\int_{A} \overrightarrow{\mathrm{E}} \cdot d \overrightarrow{\mathrm{A}}=E A\)
अर्थात् वैद्युत क्षेत्र में स्थित किसी पृष्ठ से बद्ध वैद्युत फ्लक्स वैद्युत क्षेत्र के पृष्ठ समाकल के बराबर होता है। इसका मात्रक वोल्ट-मीटर अथवा न्यूटन-मीटर²/कूलॉम है।

प्रश्न 23.
वैद्युत फ्लक्स का मात्रक और विमीय सूत्र निगमित कीजिए।
उत्तर :

प्रश्न 24.
किसी गोलीय पृष्ठ के अन्दर यदि + q आवेश रख दिया जाए तो सम्पूर्ण पृष्ठ से निकलने वाला वैद्युत फ्लक्स कितना होगा?
उत्तर :
वैद्युत फ्लक्स Φ_E =q/ε₀

प्रश्न 25.
किसी बन्द पृष्ठ से बद्ध वैद्युत फ्लक्स किस राशि पर निर्भर करता है?
उत्तर :
केवल और केवल उस पृष्ठ द्वारा परिबद्ध वैद्युत आवेश पर।

प्रश्न 26.
क्या किसी आवेश के कारण वैद्युत फ्लक्स इस बात पर निर्भर करता है कि उसको परिबद्ध करने वाले बन्द पृष्ठ की आकृति कैसी है? यदि नहीं, तो किसी आवेश के कारण वैद्युत फ्लक्स का सूत्र लिखिए।
उत्तर :
नहीं, निर्वात में स्थित आवेश q के कारण कुल वैद्युत फ्लक्स Φ_E =q/ε₀ .

प्रश्न 27.
एक अचालक बेलन एकसमान वैद्युत क्षेत्र E में पूर्णतः भीतर स्थित है तथा बेलन की अक्ष वैद्युत क्षेत्र के समान्तर है। बेलन से गुजरने वाला वैद्युत फ्लक्स कितना होगा? [2005]
उत्तर : चूँकि बेलन वैद्युत क्षेत्र के भीतर स्थित है परन्तु बेलन के भीतर कोई आवेश नहीं है; अत: गाउस के प्रमेय से Φ_E =q/ε₀ = 0 (∵ q = 0)

प्रश्न 28.
आवेशित खोखले गोलाकार चालक के भीतर वैद्युत क्षेत्र की तीव्रता कितनी होती है? [2002, 03]
हल :
वैद्युत क्षेत्र की तीव्रता शून्य होती है।

प्रश्न 29.
क्या एक खोखले गोले की अपेक्षा समान त्रिज्या के ठोस चालक गोले को अधिक आवेश दिया जा सकता है ? कारण सहित बताइए।
उत्तर :
नहीं; क्योंकि आवेशित चालक का सम्पूर्ण आवेश उसके बाहरी पृष्ठ पर रहता है न कि सम्पूर्ण आयतन में।

प्रश्न 30.
अनन्त लम्बाई की दो समान्तर प्लेटें एकसमान रूप से आवेशित हैं तथा उन पर आवेश के पृष्ठ घनत्व +σ व -σ हैं। वैद्युत क्षेत्र की तीव्रता कहाँ पर शून्य होगी? [2005]
हल :
प्रत्येक प्लेट के बाहर वैद्युत क्षेत्र की तीव्रता शून्य होगी।

प्रश्न 31.
आवेश घनत्व वाले किसी अनन्त विस्तार के समावेशित पृष्ठ के निकट r दूरी पर वैद्युत क्षेत्र की तीव्रता का सूत्र लिखिए। [2008]
उत्तर :
वैद्युत क्षेत्र की तीव्रता \(E=\frac{\sigma}{2 \varepsilon_{0}}\)

प्रश्न 32.
+σ तथा -σ पृष्ठ आवेश घनत्व वाली दो समान्तर प्लेटों के बीच वैद्युत क्षेत्र का सूत्र लिखिए। [2003, 06]
उत्तर :
वैद्युत क्षेत्र की तीव्रता E = σ/ε₀

प्रश्न 33.
समान पृष्ठीय आवेश घनत्व वाली एक धन तथा एक ऋण आवेशित प्लेटों के बीच वैद्युत क्षेत्र की तीव्रता का सूत्र लिखिए।
उत्तर :
वैद्युत क्षेत्र की तीव्रता E = σ/ε₀ जहाँ σ प्लेटों पर आवेश का पृष्ठ घनत्व है।

प्रश्न 34.
दो समतल धातु प्लेटों के बीच ‘m’ द्रव्यमान तथा ‘वं आवेश वाली द्रव बूंद को गिरने से रोकने के लिए कितने वैद्युत क्षेत्र की आवश्यकता होगी? .
[2004] …
उत्तर :
mg = qE से, अभीष्ट वैद्युत क्षेत्र \(E=\frac{m g}{q}\)

प्रश्न 35.
किसी आवेशित कण के भार को एक वैद्युत क्षेत्र द्वारा किस प्रकार सन्तुलित किया जाता है? [2009]
उत्तर :
जब आवेशित कण पर वैद्युत बल \(\overrightarrow{\mathbf{F}}=\overrightarrow{\mathbf{E}} q\) की दिशा भार \(\overrightarrow{\mathrm{mg}}\) के विपरीत, अर्थात् ऊर्ध्वाधर ऊपर की ओर हो तथा \(\overrightarrow{\mathrm{E}} q=m \overrightarrow{\mathrm{g}}\) हो।

वैद्युत आवेश तथा क्षेत्र आंकिक प्रश्नोत्तर

प्रश्न 1.
एक चालक पर 1.0 कूलॉम का ऋण आवेश है। इस पर सामान्य अवस्था से कितने इलेक्ट्रॉन अधिक हैं? .
[2000, 10]
हल :
दिया है, q= 1.0 कूलॉम, e= 1.6 x 10^-19 कूलॉम, n = ?
अत: सूत्र q= ne से, इलेक्ट्रॉनों की संख्या n = =n=\(\frac{q}{e}=\frac{1.0}{1.6 \times 10^{-19}}\) = 6.25 x 10¹⁸
क्योंकि चालक पर ऋण आवेश है; अतः चालक पर 6.25 x 10¹⁸ इलेक्ट्रॉन अधिक हैं।

प्रश्न 2.
एक चालक पर 2.4 x 10^-18 कूलॉम धनात्मक आवेश है। इस चालक पर कितने इलेक्ट्रॉन की अधिकता अथवा कमी है?
हल :
दिया है, q = 2.4 x 10^-18 कूलॉम, e= 1.6 x 10^-19 कूलॉम, n = ?
अत: सत्र = ne से. इलेक्ट्रॉनों की संख्या n = n = \(\frac{q}{e}=\frac{2.4 \times 10^{-18}}{1.6 \times 10^{-19}}=15\)
क्योंकि चालक पर धन आवेश है; अत: चालक पर 15 इलेक्ट्रॉनों की कमी है।

EXTRA SHOTS
वस्तु के धनावेशित होने का तात्पर्य है उस पर इलेक्ट्रॉनों की सामान्य अवस्था से कमी तथा ऋणावेशित होने का __तात्पर्य है उस पर इलेक्ट्रॉनों की सामान्य अवस्था से अधिकता। .

प्रश्न 3.
एक आवेशित चालक में 4000 इलेक्ट्रॉन बाहुल्य में हैं। चालक में उपस्थित कुल आवेश का मान तथा उसकी प्रकृति बताइए।
[2000, 01]
हल :
दिया है, n = 4000, e = 1.6 x 10^-19 कूलॉम, q= ?
चालक पर आवेश q= ne = 4000 x 1.6 x 10^-19 = 6.4 x 10^-16कलॉम चूँकि इलेक्ट्रॉन पर ऋण आवेश होता है; अतः चालक में उपस्थित आवेश ऋण आवेश होगा। अत: चालक पर आवेश q= 6.4 x 10-¹⁶ कूलॉम (ऋण आवेश)।

प्रश्न 4.
एक चालक पर 500 इलेक्ट्रॉनों की कमी है। इस पर आवेश की मात्रा तथा प्रकृति ज्ञात कीजिए। [2005]
हल :
दिया है, n = 500, e = 1.6 x 10^-19 कूलॉम, q= ?
चालक पर आवेश q = ne = 500 x 1.6 x 10^-19 = 8.0 x 10^-17 कूलॉम चूँकि चालक पर इलेक्ट्रॉनों की कमी है; अत: चालक में उपस्थित आवेश धन आवेश होगा। अतः चालक पर आवेश q= 8.0 x 10^-17 कूलॉम (धन आवेश)।

प्रश्न 5.
3.2 कूलॉम आवेश कितने इलेक्ट्रॉनों द्वारा निर्मित होगा? [2010, 11, 12]
हल :
दिया है, q= 3.2 कूलॉम तथा e = 1.6 x 10^-19 कूलॉम, n = ?, आवेश q = ne
n =\( \frac{q}{e}=\frac{3.2}{1.6 \times 10^{-19}}\) = 2 x 10^-19

प्रश्न 6.
12.5 x 10¹⁸ इलेक्ट्रॉनों के आवेश की गणना कीजिए।
[2018] हल : दिया है, n = 12.5 x 10⁸ तथा e= 1.6 x 10^-19 कूलॉम
आवेश q= ne = 12.5 x 10¹⁸ x 1.6 x 10^-19 = 2 कूलॉम।

प्रश्न 7.
₇N¹⁴ नाभिक पर कूलॉम में आवेश की गणना कीजिए।
हल :
₇N¹⁴ नाभिक में 7 प्रोटॉन तथा 7 न्यूट्रॉन हैं। चूँकि न्यूट्रॉन अनावेशित होता है तथा प्रत्येक प्रोटॉन पर +1.6 x 10^-19 कूलॉम आवेश होता है; अत: सूत्र q = ne से,
₇N¹⁴ नाभिक पर आवेश q = 7 x 1.6 x 10^-19 = 11.2 x 10^-19 कूलॉम।

प्रश्न 8.
दो प्रोटॉनों के बीच की दूरी 4.0 x 10^-15 मीटर है तथा इन पर आवेश 1.6 x 10^-19 कूलॉम है तो इनके मध्य लगने वाले प्रतिकर्षण बल की गणना कीजिए।
हल :

प्रश्न 9.
एक ₉₂U²³⁸ परमाणु ∝-कण उत्सर्जित करता है। यदि किसी क्षण -कण विघटित परमाणु के केन्द्र से 9.0x 10^-15 मीटर की दूरी पर हो तो ∝ -कण पर कितना बल कार्यरत होगा? [2005]
हल:
₉₂U²³⁸ परमाणु के केन्द्र (नाभिक) से ∝-कण उत्सर्जित होने के बाद नाभिक में 92 – 2 = 90 प्रोटॉन शेष बचेंगे।

प्रश्न 10.
दो सूक्ष्म गोलों में से प्रत्येक पर 10⁵ इलेक्ट्रॉनों की कमी है। यदि उनके बीच दूरी 1.0 मीटर हो तो वैद्युत बल की गणना कीजिए।
हल :
दिया है , n = 10⁵, r = 1.0 मीटर, e= 1.6 x 10^-19 कूलॉम, F = ?

प्रश्न 11.
दो धनावेश, जो कि परस्पर 0.1 मीटर की दूरी पर हैं, एक-दूसरे को 18 न्यूटन के बल से प्रतिकर्षित करते हैं। यदि दोनों आवेशों का योग 9 uC हो तो उनके अलग-अलग मान ज्ञात कीजिए।
हल :

प्रश्न 12.
दो प्रोटॉनों के बीच की दूरी की गणना कीजिए, यदि इनके बीच वैद्युत प्रतिकर्षण बल एक प्रोटॉन के भार के बराबर हो। (प्रोटॉन का द्रव्यमान mp = 1.67 x 10^-27 किग्रा, g = 9.8 मीटर/सेकण्ड²) [2007]
हल : दिया है, प्रत्येक प्रोटॉन पर आवेश q₁ = q₂ = 1.6 x 10^-19 कूलॉम
प्रोटॉन का द्रव्यमान m_p = 1.67 x 10^-27 किग्रा, g= 9.8 मीटर/सेकण्ड2, r = ?
प्रश्नानुसार, प्रोटॉनों के बीच वैद्युत बल = प्रोटॉन का भार

CLASSROOM EXPERIENCE :
प्रश्न 13.
दो सूक्ष्म गोलियों पर (80/3) x 10^-9 तथा (160/3) x 10^-9 कूलॉम आवेश हैं तथा वे वायु में एक-दूसरे से 0.10 मीटर पर स्थित हैं। उनके बीच वैद्युत बल ज्ञात कीजिए। यदि उन्हें एक तार द्वारा क्षण भर के लिए सम्बन्धित कर दें तो बल कितना हो जाएगा?
हल :
Step 1.
सर्वप्रथम प्रश्न में दिए गए आँकड़े नोट कर लेते हैं।
गोलियों पर आवेश q₁ = \(\frac{80}{3} \times 10^{-9}\) कूलॉम
q₂ = \(\frac{160}{3} \times 10^{-9}\) कूलॉम
गोलियों के बीच की दूरी (7) = 0.10 मीटर

Step 2.
कूलॉम के नियमानुसार, दोनों गोलियों के बीच कार्यरत वैद्युत बल

Step 3.
गोलियों को तार से सम्बन्धित कर देने पर प्रत्येक गोली पर आवेश दोनों गोलियों पर आवेशों के योग | के आधे के बराबर होगा। अत:

Step 4.
अब गोलियों के बीच कार्यरत वैद्युत बल

प्रश्न 14.
दो बिन्दु आवेशों को वायु में एक निश्चित दूरी पर रखने पर उनके बीच 80 न्यूटन का बल कार्य करता है। इन्हीं आवेशों को एक परावैद्युत माध्यम में इतनी ही दूरी पर रखा जाता है तो इस बल का मान 8 न्यूटन हो जाता है। माध्यम का परावैद्युतांक ज्ञात कीजिए। [2017]
हल :
दो बिन्दु आवेशों के बीच वायु में लगने वाला बल
\(F_{1}=\frac{1}{4 \pi \varepsilon_{0}} \frac{q_{1} q_{2}}{r^{2}}\)
इनके बीच परावैद्युत रखने पर,
बल \(F_{2}=\frac{1}{4 \pi \varepsilon_{0}} K \frac{q_{1} q_{2}}{r^{2}}\)
\(\frac{F_{1}}{F_{2}}=K\) अत: K = \(\frac{F_{80}}{F_{8}}\) = 10.

प्रश्न 15.
+ 2 माइक्रोकूलॉम तथा + 6 माइक्रोकूलॉम के दो बिन्दु आवेश परस्पर 12 न्यूटन के बल से प्रतिकर्षित करते हैं। यदि इन आवेशों में से प्रत्येक को – 4 माइक्रोकूलॉम का आवेश और दिया जाए तो उनके बीच कितना बल लगेगा?
हल :
दिया है, q₁ = + 2 माइक्रोकूलॉम = + 2 x 10^-6 कूलॉम
q₂ = + 6 माइक्रोकूलॉम = + 6 x 10^-6 कूलॉम F = 12 न्यूटन

प्रश्न 16.
दो धनावेश जो कि परस्पर 0.1 मीटर की दूरी पर हैं, एक-दूसरे को 18 न्यूटन के बल से प्रतिकर्षित करते हैं। यदि दोनों आवेशों का योग 9 μC हो तो उनके अलग-अलग मान ज्ञात कीजिए।
– [2017] हल : माना आवेश q₁ व q₂ हैं; अत:
दिया है , F = 18 न्यूटन,r = 0.1 मीटर, (q₁ + q₂) = 9 μC = 9 x 10^-6 कूलॉम, q₁= ?, q₂ = ?
सूत्र F = 9 x 10⁹ \(\frac{q_{1} q_{2}}{r^{2}}\) से, 18= 9 x 10⁹ \(\frac{q_{1} q_{2}}{(0.1)^{2}}\)
अथवा q₁q₂= 2 x 10^-11 = 20 x 10^-12 कूलॉम²
सूत्र (q₁ – q₂)² = (q₁ + q₂)² – 4q₁q₂ से,
(q₁ – q₂)² = (9 x 10^-6)² – 4 x 20 x 10^-12
= 81 x 10^-12 – 80 x 10^-12 = 10^-12
अत: (q₁ – q₂) = √10^-12 = 10^-6 …………..(1)
प्रश्नानुसार, q₁ + q₂ = 9 x 10^-6…………………..(2)
(2) समीकरण (1) व समीकरण (2) को हल करने पर,
q₁ = 5 x 10^-6 = 5μc तथा q₂= 9 – 5 = 4 μC