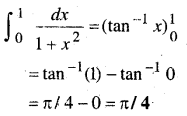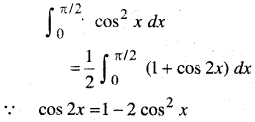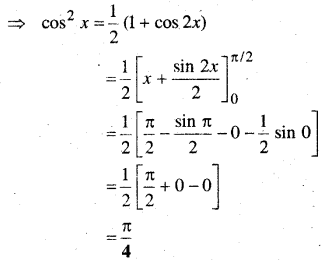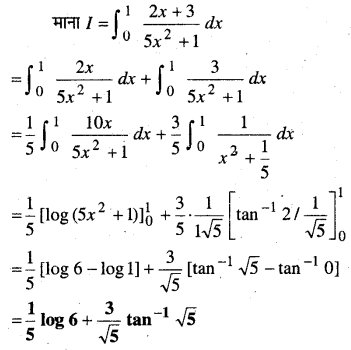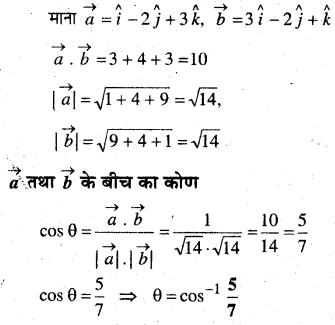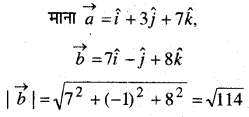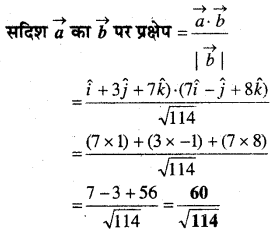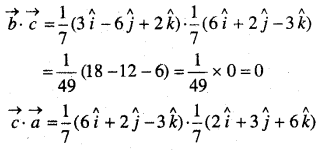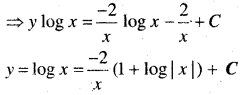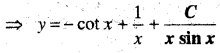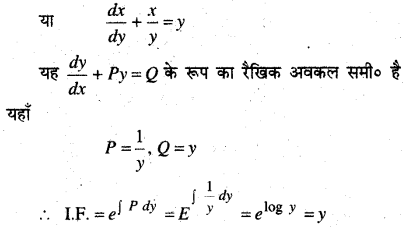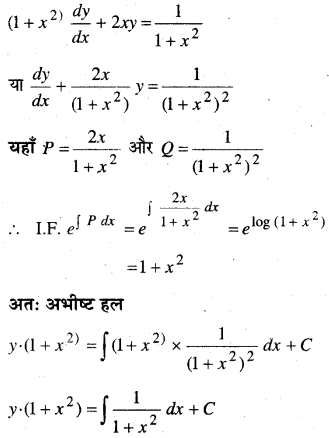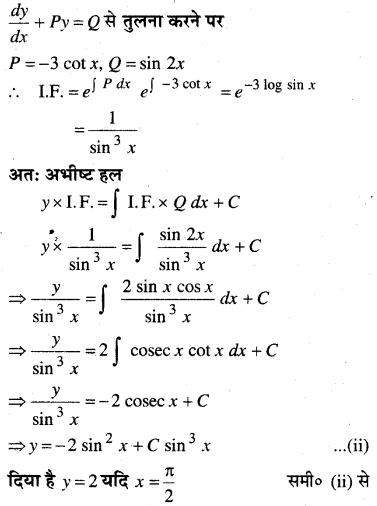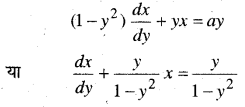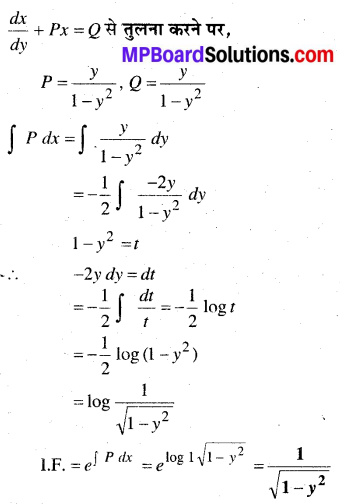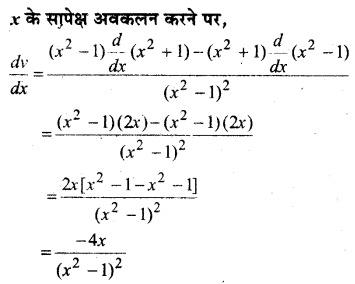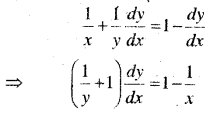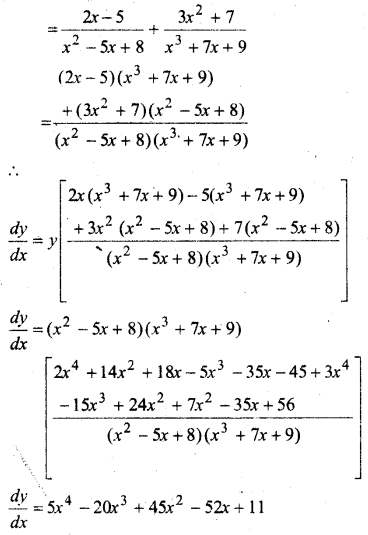Category: Class 12

In this article, we share MP Board Class 12th Maths Book Solutions Chapter 6 अवकलज के अनुप्रयोग Ex 6.1 Pdf, These solutions are solved by subject experts from the latest MP Board books.

MP Board Class 12th Maths Book Solutions Chapter 6 अवकलज के अनुप्रयोग Ex 6.1

प्रश्न 1.
वृत्त के क्षेत्रफल के परिवर्तन की दर इसकी त्रिज्या के सापेक्ष ज्ञात कीजिए जबकि
(a) r = 3cm है
(b) r = 4 cm है।
हल:
त्रिज्या वाले वृत्त का क्षेत्रफल A = πr²

प्रश्न 2.
एक घन का आयतन 8 cm³/s की दर से बढ़ रहा है। पृष्ठ क्षेत्रफल किस दर से बढ़ रहा है जबकि इसके किनारे की लम्बाई 12 cm है।
हल:
माना x लम्बाई के घन का आयतन V है।
तब V = x³

= \(\frac{8}{3}\)cm²/s
अत: घन का पृष्ठ क्षेत्रफल \(\frac{8}{3}\)cm²/s से बढ़ रहा है।

प्रश्न 3.
एक वृत्त की त्रिज्या समान रूप से 3 cm/s की दर से बढ़ रही है। ज्ञात कीजिए कि वृत्त का क्षेत्रफल किस दर से बढ़ रहा है जब त्रिज्या 10 cm है।
हल:
दिया है \(\frac{dr}{dt}\) = 3 cm/sec
वृत्त का क्षेत्रफल
A = πr²

प्रश्न 4.
एक परिवर्तनशील घन का किनारा 3 cm/s की दर से बढ़ रहा है। घन का आयतन किस दर से बढ़ रहा है जबकि किनारा 10 cm लंबा है?
हल:
माना घन के कोर की लम्बाई = x cm तब,
\(\frac{dx}{dt}\) = 3 cm/s (दिया है)
∴ घन का आयतन,

प्रश्न 5.
एक स्थिर झील में एक पत्थर डाला जाता है और तरंगें वृत्तों में 5 सेमी/सेकण्ड की गति से चलती हैं। जब वृत्ताकार तरंग की त्रिज्या 8 सेमी है, तो उस क्षण, घिरा हुआ क्षेत्रफल किस दर से बढ़ रहा है?
हल:
माना r त्रिज्या वाले वृत्ताकार तरंग का क्षेत्रफल A है
तब, \(\frac{dr}{dt}\) = 5 cm/s (दिया है)
तथा क्षेत्रफल,
A = πr²

प्रश्न 6.
एक वृत्त की त्रिज्या 0.7 cm/s की दर से बढ़ रही है। इसकी परिधि की वृद्धि की दर क्या है जब r = 4.9 cm है?
हल:
माना r त्रिज्या वाले वृत्त की परिधि c है
तथा दिया है

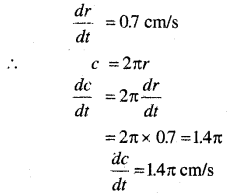
अतः परिधि 1.4 cm/s की दर से बढ़ रही है।

प्रश्न 7.
एक आयत की लम्बाई x, 5 cm/min की दर से घट रही है और चौड़ाई y, 4cm/min की दर से बढ़ रही है। जब x = 8 cm और y = 6 cm है। तब आयत के (a) परिमाप (b) क्षेत्रफल के परिवर्तन की दर ज्ञात कीजिए।
हल:
दिया है : \(\frac{dx}{dt}\) = -5cm/min तथा \(\frac{dy}{dt}\) = 4cm/min
माना आयत का क्षेत्रफल = A
परिमाप = p
लम्बाई = x cm, चौड़ाई = y cm
(a) p = 2(x + y)
\(\frac{d p}{d t}=2\left(\frac{d x}{d t}+\frac{d y}{d t}\right)\)
= 2[-5 + 4] = -2cm/min
अतः परिमाप 2 cm/min की दर से घट रहा है।
(b) A = xy

अतः क्षेत्रफल 2 cm²/min की दर से बढ़ रहा है।

प्रश्न 8.
एक गुब्बारा जो सदैव गोलाकार रहता है, एक पंप द्वारा 900 cm³ गैस प्रति सेकण्ड भर कर फुलाया जाता है। गुब्बारे की त्रिज्या के परिवर्तन की दर ज्ञात कीजिए जब त्रिज्या 15 cm है।
हल:
माना r त्रिज्या वाले गुब्बारे का आयतन V है

प्रश्न 9.
एक गुब्बारा जो सदैव लगातार गोलाकार रहता है कि त्रिज्या परिवर्तनशील है। त्रिज्या के सापेक्ष आयतन के परिवर्तन की दर ज्ञात कीजिए जब त्रिज्या 10 cm है।
हल:
माना गुब्बारे का आयतन = V
त्रिज्या = 2

प्रश्न 10.
एक 5 m लम्बी सीढ़ी दीवार के सहारे झुकी है। सीढ़ी का नीचे का सिरा, जमीन के अनुदिश दीवार से दूर 2 cm/s की दर से खींचा जाता है। दीवार पर इसकी ऊँचाई किस दर से घट रही है जबकि सीढ़ी के नीचे का सिरा दीवार से 4 cm दूर है?
हल:
माना सीढ़ी की लम्बाई AC = 5 m
BC = xm,
AB = y m,
∠ABC = 90°
समकोण ∆ABC में,
x² + y² = 5² = 25
t के सापेक्ष अवकलन करने पर,

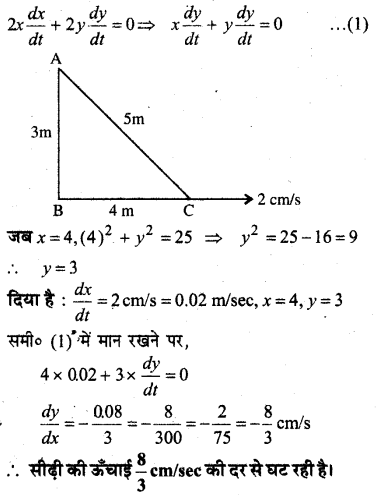
प्रश्न 11.
एक कण वक्र 6y = x³ + 2 के अनुगत गति कर रहा है। वक्र पर उन बिन्दुओं को ज्ञात कीजिए जबकि x निर्देशांक की तुलना में निर्देशांक 8 गुना तीव्रता से बदल रहा है|
हल:
वक्र का समीकरण
6y = x² + 2 …(i)

प्रश्न 12.
हवा के एक बुलबुले की त्रिज्या \(\frac{1}{2}\)cm/s की दर से बढ़ रही है। बुलबुले का आयतन किस दर से बढ़ रहा है जबकि त्रिज्या 1 cm है?
हल:
माना r त्रिज्या वाले बुलबुले का आयतन V है।
दिया है :

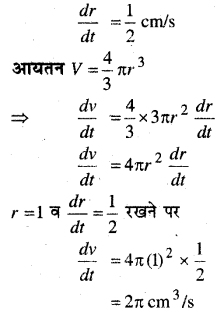
अतः बुलबुले का आयतन 2π cm³/s की दर से बढ़ रहा

प्रश्न 13.
एक गुब्बारा, जो सदैव गोलाकार रहता है, का परिवर्तनशील व्यास \(\frac{3}{2}\)(2x + 1) है। x के सापेक्ष आयतन के परिवर्तन की दर ज्ञात कीजिए।
हल:
माना गुब्बारे का आयतन = V

प्रश्न 14.
एक पाइप से रेत 12 cm³/s की दर से गिर रही है। गिरती रेत जमीन पर एक ऐसा शंक बनाती है जिसकी ऊँचाई सदैव आधर की त्रिज्या का छठा भाग है। रेत से बने शंकु की ऊँचाई किस दर से बढ़ रही है जबकि ऊँचाई 4 cm है।
हल:
माना बालू के शंकु का आयतन = V, ऊँचाई = h, त्रिज्या = r

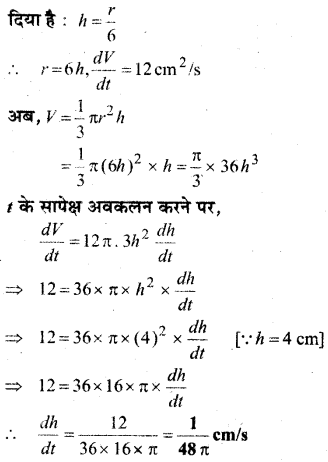
प्रश्न 15.
एक वस्तु की x इकाइयों के उत्पादन से सम्बन्धित कुल लागत C(x)(रुपये में).
C(x) = 0.007x³ – 0.003x² + 15x + 4000 से प्रदत्त है। सीमान्त लागत ज्ञात कीजिए जबकि 17 इकाइयों का उत्पादन किया गया है।
हल:
दिया है
C = 0.007x³ – 0.003x² + 15x + 4000
∴ सीमान्त लागत
(mx) = \(\frac{d c}{d x}\) = 0.021x² – 0.006x + 15
x = 17 रखने पर
mc = 0.021 × 289 – 0.006 x 17 + 15
= 6.069 – 0102 + 15
= 20.967
अतः सीमान्त लागत (mc) = 20.97 रुपये।

प्रश्न 16.
किसी उत्पाद की x इकाइयों के विक्रय से प्राप्त कुल आय R(x) रुपयों में
R(x) = 13x² + 26x + 15 से प्रदत्त है। सीमांत आय ज्ञात कीजिए जब x = 7 है।
हल:
दिया है R(x) = 13x² + 26x + 15.
∴ सीमान्त लागत (MR) = \(\frac{d R}{d x}\) = 26x + 26
x = 7 पर,
MR = 26 × 7 + 26
= 208
अतः सीमान्त लागत 3208 रुपये।

प्रश्न 17 तथा 18 में सही उत्तर का चयन कीजिए।
प्रश्न 17.
एक वृत्त की त्रिज्याr r = 6 cm पर के सापेक्ष क्षेत्रफल में परिवर्तन की दर है :
(A) 10 π
(B) 12 π
(C) 8 π
(D) 11 π
हल:
माना वृत का क्षेत्रफल = A, त्रिज्या = r
∴ A = πr²
r के सापेक्ष अवकलन करने पर,
\(\frac{d A}{d r}\) = 2πr
परन्तु r = 6 रखने पर,
∴ 2π × 6 = 12πcm²/cm
अतः विकल्प (B) सही है।

प्रश्न 18.
एक उत्पाद की इकाइयों के विक्रय से प्राप्त कुल आय रुपयों में R(x) = 3x² + 36x + 5 से प्रदत्त है। जब x = 15 है तो सीमान्त आय है :
(A) 116
(B) 96
(C) 90
(D) 126
हल:
राजस्व समीकरण है
R(x) = 3x² + 36x + 5
MR = \(\frac{d}{d x}\) R(x) = \(\frac{d}{d x}\) (3x² + 36x + 6)
= 6x + 36 = 6(x + 6)
x = 15, ∴ MR = 6 × 21 = 126 रु०
अत: विकल्प (D) सही है।

In this article, we share MP Board Class 12th Maths Book Solutions Chapter 7 समाकलन Ex 7.9 Pdf, These solutions are solved by subject experts from the latest MP Board books.

MP Board Class 12th Maths Book Solutions Chapter 7 समाकलन Ex 7.9

1 से 20 तक के प्रश्नों में निश्चित समाकलनों का मान ज्ञात कीजिए-
प्रश्न 1.
\(\int_{-1}^{1}(x+1)\) dx
हल:
समाकलन करने पर

प्रश्न 2.
\(\int_{2}^{3} \frac{1}{x}\) dx
हल:
माना I = \(\int_{2}^{3} \frac{1}{x}\) dx
= \([\log x]_{2}^{3}\) = log 3 – log 2 = log\(\frac{3}{2}\)

प्रश्न 3.
\(\int_{1}^{2}\left(4 x^{3}-5 x^{2}+6 x+9\right)\) dx
हल:

प्रश्न 4.
\(\int_{0}^{\pi / 4} \sin 2 x\) dx
हल:
माना I = \(\int_{0}^{\pi / 4} \sin 2 x\) dx

प्रश्न 5.
\(\int_{0}^{\pi / 2} \cos 2 x\) dx
हल:

प्रश्न 6.
\(\int_{4}^{5} e^{x} d x\)
हल:

प्रश्न 7.
\(\int_{0}^{\pi / 4} \tan x d x\)
हल:

प्रश्न 8.
\(\int_{\pi / 6}^{\pi / 4} \csc x d x\)
हल:

प्रश्न 9.
\(\int_{0}^{1} \frac{d x}{\sqrt{1-x^{2}}}\)
हल:

प्रश्न 10.
\(\int_{0}^{1} \frac{d x}{1+x^{2}}\)
हल:

प्रश्न 11.
\(\int_{2}^{3} \frac{d x}{x^{2}-1}\)
हल:

प्रश्न 12.
\(\int_{0}^{\pi / 2} \cos ^{2} x d x\)
हल:

प्रश्न 13.
\(\int_{2}^{3} \frac{x d x}{x^{2}+1}\)
हल:

प्रश्न 14.
\(\int_{0}^{1} \frac{2 x+3}{5 x^{2}+1} d x\)
हल:

प्रश्न 15.
\(\int_{0}^{1} x e^{x^{2}} d x\)
हल:
x² = t प्रतिस्थापित करने पर
x dx = \(\frac{1}{2}\) dt

प्रश्न 16.
\(\int_{1}^{2} \frac{5 x^{2}}{x^{2}+4 x+3}\)
हल:

प्रश्न 17.
\(\int_{0}^{\pi / 4}\left(2 \sec ^{2} x+x^{3}+2\right) d x\)
हल:

प्रश्न 18.
\(\int_{0}^{\pi}\left(\sin ^{2} \frac{x}{2}-\cos ^{2} \frac{x}{2}\right) d x\)
हल:

प्रश्न 19.
\(\int_{0}^{2} \frac{6 x+3}{x^{2}+4} d x\)
हल:

प्रश्न 20.
\(\int_{0}^{1}\left(x e^{x}+\sin \frac{\pi x}{4}\right) d x\)
हल:

प्रश्न 21 एवं 22 में सही उत्तर का चयन कीजिए-
प्रश्न 21.
\(\int_{1}^{\sqrt{3}} \frac{d x}{1+x^{2}}\) बराबर है-

हल:

अतः विकल्प (D) सही है।

प्रश्न 22.
\(\int_{0}^{2 / 3} \frac{d x}{4+9 x^{2}}\) बराबर है-

हल:

अतः विकल्प (D) सही है।

In this article, we share MP Board Class 12th Maths Book Solutions Chapter 7 समाकलन Ex 7.8 Pdf, These solutions are solved by subject experts from the latest MP Board books.

MP Board Class 12th Maths Book Solutions Chapter 7 समाकलन Ex 7.8

योगों की सीमा के रूप में निम्नलिखित निश्चित समाकलनों का मान ज्ञात कीजिए।
प्रश्न 1.
\(\int_{a}^{b} x\) dx
हल:

प्रश्न 2.
\(\int_{0}^{5}(x+1)\) dx
हल:
दिया है-f(x) = x + 1 a = 0 तथा b = 5
∴ nh = b – a = 5 – 0 = 5
परिभाषानुसार

प्रश्न 3.
\(\int_{2}^{3} x^{3}\) dx
हल:
दिया है \(\int_{2}^{3} x^{3}\) dx
यहाँ f(x) = x², a = 2, b = 3
तब nh = b – a – 3 – 2 = 1
परिभाषानुसार

प्रश्न 4.
\(\int_{1}^{4}\left(x^{2}-x\right)\) dx
हल:
\(\int_{1}^{4}\left(x^{2}-x\right)\) dx
यहाँ f(x) = x² – 2 a = 1, b = 4
तब nh = b – a = 3
परिभाषानुसार

प्रश्न 5.
\(\int_{-1}^{1} e^{x}\) dx
हल:
\(\int_{-1}^{1} e^{x}\) dx
यहाँ f(x) = e^x dx, a = -1 और b = 1
तब nh = b = a = 2
परिभाषानुसार

प्रश्न 6.
\(\int_{0}^{4}\left(x+e^{2 x}\right)\) dx
हल:
\(\int_{0}^{4}\left(x+e^{2 x}\right)\) dx
यहाँ f(x) = x + e^2x
a = 0, b = 4 तब nh = 4 – 0 = 4
परिभाषानुसार

In this article, we share MP Board Class 12th Maths Book Solutions Chapter 10 सदिश बीजगणित Ex 10.3 Pdf, These solutions are solved by subject experts from the latest MP Board books.

MP Board Class 12th Maths Book Solutions Chapter 10 सदिश बीजगणित Ex 10.3

प्रश्न 1.
दो सदिशों \(\vec{a}\) तथा \(\vec{b}\) के परिमाण क्रमशः \(\sqrt{3}\) व 2 हैं। और \(\vec{a} \cdot \vec{b}=\sqrt{6}\) हैं, तो \(\vec{a}\) और \(\vec{b}\) के बीच का कोण ज्ञात कीजिए।
हल:
दो सदिश \(\vec{a}\) और \(\vec{b}\) है के बीच का कोण हो तो

प्रश्न 2.
सदिशों \(\hat{i}-2 \hat{j}+3 \hat{k}\) और \(3 \hat{i}-2 \hat{j}+\hat{k}\) के बीच का कोण ज्ञात कीजिए
हल:

प्रश्न 3.
सदिश \(\hat{\boldsymbol{i}}+\hat{\boldsymbol{j}}\) पर सदिश \(\hat{\boldsymbol{i}}-\hat{\boldsymbol{j}}\) का प्रक्षेप ज्ञात कीजिए।
हल:

प्रश्न 4.
सदिश \(\hat{i}+3 \hat{j}+7 \hat{k}\) का, सदिश \(7 \hat{i}-\hat{j}+8 \hat{k}\) पर प्रक्षेप ज्ञात कीजिए।
हल:

प्रश्न 5.
दर्शाइए कि दिए हुए निम्नलिखित तीन सदिशों में से प्रत्येक मात्रक सदिश हैं- \(\frac{1}{7}(2 \hat{i}+3 \hat{j}+6 \hat{k})\),\(\frac{1}{7}(3 \hat{i}-6 \hat{j}+2 \hat{k}) \frac{1}{7}(6 \hat{i}+2 \hat{j}-3 \hat{k})\) यह भी दर्शाइए कि सदिश परस्पर एक-दूसरे के लम्बवत् हैं।
हल:



अतः सदिश परस्पर एक-दूसरे के लम्बवत् हैं।

प्रश्न 6.
यदि \((\vec{a}+\vec{b}) \cdot(\vec{a}-\vec{b})\) = 8 और \(|\vec{a}|=8|\vec{b}|\) हो तो \(|\vec{a}|,|\vec{b}|\) ज्ञात कीजिए।
हल:

प्रश्न 7.
\((3 \vec{a}-5 \vec{b}) \cdot(2 \vec{a}+7 \vec{b})\) का मान ज्ञात कीजिए।
हल:

प्रश्न 8.
दो सदिशों \(\vec{a}\) और \(\vec{b}\) के परिमाण ज्ञात कीजिए यदिइनके परिमाण समान हैं और इनके बीच का कोण 60° है, तथा इनका अदिश गुणनफल \(\frac{1}{2}\) है।
हल:
हम जानते हैं कि सदिश \(\vec{a}\) तथा \(\vec{b}\) के बीच का कोण

प्रश्न 9.
यदि एक मात्रक सदिश \(\vec{a}\) के लिए \((\vec{x}-\vec{a}) \cdot(\vec{x}+\vec{a})\) = 12 हो तो| \(|\vec{x}|\) ज्ञात कीजिए।
हल:

प्रश्न 10.
यदि \(\vec{a}=2 \hat{i}+2 \hat{j}+3 \hat{k}\), \(\vec{b}=-\hat{i}+2 \hat{j}+\hat{k}\) और \(\vec{c}=3 \hat{i}+\hat{j}\) इस प्रकार है कि \(\vec{a}+\lambda \vec{b}, \vec{c}\), पर लम्ब है तो λ का मान ज्ञात कीजिए।
हल:
दिया है \(\vec{a}+\lambda \vec{b}, \vec{c}\) पर लम्ब हैं।

प्रश्न 11.
दर्शाइए कि दो शून्येत्तर सदिशों \(\vec{a}\) और \(\vec{b}\) के लिए \(|\vec{a}| \cdot \vec{b}+|\vec{b}| \vec{a},|\vec{a}| \cdot \vec{b}-|\vec{b}| \vec{a}\) पर लम्ब है।
हल:

प्रश्न 12.
यदि \(\vec{a} \cdot \vec{a}\) = 0 और \(\vec{a} \cdot \vec{b}\) = 0 तो सदिश \(\vec{a}\) के बारे में क्या निष्कर्ष निकाला जा सकता है?
हल:
दिया है \(\vec{a} \cdot \vec{a}\) = 0 तथा \(\vec{a} \cdot \vec{b}\) = 0
अत: \(\vec{a}\) = 0
तब \(\vec{b}\) भी सदिश हो सकता है।

प्रश्न 13.
यदि \(\vec{a}, \vec{b}, \vec{c}\) हे मात्रक सदिश इस प्रकार हैं, कि \(\vec{a}+\vec{b}+\vec{c}=\overrightarrow{0}\) तो \(\vec{a} \cdot \vec{b}+\vec{b} \cdot \vec{c}+\vec{c} \cdot \vec{a}\) का मान ज्ञात कीजिए।
हल:

प्रश्न 14.
यदि \(\vec{a}=\overrightarrow{0}\) अथवा \(\vec{b}=\overrightarrow{0}\) तब \(\vec{a} \cdot \vec{b}=0\) परन्तु विलोम का सत्य होना आवश्यक नहीं है। एक उदाहरण द्वारा अपने उत्तर की पुष्टि कीजिए।
हल:

प्रश्न 15.
यदि किसी ∆ABC के शीर्ष A, B, C क्रमशः (1, 2, 3), (-1, 0, 0) (0, 1, 2) हैं, तो ∠ABC ज्ञात कीजिए। [∠ABC सदिशों \(\overrightarrow{B A}\) एवं \(\overrightarrow{B C}\) के बीच का कोण है।]
हल:
∠ ABC सदिशों \(\overrightarrow{B A}\) तथा \(\overrightarrow{B C}\) के बीच का कोण है

प्रश्न 16.
दर्शाइए कि बिन्दु A (1, 2, 7), B(2, 6, 3) और C(3, 10, -1) संरेख हैं।
हल:

अतः तीनों बिन्दु संरेख हैं।

प्रश्न 17.
दर्शाइए कि सदिश \(2 \hat{i}-\hat{j}+\hat{k}, \hat{i}-3 \hat{j}-5 \hat{k}\) और \(3 \hat{i}-4 \hat{j}-4 \hat{k}\) एक समकोण त्रिभुज के शीर्षों की रचना करते हैं।
हल:

अतः दिए गए सदिश समकोण त्रिभुज के शीर्ष हैं।

प्रश्न 18.
यदि शून्येतर सदिश \(\vec{a}\) का परिमाण a है और λ एक शून्येतर अदिश है तो λ\(\vec{a}\) एक मात्रक सदिश है यदि-
(A) λ = 1
(B) λ = -1
(C) a =| λ|
(D) a = \(\frac{1}{|\lambda|}\)
हल:

In this article, we share MP Board Class 12th Maths Book Solutions Chapter 5 सांतत्य तथा अवकलनीयता Ex 5.2 Pdf, These solutions are solved by subject experts from the latest MP Board books.

MP Board Class 12th Maths Book Solutions Chapter 5 सांतत्य तथा अवकलनीयता Ex 5.2

प्रश्न 1 से 8 में x के सापेक्ष निम्नलिखित फलनों का अवकलन कीजिए –
प्रश्न 1.
sin (x² + 5)
हल:
माना y = sin (x² + 5)
x के सापेक्ष अवकलन करने पर,

प्रश्न 2.
cos (sin x)
हल:
माना y = cos (sin.x)

प्रश्न 3.
sin (ax + b)
हल:
माना y = sin (ax + b)
ax + b = 1 रखने पर,

प्रश्न 4.
sec(tan (\( \sqrt{{x}} \))]
हल:
माना y = sec(tan (\( \sqrt{{x}} \))]
दोनों ओर x के सापेक्ष अवकलन करने पर,

प्रश्न 5.
\(\frac{\sin (a x+b)}{\cos (c x+d)}\)
हल:

प्रश्न 6.
cosx³ sin² (x⁵)
हल:
माना y = cosx³. sin² (x⁵)
दोनों ओर x के सापेक्ष अवकलन करने पर

प्रश्न 7.
\(2 \sqrt{\cot \left(x^{2}\right)}\)
हल:
माना y =\(2 \sqrt{\cot \left(x^{2}\right)}\)

प्रश्न 8.
cos (\( \sqrt{{x}} \))
हल:
माना y = cos\( \sqrt{{x}} \)
x के सापेक्ष अवकलन करने पर,

प्रश्न 9.
सिद्ध कीजिए कि फलन f(x) =|x – 1|, x ϵ R, x = 1 पर अवकलित नहीं है।
हल:
यहाँ f(x) = |x – 1|, x ϵ R

प्रश्न 10.
सिद्ध कीजिए कि महत्तम पूर्णांक फलन f(x) = [x], 0 < x < 3, x = 1 तथा x = 2 पर अवकलित नहीं है।
हल:
f(x) = [x]
(i) x = 1 पर,

अतः x = 2 पर f अवकलनीय नहीं है।

In this article, we share MP Board Class 12th Maths Book Solutions Chapter 9 अवकल समीकरण Ex 9.6 Pdf, These solutions are solved by subject experts from the latest MP Board books.

MP Board Class 12th Maths Book Solutions Chapter 9 अवकल समीकरण Ex 9.6

1 से 12 तक के प्रश्नों में, प्रत्येक अवकल समीकरण का व्यापक हल ज्ञात कीजिए-
प्रश्न 1.
\(\frac{d y}{d x}\) + 2y = sinx
हल:
यह \(\frac{d y}{d x}\) + 2y = Q के रूप का रैखिक अवकल समी० है, जहाँ
P = 2 तथा Q = sin x

प्रश्न 2.
\(\frac{d y}{d x}\) + 3y = e^-2x
हल:
\(\frac{d y}{d x}\) + 3y = e^-2x …(i)
यह \(\frac{d y}{d x}\)Py = Q के रूप का रैखिक अवकल समी० है यहाँ
P = 3 तथा Q = e^-2x

प्रश्न 3.
\(\frac{d y}{d x}+\frac{y}{x}\) = x²
हल:
\(\frac{d y}{d x}+\frac{y}{x}\) = x²
यह \(\frac{d y}{d x}+\frac{y}{x}\) + Py = Q के रूप का रैखिक अवकल समी० है
यहाँ

प्रश्न 4.
\(\frac{d y}{d x}\) + (sec x)y = tan x (0 ≤ x ≤ \(\frac{\pi}{2}\))
हल:
\(\frac{d y}{d x}\) + (sec x)y = tan x (0 ≤ x ≤ \(\frac{\pi}{2}\))
यह \(\frac{d y}{d x}\)Py = Q के रूप का रैखिक अवकल समी० है यहाँ
P = sec x तथा Q = tan x

प्रश्न 5.
cos² x\(\frac{d y}{d x}\) + y = tan x(0 ≤ x ≤ \(\frac{\pi}{2}\))
हत्ल :
cos² x\(\frac{d y}{d x}\) + y = tan x(0 ≤ x ≤ \(\frac{\pi}{2}\))
cos² x से भाग करने पर

प्रश्न 6.
x\(\frac{d y}{d x}\) + 2y = x² logx
हल:
दिया गया समी०

प्रश्न 7.
x log x \(\frac{d y}{d x}\) + y = \(\frac{2}{x}\) logx
हल:
दिया गया समी०

प्रश्न 8.
(1 + x²)dy + 2xy dx = cotx dx (x ≠ 0)
हल:
(1 + x²)dy + 2xy dx = cotx dx

प्रश्न 9.
x\(\frac{d y}{d x}\) + y – x + xy cot x = 0, (x ≠ 0)
हल:
दिया गया अवकल समी०

प्रश्न 10.
(x + y)\(\frac{d y}{d x}\) = 1
हल:
अवकल समीकरण,
(x + y)\(\frac{d y}{d x}\) = 1

यही अभीष्ट हल है।

प्रश्न 11.
y dx + (x – y²)dy = 0
हल:
y dx + (x – y²) dy = 0

प्रश्न 12.
(x + 3y²)\(\frac{d y}{d x}\) = y, (y > 0)
हल:
(x + 3y²)\(\frac{d y}{d x}\) = y

13 से 15 तक के प्रश्नों में प्रत्येक अवकल समीकरण के लिए दिए हुए प्रतिबन्ध को सन्तुष्ट करने वाला विशिष्ट हल ज्ञात कीजिए
प्रश्न 13.
\(\frac{d y}{d x}\) + 2y tan x = sin x; y = 0 यदि x = \(\frac{\pi}{3}\)
हल:
दिया गया समी०
\(\frac{d y}{d x}\) + 2y tan x = sin x …(i)
यह एक रैखिक अवकल समी० है

प्रश्न 14.
(1 + x²)\(\frac{d y}{d x}\) + 2xy = \(\frac{1}{1+x^{2}}\); y = 0 यदि x = 1
हल:
दिया गया समी०

प्रश्न 15.
\(\frac{d y}{d x}\) – 3y cot x = sin 2x; y = 2 यदि x = \(\frac{\pi}{2}\)
हल:
दिया है
\(\frac{d y}{d x}\) – 3y cot x = sin 2x …(i)

⇒ -2 + C
⇒ C = 4
C का यह मान समी० (ii) में रखने पर
y = 4 sin ³ – 2 sin²x

प्रश्न 16.
मूल बिन्दु से गुजरने वाले एक वक्र का समीकरण ज्ञात कीजिए यदि इस वक्र के किसी बिन्दु (x, y)पर स्पर्श रेखा की प्रवणता उस बन्दु के निर्देशांकों के योग के बराबर है।
हल:
बिन्दु (x, y) पर स्पर्श रेखा की प्रवणता = \(\frac{d y}{d x}\)
∴ दिए गए परवलय के अनुसार

∵ यह वक्र मूल बिन्दु से गुजरता है
∴ x = 0 तथा y = 0 समी० (ii) में रखने पर
⇒ 0 = -1 – 1 = Ce^° ⇒ C = 1
C का यह मान समी० (ii) में रखने पर
y = -x – 1 + e^x
या x + y + 1 = e^x

प्रश्न 17.
बिन्दु (0, 2) से गुजरने वाले वक्र का समीकरण ज्ञात कीजिए यदि इस वक्र के किसी बिन्दु के निर्देशांकों का योग उस बिन्दु पर खींची गई स्पर्श रेखा की प्रवणता के परिमाण से 5 अधिक है।
हल:
बिन्दु (x, y) से स्पर्श रेखा की प्रवणता \(\frac{d y}{d x}\) है।
तब प्रश्नानुसार


⇒ ye^-x = (x – 5) e^-x – e^x + C
⇒ y = -(x – 5) – 1 + Ce^x
⇒ y = 4 – x + Ce^x
∵ वक्र बिन्दु (0, 2) से गुजरता है, अतः
x = 0 तथा y = 2 समी० में रखने पर
⇒ 2 = 4 – 0 + Ce⁰
C = -2
C = -2 समी० (II) में रखने पर
y = 4 – x + (-2)e^x
y = 4 – x – 2e^x
Case-II
इसी प्रकार ऋण चिन्ह लेने पर,

ye^x = (5 – x) e^x + e^x + C
y = (5 – x) + 1 + Ce^-x
y = 6 – x + Ce^-x
यह वक्र बिन्दु (0, 2) से गुजरता है, अतः x = 0 तथा y = 2 लेने पर
2 = 6 – 0 + Ce⁰ ⇒ C = -4
मान प्रतिस्थापित करने पर
y = 6 – 4 – 4e^-x

प्रश्न 18.
अवकल समीकरण x\(\frac{d y}{d x}\) – y = 2x² का समाकलन गुणक है-
(A) e^-x
(B) e^-y
(C) \(\frac{1}{x}\)
(D) x
हल:
अवकल समीकरण है :

अतः विकल्प (C) सही है।

प्रश्न 19.
अवकल समीकरण (1 – y²)\(\frac{d y}{d x}\) + yx = ay (-1 < y < 1) का समाकलन गुणक है-

हल:
अवकल समीकरण है :


अतः विकल्प (D) सही है।

In this article, we share MP Board Class 12th Maths Book Solutions Chapter 5 सांतत्य तथा अवकलनीयता Ex 5.8 Pdf, These solutions are solved by subject experts from the latest MP Board books.

MP Board Class 12th Maths Book Solutions Chapter 5 सांतत्य तथा अवकलनीयता Ex 5.8

प्रश्न 1.
फलन f(x) = x² + 2x – 8, x ϵ [-4, 2] के लिए रोले के प्रमेय को सत्यापित कीजिए।
हल:
फलन f(x) = x² + 2x – 8, अंतराल [-4, 2] में संतत तथा अंतराल (-4, 2) में अवकलनीय है।
तथा f(-4) = 16 – 8 – 8 = 0
f(2) = 4 + 4 – 8 = 0
⇒ f(-4) = f(2)
अत: रोले के प्रमेय की सभी शर्ते सन्तुष्ट हैं तब रोले के प्रमेय के अनुसार एक बिन्दु CE(-4, 2), जहाँ f’ (c) = 0
⇒ f'(c) = 0
⇒ 2c + 2 =0 (::f’ (x) = 2x + 2)
⇒ c = -1
इसलिए c = -1 पर f’ (c) = 0 और c = -1 ϵ (-4, 2)

प्रश्न 2.
जाँच कीजिए कि क्या रोले का प्रमेय निम्नलिखित फलनों में से किन-किन पर लागू होता है। इन उदाहरणों से क्या आप रोले के प्रमेय के विलोम के बारे में कुछ कह सकते हैं?
(i) f(x) = |x| के लिए x ϵ [5, 9]
(ii) f(x) = |x| के लिए x ϵ [-2, 2]
(iii) f(x) = x² – 1 के लिए x ϵ [1, 2]
हल:
(i) f(x) = [x] के लिए x ϵ [5, 9]
f(x) = [x], बिन्दु x = 6, 7, 8 पर न तो संतत है और न ही अवकलनीय है।
अतः रोले प्रमेय लागू नहीं है।

(ii) f(x) = [x], x ϵ [-2, 2]
f(x) = [x], बिन्दु x = -1, 0, 1 पर न तो संतत है और न ही अवकलनीय है।
अतः रोले प्रमेय लागू नहीं है।

(iii) f(x) = (x² – 1), x ϵ [1, 2] के लिए
f(1) = 1 – 1 = 0 f(2) = 2² – 1 = 4 – 1 = 3
f(1) ≠ f(2)
यद्धपि f[1, 2] में संतत है तथा फलन (1, 2) अवकलनीय भी है परन्तु f(1) ≠ f(2).
अतः रोले प्रमेय लागू नहीं है।

प्रश्न 3.
यदि f: [-5, 5] → R एक संतत फलन है और यदि f’ (x) किसी भी बिन्दु पर शून्य नहीं होता है तो सिद्ध कीजिए कि f(-5) ≠ f(5).
हल:
यहाँ f : [-5, 5] →R
f संतत है तथा अवकलनीय है परन्तु f'(x) ≠ 0
अन्तराल (-5, 5) में रोले प्रमेय के लिए आवश्यक है-
यदि (i) [a, b] में f संतत है।
(ii) (a, b) में f अवकलित होता है।
(iii) f(a) = f(b)
तब f'(c) = 0, c ϵ (a, b)
यहाँ f'(c) ≠ 0 ⇒ f(a) ≠ f(b)
अतः f(-5) ≠ f(5)

प्रश्न 4.
माध्यमान प्रमेय सत्यापित कीजिए, यदि अंतराल [a, b] में f(x) = x² – 4x – 3, जहाँ a = 1 और b = 4 है।
हल:
∵ f'(x) = x² – 4x – 3 एक बहुपद है जो कि प्रत्येक बिन्दु पर संतत होगा।
∴ f'(x) = 2x – 4
⇒ f(x) का अस्तित्व है ∀ x ϵ (1, 4)
⇒ f(x), अंतराल (1, 4) में अवकलनीय है
माध्यमान प्रमेय द्वारा

अतः माध्यमान प्रमेय सत्यापित है।

प्रश्न 5.
माध्यमान प्रमेय सत्यापित कीजिए. यदि अन्तराल [a, b] में f(x) = x³ – 5x² – 3x, जहाँ a = 1 और b= 3 है। f'(c)= 0 के लिए c ϵ (1, 3) को ज्ञात कीजिए।
हल:
यहाँ f(x) = x³ – 5x² – 3x
[1, 3] में f संतत है तथा (1, 3) में अवकलनीय है क्योंकि यह बहुपदीय है।
f(1) = (1)³ – 5(1)² – 3 x 1
= 1 – 5 – 3 = 1 – 8 = -7
f(3) = (3)³ – 5(3)² – 3 x 3
= 27 – 45 – 9 = – 27
f(x) = 3x² – 10x – 3
f(c)= 3c² – 10c – 3

⇒ 3c² – 10c – 3 = \(\)
⇒ 3c² – 10c + 7= 0
⇒ (c – 1)(3c – 7) = 0
∴ c ≠ 1 c = \(\frac{7}{3}\) ϵ (1, 3)
यदि f'(c)= 0
तब 3c² – 10c – 3 = 0
⇒ (3c – 1)(c – 3) = 0 ⇒ c = \(\frac{1}{3}\), 3 + c ∉ (1, 3)

प्रश्न 6.
प्रश्न संख्या 2 में उपर्युक्त दिए तीनों फलनों के लिए माध्यमान प्रमेय की अनुपयोगिता की जाँच कीजिए।
हल:
(i) f(x)=[x], x ϵ [5, 9].
अन्तराल (5, 9) में f(x) = [x] बिन्दु x = 6, 7, 8 पर न तो संतत है और न ही अवकलनीय है।
अतः माध्यमान प्रमेय लागू नहीं है।
(ii) f(x) ⊂ [x], x ϵ [-2, 2]
अन्तराल [-2, 2] में | बिन्दु x= -1, 0, 1 पर न तो संतत है और न ही अवकलनीय है।
अतः माध्यमान प्रमेय लागू नहीं है।.
(iii) f(x) = x² – 1, x ϵ [1, 2]
एक बहुदीय है। यह अन्तराल [1, 2] में संतत है तथा (1, 2) में अवकलनीय है।
f(1) = (1)² – 1 = 1 – 1 = 0
f(2) = (2)² – 1 = 4 – 1 = 3
f'(x) = 2x
f'(c) = 2c

In this article, we share MP Board Class 12th Maths Book Solutions Chapter 9 अवकल समीकरण Ex 9.4 Pdf, These solutions are solved by subject experts from the latest MP Board books.

MP Board Class 12th Maths Book Solutions Chapter 9 अवकल समीकरण Ex 9.4

1 से 10 तक के प्रश्नों में, प्रत्येक अवकल समीकरण का व्यापक हल ज्ञात कीजिए।
प्रश्न 1.
\(\frac{d y}{d x}=\frac{1-\cos x}{1+\cos x}\)
हल:

प्रश्न 2.
\(\frac{d y}{d x} \sqrt{4-y^{2}}\) (-2 < y < 2)
हल:

प्रश्न 3.
\(\frac{d y}{d x}\) + y = 1(y ≠ 1)
हल:
\(\frac{d y}{d x}\) = 1 – y
\(\frac{d y}{1-y}\) = dx
समाकलन करने पर

प्रश्न 4.
sec² x tan y dx + sec² y tan x dy = 0
हल:
sec² x tan y dx = – sec² y tan x dy

प्रश्न 5.
(e^x + e^-x)dy – (e^x – e^-x) dx = 0
हल:
(e^x + e^-x)dy = (e^x – e^-x) dx = 0

प्रश्न 6.
\(\frac{d y}{d x}\) = (1 + x²) (1 + y²)
हल:


प्रश्न 7.
y log y dx – x dy = 0
हल:
दिया है :
y log y dx – x dy = 0
xy logy से भाग देने पर

प्रश्न 8.
x⁵\(\frac{d y}{d x}\) = -y⁵
हल:
x⁵\(\frac{d y}{d x}\) = -y⁵
⇒ y^-5 dy = -x^-5 dx
समाकलन करने पर

प्रश्न 9.
\(\frac{d y}{d x}\) = sin^-1x
हल:
\(\frac{d y}{d x}\) = sin^-1x
⇒ dy = sin^-1x dx
समाकलन करने पर


प्रश्न 10.
e^x tan y dx + (1 – e^x) sec²y dy = 0
हल:

11 से 14 तक के प्रश्नों में, प्रत्येक अवकल समीकरण के लिए दिए हुए प्रतिबंध को संतुष्ट करने वाला विशिष्ट हल ज्ञात कीजिए।
प्रश्न 11.
(x³ + x² + x + 1)\(\frac{d y}{d x}\) = 2x² + x; y = 1 यदि x = 0.
हल:
(x³ + x² + x + 1)\(\frac{d y}{d x}\) = 2x² + x

प्रश्न 12.
x (x² – 1)\(\frac{d y}{d x}\) = 1; y = 0 यदि x = 2
हल:
x (x² -1)\(\frac{d y}{d x}\) = 1

प्रश्न 13.
cos\(\left(\frac{d y}{d x}\right)\) = a (a ϵ R): y = 1 यदि x = 0
हल:
\(\frac{d y}{d x}\) = cos^-1 a ⇒ dy = (cos^-1a) dx
समाकलन करने पर
\(\int d y=\int\left(\cos ^{-1} a\right) d x\)
y = x cos^-1 a + C
इस समी० में y = 1 यदि x = 0 रखने पर
1= 0 + C ⇒ C = 1
C का यह मान समी० (i) में रखने पर
y = x cos^-1 a + 1
\(\frac{y-1}{x}\) = cos^-1a
⇒ cos\(\left(\frac{y-1}{x}\right)\) = a

प्रश्न 14.
\(\frac{d y}{d x}\) = y tan x; y = 1 यदि x = 0
हल:
⇒ \(\frac{d y}{y}\) = tan x dx
समाकलन करने पर
\(\int \frac{1}{y} d y=\int \tan x d x\)
logy = log sec x + log C
log y = log (C sec x)
y = C sec x …(i)
दिया है y = 1 यदि x = 0 तब समी० (i) से
1 = C sec 0 ⇒ C = 1
C = 1 समी० (i) में रखने पर ..
⇒ y = secx

प्रश्न 15.
बिन्दु (0, 0) से गुजरने वाले एक ऐसे वक्र का समीकरण ज्ञात कीजिए जिसका अवकल समीकरण y’ = e^x sinx है।
हल:
दिया है y’ = e^x sin x
या \(\frac{d y}{d x}\) = e^x sin x
⇒ dy = e^x sin x dx
समाकलन करने पर

प्रश्न 16.
अवकल समी० xy\(\frac{d y}{d x}\) = (x + 2)(y + 2) के लिए बिन्दु (1, – 1) से गुजरने वाला वक्र ज्ञात कीजिए।
हल:
दिया है xy\(\frac{d y}{d x}\) = (x + 2)(y + 2)

y – 2 log (y + 2) = x + 2 log x + C …(i)
∵ वक्र बिन्दु (1, -1) से गुजरता है अतः x = 1, y = -1
∴ -1 – 2 log (1) = 1 + 2 log (1) + C [∵ log 1 = 0]
-1 = 1 + C ⇒ C = -2
C = – 2 समी० (i) में रखने पर
y – 2 log (y + 2) = x + 2 log x + 2
⇒ y – x + 2 = 2 log x + 2 log (y + 2)
⇒ y – x’ + 2 = 2 [log x (y + 2)]
y – x + 2 = log [x² (y + 2)²]

प्रश्न 17.
बिन्दु (0, -2) से गुजरने वाले एक ऐसे वक्र का समीकरण ज्ञात कीजिए जिसके किसी बिन्दु (x, y) पर स्पर्श रेखा की प्रवणता और उस बिन्दु के ए निर्देशांक का गुणनफल उस बिन्दु के x निर्देशांक के बराबर है।
हल:
प्रश्नानुसार, y\(\frac{d y}{d x}\) = x (जहाँ \(\frac{d y}{d x}\) स्पर्श रेखा की प्रवणता है।)
y dy = x dx
समाकलन करने पर

प्रश्न 18.
एक वक्र के किसी बिन्दु (x, y) पर स्पर्श रेखा की प्रवणता, स्पर्श बिन्दु को, बिन्दु (-4, -3) से मिलाने वाले रेखाखण्डकी प्रवणता की दुगनी है। यदि यह वक्र बिन्दु (-2, 1)से गुजरता हो तो इस वक्र का समीकरण ज्ञात कीजिए।
हल:
दिया है बिन्दु (x, y) पर स्पर्श रेखा की प्रवणता = 2x [स्पर्श बिन्दु को (-4, -3) से मिलाने वाली रेखा की प्रवणता]

log (y + 3) = 2 log (x + 4) + log C
log (y + 3) = log (x + 4)² .C
⇒ y + 3 = (x + 4)².C …(i)
∵ वक्र बिन्दु (-2, -1) से गुजरता हैं इसलिए
x = -2, y = 1 रखने पर
4 = (2)² C = 4 = 4C
या C = 1
समी० (i) में C =1 रखने पर
– y + 3 = (x + 4)²

प्रश्न 19.
एक गोलाकार गुब्बारे का आयतन, जिसे हवा भरकर फुलाया जा रहा है, स्थिर गति से बदल रहा है। यदि आरम्भ में इस गुब्बारे की त्रिज्या 3 इकाई है और 3 सेकण्ड बाद 6 इकाई है, तो t सेकण्ड बाद उस गुब्बारे की त्रिज्या ज्ञात कीजिए।
हल:
माना किसी क्षण t गुब्बारे की त्रिज्या r तथा आयतन V है तब

प्रश्न 20.
किसी बैंक में मूलधन की वृद्धि r% वार्षिक की दर से होती है। यदि 100 रु० 10 वर्षों में दुगने हो जाते हैं, तो का मान ज्ञात कीजिए। (log 2 = 0.6931)
हल:
माना किसी समय पर मूलधन P हैं तब प्रश्नानुसार,

प्रश्न 21.
किसी बैंक में मूलधन की वृद्धि 5% वार्षिक की दर से होती है। इस बैंक में 1000 रु० जमा कराये जाते हैं। ज्ञात कीजिए कि 10 वर्ष बाद यह राशि कितनी हो जाएगी? (e^0.5 = 1.648)
हल:
किसी समय t पर मूलधन P हैं तब प्रश्नानुसार,

जब t = 10 वर्ष
P = 1000 e^10/20 ⇒ P = 1000e^0.5
P = 1000 × 1.648 (∵ e^0.5 = 1.648)
P = 1648 रु०
अत: 10 वर्ष बाद मूलधन 1648 रु० होगा।

प्रश्न 22.
किसी जीवाणु समूह में जीवाणुओं की संख्या 1,00,000 है। 2 घण्टों में इनकी संख्या में 10% की वृद्धि होती है। कितने घण्टों में जीवाणुओं की संख्या 2,00,000 हो जाएगी। यदि जीवाणुओं के वृद्धि की दर उनमें उपस्थित संख्या के समानुपाती है।
हल:
माना किसी समय t पर जीवाणुओं की संख्या y है।

प्रश्न 23.
अवकल समीकरण \(\frac{d y}{d x}\) = e^x+y का व्यापक इल है
(A) e^x + e^-y = C
(B) e^x + e^y = C
(C) e^-x + e^y = C
(D) e^-x + e^-y = C
हल:

In this article, we share MP Board Class 12th Maths Book Solutions Chapter 5 सांतत्य तथा अवकलनीयता Ex 5.5 Pdf, These solutions are solved by subject experts from the latest MP Board books.

MP Board Class 12th Maths Book Solutions Chapter 5 सांतत्य तथा अवकलनीयता Ex 5.5

प्रश्न 1 से 11 तक के प्रश्नों में प्रदत्त फलनों का x के सापेक्ष अवकलन कीजिए-
प्रश्न 1.
cosx. cos 2x. cos3x
हल:
माना y = cosx. cos 2x. cos3x
दोनों ओर log लेने पर
logy = log [cos x. cos 2x. cos3x]
= log cosx + log cos 2x + log cos3x
दोनों ओर x के सापेक्ष अवकलन करने पर

प्रश्न 2.

हल:

प्रश्न 3.
(log x)^{cos x}
हल:

माना y = (log x)^{cos x}
दोनों पक्षों का लघुगणक लेने पर,

प्रश्न 4.
x^x – 2sin x
हल:
माना y = x^x – 2sinx
= u – v (माना)
जबकि u = x, v = 2sinx
दोनों ओर लघुगणक लेने पर,
log u = log x^x = xlogx
x के सापेक्ष दोनों अवकलन करने पर,

प्रश्न 5.
(x + 3)² . (x + 4)³ . (x + 5)⁴
हल:
माना = (x + 3)² . (x + 4)³ . (x + 5)⁴
दोनों ओर लघुगणक लेने पर,
log y = log [(x + 3)² . (x + 4)³ (x + 5)⁴]
log y = log (x + 3)² + log (x + 4)³ + log (x + 5)⁴
[∵ log mn = log m + log n]
log y = 2log (x + 3) + 3 log (x + 4) + 4 log (x + 5) [∵ log mⁿ = n log m]
x के सापेक्ष अवकलन करने पर,

प्रश्न 6.

हल:

प्रश्न 7
(log x)^x + x ^{log x}
हल:
माना y = (log x)^x + x ^{log x}
= u + v (माना)

प्रश्न 8.
(sin x)^x + sin^-1 \( \sqrt{{x}} \)
हल:
माना y = (sin x)^x + sin^-1 \( \sqrt{{x}} \)
= u + v (माना)
∴ u = (sin x)^x
दोनों ओर लघुगणक लेने पर,
log u = log (sin x)^x = x log sin x
दोनों तरफ अवकलन करने पर,

प्रश्न 9.
x^{sin x} + (sin x)^{cos x}
हल:
माना y = x^{sin x} + (sin x)^{cos x}
माना u = x^{sin x} …(i)
तथा v = (sin x)^cosx …(ii)
∴ y = u + v …(iii)
समी० (i) व (ii) में दोनों पक्षों का लघुगणक लेने पर
log u = sin x log x तथा log v = cos x log sin x

प्रश्न 10.
x^xcosx + \(\frac{x^{2}+1}{x^{2}-1}\)
हल:

प्रश्न 11.
(x cos x)^{sin x} + (x sin x)^1/x
हल:
माना y = (x cos x)^{sin x} + (x sin x)^1/x
= u + v (माना)

प्रश्न 12 से 15 तक के प्रश्नों में प्रदत्त फलनों के लिए ज्ञात कीजिए।
प्रश्न 12.
x^y + y^x = 1
हल:
x^y + y^x = 1
दोनों पक्षों का लघुगणक लेने पर
y log x + x log y = 0 [∵log 1 0)
दोनों ओर x के सापेक्ष अवकलन करने पर

प्रश्न 13.
y^x = x^y
हल:
y = x दोनों ओर लघुगणक लेने पर
logy^x = log x^y
⇒ x log y = y log x
अब x के सापेक्ष अवकलन करने पर,

प्रश्न 14.
(cosx)^y = (cos y)^x
हल:
(cosx)^y = (cos y)^x
दोनों ओर का लघुगणक लेने पर
ylog (cos.x) = x log (cos y)
दोनों पक्षों का x के सापेक्ष अवकलन करने पर

प्रश्न 15.
xy = e^(x-y)
हल:
दोनों ओर का लघुगणक लेने पर,
logxy = loge^x-y
⇒ log x + log y = (x – y) loge
⇒ logx + logy = x – y (∵ log e = 1)
दोनों ओर x के सापेक्ष अवकलन करने पर,

प्रश्न 16.
f(x) = (1 + x) (1 + x²) (1 + x⁴) (1 + x⁸) द्वारा प्रदत्त फलन का अवकलज ज्ञात कीजिए और इस प्रकार f(1) ज्ञात कीजिए।
हल:
f(x) = (1 + x) (1 + x²) (1 + x⁴) (1 + x⁸)
∴ log f(x) = log (1 + x) + log (1 + x²) + log (1 + x⁴) + log (1 + x⁸)
दोनों ओर का अवकलन करने पर,

प्रश्न 17.
(x² – 5x + 8) (x³ + 7x + 9) का अवकलन निम्नलिखित तीन प्रकार से कीजिए-
(i) गुणनफल नियम का प्रयोग करके
(ii) गुणनफल के विस्तारण द्वारा एक एकल बहुपद प्राप्त करके
(iii) लघुगणकीय अवकलन द्वारा यह भी सत्यापित कीजिए कि इस प्रकार प्राप्त तीनों उत्तर समान है।
हल:
(i) गुणनफल नियम का प्रयोग
माना = (x² – 5x + 8).(x³ + 7x + 9)
x के सापेक्ष अवकलन करने पर,

प्रश्न 18.
यदि u, v तथा w, x के फलन हैं तो दो विधियों अर्थात् प्रथम गुणनफल नियम की पुनरावृत्ति द्वारा, द्वितीय-लघुगणकीय अवकलन द्वारा दर्शाइए कि

हल:

In this article, we share MP Board Class 12th Maths Book Solutions Chapter 5 सांतत्य तथा अवकलनीयता Ex 5.6 Pdf, These solutions are solved by subject experts from the latest MP Board books.

MP Board Class 12th Maths Book Solutions Chapter 5 सांतत्य तथा अवकलनीयता Ex 5.6

यदि प्रश्न संख्या 1 से 10 तक में x तथा y के दिए समीकरणों द्वारा, एक-दूसरे से प्राचलिक रूप में सम्बन्धित हों तो प्राचलों का विलोपन किए बिना \(\frac{d y}{d x}\) ज्ञात कीजिए।
प्रश्न 1.
x = 2at², y = at⁴
हल:
x = 2at², y = at⁴
t के सापेक्ष अवकलन करने पर,

प्रश्न 2.
x = a cosθ, y = b cosθ
हल:
x = acos θ, y = bcosθ
θ के सापेक्ष अवकलन करने पर,

प्रश्न 3.
x = sint, y = cos 2t
हल:
x = sin t, y = cos 2t
x के सापेक्ष अवकलन करने पर,

प्रश्न 4.
x = 4t, y = \(\frac{4}{t}\)
हल:
x = 4t, y = \(\frac{4}{t}\) = 4t^-1
t के सापेक्ष अवकलन करने पर,

प्रश्न 5.
x = cos θ – cos 2θ, y = sin θ – sin 2θ
हल:
x = cos θ- cos 2θ, y = sin θ – sin 2θ
θ के सापेक्ष अवकलन करने पर,

प्रश्न 6.
x = a(θ – sinθ), y = a(1 + cos θ)
हल:
x = a(θ – sinθ), y = a(1 + cos θ)
θ के सापेक्ष अवकलन करने पर,

प्रश्न 7.

हल:

प्रश्न 8.
x = a(cos t + log tan\(\frac{t}{2}\)), y = a sin t
हल:

= \(\frac{sin t}{cos t}\) = tan t

प्रश्न 9.
x = a sec θ, y = b tan θ
हल:
x = a sec θ तथा y = b tan θ

प्रश्न 10.
x = a (cos θ + θ sin θ),
y = a (sin θ – θ cos θ)
हल:
x = a (cos θ + θ sin θ), y = a (sin θ – θ cos θ)

प्रश्न 11.
यदि x = \(\sqrt{a \sin ^{-1} t}\), y = \(\sqrt{a^{\cos ^{-1} t}}\), तो दर्शाइए कि \(\frac{d y}{d x}=-\frac{y}{x}\)
हल: