Category: Class 10

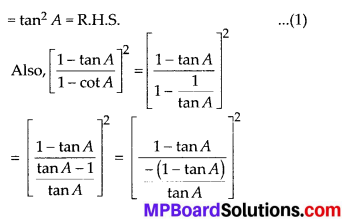
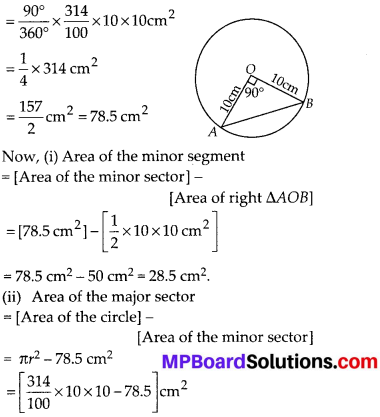
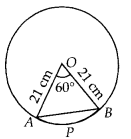
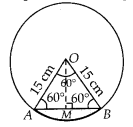
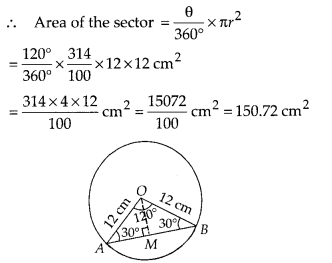
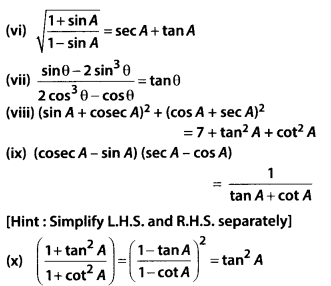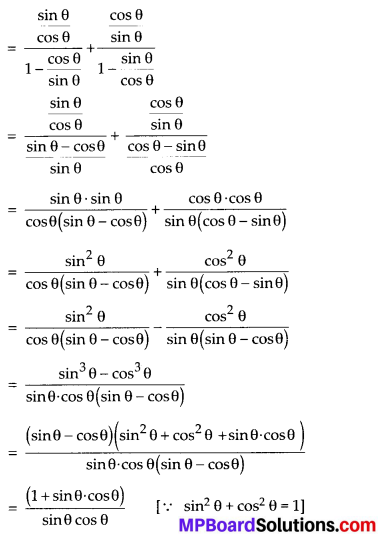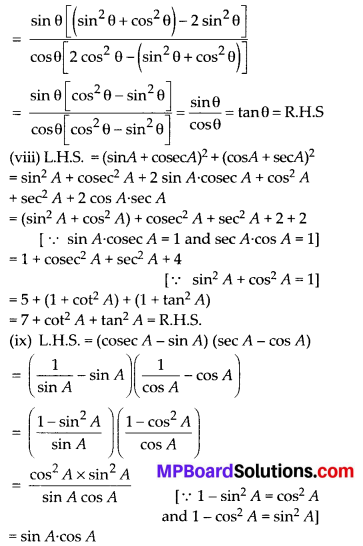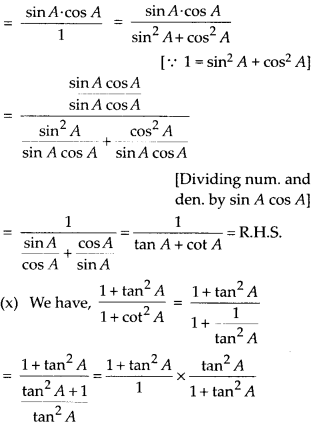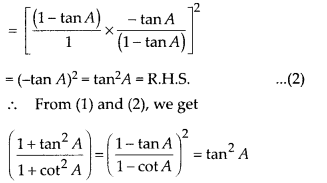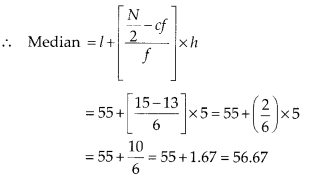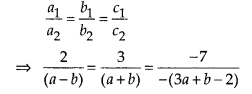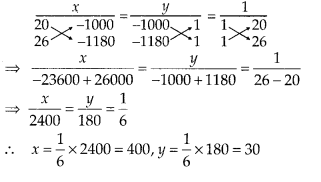In this article, we will share MP Board Class 10th Maths Book Solutions Chapter 14 Statistics Ex 14.4 Pdf, These solutions are solved subject experts from the latest edition books.

MP Board Class 10th Maths Solutions Chapter 14 Statistics Ex 14.4

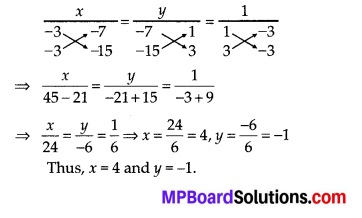
Question 1.
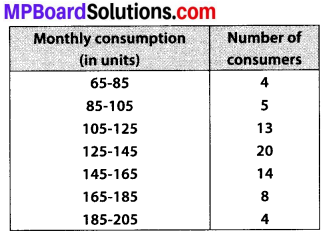
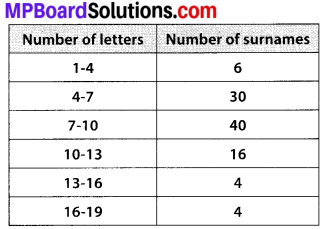
The following distribution gives the daily income of 50 workers of a factory.

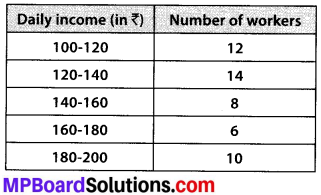
Convert the distribution above to a less than type cumulative frequency distribution, and draw its ogive.
Solution:
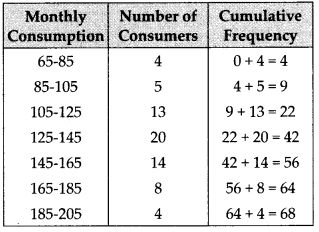
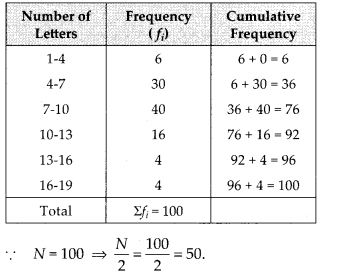
We have the cumulative frequency distribution as follows:

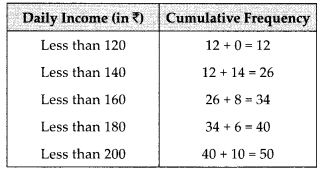
Now, we plot the points corresponding to the ordered pair (120, 12), (140, 26), (160, 34), (180, 40) and (200, 50) on a graph paper and join them by a free hand to get a smooth curve as shown below:

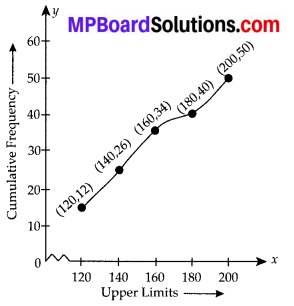
The curve so obtained is called the less than ogive.

Question 2.
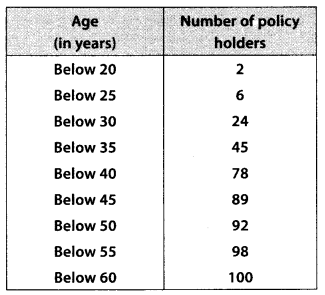
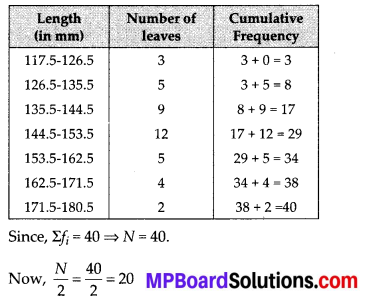
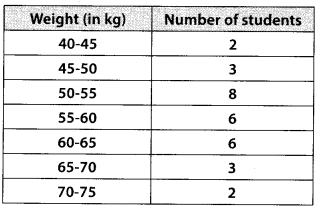
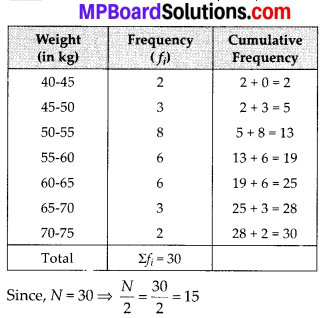
During the medical check-up of 35 students of a class, their weights were recorded as follows:

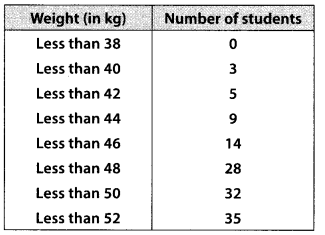
Draw a less than type ogive for the given data. Hence obtain the median weight from the graph and verify the result by using the formula.
Solution:
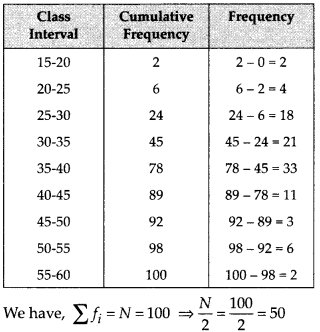
Here, the values 38, 40, 42, 44, 46, 48, 50 and 52 are the upper limits of the respective class-intervals.
We plot the points (ordered pairs) (38, 0), (40, 3), (42, 5), (44, 9), (46,14), (48, 28), (50, 32) and (52, 35) on a graph paper and join them by a free hand to get a smooth curve.
The curve so obtained is the less than type ogive.

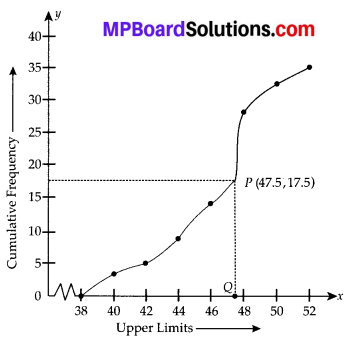
∵ N = 35
∴ \(\frac{N}{2}=\frac{35}{2}\) = 17.5
The point 17.5 is on y-axis.
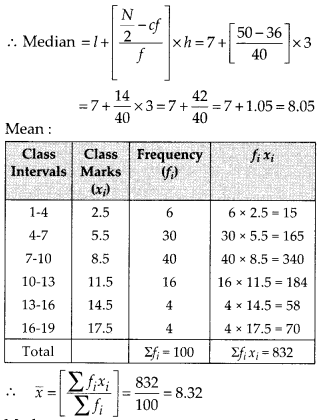
From this point (i.e., from 17.5) we draw a line parallel to the x-axis which cuts the curve at P. From this point P, draw a perpendicular to the x-axis, meeting the x-axis at Question The point Q represents the median of the data which is 47.5.
Verification:
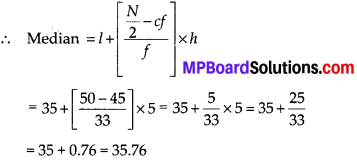
To verify the result, let us make the following table in order to find median using the formula :

Thus, the median = 46.5 kg is approximately

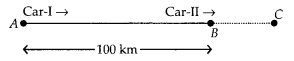
Question 3.
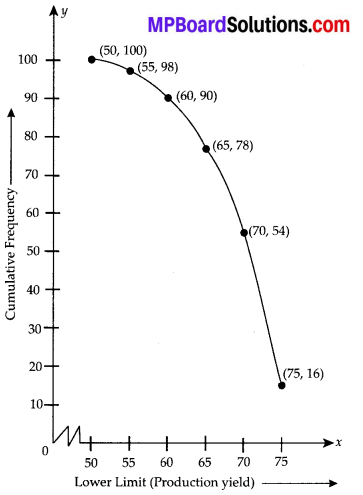
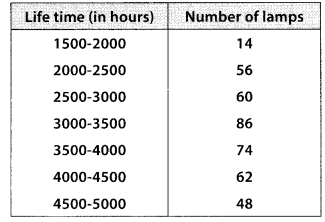
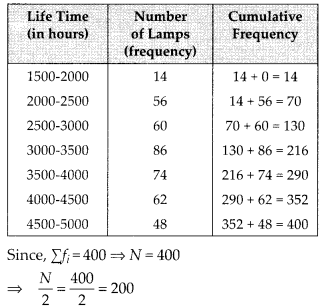
The following table gives production yield per hectare of wheat of 100 farms of a village

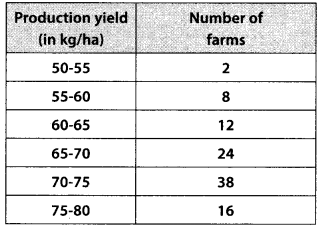
Change the distribution to a more than type distribution, and draw its ogive.
Solution:
For more than type distribution, we have

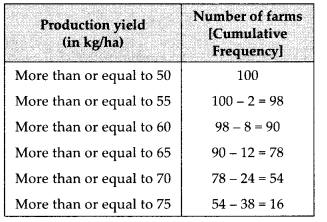
Now, we plot the points (50, 100), (55, 98), (60, 90), (65, 78), (70, 54) and (75, 16) and join the points with a free hand to get a smooth curve.
The curve so obtained is the ‘more than type ogive’.

In this article, we will share MP Board Class 10th Maths Book Solutions Chapter 8 Introduction to Trigonometry Ex 8.4 Pdf, These solutions are solved subject experts from the latest edition books.

MP Board Class 10th Maths Solutions Chapter 8 Introduction to Trigonometry Ex 8.4

Question 1.
Express the trigonometric ratios sin A, sec A and tan A in terms of cot A.
Solution:

Question 2.
Write all the other trigonometric ratios of ∠A in terms of sec A.
Solution:

Question 3.
Evaluate:
(i) \(\frac{\sin ^{2} 63^{\circ}+\sin ^{2} 27^{\circ}}{\cos ^{2} 17^{\circ}+\cos ^{2} 73^{\circ}}\)
(ii) sin 25° cos 65° + cos 25° sin 65°
Solution:
(i) \(\frac{\sin ^{2} 63^{\circ}+\sin ^{2} 27^{\circ}}{\cos ^{2} 17^{\circ}+\cos ^{2} 73^{\circ}}\)
∵ sin 63° = sin (90° – 27°) = cos 27°
⇒ sin² 63° = cos² 27°
cos² 73° = cos² (90° – 17°) = sin² 17°
∴ \(\frac{\sin ^{2} 63^{\circ}+\sin ^{2} 27^{\circ}}{\cos ^{2} 17^{\circ}+\cos ^{2} 73^{\circ}}=\frac{\cos ^{2} 27^{\circ}+\sin ^{2} 27^{\circ}}{\cos ^{2} 17^{\circ}+\sin ^{2} 17^{\circ}}=1\)
[ ∵ cos² A + sin² A = 1]

(ii) sin 25° cos 65° + cos 25° sin 65°
∵ sin 25° = sin (90° – 65°) = cos 65° [ ∵ sin (90° – A) = cos A]
cos 25° = cos (90° – 65°) = sin 65° [ ∵ cos (90° – A) = sin A]
∴ sin 25° cos 65° + cos 25° sin 65°
= cos 65° cos 65° + sin 65° sin 65°
= (cos 65°)² + (sin 65°)²
= cos² 65° + sin² 65° = 1 [∵ cos² A + sin² A = 1]

Question 4.
Choose the correct option. Justify your choice.
(i) 9 sec²A – 9 tan²A =
(A) 1
(B) 9
(C) 8
(D) 0

(ii) (1 +tanθ + secθ) (1 + cotθ – cosec0) =
(A) 0
(B) 1
(C) 2
(D) – 1

(iii) (sec A + tan A) (1 – sinA) =
(A) sec A
(B) sin A
(C) cosec A
(D) cos A

(iv) \(\frac{1+\tan ^{2} A}{1+\cot ^{2} A}=\)
(A) sec² A
(B) -1
(C) cot² A
(D) tan² A
Solution:
(i) (B): Since, 9 sec² A – 9 tan² A
= 9 (sec² A – tan² A) = 9 (1) = 9 [∵ sec² A – tan² A = 1]

(ii) (C): Here,

Question 5.
Prove the following identities, where the angles involved are acute angles for which the expressions are defined.


Solution:

MP Board Class 10th Science Solutions Chapter 7 Control and Coordination

MP Board Class 10th Science Chapter 7 Intext Questions

Class 10th Science Chapter 7 Intext Questions Page No. 119

Question 1.
What is the difference between a reflex action and walking?
Answer:
A reflex action is an automatic reaction for each stimulation in our body initiated by our sense responses e.g., we move our hand immediately after a contact with hot object. It is a direct controlled action. Walking is completely controlled by our brain. On the other hand, is a voluntary action. It requires complete coordination of muscles, bones, eyes etc.

Question 2.
What happens at the synapse between two neurons?
Answer:
The electrical impulse travels through axon and sets off the release of some chemicals (neurotransmitters) at the axon endings. These chemicals cross the gap or synapse, and start a similar electrical impulse in a dendrite of the next neuron.

Question 3.
Which part of the brain maintains posture and equilibrium of the body?
Answer:
Cerebellum is the part of the brain which maintains posture and equilibrium of the body.

Question 4.
How do we detect the smell of an agarbatti (incense stick)?
Answer:
Forebrain is responsible for thinking work. It has separate areas that are specialized for hearing, smelling, sight, taste, touch etc. The _ forebrain also has regions that collect information or impulses from various receptors. When the smell of an incense stick reaches us, out forebrain detects it. Then, the forebrain interprets it by putting it together with the information received from other receptors and also with the information already stored in the brain.

Question 5.
What is the role of the brain in reflex action?
Answer:
Reflex actions are sudden responses, which do not involve any thinking. A connection of detecting the signal from the nerves (input) and responding to it quickly (output) is called\a reflex arc. The reflex arcs can be considered as connections present between the input and output nerves which meets in a bundle in the spinal cord. The brain is only responsible of the signal and the response.

Class 10th Science Chapter 7 Intext Questions Page No. 122

Question 1.
What are plant hormones?
Answer:
The chemicals present in plants which help coordinate growth, development and responses to the environment are called plant hormones.

Question 2.
How is the movement of leaves of the sensitive plant different from the movement of a shoot towards light?
Answer:

Question 3.
Give an example of a plant hormone that promotes growth.
Answer:
Auxin is a growth-promoting plant hormone.

Question 4.
How do auxins promote the growth of a tendril around a support?
Answer:
A hormone called Auxin, synthesised at the shoot tip helps the cells to grow longer. When light is coming from one side of the plant, auxin diffuses towards the shady side of the shoot. The concentration of auxin stimulates the cells to grow longer on the side of the shoot which is away from light. Thus the plant appears to bend towards light.

Question 5.
Design an experiment to demonstrate hydrotropism.
Answer:
Take two small beakers and label them as A and B. Fill beaker A with water. Now, make a cylindrical-shaped roll from a filter paper and keep it as a bridge between beaker A and beaker B, as shown in the figure. Attach few germinating seeds in the middle of the filter paper bridge. Now, cover the entire set-up with a transparent plastic container so that the moisture is retained.

Phenomenon of Hydrotropism Observations:

• The roots of the germinating seeds will grow towards beaker A.
• This experiment demonstrates the phenomenon of hydrotropism.

Class 10th Science Chapter 7 Intext Questions Page No. 125

Question 1.
How does chemical coordination take place in animals?
Answer:
Chemical co-ordination take place by hormones Adrenal gland secrete adrenaline directly into the blood and carried to different parts of the body. Such animal hormones are part of the endocrine system which constitutes a second way of control and coordination in our body.

Question 2.
Why is the use of iodised salt advisable? .
Answer:
Iodine is main stimulator of thyroxine. It stimulates the thyroid gland to produce thyroxine hormone. It regulates carbohydrate, fat and protein metabolism in our body. Deficiency of this hormone results in the enlargement of the thyroid gland. This can lead to goitre, a disease characterized by swollen neck. Therefore, iodised salt is advised for normal functioning of the thyroid gland.

Question 3.
How does our body respond when adrenaline is secreted into the blood?
Answer:
Adrealine is secreted directly into the blood and carried to different parts of the body. The target organs or the specific tissues on which is acts include the heart. As a result, the heart beats faster, resulting in supply of more oxygen to our muscles. The blood to the digestive system and skin is reduced due to contraction of muscles around small arteries in these organs. This diverts the blood to our skeletal muscles. The breathing rate also increases because of the contractions of the diaphragm and the rib muscles.

Question 4.
Why are some patients of diabetes treated by giving injections of insulin?
Answer:
In diabetes, the level of sugar in the blood is too high and hence cause discomfort. Insulin, a naturally occuring chemical inside our pancreas act, as hormones andihelps in regulating the blood sugar levels. When due to very high suga- intake or improper secretion of insulin, balance of insulin decreasesin the body then insulin is injected to body. This is the reason why diabetic patients are treated by giving injections of insulin.

MP Board Class 10th Science Chapter 7 NCERT Textbook Exercises

Question 1.
Which of the following is a plant hormone?
(a) Insulin
(b) Thyroxin
(c) Oestrogen
(d) Cytokinin
Answer:
(d) Cytokinin is a plant hormone.

Question 2.
The gap between two neurons is called a
(a) Dendrite
(b) Synapse
(c) Axon
(d) Impulse
Answer:
(b) The gap between two neurons is called a synapse.

Question 3.
The brain is responsible for:
(a) Thinking
(b) Regulating the heart beat
(c) Balancing the body
(d) All of the above
Answer:
(d) The brain is responsible for thinking, regulating the heart beat and balancing the body.

Question 4.
What is the function of receptors in our body? Think of situations where receptors do not work properly. What problems are likely to arise?
Answer:
Receptors are sensory structures (organs/tissues or cells) present all over the body. The receptors are either grouped in case of eye Or ear, or scattered in case of skin. Functions of receptors:
(i) They sense the external stimuli such as heat or pain.
(ii) They also trigger an impulse in the sensory neuron which sends message to the spinal cord. When the receptors are damaged, the external stimuli transferring signals to the brain are not felt. For example, in the case of damaged receptors, if we accidentally touch any hot object, then our hands might get burnt as damaged , receptors cannot perceive the external stimuli of heat and pain.

Question 5.
Draw the structure of a neuron and explain its function.
Answer:
Neurons are the functional units of the nervous system.
Structure of a Neuron:

The three main parts of a neuron are axon, dendrite and cell body.

Functions of the three parts of a neuron:

1. Axon: It conducts messages away from the cell body. It is the part by which information travels as an electrical impulse.
2. Dendrite: It is the part where information is acquired, it receives information from axon of other cell or initiation point and conducts the messages towards the cell body.
3. Cell body: It is the part where impulse get converted into a chemical signal forwarding transmission. It is mainly concerned with the maintenance and growth.

Question 6.
How does phototropism occur in plants?
Answer:
When growing plants detect light, a hormone called auxin, synthesised at ‘ the shoot tip, helps the cells to grow longer towards light. When light is coming from one side of the plant, Ans: auxin diffuses towards the shady side of the shoot. This concentration of auxin stimulates the cells to grow longer on the side of the shoot which is away from the light. Thus the plant appears to bend towards light, i,e, phototropism.

Question 7.
Which signals will get disrupted in case of a spinal cord injury?
Answer:
Spinal cord is made up of nerves which supply information to think about Nerves from all over the body meet in a bundle in the spinal cord on their way to the brain. Reflex arcs are formed in this spinal cord it self, although the information input also goes on to reach the brain. So if it is injured there is obstruction for carrying impulses to other parts.

Question 8.
How does chemical coordination occur in plants?
Answer:
Different plant hormones help to coordinate growth, development and response to the environment. When growing plants detect light, a hormone called auxin, synthesised at the shoot tip, helps the cells to grow longer. Gibberellins helps in the growth of the stem. Cytokinins promote cell division.

Question 9.
What is the need for a system of control and coordination in an organism?
Answer:
The maintenance of the body functions in response to changes in the body by working together of various integrated body systems is known as coordination. All the movements that occur in response to stimuli are carefully coordinated and controlled. In animals, the control and coordination movements are provided by nervous and muscular systems. The nervous system sends messages to and away from the brain. The spinal cord plays an important role in the relay of messages. In the absence of this system of control and coordination, our body will not be able to function properly. For example, when we accidentally touch a hot utensil, we immediately withdraw our hand. In the absence of nerve transmission, we will not withdraw our hand and may get burnt.

Question 10.
How are involuntary actions and reflex actions different from each other?
Answer:
Involuntary actions cannot be consciously controlled. For example, we cannot consciously control the movement of food in the alimentary canal. These actions are however, directly under the control of the brain. On the other hand, the reflex actions such as closing of eyes immediately when bright light is focussed show sudden response and do not involve any thinking. This means that unlike involuntary actions, the reflex actions are not under the control of brain.

Question 11.
Compare and contrast nervous and hormonal mechanisms for control and coordination in animals.
Answer:
Nervous system mechanism

1. The information is conveyed in the form of electric impulse.
2. The axons and dendrites transmit the information through a coordinated effort.
3. The flow of information is rapid and the response is quick.
4. Its effects are short lived.

Hormonal system mechanism

1. The information is conveyed in the form of chemical messengers.
2. The information is transmitted or transported through blood.
3. The information travels slowly and the response is slow.
4. It has prolonged effects.

Question 12.
What is the difference between the manner in which movement takes place in a sensitive plant and the movement in our legs?
Answer:
In a sensitive plant the cells change shape by changing the amount of water in them, resulting in swelling or shrinking and there fore leading to limited movements. Movement in our legs is voluntary action done by muscle tissue regulated by central nervous system.

MP Board Class 10th Science Chapter 7 Additional Important Questions

MP Board Class 10th Science Chapter 7 Multiple Choice Questions

Question 1.
The brain box which protect internal part of brain is called:
(a) Skull
(b) Peripheral Nervous System
(c) Autonomic Nervous System
(d) Ribs
Answer:
(a) Skull

Question 2.
Secondary sexual characteristics are controlled by:
(a) Central Nervous System
(b) Peripheral Nervous System
(c) Autonomic Nervous System
(d) Endocrine gland
Answer:
(d) Endocrine gland

Question 3.
The activities of the internal organs are controlled by the:
(a) Central Nervous System
(b) Peripheral Nervous System
(c) Autonomic Nervous System
(d) Endocrine glands
Answer:
(a) Central Nervous System

Question 4.
Which pari of brain is the seat of intelligence and voluntary actions?
(a) Diencephalon
(b) Cerebrum
(c) Cerebellum
(d) Medulla oblongata
Answer:
(b) Cerebrum

Question 5.
Cell division in plant is affected by:
(a) Ethylene
(b) Auxin
(c) Gibberellin
(d) Cytokinin
Answer:
(d) Cytokinin

Question 6.
The gap between two neurons is known as……
(a) Synapse
(b) Synopsis
(c) Impulse
(d) Synaptic node
Answer:
(a) Synapse

Question 7.
Which of the follow ing is a plant hormone?
(a) Thyroxin
(b) Cytokinin
(c) Insulin
(d) Oestrogen
Answer:
(b) Cytokinin

Question 8.
Tropic movements are:
(a) In response to light
(b) In response to gravity
(c) Uni-directional
(d) Non – directional
Answer:
(c) Uni-directional

Question 9.
Artifical ripening of fruit is carried out by:
(a) Auxins
(b) Ethylene
(c) Abscisic acid (ABA)
(d) Gibberellins
Answer:
(b) Ethylene

Question 10.
The part of brain that controls respiration, heartbeat and peristalsisis:
(a) Cerebrum
(b) Cerebellum
(c) Pons
(d) Medulla
Answer:
(d) Medulla

Question 11.
The brain is responsible for:
(a) Thinking
(b) Regulating the heart beat
(c) Balancing the body
(d) All of the above
Answer:
(d) All of the above

Question 12.
Which of the following hormone is released by thyroid?
(a) Insulin
(b) Thyroxine
(c) Trypsin
(d) Pepsin
Answer:
(b) Thyroxine

Question 13.
Which body organ is surrounded by meninges?
(a) Heart and Lungs
(b) Brain and Heart
(c) Brain and Spinal Cord
(d) Spinal Cord and Lungs
Answer:
(c) Brain and Spinal Cord

Question 14.
The part of brain that controls muscular co-ordination is
(a) Cerebrum
(b) Cerebellum
(c) Pons
(d) Medulla
Answer:
(b) Cerebellum

Question 15.
Growth of the stem is controlled by:
(a) Gibberellin
(b) Auxin
(c) Abscisic acid
(d) Cytokinin
Answer:
(a) Gibberellin

Question 16.
Cause wilting of leaves? Which hormone
(a) Gibberellin
(b) Auxin
(c) Abscisic acid
(d) Cytokinin
Answer:
(c) Abscisic acid

Question 17.
Which of the following hormones contains iodine?
(a) Adrenaline
(b) Testosterone
(c) Thyroxine
(d) Insulin
Answer:
(c) Thyroxine

Question 18.
Which part of brain controls the posture and balance of the body?
(b) Cerebellum
(d) Medulla
Ans.
(b)

MP Board Class 10th Science Chapter 7 Very Short Answer Type Questions

Question 1.
What is considered as the structural and functional unit of the nervous system?
Answer:
Neuron or Nerve cell.

Question 2.
What is called an automatic response to a stimulus which is not controlled by the brain?
Answer:
Reflex action.

Question 3.
How do plants respond to stimuli without any kind of nervous systems?
Answer:
Plants respond to stimuli without any kind of nervous systems with the help of plant hormones.

Question 4.
What are the other factors which control and coordinate in plants and animals other than CNS and reflex actions?
Answer:
Hormones.

Question 5.
What is phototropism?
Answer:
The movement of a plant’s part towards light is called phototropism.

Question 6.
What we call to:

1. the movement of plant to the availability of water?
2. the movement of plant to the earth’s gravity?

Answer:

1. Hydrotropism.
2. Geotropism.

Question 7.
Which system of our body is related to hormones which constitutes a second way of control and coordination in our body?
Answer:
Endocrine system.

Question 8.
How many Endocrine glands are situated in our brain? Name them.
Answer:
Three: Hypothalamus, pituitary and pineal glands.

Question 9.
What is considered as the reflex centre of the brain?
Answer:
Medulla oblongata.

Question 10.
Which structure is related to both nervous system and endocrine system in our body?
Answer:
Hypothalamus.

Question 11.
Which part of the brain maintains posture and equilibrium of the body?
Answer:
Cerebellum.

Question 12.
Name the substance important for synthesis of thyroxine.
Answer:
Iodine is essential for the synthesis of thyroxine.

Question 13.
How thyroxine initiate growth in our body?
Answer:
Thyroxine regulates carbohydrate, protein and fat metabolism in our body and provide proper energy which causes the best balance for growth.

Qusestion 14.
Who gave the term phytohormones?
Answer:
Thimann.

MP Board Class 10th Science Chapter 7 Short Answer Type Questions

Question 1.
Write importance of control and coordination in living organisms.
Answer:

• Control and coordination increase the chances of survival by responding to stimuli.
• Different body parts function in coordination to each other as a single unit.

Question 2.
What is hyperglycemia?
Answer:
Hyperglycemia refers to high sugar level in blood. In general, diabetic patients has hyperglycemia due to insufficient release of insulin hormone. .

Question 3.
What are reasons for many drastic changes in appearance at 10-12 years of age?
Answer:
These changes are associated with puberty and are because of the secretion of testosterone in males and oestrogen in females.

Question 4.
Write down the functions performed by cerebrum.
Answer:
The cerebrum performs the following functions:

• It controls our mental abilities like thinking, reasoning, learning, memorising etc.
• It controls our feelings, emotions and speech.
• It controls all involuntary functions.

Question 5.
What are the functions of cerebellum?
Answer:
Functions of cerebellum:

• Maintains equilibrium or balance of the body.
• Coordinates muscular movement.
• Maintains posture of the body.

Question 6.
How soft and delicate brain is safe inside a human body?
Answer:
Brain is placed safely inside a bony box called cranium by the nature, within which there are 3 layers of fluid-filled (called cerebrospinal fluid) membranes (called meninges) which absorb external shock.

Question 7.
What is the role of the brain in reflex action?
Answer:
Brain has no role in reflex action response. Instead, spinal cord is the control center of a reflex action. In fact, brain becomes aware after the reflex arc has been formed.

Question 8.
What do you mean by reflex action? Give examples of reflex actions.
Answer:
It is defined as fast, unconscious, immediate, automatic and involuntary response of the body in parts or total (through effectors) to c «dmulus. It is monitored through spinal cord.

Examples of reflex actions:

• Closing of eyes with bright light.
• Knee-Jerk.
• Withdrawal of body parts when pricked by a pin.

Question 9.
What are the different types of reflexes?
Answer:
There are two types of reflexes:

• Unconditioned reflexes.
• Conditioned reflexes.

Question 10.
What is reflex arc?
Answer:
The structural and functional unit that carries our reflex action is called a reflex arc. It consists of:

• A receptor.
• Sensory nerve (afferent)
• Motor nerve (efferent)
• Spinal cord.
• Inter-neuron and effector

Question 11.
Write important functions of different plant hormones?
Answer:
The five major types of phytohormones and their functions are:

• Auxins: Promote cell division, bending of shoot towards the source of light.
• Cytokinins: Promote cell division.
• Gibberellins: Stimulate stem elongation.
• Abscisic acid: Inhibit growth, closing of stomata and dormancy.
• Ethylene( gas hormone): Promotes fruit ripening and growth.

Question 12.
How is the movement of leaves of the sensitive plant different from the movement of a shoot towards light?
Answer:
The movement of leaves of the sensitive plant, (e.g. Mimosa pudica or touch-me-not) occurs in response to touch or contact stimuli. It is a growth independent movement (nastic movement).

The movement of shoot towards light is called photo-tropism. This type of movement is directional and is growth dependent.

Question 13.
Write some points about the character of nastic movement.
Answer:
Characters of Nastic Movements in plants:

1. Growth independent movements.
2. Time of action – immediate.
3. Response to stimulus – Non-directional.
4. Motive – Change in turgor.

Examples – Folding of leaves of touch-me-not (mimosa).

Question 14.
What is chemotropism?
Answer:
Directional movement of a plant or its part in response to chemicals is called chemotropism, e.g. outward growth of the shoot from origin.

Question 15.
Define geotropism.
Answer:
Roots move in the direction of gravity (positive + ve geotropism).
Shoots move (up) against direction of gravity (negative -ve geotropism).

MP Board Class 10th Science Chapter 7 Long Answer Type Questions

Question 1.
What are the limitations of nervous system in human body? How it is overcomed?
Answer:
A chemical signal in the form of hormones would reach all cells of the body and provide the wide range of changes needed while nervous system in human body works or communicates using nerve impulses which are form of electrical impulses in limited nerve network. Electrical impulses are an excellent means of communication in human body but they have limitations like:

• They reach only those cells that are connected by nervous tissue, not each and every cell in the animal body.
• Cells cannot continually create and transmit electrical impulses.
• Hormone or endocrine system is slower than nerve cells but potentially reach all cells of the body.

Question 2.
Why is the use of iodised salt advised? Why are some patients of diabetes treated by giving injections of insulin?
Answer:
It is advised to use iodised salt to prevent goiter (enlargement of the thyroid gland). Iodine is required for the proper functioning of thyroid. Iodine stimulates the thyroid gland to produce thyroxine hormone. This hormone regulates carbohydrate, fat and protein metabolism in our body. Diabetes is a condition in which sugar level in blood is very high. Insulin hormone is released by pancreas glands which regulates the blood sugar level.

In diabetic patients, pancreas stop releasing insulin hormone. If it is not secreted in proper amounts, the sugar level in the blood rises causing many harmful effects. Due to this reason, diabetic patients are treated by giving injections of insulin. The timing and amount of hormone released are regulated by feedback mechanisms. When the sugar levels in blood rise, they are detected by the cells of the pancreas which respond by producing more insulin. As the blood sugar level falls, insulin secretion is reduced.

Question 3.
How does adrenaline act during emergency?
Answer:
During emergency situations, adrenaline hormone is released into blood stream in large quantities. It increases the heartbeat and hence supplies more oxygen to the muscles. The increase in breathing rate also increases due to contractions of diaphragm and rib muscles. It raises the blood pressure and thus, enable the body to cope up with any stress or emergency. Adrenaline hormone is secreted by the adrenal glands. It helps to regulate heart beat, blood pressure and metabolism in the times of stress or emergency to cope up with the situation.

Question 4.
What happens at the synapse between two neurons?
Answer:
Synapse is a very small gap between the last portion of axon of one neuron and the dendron of the other neuron. It acts as a one way valve to transmit impulses. This is one directional flow of impulses because the chemicals are produced only on one side of the neuron i.e., the axon’s side. Via axon, the impulses travel across the synapse to the dendron of the other neuron.

In total, synapse performs the following tasks:

1. It allows the information to pass from one neuron to another.
2. It ensures the passage of nerve impulse in one direction only.
3. It helps in information processing by combining the effects of all impulses received.

Question 5.
How do we detect the smell of any food?
Answer:
The fore-brain is the main thinking part of the brain. It has regions which receive sensory impulses from various receptors. Separate areas of the fore-brain are specialised for hearing, smell, sight and so on. Olfactoreceptors (present in nose) send the information about the smell of incense stick to fore-brain. The fore-brain interprets it along with information received from other receptors as well as with information that is already stored in the brain.

MP Board Class 10th Science Chapter 7 Textbook Activities

Class 10 Science Activity 7.1 Page No. 115

• Put some sugar in your mouth. How does it taste
• Block your nose by pressing it between your thumb and index finger. Now eat sugar again. Is there any difference in its taste.
• While eating lunch, block your nose in the same way and notice if you can fully appreciate the taste of the food you are eating.

Observations:

• The sugar tastes sweet. The taste is combined perception of tongue and nose.
• When we block our nose, the sugar taste different as now aroma through nose is hindering in proxiding the taste fell earlier. The olfactory receptors of nose are now blocked and we perceixe taste only due to gustatory receptors piesent on tongue.
• Similarly, taste of the food also can not be fully appreciated with blocked nose.

Class 10 Science Activity 7.2 Page No. 121

• Fill a conical flask with water.
• Cover the neck of the flask w’ith a wire mesh.
• Keep two or three freshly germinated bean seeds on the wire mesh.
• Take a cardboard box which is open from one side.
• Keep the flask in the box in such a manner that the open side of the box faces light coming from a window.

• After two or three days, you will notice that the shoots bend towards light and roots away from light.
• Now turn the flask so that the shoots arc away from light and the roots towards light. Leave it undisturbed in this condition for a few days.
• Have the old parts of the shoot and root changed direction?
• Are there differences in the direction of the new growth?
• What can we conclude from this activity?

Observations:

• The old parts of shoot and root does not show’ noticeable changes in the direction.,
• The new’ growth of parts of shoot and root show noticeable changes in the direction of the growth. Shoots bend towards light and roots bend away from it.
• From this activity, we can conclude that shoot shows phototropism and the roots show geotropism.

Class 10 Science Activity 7.3 Page No. 123

• Look at Figure.
• Identify the endocrine glands mentioned in the figure.
• Some of these glands have been listed in Table and discussed in the text. Consult books in the library and discuss with your teachers to find out about other glands.

Endocrine glands in human beings (a) male, (b) female.

Observations:

• The endocrine glands mentioned in the figure are: Hypothalamus, pituitary, pineal, thymus. Thyroid gland, parathyroid, adrenal, pancreas, testes and ovaries.

Class 10 Science Activity 7.4 Page No. 125

• Hormones are secreted by endocrine glands and have specific fifhctions. Complete Table 7.1 based on the hormone, the endocrine gland or the functions provided.

Some important hormones and their functions.

MP Board Class 10th Science Solutions

In this article, we will share MP Board Class 10th Maths Book Solutions Chapter 14 Statistics Ex 14.3 Pdf, These solutions are solved subject experts from the latest edition books.

MP Board Class 10th Maths Solutions Chapter 14 Statistics Ex 14.3

Question 1.
The following frequency distribution gives the monthly consumption of electricity of 68 consumers of a locality. Find the median, mean and mode of the data and compare them.

Solution:
Median:
Let us prepare a cumulative frequency table:

Now, we have N = 68 ⇒ \(\frac{N}{2}=\frac{68}{2}\) = 34
The cumulative frequency just greater than 34 is 42 and it corresponds to the class 125 – 145.
∴ 125 – 145 is the median class.
∴ l = 125, cf = 22, f= 20 and h = 20
Using the formula,
Median = l + \(\left[\frac{\frac{N}{2}-c f}{f}\right] \) × h
= 125 + \(\left[\frac{34-22}{20}\right]\) × 20
= 125 + \(\frac{12}{20}\) × 20 = 125 + 12 = 137 units.
Mean: Let assumed mean, a = 135
∵ Class size, h = 20
∴ u_i = \(\frac{x_{i}-a}{h}=\frac{x_{i}-135}{20}\)
Now, we have the following table:

∴ \(\overline{x}\) = a + h × [\(\frac{1}{N}\) Σf_iu_i] = 135 + 20 × \(\frac{7}{68}\)
= 135 + 2.05 = 137.05 units.
Mode:
∵ Class 125 – 145 has the highest frequency i.e., 20.
∴ 125 – 145 is the modal class.
We have: h = 20, l = 125 , f₁ = 20, f₀ = 13, f₂ = 14

We observe that the three measures are approximately equal.

Question 2.
If the median of the distribution given below is 28.5, find the values of x and y.

Solution:
Here, we have N = 60
Now, cumulative frequency table is:

Since, median = 28.5 (Given)
∴ Median class is 20 – 30 and l = 20, f = 20, cf = 5 + x, N = 60
∴ l + \(\left[\frac{\frac{N}{2}-c f}{f}\right] \) × h
⇒ 28.5 = 20 + \(\left[\frac{30-(5+x)}{20}\right]\) × 10
⇒ 28.5 = 20 + \(\frac{25-x}{2}\)
⇒ 57 = 40 + 25 – x
⇒ x = 40 + 25 – 57 = 8
Also, 45 + x + y = 60
⇒ 45 + 8 + y = 60
⇒ y = 60 – 45 – 8 = 7.
Thus x = 8, y = 7

Question 3.
A life insurance agent found the following data for distribution of ages of 100 policy holders. Calculate the median age, if policies are given only to persons having age 18 years onwards but less than 60 year.

Solution:
The given table is cumulative frequency distribution. We write the frequency distribution as given below :

∵ The cumulative frequency just greater than 50 is 78.
∴ The median class is 35 – 40.
Now, \(\frac{N}{2}\) = 50, l = 35, cf = 45, f = 33 and h = 5

Thus, the median age = 35.76 years.

Question 4.
The lengths of 40 leaves of a plant are measured correct to the nearest millimeter, and the data obtained is represented in the following table:

Find the median length of the leaves.
[Hint: The data needs to be converted to continuous classes for finding the median, since the formula assumes continuous classes. The classes then change to 117.5-126.5,
126.5 – 135.5 ………… 171.5 – 180.5.]
Solution:
After changing the given table as continuous classes we prepare the cumulative frequency table as follows:

The cumulative frequency just above 20 is 29 and it corresponds to the class 144.5 – 153.5.
So, 144.5 – 153.5 is the median class.
We have: \(\frac{N}{2}\) = 20, l = 144.5, f= 12, cf = 17 and h = 9
∴ Median = l + \(\left[\frac{\frac{N}{2}-c f}{f}\right] \) × h
= 144.5 + \(\left[\frac{20-17}{12}\right]\) × 9
= 144.5 + \(\frac{3}{12}\) × 9 = 144.5 + \(\frac{9}{4}\)
= 144.5 + 2.25 = 146.75
Median length of leaves = 146.75 mm.

Question 5.
The following table gives the distribution of the life time of 400 neon lamps:

Find the median life time of a lamp.
Solution:
To compute the median, let us write the cumulative frequency distribution as given below:

Since, the cumulative frequency just greater than 200 is 216.
∴ The median class is 3000-3500 and so l = 3000, cf= 130, f = 86, h = 500
∴ Median = l + \(\left[\frac{\frac{N}{2}-c f}{f}\right] \) × h
= 3000 + \(\left[\frac{200-130}{86}\right]\) × 500
= 3000 + \(\frac{70}{86}\) × 500 = 3000 + \(\frac{35000}{86}\)
= 3000 + 406.98 = 3406.98
Thus, median life time of a lamp = 3406.98 hours.

Question 6.
100 surnames were randomly picked up from a local telephone directory and the frequency distribution of the number of letters in the English alphabets in the surnames was obtained as follows:

Determine the median number of letters in the surnames. Find the mean number of letters in the surnames? Also, find the modal size of the surnames.
Solution:
Median: The cumulative frequency distribution table is as follows:

Since, the cumulative frequency just greater than 50 is 76.
∴ The class 7-10 is the median class.
We have, \(\frac{N}{2}\) = 50 , f = 7, cf = 36, f = 40 and h = 3

Mode:
Since the class 7 – 10 has the maximum frequency i.e., 40.
∴ The modal class is 7 – 10.
So, we have l = 7,h = 3, f₁ = 40, f₀ = 30, f₂ = 16

Thus, the required median = 8.05, mean = 8.32 and mode = 7.88.

Question 7.
The distribution below gives the weights of 30 students of a class. Find the median weight of the students.

Solution:
We have cumulative frequency table as follows:

The cumulative frequency just greater than 15 is 19, which corresponds to the class 55 – 60.
So, median class is 55-60 and we have \(\frac{N}{2}\) = 15,
l = 55, f = 6, cf = 13 and h = 5

Thus, the required median weight of the students = 56.67 kg.

In this article, we will share MP Board Class 10th Maths Book Solutions Pair of Linear Equations in Two Variables Ex 3.5 Pdf, These solutions are solved subject experts from the latest edition books.

MP Board Class 10th Maths Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.5

Question 1.
Which of the following pairs of linear equations has unique solution, no solution, or infinitely many solutions. In case there is a unique solution, find it by using cross multiplication method.
(i) x – 3y – 3 = 0; 3x – 9y – 2 = 0
(ii) 2x + y = 5; 3x + 2y = 8
(iii) 3x – 5y = 20; 6x -10y = 40
(iv) x – 3y – 7 = 0; 3x – 3y – 15 = 0
Solution:
(i) For x – 3y – 3 = 0, 3x – 9y – 2 = 0
∴ a₁ = 1, b₁ = – 3, C₁ = – 3, a₂ = 3, b₂ = – 9, C₂ = -2

∴ The given system has no solution.

(ii) 2x + y – 5 = 0, 3x + 2y – 8 = 0
∴ a₁ = 2, b₁ = 1, c₁ = -5, a₂ = 3, b₂ = 2, c₂ = -8

∴ The given system has a unique solution.
Now, using cross multiplication method, we have

(iii) For 3x – 5y – 20 = 0, 6x – 10y – 40 = 0

∴ The given system of linear equation has infinitely many solutions

(iv) For x – 3y – 7 = 0, 3x – 3y – 15 = 0

∴ The given statement has unique solution. Now, using cross multiplication method, we have

Question 2.
(i) For which values of a and b does the following pair of linear equations have an infinite number of solutions ?
2x + 3y = 7; (a – b) x + (a + b) y = 3a + b – 2
(ii) For which value of k will the following pair of linear equations have no solution ?
3x + y = 1; (2k – 1) x + (k – 1) y = 2k + 1
Solution:
(i) We have, 2x + 3y = 7 and
(a – b) x + (a + b) y = (3a + b – 2)
⇒ 2x + 3y – 7 = 0
and (a – b) x + (a + b) y -(3a + b – 2) = 0
a₁ = 2, b₁ = 3, c₁ = – 7, a₂ = (a- b) , b₂ = (a + b) , c₂ = -(3a + b – 2)
For infinite number of solutions,

From the first two equations, we get

Question 3.
Solve the following pair of linear equations by the substitution and cross-multiplication methods: 8x + 5y = 9; 3x + 2y = 4
Solution:
Method-1 [Substitution method]:
8x + 5y = 9 … (1)
3x + 2y = 4 … (2)

Question 4.
Form the pair of linear equations in the following problems and find their solutions (if they exist)by any algebraic method:
(i) A part of monthly hostel charges is fixed and the remaining depends on the number of days one has taken food in the mess. When a student A takes food for 20 days she has to pay ₹ 1000 as hostel charges whereas a student B, who takes food for 26 days, pays ₹ 1180 as hostel charges. Find the fixed charges and the cost of food per day.
(ii) A fraction becomes 1/3 when 1 is subtracted from the numerator and it becomes 1/4 when 8 is added to its denominator. Find the fraction.
(iii) Yash scored 40 marks in a test, getting 3 marks for each right answer and losing 1 mark for each wrong answer. Had 4 marks been awarded for each correct answer and 2 marks been deducted for each incorrect answer, then Yash would have scored 50 marks. How many questions were there in the test?
(iv) Places A and B are 100 km apart on a highway. One car starts from A and another from B at the same time. If the cars travel in the same direction at different speeds, they meet in 5 hours. If they travel towards each other, they meet in 1 hour. What are the speeds of the two cars?
(v) The area of a rectangle gets reduced by 9 square units, if its length is reduced by 5 units and breadth is increased by 3 units. If we increase the length by 3 units and the breadth by 2 units, the area increases by 67 square units. Find the dimensions of the rectangle.
Solution:
(i) Let the fixed charges = ₹ x
and charges of food per day = ₹ y
For student A : Number of days = 20
∴ Cost of food for 20 days = ₹ 20y
According to the problem,
x + 20y = 1000
⇒ x + 20y – 1000 = 0 …. (1)
For student B : Number of days = 26
Cost of food for 26 days = ₹ 26y
According to the problem,
x + 26y = 1180
⇒ x + 26y – 1180 = 0 … (2)
Solving these by cross multiplication, we get

Thus x = 400 and y = 30
∴ Fixed charges = ₹ 400
and cost of food per day = ₹ 30

(ii) Let the numerator = x
and the denominator = y

From equations (1) and (2) , we have

(iii) Let the number of correct answers = ₹ x
and the number of wrong answers = ₹ y
Case-I: Marks for all correct answers
= (3 × x) = 3x
Mark for all wrong answers = (1 × y) = y
∴ According to the condition :
3x – y = 40 ⇒ 3x – y – 40 = 0
Case-II: Mark for all correct answers
= (4 × x)=
Marks for all wrong answers = (2 × y)
= 2y
∴ According to the condition :
4x – 2y = 50
⇒ 2x – y = 25 ⇒ 2x – y – 25 = 0 … (2)
From (1)and (2) , we have a₁ = 3, b₁ = -1, c₁ = -40, a₂ = 2, b₂ = -1, c₂ = -25

Now, total number of questions = [Number of correct answers] + [Number of wrong answers]
= 15 + 5 = 20
Thus, required number of questions = 20.

(iv) Let the speed of car-I be x km/hr.
and the speed of car-II be y km/hr.
Case-I:

Distance travelled by car-I = AC
∵ AC = time × speed = 5 × x km, AC = 5x
Distance travelled by car-II, BC = 5y
Since AB = AC – BC,
100 = 5x – 5y
⇒ 5x – 5y – 100 = 0
⇒ x – y – 20 = 0 …. (1)


Thus, speed of car-I = 60 km/hr
Speed of car-II = 40 km/hr

(v) Let the length of the rectangle = x units
and the breadth of the rectangle = y units
∴ Area of rectangle = x × y = xy

Condition-II:
(Length + 3) × (Breadth + 2) = Area + 67
⇒ (x + 3) (y + 2)= xy + 67 ⇒ 2x + 3y + 6 = 67
⇒ 2x + 3y – 61 = 0….(2)
Now, using cross multiplication method in (1)and (2) , where

Thus, length of the rectangle = 17 units and breadth of the rectangle = 9 units.

MP Board Class 10th Science Solutions Chapter 5 Periodic Classification of Elements

MP Board Class 10th Science Chapter 5 Intext Questions

Intext Questions Page No. 81

Question 1.
Did Dobereiner’s triads also exist in the columns of Newlands’ Octaves? Compare and find out.
Answer:
In Newland’s Octaves, the properties of lithium and sodium were found to be the same. This arrangement is also found in Dobereiner triads.

Question 2.
What were the limitations of Dobereiner’s classification?
Answer:
Dobereiner could identify only three ‘triads’ from the elements known at that time. Hence this system of classification into triads was not found to be useful.

Question 3.
What were the limitations of Newlands’ Law of Octaves?
Answer:

The Limitations of Newlands’ Law of Oclaves is as follows:

1. It was found that the Law of Octaves was applicable only upto calcium, as after calcium every eighth element did not possess properties similar to that of the first.
2. It was assumed by Newlands’ that only 56 elements existed in nature and no more elements would be discovered in the future. But later on, several new elements were discovered, whose properties did not fit into the Law of Octaves.
3. In order to fit elements into his Table, Newlands adjusted two elements in the same slot, but also put some unlike elements under the same note.

Intext Questions Page No. 85

Question 1.
Use Mendeleev’s Periodic Table to predict the formulae for the oxides of the following elements: K, C, Al, Si, Ba.
Answer:

1. K is in I group. Its oxide is K₂O
2. C, is in IV group, its oxide is CO₂
3. Al, is in III group, its oxide is Al₂O₃
4. Si, is IV group, its oxide is SiO₂
5. Ba, is in II group, its oxide is BaO

Question 2.
Besides gallium, which other elements have since been discovered that were left by Mendeleev in his Periodic Table? (any two)
Answer:
Scandium and germanium.

Question 3.
What were the criteria used by Mendeleev in creating his Periodic Table?
Answer:
Mendeleev used the relationship between the atomic masses of the elements and their physical and chemical properties. Among chemical properties, he examined the compound formed by elements with oxygen and hydrogen. He found that if the 63 elements known at that time were arranged in the increasing order of their atomic masses, the properties of elements and also formulae of their oxides and hydrides gradually changed from element to element and at a certain interval they suddenly started almost repealing relationship was expressed by Mendeleev’s periodic law. i,e the properties of examinants are the periodic functions of their atomic masses.

Question 4.
Why do you think the noble gases are placed in a separate group?
Answer:
All noble gases are inert elements. Their properties are different from other elements and are the least reactive. Therefore, the noble gases are placed in a separate group.

Intext Questions Page No. 90

Question 1.
How could the Modern Periodic Table remove various anomalies of Mendeleev’s Periodic Table?
Answer:

1. In the Modern periodic Table atomic number of an elements is a more fundamental property than its atomic mass.
2. The anomalous position of hydrogen can be discussed after we see what are the basis on which the position of an elements in the Modern Periodic Table depends.
3. The elements present in any one group have the same number of valence electrons.
4. Atoms of different elements with the same number of occupied shells are placed in the same period.
5. In the Modern Periodic Table, a zig-zag line separated metals from non-metals.

Question 2.
Name two elements you would expect to show chemical reactions similar to magnesium. What is the basis for your choice?
Answer:
Calcium (Ca) and Strontium (Sr) is expected to show chemical reactions similar to magnesium (Mg). This is because the number of valence electrons (2) is the same in all of these three elements and since chemical properties are due to valence electrons, they show the same chemical reactions.

Question 3.
Name:

1. Three elements that have a single electron in their outermost shells.
2. Two elements that have two electrons in their outermost shells.
3. Three elements with filled outermost shells.

Answer:

1. Lithium (Li), Sodium (Na), and Potassium (K) has a single electron in their outermost shells.
2. Magnesium (Mg) and Calcium (Ca) have two electrons in their outermost shells.
3. Neon (Ne), Argon (Ar), and Xenon (Xe) have filled outermost shells.

Question 4.
Lithium, sodium, potassium are all metals that react with water to liberate hydrogen gas. Is there any similarity in the atoms of these elements?
Answer:

Lithium, sodium and potassium – These three elements have one electron in their outermost orbit.

b) Helium is an unreactive gas and neon is a gas of extremely low reactivity. What, if anything, do their atoms have in common?
Answer:
Both helium (He) and neon (Ne) have filled outermost shells. Helium has a duplet in its K shells, while neon has an octet in its L shells.

Question 5.
In the Modern Periodic Table, which are the metals among the first ten elements?
Answer:
In the modem periodic table, Lithium and Beryllium are the metals among the first 10 elements.

Question 6.
By considering their position in the Periodic Table, which one of the following elements would you expect to have maximum metallic characteristic?
Ga Ge As Se Be
Answer:
Since, ‘Be’ lies to the extreme left-hand side of the periodic table, ‘Be’ is the most metallic among the given elements.

MP Board Class 10th Science Chapter 5 Ncert Textbook Exercises

Question 1.
Which of the following statements is not a correct statement about the trends when going from left to right across the periods of the periodic table.
(a) The elements become less metallic in nature.
(b) The number of valence electrons increases.
(c) The atoms lose their electrons more easily.
(d) The oxides become more acidic.
Answer:
(c) The atoms lose their electrons more easily.

Question 2.
Element X forms a chloride with the formula XCl₂, which is solid with a high melting point. X would most likely be in the same group of the Periodic table as:
(a) Na
(b) Mg
(c) Al
(d) Si
Answer:
(b) Mg

Question 3.
Which element has:
(a) two shells, both of which are completely filled with electrons?
(b) Electronic configuration 2, 8, 2?
(c) a total of three shells, with four electrons in its valence shell?
(d) a total of two shells, with three electrons in its valence shell?
(e) twice as many electrons in its second shell as in its first shell?
Answer:
(a) Neon
(b) Magnesium
(c) Silicon
(d) Boron
(e) Carbon

Question 4.
(a) What property do all elements in the same column of the Periodic table as Boron have in common?
(b) What property do all elements in the same column of the Periodic table as Fluorine have in common?
Answer:
(a) Valency equal to 3.
(b) Valency equal to 1.

Question 5.
An atom has electronic configuration 2, 8, 7.
(a) What is the atomic number of this element?
(b) To which of the following elements would it be chemically similar? (Atomic numbers are given in parentheses.)
N(7) F(9) P(15) Ar(18)
Answer:
(a) The atomic number of this element is 17.
(b) It would be chemically similar to F(9) with configuration as 2, 7.

Question 6.
The position of three elements A, B and C in the Periodic table is shown below:

(a) State whether A is a metal or non-metal.
(b) State whether C is more reactive or less reactive than A.
(c) Will C be larger or smaller in size than B?
(d) Which type of ion, cation or anion, will be formed by element A?
Answer:
(a) A is a non-metal.
(b) C is less reactive than A because reactivity decreases down the group in halogens.
(c) C should be smaller in size than B as moving across a period, the nuclear charge increases and therefore, electrons come closer to the nucleus.
(d) A will form an anion as it will accept an electron to complete its octet.

Question 7.
Nitrogen (atomic number 7) and phosphorus (atomic number 15) belong to group 15 of the Periodic Table. Write the electronic configuration of these two elements. Which of these will be more electronegative? Why?
Answer:
Nitrogen (7) : 2, 5
Phosphorus (15) : 2, 8, 5
Nitrogen is more electronegative because Metallic character decreases across a period and increased down a group.

Question 8.
How does the electronic configuration of an atom relate to its position in the Modern Periodic table?
Answer:
In the modern periodic table, atoms with similar electronic configurations are placed in the same column. In a group, the number of valence electrons remains the same. Elements across a period show an increase in the number of valence electrons.

Question 9.
In the Modern Periodic table, calcium (atomic number 20) is surrounded by elements with atomic numbers 12, 19, 21, and 38. Which of these have physical and chemical properties resembling calcium?
Answer:
The element with atomic number 12 has the same chemical properties as that of calcium. This is because both of them have same number of valence electrons (2).

Question 10.
Compare and contrast the arrangement of elements in Mendeleev’s Periodic table and the Modern Periodic table.
Answer:

Mendeleev s Periodic table:

1. 1. Elements are arranged in the increasing order of their atomic mass.
   2. This table has 8 groups and 6 periods. And each group is subdivided as an A and B.
   3. In this table, Hydrogen has no position.
   4. No position for isotopes, because in Mendeleev period these are not discovered.

Modern Periodic table:

1. 1. Elements are arranged in the increasing order of their atomic number.
   2. It has 18 groups and 7 periods.
   3. Inert gases are placed in separate groups.
   4. In this table, a zigzag line separates Metals from Non-metals.

(or)

Mendeleev’s Periodic table vs Modern Periodic table:

1. Elements are arranged in the increasing order of their atomic masses, while in Modern Periodic table elements are arranged in the increasing order of their atomic numbers.
2. There are a total of 7 groups (columns) and 6 periods (rows) while in Mendeleev’s’ Periodic Table, there are a total of 18 groups (columns) and 7 periods (rows).
3. Elements having similar properties were placed directly under one another, while in Mendeleev’s’ Periodic Table elements having the same number of valence electrons are present in the same group.
4. In Mendeleev’s Periodic Table the position of hydrogen could not be explained, while in Modern Periodic table hydrogen is placed above alkali metals.
5. No distinguishing positions for metals and non-metals in Mendeleev’s Periodic Table while in Modern Periodic Table metals are present at the left-hand side of the periodic table whereas nonmetals are present at the right-hand side.

MP Board Class 10th Science Chapter 5 Additional Questions

MP Board Class 10th Science Chapter 5 Multiple Choice Questions

Question 1.
Which of the following statements is correct about the trends when going down in a group of the periodic table?
(a) Elements become less electropositive in nature.
(b) Element oxides become more acidic.
(c) Valence electrons increases.
(d) Elements lose their electrons more easily.
Answer:
(d) Elements lose their electrons more easily.

Question 2.
Element A forms a chloride with the formula ACl₃, which is a stable compound. A would most likely be the same group of the Periodic Table as –
(a) Na
(b) Mg
(c) Al
(d) Si
Answer:
(c) Al

Question 3.
Which of the following are coin metals?
(a) Ne, Ca, Na
(b) H₂, N₂, O₂
(c) Li, Na, K
(d) Cu, Au, Ag
Answer:
(d) Cu, Au, Ag

Question 4.
Who gave the triad arrangement of elements?
(a) Mendeleev
(b) Newlands
(c) Dalton
(d) Dobereiner
Answer:
(d) Dobereiner

Question 5.
Newlands periodic table is based on the
(a) Atomic weight
(b) Atomic number
(c) Atomic radius
(d) Atomic volume
Answer:
(a) Atomic weight

Question 6.
Which of the following is not gas in normal atmospheric condition?
(a) Helium (He)
(b) Argon (Ar)
(c) Bromine (Br)
(d) Chlorine (Cl)
Answer:
(c) Bromine (Br)

Question 7.
While moving left to right across a period, the atomic radii –
(a) Remains the same
(b) Approaches zero
(c) Decreases
(d) Increases first then decreases
Answer:
(c) Decreases

Question 8.
Which element is a metalloid?
(a) Carbon
(b) Nitrogen
(c) Oxygen
(d) Silicon
Answer:
(d) Silicon

Question 9.
Moseley’s periodic table is based on
(a) Atomic mass
(b) Mass number
(c) Atomic number
(d) Atomic volume
Answer:
(c) Atomic number

Question 10.
Which of the following is a group of highly electronegative elements?
(a) Cl, Br, I
(b) S, Se, Te
(c) Na, K, Rb
(d) Ca, Sr, Ba
Answer:
(a) Cl, Br, I

Question 11.
Which of the following elements is a non-metal?
(a) Aluminium
(b) Chlorine
(c) Sodium
(d) Silicon
Answer:
(b) Chlorine

Question 12.
As we move down in a group in Modern Periodic Table, the size of elements generally
(a) increases
(b) decreases
(c) remain the same
(d) first, increase then decrease
Answer:
(a) increases

Question 13.
As we move from top to bottom in a group in Modern Periodic Table, the electronegativity of elements
(a) Increases
(b) Decreases
(c) No change
(d) Not certain
Answer:
(b) Decreases

Question 14.
Which group of elements is considered most electropositive?
(a) Group 1
(b) Group 2
(c) Group 17
(d) Group 18
Answer:
(a) Group 1

Question 15.
Group 1 elements are also called as:
(a) Alkali metals
(b) Alkaline earth metals
(c) Halogens
(d) Noble gases
Answer:
(a) Alkali metals

Question 16.
Group 17 elements are also called as:
(a) Alkali Metals
(b) Alkaline Earth Metals
(c) Halogens
(d) Noble Gases
Answer:
(c) Halogens

Question 17.
How many elements were known when Mendeleev started his work?
(a) 100
(b) 215
(c) 65
(d) 80
Answer:
(c) 65

Question 18.
Why Mendeleev left spaces in his Periodic Table?
(a) A mistake
(b) For future elements
(c) For Isotopes
(d) For Isobars
Answer:
(b) For future elements

Question 19.
Why Lanthanoids and Actinoids are placed below in the Periodic Table?
(a) A mistake
(b) Better representation and view
(c) They were found very recently
(d) All of the above
Answer:
(c) They were found very recently

Question 20.
A period may have elements with –
(a) Variable atomic sizes
(b) Variable atomic number
(c) Variable valency
(d) All of the above
Answer:
(d) All of the above

Question 21.
Element A belongs to group 15. The formula of its hydride will:
(a) AH
(b) AH₂
(c) AH₃
(d) A₃H
Answer:
(c) AH₃

Question 22.
An electropositive element, A with 2 valence electron will form which type of oxide?
(a) AO
(b) A₂O
(c) AO₂
(d) AO₃
Answer:
(a) AO

Question 23.
Most electronegative element in our Periodic Table:
(a) Iron
(b) Nitrogen
(c) Carbon
(d) Flourine
Answer:
(d) Flourine

Question 24.
Which of the following elements where not among metals/elements named to fill the gap of Mendeleev’s Periodic Tablespaces?
(a) Cobalt
(b) Scandium
(c) Gallium
(d) Germanium
Answer:
(a) Cobalt

Question 25.
In a group, all elements have similar ………..
(a) Electronic configuration
(b) Valence electron
(c) Electronegativity
(d) All of these
Answer:
(b) Valence electron

Question 26.
Which among the following is a noble gas?
(a) C
(b) N
(c) O
(d) Ne
Answer:
(d) Ne

Question 27.
Which of the following elements has electronic configuration E = 2, 6?
(a) C
(b) N
(c) O
(d) Ne
Answer:
(c) O

Question 28.
Which of the following elements is a metalloid?
(a) B
(b) Al
(c) S
(d) P
Answer:
(a) B

Question 29.
Which of the following is not a halogen?
(a) Br
(b) I
(c) Te
(d) At
Answer:
(c) Te

Question 30.
Which element has a total of two shells, with four valence electrons?
(a) C
(b) N
(c) Br
(d) Co
Answer:
(a) C
(ii) Match column A’s description with column B’s Particulars.

Answers:

1. → 12
2. → 3
3. → 2
4. → 4
5. → 5
6. → 13
7. → 11
8. → 14
9. → 10
10. → 10
11. → 6
12. → 1
13. → 7
14. → 8

MP Board Class 10th Science Chapter 5 Very Short Answer Type Questions

Question 1.
What would be the maximum number of electrons present in the outermost shell of atoms in the first period of Periodic Table?
Answer:
Two

Question 2.
What is Solder?
Answer:
It is an alloy of lead (Pb) and tin (Sn).

Question 3.
What is anode mud?
Answer:
During electrolytic refining, the soluble impurities go into the solution, Whereas, the insoluble impurities settle down at the bottom of anode and are known as anode mud.

Question 4.
Which metal is used with iron oxide to join railway tracks or cracked machine parts?
Answer:
Aluminium.

Question 5.
Give the thermit reaction.
Answer:
Fe₂O₃(s) + 2Al(s) → 2 Fe(l) + Al₂O₃(s) + Heat

Question 6.
Roasting is used for the extraction of which ore?
Answer:
Sulphide ore.

Question 7.
Name the metal lowest inactivity series (relative reactivities of metals).
Answer:
Au or Gold.

Question 8.
Which gas is evolved when a metal reacts with nitric acid?
Answer:
Hydrogen gas.

Question 9.
Name any two metal that does not react with water at all.
Answer:
Lead, copper, gold, silver. (any two)

Question 10.
Complete the following reaction: Metal oxide + water →.
Answer:
Metal hydroxide.

Question 11.
Which material is used to coat electric wires in homes?
Answer:
PVC or Polyvinylchloride.

Question 12.
Name any two metals that are poor conductors of heat.
Answer:
Lead and mercury.

MP Board Class 10th Science Chapter 5 Short Answer Type Questions

Question 1.
What are the limitations of the Modern Periodic Table?
Answer:
The limitations of the Modern Periodic Table:
Position of hydrogen still dicey. It is not fixed till now. Position of lanthanides and actinides has not been given inside the main body of the Periodic Table. It does not reflect the exact distribution of electrons of some of the transition and inner transition elements.

Question 2.
Two elements X and Y have atomic numbers 12 and 16 respectively. Write the electronic configuration for these elements. To which period of the Modern Periodic Table do these two elements belong? What type of bond will be formed between them and why?
Answer:
Electronic configuration of X (Z= 12): 2, 8,2
Electronic configuration of Y (Z = 16): 2, 8,6
Both these elements belong to the third period. An ionic bond is formed between X and Y due to the transfer of two electrons from X to Y.

Question 3.
The present classification of elements is based on which fundamental property of elements?
Answer:
Atomic number.

Question 4.
Li, Na and K are the elements of a Dobereiner’s Triad. If the atomic mass of Li is 7 and that of K is 39, what would be the atomic mass of Na?
Answer:
According to of Dobereiner’s law of triads, the atomic mass of the middle element, in this case, Na, should be the arithmetic mean of Li and K. Thus, Arithmetic mean of Li and K = (7 + 39)/2 = 23.

Question 5.
Define Dobereiner’s law of triads.
Answer:
It states, “When elements are placed in order of the ascending order of atomic masses, groups of three elements having similar properties are obtained. The atomic mass of the middle element of the triad is equal to the mean of the atomic masses of the other two elements of the triad.”

Question 6.
Why did Dobereiner’s system of classification fail?
Answer:
The major drawback of Döbereiner’s classification was that it was valid only for a few groups of elements known during that time. He was able to identify three triads only. Also, more accurate measurements of atomic masses showed that the mid element of the triad did not really have the mean value of the sum of the other two elements of the triad. For elements of very low mass or very high mass, the law did not hold good. For example, Fluorine (F), Chlorine (Cl), Bromine (Br). The atomic mass of Cl is not an arithmetic mean of atomic masses of F and Br.

Question 7.
Explain the position of metalloids in the Modern Periodic Table.
Answer:
In the Modern Periodic Table, a zig-zag line separates metals from non-metals. The borderline elements – boron, silicon, germanium, arsenic, antimony, tellurium and polonium – are intermediate in properties and are called metalloids or semi-metals.

Question 8.
Why silicon is classified as metalloid?
Answer:
Silicon is classified as a semi-metal or metalloid because it exhibits some properties of both metals and non-metals.

Question 9.
State Newlands law of octaves.
Answer;
Elements are arranged in increasing order of their atomic masses such that the properties of the eighth element are the repetition of the properties of the first element (similar to eighth note in an octave of music).

Question 10.
X and Y are the two elements having similar properties which obey Newlands law of octaves. How many elements are there in between X and Y?
Answer:
The law states there are eight elements in an octave (row). A number of elements between X and Y are six.

Question 11.
What are the drawbacks of Newlands law of octaves?
Answer:
Following are the major drawbacks:

1. Worked well with lighter elements (upto calcium. After those elements in the eighth column did not possess properties similar to elements in the first column.
2. Newland assumed only 56 elements existed so far. Later, new elements were discovered which did not fit into octaves table.
3. Newland adjusted few elements in the same slot through their properties were quite different, e.g., Cobalt and nickel are in the same slot and these are placed in the same column as fluorine, chlorine and bromine which have very different properties than these elements. Iron, which resembles cobalt and nickel in properties, has been placed far away from these elements.

MP Board Class 10th Science Chapter 5 Long Answer Type Questions

Question 1.
What are the salient features of the Modern Periodic Table?
Answer:
In a period of the Periodic Table, the number of valence electrons increases as the atomic number increases. As a result, elements change from metal to metalloid to nonmetal to a noble gas. Atomic size is a periodic property. As atomic number increases in a period, the atomic radius decreases. As atomic number increases in a group, atomic radius increases.

Positive ions have smaller atomic radii than the neutral atoms from which they derive. Negative ions have larger atomic radii than their neutral atoms. Positive ions in the same group increase in size down the group. In a group, each element has the same number of valence electrons. As a result, the elements in a group show similar chemical behaviour.

Metallic character decreases from left to right in a period because of the increase in the effective nuclear charge. Non-metallic character increase from left to right in a period because of the increase in effective nuclear charge. Non-metallic character decreases down the group because of increase in the size of the atom.

Question 2.
What periodic trends do we observe in terms of atomic radii or atomic sizes in Modern Periodic table?
Answer:
Following two trends are observed:
1. Within each column (group), atomic radius tends to increase from top to bottom. This trend results primarily from the increase in the number of the outer electrons. As we go down a column, the outer electrons have a greater probability of being farther from the nucleus, causing the atom to increase in size.

2. Within each row (period), the atomic radius tends to decrease from left to right. The major factor influencing this trend is the increase in the nuclear charge as we move across a row. The increasing effective nuclear charge steadily draws the valence electrons closer to the nucleus, causing the atomic radius to decrease.

Question 3.
An element A with atomic number 19 combines separately with NO₃^–and (SO₄)₂^–,(PO₄)₃^–radicals:
(a) Give the electronic configuration of element A.
(b) Write the formulae of the three compounds so formed.
(c) To which group of the periodic table does the element ‘R’ belong?
(d) Does it form covalent or ionic compound? Why?
Answer:
(a) Electronic configuration of A: 2,8, 8, 1.
(b) Compounds formed are A(NO₃), A₂(SO₄) and K₃(PO₄).
(c) A has one valence electron and hence, it belongs to the first group.
(d) It forms the ionic compound.

Question 4.
Describe types of periods, blocks and trends of periodic properties along periods associated with Modern Periodic Table.
Answer:
Periods:
First period (Atomic number 1 and 2): This is the shortest period. It contains only two elements (hydrogen and helium).

Second Period: (Atomic number 3 to 10): It contains eight elements (lithium to neon).

Third period (Atomic number 11 to 18): It contains eight elements (sodium to argon).

Fourth period (Atomic number 19 to 36): Row contains eighteen elements (potassium to krypton). i.e., 8 normal elements and 10 transition elements.

5th period (Atomic number 37 to 54): Contains 18 elements (rubidium to xenon) includes 8 normal elements and 10 transition elements.

Sixth period (Atomic number 55 to 86): The longest period. It contains 32 elements (caesium to radon) has 8 normal elements, 10 transition elements and 14 inner transition elements (lanthanides).

7th period (Atomic number 87 to 118): As like the sixth period, this period also can accommodate 32 elements. Till now 26 elements have been authenticated by IUPAC.

Blocks in Periodic Table:
The periodic table includes “blocks” defined in terms of which type of orbital is being filled via the Aufbau principle. This gives us the s-block, p-block, d-block, and f-block.

Blocks:
The s-, p-, d-, and f-blocks contain elements with outer electrons in the same type of orbital. Another key link between electron arrangement and position in the periodic table is that elements in any one main group have the same number of electrons in their highest energy level. The number of elements discovered so far is 118. The last element authenticated by IUPAC is Cn112 (Copernicium).

Properties of Periods: As you proceed to the left in a period or as you proceed down within a group:

1. The metallic strength increases (Non-Metallic Strength decreases).
2. The atomic radius increases.
3. The ionization potential decreases.
4. The electron affinity decreases.
5. The electronegativity decreases.

MP Board Class 10th Science Chapter 5 Textbook Activities

Class 10 Science Activity 5.1 Page No. 84

1. Looking at its resemblance to alkali metals and the halogen family, try to assign hydrogen a correct position in Mendeleev’s Period Table.
2. To which group and period should hydrogen be assigned?

Observations:

1. No position can be fixed for hydrogen in the Mendeleev’s Periodic Table.
2. Properties of hydrogen fit with alkali metal as it combines with halogens, oxygen and sulphur to form compounds.
3. Properties of hydrogen also fit or are similar to halogen as it exists in the form of diatomic molecules and combines with metals and non-metals forming covalent compounds.

Class 10 Science Activity 5.2 Page No. 85

1. Consider the isotopes of chlorine, Cl-35 and CI-37.
2. Would you place them in different slots because their atomic masses are different?
3. Or would you place them in the same position because their chemical properties are the same?

Observations:
Two isotopes of chlorine are Cl-35 and Cl-37. Both isotopes have the same chemical properties and hence, both isotopes should be placed in the same position.

Class 10 Science Activity 5.3 Page No. 85

1. How were the positions of cobalt and nickel resolved in the Modern Periodic Table?
2. How were the positions of isotopes of various elements decided in the Modern Periodic Table?
3. Is it possible to have an element with atomic number 1, 5 placed between hydrogen and helium?
4. Where do you think should hydrogen be placed in the Modern Periodic Table?

Observations:
The position of Cobalt and Nickel were decided by placing them in the increasing order of atomic number in the Modern Periodic Table. Since isotopes are elements with the similar atomic number they are placed in the same position as its basic elements in the modern periodic table.

Class 10 Science Activity 5.4 Page No. 87

1. Look at group 1 of the Modern Periodic Table, and name the elements present in it. Write down the electronic configuration of the first three elements of group 1.
2. What similarity do you find in their electronic configurations?
3. How many valence electrons are present in these three elements?

Observations:
Elements present in Group 1 are:

Electronic configuration of the first three elements of Group I are as below:

Class 10 Science Activity 5.6 Page No. 87

1. If you look at the Modern Periodic Table, you will find that the elements Li, Be, B, C, N, O, F, and Ne are present in the second period. Write down their electronic configurations.
2. Do these elements also contain the same number of valence electrons?
3. Do they contain the same number of shells?

Observations:
No, these elements contain variable valence electrons as they belong to different groups:

Class 10 Science Activity 5.6 Page No. 88

1. How do you calculate the valency of an element from its electronic configuration?
2. What is the valency of magnesium with atomic number 12 and sulphur with atomic number 16?
3. Similarly, find out the valencies of the first twenty elements.
4. How does the valency vary in a period on going from left to right?
5. How does the valency vary in going down a group?

Observations:

1. Valency of an element can be calculated by the numbers of valence electron present.
2. Valency of Magnesium: 2
3. Valency of Sulphur: 2 Variation of valency while moving left to right in a period.
   1 → 2 → 3 → 4 → 3 → 2 → 1 → 0
4. Variation of valency while going down in a group does not change.

Class 10 Science Activity 5.7 Page No. 88

1. Atomic radii of the elements of the second period are given below:
   
2. Arrange them in decreasing order of their atomic radii.
3. Are the elements now arranged in the pattern of a period in the Periodic Table?
4. Which elements have the largest and the smallest atoms?
5. How does the atomic radius change as you go from left to right in a period?

Observations:
Decreasing order of atomic radii of following elements:

1. O < N < C < B < Be < Li
2. No in pattern.
3. Oxygen is smallest as per given data while Li is largest.
4. Atomic radius reduces while moving right in a group a, nuclear charge increase.

Class 10 Science Activity 5.8 Page No. 89

1. Study the variation in the atomic radii of first group elements given below and arrange them in increasing order.
   
2. Name the elements which have the smallest and the largest atoms.
3. How does the atomic size vary as you go down a group?

1. Sodium (Na) has the smallest atom and calcium (Ca) has the largest atom.
2. Atomic size increases as we go down a group.

Class 10 Science Activity 5.9 Page No. 89

1. Examine elements of the third period and classify them as metals and non-metals.
2. On which side of the Periodic Table do you find the metals?
3. On which side of the Periodic Table do you find the non-metals?

Observations:
Elements of the third period are:

Class 10 Science Activity 5.10 Page No. 89

1. How do you think the tendency to lose electrons change in a group?
2. How will this tendency change in a period?

Observations:
Metallic property reduces while moving right in a period.

Class 10 Science Activity 5.11 Page No. 90

1. How would the tendency to gain electrons change as you go from left to right across a period? How
2. would the tendency to gain electrons change as you go down a group?

Observations:

1. The electrons increases as we go left to right in a period up to 17th group. It decreases in the 18th
2. group. The tendency of gaining the electrons decreases as we go down a group.

MP Board Class 10th Science Solutions

In this article, we will share MP Board Class 10th Maths Book Solutions Chapter 6 Triangles Ex 6.5 Pdf, These solutions are solved subject experts from the latest edition books.

MP Board Class 10th Maths Solutions Chapter 6 Triangles Ex 6.5

Question 1.
Sides of triangles are given below. Determine which of them are right triangles. In case of a right triangle, write the length of its hypotenuse.
(i) 7 cm, 24 cm, 25 cm
(ii) 3 cm, 8 cm, 6 cm
(iii) 50 cm, 80 cm, 100 cm
(iv) 13 cm, 12 cm, 5 cm
Solution:
(i) The sides are : 7 an, 24 cm, 25 cm
Here, (7 cm)² = 49 cm²
(24 cm)² = 576 cm²
(25 cm)² = 625 cm²
∵ (49 + 576)cm² = 625 cm²
∴ It is a right triangle.
Hypotenuse = 25 cm.

(ii) The sides are: 3 cm, 8 cm, 6 cm
Here, (3 cm)² = 9 cm²
(8 cm)² = 64 cm²
(6 cm)² = 36 cm²
∵ (9 + 36) ≠ 64 cm²
∴ It is not a right triangle.

(iii) The sides are : 50 cm, 80 cm, 100 cm
Here, (50 cm)² = 2500 cm²
(80 cm)² = 6400 cm²
(100 cm)² = 10000 cm²
∵ (2500 + 6400) cm² ≠ 10000 cm²
∴ It is not a right triangle.

(iv) The sides are : 13 cm, 12 cm, 5 cm
Here, (13 cm)² = 169 cm²
(12 cm)² = 144 cm²
(5 cm)² = 25 cm²
∵ (144 + 25)cm² = 169 cm²
∴ It is a right triangle.
Hypotenuse = 13 cm.

Question 2.
PQR is a triangle right angled at P and M is a point on QR such that PM ⊥ QR. Show that PM² = QM.MR.
Solution:
In ∆QMP and ∆QPR,
∠QMP = ∠QPR [Each 90°]
∠Q = ∠Q [Common]
⇒ ∆QMP ~ ∆QPR …. (1) [AA similarity]
Again, in ∆PMR and ∆QPR,
∠PMR = ∠QPR [Each = 90°]
∠R = ∠R [Common]
⇒ ∆PMR ~ ∆QPR …… (2) [AA similarity]
From (1) and (2), we have

Question 3.
In the figure, ABD is a triangle, right angled at A and AC ⊥ BD.

Show that
(i) AB² = BC.BD
(ii) AC² = BC.DC
(iii) AD² = BD.CD
Solution:

Question 4.
ABC is an isosceles triangle right angled at C. Prove that AB² = 2AC².
Solution:
We have, right ∆ABC such that ∠C = 90° and AC = BC.

∴ By Pythagoras theorem, we have AB² = AC² + BC² = AC² + AC² = 2AC²
[∵ BC = AC (given)]
Thus, AB² = 2AC²

Question 5.
ABC is an isosceles triangle with AC = BC. If AB² = 2AC², prove that ABC is a right triangle.
Solution:
We have, an isosceles AABC such that BC = AC.

Also, AB² = 2AC²
∴ AB² = AC² + AC²
But AC =BC
∴ AB² = AC² + BC²
∴ Using the converse of Pythagoras theorem, ∠ACB = 90°
f.e., ∆ABC is a right angled triangle.

Question 6.
ABC is an equilateral triangle of side 2a. Find each of its altitudes.
Solution:
In equilateral triangle, altitude bisects the base.
⇒ AD = DB

Question 7.
Prove that the sum of the squares of the sides of a rhombus is equal to the sum of the squares of its diagonals.
Solution:
Let us have a rhombus ABCD.

∵ Diagonal of a rhombus bisect each other at right angles.
∴ OA = OC and OB = OD
Also, ∠AOB = ∠BOC [Each = 90°]
And ∠COD = ∠DOA [Each = 90°]
In right ∆AOB, we have,
AB² = OA² + OB² …… (1)
[Using Pythagoras theorem]
Similarly, in right ∆BOC,
BC² = OB² + OC² …… (2)
In right ∆COD,
CD² = OC² + OD² …… (3)
In right ∆AOD,
DA² = OD² + OA² ……. (4)
Adding (1), (2), (3) and (4)
AB² + BC² + CD² + DA²
= [OA² + OB²] + [OB² + OC²] + [OC² + OD²] + [OD² + OA²]
= 2OA² + 2OB² + 2 OC² + 2OD² = 2[OA² + OB² + OC² + OD²]
= 2[OA² + OB² + OA² + OB²]

Thus, sum of the squares of the sides of a rhombus is equal to the sum of the squares of its diagonals.

Question 8.
In the figure, O is a point in the interior of a triangle ABC, OD ⊥ BC, OE ⊥ AC and OF ⊥ AB. Show that
(i) OA² + OB² + OC² – OD² – OE² – OF² = AF² + BD² + CE²
(ii) AF² + BD² + CE² = AE² + CD² + BF²

Solution:
We have a point in the interior of a ∆ABC such that
OD ⊥ BC, OE ⊥ AC and OF ⊥ AB.
(i) Let us join OA, OB and OC.

In right ∆OAF, by Pythagoras theorem
OA² = OF² + AF² …(1)
Similarly, from right triangle ODB and OEC, we have
OB² = BD² + OD², …(2)
and OC² = CE² + OE² …(3)
Adding (1), (2) and (3), we get OA² + OB² + OC²
= (AF² + OF²) + (BD² + OD²) + (CE² + OE²)
⇒ OA² + OB² + OC²
= AF² + BD² + CE² + (OF² + OD² + OE²)
⇒ OA² + OB² + OC² – (OD² + OE² + OF²)
= AF² + BD² +CE²
⇒ OA² + OB² + OC² – OD² – OE² – OF²
= AF² + BD² + CE²

(ii) In right triangle OBD and triangle OCD, by Pythagoras theorem:
OB² = OD² + BD² and OC² = OD² + CD²
⇒ OB² – OC² = OD² + BD² – OD² – CD²
⇒ OB² – OC² = BD² – CD² ….. (1)
Similarly, we have
OC² – OA² = CE² – AE² …… (2)
and OA² – OB² = AF² – BF² ….. (3)
Adding (1), (2) and (3), we get (OB² – OC²) + (OC² – OA²) + (OA² – OB²) = (BD² – CD²) + (CE² – AE²) + (AF² – BF²)
⇒ 0 = BD² + CE² + AF² – (CD² + AE² + BF²)
⇒ BD² + CE² + AF² = CD² + AE² + BF²
or AF² + BD² + CE² = AE² + BF² + CD²

Question 9.
A ladder 10 m long reaches a window 8 m above the ground. Find the distance of the foot of the ladder from base of the wall.
Solution:
Let PQ be the ladder and PR be the wall

⇒ PQ = 10 m, PR = 8 m
Now, in the right ∆PQR, PQ² = PR² + QR²
⇒ 10² = 8² + QR²
[using Pythagoras theorem]
⇒ QR² = 10² – 8² = (10 + 8)(10 – 8)
= 18 × 2 = 36
QR = \(\sqrt{36}\) = 6m
Thus, the distance of the foot of the ladder from the base to the wall is 6 m.

Question 10.
A guy wire attached to a vertical pole of height 18 m is 24 m long and has a stake attached to the other end. How far from the base of the pole should the stake be driven so that the wire will be taut?
Solution:
Let AB is the wire and BC is the vertical pole. The point A is the stake.

Now, in the right AABC, using Pythagoras Theorem, we have

Thus, the stake is required to be taken at \(6 \sqrt{7}\)m from the base of the pole to make the wire taut.

Question 11.
An aeroplane leaves an airport and flies due north at a speed of 1000 km per hour. At the same time, another aeroplane leaves the same airport and flies due west at a speed of 1200 km per hour. How far apart will be the two planes after \(1 \frac{1}{2}\) hours?
Solution:
Let the point A represent the airport. Plane-I fly towards North,
∴ Distance of the plane-I from the airport after \(1 \frac{1}{2}\) hours = speed × time

Question 12.
Two poles of heights 6 m and 11 m stand on a plane ground. If the distance between the feet of the poles is 12 m, find the distance between their tops?
Solution:
Let the two poles AB and CD are such that the distance between their feet AC = 12m.
∵ Height of pole-1, AB = 11 m

Question 13.
D and E are points on the sides CA and CB respectively of a triangle ABC right angled at C. Prove that AE² + BD² = AB² + DE².
Solution:
We have a right ∆ABC such that ∠C = 90°.
Also, D and E are points on CA and CB respectively.
rain We have a right ∆ABC such that ∠C = 90°.

Let us join AE and BD.
In right ∆ACB, using Pythagoras theorem
AB² = AC² + BC² …… (1)
In right ∆DCE, using Pythagoras theorem,
DE² = CD² + CE² …… (2)
Adding (1) and (2), we get
AB² + DE² = [AC² + BC²] + [CD² + CE²]
= AC² + BC² + CD² + CE² = [AC² + CE²] + [BC² + CD²] …. (3)
In right ∆ACE,
AC² + CE² = AE² …… (4)
In right ∆BCD,
BC² + CD² = BD² …….. (5)
From (3), (4) and (5), we have AB² + DE² = AE² + BD² or AE² + BD² = AB² + DE²

Question 14.
The perpendicular from A on side BC of a ∆ABC intersects BC at D such that DB = 3CD (see figure). Prove that 2AB² = 2AC² + BC².

Solution:

Question 15.
In an equilateral triangle ABC, D is a point on side BC such that BD = \(\frac{1}{3}\)BC. Prove that 9AD² = 7AB².
Solution:
We have an equilateral ∆ABC; in which D is a point on BC such that BD = \(\frac{1}{3}\) BC.

Question 16.
In an equilateral triangle, prove that three times the square of one side is equal to four times the square of one of its altitudes.
Solution:
We have an equilateral ∆ABC, in which AD ⊥ BC.
Since, an altitude in an equilateral A, bisects the corresponding side.

∴ D is the mid-point

Question 17.
Tick the correct answer and justify : In ∆ABC, AB = \(6 \sqrt{3}\) cm, AC = 12 cm and BC = 6 cm. The angle B is
(A) 120°
(B) 60°
(C) 90°
(D) 45°
Solution:
(C): We have, AB = \(6 \sqrt{3}\) cm, AC = 12 cm, and BC = 6 cm

In this article, we will share MP Board Class 10th Maths Book Solutions Chapter 12 Areas Related to Circles Ex 12.2 Pdf, These solutions are solved subject experts from the latest edition books.

MP Board Class 10th Maths Solutions Chapter 12 Areas Related to Circles Ex 12.2

Unless stated otherwise, use π = \(\frac{22}{7}\).

Question 1.
Find the area of a sector of a circle with radius 6 cm if angle of the sector is 60°.
Solution:
Here, r = 6 cm and θ = 60°

Question 2.
Find the area of a quadrant of a circle whose circumference is 22 cm.
Solution:
Let radius of the circle be r.
∴ 2πr = 22

Question 3.
The length of the minute hand of a clock is 14 cm. Find the area swept by the minute hand in 5 minutes.
Solution:
Length of minute hand = radius of the circle (r) = 14 cm
∵ Angle swept by the minute hand in 60 minutes = 360°
∴ Angle swept by the minute hand in 360°
5 minutes = \(\frac{360^{\circ}}{60}\) × 5 = 30°
Now, area of the sector with r = 14 cm and θ = 30°
= \(\frac{\theta}{360^{\circ}}\) × πr² = \(\frac{30^{\circ}}{360^{\circ}} \times \frac{22}{7}\) × 14 × 14 cm²
= \(\frac{11 \times 14}{3} \mathrm{cm}^{2}=\frac{154}{3} \mathrm{cm}^{2}\)
Thus, the required area swept by the minute hand in 5 minutes = \(\frac{154}{3}\) cm²

Question 4.
A chord of a circle of radius 10 cm subtends a right angle at the centre. Find the area of the corresponding: (i) minor segment (ii) major segment.(Use π = 3.14)
Solution:
Length of the radius (r) = 10 cm
Sector angle (θ) = 90°

= [314 – 78.5] cm² = 235.5 cm²

Question 5.
In a circle of radius 21 cm, an arc subtends an angle of 60° at the centre. Find:
(i) the length of the arc
(ii) area of the sector formed by the arc
(iii) area of the segment formed by the corresponding chord
Solution:
Here, radius(r) = 21 cm and θ = 60°
(i) Circumference of the circle = 2πr
= 2 × \(\frac{22}{7}\) × 21 cm = 2 × 22 × 3 cm = 132 cm

∴ Length of the arc APB

Question 6.
A chord of a circle of radius 15 cm subtends an angle of 60° at the centre. Find the areas of the corresponding minor and major segments of the circle. (Use π = 3.14 and \(\sqrt{3}=\) = 1.73)
Solution:
Here, radius (r) = 15 cm and
Sector angle (θ) = 60°
∴ Area of the sector
\(\frac{\theta}{360^{\circ}}\) × πr² = \(\frac{60^{\circ}}{360^{\circ}} \times \frac{314}{100}\) × 15 × 15 cm²
= \(\frac{11775}{100}\) cm² = 117.75 cm²
Since ∠O = 60° and OA = OB = 15 cm
∴ AOB is an equilateral triangle.

⇒ AB = 15 cm and ∠A = 60°
Draw OM ⊥ AB,
In ∆AMO

Now area of the minor segment = (Area of minor sector) – (ar ∆AOB)
= (117.75 – 97.3125) cm² = 20.4375 cm²
Area of the major segment = [Area of the circle] – [Area of the minor segment]
= πr² – 20.4375 cm²
= [\(\frac{314}{100}\) × 15²] – 20.4375 cm²
= (706.5 – 20.4375) cm² = 686.0625 cm²

Question 7.
A chord of a circle of radius 12 cm subtends an angle of 120° at the centre. Find the area of the corresponding segment of the circle. (Use π = 3.14 and \(\sqrt{3}=\) = 1.73 )
Solution:
Here θ = 120° and r = 12 cm

Draw OM ⊥ AB
In ∆AOB, ∠O = 120°
By angle sum property,
∠A + ∠B + ∠O = 180°
⇒ ∠A + ∠B = 180° – 120° = 60°
∵ OB = OA = 12 cm
⇒ ∠A = ∠B = 30°

= 36 × 1.73 cm² = 62.28 cm²
∴ Area of the minor segment = [Area of sector] – [Area of ∆AOB]
= [150.72 cm²] – [62.28 cm²] = 88.44 cm²

Question 8.
A horse is tied to a peg at one corner of a square shaped grass field of side 15 m by means of a 5 m long rope (see figure). Find
(i) the area of that part of the field in which the horse can graze.
(ii) the increase in the grazing area if the rope were 10m long instead of 5 m. (Use π = 3.14)

Solution:
Here, length of the rope = 5 m
∴ Radius of the circular portion grazed by the horse(r) = 5 m
(i) Area of the circular portion grazed

(ii) When length of the rope is increased to 10 m, then, r = 10 m
Area of the new circular portion grazed
= \(\frac{\theta}{360^{\circ}}\) × πr² = \(\frac{90^{\circ}}{360^{\circ}} \times \frac{314}{100}\) × (10)² m²
= \(\frac{1}{4}\) × 314 m² = 78.5 m²
∴ Increase in the grazing area = (78.5 – 19.625) m² = 58.875 m²

Question 9.
A brooch is made with silver wire in the form of a circle with diameter 35 mm. The wire is also used in making 5 diameters which divide the circle into 10 equal sectors as shown in the figure. Find:
(i) the total length of the silver wire required.
(ii) the area of each sector of the brooch.

Solution:
Diameter of the circle = 35 mm
∴ Radius (r) = \(\frac{35}{2}\) mm
(i) Circumference = 2πr
= 2 × \(\frac{22}{7} \times \frac{35}{2}\) mm = 22 × 5 mm = 110 mm
Length of 1 piece of wire used to make diameter to divide the circle into 10 equal sectors = 35 mm
∴ Length of 5 pieces = 5 × 35 mm = 175 mm
∴ Total length of the silver wire = (110 + 175) mm = 285 mm

(ii) Since the circle is divided into 10 equal sectors,

Question 10.
An umbrella has 8 ribs which are equally spaced (see figure). Assuming umbrella to be a flat circle of radius 45 cm, find the area between the two consecutive ribs of the umbrella.

Solution:
Here, radius (r) = 45 cm
Since circle is divided into 8 equal parts,
∴ Sector angle corresponding to each part

Question 11.
A car has two wipers which do not overlap. Each wiper has a blade of length 25 cm sweeping through an angle of 115°. Find the total area cleaned at each sweep of the blades.
Solution:
Here, radius (r) = 25 cm
Sector angle (θ) = 115°
∴ Total area cleaned at each sweep of the blades

Question 12.
To warn ships for underwater rocks, a lighthouse spreads a red coloured light over a sector of angle 80° to a distance of 16.5 km. Find the area of the sea over which the ships are warned. (Use π = 3.14)
Solution:
Here, radius (r) = 16.5 km and sector angle (θ) = 80°
∴ Area of the sea surface over which the ships are warned

Question 13.
A round table cover has six equal designs as shown in the figure. If the radius of the cover is 28 cm, find the cost of making the designs at the rate of ₹ 0.35 per cm². (Use \(\sqrt{3}=\) = 1.7)

Solution:
Here, r = 28 cm
Since, the circle is divided into six equal sectors.

Now, area of 1 design = Area of segment APB = Area of sector ABO – Area of ∆AOB ………..(2)
In ∆AOB, ∠AOB = 60°, OA = OB = 28 cm
∴ ∠OAB = 60° and ∠OBA = 60°
⇒ ∆AOB is an equilateral triangle.
⇒ AB = AO = BO ⇒ AB = 28 cm
Draw OM ⊥ AB
∴ In right ∆AOM, we have

= 14 × 14 × 1.7 cm² = 333.2 cm² ……………(3)
Now, from (1), (2) and (3), we have
Area of segment APB
= 410.67 cm² – 333.2 cm² = 77.47 cm²
⇒ Area of 1 design = 77.47 cm²
∴ Area of the 6 equal designs = 6 × (77.47) cm² = 464.82 cm²
Hence, the cost of making the design at the rate of ₹ 0.35 per cm²
= ₹ 0.35 × 464.82 = ₹ 162.68.

Question 14.
Tick the correct answer in the following:
Area of a sector of angle p (in degrees) of a circle with radius R is

Solution:
(D) Here, radius = R
Angle of a sector (θ) = p
∴ Area of the sector

In this article, we will share MP Board Class 10th Maths Book Solutions Chapter 5 Arithmetic Progressions Ex 5.1 Pdf, These solutions are solved subject experts from the latest edition books.

MP Board Class 10th Maths Solutions Chapter 5 Arithmetic Progressions Ex 5.1

Question 1.
In which of the following situations, does the list of numbers involved make an arithmetic
progression, and why’
(i) The taxi fare after each km when the fare is ₹ 15 for the first km and 8 for each
additional km.
(ii) The amount of air present In a cylinder when a vacuum pump removes 1/4 of the
air remaining in the cylinder at a time.
(iii) The cost of digging a well after every metre of digging, when it costs 150 for
the first metre and rises by 50 for each subsequent metre.
(iv) The amount of money in the account every year, when 10000 is deposited at compound interest at 8% per annum.
Solution:
(i) Let us consider, the first term
(T₁) Fare for the first 1 km = ₹ 15
Since, the taxi fare beyond the first 1 km is ₹ 8 for each additional km.
∴ Fare for 2 km = ₹ 15 + 1 × ₹ 8
T₂ = a + 8 [where a = 15]
Fare for 3 km = ₹ 15 + 2 × ₹ 8
⇒ T₃ = a + 16
Fare for 4 km= ₹ 15 + 3 × ₹ 8
⇒ T₄ = a + 24
Fare for 5 km = ₹ 15 + 4 × ₹ 8
⇒ T₅ = a + 32
Fare for n km = ₹ 15 + (n – 1)8
⇒ T_n = a + (n – 1)8
We see that above terms form an AP with common difference 8.

(ii) Let the amount of air present in the cylinder be x

The above terms are not in A.P.

(iii) Here, the cost of digging for first 1 metre = ₹ 150
The cost of digging for first 2 metres = ₹ 150 + ₹ 50 = ₹ 200
The cost of digging for first 3 metres = ₹ 150 + (₹ 50) × 2 = ₹ 250
The cost of digging for first 4 metres = ₹ 150 + (₹ 50) × 3 = ₹ 300
∴ The terms are: 150, 200, 250, 300,…..
Since, 200 – 150 = 50 and 250 – 200 = 50
(200 – 150) (250 – 200) = 50
∴ The above terms form an AP with common difference 50.

(iv)

Question 2.
Write first four terms of the AP, when the first term a and the common difference d are given
as follows:
(i) a = 10, d = 10
(ii) a = -2, d = 0
(iii) a = 4, d = -3
(iv) a = -1, d = 1/2
(y) a = -1.25, d = -0.25
Solution:
(i) ∵ T_n = a + (n – 1)d
∴ For a = 10 and d = 10, we have:
T₁ =10 + (1 – 1) × 10 = 10 + 0 = 10
T₂ = 10 + (2 – 1) × 10 = 10 + 10 – 20
T₃ = 10 + ( 3 – 1) × 10 = 10 + 20 = 30
T₄ = 10 + (4 – 1) × 10 = 10 + 30 = 40
Thus, the first four terms are:
10, 20, 30, 40

(ii) ∵ T_n = a + (n – 1)d
∴ For a = -2 and d = 0,we have:
T₁ = -2 + (1 – 1) × 0 = -2 + 0 = -2
T₂ = -2 + (2 – 1) × 0 = -2 + 0 = -2
T₃ = -2 + (3 – 1) × 0= -2 + 0 = -2
T₄ = -2 + (4 – 1) × 0 = -2 + 0 = -2
∴ Thus, the first four terms are: -2, -2, -2, -2

(iii) ∵ T_n = a + (n – 1)d
For a = 4 and d = -3, we have:
T₁ = 4 + (1 – 1) × (-3) = 4 + 0 = 4
T₂ = 4 + (2 – 1) × (-3) = 4 + (-3) = 1
T₃ = 4 + (3 – 1) × (-3) = 4 + (-6) = -2
T₄ = 4 + (4 – 1) × (-3) = 4 + (-9) = -5
Thus, the first four terms are:
4, 1, -2, -5

(iv)

(v) ∵ T_n = a + (n – 1)d
∴ For a = -1.25 and d = -0.25, we have
T₁ = -1.25 + (1 – 1) × (-0.25) = -1.25 + 0
= -1.25
T₂ = -1.25 + (2 – 1) × (-0.25) = -1.25 + (-0.25) = -1.50
T₃ = -1.25 + (3 – 1) × (-0.25) = -1.25 + (-0.50) = -1.75
T₄ = -1.25 + (4 – 1) × (-0.25) = -1.25 + (-0.75) = -2.0

Question 3.
For the following APs, write the first term and the common difference:
(i) 3, 1, -1, -3,…..
(ii) -5, -1, 3, 7,….
(iii) \(\frac{1}{3}, \frac{5}{3}, \frac{9}{3}, \frac{13}{3}, \ldots .\)
(iv) 0.6, 1.7, 2.8, 3.9, …..
Solution:
(i) We have : 3, 1, -1, -3, …
⇒ T₁ ⇒ 3 = a = 3
T₂ = 1, T₃= -1, T₄= -3
∴ T₂ – T₁ = 1 – 3 = -2
T₄ = T₃ = -3 – (-1) = -3 + 1 = -2 ⇒ d = -2

(ii) We have : -5, -1, 3, 7,….
⇒ T₁ = -5 ⇒ a = -5, T₂ = -1, T₃ = 3, T₄ = 7
∴ T₂ – T₁ = -1 – (-5) = -1 + 5 = 4
and T₄ – T₃ = 7 – 3 = 4 ⇒ d = 4
Thus a = -5, d = 4

(iii)

Question 4.
Which of the following are APs? If they form an AP, find the common difference d and write three more terms.
(i) 2, 4, 8, 16,
(ii) 2, \(\frac{5}{2}\), 3, \(\frac{7}{2}\), ….
(iii) -1.2, -3.2, -5.2, -7.2, ……
(iv) -10, -6, -2, 2, ….
(v) \(3,3+\sqrt{2}, 3+2 \sqrt{2}, 3+3 \sqrt{2}, \ldots\)
(vi) 0.2, 0.22, 0.222, 0.2222, ….
(vii) 0, -4, -8, -12,
(ix) 1, 3, 9, 27, …..
(x) o, 2a, 3a, 4a,…
(xi) a, a₂, a₃, a₄,….
(xii) \(\sqrt{2}, \sqrt{8}, \sqrt{18}, \sqrt{32}, \dots\)
(xiii) \(\sqrt{3}, \sqrt{6}, \sqrt{9}, \sqrt{12}, \dots .\)
(xiv) 1², 3², 5², 7², ….
(xv) 1², 5², 7², 73, …..
Solution:
(i)

∴ The given numbers do not form an AP

(ii)

(iii) We have : -1.2, -3.2, -5.2, -7.2,
∴ T₁ = -1.2, T₂ = -3.2, T₃ = -5.2, T₄ = -7.2
T₂ – T₁ = -3.2 + 1.2 = -2
T₃ – T₂ = -5.2 + 3.2 = -2
T₄ – T₃ = -7.2 + 5.2 = -2
∵ T₂ – T₁ = T₃ – T₂ = T₄ – T₃ = -2 d = -2
∴ The given numbers form an AP such that d = -2.
Now, T₅ = T₄ + (-2) = -7.2 + (-2) = -9.2,
T₆ = T₅ + (-2) = -9.2 + (-2) = -11.2 and
T₇ = T₆ + (-2) = -11.2 + (-2) = -13.2
Thus, d = -2 and T₅ = -9.2, T₅ = -11.2 and T₆ = -13.2

(iv) We have : -10, -6, -2, 2,
T₁ = -10, T₂ = -6, T₃ = -2, T₄ = 2
T₂ – T₁ = -6 + 10 = 4
T₃ – T₂ = -2 + 6 = 4
T₄ – T₃ = 2 + 2 = 4
∵ T₂ – T₁ = T₃ – T₂ = T₄ – T₃ = 4 ⇒ d = 4
∴ The given numbers form an AP Now, T₅ = T₄ + 4 = 2 + 4 = 6,
T₆ = T₅ + 4 = 6 + 4 = 10,
T₇ = T₆ + 4 = 10 + 4 = 14
Thus, d = 4 and T₅ = 6, T₆ = 10, T₇ = 14

(v) We have :
3, 3 + \(\sqrt{2}\), 3 + 2\(\sqrt{2}\), 3 + 3\(\sqrt{2}\),….

(vi) We have : 0.2, 0.22, 0.222, 0.2222,….

∴ The given numbers do not form an AP

(vii) We have : 0, – 4, – 8, – 12,
∴ T₁ = 0, T₂ = -4, T₃ = -8, T₄ = -12 T₂ – T₁ = -4 – 0 = -4
T₃ – T₂ = – 8 + 4 = – 4
T₄ – T₃ = -12 + 8 = -4
∴ T₂ – T₁ = T₃ – T₂ = T₄ – T₃ = -4 ⇒ d = -4
∴ The given numbers form an AP
Now, T₅ = T₄ + (- 4) = -12 + (- 4) = -16
T₆ = T₅ + (-4) = -16 + (-4)= -20
T₇ = T₆ + (- 4) = -20 + (- 4) = -24
Thus, d = – 4 and T₅ = -16, T₆ = -20,
T₇ = -24.

(viii)

(ix) We have, 1, 3, 9, 27,….

(x) We have : a, 2a, 3a, 4a,

(xi)

(xii)

(xiii)

(xiv)
We have : 1², 3₂, 5₂, 7₂,….

(xv) We have : 1₂ , 5₂, 7₂, 7₂,….

In this article, we will share MP Board Class 10th Maths Book Solutions Chapter 6 Triangles Ex 6.4 Pdf, These solutions are solved subject experts from the latest edition books.

MP Board Class 10th Maths Solutions Chapter 6 Triangles Ex 6.4

Question 1.
Let ∆ABC ~ ∆DEF and their areas be, respectively, 64 cm² and 121 cm². If EF = 15.4 cm, find BC.
Solution:
We have ar(∆ABC) = 64 cm²
ar(∆DEF) = 121 cm² and EF = 15.4 cm[Given]
∵ ∆ABC ~ ∆DEF
∴ \(\frac { { ar }(\Delta ABC) }{ { ar }(\Delta DEF) } =\left( \frac { BC }{ EF } \right) ^{ 2 }\)
[Ratios of areas of two similar triangles is equal to the ratio of the squares of their corresponding sides]

Thus, BC = 11.2 cm

Question 2.
Diagonals of a trapezium ABCD with AB || DC intersect each other at the point O. If AB = 2CD, find the ratio of the areas of triangles AOB and COD.
Solution:
In trapezium ABCD, AB || DC. Diagonals AC and BD intersect at O.
In ∆AOB and ∆COD,

∠AOB = ∠COD [Vertically opposite angles]
∠OAB = ∠OCD [Alternate angles]
∴ Using AA criterion of similarity, we have
∆AOB ~ ∆COD

i. e., ar(∆AOB) : ar(∆COD) = 4 : 1

Question 3.
In the figure, ABC and DBC are two triangles on the same base BC. If AD intersects BC at O, show that \(\frac { { ar }(\Delta ABC) }{ { ar }(\Delta DBC) } =\frac { AO }{ DO } \)

Solution:
We have, ∆ABC and ∆DBC are on the same base BC. Also BC and AD intersect at O.
Let us draw AE⊥BC and DF⊥BC.
In ∆AOE and ∆DOF,
∠AEO = ∠DFO = 90° ……….. (1)
Also, ∠AOE = ∠DOF …………… (2)
[Vertically Opposite Angles]

Question 4.
If the areas of two similar triangles are equal, prove that they are congruent.
Solution:
We have ∆ABC and ∆DEF, such that ∆ABC ~ ∆DEF and ar(∆ABC) = ar(∆DEF).
Since the ratio of areas of two similar triangles is equal to the square of the ratio of their corresponding sides.


i.e., the corresponding sides of ∆ABC and ∆DEF are equal.
⇒ ∆ABC ≅ ∆DEF [By SSS congruency]

Question 5.
D, E and F are respectively the mid-points of sides AB, BC and CA of ∆ABC. Find the ratio of the areas of ∆DEF and ∆ABC.
Solution:
We have a ∆ABC in which D, E and F are mid points of AB, BC and CA respectively. D, E and F are joined to form ∆DEF.

Now, in ∆ABC, D and F are the mid-points of sides AB and AC.
∴ \(\frac{A D}{D B}=\frac{A F}{F C}\) = 1
∴ By the converse of the basic proportion¬ality theorem, we have,
DF||BC ⇒ DF||BE
Similarly; EF||AB ⇒ EF||BD
Since, DF||BE and DB||EF
∴ Quadrilateral BEFD is a parallelogram.
⇒ FE = BD = \(\frac{1}{2}\)AB …………. (1)
Similarly, quadrilateral ECFD is a parallelogram.
⇒ DF = EC = \(\frac{1}{2}\)BC ………… (2)
and DE = FC = \(\frac{1}{2}\)AC ………….. (3)
Now, in ∆ABC and ∆DEF

Question 6.
Prove that the ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding medians.
Solution:
We have two triangles ABC and DEF such that ∆ABC ~ ∆DEF

AM and DN are medians corresponding to BC and EF respectively.
∵ ∆ABC ~ ∆DEF
∴ The ratio of their areas is equal to the square of the ratio of their corresponding sides.

Question 7.
Prove that the area of an equilateral triangle described on one side of a square is equal to half the area of the equilateral triangle described on one of its diagonals.
Solution:
We have a square ABCD, whose diagonal is AC. Equilateral ∆BQC is described on the side BC and another equilateral ∆APC is described on the diagonal AC.

∵ All equilateral triangles are similar.
∴ ∆APC ~ ∆BQC
∴ The ratio of their areas is equal to the square of the ratio of their corresponding sides.

Tick the correct answer and justify:
Question 8.
ABC and BDE are two equilateral triangles such that D is the mid-point of BC. Ratio of the areas of triangles ABC and BDE is
(A) 2 : 1
(B) 1 : 2
(C) 4 : 1
(D) 1 : 4
Solution:
(C) : We have an equilateral ∆ABC and D is the mid point of BC. DE is drawn such that BDE is also an equilateral traingle. Since all equilateral triangles are similar,

∴ ∆ABC ~ ∆BDE
⇒ The ratio of their areas is equal to the square of the ratio of their corresponding sides.
∴ \(\frac { { ar }(\Delta ABC) }{ { ar }(\Delta BDE) } =\left( \frac { AB }{ BD } \right) ^{ 2 }\) …………. (1)
∵ AB = AC = BCfsides of equilateral AABC]
and BD = \(\frac{1}{2}\)BC [∵ D is the mid point of BC]
⇒ BC = 2BD = AB …………… (2) [∵ AB = BC]
From (1) and (2), we have

⇒ ar(∆ABC) : ar(∆BDE) = 4 : 1

Question 9.
Sides of two similar triangles are in the ratio 4:9. Areas of these triangles are in the ratio
(A) 2 : 3
(B) 4 : 9
(C) 81 : 16
(D) 16 : 81
Solution:
(D) : We have two similar triangles such that the ratio of their corresponding sides is 4 : 9.
∴ The ratio of areas of two similar triangles is equal to the square of the ratio of their corresponding sides.
∴ \(\frac { { ar }(\Delta -I) }{ { ar }(\Delta -II) } =\left( \frac { 4 }{ 9 } \right) ^{ 2 }=\frac { 16 }{ 81 } \)
⇒ ar(∆-I): ar(∆-II) = 16 : 81