Bhagya

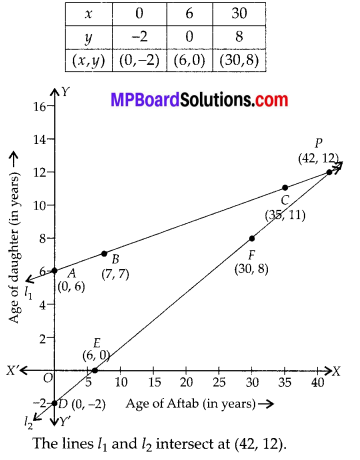
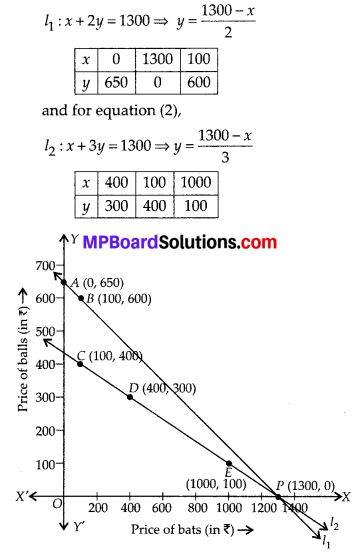
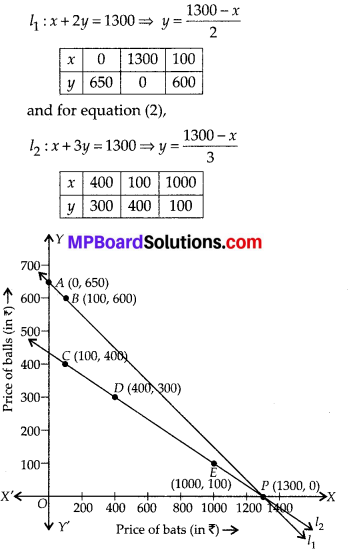
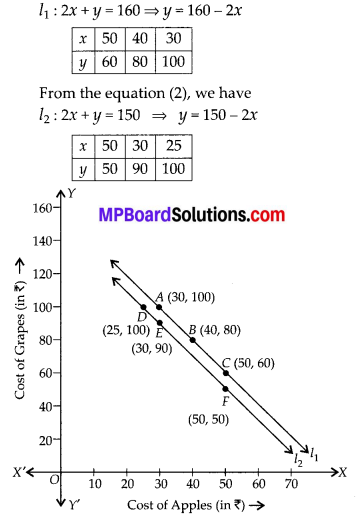
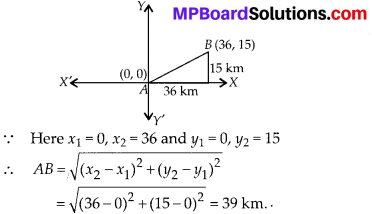
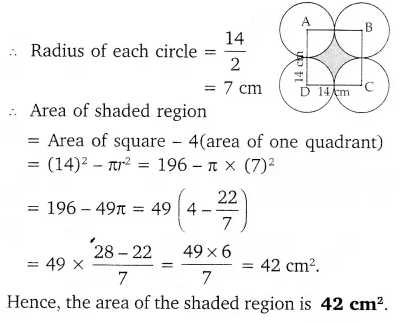
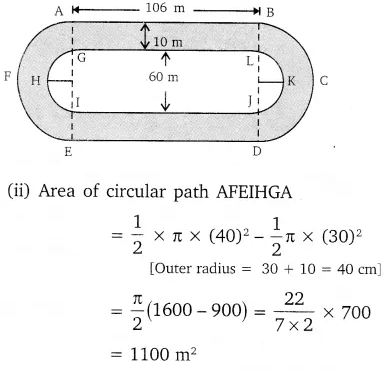
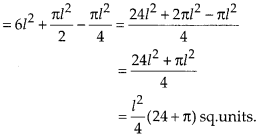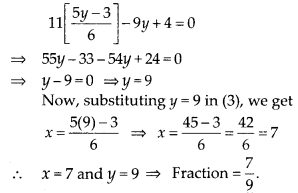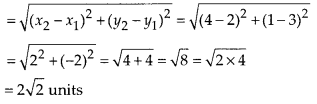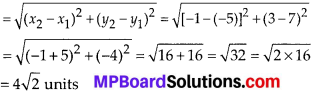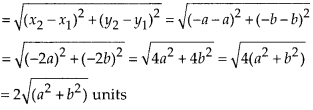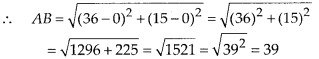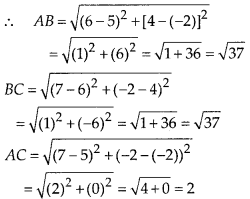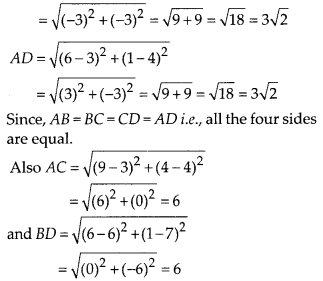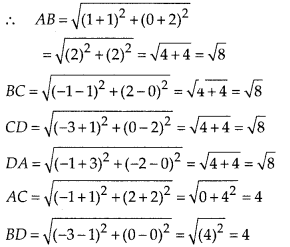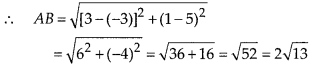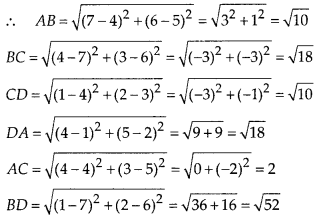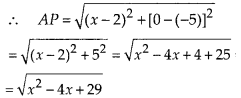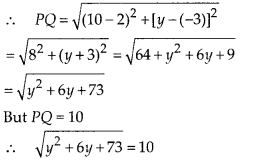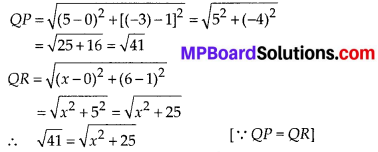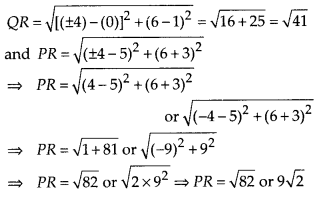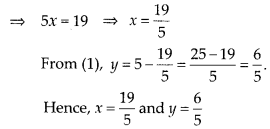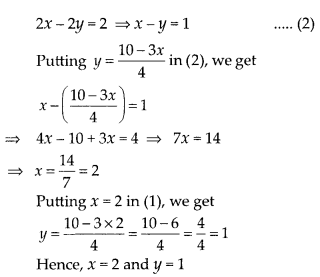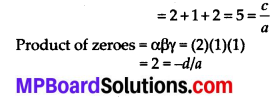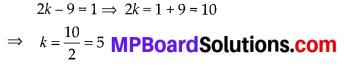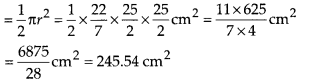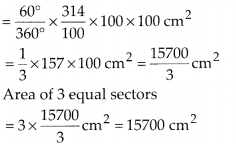In this article, we will share MP Board Class 10th Maths Book Solutions Chapter 1 Real Numbers Ex 1.4 Pdf, These solutions are solved subject experts from the latest edition books.

MP Board Class 10th Maths Solutions Chapter 1 Real Numbers Ex 1.4

Question 1.
Without actually performing the long divison, state whether the following rational numbers will have a terminating decimal expansion or a non-terminating repeating decimal expansion:


Solution:

Question 2.
Write down the decimal expansions of those rational numbers in Question 1 above which have terminating decimal expansions.
Solution:

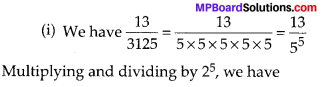
Multiplying and dividing by 2⁵, we have

Question 3.
The following real numbers have decimal expansions as given below. In each case, decide whether they are rational or not. If they are rational, and of the form \(\frac{p}{q}\), what can you say about the prime factors of q?
(i) 43.123456789
(ii) 0.120120012000120000….
(iii) \(43 . \overline{123456789}\)
Solution:
(i) 43.123456789
∴ The given decimal expansion terminates.
∴ It is rational of the form \(\frac{p}{q}\)

Hence, p = 43123456789 and q = 2⁹ × 5⁹
Prime factors of q are 2⁹ and 5⁹.

(ii) 0.120120012000120000…
∵ The given decimal expansion is neither terminating nor repeating.
∴ It is irrational number, hence cannot be written in p/q form.

(iii) \(43 . \overline{123456789}\)
∵ The given decimal expansion is non-terminating repeating.
∴ It is rational number.

Multiplying both sides by 1000000000, we have
1OOOOOOOOOx = 43123456789.123456789…
… (2)
Subtracting (1) from (2), we have
(1000000000x) – x
= (43123456789.123456789 ) – 43.123456789…
⇒ 999999999x = 43123456746

Here, p = 4791495194 and q = 111111111, which is not of the form 2^m × 5ⁿ i.e., the prime factors of q are not of the form 2^m × 5ⁿ.

In this article, we will share MP Board Class 10th Maths Book Solutions Pair of Linear Equations in Two Variables Ex 3.1 Pdf, These solutions are solved subject experts from the latest edition books.

MP Board Class 10th Maths Solutions Chapter 3Pair of Linear Equations in Two Variables Ex 3.1

Question 1.
Aftab tells his daughter, “Seven years ago, I was seven times as old as you were then. Also, three years from now, I shall be three times as old as you will be”. (Isn’t this interesting?) Represent this situation algebraically and graphically.
Solution:
At present: Let Aftab’s age = x years
His daughter’s age = y years
Seven years ago : Aftab’s age = (x – 7) years
His daughter’s age = (y – 7)years
According to the condition,
[Aftab’s age] = 7[His daughter’s age]
⇒ [x – 7] = 7[y – 7] = x – 7 = 7y – 49
⇒ x – 7y – 7 + 49 = 0 ⇒ x – 7y + 42 = 0 …. (1)
After three years : Aftab’s age = (x + 3) years
His daughter’s age = (y + 3) years
According to the condition,
[Aftab’s age] = 3[His daughter’s age]
⇒ [x + 3] = 3[y + 3]
⇒ x + 3 = 3y + 9 ⇒ x — 3y + 3 — 9 = 0
⇒ x — 3y – 6 = 0 …. (2)
Graphical representation of equation (1) and (2): From equation (1), we have :

Question 2.
The coach of a cricket team buys 3 bats and 6 balls for ₹ 3900. Later, she buys another bat and 3 more balls of the same kind for ₹ 1300. Represent this situation algebraically and geometrically.
Solution:
Let the cost of a bat = ₹ x
and the cost of a ball = ₹ y
Cost of 3 bats = ₹ 3x
and cost of 6 balls = ₹ 6y
Again, cost of 1 bat = ₹ x
and cost of 3 balls = ₹ 3y
Algebraic representation:
Cost of 3 bats + Cost of 6 balls = ₹ 3900
⇒ 3x + 6y = 3900 ⇒ x + 2y = 1300 …. (1)
Also, cost of 1 bat + cost of 3 balls = ₹ 1300
⇒ x + 3y = 1300 …. (2)
Thus, (1) and (2) are the algebraic representations of the given situation.
Geometrical representation:
We have for equation (1),

We can also see from the obtained graph that the straight lines representing the two equations intersect at (1300, 0).

Question 3.
The cost of 2 kg of apples and 1 kg of grapes on a day was found to be ₹ 160. After a month, the cost of 4 kg of apples and 2 kg of grapes is ₹ 300. Represent the situation algebraically and geometrically.
solution:
Let the cost of 1 kg of apples = ₹ x
And the cost of 1 kg of grapes = ₹ y
Algebraic representation:
2x + y = 160 … (1)
and 4x + 2y = 300
⇒ 2x + y = 150 … (2)
Geometrical representation:
We have, for equation (1),

The straight lines l₁ and l₂ are the geometrical representations of the equations (1) and (2) respectively. The lines are parallel.

In this article, we will share MP Board Class 10th Maths Book Solutions Chapter 13 Surface Areas and Volumes Ex 13.1 Pdf, These solutions are solved subject experts from the latest edition books.

MP Board Class 10th Maths Solutions Chapter 13 Surface Areas and Volumes Ex 13.1

Unless stated otherwise, take π = \(\frac{22}{7}\)

Question 1.
2 cubes each of volume 64 cm3 are joined end to end. Find the surface area of the resulting cuboid.
Solution:
Volume of each cube = 64 cm³

Let the edge of each cube = x
∴ x³ = 64 cm³
⇒ x = 4 cm
Now, Length of the resulting cuboid (l) = 2x cm = 8 cm
Breadth of the resulting cuboid (b) = x cm = 4 cm
Height of the resulting cuboid (h) = x cm = 4 cm
∴ Surface area of the cuboid = 2 (lb + bh + hl)
= 2 [(8 × 4) + (4 × 4) + (4 × 8)] cm²
= 2 [32 + 16 + 32] cm² = 2 [80] cm²
= 160 cm².

Question 2.
A vessel is in the form of a hollow hemisphere mounted by a hollow cylinder. The diameter of the hemisphere is 14 cm and the total height of the vessel is 13 cm. Find the inner surface area of the vessel.
Solution:
For hemispherical part,
radius (r)= \(\frac{14}{2}\) = 7cm
∴ Curved surface area = 2πr²
= 2 × \(\frac{22}{7}\) × 7 × 7cm²
= 308cm² 7
Total height of vessel = 13 cm

∴ Height of cylinder = (13 – 7)cm = 6 cm and radius(r) = 7 cm
∴ Curved surface area of cylinder = 2πrh
= 2 × \(\frac{22}{7}\) × 7 × 6cm² = 264cm² 7
∴ Inner surface area of vessel = (308 + 264)cm² = 572 cm²

Question 3.
A toy is in the form of a cone of radius 3.5 cm mounted on a hemisphere of same radius. The total height of the toy is 15.5 cm. Find the total surface area of the toy.
Solution:
Let h be the height of cone and r be the radius of cone and hemisphere.

∴ h = [height of toy – radius of hemi sphere]
= (15.5 – 3.5) cm = 12 cm
Also l² = h² + r² = 12² + (3.5)² = 156.25 cm²
∴ l = 12.5 cm
Curved surface area of the conical part = πrl
Curved surface area of the hemispherical part = 2πr²
∴ Total surface area of the toy = πrl + 2πr²
= πr(l + 2 r)
= \(\frac{22}{7} \times \frac{35}{10}\) (12.5 + 2 × 3.5) cm²
= 11 × (12.5 + 7) cm² = 11 × 19.5 cm²
= 214.5 cm²

Question 4.
A cubical block of side 7 cm is surmounted by a hemisphere. What is the greatest diameter the hemisphere can have? Find the surface area of the solid.
Solution:
Let side of the block, l = 7 cm

∴ The greatest diameter of the hemisphere = 7 cm
Surface area of the solid = [Total surface area of the cubical block] + [C.S.A. of the hemisphere] – [Base area of the hemisphere]
= 6 × l² + 2πr² – πr²
[where l = 7 cm and r = \(\frac{7}{2}\) cm]

Question 5.
A hemispherical depression is cut out from one face of a cubical wooden block such that the diameter l of the hemisphere is equal to the edge of the cube. Determine the surface area of the remaining solid.
Solution:
Let l be the side of the cube.

∴ Diameter of the hemisphere = l
⇒ Radius of the hemisphere (r) = \(\frac{l}{2}\)
Curved surface area of hemisphere = 2πr²
= 2 × π × \(\frac{l}{2} \times \frac{l}{2}=\frac{\pi l^{2}}{2}\)
Base area of the hemisphere = πr²
= \(\pi\left(\frac{l}{2}\right)^{2}=\frac{\pi l^{2}}{4}\)
Surface area of the cube = 6 × l² = 6l²
∴ Surface area of the remaining solid = [Total surface area of cube + C.S.A. of hemisphere – base area of hemisphere]

Question 6.
A medicine capsule is in the shape of a cylinder with two hemispheres stuck to each of its ends (see figure). The length of the entire capsule is 14 mm and the diameter of the capsule is 5 mm. Find its surface area.

Solution:
Radius of the hemispherical part

Curved surface area of one hemispherical part = 2πr²
∴ Surface area of both hemispherical parts
= 2(2πr²) = 4πr² = [4 × \(\frac{22}{7} \times\left(\frac{25}{10}\right)^{2}\)] mm²
= \(\left(4 \times \frac{22}{7} \times \frac{25}{10} \times \frac{25}{10}\right)\) mm²
Entire length of capsule = 14 mm
∴ Length of cylindrical part = [Length of capsule – Radius of two hemispherical part]
= (14 – 2 × 2.5)mm = 9mm Area of cylindrical part = 2πrh
= (2 × \(\frac{22}{7}\) × 2.5 × 9 ]mm² = (2 × \(\frac{22}{7} \times \frac{25}{10}\) × 9) mm²
Total surface area
= [Surface area of cylindrical part + Surface area of both hemispherical parts]

Question 7.
A tent is in the shape of a cylinder surmounted by a conical top. If the height and diameter of the cylindrical part are 2.1 m and 4 m respectively, and the slant height of the top is 2.8 m, find the area of the canvas used for making the tent. Also, find the cost of the canvas of the tent at the rate of ₹ 500 per m². (Note that the base of the tent will not be covered with canvas.)
Solution:

For cylindrical part:
Radius (r) = \(\frac{4}{2}\) m = 2m and height (h) = 2.1 m
∴ Curved surface area = 2πrh = (2 × \(\frac{22}{7}\) × 2 × \(\frac{21}{10}\))m²
For conical part:
Slant height (l) = 2.8 m
and base radius (r) = 2 m
∴ Curved surface area
= πrl = (\(\frac{22}{7}\) × 2 × \(\frac{28}{10}\)) m²
∴ Total surface area = [Curved surface area of the cylindrical part] + [Curved surface area of conical part]

Cost of the canvas used :
Cost of 1 m² of canvas = ₹ 500
∴ Cost of 44 m² of canvas = ₹ (500 × 44)
= ₹ 22000.

Question 8.
From a solid cylinder whose height is 2.4 cm and diameter 1.4 cm, a conical cavity of the same height and same diameter is hollowed out. Find the total surface area of the remaining solid to the nearest cm².
Solution:

For cylindrical part :
Height (h) = 2.4 cm and diameter = 1.4 cm
⇒ Radius (r) = 0.7 cm
∴ Total surface area of the cylindrical part
= 2πrh + 2πr² = 2πr [h + r]
= 2 × \(\frac{22}{7} \times \frac{7}{10}\) [2.4 + 0.7]
= \(\frac{44}{10}\) × 3.1 = \(\frac{44 \times 31}{100}\) = \(\frac{1364}{100}\) cm²
For conical part:
Base radius (r) = 0.7 cm and height (h) = 2.4 cm

Base area of the conical part
= \(\pi r^{2}=\frac{22}{7} \times\left(\frac{7}{10}\right)^{2}=\frac{22 \times 7}{100} \mathrm{cm}^{2}=\frac{154}{100} \mathrm{cm}^{2}\)
Total surface area of the remaining solid = [(Total surface area of cylindrical part) + (Curved surface area of conical part) – (Base area of the conical part)]
= \(\left[\frac{1364}{100}+\frac{550}{100}-\frac{154}{100}\right] \mathrm{cm}^{2}=\frac{1760}{100} \mathrm{cm}^{2}\)
Hence, total surface area to the nearest cm² is 18cm².

Question 9.
A wooden article was made by scooping out a hemisphere from each end of a solid cylinder, as shown in figure. If the height of the cylinder is 10 cm, and its base is of radius 3.5 cm, find the total surface area of the article.

Solution:
Radius of the cylinder (r) = 3.5 cm
Height of the cylinder (h) = 10 cm
∴ Curved surface area = 2πrh
= 2 × \(\frac{22}{7} \times \frac{35}{10}\) × 10cm² = 220cm²
Curved surface area of a hemisphere = 2πr²
∴ Curved surface area of both hemispheres
= 2 × 2πr² = 4πr² = 4 × \(\frac{22}{7} \times \frac{35}{10} \times \frac{35}{10}\) cm²
= 154 cm²
Total surface area of the remaining solid = (220 + 154) cm² = 374 cm².

In this article, we will share MP Board Class 10th Maths Book Solutions Pair of Linear Equations in Two Variables Ex 3.3 Pdf, These solutions are solved subject experts from the latest edition books.

MP Board Class 10th Maths Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.3

Question 1.
Solve the following pair of linear equations by the substitution method.
(i) x + y = 14; x – y = 4
(ii) s – f = 3; \(\frac{s}{3}+\frac{t}{2}\) = 6
(iii) 3x – y = 3; 9x – 3y = 9
(iv) 0.2x + 0.3y = 1.3; 0.4x + 0.5y = 2.3
(v) \(\sqrt{2} x+\sqrt{3} y\) = 0; \(\sqrt{3} x-\sqrt{8} y\) = 0
(vi) \(\frac{3 x}{2}-\frac{5 y}{3}\) = -2, \(\frac{x}{3}+\frac{y}{2}=\frac{13}{6}\)
Solution:
(i) x + y = 14 … (1),
x – y = 4 …. (2)
From (1) , we get x = (14 – y) …. (3)
Substituting value of x in (2) , we get
(14 – y) – y = 4 ⇒ 14 – 2y = 4 ⇒ -2y = -10 ⇒ y = 5
Substituting y = 5 in (3), we have
x = 14 – 5 ⇒ x = 9
Hence, x = 9, y = 5

(ii) s – t = 3 … (1)

From (1), we have s = (3 + t) … (2)
Substituting this value of s in (2), we get

Substituting, t = 6 in (3) we get,
S = 3 + 6 = 9
Thus, S = 9, f = 6

(iii) 3x – y = 3 … (1),
9x – 3y = 9 … (2)
From (1) , y = (3x – 3)
Substituting this value of y in (2),
9x – 3(3x – 3) = 9
⇒ 9x – 9x + 9 = 9 ⇒ 9 = 9 which is true,
Eq. (1) and eq. (2) have infinitely many solutions.

(iv) 0.2x + 0.3y = 1.3 … (1)
0.4x + 0.5y = 2.3 …. (2)
From the equation (1),

Substituting the value of y in (2), we have


Substituting the value of x in (1), we have

Question 2.
Solve 2x + 3y = 11 and 2x – 4y = -24 and hence find the value of ‘m’ for which y = mx + c
Solution:

Question 3.
Form the pair of linear equations for the following problems and find their solution by
substitution method.
(i) The difference between two numbers is 26 and one number is three times the other. Find them.
(ii) The larger of two supplementary angles exceeds the smaller by 18 degrees. Find them.
(iii) The coach of a cricket team buys 7 bats and 6 balls for 13800. Later, she buys 3 bats and 5 balls for ₹ 1750. Find the cost of each bat and each ball.
(iv) The taxi charges in a city consist of a fixed charge together with the charge for the distance covered. For a distance of 10 km, the charge paid is ₹ 105 and for a journey of 15 km, the charge paid is ₹ 155. What are the fixed charges and the charge per km? How much does a person have to pay for travelling a distance of 25 km?
(v) A fraction becomes 9/11, if 2 is added to both the numerator and the denominator. If, 3 is added to both the numerator and the denominator it becomes 5/6. Find the fraction.
(vi) Five years hence, the age of Jacob will be three times that of his son. Five years ago, Jacob’s age was seven times that of his son. What are their present ages?
Solution:
(i) Let the two numbers be X and y such that x > y
It is given that
Difference between two numbers = 26
∴ x – y = 26 … (1)
Also one number = 3 [the other number]
⇒ x = 3y … (2)
Substituting x = 3y in (1) , we get 3y – y = 26 ⇒ 2y = 26
Now, substituting y = 13 in (2) , we have
x = 3(13) ⇒ x = 39
Thus, two numbers are 39 and 13.

(ii) Let the two angles be x and y such that x > y
∵ The larger angle exceeds the smaller by 18° (Given)
∴ x = y + 18°…. (1)
Also, sum of two supplementary angles = 180°
∴ x + y = 180° … (2)
Substituting the value of x from (1) in (2) , we get,
(18° + y) + y = 180°

Substituting, y = 81° in (1) , we get
x = 18° + 81° = 99°
Thus, x = 99° and y = 81°

(iii) Let the cost of a bat = ₹ x
And the cost of a ball = ₹ y
∵ [cost of 7 bats] + [cost of 6 balls] = ₹ 3800
⇒ 7x + 6y = 3800 … (1)
Also, [cost of 3 bats] + [cost of 5 balls] = ₹ 1750
3x + 5y = 1750 …. (2)

Substituting this value of y in (1) , we have

(iv) Let fixed charges = ₹ x
and charges per km = ₹ y
∵ Charges for the journey of 10 km = ₹ 105 (Given)
∴ x + 10y = 105 … (1)
and charges for the journey of 15 km = ₹ 155
∴ x + 15y = 155 … (2)
From (1) , we have, x = 105 – 10y …. (3)
Putting the value of x in (2) , we get
(105 – 10y) + 15y = 155
⇒ 5y = 155 – 105 = 50 ⇒ y = 10
Substituting y = 10 in (3) , we get
x = 105 – 10(10) ⇒ x = 105 – 100 = 5
Thus, x = 5 and y = 10
⇒ Fixed charges = ₹ 5
and charges per km = ₹ 10
Now, charges for 25 km = x + 25y = 5 + 25(10) = 5 + 250 = ₹ 255
∴ The charges for 25 km journey = ₹ 255

(v) Let the numerator = x
and the denominator = y
∴ Fraction = \(\frac{x}{y}\)
According to the given condition,

⇒ 11(x + 2) = 9(y + 2)
⇒ 11x + 22 = 9y + 18
⇒ 11x – 9y + 4 = 0 … (1)

Substituting this value of x in (1) , we have

(vi) Let the present age of Jacob = x years
and the present age of his son = y years
∴ 5 years hence: Age of Jacob = (x + 5) years
Age of his son = (y + 5) years
According to given condition,
[Age of Jacob] = 3[Age of his son]
x + 5 = 3(y + 5) ⇒ x + 5 = 3y + 15
⇒ x – 3y -10 = 0 … (1)
5years ago : Age of Jacob = (x – 5) years,
Age of his son = (y – 5) years
According to given condition,
[Age of Jacob] = 7[Age of his son]
∴ (x – 5) = 7(y – 5) ⇒ x – 5 = 7y – 35
⇒ x – 7y + 30 = 0 … (2)
From (1) , x = [10 + 3y] … (3)
Substituting this value of x in (2) , we get
(10 + 3y) – 7y + 30 = 0
⇒ -4y = -40 ⇒ y = 10
Now, substituting y = 10 in (3) ,
we get x = 10 + 3(10)
⇒ x = 10 + 30 = 40
Thus, x = 40 and y = 10
⇒ Present age of Jacob = 40 years and present age of his son = 10 years

In this article, we will share MP Board Class 10th Maths Book Solutions Chapter 7 Coordinate Geometry Ex 7.1 Pdf, These solutions are solved subject experts from the latest edition books.

MP Board Class 10th Maths Solutions Chapter 7 Coordinate Geometry Ex 7.1

Question 1.
Find the distance between the following pairs of points:
(i) (2, 3), (4, 1)
(ii) (-5, 7), (-1, 3)
(iii) (a, b), (-a, -b)
Solution:
(i) Here x₁ = 2, y₁ = 3 and x₂ = 4, y₂ = 1
∴ The required distance

(ii) Here x₁ = -5, y₁ = 7 and x₂ = -1, y₂ = 3
∴ The required distance

(iii) Here x₁ = a, y₁ = b and x₂ = -a, y₂ = -b
∴ The required distance

Question 2.
Find the distance between the points (0, 0) and (36, 15). Can you now find the distance between the two towns /I and B discussed below as following: ‘A town 6 is located 36 km east and 15 km north of the town A’.
Solution:
Part-I
Let the points be A(0, 0) and B(36, 15)

Part-II
We have A(0, 0) and B(36,15) as the positions of two towns.

Question 3.
Determine if the points (1, 5), (2, 3) and (-2, -11) are collinear.
Solution:
Let the points be A( 1, 5), B(2, 3) and C(-2, -11). A, B and C are collinear, if
AB + BC = AC or AC + CB = AB or BA + AC = BC

Here, AB + BC ≠ AC, AC + CB ≠ AB, BA + AC ≠ BC
∴ A, B and C are not collinear.

Question 4.
Check whether (5, -2), (6, 4) and (7, -2) are the vertices of an isosceles triangle.
Solution:
Let the points be A(5, -2), 6(6, 4) and C(7, -2).

We have AB = BC ≠ AC.
∴ ∆ABC is an isosceles triangle.

Question 5.
In a classroom, 4 friends are seated at the points A B, Cand D as shown in the figure. Champa and Chameli walk into the class and after observing for a few minutes Champa asks Chameli, “Don’t you think ABCD is a square?” Chameli disagrees. Using distance formula, find which of them is correct.

Solution:
Let the horizontal columns represent the x-coordinates whereas the vertical rows represent the y-coordinates.
∴ The points are A(3, 4), B(6, 7), C(9, 4) and D(6, 1)


i.e., BD = AC ⇒ Both the diagonals are also equal.
∴ ABCD is a square.
Thus, Champa is correct.

Question 6.
Name the type of quadrilateral formed if any, by the following points, and give reasons for your answer:
(i) (-1, -2), (1, 0), (-1, 2), (-3, 0)
(ii) (-3, 5), (3, 1), (0, 3), (-1, -4)
(iii) (4, 5), (7, 6), (4, 3), (1, 2)
Solution:
(i) Let the points be A(-1, -2), B(1, 0), C(-1, 2) and D(-3, 0) of a quadrilateral ABCD.

⇒ AB = BC = CD = AD i.e., all the sides are equal.
Also, AC and BD (the diagonals) are equal.
∴ ABCD is a square.

(ii) Let the points be A(-3, 5), B(3, 1), C(0, 3) and D(-1, -4).


We see that \(\sqrt{13}+\sqrt{13}=2 \sqrt{13}\)
i. e., AC + BC = AB
⇒ A, B and C are collinear. Thus, ABCD is not a quadrilateral.

(iii) Let the points be A(4, 5), B(7, 6), C(4, 3) and D(1, 2).

Since, AB = CD, BC = DA i.e., opposite sides of the quadrilateral are equal.
And AC ≠ BD ⇒ Diagonals are unequal.
∴ ABCD is a parallelogram.

Question 7.
Find the point on x-axis which is equidistant from (2, -5) and (-2, 9).
Solution:
We know that any point on x-axis has its ordinate = 0
Let the required point be P(x, 0)
Let the given points be A(2, -5) and B(-2, 9)


∴ The required point is (-7, 0)

Question 8.
Find the values of y for which the distance between the points P(2, -3) and Q(10, y) is 10 units.
Solution:
The given points are P(2, -3) and Q(10, y).

Squaring both sides, y² + 6y + 73 = 100
⇒ y² + 6y – 27 = 0
⇒ y² – 3y + 9y – 27 = 0
⇒ (y – 3)(y + 9) = 0
Either y – 3 = 0 ⇒ y = 3
or y + 9 = 0 ⇒ y = -9
∴ The required value of y is 3 or -9.

Question 9.
If Q(0, 1) is equidistant from P(5, -3) and R(x, 6), find the values of x. Also find the distances QR and PR.
Solution:

Squaring both sides, we have x² + 25 = 41
⇒ x² + 25 – 41 = 0
⇒ x² – 16 = 0 ² x = \(\pm \sqrt{16}\) = ±4
Thus, the point R is (4, 6) or (-4, 6)
Now,

Question 10.
Find a relation between x and y such that the point (x, y) is equidistant from the point (3, 6) and (-3, 4).
Solution:
Let the points be A(x, y), B(3, 6) and C(-3, 4).
∴ AB = \(\sqrt{(3-x)^{2}+(6-y)^{2}}\)
And AC = \(\sqrt{[(-3)-x]^{2}+(4-y)^{2}}\)
Since, the point (x, y) is equidistant from (3, 6) and (-3, 4).
∴ AB = AC
⇒ \(\sqrt{(3-x)^{2}+(6-y)^{2}}=\sqrt{(-3-x)^{2}+(4-y)^{2}}\)
Squaring both sides,
(3 – x)² + (6 – y)² = (-3 – x)² + (4 – y)²
⇒ (9 + x² – 6x) + (36 + y² – 12y)
⇒ (9 + x² + 6x) + (16 + y² – 8y)
⇒ 9 + x² – 6x + 36 + y² – 12y – 9 – x² – 6x – 16 – y² + 8y = 0
⇒ – 6x – 6x + 36 – 12y – 16 + 8y = 0
⇒ – 12x – 4y + 20 = 0
⇒ -3x – y + 5 = 0
⇒ 3x + y – 5 = 0 which is the required relation between x and y.

In this article, we will share MP Board Class 10th Maths Book Solutions Pair of Linear Equations in Two Variables Ex 3.2 Pdf, These solutions are solved subject experts from the latest edition books.

MP Board Class 10th Maths Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.2

Question 1.
Form the pair of linear equations in the following problems, and find their solutions graphically.
(i) 10 students of class X took part in a Mathematics quiz. If the number of girls is 4 more than the number of boys, find the number of boys and girls who took part in the quiz.
(ii) 5 pencils and 7 pens together cost ₹ 50, whereas 7 pencils and 5 pens together cost ₹ 46. Find the cost of one pencil and that of one pen.
Solution:
(i) Let the number of boys = x and Number of girls = y
∴ x + y = 10 …. (1)
Also, Number of girls = [Number of boys] + 4
∴ y = x + 4 ⇒ x – y = – 4 … (2)
Now, from the equation (1), we have :
l₁ : x + y = 10 ⇒ y = 10 – x

And from the equation (2), we have
l₂ : x – y = -4 ⇒ y = x + 4

The lines l₁ and l₂ intersects at the point (3, 7)
∴ The solution of the pair of linear equations is : x = 3, y = 7
⇒ Number of boys = 3
and number of girls = 7
Let the cost of a pencil = ₹ x
and cost of a pen = ₹ y
Since, cost of 5 pencils + Cost of 7 pens = ₹ 50
5 x + 7y = 50 … (1)
Also, cost of 7 pencils + cost of 5 pens = ₹ 46
7x + 5y = 46 …. (2)
Now, from equation (1), we have

And from equation (2), we have

Plotting the points (10, 0), (3, 5) and (-4, 10), we get a straight line l₁ and plotting the points (8, -2), (3, 5) and (0, 9.2) we get a straight line l₂.

These two straight lines intersects at (3, 5).
∴ Cost of a pencil = ₹ 3 and cost of a pen = ₹ 5.

Question 2.
On comparing the ratios \(\frac{a_{1}}{a_{2}}, \frac{b_{1}}{b_{2}}\) and \(\frac{c_{1}}{c_{2}}\) find out whether the lines representing the following pairs of linear equations intersect at a point, are parallel or coincident:
(i) 5x – 4y + 8 = 0; 7x + 6y – 9 = 0
(ii) 9x + 3y + 12 = 0; 18x + 6y + 24 = 0
(iii) 6x – 3y + 10 = 0; 2x – y + 9 = 0
Solution:
Comparing the given equations with
a₁x + b₁y + C₁ = 0, a₂x + b₂y + c₂ = 0, we have

(i) For, 5x – 4y + 8 = 0, 7x + 6y – 9 = 0,
a₁ = 5, b₁ = -4, C₁ = 8; a₂ = 7, b₂ = 6, c₂ = -9

So, the lines are intersecting, i.e., they intersect at a point.

(ii) For, 9x + 3y + 12 = 0,18x + 6y + 24 = 0,
a₁ = 9, b₁ = 3, C₁ = 12; a₂ = 18, b₂ = 6, c₂ = 24

So, the lines are coincident.

(iii) For, 6x – 3y +10 = 0, 2x – y + 9 = 0

So, the lines are parallel.

Question 3.
On comparing the ratios \(\frac{a_{1}}{a_{2}}, \frac{b_{1}}{b_{2}}\) and \(\frac{c_{1}}{c_{2}}\), find out whether the following pair of linear equations are consistent, or inconsistent.
(i) 3x + 2y = 5; 2x – 3y = 7
(ii) 2x – 3y = 8; 4x – 6y = 9
(iii) \(\frac{3}{2} x+\frac{5}{3} y\) = 7; 9x-10y = 14
(iv) 5x – 3y = 11; -10x + 6y = -22
Solution:
Comparing the given equations with

So, lines are intersecting i.e., they intersect at a point.
∴ It is consistent pair of equations.

(ii) For 2x – 3y = 8, 4x – 6y = 9, 2x – 3y – 8 = 0 and 4x – 6y – 9 = 0

So, lines are parallel i.e., the given pair of linear equations has no solution.
∴ It is inconsistent pair of equations.

(iii)

⇒ The given pair of linear equations has exactly one solution.
∴ It is a consistent pair of equations.

(iv)

So, lines are coincident.
⇒ The given pair of linear equations has infinitely many solutions.
Thus, it is consistent pair of equations

(v)

So, the lines are coincident.
⇒ The given pair of linear equations have infinitely many solutions.
Thus it is consistent pair of equations.

Question 4.
Which of the following pairs of linear equations are consistent / inconsistent? If consistent, obtain the solution graphically:
(i) x + y = 5; 2x + 2y = 10
(ii) x – y = 8; 3x – 3y = 16
(iii) 2x + y – 6 = 0; 4x – 2y – 4 = 0
(iv) 2x – 2y – 2 = 0; 4x – 4y – 5 = 0
Solution:
(i) For, x + y = 5, 2x + 2y = 10 ⇒ x + y – 5 = 0 and 2x + 2y – 10 = 0


So, lines l₁ and l₂ are coinciding. i.e., They have infinitely many solutions.

(ii) For, x – y = 8,
3x – 3y = 16
⇒ x – y – 8 = 0
and 3x – 3y = 16

so, line are parallel
∴ The pair of linear equations are inconsistent

(iii) For 2x + y – 6 = 0, 4x – 2y – 4 = 0


The pair of linear equations are inconsistent

Question 5.
Half the perimeter of a rectangular garden, whose length is 4 m more than its width, is 36 m. Find the dimensions of the garden.
Solution:
Let the width of the garden = x m
and the length of the garden = y m
According to question,


The lines l₁ and l₂ intersect at (16, 20).
∴ x = 16 and y = 20
So, Length = 20m, and Width = 16m

Question 6.
Given the linear equation 2x + 3y – 8 = 0, write another linear equation in two variables such that the geometrical representation of the pair so formed is:
(i) intersecting lines
(ii) parallel lines
(iii) coincident lines
Solution:
Let the pair of linear equations be 2x + 3y – 8 = 0
⇒ a₁ = 2, b₁ = 3 and C₁ = -8 and a₂x + b₂y + c₂ = 0.

(i) For intersecting lines, we have:

∴ We can have a₂ = 3, b₂ = 2 and c₂ = – 7
∴ The required equation can be 3x + 2y – 7 = 0

(ii) For parallel lines, \(\frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}} \neq \frac{c_{1}}{c_{2}}\)
∴ Any line parallel to 2x + 3y – 8 = 0, can be taken as 2x + 3y -12 = 0

(iii) For coincident lines, \(\frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}}=\frac{c_{1}}{c_{2}}\)
∴ Any line parallel to 2x + 3y – 8 = 0 can be 2(2x + 3y – 8 = 0)
⇒ 4x + 6y – 16 = 0

Question 7.
Draw the graphs of the equations x – y + 1 = 0 and 3x + 2y – 12 = 0. Determine the coordinates of the vertices of the triangle formed by these lines and the x-axis, and shade the triangular region.
Solution:
Since, we have

The lines l₁ and l₂ intersect at (2, 3). Thus, co-ordinates of the vertices of the shaded triangular region are (4, 0), (-1, 0) and (2, 3).

In this article, we will share MP Board Class 10th Maths Book Solutions Pair of Linear Equations in Two Variables Ex 3.4 Pdf, These solutions are solved subject experts from the latest edition books.

MP Board Class 10th Maths Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.4

Question 1.
Solve the following pair of linear equations by the elimination method and the substitution method:
(i) x + y = 5 and 2x – 3y = 4
(ii) 3x + 4y = 10 and 2x – 2y = 2
(iii) 3x – 5y – 4 = 0 and 9x = 2y + 7
(iv) \(\frac{x}{2}+\frac{2 y}{3}\) = -1 and \(x-\frac{y}{3}\) = 3
Solution:
(i) Elimination method :
x + y = 5 … (1)
2x – 3y = 4 …. (2)
Multiplying (1) by 3, we get
3x + 3y = 15 …. (3)
Adding (2) and (3) , we get
2x – 3y + 3x + 3y = 19
⇒ 5x = 19 ⇒ x = \(\frac{19}{5}\)
Now, putting x = \(\frac{19}{5}\) in (1) , we get

Substitution Method :
x + y = 5 ⇒ y = 5 – x … (1)
2x – 3y = 4 … (2)
Put y = 5 – x in (2), we get
2x – 3(5 – x)= 4 ⇒ 2x – 15 + 3x = 4

(ii) Elimination method :
3x + 4y = 10 … (1)
2x – 2y = 2 … (2)
Multiplying equation (2) by 2, we have
⇒ 4x – 4y = 4 … (3)
Adding (1)and (3) , we get
3x + 4y + 4x – 4y = 10 + 4
⇒ 7x = 14 ⇒x = \(\frac{14}{7}\) = 2
Putting x = 2 in (1) , we get,
3(2)+ 4y = 10

(iii) Elimination method :
3x – 5y – 4 = 0 … (1)
9x = 2y + 7 ⇒ 9x – 2y – 7 = 0 …. (2)
Multiplying equation (1) by (3) , we get
⇒ 9x – 15y – 12 = 0(3)
Subtracting (2)from (3),
⇒ 9x – 15y – 12 – 9x + 2y + 7 = 0

(iv) Elimination method :

Question 2.
Form the pair of linear equations in the following problems and find their solutions (if they exist) by the elimination method:
(i) If we add 1 to the numerator and subtract 1 from the denominator, a fraction reduces 1
to 1. It becomes \(\frac{1}{2}\) if we only add 1 to the denominator. What is the fraction?
(ii) Five years ago, Nuri was thrice as old as Sonu. Ten years later, Nuri will be twice as old as Sonu. How old are Nuri and Sonu?
(iii) The sum of the digits of a two-digit number is 9. Also, nine times this number is twice the number obtained by reversing the order of the digits. Find the number.
(iv) Meena went to a bank to withdraw ₹ 2000. She asked the cashier to give her ₹ 50 and ₹ 100 notes only. Meena got 25 notes in all. Find how many notes of ₹ 50 and ₹ 100 she received.
(v) A lending library has a fixed charge for the first three days and an additional charge for each day thereafter. Saritha paid ₹ 27 for a book kept for seven days, while Susy paid ₹ 21 for the book she kept for five days. Find the fixed charge and the charge for each extra day.
Solution:
(i)Let the numerator = x
and the denominator = y

(ii) Let, present age of Nuri = x years
and the present age of Sonu = y years
Age of Nuri = (x – 5) years
Age of Sonu = (y – 5) years
According to question:
Age of Nuri = 3[Age of sonu]
⇒ x – 5 = 3[y – 5] ⇒ x – 5 = 3y – 15
⇒ x – 3y + 10 = 0 … (1)
10 years later :
Age of Nuri = (x + 10) years,
Age of Sonu = (y + 10) years,
According to question :
Age of Nuri = 2[Age of Sonu]
⇒ x + 10 = 2(y + 10) ⇒ x + 10 = 2y + 20
⇒ x – 2y -10 = 0 …. (2)
Subtracting (1) from (2),
x – 2y – 10 – x + 3y – 10 = 0 ⇒ y – 20 = 0 ⇒ y = 20
Putting y = 20 in (1), we get
x – 3(20) + 10 = 0 ⇒ x – 50 = 0 ⇒ x = 50
Thus, x = 50 and y = 20
∴ Age of Nuri = 50 years
and age of Sonu = 20 years

(iii) Let the digit at unit’s place = x
and the digit at ten’s place = y
∴ The number = 10y + x
The number obtained by reversing the digits = 10x + y
According to question,
9[The number] = 2 [Number obtained by reversing the digits]
9[10y+ x] = 2[10x + y]
90y + 9x = 20x + 2y
x – 8y = 0 …. (1)
Also sum of the digits = 9
x + y = 9 …. (2)
Subtracting (1) from (2), we have
x + y – x + 8y = 9
⇒ 9y = 9 ⇒ y = 1
putting y = 1 in (2), we get
x + 1 = 9 ⇒ x = 8
Thus, x = 8 and y = 1
∴ The required number = 10y + x = (10 × 1) + 8 = 10 + 8 = 18

(iv) Let the number of 50 rupees notes = x
and the number of 100 rupees notes = y
According to the condition,
Total number of notes = 25
∴ x + y = 25 …. (1)
Also, the value of all the notes = ₹ 2000
∴ 50x + 100y = 2000 ⇒ x + 2y = 40 …. (2)
Subtracting equation (1) from (2), we get
x + 2y – x – y = 40 – 25
⇒ y = 15
Putting y = 15 in (1),
x + 15 = 25
⇒ x = 25 – 15 = 10
Thus, x = 10 and y = 15
∴ Number of 50 rupees notes = 10
and number of 100 rupees notes = 15

(v) Let the fixed charge (for the three days) = ₹ x
and the additional charge for each extra day = ₹ y
According to question,
Charge for 7 days = ₹ 27
⇒ x + 4y = 27
[∵ Extra days = 7 – 3 = 4]
Also, charge of 5 days = ₹ 21
⇒ x + 2y = 21
[∵ Extra days = 5 – 3 = 2]
Subtracting (2) from (1), we get
x + 4y – x – 2y = 27 – 21
\(\Rightarrow \quad 2 y=6 \Rightarrow y=\frac{6}{2}=3\)
Putting y = 3 in (2), we have
x + 2(3) = 21
⇒ x = 21 – 6 = 15
So, x = 15 and y = 3
∴ Fixed charge = ₹ 15
and additional charge per day = ₹ 3

In this article, we will share MP Board Class 10th Maths Book Solutions Chapter 2 Polynomials Ex 2.3 Pdf, These solutions are solved subject experts from the latest edition books.

MP Board Class 10th Maths Solutions Chapter 2 Polynomials Ex 2.3

Question 1.
Divide the polynomial p(x) by the polynomial g(x) and find the quotient and remainder in each of the following:
(i) p(x) = x³ – 3x² + 5x – 3, g(x) = x² – 2
(ii) p(x) = x⁴ – 3x² + 4x + 5, g(x) = x² + 1 – x
(iii) p(x) = x⁴ – 5x + 6, g(x) = 2 – x²
Solution:
(i) Here, dividend p(x) = x³ – 3x² + 5x – 3, and divisor g(x) = x² – 2
∴ We have

Thus, the quotient = (x – 3) and remainder = (7x – 9)

(ii) Here, dividend p(x) = x⁴ – 3x² + 4x + 5 and divisor g(x) = x² + 1 – x = x² – x + 1
∴ We have

Thus, the quotient = (x² + x – 3) and remainder = 8

(iii) Here, dividend, p(x) = x⁴ – 5x + 6 and divisor, g(x) = 2 – x² = – x² + 2
∴ We have

Thus, the quotient = -x² – 2 and remainder = -5x +10

Question 2.
Check whether the first polynomial is a factor of the second polynomial by dividing the second polynomial by the first polynomial:
(i) t² – 3; 2t⁴ + 3t³ -2t² – 9t – 12
(ii) x² + 3x + 1; 3x⁴ + 5x³ – 7x² + 2x +2
(iii) x³ – 3x + 1; x⁵ – 4x³ + x² + 3x + 1
Solution:
(i) Dividing 2t⁴ + 3t³ – 2t² – 9t – 12 by t² – 3, we have

∵ Remainder = 0
∴ (t² – 3) is a factor of 2t⁴ + 3t³ – 2t² – 9t – 12.

(ii) Dividing 3x⁴ + 5x³ – 7x² + 2x + 2 by x² + 3x + 1, we have

∵ Remainder = 0
∴ x² + 3x + 1 is a factor of 3x⁴ + 5x³ – 7x² + 2x + 2.

(iii) Dividing x⁵ – 4x³ + x² + 3x + 1 by x³ – 3x + 1, we get

∵ Remainder = 2, i.e., remainder = 0
∴ x³ – 3x + 1 is not a factor of x⁵ – 4x³ + x² + 3x +1.

Question 3.
Obtain all other zeroes of 3x⁴ + 6x³ – 2x² – 10x – 5, if two of its zeroes are \(\sqrt{\frac{5}{3}}\) and \(-\sqrt{\frac{5}{3}}\)
Solution:
We have p(x) = 3x⁴ + 6x³ – 2x² – 10x – 5.
Given \(\sqrt{\frac{5}{3}}\) and \(-\sqrt{\frac{5}{3}}\) are zeroes of p(x).

Thus, the other zeroes of the given polynomial are -1 and -1.

Question 4.
On dividing x³ – 3x² + x + 2 by a polynomial g(x), the quotient and remainder were x – 2 and -2x + 4, respectively. Find g(x).
Solution:
Here, dividend, p(x) = x³ – 3x² + x + 2, divisor = g(x), quotient = (x – 2) and remainder = (-2x + 4)
Since, (Quotient × Divisor) + Remainder = Dividend
∴ [(x – 2) × g(x)] + [(-2x + 4)] = x³ – 3x² + x + 2
⇒ (x – 2) × g(x)
= x³ – 3x² + x + 2 – (-2x + 4)
= x³ – 3x² + x + 2 + 2x – 4
= x³ – 3x² + 3x – 2
= x³ – 3x² + 3x – 2

Thus, the required divisor g(x) = x² – x + 1

Question 5.
Give examples of polynomials p(x), g(x), q(x) and r(x), which satisfy the division algorithm and
(i) deg p(x) = deg q(x)
(ii) deg q(x) = deg r(x)
(iii) deg r(x) = 0
Solution:
(i) p(x) = 3x² – 6x + 27,
g(x) = 3 and q(x) = x² – 2x + 9.
Now, deg p(x) = deg q(x)
r(x) = 0
⇒ p(x) = q(x) × g(x) + r(x)

(ii) p(x) = 2x³ – 2x² + 2x + 3,
g(x) = 2x² – 1, and
r(x) = 3x + 2, deg q(x) = deg r(x)
⇒ p(x) = q(x) × g(x) + r(x)

(iii) p(x) = 2x³ – 4x² + x + 4,
g(x) = 2x² + 1,
q(x) = x – 2 and r(x) = 6,
deg r(x) = 0
⇒ p(x) = q(x) × g(x) + r(x)

In this article, we will share MP Board Class 10th Maths Book Solutions Chapter 2 Polynomials Ex 2.4 Pdf, These solutions are solved subject experts from the latest edition books.

MP Board Class 10th Maths Solutions Chapter 2 Polynomials Ex 2.4

Question 1.
Verify that the numbers given alongside of the cubic polynomials below are their zeroes. Also verify the relationship between the zeroes and the coefficients in each case:
(i) 2x³ + x² – 5x + 2; \(\frac{1}{2}\), 1, -2
(ii) x³ – 4x² + 5x – 2; 2, 1, 1
Solution:

Again, p(1) = 2(1)³ + (1)² – 5(1) + 2
= 2 + 1 – 5 + 2 = 0
⇒ 1 is a zero of p(x).
Also, p(-2) = 2(-2)³ + (-2)² – 5(-2) + 2
= -16 + 4 + 10 + 2 = -16 +16 = 0
= -2 is a zero of p(x).
Now, p(x) = 2x³ + x² – 5x + 2
∴ Comparing it with ax³ + bx² + cx + d, we have a = 2, b = 1, c = -5, and d = 2

Thus, the relationship between the coefficients and the zeroes of p(x) is verified.

(ii) Here, p(x) = x³ – 4x² + 5x – 2
∴ p(2) = (2)³ – 4(2)² + 5(2) – 2
= 8 – 16 + 10 – 2 = 18 – 18 = 0
⇒ 2 is a zero of p(x)
Again p(1) = (1)³ – 4(1)² + 5(1) – 2
= 1 – 4 + 5 – 2 = 6 – 6 = 0
⇒ 1 is a zero of p(x)
Now, comparing p(x) = x³ – 4x² + 5x – 2
with ax³ + bx² + cx + d = 0, we have
a = 1, b = -4, c = 5 and d = -2
Also 2, 1 and 1 are the zeroes of p(x).
Let α = 2,
β = 1,
γ = 1
Now, sum of zeroes = α + β + γ
= 2 + 1 + 1 = 4 = -b/a

Thus, the relationship between the zeroes and the coefficients of p(x) is verified.

Question 2.
Find a cubic polynomial with the sum, sum of the product of its zeroes taken two at a time, and the product of its zeroes as 2, -7, -14 respectively.
Solution:
Let the required cubic polynomial be ax³ + 6x² + cx + d = 0 and its zeroes be α, β and γ.

∴ The requied cubic polynomial is
1x³ + (-2)x² + (-7)x + 14 = 0
= x³ – 2x² – 7x + 14 = 0

Question 3.
If the zeroes of the polynomial x³ – 3x² + x + 1 are a -b, a, a + b, find a and b.
Solution:
We have p(x) = x³ – 3x² + x + 1
Comparing it with Ax³ + Bx² + Cx + D,
We have A = 1, B = -3, C = 1 and D = 1
∵ It is given (a – b), a and (a + b) are the zeroes of the polynomial.

Question 4.
If two zeroes of the polynomial
x⁴ – 6x³ – 26x²+ 138x – 35 are 2±\(\sqrt{3}\), find other zeroes.
Solution:
Here, p(x) = x⁴ – 6x³ – 26x³ + 138x – 35
∵ Two of the zeroes of p(x) are : 2 ± \(\sqrt{3}\)

(x² – 4x + 1)(x² – 2x – 35) = p(x)
⇒ (x² – 4x + 1) (x² – 7x + 5x – 35) = p(x)
⇒ (x² – 4x + 1) [x(x – 7) + 5(x – 7)] = p(x)
⇒ (x² – 4x + 1)(x – 7)(x + 5) = p(x)
i.e., (x – 7) and (x + 5) are other factors of p(x).
∴ 7 and – 5 are other zeroes of the given polynomial.

Question 5.
If the polynomial x⁴ – 6x³ + 16x² – 25x + 10 is divided by another polynomial x² – 2x + k, the remainder comes out to be x + a, find k and a.
Solution:
Applying the division algorithm to the polynomials x⁴ – 6x³ + 16x² – 25x + 10 and x² – 2x + k, we have

∴ Remainder = (2k – 9)x – k(8 – k) + 10
But the remainder = x + a (Given)
Therefore, comparing them, we have

and a = -k(8 – k) + 10
= -5(8 – 5) + 10
= -5(3) + 10 = -15 + 10 = -5
Thus k = 5 and a = -5

In this article, we will share MP Board Class 10th Maths Book Solutions Chapter 12 Areas Related to Circles Ex 12.3 Pdf, These solutions are solved subject experts from the latest edition books.

MP Board Class 10th Maths Solutions Chapter 12 Areas Related to Circles Ex 12.3

Unless stated otherwise, use π = \(\frac{22}{7}\)

Question 1.
Find the area of the shaded region in the given figure, if PQ = 24 cm, PR = 7cm and O is the centre of the circle.

Solution:
Since O is the centre of the circle,
∴ QOR is a diameter.
⇒ ∠RPQ = 90° [Angle in a semicircle]
Now, in right ∆RPQ, RQ² = PQ²+ PR² [Pythagoras theorem]
⇒ RQ² = 24² + 7² = 576 + 49 = 625
⇒ RQ = \(\sqrt{625}\) = 25 cm
∴ Radius of a circle (r) = \(\frac{25}{2}\) cm
∴ Area of ∆RPQ
= \(\frac{1}{2}\) × PQ × RP = \(\frac{1}{2}\) × 24 × 7cm²
= 12 × 7 cm² = 84 cm²
Now, area of semicircle

∴ Area of the shaded portion
= 245.54 cm² – 84 cm² = 161.54 cm²

Question 2.
Find the area of the shaded region in given figure, if radii of the two concentric circles with centre O are 7 cm and 14 cm respectively and ∠AOC = 40°.

Solution:
Radius of the outer circle (R) = 14 cm and θ = 40°

Question 3.
Find the area of the shaded region in the given figure, if ABCD is a square of side 14 cm and APD and BPC are semicircles.

Solution:
Side of the square = 14 cm
∴ Area of the square ABCD = 14 × 14 cm²
= 196 cm²

Similarly, area of semi-circle BPC = 77 cm²
∴ Total area of two semi-circle = (77 + 77) cm²
= 154 cm²
Area of the shaded part
= Area of the square ABCD – Area of semi-circles
= (196 – 154) cm² = 42 cm²

Question 4.
Find the area of the shaded region in the figure, where a circular arc of radius 6 cm has been drawn with vertex O of an equilateral triangle OAB of side 12 cm as centre.

Solution:
Area of the equilateral triangle OAB

Question 5.
From each corner of a square of side 4 cm a quadrant of a circle of radius 1 cm is cut and also a circle of diameter 2 cm is cut as shown in the figure. Find the area of the remaining portion of the square.

Solution:
ABCD of the square ABCD = (4)² cm² = 16 cm².
Area of circel inside the square = πr²
= π × (1)² = π cm².

Question 6.
In a circular table cover of (he radius 32 cm, a design Is formed leaving an equilìtcral triangle ABC in the middle as shown in the figure. Find the area of the design (shaded region).

Solution:
Let O be the centre of a circular table and ABC be the equilateral triangle.
Then we draw OD ⊥ BC
In ∆OBD, we have: cos 60° = \(\frac{\mathrm{OD}}{\mathrm{OB}}\)

Question 7.
In the figure, ABCD is a square of side 14 cm. With centres A, B, C and D, four circles are drawn such that each circle touch externally two of the remaining three circles. Find the area of the shaded region.
Solution:
Each side of the square ABCD = 14 cm

Question 8.
The given figure depicts a racing track whose left and right ends are semicircular. The distance between the two inner parallel line segments is 60 m and they are each 106 m long. If the track is 10 m wide, find:

(i) the distance around the track along its inner edge.
(ii) the area of the track.
Solution:
The distance around the track along the inner edge = Perimeter of GHI + Perimeter JKL + GL + IJ
= (π × 30 + π × 30 + 106 + 106)
= (60π + 212) m
= (60 × \(\frac{22}{7}\) + 212)m = \(\frac{2804}{7}\) m.

Similarly, area of another circular path
BCDJKLB = 1100 m²
Area of rectangular path (ABLG) = 106 × 10
= 1060 m²
Similarly, area of another rectangular path
IJDE = 1060 m²
Total area of the track
= (1100 + 1100 + 1060 + 1060) m²
= (2200 + 2120) m² = 4320 m².

Question 9.
In the given figure, AB and CD are two diameters of a circle (with centre O) perpendicular to each other and OD is the diameter of the smaller circle. If OA = 7 cm, find the area of the shaded region.

Solution:
O is the centre of the circle and OA = 7 cm
⇒ AB = 2OA = 2 × 7 cm = 14 cm
∵ AB and CD are perpendicular to each other.
⇒ OC ⊥ AB and OC = OA = 7 cm
Area of ∆ABC = \(\frac{1}{2}\) × AB × OC
= \(\frac{1}{2}\) × 14 cm × 7cm = 49 cm²
Again, OD = OA = 7 cm
∴ Radius of the small circle = \(\frac{1}{2}\) (OD)

Question 10.
The area of an equilateral triangle ABC is 17320.5 cm². With each vertex of the triangle as centre, a circle is drawn with radius equal to half the length of the side of the triangle (see figure). Find the area of the shaded region. (Use π = 3.14 and \(\sqrt{3}\) = 1.73205).

Solution:
Area of ∆ABC = 17320.5 cm²

⇒ (side)² = 40000
⇒ (side)² = (200)²
⇒ side = 200 cm
∴ Radius of each circle = \(\frac{200}{2}\) cm = 100 cm
Since, each angle of an equilateral triangle is 60°,
∠A = ∠B = ∠C = 60°
Area of a sector having angle of sector (θ), as 60° and radius (r) = 100 cm = \(\frac{\theta}{360^{\circ}}\) × πr²

Now, area of the shaded region = [Area of the equilateral triangle ABC] – [Area of 3 equal sectors]
= 17320.5 cm² – 15700 cm² = 1620.5 cm²

Question 11.
On a square handkerchief, nine circular designs each of radius 7 cm are made (see figure). Find the area of the remaining portion of the handkerchief.

Solution:
∵ The circles touch each other.
∴ The side of the square ABCD
= 3 × diameter of a circle = 3 × (2 × radius of a circle) = 3 × (2 × 7) cm = 42 cm
⇒ Area of the square ABCD = 42 × 42 cm²
= 1764 cm²
Now, area of one circle
= πr² = \(\frac{22}{7}\) × 7 × 7 cm² = 154cm²
∴ Total area of 9 circles = 9 × 154 cm² = 1386 cm²
∴ Area of the remaining portion of the handkerchief = (1764 – 1386) cm² = 378 cm²

Question 12.
In the given figure, OACB is a quadrant of a circle with centre O and radius 3.5 cm. If OD = 2 cm, find the area of the
(i) quadrant OACB,
(ii) shaded region.

Solution:
(i) Here, radius (r) = 3.5 cm

Question 13.
In the given figure, a square OABC is inscribed in a quadrant OPBQuestion If OA = 20 cm, find the area of the shaded region (Use π = 3.14)

Solution:
OABC is a square such that its side
OA = 20 cm
∴ OB² = OA² + AB²
⇒ OB² = 20² + 20² = 400 + 400 = 800
⇒ OB = \(\sqrt{800}=20 \sqrt{2}\)
⇒ Radius of the quadrant (r) = \(20 \sqrt{2}\) cm
Now, area of the quadrant OPBQ = \(\frac{1}{4}\) πr²
= \(\frac{1}{4} \times \frac{314}{100}\) × 800 cm² = 314 × 2 = 628 cm²
Area of the square OABC = 20 × 20 cm² = 400 cm²
∴ Area of the shaded region
= 628 cm² – 400 cm² = 228 cm²

Question 14.
AB and CD are respectively arcs of two concentric circles of radii 21 cm and 7 cm and centre O (see figure). If ∠AOB = 30°, find the area of the shaded region.

Solution:
∵ Radius of bigger circle R = 21 cm and sector angle θ = 30°
∴ Area of the sector OAB

Question 15.
In the given figure, ABC is a quadrant of a circle of radius 14 cm and a semicircle is drawn with BC as diameter. Find the area of the shaded region.

Solution:
Radius of the quadrant = 14 cm
Since, BC is a diameter in a semi-circle.
∴ ∠BAC = θ = 90°
Area of the semicircle ABPC
= [\(\frac{90^{\circ}}{360^{\circ}} \times \frac{22}{7}\) × 14 × 14] cm²
= 22 × 7 cm² = 154 cm²
Area of right ∆ABC
= \(\frac{1}{2}\) × 14 × 14 cm² = 98 cm²
⇒ Area of segment BPC = 154 cm² – 98 cm²
= 56 cm²

Now, area of the shaded region = [Area of semicircle BQC] – [Area of segment BRC]
= 154 cm² – 56 cm² = 98 cm²

Question 16.
Calculate the area of the designed region in the given figure, common between the two quadrants of circles of radius 8 cm each.

Solution:
Side of the square = 8 cm
Area of the square ABCD = 8 × 8 cm² = 64 cm²
Now, radius of the quadrant ADQB = 8 cm
∴ Area of the quadrant ADQB